Improving Diagnostic Efficiency with Frequency Double-Trees and Frequency Nets in Bayesian Reasoning

Abstract

Background. Medical students often have problems with Bayesian reasoning situations. Representing statistical information as natural frequencies (instead of probabilities) and visualizing them (e.g., with double-trees or net diagrams) leads to higher accuracy in solving these tasks. However, double-trees and net diagrams (which already contain the correct solution of the task, so that the solution could be read of the diagrams) have not yet been studied in medical education. This study examined the influence of information format (probabilities v. frequencies) and visualization (double-tree v. net diagram) on the accuracy and speed of Bayesian judgments. Methods. A total of 142 medical students at different university medical schools (Munich, Kiel, Goettingen, Erlangen, Nuremberg, Berlin, Regensburg) in Germany predicted posterior probabilities in 4 different medical Bayesian reasoning tasks, resulting in a 3-factorial 2 × 2 × 4 design. The diagnostic efficiency for the different versions was represented as the median time divided by the percentage of correct inferences. Results. Frequency visualizations led to a significantly higher accuracy and faster judgments than did probability visualizations. Participants solved 80% of the tasks correctly in the frequency double-tree and the frequency net diagram. Visualizations with probabilities also led to relatively high performance rates: 73% in the probability double-tree and 70% in the probability net diagram. The median time for a correct inference was fastest with the frequency double tree (2:08 min) followed by the frequency net diagram and the probability double-tree (both 2:26 min) and probability net diagram (2:33 min). The type of visualization did not result in a significant difference. Discussion. Frequency double-trees and frequency net diagrams help answer Bayesian tasks more accurately and also more quickly than the respective probability visualizations. Surprisingly, the effect of information format (probabilities v. frequencies) on performance was higher in previous studies: medical students seem also quite capable of identifying the correct solution to the Bayesian task, among other probabilities in the probability visualizations.

Highlights

• Frequency double-trees and frequency nets help answer Bayesian tasks not only more accurately but also more quickly than the respective probability visualizations.

• In double-trees and net diagrams, the effect of the information format (probabilities v. natural frequencies) on performance is remarkably lower in this high-performing sample than that shown in previous studies.

Introduction

Bayesian Reasoning in Medical Decision Making

In everyday clinical practice, physicians are often confronted with Bayesian situations. These situations include, for example, assessing how a new piece of information, such as a medical test result, affects the probability of the patient actually having a particular disease.

We illustrate the situation with a thyroid cancer problem ¹ :

Thyroid cancer problem—Probability format:

The probability of thyroid cancer for a patient in an endocrinology outpatient clinic who has a thyroid nodule is 5% (prevalence of the disease P(C)). If a patient has thyroid cancer, the probability is 40% that sonography shows a thyroid nodule with evidence of malignancy due to the presence of microcalcifications (sensitivity P(T+|C)). If a patient has no thyroid cancer, the probability is 12% that sonography shows a thyroid nodule with evidence of malignancy due to the presence of microcalcifications (false-positive rate P(T+| ¬C)).

What is the probability that this person with a thyroid nodule with microcalcifications actually has thyroid cancer?

The correct solution is 14.9% and can be calculated using the Bayes formula:

$$\begin{array}{c}P\left(C\right|T+)=\frac{P(T+|C\left)P\right(C)}{P(T+|C\left)P\right(C)+P(T+|\neg C)P(\neg C)}\hfill \\ \frac{40\%·5\%}{40\%·5\%+12\%·95\%}\approx 14.9\%\hfill \end{array}$$

Unfortunately, most physicians fail to solve Bayesian reasoning tasks with probabilities, which can sometimes have severe consequences.^2–6 It is also known that medical students have the same problems solving these tasks.

It has been shown in many studies that in such situations, the accuracy of decision making differs depending on the information format of data: probabilities (e.g., 40%) versus natural frequencies (e.g., 40 of 100 patients).^2–5 Similarly, the visualization of data—for example, with a tree diagram or with a 2 × 2-table—improves participants’ performance.^7–10 Furthermore, trainings with natural frequencies and natural frequency visualizations or experience-based formats are suggested to train the Bayesian reasoning skills of medical students.^11–14

Because of the time pressure in everyday clinical practice, however, it is important to consider both the accuracy and speed in clinical decision making to reach the correct diagnosis. ¹⁵ Determining how to improve the Bayesian reasoning process could be helpful for increasing the accuracy of medical decisions and thus minimizing important errors in patient communication and treatment. ¹⁶

Reducing Bayesian Reasoning Errors: Information Format and Visualization

Information Format

In questions in which Bayesian reasoning is applied, information can be given as probabilities or as natural frequencies. In the mathematical formalism of probability theory, probabilities instead of frequencies are used. However, probabilities and percentages are not intuitively understandable. ² Presenting natural frequencies in Bayesian tasks leads to significantly more correct results.^17–19 The thyroid cancer problem with natural frequencies reads as follows:

Thyroid cancer problem—Natural frequency format:

A total of 5000 out of 100,000 patients in an endocrinology outpatient clinic who have a thyroid nodule have thyroid cancer P(C)). In 2000 out of the 5000 patients with thyroid cancer, sonography showed a thyroid nodule with evidence of malignancy due to the presence of microcalcifications (sensitivity P(T+|C)). Of the 95,000 patients without thyroid cancer, 11,400 wrongly received sonography, which showed a thyroid nodule with evidence of malignancy due to the presence of microcalcifications (false-positive rate P(T+| ¬C)).

How many patients who have a thyroid nodule with microcalcifications actually have thyroid cancer?

Now, it is easier to see that in sum (2000 + 11,400 =), 13,400 patients receive conspicuous sonography and that only 2000 of these 13,400 actually have thyroid cancer (which is approximately 14,9%).^2–4 The beneficial effect of natural frequencies has been shown not only in the medical context but also in the economic and legal context.^9,20–22 This natural frequency facilitation effect is explained with the ecological rationality account or the nested set account.^4,23,24

Visualization

In addition to the natural frequency facilitation effect, the presentation of certain visualizations can help to improve Bayesian reasoning: (double-)tree diagrams, 2 × 2 tables, icon arrays, frequency grids, unit squares, and many more.^{8,17,22,25–33}

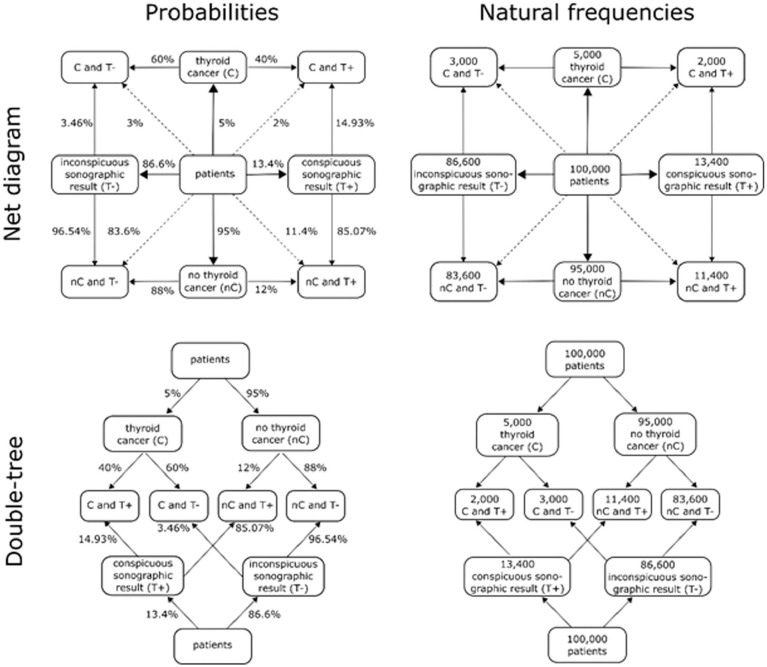
Some of these visualizations, such as (double-)tree diagrams, can be visualized rapidly with easy means, such as pen and paper, whereas other visualizations, such as icon arrays or frequency grids, require more time for preparation since they cannot be depicted easily by hand.^7,18 Furthermore, it could be shown that frequency (double-)trees lead to more accurate solutions of Bayesian tasks (whereas probability [double-]trees help less).^16,17 A more advanced version of tree diagrams are double-tree diagrams and net diagrams, which are particularly suitable for the education of medical students and physicians (see Figure 1).^16,18 Double-tree diagrams and net diagrams already contain the correct solution of the task. Compared with tree diagrams, no further calculation is necessary. Therefore, double-tree diagrams and net diagrams might even be more fruitful for improving accuracy in Bayesian reasoning situations.

Figure 1.

Net diagrams and double-trees in both information formats (probabilities v. frequencies) for the thyroid cancer case.

To date, medical students have been presented with Bayesian tasks primarily with 2 × 2-tables or with simple tree diagrams. ¹⁸ Double-trees and especially the relatively new type of visualization as net diagrams have not been investigated much. Binder et al. compared the double-tree and the net diagram with the commonly used representation 2 × 2 table and text-only version. It could be shown that 2 × 2 tables, double-trees, and net diagrams support the correct solution of Bayesian reasoning tasks if they contain natural frequencies (the corresponding probability visualizations were less helpful). ¹⁸

Time to Solve Bayesian Tasks Correctly

The working conditions of a physician in daily practice do not reflect the ideal scenario of being able to devote the individually required time to each patient, which is why physicians have to make important decisions under time pressure. ³⁴ Consequently, it is important that medical students learn how to interpret probabilities in Bayesian reasoning situations as fast as possible and that (prospective) physicians have good diagnostic efficiency, which can be defined by the time required for diagnosis divided by the number of correctly solved clinical cases. ¹⁵ Diagnostic speed seems to be higher when indications are given as natural frequencies in tree diagrams.^16,35 The more mental steps that have to be taken, the longer it takes to reach a solution to Bayesian questions. ³⁶ However, the diagnostic speed has not yet been investigated for double-trees and net diagrams, although this is interesting because the correct solution is already presented within the diagram.

Therefore, the aim of the present study is to compare the effects of information format (probabilities v. natural frequencies) and visualization (double-tree v. net diagram) on the accuracy and speed (and therefore the efficiency) of the decision-making process. We choose to investigate medical students as it is important to learn Bayesian reasoning already in medical school. The following research question will be answered: Do natural frequencies and visualizations have a positive effect on accuracy and diagnostic speed in Bayesian reasoning tasks? Our hypothesis was that natural frequency visualizations are the best to promote diagnostic efficiency. As both frequency double-trees and frequency net diagrams are recommended visualizations for Bayesian reasoning and have been shown to perform comparably well in a previous study, ¹⁸ we had no a priori hypothesis on which of these 2 diagrams perform better.

Material and Methods

Participants

In this study, 142 medical students (90 women, 51 men, 1 unknown) participated and proceeded to all cases between November and December 2020. Participants were recruited via community outreach (i.e., study flyers and word of mouth) at various university medical schools in Germany (Munich, Kiel, Goettingen, Erlangen, Nuremberg, Berlin, Regensburg). The participants were on average 24.3 years old (s = 2.9), the average clinical semester was 8.7 of a maximum of 12 (s = 2.3), the school examination grade (1 = best to 6 = worst) was $\overline{x}$ = 1.5 (s = 0.5), and the grade of the first medical examination was $\overline{x}$ = 2.3 (s = 1.0). Participants had an average of 2.7 clinical clerkships completed (s = 1.4), each lasting 1 month.

The Ethical Committee of the Medical Faculty of LMU Munich approved the study (No. 20-0871). All students were informed that participation in the study was voluntary and anonymous. After giving their written consent, each student received a financial incentive of 10 Euros.

Study Design

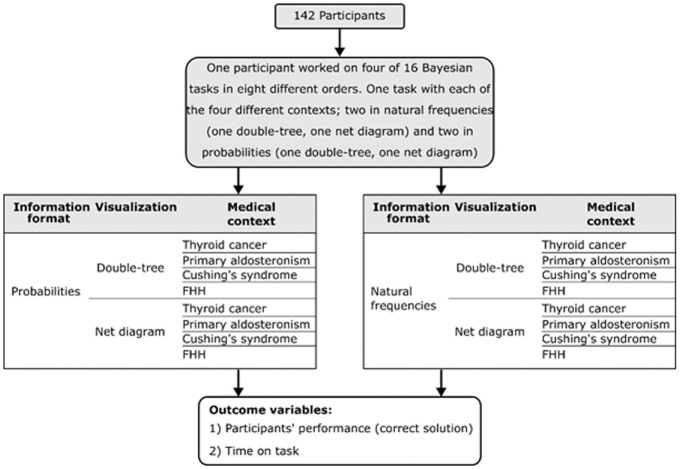
Figure 2 shows the 2 × 2 × 4 study design: 2 (information format: probabilities v. natural frequencies) × 2 (visualization: double-tree v. net diagram) × 4 (contexts: minor aim of the study). To solve the tasks, the electronic case simulation platform CASUS ³⁷ was used. First, each student completed a general sociodemographic questionnaire (age, gender, clinical semester, school examination grade, grade of the first medical examination, number of clinical clerkships, as potential control variables that may influence participants’ performance) and read an introductory text. The introductory text informed the participants about the fact that time for solving the cases was not restricted but recorded. The participants could use calculators.

Figure 2.

Study design: 2 (information format: probabilities v. natural frequencies) × 2 (visualization: double-tree v. net diagram) × 4 (medical contexts: minor aim of the study). The 4 medical contexts included thyroid cancer, primary aldosteronism, Cushing’s syndrome, and familial hypocalciuric hypercalcemia.

Material and medical context

Each student solved 4 Bayesian cases, which consisted of different medical contexts from the field of clinical endocrinology: Cushing’s syndrome, ³⁸ familial hypocalciuric hypercalcemia (FHH), ³⁹ primary aldosteronism, ⁴⁰ and thyroid cancer. ¹

Endocrinology was selected because in this field of internal medicine, there is a great discrepancy between very frequent diseases in the population. For example, diseases of the thyroid and primary aldosteronism are quite common, and diseases such as Cushing’s syndrome and FHH are very rare. This aspect can be challenging in everyday clinical practice. We chose these 4 contexts to represent the clinical reality by using 2 scenarios, Cushing’s syndrome and FHH, which are less familiar scenarios to students, whereas the scenarios thyroid cancer and primary aldosteronism are more familiar. All scenarios were covered in the curriculum.

Each case can be presented in 4 different versions: probabilities in double-trees, probabilities in net diagrams, natural frequencies in double-trees, and natural frequencies in net diagrams. Table 1 shows the thyroid cancer case exemplarily (the corresponding visualizations are displayed in Figure 1), whereas the other cases can be found in the online supplement.

Table 1.

Case Formulations for the Thyroid Cancer Context

Case Information Format	Thyroid Cancer
	Probabilities	Natural Frequencies
Medical context	Imagine you work as a physician in an endocrinology outpatient clinic. Here, among other things, thyroid sonographies are performed for suspected thyroid nodules. You have just consulted a patient whose sonography shows a thyroid nodule with evidence of malignancy due to the presence of microcalcifications. This patient would like to know how likely it is that a conspicuous sonographic finding is actually thyroid cancer. Only the following information is available for your answer, based on a sample of patients with thyroid nodules with suspected malignancy due to the presence of microcalcifications.
Visualization	• Probability double-tree, or • Probability net diagram (see Fig. 1, left)	• Frequency double-tree, or • Frequency net (see Fig. 1, right)
Question	What is the probability that this person with a thyroid nodule with microcalcifications actually has thyroid cancer?	How many patients who have a thyroid nodule with microcalcifications actually have thyroid cancer?
	Answer:_________	Answer:____ out of ____

Each participant was shown the aforementioned medical contexts and modes of presentation, which were systematically varied so that each participant received a different sequence of tasks. Every participant received 2 medical contexts in probability format (one visualized with a double-tree and the other one with a net diagram) and the other 2 in natural frequency format (one visualized with a double-tree and the other one with a net diagram). As shown in Table 1, the questions were asked in an open format. At the end of each task, participants could enter their answer in a field provided for this purpose.

Coding

Following Gigerenzer and Hoffrage, ² in the tasks with probabilities, the answer was assessed as correct if it corresponded to the exact Bayesian solution or was rounded to the nearest whole percentage point above or below. In the tasks with natural frequencies, the answer was assessed as correct if both numbers of frequency data were given correctly (e.g., in the thyroid cancer problem solution of “2000 out of 13,400,” both the 2000 and the 13,400).

Statistics

A power analysis based on previous similarly designed studies was used to select the sample size. According to these studies, the format effect is close to 100% power (95% confidence interval, 96.4% to 100%) with a sample size of approximately N = 120 students.^4,17

The R programming language was used for the statistical analysis. (Generalized) linear mixed models (with a logit link function) were used to predict 1) the performance for the Bayesian inference task and 2) the time for solving the task. In this model, we specified the probability double-tree version as the reference category and included the potential explanatory factors “natural frequencies” and “net diagram” via dummy coding.

To assess diagnostic efficiency, we used a score according to Binder et al. ¹⁶ This diagnostic efficiency score is the median time on task divided by the proportion of correct conclusions. Lower values of this score mean more correct and faster diagnoses. The median was used instead of the arithmetic mean because the completion times are highly right-skewed (as is usually the case with processing times of participants). The preplanned strategy for very long completion time was to exclude all participants with a completion time larger than 3 times the interquartile range.

The funding source had no role in the study.

Results

Participants’ Performance (Accuracy)

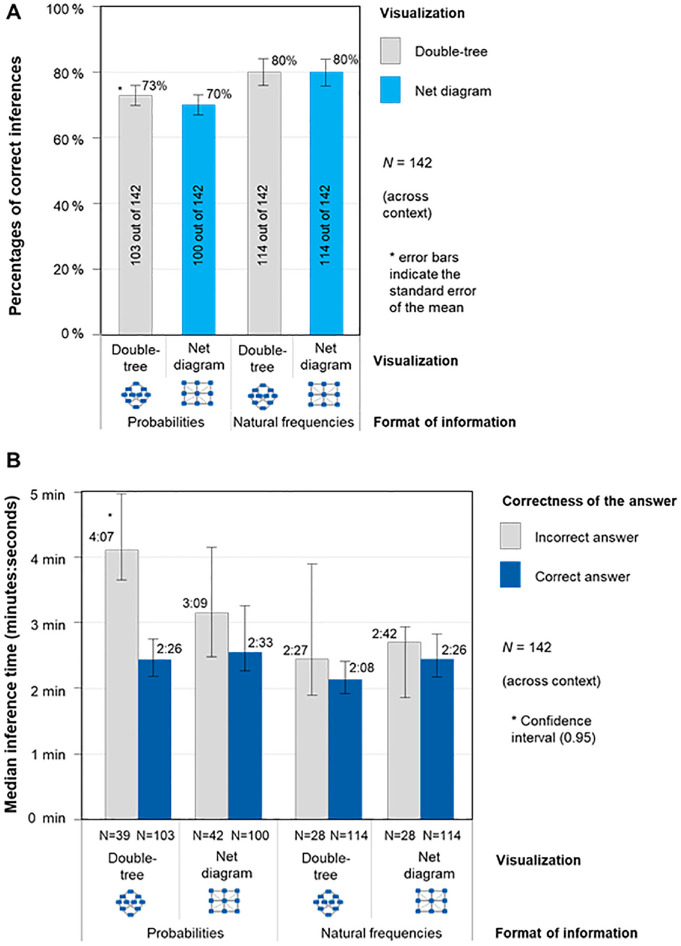
As shown in Figure 3 and Table 2, the participants’ performance was high in all versions. Participants who were presented with the probability version answered 73% of the cases correctly in the double-tree version and 70% of the cases in the net diagram version. For the natural frequency versions, the performance was the same for both visualization formats, with 80% of cases solved correctly.

Figure 3.

(A) Participants’ performance in the Bayesian reasoning tasks (across contexts). (B) Median time for solving one Bayesian reasoning task correctly or incorrectly (across contexts).

Table 2.

Overall Cross-Context Results ^a

		N	Correct inferences	Time for a diagnosis			Time for correct a diagnosis				Diagnostic efficiency-score: Median time for all diagnoses/correct inferences
				[m:ss]			N	[m:ss]			[m:ss]
				Q1	Median	Q3		Q1	Median	Q3
Probabilities	Double-tree	142	73%	1:56	2:50	4:26	103	1:44	2:26	3:40	3:53
	Net diagram	142	70%	1:46	2:50	4:16	100	1:46	2:33	3:49	4:03
Natural frequencies	Double-tree	142	80%	1:32	2:14	3:25	114	1:33	2:08	3:19	2:48
	Net diagram	142	80%	1:41	2:28	3:37	114	1:41	2:26	3:40	3:05

^aPercentages of correct inferences, time for diagnosis with median, first (Q1) and third (Q3) quartiles, score for diagnostic efficiency. The diagnostic efficiency score was calculated by dividing the median time by the percentage of correct inferences. N indicates the number of participants.

In a generalized linear mixed model for predicting accuracy, the (unstandardized) regression coefficients for natural frequencies (b₁ = 0.75, SE = 0.25, z = 2.96, P = 0.003) and the order of the task (i.e., was the task provided as the first, second, third, or fourth task; b₂ = 0.36, SE = 0.11, z = 3.12, P = 0.002) were significant. Hence, there was a learning effect. The first task was processed worse on average. Descriptive results that only refer to the first task can be found in Supplementary Figure 7 online. If only the first task is analyzed, the effect of the frequency format is even more pronounced. Other variables, however, such as the visualization, context, age, gender, and school examination grade, had no significant influence on participants’ performance. The complete model can be found in Supplementary Table 6 online.

Time for Solving the Task and Efficiency

Table 2 shows not only the median time taken by participants for each case but also the median time taken to correctly solve the task (see also Figure 3). As seen in Table 2 and Figure 3, the tasks presented with natural frequencies were solved faster. The version with the frequency double-tree was the one that was solved fastest, namely, with a median time of 2:14 min. It is also noticeable that correct solutions are consistently slightly faster than wrong answers.

A linear mixed model to estimate the time to reach a correct diagnosis was modeled excluding 8 outliers with a completion time larger than 3× the interquartile range. ⁴¹ The model showed that the visualization (double-tree v. net diagram) had no significant effect on the speed of diagnosis (P = 0.89). However, the presentation of natural frequencies (P = 0.04) and the sequence of tasks (i.e., was the task presented as the first, second, third, or fourth task; P < 0.001) had a significant effect on the speed of solution (Supplementary Table 7 online). Furthermore, the context of Cushing syndrome needed significantly more time, without changing the reported effects of the information format and sequence of the tasks.

An additional linear mixed model to estimate the time to reach a diagnosis—regardless of whether the diagnosis was correct or incorrect—shows a very similar picture (significant effect of format, P = 0.42, and sequence of the task, P = 0.003; see Supplementary Table 8 online). Furthermore, in the latter linear mixed model, the contexts Cushing syndrome and FHH needed significantly more time, without changing the reported effects of information format and sequence of the tasks. Other variables did not significantly affect completion time.

Furthermore, Table 2 shows the score to analyze diagnostic efficiency. The diagnostic efficiency score divides the median time on task by the proportion of correct inferences. The best value for diagnostic efficiency was obtained in the natural frequency double-tree version (2:48 min), whereas the worst value was obtained in the probability net diagram version (4:03 min).

Discussion

Frequency Double-Trees and Frequency Nets Increase Efficiency Compared with the Corresponding Probability Visualizations

This study investigated the influence of information format (natural frequencies v. probabilities) and different visualizations (double-tree v. net diagram) on the efficiency (i.e., accuracy and time for solving the task) of medical students in Bayesian reasoning tasks. It could be shown that frequency visualizations lead more often to correct solutions and even to faster solutions than do the corresponding probability visualizations.

Probability Double-Trees and Probability Net Diagrams Also Lead to High Performance Rates with Medical Students

In contrast to the results of Binder et al., ¹⁸ the probability double-tree and the probability net diagram led to remarkably high performance rates in our study (73% and 70%). The type of visualization double-tree and net diagram did not result in a significant difference in the performance of medical students when solving Bayesian tasks. In the study by Binder et al., participants’ performances in the probability double-tree and the probability net version (each 34%) were much lower than in the frequency double-tree (60%) and the frequency net (61%). The reason for this could be that different samples were considered: medical students in the present article and students from different disciplines in Binder et al. (whereas 117 of the students were from the field of pharmacy). The high performance of medical students in the probability versions in our study could indicate that medical students—unlike students in other disciplines—are able to distinguish P(C|T+) from the typical confounders P(T+|C) and P(C∩T+). ¹⁸ Thus, the conceptual understanding necessary to distinguish P(C|T+) from P(T+|C) and P(C∩T+) seems to have already been developed. However, the procedural knowledge necessary to calculate P(C|T+) from the prevalence, sensitivity and false-positive rate seems to be missing. In addition, here, again, natural frequencies could help.

Comparing Double-Trees and Net Diagrams with Simple Tree Diagrams

As mentioned before, double-trees and net diagrams already contain the correct solution of the Bayesian task. Thus, in our study, participants only had to select the correct solution among many other probability or natural frequency information. This explains why the performance in our study is higher and the median time is lower than those reported by Binder et al., ¹⁶ who investigated the influence of simple tree diagrams (with probabilities or frequencies) on participants’ performance and time on tasks. Solving Bayesian tasks using a simple tree diagram requires more mental steps and is therefore more complex. ³⁶

Advantages for Medical Education through Frequency Double-Trees and Frequency Nets

Presenting Bayesian problems in such a way that they can be solved quickly is of great importance in everyday medical practice. This is shown, for example, by the fact that a doctor in a family practice has an average of 5 min to treat a patient. ⁴² It is unlikely that physicians or medical students will recalculate data for every new Bayesian decision, and there is simply not enough time for that. Furthermore, medical students may not have access to the latest evidence, such as sensitivities or false-positive rates. In everyday clinical practice, one will think through new findings once and then formulate simple if-then rules that help make decisions quickly (e.g., if the new test has a higher sensitivity, the positive predictive value is getting higher than in the test before). Especially in emergency medicine, where time pressure is even higher, heuristics (instead of concrete calculations) and fast and frugal heuristics and trees would be even more helpful.^43,44

In daily clinical practice, it might be helpful to present visualizations always in the same form to medical students so that they can quickly recognize the correct solution without having to perform extra calculations. The ideal approach would be to start in training and explain to medical students how to create frequency double-trees and frequency nets on their own. Training of students to create probability or frequency diagrams is not yet included in the learning objectives catalog “NKLM” (Nationaler Kompetenzbasierter Lernzielkatalog Medizin), which applies to German universities.

The influence of the net diagram should be assessed in more detail in future research. In a net diagram, it is possible to display both the frequencies in the nodes and the probabilities at the branches. ¹⁸ In this way, all information can be presented at a glance, which can lead to fewer errors and greater diagnostic efficiency.

The results of this study might help to improve education in the medical field. Bayesian problems should be taught using natural frequencies modeled in double-trees or net diagrams. It is faster to solve these problems because this scheme is easier for students to understand. Moreover, this strategy seems to be more memorable than Bayes’ formula. ¹²

Limitations and Outlook

A limitation of this study is that we did not show if we could train medical students to draw double-trees and frequency nets on their own to solve Bayesian tasks. This should be examined in future studies for net diagrams.

In this study, medical context was not a determining factor, but decision-making ability could change if the participants were already familiar with the context. Questions could be adapted to the specific topic (e.g., endocrinological clinical cases for endocrinologists). Furthermore, mixed contexts could be used to minimize content-related bias.

Furthermore, with regard to ecological validity, the current study focuses only on the ability to solve medical Bayesian reasoning tasks. We did not focus on the correctness of decision-making of real patient cases.

Not only regarding the improvement of teaching in medicine and competence in everyday clinical practice but also in doctor–patient communication, the visual representation of data in double-trees or net diagrams could lead to positive results since it has already been shown that visual presentation of statistical information promotes better doctor–patient communication. ⁹

Furthermore, clinical guidelines could include these visualizations to standardize presentation to clinicians.

Moreover, there are findings about the influence of working memory in Bayesian reasoning: Brase and Hill (2015) ⁴⁵ stated that there should be no influence. However, Yin et al. (2020) ⁴⁶ found that the interaction between working memory and probability format was significant. Therefore, it would be interesting to implement cognitive load tasks additionally in future work.

Conclusion

When medical students are presented with the full picture of possible probabilities (or frequencies) within a visualization, they are remarkably good at selecting the correct probability (or frequency) out of the numbers given in the visualization. Visualizing natural frequencies in both double-trees and net diagrams helps medical students answer Bayesian tasks not only more accurately but also more efficiently.