Two Weights Make a Wrong: Cluster Randomized Trials with Variable Cluster Sizes and Heterogeneous Treatment Effects

Abstract

In cluster randomized trials (CRTs), the hierarchical nesting of participants (level 1) within clusters (level 2) leads to two conceptual populations: clusters and participants. When cluster sizes vary and the goal is to generalize to a hypothetical population of clusters, the unit average treatment effect (UATE), which averages equally at the cluster level rather than equally at the participant level, is a common estimand of interest. From an analytic perspective, when a generalized estimating equations (GEE) framework is used to obtain averaged treatment effect estimates for CRTs with variable cluster sizes, it is natural to specify an inverse cluster size weighted analysis so that each cluster contributes equally and to adopt an exchangeable working correlation matrix to account for within-cluster correlation. However, such an approach essentially uses two distinct weights in the analysis (i.e. both cluster size weights and covariance weights) and, in this article, we caution that it will lead to biased and/or inefficient treatment effect estimates for the UATE estimand. That is, two weights “make a wrong” or lead to poor estimation characteristics. These findings are based on theoretical derivations, corroborated via a simulation study, and illustrated using data from a CRT of a colorectal cancer screening program. We show that, an analysis with both an independence working correlation matrix and weighting by inverse cluster size is the only approach that always provides valid results for estimation of the UATE in CRTs with variable cluster sizes.

1. Introduction

Cluster randomized trials (CRTs) are commonly used to address pragmatic questions about the effectiveness of treatments and policies applied at the level of the provider, practice, or health system (Weinfurt et al., 2017). Properly addressing such questions requires the critically important step of defining the target estimand which has not been extensively discussed in the CRT literature. In real-world contexts, clusters are likely to vary in size, in which case the relative contribution from different clusters on statistical summaries and the associated target estimand can be rather different. Cook et al. (2016) discuss unequal cluster sizes and alternative estimation goals that can either target the average effect for the population of participants, or the average effect for the population of clusters. For example, large clusters can contribute more information to the average treatment effect (ATE), one of the most common estimands in CRTs (Su and Ding, 2021). Alternative estimands accommodate variable cluster sizes in different ways. For example, the unit average treatment effect (UATE) weights observations according to the inverse of cluster size so that all clusters contribute equally (Williamson and Satten, 2003; Imai et al., 2009; Seaman et al., 2014). We note that, the “U” in UATE represents the unit of randomization, which is the cluster. In addition, the UATE directly targets generalization to the expected value of treatment when applied to new clusters that are comparable to those under study.

In this paper, we present examples of how different analyses of CRT data may lead to different conclusions about treatment effectiveness when the target estimand is the UATE. This paper was motivated by analyses of the STOP CRC (Strategies and Opportunities to Stop Colorectal Cancer in Priority Populations) trial (Coronado et al. 2014) and discussions among members of the NIH Health Care Systems Research Collaboratory Biostatistics Core that investigated alternative estimation options for the UATE. We focus on analysis within the generalized estimating equations framework (GEE; Liang and Zeger, 1986). Within GEE, we consider analysis that weights each observation within a cluster by the inverse of the cluster size vs. analysis with no cluster size weighting and compare these two approaches under both an independence and exchangeable working correlation matrix. Using theoretical results, simulations, and a real data analysis, we show that it is possible to obtain either inefficient or biased estimates of treatment effect in cases where we may expect that our analysis was perfectly tuned to the target estimand. Specifically, we show that when our target estimand is the UATE, analysis of participant-level CRT data with GEE using both an exchangeable working correlation matrix and weighting by inverse cluster size is inefficient in the presence of homogeneous treatment effect, and is biased in the presence of treatment effect heterogeneity according to cluster size. That is, it is possible that “two weights make a wrong.” Moreover, we demonstrate that within GEE, only an analysis with an independence working correlation matrix and weighting by inverse cluster size always provides valid results when the UATE is the target estimand.

2. Motivating example

The STOP CRC trial is a two-arm parallel CRT conducted in the United States to evaluate a health care system-based program to improve colorectal cancer screening rates (Coronado et al., 2014). The primary outcome was a binary indicator of whether colorectal cancer screening was completed within 12 months of enrollment. There were 41,193 participants, of which 22,994 (55.8%) were female and the mean (standard deviation [SD]) age was 58.5 (6.34) years. The detailed summary of baseline characteristics is provided in table 1 of Coronado et al. (2018). The 41,193 participants were from 26 clinics (i.e., clusters), with 13 clinics each in the treatment and control arms. The number of participants in these 26 clusters (i.e., cluster size) ranged from 461 to 3,299, with mean (SD) of 1,584 (753) and coefficient of variation (CV) of 0.48. Given the cluster as an important feature of the trial and the considerable cluster size variability, the UATE is the estimand of interest because it addresses the effect of treatment on the population of clusters. Specifically, for the STOP CRC trial the targeted estimand assessed if the clinic-level rate of colorectal screening for clinics given the intervention improved relative to those clinics receiving usual care.

3. Target estimand and analytic methods

With the motivating example in mind, we consider the UATE as the target estimand. Specifically, suppose that we have n clusters of size m_i (i = 1, … , n). Let Y_ij denote the outcome for participant j = 1, … , m_i in cluster i = 1, … , n, and Z_i denote the cluster-level treatment indicator. We assume that all members of each cluster receive the allocated condition, that is, there is perfect compliance and assume that the number of clusters, n, and the cluster-specific population sizes, m_i, are fixed. Under the potential outcomes framework, our target estimand, UATE, can be expressed as

$$\tau =\frac{1}{n}\sum _i\left\{\frac{1}{m_i}\sum _j\left[Y_{ij}(1)-Y_{ij}(0)\right]\right\},$$ (1)

where Y_ij(1) and Y_ij(0) denote the potential outcomes under the treatment and control conditions, respectively. In contrast, the alternative estimand ATE can be expressed as

$$\frac{1}{{\sum }_i{m}_i}\sum _i\sum _j\left[Y_{ij}(1)-Y_{ij}(0)\right].$$

As noted above, the UATE weights each cluster equally based on the average within-cluster contrasts, therefore emphasizing the treatment effect on the population of clusters, regardless of the cluster size distribution. The formulation of the UATE estimand also reduces the influence of extremely large clusters and may provide a more generalizable interpretation for pragmatic research. Generalization of the estimand to situations where the samples within each cluster, and the sample of clusters are considered to be selected from super-populations is addressed through replacing finite sums with expected values over the within-cluster and across cluster populations respectively. In comparison, the ATE weights each participant equally based on the average within-participant contrasts, emphasizing the treatment effect on the population of participants. When all clusters have the same size or all participants have the same contrast, the UATE and ATE coincide. As we are interested in the population of clusters, to ensure valid inference for all possible settings, we choose the UATE as our target estimand.

A GEE analysis is based on the observed outcome of each participant, which under the consistency assumption (Hernán and Robins, 2020), is written as Y_ij = Z_iY_ij(1) + (1 − Z_i)Y_ij(0). For analysis with the identity link and only an intercept and the cluster-level treatment indicator in the marginal mean model, the marginal mean is specified via the following generalized linear model with identity link function

$$E\left(Y_{ij}\mid Z_i\right)={\mu }_i={\beta }_0+{\beta }_1{Z}_i.$$

We consider the following four methods of GEE analyses based on two working correlation matrices (independence vs. exchangeable) and two approaches to accommodate weighting (inverse cluster size weighting vs. no cluster size weighting):

1. independence working correlation matrix (IEE);

2. independence working correlation matrix with inverse cluster size weighting (IEEW);

3. exchangeable working correlation matrix (EEE);

4. exchangeable working correlation matrix with inverse cluster size weighting (EEEW).

4. Theoretical findings and analysis of motivating example

Assuming cluster sizes are fixed, theoretical results for the convergence of the four different estimators obtained from the four analytic methods for the mean difference estimand UATE for a continuous outcome are shown in Table 1; details of the derivations are provided in Web Appendix A. We refer to these convergence results as theoretical estimands. We do not show the theoretical results for a binary outcome but we do include a binary outcome in the simulations for an empirical investigation. The results demonstrate that, of the four analytic methods presented in the previous section using the identity link, IEEW is the only method that is always appropriate for the target estimand, UATE. Specifically, when there exists heterogeneity of treatment effects according to cluster size, only IEEW always provides unbiased estimates for UATE; in the absence of heterogeneity of treatment effects according to cluster size, all four methods are unbiased. This may be an unexpected finding given that it could be considered natural to use EEEW to accommodate both the within-cluster correlation of outcomes (via the exchangeable working correlation matrix) and the variable cluster size (via the inverse clustersize weighting). Intuitively, this is because the other three methods either do not weight by cluster size (IEE) or involve additional covariance weights that induce dependence on cluster size and therefore are sensitive to heterogeneity of the treatment effects according to cluster size (EEE, EEEW), whereas IEEW is robust to such heterogeneity.

Table 1.

Convergence of different estimators for the unit average treatment effect (UATE) estimand with a continuous outcome

Method	${\lim }_{n\to \infty }{\widehat{\beta }}_1$ a	Sufficient condition for convergence to UATEb
IEEc	$E\left\{\frac{1}{E\left(m_i\right)}\sum _j\left[Y_{ij}(1)-Y_{ij}(0)\right]\right\}$	When mi = m
IEEWd	$E\left\{\frac{1}{m_i}\sum _j\left[Y_{ij}(1)-Y_{ij}(0)\right]\right\}$	Always
EEEe	$\frac{E\left\{\frac{1}{1+\left(m_i-1\right)\rho }{\sum }_j\left[Y_{ij}(1)-Y_{ij}(0)\right]\right\}}{E\left\{\frac{m_i}{1+\left(m_i-1\right)\rho }\right\}}$	When ρ = 1, or mi = m
EEEWf	$\frac{E\left\{\frac{1}{\left[1+\left(m_i-1\right)\rho \right]m_i}{\sum }_j\left[Y_{ij}(1)-Y_{ij}(0)\right]\right\}}{E\left\{\frac{1}{1+\left(m_i-1\right)\rho }\right\}}$	When ρ = 0, or mi = m

^aThe “E” outside the curly brackets in this column indicates the expectation over clusters, based on the joint distribution of the cluster sizes as well as all potential outcomes in each cluster. In a sense, it is an expectation for the population of clusters (viewing all elements in a cluster as a random vector for which we are taking the expectation).

^bρ is the intraclass correlation coefficient (ICC).

^cIEE: Independence working correlation matrix with no cluster size weighting.

^dIEEW: Independence working correlation matrix with inverse cluster size weighting.

^eEEE: Exchangeable working correlation matrix with no cluster size weighting.

^fEEEW: Exchangeable working correlation matrix with inverse cluster size weighting.

When analyzing the STOP CRC data using the four analytic methods, we observed that, there were only small differences among the estimated treatment effects (Table 2). We hypothesized that this happened because there were small differences in treatment effect according to cluster (i.e. clinic) size. We further hypothesized that we would see greater differences in the situation where cluster size varies and where there is heterogeneity of treatment effects according to cluster size with, for example, larger clusters being associated with larger treatment effects. Simulation studies were therefore needed to provide insight into which scenarios require special attention to be paid to the choice of analytic method.

Table 2.

Analysis results of STOP CRC data using four GEE approaches

	Methodsa
	IEEb	IEEWc	EEEd	EEEWe
Treatment Effect Estimatef	0.0342	0.0357	0.0358	0.0327
Robust SE of Estimate	0.0266	0.0222	0.0223	0.0247
P-Value	0.1984	0.1079	0.1075	0.1849
Lower Bound of 95% CI	−0.0207	−0.0101	−0.0101	−0.0182
Upper Bound of 95% CI	0.0892	0.0816	0.0817	0.0837

^aModel fit under the identity link, with only the intercept and cluster-level treatment indicator in the mean model. We did not yet apply any small sample correction.

^bIEE: Independence working correlation matrix with no cluster size weighting.

^cIEEW: Independence working correlation matrix with inverse cluster size weighting.

^dEEE: Exchangeable working correlation matrix with no cluster size weighting. Mean estimated ICC from EEE = 0.0326.

^eEEEW: Exchangeable working correlation matrix with inverse cluster size weighting.

^fThe treatment effect estimate is a risk difference.

5. Simulation studies

To compare the empirical performance of the four analytic methods for continuous and binary outcomes and for both homogeneous and heterogeneous treatment effects according to cluster size, we conducted a series of simulation studies. Our goals were to evaluate the relative efficiency of alternative estimators and to test the hypothesis of treatment effect bias in the presence of heterogeneity of treatment effects according to cluster size. We therefore focused on scenarios with the potential to illustrate the severity of this bias. We focused on a two-arm parallel CRT with an equal allocation to the two arms; the target estimands were the UATE in terms of mean difference and risk difference for continuous and binary outcomes, respectively. Moreover, we considered two scenarios in relation to cluster size: (1) no heterogeneity of treatment effect according to cluster size and (2) heterogeneity of treatment effects whereby larger clusters were associated with larger treatment effects.

We fixed the total number of clusters, n = 26, to mimic the STOP CRC trial, then generated cluster sizes m_i ~ Unif(90, 110) for $i=1,\dots ,\frac{n}{2}$ and m_i ~ Unif(15, 25) for $i=\frac{n}{2}+1,\dots ,n$ so that half of the clusters had a mean size of 100 and half had a mean size of 20. Correlated continuous data were generated through the following mechanism: For each participant, we generated potential outcomes Y_ij(1) = β_i + b_i + ϵ_ij and Y_ij(0) = b_i + ϵ_ij, where $b_i~N\left(0,{\sigma }_b^2\right)$ was a cluster random intercept, and ${ϵ}_{ij}~N\left(0,{\sigma }_e^2\right)$ was a random error. We note that a linear mixed model (LMM) was used for data generation for simplicity, although analysis was via GEE, as LMM and GEE parameters should coincide under the identity link. We specified treatment effects under two scenarios whereby there was no difference in treatment effect according to cluster size (i.e. treatment effect = 2) and where larger clusters had a larger treatment effect (i.e. 4 vs. 2): β_i = β_l ∈ {2, 4} for $i=1,\dots ,\frac{n}{2}$ (large clusters) and β_i = β_s = 2 for $i=\frac{n}{2}+1,\dots ,n$ (small clusters). We fixed σ_b = 0.2 and σ_e ∈ {1, 2} to allow for different intraclass correlation coefficients (ICCs) ρ, which could be calculated as $\rho =\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }_e^2}$ (Murray, 1998). Additionally, correlated binary data in each cluster were generated from a binomial model given marginal mean and exchangeable correlation structure using the methods of Qaqish (2003). Specifically, we fixed the within-cluster correlation ρ ∈ {0.05, 0.09}; to generate Y(1), we fixed marginal means under two scenarios whereby there was no difference in treatment effect according to cluster size (i.e. marginal mean = 0.3) and where larger clusters had a larger marginal mean (i.e. 0.3 vs. 0.15): μ_i = μ_l = 0.3 for $i=1,\dots ,\frac{n}{2}$ and μ_i = μ_s ∈ {0.15, 0.3} for $i=\frac{n}{2}+1,\dots ,n$; to generate Y(0), we fixed μ_i = μ_l = 0.1 for i = 1, … , n.

Under both data generation mechanisms, for each participant, Y_ij(1) − Y_ij(0) was the true participant-level estimand, and given the cluster-level treatment indicator Z_i, the observed outcome was Y_ij = Z_iY_ij(1) + (1 − Z_i)Y_ij(0). For each scenario, 1000 data replications were generated, then analyzed using the above four GEE methods.

For each of 1000 iterations, we calculated the “true” UATE estimand τ using Eq (1), fit GEE with the intercept and treatment indicator to obtain an estimate of the treatment effect ${\widehat{\beta }}_1$ for each analytic method, then calculated the bias $(={\widehat{\beta }}_1-\tau )$ and relative bias $(=\frac{{\widehat{\beta }}_1-\tau }{\tau }\times 100\%)$ compared to the UATE for each of the four methods. Across the 1000 iterations and for each of the four methods, we calculated the mean estimate of the treatment effect, mean variance of the estimate, mean bias, mean relative bias, Monte-Carlo variance of the estimate, and empirical coverage probability of nominal 95% confidence intervals for β₁, relative to the “true” estimand τ. For continuous outcomes, for each method, we also calculated its corresponding theoretical estimand (provided in Table 1) for each of the 1000 iterations. We then calculated the mean bias, mean relative bias, and empirical coverage probability of nominal 95% confidence intervals for β₁, relative to the corresponding theoretical estimand, across those 1000 iterations.

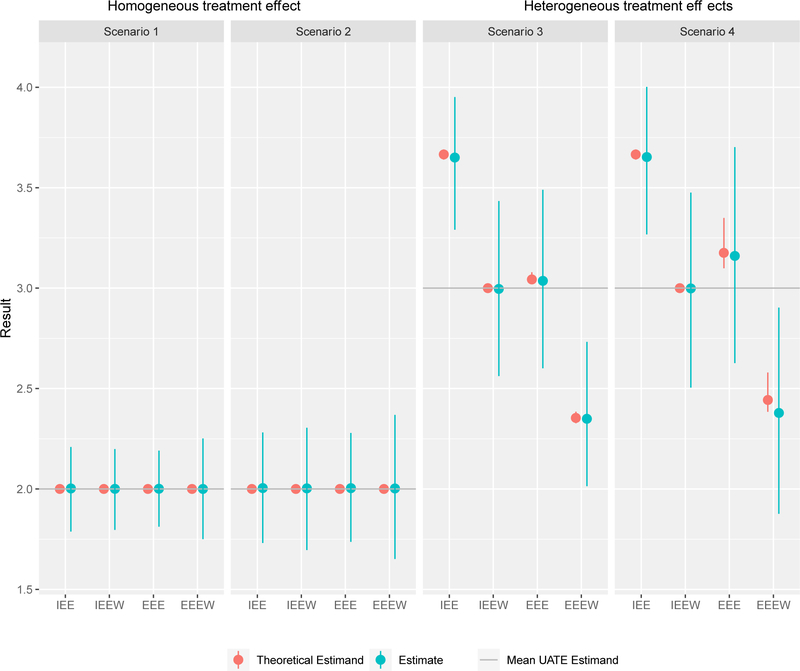
Table 3 and Table 4 summarize the scenarios and results from the above four GEE analyses for continuous and binary outcomes, respectively, relative to the “true” estimand UATE. In contrast, Figure 1 and Web Table 1 summarize the results from the four GEE analyses for continuous outcomes, relative to their respective theoretical estimands.

Table 3.

Simulation scenarios and results for continuous outcomes

Scenarioa	Parameters	Results	Methods
			IEEb	IEEWc	EEEd	EEEWe
Homogeneous treatment effect
1		Mean Estimate	2.0025	2.0009	2.0014	2.0003
	βl = 2	Mean Variance of Estimate	0.0101	0.0100	0.0089	0.0140
	βs = 2	Mean Bias	0.0025	0.0009	0.0014	0.0003
	σb = 0.2	Mean Relative Bias (%)	0.1274	0.0439	0.0725	0.0159
	σe = 1	Monte-Carlo Variance	0.0117	0.0105	0.0099	0.0163
	ρ = 0.038	Empirical Coverage	0.9200	0.9430	0.9340	0.9210
		Mean ICC	-	-	0.0338	-
2		Mean Estimate	2.0047	2.0032	2.0040	2.0030
	βl = 2	Mean Variance of Estimate	0.0170	0.0230	0.0164	0.0289
	βs = 2	Mean Bias	0.0047	0.0032	0.0040	0.0030
	σb = 0.2	Mean Relative Bias (%)	0.2341	0.1621	0.2006	0.1517
	σe = 2	Monte-Carlo Variance	0.0195	0.0237	0.0187	0.0333
	ρ = 0.010	Empirical Coverage	0.9210	0.9460	0.9230	0.9320
		Mean ICC	-	-	0.0075	-
Heterogeneous treatment effects
3		Mean Estimate	3.6505	2.9963	3.0363	2.3495
	βl = 4	Mean Variance of Estimate	0.0381	0.0839	0.0830	0.0449
	βs = 2	Mean Bias	0.6505	−0.0037	0.0363	−0.6505
	σb = 0.2	Mean Relative Bias (%)	21.6832	−0.1246	1.2101	−21.6828
	σe = 1	Monte-Carlo Variance	0.0278	0.0517	0.0553	0.0360
	ρ = 0.038	Empirical Coverage	0.1360	0.9860	0.9800	0.1740
		Mean ICC	-	-	0.3212	-
4		Mean Estimate	3.6526	2.9986	3.1603	2.3786
	βl = 4	Mean Variance of Estimate	0.0450	0.0968	0.0889	0.0752
	βs = 2	Mean Bias	0.6526	−0.0014	0.1603	−0.6214
	σbs = 0.2	Mean Relative Bias (%)	21.7544	−0.0458	5.3440	−20.7122
	σe = 2	Monte-Carlo Variance	0.0362	0.0655	0.0785	0.0703
	ρ = 0.010	Empirical Coverage	0.1670	0.9750	0.9030	0.3910
		Mean ICC	-	-	0.0878	-

^aScenarios 1 and 3 have same values of σ_b and σ_e, but Scenario 1 has homogenous treatment effect and 3 has heterogeneous treatment effects, resulting in the difference in the mean empirical ICCs. Similar patterns for Scenarios 2 and 4. The mean UATE estimand of Scenarios 1 and 2 (homogenous treatment effect) is 2; the mean UATE estimand of Scenarios 3 and 4 (heterogeneous treatment effects) is 3. The true ICC for homogeneous treatment effect (Scenarios 1 and 2) are estimated directly using $\rho =\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }_e^2}$, yielding values of 0.0385 and 0.0099, respectively. In contrast, the true ICC for heterogeneous treatment effects (Scenarios 3 and 4) are obtained via a weighted average of the ICC for the large and small clusters.

^bIEE: Independence working correlation matrix with no cluster size weighting.

^cIEEW: Independence working correlation matrix with inverse cluster size weighting.

^dEEE: Exchangeable working correlation matrix with no cluster size weighting.

^eEEEW: Exchangeable working correlation matrix with inverse cluster size weighting.

Table 4.

Simulation scenarios and results for binary outcomes

Scenarioa	Parameters	Results	Methods
			IEEb	IEEWc	EEEd	EEEWe
Homogeneous treatment effect
1	μl = 0.3 μs = 0.3 μ0 = 0.1 α = 0.05	Mean Estimate	0.2012	0.1995	0.2004	0.1985
		Mean Variance of Estimate	0.0018	0.0017	0.0015	0.0024
		Mean Bias	0.0013	−0.0003	0.0005	−0.0014
		Mean Relative Bias (%)	1.1429	−0.1097	0.4816	−0.9980
		Monte-Carlo Variance	0.0019	0.0017	0.0016	0.0028
		Empirical Coverage	0.9640	0.9890	0.9830	0.9690
		Mean ICC	-	-	0.0435	-
2	μl = 0.3 μs = 0.3 μ0 = 0.1 α = 0.09	Mean Estimate	0.2008	0.1989	0.1994	0.1976
		Mean Variance of Estimate	0.0029	0.0025	0.0024	0.0035
		Mean Bias	0.0013	−0.0007	−0.0001	−0.0020
		Mean Relative Bias (%)	1.0517	−0.3370	0.0569	−1.3874
		Monte-Carlo Variance	0.0033	0.0027	0.0026	0.0043
		Empirical Coverage	0.9560	0.9870	0.9760	0.9620
		Mean ICC	-	-	0.0775	-
Heterogeneous treatment effects
3	μl = 0.3 μs = 0.15 μ0 = 0.1 α = 0.05	Mean Estimate	0.1748	0.1244	0.1426	0.0816
		Mean Variance of Estimate	0.0019	0.0018	0.0018	0.0020
		Mean Bias	0.0498	−0.0007	0.0175	−0.0435
		Mean Relative Bias (%)	42.7613	−0.2812	15.1903	−36.9474
		Monte-Carlo Variance	0.0020	0.0017	0.0017	0.0024
		Empirical Coverage	0.8310	0.9810	0.9520	0.8690
		Mean ICC	-	-	0.0537	-
4	μl = 0.3 μs = 0.15 μ0 = 0.1 α = 0.09	Mean Estimate	0.1747	0.1245	0.1371	0.0797
		Mean Variance of Estimate	0.0030	0.0025	0.0025	0.0028
		Mean Bias	0.0496	−0.0006	0.0119	−0.0454
		Mean Relative Bias (%)	43.6007	−0.1158	10.7635	−39.5514
		Monte-Carlo Variance	0.0033	0.0024	0.0025	0.0034
		Empirical Coverage	0.8720	0.9850	0.9760	0.8890
		Mean ICC	-	-	0.0891	-

^aScenarios 1 and 3 have same values of μ_l, μ₀, and α, but have different values of μ_s, i.e. Scenario 1 has homogenous treatment effect and 3 has heterogeneous treatment effects. Similar patterns for Scenarios 2 and 4. The mean UATE estimands of Scenarios 1 and 2 (homogenous treatment effect) are 0.1999 and 0.1995, respectively; the mean UATE estimands of Scenarios 3 and 4 (heterogeneous treatment effects) are 0.1251 and 0.1251, respectively.

^bIEE: Independence working correlation matrix with no cluster size weighting.

^cIEEW: Independence working correlation matrix with inverse cluster size weighting.

^dEEE: Exchangeable working correlation matrix with no cluster size weighting.

^eEEEW: Exchangeable working correlation matrix with inverse cluster size weighting.

Figure 1. Simulation results^a of theoretical estimand and estimate for continuous outcomes (mean with 2.5^th and 97.5^th percentiles^b).

^a Scenarios 1 and 3 have same values of μ_l, μ₀ and α, but have different values of μ_s, i.e. Scenario 1 has homogenous treatment effect and 3 has heterogeneous treatment effects. Similar patterns for Scenarios 2 and 4. The mean UATE estimand of Scenarios 1 and 2 (homogenous treatment effect) is 0.200; The mean estimand of Scenarios 3 and 4 (heterogeneous treatment effects) is 0.125.

IEE: Independence working correlation matrix with no cluster size weighting.

IEEW: Independence working correlation matrix with inverse cluster size weighting.

EEE: Exchangeable working correlation matrix with no cluster size weighting.

EEEW: Exchangeable working correlation matrix with inverse cluster size weighting.

^b The lower and upper bars represent the 2.5^th and 97.5^th percentiles, respectively, of the theoretical estimands and estimated effects from 1000 simulated experiments. Note that the theoretical estimands corresponding to IEE, EEE, and EEEW only vary across replications for the two scenarios with heterogeneous treatment effects. Importantly, in all scenarios considered, there is no variation in the theoretical estimand corresponding to IEEW, which in this case is the UATE.

Inefficiency associated with two weights under homogeneous treatment effect:

For a continuous outcome, Table 3 shows Scenarios 1 and 2 under which the treatment effect does not vary by cluster size. In this case usually weighted least squares theory implies that choice of a correct covariance matrix would lead to the smallest variance. Given the structure of the model an exchangeable covariance matrix would be optimal, and this is demonstrated by EEE achieving the smallest Monte Carlo variance. Furthermore, we find that choice of two weights does not lead to bias but does lead to substantial losses in efficiency. In Scenario 1, the relative variance of EEEW to EEE is 0.0163/0.0099 = 1.65 implying a 65% increase in variance, and in Scenario 2 the relative variance is 0.0333/0.0187 = 1.78 implying a 78% increase in variance. Similar patterns are observed with a binary outcome in Table 4, Scenarios 1 and 2 with relative variances comparing EEEW to EEE of 1.75 and 1.65 respectively. In addition, when the UATE was intentionally targeted and IEEW was used then this would come at the potential cost of inefficiency. The relative variance of IEEW to EEE is 1.06–1.27 for a continuous outcome in our simulation scenarios, and 1.04–1.06 for our binary outcome simulations. Therefore, under the assumption of homogeneous treatment effect the EEE estimator is the most precise, but as we show in subsequent simulations this estimator is biased for the UATE when there is heterogeneity of effect by cluster size. Selection of IEEW ensures broadly valid targeting of the estimand, and may incur moderate losses of efficiency in some situations where methods such as EEE can be more precise yet which make additional assumptions that would be difficult to verify a priori.

Bias associated with two weights under heterogenous treatment effects:

In general, for the UATE estimand under variable cluster sizes, when there was heterogeneity of treatment effects according to cluster size, IEEW performed best among the four methods; when there was no heterogeneity of treatment effect according to cluster size, we only observed small differences in the estimated treatment effects among the four analytic methods, consistent with the theoretical results for a continuous outcome and analysis results from our motivating example. More specifically, for the UATE estimand for a continuous outcome (Table 3), IEEW resulted in mean relative bias less than 1% for the two scenarios with heterogenous treatment effects (Scenarios 3 and 4), which was much smaller than those using the other three analytic methods. In contrast, the four analytic methods provided similar mean relative bias less than 1% in the absence of treatment effects heterogeneity (Scenarios 1 and 2). Similar specific results were observed for binary outcome simulations (Table 4).

6. Discussion

In this article, we investigate different analysis methods under the GEE framework for CRTs with variable cluster sizes, when the UATE is considered as the target estimand. When inference is focused on the population of clusters, the UATE is of interest naturally in CRTs considering the data is multi-level and that clusters could be heterogeneous in size. We consider two working correlation matrices (independence vs. exchangeable) and two approaches to accommodate cluster size (inverse cluster size weighting vs. no cluster size weighting) within this framework. We conclude that an analysis using both an exchangeable working correlation matrix and weighting by inverse cluster size, which may be considered the natural analytic approach, can lead to incorrect results. That is, two weights make a wrong. The bias is minimal when there is homogeneity of treatment effects according to cluster size but unacceptable when there is heterogeneity of treatment effects according to cluster size. In addition, we show that only an analysis with an independence working correlation matrix and weighting by inverse cluster size always provides valid results for the UATE estimand. As shown in Table 1, the convergence of different estimators for the UATE estimand with a continuous outcome has the same summation expression across all four methods, but the multiplier varies. In the absence of heterogeneity of treatment effects according to cluster size, or when the cluster sizes are all equal, the four multipliers are equivalent such that the expressions converge to the same result. Similar conclusions can be drawn from the analysis of the STOP CRC data and analyses of the simulation studies. When the cluster sizes differ and there is treatment effect heterogeneity according cluster size, we do not see a clear interpretation on the theoretical estimands associated with IEE, EEE and EEEW (see Table 1). In particular, the multiplier term (inside the expectation sign) for the theoretical estimands associated with EEE and EEEW even depends on the unknown intraclass correlation coefficient, and therefore can further be specific to each trial population or endpoint. This can potentially be a source of ambiguity for interpreting the estimands, and therefore our study provides a cautionary note on their application.

Limitations of our work include the lack of small-sample correction in variance estimation (both for analysis of the STOP CRC data and in the simulation studies), the relatively limited simulation studies, and the focus on difference measures only. Regarding small-sample corrections, these are necessary to avoid finite-sample bias of standard error estimates and, depending on the setting it is expected, scenarios with fewer than 40 or 50 clusters would require such an adjustment (Murray, 1998, 2004; Feng et al., 2001). Given that there were a total of 26 clusters for both the STOP CRC data analysis and the simulation studies inspired by the STOP CRC data, we are in a setting where a small-sample correction could be deemed useful. However, given that our focus is on bias in mean estimation rather than estimates of the standard errors of treatment effects, we determined that it was an empirical question that is beyond the scope of the current article. Regarding the relatively limited size of our simulation studies, given our goal was to demonstrate a potential issue in estimation rather than to elucidate the range of settings in which bias may be an issue, we chose to focus on selected scenarios. Finally, although we focused on the mean difference and risk difference for continuous and binary outcomes, respectively, it is possible to extend our work to the estimation of casual risk ratio and odds ratio with a binary outcome. However, this interesting extension is considerably more complex, and we know of no previous work that has defined the UATE for ratio measures in the clustered outcome data setting. Future work is needed to clarify these settings.

In summary, in this article, we have focused on the UATE for CRTs with variable cluster sizes given its ability to address questions around the cluster-level impact of treatments. As such, our recommendation is to use the IEEW analytic approach and to avoid the three alternative methods, which may be more challenging to interpret when there is treatment effect heterogeneity by cluster size.