Pediatric Seizure Prediction in Scalp EEG Using a Multi-Scale Neural Network With Dilated Convolutions

Abstract

Objective: Epileptic seizure prediction based on scalp electroencephalogram (EEG) is of great significance for improving the quality of life of patients with epilepsy. In recent years, a number of studies based on deep learning methods have been proposed to address this issue and achieve excellent performance. However, most studies on epileptic seizure prediction by EEG fail to take full advantage of temporal-spatial multi-scale features of EEG signals, while EEG signals carry information in multiple temporal and spatial scales. To this end, in this study, we proposed an end-to-end framework by using a temporal-spatial multi-scale convolutional neural network with dilated convolutions for patient-specific seizure prediction. Methods: Specifically, the model divides the EEG processing pipeline into two stages: the temporal multi-scale stage and the spatial multi-scale stage. In each stage, we firstly extract the multi-scale features along the corresponding dimension. A dilated convolution block is then conducted on these features to expand our model’s receptive fields further and systematically aggregate global information. Furthermore, we adopt a feature-weighted fusion strategy based on an attention mechanism to achieve better feature fusion and eliminate redundancy in the dilated convolution block. Results: The proposed model obtains an average sensitivity of 93.3%, an average false prediction rate of 0.007 per hour, and an average proportion of time-in-warning of 6.3% testing in 16 patients from the CHB-MIT dataset with the leave-one-out method. Conclusion: Our model achieves superior performance in comparison to state-of-the-art methods, providing a promising solution for EEG-based seizure prediction.

I. Introduction

Epilepsy is a neurological disease with brain dysfunction, and it has troubled humans for thousands of years. Generally, epileptic seizures are accompanied by abnormal discharge of brain neurons and affect the patient’s behavior. As indicated by the World Health Organization (WHO), epilepsy is one of the most common neurological diseases with about 50 million people globally, and about 70% of patients could become seizure-free with appropriate treatment [1]. Nonetheless, there are as yet 30% of patients who experience the ill effects of intractable epilepsy. Hence, the study of seizure prediction is especially valuable, which could timely forecast the occurrence of seizures from scalp EEG signals for patients to take more active and effective intervention measures.

Electroencephalography (EEG) is a powerful tool for recording the brain’s electrical activity and is extensively used in the diagnosis of people with epilepsy in medicine [2]–[5]. Over the last few years, studies have shown that epileptic seizures can be predicted by EEG [6]–[9]. Most seizure prediction studies divided the consecutive epileptic EEG signals into three states: interictal (interval between seizures), preictal (before the seizure onset), and ictal (period of seizure). In general, epileptic seizure prediction can be described as a binary classification problem that distinguishes between the preictal and interictal. Many advance methods have been designed in the field of epileptic seizure prediction during the decades.

Traditionally, the EEG-based seizure prediction method focuses on feature extraction and classification. Researchers manually constructed discriminative features of EEG signals, such as time domain, frequency domain, and time-frequency domain features. For example, Chisci et al. extracted coefficients in the autoregressive models as features and classified them by improved support vector machine (SVM) [10]. Parvez et al. used phase correlation to explore EEG signals’ spatiotemporal relationship and distinguished preictal and interictal by SVM [11]. Yuan et al. used diffusion distance to extract the features and Bayesian linear discriminant analysis classifier to classify the features [12]. These methods provide a solid foundation for the prediction of epileptic seizures.

Recently, deep learning has been widely used, which could extract discriminative features automatically. Truong et al. applied convolutional neural network (CNN) to different EEG datasets and demonstrated the effectiveness of deep learning [13]. Daoud et al. took advantage of CNN in extracting significant features and classified them by recurrent neural network [14]. Ozcan et al. constructed a 3D representation according to the position of the electrode and applied 3D CNN with an image-based approach for seizure prediction [15]. Wang et al. employed directed transfer function to explore the specific information exchange between EEG channels and then used CNN for seizure prediction, achieving satisfactory performance [16]. Yang et al. proposed a dual self-Attention residual network to classify the features obtained by the short-time Fourier transform (STFT) of EEG signals [17].

Neurological studies show that the human brain is a complex system whose function depends on coordinated activity patterns over multiple temporal and spatial scales [18], [19]. For example, the alpha wave and delta wave are two classical waveforms in EEG signals. The alpha wave has a duration of 1/13 – 1/8 s (77 - 125 ms), and the delta wave with a duration of 1/4 - 2 seconds (250 - 2000 ms) [20]. That is to say, different wave in EEG signals may appear at different time scales. Similarly, the abnormal discharges in EEG may be associated with multiple distinct brain regions [21], [22]. Hence, the EEG signals are also associated with different spatial scales.

Several multi-scale methods have been designed on EEG-based seizure prediction in recent years. However, these methods fail to take full advantage of temporal-spatial multi-scale features of EEG signals so that the performance is still limited. For example, Hussein et al. used STFT to extract EEG signals’ time-frequency features and classified them with a multi-scale CNN method [23]. Similarly, Wang et al. designed a 3D multi-scale CNN model to classify the features obtained by STFT of EEG signals [24]. Qi et al. extracted preliminary features of EEG signals and then classified them using a framework of the domain adaptation CNN model with multi-scale temporal convolutions [25]. These methods still rely on extracting features of EEG signals manually, which has limited the prediction performance. To this end, in this study, we propose an end-to-end multi-scale framework for epileptic seizure prediction. The framework consists of two stages: temporal multi-scale stage and spatial multi-scale stage. In each stage, we fully explore the information of the corresponding dimension. Specifically, we use different kernel size to learn the multi-scale features of EEG signals. Then, we utilize a dilated convolution block with different dilation rates to further expand the receptive fields and systematically aggregate global information. Furthermore, we adopt a feature weighted fusion method based on an attention mechanism to achieve better feature fusion and alleviate the redundancy existing in the dilated convolution block. Finally, we evaluate our model on the CHB-MIT dataset with the leave-one-out method.

The rest of this paper is organized as follows. Section II introduces the used datasets and the proposed approaches. Section III shows our experimental results, comparison and hyperparameters selection. Section IV provides analysis and discussion. Finally, section V presents the conclusion of our work.

II. Material and Methodology

A. Data Description

The CHB-MIT scalp EEG database, [26], [27], collected at the Children’s Hospital Boston, is used to train and test the model for seizure prediction in this study. The dataset recorded the long-duration EEG of 23 pediatric patients with intractable epilepsy. All multi-channel EEG signals were acquired with a 256 Hz sampling rate according to the 10–20 international system.

Following [15], we define some relevant parameters. The preictal period is defined as 30 minutes before the onset of a seizure. The intervention time is considered as the 1-minute interval between the preictal period and the ictal period and is excluded in the training data. According to the following two conditions, the interictal period is defined: (1) more than one hour before the onset of a seizure; (2) more than one hour after the end of a seizure. In the case of two seizures occurring at a short interval, the incoming seizure is not evaluated for the lack of preictal data. The minimum interval is set to 15 minutes. To avoid the overfitting problem, we select subjects with at least three seizures and whose interictal duration was greater than three hours. In this case, we select 16 patients for our experiments, and Table 1 shows the subject information we used. To ensure the consistency of the model, we consider the common 18 channels for each patient. The consecutive recordings are divided into 4-second EEG signals with 2-second overlapping as windows for classification.

TABLE 1. Data Information of the CHB-MIT Scalp EEG Database.

Patients	Gender	Age (years)	No. of seizures	No. of preictal samples	No. of interictal samples
Pat1	F	11	7	5952	52460
Pat2	M	11	3	2606	54309
Pat3	F	14	7	5326	54666
Pat5	F	7	5	4343	53684
Pat7	F	14.5	3	2610	111228
Pat9	F	10	4	3480	109769
Pat10	M	3	7	5881	67348
Pat13	F	3	12	6687	40759
Pat14	F	9	8	6555	30386
Pat16	F	7	10	6800	18542
Pat17	F	12	3	2610	30813
Pat18	F	18	6	3956	53915
Pat19	F	19	3	1859	48573
Pat20	F	6	8	6087	36699
Pat21	F	13	4	3476	51015
Pat23	F	6	7	5525	31447

B. Temporal-Spatial Multi-Scale Convolutional Neural Network with Dilated Convolutions

To capture the multi-scale features of EEG signals, we develop the temporal-spatial multi-scale convolutional neural network with dilated convolutions. Figure 1 presents the architecture of our proposed model. The input to the model is the raw EEG signals that have not been preprocessed. EEG signals have two dimensions: time dimension (derived from different times) and space dimension (derived from different channels). To focus on these two dimensions, we not only perform convolution operations in the time dimension but also in the space dimension. Specifically, we divided this process into two stages: the temporal multi-scale stage and spatial multi-scale stage. In each stage, we firstly explore the multiscale information of EEG signals with different convolutional kernel sizes. Then we utilize a dilated convolution block to expand the receptive fields further and systematically aggregate global information. Finally, the features are classified by 2D convolutional units. Table 2 shows the specific parameters of the structure in this study.

FIGURE 1.

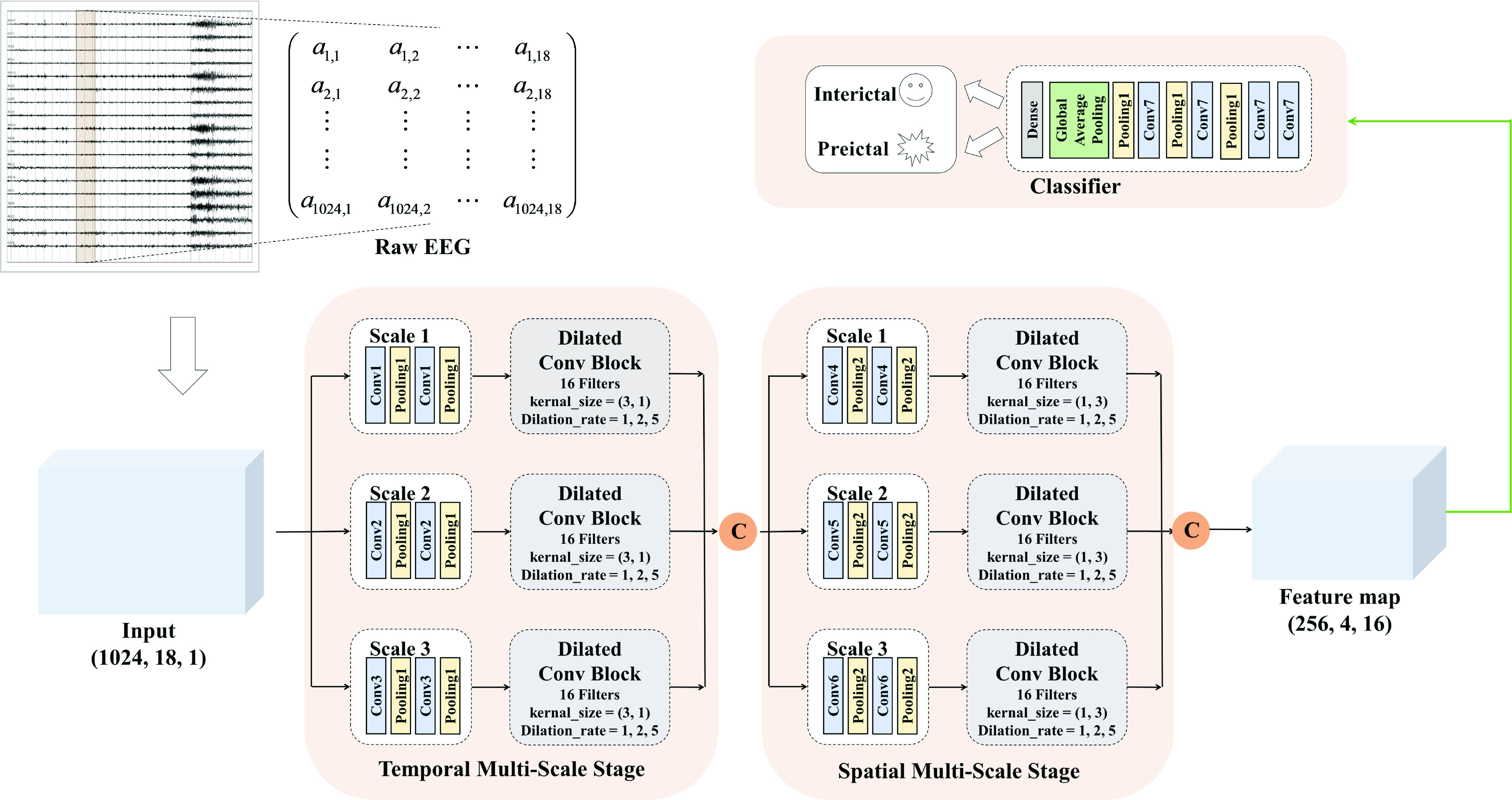
The proposed architecture of our model. Convolution unit of different scales has a different kernel size. The model parameters are represented in Table 2, and the details of the dilated convolution block are showed in Fig. 2. The symbol c above is a concatenating operator.

TABLE 2. The Parameters of Our Model.

Layer	Size	Channel	Activation function
Temporal multi-scale stage:
Conv1		16	ReLU
Conv2		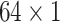16	ReLU
Conv3		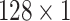16	ReLU
Pooling1		–	–
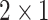Spatial multi-scale stage:
Conv4		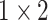16	ReLU
Conv5		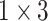16	ReLU
Conv6		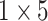16	ReLU
Pooling2		–	–
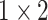Classification stage:
Conv7		16	ReLU
Dense	1	–	sigmoid

1). Multi-Scale Learning With Different Kernel Size:

Motivated by the multi-scale properties of human brain function, we designed the multi-scale framework to explore the information of EEG signals. Specifically, we use different convolution kernel sizes to learn the multi-scale features of EEG signals. In the convolution layer, the convolution kernels slide over EEG signals, and the operation is defined as follows:

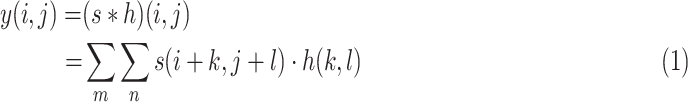Where 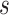is the signal, 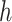is the convolution kernel, 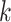and 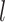are the sizes of the kernel, and 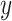is the output vector. Accordingly, kernels with different sizes capture information at different levels.

In the temporal multi-scale stage, the convolution kernels with larger sizes focus on the long-term temporal information, while the ones with smaller sizes are concentrated the local information. Then, the max-pooling layer is added after the convolutional layer for feature dimension reduction. In the spatial multi-scale stage, by considering the specific multiscale relationship between EEG channels, the convolution kernels with larger sizes focus on the information exchange over a large area of the brain, while the smaller ones pay attention to the local area.

2). Design of the Dilated Convolution Block:

Recently, dilated convolution has become popular, as it makes the kernel have a larger receptive field without increasing the number of additional parameters. The difference between dilated convolution and traditional convolution is the convolution kernel. Only part of the positions are parameters to be learned in the dilated convolution kernel, and the other positions are filled with 0.

The formula of dilated convolution is defined as:

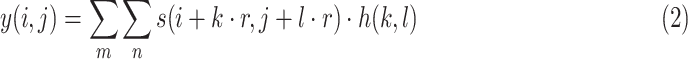where 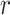is the dilation rate. It can be seen that the receptive field of dilated convolution is larger than traditional convolution under the same number of parameters. Besides, dilated convolution can also aggregate global information more effectively.

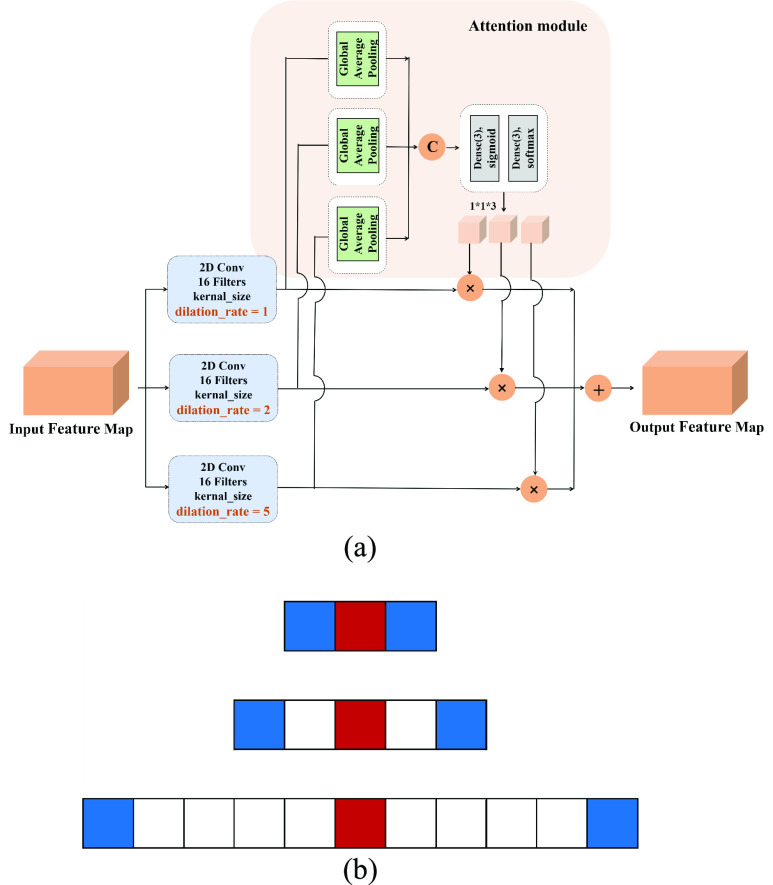
Figure 2 shows the structure of the dilated convolution block and the visualization of dilated convolution. We set the dilated convolution rate to 1, 2, 5 for the parallel paths, respectively. For better feature fusion, we adopt an attention-based approach. First, we pass each feature map obtained by parallel dilated convolution through a global average pooling layer. Then, we use the full connection layers with activation functions to learn their weights. Finally, the weighted fused feature map is considered as the output of the dilated convolution block. The overall attention process can be described as:

where 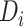is the feature map obtained by dilated convolution with different dilation rates, 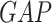denotes the global average pooling operations, Dense denotes the fully connected layer. 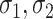denotes the sigmoid function and the SoftMax function respectively. 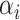is the weight of the feature map 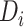, and 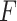is the final output of the dilated convolution block.

FIGURE 2.

(a) The architecture of dilated convolution block and (b) the visualization of dilated convolution (kernal_size = 3, dilation_rate = 1, 2, 5).

3). Design of the Classification Network:

The classification network still consists of convolutional layers and pooling layers. A global average pooling layer compresses the representation after several consecutive convolution layers and pooling layers. Also, 10% dropout is used in our network to avoid overfitting. Finally, the vector is fed into a fully connected layer with the sigmoid activation function:

and a score from 0 to 1 is obtained.

C. Training and Testing

In our experiments, the training and testing of the model are for specific patients. While training, we use an improved cross-entropy, namely focal loss as the training loss [28] to automatically downweight the contribution of easy examples during training and rapidly focus the model on hard examples. Specifically, the standard form of cross-entropy is defined as the following:

the binary form is defined by:

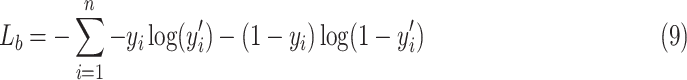and the focal loss is described as:

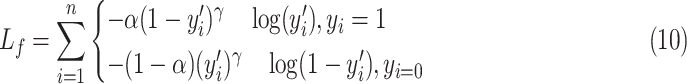where 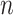is the number of training samples, 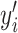is the output of the network, 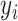is the real label for the ith sample. The parameter 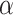is utilized to balance the negative and positive samples, and 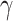is utilized to balance the hard and simple samples.

Cross-validation is a statistical method of evaluating and comparing learning algorithms by dividing data into two segments: one used to train a model and the other used to validate the model [29]. Following the work in [15], EEG data are divided into the training set, validation set, and test set for each patient. Specifically, we use leave-one-out cross-validation to split the test set. Furthermore, we split the training set and validation set using the 5-fold cross-validation method. For example, if a patient has N seizures, there are N corresponding preictal periods. We first divide all interictal data into N equal parts randomly and combine them with N preictal data to be N pairs. According to the leave-one-out method, we take out one of the pairs as a test set in each round. For the rest N-1 pairs, we divide the training set and the validation set by using the five-fold cross-validation method. In each fold, to avoid problems caused by data imbalance, interictal data was randomly down-sampled so that the ratio of preictal and interictal is set to 1: 1. Thus, the model trained and tested 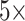N times for this patient, and the final results consist of the averages of achieved values with standard deviations.

In the model training process, we choose the best model by using early stopping to avoid overfitting. When the validation set’s loss does not decrease for ten consecutive epochs, the training stops, and the model with the minimum loss of the validation set is returned. The model is performed in Python 3.7.3 environment and using Keras 2.1.6 with a Tensorflow 1.13.1 backend.

D. Postprocess

To make the seizure prediction process closer to reality, we used the following two approaches as the same as [15]. First, we apply a 60-second causal moving average filter to the output of the classification network. Besides, to prevent continuous alarms from occurring for a short time, we set the refractory period to 30 mins. Since the ratio of preictal and interictal samples is set to 1: 1 during training, we set 0.5 as the seizure prediction alarm threshold for all patients in this study.

E. Comparative Methods

To further evaluate our model’s efficiency, we compare our model with several state-of-the-art methods. All these methods listed below are evaluated on the same database.

Zero-Crossing Intervals Analysis [29] calculated the intervals histogram through the positive zero-crossing intervals analysis of EEG signals, took the bin of the histogram as the feature of the window. Then, novel similarity and dissimilarity indices were defined to measure the distance of the current EEG dynamics to the reference preictal and interictal states, respectively. Specifically, they adopted the variational GMM of the discriminative histogram bins to compute these indices through a fully Bayesian framework. Finally, the final alarm was generated by comparing a new combined index and a patient-specific threshold.

SVM with Phase Locking Value [31] applied phase-locking value to epileptic seizure prediction and classified features by SVM.

CNN with STFT Spectral Images [13] applied short-time Fourier transform to EEG signal analysis, and the time-frequency representation of the signal as a new representation was considered as the input to the CNN.

CNN with Wavelet Transform Coefficient [32] performed the wavelet transform on the EEG signals and used the wavelet coefficient as the representation of the EEG signals. Then, they used a CNN to classify them.

3D CNN with Manual Features [15] focused on the location of the electrodes in epileptic seizure prediction, designed a representation that took spatial information into account. A 3D CNN was performed to classify them with an image-based method.

CNN with Common Spatial Pattern Statistics [33] used the common spatial pattern method to extract the most representative features of EEG signals in both the time domain and the frequency domain, and a CNN classifier was conducted to get the results.

III. Experiments and Results

In this part, extensive experiments are conducted on the CHB-MIT scalp EEG database. We describe the details of our experiments and the evaluation metrics. Moreover, the experimental results and comparisons are given below. Finally, we present the process of hyperparameters selection.

A. Experiments and Evaluation Metrics

For seizure prediction, the seizure prediction horizon (SPH) and the seizure occurrence period (SOP) need to be defined in advance [34]. SPH is the period between seizure alarm and the onset of the seizure, and SOP is the period in which seizures are predicted to occur. The prediction is correct only when the seizure occurs during SOP. In our experiments, the SPH is set to 1 minute, and the SOP is considered as 30 minutes.

For evaluation metrics, in our study, we use sensitivity (Sens, the proportion of the number of correctly predicted seizures to the total number of seizures), false prediction rate (FPR, the number of false alarms per hour), time-in-warning ( , the ratio of time spent in warning to total time) and p-value to evaluate our model.

Specifically, the exact formula of Sens is expressed as follows:

where TP is the number of correctly predicted seizures, FN + TP is the total number of seizures. The FPR is given in (12):

where FP is the number of false alarms. Then, the 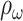is given in (13):

where Time( ) is the total duration predicted to be preictal. The p-values are computed according to [15].

B. Results and Comparison

Since most of our experiments follow the work in [15], we directly use their results reported in the literature (preictal length = 30 minutes, interictal distance = 60 minutes) to make a fair comparison with our proposed method. We present the performance of all patients in Table 3.

TABLE 3. Seizure Prediction Performance Achieved by the Proposed Method and Comparative Method for All 16 Patients.

Patients	Ozcan et al. 2019 [15]				Multi-scale network with dilated convolutions
	Sens (%)	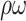(%)	FPR/h	p-value	Sens (%)	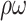(%)	FPR/h	p-value
Pat1	100.0±06.7	10.7±1.2	0.105±0.024	< 0.001	100.0±00.0	7.9±2.6	0.000±0.000	< 0.001
Pat2	100.0±12.4	11.7±3.3	0.232±0.074	0.001	100.0±00.0	0.3±0.2	0.007±0.001	< 0.001
Pat3	83.3±06.2	19.9±2.2	0.395±0.053	0.001	100.0±00.0	6.2±3.2	0.000±0.000	< 0.001
Pat5	100.0±07.5	8.3±1.1	0.101+0.030	< 0.001	100.0±00.0	6.5±1.7	0.000±0.000	< 0.001
Pat7	100.0±12.4	19.0±3.9	0.372±0.081	0.006	100.0±00.0	0.3±0.5	0.000±0.000	< 0.001
Pat9	75.0±00.0	9.7±1.3	0.180±0.030	0.003	75.0±10.8	0.9±1.0	0.020±0.001	< 0.001
Pat10	28.6±10.9	3.5±7.1	0.081±0.177	0.022	85.7±05.0	4.5±2.8	0.000±0.000	< 0.001
Pat13	60.0±07.5	9.1±5.0	0.224+0.143	0.006	83.3±06.2	6.6±4.6	0.000±0.000	< 0.001
Pat14	66.7±12.4	14.9±3.5	0.366±0.067	0.005	87.5±04.1	6.4±0.6	0.083±0.010	< 0.001
Pat16	80.0±00.0	7.6±2.9	0.000±0.096	< 0.001	87.5±04.1	19.6±8.1	0.000±0.000	0.001
Pat17	66.7±12.4	2.7±3.7	0.062±0.059	0.002	100.0±11.3	4.1±3.1	0.000±0.000	0.005
Pat18	40.0±07.5	9.3±5.3	0.167±0.118	0.067	75.0±11.9	3.5±2.7	0.000±0.000	0.006
Pat19	100.0±00.0	12.0±2.4	0.222±0.051	0.002	100.0±00.0	2.2±1.4	0.000±0.000	< 0.001
Pat20	100.0±08.3	11.7±1.7	0.098±0.037	< 0.001	100.0±00.0	13.5±2.4	0.000±0.000	< 0.001
Pat21	100.0±00.0	11.5±1.2	0.212±0.026	< 0.001	100.0±00.0	4.3±1.0	0.000±0.000	< 0.001
Pat23	100.0±00.0	9.6±0.8	0.058±0.022	< 0.001	100.0±00.0	14.5±2.1	0.000±0.000	< 0.001
Ave	79.2±6.5	10.7±2.9	0.202±0.068	n.a.	93.3±03.3	6.3±2.3	0.007±0.001	n.a.

Our model can achieve an average sensitivity of 93.3%, an average false prediction rate of 0.007 per hour, and an average proportion of time-in-warning of 6.3%. To further measure our proposed model’s validity, we compare our results with chance predictor and calculate the p-value for each patient that the significance level p is set to 0.05, and 13 out of 16 patients have p-values less than 0.001. Among the 16 patients, ten patients have a seizure prediction sensitivity of 100%, and 9 of them without false prediction. Comparing with [15], the performance of our method has been improved significantly. Specifically, our method improves sensitivity by 14.1% and reduces the false prediction rate by 0.195/h. Table 4 lists the results of other recent published seizure prediction methods using the CHB-MIT scalp EEG database. The performance obtained by our method is optimal both in Sens and FPR. It is shown that our method is superior to all other state-of-the-art methods.

TABLE 4. Comparison to Recent Epileptic Seizure Prediction Methods on CHB-MIT Scalp EEG Database.

Authors	Dataset	Features	Classifier	No. of seizures	No. of subjects	Validation methods	FPR (/h)	Sens (%)	Interictal distance (minutes)	Preictal length (minutes)
Zandi et al. 2013 [29]	CHB-MIT	Zero crossings similarity/dissimilarity index	–	18	3	–	0.165	83.81	60	40
Cho et al. 2017 [31]	CHB-MIT	Phase locking value	SVM	65	21	10-Fold CV	–	82.44	30	5
Truong et al. 2018 [13]	CHB-MIT	STFT spectral images	CNN	64	13	LOOCV	0.16	81.2	240	30
Khan et al. 2018 [32]	CHB-MIT	Wavelet transform coefficient	CNN	18	15	10-Fold CV	0.147	87.8	–	10
Ozcan et al. 2019 [15]	CHB-MIT	Spectral power Statistical moments Hjorth parameters	3D CNN	77	16	LOOCV	0.202	79.2	60	30
							0.096	85.7	240	60
Zhang et al. 2020 [33]	CHB-MIT	Common spatial pattern statistics	CNN	156	23	LOOCV	0.10	93.1	–	30
Our work	CHB-MIT	CNN	CNN	85	16	LOOCV	0.007	93.3	60	30

Abbreviations: 10-fold CV = 10-Fold Cross-Validation, LOOCV = Leave One Out Cross-Validation

C. Hyperparameters Selection

During the experiments, the hyperparameters need to be determined. In order to select the optimal convolution kernel size, we carry out experiments on all patients with different combinations of convolution kernel seize, and the average area under the curve (AUC) is used as the criteria. The results showed that most patients obtained the optimal AUC under the same combination of convolution kernel sizes. Table 5 shows the representative experimental results on patient-2 and patient-7. According to this, we set the size of kernels to 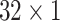, , 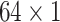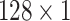for the different scales respectively in the temporal multi-scale stage and set the size of kernels to 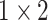, , 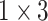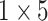respectively in the spatial multi-scale stage.

TABLE 5. Representative Results on Convolution Kernel Size Selection.

(a) Patient-2
		Space dimension
	AUC
Time dimension	(2, 3, 4)	(3, 4, 5)	(2, 3, 5)
(16, 32, 64)	0.800	0.699	0.517
(32, 64, 128)	0.517	0.749	0.880
(64, 128, 256)	0.406	0.457	0.323

Besides, we try different combinations of dilation rates based on the above optimal convolution kernel size, and the results are shown in TABLE 6. Accordingly, we determine the dilated convolution rate to 1, 2, 5 for the three scales.

TABLE 6. Experimental Results on Dilation Rate Selection.

	Dilation rate
Performance	(2, 3, 5)	(1, 3, 5)	(1, 2, 5)
Average Sens	86.2%	92.5%	93.3%
Average Fpr	0.053/h	0.015/h	0.007/h

Furthermore, we also conduct experiments with different numbers of scales (i.e., the number of branches in the model). Specifically, we set the size of kernels to 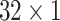, 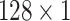for the different scales respectively in the temporal multi-scale stage and set the size of kernels to 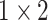, 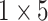respectively in the spatial multi-scale stage when the number of scales is two. When the number of scales is four, we set the size of kernels to 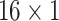, , 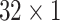, 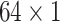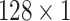for the different scales respectively in the temporal multi-scale stage and set the size of kernels to 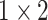, , 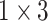, 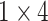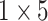respectively in the spatial multi-scale stage. The experimental results in TABLE 7 show that the model is better when the number of scales is three.

TABLE 7. Experimental Results on Scale Number Selection.

	The number of scales
Performance	2	3	4
Average Sens	88.4%	93.3%	90.7%
Average Fpr	0.014/h	0.007/h	0.014/h

IV. Discussion

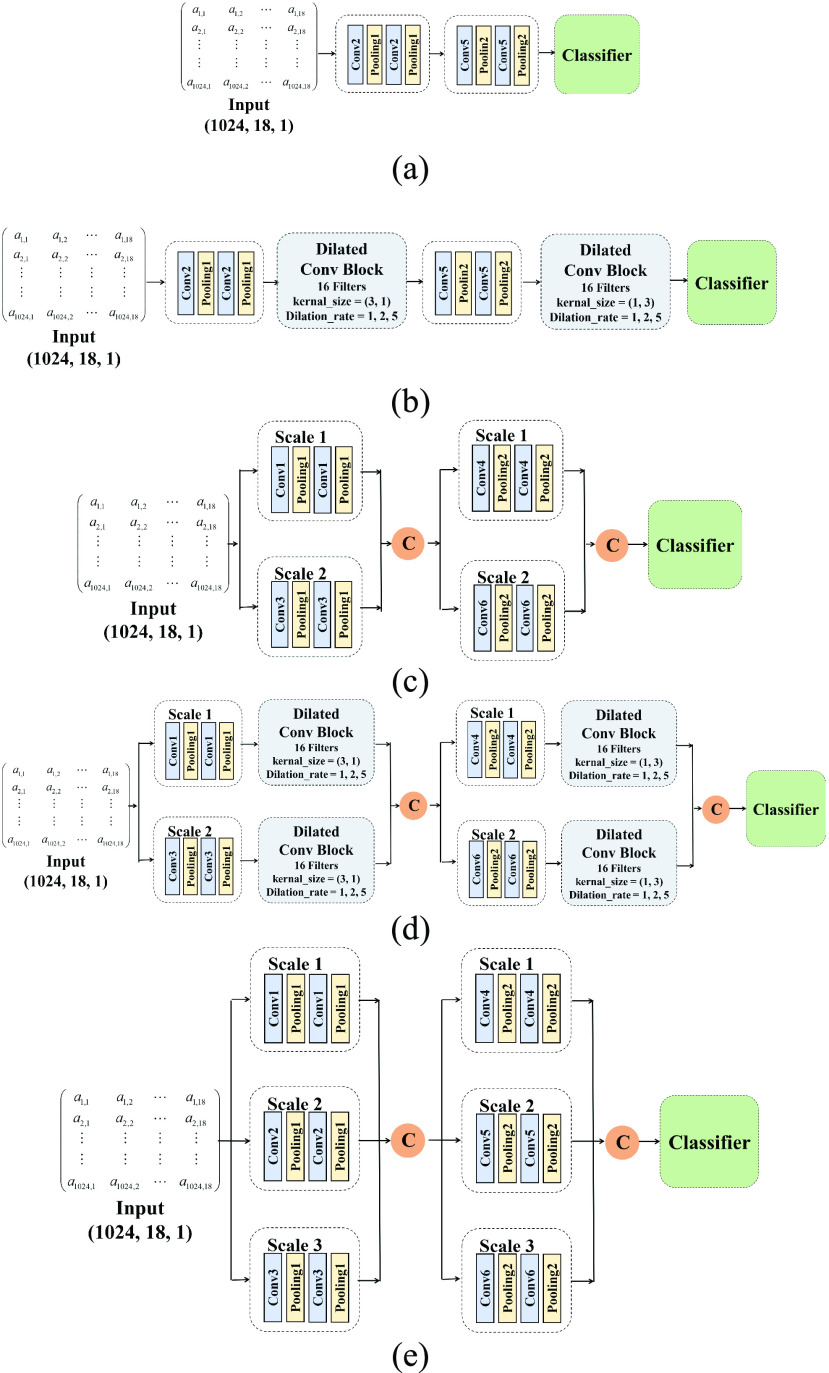
The experimental results illustrate that our model obtains excellent performance. Nevertheless, the reasons for high performance are worth discussing. Our proposed model’s better performance may be attributed to the fact that our approach considers the multi-scale characteristics of EEG signals. Furthermore, dilated convolution can expand our model’s receptive field, which may help us effectively aggregate global and local information. To further validate these viewpoints and explore the effectiveness of our model, we design ablation experiments to consider the contribution of each part of the model. Specifically, we design five models:

• (a)A single-scale network without dilated convolutions.
• (b)A single-scale network with dilated convolution.
• (c)A two-scale network without dilated convolutions.
• (d)A two-scale network with dilated convolution.
• (e)A three-scale network without dilated convolution.

Accordingly, (c) and (e) are to confirm the efficiency of multi-scale learning module, (b) and (d) are to confirm the efficiency of dilated convolutions module, and (a) is the baseline of our ablation experiments. Figure 3 presents the structure of these five models. The training and testing process is the same as the main experiment, and the comparison results are shown in Table 8.

FIGURE 3.

Structure of three models of our ablation experiments: (a) the single-scale neural network without dilated convolutions. (b) the single-scale neural network with dilated convolutions. (c) the two-scale neural network without dilated convolutions. (d) the two-scale neural network with dilated convolutions. (e) the three-scale neural network without dilated convolutions.

TABLE 8. Results of Ablation Experiments and Comparison With Baseline.

	model
Performance	Single-scale network without dilated convolutions	Single-scale network with dilated convolutions	Two-scale network without dilated convolutions	Two-scale network with dilated convolutions	Three-scale network without dilated convolutions
Average Sens	80.8%	87.3%	81.9%	88.4%	85.4%
Average Fpr	0.008/h	0.025/h	0.004/h	0.014/h	0.011/h

According to Table 8, we can infer that these two models can both give a promotion to the performance compared to the baseline for seizure prediction. Hence, the multi-scale module and dilated convolution module are both valuable for feature extraction, each of which can achieve better performance for seizure prediction. Our model combines these two modules and simultaneously extracts both aspects of EEG signal characteristics. Therefore, we obtain the best performance than these models.

In recent years, there is a trend for seizure prediction by EEG signals: before deep learning became popular, researchers were mainly searching for the most representative features of EEG signals in epileptic patients; In recent years, as computing power has improved, researchers have focused on finding the optimal representations that contain more information about EEG signals as input to the neural network. However, so far, no study has shown that there is a better representation than the original EEG signal, which has inspired us to develop methods for end-to-end seizure prediction.

Since EEG signals carry information in multiple temporal and spatial scales, it is not easy to choose a particular scale for EEG signal analysis. Hence, the introduction of a multi-scale method is essential for epileptic seizure prediction. Combined with our experimental results, the multi-scale methods can capture more valuable knowledge than the single-scale method.

Furthermore, the dilated convolution is a very effective tool for EEG signal analysis. Under the same number of parameters, the dilated convolution can significantly expand the receptive field. Also, combined with an efficient feature fusion method, the dilated convolution can systematically aggregate global and local features. With limited model parameters and considering a large receptive field, dilated convolution is feasible and effective.

V. Conclusion

In this study, we develop an end-to-end framework by using a multi-scale convolutional neural network with dilated convolutions for patient-specific seizure prediction. The proposed framework is motivated by the properties of EEG signals and neurological findings. Our model is performed on 16 epilepsy patients from the CHB-MIT scalp EEG database. After the leave-one-out validation measurement, we achieve an average sensitivity of 93.3%, an average false prediction rate of 0.007 per hour, and an average proportion of time-in-warning of 6.3%. Among the 16 patients, the sensitivity of 10 patients to seizure prediction was 100%, and 9 of them without false alarm. In contrast to the state-of-the-art methods using the same CHB-MIT scalp EEG database, our proposed method achieves the highest Sens, lowest FPR. This study provided a promising solution for EEG-based seizure prediction.

Funding Statement

This work was supported in part by the National Natural Science Foundation of China under Grant 61922075 and Grant 61701158 and in part by the USTC Research Funds of the Double First-Class Initiative under Grant YD2100002004 and Grant KY2100000123.