Native American gene flow into Polynesia predating Easter Island settlement

Summary

The possibility of voyaging contact between prehistoric Polynesians and Native Americans has long intrigued researchers. Proponents have pointed to New World crops, such as the sweet potato and bottle gourd, found in the Polynesian archaeological record, but nowhere else outside the pre-Columbian Americas^1–6, while critics have argued that these botanical dispersals need not have been human mediated⁷. The Norwegian explorer Thor Heyerdahl controversially suggested that prehistoric South Americans played an important role in the settlement of east Polynesia and particularly Easter Island (Rapa Nui)². Several limited molecular genetic studies have reached opposing conclusions, and the possibility continues to be as hotly contested today as it was when first suggested^8–12. Here, for the first time, we analyze genome-wide variation in individuals from islands spanning Polynesia for signs of Native American admixture, analyzing 807 individuals from 17 island populations and 15 Pacific coast Native American groups. We find conclusive evidence for prehistoric contact of Polynesians with Native Americans (ca. 1200 CE) contemporaneous with the settlement of remote Oceania^13–15. Our analyses suggest strongly that a single contact event occurred in eastern Polynesia, prior to the settlement of Easter Island (Rapa Nui), between Polynesians and a Native American group most closely related to the indigenous inhabitants of present-day Colombia.

A perennial question in Oceanian history concerns the possibility of prehistoric contacts between Polynesians and Native Americans. Previous genetic researchers investigating this question have focused on Easter Island (Rapa Nui). As the closest inhabited Polynesian island to the Americas, and the Polynesian island with the most elaborate megalithic culture¹⁶, Rapa Nui has been considered a likely locus for contact. High resolution analyses of HLA alleles have revealed a Native American component in modern individuals with self-identified Rapanui ancestry^8,9. However, in the only two genome-wide studies of Rapanui variation, one of eight modern individuals¹⁰, and one of five skeletal remains (three from pre-European contact era and two from post-European contact)¹¹, a Native American component was found in all samples of the former, but none of the latter. As a consequence, these studies reached opposing conclusions about pre-European contact between Polynesians on Rapa Nui and Native Americans^10,11. To date no genome-wide DNA studies have considered the possibility of pre-European Native American contact on other Polynesian islands. We have investigated both of these questions via high density genome-wide analyses of a large dataset of 166 Rapanui and 188 additional individuals from islands spanning the Pacific (Figure 1a and Supplementary Data Tables 1–2).

FIGURE 1.

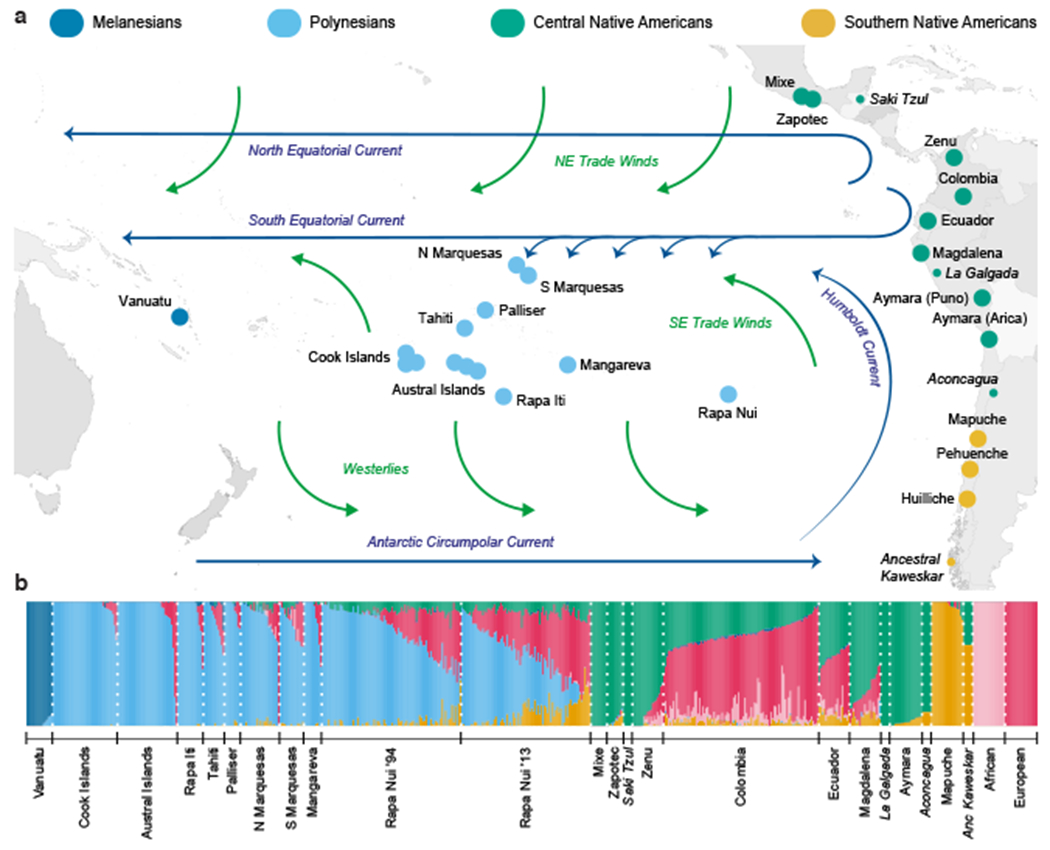
Sampled populations with unsupervised (iterative) ADMIXTURE analysis. (a) Map showing the number of individuals from each sampled population (one dot per population). (b) K=6 clustering analysis of Pacific islanders and references using the ADMIXTURE method¹⁷. The references include populations from: Europe (UK and Spain) and Africa (Yoruba)¹⁸, the Americas (Mapuche, including Pehuenche and Huilliche, from central and south Chile¹⁹, Aymara from southern Peru and northern Chile, northern Peruvians from Magdalena de Cao, Zenu from Colombia, and Zapotec and Mixe from southern Mexico²⁰), and at far-left Melanesians from Vanuatu (see Supplementary Figure 5). Each individual is represented as a narrow column, coloured to show the proportion of each ancestry cluster in that individual. Modern Colombians and Ecuadorians²¹ as well as four ancient (pre-European contact) individuals (italics, wide columns), spaced along the coast (small dots), were included to further illustrate the Native American component^19,22,23, but were not used as references due to their lower marker density. The key (at top) represents our interpretation of the six coloured clusters obtained in this unsupervised clustering analysis. (See Supplementary Data Table 5 for the distinction between early modern and ancient Oceanian cluster nomenclature.)

Multiple admixture events in Polynesia

We first performed a global ancestry analysis of our Polynesian and coastal Native American samples together with continental reference populations using ADMIXTURE (Fig. 1b, Supplementary Figs 1–8, Supplementary Data Table 3–5, see Supplementary Discussion)¹⁷ and principal component analysis (Supplementary Figure 9). We followed these variant frequency based analyses with an independent, sequence matching based analysis (local ancestry inference²⁴) in order to identify precise genomic regions of Polynesian, Native American, European, and African origin in each individual for use in later ancestry-specific analyses (Fig 3a and Supplementary Data Table 6).

FIGURE 3.

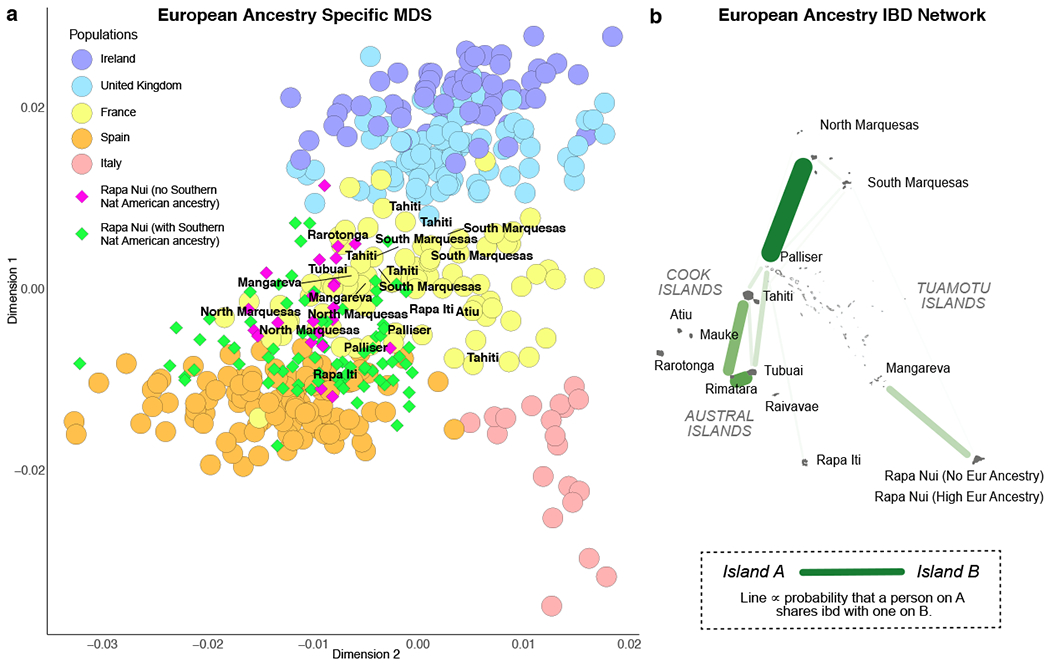
Analysis of European ancestry in Pacific islanders. (a) Our new ancestry-specific MDS applied to the European ancestry of each admixed sample from the Pacific islands together with European reference individuals from the POPRES dataset²⁹ shows French Polynesian islanders (text labels) clustering with French individuals. Rapanui (diamonds) cluster with Spain or France, depending on whether (green) or not (violet) they also have southern Native American (Chilean) ancestry. The number of samples from each country are given in Supplementary Data Table 3. (b) Identity-by-descent sharing of European ancestry segments in Polynesia is strongest (darker and thicker lines) between island clusters having the same European colonial backgrounds. The islands’ sample sizes are given in Supplementary Data Table 1.

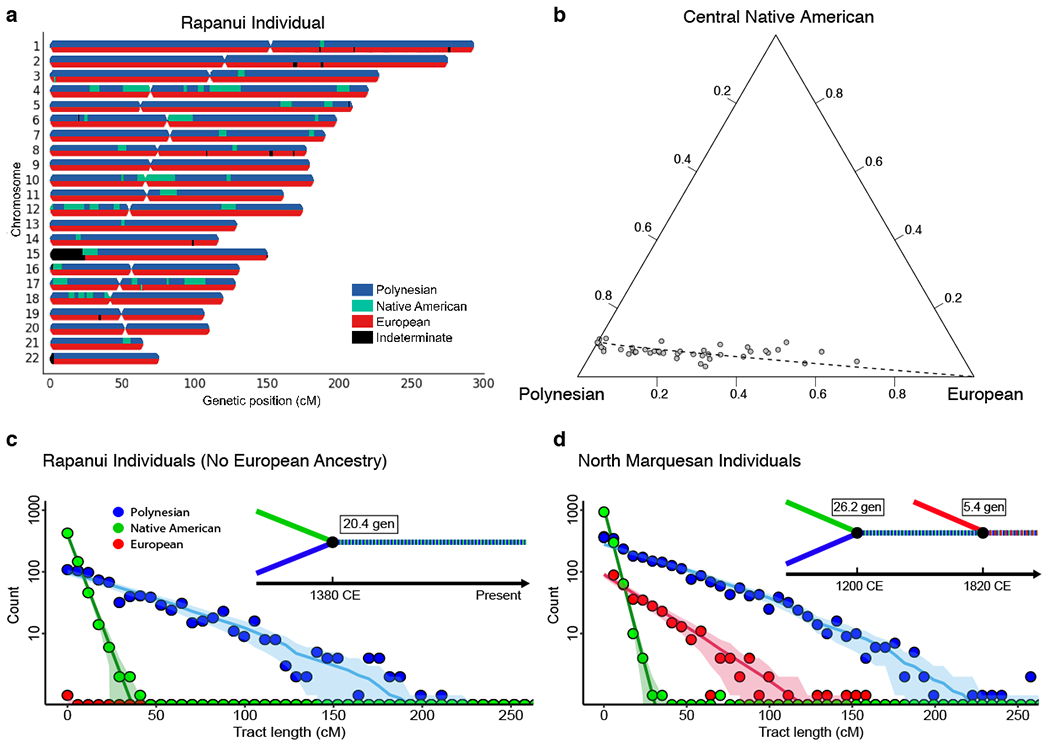
In all of these ancestry analyses, the Pacific island populations are characterized by a large Polynesian component, but with many islanders also having a European component from colonial admixture. Remarkably, in both of these independent analyses, as well as in F4 and D-statistic analyses (p<0.001), we also detect admixture in eastern Polynesia from Native Americans, even when using pre-European contact Native American references (Supplementary Figs 10–11). Looking at the ADMIXTURE plot, in the easternmost Polynesian islands (Palliser, Marquesas, Mangareva, and Rapa Nui), but on no other Polynesian islands, two Native American ancestry components can be seen. These components are characteristic of central (green) and southern (yellow) Native Americans (both modern and ancient). The southern Native American component, highest in the Mapuche and Pehuenche native peoples of Chile, increases in present-day Rapanui individuals in proportion to their European (red) ancestry component (Fig. 1b, Supplementary Figure 12, and Supplementary Data Table 7–8). This is consistent with that Native American component arriving onto Rapa Nui together with a Spanish European component via immigration of admixed Chileans following Chile’s annexation of the island. In contrast, the central Native American component, characteristic of indigenous Mexicans (Mixe and Zapotec) and indigenous Colombians (Zenu), is associated on Rapa Nui only with the Polynesian component, not with the European or southern Native American components, according to those components’ log-ratio variances (Fig. 2 and Supplementary Data Tables 7–10). This suggests that the central Native American component arrived onto Rapa Nui independently from the European component. Furthermore, unlike the southern Native American component (Chilean), the central Native American component varies little between Rapanui individuals, indicating that it stems from an older admixture event^25,26. Indeed, the Native American DNA segments in Rapanui have an aggregate length distribution that indicates initial contact several centuries before Europeans entered the Pacific (Fig. 2c). Intriguingly, the central Native American component (green) is found in the other remote eastern Polynesian islands (Palliser, Marquesas, Mangareva) and has a similarly early date (Fig. 2d).

FIGURE 2.

Relationship between Polynesian, Native American, and European ancestries. (a) Random-forest based local ancestry inference of a Rapanui individual showing small (old) Native American ancestry tracts embedded in Polynesian ancestry tracts. The ancestry of each haploid genome is coloured (top and bottom for each homologous chromosome pair); the autosome pairs are numbered along the vertical axis. (b) Ternary plot of ADMIXTURE ancestry fractions in Rapanui individuals having Polynesian, European, and central Native American, but no other, ancestries (each point corresponds to an individual). The first principal component in the centered log-ratio transform space²⁷ is projected onto the figure as a dashed curve. The ancestries’ log-ratio variances are discussed in Supplementary Data Tables 7–10. (c-d) Length distribution analyses for ancestry tracts in the six Rapanui individuals having no European ancestry (c) and in North Marquesan individuals (d). Plotted points show the aggregate tract length counts, lines show the maximum likelihood best fit tract length distributions, and shading shows the one standard deviation confidence intervals assuming Gaussian noise. The best fit admixture chronology is plotted above the timeline as a line-history with each colour representing an ancestry as indicated in the key (see a).

When we investigate the European ancestry in Polynesians, we see correspondences with the European nations that colonized each island. For example, the European component in French Polynesians clusters with French references in our new ancestry-specific MDS (Fig. 3a). Those Rapanui with southern Native American ancestry in the ADMIXTURE analysis are shifted towards the Spanish references in this European-specific MDS, consistent with those two ancestries arriving together via immigration of admixed Chileans. The remaining Rapanui having European ancestry, but no southern Native American ancestry, cluster largely with French references, which is consistent with the French origin of the first European residents on Rapa Nui²⁸. We also analyze long, shared DNA segments (>7 cM) that are inherited by related individuals and are termed identical by descent (IBD). Analyzing only genomic regions of European ancestry, the IBD relationship network mirrors European settlement patterns, with many French Polynesian islands forming one connected component, separate from Rapa Nui forms a separate component (Fig. 3b and Supplementary Data Table 11). Rapa Nui’s single European connection to Mangareva may reflect the transfer of French Catholic missionaries from Rapa Nui to Mangareva in 1871²⁸.

Native American ancestry in Polynesia

The Native American ancestry in eastern Polynesians shows a very different pattern of inter-island IBD sharing, indicating a different history of Native American contact (Fig. 4a, Supplementary Fig. 13 and Supplementary Data Table 12). To characterize the origin of this ancestry in Polynesia more precisely, we applied a novel ancestry-specific PCA to the Native American component (see Online Methods, Supplementary Figs 14–15). The first principal component is found to order the Native American references along a north-south axis, coinciding roughly with the Pacific coast of the Americas (Supplementary Fig. 14). We plot the density of the Native American references along this first principal component axis along with the location of the aggregate Native American components for each of the eastern Polynesian islands possessing such ancestry (Fig. 4b). Consistent with our ADMIXTURE analysis, which showed a central Native American component in Pacific islanders, in this analysis the Pacific islanders’ Native American ancestries all fall within, or beside, the Zenu, an indigenous Colombian population. The localization of the Native American component to Colombia-Ecuador is shown clearly by our new, lower noise, ancestry-specific MDS analysis, as well as PCA, and is consistent with the less sensitive traditional Procrustes analysis and outgroup-F3 statistic (Supplementary Figs 16–22). The only exception are the Rapanui individuals with high European ancestry. As expected, their Native American component, which likely came together with their European component via immigration of admixed Chileans into Rapa Nui, is located squarely within the Pehuenche and Mapuche native populations of central Chile (Fig. 4b and Supplementary Figs 14, 16, 18–22). The Native American ancestry component in Rapanui individuals with no European ancestry, in contrast, clusters with the Colombian Zenu, just as with the other eastern islands.

FIGURE 4.

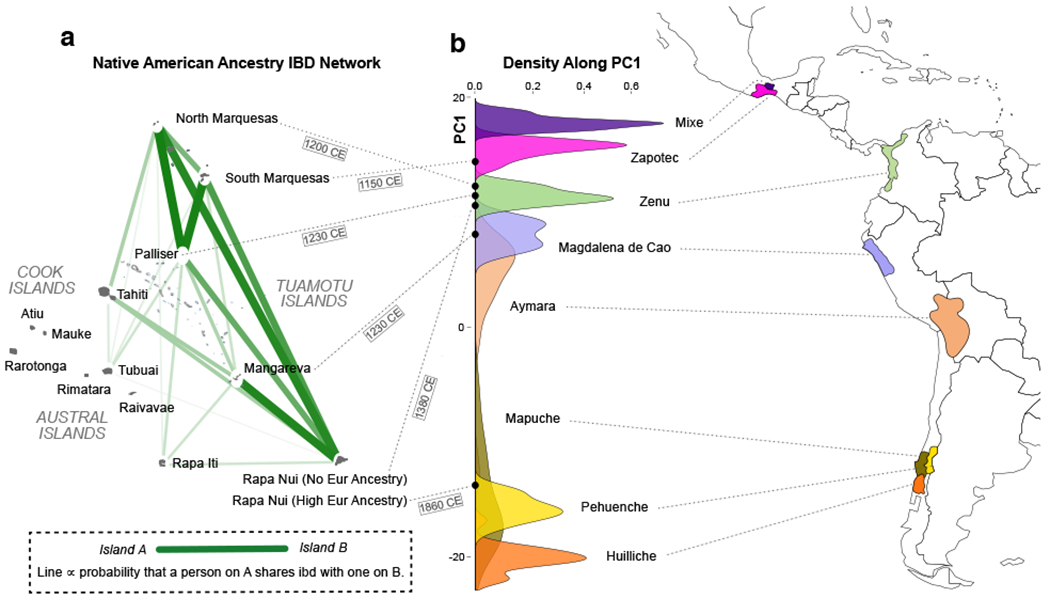
Origin and spread of early Native American ancestry in Polynesia. (a) Results of a Native American specific IBD analysis reflect the common ancestry and origin of the Native American component in easternmost Polynesia. (b) Our new ancestry-specific principal component analysis (center) separates Pacific rim Native American references along a north-south axis, as shown in a kernel density plot of the numbers of individuals from select reference populations along the first principal component axis. (See Supplementary Figs 14 and 18 for the full two-dimensional plot.) Colours indicate the reference populations’ locations in the Americas (right). The locations of the aggregate Native American specific components for each Pacific island are also plotted (black dots connected by dashed lines to their source island in (a)). The maximum likelihood date for the Native American introgression event in each island population, as determined by a Tracts analysis (Supplementary Fig. 23), is displayed under the corresponding dashed line. The numbers of samples used from each island and each American population are given in Supplementary Data Table 1.

Apart from the Chilean annexation of Rapa Nui in 1888 and sporadic interactions with ships’ crews, the only recorded events potentially connecting Pacific islanders with Native American ancestry are the Peruvian slave raids of 1862-1863. During this year, thousands of Pacific islanders were kidnapped and taken to Peru as forced laborers, including 1407 Rapanui³⁰. Following an international outcry, a few repatriation voyages were organized, but smallpox outbreaks onboard meant only a handful of passengers made it back to Polynesia alive. Only two of the islands in our dataset received any recorded returnees: Rapa Nui (15 repatriated) and Rapa Iti (9 captives from other islands resettled). With very few individuals, all self-identifying as islanders, returning to Polynesia, and with their captivity in Peru lasting only a few months, it is unlikely that this episode resulted in any introgression of Native American ancestry into Polynesia. However, such explanations have been advanced^11,31. In any case, the Native American component that we observe in the easternmost islanders, including on distant islands untouched by returnee voyages, derives from an indigenous American population lying to the north of both of our Peruvian Native American references, viz. the southern Peruvian Aymara and the northern Peruvian Magdalena (Fig. 4b and Supplementary Figs 16, 18).

Our localization of the Native American ancestry found in Polynesia is consistent with several linguistic, historical, and geographic observations that support an origin in northern South America. Although superficial similarities between the Pacific islands’ monolithic statues (found only in the remote eastern Polynesian islands) and those of the pre-Columbian site of San Augustín, Colombia have long been noted², stronger evidence has come via the Polynesian word for the sweet potato ‘kumala.’ This word has been linked to names for the food in northern South America, where it originated^2,3,32. The coastal languages that use these related names lie to the north of Peru, for example ‘cumal’ used by the Cañari of Ecuador³³, whereas the Peruvian languages that use such names are Andean and located far from the coast. It is to the north of Peru that the Pacific coast changes from desert to forests suitable for boat construction, and it is from Pacific Ecuador and Colombia that Native American voyagers are believed to have embarked for trade with Mesoamerica in large ocean-going sailing rafts made of balsa wood during the period 600 CE – 1200 CE^34–37. Wind and current simulations from the Pacific coast of the Americas have demonstrated that drift voyages departing from Ecuador and Colombia are the most likely to reach Polynesia, and they arrive with the highest probability in the South Marquesas islands, followed by the Tuamotu Archipelago⁴. Both of these archipelagos lie at the heart of the region of islands where we have found a Colombian Native American component. The trade winds and the south equatorial current move east to west at these latitudes, funneling boaters from northern South America to the archipelagos (Fig. 1a)³⁴. (In Thor Heryerdahl’s famous drift voyage from Peru to Polynesia, his Kon-Tiki raft had to be towed 80 miles offshore from Peru, because the southern current along the Peruvian coast was so unfavorable; once in the trans-Pacific currents the Kon-Tiki raft landed in the Tuamotu Archipelago.) For the same reason, these archipelagos would be the most likely origin for Polynesians discovering the Americas using their characteristic upwind exploration^38,39.

Dating Native American–Polynesia contact

To determine when the Native American component was introduced into each of the affected Polynesian populations in our dataset (Nuku Hiva in the North Marquesas, Fatu Hiva in the South Marquesas, Palliser in the Tuamotu Archipelago, Mangareva, and Rapa Nui), we modeled the length distribution of islanders’ Native American, European, and Polynesian ancestry segments using the Tracts method of Gravel et al. (Supplementary Fig. 23–24)⁴⁰. For all island populations, with one expected exception discussed below, we find that the model with the highest likelihood involves an initial Polynesian – Native American admixture event, followed centuries later by European introgression (Supplementary Data Table 13). Those later estimated European admixture dates (North Marquesas 1820 CE, South Marquesas 1830 CE, Mangareva 1750 CE, and Palliser 1790 CE) fall within the period of European colonization of Polynesia. In contrast, the dates estimated for Native American – Polynesian admixture on the islands are much earlier, and they are similar across the different islands (Mangareva 1230 CE, Palliser 1230 CE, North Marquesas 1200 CE, South Marquesas 1150 CE).

The only exception to these consistently early dates is on Rapa Nui itself, where Rapanui individuals with no European (colonial) ancestry have a slightly later estimated Native American introgression date (1380 CE; Supplementary Fig. 23a). However, this inferred date may be shifted later due to more recent Native American introgression from Chile, as already discussed. Indeed, Rapanui individuals that have high European and Native American ancestry (Fig. 4b), show Native American introgression predominantly during the colonial period (best fit, 1720 CE). According to the best fitting model, this represents Native American introgression into European ancestry first, likely occuring in Chile, followed later by addition of Polynesian ancestry (best fit, 1860 CE), likely when admixed Chileans began immigrating to Rapa Nui (Fig 6b). That latter date (1860 CE) is slightly before the annexation of Rapa Nui by Chile (1888 CE); however, by this time 12 Chileans (out of approximately 100 total inhabitants) were already recorded living on Rapa Nui⁴¹. Indeed, because of its relation to modern Chile, we find that Rapa Nui is one of the most complicated places to study and date the prehistoric Native American contact in eastern Polynesia (see Supplementary Fig. 24).

To confirm our Tracts dating of the early Native American introgression in Polynesia, we used an alternative, linkage disequilibrium (LD) based, dating method (Supplementary Fig. 23g and Supplementary Data Table 14)⁴². Unlike Tracts, this method (ALDER) does not rely on phasing or local ancestry inference, instead fitting the exponential decay of LD within an admixed target population directly using two reference populations as proxies for the ancestral sources⁴³. We used unadmixed Native Americans from Peru and indigenous Austronesians from Taiwan as references, and islanders with only Native American and Polynesian admixture (no European ancestry) as targets (6 Rapanui, 4 Mangareva, 2 Palliser, 1 North Marquesas). For these pooled individuals, we obtained an estimated admixture date of 1234 CE +/−90 years (Supplementary Fig. 23g). We note that all of our Tracts date estimates are contained within the confidence interval of this Alder estimate, except for the aforementioned special case of the Rapanui with recent Chilean ancestry.

Discussion

The Native American component within each of these widely separated remote eastern Polynesian islands has a similar introgression date, a common source in the indigenous peoples of Colombia, and a dense shared IBD network indicating shared ancestors. Each of these results is most parsimoniously explained by a single prehistoric contact event between eastern Polynesians and Native Americans. Although the island contacted is not yet clear, and perhaps is not present in our current dataset, it is likely that the contact occurred during the Polynesians’ original period of discovery and settlement of remote eastern Polynesia. Descendants of the initial contact likely transmitted their dual ancestry to new islands upon settling them; inter-island trade contact may also have played a role. Thus, the prehistoric Native American component on Rapa Nui, upon which so much research has focused^9–11, likely originates from a contact event not on Rapa Nui, but somewhere upstream in the Polynesian settlement process. This would explain a human-mediated spread of the sweet potato throughout Polynesia, if, as some have speculated, the Polynesian settlement of Rapa Nui involved no return voyaging or trade links^39,44–46.

Our earliest estimated date of contact is 1150 CE for Fatu Hiva, South Marquesas. This is close to the date estimated by radiocarbon dating for settlement of that island group¹³, raising the intriguing possibility that upon their arrival Polynesian settlers encountered a small, already established, Native American population. It was on the island of Fatu Hiva, the easternmost island in equatorial Polynesia, that Thor Heyerdahl hypothesized that Native Americans and Polynesians might have contacted one another, based on islanders’ legends stating that their forefathers had come from the east⁴⁷. The Marquesas lie at the latitude of Ecuador, and wind and current based simulations indicate that they are the most likely islands reached from South America via the strong east-to-west currents and winds at these equatorial latitudes^4,48,49.

We cannot discount an alternative explanation: a group of Polynesians voyaged to northern South American and returned⁵⁰ together with some Native Americans, or with Native American admixture, as speculated by Malaspinas et al¹⁰. We have dated the contact event to the time when Polynesian explorers were, according to some studies, making their longest range voyages (the century surrounding 1200 CE), a time when these studies suggest the Polynesian settlers discovered all remaining island groups in the Pacific, from Hawaii to New Zealand to Rapa Nui^13,46,50. The Tuamotu Archipelago, which lies at the center of the Polynesian islands in which we found a Native American component, is known to have been a Polynesian voyaging hub, and according to simulations, it is the second most likely location reached when voyaging from South America⁴. Further population genetics collaborations with these genetically understudied island populations are needed to resolve these alternative hypotheses.

In conclusion, we find strong genetic evidence for pre-Columbian human trans-Pacific voyaging contact (at the turn of the 12^th century), contemporaneous with the Polynesian voyages of discovery in the remote eastern Pacific^13,14. Previous studies on putative Polynesian - Native American contact have focused on Rapa Nui, whose modern genetic history has been influenced by a recent Chilean admixture event, and have missed the possibility, which we show to be more likely, that prehistoric contact occurred prior to the settlement of Rapa Nui. We show that evidence for early Native American contact is found on widely separated islands across easternmost Polynesia, including islands not influenced by more recent Native American contact events. Our results demonstrate the usefulness of genetic studies on modern populations, which allow for large sample sizes for unraveling complex prehistoric questions, and demonstrate the importance of combining anthropological, mathematical, and biological approaches to answer these questions.

Methods

Ethical approval

Written informed consent was obtained from all participants and research/ethics approval and permits were obtained from the following institutions: Stanford University Institutional Review Board (IRB approval No. 20839), Oxford University Tropical Research Ethics Committee (reference No. 537-14), and Ethical Scientific Committee at the Pontificia Universidad Católica de Chile (reference No. 1971092), conducted in accordance with the guidelines of the National Commission on Science and Technology (CONICYT-Chile).

Sample Collection and Genotyping

This work combines publicly available genotype data and newly generated SNP array data from samples collected over different time periods by the participating institutions (Supplementary Data Tables 1–3). Sampled populations and genotyping platforms are detailed in Supplementary Data Table 1. A total of 25 populations were genotyped at the University of California, San Francisco (UCSF) using Affymetrix (Mountain View, CA) Axiom LAT-1 arrays. Another 7 populations were genotyped using Illumina (San Diego, CA) Multi-Ethnic Genotyping Array (MEGA) or Illumina 610-Quad arrays (see Supplementary Data Table 1). Genotype calling was performed following default parameters using Affymetrix’s Genotyping Console software and Illumina’s GenomeStudio application, respectively. The average call rate was 98.5% for all newly genotyped samples. Before filtering and merging, the total number of SNPs called on the Axiom LAT-1 and Illumina MEGA platforms were 813,036 and 1,738,289 respectively. To remove genotyping errors, all samples genotyped on the same array were filtered together using Plink 1.9, eliminating the following: individuals missing more than 1% of genotypes sites (mind .01), SNPs missing in more than 1% of individuals (geno .01), and SNPs out of Hardy-Weinberg equilibrium with a p-value below 10e-110.

Data Preparation

The UCSC tool liftover was used to bring all data onto the same genome build, GRCh37 (hg19)⁵¹. When merging data from different genotyping arrays, strand flips were detected and corrected with ambiguous SNPs (SNPs whose strand definition could not be definitively matched between arrays) removed. This typically resulted in a loss of fewer than 10% of SNPs. Hence, the resulting SNP density after merging with different reference panels varied across working datasets for downstream analyses as detailed throughout the methods below. Genetic positions were assigned using the interpolated recombination map generated by the 1000 Genomes project¹⁸. Given the depth and quality heterogeneity of the ancient samples, we called pseudo-haploid genotypes for all ancient individuals to minimize potential bias derived from calling diploid genotypes²³. For each ancient genome, we discarded reads with mapping quality below 30 and bases with quality below 20.

Global Ancestry Analysis

Principal Component Analysis

Principal component analysis (PCA) was performed using EIGENSOFT 7.2.1⁵² by merging the genotyped Polynesian individuals together with reference panels from Africa, Europe, Taiwan, Melanesia, and the Americas (Supplementary Fig. 9). For African and European references, we used genotypes from 1000 Genomes individuals: 60 Yoruba (YRI), 30 British (GBR), and 30 Spanish (IBS)¹⁸. For Melanesian references we used 16 individuals from Vanuatu, for Taiwan we used 20 individuals from the Atayal and Paiwan indigenous groups, and for the Americas we used 60 individuals having only Native American ancestry (as indicated by our ADMIXTURE analysis, Fig. 1b, see below) originating from Puno, Peru (Supplementary Data Table 1). Merging of the sequence and filtered genotype data (689,899 SNPs) was done with PLINK 1.9⁵³ as was LD-pruning (--indep-pairwise 50 10 .5), which was used to greedily remove successive variants with a squared correlation greater than 0.5 in 50 SNP sliding windows with 10 SNP steps. Plotting was performed in R 3.5.2 using the ggplot2 3.1.0 package⁵⁴.

Unsupervised ADMIXTURE

To explore Native American substructure in our Polynesian individuals, we merged the Pacific island individuals above together with European (10 UK, 10 Spain), African (20 Yoruba), and Pacific coastal Native American reference populations that included Mapuche (6 Pehuenche, 14 Huilliche), Aymara (10 Puno, 10 Arica), Magdalena de Cao (19), Zenu (19), and Mexico (10 Mixe, 10 Zapotec). Samples from the two latter locations were genotyped on a second array (see Supplementary Data Tables 1,3), so the merged dataset of 489 individuals had an overlap of 134,281 SNPs. ADMIXTURE 1.3.0 was run on this dataset using unsupervised mode (Supplementary Fig. 1–2)¹⁷. According to the elbow⁵⁵ in the cross-validation plot (Supplementary Fig. 2), a good clustering is found around K=7. Because our dataset is heavily imbalanced, with the bottlenecked Rapa Nui samples (n=166) comprising nearly as much of our Pacific island dataset (47%) as all other islands combined, a cluster corresponding to Rapa Nui related Polynesian ancestry emerges (see Supplementary Fig. 4). This issue was addressed using the iterative ADMXITURE approach below.

Iterative unsupervised ADMIXTURE

To avoid the spurious clustering^56,57 that can be introduced by imbalanced sampling, such as in our Pacific island dataset, which is 47% Rapanui (described above, see Supplementary Figures 1–2 and Supplementary Discussion), without having to down-sample our Rapanui population, we employed a novel iterative unsupervised ADMIXTURE approach. Previous studies have addressed such spurious clustering, if properly recognized, by employing supervised or semi-supervised (projection) approaches⁵⁸ or by simple down-sampling of the over represented populations. We found none of those approaches to be fully satisfactory. Supervised learning requires a researcher to subjectively define clusters a priori, which does not allow ancestry patterns to emerge naturally from the data. A semi-supervised approach—for example, running unsupervised ADMIXTURE on an evenly sampled dataset, followed by projecting the remaining samples onto the clusters found—avoids these subjective biases, but generates noise in the projected samples. This noise manifests as small spurious proportions of all ancestries found in the projected samples, and stems from the fact that variants in the projected individuals were not able to inform the original clustering. We solve both of these problems at once, albeit in a computationally intensive fashion, using an iterative approach that allows every sample to participate in a fully unsupervised ADMIXTURE run, while ensuring that no one run suffers from a highly imbalanced dataset. In particular, we choose evenly sampled reference numbers as is standard for a projection-type analysis (with additional representation from Native American populations, due to their admixture with other ancestries). These were selected according to the original unsupervised ADMIXTURE (Supplementary Fig. 1) components: African, 20 Yoruba; European, 10 Spanish and 10 British; central Native American, 10 Mixe, 10 Zapotec, 19 Zenu, 20 Aymara, 19 Magdalena; southern Native American, 20 Mapuche (6 Huilliche, 14 Pehuenche); Polynesian, 2 individuals from each island; and Melanesian, 16 Vanuatuans (Supplementary Figure 5). Within the reference populations, those samples without recent admixture (typically less than 10%) according to our autosomal haplotype based local ancestry analyses (see below) were chosen. This further eliminated imbalances in the ancestry cluster sizes represented by the references. We then iteratively ran the references together with each of the remaining Polynesian samples in a series of separate fully unsupervised ADMIXTURE analyses until all samples had been analyzed. Each individual run was a standard down-sampled unsupervised ADMIXTURE analysis. By repeating many such runs, all of the overrepresented Rapanui samples could be analyzed, providing sufficient samples for our later compositional ancestry analyses (below). The results for all individuals were then plotted using ggplot2 3.1.0 and Pophelper 2.2.9⁵⁹.

Because our admixed Colombian and Ecuadorian references were genotyped on a third array (Illumina 610-Quad), different from both of the two merged above (Affymetrix Axiom LAT-1 and Illumina MEGA), combining them with our panel would have resulted in further loss of common SNP markers giving an even lower resolution for rare ancestry components. Thus, when these samples were run iteratively (separately), they were run in their own lower SNP-density (32,872 SNPs) three-way array merge with the references. Due to the lower density of SNPs, slightly more noise is evident in the ancestry assignments of these samples as compared to the higher density, neighboring American samples (see Fig. 1b). The same strategy was employed for each of our ancient Native American samples. Each ancient sample was merged separately with the references to maximize the SNP overlap (48,666 SNPs for the La Galgada sample, 114,927 SNPs for the Aconcagua sample, 25,429 SNPs for the best Saki Tzul sample, and 129,612 SNPs for the best Ancestral Kaweskar sample), then unsupervised ADMIXTURE was run on each merge. Because the ancient sample genotypes were called pseudo-haploid, the reference panel individuals were also treated as pseudo-haploid for consistency in each of these ancient sample iterative runs.

Marker Frequency Based Statistics

To further confirm the existence of Native American ancestry in Polynesia we conducted genome-wide admixture F4 and D-statistic tests across 689,899 SNPs. For the target Polynesians we pooled individuals from the islands having a greater than 1% average Native American component in our ADMIXTURE analysis (Supplementary Data Table 4), selecting all individuals without later European or African admixture, that is, with no more than .005 European and/or African ancestry: Mangareva (3), North Marquesas (1), and Rapanui (6). The F4 statistics were computed using comparison populations from Europe (UK and Spain), Africa (Yoruba), China, and Vietnam from 1000 Genomes¹⁸, along with Native Americans from Peru (Aymara) and Polynesians from Mauke, all of which had shown no admixture in our previous analyses. With the program fourpop⁶⁰, we computed F4 statistics of the form F4(target Polynesians, Mauke; X, Y), where X and Y represent all possible combinations of the other populations (Supplementary Figure 10). Standard errors were estimated by the block-jackknife with a block size of 500. As an additional verification of significance, we ran 100 coalescent simulations via fastsimcoal using the method of Meyer et. al⁶¹ to estimate the proportion of simulated jackknife blocks larger than those observed for F4(target Polynesians, Mauke; Aymara, Yoruba) (Supplementary Figure 10). None were observed. To further test whether the target Polynesian individuals carry Native American ancestry, we computed D-statistics⁴³ of the form D(Mauke, target Polynesians; H₃, Yoruba). In this case, H₃ is a set of reference populations and individuals that include pre-contact ancient Native American genomes (Supplementary Data Tables 1,3–4). We again estimated standard errors through a block-jackknife procedure (Supplementary Figure 11).

Compositional Analyses of Ancestry Proportions in Rapanui

Thanks to the large sample size of Rapanui individuals (n=166), we are able to conduct statistical analyses of this population’s ancestry proportions, and thus characterize the associations between the different ancestries. We consider first all four of the ancestry proportions identified by our iterative ADMXITURE analysis in the Rapanui: central Native American, southern Native American, European, and Polynesian. (We neglect the African component in the Rapanui, as it is present in only 12 individuals with a proportion above .005, and so these dozen individuals are simply excluded.)

Because these ancestry components (p_i for each ancestry i) are constrained to live on a simplex (that is, Σ_ip_i=1; termed compositional data), computing raw covariances and correlations between ancestry components is not informative. (As one ancestry proportion rises, the others must fall, leading to intrinsic negative covariances and correlations.) Thus, we rely on statistical methods developed for compositional data²⁷ to characterize associations between ancestry components. In particular, we compute the log ratio variance for each pair of ancestries i and j, τ_ij=Var[ln(p_i/p_j)], which together completely characterize the covariance structure of the composition²⁷ (see Supplementary Data Table 7). Smaller values of τ_ij indicate that one component does not vary much relative to the other, and larger values indicate that the ancestry components do vary freely relative to one another. We also compute the compositional analogue to correlation, ρ_ij=exp(−τ_ij²/2) (Supplementary Data Table 8)⁶². To visualize these associations, we plot the ancestry composition of each individual inside the four-component simplex, viz. a tetrahedron (Supplementary Figure 12).

We next analyze the subset of the Rapanui without a southern Native American (Chilean) component; that is, the 64 Rapanui with less than 1% southern Native American in the K = 6 iterative ADMIXTURE analysis (Fig. 1b). These individuals lie on the triangular simplex (Fig. 2b) that forms the base of the tetrahedral simplex above. Within this subset of individuals, we also compute τ_ij and ρ_ij for each of their ancestry pairings i, j (Supplementary Data Tables 9–10). To confirm the observed association between the central Native American component and the Polynesian component, we also perform a compositional (log-contrast) principal component analysis on these individuals. Since the points lie on a two-dimensional compositional simplex within ${\mathcal{R}}^3$, we map them to a 2-dimensional linear subspace of ${\mathcal{R}}^3$ (the subspace orthogonal to the vector [1,1,1]) using the centered log-ratio transform (clr)⁶². This isometry transforms each individual’s vector of ancestry components [p_i,p_j,p_k] by replacing each ancestry proportion with the log of that proportion divided by the geometric mean of all ancestry proportions, i.e. clr(p_i)=ln(p_i/(p_ip_jp_k)^1/3).

We then perform a standard singular value decomposition on the centered compositional vectors in this space to determine the principal components. Because we are now in a two-dimensional Euclidean subspace we find exactly two principal components: the first component (v₁) and the vector orthogonal to it (v₂) in this subspace, v₁ = [polynesian, european, native american]=[.411, .816, .405], and v₂ = [polynesian, european, native american] = [−.705, −.0037, .709], having corresponding singular values of σ₁ = 2.26 and σ₂ = 0.219 respectively. Thus, less than 1% of the variance in the clr-transformed space occurs along the second principal component σ₁²/(σ₁²+σ₂²) = 0.009 < 1 %. Since there is almost no variation along the second principal component, the projection of ancestries along this direction in clr-space is approximately constant, so [−.705, −.0037, .709]• ln(1 / (PEN)^1/3) [P, E, N] ≈ constant or equivalently P^−.705E^−.0037N^.709 ≈ constant, where P, E, and N are the Polynesian, European, and central Native American ancestry proportions in an individual, respectively. Exponentiating on both sides of the latter equation by (1/0.705)=1.42, we have constant≈ N^1.006E^−0.005/P≈N/P. In other words, the central Native American component (N) varies directly with the Polynesian component (P) in these Rapanui individuals, and both vary freely relative to the European component (E). Compositional analyses and plots were made in R using the Compositions 1.4.0 package⁶².

Local Ancestry Inference

References for local ancestry

For our Axiom LAT-1 array analyses (689,899 SNPs) we used a balanced set of references consisting of: African (60 Yoruban individuals), European (30 Spanish and 30 British individuals), Native American (60 unadmixed Native American Aymara individuals genotyped on the Axiom LAT-1 array), and Polynesian (60 individuals identified by ADMIXTURE, Fig. 1b, as having less than 1% non-Polynesian ancestry) (Supplementary Data Table 1,3). (Note that our local ancestry inference method, RFMix, can identify admixture in its references, if such admixture exists, through its expectation maximization iterations²⁴.) For our Illumina MEGA array analysis (896,557 SNPs), we used as reference those same European and African references together with 60 unadmixed Native American Aymara individuals genotyped on the MEGA Illumina array (Supplementary Data Table 3). For our Illumina 610-Quad array (620,901 SNPs) analyses, we used the Homburger et al. local ancestry results⁶³.

Phasing

Phasing was performed together on all samples using SHAPEITv2.837 with default parameter settings⁶⁴. Population phasing has been shown to be particularly effective in such highly related, small, founder populations⁶⁴, as are found on these remote Polynesian islands.

RFMix

The program RFMix v1.5.4 uses a conditional random field smoother to stitch together the results of random forest classifiers applied to successive windows of SNP markers to recognize local autosomal haplotype variant patterns (linked sequences of SNPs) characteristic of different ancestries²⁴ (Fig 3a). Methods that ignore SNPs’ relative positions and linkage (eg. F4 and D-statistics, ADMIXTURE, PCA) are blind to such characteristic sequence patterns. This is a semi-supervised learning approach that requires references from each ancestry of interest, as described in detail above. We ran RFMix with the recommended two expectation maximization (EM) iterations and a 2 millimorgan window size to identify genomic regions of Polynesian, European, African, and Native American ancestry in our Pacific island samples and to identify genomic regions of European, African, and Native American ancestry in our populations from the Pacific coast of the Americas. We chose these reference ancestries based on our unsupervised Admixture analyses (Supplementary Figures 1,5), which had indicated the presence of these continental ancestries in our samples.

Ancestry-Specific (AS) Analyses

To perform the ancestry-specific analyses below, all ancestries except the ancestry of interest are ‘masked’ within each sample by thresholding the posterior probabilities returned by RFMix at a 0.99 probability level for the ancestry of interest. In other words, all haploid markers along each individual’s genome that are inferred to come from a different ancestry than the one of interest are treated as missing. In addition, on Rapa Nui a high Native American ancestry population group is defined to be those Rapanui with greater than 40% of their genome in inferred Native American ancestry segments according to RFMix. This group also has much higher European ancestry than average for the island of Rapa Nui, since southern Native American ancestry and European ancestry are associated on the island (see above and Supplementary Data Table 7–8), and so this group is also referred to as ‘high European Rapa Nui’ in later analyses.

AS Principal component analysis (PCA)

The two masked haploid genomes (haplotypes) for each individual are combined to generate a genotype frequency vector with 0 representing no alternate allele seen at a marker, 0.5 representing one alternate allele and one reference allele seen, and 1 representing no reference allele seen. For markers at which both haploid genomes had missing data in a given individual, a missing value is recorded for that marker site. These genotype frequency vectors for each individual are assembled to create a masked ancestry-specific genotype frequency matrix X with N samples (rows) and p SNPs (columns). This masked matrix is then completed using the singular value decomposition (SVD), with cross-validation used to determine the optimal reconstruction dimensionality (Supplementary Figure 15 and 17), to produce a Y matrix⁶⁵. Some individuals (rows) have large numbers of masked markers, so to reduce noise in the PCA analysis we perform a weighted, rather than typical unweighted, PCA. The weights allow the principal components to be defined more heavily by the less masked, more precisely known, samples. Since the uncertainty of an estimated sample increases with the number of missing (masked) sites in that sample, we compensate by weighting each row (sample) proportional to the fraction of non-missing sites present in that row (sample). Thus, we complete the matrix using the singular value decomposition (SVD) of W^1/2Y_c, where Y_c = Y − 1/N1_N(1_N)^TW Y with Y the weight-centered, completed sample matrix, W the diagonal matrix of weights, and 1_N the N-element vector of ones. (Computing the SVD of W^1/2Y_c is equivalent to diagonalizing the Y_c^TWY_c matrix.) The diagonal elements of W are given by {w_i=f_i/∑_jf_i}_i=1.N with f_i the fraction of SNP sites present (not masked) in row i.

We apply this algorithm to the samples genotyped on the Affymetrix Axiom LAT-1 array (689,899 SNPs) and to the merge of samples genotyped on this array together with additional American Pacific coast references genotyped on the Illumina MEGA array (two-array intersection of 91,835 SNPs) (Supplementary Figure 14 and 16, respectively). In the first PCA, only individuals having at least 90,000 SNP markers in Native American tracts (unmasked SNPs) were plotted, since individuals with fewer SNPs suffer from greater noise (scatter) in their projections. For higher resolution (less noise), Native American genomic regions from all individuals on an island are also used to plot island-specific genotype frequency vectors. These genotype frequency vectors are formed by aggregating the Native American ancestry fragments from all individuals on the same island and calculating, for each marker, the ratio of the number of alternate alleles seen at that marker to the total number of unmasked alleles at that marker on that island. In the second PCA, which has far fewer SNPs from the outset, only island-specific genotype frequency vectors were plotted, except for the high Native American Rapa Nui, who each individually have sufficient numbers of Native American SNPs to be plotted separately without excessive noise.

AS Multidimensional scaling (MDS)

Ancestry-specific multidimensional scaling (MDS) makes use of the fact that distances can be computed between pairs of genotypes, even if some markers are missing (masked) in each individual, simply by normalizing by the number of markers present for comparison in each individual. This approach was first pursued by Browning et al.⁶⁶, who noticed that the resulting distance matrix may still contain missing elements; namely, when two samples have no non-missing ancestry segments in common. In this case, Browning et al. suggest completing each missing distance matrix entry using the average distance of that individual against all others (mean imputation). However, one can construct a better estimate by noting that distance matrices have a high degree of structure; in particular, their elements must obey the triangle inequality. This allows missing values to be estimated by finding all possible triangles formed by the two samples that have no overlap and a third sample with which both do overlap. The common missing leg is then taken to be the minimum, over all these triangles, of the sum of their two known legs⁶⁷. This triangulation allows the missing distance to be estimated from the known distances, rather than simply replacing it with a population wide mean, giving much more accurate estimates for individuals with large amounts of masked ancestry (as found in Pacific islanders in Native American ancestry-specific analyses). As an additional advantage, none of the inferred distances will violate the triangle inequality; this is not true for the method of Browning et al.

We implement this triangle-based algorithm to create an ancestry-specific approach to MDS that is accurate even for highly admixed samples. We use the average number of pairwise differences as a distance metric, since it is proportional to genetic drift⁶⁸.

We apply our ancestry-specific MDS method to the Native American ancestry-specific genotypes of Polynesian and American samples genotyped on Affymetrix Axiom LAT-1, Illumina MEGA, and Illumina 610-Quad (Supplementary Figure 14) and also to the European ancestry-specific genotypes of Polynesians genotyped on Affymetrix Axiom LAT-1 together with European samples from POPRES genotyped on the Affymetrix GeneChip 500K and European full genomes from the 1000 Genomes Project (see Supplementary Data Table 3 and Fig. 3a).

Procrustes

In order to confirm the findings of our new high-resolution ancestry-specific MDS and PCA methods described above, a traditional Procrustes analysis⁶⁹ was performed to combine two separate Native American ancestry-specific PCAs (ASPCAs) that were constructed by the older ASPCA method⁷⁰. The first ASPCA (Supplementary Figure 19) was constructed using American reference populations genotyped on Illumina MEGA combined with American reference populations and Polynesian populations genotyped on Axiom LAT-1 (a 91,835 SNP two-array intersection). The second ASPCA (Supplementary Fig. 20) was constructed using American reference populations genotyped on Axiom LAT-1, Illumina MEGA, and Illumina 610-Quad (a 28,653 SNP three-array intersection). The local ancestry inference used for the masking of non-Native American ancestries for these ASPCAs was performed using the full density SNP set of each of the three arrays, that is, before intersection (see local ancestry methods). The initial coordinates of the Pacific island individuals’ Native American ancestry were determined using the first ASPCA with the higher density (91,835 SNP) two-array intersection. These positions were then mapped onto the lower density (28,653 SNPs) three-array intersection of the second ASPCA, containing the full panel of American reference populations, using a Procrustes transform. The linear Procrustes mapping was identified by comparing the positions of the American references shared between the first ASPCA and the second ASPCA. Because these references have high Native American ancestry, they have few masked sites and suffer less from reduced SNPs in array intersections than the Pacific island samples (see Supplementary Fig. 20), resulting in less noisy positions.

Identity-by-Descent Segment Analysis

Germline

Identity-by-descent (IBD) segments were identified using GERMLINE 1.5.3 on the SHAPEIT phased haploid genomes using the haploid flag, allowing a maximum of 4 homozygous marker mismatches per IBD slice (-err_hom), a maximum of 1 heterozygous marker mismatch per IBD slice (-err_het), and a minimum length for IBD detection of 3 cM (-min_m)⁷¹.

Ancestry-specific Filtering

IBD segments were then filtered based on their overlap with local ancestry segments. For example, IBD segments located entirely within European ancestry segments, as previously determined by the local ancestry methods described above, are binned separately from those in Polynesian and Native American ancestries.

Ancestry-specific IBD networks

Previous publications on IBD networks have inferred the edge connections based on the average total sum of IBD shared between individuals within each pair of populations^72,73, or on the total sum shared within a specific IBD segment length range⁷⁴. Here we consider instead the number of individuals from two populations who are connected by IBD segments above a threshold length. Specifically, we consider the probability that an individual selected at random from population A shares significant IBD (greater than 7 cM, to ensure no spurious matches) with an individual selected at random from population B. This can be easily computed by dividing the total number of such inter-island individual pairs connected by >7 cM IBD by the total number of possible inter-island individual pairs. We construct two networks with edges reflecting these probabilities, one for IBD segments located entirely in European ancestry segments of the genome and another for Native American ancestry segments (Supplementary Fig. 13 and Supplementary Data Tables 11–12). We do not plot Polynesian segment IBD probabilities, as all islands were found to share Polynesian ancestors with near probability one. Networks were plotted in R using the package qgraph⁷⁵.

Dating Analyses

Tract Length Distribution Analysis

The timing of admixture events between different ancestral populations can be inferred by analyzing the length distributions of genomic segments inherited from each ancestry, aggregated over all individuals in the studied population⁴⁰. Here (Supplementary Fig. 23) we conduct our analysis separately on each island possessing at least 1% average Native American component in both our ADMIXTURE (Supplementary Data Table 5) and RFMix (Supplementary Data Table 6) analyses. We considered Polynesian, Native American, and European ancestries with genomics segments assigned by local ancestry inference using RFMix as described above. The small number of individuals with African ancestry were excluded, as above, since such ancestry is rare, likely to be post-colonial, and in any case not the focus of our dating current analysis. (12 individuals above 0.005% African ancestry were excluded from Rapa Nui, 3 from South Marquesas, and 6 from North Marquesas).

We used the Tracts method⁴⁰ to fit three models with different sequences of historical admixture for each island: (i) Polynesian-Native American admixture followed by later European admixture, (ii) European-Native American admixture followed by later Polynesian admixture, and (iii) Polynesian-European admixture followed by later Native American admixture. To optimize model parameters over the nonlinear likelihood surfaces, Python’s COBYLA optimizer was run one hundred times each with different random starts for every population and model. The best likelihood runs were chosen (Supplementary Data Table 13), and, although some random starts failed to converge, of those that did, most converged to similar maximum likelihoods and similar model parameters. The admixture model with the highest likelihood (Supplementary Data Table 13) was then selected. This method gives estimates of the time since each admixture event, measured in number of generations. To convert these to admixture dates, we used a generation time of 30 years (see Supplemental Discussion) and the sample collection dates in Supplementary Data Table 2. Tracts was also run separately, as described above, on the 64 Rapanui individuals identified as having less than 1% of a southern Native American component in our iterative ADMIXTURE analysis (see Supplementary Fig. 24).

Linkage Disequilibrium Decay Analysis

We also performed a complementary analysis of linkage disequilibrium decay using ALDER 1.0, which requires neither phasing nor local ancestry inference⁴². Observing that the Native American ancestry-specific IBD clustering network indicated common Native American ancestry in eastern Polynesia, we pooled individuals across islands for this analysis. In particular, from the islands that had a greater than 1% average Native American component in our ADMIXTURE analysis (Supplementary Data Table 5), we pooled all individuals without later European or African admixture, that is, with no more than 1% European and/or African ancestry: Mangareva (4), Palliser (2), North Marquesas (1), and Rapa Nui (6). As ancestral reference proxies, we used 30 unadmixed Native American Aymara individuals and the 22 Austronesians from the Atayal and Paiwan of Taiwan (Supplementary Data Table 1,3). A total of 690,692 SNPs were used in this analysis (see Supplementary Fig. 23g).

Because we had a large number of samples from Rapa Nui, we hoped to have increased resolution in our dating analysis there. However, all but six of the Rapanui have European admixture, so we could not use the two-population model of ALDER on the full set of Rapanui individuals, and instead used MALDER 1.0 (Supplementary Data Table 14)⁷⁶. For the Rapanui individuals, we could not pool those sampled in 1994 with those sampled in 2013 for this dating analysis, since almost one generation separates these two collections. We focused on the 1994 Rapa Nui samples, as this collection had lower amounts of the modern southern Native American and European ancestries (Supplementary Data Table 5). In addition, to reduce the complexity of the admixture model, the 13 Rapanui from the 1994 samples having African ancestry (greater than 1% in our ADMIXTURE analysis, Fig. 1b) were excluded, leaving 73 individuals. For our ancestral reference proxies, we used 30 unadmixed Native American Aymara individuals, 30 European individuals from Spain, and the 22 Austronesian individuals (Atayal and Paiwan) from Taiwan (Supplementary Data Table 1,3).