Abstract
Alterations in white matter (WM) development are associated with many neuropsychiatric and neurodevelopmental disorders. Most MRI studies examining WM development employ diffusion tensor imaging (DTI), which relies on estimating diffusion patterns of water molecules as a reflection of WM microstructure. Quantitative relaxometry, an alternative method for characterizing WM microstructure changes, is based on molecular interactions associated with the magnetic relaxation of protons. In a longitudinal study of 34 infant non-human primates (NHP) (Macaca mulatta) across the first year of life, we implement a novel, high-resolution, T1-weighted MPnRAGE sequence to examine WM trajectories of the longitudinal relaxation rate (qR1) in relation to DTI metrics and gestational age at scan. To the best of our knowledge, this is the first study to assess developmental WM trajectories in NHPs using quantitative relaxometry and the first to directly compare DTI and relaxometry metrics during infancy. We demonstrate that qR1 exhibits robust logarithmic growth, unfolding in a posterior-anterior and medial-lateral fashion, similar to DTI metrics. On a within-subject level, DTI metrics and qR1 are highly correlated, but are largely unrelated on a between-subject level. Unlike DTI metrics, gestational age at birth (time in utero) is a strong predictor of early postnatal qR1 levels. Whereas individual differences in DTI metrics are maintained across the first year of life, this is not the case for qR1. These results point to the similarities and differences in using quantitative relaxometry and DTI in developmental studies, providing a basis for future studies to characterize the unique processes that these measures reflect at the cellular and molecular level.
Keywords: quantitative relaxometry, neurodevelopment, nonhuman primate, longitudinal imaging, white matter, myelination
1. INTRODUCTION
White matter (WM) consists of bundles of myelinated axons that transfer information between clusters of neurons via electrical signal transmission and provide the structural architecture of the human brain. By establishing the underlying connectivity that mediates efficient communication between distinct brain regions, WM plays a crucial role in healthy brain development and function. Disruptions in the maturation or structural integrity of WM can result in compromised brain connectivity, and consequently, alterations in WM microstructure in early childhood are believed to be associated with psychiatric, neurological, and developmental disorders (Dean et al., 2016; Heng et al., 2010; Kim & Whalen, 2009; Tromp et al., 2019).
Within the scope of magnetic resonance imaging (MRI) techniques, developmental WM microstructural changes are most commonly evaluated in vivo using diffusion tensor imaging (DTI) (Aggarwal et al., 2021; Lebel & Deoni, 2018). DTI metrics, including fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (AD), are sensitive to a host of biophysical properties that affect WM microstructure, such as myelination, axonal coherence and packing, and tissue density (Alexander et al., 2007; Budde et al., 2011; Jones et al., 2013; Pierpaoli & Basser, 1996). Distinct from DTI, quantitative relaxometry is an alternative method for assessing microstructural brain changes in vivo. Whereas DTI measurements are derived from the diffusion patterns of water molecules in the brain, relaxometry metrics reflect the molecular interactions and energy exchanges associated with the magnetic relaxation of protons. More specifically, in MRI, two fundamental time constants, known as T1 and T2, govern both the re-growth of the longitudinal magnetization due to an energy exchange between protons and surrounding molecules, and the decay of the transverse magnetization due to the loss of phase coherence between protons interacting with one another, respectively. In turn, quantitative relaxometry encompasses the measurement of these relaxation times (qT1 or qT2) and their inverse, relaxation rates (qR1 or qR2). Importantly, relaxometry metrics are highly sensitive to the presence of the fatty myelin sheath surrounding axons, including the associated proteins, cholesterol, glycolipids, and iron-containing oligodendrocytes and glial cells (Deoni, 2010; Leppert et al., 2009). As myelination progresses over development, more protons from free water molecules bind to the various myelin-associated macromolecules, which effectively lowers the free water concentration in the given tissue, and consequently, increases observed relaxation rates (Leppert et al., 2009). Correspondingly, measured changes in longitudinal relaxation have been associated with histological markers of myelin (Lazari & Lipp, 2021; Warntjes et al., 2017).
Relaxometry metrics have been utilized to investigate age-related brain changes as well as alterations associated with various neurological and psychiatric disorders, including ischemic stroke (Hoque et al., 2007; McGarry et al., 2016), necrosis (Cheng et al., 2012; Deoni, 2010), multiple sclerosis (Burgetova et al., 2010; Gracien et al., 2016), dementia (Knight et al., 2019), traumatic brain injury (Mamere et al., 2009), ADHD (Anderson et al., 2002), major depressive disorder (Sacchet & Gotlib, 2017), and bipolar disorder (Gönenç et al., 2010; Johnson et al., 2015). Furthermore, numerous human imaging studies have used quantitative relaxometry to assess WM development in early infancy. These studies have documented large relaxation times in newborns that decrease rapidly (equivalent to increases in relaxation rates) throughout the first few years of life before leveling off between approximately 3 and 5 years of age (Deoni, 2010; Deoni et al., 2012; Eminian et al., 2018; Engelbrecht et al., 1998; Holland et al., 1986; Lebel & Deoni, 2018; Leppert et al., 2009; Masumura, 1987; Ouyang et al., 2019; Paus et al., 2001; Saito et al., 2009). These changes are thought to be driven concurrently by decreasing free water concentrations and progressive myelination marked by increasing protein and lipid concentrations (Deoni, 2010; Leppert et al., 2009; Ouyang et al., 2019; Paus et al., 2001). However, while these studies are informative and largely consistent, many of them are limited by cross-sectional designs.
Due to their conserved evolutionary development, similar brain homology, and analogous socio-emotional behaviors, nonhuman primates (NHPs), and in particular rhesus macaques, provide a useful animal model for investigating the spatiotemporal dynamics of human postnatal brain development and their relationship to the pathophysiology of early-life psychopathology (Howell et al., 2019; Kalin, 2004; Nelson & Winslow, 2009; Phillips et al., 2014; Zhang & Shi, 1993). Importantly, NHP models can be used to investigate causal relationships relevant to brain development and the risk to develop psychopathology. There are also logistical benefits to performing imaging studies in NHPs instead of humans (Raschle et al., 2012). For example, brain development in rhesus monkeys occurs at an accelerated pace compared to humans (Workman et al., 2013), allowing for robust and informative longitudinal neuroimaging studies to be carried out over a shorter window of time.
Previously, we used a longitudinal within-subjects design to characterize the spatiotemporal dynamics of developmental DTI trajectories extracted from 18 WM regions of interest (ROIs) in 34 infant rhesus monkeys assessed at 5 timepoints across the first year of life (Aggarwal et al., 2021). We documented robust logarithmic growth in DTI parameters, characterized by distinct posterior-to-anterior and medial-to-lateral gradients in WM maturation as well as especially rapid growth rates over the first 10 weeks of life that dropped precipitously thereafter. We also found that individual differences in DTI measures assessed at 3 weeks of age were significantly related to those at 1 year of age. Notably, these monkeys were also scanned with the novel, T1-weighted, MPnRAGE imaging sequence. MPnRAGE is a radial 3D sequence that samples hundreds of images along the inversion recovery curve, providing a method for producing robust quantitative qR1 (or qT1) maps (Kecskemeti et al., 2016, 2018; Kecskemeti & Alexander, 2020). Because of the potential for quantitative relaxometry to provide additional and complementary information pertaining to age-related changes in WM microstructure, we sought to investigate developmental trajectories of longitudinal relaxation rates (qR1) and to compare these to the spatiotemporal dynamics of traditional DTI parameters over the first year of life. Therefore, in this study, we analyzed the developmental trajectories of qR1 in the same 18 WM ROIs and NHP cohort as previously studied (Aggarwal et al., 2021). To our knowledge, this constitutes the first study of WM maturation in infant NHPs using qR1 relaxometry.
2. METHODS
2.1. Ethics Statement
All procedures were performed using protocols approved by the University of Wisconsin Institutional Animal Care and Use Committee.
2.2. Subjects and Housing
34 infant rhesus macaques were housed at the Wisconsin National Primate Research Center (WNPRC) in mother-infant pairs until they were weaned at approximately 6 months of age and subsequently grouped into aged-matched pairs for the remainder of the study. Standard husbandry included a 12-hour light/dark cycle, two daily feeding sessions, ad libitum access to water, and daily enrichment.
2.3. MPnRAGE (T1-Weighted) Acquisition and Data Processing
The NHP scanning protocol and scanning parameters were identical to those reported in a previous publication using this sample (Aggarwal et al., 2021). Briefly, 34 rhesus macaques (23 females, 11 males) were imaged with a 3T MR750 scanner (GE Healthcare, Waukesha, WI) at roughly 3, 7, 13, 25, and 53 weeks of postnatal age (i.e., time since birth). Whole brain, 3D T1-weighted images were acquired with MPnRAGE (Kecskemeti et al., 2016, 2018; Kecskemeti & Alexander, 2020) with 0.625 mm isotropic spatial resolution, and reconstructed to 0.47 mm isotropic resolution..
The structural MPnRAGE images for each subject were skull-stripped and then iteratively spatially normalized with non-linear, diffeomorphic registration using Advanced Normalization Tools (ANTs) software (Avants et al., 2008) to produce 34 within-subject (across time) templates. The same methodology was then implemented to co-register all 34 subject specific templates to produce a final, time-averaged, population template. The spatial transformations generated from the construction of the population template for each subject and timepoint were concatenated and the corresponding qR1 maps were warped into population space in a single interpolation step (Figure 1). Replicating the steps detailed in our previous report (Aggarwal et al., 2021), a publicly available NHP WM ROI atlas (Adluru et al., 2012; Zakszewski et al., 2014) was then warped to our population template and 52 WM ROIs were selected for analysis. In order to restrict our analysis to WM voxels, we used FMRIB’s Automated Segmentation Tool (FAST) (Zhang et al., 2001) to compute a WM mask of our population template and applied this mask to our WM atlas in population template space. qR1 values from subgroups of the 52 ROIs were averaged to represent 18 major WM fiber bundles of interest, including projection (2), commissural (2), association (9), and brainstem (5) pathways that span across the brain. All 52 ROIs and associated composite regions are listed in Table 1 and Supplemental Tables 1-3.
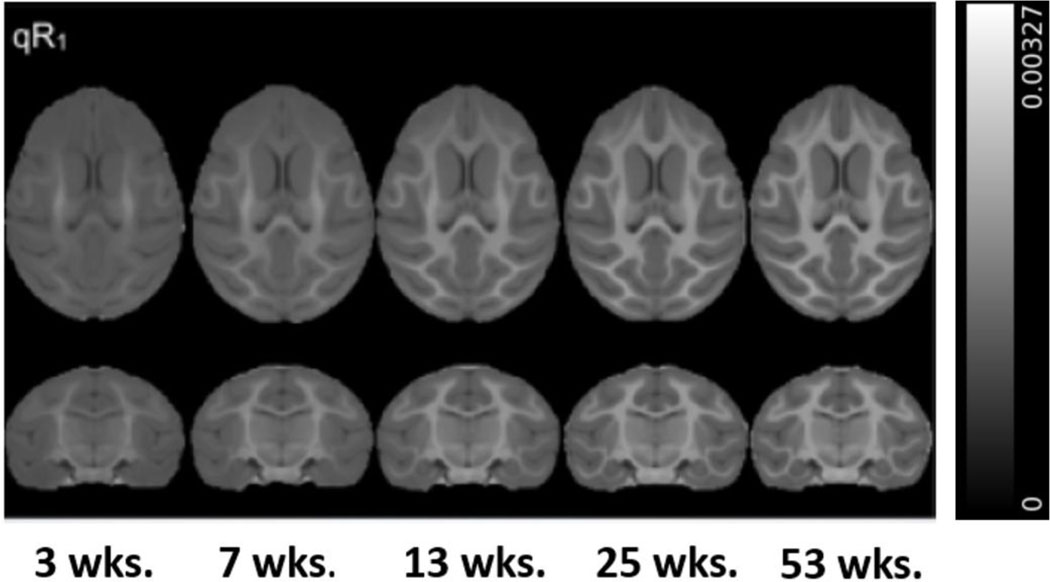
Figure 1. Axial (top) and coronal (bottom) views of the average qR1 maps (ms−1) at each age in population template space.
Note the increasing contrast and complexity of the WM over the first year of life, especially in the frontal lobes.
Table 1.
The 18 WM ROIs organized by fiber type (FromAggarwal et al., 2021.)
| Association ROIs | Commissural ROIs | Projection ROIs | Brainstem ROIs |
|---|---|---|---|
| superior longitudinal fasciculus | anterior commissure | corona radiata | cerebellar peduncles |
| superior fronto-occipital fasciculus | corpus callosum | internal capsule | cerebral peduncles |
| uncinate fasciculus | medial lemniscus | ||
| sagittal striatum | medial longitudinal fasciculus | ||
| external capsule | corticospinal tract | ||
| cingulum | |||
| stria terminalis | |||
| posterior thalamic radiation | |||
| fornix |
2.4. DTI Acquisition and Data Processing
Diffusion images were acquired and processed with procedures identical to our previously published DTI study in this sample (Aggarwal et al., 2021).
2.5. Developmental Trajectories of qR1 and Non-Linear Regression
For each subject and time point, average values of qR1 were extracted from the 18 WM ROIs and then used to construct longitudinal trajectories. Using MATLAB software, non-linear regression (via sum of squared errors [SSE] minimization) was implemented to fit these trajectories to a range of biologically relevant growth models. Candidate models included linear, quadratic, logarithmic, exponential, and Gompertz functions. Information criterion metrics, including Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), as well as sum of squared errors (SSE), were calculated to evaluate the goodness of fit for each proposed model in all WM voxels delineated by our WM mask. Model testing demonstrated that a logarithmic growth model fit best (Supplemental Table 4), corresponding to DTI trajectories (Aggarwal et al., 2021) :
| (Eq. 1) |
In this model, the parameter A represents the rate of change of qR1 and the parameter B represents the model intercept.
2.6. Linear Mixed-Effects Modeling & Individual-Level Trajectories
For a more robust and complete characterization of WM development using quantitative relaxometry, we quantified the growth of qR1 over time within the framework of a linear mixed-effects (LME) model. For all 18 WM ROIs, we modeled WM trajectories with this general form:
| (Eq. 2) |
LME models allow for precise and unbiased effect estimates by accounting for repeated within-subject measures. To enable estimation of within-subject effects, all repeated independent variables were mean-centered within-subject. Our model is linear with respect to the natural log of gestational age at scan (GestAge) and also includes the Sex (male or female), and the interaction between ln(GestAge) and Sex as covariates. Note that GestAge is the sum of the gestational age at birth (i.e., time in utero) and the postnatal age (i.e., time since birth). In the equation denoted above, we estimate four fixed effects: β0 refers to the overall model intercept and represents an estimate of the magnitude of qR1 at birth in each WM ROI; β1 refers to the main effect of GestAge (log-transformed) –our primary variable of interest; β2 refers to the main effect of Sex; and β3 refers to the interactive effect of GestAge and Sex. To account for the repeated longitudinal within-subject measurements, we also estimate two random effects: μ0 refers to the by-subject random intercept and μ1 refers to the by-subject random effect (slope) of GestAge. For each of the 34 monkeys, we calculated μ0 and μ1 for each ROI. Lastly, ε refers to the variance of the model residuals. In total, we generated 18 different LME models, one for each WM ROI. All LME modeling was performed using the lme4 package in R (Bates et al., 2015). We report effect sizes for all models with model R2 values, as well as partial-R2 and Cohen’s f2 (Selya et al., 2012) values for the specific effect of ln(GestAge).
Because our previous work found that GestAge was correlated with both brain volume and DTI parameters (Aggarwal et al., 2021), and because brain volume is also highly correlated with qR1, we performed a supplementary LME analysis of qR1 trajectories that additionally covaried for total brain volume. To this end, total brain volumes were extracted from the skull-stripped MPnRAGE structural images for each animal and timepoint using FSL software (Jenkinson et al., 2012).
2.7. Individual Differences in qR1 Across Time
To assess the extent to which individual differences in qR1 were maintained across time, we computed Pearson correlations between qR1 measures for each animal at 1 year of postnatal age (timepoint 5) and each of the preceding timepoints (3, 7, 13, and 25 postnatal weeks).
2.8. Rank Order Analysis & Clustering of qR1 Trajectories
Next, to delineate regional differences in WM status and development across the postnatal brain using quantitative relaxometry, we first ranked the magnitudes of the intercept (β0) and slope (β1) terms from the LME models generated for each WM ROI in descending order. Next, we implemented k-means clustering of the qR1 trajectories corresponding to the 18 WM ROIs. We chose to partition the data into 4 clusters. While determining the optimal number of clusters generated from a k-means algorithm is largely subjective, our cluster selection was based on analysis of multiple k-means clustering criteria and cluster interpretability (Supplemental Figure 2). All clustering and statistical procedures were performed using the kml software package in R (a k-means clustering algorithm specifically designed for clustering longitudinal trajectories) (Genolini et al., 2015).
2.9. Within-Subject and Between-Subject Correlations Between qR1 and DTI Metrics
First, to investigate longitudinal relationships between qR1 and DTI parameters across the first year of life, we performed LME modeling to compute within-subject Pearson correlations between qR1 and DTI measurements in all 18 WM ROIs, controlling for gestational age at scan. Next, cross-sectional relationships between qR1 and DTI metrics were assessed at each of the five study timepoints using multiple linear regression to compute between-subject Pearson correlations between qR1 and DTI measures at each study timepoint, again controlling for gestational age at scan. For within-subject comparisons, we calculated the partial-R2 and Cohen’s f2 values to evaluate the specific effect sizes of the relationship between DTI metrics and qR1.
2.10. Relationship Between Gestational Age at Birth and Early Postnatal WM Microstructure
To examine how variation in gestational age at birth (time in utero) affects relative WM status early in life, we computed Pearson correlations between gestational ages at birth and WM metrics (FA, MD, RD, AD, qR1) at each timepoint by implementing the following linear model in all 18 WM ROIs:
| (Eq. 3) |
This model is linear with respect to gestational age at birth (GestAgeBirth) and includes the postnatal age at scan (PostnatalAge) and Sex (male or female) as covariates. In addition to Pearson correlations, we assessed the specific effect sizes of gestational age at birth with partial-R2 and Cohen’s f2.
2.11. Statistical Correction for Multiple Comparisons
All analyses outlined above were performed in 18 WM ROIs. Therefore, all analyses were assessed for statistical significance using a Bonferroni-adjusted P-value for multiple comparisons correction (Pcorrected<0.05/18=0.0028).
2.12. Data Availability
Project data pertaining to this study can be found here: https://doi.org/10.5061/dryad.7m0cfxpvx. Additional imaging data, along with the code used for these analyses, may be able to be shared with interested parties upon request by contacting the corresponding author.
3. RESULTS
3.1. qR1 Exhibits Robust Logarithmic Growth Over the First Year of Life
The fundamental aim of this study was to implement a novel, high resolution, T1-weighted, MPnRAGE sequence to assess longitudinal within-subject qR1 trajectories across 18 WM ROIs in developing rhesus monkeys throughout the first year of life (Figures 1–2 & Table 1).
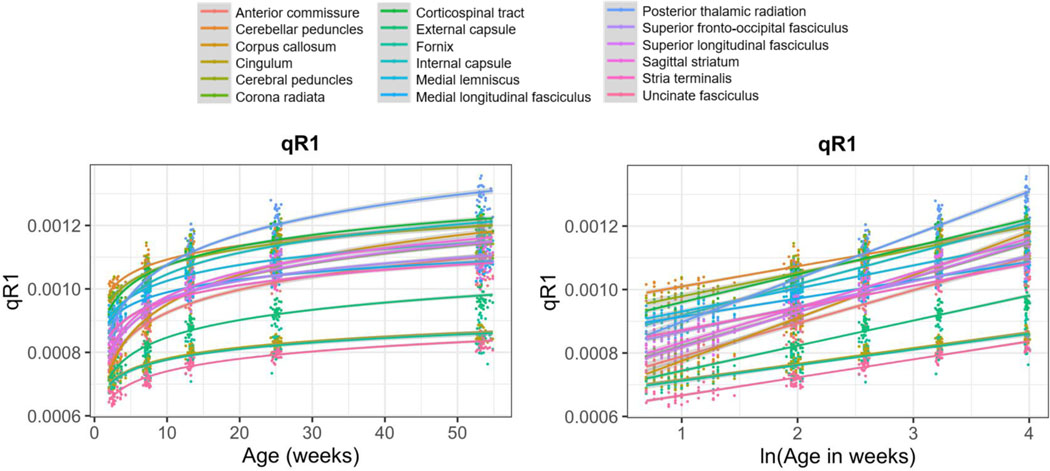
Figure 2. Logarithmic growth of qR1 across the brain.
Average within-subject qR1 trajectories over the first year of life extracted from 18 WM ROIs, shown with age (left) and log-transformed age (right). Each line represents the logarithmic (left) or linear (right) fit for a given ROI.
After testing a range of potential growth models, we confirmed a robust logarithmic relation (Supplemental Table 4) between gestational age at scan and qR1 across all 34 monkeys and five timepoints that was consistent with previously documented DTI trajectories in the same monkey cohort (Aggarwal et al., 2021). We next accounted for within-subject repeated measures as well as sex and gestational development in an LME model to test whether log-transformed gestational age at scan significantly predicted within-subject changes in qR1 over time. Results demonstrated that, for all 18 ROIs, the log-transformed GestAge term (β1) remained significant in predicting changes in qR1 over time (Pcorrected<0.05) and that the effect size of GestAge was large (mean partial-R2: 0.76; mean Cohen’s f2: 3.29). Individual-level trajectories for all 34 monkeys, along with the relative standard errors (RSE) of corresponding LME model parameters β0 and β1, are provided for 4 select WM ROIs in Supplemental Figure 3. Additionally, when controlling for total brain volume, the ln(GestAge) term (β1) was still highly significant in all 18 ROIs, accounting for unique variance beyond that accounted for by brain volume (Pcorrected<0.05). We depict the average within-subject effect of whole brain volume on whole-brain qR1 (calculated by averaging all 18 ROIs) in Supplemental Figure 4. LME model parameters for all 18 WM ROIs are provided in Supplemental Table 5.
3.2. Individual Differences in Early Postnatal qR1 Are Not Maintained Across the First Year of Life
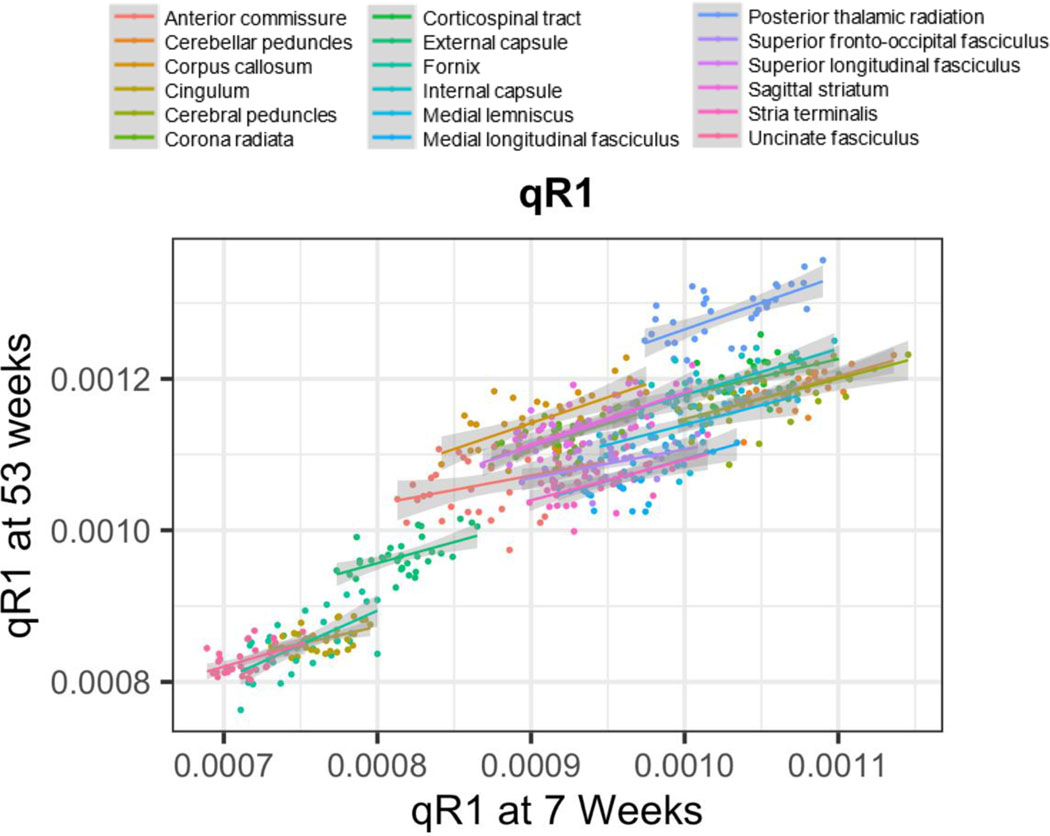
Across the sample of 34 monkeys, qR1 measurements at 3 weeks, the earliest timepoint, were significantly related to those at 1 year in only 1 out of 18 WM ROIs (the fornix), indicating that individual differences in very early postnatal longitudinal relaxation rates are generally not maintained across the first year of life (Table 2). However, qR1 measurements at 7 weeks, the second timepoint, were significantly related to those at 1 year in 14 out of 18 ROIs (Figure 3 and Table 2). The first result is in contrast with DTI metrics, for which there were meaningful relationships between 3 weeks and 1 year of postnatal age. For example, 16 of 18 FA ROI correlations, 8 of 18 RD ROI correlations, 5 of 18 MD ROI correlations, and 4 of 18 AD ROI correlations were significant after correcting for multiple comparisons (Aggarwal et al., 2021).
Table 2. Stability of early individual differences in qR1.
R2 values (and with corresponding P-values) for correlations between qR1 values at: 1) 3 weeks and 53 weeks, and 2) 7 weeks and 53 weeks for each 18 WM ROI. Significant R2 values (Pcorrected<0.05) are bolded.
| 3 ~ 53 weeks | 7 ~ 53 weeks | |||
|---|---|---|---|---|
| ROI | R2 | P-value | R2 | P-value |
| FX | 0.398 | <0.001 | 0.419 | <0.001 |
| AC | 0.023 | 0.393 | 0.110 | 0.055 |
| CBP | 0.161 | 0.019 | 0.402 | <0.001 |
| CC | 0.153 | 0.022 | 0.382 | <0.001 |
| CST | 0.237 | 0.003 | 0.232 | 0.003 |
| ML | 0.153 | 0.022 | 0.267 | 0.002 |
| CP | 0.107 | 0.060 | 0.360 | <0.001 |
| IC | 0.171 | 0.015 | 0.426 | <0.001 |
| CR | 0.125 | 0.040 | 0.422 | <0.001 |
| SS | 0.040 | 0.258 | 0.366 | <0.001 |
| EC | 0.142 | 0.028 | 0.289 | <0.001 |
| CING | 0.123 | 0.042 | 0.238 | 0.003 |
| ST | 0.145 | 0.026 | 0.331 | <0.001 |
| SLF | 0.127 | 0.038 | 0.391 | <0.001 |
| SFO | 0.095 | 0.077 | 0.224 | 0.005 |
| UF | 0.119 | 0.046 | 0.267 | 0.002 |
| MLF | 0.234 | 0.004 | 0.320 | <0.001 |
| PTR | 0.068 | 0.137 | 0.416 | <0.001 |
Figure 3.
Correlations of individual differences in qR1 at 7 and 53 weeks in 18 WM ROIs.
3.3. Regional Asynchrony in qR1 During Very Early WM Development
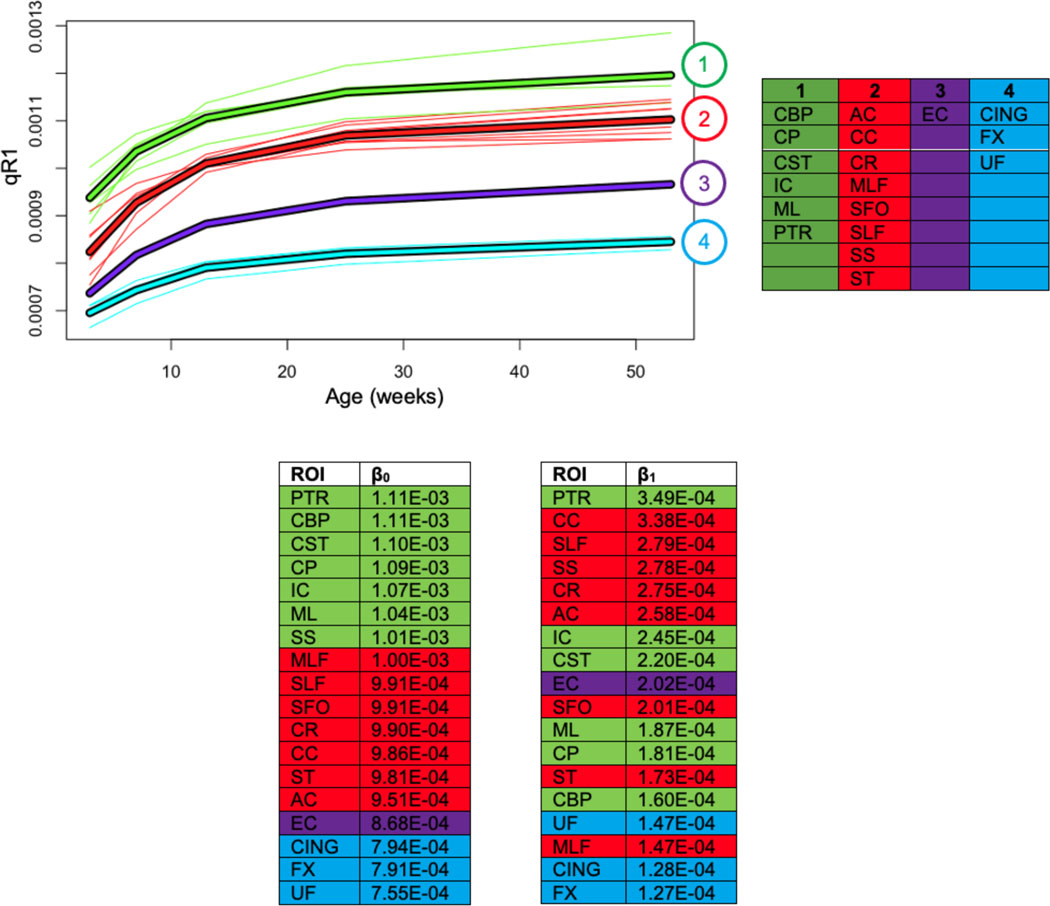
Results from k-means clustering of qR1 and rank ordering of LME parameters (β0 and β1) for the 18 WM ROIs confirm regional differences in WM microstructure changes over time (Figure 4). Based on multiple k-means clustering criteria (Genolini et al., 2015), four clusters were selected in the clustering analysis. We recapitulate previously established patterns of medial-to-lateral and posterior-to-anterior gradients of WM maturation, characterized by medial and posterior regions in clusters with higher qR1 values and lateral and anterior regions in clusters with lower qR1 values. Cluster 1, which consists of ROIs with the highest qR1 magnitudes, is comprised of the cerebral peduncles, cerebellar peduncles, corticospinal tract, medial lemniscus, internal capsule, and posterior thalamic radiation. Cluster 2 contains the corona radiata, anterior commissure, corpus callosum, medial longitudinal fasciculus, superior fronto-occipital fasciculus, superior longitudinal fasciculus, sagittal striatum, and stria terminalis. Cluster 3 consists solely of the external capsule. Finally, Cluster 4, which contains ROIs with the lowest qR1 values, includes three frontal/limbic regions –the cingulum, fornix, and uncinate fasciculus.
Figure 4. Four k-means clusters derived from the qR1 trajectories of 18 WM ROIs.
Cluster compositions, along with rank ordering of intercept and slope magnitudes (β0 and β1), are listed in the bottom two tables. Cluster 1 represents the regions that develop earliest in life and Cluster 5 represents the later developing regions, relative to each other. Rank order tables are color-coded by k-means cluster.
We note that these patterns are consistent with those elucidated from our previously reported clustering of corresponding FA trajectories (Aggarwal et al., 2021). Furthermore, by comparing the rank orders of β0 and β1 to k-means clusters of qR1 trajectories, we found that regional differentiation in the first year is related to the initial magnitudes of qR1, consistent with our corresponding rank order analysis of DTI trajectories, which exhibited a similar trend with respect to initial DTI magnitudes.
3.4. Strong Within-Subject –and Weak Between-Subject –Associations Between qR1 and DTI Metrics
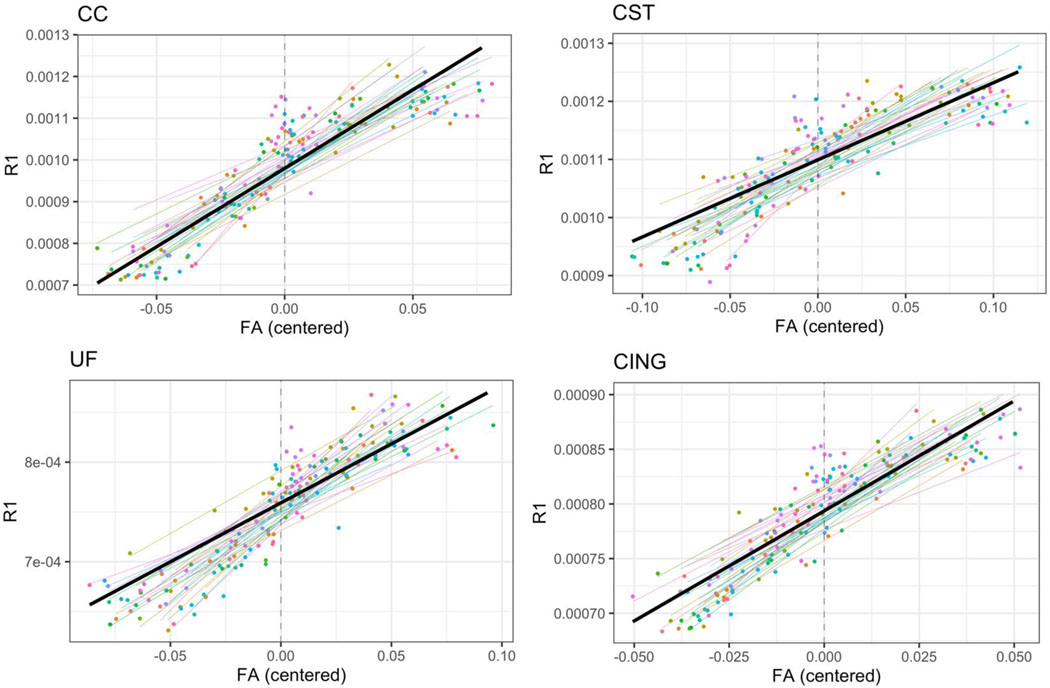
Within-subject correlations revealed a significant and robust relationship between qR1 and DTI parameters across the brain throughout the first year of life. In particular, qR1 was significantly correlated to FA in 16 of 18 ROIs (mean partial R2: 0.50), to RD in 17 of 18 ROIs (mean partial R2: 0.48), to MD in 16 of 18 (mean partial R2: 0.43) ROIs, and to AD in 10 of 18 WM ROIs (mean partial R2: 0.40). Conversely, between-subject analyses at each timepoint revealed that only a small minority of WM ROIs exhibited significant correlations between DTI metrics and qR1. For FA, the only significant associations found with qR1 were in the anterior commissure and corona radiata, and only at one or two timepoints. Within-subject correlations, as well as between-subject correlations at each timepoint, between qR1 and all DTI metrics in all 18 WM ROIs are provided in Table 3 and Supplemental Table 7, respectively. Plots of within-subject relationships of qR1 versus FA are provided for 4 select WM ROIs in Figure 5. Corresponding plots for qR1 versus RD, MD, and AD are provided in Supplemental Figure 5.
Table 3. Partial-R2 and Cohen’s f2 values for the effect of DTI parameter (FA, MD, RD, or AD) in within-subject (longitudinal) correlations between qR1 and DTI metrics extracted from 18 WM regions.
Analyses control for gestational age at scan. Significant partial-R2 and Cohen’s f2 values (Pcorrected<0.05) are bolded.
| FA | MD | RD | AD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROI | partial-R2 | Cohen’s f2 | P-value | partial-R2 | Cohen’s f2 | P-value | partial-R2 | Cohen’s f2 | P-value | partial-R2 | Cohen’s f2 | P-value |
| FX | 0.405 | 0.681 | <0.001 | 0.068 | 0.073 | 0.010 | 0.182 | 0.222 | <0.001 | 0.036 | 0.037 | 0.031 |
| AC | 0.526 | 1.110 | <0.001 | 0.481 | 0.927 | <0.001 | 0.538 | 1.165 | <0.001 | 0.381 | 0.616 | <0.001 |
| CBP | 0.512 | 1.049 | <0.001 | 0.126 | 0.144 | <0.001 | 0.326 | 0.484 | <0.001 | 0.078 | 0.085 | 0.006 |
| CC | 0.470 | 0.887 | <0.001 | 0.494 | 0.976 | <0.001 | 0.527 | 1.114 | <0.001 | 0.201 | 0.252 | <0.001 |
| CST | 0.289 | 0.406 | <0.001 | 0.233 | 0.304 | <0.001 | 0.306 | 0.441 | <0.001 | 0.033 | 0.034 | 0.061 |
| ML | 0.139 | 0.161 | 0.071 | 0.118 | 0.134 | 0.001 | 0.122 | 0.139 | <0.001 | 0.022 | 0.022 | 0.127 |
| CP | 0.321 | 0.473 | <0.001 | 0.178 | 0.217 | <0.001 | 0.264 | 0.359 | <0.001 | 0.015 | 0.015 | 0.221 |
| IC | 0.615 | 1.597 | <0.001 | 0.533 | 1.141 | <0.001 | 0.626 | 1.674 | <0.001 | 0.101 | 0.112 | 0.001 |
| CR | 0.635 | 1.740 | <0.001 | 0.650 | 1.857 | <0.001 | 0.684 | 2.165 | <0.001 | 0.663 | 1.967 | <0.001 |
| SS | 0.573 | 1.342 | <0.001 | 0.492 | 0.969 | <0.001 | 0.563 | 1.288 | <0.001 | 0.303 | 0.435 | <0.001 |
| EC | 0.580 | 1.381 | <0.001 | 0.573 | 1.342 | <0.001 | 0.627 | 1.681 | <0.001 | 0.597 | 1.481 | <0.001 |
| CING | 0.424 | 0.736 | <0.001 | 0.572 | 1.336 | <0.001 | 0.592 | 1.451 | <0.001 | 0.521 | 1.088 | <0.001 |
| ST | 0.638 | 1.762 | <0.001 | 0.120 | 0.136 | 0.002 | 0.404 | 0.678 | <0.001 | 0.105 | 0.117 | 0.004 |
| SLF | 0.608 | 1.551 | <0.001 | 0.635 | 1.740 | <0.001 | 0.675 | 2.077 | <0.001 | 0.664 | 1.976 | <0.001 |
| SFO | 0.431 | 0.757 | <0.001 | 0.531 | 1.132 | <0.001 | 0.564 | 1.294 | <0.001 | 0.361 | 0.565 | <0.001 |
| UF | 0.488 | 0.953 | <0.001 | 0.526 | 1.110 | <0.001 | 0.615 | 1.597 | <0.001 | 0.256 | 0.344 | <0.001 |
| MLF | 0.037 | 0.038 | 0.046 | 0.009 | 0.009 | 0.349 | 0.018 | 0.018 | 0.188 | 0.002 | 0.002 | 0.690 |
| PTR | 0.422 | 0.730 | <0.001 | 0.555 | 1.247 | <0.001 | 0.574 | 1.347 | <0.001 | 0.082 | 0.089 | 0.005 |
Figure 5. Within-subject relations between qR1 and FA in 4 WM regions (CC, CST, UF, and CING).
In each graph, each colored line represents a subject-specific regression line predicting qR1 from within-subject centered FA values, while controlling for gestational age at scan. Each point represents an individual scan, color-coded by subject. The bolded black line depicts the average within-subject relation of qR1 and FA.
3.5. Effect of Gestational Age at Birth on qR1 at 3 Weeks of Age
Gestational age at birth was positively correlated with mean qR1 at 3 weeks of postnatal age in 15 of 18 WM ROIs, exhibiting large effect sizes (mean partial-R2: 0.43; mean Cohen’s f2: 0.78) and explaining variance in qR1 magnitudes beyond that accounted for by postnatal age at scan and sex (Pcorrected<0.05). Longer gestational periods were associated with higher qR1 values at 3 weeks of postnatal age across the developing rhesus brain. Additionally, we note that at an uncorrected threshold (Puncorrected<0.05), gestational age at birth was positively correlated with qR1 values at 7, 13, and 25 weeks of postnatal age in several ROIs (Supplemental Tables 8-9). Strikingly, this relationship was nonexistent for DTI parameters at any postnatal age. Correlations between gestational age at birth and FA and qR1 at 3 weeks of postnatal age are provided in Table 4, while those for MD, RD, and AD are provided in Supplemental Table 10. Plots of qR1 versus gestational age at birth for 4 select WM ROIs are provided in Figure 6.
Table 4. R2 values for correlations between gestational age at birth (i.e., time in utero) and FA and qR1 at 3 weeks of age extracted from 18 WM regions, along with corresponding P-values.
Significant R2 values (Pcorrected<0.05) are bolded.
| FA | qR1 | |||
|---|---|---|---|---|
| ROI | R2 | P-value | R2 | P-value |
| FX | 0.315 | 0.314 | 0.354 | 0.004 |
| AC | 0.246 | 0.105 | 0.443 | <0.001 |
| CBP | 0.462 | 0.236 | 0.527 | <0.001 |
| CC | 0.283 | 0.582 | 0.682 | <0.001 |
| CST | 0.289 | 0.713 | 0.485 | <0.001 |
| ML | 0.246 | 0.596 | 0.298 | 0.003 |
| CP | 0.279 | 0.215 | 0.365 | 0.001 |
| IC | 0.346 | 0.076 | 0.584 | <0.001 |
| CR | 0.349 | 0.202 | 0.636 | <0.001 |
| SS | 0.401 | 0.467 | 0.541 | <0.001 |
| EC | 0.335 | 0.404 | 0.589 | <0.001 |
| CING | 0.215 | 0.726 | 0.473 | <0.001 |
| ST | 0.325 | 0.171 | 0.590 | <0.001 |
| SLF | 0.450 | 0.104 | 0.683 | <0.001 |
| SFO | 0.103 | 0.623 | 0.455 | <0.001 |
| UF | 0.382 | 0.589 | 0.431 | <0.001 |
| MLF | 0.126 | 0.387 | 0.239 | 0.007 |
| PTR | 0.161 | 0.235 | 0.563 | <0.001 |
Figure 6. Correlations between gestational age at birth (i.e., time in utero) and qR1 metrics extracted from 4 WM regions at approximately 3 weeks of postnatal age (CC, CST, UF, and CING).
Analyses control for postnatal age.
4. DISCUSSION
This study constitutes the first characterization of developmental trajectories of qR1 in WM fiber bundles across the first year of life in NHPs. While numerous studies have assessed WM trajectories of relaxometry parameters in human infants, none have offered a corresponding characterization of qR1 in developing NHPs. Here, using a longitudinal within-subjects design, we model the spatiotemporal dynamics of qR1 in 18 WM ROIs across the brain in 34 rhesus monkeys, beginning at 3 weeks of postnatal age and continuing through 53 weeks.
Overall, our analysis of qR1 trajectories indicates a logarithmic pattern of WM growth with respect to gestational age at scan across the first year of life that was marked by particularly rapid increases in qR1 over the first 6 months of life (Figure 2). Based on the relative brain maturation rates between rhesus monkeys and humans (approximately a 4:1 ratio (Workman et al., 2013)), these results are consistent with human studies, which document similar rates of growth in qT1 and qT2 that are apparent in early childhood (Deoni, 2010; Deoni et al., 2012; Eminian et al., 2018; Engelbrecht et al., 1998; Holland et al., 1986; Lebel & Deoni, 2018; Leppert et al., 2009; Masumura, 1987; Ouyang et al., 2019; Paus et al., 2001; Saito et al., 2009). More specifically, two notable studies in children found patterns similar to ours, identifying exponential changes in qT2 from birth to four years of age (Leppert et al., 2009) and logarithmic changes in both qR1 and qR2 from birth to five years (Deoni et al., 2012). The growth patterns observed in our data also exhibited regional heterogeneity in WM developmental rates (Figure 4), characterized by posterior-to-anterior and medial-to-lateral maturational gradients, consistent with our previously reported assessment of DTI trajectories in the same monkeys (Aggarwal et al., 2021). In this regard, the k-means cluster with the lowest qR1 values was comprised of the cingulum, fornix, and uncinate fasciculus, indicating that these three fiber bundles were the least structurally developed regions among the 18 we assessed. This aligns with considerable evidence which suggests that frontotemporal tracts are among the latest to myelinate and mature in both humans and NHPs (Olson et al., 2015).
Additionally, although some cross-sectional studies in specific clinical samples have shown that DTI metrics and relaxation rates are highly correlated in certain WM ROIs (Cherubini et al., 2009; Syka et al., 2015), this between-subject relation was not observed in our sample. However, we did find robust within-subject correlations between these parameters. To the best of our knowledge, other studies have not explicitly quantified longitudinal, within-subject, relationships between DTI and relaxometry parameters. Furthermore, none of these studies have examined these associations in the weeks and months immediately following birth. Here, we report widespread, significant within-subject correlations between qR1 and DTI parameters across 18 WM pathways throughout the first year of life, highlighted by particularly strong qR1 associations with RD and FA and weaker associations with AD (Figure 5, Supplemental Figure 5, & Table 3). The strong within-subject associations that we detected may reflect maturational influences that, at the individual level, have similar impacts on qR1 and DTI developmental trajectories. In this regard, genetic factors could be important. To the extent that DTI and qR1 metrics are genetically correlated and share genetic variance, it would be expected that these metrics would show strong within-subject correlations. Studies in humans and NHPs demonstrate significant heritability of DTI parameters (Geng et al., 2012; Jahanshad et al., 2013; Kochunov et al., 2010, 2014, 2015; Luo et al., 2021; Tromp et al., 2019), whereas the extent to which qR1 measures are heritable remains unknown. The reason why our study fails to detect between-subject relaxometry-DTI associations, while others report this association, is unclear. A unique feature of our study was the assessment of these inter-metric relations in NHPs very early in life, which differs from prior human studies examining the associations between these metrics in older samples (Cherubini et al., 2009; Syka et al., 2015).. While complementary, it is likely that DTI and qR1 metrics are differentially sensitive to the biophysical properties of WM microstructure (e.g., myelination, axonal packing, cell permeability) and this may be particularly evident early on in WM maturation. The lack of between-subject DTI-qR1 correlations found in our study could be explained by non-heritable factors particularly relevant to early postnatal brain development, such as environmental stimulation, stress, and maternal rearing, that not only vary considerably between individuals but early in life may also differentially affect the WM properties that are reflected in DTI and qR1 measurements. From a broader perspective, these findings underscore the importance of longitudinal designs in understanding individual differences in neurodevelopmental trajectories that are ultimately relevant to behavior and psychopathology.
Our previous DTI findings revealed meaningful relationships between measures across the first year of life, such that metrics assessed at 3 weeks old were significantly correlated with those assessed at 53 weeks old. In contrast, for qR1, we did not find significant associations for this relation. In 17 of 18 WM ROIs, qR1 values at 3 weeks were not significantly correlated with those at 53 weeks (Table 2). However, in 14 of 18 WM ROIs, individual differences in qR1 measurements at 7 weeks were found to be significantly correlated to those at 53 weeks. It is possible that the lack of stability in qR1 from 3 to 53 weeks could be due to overriding factors occurring in utero that influence early-life qR1 parameters.
Another interesting and possibly related finding is the observation that gestational age at birth is correlated with qR1 at 3 weeks of postnatal age, whereas this was not found to be the case with any DTI metric. More specifically, in 15 of 18 WM ROIs, we found significant relations between gestational age at birth and qR1 measurements at 3 weeks of postnatal age (Figure 6 & Table 4). Of note, gestational age at birth was not found to be correlated to qR1 at the later ages, after multiple comparisons correction. To our knowledge, no other studies have examined the relation between qR1 assessed early in postnatal life with gestational age at birth. The gestational period is a critical epoch of neurodevelopment that encompasses rapid macrostructural and microstructural brain changes that lay the foundation for healthy cognitive and socio-emotional function later in life, including robust white matter (WM) growth characterized by rapid myelination that begins in the second trimester (Wilson et al., 2021). As mentioned above, we did not find relations between gestational age at birth and the DTI parameters. In this regard, it is important to keep in mind that DTI measurements and qR1 are assessed with different methods and are based on different biophysical properties. For example, FA is a measure of the anisotropy of water diffusion and is thought to reflect the microstructural maturation and organization of WM fiber bundles, while qR1 is based on spin-lattice (i.e., proton-molecule) interactions that are sensitive to the presence of lipid molecules, which may provide a more direct measure of myelin content. Because qR1 was significantly related to gestational age at birth, this may indicate that longer gestational periods contribute to higher levels of postnatal myelin early in life. This finding is in contrast to that reported in two studies in human infants, demonstrating that longer gestational periods were associated with higher postnatal FA values (Broekman et al., 2014; Ou et al., 2017) and lower MD, RD, and AD values (Ou et al., 2017).
We note potential limitations that should be considered when interpreting the results from our study. First, it is important to recognize the differences between the laboratory-controlled setting used here, as compared to studies in humans in which environmental differences and variables have a much broader range. This could be important in understanding differences between NHP and human studies in relation to heterogeneity and developmental trajectories, as WM maturation is influenced by environmental factors and experience (Lebel & Deoni, 2018). Despite the suggestion that qR1 reflects myelination, caution should be used in interpreting qR1 as a direct reflection of myelin content. In general, relaxation rates may be affected by a host of biophysical processes, including myelination, iron accumulation, inflammation, edema, necrosis, changes in free water concentration, and the presence of any number of specific macromolecules (Deoni, 2010). Finally, due to the relatively low number of males (n=11) in our monkey cohort, we were unable to identify sex-related differences in developmental qR1 trajectories.
4.1. Conclusion
In summary, we present the first comprehensive characterization of WM qR1 trajectories in NHPs during the first year of life. Specifically, we established quantitative (LME) models of qR1 in 18 WM ROIs, identifying logarithmic patterns of WM development and regional heterogeneity in WM maturation rates consistent with corresponding DTI trajectories. qR1 values were highly correlated with DTI metrics on a within-subject level but at any single timepoint were largely unrelated in between-subject analyses. Unlike DTI parameters, qR1 values at 3 weeks did not predict qR1 values at 1 year, while those at 7 weeks were predictive of those at 1 year. Additionally, gestational age at birth was significantly related to qR1 measures at 3 weeks of age, which was not the case for the DTI metrics. This suggests the importance of in utero events in determining individual differences in qR1 early in postnatal life. Taken together, these results support the utility of assessing qR1 in longitudinal studies as a metric that reflects developmental changes in WM microstructure. Future work with animal models, integrating neuroimaging, behavioral, and genetic approaches, has the potential to provide a more in-depth understanding of the specific components of WM maturation captured by quantitative relaxometry and DTI metrics, as well as their relationships to the neurodevelopmental origins of adaptive and maladaptive behavior.
Supplementary Material
Highlights.
Logarithmic growth of qR1 in the first year of non-human primate life
Medial-to-lateral and posterior-to-anterior gradients of qR1 maturation
Early individual differences in qR1 are not maintained across the first year
qR1 and DTI metrics are correlated within-subjects, but not between-subjects
Gestational age at birth predicts early postnatal qR1, unrelated to DTI at any age
Acknowledgements
This research was funded by the National Institutes of Health. We thank the staffs of the Harlow Center for Biological Psychology (Marissa Riedel, Victoria Elam), Waisman Laboratory for Brain Imaging and Behavior, and Wisconsin National Primate Research Center.
Funding
This work was supported by grants from the National Institutes of Health to NHK (Grant Nos. P50-MH100031 and R01-MH081884) and grants from the National Institute of General Medical Sciences (NIH/NIGMS) - Initiative for Maximizing Student Development (IMSD – Grant No. R25 GM083252). NA is a student in the Medical Scientist Training Program (Grant No. T32-GM008692) and the Training Program in Emotion Research (Grant No. T32-MH018931). DD is supported by a Pathways to Independence Award R00 MH11056). Infrastructure support was also provided, in part, by grant U54 HD090256 from the Eunice Kennedy Shriver NICHD, National Institutes of Health (Waisman Center).
Research reported in this publication was also supported in part by the Office of the Director, National Institutes of Health under Award Number P51OD011106 to the Wisconsin National Primate Research Center, University of Wisconsin-Madison. This research was conducted at a facility constructed with support from Research Facilities Improvement Program grant numbers RR15459-01 and RR020141-01. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The funding sources played no role in the conceptualization, design, execution, or analysis of any part of the study.
NHK reported receiving grants from the National Institute of Mental Health; consulting to CME Outfitters, the Pritzker Neuropsychiatric Disorders Research Consortium, the Skyland Trail Advisory Board, the Early Life Adversity Research External Scientific Advisory Board at the University of Texas at Austin, and Corcept Therapeutics Incorporated; and serving as editor-in-chief of The American Journal of Psychiatry during the conduct of the study.
Footnotes
Declaration of Competing Interests
The other authors report no potential conflicts of interest.
REFERENCES
- Adluru N, Zhang H, Fox AS, Shelton SE, Ennis CM, Bartosic AM, Oler JA, Tromp DPM, Zakszewski E, Gee JC, Kalin NH, & Alexander AL (2012). A Diffusion Tensor Brain Template for Rhesus Macaques. NeuroImage, 59(1), 306–318. 10.1016/j.neuroimage.2011.07.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggarwal N, Moody JF, Dean DC, Tromp DPM, Kecskemeti SR, Oler JA, Alexander AL, & Kalin NH (2021). Spatiotemporal dynamics of nonhuman primate white matter development during the first year of life. NeuroImage, 231, 117825. 10.1016/j.neuroimage.2021.117825 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander AL, Lee JE, Lazar M, & Field AS (2007). Diffusion Tensor Imaging of the Brain. Neurotherapeutics : The Journal of the American Society for Experimental NeuroTherapeutics, 4(3), 316–329. 10.1016/j.nurt.2007.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson CM, Polcari A, Lowen SB, Renshaw PF, & Teicher MH (2002). Effects of Methylphenidate on Functional Magnetic Resonance Relaxometry of the Cerebellar Vermis in Boys With ADHD. American Journal of Psychiatry, 159(8), 1322–1328. 10.1176/appi.ajp.159.8.1322 [DOI] [PubMed] [Google Scholar]
- Avants B, Tustison N, & Song G. (2008). Advanced normalization tools (ANTS). Insight J, 1–35. [Google Scholar]
- Bates D, Mächler M, Bolker B, & Walker S. (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67(1), 1–48. 10.18637/jss.v067.i01 [DOI] [Google Scholar]
- Broekman BFP, Wang C, Li Y, Rifkin-Graboi A, Saw SM, Chong Y-S, Kwek K, Gluckman PD, Fortier MV, Meaney MJ, & Qiu A. (2014). Gestational Age and Neonatal Brain Microstructure in Term Born Infants: A Birth Cohort Study. PLoS ONE, 9(12), e115229. 10.1371/journal.pone.0115229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budde MD, Janes L, Gold E, Turtzo LC, & Frank JA (2011). The contribution of gliosis to diffusion tensor anisotropy and tractography following traumatic brain injury: Validation in the rat using Fourier analysis of stained tissue sections. Brain, 134(8), 2248–2260. 10.1093/brain/awr161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgetova A, Seidl Z, Krasensky J, Horakova D, & Vaneckova M. (2010). Multiple sclerosis and the accumulation of iron in the Basal Ganglia: Quantitative assessment of brain iron using MRI t(2) relaxometry. European Neurology, 63(3), 136–143. 10.1159/000279305 [DOI] [PubMed] [Google Scholar]
- Cheng H-LM, Stikov N, Ghugre NR, & Wright GA (2012). Practical medical applications of quantitative MR relaxometry. Journal of Magnetic Resonance Imaging, 36(4), 805–824. 10.1002/jmri.23718 [DOI] [PubMed] [Google Scholar]
- Cherubini A, Péran P, Hagberg GE, Varsi AE, Luccichenti G, Caltagirone C, Sabatini U, & Spalletta G. (2009). Characterization of white matter fiber bundles with T relaxometry and diffusion tensor imaging. Magnetic Resonance in Medicine, 61(5), 1066–1072. 10.1002/mrm.21978 [DOI] [PubMed] [Google Scholar]
- Dean DC, Travers BG, Adluru N, Tromp DPM, Destiche DJ, Samsin D, Prigge MB, Zielinski BA, Fletcher PT, Anderson JS, Froehlich AL, Bigler ED, Lange N, Lainhart JE, & Alexander AL (2016). Investigating the Microstructural Correlation of White Matter in Autism Spectrum Disorder. Brain Connectivity, 6(5), 415–433. 10.1089/brain.2015.0385 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deoni SCL (2010). Quantitative Relaxometry of the Brain. Topics in Magnetic Resonance Imaging : TMRI, 21(2), 101–113. 10.1097/RMR.0b013e31821e56d8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deoni SCL, Dean DC, O’Muircheartaigh J, Dirks H, & Jerskey BA (2012). Investigating white matter development in infancy and early childhood using myelin water faction and relaxation time mapping. Neuroimage, 63(3), 1038–1053. 10.1016/j.neuroimage.2012.07.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eminian S, Hajdu SD, Meuli RA, Maeder P, & Hagmann P. (2018). Rapid high resolution T1 mapping as a marker of brain development: Normative ranges in key regions of interest. PLoS ONE, 13(6). 10.1371/journal.pone.0198250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelbrecht V, Rassek M, Preiss S, Wald C, & Mödder U. (1998). Age-dependent changes in magnetization transfer contrast of white matter in the pediatric brain. American Journal of Neuroradiology, 19(10), 1923–1929. [PMC free article] [PubMed] [Google Scholar]
- Geng X, Prom-Wormley EC, Perez J, Kubarych T, Styner M, Lin W, Neale MC, & Gilmore JH (2012). White Matter Heritability Using Diffusion Tensor Imaging in Neonatal Brains. Twin Research and Human Genetics : The Official Journal of the International Society for Twin Studies, 15(3), 336–350. 10.1017/thg.2012.14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genolini C, Alacoque X, Sentenac M, & Arnaud C. (2015). kml and kml3d: R Packages to Cluster Longitudinal Data. Journal of Statistical Software, 65(1), 1–34. 10.18637/jss.v065.i04 [DOI] [Google Scholar]
- Gönenç A, Frazier JA, Crowley DJ, & Moore CM (2010). COMBINED DIFFUSION TENSOR IMAGING AND TRANSVERSE RELAXOMETRY IN EARLY ONSET BIPOLAR DISORDER. Journal of the American Academy of Child and Adolescent Psychiatry, 49(12), 1260–1268. 10.1016/j.jaac.2010.08.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gracien R-M, Reitz SC, Hof S-M, Fleischer V, Zimmermann H, Droby A, Steinmetz H, Zipp F, Deichmann R, & Klein JC (2016). Assessment of cortical damage in early multiple sclerosis with quantitative T2 relaxometry. NMR in Biomedicine, 29(4), 444–450. 10.1002/nbm.3486 [DOI] [PubMed] [Google Scholar]
- Heng S, Song AW, & Sim K. (2010). White matter abnormalities in bipolar disorder: Insights from diffusion tensor imaging studies. Journal of Neural Transmission (Vienna, Austria: 1996), 117(5), 639–654. 10.1007/s00702-010-0368-9 [DOI] [PubMed] [Google Scholar]
- Holland BA, Haas DK, Norman D, Brant-Zawadzki M, & Newton TH (1986). MRI of normal brain maturation. AJNR. American Journal of Neuroradiology, 7(2), 201–208. [PMC free article] [PubMed] [Google Scholar]
- Hoque R, Ledbetter C, Gonzalez-Toledo E, Misra V, Menon U, Kenner M, Rabinstein AA, Kelley RE, Zivadinov R, & Minagar A. (2007). The Role of Quantitative Neuroimaging Indices in the Differentiation of Ischemia From Demyelination: An Analytical Study With Case Presentation. In International Review of Neurobiology (Vol. 79, pp. 491–519). Academic Press. 10.1016/S0074-7742(07)79022-0 [DOI] [PubMed] [Google Scholar]
- Howell BR, Ahn M, Shi Y, Godfrey JR, Hu X, Zhu H, Styner M, & Sanchez MM (2019). Disentangling the effects of early caregiving experience and heritable factors on brain white matter development in rhesus monkeys. NeuroImage, 197, 625–642. 10.1016/j.neuroimage.2019.04.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahanshad N, Kochunov P, Sprooten E, Mandl RC, Nichols TE, Almassy L, Blangero J, Brouwer RM, Curran JE, de Zubicaray GI, Duggirala R, Fox PT, Hong LE, Landman BA, Martin NG, McMahon KL, Medland SE, Mitchell BD, Olvera RL, … Glahn DC (2013). Multi-site genetic analysis of diffusion images and voxelwise heritability analysis: A pilot project of the ENIGMA–DTI working group. NeuroImage, 81, 455–469. 10.1016/j.neuroimage.2013.04.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, & Smith SM (2012). FSL. NeuroImage, 62(2), 782–790. 10.1016/j.neuroimage.2011.09.015 [DOI] [PubMed] [Google Scholar]
- Johnson CP, Follmer RL, Oguz I, Warren LA, Christensen GE, Fiedorowicz JG, Magnotta VA, & Wemmie JA (2015). Brain abnormalities in bipolar disorder detected by quantitative T1ρ mapping. Molecular Psychiatry, 20(2), 201–206. 10.1038/mp.2014.157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK, Knösche TR, & Turner R. (2013). White matter integrity, fiber count, and other fallacies: The do’s and don’ts of diffusion MRI. NeuroImage, 73, 239–254. 10.1016/j.neuroimage.2012.06.081 [DOI] [PubMed] [Google Scholar]
- Kalin NH (2004). The Role of the Central Nucleus of the Amygdala in Mediating Fear and Anxiety in the Primate. Journal of Neuroscience, 24(24), 5506–5515. 10.1523/JNEUROSCI.0292-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kecskemeti S, & Alexander AL (2020). Three-dimensional motion-corrected T1 relaxometry with MPnRAGE. Magnetic Resonance in Medicine, 84(5), 2400–2411. 10.1002/mrm.28283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kecskemeti S, Samsonov A, Hurley SA, Dean DC, Field A, & Alexander AL (2016). MPnRAGE: A technique to simultaneously acquire hundreds of differently contrasted MPRAGE images with applications to quantitative T1 mapping. Magnetic Resonance in Medicine, 75(3), 1040–1053. 10.1002/mrm.25674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kecskemeti S, Samsonov A, Velikina J, Field AS, Turski P, Rowley H, Lainhart JE, & Alexander AL (2018). Robust Motion Correction Strategy for Structural MRI in Unsedated Children Demonstrated with Three-dimensional Radial MPnRAGE. Radiology, 289(2), 509–516. 10.1148/radiol.2018180180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MJ, & Whalen PJ (2009). The structural integrity of an amygdala-prefrontal pathway predicts trait anxiety. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience, 29(37), 11614–11618. 10.1523/JNEUROSCI.2335-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight MJ, Wearn A, Coulthard E, & Kauppinen RA (2019). T2 Relaxometry and Diffusion Tensor Indices of the Hippocampus and Entorhinal Cortex Improve Sensitivity and Specificity of MRI to Detect Amnestic Mild Cognitive Impairment and Alzheimer’s Disease Dementia. Journal of Magnetic Resonance Imaging, 49(2), 445–455. 10.1002/jmri.26195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov P, Glahn DC, Lancaster JL, Winkler AM, Smith S, Thompson PM, Almasy L, Duggirala R, Fox PT, & Blangero J. (2010). Genetics of microstructure of cerebral white matter using diffusion tensor imaging. NeuroImage, 53(3), 1109–1116. 10.1016/j.neuroimage.2010.01.078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov P, Jahanshad N, Marcus D, Winkler A, Sprooten E, Nichols TE, Wright SN, Hong LE, Patel B, Behrens T, Jbabdi S, Andersson J, Lenglet C, Yacoub E, Moeller S, Auerbach E, Ugurbil K, Sotiropoulos SN, Brouwer RM, … Van Essen DC (2015). Heritability of Fractional Anisotropy in Human White Matter: A Comparison of Human Connectome Project and ENIGMA-DTI Data. NeuroImage, 111, 300–311. 10.1016/j.neuroimage.2015.02.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov P, Jahanshad N, Sprooten E, Nichols TE, Mandl RC, Almasy L, Booth T, Brouwer RM, Curran JE, de Zubicaray GI, Dimitrova R, Duggirala R, Fox PT, Hong LE, Landman BA, Lemaitre H, Lopez L, Martin NG, McMahon KL, … Glahn DC (2014). Multi-site study of additive genetic effects on fractional anisotropy of cerebral white matter: Comparing meta and mega analytical approaches for data pooling. NeuroImage, 95, 136–150. 10.1016/j.neuroimage.2014.03.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazari A, & Lipp I. (2021). Can MRI measure myelin? Systematic review, qualitative assessment, and metaanalysis of studies validating microstructural imaging with myelin histology. NeuroImage, 230, 117744. 10.1016/j.neuroimage.2021.117744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebel C, & Deoni S. (2018). The Development of Brain White Matter Microstructure. NeuroImage, 182, 207–218. 10.1016/j.neuroimage.2017.12.097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leppert IR, Almli CR, McKinstry RC, Mulkern RV, Pierpaoli C, Rivkin MJ, & Pike GB (2009). T2 relaxometry of normal pediatric brain development. Journal of Magnetic Resonance Imaging, 29(2), 258–267. 10.1002/jmri.21646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Z, Adluru N, Dean DC, Alexander AL, & Goldsmith HH (2021). Genetic and environmental influences of variation in diffusion MRI measures of white matter microstructure. Brain Structure and Function. 10.1007/s00429-021-02393-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mamere AE, Saraiva L.a. L., Matos ALM, Carneiro A. a. O, & Santos AC (2009). Evaluation of Delayed Neuronal and Axonal Damage Secondary to Moderate and Severe Traumatic Brain Injury Using Quantitative MR Imaging Techniques. American Journal of Neuroradiology, 30(5), 947–952. 10.3174/ajnr.A1477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masumura M. (1987). Proton relaxation time of immature brain. Child’s Nervous System, 3(1), 6–11. 10.1007/BF00707186 [DOI] [PubMed] [Google Scholar]
- McGarry BL, Rogers HJ, Knight MJ, Jokivarsi KT, Gröhn OHJ, & Kauppinen RA (2016). Determining Stroke Onset Time Using Quantitative MRI: High Accuracy, Sensitivity and Specificity Obtained from Magnetic Resonance Relaxation Times. Cerebrovascular Diseases Extra, 6(2), 60–65. 10.1159/000448814 [DOI] [Google Scholar]
- Nelson EE, & Winslow JT (2009). Non-Human Primates: Model Animals for Developmental Psychopathology. Neuropsychopharmacology, 34(1), 90–105. 10.1038/npp.2008.150 [DOI] [PubMed] [Google Scholar]
- Olson I, Von Der Heide R, Alm K, & Vyas G. (2015). Development of the Uncinate Fasciculus: Implications for Theory and Developmental Disorders. Developmental Cognitive Neuroscience, 34. 10.1016/j.dcn.2015.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou X, Glasier CM, Ramakrishnaiah RH, Kanfi A, Rowell AC, Pivik RT, Andres A, Cleves MA, & Badger TM (2017). Gestational Age at Birth and Brain White Matter Development in Term-Born Infants and Children. American Journal of Neuroradiology, 38(12), 2373–2379. 10.3174/ajnr.A5408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ouyang M, Dubois J, Yu Q, Mukherjee P, & Huang H. (2019). Delineation of early brain development from fetuses to infants with diffusion MRI and beyond. NeuroImage, 185, 836–850. 10.1016/j.neuroimage.2018.04.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paus T, Collins DL, Evans AC, Leonard G, Pike B, & Zijdenbos A. (2001). Maturation of white matter in the human brain: A review of magnetic resonance studies. Brain Research Bulletin, 54(3), 255–266. 10.1016/S0361-9230(00)00434-2 [DOI] [PubMed] [Google Scholar]
- Phillips KA, Bales KL, Capitanio JP, Conley A, Czoty PW, ‘t Hart BA, Hopkins WD, Hu S-L, Miller LA, Nader MA, Nathanielsz PW, Rogers J, Shively CA, & Voytko ML (2014). Why Primate Models Matter. American Journal of Primatology, 76(9), 801–827. 10.1002/ajp.22281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierpaoli C, & Basser PJ (1996). Toward a quantitative assessment of diffusion anisotropy. Magnetic Resonance in Medicine, 36(6), 893–906. 10.1002/mrm.1910360612 [DOI] [PubMed] [Google Scholar]
- Sacchet MD, & Gotlib IH (2017). Myelination of the brain in Major Depressive Disorder: An in vivo quantitative magnetic resonance imaging study. Scientific Reports, 7(1), 2200. 10.1038/s41598017-02062-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito N, Sakai O, Ozonoff A, & Jara H. (2009). Relaxo-volumetric multispectral quantitative magnetic resonance imaging of the brain over the human lifespan: Global and regional aging patterns. Magnetic Resonance Imaging, 27(7), 895–906. 10.1016/j.mri.2009.05.006 [DOI] [PubMed] [Google Scholar]
- Selya AS, Rose JS, Dierker LC, Hedeker D, & Mermelstein RJ (2012). A Practical Guide to Calculating Cohen’s f2, a Measure of Local Effect Size, from PROC MIXED. Frontiers in Psychology, 3, 111. 10.3389/fpsyg.2012.00111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syka M, Keller J, Klempíř J, Rulseh AM, Roth J, Jech R, Vorisek I, & Vymazal J. (2015). Correlation between Relaxometry and Diffusion Tensor Imaging in the Globus Pallidus of Huntington’s Disease Patients. PLOS ONE, 10(3), e0118907. 10.1371/journal.pone.0118907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tromp DPM, Fox AS, Oler JA, Alexander AL, & Kalin NH (2019). The Relationship Between the Uncinate Fasciculus and Anxious Temperament Is Evolutionarily Conserved and Sexually Dimorphic. Biological Psychiatry, 86(12), 890–898. 10.1016/j.biopsych.2019.07.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warntjes JBM, Persson A, Berge J, & Zech W. (2017). Myelin Detection Using Rapid Quantitative MR Imaging Correlated to Macroscopically Registered Luxol Fast Blue–Stained Brain Specimens. AJNR: American Journal of Neuroradiology, 38(6), 1096–1102. 10.3174/ajnr.A5168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Workman AD, Charvet CJ, Clancy B, Darlington RB, & Finlay BL (2013). Modeling Transformations of Neurodevelopmental Sequences across Mammalian Species. Journal of Neuroscience, 33(17), 7368–7383. 10.1523/JNEUROSCI.5746-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zakszewski E, Adluru N, Tromp DPM, Kalin N, & Alexander AL (2014). A diffusion-tensor-based white matter atlas for rhesus macaques. PloS One, 9(9), e107398. 10.1371/journal.pone.0107398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Brady M, & Smith S. (2001). Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Transactions on Medical Imaging, 20(1), 45–57. 10.1109/42.906424 [DOI] [PubMed] [Google Scholar]
- Zhang Y, & Shi L. (1993). Phylogeny of rheusus monkeys (Macaca mulatta) as revealed by mitochondrial DNA restriction enzyme analysis. International Journal of Primatology, 14(4), 587–605. 10.1007/BF02215449 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Project data pertaining to this study can be found here: https://doi.org/10.5061/dryad.7m0cfxpvx. Additional imaging data, along with the code used for these analyses, may be able to be shared with interested parties upon request by contacting the corresponding author.