Institutional incentives for the evolution of committed cooperation: ensuring participation is as important as enhancing compliance

Abstract

Both conventional wisdom and empirical evidence suggest that arranging a prior commitment or agreement before an interaction takes place enhances the chance of reaching mutual cooperation. Yet it is not clear what mechanisms might underlie the participation in and compliance with such a commitment, especially when participation is costly and non-compliance can be profitable. Here, we develop a theory of participation and compliance with respect to an explicit commitment formation process and to institutional incentives where individuals, at first, decide whether or not to join a cooperative agreement to play a one-shot social dilemma game. Using a mathematical model, we determine whether and when participating in a costly commitment, and complying with it, is an evolutionarily stable strategy, resulting in high levels of cooperation. We show that, given a sufficient budget for providing incentives, rewarding of commitment compliant behaviours better promotes cooperation than punishment of non-compliant ones. Moreover, by sparing part of this budget for rewarding those willing to participate in a commitment, the overall level of cooperation can be significantly enhanced for both reward and punishment. Finally, the presence of mistakes in deciding to participate favours evolutionary stability of commitment compliance and cooperation.

1. Introduction

Commitments, such as contracts and agreements, are fundamental components of many social and economic interactions, ranging from personal, to institutional, to political or religious ones, in order to ensure a mutually beneficial outcome for the parties involved [1–7]. Arranging a prior commitment from all parties involved before an interaction improves the chance that people can reach mutual cooperation when individual interests are in conflict [8–10]. In most modern societies, institutions are created to enforce formal contracts and enhance cooperation, through suitable incentive structures such as punishment for wrongdoing [6,11,12]. People joining a religion share certain norms and expectations and might expect certain rewards and punishments for a given behaviour [5,13]. Commitments are important in the context of computerized multi-agent systems, where they are formalized as a tool for regulating agents’ interactions and collective behaviour [14].

Evolutionary game theory (EGT) [15] provides an appropriate tool to study the evolution of cooperative behaviour in social dilemmas, as they are governed by institutional incentives [7,16–22] and prior commitments [1,23–25]. However, prior works have not examined the interplay between different forms of incentive and commitment behaviours, including participation in and compliance with a prior commitment. On the one hand, existing institutional incentive models do not capture the commitment formation process explicitly [7,16,19,20,22]. These works fail to consider the need for improving participation in a commitment before the interaction. Indeed, since participating in a commitment usually involves a cost, for example initial time and effort spent setting up the commitment [26] and/or membership fees [27], and requires the involved parties to follow certain restrictive terms and conditions, such participation might need to be encouraged. Examples of incentives for encouraging participation are many, and have been shown to be crucial for ensuring a positive outcome, as in the contexts of climate change agreements [28], healthcare programmes for reducing smoking during pregnancy [26] and diabetes [29]. Lottery was used as a form of reward for participation in COVID-19 vaccination in many countries including the USA [30].

On the other hand, existing models of commitment formation assume that a compensation from a commitment-violating player is transferred internally to a commitment-compliant co-player, via institutional enforcement [24,31–33]. These works have thus been limited in considering what alternative mechanisms can ensure high levels of commitment compliance and cooperation. For instance, as will be analysed below, one might ask whether positive (reward) or negative (punishment) incentive is more efficient, to that end. Moreover, similar to the aforementioned institutional incentive models, these works fail to consider the possibility that enhancing participation in a commitment before interaction can maximize the benefit provided by commitments for promoting the evolution of cooperation.

Here, we aim to fill this gap by investigating, theoretically, how to distribute a per capita incentive budget effectively between enhancing the level of participation in a commitment and ensuring compliance with any adopted commitment, thereby optimizing the overall level of cooperation. Our analysis is carried out in the context of the one-shot Prisoner's Dilemma (PD) game, in which players can either cooperate (C) or defect (D). Before a PD game, players can choose whether or not to join a commitment and cooperate in the game. The commitment is formed if both players commit, and the players can decide how to act in the game conditionally on whether such a commitment is formed or not. In the former case, the committed players share a participation cost (denoted by ε, see also table 2) as a fee for maintaining the institution that provides incentives.

Table 2.

Model parameters.

parameter	symbol
population size	N
cost of cooperation	c
benefit of cooperation	b
intensity of selection	β
per capita budget	u
fraction of the budget for rewarding participation	α
cost of commitment participation	$ϵ$
error probability in participating in a commitment	χ

The present analysis is based on two well-adopted, complementary approaches in EGT, namely, evolutionarily stable strategies (ESS analysis) [34,35] and finite population dynamics [15,36]. While the former allows a simple assessment of when a strategy can resist invasion from all other strategies in a population (i.e. being an ESS), it does not capture the detailed stochastic dynamics among all strategies in co-presence. This drawback is overcome with the latter approach. We determine when participating in a costly commitment, and complying with it, is an ESS and promotes the evolution of enhanced cooperation. We examine which incentive, reward of commitment compliant behaviours or punishment of non-compliant ones, is more efficient to this end, and when. This analysis sheds light on whether the cooperation outcome can be enhanced by sparing part of the incentive budget for encouraging participation in a commitment despite reducing the incentive budget available for promoting compliant behaviours. Finally, we examine the impact of noise in a participation decision on the stability of commitment compliance and cooperation.

2. Models and methods

2.1. Model

We consider a well-mixed population of individuals who, before an interaction, can choose whether or not to voluntarily join a prior commitment dictating that, if it is formed, they then must cooperate in the interaction. Interactions are modelled using the one-shot PD game with a pay-off matrix of the form

2.1

If both players choose C (D), they both receive the same reward R (penalty P) for mutual cooperation (mutual defection). Unilateral cooperation provides the sucker’s pay-off S for the cooperative player and the temptation to defect T for the defecting one. The pay-off matrix corresponds to the preferences associated with the PD when the parameters satisfy the ordering, T > R > P > S [37]. To provide a clearer interpretation of analytical conditions presented below, we sometimes reduce the PD to its special case, the donation game [15], where T = b, R = b − c, P = 0, S = −c, with b and c standing for the benefit and cost of cooperation, respectively.

We perform a comprehensive analysis where the full set of strategies is considered. Namely, given that players can choose (i) whether to accept (A) or not (N) to join a prior commitment before a PD game, (ii) to cooperate (C) or defect (D) in the PD if the commitment is formed and (iii) to cooperate (C) or defect (D) in the PD if the commitment is not formed, in total we can define eight possible strategies. They are denoted as ACC, ACD, ADC, ADD, NCC, NCD, NDC and NDD, as summarized in table 1. Also, recall that a commitment is formed when both players in a PD commit and in that case the committed players share a participation cost ε.

Table 1.

The eight strategies with commitment/agreement formation.

strategies	accept commitment?	cooperate in presence of commitment?	cooperate in absence of commitment?
ACC	yes	yes	yes
ACD	yes	yes	no
ADC	yes	no	yes
ADD	yes	no	no
NCC	no	yes	yes
NCD	no	yes	no
NDC	no	no	yes
NDD	no	no	no

We assume that there is a per capita budget u available for providing incentives. A fraction of the budget, αu (0 ≤ α ≤ 1), is used for rewarding those who are willing to participate in a commitment (i.e. AXY players for X, Y ∈ {C, D}), increasing the chance of a commitment being formed. The remaining budget, i.e. (1 − α)u, is used for rewarding commitment-compliant players (i.e. ACC and ACD players) or punishing non-compliant ones (i.e. ADC and ADD players). When α = 0, it means the budget is used only for incentivizing commitment-compliant behaviours (i.e. pure reward and pure punishment scenarios). As we consider reward and punishment separately, without loss of generality, we assume that all the incentives described above are equally cost-efficient, where the incentive recipient’s increased or decreased amount (corresponding to reward and punishment, respectively) equals the institution’s cost.

Finally, consider that, with some small probability χ, an error might occur when players decide whether to join a commitment. It can be due to fuzzy mind or trembling hands, as well as miscommunication or environmental noise. We show that this type of noise strongly influences evolutionary dynamics, even in favour of cooperation and commitment compliance. In the electronic supplementary material, we also study other types of noise that occur in an PD interaction.

The model parameters are summarized in table 2. Next, the derivation of pay-off matrices for all the scenarios described above is provided.

2.1.1. In the absence of participation errors

First, when incentives are not in use, i.e. the no policy scenario (that is, when u = 0), the pay-off matrix for the eight strategies (table 1), reads (for row player)

2.2

An observation is that NDD and NCD are equivalent, so are NCC and NDC, because an agreement is only formed when both players agree to join. Thus, when one of these strategists are involved in an interaction, a commitment is never formed and only the move in the absence of a commitment matters. Moreover, ACC and ACD are neutral, so are ADC and ADD.

When a per capita budget u is available to reward commitment compliant behaviours, with a fraction α of it being used for rewarding participation, the pay-off matrix reads When a per capita budget u is available to reward commitment compliant behaviours, with a fraction α of it being used for rewarding participation, the pay-off matrix reads

When a per capita budget u is available to punish commitment non-compliant behaviours, with a fraction α of it being used for rewarding participation reads

where we denote γ₁ = T − ε/2 + (2α − 1)u, γ₂ = P − ε/2 + (2α − 1)u, γ₃ = R − ε/2 + αu and γ₄ = S − ε/2 + αu, just for the purpose of a neat presentation.

2.1.2. In the presence of participation errors

We assume that with a small probability χ, players made an error in the decision whether or not to join an agreement in the commitment formation stage (e.g. due to fuzzy mind or trembling hands). All the pay-off matrices above can be re-written as follows. Denote $\hspace{0.17em}\overline{A}=N$, $\overline{N}=A$, $\overline{C}=D$ and $\overline{D}=C$. For $\Pi \in \{{\Pi }_0,{\Pi }_R,{\Pi }_P\};\hspace{0.17em}{P}_j\in \{A,N\};\hspace{0.17em}{X}_j,Y_j\in \{C,D\}$, the pay-off when a player P₁X₁Y₁ against P₂X₂Y₂, ${\Pi }_{P_1{X}_1{Y}_1,P_2{X}_2{Y}_2}$, can be written as

$${(1-\chi )}^2{\Pi }_{P_1{X}_1{Y}_1,P_2{X}_2{Y}_2}+\chi (1-\chi )({\Pi }_{{\overline{P}}_1{X}_1{Y}_1,P_2{X}_2{Y}_2}+{\Pi }_{P_1{X}_1{Y}_1,{\overline{P}}_2{X}_2{Y}_2})+{\chi }^2{\Pi }_{{\overline{P}}_1{X}_1{Y}_1,\overline{P_2}{X}_2{Y}_2}.$$

2.2. Evolutionarily stable strategies

As common assumptions in ESS analysis [35], we assume that (i) mutations are rare and thus, there is at most one mutant strategy m at a time in a population of individuals with resident strategy r and (ii) mutant’s effect is negligible on the dynamics. To know if a strategy can be invaded or not by another, we need to compute the difference of absolute fitness between a mutant strategy in a population of resident strategy. If the fitness of the mutant is greater than that of the resident, the mutant invades the population and becomes resident. If the fitness of the mutant is lower, the mutant disappears and the resident resists invasion. When the two values of fitness are equal, the resident also resists invasion because in an infinitely large population, a mutant strategy cannot invade by drift. A strategy is ESS if it resists invasion from all other strategies.

2.3. Evolutionary dynamics in finite population

In finite population settings, individuals’ pay-offs represents their fitness or social success, and evolutionary dynamics is shaped by social learning [15,38], whereby the most successful agents will tend to be imitated more often by the other agents. In the current work, social learning is modelled using the so-called pairwise comparison rule [39], a standard approach in EGT, assuming that an agent A with fitness f_A adopts the strategy of another agent B with fitness f_B with probability p given by the Fermi function, $p_{A,B}={(1+{\mathrm{e}}^{-\beta (f_B-f_A)})}^{-1}.$ The parameter β represents the ‘imitation strength’ or ‘intensity of selection’, i.e. how strongly the agents base their decision to imitate on fitness difference between themselves and the opponents. For β = 0, we obtain the limit of neutral drift—the imitation decision is random. For large β, imitation becomes increasingly deterministic. In line with previous works and human behavioural experiments [40–42], we set β = 0.1 in the main text.

In the absence of mutations or exploration, the end states of evolution are inevitably monomorphic: once such a state is reached, it cannot be escaped through imitation. We thus further assume that, with a certain mutation probability, an agent switches randomly to a different strategy without imitating another agent. In the limit of small mutation rates, the dynamics will proceed with, at most, two strategies in the population, such that the behavioural dynamics can be conveniently described by a Markov chain, where each state represents a monomorphic population, whereas the transition probabilities are given by the fixation probability of a single mutant [43,44]. The resulting Markov chain has a stationary distribution, which characterizes the average time the population spends in each of these monomorphic end states.

Let N be the size of the population. Denote π_X,Y the pay-off a strategist X obtains in a pairwise interaction with strategist Y (defined in the pay-off matrices). Suppose there are at most two strategies in the population, say, k agents using strategy A (0 ≤ k ≤ N) and (N − k) agents using strategies B. Thus, the (average) pay-off of the agent that uses A and B can be written as follows, respectively,

$$\begin{array}{cc}& {\mathit{\Pi }}_A(k)=\frac{(k-1){\pi }_{A,A}+(N-k){\pi }_{A,B}}{N-1}\\ \mathrm{and}& {\mathit{\Pi }}_B(k)=\frac{k{\pi }_{B,A}+(N-k-1){\pi }_{B,B}}{N-1}.\end{array}\}$$ 2.5

Now, the probability to change the number k of agents using strategy A by ± one in each time step can be written as [39]

$$T^{\pm }(k)=\frac{N-k}{N}\frac{k}{N}{[1+{\mathrm{e}}^{\mp \beta [{\mathrm{\Pi }}_A(k)-{\mathrm{\Pi }}_B(k)]}]}^{-1}.$$ 2.6

The fixation probability of a single mutant with a strategy A in a population of (N − 1) agents using B is given by [39,44]

$${\rho }_{B,A}={(1+\sum _{i=1}^{N-1}\prod _{\hspace{0.17em}j=1}^i\frac{T^{-}(j)}{T^{+}(j)})}^{-1}.$$ 2.7

Considering a set {1, …, q} of different strategies, these fixation probabilities determine a transition matrix $M={\{T_{ij}\}}_{i,j=1}^q$, with T_ij,j≠i = ρ_ji/(q − 1) and $T_{ii}=1-\sum _{\hspace{0.17em}j=1,j\ne i}^q{T}_{ij}$, of a Markov chain. The normalized eigenvector associated with the eigenvalue 1 of the transposed of M provides the stationary distribution described above [43], describing the relative time the population spends adopting each of the strategies.

2.3.1. Risk-dominance

An important measure to compare the two strategies A and B is which direction the transition is stronger or more probable, an A mutant fixating in a population of agents using B, ρ_B,A, or a B mutant fixating in the population of agents using A, ρ_A,B. It can be shown that the former is stronger, in the limit of large N, if [15,44]

$${\pi }_{A,A}+{\pi }_{A,B}>{\pi }_{B,A}+{\pi }_{B,B}.$$ 2.8

3. Results

3.1. ESS analysis: when complying with a cooperative commitment can be an evolutionarily stable strategy

In figure 1, we study which strategies can be ESS (see Methods) across the parameter space, namely for u ∈ [0, 3], $ϵ$ ∈ [0, 3], α ∈ [0, 1] and χ ∈ [0, 0.2]. We observe that, for reward, three strategies ACD, ADD, NDD can be ESS, while NCD can also be ESS in the case of punishment. ACD is the only ESS that leads to an overall cooperative outcome (i.e. cooperative ESS), where individuals choose to accept a prior commitment and comply with it. All other possible ESS lead to a defective outcome. Namely, ADD commits to cooperate but then dishonors the commitment and defects in the interaction, and both NDD and NCD refuse to commit and defect in the interaction.

Figure 1.

Both commitment compliant and non-compliant strategies can be ESS. We show which strategies can be ESS and their frequencies across the parameters space: u ∈ [0, 3] (increment 0.05), ε ∈ [0, 3] (increment 0.05), α ∈ [0, 1] (increment 0.05) and χ ∈ [0, 0.2] (increment 0.02), i.e. the total number of configurations is thus 61 × 61 × 21 × 11 = 859551. We show the number of times (if any) each strategy is an ESS. We observe that for reward, three strategies ACD, ADD and NDD can be ESS, while in the case of punishment, NCD can also be an ESS. Other parameters: R = 1, S = −1, T = 2, P = 0.

Figure 2 shows the number of times each strategy is an ESS, for varying u, ε, α and χ separately. We observe that, in the absence of errors when deciding whether to join a commitment (i.e. χ = 0), none of the strategies can be ESS (figure 2d), for both types of incentive. For any strategy, there is always another mutant strategy to which it is neutral to in the absence of errors; namely, for AXY, it is AXY^′, while for NXY, it is NX^′Y (where X ≠ X^′, Y ≠ Y^′ ∈ {C, D}). Intuitively, in the presence of a commitment, the decision of a commitment strategy outside a commitment does not matter, while in the absence of a commitment, the decision of a non-committing strategy inside a commitment does not matter too. When error is non-negligible (χ > 0), ACD, ADD and NDD can be ESS in the case of reward, while NCD can also be ESS in the case of punishment.

Figure 2.

For commitment compliance to be evolutionarily stable, it is necessary that noise be non-negligible and the incentive budget be sufficiently high. Considering the parameters space sampled as in figure 1, i.e. u ∈ [0, 3] (increment 0.05), ε ∈ [0, 3] (increment 0.05), α ∈ [0, 1] (increment 0.05) and χ ∈ [0, 0.2] (increment 0.02), we count the number of times each strategy is ESS for varying u (a), ε (b), α (c) and χ (d). We observe that for reward, three strategies ACD, ADD and NDD can be ESS, while in the case of punishment, NCD can also be an ESS. In particular, in both cases, commitment compliant behaviour (ACD) can be ESS only if u is sufficiently large, α is not too large, and χ is greater than zero. Other parameters: R = 1, S = −1, T = 2, P = 0.

Focusing on ACD, it can be an ESS only when a sufficient per capita budget u is available (covering at least the cost of cooperation, c = 1, see electronic supplementary material for analytical proof), for both types of incentive (figure 2a). It can be ESS for the whole range of ε being considered, i.e. up to 3.0 (figure 2b). A noteworthy difference between the two types of incentive is that, when ε is sufficiently large (approximately from 2.0 onward), the number of times ACD being ESS decreases in the case of punishment, while it remains stable in the case of reward. It implies that reward might outperform punishment for a larger range of ε. Moreover, a sufficient fraction of the budget (i.e. not too large α) needs to be spent for rewarding the compliant strategies or sanctioning the non-compliant ones (figure 2c). While the frequency of ACD to be ESS decreases with α for reward, it peaks at some intermediate value of α for punishment. This suggests that it might be more important to incentivize participation for punishment than for reward, in order to increase the chance of commitment compliant behaviour (ACD) to be evolutionarily stable.

In electronic supplementary material, figures S1 and S2, we show that the observations for reward do not change for varying the benefit to cost ratio b/c. For punishment, the frequency of ACD to be ESS increases with b/c, reaching a similar frequency as in the case of reward when b/c is sufficiently high (around b/c = 3). It implies that for commitment compliant behaviours to be evolutionarily stable, it requires the social dilemma interaction to be more beneficial in the case of punishment than reward. The frequency for NCD decreases with b/c, so that NCD is no longer an ESS when this ratio is sufficiently high.

Overall, the ESS analysis provides us with some initial insights regarding when commitment compliance (ACD) can be an evolutionarily viable strategy. However, it does not show the detailed dynamics of the whole system and is limited in quantitative characterization, e.g. of the overall cooperation level in the population for a given parameters’ configuration. Also, as studied below using a stochastic evolutionary dynamics approach, ACD and some other strategies can be the most frequent strategy in the population even when they are not ESS, for example, when noise is absent.

3.2. Reward versus punishment for promoting frequent committed cooperation

We comparatively study the capability of institutional reward and punishment for promoting the evolution of commitment-compliant behaviour and cooperation. We first focus on clarifying the effects of pure incentives, considering α = 0. We then study the effect of varying α, i.e. when part of the per capita incentive budget is used to reward participation in a commitment before an interaction. We also study the impact of having some small non-negligible error probability (χ > 0).

3.2.1. Pure incentives

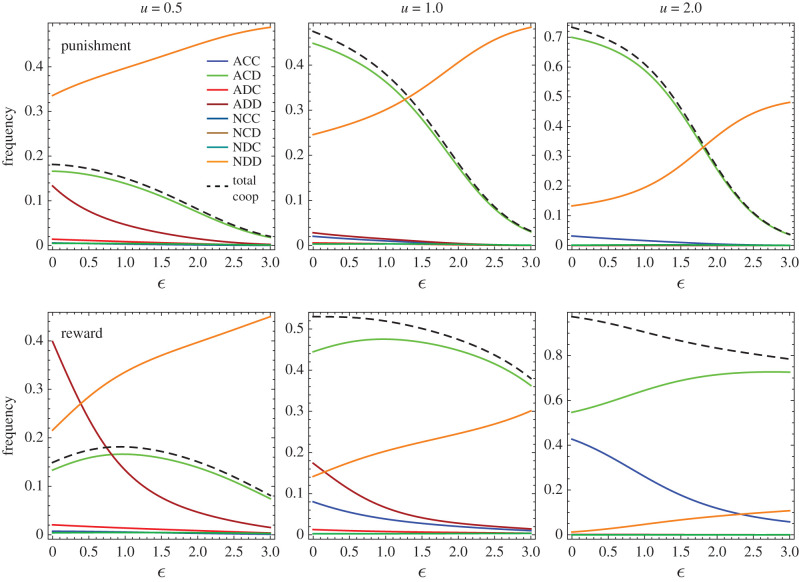
In figure 3, we compute the long-term frequency (i.e. stationary distribution) of the eight strategies (see Methods) under the pure reward and punishment policies, for varying ε and different values of u. Both reward and punishment can enable ACD to prevail when ε is small, given a sufficient budget u (u = 1 and 2). ACC is more frequent in the case of reward than punishment. ACD is frequent and even dominates the population, for a larger range of ε in the case of reward than punishment. As such, a higher level of overall population cooperation is achieved in the case of reward, for the whole range of $ϵ$. When u is small (u = 0.5), either ADD or NDD dominates the population, leading to the dominance of defection. NDD also dominates even when u is larger if ε is high, in the case of punishment.

Figure 3.

Pure incentives promote high levels of commitment compliance and cooperation. Depicted is the frequency of strategies when pure reward or punishment (α = 0) is applied, for different values of the per capita budget (u). Both reward and punishment allow ACD to prevail when ε is small. ACC is more frequent in the case of reward than punishment. ACD is frequent for a larger range of ε in the case of reward than punishment. These together lead to higher levels of cooperation in the case of reward than punishment, for the whole range of ε. Reward helps better suppress non-committers when ε is high, explaining its success. Other parameters: population size N = 100, R = 1, S = −1, T = 2, P = 0.

In the electronic supplementary material, we show the threshold of ε for which ACD is risk-dominant (see Methods) against all other strategies, except for ACC to which it is neutral. For α = 0, for a sufficient budget (namely, u > (T + P − R − S)/2 = 1), the thresholds are ε < 2(u + min{T − S, R − P}) and ε < 2min{T − S, R − P}, respectively, for reward and punishment. Thus, reward allows for a larger range of ε for which ACD is an evolutionarily viable strategy, having a high long-term frequency. Intuitively, reward enables a better suppression of non-committing strategies such as NDD because the latter do not suffer punishment since they do not commit, while reward provides a pay-off advantage for committing strategies against non-committing ones. Notably, the thresholds in numerical results are in accordance with these theoretical observations. For example, when u = 2.0, the threshold is ε < 2 for punishment and ε < 6 for reward. For u = 1.0, since ACD is also neutral to defective committers (ADC and ADD), ACD is most frequent in the population up to a slightly slower threshold than the theoretical one (i.e. ε < 2 for punishment ε < 4 for reward).

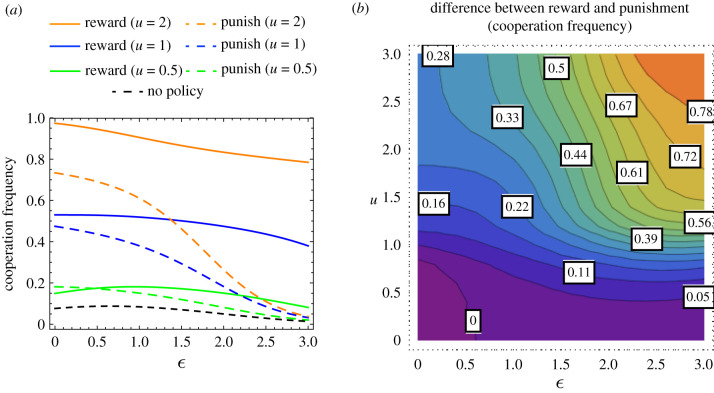
In figure 4, we compare the total cooperation frequency in the population obtained through applying pure reward and pure punishment, and also when no policy is applied. As can be seen, reward leads to a higher level of cooperation than punishment in most cases, except for when both u and ε are rather low. Also, we observe that the larger u and ε are, the more efficient reward is compared to punishment in terms of cooperation promotion (see figure 4b; also figure S3 in the electronic supplementary material). Figures S9 and S10 in the electronic supplementary material show that these observations are robust for varying the intensity of selection β.

Figure 4.

Reward leads to a higher level of cooperation than punishment provided a sufficient per capita budget u (the same for both incentives). (a) Frequency of cooperation as a function of ε when either reward of commitment compliant strategies (ACC and ACD) or punishment of non-compliant ones (ADC and ADD), is applied. The black dashed line corresponds to a reference scenario where no policy (i.e. u = 0) is applied. To ensure a high frequency of cooperation, a sufficient budget for providing incentives (u) is required. Cooperation is reduced when ε increases, for both reward and punishment. Nevertheless, reward leads to a higher level of cooperation than punishment in most cases, except for when both u and ε are sufficiently low (see u = 0.5 and $ϵ\lesssim 0.5$). (b) Contour plot showing the difference between cooperation obtained through reward and punishment, for varying u and ε. The larger u and ε are, the greater the difference is. Other parameters: population size N = 100, R = 1, S = −1, T = 2, P = 0, α = 0 (no reward for participation).

3.2.2. Incentives with rewarding participation

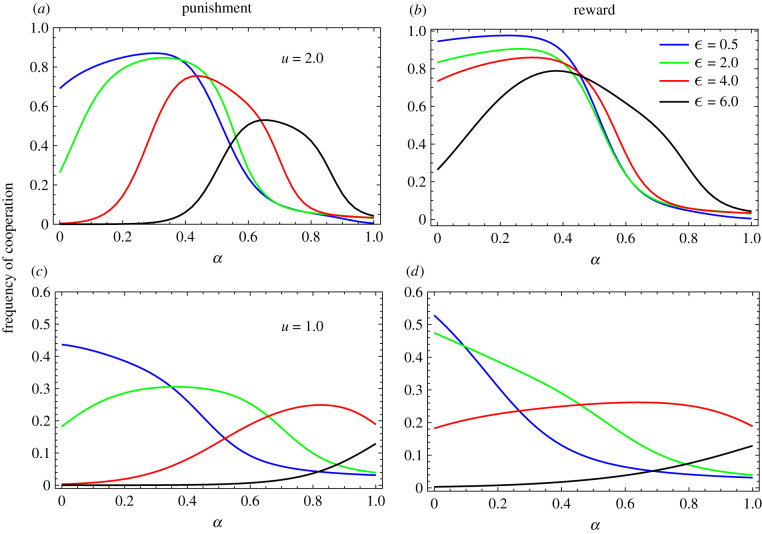
We show in figure 5, the frequency of cooperation obtained through reward or punishment when a fraction α of the per capita budget u is used for rewarding those who agree to participate. Note that the scenario where α = 0 reproduces the above described pure punishment and pure reward scenarios. For both types of incentive, reward of participation in a prior commitment can improve overall cooperation, especially with a larger available budget for incentive supply (compare top and bottom rows). We observe that, the larger the cost of commitment participation ε, the larger the fraction α of the budget should be used for rewarding participation in order for that population to reach the highest overall frequency of cooperation. Only when both u and ε are sufficiently small, it is better off not rewarding participation (see ε = 0.5 and u = 1.0).

Figure 5.

Rewarding participation can improve cooperation despite reducing the budget for incentivizing commitment compliant behaviour. Depicted is the frequency of cooperation as a function of the fraction of the budget for rewarding of participation (α), for different values of the cost of commitment participation ε. Punishment of non-compliant strategies (a,c) or reward of complaint ones (b,d), are applied as before, using the remaining budget after rewarding participation. We consider scenarios with a large (u = 2.0, top row, a,b) and small (u = 1.0, bottom row, c,d) per capita budget. When α = 0, it reproduces the results for pure punishment and reward. For both types of incentive, rewarding participation can improve the overall cooperation, especially for the larger u. For a larger ε, a larger fraction α of the budget should be used for rewarding participation to reach an optimal level of cooperation. Other parameters: N = 100, R = 1, S = −1, T = 2, P = 0.

With ${\alpha }^{\star }$ representing the value of α leading to the highest level of cooperation, figure 6 compares the level of cooperation obtained at $\alpha ={\alpha }^{\star }$, that when participation is not incentivized (i.e. α = 0), and that when no policy is in place. We observe that when u is small (u = 1.0), reward of participation leads to an improvement when ε is sufficiently large. When u is larger (u = 2.0), a significant improvement is observed for the whole range of ε being considered. In addition, we find that the improvement obtained through the reward of participation is greater for punishment than for reward, for both small and large u. This observation is in line with the ESS analysis above.

Figure 6.

Rewarding participation promotes higher levels of cooperation given a sufficient budget (u). We compare pure reward and punishment (solid red and blue lines) and when an optimal fraction (${\alpha }^{\star }$) of the budget is used for rewarding participation (red and blue dashed lines). When u is small (a), the improvement occurs when ε is sufficiently large. When u is large (b), participation can provide a large improvement for the whole range of ε. The improvement obtained through rewarding participation is more significant for punishment than for reward, for both small and large u. Other parameters: N = 100, R = 1, S = −1, T = 2, P = 0.

These notable results can be explained by looking at the frequency of strategies as a function of α, in figure S4 in the electronic supplementary material. As α approaches ${\alpha }^{\star }$, for both reward and punishment, the frequency of NDD decreases and those of ACD and ACC increase. This increase is more significant for punishment than for reward. When $\alpha >{\alpha }^{\star }$, ADD frequency starts to increase quickly and becomes dominant in the population since the remaining budget for incentivizing commitment-compliant behaviours becomes insufficient. Figure S6 in the electronic supplementary material shows that this observation is robust for other values of ε.

3.2.3. Non-negligible error in commitment participation

We study how non-negligible error when deciding whether to participate in a commitment (i.e. an AXY player would refuse to commit and act in the same way as a NXY player, and vice versa) impacts the evolutionary dynamics. When it is negligible (χ = 0), ACD cannot be an ESS nor risk-dominant against all other strategies in the population because it is always neutral to ACC. Interestingly, whenever this error probability is positive, ACD becomes always risk-dominant against ACC (see electronic supplementary material), thus making it likely to be more prevalent. Indeed, as shown in figure 7a,b depicting the frequency of the strategies and the overall level of cooperation as a function of χ, ACD becomes more frequent and ACC less frequent as χ increases. The impact is more significant in the case of reward than punishment. It leads to a slight increase in the overall level of cooperation in both cases. These observations are robust for other values of ε and u (see electronic supplementary material, figure S7).

Figure 7.

Commitment compliance and cooperation prevails in the presence of noise. (a,b) Frequency of strategies and the total level of cooperation for varying the noise probability at the commitment stage (χ), for pure punishment (a) and pure reward (b). The frequency of commitment-compliant strategy (ACD) increases in the presence of noise since it is now risk-dominant against ACC, which is not the case in the absence of noise. (c,d) Frequency of cooperation as a function of the fraction of the budget for rewarding participation (α), for different noise probabilities, for punishment (c) and reward (d). A lower optimal value of α is observed for a greater χ. Other parameters: population size N = 100, α = 0, ε = 0.5, u = 2, R = 1, S = −1, T = 2, P = 0.

Figure 7 shows that rewarding participation in a commitment can improve overall cooperation in the presence of error, especially in the case of punishment. For a larger error probability, we observe a smaller value of ${\alpha }^{\star }$ that leads to the highest level of cooperation, for both types of incentive. Moreover, we observe a slight increase in cooperation at ${\alpha }^{\star }$ for increasing χ. These observations are robust for other values of ε (see electronic supplementary material, figure S8).

4. Discussion

It has been suggested that human specialized capacity for commitment might have been shaped by natural selection [1,3,6]. Arranging a commitment from all parties involved prior to an interaction can increase the chance of reaching mutual cooperation [2,9,25,45], enabling individuals to clarify preferences or intentions from their partners before committing to a potentially costly course of actions [9,46–48]. Since individuals can decide whether not to honour an adopted commitment—there being abundant evidence of commitment breaching in both controlled experiments and real-world scenarios [6,10,45,49]—it is important to understand what mechanisms, such as positive and negative incentives, are more efficient at ensuring the cooperation-promoting benefit provided by commitments.

Herein, we have comparatively explored institutional punishment of commitment violators and reward of commitment fulfillers as potential mechanisms to enhance commitment compliance and thus the overall cooperation in the population. We have shown that, given the same, sufficiently high, per capita budget for supplying incentives, reward results in a higher level of commitment compliance and cooperation than punishment. Reward can ensure commitment compliance to be evolutionarily stable for a larger range of the commitment cost (ε) and benefit to cost ratio (b/c). This observation has useful implications for the design of institutional mechanisms for promoting pro-social behaviour, especially when communication is allowed to establish prior commitments/agreements [2,6,9]. It is important to note that the observation was obtained under the assumption that reward and punishment are equivalently cost-efficient (see Model), i.e. given the same per capita incentive budget u, they make the same impact in terms of pay-off increase or reduction, respectively, to the incentive recipient. Also, it might be more costly for institutions to provide rewards when compliant behaviour is frequent. Thus, an interesting direction is to consider how to combine reward and punishment in a cost-efficient way, taking into account that they might have different levels of cost-efficiency, as have been done in the context of social dilemmas (without considering commitment-based behaviours) [7,16–19,21]. Our results suggest that further behavioural experiments are needed to examine what incentive mechanisms are efficient and preferred (by people) for ensuring the commitment compliance and cooperation. Note that, similar to the theoretical modelling literature of incentives (see Introduction), there has been a body of behavioural experimental works comparing the effectiveness of reward and punishment for promoting cooperation in social dilemmas, see e.g. [50–52]. However, they have not studied reward and punishment in the presence of prior commitments.

Participating in a commitment can be quite costly and that might discourage players from joining the commitment in the first place. We hypothesized that by spending part of the per capita budget to incentivize participation before interaction, higher levels of compliance and cooperation might be achievable. Indeed, we have shown that the larger the cost of participation (ε), the greater fraction of this budget should to be used for encouraging participation to achieve an optimal level of cooperation. This observation confirms the importance of studying incentives in models considering an explicit process of commitment formation, which has been omitted in extant models of institutional incentives [16,18–20,22,53]. Indeed, these works have not considered commitment-based interactions nor incentives for encouraging participation in the interaction, nor its impact on the overall cooperation.

In a cooperative interaction, environmental noise is usually expected to lead to a detrimental impact on the emergence and stability of cooperation [15,54,55] and thus requires additional supporting mechanisms such as apology and forgiveness [33,56]. Surprisingly, we have shown here that the presence of some noise that causes errors when deciding to participate in a prior commitment, can stabilize commitment compliance and cooperation. In fact, ACD can be an ESS and risk-dominant against all other strategies only when the error probability is non-zero (χ > 0). A non-negligible level of noise enables ACD to break ties with the commitment-accepting unconditional cooperators (ACC), who cooperate even when a commitment is not formed and thus can be easily exploited by non-committing defectors. In the electronic supplementary material, we also considered execution noise that happens during the PD game. We showed that it has insignificant effects on the evolutionary dynamics and ESS analysis (e.g. none of the strategies can be an ESS for this type of noise).

A drawback of pro-social incentives for promoting cooperation is the possibility of antisocial reward and punishment where defectors might punish cooperators or reward other defectors, hence hindering the evolution of cooperation [57–60]. We argue that this issue disappears when a prior commitment is arranged since it becomes clear what behaviour is expected from all parties involved during the interaction. Only those who commit to cooperate can be punished for defection or rewarded for cooperation. It is not deemed justifiable to punish defectors or reward cooperators if they did commit in the first place. That is, commitments enable the freedom of choice from players, which can be important in cases where it might be contestable whether a behaviour is good [61], or when players might not be capable of cooperation, for example due to other commitments or lack of resources to carry it out.

When employing institutional incentives for sustaining pro-social behaviours, an important issue is how to set up and maintain a sufficient incentive budget. The problem of who contributes to this budget is a social dilemma in itself, and how to overcome it is a challenging problem. Several solutions have been proposed recently, including pool incentives with second-order punishments [20], democratic decisions [62] and positive and negative incentives combination [16,19]. In this work, we assume that an institution exists to facilitate the incentive providing process for promoting compliance and participation in an agreement, where those who agree to join a prior commitment contribute a participation fee (ε) to help sustain the institution. Future works might consider other non-institutional mechanisms that might underline commitment compliance and participation, such as reputation-based mechanisms (for instance, those who dishonour an adopted commitment are assigned low reputation scores) [63–65] and emotional incentives (e.g. players might feel more guilty about breaching a commitment than a mere wrongdoing without a prior commitment) [6,66,67], and even how these mechanisms might interplay and be combined with the institutional approach for further improvement [6].

Evolutionary modelling and analysis of voluntary participation has been considered in several studies [7,20,68–71], showing that cooperation can evolve even in one-shot cooperation dilemmas if players have the option to opt out. However, these works did not consider strategies conditioned on the formation of a commitment, nor incentives for encouraging the participation in it. Typically, only a subset of unconditional strategies were considered, including cooperators, defectors and non-participants. Here, we have examined a full set of strategies (table 1). In contrast to these studies, we have shown that the evolutionarily stable strategies often exhibit behaviours conditional on the formation of commitment being formed, e.g. ACD and NDC are ESS (see again figure 1). Given this crucial limitation of previous works, our model here provides a more complete picture of how prior commitments such as formal and informal contracts and agreements provide an efficient mechanism for promoting the evolution of cooperation.

In short, we have analysed here different forms of institutional incentive for promoting participation and compliance in interactions with a prior commitment formation. Our results have shown that, in this setting, using incentives for ensuring participation is as important as for enhancing compliance.

Data accessibility

All scripts used in this study are openly accessible through https://github.com/StochasticBiology/boolean-efflux.git. The data are provided in the electronic supplementary material [72].

Authors' contributions

T.A.H. designed the research, developed the model, implemented software, carried out the analysis and wrote the manuscript. T.A.H.: conceptualization, formal analysis, funding acquisition, investigation, methodology, software, validation, visualization, writing—original draft, writing—review and editing.

Competing interests

We declare we have no competing interests.

Funding

This research is supported by a Leverhulme Research Fellowship ‘Incentives for Commitment Compliance’ (RF-2020-603/9).