Viscoelastic analysis of mussel threads reveals energy dissipative mechanisms

Abstract

Mussels use byssal threads to secure themselves to rocks and as shock absorbers during cyclic loading from wave motion. Byssal threads combine high strength and toughness with extensibility of nearly 200%. Researchers attribute tensile properties of byssal threads to their elaborate multi-domain collagenous protein cores. Because the elastic properties have been previously scrutinized, we instead examined byssal thread viscoelastic behaviour, which is essential for withstanding cyclic loading. By targeting protein domains in the collagenous core via chemical treatments, stress relaxation experiments provided insights on domain contributions and were coupled with in situ small-angle X-ray scattering to investigate relaxation-specific molecular reorganizations. Results show that when silk-like domains in the core were disrupted, the stress relaxation of the threads decreased by nearly 50% and lateral molecular spacing also decreased, suggesting that these domains are essential for energy dissipation and assume a compressed molecular rearrangement when disrupted. A generalized Maxwell model was developed to describe the stress relaxation response. The model predicts that maximal damping (energy dissipation) occurs at around 0.1 Hz which closely resembles the wave frequency along the California coast and implies that these materials may be well adapted to the cyclic loading of the ambient conditions.

1. Background

Mussel byssal threads are essentially ‘fast’ mini-tendons formed in 1–5 min and immediately recruited into load-bearing service [1–3]. Similar to vertebrate tendons, byssal distal threads are highly anisotropic with parallel staggered arrays of collagens organized as bundles [4–6]. Although byssal threads exhibit strength and modulus comparable with tendon, they extend nearly 10-fold more than tendon [6–10]. Such deformability endows threads with impressive hysteresis and toughness, which, at approximately 45 MJ m⁻³, is comparable to that of Kevlar (table 1) [6,10,11]. In addition, threads can recover their mechanical properties after undergoing yield despite being completely acellular, whereas tendon damage requires cell-mediated repair [2,5,10]. The high toughness and hysteresis properties indicate that these threads use adaptive mechanisms to dissipate energy not possible in typical tendons.

Table 1.

Comparison of some mechanical properties of byssal distal thread with those of tendon and Kevlar. Tendon and Kevlar data were selected from [8].

material	modulus (GPa)	strength (GPa)	extensibility (mm/mm−1)	hysteresis (%)	toughness (MJ/m−3)
distal thread	0.9	0.08	1.10	72	45
collagen (tendon)	1.2	0.12	0.13	10	6
Kevlar	130	3.60	0.03	nd	50

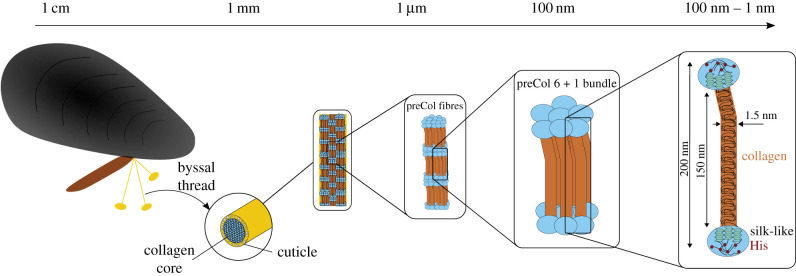
Many of the mechanical properties of byssal threads have been credited to their hierarchical composite assembly (figure 1) [2,4,5,12–16]. Individual threads are composed of a proximal region, which typically lies within the shell of the mussel, and a distal region, which extends from the shell to the plaque. The fibrous core of the distal thread (diameter approx. 150 µm) is encapsulated by a stiff outer cuticle (thickness ≤5 µm) [17–19]. The core is composed of a network of complex, collagenous, multi-domain proteins named preCols that resemble pentablock copolymers. The preCols assemble in 6 + 1 bundles which, in turn, come together to form highly ordered fibrils that are orientated parallel to the long axis of the thread [4,5,12,15,20]. The preCols have three distinct protein domains that are organized quasi-symmetrically. Starting at the N-terminus, the organization is as follows: an unstructured histidine (His)-rich N-terminus, an alanine/glycine-rich silk-like domain, a kinked central collagen core, an alanine-rich silk-like domain and finally another unstructured His-rich domain at the C-terminus (figure 1).

Figure 1.

The hierarchical assembly of mussel byssal threads spans multiple length scales. Each thread is composed of a collagen core encapsulated by a stiff cuticle. The thread core is comprised of highly ordered collagen fibres made up of preCols arranged in 6 + 1 bundles. Individual preCols are composed of a central triple helix collagen, followed by silk-like domains on both ends with His-rich domains flanking the silk-like domains.

Numerous studies have been conducted on mussel distal threads focused around the materials' elastic response [2,8–10,21–23]. Based on these studies, several energy dissipative mechanisms have been proposed. One of the postulated mechanisms is that energy is dissipated via the breaking of metal coordinate cross-links in the His-rich domains as the threads are loaded [2,10]. Another proposed mechanism is that the polyalanine and polyglycine β-sheets contained in silk-like domains unfold and reorient during the yielding phase, further contributing to energy dissipation [13]. Although these studies have shed light on many of the threads' mechanical properties, they fail to account for viscoelastic effects in the material [7,24]. Understanding their viscoelastic properties is imperative as energy dissipation is dominated by viscous processes, which are poorly understood in distal threads. Here, we propose that by studying the viscoelastic response of distal threads a better understanding will be developed of how this composite biomaterial uses diverse protein domains flanking the collagen core to dissipate energy.

When held at a constant strain, nearly all polymers (natural and synthetic) experience a decrease in stress over time through a process known as stress relaxation. During this process, energy is typically released as polymer chains are untangled and/or slide past one another [25]. Through stress relaxation experiments we sought to dissect the contribution of each domain to the relaxation response and to identify which energy dissipating mechanisms are incurred during the process. To test this, we perturbed different domains via chemical treatments and observed changes in the relaxation behaviour. Stress relaxation experiments were coupled with in situ tensile small-angle X-ray scattering (SAXS) to shed light on the effects of the various treatments on molecular spacing and hence on viscous processes incurred during relaxation.

Due to the micro-geometry of the distal threads, conducting dynamic analysis has been challenging. Work by Aldred et al. on Mytilus edulis distal threads revealed the glass transition temperature and storage modulus for relevant ecological temperatures [7]. In a different study, it was observed that, with a static load of 0.046 N, as the frequency of oscillations increased energy dissipation also increased [24]. Although these studies provide insight into the dynamic response of byssal threads, it is still unclear at which frequency distal threads dissipate maximum energy. To provide a constitutive model, in the present work, a generalized Maxwell viscoelastic model was used to analyse stress relaxation data and mathematically derive the material's viscoelastic parameters (figure 2). Using the material's viscoelastic parameters, we estimated the storage and loss moduli. This in turn allowed us to determine the relative degree of damping in the material and the frequency at which maximum damping occurs. Beyond revealing quantitative information about the distal thread's material parameters, this model provides insights into how the different domains may be responding in a manner resembling that of a spring (elastic components) or damper (viscous components).

Figure 2.

Maxwell model diagram and fitting results. (a) Representative schematic of the generalized Maxwell model: N represents the number of Maxwell elements, E_∞ denotes the long-term elastic modulus, E_i is the value for the elastic modulus for the springs in the Maxwell elements and η_i is the linear viscosity parameter for individual dashpots, i denotes respective Maxwell elements. (b) Illustration of the fitting accuracy of the 5th-order generalized Maxwell model for a native thread.

2. Method and materials

2.1. Reagents

Sodium acetate and sodium phosphate were obtained from Sigma Aldrich (St Louis, MO). Urea and ethylenediamine tetraacetic acid (EDTA) were obtained from Fisher Scientific (Pittsburgh, PA).

2.2. Thread collection

Mussels Mytilus californianus were collected from Goleta Pier near Santa Barbara, CA and stored in maricultural tanks with an open seawater circulation system maintained at 10.5–12.5°C. Individual mussels were secured onto glass plates with the use of rubber bands overnight, this prevented the mussels from moving and allowed them to deposit byssus onto the glass surface. Threads were removed within 48 h of plating and mechanically tested within 72 h. The proximal region of the threads was removed using a razor blade. Threads were stored in seawater filtered through a 0.22 µm filter.

2.3. Chemical treatments

In native conditions, distal threads were collected and stored in filtered seawater. For threads exposed only to pH changes, threads were immersed in buffered solutions (100 mM acetate, 100 mM phosphate) at pH = 5.5, 6.5 and 7.5 for a minimum of 24 h prior to testing. Buffers used for urea treatment were freshly prepared at pH = 5.5, 6.5 and 7.5 with 100 mM acetate and 100 mM phosphate and supplemented with 8 M urea. EDTA treatment buffers were prepared in the same manner as previously stated but substituting 100 mM EDTA for urea. Samples treated in their respective buffer were submerged for a minimum of 24 h prior to testing.

2.4. Stress relaxation measurements

Stress relaxation experiments were conducted on a tabletop tensile tester (Bionix 200 universal testing machine, MTS, Eden Prairie, MN), at a nominal strain rate of 1.0 min⁻¹ using a 10 N load cell and a built-in optical encoder to measure the load and displacement. All mechanical tests were performed with the distal threads fully submerged in seawater inside the Bionix 200 environmental chamber. The two ends of the threads were secured with custom-built clamps and aligned by eye on the tensile tester. Once the threads were secured, initial thread lengths were measured with a digital caliper (ABS Digimatic Caliper, Mitutoyo, Kanagawa, Japan) and recorded. All threads were pulled to a strain of 10% and held at this strain for 5–10 min. The 10% fixed strain was chosen because it is within the initial elastic regime and avoids complications arising from potential phase transitions in the microstructure [5,26]. Force, extension, and time were recorded during the duration the test. Representative stress relaxation curves are shown in the electronic supplementary material, figure S1. Stress relaxation experiments were conducted in natural seawater at temperatures of 10.5–12.5°C, which closely resemble the water temperature of collected local Mytilus californianus. It would of course be desirable for future stress relaxation experiments to be conducted at other temperatures to assess the temperature dependence of viscoelasticity.

Relaxation percentage (R%) was calculated by subtracting the force after 5 min of loading (F_{t = 5 min}) from the initial force when the sample was first strained to 10% (F_{t = 0}), and dividing by the initial force:

$$R\text{\%}=\hspace{0.17em}{\displaystyle \frac{F_{t\hspace{0.17em}=\hspace{0.17em}0}-F_{t\hspace{0.17em}=\hspace{0.17em}5\min }}{F_{t\hspace{0.17em}=\hspace{0.17em}0}}.}$$ 2.1

To enable statistically meaningful comparisons of the relaxation for the various treatments, the distributions of relaxation percentages were compared using a pairwise Student's t-test implemented in MATLAB (Mathworks, Natick, MA).

2.5. Small-angle X-ray scattering measurements

A time scale of 5 min was chosen to maintain consistency across measurements and comply with the time constraints imposed for the SAXS measurements. SAXS measurements were conducted at the BioSAXS beam line 4-2 at the Stanford Synchrotron Radiation Lightsource (SSRL) (Menlo Park,CA). Measurements were performed with a wavelength of 1 Å and a beam size of 100 × 100 µm. Diffraction patterns were acquired with a 2D CCD detector (Rayonix225HE, Rayonix Inc., Evanston, IL) with an array of 3072 × 3072 pixels and pixel size of 73 µm. Two different experiments were conducted with detector centre-to-sample distances of 1186 mm and 1215 mm. Calibrations were done using a silver behenate (AgBeh) standard.

All threads were kept submerged in their appropriate conditions for a minimum of 24 h prior to testing and pulled in a custom-built micromechanical tensile tester (electronic supplementary material, figure S2). Thread ends were first secured with a hex key in the custom-built tester clamps and aligned by eye. Once positioned, the thread length was measured using a digital caliper (ABS Digimatic Caliper, Mitutoyo, Kanagawa, Japan) and recorded. Before measurements were conducted threads were hydrated with a drop of water. A single SAXS image was acquired for each sample prior to being pulled to serve as a baseline. Threads were then pulled to 10% strain, and extensions were measured by a micrometer head that is attached to the custom-built tester (Micrometer Head MHS, Mitutoyo, Kanagawa, Japan) (electronic supplementary material, figure S2). Samples were held at a strain of 10% between 5 and 10 min, during which SAXS images were acquired every 20 s.

The two-dimensional SAXS patterns were analysed with a custom-built MATLAB function (Mathworks, Natick, MA). The SAXS reflection peak values were averaged in the meridional and equatorial directions. The one-dimensional equatorial intensities (q_e), empty beam background and variations were removed using exponentially decaying functions. No fits were necessary for the meridional reflections due to the sharp peaks (figure 3). The one-dimensional equatorial intensities were fitted with a sum of Gaussian curves. Peak positions were represented by q_m and q_e which are inversely correlated with the corresponding D-spacing, D = 2π/q and has units of nm. The molecular strain was determined as follows:

$${\epsilon }_{m,q}={\displaystyle \frac{D(t=0)-\hspace{0.17em}D(t)}{D(t=0)}\hspace{0.17em}\times 100\text{\%}.}$$ 2.2

Figure 3.

SAXS meridional scattering of mussel distal threads. (a) Integration of the peak intensity of the meridional peaks for a native thread prior to straining, at t = 20 s after initial 10% strain, and at t = 10 min held at the constant strain of 10%. (b) Representative axial staggering of the preCol bundles. D represents the axial staggering length captured from the integration of peak intensity; this value repeats every approximately 13.9 nm.

2.6. Modelling the stress relaxation

To characterize the stress relaxation phenomena observed in the uniaxial tensile relaxation test we used the generalized Maxwell model, which is depicted in figure 2. The one-dimensional representation of the model consists of N + 1 linear springs and N linear dashpot elements, where N (positive integer) represents the model order. The long-term behaviour (i.e. the response in infinitely slow loading rate or after infinite waiting time) of the model is described by the elastic modulus E_∞ of the spring in the network having no dashpot element. The other networks (i = 1 … N) contain springs with elastic modulus E_i and dashpots with linear viscosity η_i. Parameter τ_i = η_i/E_i was introduced for simplicity.

The first part of the prescribed strain history in the relaxation experiments was a ramp loading, where the sample was deformed from its undeformed configuration until the desired strain ɛ₀ during time t₀. After t₀, the strain was kept constant. Thus, the strain history is defined as

$$\epsilon (t)=\{\begin{array}{cc}\dot{\epsilon }\cdot t& t\le t_0,\\ {\epsilon }_0& t>t_0.\end{array}$$ 2.3

The resulting stress solutions are

$$\hspace{0.17em}\hspace{0.17em}\sigma (t)=\{\begin{array}{ll}{E}_{\mathrm{\infty }}\dot{\epsilon }t+\sum _{i=1}^N\left(1-\exp \left[{\displaystyle \frac{-t}{{\tau }_i}}\right]\right)\cdot E_i{\tau }_i\dot{\epsilon }& t\le t_0,\\ E_{\mathrm{\infty }}{\epsilon }_0+\sum _{i=1}^N\exp \left[{\displaystyle \frac{-(t-t_0)}{{\tau }_i}}\right]\cdot \left(1-\exp \left[{\displaystyle \frac{-t_0}{{\tau }_i}}\right]\right)\cdot E_i{\tau }_i\dot{\epsilon }& t>t_0.\end{array}$$ 2.4

An alternative representation of the solution is the following:

$$\hspace{0.17em}\hspace{0.17em}\sigma (t)={\int }_0^{t}E(t-s)\cdot \dot{\epsilon }(s)\hspace{0.17em}\mathrm{d}s,$$ 2.5

where the time-dependent elastic modulus is expressed using the Prony series representation as

$$\hspace{0.17em}\hspace{0.17em}E(t)=E_{\mathrm{\infty }}+\sum _{i=1}^N{E}_i\cdot \exp \left[{\displaystyle \frac{-t}{{\tau }_i}}\right].$$ 2.6

The instantaneous model response was characterized by the instantaneous elastic modulus $E_0=E(0)=E_{\mathrm{\infty }}+{\sum }_{i=1}^N{E}_i$. Consequently, the one-dimensional Nth-order generalized Maxwell model contains 2N + 1 material parameters, which were obtained by minimizing the error between the model prediction and the experimental data. This error can be measured by the square root of the mean of the squares of deviations as follows:

$$\hspace{0.17em}\hspace{0.17em}Q=\sqrt{{\displaystyle \frac{1}{m}\sum _{k=1}^m{({\sigma }_k^{\exp }-{\sigma }_k^{\mathrm{sim}})}^2}},$$ 2.7

where m is the number of data points. ${\sigma }_k^{\exp }$ is the experimental stress value, whereas ${\sigma }_k^{\mathrm{sim}}$ denotes the model prediction. Once the material parameters were obtained, one can express the storage and loss moduli with the parameters of the model as

$$\begin{array}{r}\hspace{0.17em}\hspace{0.17em}{E}^{\mathrm{\prime }}(\omega )=E_{\mathrm{\infty }}+\sum _{i=1}^N{\displaystyle \frac{{\tau }_i^2{\omega }^2}{{\tau }_i^2{\omega }^2+1}{e}_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{E}^{\mathrm{\prime }\mathrm{\prime }}(\omega )=\sum _{i=1}^N{\displaystyle \frac{{\tau }_i\omega }{{\tau }_i^2{\omega }^2+1}{e}_i,}}\end{array}$$ 2.8

where the relative moduli are expressed as e_i = E_i/E₀. The dimensionless quantity tanδ is defined as the ratio of the loss and storage moduli as tanδ = E″/E′. This quantity provides information about the relative degree of damping of the material and energy dissipation.

Percent stress relaxation was chosen as the metric for comparison instead of relaxation time because, based on theory, an infinite time is necessary for complete relaxation to the equilibrium configuration. Moreover, although it would be possible to calculate a relaxation time if the model contained only a single Maxwell element, our results were modelled with a series of Maxwell elements and hence no single relaxation time can be extracted.

3. Results

3.1. Stress relaxation experiments

Native threads, strained under native seawater conditions (pH ∼ 8), experienced an average stress relaxation of approximately 40%. To assess the effect of pH on stress relaxation, the relaxation percentage was calculated (at t = 5 min) for threads incubated in buffers of pH = 5.5, 6.5 and 7.5. Relaxation results are shown in table 2. Significance was assessed using a pairwise Student's t-test for the various treatment conditions (p < 0.05). A full accounting of the statistical analysis of these data is provided in the electronic supplementary material, table S1. Although collagen and the silk-like domains are quite resistant to moderate pH changes [27], the same cannot be said of the His-rich domain. The pK_a of histidine's imidazolium containing side chain (approx. 6.5) results in two discrete protonation states within the range of biologically relevant pH [28]. This leads us to deduce that at pH 5.5 approximately 90% of the histidine residues are protonated thus interfering with its ability to form metal coordinate bonds [2]. At pH 7.5, the histidine residues are largely deprotonated (approx. 91%), thus permitting the formation of reversible coordinate bonds to transition metals. When compared with pristine threads, threads treated at pH 7.5 showed no statistical difference in total relaxation: approximately 40%. Conversely, threads incubated at pH 6.5 and 5.5, corresponding to pH at or below the pK_a of histidine, respectively, experienced approximately 50% relaxation.

Table 2.

Results for percent stress relaxation after 5 min, the relaxation percentage being determined as described by equation (2.1). The average and standard deviation are presented for all conditions. Sample size varied between 4 and 12 samples.

condition	average relaxation (%)
native	38.8 ± 4.8
pH 5.5	48.0 ± 10.4
pH 6.5	48.0 ± 6.6
pH 7.5	41.7 ± 2.5
EDTA pH 5.5	53.1 ± 10.8
EDTA pH 6.5	50.0 ± 6.4
EDTA pH 7.5	48.5 ± 5.1
urea pH 5.5	23.4 ± 5.1
urea pH 6.5	24.9 ± 4.1
urea pH 7.5	33.6 ± 4.7

Chelators are agents used to sequester metal ions via coordinate bonds from materials. Chelating agents with a high affinity for metal ions are often able to partially or completely strip metal ions from proteins. To further target the metal coordinate bonds in the His-rich domains, threads were treated with the chelating agent EDTA at the equivalent pH values described above. All EDTA-treated samples showed comparable relaxation of approximately 50%. Samples treated with EDTA at pH 5.5 and 6.5 were not statistically different from samples treated with pH only (electronic supplementary material, table S1). By contrast, samples at pH = 7.5 with and without EDTA deviated by a statistically appreciable amount with the addition of EDTA increasing relaxation by approximately 7% to approximately 50%, resembling that of pH 5.5 and 6.5 treatments.

Although His-rich domains are implicated in mechanical stress response via pH and chelator treatments, the role of silk-like domains cannot be discounted [10]. The silk-like domains were perturbed using concentrated urea (approx. 8 M). Urea is a chaotropic agent known to destabilize secondary protein structure while having minimal effects on metal-coordination bonds [29–31], thus allowing the silk-like domains to be interrogated independently from the His-rich domains. Unlike samples treated with pH and EDTA, urea treatment resulted in decreased relaxation percentage at all pH values tested. Threads incubated with urea at pH 5.5 and 6.5 experienced total relaxations of 23% and 24%, respectively, a statistically significant difference from pH only treatments (electronic supplementary material, table S1). At pH 7.5, the addition of urea reduced relaxation by 5%, yielding a total relaxation of approximately 33%. Although lower than native controls, the difference was not statistically significant.

3.2. In situ tensile small-angle X-ray scattering

Previous tensile in situ SAXS measurements of byssal threads pulled to 30–50% strain found shifts in meridional peaks to lower q_m values indicating that molecular spacing between preCol bundles increased [5]. Here, in situ SAXS measurements on strained threads were conducted to assess changes in molecular spacing because of the relaxation process. It is important to note that SAXS does not capture individual protein domain unfolding but rather changes in the spacing of stagger between preCol bundles. To avoid nonlinearities resulting from yielding in the threads, the strain was held at 10%, well below the yielding regime. A representative two-dimensional scattering diffraction pattern is shown in figure S3 (electronic supplementary material). The data shown in figures 3 and 4 are in terms of the scattering vector, q, which is related to the molecular spacing objects (D-spacing) by the equation D = 2π/q.

Figure 4.

SAXS equatorial scattering of mussel distal threads. (a) Integration of the peak intensity of the equatorial peaks for a native thread prior to straining, at t = 20 s after initial 10% strain, and at t = 10 min with the constant strain of 10% (background was removed). (b) Representative hexagonal packing of the preCol 6 + 1 bundles; D represents the spacing between the centre of the collagen domain to the edge of the His-rich and silk domains.

Figure 3 shows sharp meridional reflections that arise from the highly aligned and semi-crystalline structure the preCols form along the fibre axis. The first peak (at q_m = 0.045) shows a D-spacing of approximately 13.9 nm. The remaining peaks are spaced equally apart by q_m ∼ 0.045 showing that the 13.9 nm spacing is repeated. We observed shifts in the meridional peak position upon initial loading that range between 0 and 0.9 nm corresponding to a molecular strain of 0–6.5% (calculated with equation (2.2)). EDTA-treated threads exhibited the largest molecular strain (table 3). Importantly, peak position did not exhibit additional changes over time.

Table 3.

Average axial molecular strain at t = 20 s after initial 10% bulk strain. The molecular strain is determined using equation (2.2) from scattering vector q_m. The second column shows the average molecular strain with the respective standard deviation. The third column shows the number of samples for which molecular strain (peak shifts) were captured. No further space changes were captured after the initial change at t = 20 s. The sample size varied between 2 and 7 per condition.

condition	average molecular strain (%)	number of samples with peak shifts
native	3.65 ± 3.60	4/5
pH 5.5	3.08 ± 4.19	3/7
pH 6.5	2.73 ± 3.86	1/2
pH 7.5	2.62 ± 1.66	3/3
EDTA pH 5.5	5.31 ± 0.55	3/3
EDTA pH 6.5	6.12 ± 1.13	4/4
EDTA pH 7.5	6.51 ± 1.74	4/4
urea pH 5.5	3.37 ± 4.84	4/5
urea pH 6.5	2.30 ± 1.61	5/5
urea pH 7.5	3.26 ± 1.82	3/3

The equatorial peaks reveal information about the lateral packing and straining of the preCols. Previous work by Krauss et al. showed that a number of equatorial peaks correspond to the $\sqrt{3}$ ratio of the D-spacing for an ideal hexagonal lattice and confirmed the proposed 6 + 1 bundled structures [4]. In our studies, only one peak was visible, most likely due to weak signal. This peak has been assigned to the molecular spacing from the centre of the triple-helical collagen domain to the edge of the silk-like + His domains (figure 4). Each preCol can be thought of as having a dumbbell-like structure where the silk-like + His domains are larger in diameter compared with the triple-helical collagen central domain. We observed a shift in the equatorial peak immediately upon loading (figure 4). By contrast to the meridional peaks, the equatorial peak shifted to larger q_e values over time while the thread was held at constant strain. This indicates a decrease in molecular spacing (D-spacing) after 5 min when compared to approximately 1 min under all conditions. These shifts were most pronounced for EDTA- and urea-treated samples (table 4).

Table 4.

Average lateral molecular strain at t = 20 s and the difference in strain between 20 s and 5 min. The molecular strain is determined using equation (2.2) from the scattering vector q_e. The second column shows the average molecular strain with the respective standard deviation at t = 20 s. The third column shows the change in strain between t = 20 s and t = 5 min. The negative sign indicates that the spacing between domains is decreasing. The sample size varied between 2 and 5 per condition.

condition	average molecular strain at t = 20 s (%)	average strain change between t = 20 s and t = 5 min (%)
native	−4.70 ± 2.11	−1.56 ± 0.23
pH 5.5	−1.49 ± 1.72	−1.13 ± 0.73
pH 6.5	−2.04 ± 0.67	−1.70 ± 1.55
pH 7.5	−1.62 ± 1.57	−0.50 ± 0.70
EDTA pH 5.5	−3.42 ± 0.49	−1.32 ± 0.21
EDTA pH 6.5	−3.49 ± 1.66	−0.47 ± 0.16
EDTA pH 7.5	−3.13 ± .033	−0.99 ± 0.31
urea pH 5.5	−3.59 ± 1.67	−3.15 ± 1.49
urea pH 6.5	−3.63 ± 2.53	−3.39 ± 2.22
urea pH 7.5	−6.52 ± 2.06	−2.59 ± 0.21

3.3. Fitting the generalized Maxwell model

To build a viscoelastic model describing the material response of distal threads we fit the generalized Maxwell model to our stress relaxation measurements and find that the 5th-order model provides excellent agreement in all cases. Increasing the model order did not improve the model prediction. A representative model fitting is illustrated in figure 2 where the grey curve shows the measured stress relaxation, whereas the red curve is the model prediction. One can conclude that the curves overlap one another and are almost indistinguishable. The frequency-dependent storage and loss moduli were determined from the fitted models, as well as tanδ. Representative results for a native sample are shown in figure 5.

Figure 5.

Representative storage and loss moduli along with tanδ for a native sample. (a) The loss and storage moduli were modelled using parameters obtained from the generalized Maxwell model. (b) tanδ was determined as the ratio of the loss to storage modulus. Maximum damping on average was determined to be at approximately 0.1 Hz.

The frequency values corresponding to the maximum of tanδ were calculated. These values have great importance as they represent the frequency values at which the relative damping of the viscoelastic model is greatest. One can observe that the different treatments have a minor effect on the frequency value at which the relative damping is maximal.

4. Discussion

The composite structure of the mussel byssus coupled with its unique combination of load-bearing chemistries has served as model systems for bioinspired materials engineering for decades [32–40]. The goal of this study was to investigate which components in multi-domain preCols dissipate energy via viscous processes. A pristine byssal thread can achieve an impressive 40% stress relaxation on the time scale of minutes. It has been previously demonstrated that when a bulk thread is strained up to 50%, the collagenous domain has a constant maximum molecular strain of merely 2% while the flanking domains extend up to approximately 150%; this suggests the flanking domains are largely responsible for extending and dissipating strain energy [13,20]. To test this hypothesis, byssal threads were subjected to several chemical treatments aimed at disrupting the two flanking His-rich and silk-like domains followed by stress-relaxation experiments.

EDTA greatly impacts the His-rich domain but has little effect on the silk-like domain which is devoid of metal coordination complexes [2]. Conversely, urea treatments minimally affect metal coordinate structures and hence have little effect on the His-rich domain [10,31,41]. Although urea can unravel the triple-helical structure of tropocollagens [29], in distal threads the constrained semi-crystalline collagen structure observed in SAXS remained unchanged upon urea addition [42]. As the silk-like domains in distal threads were targeted by urea treatment, the His-rich domains were left intact. The post-urea reduction in thread relaxation suggested that the silk-like domains rather than the His-rich domains were primarily responsible for the relaxation. Under EDTA/pH treatments, the opposite effect was captured with the threads relaxing more. This implies that once the His–metal bond density in the His-rich domains is compromised below a critical threshold, these domains are also recruited into relaxation at 10% strain. By contrast, in the untreated state His-rich domains are unlikely to participate in relaxation until the yield stress is approached. This indicates that when a byssal thread is held in tension at strains below the yield point, the silk-like domains contribute most to stress relief. However, given the complexity of byssus biochemistry and composite structure, inferences based on single treatments deserve a healthy measure of caution. Therefore, to gather a further understanding of what is occurring at the molecular level, in situ tensile SAXS was used.

In agreement with previous studies, the SAXS spectra contained two distinct features. First, there is a meridional peak arising from the axial spacing between the C-terminus of one collagen domain to the adjacent collagen's N-terminus. Thus, this space is occupied primarily by a small part of the collagen and the less-ordered silk-like and His-rich domains [5]. Straining a native thread to 10% led to a molecular strain of approximately 3%. As threads were held at a constant strain, no shifts were observed beyond the initial peak shift indicating the molecular spacing does not change over time. The most notable results when analysing meridional features were that threads treated with EDTA showed the highest molecular strains, approximately 6%, two times that of the other conditions. Depletion of the metal-coordinate complexes via EDTA treatment rendered the His-rich domains less loadbearing, thus adding their deformation and transferring the load to the silk-like domains following modest collagen extension [13]. As a result, the hydrogen bonds and hydrophobic interactions in the silk-like domains are ruptured as they undergo partial unfolding and extension. This may explain the increased molecular strain that accompanies EDTA treatment [43,44]. Similar behaviour has been captured by many other studies in which the β-sheets in silk fibres will orient and stretch, allowing the macromolecular chains to form interlocking regions that transfer loads between chains [45–49]. Conversely, His–metal complexes possess similar bonding energies to covalent interactions [50,51]; therefore, when loaded, the His-rich domains are able to resist deformation, resulting in the lower molecular strains observed in native threads and threads treated with urea.

Second, a single broad equatorial peak assigned as the spacing from the centre of the collagen domain to the edge of the flanking region [5] is observed with SAXS (figure 4). Our data show that although axial spacing between preCols increased upon initial loading, the lateral molecular spacing decreased. This effect was most pronounced for urea-treated threads with initial strains as high as −6.5%. Unlike the axial molecular spacing, this feature continued to decrease during stress relaxation for each condition. We suggest this arises from the rearrangement of the silk-like domains. As the silk-like domains unfold, they can reorient themselves to facilitate closer packing of the preCols. This effect was more pronounced when the system was treated with urea, likely due to the disruption of the silk-like domains.

Based on these data, we propose that at 10% strain, relaxation in the core of the thread is largely due to molecular rearrangement in the flanking domains, primarily the silk-like domains. Upon loading, the load is transferred from the His-rich domains to the silk-like domains, whereupon the silk domains begin to extend and/or reorient to relieve local stress over time. Perhaps the His-rich domains contract in order to maintain the observed constant axial spacing but this is conjecture at present. Thus, reorientation and/or molecular movement is responsible for energy dissipation during stress relaxation, similar to that of a viscous damper [25].

Our generalized Maxwell model accurately represents the relaxation behaviour of a byssal thread and allows us to further investigate the threads' viscoelastic properties. Even though nonlinear models have been developed describing the viscoelastic effects in biomaterials and other soft materials, a linear model was used because the strains at which experiments were conducted are well within the elastic regime of the threads [52,53]. Extraction of tanδ from the constitutive model indicates maximum energy dissipation (or viscoelastic damping) occurs at approximately 0.1 Hz (electronic supplementary material, figure S4). This is particularly interesting because a 22-year study of near-coast Santa Barbara and Ventura County wave statistics determined an average swell period of 11.01 s, or a frequency of 0.09 Hz [54]. This suggests that byssal threads may be adapted to cope with cyclic environmental stresses. Previous work by Carrington et al. showed a different trend suggesting that tanδ increased with the oscillation frequency [24]. However, this disagreement is not surprising as our experimental approach was significantly different: our threads were not preconditioned; moreover, their loads were greater by an order of magnitude. The relevance of our results is limited to the distal thread mechanics and do not include proximal thread viscoelastic effects. It is likely that the inclusion of the proximal thread would influence the overall damping frequency; however, the viscoelastic response of the proximal thread is inadequately characterized at this time. It would of course be desirable for future stress relaxation experiments to be conducted at other temperatures to assess the temperature dependence of viscoelasticity.

While we used the generalized Maxwell model to fit to the stress relaxation of the entire distal thread, the springs and dashpots also translate to the molecular components in the thread, e.g. the triple helix collagen behaves like a stiff spring that responds to the instantaneous load via extension of no more than 2% [13,20]. Similarly, the His-rich and silk-like domains behave as a spring and dashpot in series (Maxwell elements), with the His-rich domain extending upon initial loading just like a spring and over time the silk-like domains rearrange, behaving more like a damper and allowing the His-rich domain to contract. Although the proposed mechanism accounts for Maxwell elements in series, it is unclear as to what element behaves as the spring in parallel with these elements. One possibility is that the entire core behaves as a series of Maxwell elements while the outer stiff cuticle, known to have a modulus 10 times that of the core [19], behaves as a spring in parallel with those elements, thus providing the long-term elastic component. Although there are no known mechanics studies of the matrix proteins, they do exist as a discrete component in the system and could also be contributing to the long-term elasticity in the threads [55].

5. Conclusion

For decades, many studies have been conducted to better understand marine mussel byssus [1,17,19,35,38,39,56–59]. In this work, new insights are presented on the viscoelastic properties of marine mussel byssal threads and a mechanism for the viscous processes incurred during stress relaxation in the preCols is proposed. Evidently, as the silk-like domains were disrupted via urea treatments, there was a substantial reduction in stress relaxation. This leads us to propose that a majority of the energy dissipation occurs in the silk-like domains via molecular rearrangement. Furthermore, we propose that upon loading the collagen and His-rich domains extend. The load is then transferred from the His-rich domains to the silk-like domains causing these domains to rearrange and dissipate energy. For this reason, as the His domains were disrupted and no longer participated, the load was transferred directly to the silk-like domains leading to a higher degree of unfolding/rearrangement and hence more relaxation. Our studies were coupled with a 5th-order generalized Maxwell model, allowing us to propose various mechanisms for individual domains. It was observed that across most treatments, maximum damping occurred at around 0.1 Hz indicating Mytilus californianus distal threads may be adaptively acclimated to withstand and dissipate energy at the same frequency as ambient wave motion. Although this model was developed to describe the viscoelastic properties of mussel threads, the methodology described in this work can be applied to other highly composite biomaterials. This study has provided an alternative narrative to the mechanical response of distal threads incorporating viscoelastic effects. However, there are many areas that will need to be addressed in future research. For example, although stress relaxation was reduced by treatment by as much as 50%, it is still unclear as to where the other sources of relaxation arise from. Possible mechanisms include relaxation in the cuticle and/or the thread matrix proteins [55]. Further studies are needed in order to dissect the participation of these components in this highly complex composite material. In addition to this, it is essential that future stress relaxation experiments be conducted at other temperatures to assess the temperature dependence of the viscoelastic properties.

Data accessibility

Data and code generated through this work are made available at FigShare (doi:10.6084/m9.figshare.17563055).

The data are provided in electronic supplementary material [60].

Authors' contributions

M.A.: data curation, formal analysis, investigation, writing—original draft, writing—review and editing; E.V.: conceptualization, data curation, investigation; I.S.C.: data curation, investigation; I.R.: data curation, investigation; W.R.W.: formal analysis; A.K.: formal analysis, investigation, validation, writing—original draft; R.M.M.: supervision; J.H.W.: supervision.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Materials Research Science and Engineering Center (MRSEC) Program of the National Science Foundation (NSF) under award no. DMR 1720256 (IRG-3). A.K. and this research was supported by the Hungarian National Research, Development and Innovation Office (NKFI FK 128662). Additionally, I.S.C. and this research was supported by the LSAMP programme of the National Science Foundation under award no. HRD-1826900. M.A. acknowledges support of the NSF California LSAMP Bridge to the Doctorate Fellowship under grant no. HRD-1701365. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research, and by the National Institutes of Health, National Institute of General Medical Sciences (P30GM133894). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH.