Tendons exhibit greater resistance to tissue and molecular-level damage with increasing strain rate during cyclic fatigue

Abstract

Musculoskeletal soft connective tissues are commonly injured due to repetitive use, but the evolution of mechanical damage to the tissue structure during repeated loading is poorly understood. We investigated the strain rate dependence of mechanical denaturation of collagen as a form of structural microdamage accumulation during creep fatigue loading of rat tail tendon fascicles. We cycled tendons at three strain rates to the same maximum stress relative to their rate-dependent tensile strength. Collagen denaturation throughout the fatigue process was measured by fluorescence quantification of collagen hybridizing peptide binding. The amount of collagen denaturation was significantly correlated with fascicle creep strain, independent of the cyclic strain rate, supporting our hypothesis that tissue level creep is caused by collagen triple-helix unfolding. Samples that were loaded faster experienced more creep strain and denaturation as a function of the number of loading cycles relative to failure. Although this increased damage capacity at faster rates may serve as a protective measure during high-rate loading events, it may also predispose these tissues to subsequent injury and indicate a mechanism of overuse injury development. These results build on evidence that molecular-level collagen denaturation is the fundamental mechanism of structural damage to tendons during tensile loading.

Graphical Abstract

1. Introduction

Connective tissue overuse injuries are chronic musculoskeletal conditions caused by repeated subfailure loading of connective tissues via repetitive motion activities. These injuries afflict people from all walks of life: they constitute a primary source of athletic injury [1–3] and represent a significant proportion of occupational musculoskeletal injuries for manual laborers, musicians, and healthcare personnel [4–7]. The clinical treatment of these common pathologies continues to prove vexing due to poorly understood etiology. Commonly reported factors positively correlated with the development of musculoskeletal overuse injuries include activity intensity, duration, speed, and rapid changes in any of these factors [2, 4, 8]. Despite decades of basic research investigating the patterns and mechanisms of mechanical damage in connective tissues, we still have little understanding about when repeated loading becomes injurious and the potential mechanisms that underly the epidemiological factors associated with overuse injuries.

The working hypothesis for the development of overuse injury is that repeated loading events cause microdamage to the tissue and that injury occurs when damage accumulation exceeds the biological rate of repair [9]. This microdamage hypothesis provides a convenient framework to conceptualize the injury process, although it is agnostic to the mechanisms of damage and degeneration from the molecular to tissue scales. Cyclic fatigue loading is routinely used to investigate the mechanics of tissues subject to repeated loading. Previous studies have established that tendons subjected to creep fatigue loading undergo a progressive change in mechanics, with a triphasic pattern of increasing tissue strain (creep) and material softening with increasing loading cycles [10, 11]. Progressive structural disruption accompanies these changes in mechanics, evidenced by kinking and disorder at the fibril and fiber levels of the collagen structural hierarchy [10, 12].

Dynamic loading necessitates a consideration of rate dependence, which arises in connective tissue mechanics in many forms. At the joint scale, human motion occurs across a wide range of speeds; for example, an overhead lifting task may be performed on the order of seconds, while the acceleration phase in overhand throwing lasts on the order of 0.1 seconds [13]. At the tissue scale, faster motions can translate to greater loading; for example, the peak ground reaction force and Achilles tendon stress increase with increasing walking or running speed [14–17]. Finally, at the material scale, tendons exhibit both increased strength and modulus when they are loaded faster [18, 19], demonstrating that connective tissues are well adapted for their physiological function. A few studies have also demonstrated that disruption of molecular and fibril-level collagen organization in tendons is different following either a single fast or slow stretch to failure [20].

Our laboratory has recently focused on investigating collagen denaturation as a mechanism of damage caused by mechanical loading in tendons. We have demonstrated using collagen hybridizing peptide (CHP) binding that the collagen triple-helix denatures (unfolds) following a single application of subfailure tensile strain corresponding with tissue-level yielding [21, 22]. This molecular-level damage mechanism and the correlation between the onset of significant collagen denaturation and tissue yielding is consistent for both representative positional and energy-storing tendons [22]. We have also shown that mechanically unfolded collagen accumulates throughout the creep fatigue loading period and that this denaturation serves as the molecular mechanism of structural microdamage due to repeated loading in tendons [23]. In that study, rat tail tendon (RTT) fascicles that were cycled to the same creep stress magnitude endured more cycles before failing when cycled faster. However, the accumulation of denatured collagen as a function of the percentage of cycles to failure was independent of the cyclic strain-rate, unlike experiments that have demonstrated strain-rate dependent molecular disruption in bovine tail tendons following a single load to failure [20]. Beyond the difference between cyclic and monotonic loading, an important distinction between these experiments is the effect of viscoelastic material properties; our previous fatigue study [23] applied the same peak stress magnitude at all strain rates, while the monotonic failure experiments by Chambers et al. [20] inherently allowed the faster loaded samples to experience higher loads due to viscoelastic stiffening and strengthening. It remains unclear whether fatigue damage and failure are strain-rate dependent when the fatigue stress levels account for the viscoelasticity of tendon strength and stiffness.

Here, we investigated the strain rate dependence of denatured collagen accumulation during fatigue loading, when RTT fascicles were cycled to the same stress relative to their rate-dependent ultimate tensile strength (UTS). While previous studies have investigated a single creep stress magnitude, the creep stresses applied in the present study accounted for the changes in the viscoelastic material behavior of the RTT with strain rate. Our previous research suggested that collagen triple-helix unfolding may cause the increase in creep strain during cyclic fatigue loading; therefore, we hypothesized that the magnitude of creep strain would predict collagen molecular damage, independent of strain rate. We also expected that loading to the same stress as a percent of the effective tensile strength would normalize the number of cycles to failure, eliminating the differences between strain rates. This study provides the first investigation on the strain rate dependence of denatured collagen accumulation when accounting for the scaling of tendon strength with strain rate.

2. Materials and Methods

2.1. Mechanical testing

We chose to use RTT fascicles in this study as a representative tendon because it serves as an ideal material testing specimen due to its extremely high aspect ratio (~100:1 length:diameter). Additionally, our recent study using the rat flexor digitorum longus tendon as a representative energy-storing tendon showed that the damage mechanisms we have previously identified in the RTT fascicle are consistent between these two models of functional tendon types, further demonstrating the validity of the RTT model [22]. RTT fascicles were dissected from fresh-frozen, 6-month-old male Sprague-Dawley rat tails obtained commercially (BioIVT). It has been previously demonstrated that frozen storage and even multiple freeze-thaw cycles do not significantly affect the quasistatic and viscoelastic mechanics, multiscale deformation mechanisms, and subfailure damage mechanisms of tendons and ligaments [24–27]. Dissected samples were equilibrated before testing in 1× PBS supplemented with protease inhibitors (2 mM EDTA and 5 mM benzamidine hydrochloride) and balanced to pH 7.4. The initial cross-sectional area (CSA) was measured using a custom optical micrometer stage described previously [23]. The CSA was measured at 5 locations along the length of each sample, at 5 mm increments, and the mean area was used as the initial CSA for calculations of nominal stress. Following CSA measurement, samples were transferred to a material test system (ElectroForce 3300 Series II, TA Instruments). Sample hydration during testing was maintained by immersion in room temperature 1× PBS with protease inhibitors. Room temperature testing was used to isolate mechanical unfolding of the collagen triple-helix as the denaturation mechanism, preventing confounding local unfolding of thermally labile collagen domains or collagen fragments [21]. RTT fascicles were monotonically loaded to failure at strain rates of 0.4, 4, or 40% s⁻¹ (n=10 samples per rate; four total tails with six or nine fascicles from each tail) to establish stress levels for fatigue testing. The maximum force was normalized to the initial CSA to determine the ultimate tensile strength (44.69 ± 10.03, 60.46 ± 9.51, 83.99 ± 13.50 MPa at 0.4, 4, and 40% s^-1 respectively; mean ± SD). The grip-to-grip strain at UTS was 0.088 ± 0.013, 0.085 ± 0.009, and 0.110 ± 0.012 mm/mm at 0.4, 4, and 40% s^-1 respectively (mean ± SD).

A separate set of RTT fascicles underwent cyclic fatigue loading, following a test protocol established in our previous study [23]. A 0.03 N preload was established and samples were preconditioned for 10 cycles between 0.1 N and 10% of the strain rate specific UTS using a 0.06% s^-1 displacement controlled triangle waveform. Following preconditioning, samples were unloaded (remaining in the testing clamps) and allowed to recover for 5 minutes. A 0.03 N preload was re-established and the zero-strain length was calculated. Samples were then loaded between 0.2 N and 40% of the strain rate specific UTS at 0.4, 4, or 40% s⁻¹ using a triangle waveform until failure (n=10 per loading rate). Samples loaded to fatigue failure were used to establish the average creep behavior of RTT fascicles and to generate the failure group for CHP detection of denatured collagen (n=6 per loading rate randomly selected from each group of 10 samples for CHP staining). Additional fascicles were loaded to incremental levels of fatigue, defined by the mean strain at the peak of the loading cycle (peak cyclic strain) of fatigue failure samples, at 20, 50, and 80% of cycles to failure (n=6 at each strain level and loading rate). The samples were preconditioned as described and then loaded in creep-fatigue using the same stress levels until reaching one of the defined incremental strain levels, at which point the samples were immediately unloaded. Following testing, samples were removed from the test clamps and the clamped ends of the sample were cut away to isolate the loaded region for collagen damage quantification. All samples were stored at −70 °C in 1× PBS until CHP staining.

Creep strain was calculated from the peak cyclic strain as the change in length from the peak of the first fatigue loading cycle divided by the zero-strain length. The strain-time parameter, a measure of the cumulative strain history, was calculated as the area under the strain vs. time curve. Strain data were plotted as a function of the normalized number of cycles (cycle number divided by cycles to failure) to compare behavior between strain rates relative to sample failure. Fatigue loaded RTT fascicle samples were sourced from 20 total tails with 2–5 fascicles from each tail. The testing order was randomized so that each strain rate was represented every three samples, and for incremental fatigue tests all combinations of strain rate and subfailure fatigue level were represented every nine samples. By this randomization strategy, at least one fascicle was cycled at each strain rate for 21 of the 24 total tails represented in the study, helping control for biological variability between animals when paired with the regression analysis approach described below.

2.2. CHP staining and quantification

Fatigue loaded and unloaded samples were stained using fluorescently labeled CHP to detect and quantify denatured collagen. CHP can be used to detect and quantify denatured collagens through triple-helical hybridization with unfolded collagen α-chains [21, 28, 29]. The wet weight of the samples was measured to normalize fluorescence data by sample mass. First, liquid was removed from the surface of samples by blotting on a laboratory wipe, and then samples were immersed into a vial of 1× PBS of known mass on an analytical laboratory balance (ME304, Mettler Toledo). This measurement was repeated three times for each sample, and the mean weight of each sample was used for normalization (4.7 ± 1.6 mg average wet weight across all samples; mean ± s.d.). Samples were then stained overnight in 15 µM F-CHP (5-FAM conjugate CHP, 3Helix Inc.). F-CHP stock solution (150 µM) was heated at 80 ℃ for 10 min to thermally dissociate trimeric CHP to a monomeric state, and quenched by immersion in 4 ℃ water for 15 s. Each fascicle was placed in a vial containing 450 ml of 1× PBS and 50 ml of monomeric F-CHP stock was added, resulting in a final F-CHP concentration of 15 µM. Fascicles were incubated overnight at 4 ℃ and then unbound F-CHP was removed by washing three times in 1 ml of 1× PBS for 30 min at room temperature.

To quantify F-CHP fluorescence, stained samples were digested in 500 µl of 1 mg/ml proteinase K in water for 3 hours at 60 °C. Following digestion, 200 µl from each sample was pipetted into a 96-well plate, and samples were measured in duplicate at 485 and 525 nm excitation and emission, respectively (SpectraMax M4, Molecular Devices). Fluorescence values were normalized to the sample wet weight. The amount of denatured collagen present was calculated from normalized fluorescence, using a standard curve for RTT fascicles relating normalized CHP fluorescence to denatured collagen as measured by the trypsin digestion assay for denatured collagen [29]. Denatured collagen data were plotted as a function of the normalized number of cycles (cycle number divided by cycles to failure) to compare behavior between strain rates relative to sample failure.

2.3. Statistical analysis

Sample sizes for CHP quantification were prespecified using a power analysis based on mean and s.d. of CHP binding data from our previous study [21]. With a power of 0.8 and two-tailed α of 0.05, it was determined that n = 6 samples per group were required to detect an effect size of 0.7 (Cohen’s d). The total sample size in this study additionally complies with the suggested guideline by Harrell [30] of having a 10:1 ratio of samples per predictor variable to avoid overfitting in regression models. Denatured collagen data were analyzed using mixed-effects linear regressions, accounting for the lack of independence introduced by using multiple fascicles from each animal. Strain data (peak cyclic strain and creep strain) from samples tested to fatigue failure were analyzed using the logarithm of strain, accounting for the exponential scaling of strain with the normalized number of cycles, and using multilevel mixed-effects linear regression, accounting for repeated strain measurements from each sample. The above regression models on denatured collagen and strain data included an interaction term and mean centering of the predictor variables. Cycles to failure data were also analyzed using a mixed-effects linear regression with strain-rate as a categorical variable to compare each strain rate group, and Holm-Sidak correction for multiple comparisons was used. Significance was determined at the α=0.05 level. Experimental data are presented using unadjusted means and standard errors or standard deviations, as indicated. All regression models were performed in Stata (IC 15.1, StataCorp), using the ‘xtreg’ command for mixed-effects linear regression and the ‘mixed’ command for multilevel mixed-effects linear regression.

3. Results

3.1. Collagen denaturation normalized to failure is increased at higher strain rates

The amount and rate of denatured collagen accumulation throughout fatigue were affected by the cyclic strain rate (Fig. 1). The amount of denatured collagen, as detected by fluorescence from bound CHP, demonstrated significant effects for strain rate, fatigue level, and their interaction (p=0.010, p<0.001, p=0.027, respectively). Not only was more denatured collagen present at higher strain rates, but the rate of damage accumulation was higher as a function of the normalized number of cycles. This result contrasts with our previous findings that did not demonstrate significant strain rate dependence for the amount of denatured collagen when samples were cycled to the same magnitude of creep stress regardless of strain rate [23]. See paragraph one of Section 4 for further discussion of this topic.

Figure 1.

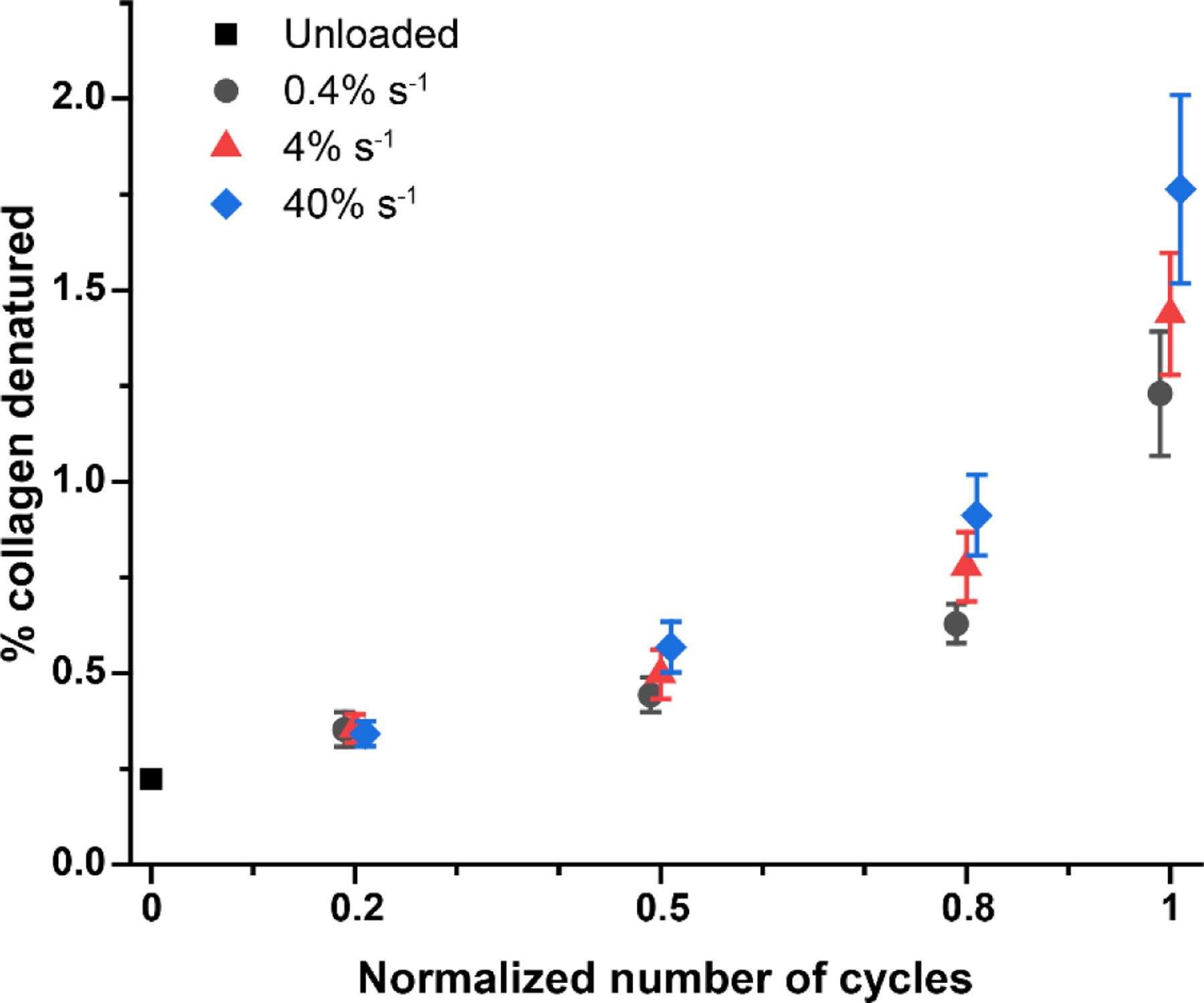
Molecular-level collagen damage as a function of the normalized number of loading cycles during cyclic fatigue loading. Denatured collagen increased with increasing number of loading cycles (p=0.010) and strain rate (p<0.001), and the rate of damage accumulation increased with increasing strain rate (p=0.027). Mean ± s.e.m; n=6 per group except n=18 unloaded samples. Normalized number of cycles represents the amount of fatigue loading relative to fatigue failure, calculated from fatigue failure samples (see Fig 2A and B) as the cycle number divided by the number of cycles to failure.

3.2. Cyclic strain rate shifts the relationship of denatured collagen and peak strain

The amount of denatured collagen was significantly correlated with both the peak cyclic strain attained by the RTT fascicles (p<0.001) and the strain rate of loading (p<0.001), with increased denaturation at higher peak strains and lower strain rates (Fig. 2A). However, the effect of strain rate was not significant (p=0.738) when denatured collagen was considered as a function of creep strain (additional strain beyond the peak of the first loading cycle) and strain rate (Fig. 2B). Consistent with our previous results, this further demonstrated that creep strain is an independent predictor of molecular-level fatigue damage. Both the peak cyclic strain and creep strain increased with increasing fatigue level (normalized number of cycles) and strain rate (p<0.001, both), mirroring the relationship between collagen denaturation and normalized number of cycles (Fig. 2C-D). Some of the vertical shift of the creep curves resulted from increased first cycle peak strain with increasing strain rate, which corresponded with the increased strain at 40% of the mean UTS in monotonically loaded samples (Fig. 3). However, there was still a clear and significant rate-dependent increase in the magnitude of creep as a function of the normalized number of cycles.

Figure 2.

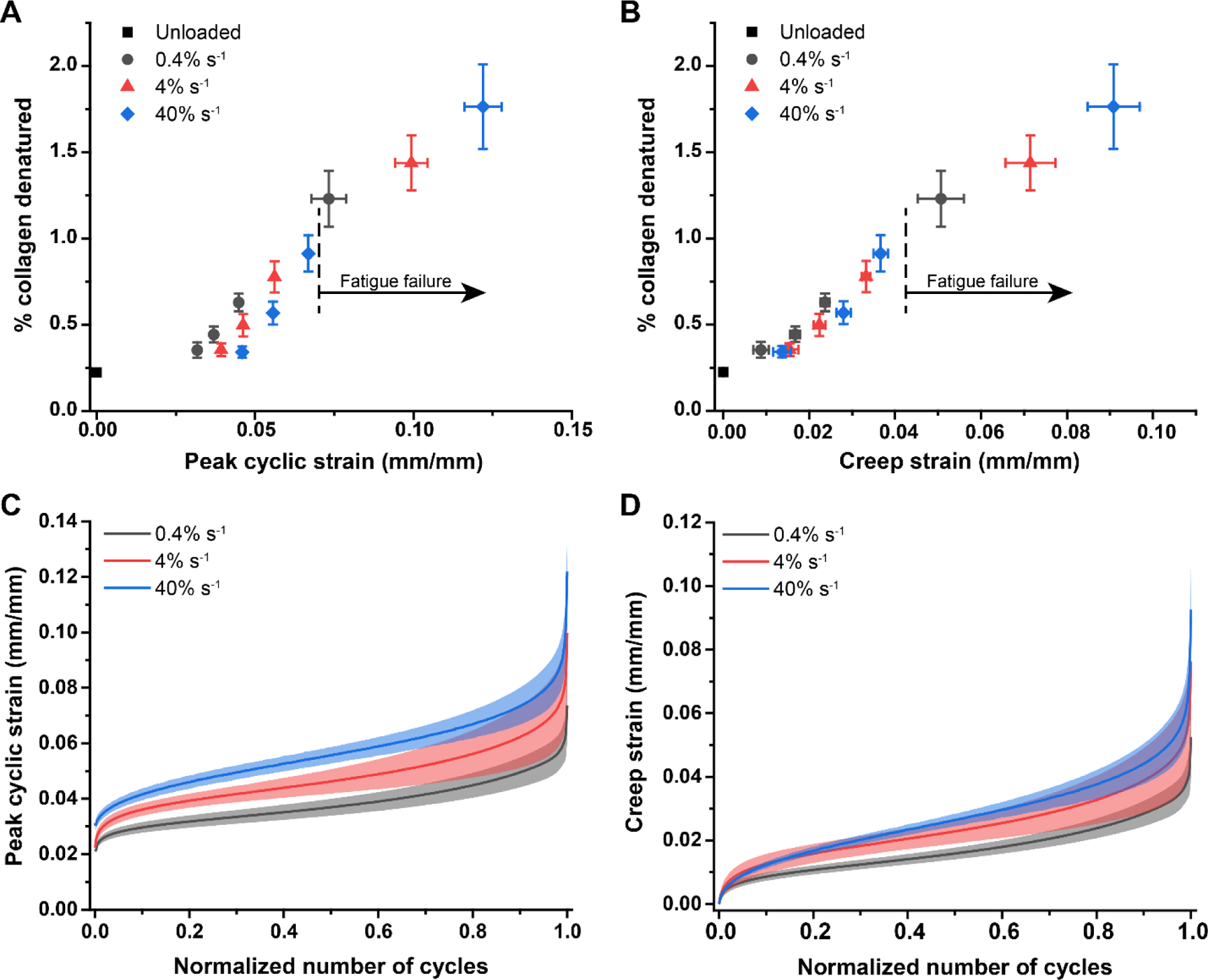
Percent denatured collagen as a function of peak cyclic strain and creep strain and strain-rate dependent fascicle creep. (A) The amount of denatured collagen increased with increasing peak cyclic strain and decreased with increasing strain rate (p<0.001 for both cases) but did not exhibit different rates of accumulation between strain rates (p=0.351). Interestingly, while samples loaded at higher strain rates accumulated less denaturation as a function of strain, they were able to withstand greater amounts of peak cyclic strain and thus denaturation before they failed (failure represented by the data point in each group). (B) When collagen denaturation was considered as a function of creep strain (normalized change in length from the peak of the first loading cycle), the overall effect of strain rate was not significant (p=0.738). However, it remained clear that samples loaded at faster strain rates withstood greater amounts of creep strain and thus denaturation before failing (failure represented by the last data point in each group). (C) Peak cyclic strain followed the typical triphasic creep pattern; high rates of creep were observed in the initial and final loading cycles, with a steady-state creep rate for the majority of the loading duration. There was a significant effect of strain rate, with higher peak cyclic strain at faster strain rates (p<0.001). (D) Creep strain similarly displayed a significant effect of strain rate (p<0.001) with samples experiencing more creep strain at faster strain rates as a function of the normalized number of cycles. Mean ± s.e.m.; n=6 per group except n=18 unloaded samples in (A) and (B). Mean ± s.d.; n = 10 per group in (C) and (D). Normalized number of cycles is the cycle number divided by the number of cycles to failure.

Figure 3.

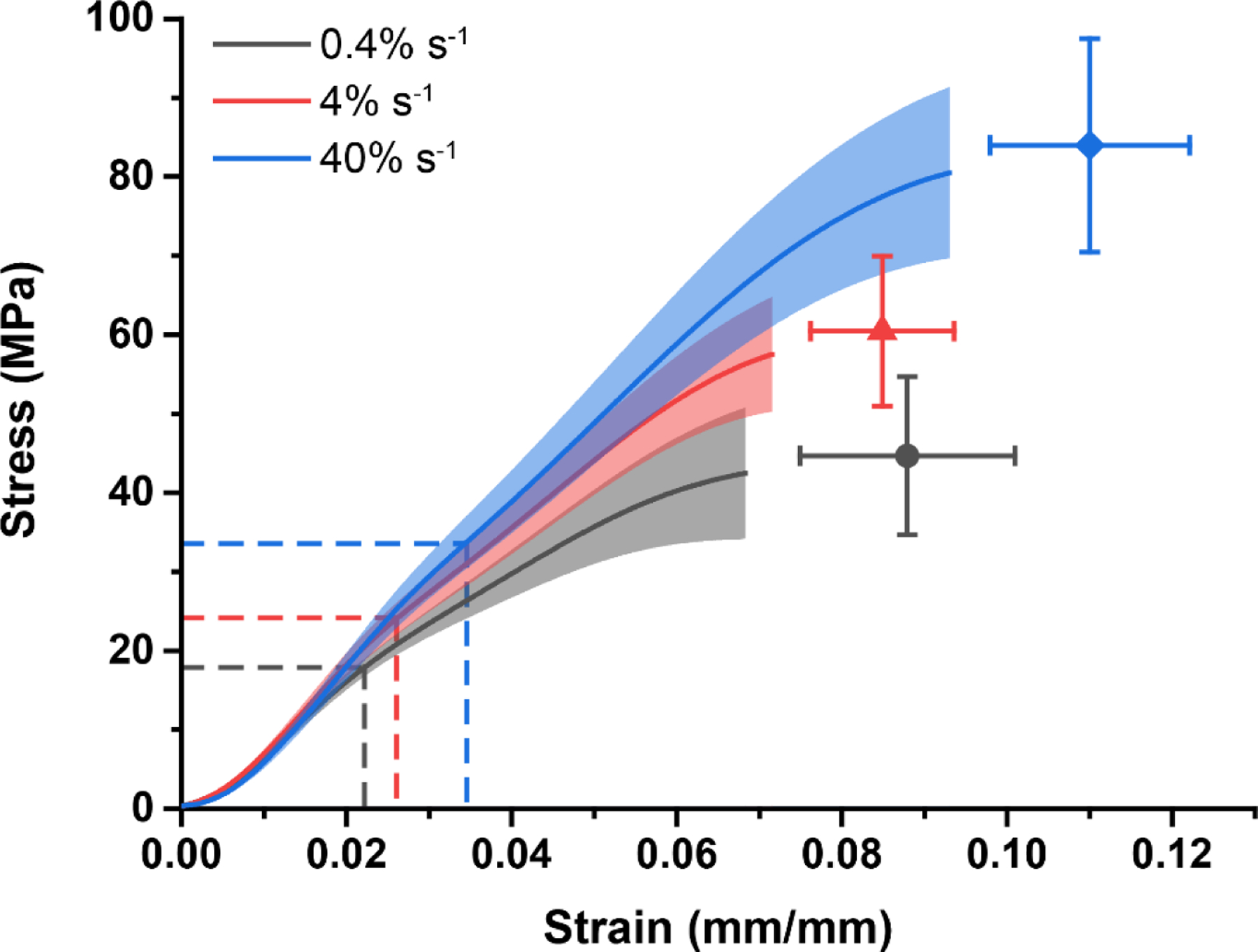
Monotonic stress-strain behavior across strain rates. The UTS increased with increasing strain rate (p<0.001). The observation of higher strain at 40% of the mean UTS with increasing strain rate corresponded to the observed vertical shift in peak cyclic strain curves (Fig. 2C), although there was not a monotonic trend in the strain at UTS (final data point). The stress-strain curve is plotted continuously to the final strain achieved by all samples, and the final point represents the ultimate stress and corresponding strain at the UTS. Mean ± s.d.; n=10 per strain rate.

3.3. Fatigue resistance of RTT is strain rate dependent

The fatigue resistance (number of cycles to failure) and fatigue lifetime (time to fatigue failure) of RTT fascicles were significantly affected by the cyclic strain rate (Fig. 4). The number of cycles to failure (Fig. 4A) displayed a threshold strain rate response, with significantly more cycles to failure at 4 and 40% s⁻¹ compared to 0.4% s⁻¹ loading (p=0.003 and p=0.006, respectively), and a non-significant difference between 4 and 40% s⁻¹ (p=0.665). The number of cycles to failure did not display a continuous effect of strain rate, demonstrated by the weak linear correlation (R²=0.07) and the non-significant main effect of strain rate (p=0.121). However, the time to failure (Fig. 4B) exhibited a significant continuous effect of strain rate with decreasing time to failure at faster strain rates (p<0.001). While samples could endure more loading cycles when loaded at faster strain rates, they failed after shorter loading duration. As a descriptor of the creep process, we expected that the amount of time the samples were under strain might be consistent across strain rate and describe a failure criterion, so strain data were integrated with respect to time to quantify the cumulative strain history. Samples cycled at faster rates spent less time at strain before failing (Fig. 4C), similar to the time to failure results.

Figure 4.

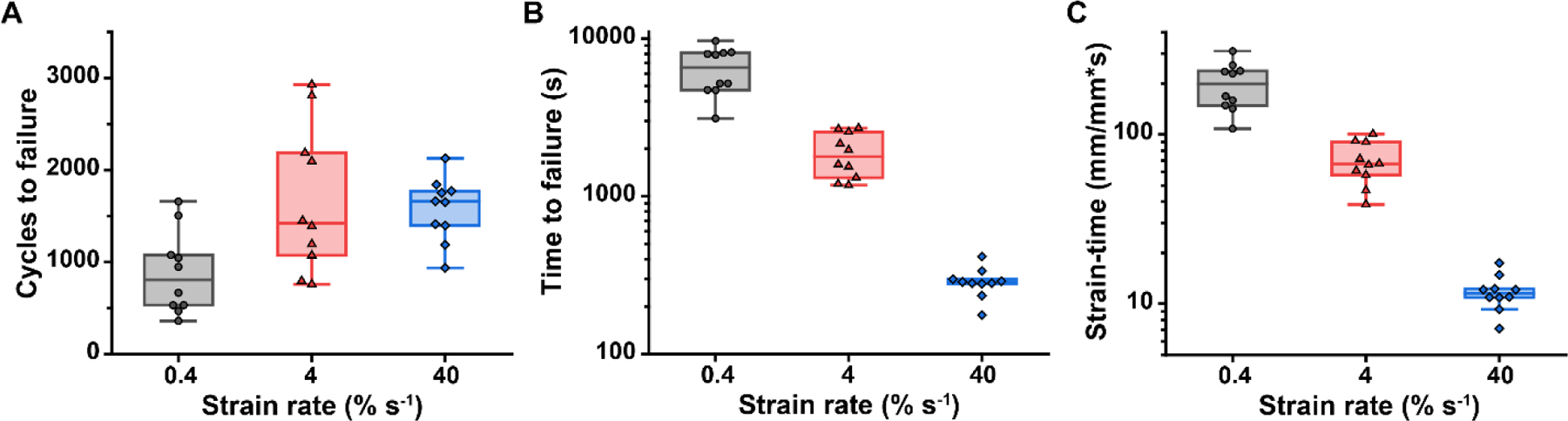
Fatigue resistance and fatigue lifetime as a function of strain rate. (A) The 4 and 40% s⁻¹ groups exhibited a higher number of cycles to failure than the 0.4% s⁻¹ group (p=0.003 and p=0.006, respectively). However, the number of cycles to failure exhibited high variability, consistent with previous studies of tendon fatigue, making it a poor predictor of tendon fatigue failure. (B) The fatigue lifetime exhibited a significant negative correlation with strain rate (p<0.001). This relationship was expected, as the number of cycles to failure was of the same order of magnitude between strain rates, but there was an order of magnitude difference between each of the strain rates. (C) The strain-time, a measure of the amount of time at strain or the strain history, also decreased with increasing strain rate (p<0.001). Median ± interquartile range (IQR) with whiskers representing the range within 1.5IQR. n=10 per strain rate; all data points are shown and were included in statistical analyses.

4. Discussion

The results of the present study definitively show that molecular damage to collagen via triple-helical unfolding accumulates throughout cyclic fatigue of RTT and that this is a mechanism of structural microdamage in tendons. The amount of collagen denaturation correlated with creep strain, independent of strain rate when the peak applied stress was scaled relative to the rate-dependent UTS. This result is consistent with our previous research that also demonstrated a rate-independent correlation of collagen denaturation with creep strain when samples were loaded to the same stress magnitude [23]. Together, these results support our hypothesis that this molecular-level damage is a mechanism of tissue-level creep and the fundamental mechanism of mechanical damage in tendons during cyclic fatigue loading. While there was a statistically significant threshold-type strain-rate dependence in the number of loading cycles at fatigue failure (Fig. 4A), the difference between dynamically loaded samples (4 and 40% s⁻¹) was not significant. Furthermore, there was only a 2-fold increase between the slowest and fastest groups (0.4 and 40% s⁻¹, respectively) compared to the 16-fold increase observed in our previous study where samples were loaded to the same stress magnitude [23]. Therefore, scaling the applied creep stress by the UTS at the strain rate of loading had the expected effect of equalizing the cycles to failure across strain rates. This result is consistent with previous studies which demonstrated that creep lifetime and cycles to failure are similar when the peak applied stress equals the predicted physiological tendon stress [31, 32].

Although tissue-level creep strain predicted the amount of collagen denaturation (Fig. 2B), neither parameter was a rate-independent indicator of damage relative to failure or failure itself. RTT fascicles that were cycled at faster strain rates sustained more denaturation as a function of the incremental fatigue level (normalized number of cycles) and at failure (Fig. 1). Multiple studies have shown that that following a monotonic load to failure, tendons that were loaded faster experienced less disruption of molecular-level packing compared to tendons that were loaded slower, as indicated by differential scanning calorimetry endotherms, although they did not have a significantly different change in enthalpy of denaturation [20, 33]. Those results suggest that a single fast loading event causes less structural disruption in the tendon, but a similar amount of overall collagen denaturation. Our previous molecular dynamics simulations of cyclic loading applied to a triple-helix molecule also demonstrated relative stabilization of the triple-helix at faster strain rates, as more loading cycles were required to reach similar levels of unfolding as the slower strain rate simulations [23]. Thus, the relative stabilization of the triple helix and triple-helical packing structure during high-rate loading may allow the tendon to endure more loading cycles to accumulate similar levels of damage and withstand more cumulative molecular-level damage before tissue-level rupture.

The strain-rate dependence of molecular damage accumulation and failure has important implications for understanding how overuse injuries develop during repetitive activities. Many dynamic human activities display a similar rate-dependent scaling of the applied load as modeled in our experimental design where we increased the cyclic stress magnitude at higher strain rates. For example, increasing either speed or step rate during walking and running is correlated with increased peak ground reaction force [14, 15], muscle forces [34], and Achilles tendon stress [16, 17]; and a faster baseball pitch velocity is correlated with higher peak shoulder and elbow moments [35]. Based on our present results, it is conceivable that tendons can endure more microdamage via collagen denaturation during a single bout of high-rate cyclic activity, which may serve a short-term protective function. However, this level of damage may be more likely to exceed the basal metabolic capacity of the tissue, and progress to injury upon repeated high-rate exertions, providing a mechanism to explain why speed is an injury risk factor for some athletic activities [2, 36]. This same process could also help explain the well-known association between overuse musculoskeletal injuries and sudden changes in athletic training and musical instrument practice intensity [6, 8, 37], and beginning new or resuming manual labor [5]. Recent research has revealed a distinct subpopulation of collagen fibrils in tendon that have turnover regulated by the circadian clock, demonstrating turnover of a structurally and mechanically important pool of collagen on the timescale of days [38], a timescale relevant to injuries that result from sudden activity changes.

While collagen denaturation is critical to the tendon damage process, tissue-level damage and failure are complex, multifactorial processes. Combined with our previous study [23], it is clear that neither the amount of collagen denaturation, amount of fascicle-level creep strain, duration of loading, number of loading cycles, nor the time at strain is an independent predictor of the relative amount of fatigue damage or fatigue failure of RTT fascicles. Even though cycles to failure demonstrated some predictive ability for dynamically loaded samples in the present study, RTT fascicles in our previous study that were loaded to the same magnitude of creep stress across strain rates showed a strong positive correlation between cycles to failure and strain rate. Additionally, the large variance in the number of cycles to failure makes it a poor criterion for evaluating the level of damage in individual tissues. We interpret our results to suggest that mechanisms other than collagen denaturation are needed to fully describe the tissue-level evolution of damage and failure in tendons due to repeated loading. It is critical to understand the interplay between collagen denaturation and hierarchical deformation mechanisms such as inter-molecular, fibrillar, and fiber sliding [39–42], biphasic fluid flow [23, 43–45], and fibril to fascicle-level helical twist [46, 47]. Importantly, these mechanisms are present to varying degrees across tendons that perform more energy-storing or positional functions. Computational damage models that incorporate both continuous (damage creation anytime the material is under load) and discontinuous (damage creation only when previous maximum strain energy is exceeded) damage mechanisms have demonstrated a powerful ability to predict the evolution of cyclic damage in soft tissues [48, 49]. New microstructurally motivated damage models that also account for solid-phase and flow-dependent viscoelasticity could prove beneficial for interpreting the growing body of multiscale experimental data and bridge the hierarchy of tissue structural organization.

It is important to acknowledge that tissue mechanical damage does not occur in isolation; it is essential to understand the biological response to mechanically denatured collagen to know how this damage persists over time, how it is detected and repaired, or how it may perpetuate pathological responses. The current and previous studies that investigated collagen molecular damage during repetitive loading in non-viable tissues provide the necessary foundation for future studies to investigate the various aspects of tendon mechanobiology that will be critical to identify proper recovery timelines following injury, altered loading, and during chronic high-load and high-rate loading. The present study focused on RTT, a specialized population of positional tendons. Studies comparing creep fatigue behavior of positional and energy-storing tendons have shown that they display similar tissue creep and softening behaviors [50, 51]. Furthermore, Lin et al. recently identified tissue yield as the threshold for significant collagen denaturation in both positional and energy-storing tendons subjected to monotonic tension (RTT and rat flexor digitorum longus tendon, respectively) [22], suggesting that collagen damage initiates and accumulates by the same mechanism across tendon types. We expect that molecular level damage during fatigue loading is also driven by the same structural mechanisms in positional and energy-storing tendons, and thus exhibits similar behavior as a function of creep strain and normalized to fatigue failure. However, the differences in yield strain and strain at UTS between positional and energy-storing tendons may result in different biological responses, which will be an important focus for future research.

5. Conclusions

This study provides new information about the rate-dependent accumulation of molecular-level collagen damage in tendons during cyclic fatigue loading. RTT fascicles were loaded to the same level of creep stress relative to their strength at the strain rate of loading (i.e., 40% of the UTS at 0.4, 4, or 40% s⁻¹), accounting for the rate-dependent material properties of tendon. Our results demonstrate that collagen denaturation during fatigue loading accumulates with increasing creep strain, independent of the cyclic strain rate. However, denatured collagen increased with strain rate as a function of loading cycles normalized to fatigue failure, and the RTT fascicles that were cycled faster ultimately endured more strain and collagen denaturation before failing. These results indicate that while tendons may be protected from acute failure during faster cyclic loading, the tissue may be at increased risk for injury development and require more recovery time compared to a similar amount of slower rate loading.

Statement of Significance.

This study is the first to investigate the accumulation of denatured collagen in tendons throughout fatigue loading when the maximum stress is scaled with the applied strain rate. The amount of denatured collagen was correlated with creep strain, independent of strain rate, but samples that were cycled faster withstood greater amounts of denaturation before failure. Differential accumulation of collagen damage between fast and slow repetitive loading has relevance toward understanding the prevalence of overuse musculoskeletal injuries following sudden changes in activity level. Since collagen is a ubiquitous biological structural component, the basic patterns and mechanisms of loading-induced collagen damage in connective tissues are relevant for understanding injury and disease in other tissues, including those from the cardiovascular and pulmonary systems.