First demonstration of tuning between the Kitaev and Ising limits in a honeycomb lattice

Abstract

Recent observations of novel spin-orbit coupled states have generated interest in 4d/5d transition metal systems. A prime example is the $J_{\text{eff}}=\frac{1}{2}$ state in iridate materials and α-RuCl₃ that drives Kitaev interactions. Here, by tuning the competition between spin-orbit interaction (λ_SOC) and trigonal crystal field (Δ_T), we restructure the spin-orbital wave functions into a previously unobserved $\mathrm{\mu }=\frac{1}{2}$ state that drives Ising interactions. This is done via a topochemical reaction that converts Li₂RhO₃ to Ag₃LiRh₂O₆. Using perturbation theory, we present an explicit expression for the $\mathrm{\mu }=\frac{1}{2}$ state in the limit Δ_T ≫ λ_SOC realized in Ag₃LiRh₂O₆, different from the conventional $J_{\text{eff}}=\frac{1}{2}$ state in the limit λ_SOC ≫ Δ_T realized in Li₂RhO₃. The change of ground state is followed by a marked change of magnetism from a 6 K spin-glass in Li₂RhO₃ to a 94 K antiferromagnet in Ag₃LiRh₂O₆.

The spin-orbital quantum state is modified by tuning the spin-orbit coupling vs. trigonal lattice distortion.

INTRODUCTION

An exotic quantum state in condensed matter physics is the $J_{\text{eff}}=\frac{1}{2}$ state in honeycomb iridate materials that leads to the Kitaev exchange interaction (1–6). The $J_{\text{eff}}=\frac{1}{2}$ state is a product of strong spin-orbit coupling (SOC) in heavy Ir⁴⁺ ions that splits the t_2g manifold into a $J_{\text{eff}}=\frac{3}{2}$ quartet and a $J_{\text{eff}}=\frac{1}{2}$ doublet. With five electrons in the 5d⁵ configuration, iridates have one electron in the spin-orbital $J_{\text{eff}}=\frac{1}{2}$ state that satisfies the prerequisites of the Kitaev interaction in a honeycomb lattice as shown by earlier studies (1–5). Here, we introduce a new spin-orbital state, $\mathrm{\mu }=\frac{1}{2}$, which we have engineered by tuning the interplay between two energy scales: the SOC (λ_SOC) and the trigonal crystal field splitting (Δ_T). The $\mathrm{\mu }=\frac{1}{2}$ state drives Ising instead of Kitaev interactions. Although the Ising limit has been discussed in several theoretical studies (7–10), a transition between the Kitaev and Ising limits has not been demonstrated until now. It has been theoretically predicted that the Kitaev limit in Na₂IrO₃ can be tuned to an Ising limit under uniaxial physical pressure (8), but the required pressure has not been achieved. The Ising limit is relevant to MPS₃ (M = Mn, Fe, and Ni) compounds (10); however, a transition from the Ising to Kitaev limit has not been discussed in those materials, even at a theoretical level. This work presents the first observation of a transition between the Kitaev and Ising limits in the same material family.

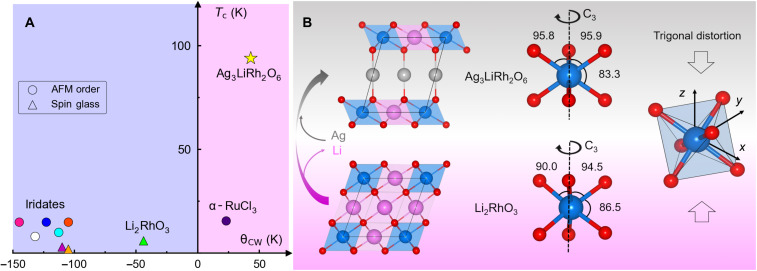
Our experiment was motivated by a survey of the average Curie-Weiss temperature (${\mathrm{\Theta }}_{\text{CW}}^{\text{avg}}$) and the antiferromagnetic (AFM) or spin-glass transition temperatures (T_N/T_g) of the two-dimensional (2D) iridium-, rhodium-, and ruthenium-based Kitaev materials (Fig. 1A and table S1). These compounds can be categorized into two groups. The first-generation Kitaev magnets include α-Li₂IrO₃, Na₂IrO₃, Li₂RhO₃, and α-RuCl₃, synthesized by conventional solid-state methods (11–19). The second-generation materials, such as H₃LiIr₂O₆, Cu₃NaIr₂O₆, and Ag₃LiIr₂O₆, have been synthesized recently by exchanging the interlayer alkali (Li⁺ and Na⁺) in the first-generation compounds with H⁺, Cu⁺, and Ag⁺ using topochemical reactions (20–26). Both the first- and second-generation iridates appear in the same region of the phase diagram in Fig. 1A. The 4d systems, namely, Li₂RhO₃ and α-RuCl₃, appear to be shifted horizontally but not vertically from the iridate block. Despite theoretical predictions of diverse magnetic phases (27, 28), it seems that all 2D Kitaev materials studied so far aggregate in the same region of the phase diagram with T_N ≤ 15 K and a $J_{\text{eff}}=\frac{1}{2}$ state. This observation prompted us to experimentally investigate the possibility of tuning the local spin-orbital state and the magnetic ground state in the same material family.

Fig. 1. Phase diagram.

(A) Critical temperature (T_c) plotted against the Curie-Weiss temperature (${\mathrm{\Theta }}_{\text{CW}}^{\text{avg}}$) using the data in table S1 for polycrystalline 2D Kitaev materials. Circles and triangles represent AFM and spin-glass transitions, respectively. The iridate materials are (from left to right) Cu₃LiIr₂O₆, Ag₃LiIr₂O₆, Na₂IrO³, Cu₃NaIr₂O₆, Cu₂IrO₃, H₃LiIr₂O₆, and α-Li₂IrO₃. (B) Structural relationship between the first- and second-generation Kitaev systems, Li₂RhO₃ and Ag₃LiRh₂O₆, with enhanced trigonal distortion in the latter, as evidenced by the change of bond angles after cation exchange.

We focused on rhodate (4d) systems where the SOC is weaker than in the iridate (5d) systems, and Δ_T has a better chance to compete with λ_SOC. Evidence of such competition can be found in earlier density functional theory (DFT) studies of the honeycomb rhodates, where a high sensitivity of the magnetic ground state to structural parameters has been reported (18, 29). To enhance Δ_T, we replaced the Li atoms between the honeycomb layers of Li₂RhO₃ with Ag atoms and synthesized Ag₃LiRh₂O₆ topochemically (Fig. 1B). The change of interlayer bonds leads to a trigonal compression along the local C₃ axis (Fig. 1B). Using crystallographic refinement (fig. S1 and tables S2 and S3), we determined the bond angles within the local octahedral (O_h) environments of both compounds and quantified the trigonal distortion by calculating the bond angle variance (9) $\mathrm{\sigma }=\sqrt{{\sum }_{i=1}^{12}{(\mathrm{\theta }-{\mathrm{\theta }}_0)}^2/(m-1)}$, where m = 12 and θ₀ = 90^∘. In an ideal octahedron, σ = 0. In Ag₃LiRh₂O₆, we found σ = 6.1(1)^∘, nearly twice the σ = 3.1(1)^∘ in Li₂RhO₃. It has been noted in earlier theoretical works (7, 8) that a trigonal distortion can reconstruct the spin-orbital states and lead to new magnetic regimes; however, it has also been noted that such a regime may not be accessible in iridate materials due to the overwhelmingly strong SOC. As shown in Fig. 1A, we induced such a change of regime between Li₂RhO₃ and Ag₃LiRh₂O₆ using chemical pressure.

RESULTS

Magnetic properties

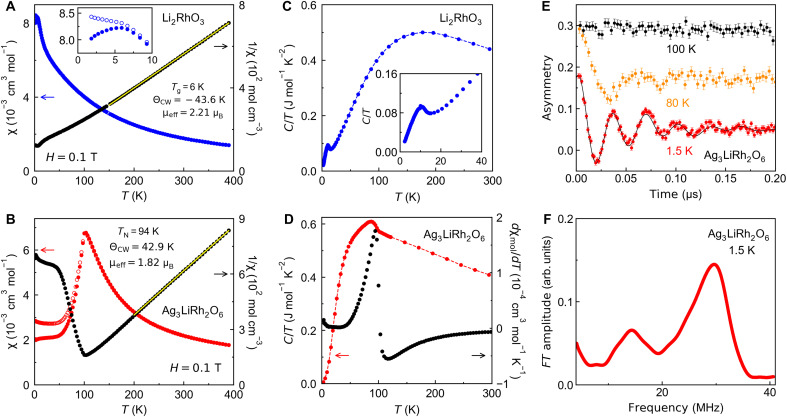
A small peak at T_g = 6.0(5) K in Li₂RhO₃ with a splitting between the zero-field-cooled (ZFC) and field-cooled (FC) susceptibility data [χ(T) in Fig. 2A] confirms the spin-glass transition as reported in earlier works (18, 30, 31). In stark contrast, Ag₃LiRh₂O₆ exhibits a robust AFM order with a pronounced peak in χ(T) and without ZFC/FC splitting (Fig. 2B). The small difference between the ZFC and FC curves at low temperatures is due to a small amount of stacking faults, which are carefully analyzed in fig. S2. A Curie-Weiss analysis in Fig. 2B yields an effective moment of 1.82 μ_B and a ${\mathrm{\Theta }}_{\text{CW}}^{\text{avg}}=42.9$ K, consistent with a prior report (32). A positive ${\mathrm{\Theta }}_{\text{CW}}^{\text{avg}}$ despite an AFM order suggests that χ(T) must be highly anisotropic, which is the case in materials with A-type or C-type AFM order. For example, Na₃Ni₂BiO₆ has a C-type AFM order [AFM intralayer and ferromagnetic (FM) interlayer] with T_N = 10.4 K and ${\mathrm{\Theta }}_{\text{CW}}^{\text{avg}}=13.3$ K (33).

Fig. 2. Magnetic characterization.

Magnetic susceptibility plotted as a function of temperature and Curie-Weiss analysis presented in (A) Li₂RhO₃ (blue) and (B) Ag₃LiRh₂O₆ (red). The ZFC and FC data are shown as full and empty symbols, respectively. Heat capacity as a function of temperature in (C) Li₂RhO₃ and (D) Ag₃LiRh₂O₆. The black circles in (D) show the derivative of magnetic susceptibility with respect to temperature. (E) μSR asymmetry plotted as a function of time in Ag₃LiRh₂O₆. For clarity, the curves at 100 and 80 K are offset with respect to the 1.5 K spectrum. The solid line is a fit to a Bessel function (see the Supplementary Materials for details). (F) Fourier transform of the μSR spectrum at 1.5 K showing two frequency components.

Both the spin-glass transition in Li₂RhO₃ and the AFM transition in Ag₃LiRh₂O₆ are marked by peaks in the heat capacity in Fig. 2 (C and D). The heat capacity peak of Ag₃LiRh₂O₆ is visible despite the large phonon background at high temperatures, confirming a robust AFM order. We report T_N = 94(3) K using the peak in dχ/dT, which is close to the peak in the heat capacity (Fig. 2D). T_N in Ag₃LiRh₂O₆ is nearly an order of magnitude larger than the transition temperature in any other 2D Kitaev material to date.

To obtain information about the local field within the magnetically ordered state of Ag₃LiRh₂O₆, we turned to muon spin relaxation (μSR) experiments. In Fig. 2E, the time-dependent μSR asymmetry curves in zero applied magnetic field show the appearance of spontaneous oscillations below 100 K, confirming the long-range magnetic order. The asymmetry spectrum at 1.5 K fits to a modified zeroth-order Bessel function (34), with the form of the fitting function indicating noncollinear incommensurate magnetic ordering (see the Supplementary Materials for details). As shown in Fig. 2F, the Fourier transform of the 1.5 K spectrum shows two peaks at 12 and 31 MHz, which we have modeled using a two-component expression. Each component has a distribution of local fields between a B_min and B_max, indicating incommensurate ordering (table S4). The center of distribution (B_min + B_max)/2 is shifted from zero, indicating a noncollinear order (34). The dominant frequency of 31 MHz in Fig. 2F corresponds to a maximum internal field of 0.231 T at the muon stopping site (using ω = γ_μB with the muon gyromagnetic ratio γ_μ = 851.6 Mrad s⁻¹ T⁻¹), which is an order of magnitude larger than the internal field of 0.015 T extracted from μSR in Li₂RhO₃ (31). The marked change of magnetism between Li₂RhO₃ and Ag₃LiRh₂O₆ in response to mild trigonal distortion, with an order-of-magnitude increase in both T_N and internal field, implies a novel underlying interaction in the ground state.

Theoretical wave functions

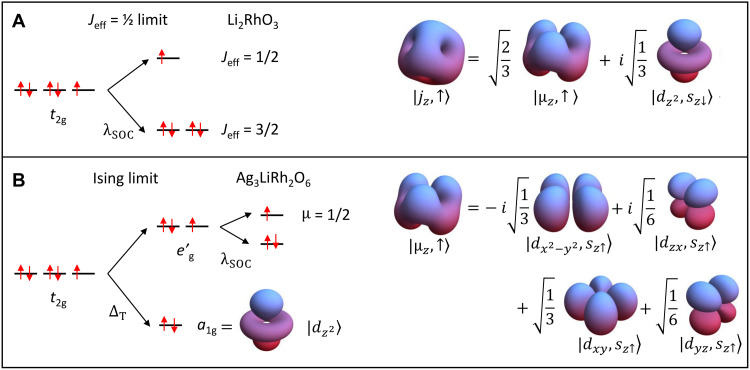
The drastic change of magnetic behavior between Li₂RhO₃ and Ag₃LiRh₂O₆ originates from a fundamental change of the spin-orbital quantum state (Fig. 3). Both Li₂RhO₃ and Ag₃LiRh₂O₆ have Rh⁴⁺ in the 4d⁵ configuration, corresponding to one hole in the t_2g manifold. Assuming that both compounds are in the Mott insulating regime (fig. S3), their low-energy physics should be described by a Kramers doublet per Rh⁴⁺ ion; i.e., they are effective spin-$\frac{1}{2}$ systems. However, the nature of the Kramers doublet may be considerably different depending on the interplay between λ_SOC and Δ_T. We illustrate this by considering two limits: the J_eff = 1/2 limit for λ_SOC ≫ Δ_T relevant to Li₂RhO₃ (Fig. 3A) and the Ising limit for Δ_T ≫ λ_SOC relevant to Ag₃LiRh₂O₆ (Fig. 3B). The wave functions of the low-energy Kramers doublet can be found in both limits using perturbation theory. The Kramers doublet in the J_eff = 1/2 limit (λ_SOC ≫ Δ_T) comprises the following two states (Fig. 3A)

$$\mid j_{z,\uparrow }\mathrm{\rangle }=\sqrt{\frac{2}{3}}\mid {\mathrm{\mu }}_z,\uparrow \mathrm{\rangle }+i\sqrt{\frac{1}{3}}\mid d_{z^2},s_{z\downarrow }\mathrm{\rangle },\mid j_{z,\downarrow }\mathrm{\rangle }=\sqrt{\frac{2}{3}}\mid {\mathrm{\mu }}_z,\downarrow \mathrm{\rangle }+i\sqrt{\frac{1}{3}}\mid d_{z^2},s_{z\uparrow }\mathrm{\rangle }$$ (1)

where {∣μ_z,↑〉, ∣μ_z,↓〉} are defined in Eq. 2 below. The J_eff = 1/2 limit has been discussed extensively in the literature, and sizable Kitaev interactions have been proposed for materials in this limit such as the honeycomb iridates (1–4), α-RuCl₃ (16), and Li₂RhO₃ (29–31). The only difference between Eq. 1 and prior works (4) is that we choose the z axis to be normal to the triangular face of the octahedron (Fig. 1B) instead of pointing at the apical oxygens.

Fig. 3. Wave functions.

(A) The J_eff = 1/2 limit, realized in Li₂RhO₃, where λ_SOC ≫ Δ_T. The probability density is visualized for the isospin-up wave function. (B) The Ising limit, realized in Ag₃LiRh₂O₆, where Δ_T ≫ λ_SOC. The probability density is visualized for the spin-up wave function. Notice the cubic and trigonal symmetries of the J_z and μ_z orbitals, respectively.

In the Ising limit (Δ_T ≫ λ_SOC), the trigonal distortion leads to new Kramers doublet states (Fig. 3B)

$$\begin{array}{c}\mid {\mathrm{\mu }}_{z,\uparrow }\mathrm{\rangle }=-i\sqrt{\frac{1}{3}}\mid d_{x^2-y^2},s_{z\uparrow }\mathrm{\rangle }+i\sqrt{\frac{1}{6}}\mid d_{\mathit{zx}},s_{z\uparrow }\mathrm{\rangle }+\sqrt{\frac{1}{3}}\mid d_{\mathit{xy}},s_{z\uparrow }\mathrm{\rangle }+\sqrt{\frac{1}{6}}\mid d_{\mathit{yz}},s_{z\uparrow }\mathrm{\rangle },\\ \mid {\mathrm{\mu }}_{z,\downarrow }\mathrm{\rangle }=i\sqrt{\frac{1}{3}}\mid d_{x^2-y^2},s_{z\downarrow }\mathrm{\rangle }-i\sqrt{\frac{1}{6}}\mid d_{\mathit{zx}},s_{z\downarrow }\mathrm{\rangle }+\sqrt{\frac{1}{3}}\mid d_{\mathit{xy}},s_{z\downarrow }\mathrm{\rangle }+\sqrt{\frac{1}{6}}\mid d_{\mathit{yz}},s_{z\downarrow }\mathrm{\rangle }\end{array}$$ (2)

Note that the states {∣j_z,↑〉, ∣j_z,↓〉} are not orthogonal to the states {∣μ_z,↑〉, ∣μ_z,↓〉}, despite being in opposite limits.

The trigonal splitting energy scale Δ_T is known to split the sixfold degenerate t_2g levels (including spin degrees of freedom) into a twofold a_1g manifold and a fourfold $e_{\mathrm{g}}^{\prime }$ manifold (Fig. 3B) (10). Choosing $\widehat{x}$ and $\widehat{y}$ directions pointing toward oxygen atoms as shown in Fig. 1B, the orbital wave functions are found to be ∣d_z²〉 for a_1g (Fig. 3B) and {∣τ_z,↑〉, ∣τ_z,↓〉} for $e_{\mathrm{g}}^{\prime }$

$$\mid {\mathrm{\tau }}_{z,\uparrow }\mathrm{\rangle }\equiv \sqrt{\frac{2}{3}}\mid d_{x^2-y^2}\mathrm{\rangle }-\sqrt{\frac{1}{3}}\mid d_{\mathit{zx}}\mathrm{\rangle }, \mid {\mathrm{\tau }}_{z,\downarrow }\mathrm{\rangle }\equiv \sqrt{\frac{2}{3}}\mid d_{\mathit{xy}}\mathrm{\rangle }+\sqrt{\frac{1}{3}}\mid d_{\mathit{yz}}\mathrm{\rangle }$$ (3)

In the materials under consideration, the trigonal distortion is a compression along the $\widehat{z}$ axis (Fig. 1B) that lowers the energy of the a_1g level (Fig. 3B). Thus, for the 4d⁵ configuration, one should focus on the fourfold $e_{\mathrm{g}}^{\prime }$ manifold. Unlike in the e_g manifold, the SOC is not completely quenched in the $e_{\mathrm{g}}^{\prime }$ manifold. We show, in the Supplementary Materials, that the d-orbital angular momentum operator $\overrightarrow{L}$, after projection into the $e_{\mathrm{g}}^{\prime }$ manifold, becomes

$$L_x\to 0, L_y\to 0, L_z\to {\mathrm{\tau }}_y$$ (4)

where τ_x,y,z are the pseudospin Pauli matrices. We therefore have, in the $e_{\mathrm{g}}^{\prime }$ manifold

$${\mathrm{\lambda }}_{\text{SOC}} \overrightarrow{\mathbf{L}}·\overrightarrow{\mathbf{s}}\to {\mathrm{\lambda }}_{\text{SOC}} L_z{s}_z={\mathrm{\lambda }}_{\text{SOC}} {\mathrm{\tau }}_y{s}_z$$ (5)

Namely, λ_SOC further splits the $e_{\mathrm{g}}^{\prime }$ manifold into two Kramers doublets: τ_y anti-aligned with s_z or τ_y aligned with s_z. The former doublet has a lower energy, so the latter doublet is half-filled in the 4d⁵ configuration. Last, the low-energy effective spin-$\frac{1}{2}$ states in the Ising limit are

$$\mid {\mathrm{\mu }}_{z,\uparrow }\mathrm{\rangle }=\mid {\mathrm{\tau }}_y=+1,s_{z,\uparrow }\mathrm{\rangle }, \mid {\mathrm{\mu }}_{z,\downarrow }\mathrm{\rangle }=\mid {\mathrm{\tau }}_y=-1,s_{z,\downarrow }\mathrm{\rangle }$$ (6)

which are nothing but the states written in Eq. 2 and illustrated in Fig. 3B.

The exchange couplings for the effective μ spins are expected to have the Ising anisotropy (easy-axis along the $\widehat{z}$ direction). To understand its origin, one may consider exchange interactions like $J{\overrightarrow{\mathbf{S}}}_i·{\overrightarrow{\mathbf{S}}}_j$ between two Rh sites i, j in the absence of the spin-orbit interaction. After λ_SOC is turned on, the $J{\overrightarrow{\mathbf{S}}}_i·{\overrightarrow{\mathbf{S}}}_j$ needs to be projected onto the Kramers doublet {∣μ_z,↑〉, ∣μ_z,↓〉} at low energies. Only the term JS_i,zS_j,z survives after the projection. In addition, the g factor of the effective μ spins in a magnetic field is also expected to be highly anisotropic. For example, the effective μ spins do not couple with a magnetic field along the $\widehat{x}$ (or $\widehat{y}$) axis in a linear fashion in this limit. A direct measurement of the magnetic response with respect to the field direction is not possible at this stage because single crystals of Ag₃LiRh₂O₆ are not available. However, indirect evidence of such anisotropic interactions may be the positive Curie-Weiss temperature in polycrystalline samples of Ag₃LiRh₂O₆ (Fig. 2B) that indicates FM interactions despite the AFM ordering. Such a behavior has been reported in Na₃Ni₂BiO₆ and attributed to a C-type AFM order where the coupling within the layers is AFM and between the layers is FM (33).

Spectroscopic evidence

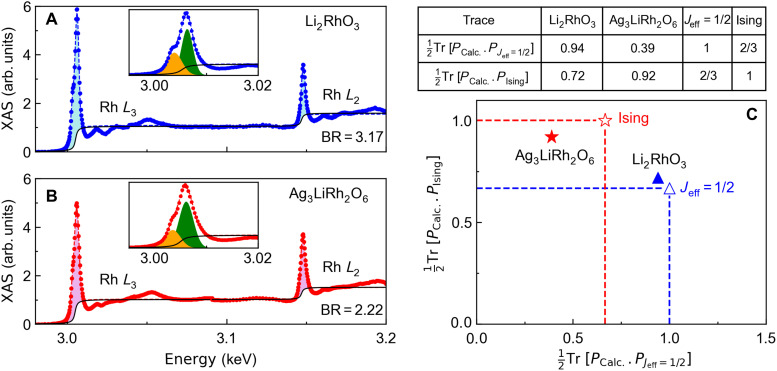
We provide spectroscopic confirmation of the above picture by measuring the branching ratio using x-ray absorption spectroscopy (XAS). Figure 4A shows the XAS data from a Li₂RhO₃ sample with the Rh L₃ and L₂ edges near 3.00 and 3.15 keV, respectively. The branching ratio, BR = I(L₃)/I(L₂) = 3.17(1), is evaluated by dividing the shaded areas under the L₃ and L₂ peaks in Fig. 4A. A similar analysis in Ag₃LiRh₂O₆ yields BR = 2.22(1) (Fig. 4B). The branching ratio is related to the SOC through BR = (2 + r)/(1 − r), where r = 〈L · S〉/n_h, with n_h being the number of holes in the 4d shell (35, 36). Using n_h = 5 for Rh⁴⁺, we obtain 〈L · S〉 = 1.40 in Li₂RhO₃ and 0.34 in Ag₃LiRh₂O₆. This is consistent with the above theoretical picture based on λ_SOC ≫ Δ_T and the J_eff limit in Li₂RhO₃ compared to Δ_T ≫ λ_SOC and the Ising limit in Ag₃LiRh₂O₆.

Fig. 4. X-ray absorption spectroscopy.

(A) XAS data from Rh L_2,3 edges of Li₂RhO₃. The data were modeled with a step and two Gaussian functions for the L₃ edge (inset) and one Gaussian function for the L₂ edge. (B) Similar data and fits for the Rh L_2,3 edges of Ag₃LiRh₂O₆. (C) Theoretically calculated traces of projector products are tabulated and plotted for both the ideal limits (empty symbols) and real materials (full symbols).

Note that the spectroscopic value of 〈L · S〉 is small but nonvanishing in Ag₃LiRh₂O₆. The fine structure of Rh L edge with a shoulder near the L₃ peak (inset of Fig. 4B) that is absent in the L₂ peak confirms a finite SOC in Ag₃LiRh₂O₆ (37). As illustrated in Fig. 3B, a weak SOC is necessary to split the $e_{\mathrm{g}}^{\prime }$ levels. The fine structure of the Rh L₃ edge can be fitted to two Gaussian curves in both Li₂RhO₃ and Ag₃LiRh₂O₆ (insets of Fig. 4, A and B). A higher ratio between the two Gaussian areas in Ag₃LiRh₂O₆ (2.42) than in Li₂RhO₃ (1.53) is consistent with a weaker SOC in the former. Supporting information about the Ag L edge is provided in fig. S4 to confirm the Ag⁺ oxidation state (38, 39).

DISCUSSION

We have demonstrated that a competition between SOC and trigonal distortion could tune a honeycomb structure between the Kitaev ($J_{\text{eff}}=\frac{1}{2}$) and Ising ($\mathrm{\mu }=\frac{1}{2}$) limits. Our magnetization, μSR, and XAS data suggest that Li₂RhO₃ is closer to the J_eff limit, whereas Ag₃LiRh₂O₆ is closer to the Ising limit. We calculated the ideal wave functions and visualized them in Fig. 3. However, a realistic material is generally situated on a spectrum between these two ideal limits. For example, minor lattice distortions (e.g., monoclinic) can further break the trigonal point group symmetry and perturb the ideal wave function.

To make our theoretical discussion more realistic, we calculated the band structure of Li₂RhO₃ and Ag₃LiRh₂O₆ from first principles and obtained a real-space tight-binding model for each compound. Details of the electronic structure calculations in the presence of Hubbard-U, SOC, and zigzag magnetic ordering are presented in figs. S5 and S6 and table S5. The full orbital content of the energy eigenstates was characterized using a combination of Quantum Espresso and Wannier90 software (40–42). This allowed us to quantitatively investigate the regimes being realized in Li₂RhO₃ and Ag₃LiRh₂O₆. Specifically, given a Kramers doublet ∣ψ₁〉 and ∣ψ₂〉, we defined the projectors

$$P_{\mathrm{\psi }}\equiv \mid {\mathrm{\psi }}_1\mathrm{\rangle }\mathrm{\langle }{\mathrm{\psi }}_1\mid +\mid {\mathrm{\psi }}_2\mathrm{\rangle }\mathrm{\langle }{\mathrm{\psi }}_2\mid$$ (7)

For example, P_Jeff=1/2 and P_Ising are projectors defined using the Kramers doublets in the J_eff = 1/2 limit (Eq. 1) and the Ising limit (Eq. 2), respectively. We then compute the traces $\frac{1}{2}\text{Tr}[P_{\text{calc}.}·P_{J_{\text{eff}}=1/2}]$ and $\frac{1}{2}\text{Tr}[P_{\text{calc}.}·P_{\text{Ising}}]$. The results are tabulated and visualized in Fig. 4C. These traces would be unity if the calculated system was in the ideal J_eff or Ising limit. Figure 4C locates Li₂RhO₃ and Ag₃LiRh₂O₆ in the vicinity of the J_eff = 1/2 and Ising (μ = 1/2) limits, respectively.

Our combined experimental and theoretical results show how to change the fabric of spin-orbit coupled states and markedly change the magnetic behavior of the Kitaev materials. Despite theoretical proposals for a diverse global phase diagram, the current Kitaev systems are all in the J_eff limit (1–5, 14, 16, 43–45). Finding an outlier, such as Ag₃LiRh₂O₆, in the phase diagram (Fig. 1A) provides the first glimpse at the diversity of magnetic phases that can be engineered using topochemical methods. Specifically, the interplay between the Kitaev and Ising limits will be a fruitful venue to search for novel noncollinear magnetic orders beyond the familiar Kitaev-Heisenberg paradigm.

MATERIALS AND METHODS

Material synthesis

Similar to other second-generation Kitaev magnets, Ag₃LiRh₂O₆ is a metastable compound. It is synthesized through a topotactic cation-exchange reaction under mild conditions from the first-generation parent compound Li₂RhO₃.

$$2\mathrm{L}{\mathrm{i}}_2\text{Rh}{\mathrm{O}}_3+3\text{AgN}{\mathrm{O}}_3⟶\mathrm{A}{\mathrm{g}}_3\text{LiR}{\mathrm{h}}_2{\mathrm{O}}_6+3\text{LiN}{\mathrm{O}}_3$$ (8)

Li₂RhO₃ was synthesized following prior published works (30, 31). To perform the topotactic exchange reaction, Li₂RhO₃ and AgNO₃ powders were mixed and heated to 350^∘C for 1 week. The excess AgNO₃ was removed with deionized water.

Characterizations

Powder x-ray diffraction was performed using a Bruker D8 ECO instrument in the Bragg-Brentano geometry, using a copper source (Cu-K_α) and a LYNXEYE XE 1D energy-dispersive detector. The FullProf suite was used for the Rietveld analysis (46). Peak shapes were modeled with the Thompson-Cox-Hastings pseudo-Voigt profile convoluted with axial divergence asymmetry. Magnetization was measured using a Quantum Design MPMS3 with the powder sample mounted on a low-background brass holder. Both the electrical resistivity (four-probe technique) and heat capacity (relaxation time method) were measured on a pressed pellet using the Quantum Design PPMS Dynacool. Electron diffraction, high-angle annular dark-field scanning transmission electron microscopy (STEM), and annular bright-field STEM were performed using an aberration double-corrected JEM ARM200F microscope operated at 200 kV and equipped with a CENTURIOEDX detector, Orius Gatan charge-coupled device camera, and GIF Quantum spectrometer (47–49). The μSR measurements were performed in a continuous-flow ⁴He evaporation cryostat (T ≥ 1.5 K) at the general purpose surface-muon instrument (50) at the Paul Scherrer Institute, and the data were analyzed using the Musrfit program (51). A pressed disk of Ag₃LiRh₂O₆ with diameter 12 mm and thickness 1.2 mm was wrapped in 25-μm silver foil and suspended in the muon beam to minimize the contribution from muons implanted in a sample holder or in the cryostat walls.

First-principles calculations

The electronic structures were computed using the open-source code Quantum Espresso (40, 41) with the experimental crystallographic information as the input. The calculation included SOC and zigzag magnetic ordering for both compounds, and the fully gapped states were achieved using a DFT + U method (52). To stabilize the noncollinear magnetic calculation, we used the norm-conserving pseudopotentials from PseudoDojo (53). For convergence reasons, we implemented the Perdew-Zunger functional in the calculation of Ag₃LiRh₂O₆, while leaving the default Perdew-Burke-Ernzerhof functional for Li₂RhO₃. To compare with the previous report of the insulating states in chemical formula Li₂RhO₃ (LRO) (18), we fixed the Hund’s coupling to J = 0.7 eV and tuned the Hubbard-U from 1 to 4 eV. Our results were consistent with the prior work. The real-space tight-binding functions (involving the Rh-4d and O-2p orbitals as well as Ag-4d orbitals for Ag₃LiRh₂O₆) were derived from the band structure using maximally localized Wannier states implemented by the Wannier90 software (42). From here, tight-binding models for a single RhO₆ cluster were constructed on the basis of the obtained real-space hopping parameters. The eigenstates of such a RhO₆ cluster were used to compute 〈L · S〉 and the traces in Fig. 4.

X-ray absorption spectroscopy

X-ray absorption near-edge structure data at Rh and Ag L_2,3 edges were collected at tender energy beamline 8-BM of the National Synchrotron Light Source II and at beamline 4-ID-D of the Advanced Photon Source, respectively. The Rh L_2,3 data were collected in total electron yield mode using powder samples in a helium gas environment. The Ag L_2,3 data were collected in partial fluorescence yield (PFY) mode with powder samples in vacuum. Silicon and nickel mirrors together with detuning of the second Si(111) monochromator crystal were used to reject high-energy harmonics. The PFY data were corrected for self-absorption (54).

Supplementary Materials

This PDF file includes:

Supplementary Text

Tables S1 to S5

Figs. S1 to S6

Other Supplementary Material for this manuscript includes the following:

Crystallographic Information File (CIF) for Li₂RhO₃

Crystallographic Information File (CIF) for Ag₃LiRh₂O₆