COMPUTATIONAL 2D and 3D MEDICAL IMAGE DATA COMPRESSION MODELS

Abstract

In this world of big data, the development and exploitation of medical technology is vastly increasing and especially in big biomedical imaging modalities available across medicine. At the same instant, acquisition, processing, storing and transmission of such huge medical data requires efficient and robust data compression models. Over the last two decades, numerous compression mechanisms, techniques and algorithms were proposed by many researchers. This work provides a detailed status of these existing computational compression methods for medical imaging data. Appropriate classification, performance metrics, practical issues and challenges in enhancing the two dimensional (2D) and three dimensional (3D) medical image compression arena are reviewed in detail.

1. Introduction

In digital era, images and image processing play significant roles in our day-to-day life. Digital images in digital platforms are rich sources of information. Utilization of digital images is in various fields such as remote sensing, satellite imaging, multimedia services, web-based applications, biological imaging etc. Medical imaging is one of the important areas wherein visualizing interior body parts of the humans as well as to view the internal structure of organs and some tissues are important for diagnostic and treatment purposes. In the last few decades, a variety of medical imaging modalities are producing high quality and content-rich digital images along with conventional radiological imaging modalities [1]. According to the Office of National Coordinator for Health Information Technology (ONC) nearly 84% of hospitals adopted the Electronic Health Record (EHR) system [2] which maintains the whole medical records of a particular patient and corresponding imaging data is now increasingly been utilized as well. The global medical imaging equipments market is projected to reach USD 36.43 billion in 2021 at a Compound Annual Growth Rate (CAGR) of 6.6% during the forecast period of 2016 – 2021 [3]. The global 3D medical imaging equipment market also grows at a CAGR of 5.58% during the period of 2016 – 2020 [4] . Due to population factor, India is the fourth largest country in Asia after the Japan, China and South Korea and counted in top 20 places globally [5] on the consumption of medical image procedures. There are various different medical imaging modalities, and their evolution takes place from the well-known and widely utilized radiological technologies such as X‐rays, Computed Tomography (CT), Mammography, Ultrasound (US), Magnetic Resonance Imaging (MRI) Single Photon Emission Computed Tomography (SPECT) and Positron Emission Tomography (PET). Figure 1 depicts the evolution of medical imaging techniques over the period from 1896 to the recent past.

Figure 1:

Evolution of medical imaging techniques

From past to the recent years in modern hospitals and diagnosis centers, huge voluminous images are being acquired and processed at unprecedented scale. With the help of medical imaging procedures, broad range of diseases and abnormalities such as cancer, infections, tumor detection, renal dysfunctions, bone fractures, mental disorders, liver and biliary diseases, dementia related disorders etc., can be identified and diagnosed even in an earlier stage, thereby enhancing the diagnosis and treatment planning.

1.1. Two-Dimensional and Three-Dimensional Medical Images

In digital image processing (DIP), a two dimensional (2D) image is represented in a computer as a 2D array having length and widths whereas a three dimensional (3D) image is stored as a 3D array which seems to have three dimensions (i.e. width, height and depth). The intensity levels of 2D image plane are referred as square shaped “Pixels”, while image plan in three-dimension represented as cubic shaped “Voxels”. In earlier days medical imaging data consists mainly of 2D images for clinical diagnostic purposes such as X-rays and CT scans. These images lacks in depth so some times its leads to misinterpret the inter-planar relationships between anatomical structures [6]. Figure 2 shows an example 2D medical image of CT human spine and X-ray image.

Figure 2:

Examples of 2D Medical Images a) X-ray chest b) CT Spine

The recent advancements in medical imaging procedures lead to 3D medical imaging modalities which can directly produce 3D images with depth information accordingly. In general, inputs of multiple 2D images are processed in order to depict the 3D space in the computational imaging systems. There are different types of 3D images that rely on modern DIP techniques. They are 3D continues images, images depicting 3D scenes and 3D objects, stereograms, range Images, hologram images, and 2D dynamic images. Among these types, general 3D medical images come under 3D continuous (in the sense of voxels) images. It works based on dimensionality of space where the image data are stored in a 3D array. This type of images is called 3D volumetric images. Normally, CT, MRI, PET and SPECT imaging techniques produce 3D volumetric images as a sequence of 2D slices; thereby producing huge volumes of medical images for a single unit of diagnostic process. Each slice is imaged the same part of the body with some minor level distance (in mm) [7]. These images are defined by function of three variables f (x, y, z). However, these images are digitized in the same way as 2D image where the cubic ordered array of sampling is applied with quantization identical with the 2D image. These images are always called as true 3D images or voxel constructed images. An example of a 3D medical image (3D head MRI) is shown in Figure 3.

Figure 3:

a) a Slice of MRI Brain b) Stack of slices c) 3D volumetric view

1.2. Medical Image Compression

In the recent years, the usage of multimedia communication is rapidly increased and leads to a demand for image data compression. Image compression is a prominent method to compactly represent an image. It reduces the actual number of bits needed to store the images which effected with low transmission costs. Basically, image compression techniques are classified into three types: lossy, lossless, and near lossless. Lossy compression is known as irreversible method where the quality degradation may occur. On the other hand, lossless compression is a reversible process which produces the reconstructed image without any loss of information. Aforesaid, wide range of medical related data and images are being acquired, processed, transferred, stored and retrieved for diagnostic purposes. The Picture archiving and communication system (PACS) is currently used in medical imaging field which uses Digital Imaging and Communications in Medicine (DICOM) standard. It comprises the compression method and TCP/IP based communication protocol for transmission. Neuroimaging Informatics Technology Initiative (Nifti), Analyze, Minc are some other existing file formats used in medical field [8]. Due to ease of access and usability of diagnostic medical records DICOM has overwhelm usage than other formats. It contains further metadata, including but not limited to pixel data information, and patient information such as name, gender, age, weight and height. The quality of medical image is very decisive factor that related to diagnostics accuracy and feasibleness. Hence, the medical domain needs large storage space for long term archival and efficient communication system to transfer images. To maintain the accuracy and quality in the medical images, the lossless compression methods are preferable because they give high reconstruction quality but with low compression performance. In addition to the lossless compression, a new compression technique called Near-lossless compression is being used in the recent years [9]. It results with better compression ratio along with appreciable reconstruction quality of reconstructed image. Figure 4 illustrates the types of medical image compression approaches. In our work, a detailed comparative review of various computational 2D and 3D medical image compression models is provided, which can help the medical imaging users in selecting optimal lossy, near lossless, and lossless compression techniques needed for their specific medical imaging modalities. We also categorize the compression models in terms of the input data, 2D/3D, modality, and present critical analysis of advantages and disadvantages of the respective models. This we believe will be useful in deciding the usage of superior image compression techniques for various medical imaging data. We further point out challenges that remain, improvements that can be acted upon in researching and developing medical imaging domain specific image compression models.

Figure 4:

Types of Image Compression

The rest of the review is organized as following sections. Section 2 presents various metrics used to assess the performance of image compression methods. In Section 3, the literature review is made with different conceptions such as lossless/near lossless and lossy compression methods on 2D and 3D medical images. In section 4, finding of research challenges and practical issues in various computational medical image compression techniques are discussed. In section 5, we conclude the work with summary of the findings from our review and further actions to be taken up for developing efficient compression techniques.

2. Evaluation Metrics for Image Compression

To assess the image compression method in the context of qualitative and quantitative measures, the following metrics are widely used in the DIP literature.

2.1. Qualitative Metrics

Qualitative metrics are measurements that are based on subjective perception of human visual system. It is also used to find the unperceived errors in the performance of compression methods. While assessing the quality of compression method with the help of quality metrics, the original image is used as a reference image to evaluate the quality of the reconstructed image. Some of the most commonly used qualitative metrics are discussed below:

• Mean Square Error (MSE): MSE represents the cumulative squared error between the reconstructed and the original image. The lower the value of MSE, lower the error.

  $$\text{MSE}=\frac{1}{MN}{\sum }_{y=1}^M{{\sum }_{x=1}^N\left[I\left(x,y\right)-I\left(x,y\right)\prime \right]}^2$$ (1)

  where M and N are the number of pixels in the x and y axis of the image, I represents the original image and I′ represents the reconstructed image. MSE value is zero when I(x, y) = I(x, y)′
• Signal to Noise Ratio (SNR): SNR is the ratio of signal power to the noise power. This ratio indicates how strong the noise corrupted the original image. It can be computed as.

  $$\text{SNR}=10\hspace{0.17em}lo{g}_{10}\frac{VAR\left(I\right)}{MSE\left(I,I\prime \right)}$$ (2)

  where VAR is variance of the original image, MSE is Mean Square Error between the original image and the reconstructed image.
• Peak Signal to Noise Ratio (PSNR): Peak Signal to Noise ratio is used to compare two images in decibels. This ratio is used as a quality measurement between the original and compressed image. The higher value of PSNR means the better quality of the reconstructed image can be obtained.

  $$\text{PSNR}=10\hspace{0.17em}lo{g}_{10}\frac{\left(2^n-1\right)}{\sqrt{MSE}}$$ (3)

  where n is maximum pixel value.
• Structural Similarity Index (SSIM): SSIM is one of the image quality metric used to measure the similarity between two images based on the characteristics of Human Visual System (HVS).

  $$\text{SSIM}=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)}$$ (4)

  where x and y are spatial patches of original image I and reconstructed image I′, μ_x and μ_y are the mean intensity values of x and y, respectively. ${\sigma }_x^2$ and ${\sigma }_y^2$ are standard deviations of x and y, respectively; and C₁ and C₂ are constants.
• Mean Structural Similarity Index (MSSIM): MSSIM index is an image quality assessment parameter relies on the characteristics of HVS and measures the structural similarity rather than error visibility between two images.

  $$\text{MSSIM}\left(I,I\prime \right)=\frac{1}{K}{\sum }_{j=1}^{K}SSIM\left(i_j,i_j^{\prime }\right)$$ (5)

  where K is the number of windows in the image. I is the original image and I′ is the reconstructed image. SSIM is similarity between I and I′.
• Percent Rate of Distortion (PRD): PRD is an average distortion measure calculated using MSE. It measures the distortion in the reconstructed image. Lower the value of PRD, the reconstructed image is less distorted.

  $$\text{PRD}\left(\%\right)=\sqrt{\frac{{\sum }_{x=1}^M{\sum }_{y=1}^N\left[I-I\prime \right]}{{\sum }_{x=1}^M{\sum }_{y=1}^N{\left[I\right]}^2}X\hspace{0.17em}100}$$ (6)

  where M and N are the number of pixels in the x and y axis of the image. I is the original image and I′ is the reconstructed image.
• Correlation Coefficient (CC): The correlation measure of the original image with compressed image is expressed in terms of Correlation Coefficient. It can be computed by,

  $$\text{CC}=\frac{{\sum }_{x=1}^M{\sum }_{y=1}^{N}I\left(x,y\right)X\hspace{0.17em}I\prime \left(x,y\right)}{\sqrt{{\sum }_{x=1}^M{\sum }_{y=1}^N{\left(I\left(x,y\right)\right)}^2}\sqrt{{\sum }_{x=1}^M{\sum }_{y=1}^N{\left(I\prime \left(x,y\right)\right)}^2}}$$ (7)

  where M and N are the number of pixels in the x and y axis of the image, I(x, y) is the original image and I′(x, y) is the reconstructed image.
• Structural Content (SC): SC is also a correlation based measure which measures the similarity between two images. Higher the value of SC implies poor the image quality.

  $$\text{SC}=\frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{\left(I\left(x,y\right)\right)}^2}{{\sum }_{i=1}^M{\sum }_{j=1}^N{\left(I\prime \left(x,y\right)\right)}^2}$$ (8)

  where M and N are the number of pixels in the x and y axis of the image. I(x,y) represents the original image and I′(x,y) represents the reconstructed image.
• Universal Image Quality Index (UIQI): It is used as an image and video quality distortion measure. It is referred as full reference image quality index. It evaluates the quality of the image based on the permutations of three factors which are luminance distortion, loss of correlation, and contrast distortion. UIQI values ranges between 0 to 1, where 1 represents being the best.

  $$\text{UIQI}=\frac{4{\sigma }_{II\prime }\overline{\iota }i\prime }{\left({\overline{\iota }}^2+\overline{\iota }{\prime }^2\right)\left({\sigma }_i^2+{\sigma }_{i\prime }^2\right)}$$ (9)

  where I represent the original image and I′ represents the reconstructed image. $I=\left\{{\text{i}}_1,{\text{i}}_2,\dots \right\}$ and $I\prime =\left\{{\text{i'}}_1,{\text{i'}}_2,\dots \right\}$. $\overline{\iota }$ is the mean of I, ${\sigma }_i^2$ is the variance of I, ${\sigma }_{II\prime }$ is covariance of I′ and ${\sigma }_i^2$ and ${\sigma }_{i\prime }^2$ are standard deviations of I and I′ respectively.

2.2. Quantitative Metrics

Quantitative metrics provides performance results in terms of numerical form. It is also used for statistical analysis of image compression methods; from that we can easily evaluate the performance of compression techniques. Here, we have listed some of the quantitative metrics that are mostly used for evaluation of image compression methods.

• Compression Ratio (CR): Compression ratio is the ratio between the original image size and the compressed image size. It can be computed as.

  $$\text{CR}=\frac{\text{Original}\hspace{0.17em}\text{Image}\hspace{0.17em}\text{size}}{Compressed\hspace{0.17em}Image\hspace{0.17em}size}$$ (10)
• Bit Per Pixel (BPP): The number of bits needed to store information on each pixel is referred as Bits Per Pixel. It is the ratio between the size of the compressed images in bits and total number of pixel. It is used to measure the compression performance in 2D images.

  $$\text{BPP}=\frac{\text{Size}\hspace{0.17em}\text{of}\hspace{0.17em}\text{compressed}\hspace{0.17em}\text{image}\hspace{0.17em}\text{in}\hspace{0.17em}\text{bits}}{Total\hspace{0.17em}number\hspace{0.17em}of\hspace{0.17em}Pixels}$$ (11)
• Bit Per Voxel (BPV): The ratio between the size of compressed 3D images in bits and total number of voxels in the image is called as BPV. It can be represented as

  $$\text{BPV}=\frac{\begin{array}{l}\text{Size}\hspace{0.17em}\text{of}\hspace{0.17em}\text{Compressed}\hspace{0.17em}\text{3D}\\ \hspace{0.17em}\hspace{1em}\text{images}\hspace{0.17em}\text{in}\hspace{0.17em}\text{bits}\end{array}}{Total\hspace{0.17em}number\hspace{0.17em}of\hspace{0.17em}Voxel}$$ (12)

3. Computational Methods for 2D and 3D Medical Images Compression

This section explores an analysis of past literature of both 2D and 3D image compression techniques proposed for medical images. Some of the existing lossy/lossless compression for different images and its ability to adopt for medical image compression techniques are also described in detail because most of the medical image compression techniques are adopted from these lossy/lossless compression methods. Moreover, transformation-based compression methods operate the image details on frequency domain which leads to intensify the efficiency of the compression algorithms. This literature review is made with different notion such as Lossless/Near Lossless and Lossy compression methods for 2D and 3D medical images that comprising diverse conceptions like transformation-based coding, object-based coding and tensor-based coding. Grounded on these concerns, the notable image compression methods on 2D and 3D images in the literature are presented and discussed in the following sections with appropriate classification.

3.1. Wavelet based Medical Image Compression Methods for 2D and 3D images

In working of wavelet in image processing is equivalent to working of human eyes. It has the major benefit that is capable to segregate the fine details in an image. It is a wave like oscillation with amplitude that starts with zero, increases and then decreases back to zero. Wavelets are a mathematical function that cut ups the data into different frequency components and then we can study each component separately with a resolution matched to its scale. Both spatial and frequency domain information are only provided by wavelet transform. By using wavelet decomposition, an image can be decomposed at different levels of resolution and can be sequentially processed from low to high resolution. Therefore, it is easy to capture local features in an image or signal. The low-pass filter performed on the rows and columns of an image constitutes an approximation LL sub band and the integration of low and high-pass filters gives details sub bands such as LH, HL and HH. LH₁, HL₁, HH₁ and LL₁ are the sub bands obtained from single level of wavelet decomposition. Further decomposition is done only on the approximation sub band to get the next level of coefficients or sub bands such as LH₂, HL₂, HH₂ and LL₂. Figure 5 depicts the resultant image of 2-level wavelet decomposition of MRI image. Another advantage of wavelet is that it supports multi resolution and it allows us to examine the signals at varying resolution with different window sizes. Very small wavelets can be used to isolate very fine details in a signal, while very large wavelets can identify coarse details. Wavelet transforms is applied to sub images, so it produces no blocking artifacts. Image compression using wavelet transforms results in an improved compression ratio as well as image quality. The following are the notable existing wavelet-based compression methods for 2D and 3D medical images.

Figure 5:

Wavelet Decomposition of MRI brain image

DeVore et al.,[10] introduced a new mathematical theory for analyzing the image compression methods based on the compression of wavelet decompositions. They analyzed the properties such as rate of error in the compressed image and smoothness of the image using Besov spaces which are derived from smoothness classes and also explained about wavelet decomposition structure for compression. Wavelet coefficients approximation and experimental results on some test images and the error rising by the quantization of the wavelet coefficients were also discussed.

A compression method based on 2D orthogonal wavelet decomposition with hierarchically coding the coefficients proposed in Lewis and Knowles [11]. It aimed to construct the combination of Human Visual System (HVS) compatible filters with the quantizer. Their method gave good compression performance and concluded that their codec is simple and effective than the existing methods namely vector quantization (VQ) and discrete cosine transform (DCT) and other sub-band coding methods.

Shapiro [12] proposed an embedded technique for encoding the wavelet coefficient namely Embedded Zerotree Wavelet (EZW) method. It is a lossy coding technique by its nature in which the coefficients larger than the threshold value are neglected or quantized. As it is a bit plane coding technique, this algorithm can be stoppable at any time when the target bitrate is achieved. There is a threshold computed using certain function and the coefficients are discriminated as significance or insignificance based on the computed threshold value. The $2^{\lfloor lo{g}_2\hspace{0.17em}{C}_{max}\rfloor }$ is chosen as an initial threshold. The significance coefficients coded with its sign and the insignificance coefficients constitute a quad tree or zero tree where the root coefficient only to be coded. The relationship between the root coefficients (parent) to other coefficients (children) are represented by a tree structure. The relationship between the parent and the child is given by (2x,2y), (2x+1,2y), (2x,2y+1), (2x+1,2y+1) where (x,y) is the coordinate of the parent.

Said and Pearlman [13] developed a wavelet coefficients coding technique based on set partitioning in hierarchical trees (SPIHT). It is an extended version of the EZW. The further advancements in this method are done in terms of low complexity and those are presented in[14] [15]. As like in the EZW, the partition of significant and insignificant pixels are done based on the threshold function. SPIHT has three ordered lists that are used to store the significant information during set portioning. They are List of Insignificant Sets (LIS), List of Insignificant Pixels (LIP) and the List of Significant Pixels (LSP). The difference between the EZW and SPIHT is only the way of coding the zero trees. The output code in SPHIT is possessed with the state-transition in zero trees. So, the number of bits or amount of bandwidth for transmitting is halved when comparing to EZW. For the same set of data used in a method by Bilgin and Zweig[16]. Xiong et al.,[17] developed a new algorithm using SPIHT associated with the 3D Integer Wavelet Packet Transform. It produced better result than the previous method using 3D CB-EZW. To achieve an efficient lossless coding, a modification was also done in the phase of arithmetic encoding by performing high order context modeling. This method gave 7.65 dB and 6.21 dB better than 2D SPIHT at 0.1 and 0.5 BPP respectively.

A notable research work on compression of 3D medical images proposed by Wang and Huang[18] using separable non uniform 3D wavelet transform for decomposition. It uses separable filter bank DWT on the 2D slices and another filter bank on the spectral/slice direction was used. They tried with several wavelet filter banks on spectral direction for the tested CT and MR images and finally the Haar wavelet found to give optimum result. Then the quantization is performed to reduce the data entropy. Finally, entropy encoding which is run length coding and Huffman is coding respectively are applied on the quantized data. It gradually reduces the image size. The experimentation results produced from this 3D method was better than the 2D wavelet compression method.

Set Partitioned Embedded block coder (SPECK) for 2D images is proposed by Islam et al.,[19]. SPECK was similar to the SPHIT algorithm and follows many properties of it such as threshold and significance checking. As this is also a wavelet-based technique, the transformed coefficients have the hierarchal pyramidal structure. SPECK partitions wavelet coefficients into blocks and sorts coefficients by using the quad tree partitioning algorithm. It also maintains two linked lists such as List of Insignificant Sets (LIS) and List of Significant Points (LSP). It is also extended for the 3D images by implementing 3D-SPECK [20]. It makes use of rectangular prisms in the wavelet transform. Each sub band in the pyramidal structure is treated as a code block which is termed as Sets with varying dimensions. The working flow of 3D-SPECK consists of four steps: the initialization step, sorting pass, refinement pass and the quantization step. It showed the better results than the other existing methods.

The 2D-EZW algorithm for 2D images could also extended to 3D images. Bilgin et al., [21] proposed the 3D version of the EZW coding (3D CB-EZW) using the integer wavelet transform. EZW was modified to work with the third dimension along with the incorporation of context based arithmetic encoding. An experiment using 3D CB-EZW was conducted on 3D medical datasets and it has achieved 10% of reduction in compressed size when compared to the normal 3D-EZW. It had a disadvantage that the encoder and decoder required a large space and no standard wavelet transform performed better for all types of datasets.

The first most implementation of 3D SPHIT to three dimensional images was done by [22]. They proposed two algorithms which employed 3D SPIHT for the hyperspectral and multispectral images. For the decomposition, wavelet is used in spatial domain, the Karhunen - Loeve Transform (KLT) is used in the frequency domain and 3D SPIHT is associated with this method. On the other hand, spectral vectors are vector quantized after using the wavelet in spatial domain along with gain driven SPIHT. They claimed that the algorithm which used KLT in the spectral domain i.e., KLT based 3D-SPIHT was performed well than all other encoding methods.

An entropy coding method, the Embedded Block Coding with Optimized Truncation (EBCOT) is proposed by Taubman [23] is a scalable compression algorithm. Because of its efficient and flexible bit-stream generation Joint Photographic Experts Group 2000 (JPEG2000) adopted the EBCOT algorithm as an encoder. In EBCOT, each sub band is divided into non-overlapping blocks of Discrete Wavelet Transform (DWT) coefficients that are known as the code block. By having this property, the highly scalable embedded bit-stream is generated rather than generating single bit stream for the whole image. It is a two-tier algorithm where the context formation and arithmetic encoding of the bit-planes are formed in tier-1. The context formation has three passes to scan all the code pixels, they are significance propagation pass, magnitude refinements pass and clean-up pass. The output of tier-1 as bit-streams passed through tier-2 and finally the compressed bit-stream is generated. Normally, EBCOT consumes more memory space and computation time due to performing context formation and bit-plane coding. Some methods were proposed to enhance the EBCOT with regarding the context formation [24][25][26]. They mainly focused on the context formation phase in a different way to accelerate the EBCOT algorithm.

The EBCOT can be extended to the three-dimensional space. The JPEG2000 for multi component images standard (JPEG2000 part-1) [27] provided a compression technique for 3D images. The variants of EBCOT for 3D images were proposed using Three Dimensional Cube Splitting Embedded Block Coding with Optimized Truncation (3D-CS EBCOT) by Schelkens [28]. Here, the 3D wavelet coefficients of prism are partitioned into small number of cubes and the cube splitting is done on each cube to generate a bit-stream. The Three Dimensional Embedded Subband Coding with Optimized Truncation (3D-ESCOT) by Xu et al.,[29] was purposefully designed for video sequences but also used for 3D images as well. In 3D-ESCOT, a subband itself considered as a block and it is to be independently coded using fractional bit-plane coding. A candidate truncation points are formed at the end of each fractional bit-plane.

The three-dimensional version of the SPHIT (3D-SPHIT) was designed by Kim and Pearlman [30], which is known as the state-of-art compression technique for three dimensional images. Indeed, they implemented the 3D-SPIHT for a video sequences which employed the coding simplicity of SPIHT and optional high performance on still images. It has dominated the Motion Picture Experts Group (MPEG-2) standard because this method does not involve in compensation and motion estimation of the data. The complicated motion estimation in MPEG-2 is neglected in 3D-SPIHT algorithm and it produced a better result than MPEG-2. Moreover, the progressive feature of SPIHT is also established in this method with high fidelity and scalability in frame rate and size.

A wavelet based coder so-called the tarp coder proposed by Simard et al.,[31] codec for 2D images. It worked based on encoding the significance coefficients through an arithmetic coder. The tarp filtering is used to figure out the probability of significance of those wavelet coefficients for arithmetic coder. Moreover, it is extended to the 3D space for 3D images and it proved its superiority over the other methods like 3D-SPHIT and JPEG2000 multicomponent standard (3D-JPEG) [32].

Benoit et al., [33] proposed a 3D sub-band coding associated with 3D lattice vector quantization and uniform scalar quantization. Distortion minimization algorithm (DMA) was used to select the quantized value where the cubic lattice lay on the concentric hyper-pyramids are used for code word searching. The proposed method was tested with a morphometer data (3D X-ray scanner data) and its performance was analyzed with Signal to Noise Ratio (SNR) and the subjective quality assessment from the radiologists. While comparing the results with 3D-DCT algorithm, this method gave better results in terms of objective and subjective quality.

Xiong et al.,proposed a lossy to lossless method for 3D medical image compression [34]. They used 3D integer wavelet transform (iWT) followed by proper bit shifts that improves the lossy compression performance and usage of memory-constrained integer wavelet transform to preserve the quality. Moreover, they used 3D-ESCOT for entropy encoder which achieves the better lossy and lossless compression for 3D medical data sets.

Yeom et al., [35] developed a compression scheme for 3D integral images using MPEG-2. The integral images were modeled as a consecutive frame of moving picture; the images are then processed with MPEG-2 as lossy scheme and expressed the impact of using it with those images in many aspects. After evaluating its performance using Group of Pictures (GOP), they compared their result with other existing methods and concluded that MPEG-2 is very fruitful for 3D integral images.

ShyamSunder et al.,[36] proposed a 3D medical image compression technique using the 3D Discrete Hartley Transform. They implemented their method in the sequence of decomposing the 3D image using 3D-DHT, quantization and then the entropy encoding. They created their own quantization method based on identifying the variation of the harmonics in frequency domain coefficients. The quantized coefficients then coded using the encoder with Run Length Coding followed by the Huffman coding. The results are compared with 3D DCT and 3D FFT to show the effectiveness of their method.

An experimentation of a wavelet based SPIHT coder for progressive transmission of DICOM images are proposed by Ramakrishnan and Sriraam in [37]. While transmitting the DICOM image, the Transfer Syntax Unique Identification (TSUID) field of the DICOM header is modified to indicate that the image is compressed using SPIHT. The header information is first sent followed by the compressed bit-stream using the lifting wavelet decomposition and coded using SPHIT. As a progressive transmission, the image reconstruction is made along with low resolution to high resolution to view an approximate image with minimum information being transmitted at the receiver end. As per the literature, it has comparable performance than the variants of JPEG methods.

The modifications in SPHIT algorithm for a lossless compression are implemented by Jyotheswar and Mahapatra in [38]. The modification is done in terms of simplification of scanning process on coefficients, usage of low dimensional addressing method instead of using the actual arrangement of wavelet coefficients. The fixed memory allocation for the data lists are also used in the place of dynamic allocation that required by the original SPHIT algorithm. Moreover, it used lifting based wavelet transform which reduced the complexity of coding and this method proved its efficiency in terms of Peak Signal to Noise Ratio (PSNR) for 3D MRI data sets.

A novel symmetry-based technique proposed in [39] used a scalable lossless compression technique to compress the 3D medical images. It utilizes 2D-IWT only for decorrelating the intensities and intra-band prediction method by exploiting the anatomical symmetries in the medical image data to reduce the energy of sub-bands. The EBCOT is used for encoding. And the 16-bit MRI and CT images were tested with this proposed method. It resulted with the average improvement of 15% compression ratios with other lossless compression methods such as 3D-JPEG2000, JPEG2000 and H.264/AVC intra-coding.

A work done by Sunil and Raj [40] was intended to assess and point out the different wavelets for 3D-DWT. The wavelet properties namely symmetry, orthogonality, impulse response, vanishing order, and frequency response were compared over certain wavelets such as orthogonal Haar, Daubechies, symlets and the biorthogonal Cohen–Daubechies–Feauveau (CDF) wavelet. Finally, they concluded that Cohen-Daubechies-Feauveau 9/7 [i.e., CDF (9, 7)] satisfied the desired properties and it may be the better wavelet for the implementation of 3D-DWT.

A 3D image compression technique to support prioritized Volume of Interest (VOI) for the medical images was proposed by Sanchez et al., in [41]. It presented the scalability properties by means to the lossless construction of images and the optimized VOI coding at any bit-rate. A scalable bit stream was created with use of modified 3D EBCOT. A progressive transmission of different VOI behaved with higher bit-rate, in conjunction with the low bit-rate background which were essential to identify the VOI in a contextual manner. The demonstrated results were being achieved higher quality than the 3D JPEG2000 VOI coding method and outperformed the MAXSHIFT and other scalable methods.

A compression method developed by Akhter and Haque [42] is used in Electrocardiogram (ECG) signals. They included the Run Length Coder (RLC) in their encoding process to compress the Discrete Cosine Transform (DCT) coefficients in time domain ECG signals. Two stages of run length encoding were performed to increase the compression ratio. It produced good compression ratio with acceptable rate of distortion which is measured in terms of Percentage Root-Mean squared Difference (PRD), Root-Mean-Square (RMS) error and Weighted Diagnostic Distortion (WDD) error indices.

A 3D medical image compression employing 3D wavelet encoders was proposed in [43]. This algorithm was validated along with four different wavelets and with some of encoders to implement it for encoding process. This method is intended to find the optimal combination of wavelets such as symmetric, decoupled and the encoding schemes such that 3D SPIHT, 3D SPECK and 3D binary set splitting with k-D trees (3-D BISK). MRI and X-ray angiogram images were tested and assessed using Multi-Scale Structural Similarity (MSSIM) index. Finally, they concluded that 3D CDF 9/7 symmetric wavelet along with the 3D SPIHT encoder produced best compression performance. To solve the expansion problem of traditional Run Length Encoder/Decoder, Cyriac and Chellamuthu [44] proposed a Visually Lossless Run Length Encoder/Decoder. In this approach, the pixel values itself store the run length value for single run thus it obviously reduces the size of the encoded vector. And this approach is appropriate for fast hardware implementation for the encoder/decoder prominent to real time applications.

A new Voxel based lossless compression algorithm was proposed by Spelic and Zalic [45] proposed for 3D CT medical images. By using Hounsfield scale, the selected ranges of the images were segmented. Then the arranged data streams were compressed by using Joint Bi-level Image Expert Group (JBIG) and segmented voxel compression algorithm. The proposed method was compared with Quadtree based algorithm, and Ghare method. This method can be used for both 2D and 3D medical image compression. By this method the user can transfer and decompress the data they need unless to do the whole data.

Lossless Video compression and image compression technique on medical images was proposed by Raza et al.,[46]. It implements the single image compression technique called super-spatial structure prediction with inter-frame coding. Also it used a two stage redundant data elimination processes called fast block-matching and Huffman coding which ultimately reduces the memory space for storing and transmission. The proposed method was evaluated with the sequence of MRI and CT images.

An image compression method presented in Setia et al., [47] used a simple haar wavelet to decompose the image. The quantization was done followed by entropy coding using Run length coding and Huffman coding as encoding algorithm. They justified that the attributes used such that Haar Wavelet Transform (HWT) is incorporated to ease the computation complexity of coding and Run Length Coding was a logical choice to carry over long runs obtained from wavelet transform coefficients. The advantage of using this method over the DCT was discussed and it gave better performance than the traditional methods.

Anusuya et al.,[48] proposed a system that implements a lossless codec using an entropy coder. The 3D medical images were decomposed into corresponding slices and the 2D-Stationary Wavelet Transforms (SWT) was applied. The EBCOT is used as an entropy encoder. They enhanced the proposed system by adopting parallel computing on the arithmetic coding stage to minimize the computation time. The proposed method produced significant results compared with JPEG and other existing methods in terms of compression ratio and computation time.

The experimentation of 2D HWT based image compression along with the variants of Run Length Encoding was presented in the work by Sahoo et al.,[49]. Initially, they stated about the zigzag scan ordering of RLE which are used in JPEG. Then, in their proposed method they processed 2D HWT to decompose and hard thresholding applied on the coefficients. The different types of RLE methods namely Conventional Run Length Encoding (CRLE), Optimized Run Length Encoding (ORLE), Enhanced Run Length Encoding (ERLE) were applied and the results are recorded. They claimed that their proposed method with variants of RLEs are much compared with the actual RLE used in JPEG as well as variants of RLEs with increasing PSNR values.

A dimension scalable lossless compression of MRI images were implemented using the lifting based Haar Wavelet Transform (HWT) along with the EBCOT coding [50]. A scalable layered bit-stream was generated through interband and intraband predictions. Moreover, lifting of wavelet coefficients predominantly helped to decode the highest quality of VOI without decoding the entire 3-D image. Their results were superior than the conventional JPEG2000 and the EBCOT method.

A new method proposed by Senapati et al [51] introduced a new 3D volumetric image compression technique using 3D Hierarchical Listless embedded block (3D HLCK). A 3D hybrid transform is applied using wavelet transform in spatial domian and the KLT in the spectral domain. The resultant coefficients in each slice undergo Z-scanning which maps two-dimensional data to one dimensional array. It uses two tables to store the information namely the Dynamic marker table (Dm) and Static marker table (Sm). It is an embedded method that uses listless block coding algorithm and encode it in an ordered-bit-plane fashion.

Bruylants et.al., [52] introduced a wavelet based 3D image compression method with some additions on wavelet such as direction adaptive wavelet filters and intra-band prediction step. They reported that the direction adaptive filter would not work on all the cases and addition of intra-band coding step improves the compression performance slightly without affecting the computational complexity. Juliet et al.,[53] proposed a novel medical image compression method to achieve a high quality compressed images at different scales and directions using ripplet transform and SPHIT encoder. The proposed method attains high PSNR and significant compression ratio when compared with conventional methods.

Xiao et al.,[54] implemented a Discrete Tchebichef Transform (DTT) orthogonal transform to improve the compression rate and reduce the computational complexity because it had the energy compaction and recursive computation properties. And they named the proposed algorithm as integer Discrete Tchebichef Transform (iDTT) and it achieved integer to integer mapping for efficient lossless image compression. It attains higher compression ratio than the iDCT and JPEG standard.

Ibraheem et al., [55] proposed a two novel compression scheme to improve the image quality. The first one is Logarithmic number system (LNS) arithmetic and the second one is a hybrid of LNS and Linear arithmetic (Log-DWT). Both schemes gave higher image quality, however it exceeds double the time of computational cost/time than the classical DWT. A hybrid medical image compression technique proposed by Perumal and Rajasekaran [56], used DWT with Back Propagation (DWT-BP) to improve the quality of compressed images. The proposed method well performed and provide better results than the classical DWT and Back Propagation Neural Network (BPNN) in terms of PSNR and CR.

Kalavathi and Boopathiraja [57] proposed a wavelet based image compression method which used 2D-DWT for decomposition. Then thresholding is performed to increase the zero coefficients in detail coefficients. After that RLC is used as an entropy encoding. In the phase of decompression inverse RLC and Inverse 2D-DWT is applied on the compressed file to get the reconstructed image. Different bit rates were used to analyze the quality of reconstructed image. For high BPP this method gave better quality reconstructed image.

Lucas et al.,[58] developed a lossless medical image compression scheme for volumetric CT and MRI medical data set which is referred as 3D-MRP based on the principal of minimum rate predictors. It also enables 2D and 3D block based classification. It achieves average coding gains of 40% and 12% over the High Efficiency Video Coding (HEVC) standard for 8 bit and 16 bit depth medical signals and it able to improve the error probability of the MRP algorithm.

Kalavathi and Boopathiraja [59] proposed compression technique for medical images. Initially the input medical image is decomposed using 2D-DWT. Then thresholding is performed on the wavelet coefficients. RLC is used as an entropy coder for the encoding process. Finally, the inverse process of RLC and inverse 2D-DWT is performed to get the reconstructed image. The evaluation of reconstructed image quality is analyzed with different bit rates. Somassoundaram and Subramaniam [60] proposed an angiogram sequence compression method using 2D bi-orthogonal multi wavelet and hybrid speck-deflate encoder algorithm. They used DICOM images and the coefficient are encoded using SPECK encoder. This method Achieves higher compression ratio with the average of 22.50 CR and the method is comparable with multiwavelet with SPIHT. The performance of the algorithm was evaluated by CR, PSNR, MSE, Universal Image Quality Index (UIQI) and SSIM metrics. Boopathiraja and Kalavathi [61] developed a near lossless compression technique for multispectral LANDSAT images. For the decomposition of the image they used a 3D-DWT. Then thresholding is performed on the decomposed image. Huffman coding is applied on the wavelet coefficients for the encoding process. The reverse process of Huffman decoding and inverse 3D-DWT is used for the process of decompression. This method reduces the space complexity with good image quality. 1.31 bpp is obtained as an average compression ratio. CR is increased by four times than the Huffman coding.

Parikh et al.,[62] implemented a high bit-depth medical image compression with HEVC. Initially, they spotted the drawback of using JPEG2000 in an image series and 3D imagery. Then, they developed a HEVC based coding for high bit depth medical images which predominantly reduce the complexity and increase the compression ratio than the JPEG2000. They contributed to HEVC by developing a Computational Complexity Reduction (CCR) model which resulted with an average of 52.47% reduction in encoding time. Additionally, they reported that their method increases the compression ratio by fifty-four percentage than the existing JPEG2000 method.

Chitra and Tamilmathi [63] proposed a lossless compression method that implements Kronecker delta notation and wavelet based techniques Brige-Massart and Parity Strategy. In this method, preprocessing is performed by applying the Kronecker delta mask followed by wavelet based compression. DWT is applied to the preprocessed image, it decomposed the image up to fourth level. The approximation coefficients were then compressed using Brige-Massart Strategy. Finally, by applying the parity threshold, they obtain a compressed image. They used MRI, CT and standard images as input datasets. The performance of proposed method was evaluated by PSNR and Compression Ratio. It revealed that the proposed algorithm is performed well on MRI images and produced an average of 39.54% more CR than the other existing methods based on Brige-Massart and Unimodal thresholding.

Boopathiraja and Kalavathi [64] proposed a wavelet based near lossless image compression technique that can be directly applied on the 3D images. They apply 3D DWT on a 3D volume and the resultant coefficients were taken to further compression process. Thresholding with mean value and using of Huffman encoding preserves the near-lossless property. The inverse processes are performed to reconstruct the images. It is evident from results of the proposed method, it saves 0.45 bit-rate averagely for given 3D volumetric images with very low MSE (closest to zero). This ensures that this method can be used in telemedicine services even to transfer a huge volume of 3D medical images to remote places or any destination point with low bandwidth communication channel.

Benlabbes Haouari, [65] proposed a novel encoding method for 3D medical image compression using Quinqunx wavelet transform combined with the SPIHT encoder for medical images. Quinqunx wavelet improve the boundaries of separable wavelets. They evaluate the method with 3D MRI and CT medical images from bit rate 0.3 bpp. The attained results gave satisfactory performance in terms of PSNR and MSSIM. And also achieved higher CR with maintaining an acceptable visual quality of the reconstructed image.

3.2. Object based Image Compression methods for 2D and 3D images

Object based coding is a compression scheme that uses segmentation approach to separate the object from the background and compresses the objects and the background regions separately to improve the compression performance. The diagnostically important portions in the medical images are termed as object of interest. In two-dimensional images, it is known to be a Region of Interest (ROI) and called as Volume of Interest (VOI) in the case of three-dimensional images. Object based image compression method provides better results than the normal whole image compression methods. It increases the compression ratio than the other compression methods. And we can easily analyze the ROI regions of the medical images. Instead of applying the compression to whole image we can apply Lossless and Lossy compression on ROI and Non-ROI regions respectively to achieve a good compression ratio. Figure 6 represents the ROI and VOI regions of medical images. The works done related with the object-based image compression methods are presented in this section. The following methods are also a subset of the above mentioned two-dimensional and three-dimensional images compression techniques.

Figure 6:

a) ROI in 2D [67] b) VOI in 3D

Earlier, the segmentation based image coding presented in Kunt et al [68]; Vaisey and Gersho [69]; Leou and Chen [70]; followed a homogenous procedure that involved the regular stages like segmentation, contour coding and text coding. These techniques need sophisticated workflows for extracting the closed contours in the segmentation process. Further, these approaches add a piece of overhead to the image coding systems because these class of codes need to be carried on the lossy level to achieve quality on images. Shen and Rangayyan [71], proposed a new segmentation based VOI detection. It uses seeded region growing method to extract the object. The discontinuity index map was used in embedded region growing procedure to produce an adaptive scanning process. It overcomes the issues of pixel being distorted by generating the low-dynamic-range error which assigns only most correlated neighbor pixels. Then, the discontinuity index map data parts were subject to encode instead of contour by the JBIG. On the tested medical images of chest and breast images, it gave better results by 4% to 28% than the other classical methods such as direct coding by JBIG, JPEG, Hierarchical Interpolation (HINT), and two-dimensional Burg prediction plus Huffman error coding methods.

Another new concept was coined in the wavelet domain namely shape-adaptive wavelet transform proposed by Li and Li [72]. It produced the same number of coefficients as the image samples within the object. Henceforth, some of the object based approaches [73][74] deployed the SA-DWT for the high dimension especially a video province was proposed which can also use for 3D imagery. As a property of identical number of coefficients in the object of the images, it reduces the size of samples to encode rather than the scaling-based ROI coding method. The object-based ROI coding easily adopted the modification or specification of ROI at the middle of the coding which cannot be done in shape-adaptive DWT. It needs to perform the transformation again and again for the new set of objects which would increase both the computational cost and complexity of the procedure.

A Medical image compression based on region of interest with application to colon CT image was proposed in Gokturk et al.,[75] they used the lossless method in ROI and motion-compensated lossy compression technique in other regions. It was mainly focused on the CT image of human colon. With certain morphological image processing techniques, the colon in the image was segmented to detect ROI. An intensity thresholding was performed in the first step to separate the tissues and the 3D extension of the Sobel’s derivative operation was used to extract the colon wall. Then, the morphological 3D grassfire operation applied for detection of colon-wall. This algorithm detects the object as slice by slice manner. Then, the proposed motion compensated hybrid coding was applied and it outperforms conventional method.

In JPEG2000 part-1[76], a max-shift ROI coding was incorporated. As a basic idea, the coefficient scaling was used in MAX-SHIFT ROI coding. Obviously, the wavelet was used to transform the whole volumetric image to the frequency domain and the coefficients in the ROI part were scaled with the scaling value s by using a given number of bit-shifts. Then the probable encoding of JPEG2000 was applied without any additional shape information to be sent. The threshold value of 2^s is used in the decoder to identify the scaled-up coefficients. However, this method suffered from distinguishing between the coefficients of actual object and outside the object. Hence, it degrades the image quality.

Liu et al.[77] proposed a Lossy-to-lossless ROI coding of chromosome images using modified SPIHT and EBCOT. As SPIHT [12] and EBCOT [17] had lack in support to ROI feature, a modified SPIHT and EBCOT for lossy-to-lossless image compression technique were developed. The shape information of ROI was coded using chain-code based shape coding scheme and the critically sampled shape-adaptive wavelet scheme was applied to get the lossy-to-lossless performance. These methods require only smaller bitrate when compared with the other whole image lossless compression schemes.

Multi rate/resolution control in progressive medical image transmission for the ROI using EZW is implemented by Dilmaghani et al [78]. In this work, a ROI coding with progressive image transmission incorporates the EZW. The wavelet coefficients of important region were multiplied by an arbitrary factor before applying EZW to preserve the quality. The frequency band of the image is subjected to different subbands and then the most significant ones were refined and encoded with EZW.

Object based coding proposed by Ueno and Pearlman [79], combined both shape-adaptive DWT and scaling based ROI named as SA-ROI. The shape-adaptive wavelet transform was used to transform the image samples within the object, which are then scaled by certain number of bit-shifts with further bit-plane encoder along with the shape information. The results of this method outperformed the conventional MAX-SHIFT ROI coding, scaling-based ROI Coding and shape-adaptive DWT coding. However, it suffers with shape information overhead leading to high computational cost and failed in reconstructing the background.

In JPEG2000 part-2[80], a Scaling-based ROI codec was adopted which shadowed the same procedure of max-shift ROI coding as the entire volume is transformed and the coefficients within and around the ROI were scaled up. Here, the selection of scaling value played an important role to enhance the image quality. Though it provided only for elliptic and rectangular objects in a 2D image, it can be easily extended to volumetric images with arbitrary shapes. But it needs to send the shape information details to the decoder and this might cause an unwanted artifact.

Gibson et al., [81] proposed a region based wavelet encoder for the angiogram video sequences. It incorporates the SPIHT based wavelet algorithm along with the texture modeling and the ROI detection stage. The basic philosophy of greater allocation of available bit-budget in the ROI was implemented. They indirectly detected the important region by the feature of angiogram imagery where different motion of heart was exploited in the background areas. It gave reasonable improvement than the conventional baseline SPIHT algorithm. But the accuracy of detected shape of ROI is questionable and this method is dedicated only for angiogram imagery.

Maglogiannis et al., [82] proposed a Wavelet-Based Compression with ROI Coding Support for Mobile Access to DICOM Images over Heterogeneous Radio Networks. In this work, they explored an application for mobile devices activating with heterogeneous radio network that supports compression and decompression of DICOM images. Regarding the compression method, it uses Distortion-Limited Wavelet Image Codec (DLWIC) [83]. This DLWIC was constructed with a base of zerotrees. For the solitary spatial domain, it took three classes of wavelet coefficient and blended. Then the significant bits are taken into account in the all the subtree to grab the zerotree property. Further, this method used QM-coder (binary arithmetic coder) for encoding. It gave comparable result compared with other techniques such as JPEG and vqSPIHT.

Valdes and Trujillo [84] proposed a Medical Image Compression Based on Region of Interest and Data Elimination in which the data elimination in an image was performed and coded using standard JPEG2000 compression method. They used DICOM images for their study. The unnecessary data around the ROI is identified and extracted through the segmentation algorithms namely K-Means clustering and Chen-Vase segmentation algorithms. Then the detected ROI was subjected to perform with flood fill algorithm and then it was coded using JPEG2000. Depending on the image context, both segmentation processes gave mixed performance. According to the experimental results, data elimination led to increase the compression ratio but also increase computation cost due to the accomplished segmentation process.

A region based medical image compression using HEVC standard was also proposed by Chen et al.,[85]. HEVC is a prediction-based technique where inter-band and intra-band predictions were made with the already discriminated non-overlapping blocks. The vatiation between the predicted block and original values were transformed using DCT and Discrete Sine Transform (DST). Then the Context adaptive binary arithmetic coding (CABAC) was used to encode the transform coefficients. The up gradation of this inter-band and intra-band prediction based HEVC approach was done to improve the lossless performance of HEVC [86][87][88].

Lossless Medical Image Watermarking (MIW) technique is proposed by Das and Kundu [89] and it is based on the concept of blind, fragile and ROI. The main objective of this work is to give solutions to the multiple problems related to medical data distribution like content authentication, security, safe archival, safe retrieval and safe transmission over the network. They use different modality images to assess the effectiveness of their method and it is simple and evident in providing security to the medical database.

Yee et al [90] proposed a new image compression format called Better Portable Graphics (BPG) which is based on HEVC. In this method image is segmented into ROI and NROI regions using flood filling algorithm. Then the lossy BPG and Lossless BPG are applied on the regions of ROI and NROI respectively. It facilitates to store more images for longer duration. This format exceeds the compression gains of all other formats like JPEG, JPEG2000, and Portable Network Graphics (PNG) by at least 10–25%.

Eben and Anitha [91] reported the enhanced Context based medical image compression method using wavelet transformation, normalization, and prediction. To obtain the approximate coefficients and detailed coefficients they used 2D wavelet transform. A mask-based predication to obtain the prediction error coefficients and are encoded using arithmetic encoding. The proposed approach produced better quantitative and qualitative results compared with JPEG2000 and other existing methods.

Devadoss and Sankaragomathi [92] proposed a medical image compression method using Burrows Wheeler Transform-Move to Front Transform (BWT-MTF) with Huffman encoding and hybrid fractal coding. They split the images into NROI and ROI then applied a lossy and lossless compression on it respectively. Hybrid fractal compresses the NROI and the proposed Burrow Wheeler Compression algorithm (BWCA) is applied on ROI to improve the compression performance. This method yields better results when evaluated with other existing methods in respect to PSNR measure.

A medical image compression technique based on region growing and wavelets algorithm was introduced by Zanaty and Ibrahim [93]. Here they first segment the image into ROI and NROI using Region Growing (RG). Then they applied wavelet methods on ROI region and NROI region is compressed by using SPHIT algorithm. They use nearaly six to seven types of wavelets and compared with one another. This combination leads to increase CR values three times more than the existing wavelet methods.

Object based hybrid lossless algorithm was proposed in [94], in this method the Volume Of Interest (VOI) yields a significant compression ratio accompanied with reduced bit rate. This method used the proposed Selective Bounding Volume (SBV) to extract VOI which reduces the complexity of reconstructing the actual 3D image volume with minimal reconstruction details. After the separation of VOI using SBV the proposed method L to A codec which is a fusion of LZW compression algorithm and Arithmetic encoding is used to compress the VOI. This method, yields double the time more compression ratio and remarkably reduces the computation time when compared to the existing methods such as Huffman, RLC, LZW and Arithmetic Coding.

Sreenivasalu and Varadarajan [95] proposed a lossless medical image compression using wavelet transform and encoding. This method consists three phases. In phase I, the input medical image is segmented into Region of Interest (ROI) and Non-ROI using Modified Region Growing (MRG) algorithm. At Phase II, segmented ROI is compressed by using DCT and SPHIT and Non-ROI is compressed by DWT then the merging is based on Huffman encoding method. By merging ROI and Non-ROI they obtained a compressed image. In Phase III the decompression takes place where the compressed bit stream of ROI is decoded using inverse DCT and SPHIT decoding decompression algorithm. Non-ROI is decompressed using Inverse DWT and Modified Huffman Decoding method. Performance analysis of the proposed method was evaluated in two phases: Segmentation and Compression. For the segmentation they use sensitivity, specificity and accuracy as a performance metrics. To evaluate the compression performance then used PSNR, CR, Cross correlation, NAE and Average Difference as a performance metrics. For the comparison of proposed method with the existing they used Possiblistic Fuzzy C-Means Clustering method (PFCM) for both segmentation and compression. They achieve the maximum of PSNR and Accuracy as 46.69 and 99.48 respectively, for MRI images.

3.3. Tensor based Three-Dimensional Image Compression Techniques

Tensor is a form of multidimensional array used to represent video and an image. It also known as N-way or Nth-order tensor is an element of the tensor product of N vector spaces. It permits us to progressively move from classical matrix-based methods to tensor methods for image processing methods and applications. Now a day, medical images are produced with multi-dimension order. To handle or process this kind of dataset, tensor facilitates the good platform. Hence, the tensor techniques can more conveniently used in the image compression field due to its nature of compact representation of the data. There are two major techniques used for tensor decomposition, first one is the Canonical Decomposition/Parallel Factors (CANDECOMP/PARAFAC), second one is the Tucker tensor decomposition.[96]

Figure 7 depicts the higher order form of PCA it is also termed as Tucker Decomposition. It decomposes a tensor into a core tensor transformed or multiplied by a matrix along each side. It can be represented as x ≈ g; A, B, C where g is called as core tensor i.e., the compression version of x. and it entries shows the level of interaction between the factor matrices A, B, C. Tensors based techniques are used in wide variety of applications such as higher order statistics, chemo metrics, blind signal separation, de-noising structured data fusion and high dimensional image compression techniques [98][99][100][101][102]. The Tensor Flow is a specialized hardware architecture created by Google which incorporated the tensor techniques [103]. These tensor techniques can more conveniently use in the image compression field due to its nature of compact representation of the data. The following works are identified as the recent works on high dimensional image compression methods which incorporates the tensor decomposition techniques.

Figure 7:

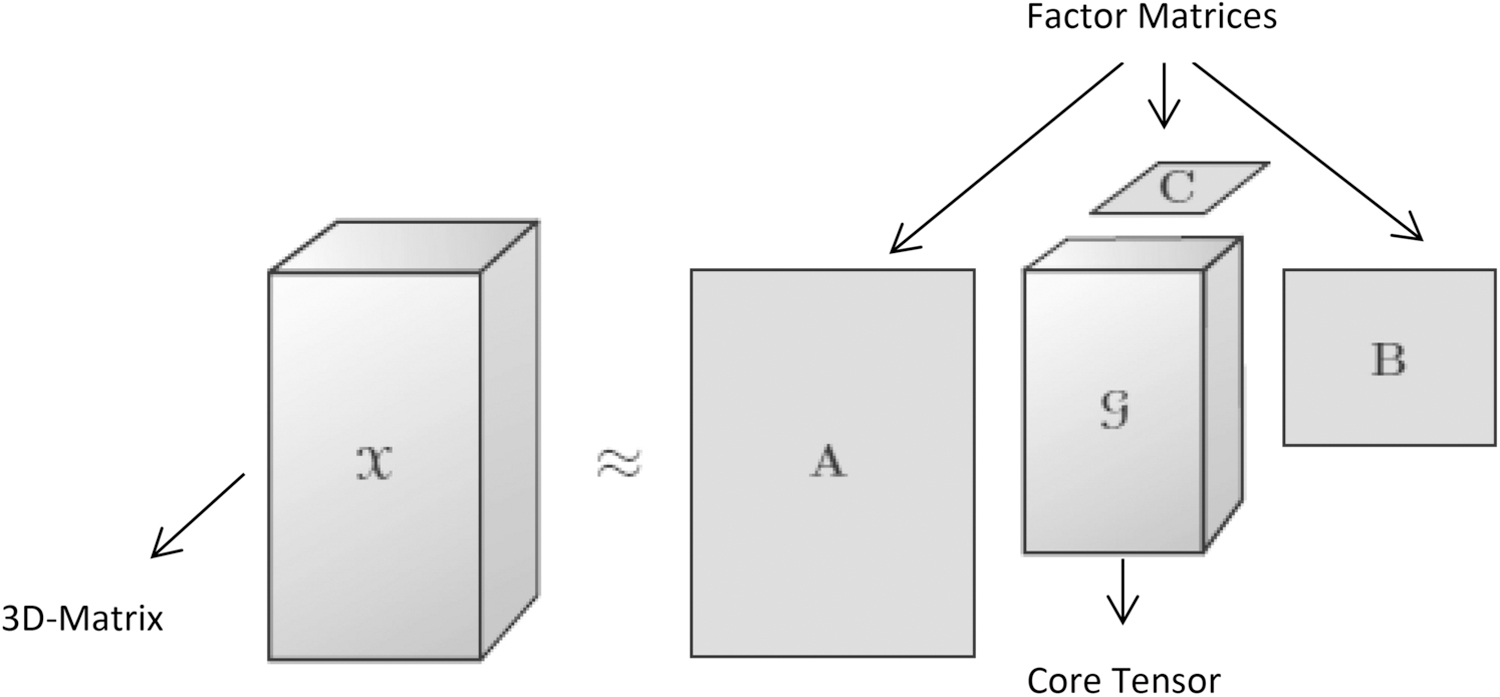
Tucker Decomposition [97]

Wu et al,. [104] proposed a hierarchical tensor-based approximation of multidimensional images. In this work, they developed an adaptive data approximation technique which used hierarchical tensor-based transformation. The given multi-dimensional image was transformed to a multi-scale structure in a hierarchical order. Then, the numbers of smaller tensor were obtained by dividing the signal in each level of hierarchy. With the common tensor approximation methods, the obtained number of tensors was transformed. They reported that the level by level sub-division of residual tensor beard the quality of approximation. This approach yields better compression ratio than the conventional methods including wavelet transforms, wavelet packet transforms and single level tensor approximation.

An optimal truncation based Tucker decomposition or Multilinear Singular Value Decomposition (MLSVD) method was proposed by Chen et al., [105]. Since, the Tucker decomposition transformed the input tensor into a core tensor and n factor matrices for an n-dimensional data, this method kept the complete core tensor. The factor matrices were then truncated with their proposed algorithm of optimal number of components of core tensor along each mode (NCCTEM). They experimented their proposed method with hyperspectral images. It gave a better reconstruction quality compared to the traditional compression methods such as symmetric 3D-SPIHT and asymmetric 3D-SPIHT schemes.

A matrix and tensor decomposition based near-lossless compression technique was proposed for multichannel electroencephalogram (MC-EEG) data by Dauwels et al.,[106]. For the selected data, they analyzed several matrix/tensor decomposition models in terms of decorrelation strategy. Both Singular Value Decomposition (SVD) and PARAFAC seemed to produce better performance and hence incorporated. In their method, input data was initially applied with SVD and PARAFAC and compressed in a lossy fashion. The residuals were quantized and encoded using modified Arithmetic coding. Hence, the near-lossless outputs were obtained, and it outperformed the similar work used in wavelet based volumetric compression technique.

A multi-dimensional or 3-order tensor based image compression technique was proposed by Zhang et al., [107]. In this method, the high dimensional input data was considered as a tensor data and tensor decomposition technology was applied. The original data was decomposed to get the approximated tensor data. Since, the input was a 3-order tensor data, it decomposed the data into the core tensor and three factor matrices along each mode. The core tensor was the compressed version, and this data could be reconstructed with the multi-linear backward projection through the factor matrices. This approach has preserved the spatial-spectral structures as much as possible and produced better performance when compared with spectral DR based methods in terms of quality preservation.

Wang et al., [108] proposed a three-dimensional image compression which employed the lapped transform and Tucker decomposition (LT-TD). In this method, each spectral channel was initially decorrelated using lapped transform. The decorrelated coefficients are rearranged into three-dimensional (3D) wavelet sub-band structure which considered as a third-order tensor. Then, the TD was performed to transform into a core tensor and factor matrices. Finally, the core tensor was encoded by bit-plane coding algorithm into bit-stream. Experimental results showed that this method influenced the compression performance by different factors including core tensors order and the quantization of factor matrices.

A lossy volumetric compression based on Tucker Decomposition and thresholding was proposed by Ballester and Pajarola [109]. They provided two contributions to the Tucker tensor decomposition or MLSVD. The first one was regarded the tensor rank selection and construction of decompression parameters in order to optimize the decomposition. For the optimal rank selection, it used the Higher Order Orthogonal Iteration (HOOI) method and logarithmic quantization. They also used coefficient thresholding, and zigzag scanning method along with logarithmic quantization as an alternative compression method for tucker decomposition. The compaction accuracy of core tensor was appreciable and gave better results than the commonly used TD methods in terms of compression performance, but it slightly suffered from reconstruction quality because of coefficient thresholding.

A work done by Fang et al.,[110] proposed a CANDECOMP/PARAFAC tensor-based compression (CPTBC). This method decomposed the original data into sum of R rank-1 tensors which produced only fewer non-zero entries. Moreover, R rank-1 tensors yield sparse coefficients with uniform distribution. As the input data was considered as a 3D-tensor, this method simultaneously exploited the spatial-spectral information of the input images. The sparseness and the uniform distribution of coefficients were directed to obtain the compact results. For the same compression performance, the visual quality of this method in terms of PSNR was much comparable over the six traditional compression methods such as MPEG4, band-wise JPEG2000, TD, 3D-SPECK, 3D-TCE and 3D-TARP. It gave more than 13, 10, 6, 4, 3, and 3 dB of PSNR values of the MPEG4, band-wise JPEG2000, TD, 3D-SPECK, 3D-TCE, 3D-TARP methods respectively.

A Patch-Based Low-Rank Tensor Decomposition (PLTD) was proposed by Du et al., [111]. It is a new framework which combined the patch-based tensor representation, nonlocal similarity, and low-rank decomposition for the compression and decompression. Instead of separate spectral channel or pixel processing, each local patch was considered as a third-order tensor. Hence, the neighborhood relationship across the spatial dimensions and the global correlation among the spectral dimension can be fully preserved. Then the clustering phase was implemented, and the similar patches were clustered by using nonlocal similarity in the spatial domain. Then, the obvious decomposition process was performed to get the approximated tensor and dictionary-matrices. The reconstructed image data can be obtained by performing the product of approximation tensor and dictionary-matrices per cluster. The advantage of this method is that it simultaneously removes the redundancies in both spatial and spectral modes. It extremely outperforms the conventional methods, but it had a disadvantage that the selection of patch size was not automated.

In ballester et al., [112], a Tensor based compression was proposed for multidimensional visual data named as TTHRESH. In this work, they mainly focused on the error controlling parameter where error target was defined in any one of the following ways such as Relative error, RMSE and PSNR. The non-truncated Higher Order Singular Value Decomposition (HOSVD) was applied and the obtained N-dimensional core was flattened as 1D vector of coefficients. Then the number of left most columns were compressed in lossless manner with RLE followed by AC. Finally, the factor matrices were compressed in order to get the cost-efficient bit budget. This method outperformed the previous tensor-based methods as well as the wavelet-based methods. Liu et al., [113] proposed a fast fractal-based compression algorithm to compress the MRI medical images. After the conversion of 3D image into 2D the sequence image-based fractal compression method is used to compress it. Then the range and domain blocks are classified by spatiotemporal similarity feature. At last residual compensation algorithm is used to attain approximate lossless compression of MRI data. Proposed method gives slightly poor compression ration than the BWT-MTF.

Tensor based medical image compression method is proposed by [114]. They used Tensor Compressive Sensing (TCS) to achieve the accuracy of 3D medical images while reconstruction. And also alternating least squares is used to optimize the TCS matrices with discrete 3D Lorenz. The proposed method conserves the intrinsic structure of tensor-based 3D images. And the proposed method attains a better compression ratio, security and decryption accuracy. Another feature of characteristic of the tensor product is used to make harder decryption for unauthorized access. Kucherov et al [115]., proposed method based on linear algebra technique intended to reduce the image file size for storing and transmitting them through network. They used the tensor based singular value decomposition. The proposed algorithm used iterative procedure with control of the Frobenius norm with the error matrix. The results are compared with other types of decomposition algorithms with the performance metrics like SNR and standard error.

4. Research Challenges and Open Issues in Medical Image Compression Techniques:

In this review, we explored an immense and great variety of medical image compression methods. These methods are better than one another in the different aspect of compression performance and also provide significant results. The following are some of the challenges and issues identified out of this literature review.

• Majority of the compression techniques are proposed for MRI, CT and X-rays based imaging data. There are some other imaging modalities such as the PET, US etc., that have not had considerable amount of research work in efficient compression models. Hence, there is a scope of work in this direction.

• The researchers mostly concentrated and used the wavelet transformations on their compression methods. The main problem with using wavelet is the choice of the choosing the right mother wavelet and decomposition levels. In general, wavelet-based method involve higher computational costs, though this can be mitigated by using in combination with downsampling operations.

• In lossy compression paradigm, pre-processing techniques and background noise removal techniques should be added and improved to achieve better compression performance.

• Our literature review also highlights that most of the medical image compression methods are hybrid techniques and they inherit the properties of both lossy and lossless techniques.

• Some of the existing compression methods [21][31][53][55][57][59][80] produce good results with the computational costs being very high. Thus, computationally efficient pipelines are required in reducing the computational costs and application time of compression techniques.

• Object based image compression schemes achieve significant results however when considering medical images lossless image compression is preferable to avoid misdiagnosis.

• Medical images hold very important details, and hence while applying a particular compression technique, it should maintain the details of the image without losing the quality of the images as well as should attain the good compression performance. Hence, the development of near lossless compression methods can improve the compression ratios than the lossless compression techniques. These are also be appropriate to support efficient telemedicine services.

• Development of tensor based methods can reduce the computational time of compression algorithm with increased performance.

• In recent days, practice over 3D and 4D (four dimensional) images are extremely increasing. Hence, there is an essential need for development of proficient compression method that can handle 3D, and 4D imaging modalities.

• To handle the Tera or even Peta bytes of medical imaging data, scalable programs have to be developed to support parallel hardware architectures like parallel-CPUs and parallel-GPUs.

5. Conclusions

The analyses of different compression methods for medical images are conducted and its merits and demerits are identified. This review illustrates the existing computational medical image compression techniques which are useful in solving the storage and bandwidth requirements for telemedicine services. Also, it helps the researcher and scientists those who are all working in this field to get insight about the various existing compression methods for 2D and 3D medical images. In this study, the existing compression techniques have been classified into three broader categories namely transformation based, object based and tensor-based compression techniques. The various performance metrics are also analyzed which are mostly used to evaluate the qualitative and quantitative properties of compression techniques.

The perusal of this past literature has addressed the necessity of near lossless compression and the object-based approaches for both 2D and 3D medical images. Generally, the reversible compression is always preferable for medical images due to the quality factor and hence meets with low compression rates. As the property of inverse proportionality between the compression rate and quality of the image takes place in any kind of compression method, there is a need to sacrifice any one of these credentials (Quality or Compression Rate). This leads to a Near Lossless compression approach which would be very effective for medical images. Though every momentum of a medical image is necessary for precise diagnostics, it can be allowed for low distortion without affecting the quality of the clinically important regions in an image during the compression. It is evident from the computational techniques explored here that, the object-based approaches work effectively for the medical image compression and mandates to converge on 3D imaging arena. This object-based coding can improvise certain compression algorithm and leads to get high fidelity on clinically significant portions. On the other hand, the cost and complexity of executing these object-based coding seems to be a constraint in terms of compression efficiency. By the consideration of all these factors, we would strongly recommend that the medical image compression techniques which incorporates the optimal object-based algorithms and near lossless properties is more suitable for an efficient 2D/3D medical image compression. In particular, wavelets and tensor-based approaches encloses the possession of resulting a progressive coding and thus the near lossless performance can be easily attained. Hence, this review work highlighted the issues in the existing computational compression models and provides initiatives to develop new compression schemes based on lossless/near lossless approaches with object-based features for 2D and 3D medical images.

Table 1:

Summary of Wavelet based Medical Image Compression methods for 2D and 3D images

Ref.	Compression Type	2D/3D	Input Data Type	Methods/Technique Used	Significance/Advantages	Limitations/Disadvantages
Devore et al.,(1992) [10]	Lossy	2D	Still images	Wavelet decomposition.	MAE is best than the MSE to measure image compression and, evaluate the error rate and smoothness of the images using besov spaces. Images are compressed with different coefficients like 128, 512, 256.	Did not mention anything about performance metrics used for evaluation. Not compared with existing methods.
Lewis and Knowles (1992) [11]	Lossy	2D	Still images	Orthogonal wavelet decomposition, Quantizer	Give better compression ratio than DCT and VQ	Introduce noise in least important parts of the image.
Shapiro (1993) [12]	Lossy	2D	Still images	DWT, Zero Tree Coding Successive approximation, AAC	User can encode the image with desired bit rate. Compared with JPEG, produced better compression rate.	Unavoidable artifacts are produced at low bit rate.
Said and Pearlman (1996) [13]	Lossless	2D	Still images	SPHIT coding	Extended version of EZW. Reduction incomputational time.	Small loss in performance
Wang and Huang (1996), [18]	Lossy	3D	CT and MRI	Separable 3D wavelet transform, Run length coding, Huffman coding, Used D4, Haar, 9/7 filter banks in the slice direction.	3D wavelet compressions give better results than 2D wavelet. Results are comparable with JPEG Compression standard. Increase the CR for 3-D is about 70% over 2-D CT images and 35% higher for MR images at a PSNR of 50 dB.	3D compression is depends on the slice distance.
Bilgin et al., (1998) [16]	Lossy/Lossless	3D	CT and MRI	EZW extended to 3D-EZW and used Context based adaptive arithmetic coding (3D-CBEZW)	3D-CBEZW gives 22% and 25% reduction in file size for CT and MRI respectively compared with 2D compression algorithms.	Progressive performance of 3D-CB-EZW is declines sharply at the boundaries of the coding units.
Xiong et al., (1998) [17]	Lossy/Lossless	3D	CT and MRI	3D-Integer wavelet Packet Transformation and SPHIT (Context modeling in arithmetic coding).	Uses a context modeling arithmetic code to improve the performance. 3DSPHIT compared with UNIX compression, JPEG-LS and 3D-CBEZW.	Computational cost is not analyzed.
Islam and Pearlman (1999) [19]	Lossy/Lossless	2D	Still Images	Set Partitioned Embedded BloCK based Coder (SPECK), Quadtree partitioning, Arithmetic coding	Low computational complexity. Fast encoding and decoding. Produced better performance and compared with EZW, SPHIT, AGP.	For some images it produced low compression rate than SPHIT.
Bilgin et al (2000) [21]	Lossy	3D	CT, MRI	Integer Wavelet Transform, 3D EZW, Context based adaptive arithmetic coding.	3D CBEZW is offers progressive lossy and lossless compression in a single bit stream. It has achieved 10% of reduction in compressed size when compared to the normal 3D-EZW. 3-D compression method provide significantly higher compression compared with 2-D methods.	The encoder and decoder required a large space and no standard wavelet transform performed better for all types of datasets
Dragotti et al., (2000) [66]	Lossy	3D	Landsat Images	3D Transform, (KLT, wavelet), SPHIT, Gain shape Vector Quantization	SPIHT extended as 3D SPIHT for multispectral Images. Compared with conventional method like 2D-SPIHT, KLT-DCT, class KLT-DCT,KLVQ	KLT takes more time for encoding
Taubman (2000) [23]	Lossy	2D	Still Images	Embedded Block Coding with Optimized Truncation(EBCOT). Daubechies 9/7 bi-orthogonal wavelet filters	It offers good compression performance with an unprecedented set of bit stream features, resolution capability, SNR scalability and a random access capability. JPEG 2000 uses EBCOT as a encoder. It uses five level of layer decomposition to different images	Consume more memory space and computation time
Xu et al., (2001) [29]	Lossy	3D	Still Images	3D-ESCOT, Extension of EBCOT in context modeling and block based motion thereading, Daubechies 9/7 bi-orthogonal wavelet filters	Block based motion threading is used to reduce the bit rate. Further it was prolonged into object based coding. For most test sequences 3D ESCOT well performed then MPEG-4.	3-D ESCOT incurs longer delay than MPEG-4
Kim and Pearlman (2002) [30]	Lossy	3D	Still Images	3D video SPHIT coding, 3D wavelet decomposition and 3D spatio temporal dependence trees, Arithmetic coder	3D-SPHIT produced a better result than MPEG-2. It is established with high fidelity and scalability in frame rate and size.	Not analyzed about computational cost and time.
Simrad et al., (2002) [31]	Lossy	2D	Gray scale image set	Uses trap filters with Non adaptive arithmetic encoder	The results are compared with JPEG, PWC and JPEG 2000. Trap gives better results than JPEG 2000	For binary images, it yields poor performance
Benoit et al. (2002) [33]	Lossy	3D	Images from X-ray, Morphometer Coronagraphy	3D wavelet transform with 3D lattice vector quantization and uniform scalar quantization, DMA	This scheme is used to code the images from 3D scanner and morphometer. Reconstructed images are significantly better than classical 3D-DCT	Computational time is high
Xiong et al., (2003) [34]	Lossy/Lossless	3D	CT, MRI	Scaling by Lifting and Scaling by bit shifts are used. 3D-IWT, Modified 3D ESCOT, Modified 3D SPHIT, Adaptive arithmetic coding.	3D-ESCOT entropy encoder achieves the better lossy and lossless compression for 3D medical data sets. Compared with Unix compression, CALIC, JPEG-LS,3D-CB-EZW, 3D-SPHIT	Scaling by bit shifts give better results than scaling by lifting in both 3D-SPHIT and 3D-ESCOT
Yeom et al (2004) [35]	Lossy	3D	Full color 3D Integral Images (II)	MPEG-2, three types of scanning topology – Parallel, Spiral, Perpendicular	Integral Images converted into video stream and compressed using MPEG2. PSNR and SNR of MPEG2 are larger than JPEG	Computational cost is not measured
Shyamsunder et al., (2006) [36]	Lossy	3D	MR images and X-Ray angiogram images	3D Hartley transform, Run length encoding and Huffman coding	Performance is compared with 3D-DCT and 3D-DFT. 3D-DHT yields better results for MR images for higher bit rates. For X-ray images 3D-DCT gives good results with the PSNR of 44.87 dB	At lower bit rates 3D-DCT give better results than 3D-DHT
Ramakrishnan and Sriram (2006) [37]	Lossy/Lossless	2D	MR Spine and X-Ray Chest images	2D lifting wavelet based set partitioning in hierarchical trees coder	It uses MSE and MSSIM metrics to access the quality of reconstructed images. It utilizes the minimum bandwidth for transmission compared with JPEG methods like JPEG, JPEG2000 and JPEG-LS. Results shows that SPHIT encoder gives low bandwidth utilization for transmission of DICOM images.	CR and MSE of JPEG-LS and JPEG are too high when compared with SPHIT at higher bit rates.
Tang and Pearlman (2006) [20]	Lossy /Lossless	3D	Hyper spectral images	3D-SPECK, 3D-DWT is applied for transformation, Adaptive arithmetic coding.	Low Computational complexity and required Low dynamic memory. Compared with 3DSPHIT, JPEG2000 Multi Component, 2D SPHIT, JPEG2000. 3D algorithms perform better than 2D algorithms.	3D-SPECK and 3D-SPHIT results are quite close.
Jyotheswar and Mahapatra (2007) [38]	Lossy/Lossless	2D/3D	Still Image and MRI Image	Lifting based Discrete Wavelet Transform and Modified SPIHT algorithm	Results are compared with original and modified SPHIT. For Higher bit rate modified SPHIT algorithm gives better results.	For lower bit rates both algorithms gives almost identical results.
Sanchez et al., (2009) [39]	Lossless	3D	MRI and CT	2D IWT, Modified EBCOT	Symmetry based technique. It resulted with the average improvement of 15% compression ratio over JPEG2000 and H.264/AVC intra-coding and 13% over 3D-JPEG2000	JPEG 2000 and H.264/AVC intra-coding achieves higher PSNR than proposed method
Sanchez et al., (2010) [41]	Lossy/Lossless	3D	MRI and CT	3D IWT, Modified 3D EBCOT.	The proposed method gives higher reconstruction qualities than 3D-JPEG2000 with VOI coding for different bit rates.	Give better results for MRI images than CT which is compared with existing methods
Akhter and Haque (2010)[42]	Lossless	2D	MIT-BIH ECG Signal	RLC, DCT, Huffman coding.	ECG signal is segmented into QRS-Complex and Non-QRS Wave. WDD index is used to evaluate the distortion quality of the reconstructed signal.	Used to test only ECG signals
Sriram and Shyamsunder (2011) [43]	Lossy/Lossless	3D	MR and X-Ray images	Four symmetric and decoupled wavelet transforms in 1st stage with encoders like 3D-SPHIT, 3D SPECK and 3D-BISK are used in 2nd stage.	3D CDF 9/7 symmetric wavelet along with the 3D SPIHT encoder produced best compression performance. It referred as optimal wavelet encoder. From the results observed that GOS of 16 slices gives the best optimum result.	Symmetrical wavelets perform better than decoupled wavelets
Cyriac and Chellamuthu (2012) [44]	Lossy/Lossless	2D	CT and MRI	Visually Lossless Run Length Encoder/Decoder	Provides faster hardware implementation for real time applications.	It works only on 8 bit images.
Spelic and Zalic (2012) [45]	Lossless	2D/3D	CT	Segmented using Hounds field scale, JBIG, Segmented Voxel compression algorithm	Ease of transfer data and ease of decompress desired data. It reduces up to 40% of the original size.	Independently compressing the segmented data, which causes coherence reduction
Raza et al., (2012) [46]	Lossless		MRI and CE	Super Spatial structure prediction with Inter-Frame coding, Fast block matching coding, Huffman coding	It ultimately reduces memory required for storage and transmission. Attains High Compression Ratio	Computational time is depends upon the size of the input image.
Setia et al., 2012 [47]	Lossy/Lossless	2D	Still Images	Haar Wavelet Transform, Run Length Coding and Huffman Coding are used for encoding	Less computational complexity. RLC gives lossless representation of data with reduced number of bits to represent a pixel in an image.	Computational cost and storage requirement are not specified.
Anusuya et al., (2014) [48]	Lossy/Lossless	3D	MRI Brain Images	Stationery Wavelet Transform, EBCOT Encoding, Bit Plane and Arithmetic coding are used.	Parallel computing is used to implement the arithmetic coder operations. The Proposed method is compared with JPEG2000 and EBCOT and give significant results in compression ratio and computation time.	CR is low for MRI when compared with JPEG2000 and EBCOT
Sahoo et al., (2014) [49]	Lossy/Lossless	2D	Still Images	2D Haar Wavelet, Hard Thresholding, RLE	HWT with HT using CRLE gives the better results than JPEG 2000	There is no novelty in proposed method. It is an existing method compared with different RLE methods.
Anusuya and Raghavan (2014) [50]	Lossy/Lossless	3D	MRI and CT images	Haar wavelet Lifiting scheme, EBCOT Block coding	Proposed method is compared with JPEG2000 and EBCOT. For CT images the proposed method gives better CR.	For MRI images proposed method gives low CR compared with JPEG2000 and EBCOT.
Senapati et al., (2014) [51]	Lossy	2D/3D	Still images	3D Hybrid transform, KLT, LEBP & CLEBP.	It reduces the encoding and decoding time. The listless implementation reduces the memory requirements. CLEBP gives better results than existing wavelet based embedded coders for the color images.	LEBP on gray scale images gives poor results than SPHIT.
Bruylants et al., (2015) [52]	Lossy/Lossless	3D	CT, MRI and US images	SD-DA-DWT, Block based intra prediction.	To improve the performance of the JPEG2000 developed its volume metric extension codec called JP3D. It significantly increases the compression performance when compared with JPEG2000 part 1. JP3D well performed in all high bit depth for US images.	Directional adaptive filters has increased computational time and memory complexities.
Juliet et al., (2016) [53]	Lossy	2D	MRI, CT	Ripplet Transform, SPHIT	It outperforms DCT in terms of CR by 5.13%, Haar wavelet by 5.47%, contourlet-based method by 6.96%, curvelet-based method by 9.43% and JPEG compression by 7.46%.	More or less proposed method performs like DCT-SPHIT
Xiao et al., (2016) [54]	Lossy/Lossless	2D	CT, MRI	Integer Discrete Tchebichef Transform	iDTT performs better in color medical image lossless compression than iDCT and JPEG-LS.	iDTT provide better results only for color medical images
Ibraheem et al., (2016) [55]	Near-Lossless	2D	MRI and X-Ray	LNS-DWT and Logarithmic DWT	Both schemes gives higher image quality than the classical DWT.	Execution speed is two times higher than the normal DWT.
Perumal and Rajasekaran (2016) [56]	Lossy/Lossless	2D	MRI, CT, and PET	Hybrid DWT-BP	Reduce the computational cost and storage. Proposed hybrid method is compared with DWT and BPNN and gives better PSNR and CR than DWT and BPNN.	MSE of DWT-BP is slightly increases than the DWT
Kalavathi and Boopathiraja (2017) [57]	Lossy	2D	Still images	2D-DWT, Thresholding, RLC	This method performance is evaluated with different bit rates. High BPP gives good quality of reconstructed image.	It gives slightly blurred image for 0.5 and 1 BPP
Lucas et al., (2017)[58]	Lossless	3D	CT and MRI	3D-MRP, 3D Shaped Predictors, Volume based optimization, Hybrid 3D-Block Classification.	Attains high compression efficiency and improves error probability and compared with JPEG-LS,JPEG2000, HEVC and CALIC.	Computational complexity is high
Kalavathi and Boopathiraja (2017) [59]	Near Lossless	2D	MRI, CT, X-Ray, US	2D-DWT, RLC	Give better results for large image than the small size images. High-quality images are reconstructed in high amount of BPP values.	This method produces little amount of blurriness for 0.5 and 1 BPP.
Somasoundaram and Subramaniam (2018) [60]	Lossy/Lossless	2D	Angiogram sequence	2D Bi-orthogonal multi wavelet transform and Hybrid speck deflate algorithm	Achieves higher compression ratio. And the method is compared with multi wavelet with SPIHT. This method provide superior performance in terms of PSNR, UIQI, SSIM, and MSE	Requires high computational time
Boopathiraja and Kalavathi (2018) [61]	Near Lossless	3D	Multispectral image	3D DWT, Thresholding and Huffman coding.	CR is increased by four times than the Huffman coding. This method reduces the space complexity with better image quality.	Comparison performed only with Huffman coding.
Parikh et al., (2018) [62]	Lossy/Lossless	3D	MR, CT, CR	ImageJ tool, HEVC encoder	HEVC compression reduces storage and bandwidth needs by up to 54% compared with J2K.. Intra HEVC compression gives 55% reduction in computational complexity.	HEVC increases the encoding time, and computational cost.
Chithra and Tamilmathi (2019) [63]	Lossy/Lossless	2D/3D	MRI and CT images	Kronecker delta notation and wavelet based techniques Brige-Massart and Parity Strategy	It is well performed on MRI images and produced better CR than the other existing methods based on Brige-Massart and Unimodal thresholding	It is not well performed for CT images
Boopathiraja and Kalavathi (2020) [64]	Near lossless	3D	MRI and CT	3D-DWT, Huffman coding	They ensure that this method can be used for telemedicine services. It saves 0.45 bit-rate averagely with very low MSE .	Computational time is high. Not compared with any existing methods.
Benlabbes Haouari, (2020) [65]	Lossy	3D	MRI and CT	Quinqunx wavelet transform, SPIHT encoder	This method achieves much higher compression rates, and also maintaining an acceptable visual quality of the reconstructed image.	Comparisons with existing methods are not specified. Evaluation made only for 0.3 bit rate.

Table 2:

Summary of Object Based Image Compression Methods for 2D and 3D Images

Ref.	Compression Type	2D/3D	Input Data Type	Methods/Techniques Used	Methods used for Object Detection/Extraction	Significant/Advantages	Limitation/Disadvantages
Leou and Chen (1991) [57]	Lossy	2D	Still Images	Contour extraction and encoding, Polyline texture extraction	Minimum spanning tree segmentation,	Simple computation structure and less computational time.	Polyline length must be specified manually. Not compared with any existing methods
Shen and Rangayyan (1997) [71]	Lossless	2D	X-Ray, Mammogram images	JBIG, Single scan neighbor pixel checking algorithm, discontinuity index map data coding.	SLIC Region growing method.	This method is compared with JPEG, HINT, JBIG, ALZ. SLIC needs only about 56% or 47% of the disk space for storing the 10 8-b/10 10-b medical images. Low computational time. Average bit rate of SLIC is 2.92	5 and 6 only had chosen as Error bits rates.
Li and Li (2000) [72]	Lossy/Lossless	3D	Test sequences from MPEG-4	Extension of ZTE and EZW, odd symmetric biorthogonal, and even symmetric biorthoganl filters are presented	SA-DWT	Very efficient technique for coding arbitrarily shaped visual objects. Locality property and self-similarity across subbands are well preserved in SA-DWT. It well performed than SA-DCT. SA-DWT provides higher PSNR values	Odd symmetric wavelet filter only give better performance than other two filters
Gokturuk et al., (2001)[75]	Lossy/Lossless	3D	Human colon CT images	Motion compensated coding,	Automatic Segmentation method using 3D morphological operation	Motion compensated coding reduces the entropy of the error image by a considerable amount of 4.38 bpp. This method is compared with DCT, PCA and Blockwise Vector quantization	It well suited only for CT medical data.
Liu et al., (2002) [77]	Lossy/Lossless	2D	Chromosome Spread Images	Modified SPHIT and EBCOT	Chain code based shape coding scheme	This method achieves improved compression performance with ROI support over other image coders. And it is compared with Winzip 8.0, JPEG-LS, JPEG-2000, Modified SPHIT and Modified EBCOT.	In lossless compression Winzip 8.0 outperforms both modified SPHIT and EBCOT
Dilmaghni et al., (2003) [78]	Lossy	2D	Mammogram and knee images	ROI coding with PIT incorporates the EZW	Progressive image transmission algorithm	It has been applied to a critical ROI of an image while the information of the rest of image is kept at low resolution. It can be applied to RIS environments.	It is only well suited for precision based progressive transmission.
Ueno and Peralman (2003) [79]	Lossy/Lossless	3D	MR-Chest	3D DWT , 3D SPHIT	SA-ROI	SA-ROI is better than SB-ROI in terms of compression performance of the object.	Poor compression performance at low coding rate
Gibson et al., (2004)[81]	Lossy/Lossless	3D	Angiogram Sequences	3D-Wavelet Transform, 3D SPHIT	Background Motion Estimation, ROI Detection	It gives better results than conventional SPHIT algorithm.	It used only angiogram imagery. For low bit rates it performed worse than the SPHIT method.
Maglogiannis (2009 )[82]	Lossy/Lossless	3D	CT, CR, and MR	Scalable wavelet based compression, DLWIC	Chain code based shape coding scheme	It is a medical application that enables the compression, retrieval and decompression of DICOM medical images.	In the case of lossy image compression, it degrade the image quality
Valdes and Trujillo (2009) [84]	Lossy/Lossless	3D	CT	K-means, Chen vase segmentation, JPEG 2000	Flood Fill Algorithm	Evaluation results shows an improvement up to 23.88% in the compression rate.	Due to the segmentation process computational cost is high.
Chen et al., (2013)[85]	Lossless	3D	MRI	Chroma sub sampling and up sampling CABAC	HEVC	Compared with HEVC intra encoding and HEVC lossless encoding and this method yields superior rate distortion performance.	Bit rate cost is high
Das and Kundu, (2013) [89]	Lossless	2D	CT, MRI, X-Ray, Mammogram	Fragile Image watermarking technique	Polygonal ROI	Authentication integrity, data hiding and Secure the medical metadata and archives lossless compression	The resultant watermarked images have higher degradation. Only tested with gray image
Yee et al., (2017)[90]	Lossy/Lossless	3D	MRI	BPG, HEVC	Flood-fill Algorithm	BPG exceeds the compression gains of all the other compression formats such as JPEG, JPEG2000, and PNG by 10–25%.	It well performed only on smaller dimensions.
Eben and Anitha, (2017) [91]	Lossy/Lossless	2D	MRI, US	Normalized Wavelet transform, Mask-based prediction, Arithmetic encoding.	Simpler and less complex interactive method of partitioning	Attains good PSNR in Low bits and high bits. compared with JPEG2000 and other conventional methods.	This algorithm provided better results for BPP greater than 0.6
Deavadoss and Sankaragoma thiet al., (2018) [92]	Near-lossless	3D	US, CT, MRI and X-ray images	BWT-MTF with Huffman coding and hybrid fractal encoding	Morphological Segmentation	Hybrid fractal used to compress NROI, and BWCA used to compress ROI. This method gives best results for US and MRI images.	BWT and MTF is high time consuming process.
Zanaty and Ibrahim (2019) [93]	Near-Lossless	2D	X-Ray, CT and MRI	Different wavelets, SPHIT	Region Growing method	Combining RG and Wavelet transform increases the CR compared with other wavelet methods	Not analyzed any particular wavelet which is well suited for the proposed method.
Boopathiraja et al., (2020) [94]	Lossless	3D	MRI, CT, and PET	LZW, Arithmetic coding	SBV	This method yields double the time more compression ratio than the other existing methods of RLC, Huffman, LZW, Arithmetic coding. It reduces the computational time.	Computational time of RLE is lesser than this proposed method
Srinivasalu and varadarajan (2020) [95]	Lossless	2D/3D	MRI images	DWT with SPHIT and DCT with MHE	Modified Region Growing	PFCM is used for both segmentation and compression	Computational time is not analyzed.

Table 3:

Summary of Tensor Based Image Compression Methods

Ref.,	Compression Type	2D/3D	Input Data Type	Methods/Techniques Used	Significant/Advantages	Limitation/Disadvantages
Wu et al., (2007) [108]	Lossless	3D	4D time varying scientific data set, 3D MI in the visible human dataset,	Adaptive data approximation technique	Hierarchical tensor approximation method is compared with Bi-orthoganal Wavelet Transform JPEG2000), Wavelet packet Transform, and Single level tensor approximation.	Storage overhead for the adaptively extracted based matrices.
Dauwels et al., (2012) [116]	Near – lossless	3D	EEG signal dataset	SVD,CUR, PARAFAC, TT, FSTD	Tensor based methods outperforms with large compression ratio. PARAFAC gives the smallest reconstruction error.	They mainly developed for EEG data set
Chen et al., (2012) [100]	Lossy	3D	Hyper spectral Images	Optimal truncation tucker	It has high compression and decompression speed than existing methods like symmetric 3D-SPIHT and asymmetric 3D-SPIHT	PSNR of the proposed method is slightly lower than the asymmetric-3D-SPHIT
Dauwels et al., (2013)[106]	Near – lossless	3D	EEG signal dataset	SVD, PARAFAC and modified arithmetic coding	This near-lossless compression scheme yields two-fivefold smaller average distortion compared to wavelet based volumetric coding.	Well suited only for MC-EEG datasets
Zhang et al., (2015) [102]	Lossy	3D	Hyperspectral Images	Tucker Decomposition, HOSVD, HOOI, Multi linear projection	TenD method is performed well better than the PCA and MNF. This method obtains the highest PSNR value and preserves the HIS data quality.	Not analyzed about computational cost.
Wang et al., (2015) [103]	Lossy	3D	Hyperspectral Images	LT-TD, PCA, HOOI, Bit plane coding	LT-TD performs better than3D-SPECK in all cases by2.24–8.8 dB.	Compared with KLT-JPEG2000, LT-TD performs worse at low bit rate, but better at high bit rates
Ballester and Pajarola (2016) [104]	Lossy	3D	CT images	HOOI, Thresholding, zig zag traversal, RLC, Huffman coding	The compaction accuracy of core tensor is appreciable and gave better compression performance than other TD methods.	Because of coefficient thresholding, reconstructed image quality is slightly worse.
Fang et al., (2017) [105]	Lossy	3D	Hyperspectral Images	CPTBC	It gives the higher PSNR (49.7 dB) than the MPEG4, band-wise JPEG2000, TD, 3D-SPECK, 3D-TCE and 3D-TARP. CPTBC method removes the noise or artifacts compared with the original data.	Computational time is higher than existing methods.
Du et al., (2017) [106]	Lossy	3D	Hyperspectral Images	PLTD, Non Local similarity, Low Rank decomposition.	This method simultaneously removes the redundancies in both spatial and spectral modes.	Patch size selection is not automated
Ballester et al., (2019) [107]	Lossy	3D	Multidimensional data	TTHRESH,HOSVD, Bit plane coding	This method achieves good accuracy at low to medium compression ratios and consistently well performs other compressors at medium to high ratios	Computational cost is high.
Wang et al., (2016) [114]	Lossy	3D	CT lungs images	HOSVD, TCS, 3D Lorenz	It achieves a high precision of decryption at a big compression ratio. Encryption makes harder for unauthorized access.	High Computational time. Not compared with any existing methods
Liu et al., (2019) [113]	Lossy	3D	MRI.	Fractal Compression, Residual compensation mechanism,	It significantly improves compression speed by 2–3 times when compared with traditional fractal compression. PSNR is higher than BWT-MTF method.	CR is slightly worse than BWT-MTF method
Dmytro Kucherov et al 2019 [115]	Lossy	3D	US images	Tensor based SVD	Higher image quality is achieved by increasing the accuracy of the truncated description approach. This algorithm satisfies adaptability feature.	It is an iterative process so it takes more computational time . Comparison with existing methods are not mentioned

Abbreviations used in this review:

2D

Two Dimensional

3D-ESCOT

Three Dimensional Cube Splitting Embedded Block Coding with Optimized Truncation

3D BISK

Three Dimensional Binary Set Splitting with k-D Trees

3D

Three Dimensional

3DHLCK

3D Hierarchical Listless embedded block

3D-DHT

3D Discrete Hartley Transform

AI

Artificial Intelligence

ALZ

Adaptive Lempel-Ziv

AAC

Adaptive Arithmetic Coding

BPNN

Back Propagation Neural Network

BPG

Better Portable Graphics

BPV

Bit Per Voxel

BWT

Burrows Wheeler Transform

BPP

Bit Per Pixel

BWCA

Burrow Wheeler Compression Algorithm

CAGR

Compound Annual Growth Rate

BTF

Bidirectional Texture Functions

CABAC

Context Adaptive Binary Arithmetic Coding

CANDECOMP

Canonical Decomposition

CALIC

Context based Arithmetic Lossless Imaging Codec

CDF

Cohen–Daubechies–Feauveau

CC

Correlation Coefficient

CE

Capsule Endoscopy

CRLE

Conventional Run Length Encoding

CCR

Computational Complexity Reduction

CUR

Column Row Decomposition

DTT

Discrete Tchebichef Transform

CLEBP

Color Listless Embedded Block Partitioning

CPTBC

CANDECOMP/PARAFAC Tensor Based Compression

DCT

Discrete Cosine Transform

DWT-BP

DWT with Back Propagation

DMA

Distortion Minimization Algorithm

ECG

Electrocardiogram

CR

Compression Ratio

DST

Discrete Sine Transform

FSTD

Fiber sampling tensor decomposition

CT

Computed Tomography

DWT

Discrete Wavelet Transform

GOP

Group of Pictures

DICOM

Digital Imaging and Communications in Medicine

EBCOT

Embedded Block Coding with Optimized Truncation

HEVC

High Efficiency Video Coding

DIP

Digital Image Processing

EEG

Electroencephalograms

HSI

Hyper Spectral Images

DLWIC

Distortion-Limited Wavelet Image Codec

EZW

Embedded Zerotree Wavelet

HWT

Haar Wavelet Transform

EHR

Electronic Health Record

HINT

Hierarchical Interpolation

IWT

integer wavelet transform

ERLE

Enhanced Run Length Encoding

HOSVD

Higher Order Singular Value Decomposition

JBIG

Joint Bi-level Image Expert Group

FSTD

Fiber Sampling Tensor Decomposition

JPEG2000

Joint Photographic Experts Group 2000

LEBP

Listless Embedded Block Partitioning

HOOI

Higher Order Orthogonal Iteration

KLT

Karhunen–Loeve Transform

LT-TD

Lapped Transform Tucker Decomposition

HVS

Human Visual System

LIP

List of Insignificant Pixels

LT-TD

Lapped Transform and Tucker Decomposition

iDTT

Integer Discrete Tchebichef Transform

LIS

List of Insignificant Sets

MSSIM

Mean Structural Similarity Index

JBIG

Joint Bi-level Image Expert Group

LNS

Logarithmic number system

MSSIM

Multi-Scale Structural Similarity Index

MHE

Merging based Huffman Encoding

LSP

List of Significant Pixels

ORLE

Optimized Run Length Encoding

MIW

Medical Image Watermarking

MC-EEG

Multichannel Electroencephalogram

PFCM

Possiblistic Fuzzy

C-Means

Clustering method

MLSVD

Multilinear Singular Value Decomposition

MFT

Move to Front Transform

PIT

Progressive Image Transmission

MRI

Magnetic Resonance Imaging

MNF

Maximum Noise Fraction

PNG

Portable Network Graphics

Nifti

Neuroimaging Informatics Technology Initiative

ONC

Office of National Coordinator for Health Information Technology

MPEG

Motion Picture Experts Group

PRD

Percent Rate Distortion

MRG

Modified Region Growing

PRD

Percentage Root-Mean squared Difference

PACS

Picture archiving and communication system

MRP

Minimum Rate Predictors

PSNR

Peak Signal to Noise Ratio

PET

Positron Emission Tomography

MSE

Mean Square Error

RLC

Run Length Coder

RG

Region Growing

PCA

Principal Component Analysis

ROI

Region Of Interest

RMSE

Root-Mean-Square Error

PLTD

Patch-Based Low-Rank Tensor Decomposition

SA-ROI

Shape Adaptive Region of interest

SA-DWT

Shape-Adaptive Discrete Wavelet Transforms

SBV

Selective Bounding Volume

SWT

Stationary Wavelet Transforms

SA-ROI

Scaling based ROI

SC

Structural Content

TCS

Tensor Compressive Sensing

SNR

Signal to Noise Ratio

SLIC

Segmentation based Lossless Image coding

SPIHT

Set Partitioning In Hierarchical Trees

SPECK

Set Partitioned Embedded block coder

TSUID

Transfer Syntax Unique Identification

SVD

Singular Value Decomposition

SPHIT

Set Partitioning In Hierarchical Trees

UIQI

Universal Image Quality Index

TC-VQ

Transform coding and Vector Quantization

SSIM

Structural Similarity Index

VOI

Volume Of Interest

UIQI

Universal Image Quality Index

VQ

Vector Quantaization

WDD

Weighted Diagnostic Distortion Index

US

Ultra Sound

WDD

Weighted Diagnostic Distortion

ZTE

Zero Tree Entropy