A practical guide to applying machine learning to infant EEG data

Abstract

Electroencephalography (EEG) has been widely adopted by the developmental cognitive neuroscience community, but the application of machine learning (ML) in this domain lags behind adult EEG studies. Applying ML to infant data is particularly challenging due to the low number of trials, low signal-to-noise ratio, high inter-subject variability, and high inter-trial variability. Here, we provide a step-by-step tutorial on how to apply ML to classify cognitive states in infants. We describe the type of brain attributes that are widely used for EEG classification and also introduce a Riemannian geometry based approach for deriving connectivity estimates that account for inter-trial and inter-subject variability. We present pipelines for learning classifiers using trials from a single infant and from multiple infants, and demonstrate the application of these pipelines on a standard infant EEG dataset of forty 12-month-old infants collected under an auditory oddball paradigm. While we classify perceptual states induced by frequent versus rare stimuli, the presented pipelines can be easily adapted for other experimental designs and stimuli using the associated code that we have made publicly available.

1. Introduction

Developmental cognitive neuroscience seeks to understand how neural representations of the world change with maturation and experience, and how individual differences in these representations affect later life outcomes. Electroencephalography (EEG) has become an increasingly important tool to address these questions. EEG measures the electrical activity on the scalp generated by population-level neuronal activity in the brain with millisecond resolution, which indirectly captures fine grained information on the temporal patterns of neuronal responses. Most studies have focused on the problem of comparing EEG activity between subject groups and experimental conditions by applying univariate statistical techniques to test for amplitude and timing differences in EEG responses. However, recent neuroimaging studies have highlighted the distributed nature of neural representations (Huth et al., 2012, Cichy et al., 2014), with even basic perceptual processes, such as phoneme categorization, shown to involve activation of multiple brain networks (Feng et al., 2021). Thus, instead of only asking whether a certain channel or time point shows amplitude differences across conditions, this distributed representation raises another important question, namely whether cognitive states can be distinguished based on the pattern of activity across multiple channels and time points.

Machine learning (ML) is particularly suited for addressing the latter question. By extracting and combining discriminative EEG attributes, such as voltage amplitude at different time points or signals at different frequency bands, which are commonly referred to as features, ML enables learning of classifiers that can distinguish different experimental conditions based on patterns of the extracted features. ML has been widely applied to adult EEG data, and successful in distinguishing stimuli as subtle as distinct English letters (Wang et al., 2018), visual colors (Hajonides et al., 2021), and individual finger movements (Liao et al., 2014), but its adoption for infant EEG data has been limited.

Initial applications of ML to infant EEG data have focused on classification of infants into groups based on age (Ravan et al., 2011) or clinical diagnosis (Stahl et al., 2012a, Stahl et al., 2012b). In this type of classification, correctly predicting group labels of the infants with high accuracy is the primary goal. More recent studies have also used ML for cognitive state classification. Above chance accuracy indicates that the EEG timeseries contain the information necessary to discriminate different cognitive states. For this interpretation to be valid, the assumption is that the classifier relies on activity patterns generated by the brain to make predictions, as opposed to using noise or movement artifacts that are correlated with stimulus (see Hebart and Baker, 2018 for a discussion on cognitive interpretation of EEG classification). In this vein, several studies have classified EEG neuronal responses to varying visual stimuli in typically and atypically developing children (Bayet et al., 2020, Mares et al., 2020, Farran et al., 2020). In the auditory domain, one study has used ML to classify event related potential (ERP) responses to speech syllables vs. tones in children with tuberous sclerosis (O'Brien et al., 2020), and a recent study has examined phoneme representations in 3-month-old infants (Gennari et al., 2021). While interest in applying ML to infant data for classifying cognitive states is growing (Emberson et al., 2017), the additional challenges compared to adult data might have restrained ML’s adoption.

Infant EEG classification has two key challenges. First, infant EEG data tend to have lower signal-to-noise ratio (SNR) than adult data due to several factors. To maximize signal once the cap is placed, electrodes are often readjusted, but infants are less tolerant of extensive electrode readjustments. Also, infants often make sudden unpredictable movements, which are less stereotyped than blink artifacts, and thus harder to remove (Georgieva et al., 2020). Finally, infants cannot be explicitly instructed to direct their attention to a given stimulus, making controlling for shifts in attention more difficult during the recording session.

The other key challenge to infant EEG classification is the shorter study duration compared to adult data, which is largely due to infants’ limited attention span. The performance of a classifier heavily depends on the number of training samples available, i.e. number of trials for classifier learning in the context of EEG classification. Therefore, the performance of a classifier learned from a single infant dataset would be limited, given the typical lower number of trials and the lower SNR compared to adult data. One way to increase sample size is to pool data across infants, which relies on extracting common brain activity patterns across infants. However, infant EEG responses are particularly influenced by individual differences in brain morphology and maturation. Inter-subject variability could thus obscure the discriminative patterns if data are naively pooled (Saha and Baumert, 2020).

In addition to determining whether information is present in the EEG responses to discriminate cognitive states, ML can further be used for identifying which brain attributes enable such discrimination. For instance, one could use classification accuracy to rank features. An example of this approach is time-resolved classification in which accuracy is estimated for each time point (with respect to stimulus onset) by combining information across EEG channels to gain insights into response dynamics (Grootswagers et al., 2017). By aggregating signals across channels, this approach has shown increased sensitivity in detecting differences across conditions and participants compared to univariate analysis (Cauchoix et al., 2014, Bayet et al., 2018, Correia et al., 2015). Other recent approaches use the classifier model weights to infer significant features under a hypothesis testing framework (Taylor and Tibshirani, 2018, Candès et al., 2018). While using ML to find discriminant brain attributes is an important problem, as an introductory tutorial to ML, we opt to focus on the most basic problem that ML addresses, namely separating samples of different classes with a single classifier. Interested readers can refer to e.g. (Belle and Papantonis, 2021) for further details on how to identify relevant features under a classification framework, and a discussion on how careful experimental designs and follow-up analyses can be used to gain insights from classification results is provided in Section 5.

In this work, we present a step-by-step tutorial on how to apply ML for infant EEG classification. We begin with an introduction to the EEG classification problem and an overview of a standard classification pipeline. We then describe the type of features that are more widely used for EEG classification, namely raw timeseries, their short time Fourier transform (STFT), Pearson’s correlation, and weighted phase lag index (wPLI) (Imperatori et al., 2019), and discuss the rationale behind the use of each feature type. We also describe connectivity features based on Riemannian geometry, which provides a mathematically elegant way for handling inter-trial and inter-subject variability (Yger et al., 2017, Yair et al., 2019, Ng et al., 2016, Sabbagh et al., 2019). These features, while not exhaustive, cover the key aspects of brain response, namely temporal and frequency information within each brain region as well as interactions between brain regions. Note that estimations of all these features except raw timeseries require multiple time points, which is partly why we focus on the problem of classifying trials in this tutorial, as opposed to classifying each time point (as done in time-resolved classification). We further describe techniques for feature selection and the type of classifiers that are better suited for the sample-to-feature ratio typical in infant EEG data. Classifier learning with data from both single and multiple infants are discussed. Lastly, we describe how to evaluate classifier performance. As an example, we apply these pipelines to infant EEG data collected under an auditory mismatch response (MMR) paradigm. The MMR is an ERP component observed in response to a deviant stimulus following a string of common, or standard, stimuli, which is used widely in infant EEG studies to assess discrimination capabilities (Cheour et al., 2000). Here, we do not classify the identity of the stimuli themselves (e.g. /ra/ vs /la/), but rather whether a deviant stimulus can be distinguished when embedded in a stream of standard stimuli (i.e. rare vs frequent stimuli). This classification task is difficult even with adult EEG data (Brandmeyer et al., 2013), which attains an accuracy of ~65%. While we focus on classifying MMR in this work, the presented pipelines are broadly adaptable to a variety of different stimuli and experimental designs.

2. Methods

2.1. EEG classification

The goal of EEG classification is to determine the cognitive state of a subject based on some attributes of the EEG data within a short time window. As a toy example, let’s say a subject is shown either a cat or a dog over many trials, and we use the voltage amplitude of two channels A and B at the time of stimulus onset as the attributes to decide if the subject is looking at a cat or a dog for each trial. Pictorially, this problem can be conceptualized as finding a curve to separate two sets of points (green for cats and purple for dogs) on the xy-plane (Fig. 1). Each point corresponds to a trial and the xy coordinates correspond to the amplitude of channels A and B. After we find a curve that well separates points corresponding to dogs from those corresponding to cats, we can test this curve with new points (Fig. 1), i.e., trials not used for finding the curve. If the curve does well in separating the new points, then this curve likely captures some true signal patterns hidden in the EEG data. In technical terms, the amplitude of channels A and B are referred to as features, and the curve is called the decision boundary. The points used for finding the decision boundary are referred to as training samples, and the new points not used for finding the decision boundary are referred to as test samples. If the decision boundary performs well on test samples, we say the corresponding classifier has high generalizability, which is a key property for evaluating a classifier. The main steps involved in EEG classification are summarized in Fig. 2, namely feature extraction and selection, classifier learning, and classifier evaluation.

Fig. 1.

Depiction of EEG classification. In this toy example, each point corresponds to a trial and the xy-coordinates correspond to voltage amplitude at channel A and B. The color of the point indicates the class to which that point belongs, and the blue curves correspond to examples of the infinitely many ways for separating the points. The goal is to learn a curve solely based on the training trials (green and purple points) where class labels are given, to separate the test trials (light green and light purple points) into their corresponding classes. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 2.

Classification pipeline. Features are first extracted from all trials, with trials divided into training and test sets. Bootstrap univariate feature selection is then performed by applying t-test to the training trials of each feature and estimating the percentage of bootstraps over which a given feature has p < 0.05, referred to as selection frequency, f. The set of features, S, with selection frequency greater a certain threshold, f_th, are used for classifier learning. Labels of test trials, I_p, are then predicted using the learned classifier weights, w, and compared against the ground truth labels, l_g, to evaluate the classifier’s performance. This procedure is repeated multiple times with random trial splits to assess variability in performance.

In real applications, we would typically extract many features to examine various aspects of brain response. Key aspects include the timing and amplitude of peaks and troughs of EEG timeseries, signals at different frequency bands, and interactions between brain regions. These aspects can be captured by standard features, such as EEG timeseries themselves, STFT of the timeseries, Pearson’s correlation between timeseries of the EEG channels, and wPLI (Imperatori et al., 2019). Recently, connectivity features based on Riemannian geometry have also been adopted for EEG classification (Yger et al., 2017, Yair et al., 2019, Ng et al., 2016, Sabbagh et al., 2019). Each of these features will be described in Section 2.2. We note that we focus here on five representative features, but many other features could be extracted to capture similar aspects of brain response.

After feature extraction, the next step is to divide the trials into training and test sets for classifier learning and evaluation, respectively. For typical infant EEG data, the number of features often exceeds the number of trials. Reducing the feature dimensionality by selecting the more discriminative features could ease classifier learning. For this, we present a common feature selection approach based on bootstrapping. Also, the number of trials is usually inadequate for exploiting deep learning. We thus describe the support vector machine (SVM) (Cortes and Vapnik, 1995), which has empirically shown robust performance for low sample-to-feature datasets. We focus on the task of binary classification where a given trial of an infant is classified as belonging to condition A or B using a single classifier. The trials can be from a single infant or from multiple infants, and we refer to training with single and multiple infants’ data as single infant classifier learning and multi-infant classifier learning, respectively. We also assume the number of trials in each class is the same, i.e. balanced classes. MATLAB scripts for extracting the aforementioned features as well as executing the classification pipeline are provided on Open Science Framework along with the associated dataset (see featureExtraction.m, main*.m, and riemannian*.m).

2.2. Feature extraction

2.2.1. Timeseries

The basis of using timeseries as features is that activation of different brain areas during task execution generates a specific spatiotemporal pattern of electrical activity across EEG channels. For instance, visual stimuli drive a large negative response in occipitotemporal channels, as well as a positive response at the vertex, which reflects signals from the occipitotemporal dipoles. Different experimental conditions could thus in theory be distinguished based on the response pattern with voltage of each channel at each timepoint of a trial taken as a feature. Hence, using timeseries provides features that capture information at millisecond resolution.

An important parameter in using timeseries as features is the expected duration of EEG responses, which defines the time length of a trial (see Section 3.2). While infants’ responses are typically slower than those observed in adults, evoked responses to visual or auditory stimuli can be quite fast. For example, by 12 months of age, visual responses to a variety of different objects can be classified by 100 ms following stimulus onset (Bayet et al., 2020). Responses to tasks that involve additional processing, such as the detection of deviance or a violation of expectation, are typically slower. For example, even in adults, classification of the MMR peaks between 200 and 300 ms following stimulus onset (Brandmeyer et al., 2013). Hence, the expected response duration depends on the experimental conditions. Typically, we only have a rough estimate of the response duration, but setting the trial length slightly longer than the response duration would not be catastrophic since less relevant time points would be either discarded during feature selection or down-weighted during classifier learning (2.3, 2.4).

While we focus on the problem of learning a single classifier to separate trials of different classes in this tutorial, it is worth noting that one could learn a separate classifier for each time point to examine response dynamics and the time following stimulus onset when classes become distinguishable (Grootswagers et al., 2017). Further, we note that within and between subject variability in response onset, shape, and duration (Saha and Baumert, 2020) can make using timeseries as features difficult. While this variability may be relatively minor for evoked sensory stimuli that drive rapid time-locked responses, response variability may be compounded for slower perceptual processes involving additional computation, such as the MMR. Thus, the same time point across trials and subjects do not necessarily correspond to each other, but such correspondence is important for using voltage at each time point as a feature for classifier learning. To deal with this temporal correspondence issue, one way is to “average” the voltage values within short time windows of each trial, and use the resulting averages as features. In fact, STFT can be viewed as an extension of this temporal averaging strategy, as discussed next.

2.2.2. Short time Fourier transform

To handle temporal variability in response, one strategy is to apply STFT to the timeseries, i.e. apply Fourier transform to short time windows within each trial, where the amplitude of each channel’s transformed timeseries at each time window and frequency bin is taken as a feature. The rationale behind using STFT stems from how EEG timeseries typically display repeated temporal patterns. By applying Fourier transform, we can estimate the frequencies at which these temporal patterns repeat. Past studies have shown that different frequency bands: delta (0–4 Hz), theta (4–7 Hz), alpha (8–12 Hz), beta (12–30 Hz), and gamma (30–100 +Hz), are involved in different mental processes, e.g. the alpha band has been shown to play a role in inhibition (Klimesch et al., 2007). Thus, patterns in the frequency spectrum can be useful for classification. Also, aggregating voltage over time samples temporally “smooths” out the response, which increases the response overlap across trials. To perform STFT, we used MATLAB’s spectrogram function with its default parameter values. The resulting STFT features provide a temporal resolution of ~100 ms for our data with a trial length of 700 ms.

2.2.3. Pearson’s correlation

A common way to bypass the problem of drawing temporal correspondence across trials is to use functional connectivity between channels as features. Functional connectivity is estimated based on the similarity between timeseries of the channels, i.e. whether the peaks and troughs line up. The assumption is that if the voltage patterns at channels A and B are highly similar, then the brain areas from which these voltage timeseries originated interact with each other. Since all time points within a trial are typically used to estimate connectivity, the resulting features do not tell us at which time points the underlying brain areas are interacting with each other. Instead, we only know that some interactions likely occur within the duration of the trial if the estimated connectivity is large.

The simplest connectivity feature is the Pearson’s correlation between timeseries between all channel pairs for each trial. The basis of using connectivity for classification is that interactions between brain regions tend to change with different experimental conditions, especially for tasks involving higher cognitive functions (Fries, 2015). A drawback of using Pearson’s correlation is that it is prone to volume conduction-induced false correlations (Bastos and Schoffelen, 2016). Specifically, signals from one source typically propagate to multiple channels, hence inducing false zero-lag correlations between spatially proximal channels (Bastos and Schoffelen, 2016). Since Pearson’s correlation is a zero-lag estimate of connectivity, i.e. temporal offsets between timeseries are ignored, volume conduction-induced false correlations would obscure the differences in connectivity patterns between experimental conditions. Further complexifying this problem is the inter-subject variability in volume conduction resulting from subject differences in brain morphology. The resulting subject-dependent false correlation patterns present a major challenge to pooling data across subjects for classifier learning (Saha and Baumert, 2020). To deal with volume conduction, a number of connectivity estimates have been proposed (Bastos and Schoffelen, 2016). Two of which are discussed next.

2.2.4. Weighted phase lag index

An important property of volume conduction is that channel measurements influenced by the same underlying source would have zero lag, as mentioned in Section 2.2.3 (Bastos and Schoffelen, 2016). Thus, one could deal with volume conduction by using connectivity estimates that are insensitive to zero lag correlation at the expense of discarding real zero lag interactions. One such connectivity estimate is wPLI, which is widely used in EEG research (Imperatori et al., 2019). Estimating wPLI involves first computing the cross-correlation between timeseries of two channels, i.e. correlations at different temporal offsets between the two timeseries. The imaginary component of the cross spectrum density (i.e. the Fourier transform of the cross-correlation) is then averaged over frequencies to estimate wPLI. Since the imaginary part of the cross spectrum density is zero when two timeseries have 0^o phase (i.e. in synchrony with no temporal offset), wPLI is insensitive to zero lag correlations, such as those arising from volume conduction.

2.2.5. Riemannian geometry-based connectivity

The application of Riemannian geometry for EEG connectivity estimation and classification has been proposed (Yger et al., 2017, Yair et al., 2019, Sabbagh et al., 2019) to account for an often-neglected property of Pearson’s correlation matrices, namely that they live in the space of covariance matrices. In vector space, basic operations, such as subtraction between two vectors is their element-wise difference. However, in covariance matrix space, subtraction becomes a nonlinear operation (see Box 1). Since most classifier learning algorithms are built upon basic vector operations, we need to convert covariance matrices into vectors, which is where Riemannian geometry comes into play. In particular, if we subtract a covariance matrix from another covariance matrix using the “proper” subtraction operation for covariance matrix space, elements of the resulting difference matrix live in a vector space. To apply this concept to EEG classification, we first estimate two covariance matrices: one with pre-stimulus time points and another with post-stimulus time points. We then “subtract” the pre-stimulus covariance matrix from the post-stimulus covariance matrix, which has the additional benefit of removing trial-specific attentional drifts and other artifacts captured by the pre-stimulus covariance matrix. A complication is that the frame of reference for subtraction is governed by the pre-stimulus covariance matrices (see Box 1 and Supplementary Materials). Since pre-stimulus covariance matrices vary across trials and subjects due to noise, attention drifts, and natural variability, the frame of reference would be different across trials, hence the resulting difference matrices would not be comparable across trials and subjects. We thus need to bring all difference matrices to a common frame of reference, which has the added benefit of further reducing inter-trial and inter-subject variability. For a more in-depth mathematical description of the Riemannian approach, please see the Supplementary Materials.

Fig. 3.

Euclidean vs. non-Euclidean geometry. (a) In Euclidean space, the shortest distance between two points (red and purple dots) is the length of the straight line (blue dotted line) connecting them. (b) On non-Euclidean curved surface, the shortest distance between two points is the length of the curve (blue dotted curve) connecting them. (c) For points that are close to each other, we can approximate their shortest distance by finding the tangent plane (green rectangular surface) at one point (red dot), projecting the other point (purple dot) onto that tangent plane, and measure their straight-line distance (blue dotted line). We note that the displayed curved surface is for concept illustration purposes only, and does not correspond to the space of covariance matrices, which is a high dimensional cone. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Box 1.

Classifier learning often entails estimation of distance between samples with feature vectors assumed to live in Euclidean space (Sabbagh et al., 2019), where the shortest distance between two samples is the length of the straight line joining them (Fig. 3a). However, covariance matrices live on a non-Euclidean curved surface (positive definite cone to be precise, which is a Riemannian manifold), so the shortest distance between two covariance matrices is not the straight-line distance (Fig. 3b). Nevertheless, a curved surface can be locally approximated by a tangent plane at a given point, i.e. analogous to how the earth is approximately flat locally and thus a local area can be mapped out with a flat 2D map. Therefore, we could estimate shortest distances between nearby points on a curved surface by projecting them to the tangent plane at a given point and computing their straight-line distances (Fig. 3c). This idea can be extended to covariance matrices, which is one of the key components of the Riemannian approach. In contrast to Pearson’s correlation, for each trial, we first estimate two covariance matrices: one with pre-stimulus time points and another with post-stimulus time points. We then “project” the post-stimulus covariance matrix onto the tangent space of the pre-stimulus covariance matrix using an operation called Log map. This projection is equivalent to subtraction in Riemannian geometry, so in effect, trial-specific attentional drifts and other artifacts captured by the pre-stimulus covariance matrix, are removed from the post-stimulus covariance matrix. However, since pre-stimulus covariance matrices typically vary across trials and subjects, the projections would be in different tangent spaces. We thus need to bring all projections to a common tangent space, which can be accomplished using an operation called parallel transport. Bringing all projections to a common space also reduces inter-trial and inter-subject variability.

2.3. Feature selection

Feature selection is often performed prior to classifier learning, especially for datasets where the number of features is orders of magnitude higher than the number of samples. When the number of features exceeds the number of samples, one could always generate an overly complex surface that well divides the training samples of different classes but poorly classifies the test samples (Fig. 4a). Such a surface would likely be fitting measurement noise instead of learning the underlying “concept” that separates the classes. By removing features that show little discriminability, the dimensionality of the space over which we search for the optimal decision boundary would be reduced, which eases the data overfitting problem. A common technique for removing features is univariate feature selection, which involves applying a t-test to training samples of each feature and retaining only those features that pass a certain p-value threshold. A threshold of 0.05 is usually used since features with moderate discriminability when examined in an univariate manner could be useful for classification when combined, and their lower discriminability would be accounted for by lower classifier weights. A problem with using t-test directly is that small perturbations to the data could easily change the selected features in small sample settings. To increase stability of feature selection, resampling is often incorporated, i.e. repeat feature selection with random subsamples of the data and see which features tend to be selected. In this work, we bootstrap the training samples 1000 times, compute the percentage of bootstrap samples for which each feature attains p < 0.05 (this percentage is commonly referred to as the selection frequency), and keep only features with a selection frequency greater than a certain threshold (Fig. 2). We note that the general approach of resampling to find stable features is not restricted to univariate statistical tests. This approach has indeed been applied to many other models, such as sparse regression and sparse graphical models (Sachdeva et al., 2021).

Fig. 4.

Classifier learning. Each dot corresponds to a sample with its class label indicated by the color. Darker and lighter shade corresponds to training and test samples, respectively. (a) In high dimensions, especially when the number of features exceeds the number of samples, using an overly complex function and allowing the classifier weights to take on arbitrarily large values would result in overfitting, i.e. fitting measurement noise, hence would not generalize well to unseen test samples. (b) SVM works by finding training samples that provide the largest margin between the classes. The solid line corresponds to the hyperplane that best separates the training samples under the SVM loss. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

For the choice of selection frequency threshold, we adopt two strategies. First, we use a lenient threshold of 50% and let the process of classifier learning decide which features are less relevant. Second, we use an information criterion specifically designed for SVM (SVMIC) (Claeskens et al., 2008) to select an optimal threshold from a range of thresholds (30–70% at 5% increments). The idea behind using an information criterion is to select a threshold that draws a balance between misclassification rate and number of features used, as described in greater detail in Box 2. Another way to automate the choice of selection frequency threshold is to perform nested cross-validation. Nested cross-validation involves subdividing the training samples of each training fold into internal training and test folds and finding the selection frequency threshold that minimizes the average internal misclassification rate across internal test folds (see (Bishop, 2006) for details). This technique is thus using the generalizability of a classifier on unseen internal test samples as the way to control for overfitting. However, nested cross-validation combined with bootstrapping is often computationally prohibitive.

Box 2.

The idea behind using an information criterion is to select features not only based on misclassification rate but also consider model complexity (often a function of the number of features). The reason is that we can always decrease the misclassification of training samples by increasing the number of features in our classifier model (through lowering the selection frequency threshold) and overfitting the training samples with an overly complex function (Fig. 4a). To apply an information criterion in selecting the optimal selection frequency threshold, we compute its value for each threshold and select the threshold that minimizes the information criterion. This threshold would draw the best balance between misclassification and model complexity. For most information criteria, such as SVMIC, model complexity is approximated as a function of the number of independent features. However, features are often correlated, e.g. due to autocorrelations in timeseries and elements of a covariance matrix are mathematically inter-related (Ng et al., 2016). Hence, approximating the number of independent features by the total number of features used in the classifier often overestimates model complexity.

2.4. Support vector machines

Recall classifier learning can be viewed as finding a curve that well separates two sets of points (Fig. 1). Since infinitely many curves can accomplish this goal, the question is how do we choose the “optimal” curve. To decide on a curve, we need to define what is optimal. For classification, low misclassification rate would be important but this criterion alone is often inadequate to find a generalizable curve, as discussed in Section 2.3. A criterion that constrains model complexity to control overfitting is also needed.

One widely-used classifier that has empirically shown robust performance in low sample-to-feature settings is SVM (Cortes and Vapnik, 1995). SVM finds samples, referred to as support vectors, that maximize the margin between the two classes and generates an optimal hyperplane that lies between the margins (Fig. 4b). This hyperplane can be represented by a classifier weight vector that reflects the relevance of each feature for classification, and the product of a given feature vector by the classifier weights provides a continuous score of the degree to which the corresponding sample belongs to a certain class. Binarization of this score based on its sign provides the predicted class label.

Details on the mathematics of SVM can be found in (Bishop, 2006), and an efficient implementation of SVM is available in MATLAB. In this work, we use fitcsvm.m with its default parameter settings for building SVM. We note that prior to classifier learning, we should normalize the features so that features with larger magnitude do not dominate the classifier learning. Typically, normalization is performed by removing the mean and dividing by the standard deviation of each feature, where the mean and standard deviation are estimated using only training samples to avoid peeking at test samples and introducing correlations between training and test sets, which might bias classification performance (see Section 2.5 for further discussion).

2.5. Classifier evaluation

To evaluate a classifier, we must apply it to test samples not seen during classifier learning to assess its generalizability. Otherwise, we could simply overfit all samples with a complex function to achieve high classification performance (Fig. 4a). We discuss here two scenarios: classifying samples from a single subject and classifying samples from multiple subjects. For the scenario with samples from a single subject, we have to split the samples into a training set for classifier learning and a test set for classifier evaluation. One way of splitting the samples is to apply K-fold cross validation, which proceeds as follows. First, we randomly split the samples into K (approximately) equal folds. We then use e.g. the first K-1 folds for classifier learning and apply the learned classifier to the left out test fold. This procedure is repeated K times with a different left out test fold each time to assess the variability in performance across samples.

As a standard practice, K is often set to 4, 5 or 10, which provides a good balance between computational cost and variability assessment. The exact choice of K depends on the number of samples available. Setting K to 10 allots more samples for training, which might be necessary in small sample settings, i.e. hard to learn generalizable classifiers with too few samples. Another common choice is to set K to the number of samples, i.e. leave-one-out cross validation. However, besides higher computational cost since more classifiers will need to be learned, leave-one-out is more prone to overestimation of performance in the presence of spurious correlations across samples. Specifically, if a test sample is highly correlated with a training sample, then it is similar to having seen this test sample during classifier learning, which biases the classification evaluation. This problem is also present for smaller K, but to a lesser extent since not all samples are mutually and equally correlated with each other in real data. Taking the above example of a highly correlated sample pair, 10-fold cross validation might assign both samples to the test set thus unseen during training, which is not possible with leave-one-out cross validation. Hence, we opt to use K-fold cross validation for classifier evaluation.

For the scenario with samples from multiple subjects, we should perform K-subject-fold cross validation. Specifically, instead of splitting samples into K folds, which would include samples from the same individual in both the training and test folds, we split subjects into K folds, perform classifier learning on samples from training subjects, and apply the classifier on samples from test subjects. This way, correlations between the training and test sets would be alleviated. The assumption is that subjects are not related, which is a typical recruitment criterion. As for the choice of K, we set K between 4 and 10 as opposed to the number of subjects (i.e. leave-one-subject-out) to reduce computational cost.

After splitting samples into training and test sets and predicting the labels of test samples, we need to decide on a metric to evaluate classification performance. Typically, classification accuracy is used, which is defined as the fraction of test samples correctly classified in a given test fold, and we compute accuracy for all test folds to estimate the variability in performance. Alternatively, we can concatenate sample labels of all test folds, estimate a single accuracy value, and repeat K-fold cross-validation multiple times to examine variability in performance. The latter approach has the advantage of considering all samples in estimating accuracy, but empirically, for each run of K-fold cross validation, the single accuracy estimate and the average accuracy over test folds tend to be very similar. We note that in the case of binary classification, if a classifier learns nothing, then it is equivalent to randomly guessing the class labels, i.e. a coin toss, hence chance level accuracy would be 50%. However, given finite samples, the estimated average accuracy across folds might not be exactly 50% for random classification. Hence, standard error of the estimated accuracy should also be considered when evaluating classifier performance.

Another often-used metric for classifier evaluation is area under the receiver operating characteristic curve (AUROC). AUROC is estimated by computing the true positive rate (TPR) and false positive rate (FPR) at various thresholds on the classification scores (i.e. the degree to which samples belong to a given class, see Section 2.4) to generate a ROC. TPR is the number of positive samples correctly labeled as positive by the classifier divided by the number of positive samples in the data, and FPR is the number of negative samples incorrectly labeled as positive by the classifier divided by the number of negative samples in the data. AUROC ranges from 0 to 1 with chance level value being 0.5. The benefit of using AUROC is that it provides a threshold-insensitive metric for classifier evaluation. However, in applications where we need to provide a clear-cut binary label for each sample, we cannot use multiple thresholds and say a sample is class A if we use threshold a and class B if we use threshold b. Instead, we have to use the optimal threshold that best separates the training samples, in which case, accuracy would be more suited as the evaluation metric since it provides a direct assessment of how well the predicted labels based on the optimal threshold match the ground truth labels.

3. Data set

3.1. EEG data collection

EEG data were generated as part of a project looking at age related changes in native phoneme discrimination (see Reh et al., 2021 for a detailed description of the study design). Data from forty 12-month-old infants were used for the present study (20 female, age in days: median = 364, min = 351, max = 418). An additional fourteen infants were tested but excluded due to failure to complete the study (n = 9), parental interference (n = 1), or failure to meet EEG data quality criteria (n = 4). Families were recruited from the Early Developmental Research Group participant database at the University of British Columbia. Parents gave written consent for their infant’s participation. Language exposure was assessed using a modified version of the language exposure questionnaire (Bosch and Sebastián-Gallés, 1997, Byers-Heinlein et al., 2017). Inclusion was restricted to those infants growing up in a monolingual English-speaking environment (defined as having at least 90% English language input). The mean English language exposure was 97%.

During the EEG recording, infants were tested on their ability to discriminate between two native English phonemes, /ra/ vs /la/. Natural tokens of the syllables [ra] and [la] were recorded by a male native English speaker, and a continuum of 200 speech sounds spanning the acoustic space between the two syllables was created using the program TANDEM-STRAIGHT (2008 ICASSP). Two tokens were selected from near the continuum ends for the current study; validation with a group of 10 adult native English speakers confirmed that the syllables were clearly discriminable as /ra/ and /la/ (Reh et al., 2021). Each syllable was 356 msec in duration. Discrimination was assessed using an ERP oddball paradigm, presented via Psychtoolbox-3 in Matlab (Mathworks, Inc.).

During recording, infants were seated on their parent’s lap in a dimly lit, sound attenuated chamber (IAC Acoustics). A single syllable, serving as the standard, was presented in repetition at a rate of 1 Hz. Following at least 4 repetitions of the standard syllable at the start of the experiment, the deviant syllable randomly occurred ~18% of the time, with the caveat that a deviant syllable never immediately followed another deviant. To explore possible directionality effects in discrimination, the deviant was counterbalanced, with half the infants hearing /ra/ as the standard and half hearing /la/. A total of 300 stimuli were presented, lasting approximately 5 min. Auditory stimuli were presented via a Fostex 6301NE speaker at a volume level of 70 dB. During the study, a short cartoon (containing no human characters or mouth movements) was presented on a Samsung 24” LCD monitor positioned in front of the infants to help them stay still and engaged. If excessive movement was disrupting the recording or the infant attempted to pull on the EEG cap, a research assistant blew bubbles to distract the infant. Throughout the experiment, parents listened to masking music through headphones.

Infant electrophysiological responses were measured using a Hydrocel Geodesic 64-channel cap (Philips-Electrical Geodesics, Inc.). To reduce infant fussiness during cap application, the facial channels (61–64) were removed from the cap by the manufacturer. Thus, only channels 1–60 are included in the present dataset. Prior to recording, infants’ head circumference and distance from nasion to inion and ear to ear were measured to select and correctly place the EEG cap. Electrode impedances were measured at or below 50 kΩ. During recording, the EEG data were acquired using the Net Amps 400 amplifier (Philips-Electrical Geodesics, Inc.), sampled at a rate of 1000 Hz and referenced to the vertex (Cz).

3.2. EEG data preprocessing

We opted to perform minimal data cleaning to avoid introducing bias or altering the EEG data in a way that influences the classification performance. Raw EEG data were exported to .mat files and initial preprocessing was executed using BEAPP (Levin et al., 2018). The PrepPipeline toolbox was used to remove line-noise (via the cleanline function (Mullen, 2012)), detect and interpolate bad channels, and re-reference the EEG data to the average reference (Bigdely-Shamlo et al., 2015). To more accurately detect noisy channels, PrepPipeline iteratively alternates between robust average re-referencing and detection and interpolation of bad channels relative to this average reference. Data were discarded if more than 10 channels were identified as bad. Following data re-referencing, the EEG data were bandpass filtered from 0.1 to 100 Hz. BEAPP uses the EEG lab function eegfiltnew, which applies a hamming windowed sinc Finite Impulse Response (FIR) filter to the data. The EEG timeseries were then split into 700 ms long trials, with syllable onset at 100 ms from the beginning of the trial. The length of this time window was informed by univariate analysis, which found evidence for MMR between 200 and 400 ms post-stimulus onset (Reh et al., 2021). A wider window was used to account for individual differences in processing speed. In addition, baseline data was included to provide contrast with the brain response, which could be exploited to improve connectivity estimation (see Section 2.2.5). Trials containing voltage deviations of larger than 200 uV were discarded. The average trial attrition rate was 9%, with a mean of 50 deviant trials retained (min = 35, max = 57). For each subject, the number of standard trials included was matched to the number of deviants to balance the classes. Preprocessed time segments of standard and deviant trials have been made publicly available on Open Science Framework.

4. Results

We applied the presented classification pipelines (see main*.m and riemannian*.m) to EEG data from forty 12-month-old infants to predict whether an infant is hearing a standard vs. a deviant sound in a classical auditory oddball paradigm. For each infant, we paired each deviant trial with the immediately preceding standard trial to ensure balanced classes, resulting in approximately 50 standard trials and 50 deviant trials per infant. We opted to use the immediately preceding standard trial since the noise background of the immediately preceding standard trial would be the most similar to that of the given deviant trial. If deviant stimulus has no effects, this choice of standard trials should make classification most difficult and least biased compared to other choice of standard trials (see Section 5 for discussion on classification bias due to attention drifts and other artifacts). Each trial comprised 700 ms time segments from 60 EEG channels, from which we extracted various features including the timeseries themselves, STFT, Pearson’s correlation, wPLI, and Riemannian geometry-based connectivity. To illustrate the challenges in classifying infant data, we first performed classification using SVM with feature selection on each infant’s data separately, i.e. the case of low SNR and low number of samples. For evaluation, we performed 10-fold cross validation and used accuracy as the evaluation metric. The average accuracy across infants is shown in Fig. 5a (see Fig. 7 for accuracy of each infant). For the majority of infants, the accuracy is 50% or below, which illustrates the difficulty level of this classification task, especially given the low SNR and limited number of samples.

Fig. 5.

Classifier learning with trials from each infant. (a) Average accuracy across infants displayed. Error bars correspond to standard errors. (b) STFT features of all trials projected to 2D space using UMAP (which is similar to principal component analysis for combining features into two dimensions but tends to better highlight clusters) to demonstrate temporal correlations across trials. The number corresponds to trial number and lighter color corresponds to later time in the experiment. A given number would appear twice: one corresponds to standard stimulus, the other corresponds to deviant stimulus. The ellipses are drawn based on the mean and standard deviation of the feature values for every 10 trials in temporal order. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7.

Accuracy breakdown at single infant level. x- and y-axis correspond to accuracy attained with single infant and multi-infant classifier learning, respectively. Each dot represents an infant. The red dotted lines correspond to chancel level accuracy. Dots above the gray dotted line implies increased accuracy with multi-infant classifier learning and vice versa. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

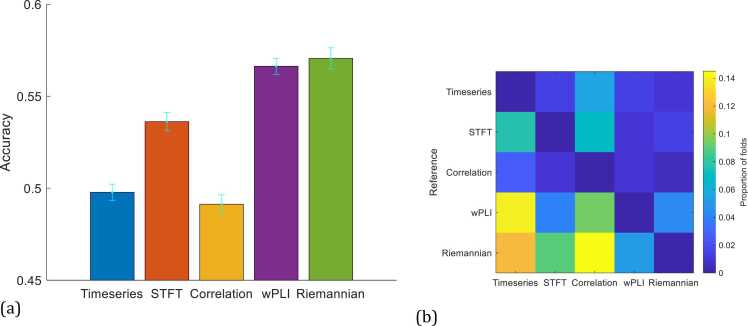
To increase sample size, we pooled data across infants. For evaluation, we again used 10-fold cross validation, but instead of leaving out 10% of the trials, we randomly left out 10% of infants for each fold to avoid correlations between samples in the training and test sets. To illustrate that classification accuracy tends to vary with different infant splits, we explicitly plotted with separate bars results from 5 runs of 10-fold cross validation (Fig. S2). The average accuracy across subject-folds is at chance level for all methods except Riemannian geometry-based connectivity, which is slightly above 50%. This result suggests that increasing sample size alone is inadequate, likely since the SNR is too low for each trial to be classified.

To increase SNR, we adopted the strategy used in traditional EEG analysis, namely averaging the trials of each infant. However, due to attention drifts among other factors, trial averaging could introduce classification bias. In particular, averaging temporally adjacent trials using a sliding window strategy would lead to bias since trials at the beginning of the experiment are quite distinct from those at the end, as shown in Fig. 5b. In particular, temporally-close trials tend to cluster together, which indicates they have similar feature vectors, whereas temporally-distant trials tend to fall in different clusters. Therefore, we opted to average H= 10 trials sampled at an (approximately) uniformly spaced time interval, i.e. deviant trials h, h+ 5, …, h+ 40, and h+ 45 were averaged for h = 1–5, and the same for standard trials. Setting H to 10 reduces the number of trials unused, i.e. 50 mod 10 = 0. Average accuracy over 20 runs of 10-fold cross-validation with H set to 10 is shown in Fig. 6a. We note that only the Riemannian approach benefited from using SVMIC to choose the optimal selection frequency threshold (Fig. S3). The reason is due to the need for estimating the number of independent features when using SVMIC (see Box 2). Specifically, bringing covariance matrices to vector space has the effect of decoupling the connectivity features (Ng et al., 2016). Hence, the number of Riemannian geometry-based connectivity features would be a closer estimate of the number of independent features compared to the contrasted features. In particular, timeseries and STFT are prone to correlation between nearby time points. Elements of Pearson’s correlation matrices are mathematically inter-related (Ng et al., 2016), and the same goes for cross spectral density matrices, which are intermediaries of wPLI estimation. Therefore, we report accuracy based on using SVMIC for only the Riemannian approach. We also note that the other option for H is to set it to 5, but was empirically found to provide inadequate SNR for classification (Fig. S4). Further, we tested 4-fold cross-validation (Fig. S5), which resulted in similar accuracy for timeseries, lower accuracy for STFT, wPLI, and the Riemannian approach, and higher accuracy for Pearson’s correlation but still near chance level. The reason for the decrease in accuracy with 4-fold cross-validation was likely due to fewer training samples per fold for classifier learning.

Fig. 6.

Classifier learning with trials pooled across infants. (a) Average accuracy over 20 runs of 10-fold cross validations displayed. Error bars correspond to standard errors across runs. (b) McNemar’s test is applied to each left out fold to test if labels of each reference method is significantly more accurate than the other methods. The proportion of folds across the 20 runs that are significantly more accurate with the reference method are displayed.

With trial averaging and data pooled across infants, average classification accuracy rose above chance level for some of the features (Fig. 6a). While the average accuracy across 20 runs of 10-fold cross validations remained at chance level with timeseries as features, average accuracy of STFT increased to 54%. The accuracy with using Pearson’s correlation remained slightly below chance level likely due to volume conduction differences across infants overwhelming the connectivity patterns, whereas using wPLI, which is insensitive to volume conduction, achieved an average accuracy of 57%. Using Riemannian geometry-based connectivity also achieved an average accuracy of 57%, demonstrating benefits of accounting for attention drifts and inter-subject variability. To test whether accuracy is statistically above chance level, we applied Fisher’s Exact test to the test folds of each run with the ground truth class labels as the reference, and computed the proportion of test folds that are significant at p < 0.05. For timeseries and Pearson’s correlation, 0% of the test folds were significant. In contrast, 35%, 85%, and 45% of the test folds have accuracy significantly above chance for STFT, wPLI, and the Riemannian approach, respectively. Further, to assess whether the increased accuracy with wPLI and the Riemannian approach are statistically significant, we applied McNemar’s test to each test fold of each run, and computed the proportion of test folds for which the increased accuracy is significant at p < 0.05. wPLI and the Riemannian approach are significantly more accurate than timeseries, STFT, and Pearson’s correlation for 9% and 12% of test folds, respectively, on average (Fig. 6b). The low proportion of test folds deemed significant was likely due to the low number of samples in each test fold for applying McNemar’s test. We note that Wilcoxon sign rank test is also widely-used for comparing accuracy across methods. This approach involves either taking the accuracy of each fold as a sample or taking the average accuracy of each run of K-fold cross-validation as a sample. However, the correlation across folds and runs of K-fold cross-validation violates the independent sample assumption in applying Wilcoxon sign rank test, hence the p-values would be underestimated. Indeed, standard errors of the accuracy estimates (i.e. error bars in Fig. 6a) are also underestimated due to correlation across folds and runs, hence why we applied Fisher Exact test to the test folds of each run to assess whether accuracy is significantly above chance level.

We further assessed the performance of multi-infant classifier learning at the individual infant level by extracting the predicted trial labels of each infant and estimating a separate accuracy value for each infant (i.e. instead of averaging accuracy across subject-folds). Except for using Pearson’s correlation, classifier learning with trials pooled across infants substantially increased accuracy over classifier learning with trials from each infant (Fig. 7). Importantly, the proportion of infants with accuracy above chancel level increased from 0.4 to 0.75 for wPLI, and 0.55 to 0.80 for Riemannian-based connectivity features, demonstrating the benefits of pooling trials across infants, provided that volume conduction and other sources of inter-subject variability are properly accounted for.

5. Discussion

We described in this introductory ML tutorial the steps involved in classifying infant EEG data, namely feature extraction, feature selection, classifier learning, and classifier evaluation. Applying the described pipeline achieved above chance level accuracy on a difficult task, namely separating infant neural responses to rare vs. frequent auditory stimuli. While similar studies have been carried out with data from adults (Brandmeyer et al., 2013), this work is, to our knowledge, the first demonstration of MMR classification with infant data. Average classification accuracy, while not high, was above chance, which is consistent with accuracy levels seen in previous infant EEG studies (Bayet et al., 2020). For the current task of MMR classification, wPLI and the Riemannian approach achieved the best classification performance, attaining an average accuracy of 57%. Also, the proportion of infants with above chance classification accuracy was > 75%, which is quite high and similar to that reported in infant fNIRS studies (Emberson et al., 2017). Considering the computational cost, if the goal is to test whether connectivity can distinguish different experimental conditions, we would recommend testing wPLI first, which is faster to compute and focuses on non-zero-lag similarity between EEG timeseries hence insensitive to volume conduction. If accuracy is insufficient, then the Riemannian approach could be explored. Although the Riemannian approach only estimates zero-lag correlation, it implicitly accounts for volume conduction and explicitly accounts for trial-specific confounds as well as inter-trial and inter-subject variability (Sabbagh et al., 2020).

Infant data have certain characteristics that make application of ML difficult, namely the relatively low SNR, low number of trials per infant, high inter-subject variability, and high inter-trial variability. We outlined strategies to address each of the above issues, but steps taken to reduce one problem may exacerbate another. For example, averaging trials improves SNR but at the expense of lowering the number of trials. Nonetheless, with the “right” balance, we found that incorporating some trial averaging does improve performance for the current classification task. Previous work on infant classification used a similar approach (Bayet et al., 2020; Gennari et al., 2020), suggesting that trial averaging could be beneficial to deal with the amount of noise in typical infant EEG data.

To deal with the low number of trials per infant, we pooled trials across infants. However, inter-subject variability, which is especially high in infant data due to differences in brain maturation and morphology during development (Gao et al., 2014), might obscure the discriminative EEG patterns. Particular to the current classification task, the MMR, also termed the mismatch negativity due to the negative voltage observed in adults (Näätänen et al., 2019), has a positive voltage in early infancy (Dehaene-Lambertz and Gliga, 2004). Studies suggest that this voltage switch is dependent on both brain maturation (Trainor et al., 2004, Kushnerenko et al., 2007, Cheng et al., 2013) and the difficulty of the experimental task (Cheng et al., 2015). Hence, an infant may display either a positive or negative mismatch response, which might explain the small number of infants for which accuracy was actually higher with classifiers learned from their own trials without pooling (see Fig. 6). Nevertheless, by accounting for inter-subject variability using wPLI and parallel transport, pooling trials across infants provided higher accuracy on average.

In addition to inter-subject variability, we must contend with high inter-trial variability in infant EEG data. The timing of stimulus-driven brain activity is less precise in infancy. Typically, infants have greater variability in response onset and duration than adults (de Haan, 2007). Over the first year of life, as myelination increases and neuronal response properties become increasingly selective, responses become more stereotyped. However, a large degree of inter-trial variability remains even in adult data. This inter-trial variability is another reason why averaging trials helps improve classifier performance.

Accuracy for single infant classifier learning was below chance on average, suggesting that the classifier discovered non-random patterns in the trials that led to misclassification. In particular, EEG timeseries are autocorrelated (Linkenkaer-Hansen et al., 2001), and the amount of autocorrelations might be exacerbated in infant data due to more attention drifts, habituation to the stimuli, and changes in SNR resulting from increased infant movements and fussiness over time. Thus, temporally adjacent trials might mistakenly get classified to the same class even when they belong to different classes (Li et al., 2020). In fact, trials being not truly independent presents a potential pitfall in EEG classification. As seen in Fig. 4b, trials are clustered by their temporal order within the experiment. If two sets of stimuli are presented one after the other instead of being interspersed, a classifier might use temporal order instead of stimulus-induced response patterns to separate the trials (Li et al., 2020). Hence, careful experimental design is needed to reduce the effects of correlated samples on classification.

Given the complexity of cognition, any of the described features (and many more) could contain information required to classify different stimuli. In the case of the MMR, its neural underpinnings have been extensively explored. Previous studies have shown differences in the timeseries domain (with the classic ERP description of the mismatch negativity) (Näätänen et al., 2019), changes in oscillatory activity (Fuentemilla et al., 2008, Hsiao et al., 2009), and differences in connectivity between brain regions (Hsiao et al., 2009, Mamashli et al., 2019). Each of these features enables us to examine neural processes from a different angle, and their relative performance partly depends on the classification task and partly depends on which confounds dominate. For example, timeseries over short windows would be well suited for stimuli that evoke rapid responses, and Pearson’s correlation would not be suited if large inter-subject variability in volume conduction patterns is present. Important to note is that features failing to classify (as was the case here for timeseries) does not imply that those features are not relevant for the given cognitive task (i.e. we should not accept the null). Rather, discriminant patterns in those features could be obscured by noise.

While the described classification pipeline does not reveal the specific time points or connections that support classification, a number of follow-up analyses can be performed to address this question. For example, one can permute the class labels to generate a null distribution for each feature’s classifier weight, and check which features have classifier weights (without label permutation) significantly higher than their respective null. In fact, techniques for estimating p-values under the classification setting without label permutation have been proposed (Taylor and Tibshirani, 2018; Candès et al., 2018). Also, specific to using timeseries as features, one could perform time-resolved classification to determine when classes become distinguishable (Grootswagers et al., 2017) as well as test if a classifier trained on one time point can generalize to other time points to gain insights on whether certain activity patterns recur in time (Kim et al., 2014).

Another approach to gain insights from classification results involves correlating accuracy with behavioral scores as well as contrasting accuracy across groups. This approach has been used in adults to examine how phoneme processing is influenced by language background (Brandmeyer et al., 2013). The results of this study revealed that, despite a high level of English proficiency and experience, classification accuracy for English phonetic contrasts was lower for native Dutch speakers than English speakers across all contrast difficulties, highlighting the importance of early language experience on the tuning of phoneme representations.

Further, insights into cognitive processes can be drawn from carefully designed experiments. While we focused on binary classification, classification over additional stimulus categories (N-way classification) can provide further insights into infants’ mental operations. For example, studies with adults have classified the entire phoneme space (Moses et al., 2016). Using a confusion matrix, one can visualize the pattern of mistakes made by the classifier, e.g. if the classifier is more likely to incorrectly classify phonemes with similar articulatory dynamics (i.e. to confuse a stop consonant ‘b’ for another stop ‘d’, as opposed to a fricative ‘f’). The underlying assumption is that classification accuracy will decrease for stimuli with similar neural representations. This is the core idea behind representational similarity analysis (Kriegeskorte et al., 2008), which has been used to explore categorical representation in the brain (e.g. for object recognition (Kaneshiro et al., 2015)).

Moreover, one could gain insights by investigating a classifier’s generalizability to unseen classes. In this case, either binary or N-way classification can be used to train a classifier on EEG data in response to a given stimulus set. The trained classifier is then tested on data from a different stimulus set, to see how well the classifier generalizes to the new stimuli. This strategy can be used to determine whether classification patterns are being driven by perceptual properties that are unique to a given stimulus set, or by more abstract properties (e.g. category membership, articulatory dynamics, etc). For example, if a classifier trained to categorize EEG data evoked by ‘b’ and ‘d’ is able to accurately classify data evoked by the stimuli ‘m’ and ‘n’, it suggests that the brain encodes information at the level of the place of articulation (Gennari et al., 2021).

To conclude, ML enables many new questions to be addressed. Instead of asking simply whether the EEG response to A differs significantly from the EEG response to B at any given channel or cluster of channels using standard group analysis, one can investigate whether the mental representations (captured by the EEG response patterns as a whole) contain information to distinguish different stimuli. In addition, one can explore how experience shapes these representations. For example, the above chance accuracy with multi-infant classifier learning provides evidence that infants share a common underlying EEG activity pattern in response to an auditory MMR. This in itself is not a surprise, given the extensive work on the MMR in infants and adults (Näätänen et al., 2019). However, the question becomes more interesting when considering the language domain more broadly. The current data set contains only data collected from infants growing up in a monolingual English-speaking environment. With the presented classification pipelines, one could probe how well the classifiers trained with data from this cohort are able to classify data from infants growing up in either bilingual households or in a different language environment entirely (e.g., Japanese where /ra/ vs /la/ are not distinguished). In addition, one can look at these questions from a developmental perspective, and begin to explore if, and when, during language development these representations begin to diverge for infants growing up in different language environments. ML thus provides the developmental cognitive neuroscience community new tools to answer questions beyond those possible with traditional group analysis.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material.

Data Availability

Data and code associated with this manuscript have been made publicly available on Open Science Framework using the following link: https://osf.io/vckms/?view_only=e77dc6e260a749d9b6f0d5181e9c8d3b.