Training gamblers to re-think their gambling choices: How contextual analytical thinking may be useful in promoting safer gambling

Abstract

Background and aims

Harmful gambling has been associated with the endorsement of fallacious cognitions that promote excessive consumption. These types of beliefs stem from intuitively derived assumptions about gambling that are fostered by fast-thinking and a lack of objective, critical thought. The current paper details an experiment designed to test whether a four-week online intervention to strengthen contextual analytical thinking in gamblers is effective in changing gamblers cognitions and encouraging safer gambling consumption.

Methods

Ninety-four regular gamblers who reported experiencing gambling-related harm were randomly allocated to either an experimental (n = 46) or control condition (n = 48), including 45 males, ranging from 19 to 65 years of age (M = 36.61; SD = 9.76). Following baseline measurement of gambling beliefs and prior week gambling consumption, participants in the experimental condition were required to complete an adaption of the Gamblers Fallacy Questionnaire designed to promote analytical thinking by educating participants on common judgement errors specific to gambling once a week for four weeks. Post-intervention measures of beliefs and gambling consumption were captured in week five.

Results

The experimental condition reported significantly fewer erroneous cognitions, greater endorsement of protective cognitions, and reduced time spent gambling post-intervention compared to baseline. The control group also reported a reduction in cognitions relating to predicting and controlling gambling outcomes.

Conclusion

Cognitive interventions that encourage gamblers to challenge gambling beliefs by reflecting on gambling involvement and promoting critical thinking may be an effective tool for reducing the time people invest in gambling activities.

Introduction

Gamblers endorse a variety of cognitive distortions that promote risky or excessive gambling (Blaszczynski & Nower, 2002; Goodie & Fortune, 2013; Miller & Currie, 2008). The types of beliefs people have and the strength with which they endorse them are related to a person's preferred style of thinking (Aarnio & Lindeman, 2005; Bloom & Weisberg, 2007; Gervais, 2015; Pennycook, Cheyne, Seli, Koehler, & Fugelsang, 2012; Swami, Voracek, Stieger, Tran, & Furnham, 2014; Willard & Norenzayan, 2013). Gamblers are more likely to demonstrate a preference for intuitively driven decision-making over more reflective or deliberative processing methods (Armstrong, Rockloff, Browne, & Blaszczynski, 2019a; Cosenza, Ciccarelli, & Nigro, 2019; Emond & Marmurek, 2010), and as a result, tend to make decisions using mental processing shortcuts that appear to be designed to generate responses quickly and effortlessly (Epstein, 2008; Hammond, 1996; Kahneman, 2003; Sadler-Smith & Shefy, 2004; Sadler-Smith, Zhang, & Sternberg, 2009). When applied to gambling, fast-intuitive thinking and a lack of critical reflection can impair judgement by strengthening the endorsement of erroneous gambling cognitions, that in turn contribute to poor gambling decisions (Armstrong, Rockloff, & Browne, 2020; Armstrong, Rockloff, Browne, & Blaszczynski, 2020; Cosenza, Ciccarelli, & Nigro, 2019; Emond & Marmurek, 2010; Leonard, 2018).

A number of studies exploring non-evidence based beliefs have found that priming analytical thinking can weaken the strength with which beliefs are endorsed (Gervais & Norenzayan, 2012; Paxton, Ungar, & Greene, 2012; Swami, Pietschnig, Stieger, & Voracek, 2011; Swami, Voracek, Stieger, Tran, & Furnham, 2014; Uhlmann, Poehlman, Tannenbaum, & Bargh, 2011). However, when applied to gambling, similar primes have failed to reduce cognitive distortions amongst gamblers (Armstrong, Rockloff, Browne, & Blaszczynski, 2019, b). In fact, Armstrong et al. (2019b) found that generalised analytic priming that involved a scrambled sentence task using keywords that facilitate analytical thinking (e.g., analyse, reason, ponder, think, rational) was counterproductive and actually increased positive gambling expectancies compared to a control condition. In some cases, gamblers may use analytical thinking to generate false narratives that justify gambling decisions, rather than seeking evidence to invalidate them (Armstrong et al., 2019b; Boudry & Braeckman, 2012; Ellerby & Tunney, 2017; Kahan, 2018).

Designing an effective intervention that neutralises the formation and reinforcement of biased gambling cognitions, and that can be implemented beyond a clinical setting, is likely to be challenging. Given the tendency for gamblers to use critical or elaborative thinking in a way that rationalises or justifies poor gambling choices (Armstrong et al., 2019b; Boudry & Braeckman, 2012; Ellerby & Tunney, 2017; Kahan, 2018), interventions designed to encourage analytical thinking must be designed with care to avoid being counterproductive. The task must elicit strong cues to the underlying rules associated with the problem, and increase vigilance in monitoring or deciphering the correct response (Kahneman, 2003). For example, simply altering the framing of a task (e.g., a statistical test rather than a lottery) is enough to cue underlying rules at play and generate greater vigilance, resulting in stronger analytical responses (Kogler & Kühberger, 2007). Interventions that are contextually relevant and serve to illustrate how gamblers are “tricked” into making biased decisions may be more effective in altering people's gambling cognitions, and in turn, their gambling behaviour (Houdé et al., 2000).

Previous research exploring the effectiveness of long-term training in gambling odds and probability was ineffective in generating behavioural changes (Williams & Connolly, 2006). This may be in part due to the nature of the training and sample characteristics. The training involved using gambling examples and themes in the provision of an education program teaching probability and odds. The aim was for students to learn the statistical nature of gambling rather than apply this learning to a gambling context. The sample consisted of university students, and while 71% reported to have gambled in the previous 6 months, majority of these had spent little time and money doing so and thus had no real motivation or reason to change their gambling behaviour.

The current paper describes the results of an experimental study exploring the effectiveness of a four-week online intervention designed to encourage gamblers to apply rational thought and statistical knowledge to overcome common gambling biases. The purpose was to determine whether training gamblers to think more analytically by solving a series of questions relating to common gambling biases developed based on the Gamblers Fallacy Questionnaire (Leonard, Williams, & Vokey, 2015) and providing performance-based feedback would be effective in reducing gambling related cognitive distortions, and subsequently, decrease real-world gambling consumption amongst regular gamblers who experience gambling related harm. It was hypothesised that gamblers in the experimental condition would report fewer erroneous and more protective gambling beliefs and have lower real-world gambling consumption at the post-intervention follow-up compared to baseline and the control condition.

Method

Participants

A brief survey screen was released via online resource provider, Mechanical Turk, to respondents with hit approval rates of >96% and a minimum of 500 completed hits. To be included in the study, participants were required to provide informed consent, be over 18 years and reside in the United States, have gambled at least weekly on any form of gambling in the past 6 months (excluding lotteries, instant scratch tickets, or raffles), and score a 1+ on The Short Gambling Harms Screen (Browne, Goodwin, & Rockloff, 2018). Participants who met the inclusion criteria were then randomly allocated to either a control or experimental condition. Of the 445 workers who completed the screening survey, 180 gamblers met the inclusion criteria, with 150 continuing to complete the baseline survey. Thirty-five cases were removed for having multiple entries or incomplete responses to the baseline survey, and 21 were removed due to attrition (failing to complete at least two of the weekly surveys or the post-intervention survey).

The final sample consisted of 94 participants (46 experimental; 48 controls), 45 males and 48 females (1 case identified as “other”), ranging from 19 to 65 years of age (M = 36.61; SD = 9.76). The majority of participants were employed full time or self-employed (78.2%, 11%; respectively), most had either a bachelors degree (34.7%) or completed some college but had no degree (24.8%); and had a median personal annual income of between $600 and $799 USD (21%).

Based on responses to the Problem Gambling Severity Index (PGSI; Ferris & Wynne, 2001), 46% met the criteria for problem gambling, 29% for moderate-risk gambling and 9% and 10% were classified as low-risk or non-problem gamblers, respectively. Seventy-three participants (77.6%) exceeded the threshold for safe gambling consumption as measured by the Consumption Screen of Problem Gambling (score of 4+; Rockloff, 2012); and reported experiencing on average 6.43 gambling harms out of the 10 captured by the SGHS (SD = 2.69; Browne et al., 2018). The most popular form of gambling was electronic gaming machines (EGMs; 32.9%), followed by sports betting (21.2%), blackjack (17.1%) and poker (16%). EGMs were also the mode of gambling on which players spent the most time (31%), and money (30.9%).

Measures

Gambling beliefs

The Gambling Related Cognition Scale (GRCS; Raylu & Oei, 2004) and the Protective Gambling Beliefs Scale (PGBS; Armstrong et al., 2019a) were used to measure participants cognitions about gambling. The GRCS requires participants to rate their level of agreement to 23 items on a 7-point Likert scale and provides five subscale scores that capture erroneous beliefs or cognitions: an illusion of control (IC), interpretive bias (IB), predictive control (PC), gambling-related expectancies (GE), and perceived inability to stop gambling (IS). Cronbach alpha for the 23 items (or total GRCS score) was 0.93.

The PGBS is a 10 item scale measuring participants level of agreement on a 4-point scale to statements concerning protective cognitions about gambling, including: gambling expectancies, the role of personal skill, and the nature of chance and probability. Cronbach alpha for the 10 PGBS items was 0.87.

Prior week gambling

Questions regarding prior week gambling asked participants to report the amount of time (hours and minutes) and money (USD) they spent gambling in the week prior to the survey and during a typical gambling session that same week.

Procedure

The study consisted of six waves of data collection, including baseline (week 0), 4× weekly surveys (week 1–4), and a post-intervention phase (week 5). The baseline survey was designed to capture pre-intervention measures of gambling beliefs and gambling participation, as well as broader gambling involvement (problem gambling severity, gambling consumption, and gambling preferences) and demographics (age and gender). Following survey questions, the participants were presented with the first intervention task. The task varied depending on condition allocation during the screening phase of the study.

The experimental condition involved completion of an analytical training task designed to educate participants on common judgement errors specific to gambling. The intervention task was an extended form of the Gambler's Fallacy Questionnaire (Leonard et al., 2015), which traditionally consists of ten multiple choice questions designed to tap into common fallacies associated with gambling. An additional 40 items were developed that challenged people's knowledge of these common gambling fallacies based on the original GFQ items (see Appendix A). Each intervention task consisted of ten items, requiring participants to select the correct response from several possibilities. Immediately following their response, participants were provided performance-based feedback informing them of whether they were correct and providing a detailed explanation of the reason(s) underlying the correct response. Once all questions had been attempted, they were given the opportunity to revisit the questions they answered incorrectly to provide a revised answer based on the feedback they had received.

The control group also received a set of ten questions; however, their questions assessed knowledge of general gambling trivia (see Appendix B). Determining a correct response on the general gambling trivia questions only requires memory retrieval of factual knowledge, and thus presumably does not activate the same cognitive processes as tasks that require insight and problem solving skills (Cabeza, Dolcos, Graham, & Nyberg, 2002; Metcalfe, 1986). Participants in the control condition were not provided any feedback (performance based or otherwise) on the general trivia questions/answers, and thus, the task should not have elicited analytically driven cognitive processing.

The weekly surveys were administered one week following baseline (week 1–4). The weekly surveys measured participants prior week gambling involvement and provided them with the relevant task depending on condition allocation (i.e., either the extended GFQ, or Gambling-trivia). In week five, participants received the post intervention survey which re-assessed participants gambling beliefs and prior week gambling, as well as some sociodemographic characteristics. Participants were encouraged to complete all surveys within 48 hours of being made available to minimise potential overlap in reports of prior week gambling. Those who had not completed the survey within the first 24 hours (approximately) were prompted with a reminder message. Participants received monetary compensation based on the length of each survey, with longer surveys (baseline and week five) offering greater incentives. Data collection commenced August 2019 and finished in September 2019.

Statistical analysis

The experiment was designed to test the impact of an analytic training task on gambling beliefs and gambling intensity. It was hypothesised that those who received the analytical training task would report fewer erroneous and more protective cognitions, and reduced gambling consumption (measured by a decrease in time and money spent gambling). Based on these predictions, the purpose of the analyses were twofold: a) to determine the extent to which the experimental manipulation changed the outcome variables from baseline (week 0) to post-intervention (week 5); and b) to compare the control and experimental conditions on the extent of change experienced during the experimental period of the study. As groups did not differ significantly in gambling beliefs or intensity at baseline, to test the latter, a difference variable was calculated for each outcome measure. This was calculated by subtracting week 5 scores from those obtained at baseline. Supplementary analyses explored changes in the 10 difference variables by PGSI category (problem versus moderate/low risk), but found no significant variation in change by group, P > 0.05, ns.

Ethics

The study procedures were carried out in accordance with the Declaration of Helsinki and granted formal ethics approval by Central Queensland University's Human Research Ethics Committee. All subjects were informed about the study and all provided informed consent.

Results

Gambling beliefs

A series of paired sample t-tests were conducted for each condition to compare baseline and week five measures of gambling beliefs. It was expected that the experimental condition would report fewer erroneous beliefs and more protective gambling beliefs at week five compared to baseline. As gambling beliefs are theoretically (and statistically) inter-related, a Bonferroni correction was applied to adjust for multiple related comparisons by dividing the P value of 0.05 by the number of comparisons being made (.05/6). The adjusted critical P value applied was 0.008.

As expected, the experimental condition had significant lower scores for: illusion of control, t (46) = 4.17, P < 0.001; interpretive bias, t (46) = 4.44, P < 0.001; predictive control, t (46) = 4.90, P < 0.001; inability to stop, t (46) = 2.88, P = 0.003; and protective gambling beliefs, t (46) = −2.39, P < 0.001. However, compared to baseline, the control condition also scored significantly lower on measures of illusion of control, t (48) = 3.54, P < 0.001; and predictive control, t (48) = 2.97, P = 0.002, at the week 5 follow-up. Table 1 presents the descriptive statistics and results of the paired sample t-tests for measures of gambling beliefs for each condition.

Table 1.

Descriptive statistics and Test of Equality for baseline and week five measures of gambling beliefs by experimental condition

		Baseline		Week 5		Test of equality
		M	SE	M	SE	t	M diff	SE diff	P
Control	IC	15.50	1.06	12.67	1.06	3.54	2.83	0.80	<0.001*
	IB	20.37	0.87	18.67	0.83	2.34	1.70	0.72	0.011
	PC	27.18	1.01	24.92	1.21	2.97	2.27	0.76	0.002*
	GE	20.25	0.72	18.97	0.83	1.80	1.27	0.70	0.039
	IS	16.92	1.20	15.25	1.25	1.96	1.67	0.86	0.028
	PGBS	27.90	0.90	29.20	0.87	−1.53	−1.31	0.86	0.066
Experimental	IC	14.00	0.99	11.30	1.01	4.17	2.69	0.64	<0.001**
	IB	19.58	0.64	16.53	0.74	4.44	3.06	0.69	<0.001**
	PC	24.89	1.27	20.47	1.12	4.90	4.41	0.90	<0.001**
	GE	19.77	0.65	19.06	0.59	1.34	0.69	0.51	0.092
	IS	16.94	1.23	14.56	1.08	2.88	2.37	0.83	0.003*
	PGBS	28.79	0.80	31.18	0.74	−4.02	−2.39	0.59	<0.001**

Note: Control n = 48, df = 47; Experimental n = 46, df = 45. *P < 0.008, **P < 0.001 (1-tailed).

A Multivariate Analysis of Variance (MANOVA) was conducted to determine whether differences exist between the control and experimental condition in belief change from baseline to week five comparing difference variables. We expected that the experimental condition would report greater changes in gambling beliefs compared to the control condition from baseline to week five. Results showed there were no significant differences between experimental conditions for any changes in beliefs from baseline to week 5, except for predictive control. The experimental condition experienced a significantly greater change in scores for predictive control compared to the control condition, F (1.92) = 3.30, P = 0.036. Table 2 presents the MANOVA and descriptive statistics for difference variables for each condition.

Table 2.

MANOVA results comparing belief change by condition

	Multivariate		Univariate
	V	F		IC	IB	PC	GE	IS	PGBS
Condition	0.091	1.32		0.02	1.82	3.30	0.43	0.35	1.05
			P	0.447	0.090	0.037*	0.258	0.277	0.154
Control			M	2.83 (0.80)	1.70 (0.72)	2.28 (0.76)	1.28 (0.70)	1.67 (0.86)	−1.31 (0.86)
			(SE)
Experimental			M	2.70 (0.64)	3.06 (0.69)	4.41 (0.90)	0.70	2.37 (0.83)	−2.39 (0.59)
			(SE)				(0.51

Note: Control n = 48; Experimental n = 46; Multivariate sourced from Roys largest root, df 6, 87; Univariate df 1.92. *P < 0.05 (1-tailed).

Gambling intensity

Listwise deletion was used for values outside three times the standard deviation that were found to be incompatible when compared to other responses. Gambling intensity measures were highly positively skewed and could not be adequately corrected through transformation. Each outcome: minutes per week gambling, minutes gambling in a typical session, dollars spent per week gambling and dollars spent gambling in a typical session, were therefore analysed using nonparametric tests.

It was expected that the experimental condition would report lower gambling intensity at week five compared to baseline, and that changes in gambling intensity would be significantly greater in the experimental condition compared to controls. To determine whether gambling intensity changed from baseline to week five, a series of Related Samples Wilcoxon Signed Rank Tests were conducted for each condition. Mann-Whitney U Tests were used to test whether the degree of change between baseline and week five significantly differed between conditions for each gambling intensity outcome. As gambling intensity measures are likely to be related, a Bonferroni correction was applied (0.05/4) resulting in an adjusted critical P value of 0.012. Table 3 presents the descriptive statistics for gambling intensity measures.

Table 3.

Descriptive statistics for baseline and week five measures of gambling intensity by experimental condition

		Baseline				Week 5				Difference
		M	SE	Mdn	Range	M	SE	Mdn	Range	M	SE
Control	MPWG	223.25	22.10	215.00	600	190.22	23.85	165	650	14.96	29.04
	MGTS	93.20	8.36	90.00	250	91.56	10.01	90.00	245	−1.40	11.41
	DSPW	176.30	40.32	100.00	1,400	206.98	37.87	92.50	1,000	4.25	54.28
	DSTS	85.95	19.70	47.50	700	95.93	18.71	60	600	−8.35	26.35
Experimental	MPWG	230.83	32.44	180	750	163.21	23.57	130	720	66.22	24.09
	MGTS	109.33	12.83	97.50	360	76.30	11.48	60.00	300	33.03	15.59
	DSPW	159.45	29.50	80.00	700	166.50	39.79	50	1,000	−10.31	31.79
	DSTS	94.43	18.08	50	500	72.86	22.36	32.50	900	20.78	16.68

Note: Control n = 44, Experimental n = 42; Minutes per week gambling (MPWG); Minutes spent gambling in a typical session (MGTS); Dollars spent per week gambling (DSPW); Dollars spent gambling in a typical session (DSTS).

Minutes per week gambling

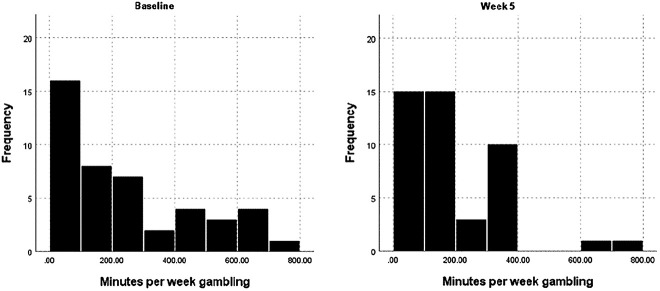
In the control condition, there were no significant differences between baseline and week 5 for minutes per week gambling, Z = −1.37, P = 0.085 (1-tailed). As expected, there was a significant difference in minutes per week gambling from baseline to week 5 for the experimental condition, Z = −2.47, P = 0.006 (1-tailed). Figure 1 below illustrates the frequency distribution of minutes per week gambling for the experimental condition at baseline and week five.

Fig. 1.

Minutes per week gambling frequency distribution for baseline and week five, experimental condition (n = 45)

A Mann-Whitney U Test was used to determine whether there were differences between the experimental and control condition for changes in minutes per week gambling over the experimental period. However, the result was non-significant, Z = 0.28, P = 0.387 (1-tailed).

Minutes gambling in a typical session

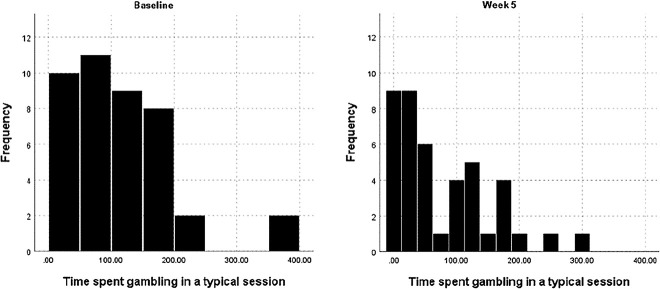
There were no significant differences between baseline and week 5 scores for minutes spent gambling in a typical gambling session for the control condition, Z = 0.02, P = 0.492 (1-tailed). However, as expected, the experimental condition spent significantly less time gambling at week 5 compared to baseline during a typical gambling session, Z = −2.57, P = 0.005 (1-tailed). Figure 2 below illustrates the frequency distribution of minutes spent gambling in a typical session for the experimental condition at baseline and week 5.

Fig. 2.

Minutes spent gambling on a typical session frequency distribution for baseline and week five, experimental condition (n = 42)

Results of a Mann-Whitney U Test showed there were no significant difference between the experimental and control condition for changes in minutes spent gambling in a typical session across the experimental period, Z = 1.68, P = 0.046 (1-tailed).

Dollars spent per week gambling

There were no significant differences in the total amount spent per week gambling between baseline and week 5 for the control condition, Z = 0.81, P = 0.210 (1-tailed), or the experimental condition, Z = 0.19, P = 0.422 (1-tailed).

A Mann-Whitney U Test demonstrated there was no significant difference between the experimental and control condition for changes in the total amount spent gambling per week across the experimental period, Z = 0.89, P = 0.187 (1-tailed).

Dollars spent gambling in a typical session

There were no significant differences in the amount spent on a typical gambling session between baseline and week 5 for the control condition, Z = 0.51, P = 0.306 (1-tailed), or the experimental condition, Z = −1.57, P = 0.058 (1-tailed).

Results of a Mann-Whitney U Test showed there were no significant difference between the experimental and control conditions in changes to the amount spent during a typical gambling session, Z = 1.56, P = 0.059 (1-tailed).

Discussion

The purpose of this study was to determine whether an online intervention designed to encourage analytical thinking and expose common gambling fallacies would be effective in generating more rational cognitions, reducing gambling intensity. While the intervention was successful in reducing erroneous beliefs across 4 of the 5 GRCS scales (illusion of control, predictive control, interpretive bias, inability to stop) and improving protective cognitions post-intervention, both conditions demonstrated fewer beliefs relating to predictive and illusionary control across the experimental phase. This change was significantly greater for the experimental group. These results suggest that the intervention: 1) made for stronger changes to beliefs relating to predictive control compared to the control group; 2) reduced endorsement of other erroneous cognitions (e.g., inability to stop gambling and interpretation of gambling outcomes; and 3) promoted safer cognitions about gambling.

Despite non-significant results for monetary expenditure, the intervention was effective in reducing the amount of time people spent gambling compared to baseline, however, changes in time spent gambling were not significantly different when comparing controls to the experimental condition. Prolonged training that challenges gambling fallacies may cause people to question their gambling choices, making gambling less enjoyable (Lin, Hung, & Li, 2012; Wohl, Young, & Hart, 2007) and encouraging people to quit sooner. It has been suggested that reduced enjoyment should equate to greater risk aversion (e.g., smaller bets) (Wohl et al., 2007), and since games of chance tend to have a negative expected value in the long term (Walker, Litvin, Sobel, & St-Pierre, 2015), that a reduction of time spent playing would naturally equate to a reduction in gambling losses and reduced gambling expenditure. However, this was not the case in the current study. It may be that a reduction in the level of enjoyment as a result of more rational approaches to gambling may encourage people to gamble more money in an attempt to make gambling more exciting.

More likely, however, is that the lack of effect is due to how gambling expenditure was quantified. Participants were asked to report “In the last week, approximately how much money have you spent gambling in total”. Gamblers tend to have varying definitions or methods for calculating gambling expenses, with some including overall turnover and others considering only net expenditure (Blaszczynski, Dumlao, & Lange, 1997; Wood & Williams, 2007). Ambiguous questionnaire items can therefore generate substantially different responses (Blaszczynski et al., 1997; Wood & Williams, 2007). Further, those with gambling problems tend to lose track of money spent and have difficulty determining whether they are financially ahead during a gambling session (Nower & Blaszczynski, 2010). Retrospective accounts of gambling expenditure are therefore likely to be unreliable for providing accurate information on the net value of money invested into gambling activities from personal bank rolls; a significant limitation of the current study. Nevertheless, it is important to note that lack of significant findings on expenditure do not imply that there was no change but may instead only reflect an inability to detect the change with self-report data. In future research, more objective measures, such loyalty card data, might provide an ability to detect a reduction in gambling expenditure. Logically, when intensity of play is constant, a reduction in time spent gambling should translate into a reduction in expenditure.

As well as the issues surrounding self-reported gambling expenditure measures, there are several other design elements that should be recognised as limitations of this study and considered when interpreting the findings. For instance, having participants monitor their gambling consumption may have prompted changes in perceived control over gambling outcomes, as demonstrated by results indicating changes to illusion of control and predictive control in both conditions. Further, the GRCS and PGBS have not been assessed for re-test reliability and the GRCS is not an exhaustive measure of gambling fallacies and biases. There may be other measures of cognitive distortions that better capture gambling cognitions that may be more or less affected by an analytic intervention. Findings of this study demonstrate the potential for cognitive interventions designed to challenge fallacious thinking by encouraging more analytic thought to be useful in attempts to reduce the time people spend gambling. However, given the intervention failed to change gambling expenditure, it would be premature to argue that the results would support such an intervention being adequate in generating and sustaining long term behavioural changes that reduces gambling related harm by itself.

In order for people to reduce gambling consumption and thus minimise their risk of experiencing gambling related harm, it is likely that cognitive interventions that challenge biased decision making would benefit from the addition of other strategies, such as behavioural feedback, that provides gamblers with realistic accounts of their actual gambling expenditure; allowing them to recognise behavioural patterns and moderate gameplay (Wohl, Davis, & Hollingshead, 2017; Wood & Wohl, 2015). Recovering gamblers report many different techniques or strategies as helpful for minimising or abstaining from gambling (Hodgins & el-Guebaly, 2000; Rodda et al., 2018). However, most studies that explore harm reduction techniques endorsed by gamblers tend to focus on behavioural strategies used by the gamblers, often overlooking the cognitive underpinnings that promote behavioural responses (Hing, Nuske, & Gainsbury, 2012; Rodda et al., 2018). Interventions, such as the one used here, to strengthen decision-making skills that are based on reflection, critical thought and reality checking, are likely to provide greater control over gambling decisions, only increasing the effectiveness of behavioural strategies for reducing gambling consumption.

While cognitive techniques have been reported to be helpful in strengthening gambling abstinence (Hodgins & el-Guebaly, 2000) and are incorporated into many problem gambling treatment therapies (Fortune & Goodie, 2012; Gooding & Tarrier, 2009), they often require gamblers to access help services in order for them to be successful. Wohl et al. (2007) suggest that some biases, such as dispositional luck, are associated with negative attitudes towards treatment seeking, and thus, failing to address gambling related cognitive distortions is likely to be a barrier to help seeking. Further, many responsible gambling initiatives operate under the assumption that being an informed consumer translates to better decision making. However, research suggests that such approaches are largely ineffective at generating behavioural changes (Cloutier, Ladouceur, & Sévigny, 2006; Miyazaki, Brumbaugh, & Sprott, 2001; Monaghan & Blaszczynski, 2005, 2007; Monaghan, Blaszczynski, & Nower, 2009; Williams & Connolly, 2006; Wynne & Stinchfield, 2004). Gamblers do not necessarily lack the statistical knowledge underpinning many gambling concepts (Delfabbro, Lahn, & Grabosky, 2006; Lambos & Delfabbro, 2007), nor are they absent of insight into the irrationality of their beliefs (Ellerby & Tunney, 2017; Gaboury & Ladouceur, 1989; Griffiths, 1994); suggesting that there is more at play than simply a lack of knowledge regarding mathematical components of probability and chance hindering behavioural changes (Williams & Connolly, 2006). When the rules of probability are disguised within a gambling context, gamblers fail to apply statistical knowledge and instead make decisions based on heuristics and emotion (Delfabbro et al., 2006; Kogler & Kühberger, 2007; Lambos & Delfabbro, 2007; Turner, Zangeneh, & Littman-Sharp, 2006). Since people's beliefs are often value-laden, closely associated with personal experiences, emotions and a sense of self and largely influenced by external factors, interventions that place all the responsibility on the consumer and fail to acknowledge other factors that influence decision making beyond personal control are likely to be ineffective and contribute to gambling stigma (Carroll, Rodgers, Davidson, & Sims, 2013).

Conclusion

Interventions that encourage people to challenge beliefs by providing conflicting evidence, removing blame and stigma, and that explain how and why these justifications are tempting (i.e., the way gambling tricks us into endorsing some beliefs that sway our decisions) are likely to be more effective in promoting cognitive changes that may generate safer gambling consumption amongst those experience gambling related harm. Early cognitive interventions designed to promote greater reflection and challenge biased gambling decisions is likely to encourage safer gambling consumption and have positive implications for treatment seeking by those who need help controlling gambling urges (Wohl et al., 2007). Interventions that are digitalised and can be accessed via the Internet means they can be administered to a wider network of gamblers, and eliminates the stigma or shame associated with accessing formal treatment services. However, a limitation of this study is that it does not delineate the cause for belief and behaviour change. While the intervention appeared successful in altering time spent gambling and gambling cognitions, it is unclear whether the intervention worked by fostering greater analytical thinking that promoted greater reflection more generally, or if it simply promoted reflection on faulty cognitions specifically about gambling; and whether behaviour change occurred as a result of a change in thinking style or due to changes in gambling beliefs. Future research should consider unpacking causation regarding changes to thinking style, gambling beliefs and gambling consumption, and explore the long-term impacts of a training-type intervention designed to strengthen critical thinking skills in gamblers to promote resilience to common gambling related cognitive distortions. Further, exploration as to how the intervention may be adapted or incorporated into other harm reduction strategies to reduce gambling expenditure is necessary to realise the goal of ameliorating gambling related harm.

Funding sources

Part of this research was supported under the Commonwealth Government's Research Training Program/Research Training Scheme. I gratefully acknowledge the financial support provided by the Australian Government and Central Queensland University. Funding agencies have had no involvement in the research design, methodology, conduct, analysis or write-up of this manuscript.

Author's contribution

TG was responsible for the study concept and design, analysis and interpretation of data, statistical analysis, obtaining funding and development of the manuscript. MR contributed to the study concept and design, analysis and interpretation of data, obtaining funding and editing the manuscript. MB contributed to the study concept and design, analysis and interpretation of data, obtaining funding and editing the manuscript. AB contributed to the study concept and design and editing the manuscript for publication.

Conflict of interest

TG has received funding for her doctoral placement from the Australian Government via the RTS program, research funding from the Victorian Responsible Gambling Foundation, and the National Association of Gambling Studies for conference attendance. MR has received research grants from the Queensland Treasury, the Victorian Treasury, the Victorian Responsible Gambling Foundation, the New Zealand Ministry of Health, the NSW Dept of Industry and Trade, the Department of Social Services, the Alberta Gambling Research Institute and Gambling Research Australia. He declares that he has no conflicts of interest in relation to this manuscript. MB received grants from the Victorian Responsible Gambling Foundation, the New Zealand Ministry of Health the NSW Dept of Industry and Trade, the Department of Social Services, the Alberta Gambling Research Institute and Gambling Research Australia. He declares that he has no conflicts of interest in relation to this manuscript. For the period 2015–2020, AB has conducted research funded directly by Australian or international government, or government-related funding agencies, and industry operators. These include Gambling Research Exchange Ontario, ClubsNSW, Dooleys Club Lidcombe, Aristocrat Leisure Industries, Gaming Technologies Association, Gambling Research Australia, Responsible Wagering Australia, Commonwealth Bank, Crown Casino, NSW Department of Trade and Investment (NSW Office of Liquor, Gaming and Racing), La Loterie Romande (Switzerland), Camelot (United Kingdom), La Française des Jeux (France), Loto-Quebec (Canada), and National Lottery (Belgium), Australian Communications and Media Authority’ and the National Association for Gambling Studies. He has received honorariums from Manitoba Gambling Research Program and GambleAware (formerly UK Responsible Gambling Trust) for grant reviews, and royalties from several publishers for books and book chapters. He has also received travel and accommodation expenses from Leagues Clubs, Gambling Research Exchange Ontario, USA National Council on Problem Gambling, Japan Medical Society for Behavioural Addiction, Le Comité d'organisation Congrès international sur les troubles addictifs, Victorian Responsible Gambling Foundation, North American Association of State and Provincial Lotteries, and New Horizons (British Columbia Lottery Corporation to attend conferences and meetings. All professional dealings have been conducted with the aim of enhancing responsible gambling and harm minimisation policies and practices, training counsellors in the treatment interventions, and advancing our understanding of the psychology of gambling.

Appendix A. Analytical training task

Baseline – Original GFQ Items

• Q1.
  Which of the following set of lottery numbers has the greatest probability of being selected as the winning combination?

  • a.
    1, 2, 3, 4, 5, 6
  • b.
    8, 18, 3, 55, 32, 28
  • c. Each of the above have an equal probability of being selected.

Feedback: When playing games of chance, each outcome is completely independent with a fixed probability. Previous outcomes therefore have no bearing on future outcomes. Despite one set of lottery numbers appearing to be selected at random and the other to present a succession or pattern, the likelihood of each individual number being a winner remains the same.

• Q2.
  Which gives you the best chance of winning the jackpot on a slot machine?

  • a.
    Playing a slot machine that has not had a jackpot in over a month
  • b.
    Playing a slot machine that had a jackpot over an hour ago
  • c. Your chances of winning the jackpot are the same on both machines

Feedback: Depending on the type of jackpot, pay out schedules can be vastly different and unpredictable. Some can be configured to pay out after a set number of spins, others based on an interval schedule and others at random. As there is no way of knowing the payout schedule of the machine you intend to play, whether the jackpot went off an hour or over a month ago provides no indication as to whether it is likely to go off again.

• Q3.
  How lucky are you? If 10 people's names were put into a hat and one name drawn for a prize, how likely is it that your name would be chosen?

  • a. About the same likelihood as everyone else
  • b.
    Less likely than other people
  • c.
    More likely than other people

Feedback: In gambling, no one person is more or less lucky than anyone else. Your perception of how lucky you are therefore has no impact on whether or not your name is likely to be drawn. Any one entry in the hat has just as much chance of being drawn as any other.

• Q4.
  If you were to buy a lottery ticket, which would be the best place to buy it from?

  • a.
    A place that has sold many previous winning tickets
  • b.
    A place that has sold few previous winning tickets
  • c. One place is as good as another

Feedback: Winning lottery numbers are not predetermined but selected at random. Therefore, at the point of purchase, one ticket is no more or less likely to be a winner than the next. The place of purchase does not give you any control over whether you purchase the winning ticket or not. Just because one venue has sold several winning tickets prior (or none), does not mean that it sells future winning tickets.

• Q5.
  A positive attitude or doing good deeds increases your likelihood of winning money when gambling.

  • a. Disagree
  • b.
    Agree

Feedback: In gambling, no one person is more or less lucky than anyone else. Despite many people believing otherwise, there is no such thing as good karma or fortune in gambling. Doing nice deeds or having a sunny disposition does not alter your chances of winning money when gambling.

• Q6.
  A gambler goes to the casino and wins 75% of the time. How many times has he or she likely gone to the casino?

  • a. 4 times
  • b.
    100 times
  • c.
    It is just as likely that he has gone either 4 or 100 times

Feedback: Generally speaking, gamblers don't tend to come out ahead in the long run. It is more likely that the gambler is ahead if they've only gambled the 4 times as gambling 100 times gives them more opportunities to lose.

• Q7.
  You go to a casino with $100 hoping to double your money. Which strategy gives you the best chance of doing this?

  • a. Betting all your money on a single bet
  • b.
    Betting small amounts of money on several different bets
  • c.
    Either strategy gives you an equal chance of doubling your money.

Feedback: Despite gambling with smaller amounts, increasing the number of bets you make also increases the opportunities to lose. Since the house is stacked against you, it's inevitable that over multiple bets, you're likely to experience more losses than wins. This means that a single bet is more likely to allow you to double your money than over multiple, smaller bets.

• Q8.
  Which game can you consistently win money at if you use the right strategy?

  • a.
    Slot machines
  • b.
    Roulette
  • c.
    Bingo
  • d. None of the above

Feedback: Outcomes of these games are determined purely by chance. Given their objectivity, they are impartial to any attempts to try to sway them. This means that the outcome will be what it will be, regardless of whether you apply a strategy to how you play. It doesn't matter what you do in terms of the numbers you pick or the lines you play, your actions will not alter the outcome and thus, whether you win or lose is still a complete gamble.

• Q9.
  Your chances of winning a lottery are better if you are able to choose your own numbers.

  • a. Disagree
  • b.
    Agree

Feedback: Lottery numbers are selected at random and so there is no strategy that you can apply to picking numbers that would give you a greater chance of winning. Each number has the same probability of coming up as the next, and so any sequence or number you choose are just as likely to win as any other.

• Q10.
  You have flipped a coin and correctly guessed ‘heads’ 5 times in a row. What are the odds that heads will come up on the next flip. Would you say…

  • a. 50%
  • b.
    more than 50%
  • c.
    or less than 50%

Feedback: Prior coin flips do not determine what side of the coin is likely to show up on your next flip. That is, each flip of the coin is completely independent from the last. It is purely a coincidence that you have received heads five times in a row and does not mean that heads is any more or less likely to come up on your next flip.

Week 1

• Q11.
  A punter is very good at picking winning horses. She wins about 1/2 of the time on every race. In the next 6 races, which sequence is most likely?

  • a.
    Win, win, win, lose, lose, lose
  • b.
    Win, lose, win, lose, win, lose
  • c.
    Win, lose, win, win, lose, lose
  • d. Any of the above are equally likely

Feedback: When playing games of chance, each outcome is completely independent with a fixed probability. Previous outcomes therefore have no bearing on future outcomes. Whether the punter wins of loses on their prior bet, or their history of wins versus losses, does not mean they will win or lose in subsequent bets.

• Q12.
  You notice a person who's been having good luck on a slot machine, it has been paying out unusually high. You haven't been so lucky playing on your machine. She collects her winnings and leaves. Are you better off:

  • a.
    To keep playing your machine
  • b.
    To switch to playing her machine
  • c. It probably doesn't matter

Feedback: Slot machines are completely random. Whether a person appears to be or feels lucky therefore has no impact on whether they win or lose. Just because one machine “appears” to pay out more, or someone seems to be “lucky”, doesn't mean that it actually is or they are. Naturally, people are more in tune to noticing wins and these wins are more memorable; which leads one to believe a machine is paying out more than what it is.

• Q13.
  Going to the races, Belinda noticed she's won every time she brought her partner to the track. Her chances of winning next time are:

  • a.
    Better if she brings her partner
  • b.
    Worse if she brings her partner
  • c. About the same, regardless of whether or not she brings her partner

Feedback: In gambling, no one person is more or less lucky than anyone else. Similarly, despite many superstitions suggesting otherwise, there is no strategy or ritual that is likely to help you win. Belinda is incorrectly attributing her wins to the presence of her partner. Her good fortune when accompanied by her partner is nothing more than a coincidence.

• Q14.
  In a true story, a Frenchman won the state lottery of $1 million Euros twice in less than 18 months. What is the best explanation for this extraordinary set of wins?

  • a.
    The Frenchman is a very lucky person
  • b.
    The Frenchman was cheating
  • c. It's highly likely that someone somewhere might win twice
  • d.
    The Frenchman had used the same set of numbers

Feedback: There are many major lottery draws across the world every year, making it highly likely that at some regular intervals, one person should experience the extraordinary occurrence of winning a major lottery twice.

• Q15.
  It's quite rare, but some people are just born winners. Those people can beat the odds, if they choose to gamble.

  • a.
    True
  • b. False

Feedback: In gambling, no one person is more or less lucky than anyone else simply because they believe they are “luckier”. Just because a person considers themselves to be a “born winner”, does not mean they can beat the odds. The odds in gambling cannot be “beaten”, since chance outcomes are beyond the control of the gambler. Gamblers with some skills on particular games, such as Poker, might win more often than less skilled gamblers, but this does not mean they can overcome or "beat the odds" of the games they play.

• Q16.
  When you roll two standard dice and add up the results, you get a number between 2 and 12. Are you more likely to get:

  • a.
    4
  • b. 6
  • c.
    You're just as likely to get a 4 or a 6

Feedback: When rolling two standard die, there is only one combination (1+1) that will give you a 2, and one combination (6+6) that will give you a 12. However, as we move towards the mid-point (7), there are more and more combinations (3+4, 5+2, 1+6) that will yield a result. Thus, you are more likely to get a sum of 6 than 4.

• Q17.
  A slot machine has a published return-to-player rate of 85%. You put in $100 and cash out all your winnings, rather than gamble with them. What amount are you most likely to leave the venue with?

  • a.
    $15
  • b.
    $85
  • c.
    $100
  • d.
    $185
  • e.
    All of the above are equally as likely outcomes

Feedback: You are most likely to leave with $85, as you only play one game with your money. If you were to cycle your winnings back into the machine, you are most likely to leave with less than $85.

• Q18.
  If you're a highly experienced and knowledgeable player, on what games might you have a better chance of winning money if you apply your knowledge?

  • a.
    Blackjack
  • b. Stud poker
  • c.
    Neither blackjack or stud poker
  • d.
    Both blackjack and stud poker

Feedback: Blackjack is a game with a very simple optimal strategy. After applying that strategy, your winnings will be entirely determined by luck. Stud poker has a more complicated strategy, and skill is involved in attempting to predict the hands and strategies of other players. Therefore, a highly skilled player can expect to do better at stud poker.

• Q19.
  You might win more money on the lottery if you let the computer choose a random set of numbers, rather than choosing numbers that are meaningful to you.

  • a. True
  • b.
    False

Feedback: Many people will pick lottery numbers based on birthdays and past lucky numbers, meaning that if you choose numbers completely at random, such as through a computer quick-pick, you'll be less likely to have to share your prize with others.

• Q20.
  What are the odds of seeing the following two sequences of coin flips? [H, H, H, H, H] and [T, H, H, T, H]

  • a. 1/32 and 1/32
  • b.
    1/64 and 1/8
  • c.
    1/8 and 1/64
  • d.
    1/128 and 1/8

Feedback: You are just as likely to see either sequence of coin flips. Prior coin flips do not determine what side of the coin is likely to show up on your next flip. That is, each flip of the coin is completely independent from the last. This means, that the odds of seeing consecutive heads is the same as seeing a sequence of tails and heads.

Week 2

• Q21.
  The roulette wheel at the casino shows a win history of black, black, red, black, red, red, red. What outcome is most likely to appear next?

  • a.
    Black
  • b.
    Red
  • c. Neither are more or less likely

Feedback: When playing games of chance, each outcome is completely independent with a fixed probability. Previous outcomes therefore have no bearing on future outcomes. Just because the previous three outcomes were red, does not mean the wheel is "due" for a black, nor does it imply that the red streak will continue.

• Q22.
  What lottery numbers could you choose that give you the best chance at winning - regardless of whether or not you share the prize?

  • a.
    A number based on your birthday
  • b.
    A quick-pick generated by a machine
  • c.
    A straight sequence such as 12, 13, 14, 15, 16, 17 …
  • d. Each of the above are equally likely

Feedback: Lottery numbers are selected at random and so there is no strategy that you can apply to picking numbers that would give you a greater chance of winning. Each number has the same probability of coming up as the next, and so any sequence or number you choose are just as likely to win as any other.

• Q23.
  In Japanese culture, 4 is considered unlucky because it is pronounced shi, which is the Japanese word of death. Often rooms numbered 4 don't exist in hospitals or hotels. When gambling, are you better off avoiding the number 4?

  • a.
    Yes, but only if you're Japanese
  • b.
    Yes, but only if you're in Japan
  • c. No, there's no need to avoid 4
  • d.
    Yes, it's probably better for everyone to avoid that number

Feedback: In games of chance, one outcome is no more or less likely than any other. Despite many superstitions suggesting otherwise, one number is no "luckier" than any other. Cultural or societal beliefs or superstitions have no bearing on the outcome of chance events. While you may feel more comfortable betting on something else, there is no reason to think 4 would be more or less likely to pay out.

• Q24.
  Often lottery players need to share a prize with others who might have chosen the same numbers. If you want to increase your chances of NOT sharing a lottery win, you should:

  • a.
    Pick numbers based on your birthday
  • b.
    Pick numbers based on a search of the most winning numbers in the past
  • c. Let a computer pick numbers for you (quick pick)
  • d.
    There is no way to pick numbers that increase your odds of NOT sharing a prize

Feedback: Many people will pick lottery numbers based on birthdays and past lucky numbers, meaning that if you choose numbers completely at random, such as through a computer quick-pick, you'll be less likely to share your prize with others.

• Q25.
  You have three coins. The first is a regular coin, the second coin has two heads, the third coin has two tails. You pick one coin at random, flip it and get tails. What is the likelihood that heads is on the other side?

  • a.
    One in six
  • b. One in two
  • c.
    Two in six
  • d.
    Two in three

Feedback: You know it can't be the T-T coin, so it's one of the other two. Two possibilities there: H-<<T>> & H-<<H>> .

• Q26.
  Do you have a better chance of rolling a 6 when you roll:

  • a. One dice
  • b.
    Two dice, adding the two results together
  • c.
    Six dice, adding all the results together

Feedback: Increasing the number of dice you roll also increases the number of possible outcomes. When you roll one dice, there are six possible outcomes, meaning your odds are 1/6. Using two die does increase the number of outcomes that will give you a six (5; 1+5; 2+4; 3+3; 4+2; 5+1), but it also increases the total number of possible outcomes to 36. Making your overall odds slightly larger than rolling one die (1/7.2). Six dice increases the number of outcomes significantly to 46,654 possible outcomes, but only provides 1 combination that will provide you with an outcome of 6, meaning your overall odds are 1/46,654.

• Q27.
  Andy wanted to play roulette at the casino. He always puts his money on red number 34. He checks the score cards for each of 4 roulette tables at the casino. The last 5 wins on Table 1 were even numbers. Table 2 was red, Table 3 was black, and Table 4 was odd. Which roulette table would give Andy the best chance of winning given his pick of red 34?

  • a.
    Table 1
  • b.
    Table 2
  • c.
    Table 3
  • d.
    Table 4
  • e. Any wheel would have equal chance

Feedback: Prior outcomes in a game of roulette do not influence what numbers of colours may come up on future spins as each outcome is independent from the last. Andy has the same chance of winning on his pick of red 34 on any of the four roulette tables, regardless of their outcome history.

• Q28.
  In a totaliser race betting system, the pooled stake is shared among those who picked the winner, after deducting a 15% commission for the operator. In what situation are you most likely to win money?

  • a. If you are an expert picker, and other bettors are amateurs
  • b.
    If you are an expert picker, and other bettors are experts also
  • c.
    If you are an amateur picker, and other bettors are amateurs also
  • d.
    If you are an amateur picker, and other bettors are experts
  • e.
    Both a and b

Feedback: In a totaliser system, any benefit of your skill is relative to the skill of other players. Therefore, you will do best in a situation where your skill exceeds that of other players.

• Q29.
  You wager $10 on blackjack and win. You decide to place another bet. This time you place a larger wager of $20 and win again. On your next bet, which wager is most likely to pay off?

  • a.
    A $5 wager
  • b.
    A $30 wager
  • c.
    A $40 wager
  • d. Any of the above are as likely as the other

Feedback: Many gamblers tend to believe the observe patterns when the gamble. While doubling your money and winning may look like you're onto a winning streak, whether you win or lose is in no way related to how much you gamble.

• Q30.
  If you win the lottery, the chance that you win another lottery is:

  • a.
    Higher
  • b.
    Lower
  • c. The same as before

Feedback: Each lottery draw is completely independent from the last. Just because you have won before, doesn't mean you're more or less likely to win again.

Week 3

• Q31.
  Joe is in the middle of a losing streak and has lost the last eight bets in a row on blackjack (twenty-one). On his next bet, is he more likely to:

  • a. Lose
  • b.
    Win
  • c.
    Neither are more or less likely

Feedback: Most gambling games, such as blackjack, have a house edge. Therefore, regardless of what has happened in the past, Joe should expect that he is most likely to lose the next bet - just as he is more likely to lose any bet. Of course, he may win, but his most likely result is losing.

• Q32.
  You have the choice between several blackjack tables at the casino. At table 1, the house has won the last four hands in a row. At table 2, on the last hand, two of the four players just received a perfect 21. At table 3, there is only one player and they have won two out of the last four hands. Which table would give you the best chance of winning blackjack?

  • a.
    Table 1
  • b.
    Table 2
  • c.
    Table 3
  • d. Either is as likely

Feedback: Whether you win or lose is not determined by what has happened in previous hands. Similarly, there is no such thing as a lucky or hot table. While a table that appears to be "hot" may be a compelling choice, just because people have won against the house, it doesn't mean that you will win, or that they will continue to win. Similarly, just because people appear to be losing, doesn't mean that they will lose on the next hand.

• Q33.
  Jim, Jane and Tom enter this week's meat-raffle at their local club. Only 5 people, including the trio, enter the raffle. Jim won the raffle last week, and Jane won the raffle two weeks before. Who is more likely to win this week?

  • a.
    Jim
  • b.
    Jane
  • c.
    Tom
  • d. Someone else

Feedback: Jim, Jane and Tom each have a 1 in 5 chance of winning the raffle. However, there are 2 other entrants who also have a 1 in 5 chance of winning. Therefore, the chance of "someone else" winning the raffle is 2 in 5 (that is, a combination of the 2 chances of other people winning). In sum, it is more likely that "someone else" will win the raffle (2 in 5 rather than 1 in 5).

• Q34.
  Your local sporting club is offering a raffle. You purchase 3 tickets and can choose to enter your tickets for whichever prize you like. There are three prizes. Prize 1 has a maximum of 50 entries. Prize 2 has a maximum of 150 entries. Prize 3 has a maximum of 500 entries. Which option gives you the best chance of winning at least one prize?

  • a.
    Entering one ticket for each prize
  • b. Entering all tickets for prize 1
  • c.
    Entering all tickets for prize 3
  • d.
    Entering 2 tickets for prize 2 and 1 ticket for prize 3

Feedback: Because prize 1 has the smallest pool of entrants, you are better off entering all your tickets for that prize, as this gives you the best odds of winning (3/50). While entering in multiple draws may seem to improve your chances of winning any prize, because entrant pools are much larger, there is less chance of you winning these draws compared to prize 1.

• Q35.
  In roulette, it's a statistical fact that red wins slightly more than black over the long term.

  • a.
    True
  • b. False

Feedback: There is no difference in the odds of winning on red or black on a roulette wheel. There are equal pockets of red and black meaning the chances of winning on either are the same.

• Q36.
  Imagine gambling on many games of chess between two equally matched players. As you gamble one more and more games, your percentage of wins is likely to:

  • a.
    Increase
  • b.
    Decrease
  • c. Get closer and closer to 50%

Feedback: Because you are equally matched, you can think of the outcome of the chess game as a coin flip. As the number of games played increases, the number of games won will tend to shift towards 50%.

• Q37.
  Jack brought $100 to a casino, and lost all his money. Which of the following is more likely:

  • a. Jack bet all of his money on a single bet
  • b.
    Jack made 10 different bets at $10 each
  • c.
    Both strategies are equally as likely ways for Jack to lose $100

Feedback: Betting many times makes it likely that you will "win a few, and lose a few". If you bet once, it is more likely that you'll either lose everything or (more hopefully) win a lot.

• Q38.
  Poor strategy can make you lose more money than a good strategy on:

  • a.
    Slot machines
  • b. Stud poker
  • c.
    Poor strategy will ensure that you lose more money on either game

Feedback: The payoff on slot machines is fixed by regulation. Large bets can make you lose money faster, but strategy has no effect on profits. In contrast, poor strategy at Stud poker can make you lose more money, on average, than someone using a better strategy.

• Q39.
  You purchase 5 instant scratch tickets. The first three return a win. On the fourth ticket, you are more likely to:

  • a.
    Win
  • b. Lose
  • c.
    Either is as likely

Feedback: Instant scratch tickets, like all forms of gambling, have a house edge. Consequently, any ticket is more likely to lose than to win, and it doesn't matter (of course) what happened earlier.

• Q40.
  You have just received a perfect 21 while playing blackjack. What are the chances that you will win the next hand?

  • a.
    Greater since your previous hand
  • b.
    Lower since your previous hand
  • c. Same as before your previous hand

Feedback: Winning prior hands in blackjack does not suggest that you will win the next hand. You might feel like you're on a "winning streak", but in reality, future events in chance-based games are not influenced by prior outcomes.

Week 4

• Q41.
  Aaron tends to win 1 out of every 2 bets he makes. Aaron won his last bet. Is Aaron more likely to win or lose his next bet?

  • a.
    Win
  • b.
    Lose
  • c. Both are equally as likely

Feedback: When playing games of chance, each outcome is completely independent with a fixed probability. Previous outcomes therefore have no bearing on future outcomes. Whether Aaron wins or loses in his prior bet, or how he has wagered in the past, has no bearing on whether he'll be successful in future bets.

• Q42.
  You decide to buy a lottery ticket and share the cost with a friend. What strategy for picking your numbers will give you the best chance of winning?

  • a.
    You pick them together
  • b.
    Your friend picks them for you
  • c.
    You pick the numbers
  • d. Each of the above is just as likely

Feedback: Lottery numbers are selected at random and so there is no strategy that you can apply to picking numbers that would give you a greater chance of winning. As each number has equal chance of being selected, whether you choose the numbers yourself does not give you any better chance of winning than if someone else were to pick them for you.

• Q43.
  Steph has entered a raffle on 5 separate occasions and has never won. Jack has entered the same raffle 3 times and won a prize each time. On each raffle, at least 10 people enter. Who is more likely to win the next raffle?

  • a.
    Jack
  • b.
    Steph
  • c. Someone else

Feedback: When at least 10 people enter the draw, each person has at most a 1 in 10 chance of winning. The chance of either Jack or Steph winning is at most 2 in 10. The chance of someone else winning is at least 6 in 10. It is more likely that someone else will win.

• Q44.
  Justin often frequents his local pokie room. The last two times he has played, he has won the jackpot on the same machine. This time, is Justin better off:

  • a.
    Playing the same machine as before
  • b.
    Playing a difference machine
  • c. There is no choice of specific machine that leaves Justin better-off

Feedback: Just because Justin has been successful in winning the jackpot twice before, doesn't mean he will win it again. There are many different types of jackpots that have different payout schedules. Some can be configured to pay out after a set number of spins, others based on an interval schedule, and others at random. As there is no way of knowing the payout schedule of the machine you intend to play, whether the jackpot has paid out to you before provides no indication as to whether it is likely to go off the next time you play. Therefore, there is no strategy that Justin can apply in picking his machine that will make him better off.

• Q45.
  If you are in a bad mood when gambling, it is less likely that you will win.

  • a.
    True
  • b. False

Feedback: In gambling, no one person is more or less lucky than anyone else and event outcomes cannot be influenced by the actions or moods of the gambler. Being in a bad mood or not feeling your best does not alter your chances of winning money when gambling.

• Q46.
  Imagine betting on a coin flip. Every time you guess correctly, you gain $1. Every time you get it wrong, you lose $1. You start with $100. When are you most likely to have a balance of $100?

  • a.
    After 1 flip
  • b. After 10 flips
  • c.
    After 100 flips
  • d.
    After 1,000 flips

Feedback: It is impossible to have a $100 balance after 1 flip, because you will either win or lose on that flip, and your bank balance will change accordingly. However, after 10 flips (an even number), it is at least possible that you might return to a balance of $100 by having 5 wins and 5 losses. It becomes progressively less likely to have a balance of exactly $100 after more flips, however, since there are exponentially more possible outcomes.

• Q47.
  Many people consider the number 7 to be a lucky number. When gambling on roulette, would you be better off putting your money on number 7 than another number?

  • a.
    Yes
  • b.
    Yes, but only if you didn't have your own lucky number
  • c. No

Feedback: In games of chance, one outcome is no more of less likely than any other. Despite many superstitions suggesting otherwise, one number is no “luckier” than any other. Cultural or societal beliefs or superstitions have no bearing on the outcome of chance events. Just because a number is considered to be luck or unlucky, does not impact whether or not the number will or won't pay out. The number 7 is no more or less likely to appear than any other number.

• Q48.
  Using a betting system when gambling on roulette will allow you to overcome the house edge.

  • a.
    True
  • b. False

Feedback: There is no betting system that can overcome the house edge on an unbiased roulette wheel.

• Q49.
  You go to the casino and want to play roulette but you only have a small amount of money. Which strategy minimizes the chances of you losing all your money quickly?

  • a. Placing an outside bet
  • b.
    Placing an inside bet

Feedback: You have a much better chance of winning a bet when betting on red and black or odd and even (outside layout), than you do betting on the inside of the layout (such as straight up on one number or a street bet covering three numbers). This means your money will last longer, but you'll receive smaller payouts compared to betting on the inside layout. The inside layout has the highest payoff but also the highest risk, whereas the outside layout is less risky but pays less. In the long run, the house edge is the same, but if your goal is to make your bankroll last as long as possible, then you are better off making the less risky outside bets.

• Q50.
  Tracey likes to bet on the winner of the local football match. Her last three picks have all won the game. In the next game, the 2 teams are equally matched. All else being equal, what are the odds that her pick for the next match will also win win the game?

  • a. 50%
  • b.
    More than 50%
  • c.
    Less than 50%

Feedback: While Tracey may be knowledgeable on football, in this instance the teams are evenly matched and therefore, it is irrelevant whether or not Tracey has some football expertise. Each gamble is independent from the last so for her next gamble, the odds of picking a winner out of two otherwise equal opponents is still 50/50.

Appendix B ‐ Example of general gambling trivia questions

Baseline

• Q1.
  Blackjack is also called:

  • a.
    Craps
  • b.
    21
  • c.
    Roulette
  • d.
    Pai Gow
• Q2.
  The background of the number on a roulette wheel are three different colours. What are they?

  • a.
    Green, yellow and red
  • b.
    Black, green and red
  • c.
    White, orange and green
  • d.
    Yellow, green and white
• Q3.
  How many numbers are there on a keno board?

  • a.
    100
  • b.
    80
  • c.
    70
  • d.
    50
• Q4.
  What is Pai Gow?

  • a.
    A dice game
  • b.
    A variation of poker
  • c.
    A variation of keno
  • d.
    A form of bingo
• Q5.
  In what country did the game Baccarat originate?

  • a.
    England
  • b.
    France
  • c.
    Italy
  • d.
    United States
• Q6.
  Slot machines that have an increasing “jackpot” along with fixed payoffs are called what?

  • a.
    Ascending
  • b.
    Progressive
  • c.
    Climbing
  • d.
    Elevated
• Q7.
  In roulette, the wheel and ball are always spun in the same direction as each other.

  • a.
    True
  • b.
    False
• Q8.
  How many decks of cards are used in a game of Baccarat?

  • a.
    1
  • b.
    8
  • c.
    2
  • d.
    4
• Q9.
  In any gambling game, what is a “series of plays”?

  • a.
    Unit
  • b.
    Session
  • c.
    Group
  • d.
    Batch
• Q10.
  In Craps, what is another term for the “Don't Pass Line”?

  • a.
    Double line
  • b.
    Black line
  • c.
    Front line
  • d.
    Dotted line

Week 1

• Q1.
  In poker, four Aces beat a straight flush.

  • a.
    True
  • b.
    False
• Q2.
  How many betting positions are there on a Baccarat table?

  • a.
    Twelve
  • b.
    Thirteen
  • c.
    Fourteen
  • d.
    Fifteen
• Q3.
  In a game of Craps, what is the person rolling the dice called?

  • a.
    Mr Lucky
  • b.
    The Shooter
  • c.
    The Roller
  • d.
    The Player
• Q4.
  You're playing blackjack and the lady next to you asks to “split”. What does that mean?

  • a.
    She wants to leave the table
  • b.
    She wants to play two hands
  • c.
    She wants to play your hand
• Q5.
  In 1899, the first modern slot machine was designed by Charles Fey of San Francisco. It was named for one of the symbols on the reels. What was the name of this early “one-armed bandit”?

  • a.
    Ace of Spades
  • b.
    Liberty Bell
  • c.
    Cherry Popper
  • d.
    Lemon Tree
• Q6.
  In sports gambling, what is the strength of a team compared to another team?

  • a.
    Power up
  • b.
    Power ratings
  • c.
    Power range
  • d.
    Press ratings
• Q7.
  What does it mean in poker when a player is “on a tilt”?

  • a.
    The player has had a string of winning hands
  • b.
    The player is emotionally upset and starts making mistakes
  • c.
    The player has just been dealt a wrong hand
• Q8.
  In a new deck of cards, what order are the suits of the cards in from top to bottom?

  • a.
    Hearts, diamonds, clubs, spades
  • b.
    Hearts, clubs, diamonds, spades
  • c.
    Clubs, diamonds, hearts, spades
  • d.
    Clubs, hearts, diamonds, spades
• Q9.
  Where is the largest casino in the world?

  • a.
    The U.S Virgin Island
  • b.
    Connecticut
  • c.
    Nevada
  • d.
    New Jersey
• Q10.
  When playing Craps, you “crap out” if you roll…

  • a.
    7
  • b.
    2, 3, or 12
  • c.
    11
  • d.
    7 or 11

Week 2

• Q1.
  Each numbered slot on a roulette wheel is coloured either black or red with the exception of “0” and “00” slots. What colour are they?

  • a.
    White
  • b.
    Green
  • c.
    Blue
  • d.
    Yellow
• Q2.
  When playing blackjack and you receive a blackjack, what payoff will you generally receive?

  • a.
    2 to 1
  • b.
    Depends on how much money you wagered
  • c.
    Even money
  • d.
    3 to 2
• Q3.
  What Las Vegas Casino hotel suffered a hotel fire on November 21, 1980?

  • a.
    Fremont
  • b.
    Stardust
  • c.
    MGM Grand
  • d.
    Flamingo
• Q4.
  In Craps, what two numbers are called natural?

  • a.
    2 and 10
  • b.
    7 and 11
  • c.
    3 and 8
  • d.
    6 and 12
• Q5.
  In racetrack betting, if you bet a horse to “show”, what does that horse have to do in order for you to win?

  • a.
    Finish either first, second or third
  • b.
    Finish either first or second
  • c.
    Finish first
  • d.
    None of these
• Q6.
  In Baccarat, who is also known as the “Croupier”?

  • a.
    The underdog
  • b.
    The player on the right
  • c.
    The dealer
  • d.
    The highest bidder
• Q7.
  What is a players total available gambling money?

  • a.
    Banque
  • b.
    Bank book
  • c.
    Cheque
  • d.
    Bankroll
• Q8.
  In sports gambling, how much is a “nickel” wager worth?

  • a.
    c
  • b.
    100
  • c.
    500
  • d.
    50
• Q9.
  In slots, which part of the slot machine shows the payoffs for winning combinations?

  • a.
    The pay line
  • b.
    The pay out
  • c.
    The pay back
  • d.
    The pay table
• Q10.
  How many numbers are drawn in each game of keno?

  • a.
    20
  • b.
    80
  • c.
    10
  • d.
    40

Week 3

• Q1.
  In roulette, when playing a wheel with a “0” and a “00”, you place your bet on a number. What are the payoffs if the ball lands on your number?

  • a.
    39 to 1
  • b.
    38 to 1
  • c.
    35 to 1
  • d.
    40 to 1
• Q2.
  When playing Pai Gow poker, how many cards do you receive from the dealer?

  • a.
    2
  • b.
    5
  • c.
    7
  • d.
    3
• Q3.
  What are the majority of casino tokens or chips made from?

  • a.
    Clay
  • b.
    Metal
  • c.
    Plastic
  • d.
    Wood
• Q4.
  In blackjack, what is the term for betting that you will beat the dealer with just one more card than the two dealt?

  • a.
    Doubling out
  • b.
    Doubling up
  • c.
    Doubling down
  • d.
    Doubling off
• Q5.
  In Craps, what is the name of the first roll of the dice?

  • a.
    Throw-out roll
  • b.
    Come-out roll
  • c.
    Start-off roll
• Q6.
  In gambling, what is the advantage over an opponent called?

  • a.
    Edge
  • b.
    Cover
  • c.
    Overage
  • d.
    Comparison shot
• Q7.
  In sports betting, what is it called when one bets the favourite by giving up points?

  • a.
    Bluffing
  • b.
    Toeing the line
  • c.
    Laying the odds
  • d.
    Laying the points
• Q8.
  What are the rotating barrels on which the symbols appear on a slot machine called?

  • a.
    Carousels
  • b.
    Reels
  • c.
    Wheels
  • d.
    Handles
• Q9.
  What European city is home to the world's first casino?

  • a.
    London
  • b.
    Paris
  • c.
    Venice
• Q10.
  When playing poker, which of the hands below are the highest?

  • a.
    Flush
  • b.
    Full house
  • c.
    Straight
  • d.
    Three of a kind

Week 4

• Q1.
  When you are going to be rolling the dice on the come-out in craps, what numbers do you have to roll to establish the point?

  • a.
    Any odd number
  • b.
    7 or 11
  • c.
    4, 5, 6, 7, 8, 9, or 10
  • d.
    2, 3, or 12
• Q2.
  In a casino card game, you are dealt two cards down and four up, and then one more down. Betting takes place through the deal. What game are you playing?

  • a.
    Blackjack
  • b.
    Omaha
  • c.
    Baccarat
  • d.
    Stud Poker
• Q3.
  How many spaces are there on a standard roulette wheel which includes zero and double zero?

  • a.
    39
  • b.
    37
  • c.
    38
  • d.
    36
• Q4.
  What is the nickname for the overhead camera that monitors player and dealer behaviour in a casino?

  • a.
    Candid camera
  • b.
    Peek-a-boo
  • c.
    Eye in the sky
  • d.
    See all spot
• Q5.
  How much is an Ace worth in a game of blackjack?

  • a.
    1
  • b.
    11
  • c.
    Either 1 and 11
  • d.
    None of these options
• Q6.
  In Baccarat, what is the wooden device that can hold up to 8 decks at a time?

  • a.
    The carousel
  • b.
    The palette
  • c.
    The shoe
  • d.
    The hand
• Q7.
  Where did poker originate in the US?

  • a.
    New York
  • b.
    Atlantic City
  • c.
    Texas
  • d.
    New Orleans
• Q8.
  All traditional slot machines have a light on top in the shape of a stick. What are those lights called?

  • a.
    Lampposts
  • b.
    Lanterns
  • c.
    Chandeliers
  • d.
    Candles
• Q9.
  In Texas Hold Em Poker, what comes first?

  • a.
    The turn
  • b.
    The flop
  • c.
    The river
• Q10.
  The rake is a commission fee taken by a casino in many card-based games.

  • a.
    True
  • b.
    False

Some general gambling trivia questions were sourced or developed from the following online gambling quiz and trivia websites:

www.funtrivia.com.

www.proprofs.com/quiz-school/story.php?title=pp-about-gambling.

www.play.howstuffworks.com/quiz/casino-game-quiz.

www.les-croupiers.co.uk/tag/roulette-2/.

www.oilfieldchili.com/how/in-sports-gambling-how-much-is-a-nickel-wager-worth.html.

www.boomtownbiloxi.com/-/media/png/midwest/boom-town/pdfs/btc-tablegames-craps-link.pdf.