Abstract
The structure of pollen grains, which is typically characterized by soft apertures in an otherwise stiff exine shell, guides their response to changes in the humidity of the environment. These changes can lead to desiccation of the grain and its infolding but also to excessive swelling of the grain and even its bursting. Here we use an elastic model to explore the mechanics of pollen grain swelling and the role of soft, circular apertures (pores) in this process. Small, circular apertures typically occur in airborne and allergenic pollen grains so that the bursting of such grains is important in the context of human health. We identify and quantify a mechanical weakness of the pores, which are prone to rapid inflation when the grain swells to a critical extent. The inflation occurs as a sudden transition and may induce bursting of the grain and release of its content. This process crucially depends on the size of the pores and their softness. Our results provide insight into the inactive part of the mechanical response of pollen grains to hydration when they land on a stigma as well as bursting of airborne pollen grains during changes in air humidity.
Significance
Pollen grains undergo significant changes in their water content during transfer from the anther to the stigma. Airborne pollen grains are particularly sensitive to atmospheric changes. In a humid environment, they swell and may rupture, releasing their cytoplasmic content, which may provoke allergic reactions in sensitive individuals. The mechanics of this process are poorly understood, and it is not known why pollen grains of some species are more resistant than others. We show that grain bursting critically depends on the presence of pores, soft spots in the grain wall. The occurrence of bursting is determined by the interplay between pore softness and pore size.
Introduction
The ability of pollen grains to adapt to physical and biochemical changes in their environment is essential for their survival. When pollen grains leave the environment of the anther, they start to lose water, and this process activates a variety of protective mechanisms (1,2). Upon landing on a stigma, they take in exudate from its cells, swell, and eventually germinate, forming a pollen tube through which they fertilize the flower (3,4). Although growth of the pollen tube is an active response of the pollen grain, which requires coherent mobilization of numerous cellular mechanisms, precise regulation of osmotic forces (5), and deposition of biopolymers in the growing tube (6,7), the mechanical response of pollen grains to changes in their water content is, to a large degree, inactive and a consequence of their mechanical constitution (8, 9, 10). This mechanical makeup has its drawbacks, however, because it can induce an extreme response of the grains in a non-reproductive context. When the environmental conditions change suddenly (e.g., when the relative humidity of the atmosphere increases significantly), such a response may lead to the bursting of pollen grains (9,11). This typically occurs in windborne pollen grains when they have been lifted up from the anthers into the atmosphere. For instance, the concentration of grass allergens in the non-pollen-containing fraction of ambient air has been shown to correlate with air humidity (12), which, in turn, is related to the bursting of the pollen grains (11).
Understanding pollen bursting is important not only from the perspective of grain viability and plant fertilization but also in the context of human health because ruptured airborne grains can release respirable fragments that can provoke allergic reactions in exposed sensitive individuals (13, 14, 15). In regions of intense agricultural activity, for example, some monocultures—particularly those pollinated by wind—can produce huge quantities of pollen prone to bursting (16), and similar problems occur with urban horticultural planning (13,17). Although grain bursting and the consequential release of its content is not characteristic only of allergenic pollen, being a general feature of pollen that hydrates rapidly (9), it is a necessary process for realization of the allergenic potential of a species (11,16). Pollen allergens released in the atmosphere when the grains burst can affect human health for a long time, even when the pollen grains are destroyed and no longer viable (15). The grains, and in particular the cytoplasmic fragments they release when they burst, can also act as effective nucleation sites for cloud condensation (18, 19, 20), which can influence precipitation (21). Bursting of pollen grains in the atmosphere is thus relevant medically and meteorologically. Last, the spatial distribution of stresses effected by the inactive mechanical response of the grain could tag the site where the pollen tube originates and trigger and guide the active mechanisms for its growth (5,22). These examples highlight the importance of a quantitative description of pollen grain swelling and bursting to understand a wide range of phenomena in different environments and on very different scales.
Any model constructed to represent the influence of changing water content on pollen grain volume and shape needs to account for the inhomogeneities in the grain wall. Pollen grain walls of an overwhelming majority of gymnosperm and angiosperm species have discernible regions called apertures, which are known to differ in chemical and structural composition from the rest of the wall (3). The larger part of the pollen shell contains a rigid layer, called the exine, which is mostly made of sporopollenin. The apertures are regions in the shell where the exine layer is thinned or entirely absent and mostly consist of cellulose and pectin, making them typically (much) softer than the exine (23,24). Apertures thus act as flexible regions in an otherwise stiff pollen shell. Because the exchange of water between the pollen grain and its surroundings takes place mostly through the apertures (1,25), their closure and concomitant infolding of the pollen grain provides a mechanical response that prevents further desiccation and destruction of the grain. It has been shown recently that the success of this process requires a tuned mechanical flexibility of the grain wall so that closing of the apertures also pulls in the hard, exine parts of the grain (8,10) without inducing rupture in the wall material.
Much less is known about the influence of different features of pollen morphology on the swelling and bursting of the grains, which can happen by rupture of the apertures or the exine (9). Our aim is to investigate how pollen grains passively respond to (re)hydration and what role apertures play in this process. We focus on pollen grains with circular apertures called pores (3), which is the dominant type of pollen of anemophilous (wind-pollinated) plants (26). Experiments have shown that pores mechanically respond to hydration (3,9,25), but a theoretical description of this process it still lacking. To describe the swelling and possible rupture of porate pollen grains, we formulate an elastic model of the grain akin to one established previously to describe the shape changes in drying grains (10). We examine how the presence of pores influences the swelling of pollen grains as their volume increases because of the influx of fluid from the environment. The increase in grain volume is shown to cause rapid inflation of the pores, which results in huge strain on the pore material. We explore how the size, number, and distribution of pores influence deformation of the pollen grain and its resistance to pore inflation and bursting. Our results provide quantitative theoretical insight into the inactive mechanisms behind the bursting of pollen grains, and the model we use can be generalized to study the swelling of other types of aperturate pollen grains as well.
Materials and methods
Elastic model of the pollen grain
Construction of the elastic triangular mesh of the pollen grain and the elastic energy functional assigned to it closely follows the method used previously by Božič and Šiber (10). We assume that there exists an unstrained state of the pollen grain of volume , which is perfectly spherical and represents the reference, equilibrium state of the problem. The pollen grain can desiccate, which leads to a reduction of its volume , or it can further hydrate, leading to an increase in its volume .
Elastic energy of the grain
The elastic energy of the pollen wall can be formulated so that the microscopic energies effectively reside in the edges of the mesh:
| (1) |
The first and the second term in Eq. (1) are the stretching and the bending energy, respectively. The mesh (triangle) edges i have lengths , which, in general, differ from their equilibrium lengths in the unstrained state. The stretching energy of an edge is proportional to the square of its extension ; i.e., each edge i acts as a Hookean spring with a spring constant . The bending energy associated with the i-th edge can be expressed via the angles between the two triangle faces that share the edge. The bending energy depends on the difference between the actual and the equilibrium angles ( and , respectively).
The bending and stretching elastic constants of an edge can take on two different values, depending on whether the edge belongs to the exine or to the pore region of the grain wall, because the two regions have different elastic properties: for edges in the exine region, and , and for edges in the pore region, and . The values of the elastic constants in the pore region are scaled by a softness parameter (8) so that and . Edges that have bounding vertices in different regions, one in the exine and the other in the pore region, are assigned a stretching constant of . Similarly, when the geometrical centers of two faces sharing an edge are in different regions, the edge is assigned a bending constant of .
We also introduce a dimensionless quantity , which signifies the relative contributions of the bending and stretching energies and is defined as
| (2) |
This quantity, defined through microscopic elastic constants and used already in our previous work (10), differs from the Föppl-von Kármán number of the exine (or pore) sheet defined through continuum elastic constants by a factor on the order of unity. This is a consequence of the discrete form of bending energy we use (second term in Eq. (1)), whose continuum limit depends on the topology of the shape (27, 28, 29). For a more detailed discussion of the our model, we refer the reader to our previous work (10).
Mesh triangulation
This mesh obtained from the marching triangulation (30) is preconditioned so that the local elastic responses in the mesh without the pores () are as uniform as possible. When the mesh is optimized, the resulting edge lengths and angles are defined to be the equilibrium values of the edge lengths and angles, and this produces the set of constants and in the energy functional in Eq. (1). When such a mesh is inflated for a grain without pores, the strains are checked to be nearly uniform and isotropic throughout the mesh, as they must be according to Eq. (5). Indeed, they differ from the analytical prediction by at most . For the results shown in this work, the stress- and strain-free state is a spherical shell of radius , where a is the mean length of the mesh edge. The mesh has vertices, edges, and faces, and , as it must be according to the Euler formula for polyhedra (31).
Minimization procedure
The energy functional in Eq. (1) is minimized with respect to the coordinates of the mesh vertices using the conjugate gradient method of Hager and Zhang (32). The volume of the mesh is constrained by adding an extra term to the energy functional of the form
| (3) |
where is the volume penalization constant. The constant must be chosen with care because values that are too small do not constrain the volume to a sufficient precision, whereas values that are too large may result in problems with the convergence of the minimization. The appropriate value of the constant can be determined by a sequence of minimizations in which the constant is multiplied by a factor of in each step, as described, for instance, by Šiber (33). When the minimization is finished, the penalty energy, because of the constraint in Eq. (3), must be a negligible percentage of the total elastic energy of the mesh. When the minimal shape for a given relative additional volume is obtained, all mesh vertices are randomly jittered, i.e. displaced typically between 0 and 0.1a in random directions, and the minimization is repeated. The volume is then increased or decreased, depending on whether the minimization proceeds along the forward or the backward path, respectively.
Strains in the pollen grain
To effectively measure the magnitude of the strains in the pollen grain, we define a suitably averaged measure of strain in each vertex v of the mesh. This quantity is obtained from the area of all triangles sharing the vertex ν,
| (4) |
where is the area of all triangles around the vertex v in the strain-free state of the mesh. In the case of small deformations, the scalar in Eq. (4) can be thought of as the average value of the magnitudes of principal strains. The averaged measure of strain in the entire pore is then calculated by summing the quantities over all vertices v that belong to the pore region and dividing the result by the total number of vertices in the pore.
Results
Mechanical properties of porate pollen grains
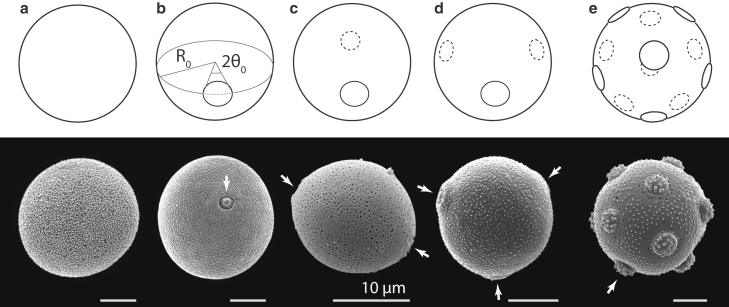
Pollen species with porate grains are ubiquitous, particularly in anemophilous plants (26), and represent a large proportion of allergenic pollen species (15). Their pollen grains can have different shapes with a more or less pronounced asphericity. Here we assume that the grains are perfectly spherical in the equilibrium state (thus neglecting any initial asphericity) with an equilibrium radius . Although the model we use allows different equilibrium grain shapes, the assumption of spherical grains reduces the number of parameters of the model and allows simpler identification and classification of the important features of grain swelling. The porate pollen grains can be further characterized by the number N of identical (circular) pores they contain, their distribution, and the angular span of each pore (see the examples in Fig. 1).
Figure 1.
Porate pollen. Classes of porate pollen considered in this study. (a–e) inaperturate () (a), monoporate () (b), diporate () (c), triporate () (d), and pantoporate (; in this case, ) (e). (b) also illustrates the parameters of the pore geometry—its equilibrium, unstrained radius , and the pore opening angle . Pore size in each schematic porate pollen is . The bottom part of each panel shows a scanning electron microscopy image of a pollen grain representative of the class: (a) P. alba, (b) P. pratense, (c) Besleria solanoides, (d) B. pendula, and (e) S. aquatica. The scale bars represent 10 , and the arrows point to the grain pores. In (e), only one of the 12 pores is indicated. Pollen images are reprinted with permission from the Society for the Promotion of Palynological Research in Austria; images courtesy of PalDat (2000 onward, www.paldat.org).
Inaperturate pollen—pollen without any apertures—with can be considered an extension of the geometric class of porate pollen and represents, at least on the level of our model, mechanically the simplest case of a porate pollen grain. The genus Populus, for instance, contains many anemophilous species with inaperturate pollen, some of which are also moderately allergenic (e.g., Populus alba) (34). Monoporate pollen () is characteristic of most of the species in the Poaceae family (grasses) (3), to which some of the most allergenic anemophilous plant species belong (e.g., Phleum pratense) (15). Diporate pollen grains (), with the two pores situated diametrically on the equator of the grain, can be found, for instance, in Morus alba, although the grains of this species can also have three and four pores. Triporate pollen (), with the three pores arranged equidistantly on the equator of the grain, are typical for Ambrosia artemisiifolia and the majority of species in the Betulaceae family, although some Betulaceae species also have five () equatorially situated pores (e.g., Alnus glutinosa). Lastly, Amaranthus species are typically pantoporate—they have many pores ( to 60) distributed nearly uniformly on the grain surface (35). The opening angles of the pores can be estimated from microscopic images of hydrated grains (3) and in general depend on the species, but they are typically about (36,37), such as in Betula pendula (Fig. 1 c) and Ulmus parvifolia (3). In two more extreme examples, the pore angles of Stellaria aquatica (Fig. 1 e) and Zea mays are about (38) and to 0.07 (39), respectively.
The Föppl-von Kármán number, , of pollen grains is typically in the range of to (10). The softness parameter of the pores has been estimated in our previous study to be in the range of to 0.1 (10). It is a relatively simple feat to measure the volume of a pollen grain as it hydrates by measuring its dimensions (40,41). This is why we perform elastic calculations at a given volume of the grain, treating it as a mechanical constraint. The minimization of the elastic energy yields simultaneously the grain shape and the distribution of elastic strains in the grain wall (in the pore and in the exine regions).
Swelling of inaperturate pollen grains
As a pollen grain hydrates, its volume increases, and its shape changes depending on its elasticity and the distribution, size, and shape of the pores. It is instructive to first consider the swelling of an inaperturate pollen grain—a perfectly homogeneous and spherical elastic shell of radius enclosing a volume . Such a shell responds to an increase in its interior volume V by an isotropic increase in its radius R. The influence of pores on pollen grain deformation can then be compared with this idealized case, which approximates a perfectly spherical inaperturate pollen grain (; Fig. 1 a).
The extensional strains in a homogeneous spherical shell are the same everywhere and can be obtained from
| (5) |
where represents the relative increase in the arbitrarily oriented infinitesimal lengths in the surface of the shell as they extend from in the initial state to in the swollen state (42). Similarly, denotes the corresponding increase in the radius of the shell when its volume increases by (43). For small values of relative additional volume, Eq. (5) reduces to . This can be applied to the case of inaperturate pollen; when the strain in the exine exceeds a critical value (i.e., when the additional volume v becomes large enough), the grain wall will break. For example, if the rupture strain of the exine is , then the inaperturate grain can increase its volume by before it ruptures. This estimate is, in fact, of the correct order of magnitude; a rupture strain of has been measured in inaperturate pollen of Cryptomeria japonica (44), and similar values are found in experiments on exine deformation and rupture (45). The estimate effectively presumes that the material deforms elastically all the way until fracture. This appears to be a good approximation for exine and cellulose films (45, 46, 47).
Swelling of monoporate pollen grains
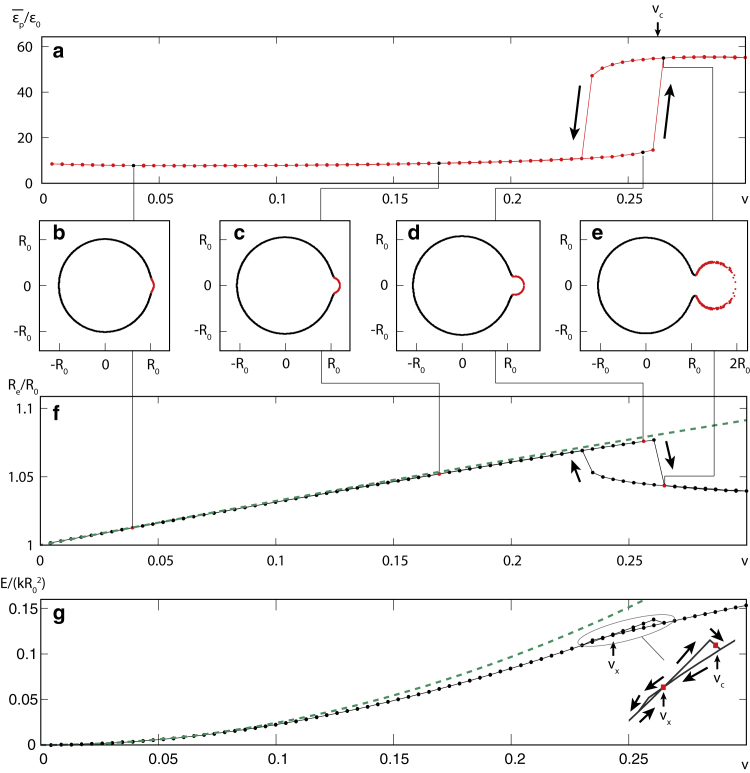
If there are pores in the pollen grain, they can relieve some of the swelling strain and, thus, change the nature of the grain fracture. We first investigate how the presence of a single soft pore (; Fig. 1 b) influences the swelling of pollen grains. Fig. 2 illustrates and quantifies this process of an increase in the volume of a pollen grain with , , and . Fig. 2 a shows the effect of increasing volume on the pore strain, which is averaged over the entire pore surface, , and scaled by the strain, which would be characteristic for an inaperturate grain of the same volume, (i.e., when or ; Eq. (5)). The most notable feature of hydration of the monoporate grain is the sudden jump in pore strain, which, for this particular choice of elastic parameters, occurs at a relative additional volume of . At this point, the average scaled pore strain increases from to . An even more drastic increase is observed in the maximum scaled pore strain, which is located at the outermost point of the pore and increases from to . Note here that this is a scaled quantity, where is about 0.09 at , meaning that the maximum pore strain jumps from about just before the transition to about after the transition. The sudden transition observed in the pore strain exhibits hysteresis, as seen by the non-equivalence of the forward and backward minimization paths of gradual increase and decrease of internal volume, respectively (marked by arrows in Fig. 2 a).
Figure 2.
Swelling of a monoporate pollen grain. (a) Pore strain averaged over the pore area and scaled by strain in a homogeneous (inaperturate) grain (given by Eq. (5)) as a function of relative additional volume . (b–e) Cross-sectional projections of the mesh points of the model for , 0.17, 0.256, and 0.265. In these panels, the pore and exine materials are denoted by red and black dots, respectively. The procedure used to generate these projections is described in the supporting material. (f) Dimension of the bounding box of the exine part of the pollen grain in the direction perpendicular to the axis connecting the centers of the grain and the pore (i.e., along the ordinate axis in b–e). The dashed line indicates the increase in radius that would occur in an inaperturate, homogeneous grain, . (g) Total energy of the pollen grain mesh scaled by (black line with symbols). The dashed line indicates the continuum limit of the stretching energy in the elastic discrete model of an inaperturate, homogeneous grain, . The inset shows the magnified region of v where the hysteresis occurs. Elastic parameters of the pollen grain are , , and throughout. To see this figure in color, go online.
Fig. 2, b–e, shows the cross-sectional projections of the triangular mesh of the model grain at different relative additional volumes, , 0.17, and 0.256 (just before the transition), and 0.265 (just after the transition). The sudden inflation of the pore (shown in red) at the critical volume is very pronounced. The mean radius of the exine region of the pollen grain (shown in black) increases until the transition point at and suddenly decreases afterward. This change is quantified in Fig. 2 f, which shows the effective radius of the pollen grain in the direction perpendicular to the line joining the centers of the grain and the pore (ordinate axis in Fig. 2, b–e). The dashed line shows the increase in the exine radius, which would be expected in the case of an inaperturate grain, . The mean radius of the exine region follows this dependence quite closely for small v, but the increase slows down as the grain volume approaches and the exine abruptly deflates at the critical volume, compensating in this way for the sudden inflation of the pore.
The inflation of the pore can also be traced in the elastic energy of the pollen grain, as shown in Fig. 2 g, where a sudden drop in energy is observed at . This calculation also reveals two different energy behaviors that represent two different states of the system. In one of them, the pore still encloses a fairly small volume and has not yet bulged out, whereas in the other, the pore has bulged out and the exine has relaxed. Intriguingly, the two energy behaviors cross at volume , which suggests that the true energy minimum of the system cannot be reached for all volumes; i.e., the pore needs to sufficiently deform before it can bulge out and transition to a lower-energy state. This is illustrated in the inset of Fig. 2 g, which shows the magnified portion of the forward and backward minimization paths near the intersection of the two energy curves. The inflation of the pore during grain swelling results in lower elastic energies of the grain compared with an inaperturate grain of the same volume. The stretching elastic energy of the latter, , which is the analytical limit of the stretching energy encompassed by the microscopic numerical model in such a situation, is shown by a dashed line.
Mechanics of the bursting transition
When the increase in volume of a monoporate pollen grain reaches a critical relative additional volume , the strains in the pore increase manyfold, which can cause it to burst. It is therefore appropriate to call the sudden inflation a bursting transition. Bursting of a monoporate grain can be viewed as a transition of the pore through a state when it is maximally curved—this is the state when the inflated pore resembles a hemisphere (Fig. 2 d). Up to that point, the pore can resist the internal pressure mainly by increasing its curvature because the reaction force of the inflated pore is proportional to the inverse radius of curvature (see the discussion in the supporting material). Past that point, however, the pore radius must increase because of the geometry of the problem, and to resist the additional pressure, the tension in the pore material must increase to resist the same pressure at a larger pore radius. This leads to sudden inflation of the pore.
The physical mechanism behind the bursting transition can be quantified by equating the normal reaction forces of the exine and the pore at the poles because they must resist the same internal pressure in the grain (42,43). When this analysis is performed for the maximal curvature of the pore (i.e., when the pore attains a (nearly) hemispherical shape), one obtains the following equation for the critical relative additional volume of the grain at which the sudden pore inflation occurs (see the supporting material for details of the derivation):
| (6) |
The relation was derived assuming a negligible influence of the bending energies on the transition, which can be seen by the lack of dependence of on . When and , conditions likely to be fulfilled by most pollen grains, the expression for the critical volume reduces to
| (7) |
Although Eqs. (6) and (7) give only rough estimates of the critical volume of the bursting transition, they are important because they demonstrate that, for the mechanical parameters typical for pollen grains, the critical volume for bursting should primarily depend on the ratio of the softness of the pore (compared with the exine) and the pore size.
To fully inflate (and eventually burst), the pore must pass through a hemispherical state. However, even when the pore has not yet sufficiently inflated to reach the hemispherical shape, there might exist inflated states of the pore (i.e., pores larger than a hemisphere) with lower elastic energies. Such states are, however, not geometrically accessible because they can be reached only after the pore passes through the hemispherical state. In this case, the hemispherical state of the pore represents a geometrical hindrance or a bottleneck and acts as an effective energy barrier. This effect is somewhat similar to the “blowout” or bursting instability observed in inflation of flat circular membranes (48,49). In our numerical simulations, the energy barrier can be most easily detected by the hysteretic nature of the minimization, as demonstrated in Fig. 2. It is also worth mentioning here that the analogy between pore inflation and “blowing a balloon confined in a rigid box” has been noted previously by Matamoro-Vidal et al. (9) in discussions of experiments on pollen swelling.
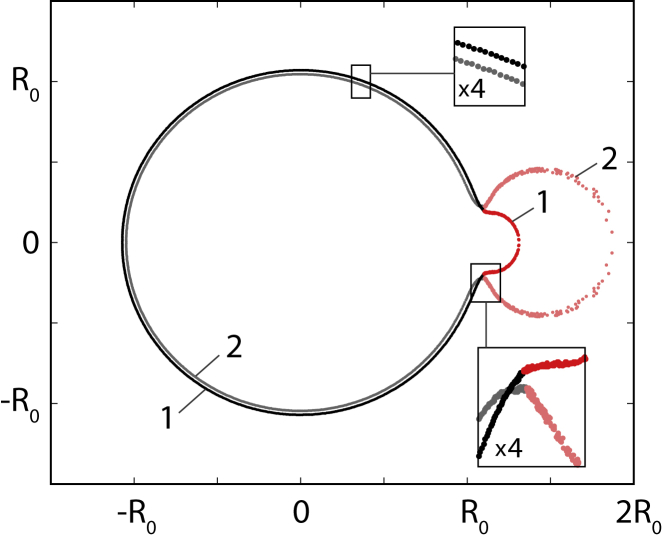
With this insight, we can now rationalize the two characteristic volumes and , which were detected in the dependence of the elastic energy of the pollen grain on its volume (Fig. 2 g). The first of the characteristic volumes, , is the relative additional volume at which the state with the inflated pore (larger than a hemisphere) becomes advantageous with respect to the total elastic energy. The second characteristic volume, , is the critical relative additional volume when the internal pressure becomes large enough to surmount the energy barrier of the hemispherical shape and allows the pore to attain the inflated shape. This critical volume, which can be identified in the forward minimization procedure, is relevant for hydration of pollen grains. The analytical considerations given by Eq. (6) also pertain to this volume. The volume where the energy curves cross () can be detected by combining the results of the forward and backward minimization procedures (see Fig. 2 g). Thus, at , there exist two different states of the grain with the same energy (shown in an example in Fig. 3). In one of those states, denoted by 1 in Fig. 3, the pore has not yet reached the critical, hemispherical shape, whereas in the other state, denoted by 2 in Fig. 3, the pore has inflated. These two shapes are obtained in the forward and backward minimization paths at , respectively.
Figure 3.
Two states of the grain with the same elastic energy. Cross-sectional projections of two states of the grain (shown in light and dark shades, respectively) with the same elastic energy at (as marked in Fig. 2g). Insets show the magnified regions of the grain cross-sections. Elastic parameters of the grain are , , and . To see this figure in color, go online.
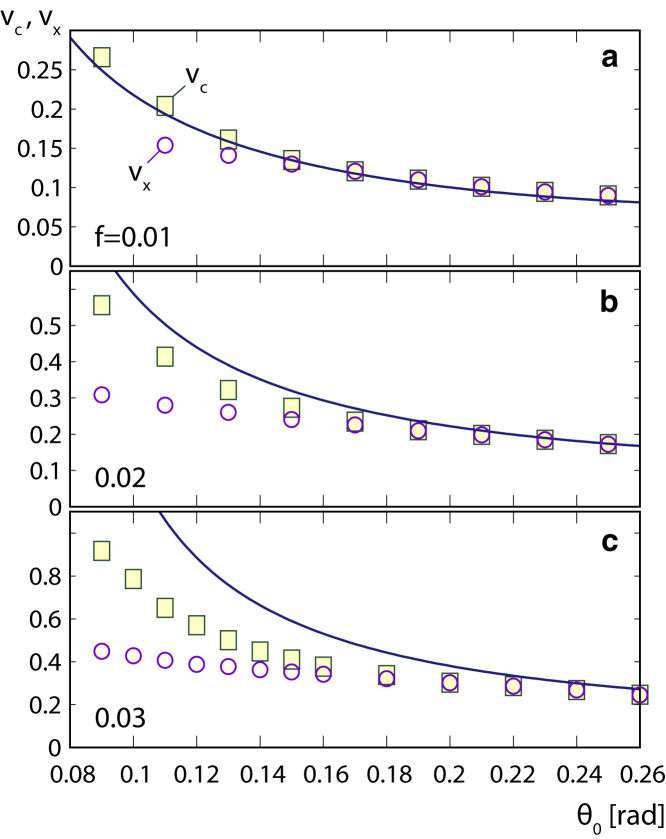
Bursting transition and pore size and softness
To further corroborate the physical interpretation of the volumes and , we show in Fig. 4 how these volumes change with the pore opening angle and different values of the pore softness parameter f. In particular, we examine the range of relevant for porate pollen grains; see the examples in Fig. 1 for an illustration of the different pore sizes. One can observe that the analytical prediction of Eq. (6) becomes progressively worse as f increases. This is to be expected because the equation stops making sense as f becomes comparable to , which can happen for small pore opening angles or sufficiently large f, and it has a divergence at . Nevertheless, the simple physical reasoning behind Eq. (6) explains the salient features of the numerical results in the range of parameters f and typical for monoporate pollen grains. It is worth reiterating that the critical volume at which the pore inflates and bursts does not depend on the elasticity of the exine or the pore alone but on the softness of the pore compared with the exine (softness parameter f). When the pores are sufficiently large, the energy barrier for the pore inflation disappears, and the two characteristic volumes become identical: . The rather rapid inflation of the pore still persists, although it now becomes a continuous phenomenon. Furthermore, the hysteresis of the numerical calculation disappears, which indicates disappearance of the energy barrier for the bursting transition; for , for instance, this happens for opening angles larger than (Fig. 4 b). The increase in strains in the pore during the bursting transition becomes smaller as the pore gets larger.
Figure 4.
Critical volumes and pore softness. Critical relative additional volume , at which a pore rapidly inflates (squares), and relative additional volume , at which the state with the inflated pore has a lower total energy (circles), as a function of the pore opening angle for monoporate grains with . Results are shown for three different pore softness parameters: (a) , (b) 0.02, and (c) 0.03. Full lines show the prediction of Eq. (6). To see this figure in color, go online.
Bursting of pollen grains with two or more pores
Swelling of monoporate grain eventually leads to inflation and bursting of the pore, unlike in the case of inaperturate pollen, where swelling causes fracture of the exine when the strains become too large. Pore size and softness limit the amount of swelling a grain can tolerate before it ruptures. Simple analytical considerations of the bursting transition suggest that the critical volume is not significantly modified by the number of pores in the grain as long as these are sufficiently small. More precisely, as long as , the critical volume of a grain with N pores,
| (8) |
should essentially remain the same as in the case of monoporate grains. One could argue that the final state of the inflated pores is now less strained because the additional volume is distributed among several pores. However, numerical calculations indicate that inflation past the critical point is always asymmetric. Even the slightest difference between the pores leads to a situation where one of the pores inflates much more than the rest and bursts. This is shown in Fig. 5 for a pantoporate pollen grain with pores, where a single pore suddenly inflates after the bursting transition, whereas the other 11 pores deflate. The surface of the pollen grain is colored in accordance with the local strain in the grain so that the darkest blue and the brightest yellow represent the smallest and largest values of averaged strain when it is larger than it would be in an inaperturate grain with the same volume. One can observe that regions with an increased strain compared with an inaperturate grain are restricted exclusively to the pores. On the other hand, the strains in the exine are quite uniform (gray regions) and reach only about of the value that they would in an inaperturate grain (see the inset in Fig. 5). These two observations demonstrate that the pores act to relieve some of the strain on the exine, the more so the smaller the ratio , i.e. the softer and larger the pores are (see also the supporting material).
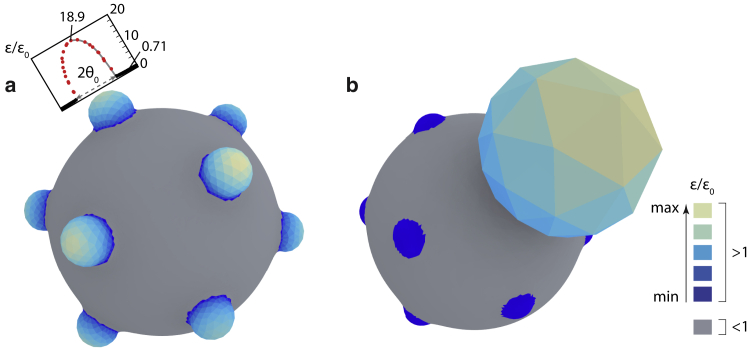
Figure 5.
Pore inflation in pantoporate pollen grain. Pantoporate grain with pores arranged around icosahedron vertices (a) right before the bursting transition () and (b) just after it (). The large sphere-like bulge in the upper right portion of (b) is the inflated pore. Mesh triangles are colored in accordance with the scaled local strain . The parts of the grain where the strains are smaller than in the inaperturate case () are colored in gray. The parts where are colored using the color scale shown in the legend so that blue and yellow correspond to smallest and largest values of , respectively. The maximal relative strains in the grains in (a) and (b) are and 178, respectively; in both cases, corresponding to the brightest yellow. The inset in (a) shows the cross-sectional profile of the relative strains in the plane that contains the maximally strained point of the pore (its pole) and the grain center. The points corresponding to the pore and the exine are indicated by red and black circles, respectively. The x axis in this diagram is the angular coordinate of the mesh points in the chosen cross-section and is appropriately scaled to match the 3D representation. Elastic parameters of the pollen grain are , , and . To see this figure in color, go online.
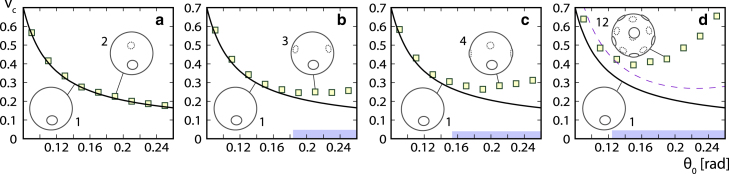
In Fig. 6, we show the bursting volumes of pollen grains with and , 3, and 4 pores arranged equidistantly along the equator of the grain as well as of a pantoporate grain with pores arranged on the vertices of an icosahedron. Diporate pollen grains with two diametrically positioned pores behave essentially the same as monoporate grains (Fig. 6 a); their critical volumes differ very little, and the two pores in diporate grains do not interact in the relatively wide range of pore opening angles considered. However, as the number of pores increases, critical volumes of porate grains begin to deviate from the values obtained in monoporate grains, which can be interpreted as a consequence of an effective elastic interaction between the pores. This effect occurs only for sufficiently large pore opening angles, when the pores themselves become large and move closer to each other. The region of where this effect becomes noticeable is shown by thick light-blue lines on x axes in Fig. 6, b–d. As the number of pores in pollen grains increases, the range of pore sizes where pores interact with each other increases as well, and the pores start to interact at ever smaller values of . The effect of the pore-pore interaction cannot be accounted for solely by the volume they share, as predicted by Eq. (8), because this provides only a barely visible correction for and 4 pores (because is a rather small quantity). In the case of pores, Eq. (8) significantly underestimates the correction to the monoporate case, which can be seen by comparing the dashed line in Fig. 6 d with the numerically obtained results.
Figure 6.
Critical volumes for grains with 1, 2, 3, 4 and 12 pores. Critical volume for pollen grains with and as a function of pore opening angle in grains with (a) , (b) 3, (c) 4, and (d) 12 pores. Numerical results are denoted by symbols, and full lines represent numerically obtained critical volumes of monoporate grains. The dashed line in (d) shows the results of Eq. (8) for . Thick light-blue lines above the x axes in (b)–(d) indicate the approximate regions of in which the pores interact with each other. To see this figure in color, go online.
These discrepancies can be understood by examining the mean distance between the pores. In the case of N pores distributed equidistantly along the equator, the pores start to touch each other when . At this point, the entire geometry of the problem fundamentally changes, and the N individual pores merge into a single pore, forming an equatorial poral belt. Pollen grains with a ring-like aperture at the equator can indeed be found; e.g., in Zamioculcas zamiifolia and Gonatopus angustus in the Araceae family. Geometric aspects of the problem—other than the volume occupied by the pores—are not accounted for by Eq. (8), and the deviation of the critical volume from the monoporate case indicates an elastic interaction between the pores mediated by the exine between them. A physical explanation of this effect requires considerations of the pore packing on the grain surface, their mutual distance, and the total area they cover, which is a problem of characteristic lengths and areas rather than volumes. For our purposes, it is important to note that, for pore sizes typical for allergenic grains, , the pores can be considered to be independent even when they are numerous because the critical volumes below are quite similar for to 4 and even for . In this region, the predictions of Eq. (8) are essentially fulfilled.
Discussion
The mechanical model of the pollen grain used in this study predicts that the pores deform significantly more than the exine as a pollen grain swells. The presence of pores relieves the stress on the exine and reduces it below the values it would attain were the pores not present (Fig. 5). At the same time, the pores are also the weak parts of the grain wall that are likely to rupture first when the grain reaches a certain level of hydration because they undergo rapid inflation at a critical relative additional volume of the grain. This pore bursting mechanism, where the pore bulges out and assumes a hemispherical shape just before rupture, has been observed in experiments (13,50) and is similar to one of the grain rupture mechanisms proposed by Matamoro-Vidal et al. (9) for pollen grains with a resistant exine and delicate intine, which, in our model, corresponds to low values of f. Another mechanism observed by Matamoro-Vidal et al. (9), swelling of the grain without pore or exine bursting and without significant bulging of the pore, is also included in our model and is typical for grains with rather small pores. The pores are less prone to bursting as they become smaller (Fig. 4), and because the critical volume of bursting is inversely proportional to (Eq. (7), smaller pores do not undergo the bursting transition until the grain swells to a large extent. In this case, this also means that the exine becomes more strained and that it can break before the pores do. Fracture of the exine was also observed by Matamoro-Vidal et al. (9), but only in inaperturate pollen grains with a relatively thin exine. These observations and our model therefore suggest that the pores are, in general, indeed the weak spots of the grain and that they will—when present—typically rupture first. Although the calculated strains in the pores can become huge at the bursting transition (see, e.g., Fig. 2), where our assumption of Hookean elasticity (Eq. (1)) is likely to break down, the transition also survives in a more general, non-Hookean parametrization of the stretching energy (see the supporting material).
The critical volumes predicted by our model can be related to values observed in experiments. When the increase in mass of pollen grains was measured at different relative humidities (RHs) (20), it was found that until the grains absorb water internally, whereas for even larger values of RH, a water layer forms on the external surface of the grains. At , the mass of pollen grains increases by about , a number that does not appear to vary much between different pollen types (20). Maximal volume expansion of pollen grains in the atmosphere can thus roughly be estimated to be about , which is similar to the typical values of obtained in our study. This suggest that our model covers the salient aspects of pollen grain swelling and provides a correct estimate of the characteristic energies involved. In particular, the model supports the observation that pollen grains in the atmosphere are in a critical environment where changes in humidity may easily lead to grain bursting, depending on the structure of the grains (11). Grains with sufficiently hard and small pores can sustain a large volume increase without their pores bursting. Although colpate pollen (pollen with elongated apertures) is not the subject of this work, it is nevertheless of interest to note that some colpate pollen (e.g., Petunia hybrida), can swell to a huge extent, increasing its volume two or three times upon hydration (40).
Diameters of pollen grains and the size of their pores show a significant correlation across different species of grasses (36,37), which suggests that their pore opening angles are approximately constant and can be estimated to be in the range of to 0.09 (at least in the grass species studied). Such a low value of suggests that the pores of pollen grains of grasses are, interestingly, not particularly prone to bursting. This is partially confirmed by experiments (11) where it was found that, although of B. pendula pollen grains release subpollen particles when hydrated for 10 min, only of P. pratense pollen grains do so under the same conditions. The mean pore opening angle of monoporate grains of P. pratense (Fig. 1 b) can be estimated to be about , whereas the pores of triporate pollen grains of B. pendula have a significantly larger opening angle of (3) (Fig. 1 d). This fact alone might explain the more frequent rupture of Betula pollen in a humid atmosphere.
On the other hand, such simple reasoning does not explain the fact that triporate pollen grains of Parietaria judaica with (3) burst five times less frequently than pollen grains of P. pratense even though they have similar pore opening angles. One should, however, keep in mind that the argument depends on the assumption of a similar value of aperture softness f, and different values of f can be expected in different pollen species (51), not only because of the differences in apertures and their thickness but also because of the differences in exine thickness and composition since f is a parameter that depends on the relative softness of the apertures. Although the values of f in porate pollen grains are in general unknown, it is nevertheless possible to estimate them in some cases. Rupture of pentoporate pollen grains of U. parvifolia has been recorded in a video sequence by Miguel et al. (13), and individual frames can be used to determine and because the volumes right before and after pore rupture can be determined from the sizes of the grain in different frames. This analysis gives and , which enables one to combine the two numbers and estimate the pore softness to be (Fig. 4), in line with previous estimates (8,10).
Pore sizes in pollen of grasses appear to be particularly small, which could signify an evolutionary path that, on one hand, allows a soft spot in the grain to ease pollen tube growth and, on the other hand, maximally reduces its size to retain the mechanical consistency of the grain. The minimal pore size is constrained by the size of the sperm cell, which has to pass through the pore into the pollen tube, and a comparison of typical sizes indeed suggests that the pores in grasses are maximally reduced. There also exist pollen grains with a number of quite large pores; for example, the pantoporate grains of Gypsophila perfoliata and S. aquatica (Fig. 1 e). Such an evolutionary solution enables accommodation of large additional volumes before one of the pores bursts. This is manifested by the characteristic shape of the dependence of on in Fig. 6 d, where increases with for sufficiently large pores. This shows that large critical volumes can be obtained not only by a single small pore but also by many large pores ( for the parameters used in Fig. 6). In this respect, it is interesting to note that pantoporate pollen grains appear to have evolved independently many times in different clades of flowering plants (52).
Thinning of the pollen wall in the form of an aperture enables efficient initiation of pollen tube growth but, at the same time, is a mechanical weakness of pollen grain. The same mechanical devices that would, under proper conditions, aid pollen tube germination can lead to grain rupture and the release of cytoplasm when the grain hydrates in an environment with inadequate osmolarity and ionic content, as might happen in the atmosphere. We have shown that the relative additional volume , which can be sustained by a nearly spherical porate grain, and the potential of the grain to rupture are determined predominantly by the ratio (Eq. (7)), a dimensionless parameter combining pore softness and its size. Other properties of the pollen grain, such as the number of pores, their precise distribution, and the contribution of bending in the process of bursting appear to be less important as long as the pores are sufficiently small.
Author contributions
A.Š. designed and performed the research. A.B. and A.Š. analyzed the data and wrote the paper.
Acknowledgments
A.B. acknowledges funding from the Slovenian Research Agency ARRS (Research Core Funding No. P1–0055).
Editor: Padmini Rangamani.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.01.019.
Supporting material
References
- 1.Firon N., Nepi M., Pacini E. Water status and associated processes mark critical stages in pollen development and functioning. Ann. Bot. 2012;109:1201–1213. doi: 10.1093/aob/mcs070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hoekstra F.A. In: Desiccation and Survival in Plants: Drying without Dying. Black M., Pritchard H.W., editors. CAB International; 2002. Pollen and spores: desiccation tolerance in pollen and the spores of lower plants and fungi; pp. 185–205. [Google Scholar]
- 3.Halbritter H., Ulrich S., et al. Frosch-Radivo A. Springer; 2018. Illustrated Pollen Terminology. [Google Scholar]
- 4.Evert R.F., Eichhorn S.E. W. H. Freeman and Company; 2013. Raven Biology of Plants. [Google Scholar]
- 5.Hamilton E.S., Jensen G.S., et al. Haswell E.S. Mechanosensitive channel MSL8 regulates osmotic forces during pollen hydration and germination. Science. 2015;350:438–441. doi: 10.1126/science.aac6014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cameron C., Geitmann A. Cell mechanics of pollen tube growth. Curr. Opin. Genet. Dev. 2018;51:11–17. doi: 10.1016/j.gde.2018.03.008. [DOI] [PubMed] [Google Scholar]
- 7.Rakusová H., Geitmann A. Pollen Tip Growth. Springer; 2017. Pollen tip growth: control of cellular morphogenesis through intracellular trafficking; pp. 129–148. [Google Scholar]
- 8.Katifori E., Alben S., et al. Dumais J. Foldable structures and the natural design of pollen grains. Proc. Natl. Acad. Sci. U S A. 2010;107:7635–7639. doi: 10.1073/pnas.0911223107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Matamoro-Vidal A., Raquin C., et al. Gouyon P.-H. Links between morphology and function of the pollen wall: an experimental approach. Bot. J. Linn. Soc. 2016;180:478–490. [Google Scholar]
- 10.Božič A., Šiber A. Mechanical design of apertures and the infolding of pollen grain. Proc. Natl. Acad. Sci. U S A. 2020;117:26600–26607. doi: 10.1073/pnas.2011084117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cecchi L., Scala E., et al. Asero R. Allergenicity at component level of subpollens particles from different sources obtained by osmolar shock: a molecular approach to thunderstorm-related asthma outbreaks. Clin. Exp. Allergy. 2020;51:253–261. doi: 10.1111/cea.13764. [DOI] [PubMed] [Google Scholar]
- 12.Buters J., Prank M., et al. Cecchi L. Variation of the group 5 grass pollen allergen content of airborne pollen in relation to geographic location and time in season. J. Allergy Clin. Immunol. 2015;136:87–95. doi: 10.1016/j.jaci.2015.01.049. [DOI] [PubMed] [Google Scholar]
- 13.Miguel A.G., Taylor P.E., et al. Flagan R.C. Meteorological influences on respirable fragment release from Chinese Elm pollen. Aerosol Sci. Technol. 2006;40:690–696. [Google Scholar]
- 14.D’Amato G., Liccardi G., Frenguelli G. Thunderstorm-asthma and pollen allergy. Allergy. 2007;62:11–16. doi: 10.1111/j.1398-9995.2006.01271.x. [DOI] [PubMed] [Google Scholar]
- 15.Sofiev M., Bergmann K.-C., editors. Allergenic Pollen: A Review of the Production, Release, Distribution and Health Impacts. Springer Science & Business Media; 2012. [Google Scholar]
- 16.Diethart B., Sam S., Weber M. Walls of allergenic pollen: special reference to the endexine. Grana. 2007;46:164–175. [Google Scholar]
- 17.Shams M., Fineman S. High Chinese elm pollen counts in the fall in Atlanta, Georgia, 2009–2015. Ann. Allergy Asthma Immunol. 2016;117:553–554. doi: 10.1016/j.anai.2016.08.011. [DOI] [PubMed] [Google Scholar]
- 18.Diehl K., Quick C., et al. Jaenicke R. The ice nucleating ability of pollen. Atmos. Res. 2001;58:75–87. [Google Scholar]
- 19.Pope F.D. Pollen grains are efficient cloud condensation nuclei. Environ. Res. Lett. 2010;5:044015. [Google Scholar]
- 20.Griffiths P.T., Borlace J.-S., et al. Pope F.D. Hygroscopic growth and cloud activation of pollen: a laboratory and modelling study. Atmos. Sci. Lett. 2012;13:289–295. [Google Scholar]
- 21.Wozniak M.C., Solmon F., Steiner A.L. Pollen rupture and its impact on precipitation in clean continental conditions. Geophys. Res. Lett. 2018;45:7156–7164. [Google Scholar]
- 22.Parre E., Geitmann A. More than a leak sealant. The mechanical properties of callose in pollen tubes. Plant Physiol. 2005;137:274–286. doi: 10.1104/pp.104.050773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Edlund A.F., Zheng Q., et al. Preuss D. Pollen from Arabidopsis thaliana and other Brassicaceae are functionally omniaperturate. Am. J. Bot. 2016;103:1006–1019. doi: 10.3732/ajb.1600031. [DOI] [PubMed] [Google Scholar]
- 24.Wang R., Dobritsa A.A. In: Annual Plant Reviews Online. Roberts J., editor. Vol. 1. John Wiley & Sons; 2018. Exine and aperture patterns on the pollen surface: their formation and roles in plant reproduction; pp. 1–40. [Google Scholar]
- 25.Vieira A.M., Feijó J.A. Hydrogel control of water uptake by pectins during in vitro pollen hydration of Eucalyptus globulus. Am. J. Bot. 2016;103:437–451. doi: 10.3732/ajb.1500373. [DOI] [PubMed] [Google Scholar]
- 26.Ackerman J.D. Abiotic pollen and pollination: ecological, functional, and evolutionary perspectives. Plant Syst. Evol. 2000;222:167–185. [Google Scholar]
- 27.Seung H.S., Nelson D.R. Defects in flexible membranes with crystalline order. Phys. Rev. A Gen. Phys. 1988;38:1005–1018. doi: 10.1103/physreva.38.1005. [DOI] [PubMed] [Google Scholar]
- 28.Lidmar J., Mirny L., Nelson D.R. Virus shapes and buckling transitions in spherical shells. Phys. Rev. E. 2003;68:051910. doi: 10.1103/PhysRevE.68.051910. [DOI] [PubMed] [Google Scholar]
- 29.Gompper G., Kroll D.M. Random surface discretizations and the renormalization of the bending rigidity. J. Phys. 1996;6:1305–1320. [Google Scholar]
- 30.Hartmann E. A marching method for the triangulation of surfaces. Vis. Comput. 1998;14:95–108. [Google Scholar]
- 31.Šiber A. Icosadeltahedral geometry of geodesic domes, fullerenes and viruses: a tutorial on the T-number. Symmetry. 2020;12:556–1–556–22. [Google Scholar]
- 32.Hager W.W., Zhang H. Algorithm 851: CG_DESCENT, a conjugate gradient method with guaranteed descent. ACM Trans. Math. Softw. 2006;32:113–137. [Google Scholar]
- 33.Šiber A. Buckling transition in icosahedral shells subjected to volume conservation constraint and pressure: relations to virus maturation. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2006;73:061915. doi: 10.1103/PhysRevE.73.061915. [DOI] [PubMed] [Google Scholar]
- 34.Celik G., Mungan D., Misirligil Z., et al. Poplar pollen-related allergy in Ankara, Turkey: how important for patients living in a city with high pollen load? Allergy Asthma Proc. 2005;26:113–119. [PubMed] [Google Scholar]
- 35.Borsch T. Pollen types in the Amaranthaceae. Morphology and evolutionary significance. Grana. 1998;37:129–142. [Google Scholar]
- 36.Joly C., Barillé L., et al. Visset L. Grain and annulus diameter as criteria for distinguishing pollen grains of cereals from wild grasses. Rev. Palaeobot. Palynol. 2007;146:221–233. [Google Scholar]
- 37.Jan F., Schüler L., Behling H. Trends of pollen grain size variation in C3 and C4 Poaceae species using pollen morphology for future assessment of grassland ecosystem dynamics. Grana. 2015;54:129–145. [Google Scholar]
- 38.Wan C., Liu J. The morphology and systematics of the pollen of Stellaria. Palynology. 2017;41:1–14. [Google Scholar]
- 39.Haas J., Creamer W., et al. Rodríguez C.V. Evidence for maize (Zea mays) in the late archaic (3000–1800 B.C.) in the Norte Chico region of Peru. Proc. Natl. Acad. Sci. U S A. 2013;110:4945–4949. doi: 10.1073/pnas.1219425110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gilissen L.J. The influence of relative humidity on the swelling of pollen grains in vitro. Planta. 1977;137:299–301. doi: 10.1007/BF00388166. [DOI] [PubMed] [Google Scholar]
- 41.Zuberi M.I., Dickinson H.G. Pollen-stigma interaction in Brassica. III. Hydration of the pollen grains. J. Cell Sci. 1985;76:321–336. doi: 10.1242/jcs.76.1.321. [DOI] [PubMed] [Google Scholar]
- 42.Šiber A., Ziherl P. CRC Press, Taylor & Francis Group; 2017. Cellular Patterns. [Google Scholar]
- 43.Božič A.L., Šiber A. Electrostatics-driven inflation of elastic icosahedral shells as a model for swelling of viruses. Biophys. J. 2018;115:822–829. doi: 10.1016/j.bpj.2018.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang Q., Nakamura S., et al. Miwa M. Release behavior of small sized daughter allergens from Cryptomeria japonica pollen grains during urban rainfall event. Aerobiologia. 2012;28:71–81. [Google Scholar]
- 45.Liu T., Zhang Z. Mechanical properties of desiccated ragweed pollen grains determined by micromanipulation and theoretical modelling. Biotechnol. Bioeng. 2004;85:770–775. doi: 10.1002/bit.10908. [DOI] [PubMed] [Google Scholar]
- 46.Wang K., Abdala A.A., et al. Khraisheh M.K. In: Membrane Characterization. Hilal N., Ismail A., et al.Oatley-Radcliffe D., editors. Elsevier; 2017. Mechanical characterization of membranes; pp. 259–306. Chap. 13. [Google Scholar]
- 47.Suryanto H., Muhajir M., et al. Yanuhar U. The mechanical strength and morphology of bacterial cellulose films: the effect of NaOH concentration. IOP Conf. Ser. Mater. Sci. Eng. 2019;515:012053-1–012053-7. [Google Scholar]
- 48.Bogen D.K., McMahon T.A. Do cardiac aneurysms blow out? Biophys. J. 1979;27:301–316. doi: 10.1016/S0006-3495(79)85219-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Reuge N., Schmidt F.M., et al. Abbé F. Elastomer biaxial characterization using bubble inflation technique. I: experimental investigations. Polym. Eng. Sci. 2001;41:522–531. [Google Scholar]
- 50.Taylor P.E., Flagan R.C., et al. Glovsky M.M. Release of allergens as respirable aerosols: a link between grass pollen and asthma. J. Allergy Clin. Immunol. 2002;109:51–56. doi: 10.1067/mai.2002.120759. [DOI] [PubMed] [Google Scholar]
- 51.Hargrove L., Simpson M.G. Ultrastructure of heterocolpate pollen in Cryptantha (Boraginaceae) Int. J. Plant Sci. 2003;164:137–151. [Google Scholar]
- 52.Prieu C., Sauquet H., et al. Albert B. More than sixty origins of pantoporate pollen in angiosperms. Am. J. Bot. 2017;90:924–930. doi: 10.3732/ajb.1700289. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.