Feedback-controlled dynamics of neuronal cells on directional surfaces

Abstract

The formation of neuronal networks is a complex phenomenon of fundamental importance for understanding the development of the nervous system. The basic process underlying the network formation is axonal growth, a process involving the extension of axons from the cell body and axonal navigation toward target neurons. Axonal growth is guided by the interactions between the tip of the axon (growth cone) and its extracellular environmental cues, which include intercellular interactions, the biochemical landscape around the neuron, and the mechanical and geometrical features of the growth substrate. Here, we present a comprehensive experimental and theoretical analysis of axonal growth for neurons cultured on micropatterned polydimethylsiloxane (PDMS) surfaces. We demonstrate that closed-loop feedback is an essential component of axonal dynamics on these surfaces: the growth cone continuously measures environmental cues and adjusts its motion in response to external geometrical features. We show that this model captures all the characteristics of axonal dynamics on PDMS surfaces for both untreated and chemically modified neurons. We combine experimental data with theoretical analysis to measure key parameters that describe axonal dynamics: diffusion (cell motility) coefficients, speed and angular distributions, and cell-substrate interactions. The experiments performed on neurons treated with Taxol (inhibitor of microtubule dynamics) and Y-27632 (disruptor of actin filaments) indicate that the internal dynamics of microtubules and actin filaments plays a critical role for the proper function of the feedback mechanism. Our results demonstrate that axons follow geometrical patterns through a contact-guidance mechanism, in which high-curvature geometrical features impart high traction forces to the growth cone. These results have important implications for our fundamental understanding of axonal growth as well as for bioengineering novel substrate to guide neuronal growth and promote nerve repair.

Significance

Decades of research have shown that environmental guidance cues (biochemical, mechanical, geometrical) control the dynamics of neuronal axons, and the wiring up of the nervous system. However, a detailed quantitative model of the axonal growth is still missing. We demonstrate that axonal dynamics on substrates with periodic micropatterns is governed by a closed-loop feedback control mechanism that leads to axonal alignment on these surfaces. Axons follow geometrical patterns through a contact-guidance mechanism, in which high-curvature geometrical features impart high traction forces to the tip of the axon. We develop a quantitative theoretical model that incorporates mechanical interactions between the axon and the growth substrate. This model fully accounts for the experimental data, including diffusion coefficients, speed distributions, and angular alignment.

Introduction

Neurons are the basic constituents that make up the nervous system, establishing neuronal networks to transmit information throughout the body. During their growth, neurons extend axons and dendrites, which navigate to other neurons and build complex interwoven networks that in many organisms grow to contain billions of synapses. The extension of the axon is guided by its growth cone, a dynamical unit that is located at the distal tip of the axon (1,2). To navigate its environment, the growth cone uses environmental cues such as electrical, chemical, mechanical, and geometrical stimuli (1, 2, 3, 4). The dynamics of the growth cone throughout the external environment is controlled by the cell cytoskeleton, a flexible ensemble of actin and microtubule filaments and their associated molecular motors (1, 2, 3, 4, 5, 6, 7).

Previous research has characterized many of the molecular pathways (1, 2, 3, 4, 5, 6, 7) responsible for intercellular signaling in developing neuronal systems (2,5, 6, 7, 8); however, the description of the fundamental mechanisms behind the growth cone response to geometrical and mechanical cues has not been determined at the same level of detail. Much of the research into geometrical and mechanical cues has studied neurons on substrates in vitro where the geometry of the substrate can be controlled. These studies have shown that neurons grown on substrates with periodic geometrical features develop different growth patterns as a population compared with neurons grown on surfaces lacking a periodic geometry (3,5,9, 10, 11, 12, 13, 14). Observational differences include populations of axons that are markedly longer and that strongly tend to align their growth along preferred spatial directions (9,10,12,13,15, 16, 17, 18). Most of this previous work has focused on qualitative or semi-quantitative models to describe the influence of a substrate with controlled geometrical features on neuronal development. However, a detailed quantitative model of the growth dynamics on these substrates that incorporates the mechanisms of axonal alignment and cell-surface interactions is still missing.

Fundamentally, axonal growth on surfaces with controlled geometries arises as the result of an interplay between deterministic and stochastic components of growth cone motility (12,18, 19, 20, 21). An example of a deterministic influence is the presence of a preferred direction of growth along a specific geometrical pattern on a substrate (18,21). Examples of stochastic influences are the effects of polymerization of cytoskeletal features such as actin filaments and microtubules, cell signaling, low concentration biomolecule detection, biochemical reactions within the neuron, and the formation of lamellipodia and filopodia (1,2,7,22). The resultant growth cannot be predicted for individual neurons due to this stochastic-deterministic interplay; however, the defining features of a population of neurons can be modeled by probability functions that satisfy a set of well-defined stochastic differential equations (12,19,20). Foremost examples include the Langevin and Fokker-Planck equations, which have been used previously to capture the effects of both deterministic and stochastic influences on cellular motion, which is treated as a form of biased random motion (9,12,19,20,23, 24, 25, 26, 27).

In previous work (20,21) we have shown that axonal dynamics on uniform glass surfaces is described by an Ornstein-Uhlenbeck (OU) process, defined by a linear Langevin equation and stochastic white noise (28,29). We have also reported that neurons cultured on poly-D-lysine(PDL)-coated polydimethylsiloxane (PDMS) substrates with periodic parallel ridge micropatterns of spatial periodicity d (henceforth referred to as the pattern spatial period) grow axons parallel to the surface patterns (18,21). We have studied axonal growth as a function of time on these micropatterned surfaces and found that axonal alignment increases as a function of time (18). While initially the growth can be represented as an OU process, at times greater than 48 h axonal growth can no longer be described as standard diffusion, following instead a superdiffusive behavior. This growth is characterized by non-Gaussian speed distributions and power law dependence of the axonal mean square length with time (18). Moreover, axonal dynamics is described by non-linear Langevin equations, involving quadratic velocity terms and non-zero coefficients for the angular orientation of the growing axon (21). In another paper, we have used the Langevin and Fokker-Planck equations to quantify axonal growth on surfaces with ratchet-like topography (asymmetric tilted nanorod: nano-ppx surfaces), and we have investigated the diffusion coefficient of axons on this type of surface geometry (12). It was shown that the axonal growth is aligned with a preferred spatial direction as a result of a “deterministic torque” that drives the axons to directions determined by the substrate geometry. We have also measured the angular distributions and the coefficients of diffusion and angular drift on these substrates (12).

In this paper, we demonstrate that the motion of axons on surfaces with micropatterned periodic geometrical patterns is governed by a closed-loop feedback control mechanism that leads to axonal alignment on these surfaces. We develop a quantitative stochastic framework based on the Fokker-Planck equation that treats each growth cone as a system with a closed feedback loop. We demonstrate that a simple mechanical model based on the axon bending-induced strain justifies the use of the Fokker-Planck equation and allows us to extract the main dynamical parameters for both untreated and chemically modified neurons. This theoretical model fully accounts for the experimental data measured on ensembles of axons, including speed distributions and angular alignment. Furthermore, our experiments show that inhibition of cytoskeletal dynamics by treatment of neurons with Taxol (inhibitor of microtubules) and Y-27632 (inhibitor of myosin II and actin dynamics) results in a significant decrease of the axonal alignment by altering the feedback mechanism of the cell. Feedback control means that the growth cone is guided toward a target by using information retrieved from the environment (external stimuli). This is a powerful technique for describing the dynamical properties of many types of physical and biological systems, including particle trapping (30, 31, 32), optical tweezers (33, 34, 35), neuron firing (36,37), and cellular dynamics (38, 39, 40). We demonstrate that this approach provides significant insight into the neuronal response to external mechanical and topographical stimuli. In particular, our results show that axonal dynamics is controlled by a contact-guidance mechanism, which stems from cellular feedback in an external periodic potential imparted by the surface geometry. This work has a significant impact for designing new platforms for guiding growth and regeneration of neurons and provides new insights for developing a general model to describe cellular motility.

Materials and methods

Surface preparation, cell culture, and imaging

The periodic micropatterns on PDMS surfaces are made of parallel ridges separated by troughs. Each surface is characterized by a different value of the pattern spatial period d, defined as the distance between two neighboring ridges (Fig. 1 a). To make these periodic patterns we used a simple fabrication method based on imprinting diffraction grids with different grating constants onto PDMS substrates (additional experimental details are given in supporting material).

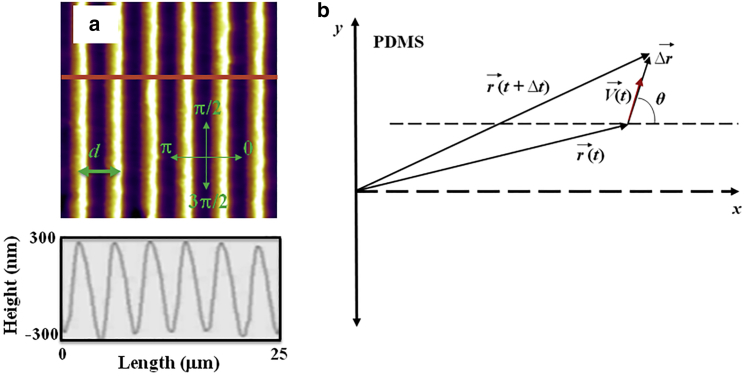
Figure 1.

(a) Top: AFM topographic image of a PDL-coated PDMS-patterned surface. Bottom: line scan (cross section) along the red line shown in the AFM image. (b) Coordinate system and the definition of the angular coordinate θ. The x axis is defined as the axis perpendicular to the direction of the PDMS patterns. The directions corresponding to θ = 0, π/2, and 3π/2, and the pattern spatial period d are also shown in (a). The line scan in (a) shows that the micropatterns are periodic in the x direction with the spatial period d = 4 μm, and have a constant profile shape with a depth of approximately 0.6 μm. To see this figure in color, go online.

The direction of the patterns is shown in Fig. 1 by the parallel bright stripes (ridges), and by the parallel dark stripes (troughs). We have performed control experiments that demonstrate that the micropatterns used in our experiments have constant shape and depth. Examples of topographical images are presented in Figs. 1 a and S1 a). The micropatterned surfaces were spin-coated with PDL (Sigma-Aldrich, St. Louis, MO) solution of concentration 0.1 mg/mL. Neuronal cells were imaged using an MFP3D atomic force microscope (AFM) equipped with a BioHeater closed fluid cell, and an inverted Nikon Eclipse Ti optical microscope (Micro Video Instruments, Avon, MA). Control experiments demonstrate that the topographical and mechanical properties of the micropatterned PDMS substrates do not change significantly among surfaces with different spatial periods or upon coating with PDL (Figs. S1 b, S2, and S3).

The cells used in this work are cortical neurons obtained from embryonic day 18 rats. For cell dissociation and culture we have used established protocols presented in our previous work (9,12,18,20,21,41, 42, 43). Cortical neurons were cultured on micropatterned PDMS substrates coated with PDL. The cells were cultured at a surface density of 4000 cells/cm². We have previously reported that neurons cultured at relatively low densities (in the range 3000–7000 cells/cm²) are optimal for studying axonal growth on surfaces with different mechanical, geometrical, and biochemical properties (9,12,18,21,41).

Fluorescence images were acquired using a standard fluorescein isothiocyanate (FITC) filter: excitation, 495 nm and emission, 521 nm (details on acquiring the fluorescence images are provided in the supporting material). For the experiments on chemically modified cells, we treated the neurons with either (1) Taxol (10 μM concentration) or (2) the chemical compound Y-27632 (10 μM concentration), which were added to the neuron growth medium at the time of plating. Previous work has shown that a Taxol concentration of 10 μM is very effective in suppressing the microtubule dynamics (12,22,41), and that 10 μM Y-27632 is very efficient in disrupting actin polymerization and the formation of actin bundles, thus reducing traction forces between the neurons and the growth substrates (42).

Data analysis

Growth cone position, axonal length, and angular distributions were measured and quantified using ImageJ (National Institutes of Health). The displacement of the growth cone was obtained by measuring the change in the center of the growth cone position. Examples of images that show the tracked position for axons are shown in Fig. S4. To measure the growth cone velocities, the samples were imaged every Δt = 5 min for a total period of 1 h per sample. The 5-min time interval between measurements was chosen such that the typical displacement $\Delta \overrightarrow{r}$ of the growth cone in this interval satisfies two requirements: (1) it is larger than the experimental precision of our measurement (∼0.1 μm) (20,21); (2) the ratio $\Delta \overrightarrow{r}/\Delta t$ accurately approximates the instantaneous velocity $\overrightarrow{V}$ of the growth cone. The speed of the growth cone is defined as the magnitude of the velocity vector $V\left(t\right)=\left|\overrightarrow{V}\left(t\right)\right|$, and the growth angle θ(t) is measured with respect to the x axis (growth angle and the x axis are defined in Fig. 1).

To obtain the speed distributions (Figs. 3 c, d, S6 c, d, and S7), the range of growth cone speeds at each time point was divided into 15 intervals of equal size $\left|\Delta {\overrightarrow{V}}_0\right|.$ Experimental data (Fig. S4) show that, over a distance of ∼20 μm, the axons can be approximated by straight line segments, with a high degree of accuracy. Therefore, to obtain the angular distributions for the growth angle θ (Figs. 3 a, b, 4 c, d, S6 a, and b), we tracked all axons using ImageJ and then partitioned them into segments of 20 μm in length, following the same procedure outlined in our previous work (18,21). Next, we recorded the angle that each segment makes with the x axis (schematic shown in Fig. 1). The total range [0, 2π] of growth angles was divided into 18 intervals of equal size $\Delta {\theta }_0=\pi /9$ (Figs. 3 a, b, 4 c, d, S6 a, and b). Experimentally, the average for the absolute value of sin θ for each type of surface is obtained according to the formula:

$$⟨\left|\text{sin}\theta \right|⟩=\frac{1}{N}\cdot \sum _{i=1}^N\left(\left|\text{sin}{\theta }_i\right|\right)$$ (1)

where N is the total number of axonal segments of 20 μm in length, measured on a given type of surface, and ${\theta }_i$ represents the angle that i^th segment makes with the x axis.

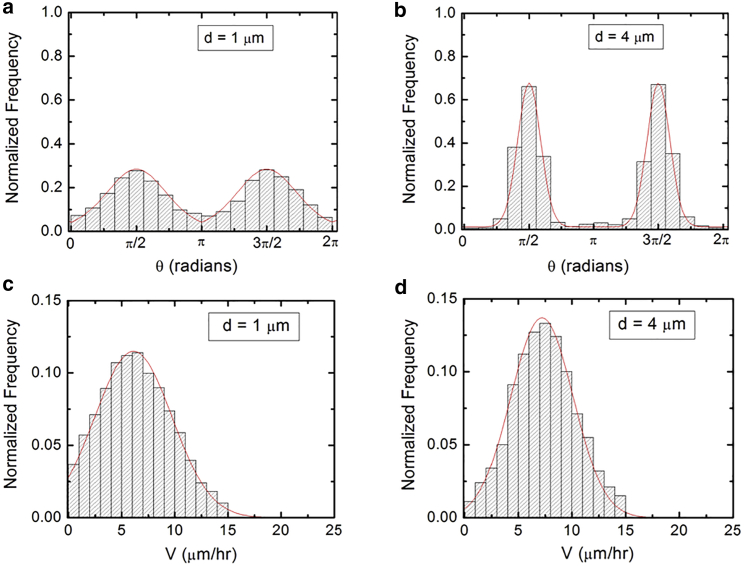
Figure 3.

(a and b) Examples of normalized experimental angular distributions for axonal growth measured on micropatterned PDMS surfaces with different pattern spatial periods d. The continuous red curves in each figure are the predictions of the theoretical model discussed in the main text. The vertical axis (labeled normalized frequency) represents the ratio between the number of axonal segments growing in a given direction and the total number N of axon segments. Each axonal segment is of 20 μm in length (see section “data analysis”). All distributions show data collected at t = 40 h after neuron plating. (a) Angular distribution obtained for N = 1404 different axon segments on surfaces with d = 1 μm. (b) Angular distribution obtained for N = 1560 different axon segments on surfaces with d = 4 μm. The data show that the axons display strong directional alignment along the surface patterns (peaks at $\theta =\pi /2\text{and}\theta =3\pi /2$), with the highest degree of alignment (sharpness of the distribution) measured for d = 4 μm. (c and d) Examples of normalized speed distributions for growth cones measured on micropatterned PDMS surfaces with different pattern spatial period d. (c) Speed distribution for N = 210 different growth cones measured on surfaces with d = 1 μm. (d) Speed distribution for N = 242 different growth cones measured on surfaces with d = 4 μm. The continuous red curves in each figure represent the predictions of the theoretical model discussed in the main text. To see this figure in color, go online.

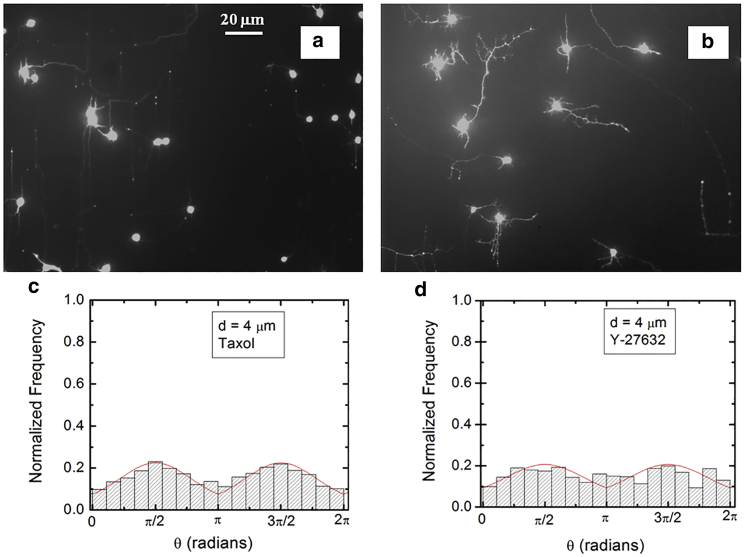
Figure 4.

(a and b) Examples of axonal growth for cortical neurons treated with chemical compounds that inhibit the cytoskeletal dynamics: (a) Taxol and (b) Y-27632. The growth substrates are PDL-coated PDMS surfaces with periodic micropatterns with the pattern spatial d = 4 μm. The images are captured at t = 40 h after neuron plating. The scale bar shown in (a) is the same for both images. (c and d) Normalized experimental angular distributions corresponding to the images shown in (a) and (b), respectively. The neurons treated with Taxol or Y-27632 show a significant decrease in the degree of alignment with the surface patterns, compared with the untreated cells (Figs. 2 and 3). The continuous red curves in each figure are the predictions of the theoretical model discussed in the main text. To see this figure in color, go online.

Results

Axonal alignment and speed distributions for untreated neurons

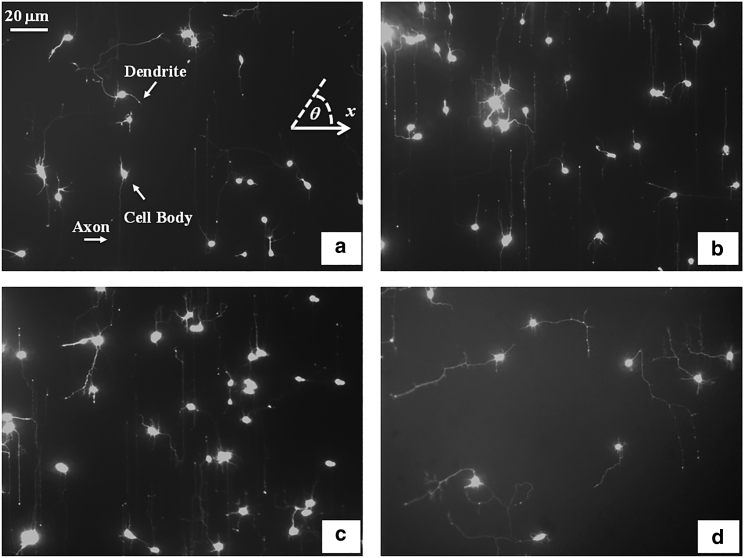
Cortical neurons are cultured on PDL-coated PDMS surfaces with parallel micropatterns (periodic parallel ridges separated by troughs). The surfaces differ by the value of the pattern spatial period d defined as the distance between two neighboring ridges (Fig. 1). We analyze the growth of both untreated and chemically modified neuronal cells on surfaces with spatial periods in the range d = 1–10 μm (in increments of 1 μm). Fig. 2 shows examples of images of axonal growth for untreated cells, captured at t = 40 h after cell plating. Examples of the corresponding axonal normalized angular and speed distributions are shown, respectively, in Fig. 3 a and c (for d = 1 μm), and Fig. 3 b and d (for d = 4 μm). Additional angular and speed distributions are shown in Fig. S6. We have previously demonstrated (21) that axons of untreated neurons display maximum alignment along PDMS patterns for surfaces where the pattern spatial period d matches the linear dimension of the growth cone l, where l is in the range 3–6 μm. The experimental data shown in Fig. 2 b and c are in agreement with our previous findings. Furthermore, the speed distributions for these growth cones are close to Gaussian distributions, which are expected for t = 40 h after cell plating (18). We note that, in contrast to axons, dendrites do not display angular alignment along the surface micropatterns (examples of angular distributions for dendrites are shown in Fig. S5).

Figure 2.

Examples of cultured cortical neurons on PDL-coated PDMS surfaces with periodic micropatterns. The main structural components of a neuronal cell are labeled in (a). The angular coordinate θ used in this paper is defined in the inset of (a). All angles are measured with respect to the x axis, defined as the axis perpendicular to the direction of the PDMS patterns (see Fig. 1). The pattern spatial period is d = 1 μm in (a); d = 4 μm in (b); d = 6 μm in (c); d = 9 μm in (d). All images are captured 40 h after neuron plating. The scale bar shown in (a) is the same for all images.

Axonal alignment and speed distributions for neurons treated with Taxol and Y-27632

To further investigate the axonal dynamics on PDMS surfaces with periodic micropatterns, we measure angular and speed distributions for neurons treated with chemical compounds known to inhibit the dynamics of the cell cytoskeleton. Fig. 4 a shows an example of axonal growth for neurons treated with 10 μM Taxol. Fig. 4 b shows a similar image obtained for neurons treated with 10 μM Y-27632. The pattern spatial period of the PDMS surfaces is d =4 μm for both images. Taxol is a chemical compound that is commonly used to inhibit the normal functioning of the cytoskeleton, due to the disruption of microtubule dynamics (12,22,41). Y-27632 is known to inhibit the formation of actin bundles and the reorganization of actin-based structures during neuronal growth (42,44). Both of these compounds have been shown to be effective at the concentration of 10 μM used in our experiments (12,22,41,42,44). The normalized angular distributions for axonal growth are shown in Fig. 4 c for Taxol and in Fig. 4 d for Y-27632. The neurons treated with either Taxol or Y-27632 show a dramatic decrease in the degree of alignment with the surface patterns compared with the unmodified cells (Figs. 2 and 3). The data show that while the axonal directionality is greatly reduced by the chemical treatment, the treated neurons still grow long axons and form cell-cell connections (Fig. 4 a and b). These results demonstrate that the disruption of the cytoskeletal dynamics for chemically treated neurons affects only the degree of alignment with the surface pattern, leaving the navigation of the growth cone and axonal outgrowth uninhibited.

Stochastic model of axonal growth on surfaces with periodic micropatterns

Axonal motion on the PDMS substrates is characterized by both deterministic and stochastic components (12,18, 19, 20, 21). The dynamics of the growth cones is described by the spatial probability distribution $p(\overrightarrow{r},t)$, whose time evolution is governed by the Smoluchowski (spatial Fokker-Planck) equation (28,29):

$$\frac{\partial }{\partial t}p\left(\overrightarrow{r},t\right)=D\cdot {\nabla }^{2}p\left(\overrightarrow{r},t\right)+\frac{1}{\gamma }\nabla \cdot \left(p\left(\overrightarrow{r},t\right)\cdot \nabla V\left(\overrightarrow{r}\right)\right)$$ (2)

where D represents the diffusion (cell motility) coefficient, $\gamma$ is the damping coefficient (friction constant of the corresponding Langevin equation), and $V\left(\overrightarrow{r}\right)$ is the effective potential that determines the axonal motion. The net force per unit mass acting on the growth cone is $\overrightarrow{f}=-\nabla V\left(\overrightarrow{r}\right)$ (21). We write the effective potential as a sum of three terms:

$$V\left(\overrightarrow{r}\right)=V_{ext}\left(\overrightarrow{r}\right)+V_F\left(\overrightarrow{r}\right)+V_{int}\left(\overrightarrow{r,}p\right)$$ (3)

where $V_{ext}\left(\overrightarrow{r}\right)$ is the neuron-substrate coupling potential (external potential imposed by the substrate geometry), $V_F\left(\overrightarrow{r}\right)$ is the potential responsible for the closed-loop feedback (to be discussed below), and $V_{int}(\overrightarrow{r},p)$ is the neuron-neuron interaction potential (quantifies the interactions between neuronal cells).

In this paper, we consider the motion of an ensemble of N growth cones when the neuron-neuron signaling potential $V_{int}(\overrightarrow{r},p)$ is negligible compared with the neuron-substrate interactions described by the periodic potential (see Eq. 4 below). This is indeed the case for the low values of the cell culture density (4000 cells/cm²) used in our experiments, as shown in previous work (9). The micropatterned PDMS substrates have uniform geometry in the y direction, and periodic geometry along the x axis (Fig. 1). Thus, the mechanical coupling between the growth cone and the substrate results in a constant potential along the y direction, and a periodic external potential along the x axis:

$$V_{\text{ext}}\left(x\right)=V_0\cdot {\sin }^2\frac{\pi x}{d}$$ (4)

where V₀ is the maximum strength of the external potential imposed by the surface geometry, d represents the pattern spatial period, and x is the coordinate along the x axis defined in (Fig. 1 b). We note that the PDMS surfaces are coated with a uniform layer of PDL (Figs. S1–S3), and thus the substrate chemistry contributes with a constant value to $V_{ext}\left(\overrightarrow{r}\right)$ and does not influence the axonal dynamics described by Eq. (2).

Experimental data show that the motion of growth cones along the x axis on the micropatterned surfaces is similar to the dynamics of particles inside a harmonic trap centered on the mean position, similar to the dynamics of polarizable colloids inside optical traps (30,33, 34, 35,45). This type of dynamics is described by the harmonic potential (30,34,35):

$$V_{\text{F}}\left(x,p\right)=V\cdot {\left(x-⟨x⟩\right)}^2$$ (5)

where V is the strength of the harmonic confinement, and $⟨x\left(t\right)⟩$ is the time-dependent growth cone mean position along the x axis. We emphasize that in our model the time evolution of the probability density in Eq. 2 is explicitly written in real space, as opposed to velocity space treated in previous work (18,20,21), and thus it allows us to separate the effects of periodic geometry (V_ext given by Eq. 4) from the feedback control (V_F given by Eq. 5).

Equations 3, 4, and 5 imply that the spatial probability distribution $p(\overrightarrow{r},t)$ admits the following separation of variables: $p(\overrightarrow{r},t)=p(x,t)\cdot p(y,t)$ where $p(x,t)$ and $p(y,t)$ represent the cellular probability distributions in the y and x directions respectively. Furthermore, the approximation $V_{int}\left(\overrightarrow{r},p\right)$ = 0 and the uniform geometry in the y direction implies that $p(y,t)$ is a constant, and thus:

$$p(\overrightarrow{r},t)=A\cdot p(x,t)$$ (6)

where A is an overall normalization constant.

With the geometrical and feedback potentials given by Eqs. 4 and 5, and the probability distribution given by Eq. 6, the equation of motion for the growth cone (Eq. 2) in the x direction becomes:

$$\frac{\partial }{\partial t}p\left(x,t\right)=D\cdot \frac{{\partial }^2}{\partial x^2}p\left(x,t\right)+\frac{1}{\gamma }\frac{\partial }{\partial x}\left(p\left(x,t\right)\cdot \frac{\partial }{\partial x}\left(V_{ext}\left(x\right)+V_F(x,⟨x⟩\right)\right)$$ (7)

with the time-dependent growth cone mean position along the x axis:

$$⟨x\left(t\right)⟩=\frac{1}{N}\int dxxp\left(x,t\right)$$ (8)

The model described by Eqs. 4, 5, 6, 7, and 8 predicts that the overall motion for the axons has two components: (1) a uniform drift along the directions of minimum $V_{\text{ext}}\left(x\right)$ (i.e., along the y axis in Fig. 1), and (2) a random walk around these equilibrium positions. This is indeed what is observed experimentally. At early times the growth cone dynamics resembles a Brownian motion, resulting in a slow increase in the mean growth cone position $⟨x⟩$ along the x axis. As time progresses, the feedback control, which depends on $⟨x⟩$, steers the axonal motion along the minimum values of the periodic potential; i.e., along the micropatterned parallel PDMS lines (Figs. 1 and 2). Furthermore, in the absence of the confinement imposed by the periodic potential (Eq. 4) and feedback control potential (Eq. 5), the equation of motion for the growth cones (Eq. 2) reduces to a regular diffusion (OU) process characterized by exponential decay of the autocorrelation functions with a characteristic time $\tau =\frac{1}{\gamma }$, axonal mean square length that increases linearly with time, and velocity distributions that approach Gaussian functions (28,29). In our previous work we have shown that this is indeed the case for axonal growth on PDL-coated glass and PDMS surfaces characterized by large pattern spatial periods: d > 9 μm (21).

To model the motion of the growth cones on micropatterned PDMS periodic surfaces we solve Eq. 7 numerically, subject to the stationary solutions (18,28,29):

$$p\left(x\right)=\left(1/Z\right)\cdot \exp \left(-\left(V\cdot x^2+V_{\text{ext}}\left(x\right)\right)/D\cdot \gamma \right)$$ (9)

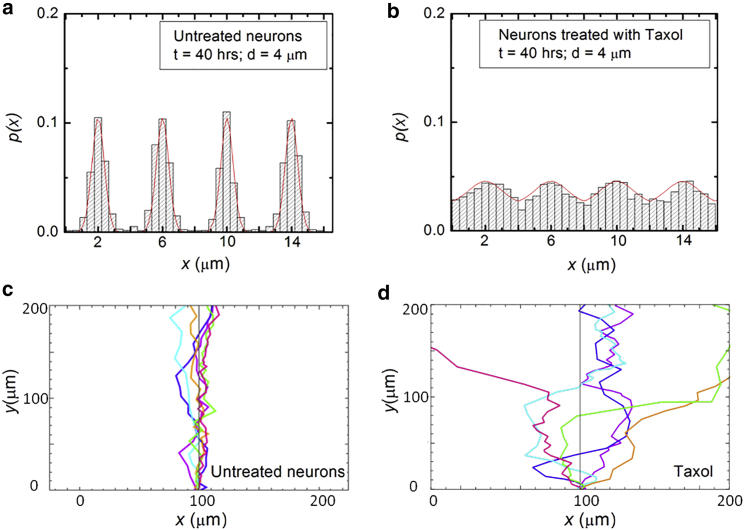
where Z is a normalization constant. Fig. 5 a and b show examples of experimentally measured probability distributions for the motion of the growth cones in the x direction. Fig. 5 a shows data obtained for untreated neurons, while Fig. 5 b displays data obtained for neurons treated with Taxol. The pattern spatial period for both Fig. 5 a and b is d = 4 μm. The red curves in Fig. 5 a and b represent fits to the data with the solutions of the theoretical model given by Eq. 7. For the case of untreated neurons, the solutions of Eq. 7 fit the experimental data for the probability distribution $p(x,t)$ (Fig. 5 a) with the following values of the growth parameters: diffusion coefficient $D=(22\pm 4)\text{μ}{\text{m}}^2/\text{hr}$, damping coefficient $\gamma =(0.14\pm 0.05){\text{hr}}^{-1}$, and strengths of the external and feedback potentials $V_0=(1.9\pm 0.3)\text{μ}{\text{m}}^2/{\text{hr}}^2$, and $V=(0.23\pm 0.08){\text{hr}}^{-2}$, respectively. The values for the diffusion and damping coefficients are close to the ones we have previously reported for growth cones on glass and PDMS surfaces (18,20,21). The probability distribution in the case of neurons treated with Taxol (Fig. 5 b) is fitted with the solutions of Eq. 7 for the following values of the growth parameters: diffusion coefficient $D=(14\pm 3)\text{μ}{\text{m}}^2/\text{hr}$, damping coefficient $\gamma =(0.11\pm 0.03){\text{hr}}^{-1}$, and strengths of the external and feedback potentials $V_0=(0.6\pm 0.2)\text{μ}{\text{m}}^2/{\text{hr}}^2$, and $V=(0.08\pm 0.04){\text{hr}}^{-2}$, respectively. We note that the values for the growth parameters decrease either upon the chemical treatment of the neuron or with increasing spatial period d (see Table S1 for a summary of these parameters).

Figure 5.

(a and b) Examples of experimentally measured probability distributions for the motion of the growth cones in the x direction. The red curves represent fits to the data with the solutions of the theoretical model given by Eq. 7. The fit parameters are the diffusion (cell motility) coefficient D, the damping coefficient γ, and the magnitudes V₀ and V of the external and feedback potential, respectively. (a) Data obtained for N = 331 untreated neurons measured at t = 40 h on PDMS surfaces with d = 4 μm. (b) Data obtained for N = 298 neurons treated with Taxol measured at t = 40 h on PDMS surfaces with d = 4 μm. (c and d) Simulated neuronal growth for untreated (c) and Taxol-treated neurons (d). The simulations are performed by using the values of the growth parameters obtained from the fit of the experimental data with solutions of Eq. 7 (see main text). To see this figure in color, go online.

We use the solutions of Eq. 7 for the probability distribution to simulate axonal growth trajectories, as well as axonal speed and angular distributions. The simulations are performed using the above values for the growth parameters and strengths of the periodic and feedback potentials (obtained from the data fit in Fig. 5 a and b) with no additional adjustable parameters (see the supporting material for simulation details). Fig. 5 c and d show examples of simulation results for untreated (Fig. 5 c) and Taxol-treated neurons (Fig. 5 d) grown on surfaces with d = 4 μm. Similar experimental data and simulations obtained for untreated neurons grown on surfaces with d = 6 μm, as well as neurons treated with Y-27632, are shown in Fig. S8. Simulations performed for untreated neurons cultured on surfaces with d = 9 μm and d = 10 μm are shown in Fig. S9. We emphasize that the angular distributions and speed distributions obtained from these simulations match the experimental data for untreated (Figs. 3 and S6), Taxol-, and Y-27632-treated neurons (Figs. 4 and S7) without the introduction of any additional parameters. The simulated axon trajectories in Figs. 5 c and S8 c reproduce the high degree of alignment observed experimentally for untreated neurons grown on surfaces with d = 4 μm or d = 6 μm (Fig. 2 b and c, Figs. 3 b and S6 a). Figs. 5 d and S8 d show simulated growth trajectories with intermediate degree of alignment (similar to the data measured on Taxol- and Y-27632-treated neurons in Fig. 4). Fig. S9 shows simulated axon trajectories with low degree of alignment, similar to the growth data measured on surfaces with d = 9 μm and d = 10 μm (Fig. S6 b). In the limit of very large d, the dynamics reduces to simple Brownian motion, as discussed above. The Table S1 presents a summary of the values for the growth parameters obtained from the comparison between the theoretical model (solutions of Eq. 7) and the experimental data for different cells and substrates. The decrease in the parameters V and V₀ observed for chemically treated cells, as well as for untreated neurons cultured on surfaces with large d, reflects the lower degree of alignment measured in these cases.

Mechanical model for axonal dynamics

We justify the stochastic model described in the previous section by introducing a simple mechanical model that takes into account the cell-substrate interactions when the axon grows close to the top of the micropattern; this is indeed the case for most axons at t = 40 h after cell culture as we have shown in (18) (see also Fig. S10). We first note that the micropatterned PDMS lines can be approximated locally with semi-cylinders with radius of curvature R (Fig. S1 a). The model considers the bending-induced strain sustained by the axon while growing close to the top of the semi-cylindrical surface: axonal adhesion to the micropattern leads to axonal bending, which in turn leads to increased mechanical strain energy in the axon cytoskeleton. The mechanical strain energy E depends on the axon bending stiffness B, and the local surface curvature $K(\theta ,R)$ (4,46):

$$E=\frac{1}{2}B\cdot K^2(\theta ,R)$$ (10)

In the case of axonal growth on the micropatterned surfaces, the curvature of the axon on the surface of the semi-cylinder is given by:

$$K(\theta ,R)=\frac{\left|\text{cos}\left(\theta \right)\right|}{R}$$ (11)

where R is the radius of curvature of the semi-cylindrical pattern. Under the assumption of maximum entropy (close to growth equilibrium), the probability of axon growing in a given direction is given by Boltzmann distribution:

$$p\left(\theta \right)=A_1\cdot \text{exp}\left(-\frac{E}{E_0}\right)$$ (12)

where E₀ is the characteristic energy scale for axonal bending, and A₁ is an overall normalization constant. By combining Eqs. 10, 11, and 12 we can write the following expression for the angular probability distribution:

$$p\left(\theta \right)=A\cdot \text{exp}(-\frac{B}{E_0\cdot R^2}\cdot co{s}^2\left(\theta \right))$$ (13)

When the axon grows close to top of the semi-cylindrical pattern, the external potential V_ext is approximatively constant (close to its maximum value; see Eq. 4). In this limit, Eq. 13 has the general form of Eq. 9, given that the relationship between the displacement in the x direction and the axon growth angle θ is $\Delta x=\Delta r\cdot \text{cos}\left(\theta \right)$ (Fig. 1 b), where $\Delta r=20\text{ μm}$ (see section “data analysis”). Therefore, a direct comparison between Eq. 13 (derived from the mechanical beam model) and Eq. 2 (solution of the stochastic Fokker-Planck equation) leads to the following relationship between the stochastic parameters (diffusion coefficient $D$, damping coefficient $\gamma$, strength of the feedback potential V) and the mechanical parameters (axon bending stiffness B, the characteristic energy scale E₀, and the surface radius of curvature R):

$$\frac{V\cdot \Delta L^2}{D\cdot \gamma }=\frac{B}{E_0\cdot R^2}$$ (14)

We emphasize that Eq. 13 is a special case of Eq. 9 (obtained at growth equilibrium and when the growth cone is close to the top of the micropattern). However, we can use Eq. 14 (derived by direct comparison between Eqs. 9 and 13) together with the values for the stochastic parameters found in the previous section to calculate the ratios between the axon bending modulus B and the characteristic energy scale E₀ for untreated as well as chemically modified neurons. The radius of curvature of the micropatterns could be measured directly by AFM (Fig. S1 a). For example, for neurons grown on surfaces with d = 4 μm, the AFM measurements give R ∼ 0.5 μm. From Eq. 14 we then obtain $B/E_0=(6.9\pm 0.9)\text{ μ}{\text{m}}^3$ for untreated neurons, and $B/E_0=(5.5\pm 0.9)\text{ μ}{\text{m}}^2$ for neurons treated with Taxol. The corresponding value for Y-27632-treated cells is $B/E_0=(5.1\pm 0.9)\text{ μ}{\text{m}}^2)$ (all values are obtained for cells cultured on surfaces with d = 4 μm). A summary of the values for B/E₀ for different types of surfaces and chemical treatment is given in Table S1. Eq. 14 gives only the ratio between the bending modulus B and the characteristic energy scale E₀ for mechanical interactions between the axons and the PDMS micropatterns on the growth substrate. Assuming a constant energy scale E₀ for all these cases, we can perform a joint fit for all data points using the maximum likelihood method (12,20). The constant value of the characteristic energy scale that maximizes the likelihood of measuring the given data set is $E_0=(3.2\pm 0.7)\cdot {10}^{-15}\text{ J}$. Using this constant value for E₀ we obtain the following values for the axonal bending rigidities: $B=(23.7\pm 0.8)\text{J}\cdot \text{μ}{\text{m}}^2$ for untreated neurons, $B=(17.6\pm 0.8)\text{J}\cdot \text{μ}{\text{m}}^2$ for neurons treated with Taxol, and $B=(16.3\pm 0.8)\text{J}\cdot \text{μ}{\text{m}}^2$ for neurons treated with Y-27632 (cells cultured on surfaces with d = 4 μm). These values for the axonal bending rigidity are comparable with the values for axon bending rigidity reported in the literature (4,43,46,47), and are consistent with our previous values for the elastic modulus of the neuronal cells (41, 42, 43), if we assume a simple rigid beam model for the axon (48).

Feedback control dynamics for axonal growth in periodic potentials

The stochastic model described in the previous sections shows that the feedback potential V_F depends on the dynamical state of the whole system, through the ensemble average $⟨x\left(t\right)⟩$ (Eq. 5). Thus, this model implies that the axonal motion on surfaces with periodic geometries exhibits a simple closed-loop behavior: the growth cone detects the geometrical cues on the surface and tends to align its motion along certain preferred directions that maximize the cell-surface interactions. In general, closed-loop feedback control means that the system is steered toward a target behavior by using information that is retrieved from the environment through continuous measurements.

To further investigate this model, we determine the average value for |sinθ| (absolute value for the sine of the axonal growth angle), which measures axonal alignment for each type of surface. We use the absolute value |sin θ| due to the growth symmetry with respect to the x axis (directions $\theta =0\text{and}\theta =\pi$ are equivalent; see Figs. 1 and 2). As shown in references (38, 39, 40) on work performed for galvanotaxis and chemotaxis dose-response curves for the motion of human granulocytes and keratinocytes, the feedback control model leads to the following expression for the average of the absolute value for the sine of the growth angle:

$$⟨\left|\text{sin}\theta \right|⟩\equiv {\int }_0^{2\pi }p\left(\theta \right)\cdot \left|\text{sin}\theta \right|d\theta =\frac{I_1(\alpha \cdot d)}{I_2(\alpha \cdot d)}$$ (15)

where I₁ and I₀ are the modified Bessel functions of the first kind, and $\alpha$ is a parameter with dimensions of inverse length.

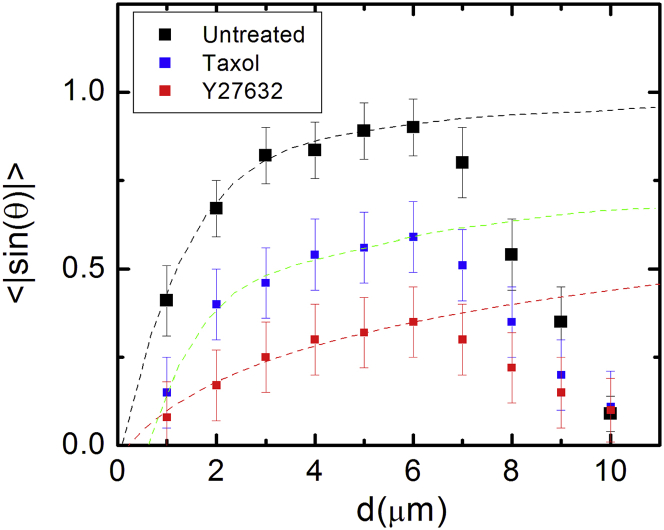
Fig. 6 shows the variation of the experimentally measured values for $⟨\left|\text{sin}\theta \right|⟩$ with the pattern spatial period d, for untreated neurons (black squares), as well as for neurons treated with Taxol (blue squares) and Y-27632 (red squares). The dotted curves represent fits to the data with the predictions of the closed-loop feedback model given by Eq. 15. Only the data points in the range d = 1 to 6 μm are included in the fit. The data demonstrate that axonal dynamics on micropatterned PDMS surfaces is described by a simple linear response model, when the pattern spatial period is in the range d = 1 to 6 μm, that is when d matches the linear dimension of the growth cone: $d\approx l$. This conclusion applies to both untreated cells and cells treated with Taxol and Y-27632. This type of response is known as “automatic controller” in the theory of feedback control systems (49) and it is exhibited by a large class of biological and non-biological systems as discussed below. In our experiments, the pattern spatial period d plays the role of an effective control parameter that determines the axonal alignment, similar to the electric field in the case of galvanotaxis of human granulocytes and keratinocytes (23,38), or the concentration gradient in the case of cellular chemotaxis (39). Furthermore, Fig. 6 demonstrates that the response of the automatic controller is affected by the inhibition of cytoskeletal dynamics: the actual response (measured by the coefficient α) is different for the untreated and chemically treated cells (see the caption in Fig. 6, and Table S1).

Figure 6.

Variation of the average value for |sin θ| (absolute value for the sine of the axonal growth angle) with the pattern spatial period d. The black squares represent the values for $⟨\left|\sin \theta \right|⟩$ obtained from the experimental data for untreated neurons. The blue squares correspond to the experimental data obtained for neurons treated with Taxol, while the red squares correspond to the data measured for neurons treated with Y-27632. Error bars indicate the standard error of the mean for each data set. The dotted curves represent fit of the data points with Eq. 15, performed in the range d = 1 to 6 μm. The graph shows that data points in this range are fitted by the feedback control model for the following values of the parameters: $\alpha =(1.9\pm 0.4)\text{μ}{\text{m}}^{-1}$ for untreated neurons, $\alpha =(0.5\pm 0.2)\text{μ}{\text{m}}^{-1}$ for neurons treated with Taxol, and $\alpha =(0.3\pm 0.2)\text{μ}{\text{m}}^{-1}$ for neurons treated with Y-27632. To see this figure in color, go online.

Discussion

Neurons respond to a variety of external cues (biochemical, mechanical, geometrical) while wiring up the nervous system in vivo (1,2,4, 5, 6, 7). In many cases these cues consist of periodic geometrical patterns with dimensions of the order of a few micrometers (1,4,5). Examples of physiological growth scaffolds include curved brain folding (4, 5, 6), radial glial fibers (4,5), and extracellular matrix tracks (1,2,6,7). Our results show that growth substrates containing micropatterned periodic features promote axonal growth along the direction of the pattern. The range for the micropattern spatial periods in our experiments (d = 1 to 10 μm) is relevant both for neuronal growth in vivo as well as for many proposed biomaterial implants for nerve regeneration (13,17). Furthermore, our experiments show that neurons grown on PDMS substrates display a significant increase in the overall axonal length and a high degree of alignment when the pattern spatial period d matches the linear dimension of the growth cone: $d\approx l$.

We have shown that the Fokker-Planck equation with closed-loop feedback control and periodic external potential (Eqs. 1, 2, 3, 4, 5, 6, 7, 8, and 9) provides a general stochastic framework that describes the main characteristic of the axonal dynamics on micropatterned PDMS substrates. The limitations of this model are due to its phenomenological nature: the growth parameters are obtained from fit to experimental data, and not predicted from the underlying cellular biophysics. However, we have demonstrated that a simple mechanical model based on the axon bending-induced strain (Eqs. 10, 11, 12, and 13) justifies the use of the Fokker-Planck equation and allows us to extract the main dynamical parameters that characterize axonal growth for both untreated and chemically modified neurons. Our results show that the additional cues necessary to guide the axonal dynamics result from the interplay between the geometrical features of the substrate and the physical properties (stiffness) of the nerve process.

The theoretical model captures all the characteristics of axonal growth on the PDMS surfaces for untreated and chemically modified neurons, including diffusion (cell motility) coefficients, and angular and speed distributions (Figs. 2, 3, 4, 5, and S6–S8). Furthermore, Eqs. 2, 3, 4, 5, 6, 7, 8, and 9 imply a simple closed-loop automatic controller model for axonal motion: the growth cone detects geometrical features on the substrate and orients its motion in the directions that maximize the interaction between the axon and the substrate. This behavior is displayed by both untreated and chemically modified neurons, as shown in Fig. 6. In this figure, each data set (for untreated, Taxol-, and Y-27632-treated cells) is fitted with a unique parameter α, which demonstrates a linear response characteristic to a proportional controller: the response is proportional to the signal received from the guidance cue (38,39). The coefficients α obtained from the data fit (Fig. 6 and Table S1) measure the neuronal responses to periodic geometrical cues, and play a similar role to the galvanotaxis and chemotaxis coefficients used to describe the cellular motion in external electric fields or chemical gradients (23,38, 39, 40).

Models based on the theory of automatic controllers have been successfully used by other groups to characterize the galvanotaxis (motion in external electric fields) of human granulocytes and keratinocytes (23,38), as well as the chemotactic response of bacteria and of various types of virus-modified cells (39,40). We note that the closed-loop feedback displayed by neurons is different than the case of external (or open-loop) control, where the parameters are set externally without involving the reaction of the system. Open-loop control does not involve measurements of the environment and it is the type of control encountered in systems with predictable dynamics. Examples of open-loop systems include many types of devices, such as fluorescent lamps or watches controlled by quartz crystals (49), or systems under the influence of oscillating forces, such as mixing devices or ratchet structures (50, 51, 52). In the case of complex dynamics, such as the stochastic motion of cells, closed-loop feedback control is a much more reliable control mechanism. In the case of neurons, the closed-loop feedback control underlies the mechanism of axonal alignment on micropatterned PDMS substrates. Within this model, the growth cone behaves similarly to a device that senses geometrical cues, and as a result generates traction forces that align the axon with the surface pattern.

The parameters V₀, V, α, and B/E₀ (see Table S1) are obtained from the comparison between experimental data and the theoretical model, and represent a measure of the interactions between cells and the geometrical cues on the growth substrates. These parameters allow for a meaningful comparison of the cellular response to geometrical cues among different types of cells and growth substrates. For example, the high degree of alignment observed for untreated neurons grown on surfaces with $d\approx l$ (e.g., d = 4 μm or d = 6 μm) is reflected by the higher strengths of the geometrical and feedback potentials V₀ and V compared with neurons grown on surfaces with other pattern spatial periods (e.g., d = 1 μm or d = 9 μm; see Table S1). Furthermore, the reduction in axonal alignment observed for chemically treated cells is measured quantitatively by the significant decrease in the values of the parameters V₀, V, and α, compared with the corresponding values obtained for untreated neurons grown on the same type of micropatterned surface (d = 4 μm). Table S1 shows a decrease by a factor ∼3 to 4 in the values of V₀ and V for chemically treated cells compared with the untreated neurons grown on the same type of substrate. The unique fit parameter α obtained in each case (untreated, Taxol-, and Y-27632-treated cells) for neuronal growth on surfaces with pattern spatial period in the range d = 1 to 6 μm demonstrates a linear response characteristic to a proportional controller. However, the value of α for Taxol-treated cells is a factor of ∼4 smaller than the value for the corresponding parameter obtained for untreated cells (Fig. 6 and Table S1). This result is in very good quantitative agreement with the experimentally observed decrease in the peak of the angular distributions for Taxol-treated cells (Fig. 4 c compared with Fig. 3 b). A similar decrease in the value of α is measured for neurons treated with Y-27632 (Fig. 6 and Table S1). The smaller value of the parameter α for the chemically treated neurons implies a less effective guidance mechanism for these cells compared with the untreated ones. Within the feedback control model, these results show an alteration of the automatic controller responsible for directional motion of axons in the case of chemically treated neurons.

The comparison between the stochastic and mechanical model given by Eqs. 10, 11, 12, and 13 allows us to calculate the ratios between the axon bending modulus B and the characteristic energy scale of axon-substrate interactions E₀, for untreated as well as chemically modified neurons (Eq. 14). This ratio is almost constant for untreated neurons grown on surfaces with different pattern spatial periods d (Table S1), showing a constant axon-surface bending energy. The model also shows a statistically significant decrease in the value B/E₀ for cells treated with Taxol or Y-27632 (Table S1), and thus indicates a decrease in the bending rigidity for chemically modified neurons, which is consistent with the alteration of cytoskeletal dynamics and axon-substrate coupling forces for these cells, as discussed below.

The biophysical mechanisms responsible for the observed changes in the dynamical behavior involve changes in the cell-substrate coupling forces, which could occur through different cellular processes. Growth cones are filled up with actin filaments, which polymerize at their leading edge (1, 2, 3, 4, 5, 6, 7). At the same time, myosin II motors pull on actin filaments and generate traction forces via point contacts (e.g., integrins, viniculin, talin). Furthermore, interactions between actin filaments and microtubules modify the distribution of mechanical stress in the growth cone and affect its adhesion properties, and its ability to navigate and turn. In consequence, both microtubules and actin filaments inside the growth cone act as stiff load-bearing structures that generate surface adhesion and traction forces (1,2,4). Inhibition of microtubule or actin dynamics will therefore result in a decrease in cell-substrate interactions and cellular adhesion. Our experiments are consistent with these predictions: we have demonstrated that disruption of the cytoskeletal dynamics for cells treated with Taxol (inhibitor of microtubule dynamics), and Y-27632 (disruption of actin filaments) results in a decrease in the degree of alignment and a reduction in cell-substrate interactions (Figs. 4, 5 b, d, S8 b, d; Table S1).

These results support previous work that has shown that neurons follow geometrical patterns through a contact-guidance mechanism (12,21,53). Contact guidance is the behavior displayed by many different types of cells that can change their motion in response to geometrical cues present in the surrounding environment. This property has been observed for several types of cells, including neurons, fibroblasts, and tumor cells (12,17,21,53). Previous work (17,53, 54, 55) has shown that growth cones develop several different types of curvature-sensing proteins, such as amphipathic helices and bin-amphiphysin-rvs (BAR) domains, that act as sensors of geometrical cues and are involved in the generation of traction forces. Moreover, the degree of directional alignment of cellular motion is increasing with the increase in the density of curvature sensing proteins (17,53, 54, 55). In our experiments, the growth cone filopodia and lamellipodia wrap around the ridges of the PDMS micropatterns (18), which results in a minimal contact area with the surface, and thus a maximum density of curvature-sensing proteins. Consequently, high-curvature geometrical features such as ridges on PDMS substrates will impart higher forces to the focal contacts of filopodia wrapped over these features, compared with the low-curvature patterns. This means that the contact-guidance mechanism leads to an increase in the traction force along the direction of the surface pattern (defined as the y direction in Fig. 1), which ultimately results in the observed directional alignment of axons on these surfaces.

Proper wiring of the nervous system in vivo is carried out precisely and robustly as growth cones respond to their environment by integrating external cues. While the fundamental stochastic nature of self-wiring obscure the details of how it is achieved, it is likely that there are general emergent rules that apply across large patterns of connections (56,57). Previous growth models have simulated multiple axons growing in complex domains with multiple guidance factors (56,57). However, many of the parameters that control axonal dynamics have not been quantified. In previous work we have investigated axonal growth on substrates with different geometrical patterns, and have measured speed and acceleration distributions as a function of substrate geometry (21), axonal alignment as a function of time (18), as well as axonal angular distributions, angular drift, and diffusion coefficients (12,18,21). In this paper, we show that axonal stiffness and substrate curvature can act together to direct axonal growth on filamentous surfaces. This work also opens up several important directions for future investigations of surface-driven axonal growth. For example, the ability to control and direct biomechanical responses in vitro has important consequences for neural repair and tissue engineering, along with in vitro-in vivo device interfaces. Such control is critical, for example, to repair nerve damage, to guide and optimize nerve interfaces to prosthetics, and to integrate medical devices for physiological functions.

The role played by curvature-sensing proteins and other cellular processes, such as changes in expression of BAR proteins, or the opening of stress activated ion channels, which could lead to changes in the cell-substrate coupling forces, will be investigated in future experiments. This future work will involve the measurement of both cell-surface coupling forces using traction-force microscopy and the density of cell-surface receptors and curvature-sensing proteins using fluorescence techniques. The effect that these biomolecules have on the generation of traction forces can be determined in experiments where their activity is selectively inhibited while simultaneously measuring cell-substrate interactions and the axonal dynamics. Furthermore, combined with traction-force experiments, the automatic controller model presented here could be further extended to account for the explicit dependence of the growth parameters on the mechanical and biochemical guidance cues, such as changes in the geometry or stiffness of the growth substrate, or external chemical gradients. This general model could also be applied to other types of cells to give new insight into the nature of cellular motility. In principle, these future investigations will enable researchers to quantify the influence of environmental cues (geometrical, mechanical, biochemical) on cellular dynamics, and to relate the observed cell motility behavior to cellular processes, such as cytoskeletal dynamics, cell-surface interactions, and signal transduction.

Conclusion

In this paper, we have performed a detailed analysis of axonal growth on micropatterned PDMS surfaces. We have demonstrated that the axonal dynamics on these surfaces is described by a theoretical model based on the motion of a closed-loop automatic controller in a periodic external potential imparted by the surface geometry. We have used this model to measure the parameters that characterize the axonal growth. Our results show that the motion of the growth cone is mediated by a contact-guidance mechanism, which originates from cellular feedback in an external periodic potential: the growth cone responds to geometrical cues by directing its motion along the surface micropatterns. This work implies that the cues that guide the axonal dynamics result from the interplay between the geometrical features of the substrate and the physical properties (stiffness) of the nerve process. The general model presented here could be applied to describe the dynamics of other types of cells in different environments, including external electric fields, substrates with various mechanical properties, and biomolecular cues with different concentration gradients.

Author contributions

Data acquisition, data analysis, experimental work, and writing of the manuscript, M/D; data acquisition, data analysis, experimental work, and writing of the manuscript, J.P.S.; data acquisition, data analysis, experimental work, and writing of the manuscript, D.D.B.; conceptualization, methodology, data analysis, development of the theoretical model, project administration, funding acquisition, and writing of the manuscript, C.S. All authors have read and agreed to the final version of the manuscript.

Editor: Paul Janmey.