Abstract
The cone-straight nozzle has been commonly utilized in various applications, such as cleaning, cutting, and drilling, and hence investigated extensively with simulations and experiments. However, the internal flow patterns and dynamics, as well as the influence of internal flow on jetting performance, remain unclear. In this study, we carry out both experiments and computational fluid dynamics to understand the effect of different converging angles of the cone-straight nozzle on internal and external flow patterns. Nozzle flows are simulated by a large eddy simulations model and further compared with the experimental flow fields obtained by a particle image velocimetry (PIV) method. Nozzles with different converging angles and throat lengths have been used experimentally. The influence of nozzle converging angle, throat length, and inlet flow speed on flow field, skin friction resistance, and viscous force is discussed. Associated boundary layer transition and separation are investigated comparatively. The flow discharge coefficient and flow core length are measured by the PIV test system with a high-pressure pump. The experimental results show that a specific converging angle and flow speed can cause the boundary layer transition and separation. Skin friction resistance increases first and then decreases with the increase of inlet flow speed when the angle is larger than 20°. The resistance decreases gradually when the angle is lower than 15°. Importantly, the skin friction resistance remains a lower level when the converging angle is 15°, in agreement with the previous research results. The experimental results show that the nozzle with a converging angle of 10° or 15° has a higher discharge coefficient and a better cluster capacity. The nozzle with a throat length of 3 times the outlet diameter has a longer flow core. Considering the nozzle size, the nozzle with a converging angle of 15° and a throat length of 3 times the diameter of the outlet is suggested when the nozzle is used in jetting for obtaining a longer jetting distance.
1. Introduction
Water jet is an emerging technology developed rapidly in recent years and used in many fields. This method uses a pump to generate high-speed fluid with sufficient kinetic energy to cut materials, perforate, break coalbeds and rock, and wash wellbore.1−6 Tailored to different applications, several nozzle structures or shapes have been proposed, such as a self-excited oscillation jet nozzle and a venturi nozzle. The self-excited oscillation jet nozzle including the Organ nozzle and the Helmholtz nozzle7 can generate both pulsing and cavitation jets. Venturi nozzles are often used in the aerospace industry, energy, and metering, for instance, in the transmission of flow standards,8 gas flow measurement, and the maximum flow limitation of the flow system.9 Spray nozzles are used in irrigation due to their better atomizing ability. The rotating multi-orifice nozzle can be used in drilling in petroleum fields.10,11 Some other non-circle nozzles have been investigated in recent years for abrasive jet cutting and spray irrigation.12−14 Among these, cone-straight nozzles are most widely used in the petroleum field due to their relatively simple processing.
Nozzle geometry directly affects the performance of jets, which are further used for subsequent applications such as cleaning, cutting, and drilling. The cone-straight nozzle’s geometry comprises a converging section, a throat section, and a reaming section. The converging section is used to concentrate the fluid and energy, the throat section to stabilize the flow status, and the reaming section to control jet exit diffusion angle and control cavitation. However, the reaming section does not often exist when nozzles are utilized in the petroleum field, so it is not considered in this article.
The primary parameters of the nozzle geometry are the converging angle and throat length and have been investigated by experiments and simulations. Many researchers have investigated the influences of various parameters on a jetting angle, jetting length, and impact force,15−17 especially in breaking rocks, such as coalbed,3 sandstone, and gas hydrate. The researchers concluded that the nozzle has a critical converging angle and throat length that can obtain the longest flow core. The better converging angle is 13–15°, and the better throat length is 2–4 times the nozzle diameter.
Some researchers focused on the studies of the nozzle outline, and a streamlined curve (e.g., Sine curve, Gaussian curve, and Widosinski curve18) is used as the nozzle geometry. Many simulations are simulated to discover the difference in flow speed distributions and pressure loss between the cone-straight nozzle and streamlined nozzle. Jiang et al. investigated the internal flow characteristics with simulations but only focused on one type of nozzle and analyzed the near-wall flow field.19 They found that the pressure loss is lower when the fluid flows through a streamlined nozzle.
Some researchers paid more attention to jet noise when the jetting fluid was gas. The jet noise and nozzle exit boundary layer is an evaluation of the flow turbulence when the fluid is gas. Jet noise is an essential factor for evaluating turbulent jetting. Based on the research results, the nozzle exit boundary layer plays an essential role in the outer flow field. Some simulations showed the influence of flow state on jet noise and found that the nozzles involving turbulent boundary layers were quietest. In contrast, the nozzle involving a “nominally laminar” boundary layer was loud, especially on the high-frequency side of the sound pressure level spectrum. The noisier nozzle involves a highly disturbed laminar, or nominally laminar, boundary layer state instead of a turbulent state.20,21,37 Some nozzles were designed and tested to obtain more credible results, such as the ASME nozzle and conical nozzle. The results showed that the high-frequency jet noise is reduced when the laminar layer transitions to turbulence. The influence of the boundary layer on jet noise and the outer turbulent shear layer was discussed. The effects of moderate Reynolds numbers on subsonic round jet noise with highly disturbed nozzle exit boundary layers were also investigated.22,23
Hariharan et al. conducted (Particle Image Velocimetry) PIV measurements and analyzed the viscous shear stress, velocity distribution, and pressure distribution of the nozzle area. Their results supported the validation of their computational fluid simulations.24 The flow characteristics of pressure oscillation and velocity phase diagrams of different self-excited oscillating modes were analyzed. A full Navier–Stokes viscous laminar model was established for non-equilibrium condensing steam flow.25 A curve-fit equation obtained by experiments representing the average trend is provided to predict the throat-to-shock-location distance at a given nozzle pressure ratio.26 The discharge coefficient dependency of critical-flow venturi nozzle on Reynolds number and wall temperature was investigated by a series of two-dimensional axisymmetric and adiabatic computational fluid dynamics (CFD) simulations. The results showed that the wall temperature effect is stronger for small nozzle diameters. The research also presented that the CFD simulations can predict the transition of the boundary layer of inner flow.27 Xiao Yu performed some experiments and simulations [large-eddy simulations (LES)] and found that the shear stress appeared at the nozzle throat.28 A new turbulence model was proposed, which could predict the boundary layer transition of CFVNs. The experimental results showed a good agreement with the simulations.29 All the results showed that the CFD could predict the boundary layer transition.
The discharge coefficient is an essential factor in evaluating the nozzle. The discharge coefficient equation was derived and verified by measurement data and subsequently improved.30,31 Some researchers also focused on the internal flow state transfer and found that the flow in the nozzle remains subsonic, accompanied with a reduction in turbulence in the convergent portion and amplification in the divergent portion.32 Wall roughness plays a vital role in boundary layer transition, skin friction, and pressure drop. The effect of wall roughness on flow through converging–diverging nozzles was studied before. The cooling and roughness effects on the transition of nozzle throats and blunt bodies were investigated by experiments in the wind tunnel.33,34
However, most researchers have focused on the studies of gas flow rather than a fluid flow, and the detailed flow field inside the nozzle has not been revealed clearly, especially near the nozzle wall. Few researchers focused on the flow resistance inside the nozzle. In this study, cone-straight nozzles with different converging angles are simulated by an LES model. In addition, the internal flow patterns are measured by a PIV method under a lower flow speed. The external flow field of the cone-straight nozzle is measured by a high-pressure pump system under high jet pressure.
According to the results of our literature research and previous work, we made some hypotheses before conducting simulations and experiments. First, the nozzle profile can affect the flow characteristics inside and outside the nozzle directly. Second, there will be boundary layer separation and transition inside the cone-straight nozzle for its converging section. Third, nozzles with specific converging angles and throat lengths could generate an optimal jetting performance with lower flow resistance.
2. Simulations
LES can capture transitional and turbulent flows with a relatively loose grid compared with Direct Numerical Simulation. A wall-adapting local eddy-viscosity model (WALE) is used to calculate smaller grids.35 LES has been proven to be an effective model to simulate boundary layers29,36 and is used in this article.
2.1. Geometry
To reduce the amount of computation, a 3D nozzle is simplified to 2D, as shown in Figure 1. D represents the inlet diameter, d represents the throat diameter, α is the converging angle, and L is the length of the throat. Listed in Table 1 are the parameter sets used in our simulations.
Figure 1.
Nozzle geometry.
Table 1. Sets of Simulations.
| converging angle, α (degree) | 10 | 15 | 20 | 25 |
| inlet flow speed, U (m/s) | 1/5/10 | 1/5/10 | 1/5/10 | 1/5/10 |
2.2. Grid
The boundary layer must be considered
to capture the flow state near the nozzle wall. The grid must be fine
enough; the first layer height is used to generate the grid, and y+ (
) is used to evaluate the quality of the
grid. The max inlet flow speed is set to 10 m/s, the first layer height
is set to 10–6 m, and the growth rate is set to
1.15. The boundary layer is set to 20 layers, and the value along
the nozzle is shown in Figure 2. Most values of y+ are lower than 1, and all values
are lower than 2. To further reduce the calculation time, the calculation
domain is symmetrical. The maximum surface size of the main flow field
is set to 0.001 m. The number of grids is reduced from 860 000
to 360 000. The max skewness of the grid is 0.76, and the quality
of the grid is good and acceptable.
Figure 2.
Distribution of Y+ along the wall.
2.3. Numerical Model
To fully distinguish the turbulent structure near the wall, the normal phase adopts non-uniform mesh refinement. The periodic boundary condition is adopted, and the wall condition is a no-slip boundary condition.
The flow state inside the nozzle is unstable when the flow speed is high with curved flows and eddies. The grid near the wall should be fine enough, so the enhanced wall treatment is adopted first. The RNG k-epsilon turbulence model is used to obtain a steady flow field, and the calculation result will be set as the initial conditions of the LES simulation. The WALE sub-grid model is chosen for the unsteady-state solution, the numerical method has the third-order accuracy in space, and the time step is set to 10–7 to 10–6 s.
The simulation data is compared to the existing DNS data,37 and our PIV experimental data is shown in Figure 3. The LES data is in agreement with the DNS data and PIV data. The maximum error is 3%, which proves the accuracy of the LES model used.
Figure 3.
Comparison of LES data and PIV data.
Besides, an experimental setup was built, and some flow tests were done. The setup, shown in Figure 4, is composed of the PIV component, gear pump, and experiment rack. A transparent nozzle is designed and processed, and the experimental data is compared to the LES data shown in Figure 5, showing a good agreement. The LES model is proven to be accurate to some extent. The numerical simulation is used to study the internal flow of the fluid flowing through the cone-straight nozzle.
Figure 4.
Experiment setup.
Figure 5.
Comparison of the PIV data and LES data.
2.4. Results and Discussion
Based on the numerical simulation results, the influence of converging angle and inlet fluid speed on flow speed distribution and flow resistance are analyzed separately.
2.4.1. Influence of Nozzle Geometry on the Flow Field
Figure 6 shows the flow speed contours of cone-straight nozzles with different converging angles when the inlet flow speed is set to 1 m/s. The flow fields inside the nozzles show a similar trend with a speed peak at the entrance of the throat section. The flow speed near the wall of the converging section is lower, gradually increases along the vertical wall direction, and then tends to be stable. When the fluid is accelerated along the centerline, the speed peak value appears in the main flow field. The flow speed at the entrance of the throat section first increases along the vertical wall direction and then decreases and finally stabilizes. In addition, a peak flow speed value appears at the entrance of the throat section.
Figure 6.
Vortex generation near the throat wall of the different nozzles with different inlet flow speeds (1, 5, and 10 m/s from left to right).
When the inlet flow speed is set to 5 m/s or higher, the vortex appears near the whole throat section when the converging angle is 15o degrees, 20°, and 25°, while the vortex does not appear in a nozzle with 10° of converging angle. The intensity of the vortex increases with the converging angle. When the converging angle is smaller, the distribution of the vortex is more uniform, and the periodicity of the vortex is more robust. To display the vortex distribution more intuitively, the flow speed distribution (“U”) is depicted in Figure 7. Some lines parallel to the nozzle wall are monitored, and the flow speeds on those parallel lines are displayed in Figure 7. We marked some circles where the vortex is generated and developed, and the flow speed near the wall is more fluctuated. The closer to the center of the flow field, the smaller the fluctuations. The positions corresponding to the red circle are the positions where the vortex is generated. The vortex develops along the throat section, and the size of the vortex becomes greater. The approximately uniform distribution of flow speed indicates the appearance of the vortex, and a pulsation period represents the appearance of a vortex. However, the homogeneity of flow speed distribution near the wall of the throat section deteriorates with the increase of the converging angle.
Figure 7.
Flow speed distribution near the wall of the throat section.
Figure 8 shows the influence of the converging angle on the peak value of flow speed. It is evident that the greater the converging angle, the sharper the speed peak. When only one nozzle geometry is considered, the flow speed distribution in the throat section is shown in Figure 9. The flow speed peak only survives a short distance and then disappears. The difference of flow speed distribution of nozzles with a different converging angle in the throat section only appears near the wall surface.
Figure 8.
Flow speed distribution at (left) and after (right) the entrance of the throat section.
Figure 9.
Flow speed distribution (“U”) in converging section (left) and throat section (right).
When the fluid flows into the converging section, it will be agitated by the converging surface, and the flow state near the wall will be turbulent. The boundary layer will change from the original laminar flow state to turbulent flow, and the small vortex appears at the corner and then the fluid will be compressed in the entire converging section. Due to the lower turbulence intensity, the small vortex cannot survive, and the vortex disappears after flowing through the first corner. The near-wall flow becomes more stable until arriving at the second corner. The fluid flow direction near the wall is parallel to the wall when the fluid passes through the converging section. The fluids with different flow directions will meet and collide near the throat. The closer to the nozzle center axis, the more serious the collision and the more profound the fluid momentum loss. The higher the flow speed, the more severe the collision, and the more severe the fluid momentum loss. Therefore, the flow speed peak appears near the wall of the nozzle throat. When the turbulent flow flows into the throat section, the intensity of turbulence will be suppressed. The main flow will become relatively stable. The converging angle mainly influences the flow field of the throat section. The greater the converging angle, the greater the crossing angle of flow speed direction. The more intense the fluid collision, the greater the turbulence.
When the inlet flow speed is low, the vortex near the entrance of the converging section and throat section cannot survive, and the flow near the wall of the entire nozzle exhibits a laminar flow pattern. When the inlet flow speed is higher, the sequential vortex appears at the nozzle throat with a larger converging angle. When the inlet flow speed is high enough, the sequential vortex appears in all nozzles. The greater the converging angle, the more chaotic the vortex sequence. The vortex appearance indicates the existence of boundary layer transition and separation phenomena. The boundary layer transition occurs near the entrance of the converging section and throat section, and the boundary layer separation occurs near the entrance of the throat section.
2.4.2. Influence of Nozzle Geometry on Skin Friction
When the flow resistance is considered, the skin friction resistance is a factor that should not be ignored. To investigate the influence of converging angle and the inlet flow speed distribution of skin friction resistance, we integrate and solve the skin friction coefficient, and the whole skin friction is obtained
 |
1 |
 |
2 |
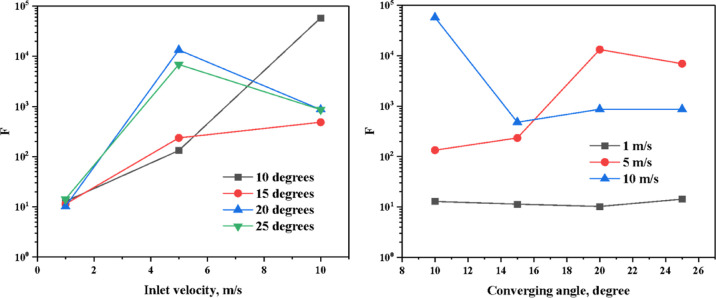
Figure 10 shows the skin friction resistances of different nozzles; when the inlet flow speed is low, there is little difference among the nozzles with different converging angles. When the inlet flow speed is higher, there is a big difference among nozzles.
Figure 10.
Influence of inlet flow speed (left) and converging angle (right) on skin friction resistance.
When the converging angle is 10°, the flow near the wall is mainly laminar. The skin friction resistance increases exponentially with the increase of flow speed. It reaches the maximum value of each group of simulations in this article when the inlet flow speed is set to 10 m/s. When the converging angle is 15°, the growth trend of skin friction resistance is similar to that of 10°, but the increase rate is much smaller than the increase of 10°. When the converging angle is 20° or 25°, it shows a big difference with a nozzle with 10 degrees of converging angle, and the peak value appears at 5 m/s of the inlet flow speed; the skin friction resistance increases first and then decreases with the increase of inlet flow speed. The peak value is much smaller than that of a nozzle with 10° and larger than that of a nozzle with 15°. The skin friction resistance of nozzles with a converging angle of 20 and 25° is close in value when the inlet flow speed is set to 1 and 10 m/s. However, it shows a big difference when the inlet flow speed is set to 5 m/s.
The length of the converging section plays an essential role in skin friction resistance when the inlet flow speed is low. The flow state of the boundary layer is laminar, and the resistance decrease with the increase of the converging angle because of the decrease of the converging length. While the resistance in the throat section does not follow the role fully, the skin friction resistance in the throat section of 25 degrees of converging angle is the maximum value among them when the inlet flow speed is set to 1 m/s. When the flow inside the nozzle is more turbulent, the boundary layer is turbulent, and the vortex appears near the wall of the throat section. The converging angle plays a significant role in the skin friction resistance of the throat section. Above all, it is evident that the nozzle with 15 degrees of converging angle has a smaller skin friction resistance no matter if the inlet low speed is low or high based on our simulations.
2.4.3. Influence of Nozzle Geometry on Boundary Layer Thickness
Boundary layer transition and separation directly affect the appearance of the vortex near the wall of the throat section. The boundary layer thickness, transition, and separation are considered in this article; the boundary layer transition and separation directly affect the appearance of vortex near the wall of the throat section.
The boundary layer thickness refers to the distance from the wall to the location with 99% of the centerline speed value along the vertical wall. Given the fact that the flow direction near the wall of the converging section is different from the main flow direction, we deal with the converging section separately. We take the flow speed distribution along the vertical direction of the converging section wall, find the position of the maximum flow speed at 99%, and calculate the boundary layer thickness.
Figure 11 shows the boundary layer thickness of different nozzles with different inlet flow speeds. The boundary layer thickness decreases along the converging direction, reaches the lowest value at the entrance of the throat section, and then gradually increases along the throat section, finally showing a stable state of fluctuations. Figure 11a shows the boundary layer thickness distribution of the nozzle with 10 degrees of converging angle; the profile is smooth, which shows that the flow near the wall is more stable than other nozzles. The flow contours also do not show the existence of a vortex. When the converging angle is set to 25°, the vortex appears when the inlet flow speed is set to 1 m/s, which means that the boundary layer separation occurs earlier than the nozzle with a smaller converging angle. When the converging angle is set to 15° or higher, there are fluctuations at the boundary layer thickness profile when the inlet flow speed is set to 5 m/s or higher. This suggests that the nozzle has a critical converging angle that can induce the boundary layer separation earlier. The greater the converging angle, the earlier the boundary layer separation occurs. When the inlet flow speed is the same, the greater the converging angle, the more severe the boundary layer thickness fluctuation, and the more chaotic the vortex structure.
Figure 11.
Distribution of boundary layer along the wall. (a) Nozzle with a converging angle of 10°. (b) Nozzle with a converging angle of 15°. (c) Nozzle with a converging angle of 20°. (d) Nozzle with a converging angle of 25°).
2.4.4. Influence of Nozzle Geometry on Viscous Force
The viscous force is analyzed only under an inlet flow speed of 1 m/s. All the results are calculated according to the XY coordinate system. However, according to the definition of viscous force, it should be proportional to the velocity gradient in the vertical flow direction, so the coordinate system needs to be converted to the MN coordinate system shown in Figure 12. The conversion equation of the coordinate system is as follows.
Figure 12.
Coordinate transfer.
The data we can get is, the viscous force equation
is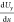 
given by
 |
3 |
The equation in MN coordinate system is as follows
 |
4 |
We decompose the 
along the XY axis; then,
the formula can be presented as
 |
5 |
 |
6 |
The viscous force equation in the MN coordinate system can be written as follows
 |
7 |
and 
in the MN coordinate system can be decomposed
as follows
 |
8 |
 |
9 |
Then, the viscous force in the MN coordinate system can be obtained according to the data in the XY coordinate system; the equation used in the converging section is given by
 |
10 |
When we consider the flow state in the throat section, we assume that the direction of flow is parallel to the axis of the throat section. The equation of viscous force used in the throat section is given by
 |
11 |
When integrating the viscous force, only the viscous force within the thickness of the boundary layer is calculated because only the speed of the fluid flowing near the wall is parallel to the wall surface in the converging section, and the viscous force in the main flow field is negligible. Monitoring points are selected uniformly in the converging section and throat section.
Figure 13 shows the distribution of the viscous force of the converging and throat sections of the nozzle with 10 degrees of converging angle. The “Distance” in Figure 13 is the vertical distance from the monitoring point to the nozzle wall. The peak values in monitoring points appear near the wall and then decrease along the vertical wall direction. Finally, the viscous force approaches zero outside the boundary layer, implying that the viscous force in the main flow field can be ignored. When comparing the viscous force at different locations, it can be found that the peak value appears at the entrance of the throat section. The positions where the viscous force tends to zero can indicate that the boundary layer thickness decreases along the converging direction. It is in good agreement with the trend of the boundary layer thickness discussed above.
Figure 13.
Distribution of viscous force in converging section (left) and throat section (right).
Figure 14 shows the viscous force of all nozzles. We integrate the viscous force inside the boundary layer of monitoring points to investigate the viscous force distribution along the whole flow field inside the nozzle. The peak value of viscous force in all nozzles appears near the entrance of the throat nozzle. In contrast, the peak value decreases with the increase of the converging angle. The viscous force increases along the direction of flow in the converging section decreases and finally becomes stable along the direction of flow in the throat section. When we integrate the whole vicious force inside the nozzle, it is evident that the value of the viscous force of the nozzle with 10 degrees of converging angle is the largest, and the value decreases with the increase of converging angle.
Figure 14.
Viscous force along the centerline in nozzles with different converging angles.
When the nozzle inlet diameter and throat diameter are consistent, the longer the converging section, the larger the viscous force, and the viscous force in the throat section remains constant when the flow is lower, and the flow state is laminar.
2.4.5. Influence of Nozzle Converging Angle on Static Pressure
In our simulations and experiments, gravity can be ignored, so the static pressure is caused by the fluid pressure on the wall in the flow field. The heterogeneity of fluid flow can cause fluctuations in static pressure on the wall.
Figure 15 shows the static pressure curves of different nozzles with different inlet flow speeds. When the inlet flow speed is set to 1 m/s, the static pressures of the nozzle with 15 and 20° of converging angle are greater than others. The static pressure of the nozzle of 25° of converging angle is the lowest; there are no fluctuations in the curves of the nozzles with a converging angle of 15° and 10°. The static pressure curve has small fluctuations when the converging angle is 20°; there is a significant fluctuation when the converging angle is 25°. All the static pressure near the entrance of the throat section is negative, and the fluctuation values are negative. There are some differences when the inlet flow speed is set to 5 m/s. The static pressure on the inner wall of the nozzle fluctuates except for the converging angle of 10°, and the static pressures of the nozzles with the converging angles of 15 and 20° are relatively small. There is negative pressure among all the nozzles. When the inlet flow speed is set to 10 m/s, all curves fluctuate, and the curve of 15° is relatively small.
Figure 15.
Distribution of static pressure along the wall of different nozzles. (a) Inlet flow speed is set to 1 m/s. (b) Inlet flow speed is set to 5 m/s. (c) Inlet flow speed is set to 10 m/s.
The static pressure increases with the increase of flow speed. The higher the flow speed, the more severe the intensity of fluctuations, and the fluctuations only appear in the throat section. The fluctuation indicates a pulsion of flow speed, which matches the appearance of the vortex in the throat section. The intensity of fluctuations can indicate the appearance of boundary layer separation to some extent. As shown in Figure 15a, the boundary layer separation only occurs in the nozzle with a converging angle of 25°. The boundary layer separation happens when the velocity is high enough. From the profile of static pressure, the greater the converging angle, the earlier the boundary layer separation occurs, and the results are in good agreement with the above discussion.
Static pressure can be used as a consideration when considering nozzle structure optimization. It can also characterize the speed pulsation; its size and fluctuation can characterize the intensity of turbulence. As Figure 15 shows, when the converging angle is 15°, the rate of static pressure increases with the flow speed is the smallest, and when the converging angle is 20°, the rate of increase is the largest. From this perspective, the nozzle could have better flow stability when the converging angle is 15°.
2.4.6. Influence of Nozzle Converging Angle on Outflow Field
The outflow states of the different nozzles with different inlet velocities are shown in Figure 16. When the inlet flow speed is set to 1 m/s, the contours show no difference except for the nozzle with a converging angle of 25°. When the inlet flow speed is set to 5 m/s, it is apparent that the most unstable outflow stream is the nozzle with a converging angle of 15°. When the inlet flow speed is set to 10 m/s, there is almost no difference in flow speed contours except for the nozzle with a converging angle of 10°.
Figure 16.
Outflow field of different nozzles with different inlet velocities. (a) 1. (b) 5. (c) 10 m/s.
According to the above discussion, the boundary layer separation occurs in the nozzle with a converging angle of 25° when the inlet flow speed is set to 1 m/s; only the nozzle with a converging angle of 25° shows fluctuations. This means that the states of outflow of the three nozzles are identical, and there is no boundary layer separation near the throat wall among the three nozzles. While there is a sequence of vortex appearing near the wall of the throat section on the nozzle with a converging angle of 25°, the vortex near the wall do not disappear outside the nozzle but gradually developed and has a more significant impact on the central flow core, resulting in fluctuations in a flow core. All of these can indicate that the boundary layer near the nozzle outlet affects the outflow. When the inlet flow speed is set to 5 m/s, the boundary layer transition and separation appear in that inlet flow speed. The vortex in the boundary layer near the wall of the throat section of that nozzle can survive a long distance in the outside flow field; the vortex in the outside flow field develops the longest distance among the four nozzles, in agreement with Figure 16.
There is no vortex appearing near the wall of the throat section of the nozzle with a converging angle of 10° under the three simulation conditions. The separation does not occur in the boundary layer of the throat section; there is no vortex appearing in the outside flow field, and the flow core is more stable.
When the flow speed is low, the flow state of the boundary layer remains laminar along the throat section. There is no vortex appearing in the boundary layer on the throat section. The boundary layer flow will remain stable when flow into the outside flow field. That is why, the flow core is stable when the inlet flow speed is set to 1 m/s among the three nozzles with a smaller converging angle. When the separation vortex is just generated at the critical flow speed, a uniformly spaced vortex sequence can be generated near the wall of the throat section; the vortex will survive in the outside flow field and develop slowly, and the sequence vortex can survive a long distance, which shows unstable flow speed contour as the contours of the nozzle with a converging angle of 15° under an inlet flow speed of 5 m/s. When the flow speed gradually increases, the distribution of the vortex near the wall will become more uneven. The distance between adjacent vortices gradually increases along the flow direction. The vortex will develop fast in short distances when flowing into the outside flow field. Therefore, it is not easy to see the difference between the three nozzles with greater converging angles. Still, there will be a difference in the length of the flow core, which will be discussed in the experiment section.
Above all, when the flow speed is low, the nozzle with a smaller converging angle can generate a more stable flow core. The flow resistance will increase with nozzle length. According to the discussions of skin friction resistance and viscous force, the nozzle with a converging angle of 15° is suggested.
When the flow speed is high, boundary layer transition and separation appear near the wall of the throat section, and the viscous force can be ignored. What we should consider is the flow stability inside and outside the nozzle. The best way to obtain a stable flow is to avoid the appearance of the vortex. Each nozzle has a critical flow speed. There will be no vortex when the flow speed is lower than the critical value. While the longer length will affect the flow resistance, the flow core length should be considered, this part will be discussed later by experiments, but there is a critical converging angle that can obtain the longest and most stable flow core.
3. Experiments with a Higher Flow Speed
We carried out CFD simulations to investigate the flow dynamics inside a cone-straight nozzle and found that the nozzle with a specific converging angle would have a critical angle below which the boundary layer will not separate. External flow patterns are easier to be investigated by experiments. We hence carried out some experiments to study the external flow patterns. The throat length also affects the development of the near-wall flow, and the outer flow has been tested with a high-pressure pump and a PIV test system. In this study, 16 different cone-straight nozzles were used in the experiments, and their parameters are listed in Table 2. The metal nozzles are shown in Figure 17. The discharge coefficient and flow core length were measured experimentally.
Table 2. Experimental Parameters.
| converging angle/° | throat length | outlet diameter/mm | measure pressure/MPa |
|---|---|---|---|
| 10 | 0, 4, 8, 12, 16 | 4 | 0–25 |
| 15 | 0, 4, 8, 12, 16 | 4 | 0–25 |
| 20 | 0, 4, 8, 12, 16 | 4 | 0–25 |
| 25 | 0, 4, 8, 12, 16 | 4 | 0–25 |
Figure 17.
Experimental metal nozzle.
3.1. Experiment Setup
The flow-core length is measured, and the measurements of the flow coefficient for various nozzles with different profiles are carried out with the experimental setup shown in Figure 18. The experimental setup consists of three main components: the high-pressure pump, blessing, and the visualization device, and the experiments are carried out using particle image velocimetry.
Figure 18.
Experimental setup.
The high-pressure pump is a device that supplies the power and fluids, including the pump, water tank, pressure sensor, flow sensor, and control panel. The range of the high-pressure pump is 0–60 MPa, the displacement of the high-pressure pump is 0–100 L/min, and the power is 250 kW. The pressure gauge range is 60 MPa, and the measurement accuracy is 0.1 MPa. The flow meter range is 0–200 L/s, and the accuracy is 0.03. The high-pressure pump can generate fluids with high pressure. When the fluid flows through the nozzle, due to the reduced cross-sectional area of the flow, the fluid pressure energy will be converted into kinetic energy. The fluid will be accelerated and a higher flow speed is obtained.
The Particle Image Velocimetry system used is the Dantec standard Nd:YAG PIV laser system (wavelength 532 nm) with a pulse energy of up to 135 mJ per pulse, which is used to form an axial laser sheet parallel to the flow. A digital camera positioned perpendicularly to this laser sheet is used to capture the illuminated images. The maximum laser emission frequency is 7 Hz, and the PIV camera is a 16-bit sCMOS camera (LaVision, sCMOS, 2550 × 2160 pixels) with a Nikon macro lens equipped with a band-pass filter. The time interval between the two lasers is set to 2–6 μs depending on different flow velocities. The laser emission frequency is set to 5 Hz. Fifty images are captured for one experiment to obtain a stable flow speed.
3.2. Experimental Results and Discussion
3.2.1. Flow Core Length
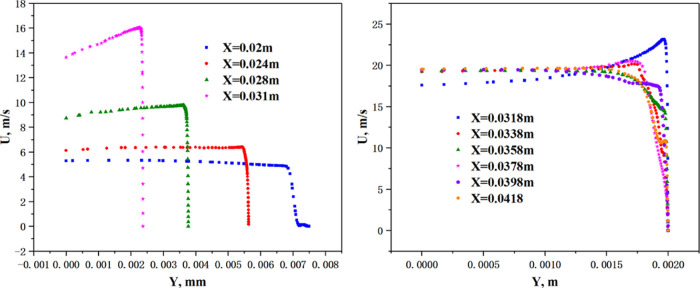
When the flow speed is high, cavitation can occur, and cavitation bubbles affect the quality of the image. We hence captured the outer flow field at a relatively low flow rate by adjusting the jetting pressure (∼0.3 MPa) to ensure no cavitation. The original image is shown in Figure 19a, and the particle density is higher than 100 per unit and good for analyzing the flow field.
Figure 19.
Flow field of the nozzle with a converging angle of 15°. (a) Original PIV image. (b) Without throat section. (c) 4 mm of throat length. (d) 8 mm of throat length. (e) 12 mm of throat length. (f) 16 mm of throat length.
Figure 19 shows the flow field of the cone-straight nozzle with a converging angle of 15° with different throat lengths. To quantitatively analyze the length of the isokinetic nucleus, we have done dimensionless analysis and defined a dimensionless flow core length, R, expressed as
 |
12 |
Lv90 represents the distance from nozzle exit at 90% of maximum speed, while Lv40 at 40%.
The flow core length of the 16 nozzles is shown in Figure 20. The flow core length of nozzles with different angles decreases first and then increases—and finally decreases with the throat length. The nozzle with a throat length of 12 mm (3 times the diameter of the nozzle outlet) can obtain the longer flow core, which is consistent with previous research results. The nozzle with a converging angle of 10 or 15° has a longer flow core than the other two types of the nozzle.
Figure 20.
Relationship between the flow core length and throat length.
Figure 21 shows the relationship between the jet angle and throat length of a nozzle with a converging angle of 15°. The jet angle decreases first and then increases with the throat length. The nozzle with a throat length of 8 mm or 12 mm (2 or 3 times the diameter of the nozzle outlet) has a relatively small jet angle, which means that the nozzle has a better cluster capacity.
Figure 21.
Relationship between the jet angle and throat length.
From the results of the visualization experiment by the PIV test system, we found that the nozzle with a converging angle of 15° has a longer flow core length and a better cluster capacity, which is consistent with the numerical simulation results described in Section 2.
3.2.2. Flow Discharge Coefficient
The flow discharge coefficient is an important evaluation parameter for evaluating nozzle energy conversion efficiency and has been investigated in this study. The measurements are done with a jetting pressure of 0–25 MPa.
The flow discharge coefficient equation is derived from the equation38 expressed as
 |
13 |
 |
14 |
Figure 22 shows the relationship between the discharge coefficient and jetting pressure for four types of nozzles with different converging angles. The flow discharge coefficient increases with the jetting pressure and then becomes stable. The flow discharge coefficient of the nozzle with a converging angle of 15° has the best energy transfer efficiency when the throat length is 16 mm (4 times the diameter of the outlet).
Figure 22.
Flow discharge coefficient along with the jetting pressure.
Figure 23 shows the stable value of the flow discharge coefficient of all the nozzles. There are differences in discharge coefficient trends among the four types of nozzles. The nozzle with a converging angle of 15° has a higher flow discharge coefficient when the throat length is 0, 4, 8, and 16 mm. The nozzle with a converging angle of 15 or 20° has the lowest discharge coefficient when the throat length is 3 times the diameter of the nozzle outlet. The nozzle with a converging angle of 10° has the highest discharge coefficient. The discharge coefficient of nozzles with a converging angle of 25° shows a fluctuation. The main difference occurs when the throat length is 3 times the diameter of the outlet. Hence, the nozzle with 3 times the diameter of the outlet has the better cluster capacity and has the longer flow core length. The difference needs to be investigated in future work.
Figure 23.
Relationship between the flow discharge coefficient and throat length.
Many influencing factors affect the nozzle flow discharge coefficient, such as the converging angle and the length of the throat section. The overall length of the nozzle affects the nozzle flow coefficient. The nozzle with a converging angle of 10° is almost 3 times the length of the nozzle with a converging angle of 25° without the throat section. This may be the reason that the nozzle with a converging angle of 10° has the lowest discharge coefficient when the throat length is zero. With the increase of the throat length, the internal flow patterns are changed, and the discharge coefficient increases first when the converging angle is 10, 20, and 25°, while the nozzle with a converging angle of 15° does not.
Above all, the flow core length and flow discharge coefficient can evaluate the quality of the cone-straight nozzle to some extent. From the discussion of experimental results, we know that the nozzle with a converging angle of 10 or 15° will have a longer flow core, a better cluster capacity, and a higher discharge coefficient, which is consistent with the simulation results.
4. Conclusions
An LES model is used to simulate the flow inside and outside cone-straight nozzles. The simulation data is in agreement with the existing DNS data. An experimental setup is built to carry out some experiments under lower flow speed to validate the accuracy of the LES model. Flow field measurements are done to reveal the real flow patterns and flow speed development. Four types of nozzles with different converging angles are simulated under three different inlet flow speeds. In total, 16 different nozzles are used in the experiments at different pressures. The conclusions are summarized below.
The converging angle directly affects the transition and separation of the boundary layer in the throat section. The thickness of the boundary layer has the minimum value at the entrance of the throat section. The boundary layer is compressed along the converging direction. The greater the converging angle, the more severe the flow fluctuations. The higher the flow speed, the more powerful the fluctuations. The nozzle converging angle directly affects the skin friction resistance. The nozzle with a converging angle of 15° has a smaller resistance among the four nozzles.
The boundary layer at the nozzle exit affects the stability of the flow core outside the nozzle. The vortex will develop fast in the flow field outside the nozzle and affect the state of the flow core. The converging angle has an important effect on the flow state.
The nozzle with a converging angle of 10 or 15° and 3 times the diameter of the outlet has a longer flow core length, a better cluster capacity, and a higher discharge coefficient. Considering the nozzle size, the nozzle with a converging angle of 15°, with a throat length of 3 times the outlet, is suggested to obtain a more stable and longer flow core at a low flow speed.
Acknowledgments
The authors would like to thank the financial support from the National Natural Science Foundation of China (grant no. 51827804), 111 Plan (grant no. B17045), and the National Science Fund for Distinguished Young Scholars (grant no. 51725404).
Glossary
Abbreviations
- D1
inlet diameter, mm
- α
converging angle, degree
- L
length of throat section, mm
- D2
outlet diameter, mm
- U
flow speed, m/s
- Uc
flow speed at the centerline, m/s
- R
radius of the monitored point, m
- D
diameter of the pipe, m
- yp
real distance to the wall
- yp+
dimensionless distance to the wall
- μτ
shear velocity
- y+
dimensionless distance to the nozzle wall
- X
nozzle axis coordinate
- Y
radial coordinate
- ρ
density, kg/m3
- ν
dynamic viscosity, Pa*s
- τw
wall shear stress, Pa
- Cf
skin friction coefficient
- F
skin friction resistance, n
- Ux
velocity component along the X coordinate
- Uy
velocity component along the Y coordinate
- Uxm
component of Ux along the M coordinate
- Uym
component of Uy along the M coordinate
- Uxn
component of Ux along the N coordinate
- Uyn
component of Uy along the N coordinate
- τ
shear stress, Pa
- R
represent the flow core length, %
- Lv90
distance from nozzle exit at 90% of maximum speed, m
- Lv40
distance from nozzle exit at 40% of maximum speed, m
- C
flow discharge coefficient,
- Q
flow discharge, m3/s
- A
nozzle exit cross-sectional area, m2
- ΔP
jetting pressure, Pa
The authors declare no competing financial interest.
Notes
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- Ping L.; Yangzhu H. Current Status and Development Projects of Water Jet Technology. Coal Min. Mach. 2009, 30, 10–12. [Google Scholar]
- Gensheng L.; Zhonghou S. High-pressure water jet theory and its application in petroleum engineering. Pet. Explor. Dev. 2005, 1, 2. [Google Scholar]
- Huanjian S. Coal Seam Slotted Nozzle Structure Optimization and Test. Coal Min. Safety 2020, 51, 10–13. 10.13347/j.cnki.mkaq.2020.04.003. [DOI] [Google Scholar]
- Wentao M.; Junfeng P.. Numerical simulation of water jet flow field and rock breaking characteristics with different nozzle structures. Coal Min. Mach. 2019, 9, 10.13436/j.mkjx.201909006. [DOI] [Google Scholar]
- Folkes J. Waterjet—An innovative tool for manufacturing. J. Mater. Process. Technol. 2009, 209, 6181–6189. 10.1016/j.jmatprotec.2009.05.025. [DOI] [Google Scholar]
- Guha A.; Barron R. M.; Balachandar R. An experimental and numerical study of water jet cleaning process. J. Mater. Process. Technol. 2011, 211, 610–618. 10.1016/j.jmatprotec.2010.11.017. [DOI] [Google Scholar]
- Jian H.; Tengfei C.; Yan P. Analysis of Jet Characteristics of Organ Tube Nozzle and Helmholtz Nozzle. Coal Min. Safety 2017, 48, 134–137. [Google Scholar]
- Hayakawa M.; Ina Y.; Yokoi Y.; Takamoto M.; Nakao S.-i. Development of a transfer standard with sonic Venturi nozzles for small mass flow rates of gases. Flow Meas. Instrum. 2000, 11, 279–283. 10.1016/S0955-5986(00)00032-7. [DOI] [Google Scholar]
- Nakao S.-i.; Takamoto M. Development of the calibration facility for small mass flow rates of gases and the sonic Venturi nozzle transfer standard. JSME Int. J., Ser. B 1999, 42, 667–673. 10.1299/jsmeb.42.667. [DOI] [Google Scholar]
- Jiang T.; Huang Z.; Li J.; Li H. Effect of parameters on threshold pressure of sandstone tested by water jet. Int. J. Rock Mech. Min. Sci. 2021, 139, 104640. 10.1016/j.ijrmms.2021.104640. [DOI] [Google Scholar]
- Jingbin L.; Zhongwei H.; Guangqing Z.; Xin L.; Huan L. Rock breaking characteristics of the self-rotating multi-orifices nozzle applied to coalbed methane radial jet drilling. Int. J. Rock Mech. Min. Sci. 2020, 136, 104483. 10.1016/j.ijrmms.2020.104483. [DOI] [Google Scholar]
- Jiayu L.; Ailun W.; Jin J.; Bin J. Comparative study of water jet flow field between special-shaped nozzle and conical nozzle. Light Ind. Mach. 2019, 37, 19–24. [Google Scholar]
- Xiaoyin Z.; Hong L.; Yue J. Experimental study on water distribution uniformity of low-pressure nozzles with special-shaped nozzles. J. Irrig. Drain Eng. 2017, 35, 448–453. [Google Scholar]
- Haining Z.; Lu B.; Jiari Z.; Shupeng C. Research on the visualization of the internal flow field of the special-shaped nozzle. J. Hunan Univ. Technol. 2013, 43–47. [Google Scholar]
- Wenjie L.; Xiaoyang C. Study on optimization simulation of high pressure water jet nozzle based on Fluent. Energy Environ. Prot. 2020, 3. [Google Scholar]
- Xinying C. Hydraulic fracturing sand annulus jet nozzle structure analysis and optimization. Oil Field Equip. 2019, 48, 41–45. [Google Scholar]
- Tingbin C.; Wenling L.; Xiaoxiao L.; Zhengbiao J.; Yilong G. Design and optimization of jet nozzle structure based on Fluent. J. Chengdu Univ. 2019, 17. [Google Scholar]
- Minxia L.; Xiuhui L. A Practical Study on the Expansion Method of the Contraction Section of the Wind Tunnel of the Vydolcinski Curve. Appl. Energy Technol. 2010, 1–4. [Google Scholar]
- Jiang T.-W.; Huang Z.-W.; Li J.-B.; Zhou Y.-S. Internal Flow Mechanism of Cone-straight Nozzle. Pet. Sci. 2021, 18, 1507–1519. 10.1016/j.petsci.2021.08.008. [DOI] [Google Scholar]
- Brès G. A.; Jordan P.; Jaunet V.; Le Rallic M.; Cavalieri A. V. G.; Towne A.; Lele S. K.; Colonius T.; Schmidt O. T. Importance of the nozzle-exit boundary-layer state in subsonic turbulent jets. J. Fluid Mech. 2018, 851, 83–124. 10.1017/jfm.2018.476. [DOI] [Google Scholar]
- Zaman K. B.Increased Jet Noise Due to a“nominally Laminar” State of Nozzle Exit Boundary LayerNASA; Glenn Research Center, 2017. [Google Scholar]
- Fontaine R. A.; Elliott G. S.; Austin J. M.; Freund J. B. Very near-nozzle shear-layer turbulence and jet noise. J. Fluid Mech. 2015, 770, 27–51. 10.1017/jfm.2015.119. [DOI] [Google Scholar]
- Karon A. Z.; Ahuja K. K.. Reduction of Jet Noise by the Nozzle-Exit Boundary Layer. 23rd AIAA/CEAS Aeroacoustics Conference, 2017; p 3859.
- Hariharan P.; Giarra M.; Reddy V.; Day S. W.; Manning K. B.; Deutsch S.; Stewart S. F. C.; Myers M. R.; Berman M. R.; Burgreen G. W.; Paterson E. G.; Malinauskas R. A. Multilaboratory particle image velocimetry analysis of the FDA benchmark nozzle model to support validation of computational fluid dynamics simulations. J. Biomech. Eng. 2011, 133, 041002. 10.1115/1.4003440. [DOI] [PubMed] [Google Scholar]
- Wang C.; Wang X.; Ding H. Boundary layer of non-equilibrium condensing steam flow in a supersonic nozzle. Appl. Therm. Eng. 2018, 129, 389–402. 10.1016/j.applthermaleng.2017.10.015. [DOI] [Google Scholar]
- Zaman K.; Bencic T.; Clem M.; Fagan A.. Shock-induced boundary layer separation in CD nozzles and its impact on jet noise. 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2011; p 1031.
- Nozzles V.Numerical Assessment of Discharge Coefficient and Wall Temperature Dependence of Discharge Coefficient for Critical-Flow, 2016.
- Manchester E. L.; Xu X. Y. The effect of turbulence on transitional flow in the FDA’s benchmark nozzle model using large-eddy simulation. Int. J. Numer. Method Biomed. Eng. 2020, 36, e3389 10.1002/cnm.3389. [DOI] [PubMed] [Google Scholar]
- Ünsal B.; Rathore K.; Koç E.. Numerical findings on the boundary layer transition of critical-flow venturi nozzles, 17th International Flow Measurement Conference, 2016; pp 1–5.
- Ishibashi M. Discharge coefficient equation for critical-flow toroidal-throat venturi nozzles covering the boundary-layer transition regime. Flow Meas. Instrum. 2015, 44, 107–121. 10.1016/j.flowmeasinst.2014.11.009. [DOI] [Google Scholar]
- Ishibashi M.; Takamoto M. Instrumentation Theoretical discharge coefficient of a Engineering critical circular-arc nozzle with laminar boundary layer and its verification by measurements using super-accurate nozzles. Flow Meas. Instrum. 2000, 11, 305–313. 10.1016/S0955-5986(00)00029-7. [DOI] [Google Scholar]
- Mahapatra S.; Nelaturi A.; Tennyson J.; Ghosh S. Large-eddy simulation of compressible turbulent flow in convergent-divergent nozzles with isothermal wall. Int. J. Numer. Methods Heat Fluid Flow 2019, 78, 108425. 10.1016/j.ijheatfluidflow.2019.108425. [DOI] [Google Scholar]
- Demetriades A. Cooling and roughness effects on transition on nozzle throats and blunt bodies. J. Spacecr. Rockets 1992, 29, 432–436. 10.2514/3.25482. [DOI] [Google Scholar]
- Krishnamurty V. S.; Shyy W. Effect of Wall Roughness on the Flow Through Converging - Diverging Nozzles. J. Propul. Power 1997, 13, 753–762. 10.2514/2.5248. [DOI] [Google Scholar]
- Jianyang Y.; Ruoyu W.; Fu C.; Yanping S. Comparative analysis and application of different sub-lattice models. J. Eng. Thermophys. 2016, 37, 2311–2318. [Google Scholar]
- Bogey C.; Bailly C. Influence of nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 2010, 663, 507–538. 10.1017/S0022112010003605. [DOI] [Google Scholar]
- Eggels J. G. M.; Unger F.; Weiss M. H.; Westerweel J.; Adrian R. J.; Friedrich R.; Nieuwstadt F. T. M. Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 1994, 268, 175–210. 10.1017/S002211209400131X. [DOI] [Google Scholar]
- Jingbin L.; Gensheng L.; Zhongwei H.; Xianzhi S. Analysis of energy conversion efficiency of porous nozzles. Fluid Mach. 2017, 45, 20–25. [Google Scholar]