Elucidation of the key role of Pt···Pt interactions in the directional self-assembly of platinum(II) complexes

Significance

Molecular self-assembly provides a bottom-up platform to design supramolecular functional materials, attracting numerous interests in material sciences. The utilization of platinum(II) complexes as building blocks of supramolecular assemblies opens up the unique noncovalent Pt···Pt interaction as one of the driving forces, imparting the supramolecular materials with rich spectroscopic features. However, the exact role of Pt···Pt interactions in molecular assembly remains elusive. The current study combines experimental and computational techniques to elucidate the role of Pt···Pt interactions in the self-assembly process of a representative amphiphilic platinum(II) complex. This work demonstrates the directional role of Pt···Pt interactions in assisting the molecular assembly in an anisotropic manner, achieving the formation of ordered self-assembled structures.

Abstract

Here, we report the use of an amphiphilic Pt(II) complex, K[Pt{(O₃SCH₂CH₂CH₂)₂bzimpy}Cl] (PtB), as a model to elucidate the key role of Pt···Pt interactions in directing self-assembly by combining temperature-dependent ultraviolet-visible (UV-Vis) spectroscopy, stopped-flow kinetic experiments, quantum mechanics (QM) calculations, and molecular dynamics (MD) simulations. Interestingly, we found that the self-assembly mechanism of PtB in aqueous solution follows a nucleation-free isodesmic model, as revealed by the temperature-dependent UV-Vis experiments. In contrast, a cooperative growth is found for the self-assembly of PtB in acetone–water (7:1, vol/vol) solution, which is further verified by the stopped-flow experiments, which clearly indicates the existence of a nucleation phase in the acetone–water (7:1, vol/vol) solution. To reveal the underlying reasons and driving forces for these self-assembly processes, we performed QM calculations and show that the Pt···Pt interactions arising from the interaction between the p_z and d_z² orbitals play a crucial role in determining the formation of ordered self-assembled structures. In subsequent oligomer MD simulations, we demonstrate that this directional Pt···Pt interaction can indeed facilitate the formation of linear structures packed in a helix-like fashion. Our results suggest that the self-assembly of PtB in acetone–water (7:1, vol/vol) solution is predominantly driven by the directional noncovalent Pt···Pt interaction, leading to the cooperative growth and the formation of fibrous nanostructures. On the contrary, the self-assembly in aqueous solution forms spherical nanostructures of PtB, which is primarily due to the predominant contribution from the less directional hydrophobic interactions over the directional Pt···Pt and π−π interactions that result in an isodesmic growth.

Supramolecular assembly, which uses randomly oriented molecules to form ordered structures, offers a bottom-up approach to design functional materials at multiscale levels (1–4). This organization of molecular building blocks in a noncovalent manner is highly prevalent in nature and vital for living organisms; examples include protein folding, bilayer membrane formation, DNA, and viruses (2, 5–7). Scientists have also designed numerous functional materials by strategically altering molecular building blocks, as slight modifications in these building blocks may significantly change the morphology of the assembled structures due to a change in the relative strength of various noncovalent interactions (NCIs) (8–10). In particular, amphiphiles, which contain both hydrophilic and hydrophobic parts, have demonstrated the ability to assemble into various nanostructures (e.g., micelles, nanotubes, nanorods, nanosheets, and vesicles), attracting broad interests of chemists and material scientists. These assembled structures are determined at thermodynamic equilibrium by the balance of various nonbonded interactions, such as hydrophobic interactions, hydrogen bonding, and π−π interactions (9, 11–13) and have broad implications in various applications, ranging from drug delivery, biosensors, cell imaging, to optoelectronic devices (8, 14–16).

Unlike organic and polymer amphiphiles (17–21), metallo-amphiphiles are relatively less extensively explored (10). The amphiphilic platinum(II) complex, termed Pt(II) amphiphile, is a special family of metallo-amphiphiles that displays the coexistence of the unique Pt···Pt interaction between pairs of Pt(II) complexes and other nonbonded intermolecular interactions such as π−π interactions (4, 22, 23). By reducing solvation through the introduction of nonsolvents, intermolecular Pt···Pt interactions can be turned on through the proximity of the molecules and can serve as an additional driving force for the self-assembly (14, 24, 25) and consequently results in the formation of assembled nanostructures that are different from those without the contribution from Pt···Pt interaction. For example, an oligo(p-phenylene ethynylene)-containing amphiphilic alkynylplatinum(II) terpyridine complex has been found to exhibit the formation of nanotubes assisted by the intermolecular Pt···Pt and π−π interactions (25). Upon the introduction of the sterically demanding bulky substituent groups on the terpyridine ligands of the amphiphilic complex, in stark contrast to the formation of nanotubes, helical ribbons are formed and attributed to a lesser extent to intermolecular Pt···Pt interactions (25). In addition, the amphiphilic Pt(II) complexes with sulfonate pendants could assemble into ordered nanoaggregates, such as vesicles and nanofibers, in solutions through the switching-on of the intermolecular Pt···Pt interactions upon the variation of solvent polarity (26).

Formation of directional nanostructures has also been demonstrated in a polyhedral oligomeric silsesquioxane (POSS)-containing alkynylplatinum(II) complex (27). Upon addition of hexane, a nonpolar nonsolvent, to a tetrahydrofuran (THF) solution of the well-dispersed platinum(II) complex, self-assembly driven by directional Pt···Pt interactions led to the formation of one-dimensional rod-like nanostructures (27). Conversely, the addition of water, which is another nonsolvent but it is polar, to the same THF solution of the well-solvated platinum(II) complex led to ring-like aggregates instead since the driving force becomes dominated by the less directional dispersion interaction from the hydrophobic POSS moieties with less involvement of the directional Pt···Pt interactions (27).

These observations suggest that the presence of Pt···Pt and π−π interactions allows the Pt(II) complexes to self-assemble into more ordered structures, implying the directionality of the Pt···Pt interactions. However, the self-assembled structures and characteristics of most of these works were investigated by experiments such as emission spectroscopy, electron microscopy, NMR, X-ray crystallography, and various X-ray methods, which are only capable of being used to study the assembled nanostructures at thermodynamically equilibrated states (9, 27, 28). The dynamic details of the self-assembly process are limited.

The emergence of the characteristic metal-metal-to-ligand charge transfer (MMLCT) absorption bands upon the formation of Pt···Pt interactions in the Pt(II) aggregate can serve as a probe to monitor the self-assembly mechanism through the temperature-dependent ultraviolet-visible (UV-vis) absorption spectroscopy. The following two mathematical models are available to describe the underlying self-assembly processes: the nucleation–elongation model (29) and the isodesmic model (30). In the nucleation–elongation model, the formation of a nucleus is required at the elongation temperature (T_e) before subsequent elongation processes take place. Thus, this model describes a cooperative growth mechanism of the assemblies. On the other hand, the isodesmic model is used to quantify the isodesmic growth mechanism of the assemblies, and it is known as the equal-K model, in which every monomer addition to the supramolecular polymer is governed by a single equilibrium constant K_e. In particular, the formation of nanofibers has been observed in a series of oligo(p-phenyleneethynylene)s-containing amphiphilic dinuclear alkynylplatinum(II) complexes with 2,6-bis(N-alkylbenzimidazol-2′-yl)pyridine pincer ligand, exhibiting the cooperative growth or isodesmic growth mechanism assisted by the formation of intermolecular Pt···Pt interactions in the self-assembly (31). More importantly, the thermodynamic parameters can be obtained from these temperature-dependent experiments, which provide an in-depth understanding into the self-assembly processes. However, the dynamics of the self-assembly of the amphiphilic Pt(II) complexes is relatively less explored, probably attributed to the fast aggregation kinetics in the millisecond time regime.

Computer simulations such as dissipative particle dynamics (32–34), Brownian dynamics (35–37), and molecular dynamics (MD) simulations (38–41) have shown to be a valuable alternative to complement experiments in studying the dynamics of the self-assembly process. In particular, MD simulations are a powerful tool that can provide dynamical information of the self-assembly processes at atomistic resolutions. To perform MD simulations for the self-assembly of amphiphilic Pt(II) complexes, precise characterization of the unique Pt···Pt interactions is crucial. Unfortunately, accurate force field parameters for Pt(II) are not available in commonly used force fields. Therefore, we adopted an effective strategy to develop the force field parameters for the Pt(II) atom in Pt(II) complexes for all-atom MD simulations.

In this work, we combined experimental and computational techniques to elucidate the role of Pt···Pt interactions in the self-assembly process of a representative amphiphilic Pt(II) complex, PtB (Fig. 1A). First, we monitored the fraction variations of the assembled aggregates at different temperatures using UV-Vis spectroscopy in aqueous solution and found that the temperature dependence of the aggregate fraction for PtB follows the nucleation-free isodesmic model. Second, we monitored the fraction variations of the assembled aggregates as a function of temperature by UV-Vis spectroscopy in acetone–water (7:1, vol/vol) solution and found that the temperature dependence of the aggregate fraction for PtB follows the nucleation–elongation model, which is further supported by the kinetic stopped-flow experiments. Third, combining the MD simulations, principal interacting orbitals (PIO), and NCI analysis, we demonstrated the key role of the Pt···Pt interactions in facilitating self-assembly and unraveled the intrinsic origin of the directional Pt···Pt interactions to be arising from the interaction between the p_z and d_z² orbitals. Finally, we rationalize the PtB self-assembly for the formation of the vesicles and fibers and provide theoretical insights for the design of the Pt(II) complex and precise control of the self-assembly process.

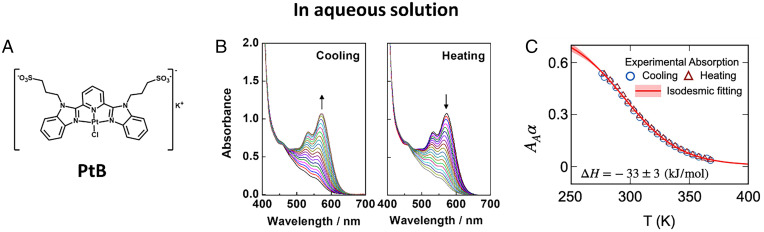
Fig. 1.

Temperature-dependent UV-Vis absorption spectra and fitted curves for the self-assembly of Pt(II) complex PtB in aqueous solution. (A) Chemical structure of PtB. (B) The UV-Vis absorption spectra of PtB in water ([Pt] = 10⁻⁴ M) upon decreasing temperature from 368 to 276 K (Left panel) and increasing temperature from 276 K to 368 K (Right panel). (C) The aggregation fraction obtained by the UV-Vis absorption spectra at 600 nm (circles and triangles) as a function of temperature, fitted to the isodesmic model (red curve; SI Appendix, Eq. S2). $A_A$ corresponds to 100% of the aggregate fractions. The red triangles and blue circles are the fractions obtained upon increasing and decreasing temperature between 276 K and 368 K, respectively (SI Appendix, Fig. S1 for details). The light-red region shows the range of error when fitted to the isodesmic model. The change in enthalpy during elongation in the isodesmic growth is −33 ± 3 kJ mol⁻¹.

Results and Discussion

Self-Assembly via an Isodesmic Model in Aqueous Solution Unraveled by Thermodynamic Experiments.

The rich spectroscopic and luminescence properties of the amphiphilic Pt(II) complex can serve as a probe for the study of supramolecular assemblies, as the temperature-dependent degree of aggregation α, obtained by the spectroscopic change of the UV-Vis absorption spectra (Fig. 1B and SI Appendix, Fig. S1 for details), can reveal the growth mechanism of supramolecular assemblies. In our UV-Vis absorption experiments in aqueous solution, we found that the assembly of PtB molecules follows the nucleation-free isodesmic model (see Fig. 1C), where the equilibrium constants of aggregation are high at both low temperatures (e.g., $K_{\mathrm{e}}^{300\mathrm{K}} = 2.4\times {10}^3 {\mathrm{M}}^{-1}$) and high temperatures (e.g., $K_{\mathrm{e}}^{368\mathrm{K}} = 2.6\times {10}^2 {\mathrm{M}}^{-1}$). This indicates that the elongation processes for this self-assembly mechanism in aqueous solution are highly favorable at all temperatures. Moreover, no hysteresis was observed in the PtB assembly since the α against temperature curve obtained from heating (red triangle) and cooling (blue circle) experiments can overlap well (Fig. 1C). This observation further suggests that the intermolecular Pt···Pt interaction and π−π stacking (as indicated by the characteristic low-energy absorption band at 570 nm in Fig. 1B) can simultaneously drive the self-assembly process across a wide range of temperatures (26).

In aqueous solution, hydrophobic interactions also serve as a driving force for the self-assembly of PtB with reduced solvation. Since the hydrophobic interactions are nondirectional, the assembly of PtB by hydrophobic interactions alone is expected to be less ordered with relatively less well-defined nanostructures (42). However, transmission electron microscopy (TEM) and confocal microscopic experiments detect the highly ordered assembled structures of PtB in aqueous solution. These observations suggest that the directional Pt···Pt and π−π interactions and the less directional hydrophobic interactions should play crucial roles in directing and maintaining the formation of ordered PtB structures. Furthermore, it is interesting to note that several previously reported amphiphilic Pt(II) complexes can self-assemble via the cooperative growth mechanism and the cooling curves of α can be fitted to the nucleation–elongation model (e.g., bi-PtB and bi-PtT in SI Appendix, Fig. S1) (25, 43). The cooperativity of the supramolecular system has been found to be governed by a number of factors including the hydrophobicity of the complexes (31) and the solvent composition and temperature as well as a delicate balance of the NCIs (31, 44, 45). Unfortunately, the changes in the absorbance of PtB in aqueous solution are too small to obtain meaningful data with certainty, hindering the further investigation into the kinetics of the formation of the spherical aggregates using the stopped-flow technique.

Self-Assembly via a Cooperative Growth Mechanism in Acetone–Water (7:1, vol/vol) Solution Unraveled by the Thermodynamic and Kinetic Experiments.

We have further investigated the self-assembly mechanism of PtB at acetone–water (7:1, vol/vol) solution by the variable-temperature UV–vis absorption studies. Upon decreasing the temperature of a solution of PtB in the acetone–water (7:1, vol/vol) mixture from 353 to 263 K, there is a growth of the absorption at 594 nm associated with the formation of the intermolecular Pt···Pt interaction (Fig. 2A). The plot of α against temperature at 594 nm of the cooling curve of such solution is found to be clearly nonsigmodal (Fig. 2B), indicating a cooperative supramolecular growth mechanism. Hence, the nucleation–elongation model has been employed to further investigate the cooperative growth process. The thermodynamic parameters for the self-assembly process of PtB in the acetone–water (7:1, vol/vol) mixture have also been obtained, in which the change in enthalpy during the self-assembly for elongation (H_e) and the T_e are found to be about $-15.8\pm 2.3$ kJ mol⁻¹ and $342$ K, respectively. The corresponding equilibrium constants at room temperature and near elongation temperature are $K_{\mathrm{e}}^{298\mathrm{K}} = 2.6\times {10}^3 {\mathrm{M}}^{-1}$ and $K_{\mathrm{e}}^{328\mathrm{K}} = 1.4\times {10}^2 {\mathrm{M}}^{-1}$, respectively (Fig. 2B). In addition, the equilibrium constant for the nucleation phase (K_a) is found to be relatively small at $5.0\times {10}^{-6}$, confirming the existence of a rate-limiting nucleation step. Such a discrepancy in the growth mechanism of the assembly of PtB in water and in the acetone–water (7:1, vol/vol) mixture is believed to be originating from a delicate balance of noncovalent intermolecular interactions in the self-assembly (28). In water, the isodesmic growth of PtB is believed to arise from the predominant contribution of the nondirectional hydrophobic interactions, with a lesser contribution from the rather loosely packed directional Pt···Pt and π−π interactions associated with the less-ordered packing from the Pt(II)-pincer moieties of PtB, as revealed from the less red-shifted MMLCT absorption band at 570 nm that lead to the formation of spherical aggregates. In stark contrast, the hydrophobic interactions are believed to be attenuated due to the improved solvation of the hydrophobic moieties of the PtB complex at high ratio of acetone in the acetone–water (7:1, vol/vol) mixture. Thus, the cooperativity of PtB in the acetone–water (7:1, vol/vol) mixture is believed to originate from the stronger presence of the directional Pt···Pt and π−π stacking interactions, while at a lesser extent from the nonspecific hydrophobic interactions. This statement is supported by our experimental observation of the highly aligned and ordered Pt(II)-pincer moieties of PtB, as revealed from a more red-shifted MMLCT absorption band at 594 nm. In the acetone–water mixture, the balance of various nonbonded interactions will ultimately lead to the cooperative growth of PtB into nanofibers. It is interesting to note that in the acetone–water (7:1, vol/vol) mixture, despite an increasing content of an organic solvent, acetone that can better solvate the hydrophobic moieties, the hydrophobic interactions are attenuated to only a certain extent rather than completely or to a large extent given the rather polar character of acetone, leading to the coexistence of Pt···Pt, π−π and hydrophobic interactions, i.e., predominantly Pt···Pt and π−π interactions assisted by hydrophobic interactions that led to a cooperative growth mechanism.

Fig. 2.

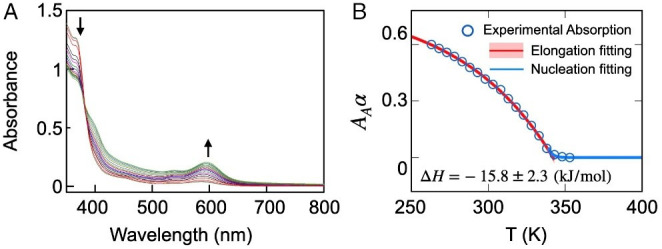
Temperature-dependent UV-Vis absorption spectra and fitted curves for the self-assembly of Pt(II) complex PtB in the acetone–water (7:1, vol/vol) mixture. (A) The UV-Vis absorption spectra of PtB in the acetone–water (7:1, vol/vol) mixture upon decreasing temperature from 353 K to 263 K. (B) The aggregation fraction obtained by the UV-Vis absorption spectra at 594 nm (circles) as a function of temperature, fitted to the elongation model (red curve; SI Appendix, Eq. S4) and nucleation model (blue curve; SI Appendix, Eq. S5). The blue circles are the fractions obtained upon decreasing temperature from 353 K to 263 K. The light-red region shows the range of error when fitted to the elongation model. The change in enthalpy during the elongation is found to be −15.8 ± 2.3 kJ/mol.

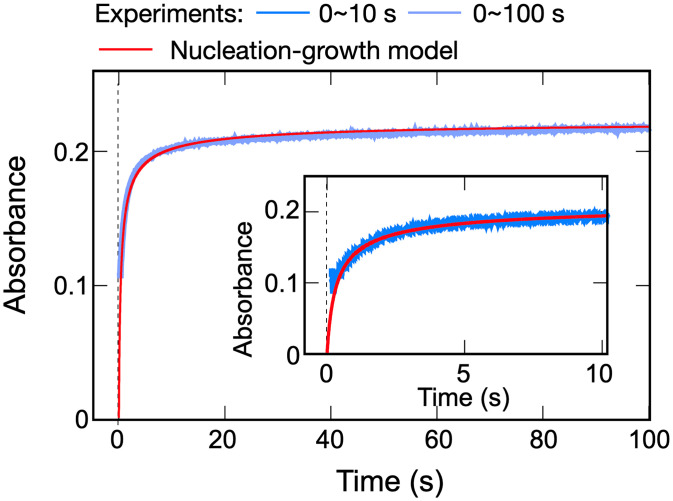
The cooperative dynamics of PtB self-assembly in acetone–water (7:1, vol/vol) mixture can be directly measured by the stopped-flow experiment. The color of the solution changes from green to blue, which is attributed to the increase in the MMLCT absorption band associated with the formation of intermolecular Pt···Pt interaction, leading to nanorod morphologies. The absorbance changes at 594 nm at various time intervals are shown in Fig. 3. To derive the kinetic rates from the stopped-flow experiments, we fitted the experimental data to a nucleation-growth model that takes into account the following three kinetic processes: the formation of nucleus, further growth of fibril aggregates, and merging of small aggregates into larger ones (SI Appendix, section 2.3 for details). This nucleation–elongation model was based on our previous work that describes the aggregation of hydrophobic moieties via a classical nucleation–elongation theory (46). As shown in Fig. 3, the stopped-flow experimental data can be well fitted to the kinetic nucleation–growth model and clearly indicates the existence of the nucleation phase in the self-assembly process (see SI Appendix, section 2.3 for fitting details). At $t = 0.1 s$, we obtained the nucleation rate of $1.1\times {10}^{-6} \mathrm{M} {\mathrm{s}}^{-1}$ with a critical nucleus size of ∼104. As time elapses, the nucleation rate sharply decreases and plays a negligible role at t = 1 s. At this stage, the elongation dominates the growth with a rate of 10.6 s⁻¹ (t = 0.1 s) and gradually decreases with the consumption of PtB monomers and merging of the existing aggregates, e.g., 1.50 s⁻¹ at t = 1 s, 0.31 s⁻¹ at t = 10 s, and 0.076 s⁻¹ at t = 100 s. These observations confirm the existence of an activated nucleation process of PtB assembly in the acetone–water (7:1, vol/vol) mixture.

Fig. 3.

Time-dependent UV-Vis spectral change in the stopped-flow experiment and fitting to a kinetic nucleation–elongation model. In the stopped-flow experiment, PtB was dissolved in a acetone–water (3:1, vol/vol) mixture, then mixed with acetone, and finally reached a volume ratio of acetone–water of 7:1 (vol/vol). The total concentration of PtB is 2.25 × 10⁻⁴ M. The experiments were conducted at room temperature (298 K). The absorbance changes at 594 nm were measured as an indication of the degree of aggregation. The blue and light-blue curves are the experimental result performed at 0∼10 and 0∼100 seconds, respectively. The experimental data were fitted to the extended kinetic nucleation–growth model (red curve; SI Appendix, section 2.3 for fitting details).

Quantum Mechanics Calculations and MD Simulations Reveal that Pt···Pt Interactions Play Key Roles in the Self-Assembly Process.

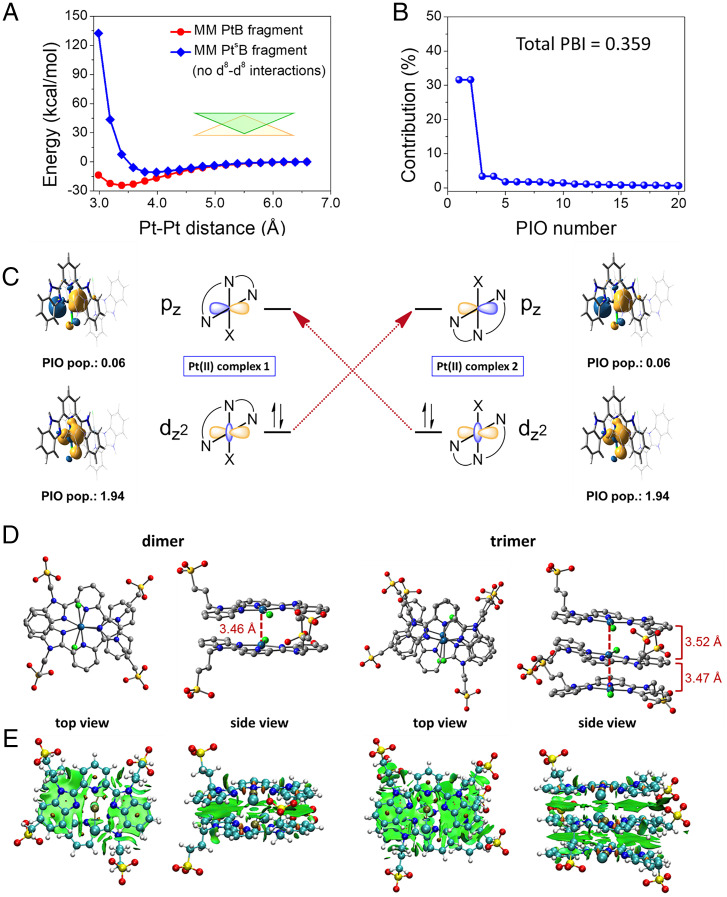
In the previous section, we discovered that the PtB self-assembly follows a nucleation-free isodesmic model in aqueous solution but a cooperative growth nucleation–elongation model in the acetone–water (7:1, vol/vol) solution. To reveal the microscopic role that the Pt···Pt interactions play in PtB self-assembly, we examined the strength and directionality of the Pt···Pt interaction using QM calculations on the dimer of the extracted core fragment from the PtB complex (i.e., PtB-core; Fig. 4A and SI Appendix, Fig. S3). We found that the intermolecular interactions between the dimer of PtB-core are strong and can reach a minimum of ∼−25 kcal mol⁻¹ when the Pt···Pt distance ∼3.38 Å (black curve in Fig. 4B). In order to examine the contributions of the d⁸–d⁸ interaction to this energy profile, we also computed the dimer energy profile using molecular mechanics (MM) on a control system, as follows: Pt^sB, where the d⁸–d⁸ interactions between two Pt(II) atoms are not considered (SI Appendix, section 2.7 for details). Without d⁸–d⁸ interactions, the potential energy profile in the vertical direction of the extracted core fragment of Pt^sB complex (Pt^sB-core) is significantly higher than that of the PtB-core (e.g., 31.8 kcal mol⁻¹ higher at the minimum when Pt···Pt distance is 3.38 Å; Fig. 5A and SI Appendix, Fig. S4A). This could lead to the large difference in flexibility of the self-assembled structures. In addition, the direct interaction between two Pt atoms in the PtB dimer computed by MM using our fitted force field parameters is very strong, reaching −2.52 kcal/mol at a Pt···Pt distance of 3.38 Å (SI Appendix, sections 2.4 and 2.5 and Table S1 for fitting details), which is comparable to the π-π interactions in a benzene dimer (about 2 to 3 kcal mol⁻¹) (47). This comparative strength demonstrates the importance of the Pt···Pt interaction during the self-assembly of Pt(II) complexes. In addition, the antiparallel-packing of both PtB-a and PtB-b in their crystal structures also suggests an important role of the directional Pt···Pt interactions in maintaining ordered packing of these complexes (see Fig. 4 C–F).

Fig. 4.

Fitting and validation of the force field parameters for the PtB complex. (A) Chemical structure of the PtB-core. (B) The potential energy profiles as a function of Pt···Pt distance for PtB-core dimer in the PtFF model were calculated using QM (black curves) and MM (red curves). (C and E) Chemical structures of Pt(II) complex PtB-a and PtB-b used for force field parameters validation. (D and F) The snapshots of supercell extracted from the PtB-a and PtB-b crystal structures in the PtFF model, respectively.

Fig. 5.

The orbital interactions between two monomers of PtB-core and the noncovalent intermolecular interactions of PtB oligomers. (A) The potential energy profiles for dimer of PtB-core calculated from MM with (the red curve), as well as without considering d⁸–d⁸ interactions along the vertical direction of Pt···Pt interactions (the blue curve). The green and orange triangles represent the shape of the complex. (B) Screen plot of the contributions (normalized squared singular values) of the top 20 PIO pairs ordered by decreasing singular values. The clear gap between the second and third PIO pair indicates that the intermonomer orbital interactions are mainly dominated by two interactions, which collectively contribute >60% of the total. The total PBI was 0.359 for this pair of Pt(II) complexes. (C) The two dominant PIO pairs. PIO of PtB-core 1 (PIO population of 1.94, closely resembles dz² orbital) donates to the PIO of PtB-core 2 (PIO population of 0.06, resembles p_z orbital), whereas the other one is the converse donation from the dz² orbital of PtB-core 2 to the p_z orbital of PtB-core 1. The PBI of both interactions is around 0.114 (contributing 31.6% of the total orbital interactions amounting to the total PBI of 0.359) shown in B. This indicates that they are not traditional covalent bonds but reasonable secondary interactions. (D and E) The ground-state geometries of the dimer and trimer of PtB optimized and the corresponding NCI plots at the M06 level.

The origin of Pt···Pt interactions was believed to be attributed to the highly accessible nature in the z-direction of the platinum(II) complex due to its square-planar geometry (48–51). Thus, the head-on overlapping of two d_z² orbitals and two empty p_z orbitals from adjacent platinum(II) complexes in close proximity along the z-direction is made possible, which would lead to the formation of two fully filled dσ and dσ* orbitals and two empty pσ and pσ* orbitals, respectively (50, 51). A significant configuration mixing between dσ and pσ orbitals and between dσ* and pσ* orbitals would be favored because these orbitals possess the same orbital symmetry (50, 51). This would lead to a fractional bond order between the Pt(II) centers, which is known as the Pt···Pt interactions. Theoretical calculations on closed-shell interaction by Pyykkö et al. (52–55) realize the stabilization of metal–metal interactions, in which the correlation effect, which is strengthened by the relativistic effect, is suggested to be responsible for the metal–metal interaction. Recent theoretical studies of the closed-shell interactions in d¹⁰ organometallic complexes by Che realize the repulsive nature of the metal–metal interaction which is found to be induced from the significant mixing of the (n+1)s and nd orbitals of the metal center. Such a metal−metal Pauli repulsion is found to be suppressed by the mixing of the (n+1)p and nd orbitals. Although the metal−metal interactions are repulsive when there is a significant mixing of (n+1)s and nd orbitals, the short metal−metal distance, which is shorter than the sum of the van der Waals’ radii between the metal centers, is made possible in d¹⁰ organometallic complexes by the attractive dispersive forces between the ligands (56).

To elucidate the intrinsic mechanism of Pt···Pt interactions, PIO analysis was performed for the PtB-core dimer. PIO analysis (57, 58) performs two rounds of principal component analysis (PCA) on the cross-fragment block of the density matrix, which gives rise to two sets of linearly combined orbitals (one set on each fragment) ordered by their contribution to the cross-fragment interactions. PIO analysis of the dimer indicates that the d⁸–d⁸ interaction is the most important interacting orbital that holds the two monomers together. Moreover, a close examination of the two sets of PIOs revealed that two significant pairs of orbitals dominate the cross-fragment orbital interactions (Fig. 5B), namely, donations from the d_z² orbital of one monomer to the p_z orbital of the other (shown schematically nearby real molecular orbitals in Fig. 5C). Therefore, the d⁸–d⁸ orbital interactions arise from the vertical interactions between the p_z and d_z² orbitals, which are directional and belong to the long-range dispersion interactions among Pt(II) complexes.

We have also investigated the NCIs in the dimer and trimer of PtB by QM calculations under the framework of density functional theory. The ground-state geometries of the dimer and trimer have been optimized at the M06 level. The optimized structures and their corresponding NCI plots are shown in Fig. 5 D and E, respectively. The Pt···Pt distance in the dimer and trimer were computed to be 3.46 to 3.52 Å, indicating the presence of Pt···Pt interactions in both the dimer and trimer. In addition, the interplanar distance of the coordination planes were found to be 3.3 to 4.0 Å, indicating the presence of π–π interactions in both the dimer and trimer. The above results are further supported by the results of the NCI analysis (Fig. 5E), indicating that both the Pt···Pt interactions and the ligand–ligand π−π dispersive interactions play important roles in enhancing the intermolecular interactions, which give rise to highly ordered directional nanostructures.

To further elucidate the role of Pt···Pt interactions in the dynamics of self-assembly, we have further performed MD simulations. One challenge for the MD simulations of the Pt(II)-containing complex is the lack of accurate force field parameters. Previously reported force field parameters for Pt(II) complexes (59, 60) yield inconsistent results with the QM calculations for the PtB-core dimer. In particular, there exists an ∼30 kcal mol⁻¹ discrepancy in relative potential energy between the MM and QM calculations at the interaction minimum for a PtB-core dimer (Fig. 5A and SI Appendix, Fig. S4). To address this issue, we have developed force field parameters of the Pt(II) atom (termed PtFF; Methods and SI Appendix, sections 2.4 and 2.5 for fitting details). We first extracted the PtB-core from the amphiphilic Pt(II) complexes (Fig. 4A). Then, we obtained the force field parameters of Pt(II) atoms by minimizing the differences between the relative potential energy profiles as a function of Pt···Pt distance obtained by QM and MM calculations for two antiparallel-aligned PtB-core in vertical direction (Fig. 4B). As shown in Fig. 4B, the relative potential energy profile as a function of Pt···Pt distance of MM can reproduce that from QM calculations in the vertical direction, as well as the long axis and short axis of the Pt(II) plane (SI Appendix, Figs. S2 and S4B). Furthermore, we show that our PtFF parameters can maintain the supercell structures when applied to simulate the PtB-a and PtB-b crystals (48, 49) (with the root mean square distance of 0.049 Å and 0.081 Å, respectively; Fig. 4 D and F).

Using the developed force field parameters, extensive all-atom MD simulations were performed to unravel the role of Pt···Pt interactions in the early stage of the self-assembly process. As shown in Fig. 6A and SI Appendix, Fig. S5, all the self-assembled oligomers (i.e., the dimer, trimer, hexamer, and decamer) of PtB in aqueous solutions can form linear self-assembled structures packed in a helix-like fashion. Since three types of intermolecular interactions drive this self-assembly process (Pt···Pt interactions, π-π stacking, and hydrophobic interactions), we designed the following two control systems to determine the role of these interactions: in the first control system, Pt^sB (not considering the d⁸–d⁸ interaction; SI Appendix, section 2.7 for details), and in the second control system, Pt-free, we removed the platinum atom from PtB. In sharp contrast to the PtB system, the molecular packing in the Pt^sB simulations is much more flexible and forms curved structures (Fig. 6A). This flexibility difference can be characterized by the structural fluctuations of the assembled oligomers (i.e., decamer) and be quantified by root mean square fluctuation (RMSF) values of the central Pt atoms in the assembled decamers (Fig. 6B). We found that the RMSF for the Pt atoms in PtB decamers is always smaller than those in Pt^sB decamers (Fig. 6B). Furthermore, structural analysis of the assembled PtB decamers reveals that the PtB decamers preferentially pack in an antiparallel head-to-tail fashion (rotational angle of neighbor PtB planes distributed in ∼150°), as shown in Fig. 6C. In contrast, the assembled Pt^sB decamers have similar parallel (∼15°) and antiparallel (∼150°) fractions (Fig. 6C), showing no preference in the way they assemble. We also found that the angle distribution between two adjacent planes of PtB decamers from MD simulations is narrower than that of Pt^sB, suggesting a more ordered and dense packing of the PtB decamer with less fluctuation (Fig. 6D). Furthermore, in the Pt-free system, we found that the delocalized π-plane of the original PtB disappears without Pt coordination (shown in SI Appendix, Fig. S6). When both Pt···Pt interactions and π–π interactions were absent, the initial randomly distributed Pt-free monomers only assembled into amorphous oligomers (SI Appendix, Fig. S6) with the hydrophobic aromatic rings inside and the hydrophilic sulfate ions outside dispersing in bulk water. These findings are consistent with the observed irregular nanostructure reported in experimental results (24) and indicate the importance of the directional Pt···Pt and π–π interactions to form ordered structures in the self-assembly of Pt(II) complexes.

Fig. 6.

Pt···Pt interaction plays a crucial role in the self-assembly of PtB. (A) Snapshots of typical assembled PtB and Pt^sB aggregates (both Side view and Top view). (B) The RMSFs of all Pt atoms after least-squares aligning to the reference frame of the assembled decamer, and the error bars represent the SD. The blue and red curves represent PtB and Pt^sB, respectively. (C) The distributions of rotational angles for PtB (the red curve) and Pt^sB (the blue curve) molecules against their corresponding adjacent neighbors. Angles between 0° and 90° correspond to a parallel alignment of adjacent molecules, where the Cl atom of both molecules is pointing in the same direction. Angles between 90° and 180° correspond to an antiparallel alignment, where the Cl atom of both molecules is pointing in the opposite direction. (D) The distribution of angles between adjacent PtB planes for both PtB (the red curve) and Pt^sB (the blue curve), where 0° stands for parallel/antiparallel alignments and 90° stands for perpendicular alignments.

Interplay of Pt···Pt Interactions and Other NCIs Leading to Distinct Self-Assembled Morphology under Different Solvent Conditions.

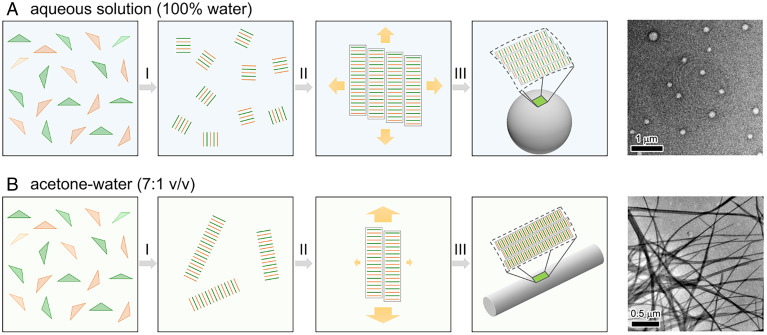
Based on our findings, we propose the self-assembly mechanism for the PtB complex in both the aqueous solution (Fig. 7A) and in the acetone–water (7:1, vol/vol) solution (Fig. 7B). In water, the isodesmic growth of PtB is believed to be attributed to the predominant contribution from the less directional hydrophobic interactions over the directional Pt···Pt and π−π interactions, leading to the formation of spherical aggregates. Initially, the linearly and antiparallelly packed structures of oligomers (like those observed in MD simulations, Fig. 6A) start to form when the solution becomes oversaturated below the elongation temperature (Fig. 7 A, I). Then, the oligomers continue to grow longitudinally and align parallelly (like the crystal structures in Fig. 4 D and F) to expand into large-scale nanosheets isotropically because of the predominant and less directional hydrophobic interactions (Fig. 7 A, II). It should be noted that the large-scale nanosheet requires the PtB structures to be packed in an ordered manner, and without the Pt···Pt interaction, the Pt^sB oligomers would lose the long-range order (as shown in Fig. 6A) and form a less-ordered aggregate. Finally, the nanosheets will bend into closed structures (like vesicles) due to the unfavorable energy at the water-surface interface of the nanosheets (Fig. 7 A, III). Consequently, the self-assembled structures will grow into a spherical vesicle (diameter, ∼100 nm) that can be observed using TEM (Fig. 7A) (26).

Fig. 7.

The d⁸–d⁸ interactions direct the self-assembly process of PtB molecules. Schematic pictures for the self-assembly of PtB at different solvent conditions, as follows: the aqueous solution (A) and acetone–water (7:1, vol/vol) solution (B). The TEM images show the comparison of the assembled structures under different solvent conditions (26). Reprinted with permission from reference 26.

In the acetone–water (7:1, vol/vol) solution, the hydrophobic interactions are believed to be attenuated due to the solvation of the hydrophobic moieties of the PtB complexes in high acetone content. Thus, the cooperativity of PtB in the acetone–water (7:1, vol/vol) mixture is achieved by the predominant contribution from directional Pt···Pt and π−π stacking interactions with a lesser extent of the hydrophobic interaction, ultimately leading to the anisotropic and cooperative growth of PtB complexes into nanofibers. Initially, the linearly and antiparallelly packed structures of oligomers form (Fig. 7 B, I). Different from the nucleation-free case in aqueous solution, much less oligomers form here in the nucleation step. The oligomers continue to elongate longitudinally along the direction perpendicular to Pt plane (Fig. 7 B, II), with the parallel alignment of two oligomers less favored. Therefore, the oligomers in acetone–water (7:1, vol/vol) solution grow longitudinally and anisotropically with less extent of lateral aggregation into nanosheets. Finally, the nanofiber formed due to anisotropic growth mainly attributed to the formation of directional Pt···Pt and π−π stacking interactions (Fig. 7 B, III). Consequently, the self-assembled structures will grow into a fiber (diameter, ∼10 nm) that can be observed using TEM (Fig. 7B) (26).

Conclusions

In this paper, we combine temperature-dependent UV-Vis spectroscopy experiments, stopped-flow kinetic experiments, QM calculations, and MD simulations to elucidate the key role of Pt···Pt interactions in directing the self-assembly of amphiphilic Pt(II) complexes. At the macroscopic level, we show that the self-assembly dynamics of PtB interestingly follow the nucleation-free isodesmic model in the aqueous solution but the cooperative growth model in the acetone–water (7:1, vol/vol) solution. At the microscopic level, we revealed that the Pt···Pt interaction is one of the major forces for directing the PtB self-assembly and maintaining the assembled structures. In particular, we found that the strength of the direct interactions between two Pt atoms in a PtB dimer (which can reach −2.52 kcal/mol) is comparable to the π−π interactions in a benzene dimer (48), and thus the Pt···Pt interaction can account for both the driving forces of self-assembly in solutions and the close packing of the crystal structure. More interestingly, the strong Pt···Pt interaction is directional and arises from the interactions between the p_z and d_z² orbitals in solution, playing a crucial role in guiding the assembly process and maintaining the ordered structures. This unraveled directional Pt···Pt interaction provides more insight into the rational design of building blocks for Pt(II) complexes that have various morphologies. Finally, we expect that our developed force field parameters are transferable and applicable to other Pt(II) complexes and could therefore be helpful when investigating their self-assembly mechanism using MD simulations.

Methods

Experimental Setup.

The temperature-dependent UV-visible spectra were recorded on a Varian Cary 50 UV-Vis spectrophotometer with the monitoring of temperature using a Varian Cary single-cell Peltier thermostat or on a Horiba Duetta spectrofluorometer with a temperature-controlled SampleSnap-1Pelt single-cell Peltier holder. TEM experiments were recorded on a Philips CM100 transmission electron microscope with an accelerating voltage of 200 kV.

Force Field Parameters Fitting Procedure.

To perform all-atom MD simulations of the self-assembly process for Pt(II) complexes, we first obtained the force field parameters for the Pt(II) complexes. Here, the force field parameters were termed as PtFF. The force field fitting procedures are as follows. 1) We selected typical core fragments from Pt(II) complexes termed PtB-core (Fig. 4A). 2) We optimized the structure of the PtB-core dimer at the TPSS-D3/def2-TZVP level (61–63), which showed the most stable antiparallel packing (shown in SI Appendix, Fig. S3) consistent with experimental observations (49, 64). 3) We calculated the total potential energy of the dimer at various Pt···Pt distances along the vertical direction using QM. 4) Then, we obtained the LJ parameters of Pt(II) by minimizing the difference between the relative potential energy profiles as a function of Pt···Pt distance in the vertical direction obtained from QM with that obtained by the MM calculations. 5) We verified our force field parameters by comparing the relative potential energy profiles as a function of Pt···Pt distance along the long axis and along the short axis of the antiparallel PtB-core dimer obtained by QM and MM calculations. Here, the long axis corresponds to the direction parallel to the line connecting two bzimpy moieties of the ligand, and the short axis corresponds to the direction along the Pt-Cl bond of the PtB-core (see schematic definition in SI Appendix, Fig. S2). As shown in SI Appendix, Fig. S4B, the obtained MM profiles of the PtB-core dimer in these two directions could reproduce the QM profiles, and the energy difference between QM and MM profiles are within 0.4 kcal mol⁻¹ with a Pt···Pt distance in the range from 3.3 Å to 6.6 Å. 6) We further validated our force filed parameters by showing that the crystal structures of representative Pt(II) complexes are stable in MD simulations (SI Appendix, section 2.6 and Tables S2–S5 for details).

Setup All-Atom MD Simulations.

All MD simulations were performed by the GROMACS (version 4.5.5) package (65). To understand the self-assembly mechanism of amphiphilic Pt(II) complexes, oligomer formation at the early stage of the self-assembly process in aqueous solution was performed for the representative Pt(II) complex PtB. Here, PtB oligomers with aggregate sizes 2, 3, 6, and 10 were considered (Fig. 6A and SI Appendix, Fig. S5). For each oligomer system, we first performed energy minimization followed by a 2-ns MD simulation with position restraints on the heavy atoms under the canonical (NVT) ensemble. Then, 10 production MD trajectories (100 ns for each trajectory) were carried out for each PtB oligomer size under the isothermal–isobaric (NPT) ensemble. The long-range electrostatic interactions were considered by the Particle Mesh Ewald method. All water molecules here were modeled by the three-site (TIP3P) force field. The integration time step was 2.0 fs (SI Appendix, sections 2.5–2.7 for more details).

PIO Analysis.

PIO analysis is a recently developed framework used to analyze the orbital interaction between two chemical fragments (57, 58). It works by applying two rounds of PCA (66), namely, one on the row space and the other on the column space (or collectively as a singular value decomposition) on the interfragment block of the density matrices, resulting in a minimal set of PIOs that best describes the interfragment interactions. After the diagonalization, the PIOs (as the row and the column principal components) together with PIO-based bond index (PBI) serve as the optimal low-rank approximation of the interfragment matrix block. As exemplified in Fig. 5 B and C, the transformed matrix will usually contain a few dominant elements (in this case two), and these dominant elements will serve as a good indicator of what chemical interactions are present between the two fragments. For the interaction between two PtB-cores in this paper, the dominant interaction was found to be a pair of d⁸–d⁸ interactions formed by the d_z² and p_z orbitals of the Pt centers.

Data Availability

All study data are included in the article and/or SI Appendix.