Bending-torsional elasticity and energetics of the plus-end microtubule tip

Significance

The mechanochemical basis of microtubule growth, which is essential for the normal function and division of eukaryotic cells, has remained elusive and controversial, despite extensive work. In particular, recent findings have created the paradox that the microtubule plus-end tips look very similar during both growing and shrinking phases, thereby challenging the traditional textbook picture. Our large-scale atomistic simulations resolve this paradox and explain microtubule growth and shrinkage dynamics as a process governed by energy barriers between protofilament conformations, the heights of which are in turn fine-tuned by different nucleotide states, thus implementing an information-driven Brownian ratchet.

Abstract

Microtubules (MTs), mesoscopic cellular filaments, grow primarily by the addition of GTP-bound tubulin dimers at their dynamic flaring plus-end tips. They operate as chemomechanical energy transducers with stochastic transitions to an astounding shortening motion upon hydrolyzing GTP to GDP. Time-resolved dynamics of the MT tip—a key determinant of this behavior—as a function of nucleotide state, internal lattice strain, and stabilizing lateral interactions have not been fully understood. Here we use atomistic simulations to study the spontaneous relaxation of complete GTP-MT and GDP-MT tip models from unfavorable straight to relaxed splayed conformations and to comprehensively characterize the elasticity of MT tips. Our simulations reveal the dominance of viscoelastic dynamics of MT protofilaments during the relaxation process, driven by the stored bending-torsional strain and counterbalanced by the interprotofilament interactions. We show that the posthydrolysis MT tip is exposed to higher activation energy barriers for straight lattice formation, which translates into its inability to elongate. Our study provides an information-driven Brownian ratchet mechanism for the elastic energy conversion and release by MT tips and offers insights into the mechanoenzymatics of MTs.

Microtubules (MTs) span the intracellular space, define the position of the nucleus, build the spindle needed to segregate genetic material, and define the shape of axons and cilia as well as transport networks (1). They are dynamic noncovalent polymers formed by tubulin dimers that hydrolyze GTP to GDP upon self-assembly. The polymerization dynamics and mechanical properties of MTs—which determine both network architecture and directional force generation—are central to cell physiology. MTs are structurally stiff due to the large and hollow cross-sections but highly dynamic at their plus-end tips, while the minus-end tip dynamics are usually suppressed by MT nucleation complexes (2). During growth, the plus-end tips stochastically transition to periods of rapid shortening (referred to as catastrophe events), depending on polymerization conditions, the shape ruggedness of MT ends, the content and distribution of GTP-tubulin in the lattice, and occasionally on posttranslational modifications and MT-associated proteins (3–7). This power stroke provides the directional force that drives, particularly, the segregation of chromosomes during mitosis (8–10). The elastic energy released by MT protofilaments (PFs) curling outward is transmitted mechanically to kinetochore–MT ring complexes (11–14), which translates into directional and concerted chromosome movement.

With its well-separated modes of operation—chemomechanical energy conversion, storage, and release—this protein engine is an excellent object for studies on nanomechanics. The ultimate goal is to understand the functioning of this astounding out-of-equilibrium machine at the atomic scale. The kinetics of MT assembly and catastrophe have been fairly well characterized (15–19) compared to the MT tip structure, the dynamics of which are hard to time resolve at high resolutions with modern techniques and despite its critical role in setting up these kinetic rules. Although an early cryoelectron microscopy (cryo-EM) study (20) found that MT tips are rather blunt when growing and flared when shrinking, further studies reported a much wider range of shapes for growing MT tips (21–25). Meanwhile, a model of consensus is emerging in which MTs have rugged and splayed tips with PFs curling outward from the lumen, irrespectively of their polymerization state (26–29).

Despite the wealth of available structural data, the mechanistic details of this energy conversion and transduction are still not fully understood. It is known, from optical tweezer assays (8, 9, 30) and force–velocity measurements (31, 32), that disassembling MTs (most likely almost exclusively GDP-MTs) are capable of developing large pulling forces in the range of 30 to 65 pN in the presence of load-bearing attachment to kinetochores, while growing MTs (most likely densely capped by GTP-tubulin) can generate pushing forces up to 3 to 4 pN through incorporation of tubulin dimers (Fig. 1A). What still remains enigmatic is, however, why these opposing behaviors exist if growing and shrinking MTs apparently have very similar tip structures and what role the flared tip morphology plays in the mechanism of MT catastrophe. The interplay of intrinsic PF strain and stabilizing lateral interactions is complex, and very little is known about the transient dynamics of the MT tip along its internal degrees of freedom that might be strongly affected by GTP hydrolysis but have not been resolved previously. A clear mechanochemical picture that fairly describes all these phenomena is not yet available.

Fig. 1.

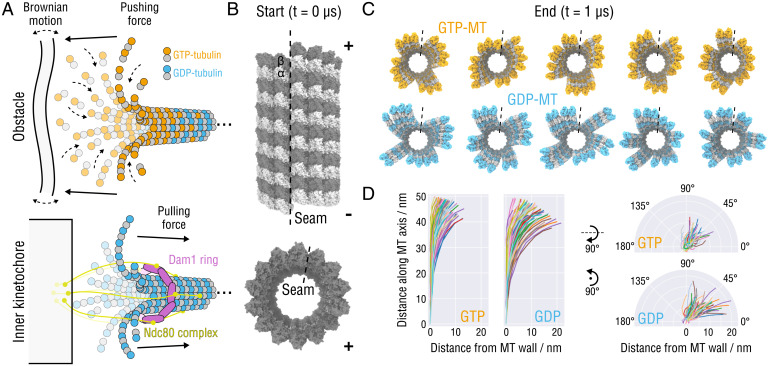
Splaying relaxation of the MT plus-end tip. (A) Biochemical basis of force generation by polymerizing and depolymerizing MTs (adapted from refs. 9, 11, 14, 26). (Top) An MT growing against an intracellular obstacle, e.g., lipid membranes, organelles, or other protein complexes. Stochastic fluctuations allow for incorporation of tubulin dimers into the lattice, leading to a displacement or deformation of the obstacle (assuming the minus-end is fixed). (Bottom) Schematic showing the attachment of the MT tip to the Ndc80-Dam1 kinetochore complex that is thought to slide toward the minus-end using the mechanical force transmitted from peeling PFs during MT depolymerization (assuming the minus-end is fixed). (B) Side and top views of the starting MT tip structure. Atomistic structures are shown in surface representation. The lowest row of tubulin monomers at the minus-end were restrained during the simulations. The position of the seam is indicated with a dashed line. (C) Top view of the GTP- (orange) and GDP-MT (blue) tip structures after $1\hspace{0.17em}\text{μ}$s of simulation. The seams are indicated with dashed lines. (D) Traces of the PFs aligned with respect to the minus-end monomer and projected onto the radial (Left) and axial (Right) planes. Random colors were assigned for clarity.

To answer these questions, we carried out atomistic molecular dynamics (MD) simulations of the complete MT plus-end tip both in GTP and in GDP state starting from an initially straightened MT structure (all PFs are straight) and analyzed the subsequent splaying of individual PFs driven by their outward curling. We assumed that this relaxation process is directly related to the twist-bending stiffness of individual PFs and inversely related to the lateral interaction free energies. Quantifying the elementary intra- and inter-PF contributions to the overall thermodynamics and kinetics of MT tip splaying allowed us to infer the basic energetic criteria for the MT plus-end tip stability and to propose a mechanism of MT catastrophe that does not involve differences in the shapes of growing and shrinking MT tips.

Results and Discussion

Relaxation Dynamics and Heterogeneity of MT Plus-End Tips.

At the MT tip, the elastic energy stored by straightened PFs is only insufficiently balanced by the total energy of lateral dimer–dimer interactions, which results in MT structures featuring irregularly splayed, curved PFs (26–29). Recent atomistic MD simulations have predicted substantial differences in the bending rigidity of GTP- and GDP-bound free dimers, single PFs, and tubulin octamers (33–38). Concomitantly, it has been proposed that the formation/breakage of lateral dimer–dimer contacts might also be nucleotide-dependent (39–41). Hence, we first asked if the nucleotide state affects the overall dynamics of complete MT tips, where all these factors come together and can be assessed simultaneously.

To this end, we constructed two initial atomistic models of GTP- and GDP-MT tips by consecutively stacking three identical MT segments, each comprising two layers of dimers (Fig. 1B). The length of the MT segments to be simulated was chosen based on the following consideration. The segments should be long enough to capture essential topological features of flared MT plus-ends observed experimentally. The average length of PFs at the tip of in vitro growing GTP-MTs and depolymerizing GDP-MTs was reported to be 36 ±15 and 43 ±16 nm, respectively (table 3 in ref. 26). In a follow-up study, the PF length at the tip of growing GTP-MTs was estimated as 36 ±28 nm (averaged over three concentrations; figure 5 in ref. 28). The most recent cryoelectron tomography (cryo-ET) study (figure 2 in ref. 29) reported 24 ±17 nm for dynamic plus-end PFs. With six tubulin dimer layers (each PF has a length of 6 × 8 nm = 48 nm), our MT tip models are well within these experimentally measured ranges and even exceed the reported mean PF lengths, yet are still computationally feasible. Each model was then optimized against high-resolution cryo-EM densities of GMPCPP- or GDP-MTs (37, 42, 43) (see Materials and Methods for a detailed construction and optimization protocol). Immobilization of the minus-end tip was modeled by harmonically restraining the lowest row of tubulin monomers to their initial positions. Relaxation of the preequilibrated tip models was then quantified in five independent 1-µs simulations for each nucleotide state (later extended beyond 2 µs; see Materials and Methods for a detailed simulation protocol). Relaxed tip structures are shown in Fig. 1C. Movies S1 and S2 visualize the relaxation process of all simulated tip structures from the top and side perspectives, respectively. The extent of differences between the individual runs can be also followed in SI Appendix, Fig. S1, showing rmsd values from the starting straight conformations as a function of time. Finally, to rule out the possibility of the splaying behavior being a force-field artifact, we performed five additional 800-ns relaxation simulations per nucleotide state using a different force field (Materials and Methods). Relaxed tip structures for this alternative set of simulations are shown in SI Appendix, Fig. S2A. Implications of the force-field choice for the results of this study are discussed in Conclusions.

The final tip structures after 1 µs of relaxation qualitatively resemble experimental observations (26–29). Overall, it is seen that the initial straight configuration is highly unstable. Notably, the relaxation is somewhat stochastic in that it does not follow the same pattern in every simulation. Rather, the MT tips crack open at different lateral interfaces, with none of them being unique, except for the seam that splays faster and more strongly than other interfaces in all performed simulations, as will be discussed further below. To compare the GTP and GDP tips directly, we aligned the PFs of the final tip structures with respect to the first minus-end monomer and projected their traces onto the radial and axial plains (Fig. 1D; calculation of traces is explained in SI Appendix, Fig. S10). Our analysis shows a stronger tendency of the simulated GDP-MT tips to splay and a stronger tendency of their PFs to bend radially. We note that the obtained projections do not fully reflect the equilibrium distribution of individual PF curvatures because 1) our MT tip models are—by construction—too large to converge within 1 µs (rmsd values in SI Appendix, Fig. S1 continue to increase even after 1 µs of simulation), and 2) most PFs are still stabilized by lateral neighbors.

We further observed that all of the simulated MT tips additionally accumulate a twist when looked at from the plus-end perspective (Fig. 1 C and D and Movies S1 and S2). Closer inspection of the simulation trajectories showed that this motion is strictly clockwise and caused by the bent PFs twisting similarly clockwise about their centerlines. Crystallographic data (44–46) and previous MD studies (33, 35, 41) show that such torsional motions are an intrinsic property of tubulin dimers and PFs. This reflects the structurally complex nature of the bending-torsional coupling at the MT plus-end.

Essential Dynamics and Energetics of PF Fluctuations.

The complex bending-torsional coupling and the clockwise lattice twist of the individual PFs at the MT tip, particularly pronounced in GDP-MTs, suggests that the usually employed single angular variables describing the nucleotide-dependent radial bending angles between adjacent tubulins (28, 38, 47–49) may be insufficient to fully explain the conformational dynamics of PFs. We therefore asked, what are the essential collective variables (CVs) that quantitatively describe bending-torsional PF fluctuations in our atomistic simulations and exactly how are these affected by the nucleotide state?

To investigate the bending-torsional PF dynamics in more detail, we carried out additional simulations of isolated minus-end–fixed PFs in both nucleotide states and analyzed their equilibrium dynamics. Straight PFs comprising three longitudinally connected tubulins were extracted from the complete MT lattices (Materials and Methods), and their fluctuations were then quantified in a set of 20 independent 4-µs simulations for each nucleotide state. Principal component analysis (PCA; Materials and Methods) was performed on the backbone atoms of the PF structures aligned with respect to the minus-end monomer to capture their collective motion.

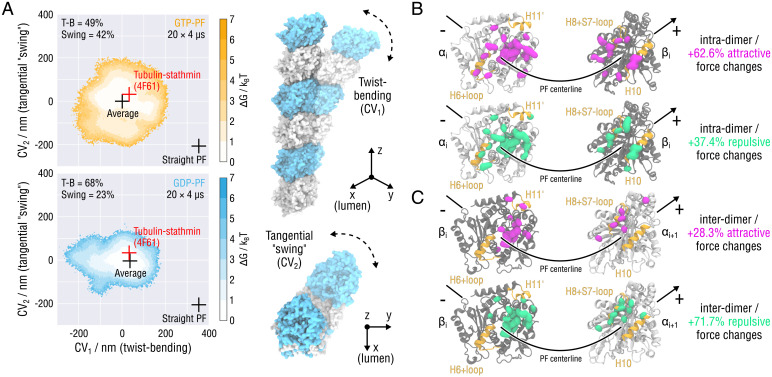
Two major conclusions can be drawn from this analysis. First, more than 90% of the equilibrium fluctuation variance can be explained by only two principal modes of motion. Mode 1 represents the bending-torsional PF motion observed in the large-scale MT tip simulations (Movie S3). We refer to this mode as twist-bending, and the corresponding CV used to compute free energy projections is denoted as CV₁. Mode 2 describes a tangential motion of the PF perpendicular to the radial plane (Movie S3). We refer to this mode as tangential swing, and, by analogy, the corresponding CV is denoted as CV₂. Fig. 2A shows the corresponding free energy profiles projected onto the joint (CV₁, CV₂)-space. SI Appendix, Fig. S3 additionally illustrates the equilibrium distributions of PF traces projected onto the radial and axial planes. To verify if the minimum free energy conformations seen in our simulations agree with PF conformations observed experimentally, we also projected the crystal structure of the tubulin-stathmin oligomer complex [Protein Data Bank (PDB) ID 4F61 (46)] onto our calculated free energy profiles (Fig. 2A, red crosses, and Materials and Methods). The projected crystal structure aligns well with the free energy minima predicted in our PF simulations, suggesting that the observed relaxed PF conformations are energetically and structurally reasonable. Importantly, bending of the PFs and twisting about their centerlines do not come out as separate eigenmodes in the PCA but are highly correlated, which strongly suggests that using only a single bending angle describing the local radial PF curvature may miss a large part of the actual conformational dynamics of individual PFs.

Fig. 2.

Essential dynamics of PF fluctuations and structural determinants of PF twist-bending. (A) Free energy landscapes of the minus-end-fixed PF conformations obtained by 20 × 4-µs all-atom MD simulations for each nucleotide state (Materials and Methods). Color coding is the same as in Fig. 1. Black crosses denote the straight and relaxed (average) PF conformations. The free energy minimum corresponds to the average PF conformation. Red crosses indicate the conformation of the experimental structure of the PF oligomer cocrystallized with the stathmin protein [PDB ID 4F61 (46)]. Also shown schematically are PF rearrangements along the conformational modes 1 and 2 (see also Movie S3). (B) Intradimer and (C) interdimer contact clusters and pairwise interaction forces obtained by the FDA. Relative changes are shown reflecting shifts in the pairwise contact forces after GTP hydrolysis. Amino acid residues contributing to negative shifts (more attractive forces) are marked with magenta blobs, whereas those contributing to positive shifts (more repulsive forces) are marked with green blobs. A lower limit cutoff of 50 pN for both negative and positive force changes was applied to highlight high-force clusters. α- and β-tubulins are shown as silver and gray ribbons, respectively. Highlighted in yellow are residues involved in the H6 (+ loop), H8 (+ loop), H10, and H11${}^{\prime }$ helices.

Second, the conformational dynamics of PFs depends strongly on the nucleotide state. According to the PCA results, the overall conformational flexibility of GDP-PFs is reduced by 31% compared to that of GTP-PFs (Materials and Methods). In order to estimate the free energy stored in straight GTP- and GDP-PFs, $\mathrm{\Delta }{G}_0$, we fit a two-dimensional harmonic function to the free energy landscapes in Fig. 2A. The fits were then used to extrapolate the profiles to the region containing the straight PF conformation, which was not sampled in our unbiased PF simulations. This procedure yielded $\mathrm{\Delta }{G}_0=19.9\pm 0.4$ k_BT (GTP-PF) and $\mathrm{\Delta }{G}_0=28.7\pm 0.5$ k_BT (GDP-PF). SI Appendix, Fig. S4 additionally shows one-dimensional marginal projections of the free energy profiles in Fig. 2A with the corresponding harmonic fits to illustrate the goodness of fit. We emphasize that these estimated energies rest on a harmonic approximation though, not on direct sampling. Further, whereas for the GTP-PFs both bending-torsional (mode 1) and tangential swing (mode 2) components explain almost equal fractions of the conformational flexibility (49 and 42%, respectively), this distribution is shifted substantially to 68 and 23% for the GDP-PFs, respectively. Neglecting the remaining variance unexplained by modes 1 and 2 (less than 10%), the decomposition provided by the PCA suggests an allosteric mechanism that couples the PF bending-torsional dynamics to the change of the nucleotide state. More specifically, the rate and the exact modality (i.e., stronger or weaker mode 2) of PF straightening would be largely changed upon GTP hydrolysis.

To the best of our knowledge, the tangential swing component has not been reported in previous MD studies (35, 41, 50, 51), most likely due to shorter simulation times. Speculating about its role in the plus-end tip dynamics, we propose that lower tangential stiffness might facilitate the stochastic formation of lateral PF–PF contacts through spontaneous collisions. The role of the lateral contacts in these processes will be elucidated further below.

Structural Determinants of the Intradimer and Interdimer Coupling in PFs.

As the mechanical coupling along the PF shaft is a key determinant of the overall bending-torsional elasticity, we analyzed the longitudinal interactions both within and between the tubulin dimers in more detail. To this end, we identified pairs of residues that contribute the most to the intradimer and interdimer interactions in our equilibrium PF simulations, thus forming a network that stabilizes the PF and modulates its essential conformational dynamics (Fig. 2A). Here we first used the time-resolved force distribution analysis (FDA) (52, 53) to follow the dynamics of all internal forces within the PFs in GTP and GDP state (Materials and Methods). We then averaged the obtained forces and filtered out those force contributions that were unrelated to the intradimer and interdimer contacts. By convention, negative (positive) pairwise forces are attractive (repulsive) forces, and hence, negative (positive) changes in the pairwise forces denote stronger (weaker) intradimer and interdimer interactions.

SI Appendix, Fig. S5 shows the identified contact clusters for each nucleotide state. Two main regions exhibit strong (absolute values larger than 50 pN) pairwise residue forces. The first one is located mainly in the vicinity of the hydrophobic contact [anchor point (42)] between the H8 helix plus the accompanying H8–S7 loop of the top monomer and the H11${}^{\prime }$ helix of the bottom monomer, as well as around the nucleotide binding pocket. In this region, not all of the interactions are clustered near the putative outside of the MT surface; some of them reach out to the putative PF–PF contact zones, which partially explains the nonradial nature of PF bending. The second region is located near the putative inside of the MT surface. Here the portion of the highly conserved H10 helix of the top monomer that is closer to the MT lumen interacts with the H6 helix plus the adjacent loop of the bottom monomer. Interestingly, this contact cluster is only present at the intradimer interface, which might explain the higher PF flexibility at the interdimer interfaces, as also reported previously (35).

Fig. 2 B and C shows changes in the average pairwise residue forces after GTP hydrolysis. Contrary to our initial expectation that GTP hydrolysis would only affect the force distribution at the interdimer interface (indeed, the negatively charged γ-phosphate and Mg²⁺ are removed), we found that posthydrolysis changes in the PF structure have opposite effects at the intradimer and interdimer interfaces. First, the overall rearrangements near the nucleotide binding pocket result in a cumulative weakening of the interdimer interface: +71.7% of repulsive pairwise forces vs. only +28.3% of attractive pairwise forces (Fig. 2C). This finding correlates well with a recent MD study showing that GTP hydrolysis results in an $\sim 4$ k_BT longitudinal bond weakening (38) as well as with our previous finding that the longitudinal bonds in GDP-PFs are more fragile when subject to mechanical stretching (37). We note, however, that the FDA provides only the enthalpic contribution to the longitudinal stability because the entropic penalty for eliminating solvent from tubulin’s surface is not taken into account. Second, inspection of the average pairwise force changes at the intradimer interface points to a cumulative strengthening: +62.6% of attractive pairwise forces vs. +37.4% of repulsive pairwise forces (Fig. 2B). This stabilization arises mainly from rearrangements near the nucleotide binding pocket as well as from altered interactions between the H10 and H6 helices. Because the hydrolysis reaction does not happen at the intradimer interface (54), we speculate that the conformational changes triggered by GTP hydrolysis [lattice compaction around the longitudinal interdimer interface (37, 42, 55, 56)] propagate upstream, allosterically causing additional intradimer tensions.

The Behavior of Lateral Contacts during MT Tip Relaxation.

In the absence of lateral neighbors, PFs tend to adopt curved-twisted conformations due to the heterogeneous interaction profiles at their intradimer and interdimer interfaces (Fig. 2 A and B). However, straight PFs inside the MT lattice need to be stabilized via specific interlocking of α- and β-tubulin monomers (Fig. 1 B–D). This draws attention to the lateral contacts, the exact role of which in the MT stability is still controversially debated (57). With two notable exceptions (40, 41), simulation studies have proposed that the stability of lateral PF–PF contacts is unaffected by the nucleotide state (34, 36, 37). However, in only one of these studies (36), the lateral binding free energy was computed explicitly using enhanced sampling techniques, although with relatively short sampling times. Furthermore, the available MD simulation evidence does not account for and cannot rule out that kinetic aspects of the lateral PF–PF association also play an active role in the MT growth and shrinkage. Indeed, super coarse-grained Brownian dynamics modeling benchmarked against in vitro experiments measuring MT-based pulling and pushing forces points to such a possibility (28). Nevertheless, accurate kinetic and energetic insights are currently missing.

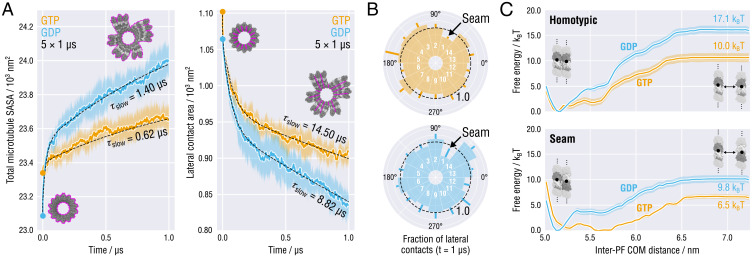
The nonequilibrium nature of the MT tip relaxation in our simulations and improved sampling compared to previous studies provide additional time-resolved information to address this question. In particular, one would expect that if MTs grow when lateral contacts are strong and disassemble when they are weakened, lateral contacts exposed at the GDP-MT tip would disengage first, followed by PF twist-bending, while they would stay more intact for the GTP-MT tip. To test this idea, we calculated both the total MT solvent accessible surface area (SASA) and the total lateral contact area over the course of our simulations (Fig. 3A). SI Appendix, Fig. S2B also shows the total MT SASA calculated using the alternative set of relaxation simulations with a different force field. In accordance with the final structures in Fig. 1C, GTP- and GDP-MTs gain ∼1.4 and ∼4.0% of their initial SASA, respectively, due to splaying during the first 1 µs. Unexpectedly, however, lateral contact splaying contributes only ∼59 and ∼20% to the total gain. This finding implies that MTs lose ∼21% of their lateral contacts during the first 1 µs, regardless of the nucleotide state. In addition, we compared the characteristic relaxation time of the MT SASA and the total contact area (Fig. 3A; relaxation time constants are provided), which revealed that the former is almost an order of magnitude faster for both GTP- and GDP-MTs. It is therefore mainly the PF twist-bending that drives the increase of the MT SASA, which in turn sets the lateral contacts under stress and causes them to partially dissociate.

Fig. 3.

Time dynamics, heterogeneity, and energetics of MT tip splaying. (A) Time evolution of the total MT SASA (Left) and the lateral contact area (Right), both averaged over the five independent tip relaxation runs shown in Fig. 1C (same color coding for GTP- and GDP-MTs was used). Black dashed lines depict fits with a two-component exponential decay function. Characteristic decay times of the slow components are indicated. (B) Lateral contacts preserved after 1 µs of simulation relative to the initial state (indicated with a black dashed line). Positions of the seam are indicated. (C) Free energy profiles of homotypic (Top) and seam-like (Bottom) tubulin–tubulin lateral interactions in straight infinitely long PFs as a function of the inter-PF COM distance. Color coding as in A and B. Statistical errors are shown as shaded areas (Materials and Methods).

It may also appear puzzling that the lateral contacts both at GTP-MT and GDP-MT tips are lost at the rate of $\sim {10}^5$ s^–1 (Fig. 3 A, Right), which might be too fast and incompatible with the rate of MT growth. However, the observed MT tip fluctuations do not reflect the equilibrium dynamics but rather the ongoing relaxation of this system toward a metastable state. It is therefore likely that calculating the rate of lateral contact loss using only the first 1 µs of the tip relaxation dynamics leads to an overestimation of that rate. To test this hypothesis, we extended all of the 10 MT tip simulations (up to $\sim 2.4\hspace{0.17em}\text{μ}$s for GTP-MTs and $\sim 2.3\hspace{0.17em}\text{μ}$s for GDP-MTs) and calculated both total MT SASA and lateral contact area as a function of time (SI Appendix, Fig. S6). While the total MT SASA continues to grow at a rate comparable with that before the trajectory extension, we observe a slowdown for the lateral contact area loss. More specifically, the decay constants of the lateral relaxation process increased by ∼50 and ∼30% for GTP-MTs and GDP-MTs, respectively, after doubling the sampling time. Therefore, we speculate that although the MT tip splaying is indeed very fast (especially within the first 1 µs of relaxation), the process of lateral contact loss gradually slows down with the time and most likely levels off even before the curvatures of individual PFs fully equilibrate, which prevents MT tips from dissociating very rapidly and entirely. Given the decay curves in Fig. 3 A, Right, and SI Appendix, Fig. S6, Right, we also conclude that the lateral contact area relaxes faster in posthydrolysis MT tips and converges to a lower value, which is consistent with the larger number of PF clusters observed in GDP-MT tips (Fig. 1C).

Finally, the MT geometry imposes that at one specific lateral interface, called the seam, α- and β-tubulins form heterotypic contacts (Fig. 1B). Structural studies have speculated that the seam is a weak interaction site in the MT lattice and may represent evolutionary tuning to reduce the intrinsic stability of the regular MT lattice (42, 55, 58). Indeed, introducing additional seams into the dynamic MT lattice substantially increases the catastrophe frequency and the depolymerization rate, yet not the growth rate (58). To determine the contribution of the seam to the overall loss of lateral interfaces, we calculated the fraction of pairwise PF contacts preserved after 1 µs of simulation (Fig. 3B and Materials and Methods). Interestingly, some lateral contacts—despite the global trend—increased their interaction surfaces during relaxation. We think this is caused by the uneven distribution of PF twist-bending strains at the tip, which transiently pushes the PFs into each other. Regardless of the nucleotide state and in all relaxation runs, the seam PFs disengaged significantly faster than the average of the homotypic PFs (a preserved fraction of 0.43 to 0.59 compared to ∼0.80 for the average homotypic interface), supporting the view that MT plus-ends have a higher tendency to splay at the seam. It is, however, unlikely that the seam is the primary initiator of lattice opening, as proposed originally (42, 55), because statistically, it is still more favorable to crack open at any of the more numerous homotypic interfaces.

The Role of Lateral Contact Energetics in MT Lattice Integrity.

It seems counterintuitive that the relative loss of lateral interfaces per microsecond is not drastically distinct between the two nucleotide states (Fig. 3 A and B), as the GDP-MT should exert a much stronger tearing load on the lateral contacts due to the much higher PF bending-torsional stiffness (Figs. 1 B–D and 2A). Moreover, it is unclear why, then, the MTs splay faster at the seam while the seam PFs presumably have bending-torsional properties not largely different from the rest of the MT shaft. Because the preparation of and the simulation conditions for the GTP-MT and GDP-MT models were identical, these observations might point to substantial differences in the lateral PF–PF affinities: namely, stronger lateral interactions between GDP-PFs compared to those between GTP-PFs and stronger homotypic lateral interactions compared to seam-like ones.

To test this hypothesis, we need to assess the elementary contribution of a laterally coupled PF pair to the thermodynamic stability of the MT lattice as a function of both nucleotide state and lateral contact topology. To this end, we used a simulation setup that comprises a pair of laterally coupled tubulin dimers, as described previously (37, 59) (Materials and Methods). The system is made periodic along the main MT axis to keep the dimers aligned, and the dimers interact with their copies through periodic boundaries. The setup hence mimics two infinite neighboring PFs as they would be found in the shaft of a very long MT. Initial configurations of the homotypic and seam PF setups were derived from the full MT lattice models (Materials and Methods). We used umbrella sampling with preequilibrated configurations obtained from 1-µs unrestrained MD simulations of the initial double-PF models. In the umbrella simulations, an external force applied to the inter-PF center of mass (COM) distance was employed to restrain the straight PFs at a desired distance from one another.

We note that although neighboring PFs at the MT plus-end do not move along this coordinate initially, they do so at slightly later stages collectively with the outward splaying motion. A quantitative description of the tangential separation of PFs is required for a proper understanding of the energetic balance between PF splaying and cluster formation. Since the actual umbrella sampling is performed only with the two dimers in the periodic box, the free energy calculation reflects the per-dimer contribution to the thermodynamic stability of lateral contacts.

Fig. 3C shows the resulting free energy profiles. Convergence analysis served to ensure that the sampling was sufficient to statistically discriminate between the four tested conditions (SI Appendix, Fig. S7). Our analysis reveals that initially—for all tested cases—the free energy rises steeply as the PFs move away from each other from their equilibrium distance ∼5.2 to roughly 6.5 nm. Clearly, this free energy stabilizes the lateral contact around its natural conformation. After ∼6.5 nm the free energy levels off, which is indicative of a high-energy transition state in which the lateral contacts have disengaged completely. More importantly, as can also be seen in Fig. 3C, the energy required to cause the contact to disengage depends strongly on both nucleotide occupancy of the β-tubulin subunits and topology (seam vs. homotypic).

For the homotypic lateral contact, the system in the GDP state has to reach a substantially higher energy $\mathrm{\Delta }{G}^{*}\approx 17.1$ k_BT prior to contact rupture compared to only $\mathrm{\Delta }{G}^{*}\approx 10.0$ k_BT for the system in the GTP state. Even though our data do not directly explain the origin of the observed 7-k_BT difference in the lateral contact stability, we do not think this energy difference results from altered surface charge distributions or solvation shells because of the high structural similarity of the prehydrolysis and posthydrolysis states of PFs (both initially differ by only ∼0.2-nm compaction in the longitudinal dimension). Rather, it is conceivable that—like in the case of longitudinal contacts (Fig. 2B)—changes at the interdimer interfaces cause subtle structural changes in the vicinity of lateral contacts, hence raising the lateral contact free energy. For the seam lateral contact, the relationship between the barrier height and the nucleotide state changes considerably (Fig. 3 C, Bottom). The free energy of the transition state depends only weakly on the nucleotide state ($\mathrm{\Delta }\mathrm{\Delta }{G}^{*}\approx 3.3$ k _BT) and is also systematically lower than that of the homotypic system. Also, here the observed contact weakening can be most likely attributed to the noncanonical contact structure because the seam PFs themselves are not expected to have largely different mechanical properties.

The Free Energy Barrier for PF Cluster Formation and Rupture at the MT Tip.

When PFs at the MT plus-end begin to splay, two main processes are observed: 1) relaxation of the PF curvatures due to twist-bending and tangential swinging of each PF and 2) rupture of the lateral contacts that propagates from the plus- to the minus-end (schematically illustrated in Fig. 4A and see also Movies S1 and S2). We conveniently describe process 1 in terms of the PFs’ eigenmodes (Fig. 2A and Movie S3). Process 2 is then locally described by the separation of pairs of tubulin dimers, where the dimers in each pair are approximately aligned and where each pair approximately follows the separation pathway shown in Fig. 3C. Therefore, by combining the elastic energy and the per-dimer lateral stability contributions, we assume that it is possible to deduce a plausible description of the PF–PF rupture energetics and the corresponding energy barriers for PF cluster formation.

Fig. 4.

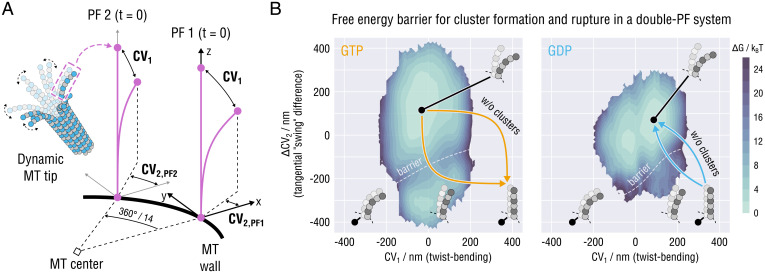
Schematic illustrating the proposed mechanism of PF cluster formation and rupture. (A) Exemplary structure of the splaying MT tip determined by the competition between the stabilizing inter-PF interactions and the twist-bending dynamics of individual PFs as indicated. Schematic visualization of a pair of neighboring PFs (purple lines). For illustration, other PFs at the MT tip are not considered, and the MT body, to which the PFs are rigidly attached, is shown as a black thick line. Both the distance between the PFs and their lengths are drawn not to scale for clarity. Given this simplified representation, the order parameters that determine the extent of PF outward bending and splaying are expressed in terms of the PFs’ eigenmodes: twist-bending or CV₁ and the difference in tangential separation between the PFs or $\mathrm{\Delta }C{V}_2=C{V}_{2,{\text{PF}}_2}-C{V}_{2,{\text{PF}}_1}$. (B) Free energy profiles describing the bending and splaying dynamics of the double-PF system as a function of the nucleotide state, generated by resampling the results of Figs. 2A and 3C (Materials and Methods).

To verify this assumption, we considered a simplified subsystem consisting of only two neighboring PFs at the MT plus-end tip (Fig. 4A). The knowledge of the energetics of PF curving and lateral PF–PF association was merged into a joint free energy landscape of the coupled PF dynamics using a resampling scheme described in Materials and Methods. Briefly, our procedure defines the PF conformations by two order parameters: CV₁ reflecting the extent of each PF’s deviation from the equilibrium conformation owing to twist-bending and $\mathrm{\Delta }C{V}_2=C{V}_{2,{\text{PF}}_2}-C{V}_{2,{\text{PF}}_1}$ expressing the extent of tangential separation between the PFs. Fig. 4B shows the reconstructed free energy landscapes for the motion of the coupled PF system in each nucleotide state.

Three interesting observation can be made. First, both landscapes exhibit two free energy minima corresponding to the states of fully uncoupled and splayed PFs and partially coupled straightened PFs. Second, the free energy landscapes suggest the following pathway for the formation of the straight MT lattice at the plus-end tip: partial straightening of the PFs through lateral association (i.e., formation of PF clusters) followed by spontaneous formation of a straight MT wall from this high-energy metastable state. Of course, it cannot be ruled out that a straight MT wall is formed via simultaneous and full straightening of the PFs, avoiding metastable PF clusters. However, such an event would involve a much higher free energy penalty. Third, GTP hydrolysis modulates the shape of the free energy landscape to make the formation of both metastable clusters and straight MT wall more unfavorable (Fig. 4 B, Left vs. Right). Specifically, the energy barrier that the GDP system would have to overcome while exploring the landscape in Fig. 4 B, Right, to achieve the straight MT state raises considerably owing to both higher GDP–PF rigidity and higher PF–PF interaction free energy. One should be, however, aware of two limiting assumptions of this type of calculation: 1) we neglect the rotation angle of one dimer with respect to the other in a lateral pair, i.e., imperfect dimer alignment during PF curling, and 2) we neglect the intrinsic bending of dimers, i.e., assume that they remain in a straight conformation during PF curling.

Given the thermodynamics of the plus-end PF elasticity and the kinetics of MT lattice splaying (Figs. 1–4), the stability of the MT tip structure might be determined by the dynamic equilibrium between the straight(er) coupled and curved uncoupled states of neighboring PFs (schematically illustrated in Fig. 4A). We propose that the tendency of each PF to twist-bend and disconnect from its nearest neighbors would be balanced out by the lateral interactions, resulting in a complex potential energy landscape of the MT tip having multiple minima separated by energy barriers. One of these minima would correspond to fully splayed MT tips akin to the ones observed experimentally (26, 28), while the many others would correspond to tips with metastable clusters of less curved PFs akin to those observed in the most recent cryo-ET study (29). Both minima depths and barrier heights would be tightly controlled by the nucleotide. Therefore, if building PF clusters were favorable and the barriers for their formation were low (e.g., at a GTP-MT tip), the MT tip would then favor, by biased diffusion, the pathway through these metastable states toward the straight MT lattice, provided there is sufficient and timely delivery of GTP-tubulin to the tip. Otherwise, if the barriers were high and PF cluster formation unfavorable (e.g., at a GDP-MT tip), the net MT growth would no longer be possible even under sufficient GTP-tubulin concentrations, resulting in a catastrophe event.

Conclusions

From the nonequilibrium atomistic simulations of complete MT plus-end tips, we have derived a thermodynamic and kinetic description of the MT plus-end tip splaying dynamics, providing a mechanistic interpretation for recent structural experiments. The simulated splayed shapes of MT tips (Fig. 1 C and D and SI Appendix, Fig. S2A) are generally consistent with cryo-ET measurements (18, 25–27, 29), further supporting the view that blunt straight MT tips are strongly energetically disfavored, irrespective of the nucleotide state. Interestingly, some cryo-ET measurements (26, 28) find that PFs are fully splayed (no PF clusters) and bend almost entirely within their radial plains containing the main MT axis [out-of-plane deflection of <4 nm over 30 to 50 nm of PF length (26)], whereas other cryo-ET studies identify PF clusters at the plus-end MT tips (25, 27, 29). Our nonequilibrium large-scale simulations now clearly capture such metastable states with sticky PF clusters (Fig. 1C; SI Appendix, Fig. S2A; and Movies S1 and S2).

We believe there are two possible explanations for why our results do not fully agree with some of the recent studies (26, 28) showing fully splayed MT tips. 1) Our simulations have simply not converged (even after $\sim 2.4$ µs of simulation; SI Appendix, Fig. S1). It cannot be ruled out that if extended to hundreds of µs, the observed PF clusters in our MT tip models will eventually disengage. However, such all-atom MD simulations are currently infeasible. 2) The manual analysis of cryo-ET images with low signal-to-noise ratio is difficult and prone to errors, which might have complicated the detection of clusters of short, curling PFs despite their presence in the data. Indeed, the more recent study using the same techniques but improved analysis methods has been able resolve PF clusters (29).

Our simulations also show somewhat larger PF deflections (Fig. 1D; $\mathrm{\lesssim }$10 and $\mathrm{\lesssim }$15 nm over 40 to 50 nm of PF length for GTP- and GDP-MTs, respectively). The larger deflections might be caused by the fact that most of the PFs are transiently stabilized by lateral interactions. Furthermore, approaching a metastable state with PF clusters transiently produces an uneven distribution of PF twist-bending and tangential swing strains at the tip and causes a global clockwise twist of the entire MT tip (Fig. 1C and SI Appendix, Fig. S2A). The observed twist agrees well with the most recent high-resolution cryo-ET reconstructions (29). Their structural analysis of dynamic MT tips showed that—very much like our simulated structures shown in Fig. 1C and SI Appendix, Fig. S2A—the majority (84%) of MT end flares were helically bent, showed a clear clockwise twist, and had clusters of coupled PFs. The fact that our theoretical predictions were confirmed independently further corroborates that twisted MT tips with partially associated PFs are possibly transient, functionally relevant, and nucleotide-dependent intermediates, the exact role of which for the MT dynamics and their regulation by MT-associated proteins is yet to be elucidated. To the best of our knowledge, this behavior has not been accounted for and/or predicted by any of the published physical models of MT dynamic instability.

As in all computational studies using atomistic force fields as a foundation to describe the dynamics of a biomolecular system, there is a possibility that the reported results, e.g., the splaying behavior of MT tip models or the formation of PF clusters, are an artifact of the force-field choice. Here we have made use of the CHARMM22* force field (60), which provided a reasonable physical description of the tubulin dynamics in our previous studies (33, 37, 43). Usage of this force field also in this study has been our intention to maintain continuity in the physical description, to build on previous successful tests against experimental data, and to enable a direct comparison to our previous results. Our additional simulations of the same MT tip models with the newer CHARMM36m force field (61), however, convincingly demonstrate similar MT structures and a similar relaxation behavior (SI Appendix, Fig. S2). The specific force-field choice (whether CHARMM22* or CHARMM36m), thus, does not have a significant effect on the behavior of MT plus-end tips in the simulations.

Our conformational analysis shows that substantially more free energy is required to spontaneously form straight GDP-PFs than straight GTP-PFs at the MT tip (Fig. 2A), in good agreement with the recent experimental observation that subpopulations of straight GDP-oligomers occur extremely rarely (62) as well as with recent computational studies (33–35, 37, 38). Moreover, not only does GTP hydrolysis appear to affect the conformational rigidity of PFs, but its influence is also highly anisotropic, with GTP-PFs being more flexible with respect to both outward twist-bending and tangential swing and GDP-PFs being more rigid but particularly rigid to motions in the tangential direction. We hypothesize that the prehydrolysis and posthydrolysis modes of PF motion have different effects on the collective dynamics of the MT tip. During MT assembly, flexible GTP-PFs might have an elevated rate of both spontaneous straightenings and encounters with neighboring GTP-PFs, while the higher twist-bending and, especially, tangential rigidity of GDP-PFs would reduce this rate and cause high tearing loads on lateral interfaces during MT disassembly.

The observed dependence of the mechanical properties of individual PFs on the nucleotide state may be a prototypical example for an intersubunit cooperativity that does not involve significant backbone rearrangements but is capable of causing large-scale conformational effects, as recently demonstrated for other protein nanomachines such as the F₁-ATPase (63) or the bacterial MreB filaments (64). As revealed by our FDA, also in the MT system this communication is mediated by groups of strong pairwise residue interactions concentrated mainly near the nucleotide binding pocket as well as the H8 helix, the H8–H7 loop, and the accompanying H11${}^{\prime }$ helix at the intradimer and interdimer interfaces (Fig. 2 B and C and SI Appendix, Fig. S5).

The free energy calculations in conjunction with the nonequilibrium relaxation simulations of complete MT tips enable us to address a key question about the dependence of the lateral tubulin–tubulin contact stability on the nucleotide state and the contact topology (homotypic vs. seam). While the presented estimates of the lateral interaction energies are magnitude-wise consistent with previous ones derived from atomistic simulations with or without enhanced sampling (36, 65), we have been able to discern in detail the effects of the nucleotide state on the lateral contact stability owing to ∼100-fold more MD sampling (Fig. 3C and SI Appendix, Fig. S7). We have found that GTP hydrolysis, in fact, increases the lateral contact stability by ∼7.1 k _BT (homotypic) or ∼3.3 k_BT (seam). Contrary to our initial skepticism, the subsequent convergence analysis has confirmed that this stabilization effect is not due to insufficient sampling (SI Appendix, Fig. S7). Moreover, the fact that both GTP- and GDP-MT tips lose approximately the same fraction of lateral contacts within 1 µs of simulation (Fig. 3 A, Right)—despite the much higher conformational strain stored initially in the GDP-MT tips—can only be explained by more stable lateral contacts between GDP-PFs. Although counterintuitive, we believe that the hydrolysis-driven stabilization of lateral contacts in the MT lattice, accompanied by the increase of longitudinal strain in PFs, is a necessary condition for regulating MT dynamics and triggering MT catastrophe.

The role of the seam in regulating the MT dynamics has been elusive. Here we have shown that although MT tips crack open at different lateral interfaces, the rate of PF splaying at the seam is significantly elevated (Fig. 3B), in accordance with the original hypothesis by Nogales and colleagues (42, 55). This observation is further supported by the calculated lateral free energies (Fig. 3 C, Bottom) that more weakly depend on the nucleotide state and are systematically lower than those for the homotypic interface. These results confirm that the functional effect of the seam might be exactly the opposite of a homotypic interface: namely, to provide a kinetic destabilization of the entire MT tip by lowering the energy barrier for lateral contact dissociation, especially during MT shrinkage (Fig. 4 B, Right). This mechanism would explain why MTs containing more than one seam exhibit more frequent catastrophe events and shrink faster than single-seam dynamic MTs (58), yet the excess presence or absence of seams does not necessarily affect the bending rigidity of MTs (66). Rather, the presence or absence of kinetically unstable seams may offer an additional mechanism to regulate MT polymerization and depolymerization kinetics.

At first glance, the existence of strongly flared MT tips with fully or partially splayed PFs may seem to contradict the widely accepted stabilizing cap hypothesis, i.e., the presence of a GTP-rich structure at the ends of growing MTs that is critical for MT stability (3, 4, 67). In its prevailing formulation, the loss of this GTP cap is thought to expose the unstable GDP-MT lattice, which subsequently triggers MT depolymerization either by inducing curved PF conformations that are inconsistent with the straight MT lattice (68, 69) or by weakening the lateral contacts between PFs (39, 41, 51, 57), or both. However, we believe that the results of our computational study in conjunction with the recent cryo-ET observations (18, 26, 27, 29) do not contradict the stabilizing cap hypothesis as a concept. Rather, we argue that the mechanism of MT growth and catastrophe is more complex than what has been proposed previously.

The stabilizing GTP cap is a target for end-binding (EB) proteins, which has enabled more detailed characterization of its behavior as a function of the stochastic fluctuations in MT length and immediately before a catastrophe (42, 70–72). In particular, it has been shown that 1) stabilizing cap lengths can vary considerably; 2) longer caps, on average, lead to longer MT lifetimes; and 3) catastrophe is triggered before the stabilizing cap is lost completely. More recent studies (19, 73, 74) have provided a more comprehensive description of the structure of the hypothetical GTP cap. Essentially, these studies suggest that the stabilizing MT cap is a complex, multilayer region spanning hundreds of nanometers of MT length, with strongly heterogeneous patchworks of tubulin conformations and nucleotide states in overlapping areas.

However, there are still significant controversies regarding the origin of the large variation in delay times between the cessation of MT growth and the MT collapse [e.g., after tubulin washout (72)], which potentially indicates the presence of additional stochastic effects at the extreme MT plus-end that we are not yet aware of. Moreover, there is still no agreement on the mechanistic origin of the MT aging effect, i.e., the gradual increase of the catastrophe probability as MTs elongate (15, 75, 76). The stabilizing cap hypothesis also does not explain exactly what interactions at the MT tip guarantee its momentary stability and/or trigger the onset of catastrophe—not least because the ultrastructure and dynamics of the MT plus-end are hard to time resolve at a high resolution.

Accurate simulations of large-scale MT tip models based on high-resolution cryo-EM data might be, thus, a uniquely suitable method to bridge the information from static high-resolution structural data and the conformational dynamics of individual PFs at the extreme MT ends, which likely govern dynamic instability. Our results suggest that the stochastic formation/dissociation of metastable PF clusters regulated by nucleotide-dependent free energy barriers might be the missing link. The rates of both spontaneous PF straightening and lateral association between PFs [$\mathrm{\lesssim }{10}^5$ s^–1 (28, 36, 65, 77, 78)] are substantially larger than the rates of tubulin turnover and GTP hydrolysis at the MT tip [0.2 to 40 s^–1 at 10- to 15-µM free tubulin (17–19, 71)]. Although the classical GTP cap model can explain the main kinetic features of MT behavior, this timescale separation implies that the dynamics and energetics of the extreme MT tip additionally control the MT growth and catastrophe.

When a MT with a long stabilizing cap grows stably, its extreme tip and the constituting PFs are almost in pure GTP state. Such a tip is prone to self-closure and subsequent elongation because the GTP-PFs are mechanically soft and easily form lateral clusters through stochastic fluctuations in the tangential direction. More specifically, the configuration of the free energy landscape of the MT tip is such that it stochastically favors pathways that guide it through conformational states with metastable PF clusters toward the fully closed MT lattice upon addition of new tubulin dimers to its flaring PFs. On the contrary, a significant loss of the stabilizing cap leads to a situation in which the PFs at the extreme MT tip can be in different nucleotide states, i.e., more GDP-like. PF clusters are then disfavored because the GDP-PFs (or PFs including a large fraction of GDP-tubulin) are mechanically stiffer, especially in the tangential direction. In this case, the configuration of the free energy landscape of the MT tip changes gradually to increase the energy barriers for the formation of PF clusters, which strongly reduces the collective probability to form a straight MT lattice. This process resembles an information-driven Brownian ratchet (79, 80) that is only capable of rolling uphill (MT growth) when the corresponding free energy barriers are low (GTP-MT tip with PF clusters), but which are themselves a function of the system’s state (lattice formation triggers GTP hydrolysis). As a result, there is an information feedback loop (GTP hydrolysis raises the barriers) between the current state of the system and the next energy barriers that should be modified.

Interestingly, the proposed model agrees with the broad distribution of delay times between tubulin washout and MT catastrophe (72). This phenomenon could be explained by the time the tip PFs require to reequilibrate. Since this process would involve diffusion on a rugged, multidimensional free energy landscape, it would make the start of MT catastrophe itself a broadly distributed random variable. Furthermore, the proposed model provides a possible explanation for the destabilizing effect of EBs via acceleration of the MT plus-end maturation (71). Assuming that EBs must take action rather early in the MT growth process, it is conceivable that the metastable PF clusters are one of the primary targets of EBs, which also agrees with EB binding sites being located between PFs (42, 70).

Materials and Methods

Construction of MT Tip Models.

Initial models for the tubulin dimers were obtained from PDB IDs 3JAT (GMPCPP) and 3JAS (GDP) (42) by extracting the central dimer from the 3 × 2 lattice patches (chains A and H in the original PDBs). GMPCPP was converted into GTP by replacing the carbon atom between α- and β-phosphate with an oxygen atom. The missing loop in the α-subunit (residues 38 to 46) was modeled in for structure consistency using MODELER version 9.17 (81) but excluded from further refinement. Similarly to our previous study (37), the flexible C termini (α:437–451 and β:426–445) were not included in our simulations to reduce the system size and to achieve the best possible sampling.

Asymmetric (C1) reconstructions of 14-PF GMPCPP- and GDP-MTs decorated with kinesin [kindly provided by Rui Zhang, Washington University in St. Louis, St. Louis, MO (42)] were used to construct the all-atom models of MT lattices. Although the C1 reconstructions have a lower resolution (4.0 to 4.1 Å compared to 3.5 Å for the symmetrized ones), they reflect the correct seam location and topology as well as the slightly increased PF–PF distance at the seam. Subsection of the cryo-EM maps enclosing two layers of dimers in the axial direction were extracted, and copies of the atomistic dimer models were rigid-body fitted into the subsection densities (SI Appendix, Fig. S8). The constructed models were solvated in a triclinic water box of size 33.2 × 33.2 × 25.8 nm³ and subsequently neutralized with 150 mM KCl.

Refinement was done with correlation-driven MD (CDMD) (43), following our previously published protocols (37, 43). Briefly, we employed a cold-fitting protocol (NPT ensemble, T = 100 K, P = 1 atm) containing three phases: short restraint-free equilibration for 10 ns; refinement with a resolution and force constant ramp for 35 ns; and finally, 15 ns of simulated annealing. The sigma parameter controlling the simulated map resolution was ramped from 0.6 to 0.2 nm. The force constant was ramped from 1 × 10⁵ to 1 × 10⁶ kJ/mol.

The final MT plus-end models were constructed by grafting three copies of the refined subsection models onto one another by applying a translation operation to each copy that conforms to the dimer periodicity [also known as dimer rise; ∼8.31 nm for GTP-MTs and ∼8.15 nm for GDP-MTs (42, 56)] and removing the terminal α-tubulin monomers from the plus-end (Fig. 1B). The resulting tip structures (79 α-tubulins and 84 β-tubulins) were kept blunt to maximize the initial lateral contact area.

Relaxation Simulations of MT Tips.

The CHARMM22* force field (60) and the CHARMM-modified TIP3P water model (82) were used in all simulations. GTP/GDP parameters were adapted from those for ATP/ADP implemented in the CHARMM22/CMAP force field (82, 83). Titration curves of histidines were calculated using the GMCT package (84) and assigned as described previously (33).

The final MT tip structures were centered and resolvated in a larger periodic box of size 50 × 50 × 63 nm³ to accommodate larger splayed conformations and to avoid collisions of the PFs belonging to periodic images (at least on microsecond time scales). As in the refinement simulations, the solvated tip structures were neutralized with 150 mM KCl, yielding an atomic system with ∼15.6 million atoms. All subsequent MD simulations were carried out with GROMACS 2019 (85). Lennard–Jones and short-range electrostatic interactions were calculated with a 0.95-nm cutoff, while long-range electrostatic interactions were treated using particle-mesh Ewald summation (86) with a 0.12-nm grid spacing. The bond lengths were constrained using the LINCS algorithm (87) (hydrogen bonds during initial equilibration and all bonds in the production runs). Velocity rescaling (88) with a heat bath coupling constant of 0.5 ps was used to control the temperature for solute and solvent separately. Applying virtual site constraints (89) allowed us to increase the integration step size to 4 fs in the production runs. Center-of-mass correction was applied to solute and solvent separately every 100 steps. To mimic the minus-end attachment, we applied position restraints with the force constant k = 350 kJ/mol/nm² to the bottom layer of monomers (nine α-tubulins and five β-tubulins in total).

With the above parameters fixed, the equilibration protocol consisted of the following steps: 1) energy minimization using steepest descent, 2) short NVT equilibration for 1 ns at T = 100 K with position restraints on all heavy atoms and using a 1-fs integration time step, 3) gradually heating up the system to 300 K within 5 ns in the NVT ensemble using a 2-fs integration time step, 4) equilibration in the NPT ensemble for 5 ns [Berendsen barostat (90) with a 5-ps coupling constant] using a 2-fs time step, 5) gradual release of the position restraints (except those mimicking the minus-end attachment) within 10 ns in the NPT ensemble [isotropic Parrinello–Rahman barostat (91) with a 5-ps coupling constant] using a 4-fs time step, and 6) preequilibration for 5 ns in the NPT ensemble (same as in step 5) using a 4-fs time step. The last frame of step 6 was used to spawn five independent relaxation runs for each nucleotide state.

To additionally test the dependence of the MT relaxation behavior on the force-field choice, we performed 10 additional, large-scale relaxation simulations of the MT tip models using the newer CHARMM36m (61) force field, i.e., five simulations per nucleotide state, each covering at least 800 ns of sampling. The same water model and GTP/GDP parameters were used. The simulation parameters were identical, except that the Lennard–Jones and short-range electrostatics cutoffs were set to 1.0 nm as recommended in the original study (61).

Simulations of Single Finite PFs and Infinite Coupled PFs.

Straight GTP-PFs and GDP-PFs comprising three longitudinally coupled tubulin dimers were extracted from a seam-distant location of the respective MT tip models (SI Appendix, Fig. S9). The single-PF systems were then solvated in a water box of size 13.5 × 13.5 × 28.0 nm³ and neutralized with 150 mM KCl. The box size was sufficient to avoid collisions with periodic images. The PFs were then equilibrated as described in the previous section, and the equilibrated structures were used to span 20 independent 4-µs production runs for each nucleotide state.

Double-PF systems were prepared as described in our recent study (37). Briefly, for each nucleotide state, we extracted two 2 × 2 tubulin patches, one from a seam-distant location mimicking a homotypic interface and the other from the seam (SI Appendix, Fig. S9). The patches were then solvated in a water box of size 12.7 × 12.7 × 21.0 nm³ and neutralized with 150 mM KCl. These finite double-PF models were converted into infinite double-PF models by removing the extra tubulin dimers and nucleotides. Water and ion atoms were then trimmed to conform to the experimental value of the axial periodic dimension, namely, ∼8.31 nm for GMPCPP-MTs and ∼8.15 nm for GDP-MTs (42). The number of ions in the trimmed water shell was fixed to keep the systems neutral and to maintain the ionic strength of 150 mM KCl. The double-PF systems were equilibrated as described in the previous section with the only difference being that we used the semiisotropic Parrinello–Rahman barostat to control the system size fluctuations in the axial (along the PF) and transverse (perpendicular to the PF) directions separately. The equilibrated structures were used to spawn a 1-µs production run for each nucleotide state.

Calculation of the PF–PF Association Free Energy Profiles.

Our approach to calculate the lateral PF–PF interaction free energies relied on a previous study (36). We employed the umbrella sampling technique (92) in conjunction with the weighted histogram analysis method (WHAM) (93, 94). We first defined the inter-PF COM distance to be the reaction coordinate. The biasing potential was tuned to be 4,000 kJ/mol/nm² and was applied to restrain only the transverse component of the inter-PF distance. To cover the full range of inter-PF interactions, the distance between 5.0 and 7.2 nm was split into windows, each being separated by 0.05 nm from its nearest neighbors. This partitioning of the reaction coordinate space yielded sufficient overlap between neighboring windows in the absolute majority of cases. In those cases, where the overlap was still $\mathrm{\lesssim }$30%, new windows were added. The production runs were used for seeding the umbrella simulations, where each seed was separated from all the others by at least 50 ns in time. Seeding structures for those windows that were not initially covered by the unrestrained simulations of the double-PF systems were derived from neighboring windows located 0.05 nm away in the reaction coordinate space. Each window was then simulated for 1 µs, and the autocorrelation times of the inter-PF COM fluctuations were assessed. If an autocorrelation time was above the average, the respective umbrella window simulation was extended to 1.3 µs. For determining the convergence of the free energy profile for each condition (nucleotide state and contact topology), we calculated the profiles using WHAM as a function of the length of umbrella window trajectories with an increment of 100 ns (SI Appendix, Fig. S7). Free energy uncertainties were estimated using Bayesian bootstrapping (94) of the complete histograms scaled by inefficiency factors g_i = 1/(1 + ${\tau }_i)$, where τ_i is the autocorrelation time of umbrella window i (95, 96).

PCA of PF Dynamics.

To quantify the highest-variance (lowest-energy) uncorrelated motions of the single PF conformational dynamics, the PCA (97) was carried out. First, for each independent single PF trajectory, we extracted all backbone atoms, while excluding the first 1 µs of the respective trajectory from the analysis. Second, all backbone trajectories were superimposed relative to the minus-end α-tubulin. Then, all independent trajectories belonging to the same nucleotide state were concatenated, and the atomic displacement covariance matrix was calculated. The covariance matrix was diagonalized to yield the eigenvalues $\left\{{\lambda }_i\right\}$ and eigenvectors $\left\{{\mathbf{v}}_i\right\}$. Finally, the concatenated trajectory for each nucleotide state was projected onto the first and second eigenvectors of the this matrix. The projection histograms were then calculated to obtain the equilibrium distributions $p({\xi }_1,{\xi }_2)$ converted to the free energy profiles $G({\xi }_1,{\xi }_2)=-$ k_BT ln $p({\xi }_1,{\xi }_2)$ (Fig. 2A). Note that the projections were not rescaled by $\sqrt{N}$ (N is the number of backbone atoms), which is why the magnitudes of eigenmotions in Figs. 2A and 4B are not to scale. The relative contribution of eigenmode i can then be expressed as ${\lambda }_i/{\displaystyle {\sum }_{j=1}^{3N-6}{\lambda }_j}$.

Joint Free Energy Landscape of Coupled PF Dynamics Obtained through Resampling.

To assess the combined effect of PF elasticity and PF–PF interaction on the dynamics of neighboring PFs, we employed a resampling scheme using the data available from the single-PF simulations (Fig. 2A) and the umbrella sampling of lateral interactions (Fig. 3C). To mimic the presence of a lateral neighbor, we first copied the full ensemble of PF conformations and rotated the copy by 2π/14 radians along the MT circumference away from the original (Fig. 4A). We then used the PFs’ eigenmodes to describe the conformations of the PF neighbors: namely, CV₁ reflecting the extent of each PF’s deviation from the equilibrium conformation and $\mathrm{\Delta }C{V}_2=C{V}_{2,{\text{PF}}_2}-C{V}_{2,{\text{PF}}_1}$ expressing the extent of tangential separation between the PFs.

With the order parameters CV₁ and $\mathrm{\Delta }C{V}_2$ defined, the resampling procedure was as follows. The parametric space $(C{V}_1,\mathrm{\Delta }C{V}_2)$ was partitioned into bins of finite size. For each bin $(C{V}_1,\mathrm{\Delta }C{V}_2)$, all corresponding PF conformations were found and extracted from the PF ensembles (original and copy), and all possible pairs of PFs were constructed without replacement. For each PF pair k in bin i, the lateral interaction free energy was computed as $\mathrm{\Delta }{G}^{(i,k)}={\displaystyle {\sum }_{j=1}^3\mathrm{\Delta }}{G}_{\mathit{lat}}^{(i,k)}(d_j)$, where $\left\{d_j\right\}$ are the COM–COM distances between the neighboring dimers and $\mathrm{\Delta }{G}_{\mathit{lat}}(d)$ is the lateral interaction free energy landscape (Fig. 3 C, Top). The weighted probability distribution of the PF pair conformations that also accounts for lateral interactions between the PFs was then obtained by bin counting, where each observation k in bin i was weighted by $w^{(i,k)}\propto \text{exp}[\text{}-\mathrm{\Delta }{G}^{(i,k)}/{\text{k}}_{\text{B}}\text{T}]$. The weighting ensures that those PF conformations likely to form a strong lateral interaction contribute more to the total probability distribution, thus creating a metastable state at low $\mathrm{\Delta }C{V}_2$ values (Fig. 4B).

Data Analysis and Availability.

All postprocessing calculations were done using GROMACS internal tools (85), Python 2.7 (98), and Numpy (99). Graphs were produced with the Matplotlib v2.2.5 (100) and Seaborn v0.9 (101) libraries. All structure and map manipulations were performed using UCSF Chimera v1.14 (102) or Visual Molecular Dynamics (VMD) v1.9.3 (103). The VMD software was further used for visualization of all MT and PF structures as well as for producing the movies. Atomic coordinates of the initial MT tip models are provided as Datasets S1 and S2. The raw MD trajectories (>2 TB of data) that support the findings of this study are available through a specialized file hosting service of the authors’ institute: https://data.goettingen-research-online.de/dataverse/pnas2022_mt_splaying_igaev_grubmueller.