A variable refractory period increases collective performance in noisy environments

Significance

In biological and artificial systems, synchronization is an important means of achieving coordination. During hunting, social spiders alternate their moving and stopping phases in unison as they move toward their prey. We combined fieldwork and modeling to investigate the behavioral rules that lead to the emergence of synchronized oscillations in hunting groups. We showed that an individual's decision to move depends on the relative intensity of vibrations emitted by the prey and the moving spiders. This rule allows the group to adapt quickly to any change in prey size or the number of spiders involved in the hunt. Such synchronization ensures that the spiders can locate their prey without being disturbed by signals from conspecifics and thus improves hunting performance.

Abstract

Synchronized oscillations are found in all living systems, from cells to ecosystems and on varying time scales. A generic principle behind the production of oscillations involves a delay in the response of one entity to stimulations from the others in the system. Communication among entities is required for the emergence of synchronization, but its efficacy can be impaired by surrounding noise. In the social spider Anelosimus eximius, individuals coordinate their activity to catch large prey that are otherwise inaccessible to solitary hunters. When hunting in groups, dozens of spiders move rhythmically toward their prey by synchronizing moving and stopping phases. We proposed a mechanistic model implementing individual behavioral rules, all derived from field experiments, to elucidate the underlying principles of synchronization. We showed that the emergence of oscillations in spiders involves a refractory state, the duration of which depends on the relative intensity of prey versus conspecific signals. This flexible behavior allows individuals to rapidly adapt to variations in their vibrational landscapes. Exploring the model reveals that the benefits of synchronization resulting from improved accuracy in prey detection and reduced latency to capture prey more than offset the cost of the delay associated with immobility phases. Overall, our study shows that a refractory period whose duration is variable and dependent on information accessible to all entities in the system contributes to the emergence of self-organized oscillations in noisy environments. Our findings may inspire the design of artificial systems requiring fast and flexible synchronization between their components.

Oscillations are ubiquitous in biological systems, from biochemical reactions in cells to predator–prey interactions in ecosystems and on time scales ranging from fractions of a second to years. Considerable attention has been given to the study of the underlying mechanisms, from the simplest to the most complex systems, and a limited number of common elements have been recognized as essential for giving rise to temporal oscillations (1–3). Basically, there are two broad categories of mechanisms leading to the production of oscillations on a collective scale: either the entities of the system have their own rhythm and the oscillations require the adjustment of their phases, or the entities of the system have no intrinsic rhythmic activity and the oscillations result from the ability of one element to excite another component of the system. In both cases, the production of oscillations relies on the interactions between the components of the system. Communication is essential for regulating interactions between entities and for the expression of feedback loops that are necessary for the emergence of collective behaviors in self-organized systems, which are notably characterized by an absence of centralized control (4). Achieving optimal collective performance therefore requires minimizing the negative impact of noise on communication to increase the signal-to-noise ratio and improve the quality of information processing.

A critical ingredient for generating oscillatory behavior is the existence of a sufficiently large delay in the response of the excitable entities making up the system. In cellular systems for instance, the presence of intermediate steps in feedback loops generate delays that are sources of oscillations in the production of gene transcripts (5). This delay may also take the form of a refractory period that requires an entity that has just been excited to remain inactive for a certain time before returning to its original state (6). Such a mechanism explains, for example, the genesis of the heartbeat with cells alternating between phases of activity and inactivity (7) or, on another scale, the propagation of the Mexican wave, where spectators in stadiums stand up and sit down in a coordinated manner (8). Most studies aimed at generating synchronization in artificial systems (e.g., robotic swarms) use agents with periodic behavior (9), but the implementation of a refractory period coupled with the mutual excitability of entities represents an interesting alternative to coordinate the activities of a multitude of interacting elements.

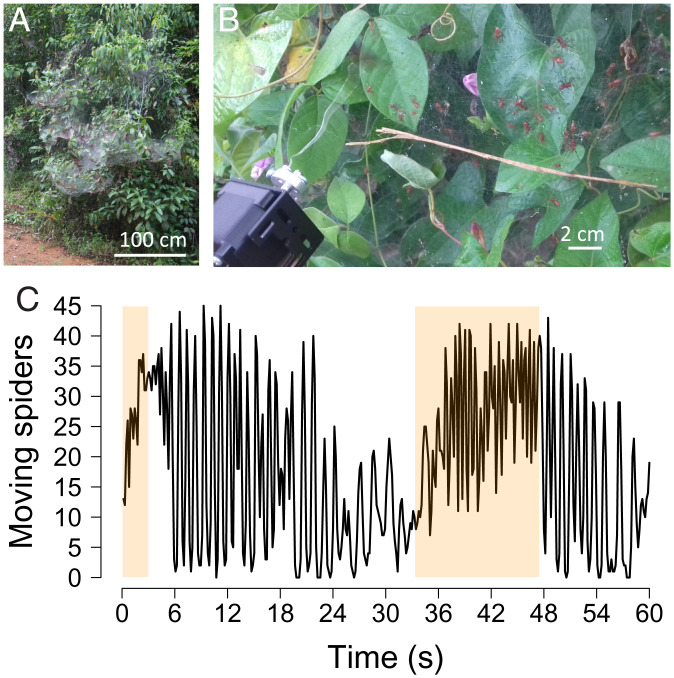
Understanding the genesis of oscillations in animal groups requires characterizing the signals involved in social interactions and identifying the individual behavioral rules that generate the feedback and delays necessary for the production of rhythmic behavior on a collective scale. Groups of animals exhibit synchronized behaviors leading to the propagation of regular waves of activity or signaling in a variety of contexts. A paradigmatic example is found in fireflies, where males delay the emission of their light signal in response to a signal from a conspecific, leading assemblies to flash rhythmically (10). One remarkable example of synchronization leading to collective oscillations is found in the social spider Anelosimus eximius during cooperative hunts (Movie S1). Among the 50,000 species of spiders described so far, about 20 have evolved toward permanent sociality (11). These species are characterized by a series of traits that include cooperation in prey capture, web construction, colony defense, and brood care (12, 13). A. eximius inhabits tropical rainforests of northern South America, and colonies can comprise thousands of individuals (12, 14). Nests, which can measure several meters in width and length, are typically composed of a horizontal basket-shaped silken sheet and a network of vertical threads, connected to the vegetation, used to intercept flying prey (Fig. 1A). Spiders cooperate during hunting, and collectively, they can catch very large prey, up to 700 times the weight of an individual spider (15). When approaching the prey, spiders rapidly synchronize their displacements by alternating phases of mobility and immobility (16) (Fig. 1 and Movie S1). Many solitary spiders that hunt alone also exhibit pausing behaviors (17–19), the challenge with social spiders is to explain the coordination of the many hunters leading to the emergence of synchronized waves of moves. Although this collective behavior was a source of inspiration in the field of swarm intelligence to develop model of optimization (20), the mechanisms underlying the emergence of the periodic oscillations in hunting spiders still remains poorly understood.

Fig. 1.

Collective hunting in social spiders. (A) Web of the social spider A. eximius in French Guiana. (B) A dead fly connected to a vibration generator was brought into contact with the web to trigger collective hunting behavior in a group of social spiders. (C) Activity patterns in a group of spiders engaged in a hunt triggered by the lure. Individuals alternate synchronously between moving and stopping when hunting. The colored areas indicate when the lure was contacting the web. (Copyright R. Jeanson/CNRS.)

Spiders live in a vibrational world (21). They are exposed to multiple vibrations whether these are produced by conspecifics and involved in the regulation of social interactions or whether they are produced by prey struggling in the web and used by the spiders to orient themselves during the hunt. We proposed that social spiders use vibrational information to coordinate the behavioral transition between movement and immobility phases during collective hunting. Our hypothesis was that they switch between behavioral states depending on the surrounding noise produced by the moving spiders relative to the signal emitted by the prey. We developed a numerical model implementing only behavioral rules measured in field experiment to validate our hypothesis. We then used this model to identify the respective contribution of the rules driving the emergence of oscillations and to explore how synchronization is beneficial during group hunting in a noisy environment.

Results

Individual Behaviors.

We performed field experiments in French Guiana. Collective hunts were triggered with a custom vibrating lure that elicits behaviors in spiders similar to those observed when a prey falls into the web: individuals rapidly develop synchronized oscillations between phases of mobility and immobility. The use of a lure, instead of live prey, allowed us to stimulate the same groups of spiders several times without their motivation being affected by the consumption of the prey (Fig. 1B). When spiders are engaged in a hunt, they continue to move synchronously for a few seconds when the vibrations temporarily stop or when the natural prey escapes (Fig. 1C). By placing or removing the lure from the web, we were able to distinctly quantify the response of spiders to vibrations produced by conspecifics or by the lure. We used a timestep of 0.08 s to analyze video-recorded hunting.

Probability of moving in response to vibrations.

We aimed at determining how immobile spiders reacted to the vibrations produced by one or more moving spiders or by the lure. We used the behavioral response of spiders to vibrational stimuli to infer how the signal produced by the lure or conspecifics was attenuated when propagating on the web. Earlier work documented a sigmoidal relationship between the intensity of the stimulus and the neuronal response to vibrations in spiders (22). Therefore, we modeled the behavioral response of spiders to the vibrations V using a sigmoidal function: the probability of moving P_move increases exponentially at low stimulus intensity and at a decelerating rate at large intensity. This gives the following:

$$P_{\mathit{move}}=\frac{1}{1+e^{\left(\text{σ}-V\right)}},$$ [1]

where σ is a constant.

Since attenuation of vibrations with distance on a web is exponential (23), the intensity of the signal at a distance d from the source of vibrations is the following:

$$V=V_0{e}^{-kd},$$ [2]

where V₀ is the intensity of vibrations at the origin, and k is a constant that determines how fast vibrations are attenuated. Therefore, we had to determine the values of V₀ and k for vibrations produced either by the spiders or by the lure.

We assumed that an individual detected the local vibration, whether produced by a single spider or by a combination of spiders. Because vibrations are approximately additive, the intensity of the vibrations V_spider produced by N moving spiders that are perceived by a stopped spider is given by the following:

$$V_{\mathit{spider}}={\displaystyle {\sum }_{i=1}^N{V}_{0_{\mathit{spiders}}}\hspace{0.17em}{e}^{-k_{\mathit{spider}}{d}_i}},$$ [3]

where $V_{0_{\mathit{spider}}}$ is the intensity of spider vibrations at the origin (the vibrations at the origin being assumed identical for all moving spiders), d_i the distance between the stopped spider and each moving spider i, and k_spider the coefficient of attenuation of spider vibrations.

From Eqs. 1 and 3, the probability of moving for a stopped individual in response to N moving spiders is thus given by the following:

$${\text{P}}_{\mathit{move}, \mathit{spider}}=\frac{1}{1+e^{\left({\sigma }_{\mathit{spiders}}-{{\displaystyle \sum }}_{i=1}^N V_{0_{\mathit{spider}}} e^{-k_{\mathit{spider}}{d}_i}\right)}}.$$ [4]

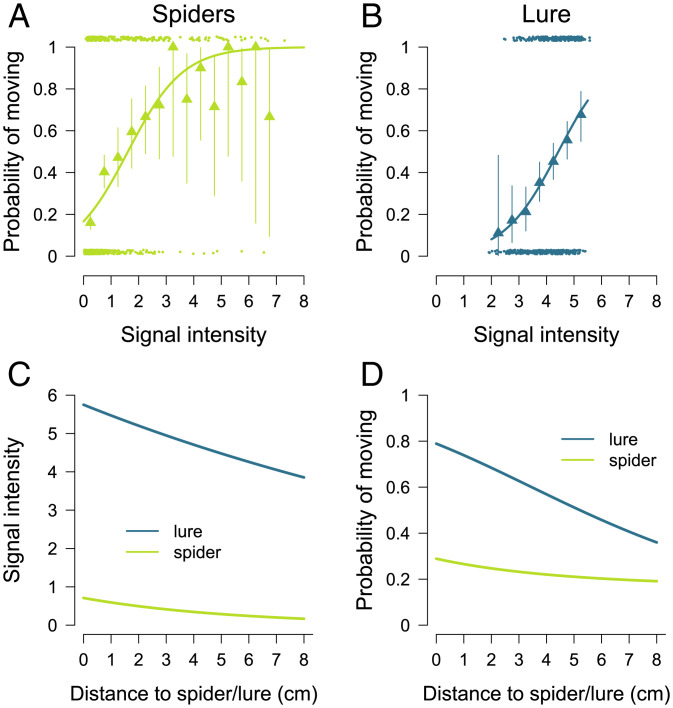
In order to estimate the parameters $V_{0_{\mathit{spider}}}$, k_spider, and σ_spider, we analyzed by eye four hunting sequences, each lasting 10 to 14 s and involving 26 to 46 spiders (SI Appendix, Fig. S1). When the lure was absent, we identified each moment (t₀) when one or more spiders (initiators) moved spontaneously after all spiders had been stopped for at least one timestep. We then determined whether the spiders that were immobile at timestep (t₀) started moving at the next step (t₁) in response to the vibrations produced by the initiator(s). For each individual, this allowed us to obtain the probability that it started moving in response to the movements of N spiders by considering their distance. We used a maximum log-likelihood approach to find the values of the parameters $V_{0_{\mathit{spider}}}$, k_spider, and σ_spider (Eq. 4) that maximize the probability of observing the experimental data (Fig. 2A and SI Appendix, Fig. S2). In absence of the lure, the best fit was obtained with $V_{0_{\mathit{spider}}}$ = 0.71, k_spider = 0.18 cm⁻¹ and σ_spider = 1.62.

Fig. 2.

Individual response to signal intensity. Probabilities of moving in response to vibrations produced by spiders (A) or the lure (B). The dots (n = 830 for the spiders, n = 550 for the lure) give the observed events (move or not) as a function of the intensity of the signal received by a stopped individual at the preceding timestep (the positions of the dots were shifted along the y-axis for illustrative purpose). The triangles indicate the experimental proportion ±95% CI of spiders that moved as a function of signal strength by 0.5 interval. The lines give the predicted probabilities obtained with Eq. 4 for spiders (${\text{V}}_{0_{\text{spider}}}$ = 0.71, k_spider = 0.18 cm⁻¹, and σ_spider =1.62) and Eq. 5 for the lure (${\text{V}}_{0_{\text{lure}}}$ = 5.74, k_lure = 0.05 cm⁻¹, and σ_lure = 4.42). (C) Predicted intensity of the signal perceived by a spider as a function of its distance from the lure or a single moving spider. (D) Predicted probability of moving in response to the lure or a single moving spider as a function of the distance to the immobile spider.

We next aimed at estimating the response of spiders to the lure. We needed to identify events where all spiders were motionless before the lure was activated in order to measure the spiders' response only to the lure and not to conspecifics. We used 18 hunting sequences with a mean of 30 spiders (minimum = 13, maximum = 78) that were immobile for at least 0.08 s. After all spiders had stopped, we determined which individuals moved in the timestep beginning with the movement of the first spider after the lure had approached the web. As we did to model the response to spider vibrations, we modeled the response to lure with a sigmoid function:

$$P_{\mathit{move}, \mathit{lure}}=\frac{1}{1+e^{\left({\sigma }_{\mathit{lure}}- V_{0_{\mathit{lure}}}{e}^{-k_{\mathit{lure}}d}\right)}},$$ [5]

where d is the spider’s distance to the lure, $V_{0_{\mathit{lure}}}$ is the intensity of lure vibration at the origin, and k_lure the coefficient of attenuation of lure vibration.

Fitting our experimental dataset with Eq. 5, we obtained $V_{0_{\mathit{lure}}}$ = 5.74, k_lure = 0.05 cm⁻¹, and σ_lure = 4.42 (Fig. 2B).

We then used the parameters obtained for both fits to calculate the intensity of the signal produced by moving spiders or by the lure. The comparison between the observed proportions of spiders that moved as a function of signal intensity and the corresponding theoretical probabilities revealed quantitative agreement for both spider and lure response, which means that we satisfactorily modeled the behavioral responses of spiders to stimuli (Fig. 2 A and B). At any distance from a focal individual, the intensity of the signal produced by the lure was greater than the strength of the signal produced by one moving spider (Fig. 2C). The individual probability of moving decreased with the distance from the source of vibration and was greater in response to the lure than to a single moving spider (Fig. 2D).

Probability of stopping in presence and absence of the lure.

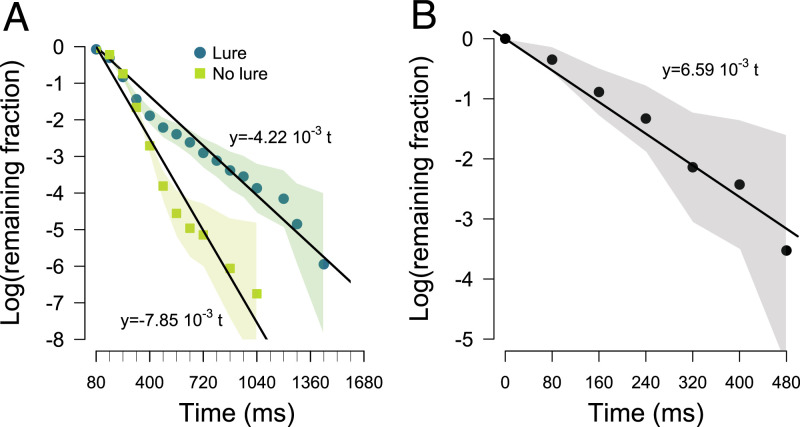
In the absence of the lure, we detected no correlation between the time spent moving and the maximum intensity of spider vibrations perceived during the move (Pearson correlation test: t = −1.377, df = 856, r = −0.047, and P = 0.169) (SI Appendix, Fig. S3). This suggested that the activity of other spiders had no influence on the probability of stopping. The durations of moves were twice as long in the presence than in the absence of the lure (log-rank test: χ² = 6.3, df = 1, and P = 0.01). The survival curves for the duration of moves recorded in the presence or absence of the lure were plotted on a log-linear scale and fitted with linear regressions (Fig. 3A). The slope of each regression line gave the individual probability per unit time that a moving spider would stop when the lure was active or not (Fig. 3A).

Fig. 3.

(A) Survival curves of the durations of moves in presence (n = 858) and absence (n = 383) of the lure. Colored bands are 95% CI. (B) Survival curve of the durations of the phases of silence (n = 34).

Spontaneous probability of moving in absence of vibrations.

We assessed the individual probability of moving spontaneously (i.e., not in response to any external vibration) when all spiders were stopped in absence of the lure. We plotted on a log-linear scale the survival curves of the durations of the phases of silence recorded in the four hunting sequences used to quantify the response of spiders to vibrations (Fig. 3B). The slope gives the probability per unit of time that at least one spider started to move. Assuming that each spider was equally likely to start moving spontaneously, the individual probability of moving per unit of time was given by the slope divided by the number of spiders likely to move. Using a number of spiders of 25 (i.e., the average number of individuals involved in the sequences used to calculate the slope), we obtained an individual probability of moving spontaneously per unit of time equaling 2.63 10⁻⁴ ms⁻¹.

Characterization of the refractory state.

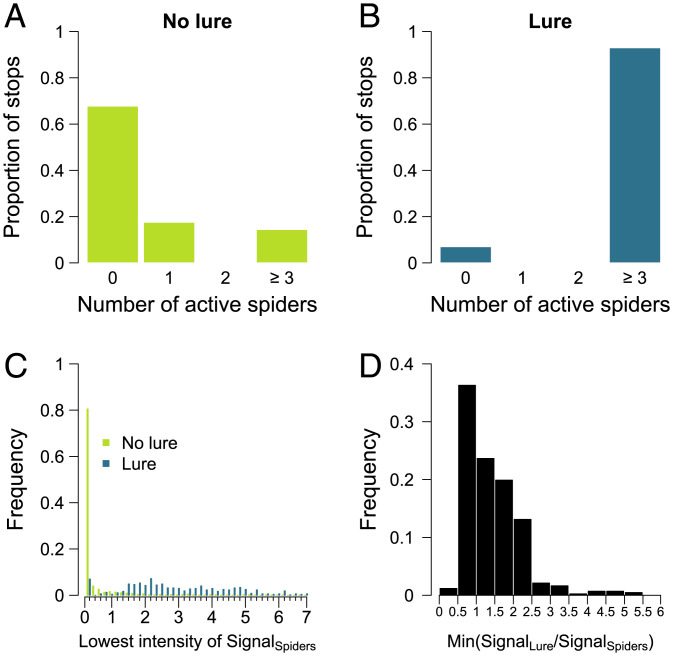
After a spider stopped, we needed to identify what condition had to be met for it to return to an excitable state and respond again to vibrations emitted by its conspecifics. We considered the vibrational information emitted by conspecifics or by the lure that was received by each spider at each timestep (0.08 s) of its stop to determine whether a refractory state existed and, if so, whether its expression was dependent on the presence of the lure. In the absence of the lure, ∼70% of the stops preceding an individual’s move were characterized by a period of at least 0.08 s where all spiders were immobile (Fig. 4A). In contrast, when the lure was active, less than 10% of the stops contained a period when all spiders were stopped (Fig. 4B). We then used Eq. 3 to calculate the intensity of the signal produced by moving individuals that a stationary spider perceived for each timestep during its stop in absence or presence of the lure. The values of the lowest spider signal intensity recorded during one timestep during each stop was greater in the presence of the lure than in its absence (Fig. 4C). This implied that the spiders did not resume their movement until the vibrations of the conspecifics were very low, whereas in the presence of the lure, the spiders could resume their movement even if they perceived relatively higher vibrations from the conspecifics. Last, we calculated the ratio of the intensity of the signal produced by the lure divided by the intensity of the signal produced by moving spiders at each timestep when a spider was stopped. A stopped spider experienced a minimum ratio of the lure signal over the spider signal greater than 0.5 in 99% of the observed cases (n = 438) (Fig. 4D). This meant that during almost every stop in the presence of the lure, the signal intensity of the lure received by the stopped spider was more than one-half the signal strength produced by moving spiders for a least one timestep. Based on these results, we proposed the rule that an individual that had just stopped entered a refractory state and could not resume movement as long as the strength of the signal emitted by the lure was less than one-half the strength of the signal produced by the mobile spiders. When the lure was absent, this meant that the spiders all had to observe a phase of silence to allow them to become active again. Therefore, the duration of the refractory phase was not fixed and could vary depending on the vibrational landscape perceived by a stopped spider.

Fig. 4.

Influence of the presence of the lure on the decision to move. (A and B) Proportion of stops where 0, 1, 2, or 3 spiders were active in absence (n = 1,179) or presence (n = 471) of the lure. (C) Lowest intensity of the signal produced by spiders (Signal_Spiders) perceived during one timestep by an individual when stopped in presence or absence of the lure. (D) Histogram of the minimum value of the ratio of lure signal divided by spider signal perceived by stopped individuals during one timestep before resuming movement (n = 438).

Spider velocity.

The speed of spiders was obtained by dividing the distance of each move (i.e., distance between the positions of two successive stops) by the duration of the movement. We detected no difference in spider’s velocity in presence or absence of the lure (Student’s t test on log transformed data: t_760.43 = −1.38, P = 0.17). Pooling the data recorded in presence and absence of the lure, the experimental distribution of velocities was fitted with a lognormal distribution (geometric mean ×/SD = 0.17 ×/0.93, n = 1,241) (SI Appendix, Fig. S4A).

Orientation of spider movement in relation to the lure.

For each moving spider, we determined the orientation of its move with respect to the lure (i.e., the value of the angle between the starting and ending position of its move and the position of the lure). When the lure was not active, we used the coordinates of its last active position. In our experimental conditions where we rapidly alternated the presence and absence of the lure and moved the lure between two successive stimulations, we detected a marginal difference in the angular distribution of movements when the lure was present or not (Watson–Wheeler test: W = 6.834, df = 2, and P = 0.033). Although the spiders tended to move predominantly in a forward direction, the distribution of angles obtained under our experimental conditions revealed that their movements did not go in a straight line toward the prey and showed frequent reorientations (SI Appendix, Fig. S4B).

Emergence of Oscillations.

We developed a two-dimensional spatially explicit agent–based model written in R to explore the contribution of social interactions on the emergence of synchronization during collective hunting (SI Appendix, Fig. S5).

To compare simulations and observations, we analyzed 12-s portions of hunting sequences (n = 20) to characterize activity patterns in hunting groups of different sizes (mean = 30 spiders, minimum = 12, and maximum = 60). Each of the 20 sequences included episodes where the lure was active or not. For each sequence, we calculated a score of synchronization for the periods when the lure was inactive and a score for the periods when the lure was active (Materials and Methods). This score of synchronization ranges between −1 and 1 (0 = no synchronization, 1 = maximum synchronization). Next, we ran simulations where the initial positions of the spiders corresponded to the same spatial coordinates as the spiders tracked in the experiments. For each simulated sequence, the lure was active at the same timestep and at the same position as in the experiments. In our model, a spider could either be stopped (inactive) or moving (active) (SI Appendix, Fig. S5). At the beginning of each simulation, individuals were initialized in the inactive state. At each timestep (0.08 s/cycle), the velocity of each active individual was drawn randomly from the lognormal distribution fitted from the experimental data (SI Appendix, Fig. S4A). For each movement of a spider, the value of the angle of its movement relative to the position of the lure was drawn from the experimental distribution (SI Appendix, Fig. S4B). Moving spiders had a constant probability of stopping per unit time, the value of which depended on the presence or absence of the lure (Fig. 3A). When an individual just stopped, it entered a refractory state and could not become active (neither spontaneously nor in response to vibrations) as long as the amount of lure’s vibrations was lower than one-half the amount of spiders’ vibrations (Fig. 4D and SI Appendix, Fig. S5). A stopped individual that exited its refractory state became activable and could start moving either spontaneously or in response to the vibrations produced by the spiders or the lure. The probability of moving for a stopped spider in response to vibrations was given by Eqs. 4 and 5. In absence of the lure, a stopped individual must not perceive any spider vibration during at least one timestep to get out of its refractory state. When the lure was switched off, the spiders moved toward the previous position of the lure. We performed a total of 20 simulations for each of the 20 observed sequences.

At the individual level, longer stopping times were obtained in the absence than in the presence of the lure in the simulations, just as was observed in the experiments, though the difference in the simulated data were more pronounced than in the observed data (SI Appendix, Fig. S6 A and B). It is important to note that our simulations reproduced the observed patterns while no rule governing the duration of stops in the presence of vibration was explicitly implemented but only a rule governing the refractory period and the probability of responding to the lure or to other spiders.

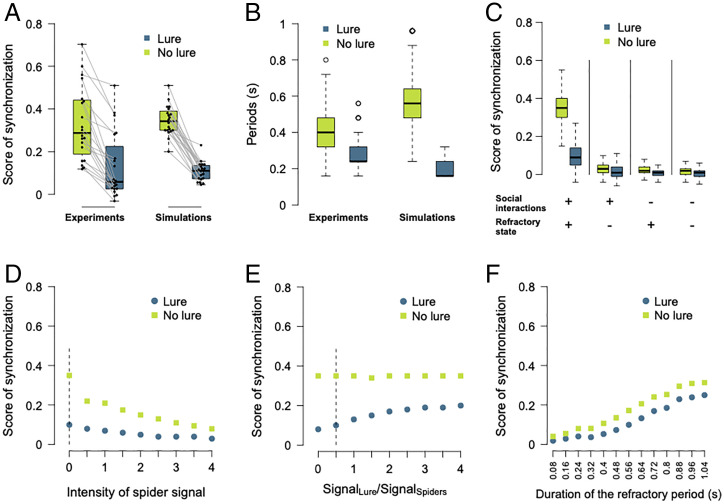
At the collective level, the intensity of synchronization was greater when the lure was inactive than active in both experiments (paired Student’s t test: t₁₉ = −7, P < 0.001) and simulations (linear mixed model [LMM]: F_1,779 = 3,864.1, P < 0.001) (Fig. 5A and SI Appendix, Figs. S1 and S7A). Similarly, we found that the periods between successive peaks of spider activity were longer in the absence than in the presence of the lure in both experiments (LMM: t_1,230.25 = 33.93, P < 0.001) and simulations (LMM: F_1,3738 = 6,753.4, P < 0.001) (Fig. 5B). Our model being validated, we then aimed to examine the contribution of the different identified rules and associated values in the emergence of synchronization. The exploration of the model showed that both the refractory state and the social amplification associated with the increase in the probability of moving as a function of the number of active individuals were necessary for the emergence of synchronized oscillations (Fig. 5C and SI Appendix, Fig. S7B). Simulations implementing a relaxation of the rule controlling the exit of the refractory state in the absence of lure and allowing spiders to resume movement even if other spiders are moving (i.e., no full silence) still exhibited a higher degree of synchronization in the absence of lure than in the presence of lure, even though the difference progressively diminished when the spider signal below which an individual can leave the refractory state was increased (Fig. 5D). Similarly, varying the ratios of the lure signal to the spider signal beyond which the spider can leave the refractory state did not abolish the greater synchrony observed in the absence of the lure. The gradual increase in the level of synchrony in the presence of the lure when the ratio was increased is explained by the fact that more spiders must be silent to allow the refractory state to end (Fig. 5E). All these results demonstrate that the rules identified are robust and do not depend strictly on the values of the parameters. Finally, we examined the impact the implementation of a refractory state of a fixed duration on the intensity of the synchronization (all other parameters values being those measured experimentally). Under this condition, similar levels of synchronization were obtained in the presence and absence of the lure, which is inconsistent with empirical observations (Fig. 5F). To reach a synchronization intensity similar to that of our experiments, a fixed refractory period of at least 1.04 s would be required, which is much higher than the average stop duration found in our experiments in presence (median: 0.16 s) or in absence of the lure (median: 0.48 s) (Fig. 5F and SI Appendix, Figs. S6A and S7C). Overall, our analysis revealed that the synchronized oscillations in hunting groups of spiders emerged spontaneously from the existence of a refractory state, the duration of which depended on the behavior of the conspecifics and was variable (SI Appendix, Fig. S6C).

Fig. 5.

Synchronization in experiments and simulations. Boxplots of (A) scores of synchronization and (B) periods between activity peaks in experimental (n = 20) and simulated hunting sequences when the lure was alternately present or absent. We simulated each of the 20 observed sequences 20 times. At the beginning of each simulation, the spatial coordinates of the individuals were identical to those of the spiders in the corresponding observed sequence. In A, each point on the boxplots of the simulated data gives the median of the scores obtained in the 20 simulations. Each gray line connects the scores of synchronization obtained in the same hunting sequence in presence and absence of the lure. In B, the values of the periods between the activity peaks were pooled for all peaks in all simulations. (C) Score of synchronization in simulations (n = 20 for each of the 20 hunting sequences) where the refractory state was implemented (+) or not (−) and when the probability of moving varied (+) or not (−) as a function of the number of active spiders (social interactions). Horizontal line in each box represents the median, and the Lower and Upper hinges indicate the first and third quartiles. Lower and higher whiskers extend to the most extreme values within 1.5 interquartile ranges from the first and third quartiles, respectively. (D) Score of synchronization in simulations for different intensities of spider signal below which an individual can leave the refractory state in absence of the lure. Dashed lines indicate the experimental values. (E) Score of synchronization in simulations for different ratios of the lure signal over the spider signal beyond which the spider can leave the refractory state. Dashed lines indicate the experimental. (F) Score of synchronization in simulations implementing a refractory period of a fixed duration. From (D–F), each point gives the median score obtained for 20 simulations of each of the 20 hunting sequences. See SI Appendix, Fig. S7 for an illustration of representative activity patterns for the different conditions tested.

Benefits of Synchronization.

It is generally accepted that synchronization of spiders hunting in groups reduces vibrational noise, thereby improving the ability of the spiders to locate the epicenter of the vibrations emitted by the prey (16, 24). A massive and rapid accumulation of spiders on the prey is all the more important as the webs of A. eximius are not sticky and the risk is high of the prey escaping before being seized by spiders (15). However, the advantages of synchronization in spider groups have not been explicitly addressed, as it is not possible, on an experimental basis, to prevent spiders from synchronizing during hunting. We therefore used our numerical model to study the extent to which coordinated alternation between phases of movement and pause is possibly beneficial to hunting spiders. We compared two extreme situations where the detection of prey position by spiders was or was not impacted by noise from moving spiders (SI Appendix, Fig. S8). Combined with the study of the influence of noise, we also explored the impact of the presence or absence of the refractory state on the movement of spiders. When noise had no impact, the spiders were able to accurately locate the prey position and move directly to it without being disturbed by the vibrations emitted by the conspecifics. This gives the best theoretical performance that can be used as a reference to assess how the presence of vibratory noise and the implementation of a refractory state influence the efficiency of the group. When noise was influential, we assumed that spider vibrations above a given threshold decreased an individual's ability to locate the epicenter of the lure's vibrations and that spiders oriented themselves randomly on the web. Based on our experimental results, we considered that the spider moved directly toward the prey when the vibration intensity of the prey was greater than or equal to one-half that of the spiders and randomly otherwise.

We explored the time taken for 50% of the group to reach the prey for each condition in groups of 10 to 100 individuals and in the presence of prey signal of increasing intensity (i.e., to mimic prey of increasing size) (Fig. 6). Whatever the size of the group, spiders reached the prey within 40 s when noise was not influential in the absence of a refractory state. Under this condition, spiders could always detect the prey and determine its position regardless of the intensity of the conspecifics’ vibrations without needing to stop (Fig. 6A). In the absence of a detrimental influence of noise, the implementation of a refractory state led to an increase in the time required for 50% of the group to reach the prey, highlighting the detrimental influence of pausing behaviors in hunting efficiency (Fig. 6B). The time to reach the prey varied with group size and prey signal strength because the duration of the refractory state, which depends on the signal-to-noise ratio, was greater when the prey signal was weak or the spiders were numerous and therefore noisy. The combination of the presence of noise and the absence of a refractory strongly impaired spiders' orientation and their ability to reach the prey, except for small group size and large prey signal (Fig. 6C). The implementation of a refractory state when noise was influential significantly improved hunting performance (Fig. 6 D and E). These simulations, which incorporate the behavioral rules observed in spiders, predict that if the number of spiders recruited to the hunt scales with prey signal strength (25, 26), then the time to reach the prey is relatively constant and hunting efficiency is maintained. In the scenario where the angle of movement was determined upon exiting the refractory state (Fig. 6D), not when the spider began to move (Fig. 6E), spiders reached the prey faster (because the amount of noise perceived by a spider changed between the time it left the refractory state and the time it started moving again). Finally, the implementation of a refractory period of fixed duration [set here at 0.16 s, which is equal to the median duration of the stops in the presence of the lure in the experiments (SI Appendix, Fig. S7)] had severe consequence on the latency to contact the prey (Fig. 6E). Overall, our results provide strong evidence that a refractory state of variable duration allows spiders to significantly minimize the negative consequences of the noise inevitably produced by moving conspecifics and thus proves to be an effective behavioral strategy for optimizing hunting success.

Fig. 6.

Prey capture efficiency. Each panel indicates the time required for 50% of the group to reach the prey as function of group size and prey signal intensity (varying $V_{0_{\mathit{lure}}}$ in Eq. 5). Spiders obeyed or not a refractory state (refractory versus no refractory) and were influenced or not by the noise (noise versus no noise) produced by the moving spiders. The lure was active during the entire simulation. Simulations implementing an absence of refractory period and noise gives the best theoretical performance (A). B and C give the latency to reach the prey when only the refractory period or only the noise was implemented. In the presence of a refractory state and noise, spiders determined the noise level and the angle of their move toward the prey either when leaving the refractory state (D) or when starting to move (E). For all conditions, the duration of the refractory state was variable and ended when the strength of the signal emitted by the prey was more than one-half the strength of the signal produced by the mobile spiders except in (F), where the duration of the refractory period was fixed and equal to 0.16 s. Spiders that did not reach their prey within 120 s received a +120 value. The dotted line indicates the value of ${\text{V}}_{0_{\text{lure}}}$ measured experimentally.

Discussion

Our study showed that the key mechanism driving the emergence of synchronization during hunting in social spiders is the decision rule for leaving the refractory state, which depends on the signal-to-noise ratio. Compared to other biological systems where synchronization involves a refractory period whose duration is relatively fixed and not influenced by external conditions (27–29), the duration of the refractory phase in social spiders is variable and modulable in response to variations in the signal-to-noise ratio. Our exploration of the model revealed that a long refractory period relative to the duration of activity would be required to generate synchronization, which is not consistent with empirical observations and was found to be detrimental to collective performance. The existence of a refractory state of a variable duration gives spiders the unique advantage of being able to behave flexibly in response to the many factors that can potentially influence the transmission of vibrational signals across the web. These factors include prey species and size, which can produce vibrations of different frequencies or intensities (23) or abiotic conditions that can alter the mechanical properties of the silk (30). For example, synchronization occurred when hunting moths but not grasshoppers possibly because the later produce more intense vibrations (15). The behavioral rules involved in collective hunting should therefore allow spiders to optimize prey capture by dynamically adapting to any changes occurring during the hunt, such as distance to prey or the number of conspecifics engaged in the hunt.

In social spiders, oscillations during collective hunting have been documented in A. eximius, but mentions of synchronized movements have also been made in two other species (13, 31). Solitary spiders could potentially constitute a largely unsuspected reservoir of collective behaviors that deserve further attention. Indeed, the vast majority of species of spiders are solitary at adulthood, but most, if not all, show a transient tolerant and gregarious phase during their early developmental stage (32). By living in groups, juvenile spiders may face the same constraints as social spiders and may have developed strategies to optimize collective capture of prey, as suggested by anecdotal reference to the existence of synchrony in groups of juveniles of the subsocial species Amaurobius ferox (33). Experimental efforts should be made to document the existence of oscillations in solitary species and to identify whether the underlying behavioral rules are universally shared across species, whether transiently or permanently social.

In other biological systems also composed of excitable entities, such as neuronal assemblies or cardiac tissue, variations in the duration of refractory periods can result in electrophysiological alterations. In the heart, for example, differences in refractoriness between atrial cells can trigger arrhythmias because proximal regions can be re-excited, when they should not, due to the lack of uniformity of excitability recovery (34, 35). In systems whose functional properties depend closely on temporal stability and uniformity of refractory periods, the duration of the refractoriness relies primarily, if not solely, on the entity itself. In other words, the exit from the refractory period depends on the time already spent in this state and not on the behavior of other entities. The stability of such systems therefore requires a strict control in the expression of the refractory period at the individual level. This differs from the contribution of the refractory period at work in the system we studied here, where the exit from the refractory state does not depend on the history of each individual (i.e., the time spent in the refractory period) but is conditioned by the immediate behavior of the whole group. Indeed, the information about the state of the system propagates throughout the network and is almost immediately accessible to all units, although the intensity of the information available varies according to individuals and their location on the web. By integrating all available information, the system components can therefore synchronize quickly without paying the cost of the long immobility delays that a fixed refractory period would impose.

In conclusion, the mechanisms unraveled in our study provide flexibility and robustness at the collective level while avoiding the risks of desynchronization inherent to the errors or inaccuracies of individual components. From an engineering point of view, our findings are relevant to design self-organizing procedures to enable the cooperation of a multitude of agents in decentralized artificial systems such as swarm robots (9, 36). The implementation of a variable refractory period, whose expression is conditional on the noise-to-signal ratio, has the potential to be an original bioinspired strategy of communication to achieve reliable, fast, and flexible coordination in noisy environments while minimizing the complexity of operations at the individual level.

Materials and Methods

Field Sites.

In the study, we observed two colonies in French Guiana, one localized along the Route de Kaw (N4° 33.370' W52° 10.842') (colony A) and one close to the dam of Petit-Saut (N5° 17.887' W53° 03.015') (colony B) between September 27 and October 3, 2019.

Vibratory Lure.

The lure performed oscillations around a position by means of alternating and controlled rotations of a stepper motor. A return cycle of the stepper motor generates one vibration. A set of potentiometers was used to modify the duration of the step (adjustable from 64 μs to 4.2 s), the latency (adjustable from 32 μs to 2.1 s), the number of steps (adjustable from 1 to 33), and the vibration duration (i.e., the number of return cycles is adjustable from 1 to 33). It was also possible to add noise to each parameter. A freshly captured dead horsefly or a leaf fragment was placed at the end of a piece of light and flexible wire that was attached to the axis of rotation of the motor. The vibrator was then activated, and the lure was put in contact with the web. We found by trial and error a combination of parameters that seemed optimal to trigger a high number of hunting sequences. Our multiple observations give us confidence that the collective movements during the approach to the epicenter of the vibrations were equivalent when spiders were presented with the lure or with a live prey. Once an appropriate set of parameters was found, it was possible to generate relatively reproducible vibrations. Upon contact with the web, the vibrator triggered the movement of the spiders in the direction of the source of vibrations. In the experiments, the lure was alternately placed in contact with the web or away from the web for short periods of time to determine the influence of spider interactions on synchronization. We stimulated different parts of the nest one after the other to recruit different groups of spiders. It was also possible to stimulate the same part of the web several times (up to five) before the spiders lost their motivation to hunt, which is clearly detectable by their lack of reaction to lure vibrations and their retreat under the leaves of the nest. After a few hours, the spiders resumed their hunting activities and reacted again to the lure.

Video Recordings.

We recorded hunts with a high-definition camcorder JVC EverioR (GZ-RX645AE) at a rate of 50 frames per second (noninterlaced). The camera was mounted on a stand and placed in front of a part of the web. Each video began by recording a scale (graduated ruler or checkered paper) placed on the web to allow us to estimate the distance between the spiders during the subsequent analysis of hunting sequences. For the analysis, we selected portions of the hunting web where the spiders could be considered to be moving in two dimensions (see Movie S1 for a representative example). Although we could not guarantee that a spider moving outside the camera's field of view did not influence the behavior of the spiders, we were confident that this effect was minimal, as we took particular care to record the majority of spiders and distant spiders have little influence on the behavior.

We analyzed four hunts to determine precisely the position of each individual involved in the hunt in order to finely quantify the rules of spider behavior (1 image/0.08 s). Three of these four hunting sequences (Sequences 1 to 3 in SI Appendix, Fig. S1) were obtained on three different days with colony B, and one sequence (Sequence 4 in SI Appendix, Fig. S1) was obtained on colony A. We assessed the individual spider response to the lure using 4 sequences obtained on colony A for 2 d and 14 hunting sequences obtained on colony B for 3 consecutive d (1 image/0.08 s). In addition, we analyzed another 20 hunting sequences (obtained using colony B on three different days) at a rate of one image every 0.16 s to quantify the intensity of synchronization in the presence and absence of the lure and to compare these values with those obtained in the numerical simulations. All hunting sequences were analyzed with eye.

Measure of Synchronization.

We estimated the degree of synchronization in experiments and simulations using the Fleiss’ Kappa coefficients (37) using the R package “irr” (38). Kappa coefficients vary between −1 and 1, with 1 indicating that the stops and moves of all individuals would be perfectly synchronized and 0 that there would be no synchronization. In each observed and simulated sequence, we calculated a score of synchronization when the lure was active and a score when the lure was inactive (i.e., two scores for each sequence). Spiders in experimental sequences whose spatial coordinates could not be determined during the entire sequence because they were temporarily hidden by a leaf, or entered or left the field of view during the sequence, were not included in the calculation of the score. In the corresponding simulated sequences (Simulations), these individuals were also not included in calculating the level of synchronization (so that the score of synchronization was based on the same number of individuals in both experiments and simulations). The scores of synchronization obtained in experimental sequences in the presence and absence of the lure were compared by a paired Student’s t test.

Peaks Detection.

We aimed at determining the time intervals (i.e., periods) between successive peaks of spider activity during hunting sequences. We used the function fpeaks from the R package “seewave” which detect peaks in time series (39). We checked by eye on a subset of sequences the accuracy of peak detection. We used a LMM (lmer function of the lme4 package in R) to compare the time intervals between consecutive peaks of activity where the lure was active or not active in experimental sequences with sequence ID as a random factor (to account for the collection of multiple values of time intervals in each sequence).

Simulations.

In a first series of simulations, we used the same initial spatial configuration of spiders and timing of lure activation than in the 20 observed hunting sequences to compare the collective patterns in the experiments and simulations. Spiders that were observed in less than one-half the duration of the experimental sequence were not included in the simulations. For each set of simulations (n = 20) for each sequence (n = 20), we determined the median score of synchronization. The simulations were performed with a timestep of 0.08 s but analyzed at a timestep of 0.16 s to match the sampling rate of the experimental sequences used to calculate the intensity of synchronization and the periods between peaks. First, we performed simulations implementing only the parameter values of behavioral rules obtained empirically to compare the level of synchronization between experiments and simulations in order to validate our model. We compared the scores of synchronization and the periods between peaks of activity obtained in the presence and absence of the lure in simulations with LMMs using sequence ID as random factor.

Then, we used the model to explore the respective contribution of the refractory state and social amplification on activity patterns. Thus, we ran simulations (n = 20 for each of the 20 hunting sequences) where the refractory state was implemented or not and where the probability of moving varied or not as a function of the number of active spiders (SI Appendix, Fig. S5). In the absence of the implementation of the refractory state, a stopped spider could resume movement without the requirement that all spiders be stationary when the lure was inactive or that the signal from the lure be greater than or equal to one-half the signal of spiders. In the absence of the implementation of social interactions, a stopped spider could begin to move either spontaneously or in response to the vibrations of the lure but was not influenced by the activity of other spiders. Next, we aimed to examine the sensitivity of the values conditioning the exit of the refractory state on the production of synchronized activity patterns. Therefore, we ran simulations where we varied either the intensities of spider signal below which an individual can leave the refractory state in absence of the lure or the ratios of the lure signal over the spider signal beyond which the spider can leave the refractory state. These simulations allowed determining the sensitivity of the values associated to behavioral refractory state to the production of synchronized activity patterns. Finally, we tested whether the implementation of a refractory state of fixed, rather than variable, duration allowed the production of synchronized activity patterns. In this condition, a spider was in a refractory state for a fixed amount of time (range tested from 0.08 to 1.04 s) and could then become active without requiring the other spiders to be immobile or the ratio of the lure signal over the spider signal to exceed a particular threshold.

In a second series of simulations, we aimed to explore how synchronized alternations of mobility and stop phases is beneficial to groups of hunting spiders in the presence of vibrational noise and prey of different size. We simulated prey of different size by varying the value of $V_{0_{\mathit{lure}}}$ (i.e., the signal intensity at epicenter of the prey’s vibrations) but using the same attenuation as found in our field experiments. We ran simulations where the spider obeyed or not a refractory state and where the noise produced by the moving spiders was detrimental or not detrimental to the spider’s orientation toward the prey (SI Appendix, Fig. S8). We also examined the impact of a fixed refractory period (using a value of 0.16 s that corresponds to the median stopping time of spiders in the presence of the lure) on hunt efficiency. For each simulation, we determined the time required for 50% of the group to reach the prey (distance < 1 cm). We simulated groups of spiders of different sizes (10 to 100 spiders) that were randomly distributed in a circle whose radius varied with group size (initial density for all conditions: one spider per 4 cm²) at a distance D = 40 cm from the lure (SI Appendix, Fig. S9). The lure was permanently active. We varied the value of $V_{0_{\mathit{lure}}}$ between 1.25 and 20.75 to simulate the production of more intense vibrations by the prey.

We used R 3.3.3 to analyze data and to implement the agent-based simulations.

Data Availability

R scripts and datasets to reproduce our analyses have been deposited at Zenodo and can be accessed at https://doi.org/10.5281/zenodo.5841117 (40).