A Statistical Review: Why Average Weighted Accuracy, not Accuracy or AUC?

Abstract

Sensitivity and specificity are key aspects in evaluating the performance of diagnostic tests. Accuracy and AUC are commonly used composite measures that incorporate sensitivity and specificity. Average Weighted Accuracy (AWA) is motivated by the need for a statistical measure of diagnostic yield that can be used to compare diagnostic tests from the medical costs and clinical impact point of view, while incorporating the relevant prevalence range of the disease as well as the relative importance of false positive versus false negative cases. We derive the variance/covariance estimators and testing procedures in four different scenarios comparing diagnostic tests: (i) one diagnostic test vs. the best random test, (ii) two diagnostic tests from two independent samples, (iii) two diagnostic tests from the same sample, and (iv) more than two diagnostic tests from different or the same samples. The impacts of sample size, prevalence, and relative importance on power and average medical costs/clinical loss are examined through simulation studies. Accuracy has the highest power while AWA provides a consistent criterion in selecting the optimal threshold and better diagnostic tests with direct clinical interpretations. The use of AWA is illustrated on a three-arm clinical trial evaluating three different assays in detecting Neisseria gonorrhoeae (NG) and Chlamydia trachomatis (CT) in the rectum and pharynx.

Introduction

Accurate and timely diagnostic information is critical for successful medical management. Traditional assessment of a diagnostic accuracy such as sensitivity, specificity, positive predicted value (PPV), negative predicted value (NPV) [1,2] focus on one aspect of the performance of diagnostic tests. Unless synthesized it is difficult to pragmatically evaluate and choose between diagnostic tests. For instance, both high sensitivity and specificity are desirable, but increases in one usually leads to decreases in the other. This creates challenges in choosing the optimal thresholds for biomarkers. When deciding between different tests, there is often no winner that is superior in all aspects, which again creates a challenge for diagnostic selection. We illustrate the difficulty in evaluating diagnostic tests using a hypothetical example of two diagnostic tests: one with a higher sensitivity (Diagnostic Test A: Sensitivity=0.90, specificity=0.60) and the other with a higher specificity (Diagnostic Test B: Sensitivity=0.70, specificity=0.65). Which diagnostic should be selected to optimize clinical decision-making? Clearly, the answer depends on the purpose of the tests and the clinical context including the relative importance of sensitivity and specificity, and the prevalence of disease. Global assessment that accounts for sensitivity and specificity, disease prevalence, and the relative importance of false positive and negative errors is needed to inform decision-making.

Clinically, composite statistical measures that integrate the two pieces of information and provide a global assessment that non-composed sensitivity and specificity analyses cannot provide are desirable in evaluating performances of diagnostic tests and choosing appropriate thresholds. Area under the receiver operating characteristics curve (AUC) [3] incorporates sensitivity and specificity by integrating true positive rates over the possible range of false positive rate values when the threshold between positive and negative diagnostic results moves from minimum to maximum. However, the prevalence of the disease status dictates the absolute numbers in the population affected by false negative rate (i.e. 1-sensitivity) or false positive rate (i.e. 1-specificity), respectively, which are key in evaluating the performance of a diagnostic test. For example, when prevalence is high, a good diagnostic procedure would place more emphasis on sensitivity rather than specificity. But in cases of rare infectious diseases, greater emphases would be switched to specificity. Furthermore, prevalence often varies across different patient populations and across studies. But AUC does not incorporate prevalence information, hence it is invariant to different prevalence values or distributions. That is, researchers making selections based on the AUC are ignoring potentially valuable prevalence information.

Accuracy, the percent of correct diagnosis in the pooled sample of infections and uninfected controls, is another composite measure incorporating both sensitivity and specificity, which further reflects prevalence [4,5]. In the example above, the accuracy values for the two hypothetical diagnostic tests A and B in discriminating an infection with prevalence of 20% are, respectively,

$$\begin{gathered} {\mathit{\text{Accuracy}}}_A=\mathit{\text{Prevalence}}\cdot \mathit{\text{Sensitvity}}+\left(1-\mathit{\text{Prevalence}}\right)\cdot \mathit{\text{Specificity}} \\ =0.2\cdot 0.9+0.8\cdot 0.6=0.66; \end{gathered}$$

$$\begin{gathered} {\mathit{\text{Accuracy}}}_B=\mathit{\text{Prevalence}}\cdot \mathit{\text{Sensitvity}}+\left(1-\mathit{\text{Prevalence}}\right)\cdot \mathit{\text{Specificity}} \\ =0.2\cdot 0.7+0.8\cdot 0.65=\mathrm{0.66.} \end{gathered}$$

This example shows that different sensitivity and specificity combinations may produce the same accuracy. However, do equal accuracy values infer equivalent clinical performances? Not necessarily because the accuracy measurement assumes that sensitivity and specific are equally important. Therefore, accuracy does not reflect the difference in medical costs and quality of life associated with a false negative versus those with a false positive. It is important for pragmatic assessment to reflect the relative importance between sensitivity and specificity, since the impacts of mistakenly identifying a non-infected individual and missing a truly infected case could be dramatically different. Take bacterial infection as an example, false positive error could result in unnecessary prescription of antibiotic while false negative error could result in wrongly withholding the necessary antibiotic. Patients and clinicians weigh these two types of errors quite differently according to individual-specific situations.

Recently, Evans et al (2016) [6,7] proposed the average weighted accuracy (AWA) method to incorporate the relative importance of diagnostic errors as well as a plausible range of the prevalence of disease, to produce a pragmatic evaluation of diagnostic yield. AWA can be used to choose the optimal threshold for biomarkers, evaluate the global utility of a diagnostic test and compare test alternatives. This manuscript evaluates the three composite measures, AUC, accuracy and AWA, studying the pros and cons of each measure and guiding the choice of appropriate statistical measures in evaluating diagnostic tests. Section 2 provides an overview of the concepts, formulation and hypothesis testing procedures using AUC, accuracy and AWA, respectively. Typical clinical scenarios are simulated and the performances of the three statistics are compared in Section 3. We use a three-arm cross-sectional diagnostic study to illustrate the applications of AWA in clinical studies in Section 4, followed by extra discussion in Section 5.

Methods

We lay out the mathematical definition, variance derivation and hypothesis testing procedure of AWA in detail. We summarize the properties of the accuracy and AUC statistics, where the hypothesis testing procedures are similar except the variance and covariance formula.

Sensitivity and specificity are denoted by Se and Sp, respectively.

$$Se\equiv P\mathit{\text{(diagnosis positive}}|\mathit{\text{ infection positive}}),$$

$$Sp\equiv P\mathit{\text{(diagnosis negative}}|\mathit{\text{infection negative}}).$$

We estimate Se and Sp by the positive percentage agreement and negative percentage agreement in the sample, denoted by $\widehat{Se}$ and $\widehat{Sp}$, respectively. Where $\widehat{ Se}=\sum _{i=1}^{n_{+}}\frac{I({Dx}_i=1)}{n_{+}}$ and $\widehat{ Sp}=\sum _{i=1}^{n_{-}}\frac{I({Dx}_i=0)}{n_{-}}$, that is, the observed percentage of positive diagnostic (i.e. ${Dx}_i=1$) results among the truly infected samples and the observed percentage of negative diagnostic (i.e. $D{x}_i=0$) results among the true non-infection samples, respectively. Here n₊ and n₋ represent the number of true infections and non-infections in the sample, respectively; and ${Dx}_i$ is the diagnostic test result on the ith subject (1 for positive and 0 for negative).

Let r be the relative importance of false positive versus false negative. For example, when r=0.5, it is assumed that the costs and damages resulting from reporting two false positive cases are equivalent to those from missing one true positive case. Let p denote the percentage of subjects without the infection under study in the population, that is, one minus the prevalence of the target infection. The weighted accuracy is defined as follows

$$\widehat{WA}=\frac{\text{rp}\widehat{Sp}+(1-\text{p})\widehat{Se}}{rp+1-p}.$$

Accuracy can be viewed as a special case of WA where the relative importance is one, which is usually not true in most clinical situations. If we integrate the percentages of non-disease cases over the plausible and relevant range of the infection, say [a,b], we get the average weighted accuracy (AWA), estimated by

$$\widehat{AWA}=c_{se}\widehat{Se}+c_{sp}\widehat{Sp},$$

$$c_{\text{se}}=-\frac{1}{\text{r}-1}+\frac{r}{{\left(r-1\right)}^2\left(b-a\right)}ln\left(\frac{1+b\left(r-1\right)}{1+a\left(r-1\right)}\right),$$

$$c_{sp}=\frac{r}{r-1}-\frac{r}{{\left(r-1\right)}^2\left(b-a\right)}ln\left(\frac{1+b\left(r-1\right)}{1+a\left(r-1\right)}\right).$$

The standard error of $\widehat{AWA}$ is calculated as

$$SE\left(\widehat{AWA}\right)=\sqrt{\frac{{c_{se}}^2\widehat{Se}(1-\widehat{Se})}{n_{+}}+\frac{{c_{sp}}^2\widehat{Sp}(1-\widehat{Sp})}{n_{-}}.}$$

(1). Compare a diagnostic test vs. the best random test

In the case of a random test,

$$Se=P\mathit{\text{(test positive}}|\mathit{\text{disease positive}})=P\left(\mathit{\text{test positive}}\right)$$

$$Sp=P\mathit{\text{(test negative}}|\mathit{\text{disease negative}})=P\left(\mathit{\text{test negative}}\right).$$

Let the probability of the diagnostic test giving a positive result be p_r,. The AWA corresponding to a random test is

$${AWA}_{RT}=c_{se}{p}_r+c_{sp}\left(1-p_r\right).$$

The best random test (BRT) refers to the random test with the choice of p_r maximizing AWA_RT

$${AWA}_{BRT}={max}_{p_r\in \left[\mathrm{0,1}\right]}\left\{{AWA}_{RT}\right\}=\left\{\begin{array}{c}{c}_{se}, c_{sp}<c_{se}\\ c_{sp}, c_{sp}\ge c_{se}\end{array}\right.$$

The performance of a diagnostic test under evaluation is first compared to that of the BRT because only diagnostic tests significantly superior than the free BRT are worth further pursuing. In the comparison of a diagnostic (Dx) test versus BRT in terms of AWA, the test statistic goes as follows

$$\frac{{\widehat{AWA}}_{Dx}-{AWA}_{BRT}}{SE\left({\widehat{AWA}}_{Dx}\right)}=\frac{(c_{se}{\widehat{Se}}_{Dx}+c_{sp}{\widehat{Sp}}_{Dx}-{AWA}_{BRT})}{\sqrt{\frac{{c_{se}}^2{\widehat{Se}}_{Dx}(1-{\widehat{Se}}_{Dx})}{n_{+}}+\frac{{c_{sp}}^2{\widehat{Sp}}_{Dx}(1-{\widehat{Sp}}_{Dx})}{n_{-}}}},$$

which follows a standard normal distribution under the null.

(2). Compare two diagnostic tests on two independent samples

The difference between two AWA estimates is

$${\widehat{AWA}}_1-{\widehat{AWA}}_2=\left(c_{se}{\widehat{Se}}_1+c_{sp}{\widehat{Sp}}_1\right)-\left(c_{se}{\widehat{Se}}_2+c_{sp}{\widehat{Sp}}_2\right).$$

Here subscripts 1 and 2 denote the two diagnostic tests, respectively. The standard error of the difference goes as follows

$$SE\left({\widehat{AWA}}_1-{\widehat{AWA}}_2\right)=\sqrt{\frac{{c_{se}}^2{\widehat{Se}}_1(1-{\widehat{Se}}_1)}{n_{1+}}+\frac{{c_{sp}}^2{\widehat{Sp}}_1(1-{\widehat{Sp}}_1)}{n_{1-}}+\frac{{c_{se}}^2{\widehat{Se}}_2(1-{\widehat{Se}}_2)}{n_{2+}}+\frac{{c_{sp}}^2{\widehat{Sp}}_2(1-{\widehat{Sp}}_2)}{n_{2-}},}$$

where n₁ and n₂ refer to the two independent samples for maker 1 and marker 2, respectively. Under H₀, the test statistics is

$$\frac{{\widehat{AWA}}_1-{\widehat{AWA}}_2}{SE\left({\widehat{AWA}}_1-{\widehat{AWA}}_2\right)}~N\left(\mathrm{0,1}\right).$$

(3). Compare two diagnostic tests on the same sample

The numerator of the test statistic measuring the difference between two AWA values is the same as the numerator in the case of two tests on two samples

$${\widehat{AWA}}_1-{\widehat{AWA}}_2=\left(c_{se}{\widehat{Se}}_1+c_{sp}{\widehat{Sp}}_1\right)-\left(c_{se}{\widehat{Se}}_2+c_{sp}{\widehat{Sp}}_2\right).$$

But the variance of the difference estimator from the same sample needs to incorporate the covariance between $({\widehat{ Se}}_1,{\widehat{ Se}}_2)$ and the covariance between $({\widehat{ Sp}}_1,{\widehat{ Sp}}_2)$.

$$Var\left({\widehat{AWA}}_1-{\widehat{AWA}}_2\right)={c_{se}}^2\left\{{\widehat{Se}}_1\left(1-{\widehat{Se}}_1\right)/n_{+}+{\widehat{Se}}_2\left(1-{\widehat{Se}}_2\right)/n_{+}-2cov({\widehat{Se}}_1,{\widehat{Se}}_2)\right\}+{c_{sp}}^2\left\{{\widehat{Sp}}_1\left(1-{\widehat{Sp}}_1\right)/n_{-}+{\widehat{Sp}}_2\left(1-{\widehat{Sp}}_2\right)/n_{-}-2cov({\widehat{Sp}}_1,{\widehat{Sp}}_2)\right\}.$$

Here the covariances are estimated from the observed percentage of agreement between the two diagnostic tests Dx₁ and Dx₂ in the sample

$$\mathit{\text{cov}}\left({\widehat{Se}}_1,{\widehat{Se}}_2\right)\equiv E\left({\widehat{Se}}_1{\widehat{Se}}_2\right)-E\left({\widehat{Se}}_1)E({\widehat{Se}}_2\right)=\left(\sum _{i=1}^{n_{+}}\frac{I\left(D{x}_{1i}=1\right)I\left(D{x}_{2i}=1\right)}{n_{+}}-{\widehat{Se}}_1{\widehat{Se}}_2\right)/n_{+},$$

$$\mathit{\text{cov}}\left({\widehat{Sp}}_1,{\widehat{Sp}}_2\right)\equiv E\left({\widehat{Sp}}_1{\widehat{Sp}}_2\right)-E\left({\widehat{Sp}}_1)E({\widehat{Sp}}_2\right)=\left(\sum _{i=1}^{n_{-}}\frac{I\left(D{x}_{1i}=0\right)I\left(D{x}_{2i}=0\right)}{n_{-}}-{\widehat{Sp}}_1{\widehat{Sp}}_2\right)/n_{-}.$$

Where ${Dx}_{1i}=1$ and 0 represent positive and negative diagnosis from diagnostic test one on subject i, and ${Dx}_{2i}=1$ or 0 represents the diagnostic result from test two.

(4). Test the equality of AWAs from multiple (K) diagnostic tests

The variance and covariance estimators in subsection (2) and (3) can also be used to construct the covariance matrix of $\widehat{\underset{\_}{AWA}}=\left(\begin{array}{ccc}{\widehat{AWA}}_1,& \cdots ,& {\widehat{AWA}}_K\end{array}\right)$, denoted by ∑. Then a linear combination $L*\widehat{\underset{\_}{AWA}}$ can be used to test H₀: AWA₁ = ⋯ = AWA_K. Here * denotes matrix multiplication; and L is a (K − 1) × K matrix with one $1-\frac{1}{K}$ value in each row and $-\frac{1}{K}$ otherwise, furthermore all $1-\frac{1}{K}$ values locate in different columns. The variance-covariance matrix of $L*\widehat{\underset{\_}{AWA}}$ is L * Σ * L`, then $\left(L*\underset{\_}{\widehat{AWA}}\right)`*{\left(L*\Sigma *L`\right)}^{-1}*\left(L*\underset{\_}{\widehat{AWA}}\right)$ follows a χ² distribution with degree of freedom K-1 under the null hypothesis of K equal AWAs.

(5). Variance and covariance of accuracy

Accuracy is the weighted average of sensitivity and specificity where the weights are the proportions of population with and without the infection of interests

$$\widehat{\mathit{\text{Accuracy}}}=p\widehat{Se}+\left(1-p\right)\widehat{Sp}.$$

The standard error of estimated accuracy for a single diagnostic marker is

$$SE\left(\widehat{\mathit{\text{Accuracy}}}\right)=\sqrt{\frac{p^2\widehat{Se}\left(1-\widehat{Se}\right)}{n_{+}}+\frac{{\left(1-p\right)}^2\widehat{Sp}\left(1-\widehat{Sp}\right)}{n_{-}}.}$$

The standard deviation of the difference between two accuracy measures for two diagnostic markers estimated from two independent samples is

$$SE\left({\widehat{\mathit{\text{Accuracy}}}}_1-{\widehat{\mathit{\text{Accuracy}}}}_2\right)=\sqrt{\frac{p^2{\widehat{Se}}_1\left(1-{\widehat{Se}}_1\right)}{n_{1+}}+\frac{{\left(1-p\right)}^2{\widehat{Sp}}_1\left(1-{\widehat{Sp}}_1\right)}{n_{1-}}+\frac{p^2{\widehat{Se}}_2\left(1-{\widehat{Se}}_2\right)}{n_{2+}}+\frac{{\left(1-p\right)}^2{\widehat{Sp}}_2\left(1-{\widehat{Sp}}_2\right)}{n_{2-}}.}$$

Furthermore, the variance of the difference between two correlated accuracy measures for two diagnostic markers estimated from the same sample is

$$\mathit{\text{Var}}\left({\widehat{\mathit{\text{Accuracy}}}}_1-{\widehat{\mathit{\text{Accuracy}}}}_2\right)=p^2\left\{{\widehat{Se}}_1\left(1-{\widehat{Se}}_1\right)/n_{+}+{\widehat{Se}}_2\left(1-{\widehat{Se}}_2\right)/n_{+}-2cov\left({\widehat{Se}}_1,{\widehat{Se}}_2\right)\right\}+{\left(1-p\right)}^2\left\{{\widehat{Sp}}_1\left(1-{\widehat{Sp}}_1\right)/n_{-}+{\widehat{Sp}}_2\left(1-{\widehat{Sp}}_2\right)/n_{-}-2cov\left({\widehat{Sp}}_1,{\widehat{Sp}}_2\right)\right\}$$

The testing procedures using the accuracy statistic under the four scenarios in subsections (1) to (4) use similar formula as those derived for AWA except that we plug in the variance and covariance of accuracy instead of those of AWA.

(6). Variance and covariance of AUC

AUC is usually estimated by the percent of concordant pairs, that is, pairs whose case has a higher marker value than the control, among all the possible pairs made of one infected subject and one uninfected subject. Let i=1,…, n₊ be the sample of participants with the infection condition and j=1,…, n₋ be the sample of participants without the infection. The

$$\widehat{AUC}=\frac{1}{n_{+}{n}_{-}}{\sum }_{j=1}^{n_{-}}{\sum }_{i=1}^{n_{+}}\psi \left(X_i,Y_j\right),\text{where }\psi \left(X,Y\right)=\{\begin{array}{cc}1& X>Y\\ 0.5& X=Y\\ 0& X<Y\end{array}.$$

Let $\theta =E\left(\widehat{AUC}\right)=\text{Pr}\left(X>Y\right)+0.5\text{ Pr}\left(X=Y\right)$. We employ the variance and covariance formula in DeLong, DeLong & Pearson (1988) [8],

$$\mathit{\text{Var}}\left(\widehat{AUC}\right)=\frac{\left(n_{+}-1\right)\left\{E\left[\psi \left(X_i,Y_j\right)\psi \left(X_i,Y_k\right)\right]-{\theta }^2\right\}+\left(n_{-}-1\right)\left\{E\left[\psi \left(X_i,Y_j\right)\psi \left(X_k,Y_j\right)\right]-{\theta }^2\right\}+\left\{E\left[\psi \left(X_i,Y_j\right)\psi \left(X_i,Y_j\right)\right]-{\theta }^2\right\}}{n_{+}{n}_{-}}$$

$$\mathit{\text{COV}}\left({\widehat{AUC}}^A,{\widehat{AUC}}^B\right)=\frac{\left(n_{+}-1\right)\left\{E\left[\psi \left(X_i^A,Y_j^A\right)\psi \left(X_i^B,Y_k^B\right)\right]-{\theta }^A{\theta }^B\right\}+\left(n_{-}-1\right)\left\{E\left[\psi \left(X_i^A,Y_j^A\right)\psi \left(X_k^B,Y_j^B\right)\right]-{\theta }^A{\theta }^B\right\}+\left\{E\left[\psi \left(X_i^A,Y_j^A\right)\psi \left(X_i^B,Y_j^B\right)\right]-{\theta }^A{\theta }^B\right\}}{n_{+}{n}_{-}}$$

Here the subscripts i, j and k indicate independent and different subjects in the samples; the superscripts A and B indicate the two diagnostic tests under comparison; and the test results X and Y are 1 for positive and 0 for negative.

Simulation Design

A simulation study was conducted to evaluate the performance of AWA under the first three scenarios in subsections (1)–(3). The biomarker value of the patients with and without the disease of interests are assumed to follow bivariate normal distributions with mean (μ_A, μ₀) and covariance $\Sigma =\left(\begin{array}{cc}{\sigma }_A^2& {{\rho }_A\sigma }_A^2\\ {\rho }_A{\sigma }_A^2& {\sigma }_A^2\end{array}\right)$. Without loss of generality, we center and standardize the data so that μ₀=0 and σ_A = 1. Similarly, the values of marker B among the infected and uninfected populations are distributed as bivariate normal with mean (μ_B, 0) and covariance $\Sigma =\left(\begin{array}{cc}{\sigma }_B^2& {\rho }_B{\sigma }_B^2\\ {\rho }_B{\sigma }_B^2& {\sigma }_B^2\end{array}\right)$. Here we assume the variances of the same marker in the diseased and non-diseased populations are the same to single out the effects of distance in means and the effects of the sizes of variances. The conclusions can be borrowed into cases where the diseased and non-diseased populations have different variances. Two sets of optimal thresholds are calculated by maximizing either AWA or accuracy, respectively, under each parameter setting. The sensitivity and specificity are calculated using the survival probabilities and the cumulative distribution probabilities of the underlying distributions at the selected optimal thresholds. Similarly, AWA, accuracy and their variances and covariances are calculated at the two sets of optimal thresholds. The AUC and the corresponding variances and covariances are calculated using the joint probability of a pair of marker values from the infected population are both larger or both smaller than the markers’ values from a random uninfected subject, which are obtained by two-dimensional numeric integration over the joint probability density function of the bivariate normal distributions. In addition, the ROC curve, which the AUC is based on, is plotted to illustrate the diagnostic ability of the binary classifier as its discrimination threshold is varied.

Three scenarios corresponding to subsections (1), (2) and (3) in the Methods section are examined – a diagnostic test where the biomarker values in the diseased population have mean 0.5 and variance 1 vs. best random test, two diagnostic tests from two independent samples, and two diagnostic tests from the same sample, whose biomarkers are distributed as N(0.6, 1) and N(0.5, 0.5), respectively, in the infected populations. Two different sample sizes 500 and 1000, low (5%, 10%) and high (10%, 30%) prevalence ranges, as well as two common relative importance levels 0.1 and 0.25 are tested. The powers from the three statistics (AWA, accuracy and AUC) are compared. Furthermore, we put the medical costs and clinical loss associated with one false negative case to be one and the medical costs and clinical loss associated with one false positive case be r. The relationship between total medical costs and clinical loss versus AWA, accuracy and AUC are further compared side by side.

Simulation Result

In Figure 1, we plot the relationships between average medical costs and the three statistics (AWA/Accuracy/AUC) when the threshold of the biomarker changes from minimum to maximum. Four different scenarios examining high and low prevalence as well as high and low relative importance are plotted. In all scenarios, AWA is reversely related to medical cost. And the value of AUC is invariant to the choice of thresholds which are expected to incur quite different medical costs. The pattern of accuracy versus medical cost varies depending on the prevalence and relative importance of the diagnostic errors. For low prevalence and high relative importance, accuracy goes down while the medical cost goes up; in cases with high prevalence and low relative importance, accuracy goes up together with medical cost. For the other two scenarios, minimum medical costs occur in the middle of the range of possible accuracy values, that is, neither the highest nor the lowest accuracy. If clinicians aim for an “optimal” threshold using the criterion of minimum medical costs, AUC provides no information about medical costs, accuracy provides confusing information about medical costs because the relationship between accuracy and medical costs could be either positive or negative. AWA can be used as a reliable criterion to choose optimal threshold because the threshold that maximizes AWA also minimizes expected medical costs at the same time. When the importance of the false positive and false negative are equivalent (relative importance r=1), the AWA is the same as accuracy, the two lines overlap. (Figure 1, r=1)

Figure 1.

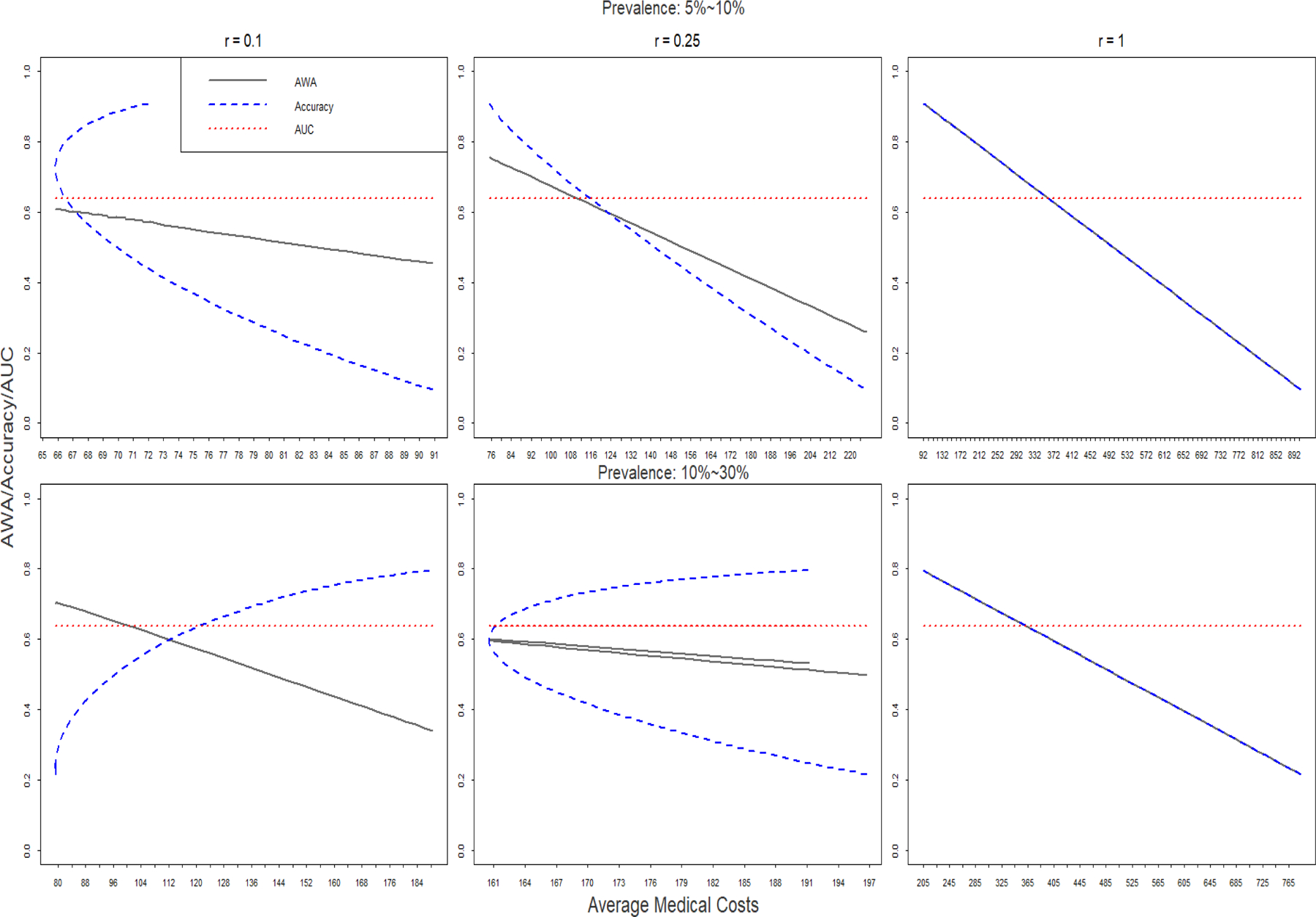
Relationships between AWA, Accuracy and AUC versus medical costs.

Combinations of specificity and sensitivity are determined by placing cut-offs on biomarker distribution under null and alternative respectively. Regardless of the choice of optimal relative importance (r) and prevalence (p), the corresponding ROC remains the same. (Figure 2)

Figure 2.

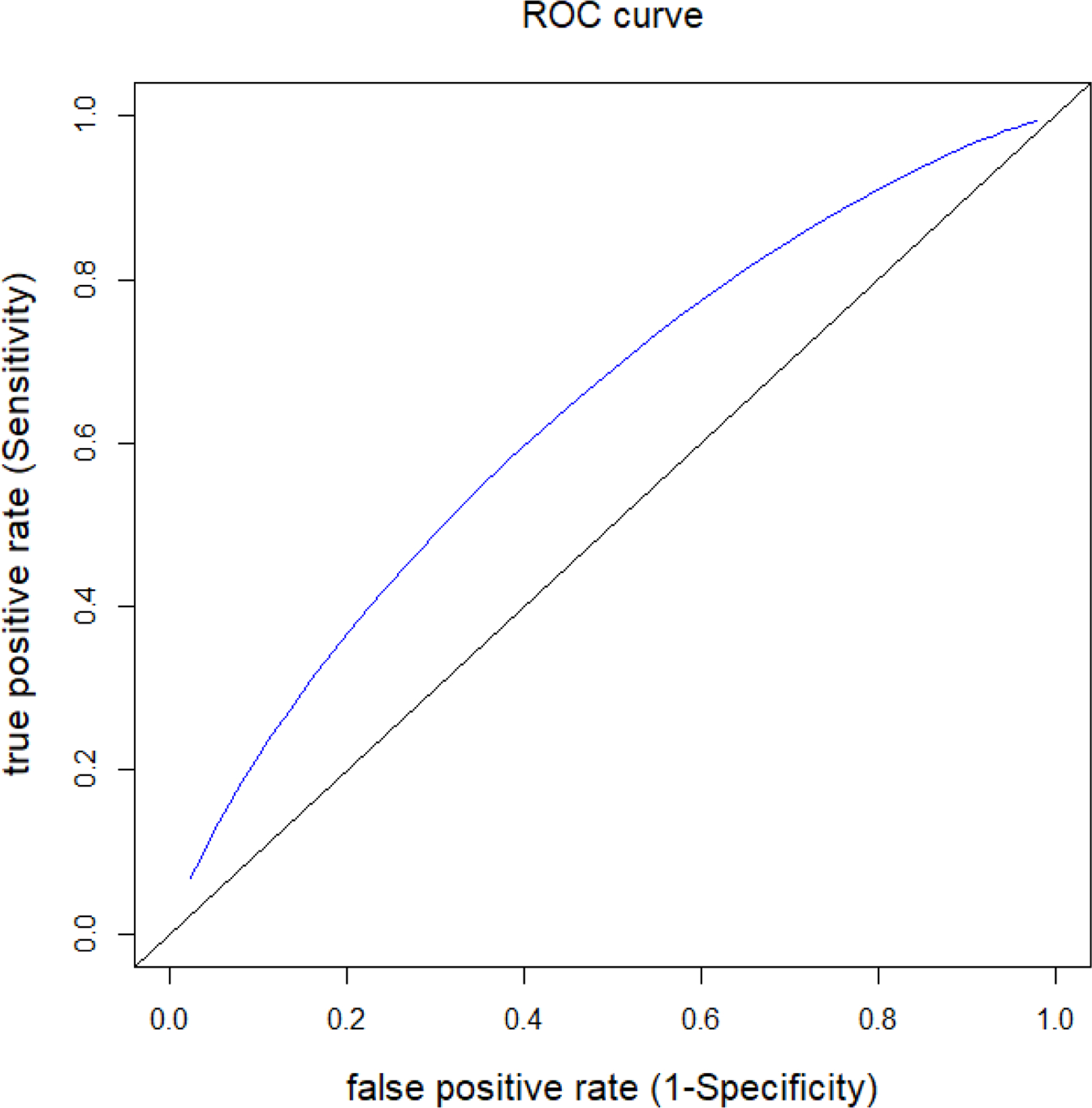
ROC for evaluating true positive/false positive value of the diagnostic test.

The results of the simulations from the three scenarios in subsection (1)–(3) of the Methods section are listed in Tables 1–3, respectively.

Table 1.

Power and medical costs using AWA, Accuracy or AUC in comparing a diagnostic test (Dx) and the best random test (BRT). The biomarker values from the diagnostic test in the infected population are distributed as N(μ₁=0.5,σ₁=1).

Method	Sample Size (N)	Relative Importance (r)	Prevalence Range (p)	Prevalence (median)	Biomarker (μ1)	Threshold (cut-off)	Sensitivity (Dx)	Specificity (Dx)	AWA, Accuracy or AUC (Dx)	SD (Dx)	Sensitivity (BRT)	Specificity (BRT)	AWA, Accuracy or AUC (BRT)	Power	Medical Cost (Dx)	Medical Cost (BRT)
AWA	500	0.25	5%−10%	0.075	0.5	2.517	0.022	0.994	0.757	0.0064	0	1	0.756	0.0651	37.36875	37.5
	500	0.25	5%−10%	0.075	1	1.633	0.263	0.949	0.782	0.0192	0	1	0.756	0.375	33.534375	37.5
	500	0.25	10%−30%	0.2	0.5	0.33	0.568	0.629	0.599	0.0272	0	1	0.51	0.948	80.3	100
	500	0.25	10%−30%	0.2	1	0.54	0.677	0.705	0.692	0.0257	0	1	0.51	1	61.8	100
	500	0.1	5%−10%	0.075	0.5	0.702	0.42	0.759	0.608	0.0374	0	1	0.608	0.4	32.89625	37.5
	500	0.1	5%−10%	0.075	1	0.726	0.608	0.766	0.696	0.037	0	1	0.556	0.983	25.5225	37.5
	500	0.1	10%−30%	0.2	0.5	−1.442	0.974	0.075	0.704	0.0118	1	0	0.7	0.0982	39.6	40
	500	0.1	10%−30%	0.2	1	−0.346	0.911	0.365	0.747	0.0212	1	0	0.7	0.718	34.3	40
	1000	0.25	5%−10%	0.075	0.5	2.517	0.022	0.994	0.757	0.0045	0	1	0.756	0.0723	74.7375	75
	1000	0.25	5%−10%	0.075	1	1.633	0.263	0.949	0.782	0.0135	0	1	0.756	0.591	67.06875	75
	1000	0.25	10%−30%	0.2	0.5	0.33	0.568	0.629	0.599	0.0192	0	1	0.51	0.998	160.6	200
	1000	0.25	10%−30%	0.2	1	0.54	0.677	0.705	0.692	0.0182	0	1	0.51	1	123.6	200
	1000	0.1	5%−10%	0.075	0.5	0.702	0.42	0.759	0.608	0.0265	0	1	0.556	0.627	65.7925	75
	1000	0.1	5%−10%	0.075	1	0.726	0.608	0.766	0.696	0.0262	0	1	0.556	1	51.045	75
	1000	0.1	10%−30%	0.2	0.5	−1.442	0.974	0.075	0.704	0.0084	1	0	0.7	0.126	79.2	80
	1000	0.1	10%−30%	0.2	1	−0.346	0.911	0.365	0.747	0.015	1	0	0.7	0.933	68.6	80
Accuracy	500	0.25	5%−10%	0.075	0.5	3	0.0062	0.999	0.924	0.0003	1	0	0.075	1	36.760625	115.625
	500	0.25	5%−10%	0.075	1	3	0.0228	0.999	0.925	0.0024	1	0	0.075	1	37.383125	115.625
	500	0.25	10%−30%	0.2	0.5	3	0.0062	0.999	0.8	0.0022	1	0	0.2	1	99.48	100
	500	0.25	10%−30%	0.2	1	1.886	0.1877	0.97	0.814	0.0103	1	0	0.2	1	84.23	100
	500	0.1	5%−10%	0.075	0.5	3	0.006	0.999	0.924	0.0018	1	0	0.075	1	37.32125	46.25
	500	0.1	5%−10%	0.075	1	3	0.0228	0.999	0.925	0.0024	1	0	0.075	1	36.69125	46.25
	500	0.1	10%−30%	0.2	0.5	3	0.0062	0.999	0.8	0.0022	1	0	0.2	1	99.42	40
	500	0.1	10%−30%	0.2	1	1.886	0.1877	0.97	0.814	0.0103	1	0	0.2	1	82.43	40
	1000	0.25	5%−10%	0.075	0.5	3	0.0062	0.999	0.924	0.0013	1	0	0.075	1	74.76625	231.25
	1000	0.25	5%−10%	0.075	1	3	0.0228	0.999	0.925	0.0017	1	0	0.075	1	73.52125	231.25
	1000	0.25	10%−30%	0.2	0.5	3	0.0062	0.999	0.8	0.0015	1	0	0.2	1	198.96	200
	1000	0.25	10%−30%	0.2	1	1.886	0.1877	0.97	0.814	0.0073	1	0	0.2	1	168.46	200
	1000	0.1	5%−10%	0.075	0.5	3	0.0228	0.999	0.925	0.0017	1	0	0.0017	1	73.3825	92.5
	1000	0.1	5%−10%	0.075	1	3	0.0228	0.999	0.924	0.0017	1	0	0.0017	1	73.3825	92.5
	1000	0.1	10%−30%	0.2	0.5	3	0.0062	0.999	0.8	0.0015	1	0	0.2	1	198.84	80
	1000	0.1	10%−30%	0.2	1	1.886	0.1877	0.97	0.814	0.0073	1	0	0.2	1	164.86	80
AUC	500	0.25	5%−10%	0.075	0.5				0.638	0.0466			0.5	0.906
	500	0.25	5%−10%	0.075	1				0.76	0.0401			0.5	1
	500	0.25	10%−30%	0.2	0.5				0.638	0.0307			0.5	0.998
	500	0.25	10%−30%	0.2	1				0.76	0.0264			0.5	1
	500	0.1	5%−10%	0.075	0.5				0.638	0.0466			0.5	0.906
	500	0.1	5%−10%	0.075	1				0.76	0.0401			0.5	1
	500	0.1	10%−30%	0.2	0.5				0.638	0.0307			0.5	0.998
	500	0.1	10%−30%	0.2	1				0.76	0.0264			0.5	1
	1000	0.25	5%−10%	0.075	0.5				0.638	0.033			0.5	0.994
	1000	0.25	5%−10%	0.075	1				0.76	0.0284			0.5	1
	1000	0.25	10%−30%	0.2	0.5				0.638	0.0217			0.5	1
	1000	0.25	10%−30%	0.2	1				0.76	0.0187			0.5	1
	1000	0.1	5%−10%	0.075	0.5				0.638	0.033			0.5	0.994
	1000	0.1	5%−10%	0.075	1				0.76	0.0284			0.5	1
	1000	0.1	10%−30%	0.2	0.5				0.638	0.0217			0.5	1
	1000	0.1	10%−30%	0.2	1				0.76	0.0187			0.5	1

Table 3.

Power and medical costs using AWA, Accuracy or AUC in comparing two diagnostic tests from the same sample. The biomarker values from the two diagnostic tests in the infected population are distributed as N(μ₁=0.6,σ₁=1) and N(μ₂=0.5,σ₂=0.5), respectively.

Method	Sample Size (N)	Relative Importance (r)	Prevalence Range (p)	Prevalence rate	Threshold (Dx1)	Sensitivity (Dx1)	Specificity (Dx1)	AWA, Accuracy or AUC (Dx1)	Threshold (Dx2)	Sensitivity (Dx2)	Specificity (Dx2)	AWA, Accuracy or AUC (Dx2)	SD (Dx1-Dx2)	Power	Medical Cost (Dx1)	Medical Cost (Dx2)
AWA	500	0.25	5%−10%	0.075	2.189	0.056	0.986	0.759	0.817	0.263	0.949	0.782	0.0197	0.309	37.01875	33.534375
	500	0.25	10%−30%	0.200	0.366	0.592	0.643	0.618	0.27	0.677	0.705	0.692	0.0307	0.773	76.5	61.8
	500	0.1	5%−10%	0.075	0.677	0.469	0.751	0.626	0.363	0.608	0.766	0.696	0.0436	0.485	31.42875	25.5225
	500	0.1	10%−30%	0.200	−1.11	0.956	0.134	0.709	−0.173	0.911	0.365	0.747	0.0232	0.489	39.04	34.3
	1000	0.25	5%−10%	0.075	2.189	0.056	0.986	0.759	0.817	0.263	0.949	0.782	0.0139	0.491	74.0375	67.06875
	1000	0.25	10%−30%	0.200	0.366	0.592	0.643	0.618	0.27	0.677	0.705	0.692	0.0217	0.959	153	123.6
	1000	0.1	5%−10%	0.075	0.6	0.5	0.726	0.626	0.363	0.608	0.766	0.696	0.0308	0.738	62.845	51.045
	1000	0.1	10%−30%	0.200	−1.11	0.956	0.134	0.709	−0.173	0.911	0.365	0.747	0.0164	0.74	78.08	68.6
Accuracy	500	0.25	5%−10%	0.075	3	0.008	0.999	0.924	1.506	0.022	0.999	0.925	0.0029	0.102	37.315625	36.790625
	500	0.25	10%−30%	0.200	2.61	0.022	0.995	0.801	0.943	0.188	0.97	0.814	0.0105	0.342	98.3	84.2
	500	0.1	5%−10%	0.075	3	0.008	0.999	0.924	1.506	0.022	0.999	0.925	0.0029	0.102	37.24625	36.72125
	500	0.1	10%−30%	0.200	2.61	0.022	0.995	0.801	0.943	0.188	0.97	0.814	0.0105	0.342	98	82.4
	1000	0.25	5%−10%	0.075	3	0.008	0.999	0.924	1.506	0.022	0.999	0.925	0.0021	0.132	74.63125	73.58125
	1000	0.25	10%−30%	0.200	2.61	0.022	0.995	0.801	0.943	0.188	0.97	0.814	0.0074	0.542	196.6	168.4
	1000	0.1	5%−10%	0.075	3	0.008	0.999	0.924	1.506	0.022	0.999	0.925	0.0021	0.132	74.4925	73.4425
	1000	0.1	10%−30%	0.200	2.61	0.022	0.995	0.801	0.943	0.188	0.97	0.814	0.0074	0.542	196	164.8
AUC	500	0.25	5%−10%	0.075				0.664				0.76	0.0491	0.621	153.125	153.125
	500	0.25	10%−30%	0.200				0.664				0.76	0.032	0.911	200	200
	500	0.1	5%−10%	0.075				0.664				0.76	0.0491	0.621	83.75	83.75
	500	0.1	10%−30%	0.200				0.664				0.76	0.032	0.911	140	140
	1000	0.25	5%−10%	0.075				0.664				0.76	0.0491	0.868	306.25	306.25
	1000	0.25	10%−30%	0.200				0.664				0.76	0.0226	0.995	400	400
	1000	0.1	5%−10%	0.075				0.664				0.76	0.0347	0.868	167.5	167.5
	1000	0.1	10%−30%	0.200				0.664				0.76	0.0226	0.995	280	280

The impacts of sample size, prevalence and relative importance on the performance of the three statistical measures are similar throughout the three tables. Larger sample sizes increase the precision of all three estimators, which leads to greater power. Larger sample sizes also require higher medical cost due to the increased number of misdiagnosis cases. There is an interaction between the relative importance of the diagnostic error (r) and prevalence (p). When r is small (0.1), a higher prevalence is associated with a lower optimal threshold of biomarker that maximizes AWA, and it leads to a higher sensitivity and lower specificity. AWA of the diagnostic test increases but power decreases with prevalence. On the other hand, when r is relatively large (0.25), AWA is maximized at a greater threshold for biomarker value, hence lower sensitivity and higher specificity. For large r values, AWA decreases and power increases with the prevalence rate. Both higher prevalence and higher relative importance lead to a greater medical cost. For the accuracy measure, higher prevalence lead to lower thresholds and specificity, but higher sensitivity, power and medical costs.

In terms of power in detecting differences between tests, accuracy has the highest power and AUC has the lowest power for evaluating the diagnostic test against best random test, or two diagnostic tests from either two independent samples or the same sample. AWA has higher power than AUC, but lower power than accuracy.

Impact of Relative Importance

Table 4 shows the power of AWA under the three scenarios in Table 1–3. When r is misspecified, the power may be higher or lower than the AWA using the correct r because r is selected for clinical interpretability, not based on minimum variance or maximum power. Therefore, it is possible that misspecified r leading to an AWA with higher power in comparing diagnostic tests. For example, when comparing two diagnostics applied in two independent samples, when prevalence is in the 5%−10% range, using r value of 0.1 would give higher power than r value of 0.25, even if the true value of r is 0.25. However, misspecified r will lead to choosing threshold too high (when r is over-estimated) or too low (when r is under-estimated) for the biomarker as well as bias in the estimation of AWA and the corresponding medical costs.

Table 4:

Power and medical costs using AWA in hypothesis testing.

Scenario	Prevalence Range	Relative Importance	Power	Medical Cost
Diagnostic vs Best Random Test	5%−10%	0.1	0.627	66
	5%−10%	0.25	0.072	75
	10%−30%	0.1	0.126	79
	10%−30%	0.25	0.998	161
Independent sample: Diagnostic 1 vs Diagnostic 2	5%−10%	0.1	0.455	63
	5%−10%	0.25	0.294	74
	10%−30%	0.1	0.474	78
	10%−30%	0.25	0.742	153
One sample: Diagnostic 1 vs Diagnostic 2	5%−10%	0.1	0.738	63
	5%−10%	0.25	0.491	74
	10%−30%	0.1	0.74	78
	10%−30%	0.25	0.959	153

The performance of AWA varies by the choice of relative importance (r). However, in practice, the relative importance of r can often be accurately determined using cost-effectiveness analysis or clinicians’ clinical judgement. This information can often be accurately measured and should reflect the clinical representation of such value. [9] For instance, the relative importance can be by the expert opinion from the clinicians through a survey of experts. Even in cases of misspecified r, as long as the difference between the chosen r and the true r is not too large, the estimates of medical costs are close, especially for infections with low prevalence (5%−10%).

Example Application

Diagnostic Assays to detect Neisseria gonorrhoeae and Chlamydia trachomatis (GC) infection

The master protocol for multiple infection diagnostics (MASTERMIND) GC study [10] was a cross-sectional, single visit study evaluating the performance of three commercial nucleic acid amplification tests (NAATs including Xpert® Assay (Cepheid), APTIMA Combo 2® Assay (Hologic) and Abbott RealTime Chlamydia trachomatis and Neisseria gonorrhoeae assay (Abbott)) to detect Neisseria gonorrhoeae (NG) and Chlamydia trachomatis (CT) in the rectum and pharynx. The study enrolled 2767subjects who had four pharyngeal and four rectal swabs collected as part of a one-time study visit. Each swab was used for a specific NAAT testing. A composite reference standard, defined by the results of two other NAATs, was used to determine the anatomic site infected status (ASIS). For a full description of the study, see [11].

169 subjects were excluded due to protocol violation and after applying the exclusion criteria. The final study population included 2598 participants, who attended a participating clinic for evaluation of STDs, and were ≥ 18 years of age at date of screening, be willing to provide informed consent, and comply with study procedures including collection of 4 swabs each from the pharynx and rectum for NG and CT testing. The subjects who received any systemic antibacterial drug in the past 14 days, or received myelosuppressive chemothrerapy in the past 30 days were excluded from the study. The estimated sensitivity and specificity, and associated 95% confidence intervals of the three assays at two locations for the two target infections are listed in Table 5.

Table 5.

Estimated specificity and sensitivity and associated 95% confidence intervals for each platform by specimen site and specie type.

		Panther		Abbott		Xpert
		$\widehat{\mathit{S}\mathit{e}}$	$\widehat{\mathit{S}\mathit{p}}$	$\widehat{\mathit{S}\mathit{e}}$	$\widehat{\mathit{S}\mathit{p}}$	$\widehat{\mathit{S}\mathit{e}}$	$\widehat{\mathit{S}\mathit{p}}$
CT	pharynx	0.900 (0.786,0.956)	1 (0.998,1)	0.840 (0.715, 0.917)	1 (0.998,1)	0.959 (0.863, 0.989)	1 (0.998,1)
	rectal	0.894 (0.846,0.928)	0.998 (0.995,0.999)	0.846 (0.792, 0.888)	1 (0.998,1)	0.874 (0.824,0.911)	1 (0.998,1)
NG	pharynx	0.960 (0.923, 0.980)	0.999 (0.997, 1)	0.865 (0.818,0.905)	1 (0.998,1)	0.955 (0.917,0.976)	1 (0.998,1)
	rectal	0.965 (0.929, 0.983)	0.999 (0.997, 1)	0.887 (0.836, 0.924)	1 (0.998,1)	0.921 (0.876,0.951)	1 (0.998,1)

The estimated AWA is calculated using the estimated sensitivity and specificity of each NAAT platform assay, assuming the relative importance of diagnostic error of 0.25, and disease prevalence of NG in the rectum, NG in the pharynx, CT in the rectum and CT in the pharynx to be of 10% each, ranging from 7.5% to 15%. We first compare each of the three platforms to BRT at each specimen sites and for each specie type. Four additional statistical tests are performed for comparing the equality of the AWAs using the three platforms for the two specimen sites and two species, respectively. The testing procedures for the hypotheses of three equal AWAs follow the derivations in subsection (4) of the Methods section.

TEST versus BRT

The null and alternative hypotheses are as follows:

$$H_0:{AWA}_i={{AWA}_{BRT}vs.H}_a:{AWA}_i\ne {AWA}_{BRT},i=\mathrm{1,2},3$$

For all species and sites, the estimated AWA of the platform test is greater than the AWA of BRT at the significance level of 0.004 (note: the significance level is adjusted based on Bonferroni correction 0.05/12) (Table 6).

Table 6.

Testing AWAs of the three platforms versus BRT by specimen site and species (AWA of the BRT=0.666).

Platform	Species	Sites	AWA	Difference(95% CI) in AWA between platform and BRT	Test statistics	p-value
Panther	CT	pharynx	0.966	0.301 (0.273,0.328)	21.213	<0.001
		rectal	0.963	0.297 (0.284,0.311)	42.520	<0.001
	NG	pharynx	0.986	0.320 (0.311,0.329)	69.175	<0.001
		rectal	0.988	0.322 (0.313,0.330)	73.555	<0.001
Abbott	CT	pharynx	0.946	0.281 (0.247,0.314)	16.202	<0.001
		rectal	0.948	0.283 (0.267,0.298)	34.843	<0.001
	NG	pharynx	0.955	0.289 (0.273, 0.304)	36.429	<0.001
		rectal	0.962	0.296 (0.282,0.311)	39.928	<0.001
Xpert	CT	pharynx	0.986	0.320 (0.302,0.339)	33.854	<0.001
		rectal	0.958	0.292 (0.277,0.306)	39.330	<0.001
	NG	pharynx	0.985	0.319 (0.310,0.329)	65.474	<0.001
		rectal	0.974	0.308 (0.295,0.320)	48.648	<0.001

Comparison the equality of the AWAs from the three TESTs

The null and alternative hypotheses are as follows:

$$H_0:L*\underset{\_}{AWA}=\left(\begin{array}{c}AW{A}_1-\overline{AWA}\\ AW{A}_2-\overline{AWA}\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right) vs.H_a:L*\underset{\_}{AWA}\ne \left(\begin{array}{c}0\\ 0\end{array}\right),$$

$\mathit{\text{where\hspace{0.17em}}}\overline{AWA}=\frac{AW{A}_1+AW{A}_2+AW{A}_3}{3}\mathit{\text{and\hspace{0.17em}}}L=\left(\begin{array}{ccc}1-1/3& -1/3& -1/3\\ -1/3& 1-1/3& -1/3\end{array}\right)$.

Furthermore, the variance and covariance matrix for $\widehat{\underset{\_}{AWA}}$ is

$$\mathit{\text{Σ}}=\left(\begin{array}{ccc}\mathit{\text{Var}}\left({\widehat{AWA}}_1\right)& \mathit{\text{Cov}}\left({\widehat{AWA}}_{21}\right)& \mathit{\text{Cov}}\left({\widehat{AWA}}_{31}\right)\\ \mathit{\text{Cov}}\left({\widehat{AWA}}_{12}\right)& \mathit{\text{Var}}\left({\widehat{AWA}}_2\right)& \mathit{\text{Cov}}\left({\widehat{AWA}}_{32}\right)\\ \mathit{\text{Cov}}\left({\widehat{AWA}}_{13}\right)& \mathit{\text{Cov}}\left({\widehat{AWA}}_{23}\right)& \mathit{\text{Var}}\left({\widehat{AWA}}_3\right)\end{array}\right)$$

Therefore, the test statistics are calculated as $x^2=\left(L*\widehat{\underset{\_}{AWA}}\right)\text{'}*{(L*\Sigma *L`)}^{-1}*\left(L*\widehat{\underset{\_}{AWA}}\right)$, which follow a chi-square distribution with degree freedom of 2, as shown in Table 7. Except for the species CT and rectal site, in all the other scenarios, the AWAs from the three platforms are not equal at significance level 0.05. Using AWA as the measure of performance, the Abbott platform seems to be inferior than the other two although the highest AWA may be from either Panther or Xpert.

Table 7.

AWAs from three platforms by specimen site and species and the Chi-square test for the equality of the three AWAs.

		Panther	Abbott	Xpert	Chi-square statistic	p-value
CT	pharynx	0.966	0.946	0.986	19.002	<0.001
	rectal	0.963	0.948	0.958	4.601	0.100
NG	pharynx	0.986	0.955	0.985	37.069	<0.001
	rectal	0.988	0.962	0.974	7.896	0.019

Discussion

The clinical impact of diagnostic test should be evaluated in the context of diagnostic yield, which depends not only on the test’s ability to discriminate disease from non-disease (sensitivity and specificity), but also on the prevalence of disease and the relative importance of a false positive vs. false negative. AWA is a measure of diagnostic yield that incorporates these components and provides a pragmatic evaluation of the diagnostics under investigation. AWA is expected to yield a better power than cases when sensitivity or specific is used alone, as it utilizes entire study sample (both disease and non-disease population) in estimation and hypothesis testing compared to the segmented evaluation of sensitivity and specificity. The criterion of evaluating the performance of a diagnostic test should not be based only on the statistical properties (etc. power), but also on its clinical value (e.g. measured by medical cost or clinical importance). This paper examined the statistical properties and practical value of AWA as compared to two other composite statistical measures, AUC and accuracy, with respect to power and clinical cost. AWA is not the statistical measure with the highest power but it always has a simple reverse relationship with medical cost and is most informative in selecting the optimal biomarker thresholds and best diagnostic tests in terms of clinical importance based on optimizing diagnostic yield. AWA is an effective measure of cost-utility reflecting the relative cost between false positive and false negative diagnosis of a diagnosis test and providing a pragmatic evaluation of the diagnostic test based on the disease population.

Table 2.

Power and medical costs using AWA, Accuracy or AUC in comparing two diagnostic tests in two independent samples. The biomarker values from the two diagnostic tests in the infected population are distributed as N(μ₁=0.6,σ₁=1) and N(μ₂=0.5,σ₂=0.5), respectively.

Method	Sample Size (N1, N2=500)	Relative Importance (r)	Prevalence Range (p)	Prevalence rate	Threshold (Dx1)	Sensitivity (Dx1)	Specificity (Dx1)	AWA, Accuracy or AUC (Dx1)	SD (Dx1)	Threshold (Dx2)	Sensitivity (Dx2)	Specificity (Dx2)	AWA, Accuracy or AUC (Dx2)	SD (Dx2)	SD (Dx1-Dx2)	Power	Medical Cost (Dx1)	Medical Cost (Dx2)
AWA	500	0.25	5%−10%	0.075	2.189	0.056	0.986	0.759	0.01	0.817	0.263	0.949	0.782	0.0192	0.0216	0.274	37.01875	33.534375
	500	0.25	10%−30%	0.200	0.366	0.592	0.643	0.618	0.027	0.27	0.677	0.705	0.692	0.0257	0.0373	0.628	76.5	61.8
	500	0.1	5%−10%	0.075	0.677	0.469	0.751	0.626	0.0378	0.363	0.608	0.766	0.696	0.037	0.053	0.374	31.42875	25.5225
	500	0.1	10%−30%	0.200	−1.11	0.956	0.134	0.709	0.0152	−0.173	0.911	0.365	0.747	0.0212	0.0261	0.419	39.04	34.3
	1000	0.25	5%−10%	0.075	2.189	0.056	0.986	0.759	0.0071	0.817	0.263	0.949	0.782	0.0192	0.0204	0.294	74.0375	67.06875
	1000	0.25	10%−30%	0.200	0.366	0.592	0.643	0.618	0.0191	0.27	0.677	0.705	0.692	0.0257	0.032	0.742	153	123.6
	1000	0.1	5%−10%	0.075	0.677	0.469	0.751	0.626	0.0268	0.363	0.608	0.766	0.696	0.037	0.0457	0.455	62.8575	51.045
	1000	0.1	10%−30%	0.200	−1.11	0.956	0.134	0.709	0.0107	−0.173	0.911	0.365	0.747	0.0212	0.0238	0.474	78.08	68.6
Accuracy	500	0.25	5%−10%	0.075	3	0.008	0.999	0.924	0.0019	1.506	0.022	0.999	0.925	0.0024	0.003	0.0989	37.315625	36.790625
	500	0.25	10%−30%	0.200	2.61	0.022	0.995	0.801	0.004	0.943	0.188	0.97	0.814	0.0103	0.011	0.319	98.3	84.2
	500	0.1	5%−10%	0.075	3	0.008	0.999	0.924	0.0019	1.506	0.022	0.999	0.925	0.0024	0.003	0.0989	37.24625	36.72125
	500	0.1	10%−30%	0.200	2.61	0.022	0.995	0.801	0.004	0.943	0.188	0.97	0.814	0.0103	0.011	0.319	98	82.4
	1000	0.25	5%−10%	0.075	3	0.008	0.999	0.924	0.0014	1.506	0.022	0.999	0.925	0.0024	0.003	0.106	74.63125	73.58125
	1000	0.25	10%−30%	0.200	2.61	0.022	0.995	0.801	0.0028	0.943	0.188	0.97	0.814	0.0103	0.011	0.334	196.6	168.4
	1000	0.1	5%−10%	0.075	3	0.008	0.999	0.924	0.0014	1.506	0.022	0.999	0.925	0.0024	0.003	0.106	74.4925	73.4425
	1000	0.1	10%−30%	0.200	2.61	0.022	0.995	0.801	0.0028	0.943	0.188	0.97	0.814	0.0103	0.011	0.334	196	164.8
AUC	500	0.25	5%−10%	0.075				0.638					0.76		0.0608	0.474	153.125	153.125
	500	0.25	10%−30%	0.200				0.664					0.76		0.04	0.774	200	200
	500	0.1	5%−10%	0.075				0.664					0.76		0.0608	0.474	83.75	83.75
	500	0.1	10%−30%	0.200				0.664					0.76		0.04	0.774	140	140
	1000	0.25	5%−10%	0.075				0.664					0.76		0.0515	0.586	306.25	306.25
	1000	0.25	10%−30%	0.200				0.664					0.76		0.0339	0.882	400	400
	1000	0.1	5%−10%	0.075				0.664					0.76		0.0515	0.586	167.5	167.5
	1000	0.1	10%−30%	0.200				0.664					0.76		0.0339	0.882	280	280

^*The cost of a false negative is defined as 1, and the cost of a false positive is assumed to be r.

Author bio

Dr. Scott Evans is a Professor of Epidemiology and Biostatistics and the Director of the George Washington University Biostatistics Center. Professor Evans interests include the design, monitoring, analyses, and reporting of and education in clinical trials and diagnostic studies. He is the author of more than 100 peer-reviewed publications and three textbooks on clinical trials including Fundamentals for New Clinical Trialists. He is the Director of the Statistical and Data Management Center (SDMC) for the Antibacterial Resistance Leadership Group (ARLG), a collaborative clinical research network that prioritizes, designs, and executes clinical research to reduce the public health threat of antibacterial resistance. Professor Evans is a member of the Board of Directors for the American Statistical Association (ASA) and the Society for Clinical Trials (SCT) and is a former member of the Board for the Mu Sigma Rho (the National Honorary Society for Statistics). He is a member of an FDA Advisory Committee, the Steering Committee of the Clinical Trials Transformation Initiative (CTTI), and serves as the Chair of the Trial of the Year Committee of the SCT. Professor Evans is the Editor-in-Chief of CHANCE and Statistical Communications in Infectious Diseases (SCID), and the Co-Editor of a Special Section of Clinical Infectious Diseases (CID) entitled Innovations in Design, Education, and Analysis (IDEA).

Dr. Evans is a recipient of the Mosteller Statistician of the Year Award, the Robert Zackin Distinguished Collaborative Statistician Award, and is a Fellow of the American Statistical Association (ASA) and the Society for Clinical Trials (SCT).

Dr. Qing Pan is tenured associate professor of Statistics at George Washington University. She received a B.S. in Biotechnology from Beijing University in 2000, an M.S. in Statistics from University of Georgia in 2003 and a Ph.D. in Biostatistics from University of Michigan in 2007. Dr. Pan’s research focuses on novel statistical and machine learning methods with applications in biostatistics and bioinformatics including survival analysis, electronic health records, network analysis and “omics” data. She was/is an important investigator in the Prospective Payment System for End Stage Renal Disease, Scientific Registry of Transplant Recipients, Diabetes Prevention Program, Antibacterial Resistance Leadership Group.

Dr. Yunyun Jiang, Assistant Research Professor of Epidemiology and Biostatistics, Milken Institute School of Public Health at George Washington University. She is a biostatistician for the Antibacterial Resistance Leadership Group (ARLG) research network, a network that develops, designs and implements the transformational trials to change clinical practice and reduce the impact of antibacterial resistance and antimicrobial resistance. Her current research focuses on the development of novel statistical methodologies that will advance the ARLG mission, specifically innovative approaches to design, monitoring, and analyses of antibacterial studies (clinical trials, diagnostic studies, and master protocols). She received her Ph.D. in Biostatistics from Medical University of South Carolina, with her dissertation research focus on the design and implementation of Bayesian response adaptive randomization in phase III confirmatory clinical trials. Her research interests include clinical trial design, conduct and analysis.

Dr. Ying Liu obtained her Ph. D in applied statistics from UC Riverside. Her thesis topic is MCMC and Bayesian analyses. Then she worked with Dr. Scott Evans as a research associate at the center for Biostatistics in AIDS research at Harvard, during which she did research on sequentially multiple assignment randomized trials (SMART) and diagnostic studies. Currently she works for Biogen on Alzheimer’s disease. Her research interests include propensity score methods, longitudinal analyses and Bayesian analyses.