Reveal, Don’t Conceal: Transforming Data Visualization to Improve Transparency

Abstract

Reports highlighting the problems with the standard practice of using bar graphs to show continuous data have prompted many journals to adopt new visualization policies. These policies encourage authors to avoid bar graphs and use graphics that show the data distribution; however, they provide little guidance on how to effectively display data. We conducted a systematic review of studies published in top peripheral vascular disease journals to determine what types of figures are used, and to assess the prevalence of suboptimal data visualization practices. Among papers with data figures, 47.7% of papers use bar graphs to present continuous data. This primer provides a detailed overview of strategies for addressing this issue by 1) Outlining strategies for selecting the correct type of figure based on the study design, sample size and the type of variable, 2) Examining techniques for making effective dot plots, box plots and violin plots and 3) Illustrating how to avoid sending mixed messages by aligning the figure structure with the study design and statistical analysis. We also present solutions to other common problems identified in the systematic review. Resources include a list of free tools and templates that authors can use to create more informative figures, and an online simulator that illustrates why summary statistics are only meaningful when there are enough data to summarize. Finally, we consider steps that investigators can take to improve figures in the scientific literature.

Introduction

Informative figures that allow readers to critically evaluate data are essential; however, a systematic review demonstrated that the figures commonly used in basic biomedical science obscure the data.¹ Figures highlight the most important findings in publications, posters and talks. The data underlying published studies typically are not available² or are not reusable.³ Success rates for requesting data from authors decline precipitously with time since publication.⁴ Until open science becomes more widespread, our knowledge of the data underlying study conclusions will be forever limited by what the authors choose to show.

Many journals have recently introduced policies that encourage or require authors to use more informative figures that show the data points or distribution, including PLOS Biology⁵, eLife⁶, the Journal of Biological Chemistry⁷ and Nature Publishing Group⁸. We conducted a systematic review of studies published in top peripheral vascular disease journals to determine what types of figures are commonly used to present data, and to assess the prevalence of suboptimal data visualization practices. The results show that the inappropriate use of bar graphs to present continuous data is a major problem in peripheral vascular disease journals. This primer provides a detailed overview of strategies for addressing this problem by 1) Outlining techniques for selecting the correct type of figure based on the study design, sample size, and type of outcome variable, 2) Examining techniques for creating effective dot plots, box plots and violin plots, and 3) Showing how to avoid sending mixed messages by aligning the structure of the figure with the study design and goals of the analysis. We also present solutions to other common visualization problems identified in the systematic review. Finally, we provide links to free tools and templates that make it easy for authors to prepare informative figures.

Visualization Problems in Peripheral Vascular Disease Journals

The systematic review included all original research articles published in September 2018 in the top 25% of peripheral vascular disease journals, ranked according to 2017 impact factor (n=206 papers from 13 journals, Supplementary figure 1, Supplementary table 1). Detailed methods and results are presented in the supplement. The protocol and data were deposited in a public repository.⁹ 180 papers (87.4%) included a data figure. Table 1^10–14 provides a brief overview of findings and presents steps that authors can take to correct common visualization problems (Figure 5).

Table 1:

Correcting Common Visualization Problems in Peripheral Vascular Disease Journals

Replace bar graphs with figures that show the data distribution: 47.7% of papers used bar graphs to present continuous data, typically for small datasets. The median sample size for the smallest and largest groups shown in a bar graph were 3 (interquartile range 3–5) and 10 (7 – 17). This suggests that most bar graphs should be replaced with dot plots (Figure 1, 2).

Consider adding dots to box plots: The median sample size for the smallest and largest groups shown in a box plot were 20 (interquartile range 11.5–56) and 66 (17.5–302.5). There are no clear guidelines for the sample size at which a dataset becomes large enough to use box plots, however, these data show that box plots are sometimes used for small samples. In these cases, authors should combine the box plot with a dot plot and emphasize the box plot, as shown in Figure 3.

Change journal policies: Only three of the 13 peripheral vascular disease journals examined had policies requesting that authors replace bar graphs with more transparent figures that show the data points or distribution.

Use symmetric jittering in dot plots to make all data points visible: Among papers with dot plots (n = 39), 46.2% included overlapping data points that were not clearly visible. Figure 4 illustrates strategies for making all points visible.

Use semi-transparency or show gradients to make overlapping points visible in scatterplots and flow-cytometry figures: Scatterplots in 89.2% of papers (33/37) had overlapping points, however only 12.1% of papers (4/33) used techniques like semi-transparency, shaded color gradients, or gradient lines to make overlapping points visible. 76.5% of papers with flow cytometry plots (13/17) used gradients to identify regions with many overlapping points. Semi-transparency works best for small datasets with few overlapping points (Supplemental figure 2). Gradients should be shown for large datasets with many overlapping points, including flow cytometry plots.

Consider adding a flow chart or study design diagram: Only 63/206 (30.6%) of the papers had a flow chart or a study design diagram. These figures make it easy to understand the study design, and to follow the flow of participants or animals through the experiment. The Experimental Design Assistant tool is extremely useful for creating flow charts when planning animal studies.11 This tool also provides extensive feedback to facilitate rigorous experimental design and transparent reporting of key features like blinding and randomization. The STROBE guidelines recommend using flow charts for observational studies.10 The CONSORT guidelines12 include sample flow charts for randomized controlled trials.

Use color blind safe color maps: The most common form of color blindness affects up to 8% of men and 0.5% of women of Northern European ancestry.14 While 12.6% of papers (26/206) used a color map on a graph or clinical image, only 15.4% of these papers (4/26) used color maps in which key features were visible to someone with deuteranopia. Most papers with heat maps used color palettes that were not color blind safe (7/12, 58.3%). Free tools like Color Oracle13 allow investigators to quickly see how figures might look to a colorblind person (Figure 5). Investigators should avoid non-color blind safe color maps (i.e. rainbow, red/green) and choose colorblind safe alternatives. This may require working with device manufacturers, as many rainbow color maps appeared to have been generated by flow cytometry or ultrasound software.

Figure 5: Select Color Blind Safe Color Maps.

This figure illustrates how heat maps created using different color palettes would appear to someone with normal color vision (top row) vs. someone with the most common form of color blindness (bottom row). Color blindness was simulated using Color Oracle.¹³

The inappropriate use of bar graphs to display continuous data was the most common visualization problem in peripheral vascular disease journals. Bar graphs showing continuous data were the most common figure type, appearing in 47.7% of papers (Supplemental table 2). These figures do not allow readers to critically evaluate the data.¹ This is problematic, as many different data distributions can lead to the same bar or line graph and the actual data may suggest different conclusions from the summary statistics alone.¹ Bar graphs also misleadingly assign importance to the bar height and distort our perception of how the differences between means compare to the variability in the data.¹⁵ As the y-axis typically starts at zero and ends above the highest error bar, bars often include biologically impossible values (Zone of Irrelevance, Figure 1) while omitting high values that were observed in the sample (Zone of Invisibility). Bars also introduce within-the-bar bias, where viewers erroneously believe that data points are more likely to fall inside the bar than outside (above) the bar.¹⁶ Investigators should use more informative alternatives to bar graphs, such as dot plots, box plots and violin plots, especially for the situations outlined in Table 2.^17–21

Figure 1: Why one shouldn’t use a bar graph, even if the data are normally distributed.

Bar graphs arbitrarily assign importance to the height of the bar, rather than focusing attention on how the difference between means compares to the range of observed values. Panel A: The bar height represents the mean. Error bars represent one standard error. The y-axis starts at zero and ends just above the highest error bar. Panel B: Adding data points reveals that the bar graph in Panel A includes low values that never occurred in the sample (Zone of Irrelevance) and excludes observed values above the highest error bar (Zone of Invisibility). Panel C: The dot plot emphasizes how the difference between means compares to the range of observed values. The y-axis includes all observed values. Reprinted from Weissgerber et al.²² under a CC-BY license. Abbreviations: SE, standard error.

Table 2:

Situations Where Showing the Data Points or Distribution is Particularly Important

Transparent figures are particularly important for situations described below:

Small sample size studies: Dot plots are crucial for small studies, as summary statistics for small samples can be quite different from those of the population from which the sample was drawn.17

Responses are highly variable: When a paper asserts that responses are highly variable, figures showing the data distribution are necessary to support this conclusion. Understanding the factors that contribute to variability between individuals can provide critical insight into pathophysiology, as well as the potential utility of tests and treatments. A blog post18 based on a study19 examining highly variable weight regain patterns among participants of the “Biggest Loser” television series illustrates how examining individual-level data may provide additional insight.

Heterogeneity or subgroups are expected: Bar and line graphs mask heterogeneity and conceal subgroups. Data points must be visible if we want to understand heterogeneity or identify subgroups. The hypertensive pregnancy disorder preeclampsia is one example. Many pathways can lead to the diagnostic signs of hypertension and proteinuria, for example, and the relative contribution of each pathway likely varies from woman to woman.20 Markers for any pathway are likely to be normal in some preeclamptic women and abnormal in others.21 Showing the data distribution allows others to examine the overlap between groups and estimate the proportion of patients with abnormal values.

The standard deviation is larger than the mean and the variable cannot be negative: This indicates that the data are skewed and the mean and standard deviation are misleading.

Previous studies suggest that the variable is not normally distributed in the study population or in related populations.

Selecting the Best Graphic for the Data

Effective figures in scientific papers should: 1) Immediately convey information about the study design and statistical analysis, 2) Illustrate important findings and 3) Allow the reader to critically evaluate the data.²² The type of figure that is selected will depend on the study design. When working with continuous data, dot plots, box plots and violin plots may be used to compare independent groups in cross-sectional or experimental studies, whereas line graphs are commonly used to present data from longitudinal studies or studies with matched participants. Table 3 lists free tools and resources for creating these graphs.^{1, 15, 22–31}

Table 3:

Free resources to create figures for small datasets

Figure	Program	Resource
Static or interactive dot plots, box plots & violin plots	Web-based tool; features for showing subgroups & clusters of non-independent data *	http://statistika.mfub.bg.ac.rs/interactive-dotplot/ 22
Dot plots, box plots & violin plots	Web-based tool (SHINY app)	https://huygens.science.uva.nl/PlotsOfData/ 27
Combination of dot plots, box plots and kernel density plots	Tutorial for R, Python, Matlab – this visualization is only appropriate for large datasets	https://wellcomeopenresearch.org/articles/4-63/v1 30
Dot plots	Excel templates, GraphPad PRISM instructions	Supplemental files of Weissgerber et al., 2015 1
	SPSS code	https://www.ctspedia.org/wiki/pub/CTSpedia/TemplateTesting/Dotplot_SPSS.pdf 23
	R code	Blog post by Jamie Ashander 25 Blog post by Ben Marwick 26
Box plots	Web-based tool (for independent or clustered /grouped data; SHINY app) *	https://lancs.shinyapps.io/ToxBox 28
	Web-based tool (for independent data; SHINY app)	http://boxplot.tyerslab.com/ 15
	R code	Blog post by Jamie Ashander 25
Violin plots	Web-based tool (for independent data; SHINY app)	https://interactive-graphics.shinyapps.io/violin/ 24
Paired data: Spaghetti plots & dot plots of change scores	Excel templates, GraphPad PRISM instructions	Supplemental files of Weissgerber et al., 2015 1
	R code	Blog post by Jamie Ashander 25 Blog post by Ben Marwick 26
Interactive line graphs	Web-based tool; features for showing lines for any individual, focusing on groups or time points of interest, viewing change scores for any two conditions	http://statistika.mfub.bg.ac.rs/interactive-graph/ 29
Various types of graphs	Excel, R code, Stata	http://faculty.washington.edu/kenrice/heartgraphs 31

^*Grouped or clustered data refers to measurements performed in subjects, specimens or samples that are related to each other. This might include replicates, or animals from the same litter.

Comparing independent groups:

More informative alternatives to the bar graph include dot plots, box plots and violin plots. Figure 2 provides detailed information about how to determine which type of figure to use and describes best practices. When creating dot plots, avoid programs that create “histograms with dots” by grouping the data points into bins, and then moving all data points to the center of their respective bins.³² These fake dot plots can be misleading, especially for small datasets. Every point should be visible in dot plots (Figure 3, Step 1). Emphasizing mean or median lines and de-emphasizing data points conveys a clear message, while allowing readers to critically evaluate the data (Figure 3, Step 2). This is especially useful for complex graphs with many groups. Similar principles can be applied when combining dot plots with box or violin plots (Figure 4C, D). Avoid adding dot plots to bar graphs. The bar does not add information and often obscures data points.

Figure 2: Figures for comparing groups in cross-sectional or experimental studies.

When choosing among different types of graphs, it is important to consider the study design, sample size and data distribution. This figure provides a detailed overview of different types of graphs, describes when to use each graph and lists best practices for clear data presentation.

Figure 3: Strategies for making effective dot plots.

The initial graph is hard to interpret because it has many overlapping data points (A). Strategies for making all points visible include decreasing the size of the data points (B), making the data points semi-transparent (C), and using random (D) or symmetric (E) jittering. The bottom row illustrates how to clearly show the main finding, while allowing readers to critically evaluate the data. Increasing the white space between groups (G) and emphasizing the summary statistics (H) makes the graph (F) much easier to interpret.

Figure 4: Combining dot plots with box or violin plots.

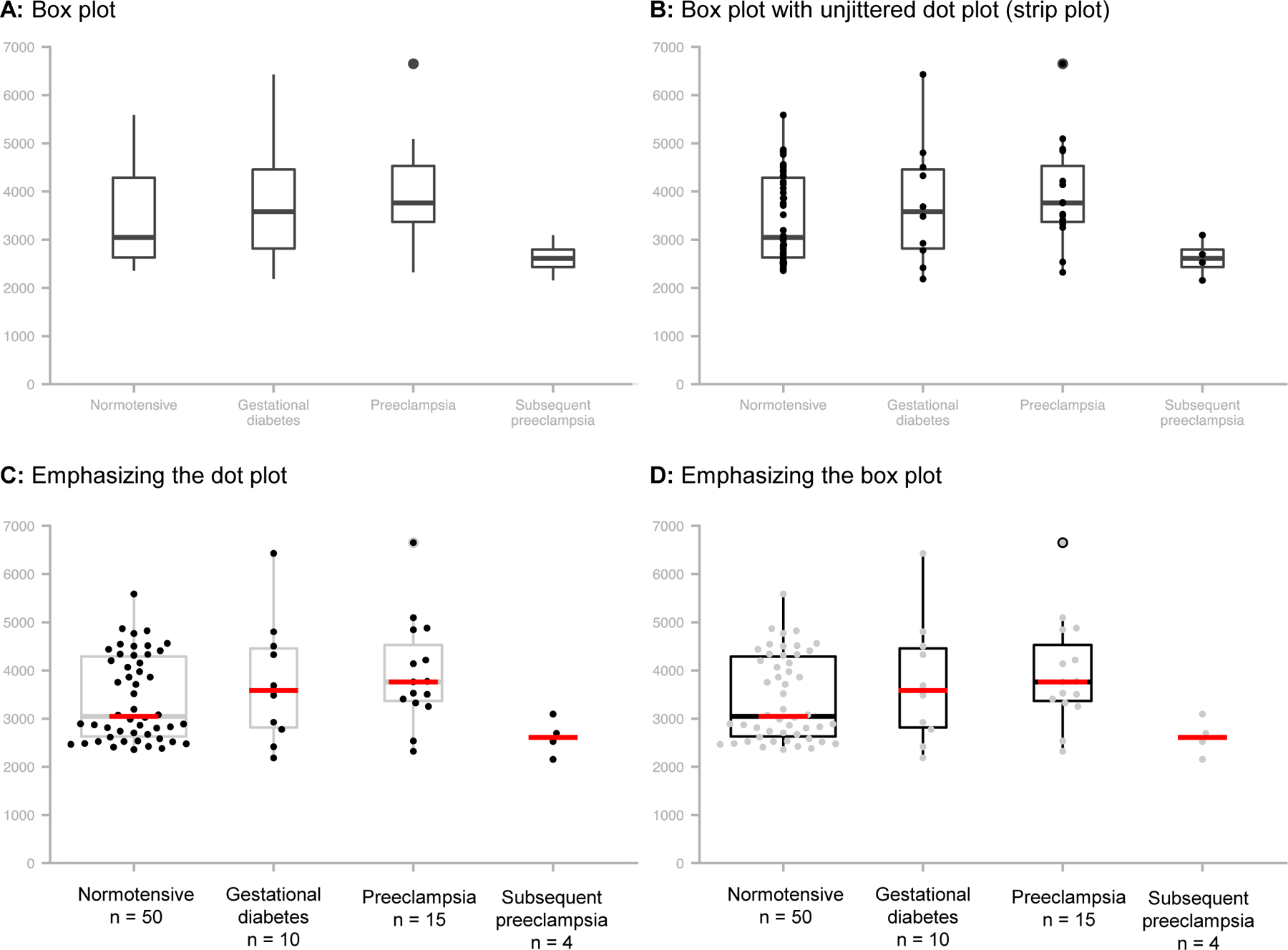
Panel A shows the data distribution, but provides no information about sample size. The overlapping points in Panel B offer little additional insight. Panels C and D allow readers to evaluate the data by including symmetrically jittered data points, making the box plot width proportional to the sample size and listing the sample size on the x-axis. Only the dot plot is shown for the last group, as the sample size was too small for a box plot. This dataset includes small groups (n = 10–15); therefore it would be better to emphasize the dot plot (C). If all groups have larger sample sizes, investigators can choose whether to emphasize the dot plot (C) or the box plot (D).

Longitudinal, repeated measures, or matched data:

Line graphs were the second most common type of graph in peripheral vascular disease journals, appearing in 34.4% of papers. These graphs are used for longitudinal or repeated measures studies with two or more time points or conditions. The lines indicate that the same measurement was repeated on each participant, specimen or sample. Lines can also show matched or related observations. The simplest design is paired data, in which measurements are performed on the same participants at two time points or under two experimental conditions, or two different participants are matched for important characteristics. Previous publications provide advice on visualizing paired data.^{33, 34}

As with bar graphs, many datasets can lead to the same line graph. There are some alternatives for small datasets that allow readers to go beyond the summary statistics. We recently introduced a free web-based tool for creating interactive line graphs for publications.²⁹ Users can gain additional insight by examining different summary statistics, viewing lines for any individual in the dataset, focusing on groups, time points or conditions where important changes are occurring, and examining change scores for any two time points or conditions. These features make it easier to assess overlap between groups and determine whether all individuals respond the same way. Alternatives to the line graph are useful for certain types of datasets, as described in the supplement of a recent paper.²⁹ These include lasagna plots,³⁵ small multiples,³⁶ spaghetti plots³⁷ and showing lines for selected individuals on a dot plot.³⁸

All means are not equally meaningful: When to show summary statistics

Bar and line graphs create the illusion of certainty by focusing readers’ attention on differences in summary statistics, while erroneously suggesting that all means are equally meaningful. This assumption is particularly problematic for small datasets, as summary statistics for small samples can be very different from the true population values (Figure 6). Preclinical and basic biomedical science studies typically have fewer than 15 observations per group, and three to six observations per group are common (supplemental results).^{1, 39} Figure 6A shows how the summary statistics might change if we repeated the same experiment 100 times, with 5 or 20 observations per group. The smaller the sample size, the greater the variability in the summary statistics and the higher the probability that a sample will yield estimates that are very different from the true population value. Figure 6B illustrates that increasing the sample size allows one to move from the turbulent “Seas of Uncertainty”,⁴⁰ where summary statistics can be wildly imprecise, into the “Corridor of Stability”.⁴¹ Investigators can explore the effects of sample size on summary statistics by using a free online simulator with interactive versions of these figures (https://rtools.mayo.edu/size_matters/, Simulator 1⁴²).

Figure 6: Summary statistics are only meaningful when there are enough data to summarize.

Panel A illustrates how the sample mean (red/blue dots) and standard deviation (red/blue error bars) might change if we repeated the same experiment 100 times, with n = 5 or n = 20. The black line and gray shaded region show the population mean and standard deviation. If all samples gave precise estimates, each sample mean would be on the black line and the error bars would fill the gray region. Panel B illustrates how cumulative means change with increasing sample size. The sample mean is calculated for three participants. New participants are added one at a time. The colored lines illustrate how the sample mean changes as each new participant is added. The experiment is repeated 100 times. The black line shows the true population mean. When n is small, the sample means are often quite different from the population mean (Seas of Uncertainty). As n increases, the sample means converge on the population mean (Corridor of Stability). Interactive version: https://rtools.mayo.edu/size_matters/.⁴² The terminology of Seas of Chaos/Uncertainty and Corridor of Stability was used in papers examining the effects of sample size on correlation coefficients⁴¹ and effect sizes.⁴⁰ Abbreviations: SD, standard deviation.

An additional problem with showing mean and standard error or standard deviation for small samples is that these summary statistics are most appropriate for normally distributed data. Very small samples do not provide enough data to distinguish between normal, skewed or bimodal distributions (Figure 7). Normality tests are underpowered when n is small and often fail to detect non-normal distributions. Interactive versions of this figure, and a table showing the percentage of samples that would fail a normality test, are available in the online simulator (https://rtools.mayo.edu/size_matters/, Simulator 1⁴²). Investigators can use this tool to actively explore potential effects, instead of relying on arbitrary thresholds. Results may vary from those shown in the simulator based on the degree of skewness or the separation between bimodal peaks.

Figure 7: Small samples do not contain enough information to determine the distribution.

Random samples of different sizes (n = 100, n = 20 and n = 5) were drawn from populations with a normal, skewed or bimodal distribution (red violin plots). One can clearly identify the different data distributions when n = 100. Determining the data distribution becomes more difficult when n = 20 and is impossible when n = 5. Interactive version: https://rtools.mayo.edu/size_matters/.⁴²

The simulator illustrates that dot plots of very small samples help readers to evaluate the data, but don’t reveal the data distribution. As sample size increases, data distributions can be identified and summary statistics become more precise. This explains why dot plots with mean or median lines are the best choice for very small datasets – error bars, box plots and violin plots are only meaningful when there are enough data to summarize. These features can be added when the sample size is large enough to give reasonably precise estimates. In most bar graphs in our sample, error bars show the standard error (66.3%) rather than the standard deviation (20.9%) or 95% confidence interval (2.3%). As described previously, standard errors are sample size dependent and provide information about the precision of the mean, rather than the variability in the data.⁴³ If the sample size varies among groups, avoid creating a false sense of certainty by only showing error bars, box plots or violin plots for larger groups. In Figure 4, the box plot was removed for the group with four observations. When combining plots for small samples, investigators should emphasize what is known (the data points) and de-emphasize what is uncertain (the box/violin plot). For larger samples, investigators can choose whether to emphasize the dot plot (Figure 4C) or the box/violin plot (4D).

Practice Good Statistical Hygiene

The figure structure provides visual cues about the study design and statistical analysis. Misleading structures confuse readers (Figure 8). The experiment shown in Figure 7 was designed to compare normotensive and hypertensive patients. Concentrations of three different vascular biomarkers (dependent variables) were each compared using a t-test (normotensive vs. hypertensive). Sometimes published papers present different dependent variables in the same graph (Figure 8A). This erroneously suggests that t-tests would not be appropriate, as the authors wanted to compare biomarkers (A vs. B vs. C) in addition to examining the effects of hypertension. In contrast, presenting each biomarker in a separate panel (Figure 8B) shows that the goal was to compare hypertensive and normotensive patients, and not to compare biomarkers. For small studies, each graph should present one statistical analysis and include all groups that were part of that analysis. Figure 9 illustrates how to structure figures and panels for common analyses.

Figure 8: Avoid sending mixed messages – Why the figure structure should match the study design and statistical analysis.

The experiment was designed to compare normotensive and hypertensive patients. Separate analyses were performed for each dependent variable (biomarkers A, B and C). Panel A illustrates a common strategy for presenting this type of data. Including all dependent variables on the same graph erroneously suggests that the authors intended to compare biomarkers A, B and C. Panel B avoids confusion by presenting each biomarker separately. Abbreviations: HTN, hypertensive; NT, normotensive.

Figure 9: How to structure figures for common analyses.

This figure illustrates how to structure figure panels and groups for common types of analyses, including comparing groups, repeating the same analysis on different dependent variables, comparing groups with pooled subgroups, stratified analyses, and testing for an interaction. Abbreviations: HTN, hypertensive; NT, normotensive.

The statistical methods, figure legend and results should contain the information needed to reproduce the analysis. Specifying the statistical test in the figure legend makes it easy for readers to determine what the authors were comparing and to confirm that the statistical methods match the design. When this is not possible, list table or figure numbers next to each technique in the statistical methods. If data are normally distributed but means and standard deviations are not evident from the figure, report these statistics in the legend or in the results. Readers may need exact values to confirm the statistical results, perform power calculations or conduct meta-analyses. Reporting test statistics, degrees of freedom and exact p-values (p = 0.43), instead of thresholds (p < 0.05), is essential to allow others to confirm the test results.⁴⁴ Exact sample sizes for each group should be reported in the figure or legend, for example, by listing sample sizes below the group name on the x-axis. Do not report a range of sample sizes. This conceals information needed to reproduce the analysis and raises questions about whether unequal sample sizes were planned, or may be due to the unexplained exclusion of participants or samples.

It is necessary to show outliers or excluded observations in figures, provide explanations (if known) and state how outliers were handled in the analysis. Excluding one or two outliers that oppose the expected effect in small studies can dramatically increase the odds of finding a significant effect when none exists.³⁹ If showing extreme outliers alters the scale such that the remaining data are not clearly visible, omit the outlier from the graph and report the value in the legend. Flow charts that illustrate the planned number of participants, animals or samples for each experiment and show the reasons for attrition or exclusion of each subject or specimen are underutilized in preclinical and observational studies. This information is needed to confirm that exclusions were unbiased.

Papers that show data points or provide open data allow others to reproduce the analysis and determine whether using different analytic techniques would have yielded different results. Transparent reporting and open data are becoming increasingly important as scientists, funding agencies and journals implement new strategies to improve scientific rigor and reproducibility.⁴⁵ These include reducing our reliance on hypothesis testing and the widespread use of the p<0.05 threshold for statistical significance and training investigators in the strengths and weaknesses of this approach compared to other techniques (i.e. effect sizes, Bayesian analysis, etc.).^{17, 46, 47}

Additional Graphs and Resources

This section briefly reviews visualization techniques for other common situations in the basic biomedical sciences and introduces some new visualization tools.

Two-Way ANOVA:

A two-way ANOVA could refer to several different tests, each of which is appropriate for a different study design and requires a different figure structure.⁴⁸ Authors should avoid confusion by specifying whether a repeated measures ANOVA was used, and whether each independent variable was analyzed as a between-subjects or a within-subjects factor. The figure structure should match the study design and analysis (Supplementary figure 3).

Static Graphs Comparing Effect Sizes:

P-values indicate whether groups are significantly different, but they do not assess the size of the difference or determine whether this difference is biologically meaningful. A new web-based tool creates graphs that highlight the size of the difference between groups.⁴⁹

Comparing Differences in Variability:

Common statistical tests compare differences in means or ranks, however sometimes scientists want to compare differences in variability (i.e. Is the range of observed values larger in males than in females?). Investigators with larger samples can compare variability by graphing shift functions.⁵⁰

Interactive Graphics:

Free online tools allow scientists with no programming expertise to quickly make interactive dot plots, box plots and violin plots²² or interactive line graphs²⁹ for publications. Investigators who use R can create customized interactive graphics using SHINY.⁵¹

What Can Scientists Do To Improve Data Presentation In The Scientific Literature?

Scientists, journal editors and funding agencies can use several strategies to promote better data visualization.

1. Use transparent figures for papers, posters and talks.

2. Support data presentation choices, as one would any other aspect of the study. Provide references that illustrate the importance of showing the data distribution^{1, 28, 52} when asked.

3. When reviewing papers, request informative figures that allow others to critically evaluate the data.

4. Talk to journal editors about strategies for improving data presentation. Encourage them to consult editorials,^{7, 53} presentations⁵⁴ and policies^{5, 8, 55, 56} of journals that have implemented policy changes. Policy changes are most effective when they are integrated into the review process. Decision letters should include comments requesting data visualization changes, with citations to show why this is important and how to create more informative graphics.

5. Organize data visualization training for researchers at all career stages.^{1, 57} Record sessions for later viewing.

Conclusions

Better data visualization practices are needed to promote transparency in small sample size studies.¹ The strategies and resources outlined in this review are designed to promote transparency by improving the quality of figures, while assisting scientists, academic journals and funding agencies in making lasting improvements to data visualization in the scientific literature.