GWAS of longitudinal trajectories at biobank scale

Summary

Biobanks linked to massive, longitudinal electronic health record (EHR) data make numerous new genetic research questions feasible. One among these is the study of biomarker trajectories. For example, high blood pressure measurements over visits strongly predict stroke onset, and consistently high fasting glucose and Hb1Ac levels define diabetes. Recent research reveals that not only the mean level of biomarker trajectories but also their fluctuations, or within-subject (WS) variability, are risk factors for many diseases. Glycemic variation, for instance, is recently considered an important clinical metric in diabetes management. It is crucial to identify the genetic factors that shift the mean or alter the WS variability of a biomarker trajectory. Compared to traditional cross-sectional studies, trajectory analysis utilizes more data points and captures a complete picture of the impact of time-varying factors, including medication history and lifestyle. Currently, there are no efficient tools for genome-wide association studies (GWASs) of biomarker trajectories at the biobank scale, even for just mean effects. We propose TrajGWAS, a linear mixed effect model-based method for testing genetic effects that shift the mean or alter the WS variability of a biomarker trajectory. It is scalable to biobank data with 100,000 to 1,000,000 individuals and many longitudinal measurements and robust to distributional assumptions. Simulation studies corroborate that TrajGWAS controls the type I error rate and is powerful. Analysis of eleven biomarkers measured longitudinally and extracted from UK Biobank primary care data for more than 150,000 participants with 1,800,000 observations reveals loci that significantly alter the mean or WS variability.

Introduction

Biomarker trajectories are important phenotypes that reflect the evolution of an individual’s health or disease progression.^{1, 2, 3} With the increasing use of electronic health records (EHRs) linked with biobanks, large scale and repeatedly measured EHR-based quantitative laboratory-derived phenotypes are becoming highly influential in genetic studies of human health.^{4, 5, 6} For example, a recent LabWAS tool demonstrates the broad impact of using such “real world” measurements for genetic association studies.⁷ LabWAS summarizes longitudinal measurements by taking the mean for analyses. Although proven to be robust, this approach may lose power by ignoring the many rich features in the whole trajectories. Identifying genetic and clinical factors associated with these longitudinal trajectories can quantify the susceptibility to the onset of disease and disease progression, which ultimately offers new opportunities for early clinical prevention.^{1,8, 9, 10}

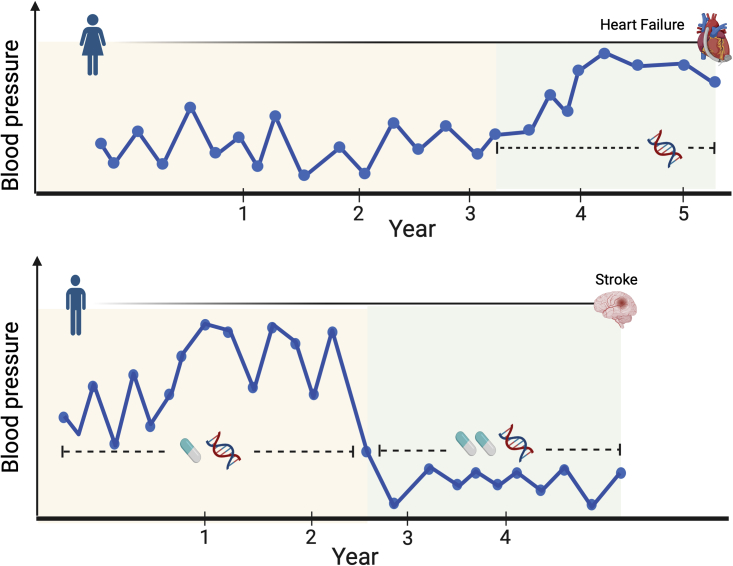
Besides mean level trajectory patterns, the biomarker fluctuations may also differ between individuals; some individuals show higher levels of variation around their mean than others (Figure 1). This intra-individual variability or within-subject (WS) variability^11,12 has been shown to be an important risk factor for disease. For example, among diabetes patients, visit-to-visit intra-individual fasting glucose variability is a risk factor for the development of vascular complications,^{13, 14, 15} independent of the glycemic control of the mean; blood pressure variability has been associated with the increased risk of heart failure¹⁶ and stroke.¹¹ Experimental research has revealed the biological basis of glycemic variability and diabetic kidney injury.¹⁷ WS variability in reaction times has also been suggested as a leading endophenotype for neurocognitive disorders, such as attention deficit hyperactivity disorder and schizophrenia.^18,19 As the wearable devices gain more and more popularity, WS variability becomes a clinical metric of disease management, such as the glucose coefficient of variability output from the continuous glucose monitoring (CGM) device report.^20,21

Figure 1.

Illustration of TrajGWAS

TrajGWAS identifies the genetic factors that shift the mean or alter the within-subject (WS) variability of a biomarker trajectory (e.g., blood pressure measurements over visits), which changes with time-varying covariates (e.g., medication history) or time-invariant covariates (e.g., sex).

WS variability differs from the between-subject (BS) variability, which also has recently attracted much attention. Variance quantitative trait loci (vQTLs) analysis seeks to identify loci that show different trait variances among groups of individuals with different variant genotypes.^{22, 23, 24, 25} Such phenotypic variance heterogeneity can be caused by gene-by-environment interaction, selection, epistasis, or phantom vQTLs. vQTL analysis is typically performed on a cross-sectional cohort, while TrajGWAS requires longitudinal data. In contrast to vQTL, TrajGWAS investigates genetic contributions to the WS variability instead of BS variability. Thus, TrajGWAS and vQTL analyses can provide complementary insights into the etiology of a disease. As an interesting example, we find that the well-known FTO (MIM: 610966) vQTL for body mass index (BMI)²⁶ (p value = $1.16\times {10}^{-102}$) is not associated with the WS variability (p value = $1.18\times {10}^{-4}$) at the genome-wide significance level.

Identifying genome-wide genetic contributions to longitudinal trajectories, including both mean and WS variability, is both methodologically and computationally challenging. Despite recent efforts,^{27, 28, 29} no existing software is able to analyze massive longitudinal traits at the biobank scale. The linear mixed effect model (LMM) is a powerful and popular method for longitudinal data analysis. Generalizations such as the mixed-effects location scale model³⁰ allow for simultaneous modeling of the mean and variability of the longitudinal measurement, increase power, and reduce bias. It leverages information across individuals to produce more precise estimates.³¹ However, the expensive numerical integration required in each iteration prohibits many modern data applications. For example, the run times of the full likelihood approach with MixWILD software^32,33 on two simulated datasets with 1,000 individuals and ten observations per individual ranged from 40 min to $10+$ h depending on the different modeling assumptions being made. MLwiN,³⁴ a multi-level model (a type of mixed effect model), has been used to estimate the mean trajectories while accounting for the change in scale and variance of measures over time.¹ However, none of these tools were designed for modern genome-wide scans. The heuristic strategies being employed in practice involve a two-stage model: (1) summarize a subject-level measure of the variation of the longitudinal measurement such as standard deviation (SD), average real variability (ARV), or the coefficient of variation (CV); (2) model those as the responses with covariates.^12,35,36 This framework makes an implicit assumption that an individual’s variability remains constant over time and cannot be affected by time-varying covariates (Figure 1). Yet intra-individual variability is affected by both time-varying (e.g., medication use or adherence to the treatment regime) and time-invariant features (e.g., sex and genes). Regressing the subject-level variability summaries on predictors leads to serious bias.³¹ The simulation study in supplemental methods, section C, shows that, without properly adjusting for time-varying covariates, the heuristic method can seriously inflate the type I error.

Building upon our recent methods, within-subject variance estimator by robust regression (WiSER),³⁷ we derive an ultra-fast score test, which only requires fitting one null model across the whole genome-wide set. This testing strategy scales linearly in the number of individuals. We also develop and implement a saddlepoint approximation (SPA) for our score test to ensure well-controlled type I error rates for single rare variant testing with minor allele frequencies (MAFs) as low as 0.001.

Material and methods

An LMM framework for testing genetic effects on the trajectory mean and WS variability

Our modeling assumptions are as follows. Assume there are m independent individuals, individual i has $n_i$ longitudinal measurements of a biomarker, and $n={\sum }_{i=1}^m{n}_i$ is the total number of observations. Consider an LMM for modeling different sources of variation in a biomarker in the longitudinal setting

$$y_{ij}={\mathit{x}}_{ij}^T\mathit{\beta }+g_i{\beta }_g+{\mathit{z}}_{ij}^T{\mathit{\gamma }}_i+{\mathrm{\epsilon }}_{ij},$$ (Equation 1)

where $y_{ij}$ is individual i’s measurement at occasion $j\in \left\{\mathrm{1,2},\dots ,n_i\right\}$, ${\mathit{x}}_{ij}$ is the $p\times 1$ vector of regressors with corresponding regression coefficients $\mathit{\beta }$, $g_i$ is the genotype dosage of individual i with corresponding genetic mean effect ${\beta }_g$, and ${\mathit{z}}_{ij}$ is the $q\times 1$ vector of covariates with corresponding random effects ${\mathit{\gamma }}_i$. The WS variability is captured by the random terms ${\epsilon }_{ij}$ with mean zero and inhomogeneous variance

$${\sigma }_{{\mathrm{\epsilon }}_{ij}}^2=\text{exp}\left({\mathit{w}}_{ij}^T\mathit{\tau }+g_i{\tau }_g+{\omega }_i\right),$$ (Equation 2)

where ${\mathit{w}}_{ij}$ is the $\ell \times 1$ vector of covariates with corresponding fixed effects $\mathit{\tau }$, ${\tau }_g$ is the genetic effect on the WS variability, and ${\omega }_i$ is a random intercept. We assume that the random effects ${\left({\mathit{\gamma }}_i^T,{\omega }_i\right)}^T$ are independent of ${\epsilon }_{ij}$, have mean zero, and have covariance

$$\text{Var}\left(\begin{array}{l}{\mathit{\gamma }}_i\hfill \\ {\omega }_i\hfill \end{array}\right)={\mathbf{\Sigma }}_{\mathit{\gamma }\omega }=\left(\begin{array}{ll}{\mathbf{\Sigma }}_{\mathit{\gamma }}\hfill & {\mathit{\sigma }}_{\mathit{\gamma }\omega }\hfill \\ {\mathit{\sigma }}_{\mathit{\gamma }\omega }^T\hfill & {\sigma }_{\omega }^2\hfill \end{array}\right).$$

Covariates ${\mathit{x}}_{ij}$, ${\mathit{z}}_{ij}$, and ${\mathit{w}}_{ij}$ typically contain an intercept and can include both time-invariant covariates, e.g., sex and baseline measurements, and time-varying covariates, e.g., age at measurement, medication history, and life-style indicators. Individuals can have varying numbers of observations, which do not need to be aligned.

Given a longitudinal biomarker of interest, our primary goal is to test (1) the mean effect of genotype, $H_0:{\beta }_g=0$, i.e., whether a genotype shifts the mean of the biomarker trajectory; (2) the WS variance effect of genotype, $H_0:{\tau }_g=0$, i.e., whether a genotype changes the WS variation of the biomarker trajectory around its mean; and (3) the joint effect, $H_0:{\beta }_g={\tau }_g=0$, i.e., whether a genotype affects either the mean, or the WS variation, or both. Although for the models in Equation 1 and Equation 2 we use scalar $g_i$ to represent a single genotype, our method and software can also test a group of genotypes or gene-by-environment (G $\times$ E) effects.

The models in Equation 1 and Equation 2 are similar to a multiple location scale model considered by Dzubur et al.,³³ who assume normality of the random effects ${\left({\mathit{\gamma }}_i^T,{\omega }_i\right)}^T$ and ${\mathrm{\epsilon }}_{ij}$ and resort to the maximum likelihood estimation (MLE). Because each iteration of the MLE algorithm requires expensive numerical integration, it is not only distributionally restrictive but also computationally prohibitive. Both limitations prevent its application to genome-wide association studies (GWASs) of biobank data. Instead, we employ our recent estimation method, WiSER,³⁷ which is robust to the misspecification of the trait distribution (conditional on random effects) and the random effects distribution. The estimation algorithm is free of numerical integration and scales linearly in the total number of longitudinal measurements. For example, the run times of the full likelihood approach with the MixWILD software^32,33 on two simulated datasets with 1,000 individuals and ten observations per individual range from 40 min to $10+$ h according to the different modeling assumptions being made, while WiSER takes less than half a second.

Briefly, the WiSER estimator is defined as

$$\begin{array}{l}\hat{\mathit{\beta }},{\hat{\beta }}_g=\text{arg}\underset{\mathit{\beta },{\beta }_g}{\text{min}}\frac{1}{2}\sum _{i=1}^m{\left({\mathit{y}}_i-{\mathit{X}}_i\mathit{\beta }-g_i{\beta }_g\right)}^T{\left({\mathit{V}}_i^{\left(0\right)}\right)}^{-1}\left({\mathit{y}}_i-{\mathit{X}}_i\mathit{\beta }-g_i{\beta }_g\right)\\ \hat{\mathit{\tau }},{\hat{\tau }}_g,{\hat{\mathbf{\Sigma }}}_{\mathit{\gamma }}=\text{arg}\underset{\mathit{\tau },{\tau }_g,{\mathbf{\Sigma }}_{\mathit{\gamma }}}{\text{min}}\frac{1}{2}\sum _{i=1}^m\text{tr}\left({\left({\mathit{V}}_i^{\left(0\right)}\right)}^{-1}{\mathit{R}}_i{\left({\mathit{V}}_i^{\left(0\right)}\right)}^{-1}{\mathit{R}}_i\right),\end{array}$$ (Equation 3)

where ${\mathit{R}}_i=\left({\mathit{y}}_i-{\mathit{X}}_i\hat{\mathit{\beta }}-g_i{\hat{\beta }}_g\right){\left({\mathit{y}}_i-{\mathit{X}}_i\hat{\mathit{\beta }}-g_i{\hat{\beta }}_g\right)}^T-{\mathit{V}}_i\left(\mathit{\tau },{\tau }_g,{\mathbf{\Sigma }}_{\mathit{\gamma }}\right)$,

$${\mathit{V}}_i\left(\mathit{\tau },{\tau }_g,{\mathbf{\Sigma }}_{\mathit{\gamma }}\right)=\left(\begin{array}{lll}\text{exp}\left({\mathit{w}}_{i1}^T\mathit{\tau }+g_i{\tau }_g\right)\hfill & \hfill & \hfill \\ \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & \text{exp}\left({\mathit{w}}_{i{n}_i}^T\mathit{\tau }+g_i{\tau }_g\right)\hfill \end{array}\right)+{\mathit{Z}}_i{\mathbf{\Sigma }}_{\mathit{\gamma }}{\mathit{Z}}_i^T,$$ (Equation 4)

and ${\mathit{V}}_i^{\left(0\right)}={\mathit{V}}_i\left({\mathit{\tau }}^{\left(0\right)},{\tau }_g^{\left(0\right)},{\mathbf{\Sigma }}_{\mathit{\gamma }}^{\left(0\right)}\right)$ is an initial estimator of $\text{Var}\left({\mathit{Y}}_i\right)$. Model parameters are the mean fixed effects $\mathit{\beta }$ and ${\beta }_g$, WS variance fixed effects $\mathit{\tau }$ and ${\tau }_g$, and the random effects covariance ${\mathbf{\Sigma }}_{\mathit{\gamma }}$. In the special case ${\mathit{V}}_i^{\left(0\right)}={\mathit{I}}_{n_i}$, WiSER reduces to a method of moments (MoM) estimate because the objective functions in Equation 3 are simply the least-squares losses for the first two moments of ${\mathit{Y}}_i$. Using an initial estimate ${\mathit{V}}_i^{\left(0\right)}$ improves the estimation efficiency of WiSER. In practice, we set the initial ${\mathit{V}}_i^{\left(0\right)}$ according to a least-squares estimator of $\mathit{\tau }$ and ${\mathbf{\Sigma }}_{\mathit{\gamma }}$. WiSER enjoys a double robustness property. It is robust to the misspecification of both the distribution of random effects ${\left({\mathit{\gamma }}_i^T,{\omega }_i\right)}^T$ and the distribution of ${\mathit{Y}}_i$ conditional on random effects. In TrajGWAS, we employ a score test that only requires fitting one null model, with ${\beta }_g={\tau }_g=0$, across the genome-wide tests. Compared with the Wald test proposed by German et al.,³⁷ which requires fitting WiSER for each genotype, it is much faster and enables fast longitudinal trajectory GWAS analysis at biobank scale.

Robust and scalable score testing

Let ${\theta }_1\in \mathbb{R}$ be the genetic effect ${\beta }_g$ or ${\tau }_g$. We are interested in testing the null hypothesis ${\theta }_1=0$. Let ${\mathit{\theta }}_2\in {\mathbb{R}}^{p+\ell +q\left(q+1\right)/2}$ collect all parameters in the null model. We first derive the score (gradient of the WiSER loss function) ${\mathit{\psi }}_{H_1}$ under the full model and then evaluate it under the null model, i.e., ${\mathit{\psi }}_{H_1}\left(\tilde{\mathit{\theta }}\right)$, where $\tilde{\mathit{\theta }}=\left(0,{\hat{\mathit{\theta }}}_2\right)$ and ${\hat{\mathit{\theta }}}_2$ is the estimate under the null model. The generalized score test statistic³⁸ is

$$T=\frac{1}{m}{\left[\stackrel{m}{\sum _{i=1}}{\mathit{\psi }}_{H_1,i}\left(\tilde{\mathit{\theta }}\right)\right]}^T{\mathit{V}}_{{\mathit{\psi }}_{H_1}\left(\tilde{\mathit{\theta }}\right)}^{-1}\left[\stackrel{m}{\sum _{i=1}}{\mathit{\psi }}_{H_1,i}\left(\tilde{\mathit{\theta }}\right)\right],$$

where ${\mathit{V}}_{\mathit{\psi }}$ is the variance of score $\mathit{\psi }$. The score test statistic T is asymptotically distributed as ${\chi }_1^2$ under the null model. In supplemental methods, section A, we show that the scores for testing ${\beta }_g=0$ and ${\tau }_g=0$ are

$$S_{{\beta }_g}=\stackrel{m}{\sum _{i=1}}\left[1_{n_i}^T{\left({\mathit{V}}_i^{\left(0\right)}\right)}^{-1}{\hat{\mathit{r}}}_i\right]g_i=:{\mathit{c}}_{{\beta }_g}^T\mathit{g}$$

and

$$S_{{\tau }_g}=-\stackrel{m}{\sum _{i=1}}\left\{1_{n_i}^T\text{diag}\left[\left(\begin{array}{lll}{e}^{{\mathit{w}}_{i1}^T\hat{\mathit{\tau }}}\hfill & \hfill & \hfill \\ \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & e^{{\mathit{w}}_{i{n}_i}^T\hat{\mathit{\tau }}}\hfill \end{array}\right){\left({\mathit{V}}_i^{\left(0\right)}\right)}^{-1}{\hat{\mathit{R}}}_i{\left({\mathit{V}}_i^{\left(0\right)}\right)}^{-1}\right]\right\}{g}_i=:{\mathit{c}}_{{\tau }_g}^T\mathit{g}$$

respectively. The quantities ${\hat{\mathit{r}}}_i={\mathit{y}}_i-{\mathit{X}}_i\hat{\mathit{\beta }}$, ${\hat{\mathit{R}}}_i$, $\hat{\mathit{\tau }}$, and ${\mathit{V}}_i^{\left(0\right)}$ are readily available from the fitted null model. Calculation of each score involves linear combination of the genotype dosages with the coefficient vector ${\mathit{c}}_{{\beta }_g}$ or ${\mathit{c}}_{{\tau }_g}$ pre-computed and cached. In supplemental methods, section A, we show that the calculation of variance ${\hat{\mathit{V}}}_{\mathit{\psi }}$ costs $O\left(1\right)$ flops. Therefore, forming each score test statistic costs $O\left(m\right)$ flops, where m is the number of individuals, usually much smaller than the total number of longitudinal measurements n. This extreme computational efficiency makes TrajGWAS easily scalable to biobank data with ${10}^5\sim {10}^6$ samples and millions of SNPs.

Saddlepoint approximation for rare variant testing

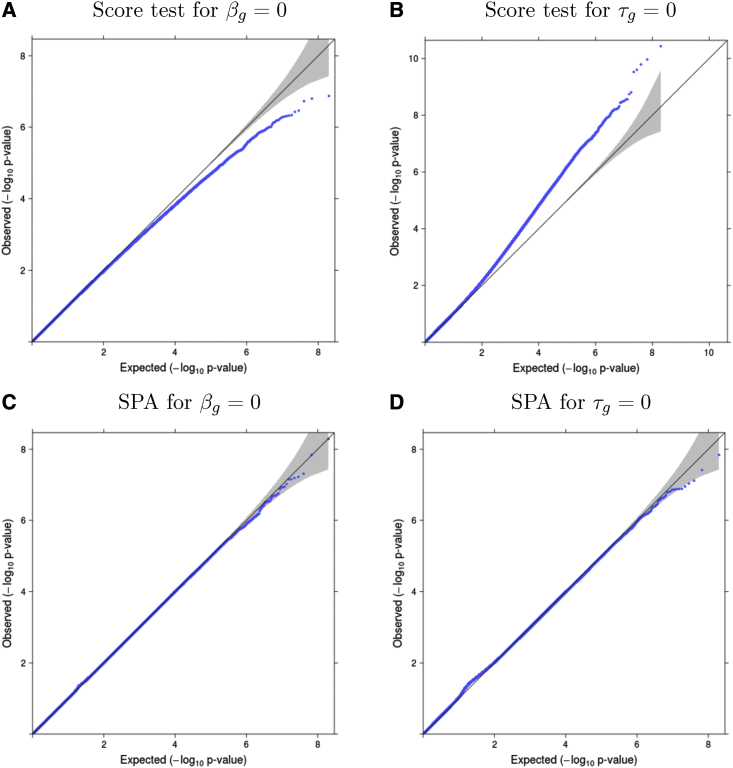
It is well-known that asymptotic score tests may yield deflated or inflated type I errors at stringent significance levels for rare variants with MAF $<$ 0.01.^39,40 Figures 2A and 2B show that, when testing a null variant with MAF $=0.01$, the score test shows deflation in testing ${\beta }_g$ and inflation in testing ${\tau }_g$. To calibrate the null distribution for score statistics when testing rare variants, we apply a saddlepoint approximation (SPA).^{39, 40, 41, 42, 43} This approach uses the entire cumulant generating function (CGF) to approximate the null distribution instead of the first two moments as in the normal approximation and Satterthwaite method,⁴⁴ resulting in superior performance. For testing a single variant, we directly use the score, $S_{{\beta }_g}$ or $S_{{\tau }_g}$, as the test statistic. Since the CGFs of $S_{{\beta }_g}$ and $S_{{\tau }_g}$ do not have a simple closed-form expression, we use the empirical CGF based on the empirical moment generating function (MGF). Details are provided in the supplemental methods, section B. Because the normal approximation of the score test performs well near the mean of the distribution, to save on computation, we only apply SPA when the observed score statistic is large. Following Bi et al.,³⁹ SPA is applied when $\left|S_{{\beta }_g}\right|>r\sqrt{\text{Var}\left({\mathit{c}}_{{\beta }_g}\right)\text{Var}\left(\mathit{g}\right)}$ and $\left|S_{{\tau }_g}\right|>r\sqrt{\text{Var}\left({\mathit{c}}_{{\tau }_g}\right)\text{Var}\left(\mathit{g}\right)}$ for testing ${\beta }_g$ and ${\tau }_g$, respectively. In this paper, we use $r=0.75$ for all analyses. A smaller value of r leads to more tests having SPA applied and increased computational time. For the joint test of null hypothesis ${\tau }_g={\beta }_g=0$, we compute p values for both $S_{{\tau }_g}$ and $S_{{\beta }_g}$ and then take their harmonic mean.⁴⁵

Figure 2.

Quantile-quantile (QQ) plots of p values for simulation studies

(A and B) Quantile-quantile (QQ) plots of p values from the score test for testing β_g (A) and for testing τ_g (B), where m = 6,000, n_i = 6 to 10, and minor allele frequency (MAF) = 0.01, based on 10⁹ replicates.

(C and D) QQ plots of SPA-corrected p values for testing β_g (C) and for testing τ_g (D); simulations are based on m = 6,000, n_i = 6 to 10, and minor allele frequency (MAF) = 0.01. SPA corrects the deflation or inflation that occurs in the score test at low MAFs. QQ plots for all simulation scenarios are shown in Figures S2–S5.

Simulations

We carry out simulations to evaluate type I error rates and power of TrajGWAS. For each subject, we generate the response according to the models in Equation 1 and Equation 2. In our simulations, the random mean effect ${\mathit{\gamma }}_i$ is intercept only so ${\mathit{Z}}_i$ is a single column of 1’s. ${\mathit{X}}_i$ and ${\mathit{W}}_i$ contain a random time-invariant binary variable (0 or 1) in their second columns, a time-invariant standard normal variable in their third columns, and a time-varying standard normal variable in their fourth columns. The true regression coefficients are $\mathit{\beta }={\left(10.0,5.0,0.5,-0.3\right)}^T$ and $\mathit{\tau }={\left(0.25,0.3,-0.15,0.1\right)}^T$. We generate the random effects $\left({\gamma }_i,{\omega }_i\right)$ from the multivariate normal distribution with mean zero and covariance ${\mathbf{\Sigma }}_{\mathit{\gamma }\omega }=\left(\begin{array}{ll}2.0\hfill & 0.0\hfill \\ 0.0\hfill & 0.1\hfill \end{array}\right).$

For both type I error and power simulations, we consider 12 scenarios with different combinations of (1) sample sizes: $m=\mathrm{6,000}$ and $m=\mathrm{100,000}$, (2) number of repeated-measurements: $n_i=6\text{ to }10$ and $n_i=10\text{ to }30$, and (3) MAF: 0.01, 0.05 and 0.3 for $m=\mathrm{6,000}$ and 0.001, 0.05 and 0.3 for $m=\mathrm{100,000}$. Results of both the score test and SPA are reported.

Type I error

To evaluate type I error rates at genome-wide significance level $\alpha =5\times {10}^{-8}$, for each scenario we generate 1,000 datasets each with ${10}^6$ variants following Hardy-Weinberg equilibrium, yielding ${10}^9$ total replicates.³⁹ We report type I error rates for testing the genetic contribution to both the mean, ${\beta }_g$, and the WS variance, ${\tau }_g$.

Power

To evaluate the power for testing ${\tau }_g$ and ${\beta }_g$, we generate 100 datasets under the alternative model for each scenario. In each dataset, the alternative model uses the parameters in simulations and contains ten causal variants each with the same effect size, selected specific to each scenario in order to show the spread of power. We compare power of the score test and SPA at the significance level $\alpha =5\times {10}^{-8}$.

Application to the UK Biobank study

We conduct TrajGWAS analysis by using longitudinal biomarker measures extracted from the UK Biobank primary care data, including systolic blood pressure (SBP), diastolic blood pressure (DBP), pulse pressure (PP), high-density lipoprotein (HDL) cholesterol, low-density lipoprotein (LDL) cholesterol, total cholesterol (TC), triglycerides, glucose (fasting and random), hemoglobin A1C (HbA1c), and body mass index (BMI). Record-level access to primary care data is obtained by requesting field 42040 (“GP clinical event records”) from the UK Biobank showcase. We combine a previously reported and validated semi-supervised approach⁴⁶ and in-house extraction criteria to create clinical biomarker phenotypes. We matched and compared empirical cumulative distributions of extracted lab values from the primary care database and those provided through the UK Biobank assessment center to infer the measurement units and for further quality control (Figure S16). Detailed data extraction, unit conversion, and quality control procedures are documented in the supplemental methods, section D.

For each GWAS, we use the standardized biomarker phenotypes for TrajGWAS analysis by subtracting the overall mean from each measurement and dividing by the standard deviation and we adjust for ten principal components (PCs) on the mean component. Using the PCs to adjust both the mean and WS variance makes no differences for the final results. Each biomarker uses a different covariate adjustment scheme, which is detailed in supplemental methods, section E. In general, we adjust for sex, age, age², and age $\times$ sex for both mean and WS variability; age and age² are treated as time-varying covariates. The selection of covariates is guided by previous GWAS analyses^4,47,48 and the mean profile plots are shown in the Figure S15. Non-significant covariates in the null model are then removed from the GWAS analysis. In addition, we include self-reported diabetes status as a time-fixed covariate for glycemic measures (HbA1c and random and fasting glucose). Diabetes status included as a time-varying indicator is also explored (supplemental methods, section F). Summary of the covariates included and adjustments made for medication is summarized in supplemental methods, section E.

Controlling the effect of medication on the biomarkers is important in the analysis. Most widely used methods for such adjustments are (1) treatment modeled as an additional covariate (“indicator”);^{49, 50, 51} (2) adding a sensible constant (“shifting”) to the treated subjects;^{48,52, 53, 54, 55} and (3) censored normal regression.⁵⁶ Shifting and censored normal regression are often recommended for their superior performances over the indicator method.⁵⁶ In this paper, we use the shifting method if a sensible value for adjustment is available through previous studies and use the indicator method for others. We compare adjustment by shifting and adjustment by an additional covariate in Figures S21–S24. For blood pressures, we add 15 mmHg for SBP and 10 mmHg for DBP⁵⁵ for subjects taking blood-pressure-lowering medication before standardization. For lipids, following previous GWAS analysis,⁴⁷ we add 0.208 mmol/L for triglycerides, 1.347 mmol/L for total cholesterol, 1.290 mmol/L for LDL cholesterol, and subtract 0.060 mmol/L for HDL cholesterol for participants on lipid-controlling treatments. For glycemic measures (HbA1c and random and fasting glucose), a sensible value for adjustment was not available, so they are adjusted with the indicator method.

To evaluate and compare the genetic association of trajectory means, i.e., ${\beta }_g$, we create lists of previously reported genetic associations for each analyzed trait by using the GWAS Catalog⁵⁷ queried by the R package gwasrapidd⁵⁸ (curated on 7/8/2021). We search the catalog for phenotypes matching our analyzed biomarkers by using syntax, “efo_trait=,” and keep SNPs with p value less than genome-wide significance level $<5\times {10}^{-8}$.

Results

Simulation

Table 1 reports the empirical type I error rates of the score test and SPA at an $\alpha =5\times {10}^{-8}$ threshold, based on ${10}^9$ simulation replicates. At lower MAFs, the score test for ${\tau }_g$ has substantially inflated type I errors, whereas SPA leads to well-calibrated type I error rates. Inflation in the score test for ${\tau }_g$ at less common alleles (MAF = 0.05) is large for smaller sample sizes and fewer repeated measures. The amount of type I error inflation decreases as the MAF and the number of repeated measures increase. For ${\beta }_g$, the score test is conservative at lower MAFs and SPA corrects the type I error in the right direction. For common alleles such as MAF = 0.3, score test and SPA do not differ much in the type I error rates for either ${\tau }_g$ or ${\beta }_g$. Overall SPA has appropriate type I error at the $\alpha =5\times {10}^{-8}$ significance level across all scenarios. Figure 2 illustrates how SPA corrects type I error in both directions by displaying QQ plots from a random sample of 100 million replicates of the $m=6000,n_i=6$ to 10, MAF = 0.01 scenario. Additional QQ plots are presented in Figures S2–S5.

Table 1.

Empirical type I error rates for the simulation studies

Simulation conditions			Empirical type I error rate (standard error)$\times {10}^{-8}$
Sample size m	$n_i$	MAF	${\beta }_g$score	${\beta }_g$SPA	${\tau }_g$score	${\tau }_g$SPA	Joint score	Joint SPA
6,000	6 to 10	0.01	0.30 (0.17)	4.00 (0.63)	138.50 (3.72)	3.50 (0.59)	80.80 (2.84)	4.10 (0.64)
6,000	6 to 10	0.05	3.30 (0.57)	4.10 (0.64)	34.50 (1.86)	6.30 (0.79)	22.90 (1.51)	5.90 (0.77)
6,000	6 to 10	0.3	4.10 (0.64)	4.20 (0.65)	4.80 (0.69)	4.30 (0.66)	4.80 (0.69)	4.40 (0.66)
6,000	10 to 30	0.01	0.40 (0.20)	6.00 (0.77)	42.70 (2.07)	4.00 (0.63)	23.20 (1.52)	4.20 (0.65)
6,000	10 to 30	0.05	4.00 (0.63)	4.90 (0.70)	20.50 (1.43)	5.10 (0.71)	12.80 (1.13)	5.50 (0.74)
6,000	10 to 30	0.3	4.50 (0.67)	5.20 (0.72)	6.60 (0.81)	6.00 (0.77)	5.20 (0.72)	6.00 (0.77)
100,000	6 to 10	0.001	1.20 (0.35)	4.80 (0.69)	136.80 (3.70)	4.40 (0.66)	80.90 (2.84)	3.90 (0.62)
100,000	6 to 10	0.05	5.00 (0.71)	5.00 (0.71)	6.20 (0.79)	5.10 (0.71)	5.80 (0.76)	5.60 (0.75)
100,000	6 to 10	0.3	4.10 (0.64)	4.00 (0.63)	5.30 (0.73)	5.50 (0.74)	5.40 (0.73)	5.30 (0.73)
100,000	10 to 30	0.001	2.40 (0.49)	5.80 (0.76)	50.80 (2.25)	4.80 (0.69)	28.50 (1.69)	5.40 (0.73)
100,000	10 to 30	0.05	5.40 (0.73)	5.10 (0.71)	7.60 (0.87)	6.50 (0.81)	7.20 (0.85)	6.20 (0.79)
100,000	10 to 30	0.3	6.30 (0.79)	6.10 (0.78)	4.00 (0.63)	3.90 (0.62)	5.40 (0.73)	5.70 (0.75)

Empirical type I error rates (standard error) for the score test and SPA ($\times {10}^{-8}$) at a significance level $5\times {10}^{-8}$ based on ${10}^9$ simulation replicates. The score test shows inflated type I error at low minor allele frequencies (MAFs) for testing ${\tau }_g$ where SPA (saddlepoint approximation) has proper type I error rates. Joint score and joint SPA are based on the harmonic means of the respective ${\beta }_g$ and ${\tau }_g$ p values.

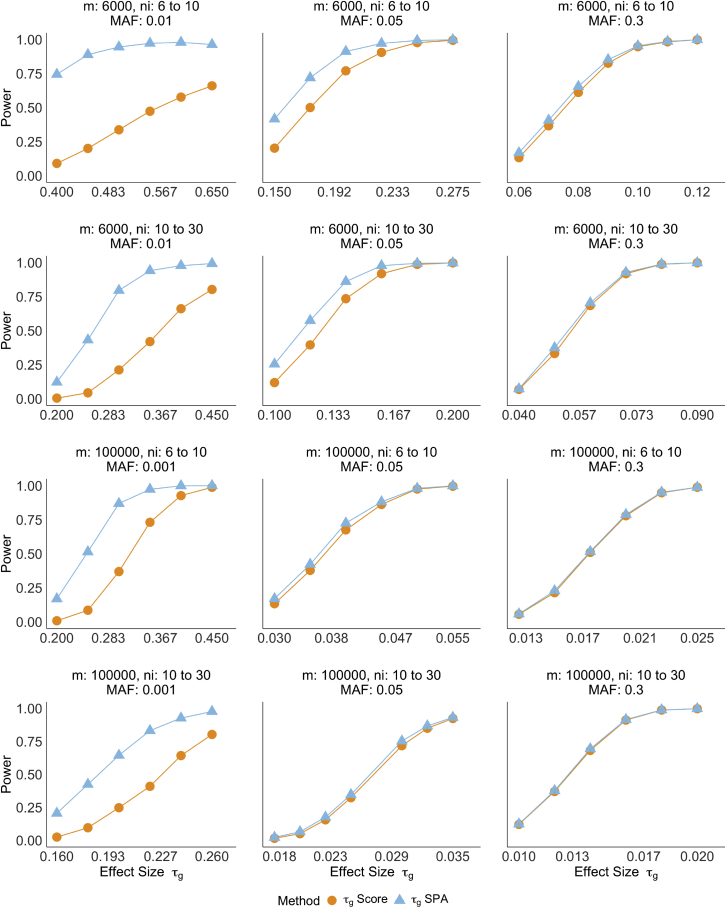
Power curves for testing ${\tau }_g$ and ${\beta }_g$ across 12 scenarios are displayed in Figure 3 and Figure S6, respectively. Although the score test is unable to adequately control type I error for rare variants, we still report power based on the nominal power at the $\alpha =5\times {10}^{-8}$ significance level. Using the empirical significance levels estimated from the type I error simulations would result in even lower power for the score test than what is shown in the figure. SPA achieves higher power at the $\alpha =5\times {10}^{-8}$ significance level than the score test when the MAF is low, but the power of the two methods are nearly identical for common variants and large sample sizes. In conjunction with the type I error results, this indicates that SPA is able to better model the tail of the test statistic distributions for rare variants. When the variants are common, both approaches converge to the same results.

Figure 3.

Empirical powers of testing ${\beta }_g$ with score test and SPA

Each row contains the same sample size m and number of observations per individual $n_i$. Power is evaluated at the significance level $\alpha =5\times {10}^{-8}$. Each scenario is based on 1,000 replicates.

Computational efficiency

With careful implementation, each iteration of the optimization algorithm for fitting the WiSER null model scales linearly in the total number of observations n. For testing a single SNP, our score test with SPA scales linearly with the sample size m. Therefore, our TrajGWAS analysis based on WiSER can be applied to longitudinal genetic association analysis at biobank scale. For example, analyzing SBP for 10,805,717 imputed variants on all autosomal chromosomes takes about 150 central processing unit (CPU) h with SPA and 139 CPU h without SPA. The computation is split into 16 chunks per chromosome, resulting in 352 separate computational jobs that can run simultaneously on computing clusters. Under these conditions, each job runs within an hour with and without SPA.

Real data analysis

About 44% of the 500,000 UK Biobank participants are linked to their primary care EHR data. These EHR data are recorded with four controlled clinical terminologies: (1) Read version 2 (Read v2); (2) Clinical Terms Version 3 (CTV3); (3) British National Formulary (BNF); and (4) the Dictionary of Medicines and Devices (DM+D). Only Read v2 and CTV3 are relevant for biomarker extraction. Using previously validated algorithms,^46,59 we generate unified lists of Read v2 and CTV3 clinical terms, and extract measurements for all biomarkers from the clinical event records (gp_clinical table). Terms used for extraction are shown in Table S2. Ten longitudinal clinical measurements are extracted: blood pressures (SBP and DBP), HDL, LDL, total cholesterol, triglycerides, blood glucose (fasting and random), HbA1c, and BMI (supplemental methods, section D). Extracted records cover 55,000 to 150,000 participants. The flowcharts for creating the cohort for each biomarker are displayed in Figures S7–S14. There are more repeated-measures of SBP and DBP (median (IQR) = 12 (6, 24)) than of the lipid values (e.g., median (IQR) = 4 (2, 8) for HDL). See Table 2 for details. Taking blood pressure as an example, we exclude observations with no date or invalid date information, or missing BMI measures at recruitment, resulting in 2,598,484 observations. The sample size for GWAS analysis ranges from 55,949 (fasting glucose) to 148,870 (blood pressure). Patterns of the mean profile over age groups vary across different biomarker groups (Figure S15). DBP, LDL, and total cholesterol show strong non-linear, age-dependent trends.

Table 2.

Sample size m, the number of repeated-measurements $n_i$, and summary statistics for eleven biomarkers extracted from the UK Biobank primary care data

	m	$n_i$	$y_{ij}$	Female	Age	BMI
Biomarker	Sample size	Median (IQR)	Mean (SD)	%	Mean (SD)	Mean (SD)
SBP (mmHg)	148,870	12 (6, 24)	135.0 (15.3)	54.1	56.0 (8.7)	27.5 (4.8)
DBP (mmHg)	148,870	12 (6, 24)	81.0 (8.7)	54.1	56.0 (8.7)	27.5 (4.8)
PP (mmHg)	148,870	12 (6, 24)	53.9 (9.6)	54.1	56.0 (8.7)	27.5 (4.8)
HDL (mmol/L)	129,069	4 (2, 8)	1.5 (0.4)	53.1	59.5 (7.8)	27.7 (4.8)
LDL (mmol/L)	98,556	3 (1, 6)	3.2 (0.9)	52.3	59.3 (7.8)	27.8 (4.8)
Total cholesterol (mmol/L)	133,590	5 (2, 10)	5.4 (0.9)	53.3	58.7 (7.9)	27.6 (4.8)
Triglycerides (mmol/L)	124,092	4 (2, 8)	1.6 (1.0)	48.1	60.6 (7.8)	28.6 (5.0)
Fasting glucose (mmol/L)	55,949	2 (1, 3)	5.5 (1.4)	47.7	60.4 (7.6)	28.7 (5.1)
Random glucose (mmol/L)	97,162	2 (1, 4)	5.7 (2.1)	51.9	59.8 (8.2)	28.5 (5.1)
HbA1c (%)	70,589	2 (1, 4)	6.7 (1.4)	43.4	62.4 (7.8)	30.4 (5.7)
BMI	144,414	5 (3, 9)	28.3 (5.7)	54.9	57.3 (9.9)	–

The eleven biomarkers are as follows: SBP, systolic blood pressure; DBP, diastolic blood pressure; PP, pulse pressure = SBP – DBP; HDL, high-density lipoprotein; LDL, low-density lipoprotein; total cholesterol; triglycerides; random glucose; fasting glucose; HbA1c, hemoglobin A1C; and BMI, body mass index.

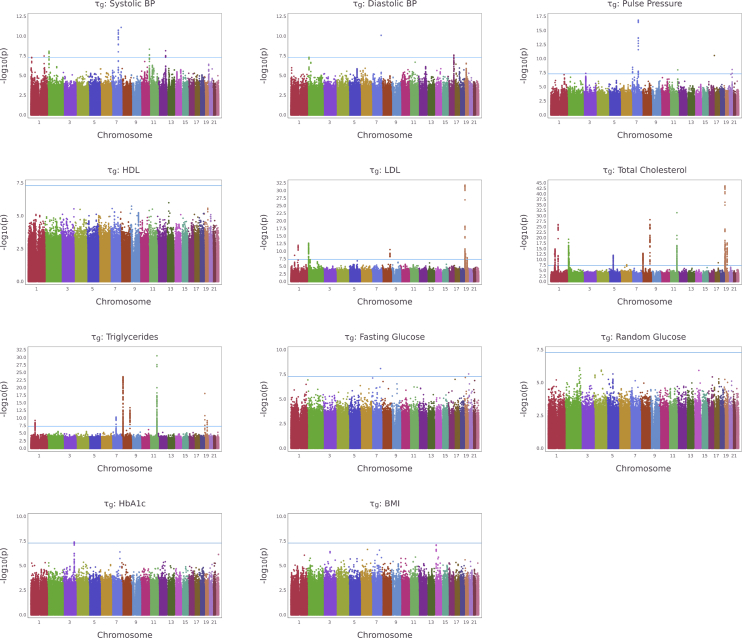
We then apply TrajGWAS to UK Biobank imputed genetic data among European ancestry for these ten longitudinal clinical measures and one derived phenotype pulse pressure (PP = SBP − DBP). SNPs with MAF greater than 0.002 and imputation quality score (infoscore or $r^2$) greater than 0.3 are included in the analyses. The Manhattan plots (Figure 4 for ${\tau }_g$ and Figure S17 for ${\beta }_g$) and quantile-quantile (QQ) plots (Figures S18 and S19) show that TrajGWAS successfully identifies a large number of loci. Concordant with the simulation study, the QQ plots suggest that SPA controls type I error rates well. Highly polygenic traits with a larger number of associated variants have, on average, larger genomic control factor $\left({\lambda }_{GC}\right)$ values (Figures S18 and S19). Additionally, since SPA is not applied when the score statistics are close to the mean, the median p values used for calculation of the genomic control factor may be miscalibrated.⁴⁰ Thus, even though many QQ plots appear normal for ${\tau }_g$, the reported ${\lambda }_{GC}$ is inflated for some traits. To give a complete picture, we report ${\lambda }_{GC}$ calculated at different p value quantiles for each trait in Table S3.

Figure 4.

Manhattan plots for testing ${\tau }_g$ for longitudinal markers in the UK Biobank study

Manhattan plots for testing ${\tau }_g$, the effects of the WS variability, for 11 longitudinal biomarkers in the UK Biobank study. The blue line represents the genome-wide significance level, $5\times {10}^{-8}$.

Next, we compare associations identified by TrajGWAS with those reported in the GWAS Catalog. We extract association results from the GWAS Catalog by using the Experimental Factor Ontology (EFO) trait labels and keep the unique associations, i.e., SNPs, with p value $<5\times {10}^{-8}$. The number of associations from TrajGWAS analysis is shown in the second and third columns of Table 3. Data in the GWAS Catalog are mapped to genome assembly GRCh38, while UK Biobank SNPs are mapped to GRCh37. We remove the queried SNPs with no genomic coordinates and convert GWAS Catalog associations to genome assembly GRCh37. The numbers of associated SNPs are shown in the fourth column of Table 3. Using the associations reported in the GWAS Catalog as positive controls, we evaluate whether SNPs associated with the mean from our TrajGWAS analysis can replicate previous findings (fifth column of Table 3). For eight out of eleven markers, we have replication rates higher than 80%, validating high quality of EHR-based biomarker phenotyping and TrajGWAS analysis. The analysis of HbA1c has the lowest replication rate 59.65%. This may be due to the relatively small sample size among all biomarkers and the differences in distribution of HbA1c measures from EHR (see Figure S16). The last column of Table 3 lists the numbers of SNPs TrajGWAS identifies as “novel,” i.e., not in linkage disequilibrium (LD) with the existing SNPs in the GWAS Catalog (defined as being greater than one megabase from any SNP in the GWAS Catalog). Tables S4–S11 provide additional annotations for these “novel” SNPs. As an example, for total cholesterol, there are 177 and 209 SNPs associated with mean and WS variability that are at least 1 Mb away from the existing reported GWAS Catalog SNPs, respectively. Additional annotations shown in Table S8 demonstrate that the majority of SNPs reported to be “novel” for total cholesterol are relevant to lipids traits as well as psychiatric disorders. These findings are consistent with the possibility of a disease-specific lipid pathway underlying the pathophysiology of psychiatric disorders.⁶⁰

Table 3.

Summary of TrajGWAS results

Biomarkera	Num. of sig. loci for${\beta }_g/{\tau }_g$b,c	Num. of sig. SNPs for${\beta }_g/{\tau }_g$d	Num. of sig. SNPs in GWAS Cataloge	Replication rate${\beta }_g$f	Num. of sig. SNPs for${\beta }_g/{\tau }_g>1$Mb from GWAS Catalog SNPsg
SBP	269/8	4,720/32	1,738	82.48%	0/1
DBP	368/3	7,374/5	917	79.65%	615/0
PP	371/8	6,895/32	876	89.34%	93/0
HDL	1,443/0	14,068/0	1,953	88.62%	24/0
LDL	826/23	8,160/434	1,654	83.57%	0/0
Total cholesterol	1,356/92	16,002/1,525	1,270	95.06%	177/209
Triglycerides	1,172/55	11,796/820	1,693	87.57%	2/0
Fasting glucose	166/2	1,540/2	110	86.67%	144/2
Random glucose	81/0	824/0	256	73.63%	10/0
HbA1c	73/1	1,820/4	651	59.65%	11/0
BMI	220/0	3,651/0	3,507	86.95%	1/0

^aExperimental Factor Ontology (EFO) trait labels (see web resources) used for query are as follows: SBP, “systolic blood pressure (EFO_0006335)”; DBP, “diastolic blood pressure (EFO_0006336)”; PP, “pulse pressure measurement (EFO_0005763)”; HDL, “high-density lipoprotein cholesterol measurement (EFO_0004612)”; LDL, “low-density lipoprotein cholesterol measurement (EFO_0004611)”; total cholesterol, “total cholesterol measurement (EFO_0004574)”; triglycerides, “triglyceride measurement (EFO_0004530)”; HbA1c, “HbA1c measurement (EFO_0004541)”; fasting glucose, “fasting blood glucose measurement (EFO_0004465)”; random glucose, “glucose measurement (EFO_0004468)”; BMI, “body mass index (EFO_0004340)” and “longitudinal BMI measurement (EFO_0005937).”

^bSignificant SNPs for each biomarker are clumped via PLINK 1.9.⁶¹ Index variants are chosen greedily starting with the SNPs with lowest p value among those SNPs having p value $\le 5\times {10}^{-8}$. Sites that are $<250$ kb away from an index variant and $r^2>0.5$ with the index variant are assigned to that index variant’s clump.

^cThe number of significant loci (after clumping).

^dThe number of significant SNPs $\left(<5\times {10}^{-8}\right)$ on ${\beta }_g$ and ${\tau }_g$.

^eNumber of GWAS Catalog SNPs with p value $<5\times {10}^{-8}$ (all SNPs are converted to genome build 37; the SNPs with no genomic coordinates are removed; and GWAS Catalog stores the most significant SNP from each independent locus).

^fPercent of significant SNPs from GWAS Catalog that are nominally significant in ${\beta }_g$ (p value $<0.05$) in the TrajGWAS analysis.

^gThe number of SNPs at least 1 megabase (Mb) away from any previously reported SNP for the given biomarker in the GWAS Catalog.

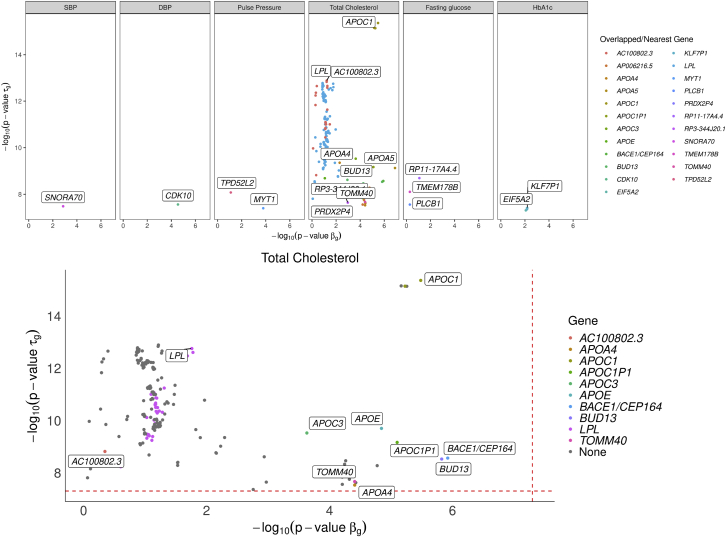
The majority of genes that affect WS variability of a trajectory also affect mean, but not always. Figure 5 highlights the 235 SNPs that are significantly associated with WS variability but not with mean levels with p values and gene annotations. Consistent with our simulation, with too few longitudinal measures, it is hard to detect ${\tau }_g$ at genome-wide significance level, e.g., random glucose (median $n_i=2$), fasting glucose (median $n_i=2$), and HbA1c (median $n_i=2$). For traits with median $n_i>4$, there are signals in ${\tau }_g$. In particular, TrajGWAS identifies a genome-wide significant association between WS variability of total cholesterol and variants in the LPL gene (MIM: 609708), whereas they are not associated with the mean values. LPL is a protein-coding gene for lipoprotein lipase, which is expressed in heart, muscle, and adipose tissue. Severe mutations that cause LPL deficiency result in type I hyperlipoproteinemia, while less extreme mutations in LPL are linked to many disorders of lipoprotein metabolism.⁶² Several GWASs have identified the association of LPL with different lipid-related phenotypes.^63,64 Figure S20 displays a boxplot of within-sample variance of residuals for subjects with 0, 1, and 2 copies of reference allele of rs6993414, the most significant SNP in terms of ${\tau }_g$ on LPL. It shows there are big differences in the tail distributions between them. Other examples include the association between HbA1c WS variability and the EIF5A2 gene (MIM: 605782). EIF5A2 is a protein-coding gene associated with type 2 diabetes and cancer.⁶⁵ Interestingly, a variant, rs8192675, and its proxies show the strongest association with HbA1c response to metformin; its LD block covered three genes and EIF5A2 is one of them.⁶⁶

Figure 5.

SNPs that significantly change the WS variability while not significantly shifting the mean

SNPs that significantly change the WS variability of longitudinal biomarkers (top) and total cholesterol (TC) trajectory (bottom) while not significantly shifting the mean of their trajectories. Each dot is a SNP that passes the genome-wide significance level (dashed line) for ${\tau }_g$ but not for ${\beta }_g$.

TrajGWAS differs from the vQTL, which is predominantly used among cross-sectional studies and for G $\times$ E interaction screening. For a BMI analysis adjusted for age, sex, and ten PCs with the OSCA software (see web resources), 13 of the 22 vQTLs previously reported in Wang et al.²⁵ have a significant vQTL on the same gene (p value $<2\times {10}^{-9}$) in our cohort. One well-known vQTL for BMI is the FTO gene, and variants in this gene are previously found to be associated with BS variance of BMI with very low p values.²⁵ Our cohort yields the lowest p value of $1.16\times {10}^{-102}$ for vQTL analysis. However, ${\tau }_g$ for WS variability of TrajGWAS minimum p value in the same region is $1.18\times {10}^{-4}$, showing no significant SNP association with WS variability.

Discussion

We provide a genome-wide trajectory analysis tool, TrajGWAS, for simultaneous testing of genetic effects on the mean and WS variability of a longitudinal biomarker for biobank-scale studies. The method relies on a mixed-effects location scale model but has several advantages over existing methods. For example, the likelihood-based approach for fitting the mixed effect location scale model requires computationally intensive numerical integration, making it infeasible to implement for genome-wide scans of biobank data.^30,32,33 TrajGWAS relies on M-estimation asymptotics and is both computationally efficient and robust to distributional assumptions. It also does not assume the WS variability is constant and can capture and control for the effects of time-varying covariates such as medication usage and age. We use empirical SPA to calibrate p values so that type I error rates can be well controlled for rarer variants and when the number of repeated measures is small. Through extensive simulation studies and application to UK Biobank data, we demonstrate that TrajGWAS scales well for millions of markers, hundreds of thousands of individuals, and multiple random effects while retaining well-controlled type I error rates and power. One limitation of the SPA approach is that its construction only works for a single univariate hypothesis. Thus, for the joint test ${\beta }_g={\tau }_g=0$, we resort to the less satisfactory harmonic mean approach,⁴⁵ which might compromise power.

Although originally motivated by the study of longitudinal biomarkers, TrajGWAS is also applicable to genome-wide scans of multiple, correlated phenotypes. The flexible LMM framework is apt to capture the correlations between traits and yields correct and powerful inference. TrajGWAS can also be used as a scanning tool by only testing SNPs that pass a threshold with the much slower but more powerful likelihood-based approaches. Although this paper focuses on genetic effects for the mean and WS variability, many studies are also interested in BS variance. It is possible to adapt this framework for modeling BS variability, but it comes at the cost of excluding random slopes in the model that are important in many situations.

Our findings raise a potential red flag for some existing Mendelian randomization (MR) analyses. A core assumption in MR is that the genetic determinant used as an instrument, G, only affects the outcome, Y, through the exposure, X (no horizontal pleiotropy). Many studies use mean levels of measurements as the exposure (e.g., blood pressure and cholesterol levels). This assumption may be violated in cases where (1) the outcome is associated with WS variability of the exposure independent of mean levels, such as blood pressure and glucose variability,^14,16 and (2) variants that affect both mean and WS variability are used as instruments. In our TrajGWAS analysis, we find many SNPs that affect the mean also affect the WS variability. This suggests that the causal effects of the exposures on the outcomes estimated through these MRs may be biased because of a failure to account for the effect of the genetic determinant on the outcome acting through a second exposure (WS variability). This application gap may also provide an opportunity for new MR method development by considering both exposures.

Our method can incorporate time-varying covariates adjustment for both mean and WS variability. It makes controlling for disease status and medication usage over time possible, which sometimes increases the power (supplemental methods, section F). However, caution must be taken when considering disease and medication covariate adjustment. As medications types or disease status may be reversely correlated with biomarkers, the true genetic susceptibility can be obscured. How to best account for these effects remains an important question in future EHR-based longitudinal biomarker studies. One possible direction is a joint model that can model the biomarker trajectory, while simultaneously learning the association between disease trajectory (e.g., comorbidity events).

In conclusion, we present an ultra-efficient biobank-scale trajectories analysis tool that makes EHR-derived longitudinal traits analysis possible at very large scales. By modeling both mean effects and within subject variability, our method can provide insights that are not evident when the effects of genetic variants are only considered for the mean.

Published: February 22, 2022

Data and code availability

The data that support the findings of this study are available from UK Biobank repositories. The UK Biobank data are retrieved under Project ID: 48152. Data are available at https://www.ukbiobank.ac.uk with the permission of the UK Biobank. The code generated during this study are available at https://github.com/OpenMendel/TrajGWAS.jl. GWAS summary statistics are available at https://kose-y.github.io/TrajGWAS-resources/.

Web resources

• Experimental Factor Ontology, https://www.ebi.ac.uk/ols/ontologies/efo

• GWAS Catalog, https://www.ebi.ac.uk/gwas/home

• gwasrapidd R package, https://github.com/ramiromagno/gwasrapidd

• OSCA software, https://cnsgenomics.com/software/osca

• UK Biobank, https://www.ukbiobank.ac.uk/