Abstract
The SARS-Cov-2 has spread differently over space and time worldwide. By monitoring the contagion’s time evolution, the November 3 2020 the Italian government introduced differentiated regime of restrictions among its regions. This experiment demonstrated that public health policies can be effectively designed by means of clustering. This paper proposes a fuzzy clustering model where spatial and temporal dimensions of the disease spread are optimally weighted. The resulting model is applied with the aim of identifying groups of Italian regions with similar contagion spread. We found that two groups of regions sharing similar patterns of COVID-19 spread over both space and time exist. Appropriate public health policies can be designed on the basis of this evidence.
Keywords: Spatial auto-correlation, Time series, Fuzzy clustering, LISA, COVID-19, Policy design
1. Introduction
The spread of COVID-19 among the Italian regions and provinces did not follow a uniform spatio-temporal pattern (Dickson et al., 2020). This fact motivated specific measures at regional level to prevent and contain the epidemic.
Starting from January 2020, a total of 844 legislative acts have been issued by the Italian government to manage the spread of the coronavirus, with an average of 35 per month.1 To further contain the contagion spread, on November 3 2020 a new measure2 was experimented. This measure introduced a differentiated regime of restrictions among the Italian regions. More in detail, each region has been assigned to a color cluster based on the temporal trend of the epidemic and the risk of contagion. In a first cluster indicated with the yellow color, all the regions with a moderate risk of contagion were grouped. In a second cluster, the orange one, there were regions with medium-high risk, while those with the highest risk of contagion were placed in the cluster with red color.
In practice, the Italian government showed how the containment of COVID-19 spread can be done by means of geographical areas clustering, demonstrating its usefulness also for public health policy decisions. In other words, clustering can be used for the definition of differentiated local treatments. However, while it is well known that COVID-19 spread has a spatial dimension (Cordes and Castro, 2020), the Italian government limited the attention on the contagion time evolution. In what follows, following recent contributions on the topic (e.g. see D’Urso et al., 2021a, D’Urso et al., 2021b, Lopez-Oriona et al., 2021), we argue that spatial dimension has to be taken into consideration together with the temporal one for a more correct classification. Indeed, recently there has been an increasing interest in the development of spatial and spatio-temporal clustering algorithms for epidemiological data.
Following Fouedjio (2016) clustering of spatial data can be done by considering either non-spatial clustering models based on spatial dissimilarity measures or spatially constrained clustering approaches. Within the first category, the clustering approaches define the dissimilarity among the objects by means of geographical coordinates, i.e. considering simple spatial proximity, or consider a dissimilarity measure constructed on the basis of spatial features such as the variogram (e.g. Oliver and Webster, 1989, Romano et al., 2015) or the spatial auto-correlation (e.g. Scrucca et al., 2005, Holden and Evans, 2010). The second category is instead based on spatial contiguity constraints rather than spatial dissimilarity measures (e.g. Pham, 2001, Romary et al., 2015, D’Urso and Vitale, 2020). In other words, these clustering approaches consider non-spatial distances but introduces a penalty term in the objective function to enhance clustering in the same group neighboring statistical units.
Clustering of time series object can be done in different ways as well. The time series clustering approaches can be divided into three main groups (Maharaj et al., 2019): observation-based, feature-based and model-based. The first uses raw data and the distances are directly computed on the observed time series. Differently, the second approach aims to group time series by taking into account some features such as the auto-correlation function (ACF) or the partial autocorrelation function (PACF) (e.g. see Caiado et al., 2006, D’Urso and Maharaj, 2009). Some of the methods belonging to this class, are based on the frequency domain features like the periodogram with its transformations (Maharaj and D’Urso, 2011) or the cepstral (D’Urso et al., 2020). The model-based approached are instead based on the assumption that the time series are generated by the same statistical model, such as the ARMA (Piccolo, 1990) or the GARCH (D’Urso et al., 2016) processes, but with different parameter. Model-based approaches can be also defined on the basis of probability distribution parameters (e.g. see D’Urso et al., 2017, Cerqueti et al., 2021).
In many applications, however, it can be reductive considering only spatial or temporal dimension because both of them have provide important information. This is surely the case of epidemiological data and, specifically, of COVID-19 spread modeling (D’Urso et al., 2022, Vitale et al., 2021). Among different approaches for clustering spatio–temporal data we can mention the use of a time series clustering model based on a spatial dissimilarity measure (Izakian et al., 2012), model-based clustering approaches (Disegna et al., 2017) or the use of time series distance with the inclusion of contiguity constraints (Coppi et al., 2010, D’Urso et al., 2019, D’Urso et al., 2021a).
As noted by D’Urso and Massari (2019), spatial and temporal data are of different types. In this paper, following a Partition Around Medoids (PAM) approach, we propose a fuzzy clustering model for spatio-temporal data where both temporal and spatial information are properly considered in the definition of a unique spatio-temporal distance. Specifically, we apply the (D’Urso and Massari, 2019) fuzzy clustering model with mixed-data type in a spatio-temporal framework, considering a particular mixed distance measure for spatial and temporal data. By adopting a fuzzy approach, we admit that each statistical unit can be in more than one cluster with a certain level of probability. Indeed, the fuzzy approach implicitly indicates the presence of a second-best cluster — sometimes, almost as good as the first best; this is a property that is missing in the traditional clustering methods. Moreover, in the real world, the identification of a clear boundary between clusters is not an easy task, so a fuzzy approach is more attractive than a deterministic one. The properties of fuzzy clustering can be particularly useful when dealing with COVID-19 policy design application. Usually fuzziness can be exploited to avoid the classification of some units. However, in this framework, uncertainty cannot be seen as an indication of policy avoidance. When cluster assignment of an unit is uncertain, the definition of the right treatment can be difficult. Knowing that a statistical unit has an uncertain cluster assignment allows policy makers to deeply investigate the characteristics of such a unit in order to define the most appropriate treatment. Clearly, with an hard clustering algorithm the risk of assigning an inappropriate treatment is definitely higher, because policy makers have no information about classification uncertainty for each statistical unit in the sample.
The proposed clustering algorithm is applied for the definition of clusters of Italian regions with similar COVID-19 spread. The results can be useful for the definition of new public health policy, where a different level of restrictions could be imposed to different geographical areas according to the spatio-temporal features of the disease spread.
The structure of the paper is the following. Section 2 presents the clustering model, while Section 3 discusses the application and the data used. Section 4 provides a discussion of the main results and Section 5 concludes.
2. Methodology
2.1. The clustering model
Let us consider statistical units observed over time and space. Then, let us consider a matrix containing in each th column the temporal pattern of a variable of interest for several geographical units . Aim of the clustering procedure is to group the units in terms of similarity over both time and space. In what follows we propose a clustering approach that consider a spatio-temporal dissimilarity measure. By exploiting the fact that spatial and temporal data are of different type, we apply the (D’Urso and Massari, 2019) fuzzy clustering algorithm for mixed data type in a spatio-temporal framework. In other words, we define a spatio-temporal distance that is constructed by optimally weighting both temporal and spatial distances.
More in detail, the resulting clustering approach is based on the following minimization problem:
| (1) |
under the constraints:
| (2) |
where is the number of clusters, is the membership degree of the th unit to the th cluster with the fuzziness parameter. In this framework, we define the spatial distance to which is assigned a weight , and the temporal distance with its relative weight. By solving the minimization problem (1), we have the following solutions:
| (3) |
for the membership degrees and:
| (4) |
| (5) |
for the weights. The proof of these results can be obtained following those provided by D’Urso and Massari (2019). The main issues related to the presented clustering algorithm are the definition of the number of clusters and the fuzziness parameter .
It is well known that values of equal to 1 results into an hard partition, where the membership of an th unit to a th cluster can be either 1 or 0. Therefore, in order to introduce fuzziness in the clustering problem the parameter has to be set . However, also large values of are not appropriate because for the membership degrees are equal to . Overall, there not exist a theoretical rule for selecting the fuzziness parameter , but most of literature considers a value of (e.g. see Bezdek et al., 1984). Similarly, some studies have also shown that the performance of fuzzy clustering algorithms is not so sensitive to the variation of (e.g. see Choe and Jordan, 1992).
Then, we address the problem of selecting the number of clusters by means of the Fuzzy Silhouette (FS) criterion (Campello, 2007). The Fuzzy Silhouette makes explicit use of the fuzzy partition matrix with elements and considers the information on the membership degrees contained in . In the case of high membership, it stresses the importance of units closely placed with respect to the cluster prototypes. In the case of small membership, it reduces the importance of the units placed in overlapping areas. In details, the FS is computed as follows:
| (6) |
with:
The value is the average distance between the th unit and the cluster to which it belongs with the highest membership degree and is the average distance between the th unit and those of the other clusters. Moreover, and are the first and second largest elements of the th row of the fuzzy partition matrix, respectively and is a weighting coefficient, usually set equal to 1.
2.2. Distance measures
First of all, we have to define a dissimilarity measure to account for the spatial nature of the phenomenon under consideration. We measure the spatial dimension of the disease spread instantaneously, i.e. at time 3 by means of the spatial auto-correlation. Spatial auto-correlation is a measure of similarity among neighboring statistical units. As stated by Tobler (1970) “everything is related to everything else, but near things are more related than distant things”. Finding a positive spatial auto-correlation means that adjacent units have similar characteristics, while the units are different in the case of a negative value. Usually, spatial-autocorrelation is measured by means of the global Moran’s index (Moran, 1948).
However, even if extremely useful, the global Moran’s statistics is not able to provide a deeper understanding about which statistical units is similar or different to neighborhood ones. In other words, the global Moran statistics only provides a general picture about the spatial correlation of a variable.
A local measure of spatial auto-correlation can be found in the Local Moran’s statistics (Anselin, 1995). The Local Moran’s is similar to the global Moran’s in the extent to which it provides a measure of how similar locations are to their neighbors. Nevertheless, the second one is computed at local level, such that each statistical unis has its own spatial auto-correlation statistics. Local Indicators of Spatial Association (LISA) have been often used for the determination of spatial clusters (e.g. Moraga and Montes, 2011, Martínez Batlle and van der Hoek, 2018, Pfeiffer et al., 2008). Some other papers (Scrucca et al., 2005, Stojanova et al., 2013) have used LISA as inputs of unsupervised learning techniques, by considering only spatial information for clusters definition.
In this paper, we define the spatial distance, , as the squared Euclidean distance between local spatial auto-correlations, estimated by means of Local Moran’s (Anselin, 1995):
| (7) |
with and are the values of the variable in the areas and respectively. The local Moran’s allows to account for spatial auto-correlation between neighbor statistical units. Positive values indicates that areas and have similar characteristics. On the contrary, negative values suggest a dissimilarity between and .
Once the spatial distance has been defined, we have to discuss a suitable time series distance. As we have seen in the introduction there are several ways of measuring distances between time series. In this paper we propose to follow a feature-based approach, where the time distance is computed according to the auto-correlation structure. Hence, the proposed clustering model consider both spatial and temporal auto-correlation.
Let us define the estimated autocorrelation at lag of the time series associated to the th statistical unit. By considering the usual sample auto-correlation estimator:
| (8) |
with the time series for the th unit, the average and a sufficiently large set of auto-correlation. Usually, common choices for are or (Díaz and Vilar, 2010). Then, we consider the following Ljung and Box (1978) statistics:
where is the length of the time series, is the th autocorrelation coefficient. A large value of the statistics indicates that there is a significant auto-correlation structure in the time series. Therefore, as suggested by Bastos and Caiado (2021), the time distance can be computed as the squared Euclidean distance between estimated statistics.
3. Application to Italian regions
As previously stated, we use the proposed clustering model with the aim of obtaining clusters of Italian regions that share similar spatio-temporal patterns in the COVID-19 spread. Indeed, the Italian government introduced the application of differentiated local treatments on the basis of contagion spread evolution. However, the potential usefulness of clustering has not been totally explored. Clustering algorithms allow the definition of a partition on the basis of an objective measurement of dissimilarities among the statistical units. In presence of territorial units with many variables, the definition of similarity degree among the units becomes a difficult task. The resulting clusters can be used to orientate public health policy (e.g. see D’Urso et al., 2021a).
We collect the data4 about several indicators of COVID-19 spread from the 20th February 2020 to the 20th April 2021 in order to consider the dates with the highest spread of contagion. Hence, we have statistical units with an observed time series length of .
The considered dataset contains several indicators such as the number of occupied beds in intensive cares, the number of positive cases or the number of deaths per 1000 inhabitants. For each of the considered variables we have time series highlighting the differences in temporal trends among the Italian regions.
The decision about which variable to consider in the clustering model is surely difficult and depends by the policy makers. For example, the number of occupied beds in intensive care was considered by the Italian authorities as one of the most important indicators to track the severity of pandemic.
To show how clustering results change with different target variables, in what follows we provide clustering results according to both the number of cases per 1000 inhabitants and the occupied beds in intensive cares 1000 inhabitants.
The number of positive cases at 20th April 2021 is showed in Fig. 1.
Fig. 1.
Number of positive COVID-19 cases per 1000 inhabitants 20/04/2021.
The number of positive cases was relatively high in most of south regions, especially Campania and Puglia, while in the north with the only exception of Emilia-Romagna, the cases were relatively low. Overall, it is evident a certain degree of similarity between neighboring regions, such as the case of Campania, Basilicata and Puglia or Lobardia and Piemonte in the north. The number of occupied beds in intensive care is shown in Fig. 2.
Fig. 2.
Occupied intensive care beds per 1000 inhabitants 20/04/2021.
Fig. 2 highlights a completely different picture, with the norther regions having the most negative values. Fig. 2 explains why many north regions were assigned to more severe color clusters than others of the south. Also in this case spatial heterogeneity and auto-correlation emerge. In general, it is evident that the consideration of alternative indicators suggest different results in terms of pandemic spread.
Nevertheless, together with the spatial dimension of the phenomenon, also the time pattern of the contagion is important and has to be considered. Time dimension of occupied intensive care beds per 1000 inhabitants for all the Italian regions is showed in Fig. 3.
Fig. 3.
Occupied intensive care beds per 1000 inhabitants: time evolution of some Italian regions.
From Fig. 3 it is evident that the time evolution follow a different pattern across different regions as well. For example, regions in the south of Italy like Calabria, Sicily and Puglia show increasing occupied intensive care beds in the last time periods, while the other Italian regions show decreasing patterns. Moreover, almost all the time series are characterized by very low values during the summer months.
Similarly, Fig. 4 shows the time pattern of positive cases for the Italian regions.
Fig. 4.
Positive cases per 1000 inhabitants: time evolution of Italian regions.
Also in this case many differences can be highlighted. For example, Sardegna, Campania and Puglia seem to have very similar time patterns in terms of positive cases number. However we have already explained that the definition of a proper similarity between time series should not be based on raw data. Instead, alternative features should be considered, such as the auto-correlation structure. Moreover, also spatial dimension of the disease spread has to properly taken into account in the clustering process.
For these reasons we claim that the usage of spatio-temporal statistical models can be of relevance in designing novel public health policies as the Italian government has shown. In what follows we propose the use of the spatio-temporal application of the D’Urso and Massari (2019) fuzzy clustering algorithm, with the aim of defining groups of homogeneous Italian regions in terms of COVID-19 spread over the time but also accounting for instantaneous differences among geographical units.
4. Results and discussion
4.1. Target I: occupied beds in intensive care
In what follows we consider the occupied beds in intensive care as the interesting variable to build the clusters of regions. A crucial aspect of any clustering procedure is the selection of the number of clusters . At this aim, following previous studies, we use the Fuzzy Silhouette (FS) criterion of Campello (2007). According to the FS criterion we choose clusters of regions (see Fig. 5).
Fig. 5.
Campello (2007) Fuzzy Silhouette: values for different clusters .
The optimal weights selected by means of the solution of the problem (1) are shown in the Table 1.
Table 1.
Weights assigned to the spatial and temporal distance.
| Weights | 65.27% | 34.72% |
From Table 1 we conclude that the spatial dimension is more important in clusters definition but at the same time the time dimension is not negligible.
The clustering results with the membership degrees are reported in Table 2.
Table 2.
Clustering results: membership degrees.
| Regions | Medoids |
|
|---|---|---|
| Molise | Piemonte | |
| Abruzzo | 0.00 | 1.00 |
| Basilicata | 0.94 | 0.06 |
| Calabria | 0.97 | 0.03 |
| Campania | 0.54 | 0.46 |
| Emilia-Romagna | 0.01 | 0.99 |
| Friuli Venezia Giulia | 0.00 | 1.00 |
| Lazio | 0.01 | 0.99 |
| Liguria | 0.00 | 1.00 |
| Lombardia | 0.02 | 0.98 |
| Marche | 0.00 | 1.00 |
| Molise | 1.00 | 0.00 |
| Piemonte | 0.00 | 1.00 |
| Puglia | 0.21 | 0.79 |
| Sardegna | 0.19 | 0.81 |
| Sicilia | 0.02 | 0.98 |
| Toscana | 0.03 | 0.97 |
| Umbria | 0.01 | 0.99 |
| Valle d’Aosta | 0.92 | 0.08 |
| Veneto | 0.02 | 0.98 |
| Trentino-Alto Adige | 0.01 | 0.99 |
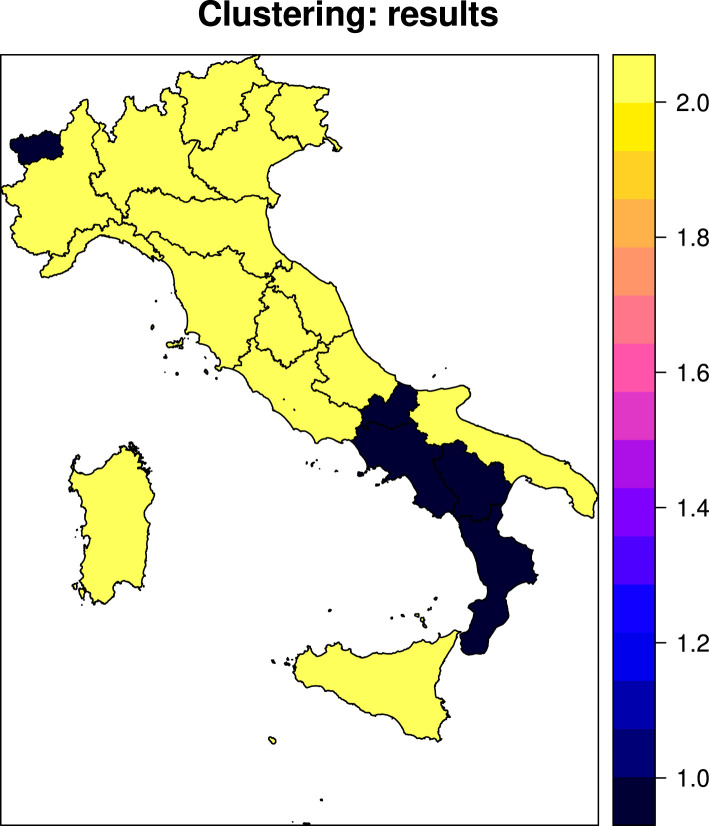
The medoids, Molise and Piemonte, follow a territorial difference, i.e. south and north of Italy. Table 2 shows the membership degrees of the territorial units. Overall, we do not observe very fuzzy classification for most of the Italian regions, with Campania being the only exception. Note the cluster 1 (Molise medoid) includes specifically regions located in the south of Italy. However, not all the southern regions belong to the first cluster, being more similar to those located in the center and north of Italy. Fig. 6 allows to visualize the clusters, in terms of crisp classification, geographically.
Fig. 6.
Fuzzy clustering (occupied beds in intensive care): crisp classification.
Overall, in terms of intensive care beds the clustering model highlights two clear geographical clusters: some neighboring regions of south Italy and those in the north and center with the islands. The only north regions that is placed in the same “south cluster” is the Valle d’Aosta.
Then, to geographically visualize also the uncertainty in the classification, Fig. 7 shows the membership degrees in a map. The lighter (darker) is the color of the th region the more (less) likely it belongs to the cluster in Fig. 6.
Fig. 7.
Fuzzy clustering model (occupied beds in intensive care): membership degrees.
As showed in Table 2, with the exclusion of Campania, the overall uncertainty in the assignment is not problematic. This means that the Campania region cannot be assigned automatically to a cluster and it would deserve a deeper investigation by policy makers.
4.2. Target II: positive cases
In what follows, we present another example by considering the number of positive cases as the variable of interest for clustering. According to the FS criterion, we choose again clusters of regions (see Fig. 8).
Fig. 8.
Campello (2007) Fuzzy Silhouette: values for different clusters .
The optimal weights selected by means of the solution of the problem (1) are shown in the Table 3.
Table 3.
Weights assigned to the spatial and temporal distance.
| Weights | 50.71% | 49.29% |
From Table 3 we conclude that the spatial and time dimension are of equal importance. Also in this case, two clusters are identified. The clustering results, with membership degrees, are shown in Table 4.
Table 4.
Clustering results: membership degrees.
| Regions | Medoids |
|
|---|---|---|
| Piemonte | Toscana | |
| Abruzzo | 0.12 | 0.88 |
| Basilicata | 0.97 | 0.03 |
| Calabria | 0.60 | 0.40 |
| Campania | 0.19 | 0.81 |
| Emilia-Romagna | 0.16 | 0.84 |
| Friuli Venezia Giulia | 0.15 | 0.85 |
| Lazio | 0.18 | 0.82 |
| Liguria | 0.07 | 0.93 |
| Lombardia | 0.14 | 0.86 |
| Marche | 0.26 | 0.74 |
| Molise | 0.15 | 0.85 |
| Piemonte | 1.00 | 0.00 |
| Puglia | 0.28 | 0.72 |
| Sardegna | 0.31 | 0.69 |
| Sicilia | 0.17 | 0.83 |
| Toscana | 0.00 | 1.00 |
| Umbria | 0.15 | 0.85 |
| Valle d’Aosta | 0.02 | 0.98 |
| Veneto | 0.24 | 0.76 |
| Trentino-Alto Adige | 0.64 | 0.36 |
Differently from the previous experiment, in this case the two medoids (Piemonte and Toscana) are located in the north of Italy. The uncertainty in the classification is not problematic also in this case, with the Calabria and Trentino-Alto Adige having the lowest membership degrees (0.6 and 0.64) to the cluster 1. Differently from the previous experiment with intensive care, since the cluster 2 included both northern and southern regions, we now observe two clusters that are less spatially constrained. This happen because, differently from Table 1, in this second setting the temporal dimension has a much greater relevance, almost of the same importance of the spatial one (see Table 3).
In Fig. 9 is shown the map with the crisp assignments that allows for a better visualization of the clusters over the space. In terms of positive cases, we observe that most of the regions are placed in the yellow cluster while few of them are in the blue one. While Calabria and Basilicata are neighbors in the blue cluster, Piemonte and Trentino-Alto Adige are not. On the contrary, most of the yellow cluster regions are neighbors. This happen, as explained previously, because now the temporal dimension has greater relevance in defining the clusters.
Fig. 9.
Fuzzy clustering (positive cases): crisp classification.
Then, in order to visualize geographically the uncertainty in the classification, Fig. 10 shows the membership degrees.
Fig. 10.
Fuzzy clustering (positive cases): membership degrees.
The lighter (darker) is the color of the th region the more (less) likely it belongs to the cluster in Fig. 9. Confirming the evidences shown in Table 4, the membership degrees highlights an overall low uncertainty in the classification, since the lowest value (Calabria) is greater than 0.6.
4.3. Discussion
The most important result to be highlighted is that we found the presence of the clusters of regions in terms of disease spread rather than the three. This result hold for both the considered target variables. The relatively high values of the Fuzzy Silhouette indicate that the clusters are well defined in terms of both compactness and separation. This means that one of the three clusters of color does not respect the actual differences among the Italian regions. Moreover, clusters’ composition is very similar for both the considered variables, i.e. positive cases and occupied beds in intensive care. These findings open up for a discussion related to the effectiveness of the proposed containment measures.
According to some recent studies, the clusters of colors had overall positive effects on the reduction of the disease spread (Manica et al., 2021, Pelagatti and Maranzano, 2021). Clearly, the different type of restrictions generated lower or greater reduction rates in the COVID-19 infection rates. Obviously, the regions placed in the yellow cluster showed a slower decrease of infections if compared with regions in orange and red clusters. For example, according to Manica et al. (2021), while regions in the yellow cluster experimented a reduction about 18% of the infection rates, orange and red clusters showed reduction of 34% and 45% respectively. Therefore, as expected the red cluster has been the most successful in reducing the pandemic spread, especially respect to the orange one (Panarello and Tassinari, 2021).
As noted by Panarello and Tassinari (2021), the restrictions introduced by the governments are not sufficient by themselves without citizens’ compliance. Mobility restrictions had a huge negative psychological impact on citizens (Yao et al., 2021) and generated considerable losses in economic terms. With this respect, we have to stress that the orange cluster is characterized by more severe restrictions than the yellow one. For example, food services such as restaurants and pubs, that are essential for social life, were suspended while in the yellow cluster they were allowed until 10pm in the evening. Moreover, while nobody was allowed to leave the region and municipality of residence, in the yellow cluster citizens were instead allowed to move freely. On the basis of these considerations, we can argue that the orange color cluster, with mild-severity restrictions, could be removed.
Clearly, these findings are far to be conclusive. Indeed, evaluating what would be the effects of two differentiated local treatments rather than three is difficult and out of the scope of this paper. By commenting the results, we should also have in mind the main limitation of automatic algorithms like the proposed clustering procedure. Indeed, clustering algorithms can only provide an indication of the degree of similarity across geographical areas. Conversely, they are not able to specify the degree of the pandemic severity within each cluster. To get more insights deeper investigations are needed.
In general, we can argue that the choice of treatments has to be made on the basis of within cluster analyses conducted by policy makers with the help of public health authorities. Nevertheless, as argued by D’Urso et al. (2021a), clustering algorithms can be interestingly used by national and local authorities to deeply understand the contagion evolution, similarities among statistical units over time and space. On the basis of the obtained results, more effective policies can be designed to mitigate the effects of the pandemic.
5. Conclusion
With the legislative act of November 3 2020 the Italian government introduced a differentiated regime of restrictions among the Italian regions, showing how the containment of COVID-19 spread can be done by means of geographical areas clustering. In particular, yellow cluster is characterized by not severe policies, while orange and red ones by mild and severe restrictions. The clusters of colors, used for the definition of specific local treatments, had overall positive effects on the reduction of the disease spread at the time we are writing. Specifically, the red cluster has been the most successful in reducing the pandemic spread especially f compared to the orange one. Clearly, the yellow cluster has been the less effective, but guaranteed more freedom to citizens, that have been negatively affected by the pandemic also from the mental health point of view.
In this paper we ask whether the three clusters of colors were really reflecting the actual differences among the Italian regions in terms of contagion spread. To this aim, we propose a clustering algorithm that accounts for the differences in both the temporal trend and spatial structure among the Italian regions. In particular, following a Partition Around Medoids (PAM) approach, we apply the D’Urso and Massari (2019) fuzzy clustering model with mixed-data type in a spatio-temporal framework, considering a particular mixed distance measure for spatial and temporal data.
What we show is that, in the case of intensive care beds, the algorithm assigns an higher weight to the spatial dimension than the temporal one, thus confirming the relevance of spatial dimension in the understanding of contagion spread over the regions. By considering positive cases, however, both dimensions have the same degree of relevance. Second, we show that two groups of regions sharing different patterns of COVID-19 spread exist. Clearly, evaluating the effects of two differentiated local policies is difficult task, out of the scope of this paper. However, clustering algorithms can successfully used to identify objective degree of similarity across geographical areas. Therefore, we advocate the use of clustering algorithms for the design of more effective health policies. For an accurate implementation of differentiated local policies, deeper within cluster analyses has to be conducted by experts and epidemiologists.
A future development of this work should be devoted to the simultaneous analysis of multiple target variables, by considering multivariate time trajectories in the space as discussed recently in Lopez-Oriona et al. (2021).
Footnotes
This number of legislative acts refers to the time period between 1th January 2020 and 1th January 2022. Detailed information about the legislative acts about COVID-19 in Italy can be found at the following link https://www.openpolis.it/coronavirus-lelenco-completo-degli-atti/.
Published on the Gazzetta Ufficiale (n.275 of 04-11-2020 - Suppl. Ordinario n. 41) on November 3 2020 “Ulteriori disposizioni attuative del decreto-legge 25 marzo 2020, n. 19, convertito, con modificazioni, dalla legge 25 maggio 2020, n. 35, recante” Misure urgenti per fronteggiare l’emergenza epidemiologica da COVID-19.
Where is the last observation in the sample (i.e. today). Therefore, the spatial distance can be seen as an instantaneous measure. Alternative approaches can be also defined on the basis of weekly or monthly averages rather than instantaneous values.
Data can be retrieved at the following link: https://github.com/pcm-dpc/COVID-19/tree/master/dati-regioni.
References
- Anselin L. Local indicators of spatial association—LISA. Geogr. Anal. 1995;27(2):93–115. [Google Scholar]
- Bastos J.A., Caiado J. On the classification of financial data with domain agnostic features. Internat. J. Approx. Reason. 2021;138:1–11. [Google Scholar]
- Bezdek J.C., Ehrlich R., Full W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984;10(2–3):191–203. [Google Scholar]
- Caiado J., Crato N., Peña D. A periodogram-based metric for time series classification. Comput. Statist. Data Anal. 2006;50(10):2668–2684. [Google Scholar]
- Campello R.J. A fuzzy extension of the rand index and other related indexes for clustering and classification assessment. Pattern Recognit. Lett. 2007;28(7):833–841. [Google Scholar]
- Cerqueti R., Giacalone M., Mattera R. Model-based fuzzy time series clustering of conditional higher moments. Internat. J. Approx. Reason. 2021;134:34–52. [Google Scholar]
- Choe H., Jordan J.B. [1992 Proceedings] IEEE International Conference on Fuzzy Systems. IEEE; 1992. On the optimal choice of parameters in a fuzzy c-means algorithm; pp. 349–354. [Google Scholar]
- Coppi R., D’Urso P., Giordani P. A fuzzy clustering model for multivariate spatial time series. J. Classification. 2010;27(1):54–88. [Google Scholar]
- Cordes J., Castro M.C. Spatial analysis of COVID-19 clusters and contextual factors in new york city. Spatial Spatio-Temporal Epidemiol. 2020;34 doi: 10.1016/j.sste.2020.100355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Díaz S.P., Vilar J.A. Comparing several parametric and nonparametric approaches to time series clustering: a simulation study. J. Classification. 2010;27(3):333–362. [Google Scholar]
- Dickson M.M., Espa G., Giuliani D., Santi F., Savadori L. Assessing the effect of containment measures on the spatio-temporal dynamic of COVID-19 in Italy. Nonlinear Dynam. 2020;101(3):1833–1846. doi: 10.1007/s11071-020-05853-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Disegna M., D’Urso P., Durante F. Copula-based fuzzy clustering of spatial time series. Spatial Stat. 2017;21:209–225. [Google Scholar]
- D’Urso P., De Giovanni L., Disegna M., Massari R. Fuzzy clustering with spatial–temporal information. Spatial Stat. 2019;30:71–102. [Google Scholar]
- D’Urso P., De Giovanni L., Massari R. GARCH-based robust clustering of time series. Fuzzy Sets and Systems. 2016;305:1–28. [Google Scholar]
- D’Urso P., De Giovanni L., Massari R., D’Ecclesia R.L., Maharaj E.A. Cepstral-based clustering of financial time series. Expert Syst. Appl. 2020;161 [Google Scholar]
- D’Urso P., De Giovanni L., Vitale V. Spatial robust fuzzy clustering of COVID 19 time series based on B-splines. Spatial Stat. 2021 doi: 10.1016/j.spasta.2021.100518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Urso P., De Giovanni L., Vitale V. A D-vine copula-based quantile regression model with spatial dependence for COVID-19 infection rate in Italy. Spatial Stat. 2022 doi: 10.1016/j.spasta.2021.100586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Urso P., Maharaj E.A. Autocorrelation-based fuzzy clustering of time series. Fuzzy Sets and Systems. 2009;160(24):3565–3589. [Google Scholar]
- D’Urso P., Maharaj E.A., Alonso A.M. Fuzzy clustering of time series using extremes. Fuzzy Sets and Systems. 2017;318:56–79. [Google Scholar]
- D’Urso P., Massari R. Fuzzy clustering of mixed data. Inform. Sci. 2019;505:513–534. [Google Scholar]
- D’Urso P., Mucciardi M., Otranto E., Vitale V. Community mobility in the European regions during COVID-19 pandemic: A partitioning around medoids with noise cluster based on space–time autoregressive models. Spatial Stat. 2021 doi: 10.1016/j.spasta.2021.100531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Urso P., Vitale V. A robust hierarchical clustering for georeferenced data. Spatial Stat. 2020;35 [Google Scholar]
- Fouedjio F. A hierarchical clustering method for multivariate geostatistical data. Spatial Stat. 2016;18:333–351. [Google Scholar]
- Holden Z.A., Evans J.S. Using fuzzy C-means and local autocorrelation to cluster satellite-inferred burn severity classes. Int. J. Wildland Fire. 2010;19(7):853–860. [Google Scholar]
- Izakian H., Pedrycz W., Jamal I. Clustering spatiotemporal data: An augmented fuzzy c-means. IEEE Trans. Fuzzy Syst. 2012;21(5):855–868. [Google Scholar]
- Ljung G.M., Box G.E. On a measure of lack of fit in time series models. Biometrika. 1978;65(2):297–303. [Google Scholar]
- Lopez-Oriona A., D’Urso P., Vilar J.A., Lafuente-Rego B. Spatial weighted robust clustering of multivariate time series based on quantile dependence with an application to mobility during COVID-19 pandemic. IEEE Trans. Fuzzy Syst. 2021 [Google Scholar]
- Maharaj E.A., D’Urso P. Fuzzy clustering of time series in the frequency domain. Inform. Sci. 2011;181(7):1187–1211. [Google Scholar]
- Maharaj E.A., D’Urso P., Caiado J. CRC Press; 2019. Time Series Clustering and Classification. [Google Scholar]
- Manica M., Guzzetta G., Riccardo F., Valenti A., Poletti P., Marziano V., Trentini F., Andrianou X., Urdiales A.M., del Manso M., et al. 2021. Effectiveness of regional restrictions in reducing SARS-CoV-2 transmission during the second wave of COVID-19, Italy. MedRxiv. [Google Scholar]
- Martínez Batlle J.R., van der Hoek Y. Clusters of high abundance of plants detected from local indicators of spatial association (LISA) in a semi-deciduous tropical forest. PLoS One. 2018;13(12) doi: 10.1371/journal.pone.0208780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moraga P., Montes F. Detection of spatial disease clusters with LISA functions. Stat. Med. 2011;30(10):1057–1071. doi: 10.1002/sim.4160. [DOI] [PubMed] [Google Scholar]
- Moran P.A. The interpretation of statistical maps. j. r. Statist. Sot. B. 1948:10–243. [Google Scholar]
- Oliver M., Webster R. A geostatistical basis for spatial weighting in multivariate classification. Math. Geol. 1989;21(1):15–35. [Google Scholar]
- Panarello D., Tassinari G. One year of COVID-19 in Italy: are containment policies enough to shape the pandemic pattern? Socio-Economic Planning Sciences. 2021 doi: 10.1016/j.seps.2021.101120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelagatti M., Maranzano P. Assessing the effectiveness of the italian risk-zones policy during the second wave of COVID-19. Health Policy. 2021;125(9):1188–1199. doi: 10.1016/j.healthpol.2021.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer D., Robinson T.P., Stevenson M., Stevens K.B., Rogers D.J., Clements A.C., et al. Oxford university press Oxford; 2008. Spatial analysis in epidemiology, vol. 142. [Google Scholar]
- Pham D.L. Spatial models for fuzzy clustering. Comput. Vis. Image Underst. 2001;84(2):285–297. [Google Scholar]
- Piccolo D. A distance measure for classifying ARIMA models. J. Time Series Anal. 1990;11(2):153–164. [Google Scholar]
- Romano E., Mateu J., Giraldo R. On the performance of two clustering methods for spatial functional data. AStA Adv. Stat. Anal. 2015;99(4):467–492. [Google Scholar]
- Romary T., Ors F., Rivoirard J., Deraisme J. Unsupervised classification of multivariate geostatistical data: Two algorithms. Comput. Geosci. 2015;85:96–103. [Google Scholar]
- Scrucca L., et al. Clustering multivariate spatial data based on local measures of spatial autocorrelation. Quaderni Dipart. Econ. Finanza E Stat. 2005;20(1):11. [Google Scholar]
- Stojanova D., Ceci M., Appice A., Malerba D., Džeroski S. Dealing with spatial autocorrelation when learning predictive clustering trees. Ecol. Inform. 2013;13:22–39. [Google Scholar]
- Tobler W.R. A computer movie simulating urban growth in the detroit region. Econ. Geogr. 1970;46(sup1):234–240. [Google Scholar]
- Vitale V., D’Urso P., De Giovanni L. Spatio-temporal object-oriented Bayesian network modelling of the COVID-19 Italian outbreak data. Spatial Stat. 2021 doi: 10.1016/j.spasta.2021.100529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao H., Liu W., Wu C.-H., Yu Y.-H. The imprinting effect of SARS experience on the fear of COVID-19: The role of AI and big data. Soc.-Econ. Plan. Sci. 2021 doi: 10.1016/j.seps.2021.101086. [DOI] [PMC free article] [PubMed] [Google Scholar]