Abstract
Exchange rates are affected by the impact of disparate types of new information as well as the couplings between these modalities. Previous work mainly predicted exchange rates solely based on market indicators and therefore achieved unsatisfactory results. In response to such an issue, this study develops an inventive multimodal fusion-based long short-term memory (MF-LSTM) model to forecast the USD/CNY exchange rate. Our model consists of two parallel LSTM modules that extract abstract features from each modality of information and a shared representation layer that fuses these features. In terms of the text modality, bidirectional encoder representations from transformers (BERT) is applied to conduct a sentiment analysis on social media microblogs. Compared to previous studies, we incorporate not only market indicators but also investor sentiments into consideration, treating the two types of data differently to match their exclusive characteristics. In addition, we apply the multimodal fusion technique and contrive a deep coupled model rather than a shallow and simple model to reflect the couplings between the two modalities. As a consequence, the experimental results obtained over a 15-month period exhibit the superiority of the proposed approach over nine baseline algorithms. The purpose of our study is to demonstrate that it is practicable and effective to incorporate multimodal fusion into financial time series forecasting.
Keywords: Multimodal fusion, MF-LSTM, Sentiment analysis, Exchange rate forecasting
Introduction
The foreign exchange market has become the largest financial market on the globe, with a daily volume of $6.6 trillion [1]. However, with the rapid increase in the size of the market in recent decades, the risk of foreign exchange has also been greatly accentuated. After the debacle of the Bretton Woods system, more flexible policies regarding exchange rates were adopted by most central banks, contributing to the volatile nature of the Forex market. These unanticipated fluctuations impose threats to not only the profits of multinational corporations but also the stability of financial systems. For illustration, the devaluation plan for the Mexican peso against the U.S. dollar implemented in 1994 triggered an unexpected plunge in the Mexican Peso Index, which eventually led to a severe recession in the Mexican economy, with a 6.2% decline in gross domestic product (GDP) over the following year1. Consequently, the exigency of forecasting the directions and extents of these fluctuations began to rise. In addition, the internationalization of CNY has profoundly influenced the global market. In 2020, US$2.591 trillion worth of goods and services were exported by China, accounting for 13.8% of overall global exports2. In addition, China brought in US$ 163 billion of inflows in 2020, surpassing the United States as the largest recipient of foreign direct investment (FDI)3. Nevertheless, trade conflicts with the United States and the COVID-19 pandemic have also brought risks to China’s economy. In terms of such magnitude, correspondingly, any exchange rate fluctuation might incur an enormous aftershock. Therefore, forecasting exchange rates with accuracy and robustness is crucial for international trade practitioners, global investors, and policy makers.
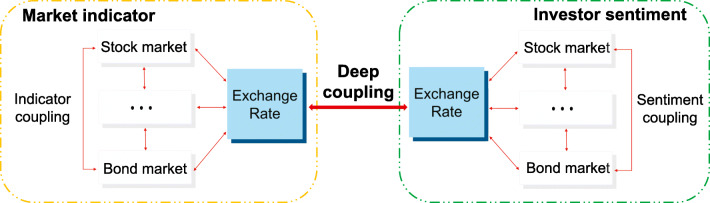
Unfortunately, there is still no panacea to address this issue. Such a predicament can be ascribed to three main reasons. First, an exchange rate is determined by an intricate system with complicated coupled relationships [2], as shown in the left part of Fig. 1. Factors comprising stock market movements and macroeconomic policies not only possess distinctive conduction mechanisms and impose various effects on the Forex market but also interact with each other. In addition, the factors that belong to each country’s markets are also related. Second, Forex market participants do not make decisions solely based on the numerical market indicator data. Investor sentiments aroused by new information can also exert coupled effects among themselves concerning markets and countries, as displayed in the right part of Fig. 1, eventually affecting the corresponding exchange rates [3]. Two theories can expound on this phenomenon. On the one hand, according to the effective market hypothesis (EMH), the stock market is capable of making rapid adjustments to new information [4, 5]. This hypothesis was further applied to the Forex market in [6]. That is, new information in different markets and regions, including financial news and social media texts, can be absorbed by Forex market participants through investor sentiments. Ergo, market expectations and exchange rates will change accordingly. On the other hand, behavioral finance theory argues that some agents are not fully rational [7]. When facing new information, irrationality such as herd behavior, thought contagion, and risk aversion affects market movement [8]. Additionally, these irrationalities within a single market can be conveyed far beyond the original sphere. For example, when encountering unpredictable calamities in the British stock market, panic may disseminate and compel practitioners to make overreact. These investor sentiments may even be transmitted to the USD/CNY Forex market and trigger fluctuations. Even though the above two theories have disparate perception with regard to how market movements reflect all sorts of new information, a consensus regarding the effect of new information can be derived – information related to each market is capable of generating investor sentiments, ultimately affecting the exchange rate. Third, there are also deep couplings between market indicators and investor sentiments, as shown in the middle of Fig. 1. Since the mechanism that determines an exchange rate has three types of couplings with exclusive characteristics and the two forms of information are distinctive in modality, any attempt that considers only a single modality of information, whether that be numerical market indicator data or text data regarding investor sentiments, tends to fail in terms of obtaining accurate forecasts. Thus, to cope with the above problems, it is logical that a qualified forecasting methodology should capture both the inherent interactions among the market indicators and investor sentiments within these markets, as well as the couplings between the two modalities of new information.
Fig. 1.
Hidden mechanisms beneath the exchange rate
When confronting such a challenge, however, it is arduous for existing methods to represent sophisticated coupled structures while incorporating various modalities of information. Traditionally, economists have applied econometric methods (e.g., the autoregressive integrated moving average (ARIMA) approach [9]) for financial time series forecasting. Nonetheless, the processed time series are assumed to be rigidly linear and stationary [10]. As a result, these methods are rendered feeble when facing nonlinear hidden patterns within exchange rates and the impacts of various information. In addition, although machine learning techniques (e.g., decision trees [11] and support vector machines (SVMs) [12]) are capable of incorporating diverse factors without such stringent restrictions, these shallow structures may ignore the distinctive conduction mechanisms of the market, as well as coupled effects. Furthermore, different modalities of data owns distinctive characteristics. It is logical that any approaches should treat them separately. Therefore, using a single and shallow structure to process multiple types of data actually ignores the differences between them, which is likely to generate unfavorable results. Nevertheless, in recent years, two methods have exhibited the potential to resolve these difficulties. The first is the long short-term memory (LSTM) approach proposed by Schmidhuber and Hochreiter. Through its memory cells and gates, LSTM fixes the exploding and vanishing gradient problems formerly exhibited by recurrent neural networks (RNNs) [13]. Such a merit contributes to the excellent performance of LSTM in learning both long-term and short-term dependencies [14]. Hence, the LSTM model was later applied to numerous time series forecasting tasks, and achieved excellent results [15–17]. Another candidate method is multimodal fusion (MF), in which multiple types of media, their related features, or the intermediate decisions are incorporated to complete an analysis task [18]. In particular, since a hierarchical architecture can be automatically learned for each modality via deep learning, deep multimodal learning achieves undeniable success in domains such as object recognition tasks [19], medical applications [20], and autonomous systems [21]. It is noteworthy that this ability is consistent with the elaborate nature of the Forex market – different modalities of information exert distinctive impacts on exchange rates. However, to our knowledge, this method has not been applied to forecast foreign exchange rates. It is still an issue to formulate a deep learning model that is able to reflect the effects of factors within each type of information as well as the couplings of multiple modalities for the complex currency market.
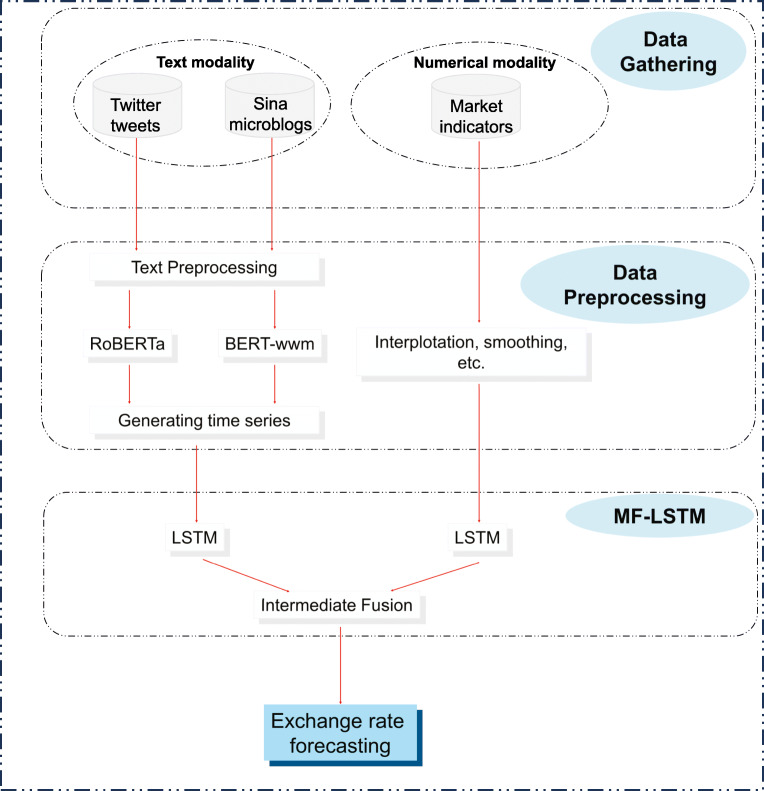
To address the above challenge, this study devises a novel multimodal fusion-based long short-term memory (MF-LSTM) approach to forecast the USD/CNY exchange rate. We manifest the framework of our study in Fig. 2. The main contributions of this paper are as follows:
Sentiment analysis: We leverage state-of-the-art sentiment analysis models based on bidirectional encoder representations from transformers (BERT) to extract the daily sentiments in the Forex market from both countries’ social media platforms. More than a million pieces of microblogs are processed to create sentiment series.
Model structure: The deep multimodal fusion (MF) method is applied to exchange rate forecasting for the first time. In terms of our MF-LSTM model, two LSTM models are deployed in the first layer to learn from the influencing factors within market indicators and social media sentiments separately. In the second layer, to represent the couplings of each modality, a shared representation layer is applied to fuse the two abstract features acquired from the first layer. Finally, a fully connected layer is fed by the coupled features learned from the previous layer to perform the exchange rate forecasting task.
Experimental results: By implementing the deep multimodal fusion technique, our model is able to significantly outperform all baseline approaches with regard to technical and statistical results, demonstrating that deep MF is useful for exchange rate forecasting. Additionally, it is feasible and quite effective to incorporate this method into an LSTM-derived model for time series prediction.
Fig. 2.
Flowchart of our work
The rest of this paper is organized as follows. In Section 2, we introduce the methodology of the basic BERT model and our MF-LSTM model. In Section 3, we describe the experimental settings, including the utilized data gathering and preparation approaches, as well as the model settings. Then, our model is compared with other algorithms regarding various technical and statistical indicators. In Section 4, the main findings and limitations of our work are presented. We also describe three perspectives from which future studies may build upon our research. Finally, we conclude our study in Section 5.
Methodology
Basic BERT model
Devlin et al. [22] proposed bidirectional encoder representations from transformers (BERT) in 2018. It achieved excellent performance in 11 natural language processing (NLP) tasks and was widely used in the NLP field. Serving as the basis of BERT, transformer encoders can be stacked to extract the deep relationships among words and sentences. Addditionally, multi-head attention allows the model to jointly learn information of input vectors Xa from different positions, resulting in superior performance. This mechanism can be described as follows:
| 1 |
where Q, K, and V are different representations of the input vector Xa. Through a softmax computation, the attention output V1 is obtained.
Then Va = Xa + Vl is normalized and thrown into a feed-forward neural network. As a result, the output of a transformer Vt is reached as follows:
| 2 |
Finally, since BERT consists of bidirectional stacked transformers, for any input vector Xa, the output of BERT Vb can be acquired via repeating the process above.
Elementary LSTM model
We describe the basic structure of an LSTM model in this part. At time t, it consists of a memory cell Ct with three distinctive gates – a forget gate ft determines the disposal of information from the previous memory cell Ct− 1, an input gate it keeps the remaining information, and an output gate ot defines the output information of the current cell Ct. The working mechanism of an LSTM model can be described as follows:
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
where ht and Xt denote the hidden state and input variable at time t, respectively. W and U are weight matrices of the variables, and b is a bias vector. represents the candidate input in cell Ct. As shown in (3), at the forget gate ft, the input Xt and ht− 1 are processed by a sigmoid function. Hence, a value ranging from 0 to 1 is obtained, which specifies how much information in Ct− 1 should be forgotten. For example, if the value is 0, all information are forgotten and will not affect later states. (4)–(6) constitute the next steps. Through another sigmoid function, the input gate it decides how much current information in should be stored. For example, if the value is 1, all information are preserved for future operations.Then a tanh function generates a candidate vector and the cell state Ct is updated according to (5) and (6). Finally, (7) and (8) depict the output process: hidden state or current output ht is obtained through the output gate ot.
Through the three-gate mechanism, the LSTM model manages to preserve the long-term information while avoiding the problem of exploding and vanishing gradient. Apparently, this hallmark is very useful to identify the impact of various influencing factors within each modality.
MF-LSTM model
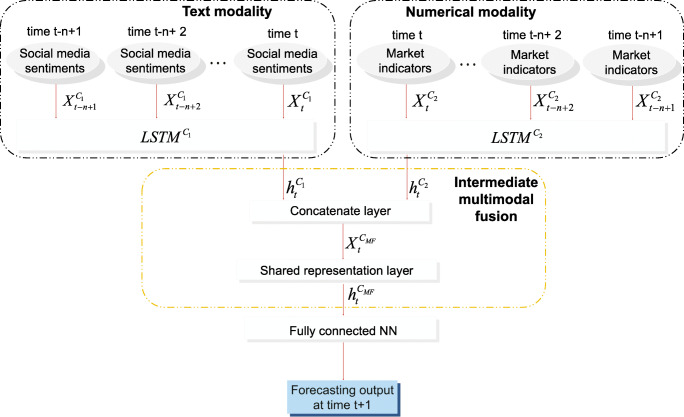
Although the basic LSTM model exhibits great performance in multivariate time series forecasting, it is not capable of analyzing different influencing factors within multiple modalities at the same time, let alone the coupling effects between these modalities. Therefore, to simulate the impact exerted by different sources of information, we propose the MF-LSTM model, which is characterized in Fig. 3. It consists of three layers. Two LSTM models are embedded at the first layer, where the first one depicts the couplings of social media sentiments in the text modality and the second one represents the couplings of market indicators in the numerical modality, so as to learn from disparate modalities separately. Suppose the window length is n, features of the two modalities from time t − n + 1 to time t are served as the input of the first layer. Next, the hidden state features obtained from the two LSTM modules are concatenated and fed into a shared representation layer, which represents the couplings between the modalities via intermediate multimodal fusion [23]. Finally, a dense layer is deployed in the third layer. Obviously, it applies a nonlinear transformation to the deep interactions learned from the previous layer and converts them into the exchange rate forecasting results.
Fig. 3.
Structure of the MF-LSTM model
Representation of text modality couplings
Specifically, in the first LSTM, suppose there are N series of social media sentiments, where αit represents a daily sentiment value of certain social media keyword. Correspondingly, denotes a single sentiment time series. At time t, is fed into the first LSTM (LSTMC1) module, where ERt equals the current USD/CNY exchange rate. In our work, due to the LSTM’s requirement of three-dimentional input, the shape of is (batch_size, 1, 9) because we predict the value at time t + 1 and there are 9 social media keywords, as discussed in the following experimental setting part. Through the three-gate-mechanism shown in (3), (4) and (7), the LSTM model shall explore the couplings of social media indicators and generate a hidden state feature from the text modality consequently:
| 9 |
where the shape of is (batch_size, 50) because there are 50 cells in LSTMC1 (please refer to Table 4).
Table 4.
Model settings
| Algorithms | Sentiment series | Market indicators | Historical USD/CNY rate | Parameters |
|---|---|---|---|---|
| ARIMA | X | X | O | Order = (2,1,2) |
| BPNN | O | O | O | Hidden units: 52; Activation function: ReLU; Learning rate: 0.05} |
| ELM | O | O | O | Hidden units: 77; Activation function: sigmoid} |
| SVR | O | O | O | Kernel function: sigmoid; C: 100.0; γ: 0.1} |
| CNN | O | O | O | Convolutional layer: Conv1D, Filter: 64, Kernal size: 2; Pooling layer: MaxPooling1D, Pool size: 2; Optimizer: Adam; Activate function: ReLU |
| LSTM-single | X | X | O | Hidden units: 32; Learning rate: 0.0001; Epoch: 200 |
| LSTM-market | O | O | O | Hidden units: 60; Learning rate: 0.0001; Epoch: 200 |
| LSTM-sentiment | O | X | O | Hidden units: 50; Learning rate: 0.0001; Epoch: 200 |
| LSTM-all | X | O | O | Hidden units: 64; Learning rate: 0.0001; Epoch:200 |
| MF-LSTM | O | O | O | Hidden units: 50(LSTMC1), 60(LSTMC2), 64(FC layer); Learning rate: 0.0001; Epoch: 200 |
O means that the factor is applied, while X means not
Representation of numerical modality couplings
Similarly, in the second LSTM, suppose there are M series of market indicators. At time t, serves as the input of the LSTM model. In our work, the shape of is (batch_size, 1, 14) because there are 14 market indicators. Subsequently, the hidden patterns learned from the numerical modality (LSTMC2) is obtained as:
| 10 |
where the shape of is (batch_size, 60) because there are 60 cells in LSTMC2 (please refer to Table 4).
Intermediate fusion and MF-LSTM-based forecasting
The next step is to fuse the hidden features acquired from each modality. Initially, two outputs from the first layers are concatenated as the input of the second layer at time t:
| 11 |
where the shape of the contatenated is (batch_size, 110).
Then is thrown into a shared representation layer, which represents the coupled effects between the two modalities:
| 12 |
where δ and Wh denote the ReLU activation function and weight matrix, respectively. The shape of is (batch_size, 64).
Finally, a dense layer is deployed to process and the exchange rate prediction ERt+ 1 at time t + 1 is obtained:
| 13 |
Experimental settings and results
Data Gathering
Social media sentiments
To comprehensively display the public sentiment related to the USD/CNY exchange rate comprehensively, we first construct an original unprocessed dataset. Considering the characteristics and availability of social media data, certain social networking or chatting tools such as Facebook and WeChat apparently cannot fulfill the purpose of our study. Therefore, Twitter and Sina Weibo are elected as the data sources of our text modality. Twitter is an American microblogging platform. It provides some-to-many microblogging services that are more suitable for our study. Sina Weibo is the largest Chinese microblogging website. The original unprocessed dataset applied in this work contains 419,228 English tweets with 7 keywords and 912,363 Chinese microblogs collected from 1/1/2015 to 4/1/2021 via the official application programming interfaces (APIs) of these websites. The 9 total keywords are listed in Table 1 (Mandarin keywords are translated into English in this table) Unfortunately, tradeoffs are made during the selection of keywords. For example, when searching “USD/CNY” on Twitter, we find too few results to reflect user opinions on each day. As a result, this word is replaced with “Dollar Index”. Additionally, the search results of other keywords on Sina Weibo teem with noise (e.g., advertisements). Thus, after conducting data processing, only 2 keywords are preserved for our study. Nevertheless, these remaining keywords are all in accordance with the selection of market indicators.
Table 1.
Selected market indicators and social media keywords
| Category | Market indicator | Social media keyword | |
|---|---|---|---|
| Sina Weibo | |||
| Commodity market | Gold price | “Gold price” | |
| Silver Price | “Silver price” | ||
| WTI crude oil price | “Oil price” | ||
| Stock market | Shanghai Securities Composite Index | N/A | “CN stock market” |
| Shenzhen Component Index | |||
| Dow Jones Index | “US stock market” | N/A | |
| S&P 500 Index | |||
| NASDAQ Index | |||
| NYSE Index | |||
| Bond market | China 10-year bond yield | N/A | N/A |
| U.S. 10-year Treasury bond yield | “US bond market” | ||
| Interest rate | Shibor O/N rate | N/A | N/A |
| Federal fund rate | “US interest rate” | ||
| Exchange rate | USD/CNY rate | “Dollar index” | “USD/CNY” |
Before applying BERT models to perform sentiment analysis, it is essential to preprocess the original dataset [24]. Notably, since Twitter and Sina Weibo users type various nonstandard language such as slang terms and emojis in their microblogs, and because these terms can help improve the sentiment classification results [25, 26], we choose to preserve them. Therefore, the collected social media text is preprocessed as follows:
Removing noisy microblogs: Microblogs sent by foreign users or from overseas regions are deleted. In addition, duplicates of any Sina microblogs and Twitter tweets are removed.
Removing useless symbols and stopwords: Address signs (@), hashtags (@), URLs, and stopwords (e.g., “the”) are excluded.
Lemmatization for English tweets: English words are processed to return to the basic dictionary morphology. For example, an “s” or “es” at the end of a plural word is removed. Please note that Mandarin text does not need to go through this step due to its syntax characteristics.
Tokenization: Phrases, sentences, or paragraphs are split into individual words to fulfill the requirements of BERT models.
To obtain the sentiment time series of these keywords, it is necessary to extract the sentiment of each microblog. Consequently, inspired by the concept of transfer learning, we leverage two BERT-based models, the robustly optimized BERT approach (RoBERTa) and BERT with whole-word masking (BERT-wwm), for the sentiment analysis task. Since the invention of BERT, several improved models have been presented. For illustration, Cui et al. [27] proposed the BERT-wwm model. Compared to BERT, it takes the syntax difference between Mandarin and English into account, using the whole-word masking technique to improve the model performance on common NLP tasks with Chinese text. Additionally, Liu et al. [28] proposed RoBERTa, which is also based on BERT. In addition to applying more training data, the authors adopted a dynamic masking method to optimize the obtained results.
The two models above are selected for our sentiment analysis task. Since BERT-derived models are capable of effectively capturing the deep relationships among words and sentences, only the parameters of the output layer need to be fine-tuned. Therefore, for Sina microblogs, we train the BERT-wwm model on an appropriate dataset4. For English tweets, the Twitter-RoBERTa-base sentiment model is imported from Hugging Face. Since this model has already been fine-tuned on approximately 58 million tweets, there is no need to conduct further training [29].
The sentiment orientations in our work are defined as -1 (negative), 0 (neutral), and 1 (positive). To examine the sentiment classification performance of the models, two experts in the field of international finance are invited to label 1% of the large preprocessed dataset, which is evenly sampled in terms of years and keywords. The consistency of the annotation results reaches 95.7%, indicating the effectiveness of the annotation process. Table 2 presents the number of three sentiment orientations regarding each social media keyword in our manually labeled test set. We ensure that the distribution of three sentiment orientations in the evaluation dataset is in accordance with that of the whole dataset. In addition, it can be observed that the distribution in general fit the market condition. For example, in our observation period, there are 892 days that the NASDAQ Index goes up and 681 days that the Index goes down. In terms of the “US stock market” of our dataset, the percentage of positive orientation (27.9%) is significantly higher that of negative orientation (16.9%), which reflects the real market condition.
Table 2.
Evaluation dataset of sentiment analysis
| Social media keyword | Positive | Neutral | Negative | Total |
|---|---|---|---|---|
| “Gold price” | 76 | 194 | 119 | 389 |
| “Silver price” | 53 | 89 | 71 | 213 |
| “Oil price” | 108 | 109 | 184 | 401 |
| “CN stock market” | 384 | 1,207 | 1,882 | 3,473 |
| “US stock market” | 285 | 563 | 173 | 1,021 |
| “US bond market” | 201 | 637 | 299 | 1,137 |
| “US interest rate” | 162 | 387 | 313 | 862 |
| “Dollar index” | 276 | 538 | 183 | 997 |
| “USD/CNY” | 1,156 | 695 | 673 | 2,524 |
Then, the sentiment orientation results produced by the two models are evaluated on these manually labeled microblogs. Three evaluation methods based on a confusion matrix are as follows:
- Precision: Precision is the ratio of correctly classified positive observations to the total number of predicted positive observations. High precision indicates a low false-positive rate. It can be described by the following formula:
14 - Recall: Recall (sensitivity) is the ratio of correctly classified positive observations to the number of total observations in the actual class:
15 - F1_score: The F1_score refers to the weighted average of the precision and recall metrics, which takes both false positives and false negatives into account:
16
The sentiment evaluation results are shown in Table 3, demonstrating the sentiment classification efficacy of the models.
Table 3.
Sentiment evaluation results
| Evaluation methods | BERT-wwm | RoBERTa |
|---|---|---|
| Precision | 0.83 | 0.81 |
| Recall | 0.84 | 0.79 |
| F1_score | 0.83 | 0.80 |
After that, the sentiment time series of these keywords are calculated based on the sentiment orientation results of each microblog. Here we employ a straightforward method:
| 17 |
where αkt denotes the sentiment value of a keyword on day t. and are the total numbers of positive and negative microblogs containing a keyword on day t, respectively. Correspondingly, the social media sentiment time series of each keyword is obtained.
Market indicators
Market indicator data covering the period from 1/1/2015 to 4/1/2021 are collected from the Wind Database5. The daily USD/CNY central parity rate is designated as the prediction target. Thirteen factors along with the exchange rate are displayed in Table 1. Due to the existence of nontrading days, each missing value is filled with the value of the previous trading day.
Data preparation
Raw time series are often skewed by a multitude of outliers. The use of such numerical features directly may cause issues that impair the forecasting performance of the tested models. Hence, the trailing moving average method is applied in our work for feature engineering: αkt = mean(obs(t − 2),obs(t − 1),obs(t)), where obs(t) is the current observation value of the time series on day t. Then all processed data is normalized to [0,1] by , where It denotes the raw value of the time series on day t, because the LSTMs in the first layer of our model are sensitive to the scale of the inputs. The dataset is split into training, validation, and test sets at a ratio of 6:2:2. That is, the data ranging from 1/1/2020 to 4/1/2021 are selected to examine the forecasting performance of our model.
Evaluation methodology
Technical perspective
- R2 R2, also known as the coefficient of determination, is a technical indicator that represents the proportion of the variance of a dependent variable that can be explained by the independent variables in a regression model. Suppose that yt and denote the original and predicted values at time t during the given time period (N days); then a high R2 result means that the model fits the data well.
18 - Mean absolute error (MAE) The MAE represents the average of the absolute differences between the original and predicted values. It is the most intuitive and common forecasting evaluation method. A small value indicates a higher forecasting accuracy. The meanings of the symbols below are consistent with those in the previous equation.
19 - Mean squared error (MSE) The MSE is the mean of the squared differences between the original and predicted values. It measures the variance of the residuals. A small value represents a better forecasting performance.
20 - Root mean square error (RMSE) The RMSE is the square root of the mean of the square of all errors. As with the MSE, a small value indicates a better forecasting performance.
21
Statistical perspective
Sometimes favorable results obtained from a technical perspective do not equate with promising forecasting performance, as they might be biased. It is still necessary to execute statistical tests to conclude whether the forecasting accuracy is significant from a statistical perspective. Consequently, the Pesaran-Timmermann (PT) test [30] and Diebold-Mariano (DM) test [31] are leveraged in our work.
-
PT test The PT test aims to examine the forecasting performance of model in terms of the direction of movement. The PT value can be obtained through the following steps.
For any time t during the whole time period (T days), we first define22 23
Now y and denote the time series of the original and predicted values, respectively, then24 25 26
Finally, we have the following test statistic:27 28 If the obtained p value is less than the given threshold, the null hypothesis can be rejected, indicating a good prediction result.
- DM test Suppose y(t) and are the original and predicted values at time t, respectively, the forecasting error of model i can be defined as . Correspondingly, the loss difference between model i1 and model i2 is constructed as , where g() is the MSE loss fuction. Then, the DM value is described as follows:
where . is the standard error of time series d, in which represents the consistent estimator of fd(0). As in the PT test, if the obtained p value is less than the given threshold, the null hypothesis can be rejected, which means that the difference between the prediction capabilities of model i1 and model29
Baseline algorithms
To test the forecasting performance of the proposed MF-LSTM model, we compare it with the following algorithms. The model settings are listed in Table 4. We use GridSearchCV to help determine an optimal set of hyperparameter values, which is a widely used and effective method for hyper-parameter optimization.
ARIMA This is a traditional time series forecasting method. The model output is derived from the historical USD/CNY rate data.
Support vector regression (SVR) Though it is equipped with shallow structures, as a classic machine learning method, SVR can still incorporate various factors without stringent restrictions. We compare it with the following deep learning methods.
Backpropagation neural network (BPNN) BPNNs are widely used for various tasks. The backpropagation algorithm computes the loss function gradient multiple times to update the weights of hidden units so that the loss can be minimized.
Extreme learning machine (ELM) An ELM is a feedforward NN. No parameters need to be manually tuned through gradient descent. Compared to a BPNN and SVR, an ELM usually exhibites a better generalization performance.
Convolutional Neural Network (CNN) CNNs are deep learning models that are widely used in Computer Vision (CV) [32, 33], NLP [34], time series prediction [35], etc. The forecasting performances of a CNN and LSTM are compared.
LSTM-single This is a single LSTM that only applies the historical data of the USD/CNY exchange rate to the prediction task.
LSTM-sentiment LSTM-sentiment is LSTMC1 in the first layer of our MF-LSTM model. It only takes the sentiment time series into account.
LSTM-market LSTM-market is LSTMC2 in the first layer of our MF-LSTM model, and it only considers the market indicators.
LSTM-all This is a single LSTM model that considers both sentiment time series and market indicators. The difference in forecasting performance between this model and MF-LSTM reflects the effect of MF.
Results
To determine the optimal lag order, we compare the six-month-window forecasting results obtained by the LSTM-all model with several lag length settings, which are shown in Table 5.
Table 5.
Forecasting performance with different lag orders
| Lag time | R2 | MAE | MSE | RMSE |
|---|---|---|---|---|
| 1 | 0.9788 | 0.0145 | 0.0004 | 0.0208 |
| 2 | 0.9767 | 0.0147 | 0.0004 | 0.0212 |
| 3 | 0.9702 | 0.0154 | 0.0006 | 0.0249 |
| 4 | 0.9612 | 0.0265 | 0.0013 | 0.0362 |
| 5 | 0.9537 | 0.0384 | 0.0021 | 0.0457 |
Based on the results, it can be concluded that the optimal lag length is 1 day, which is consistent with the observation in [36]. Such a result may imply that the Forex market can swiftly absorb the new information from both the text and numerical modalities and make corresponding adjustments.
Forecasting performance results
Table 6 displays the forecasting performance of the ten models in terms of the MAE, MSE, and RMSE metrics with a six-month window length. Note that we also list the results of two scenarios (MF-LSTM-US and MF-LSTM-CN), in which the market indicators and social media sentiments belonging to each country are exclusively applied to the MF-LSTM model, to determine which side exerts more influence on the USD/CNY exchange rate.
Table 6.
Technical results of different algorithms
| Algorithms | R2 | MAE | MSE | RMSE |
|---|---|---|---|---|
| ARIMA | 0.9392 | 0.0271 | 0.0014 | 0.0369 |
| SVR | 0.9582 | 0.0248 | 0.0011 | 0.0335 |
| BPNN | 0.9447 | 0.0256 | 0.0012 | 0.0347 |
| ELM | 0.9578 | 0.0239 | 0.0009 | 0.0312 |
| CNN | 0.9603 | 0.0232 | 0.0009 | 0.0299 |
| LSTM-single | 0.9655 | 0.0235 | 0.0009 | 0.0304 |
| LSTM-sentiment | 0.9689 | 0.0234 | 0.0008 | 0.0286 |
| LSTM-market | 0.9723 | 0.0191 | 0.0006 | 0.0240 |
| LSTM-all | 0.9788 | 0.0145 | 0.0004 | 0.0208 |
| MF-LSTM-US | 0.9765 | 0.0193 | 0.0006 | 0.0248 |
| MF-LSTM-CN | 0.9693 | 0.0227 | 0.0008 | 0.0289 |
| MF-LSTM | 0.9851 | 0.0122 | 0.0002 | 0.0154 |
Six-month window length
Apparently, it can be concluded that the proposed MF-LSTM model exceeds all baseline algorithms regarding the technical indicators. In addition, three observations can be obtained. First, the LSTM-derived models generally outperform the ARIMA, SVR, BPNN, ELM, and CNN approaches. Second, the MAE values of MF-LSTM are 15.9%, 36.1%, and 47.8% lower than those of LSTM-single, LSTM-sentiment, LSTM-market, and LSTM-all. Third, the LSTM-market model is superior to LSTM-sentiment when a six-month window length is utilized. Last, MF-LSTM-US holds an advantage over MF-LSTM-CN, with a lower RMSE value (0.0252).
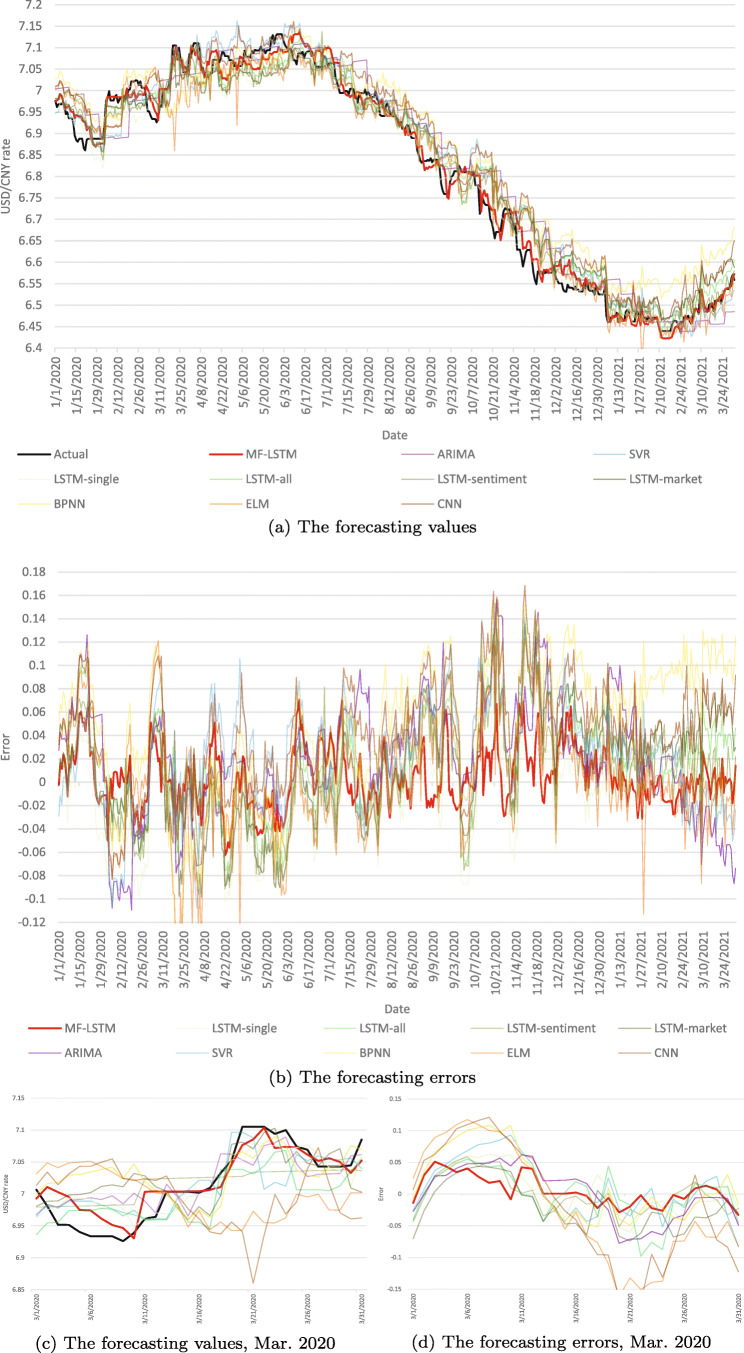
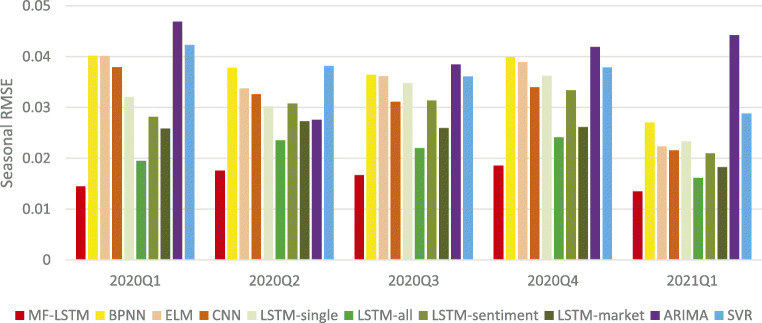
Figure 4 shows the forecasting accuracies and errors of the ten approaches for the period from 1/1/2020 to 4/1/2021. For a clearer view, Fig. 4c and d are extractions (Mar. 2020) from Fig. 4a and b, respectively. It can be observed from Fig. 4a that the MF-LSTM arguably fits the historical USD/CNY rate well. Moreover, the forecasting performance discrepancy is clearer in Fig. 4b. Furthermore, Fig. 5 depicts the forecasting RMSE of of different algorithms in 5 seasons. Notably, the USD/CNY exchange rate fluctuated severely in 2020Q1 due to the effect of the COVID-19 pandemic. During this period, our MF-LSTM model still significantly outperforms all other algorithms, exhibiting great resilience and robustness. Overall, our approach has the smallest forecasting errors throughout the whole period, especially on days with very high volatility. (Table 7)
Fig. 4.
Forecasting results of different algorithms with a six-month window length
Fig. 5.
Seasonal forecasting RMSE
Table 7.
Seasonal forecasting RMSE of different algorithms
| Algorithms | 2020Q1 | 2020Q2 | 2020Q3 | 2020Q4 | 2021Q1 |
|---|---|---|---|---|---|
| ARIMA | 0.0469 | 0.0275 | 0.0385 | 0.0419 | 0.0442 |
| SVR | 0.0423 | 0.0382 | 0.0361 | 0.0379 | 0.0288 |
| BPNN | 0.0402 | 0.0378 | 0.0365 | 0.0399 | 0.0270 |
| ELM | 0.0401 | 0.0338 | 0.0361 | 0.0389 | 0.0224 |
| CNN | 0.0380 | 0.0326 | 0.0311 | 0.0340 | 0.0216 |
| LSTM-single | 0.0321 | 0.0302 | 0.0348 | 0.0362 | 0.0234 |
| LSTM-sentiment | 0.0281 | 0.0308 | 0.0314 | 0.0334 | 0.0210 |
| LSTM-market | 0.0259 | 0.0273 | 0.0260 | 0.0261 | 0.0182 |
| LSTM-all | 0.0195 | 0.0236 | 0.0220 | 0.0242 | 0.0161 |
| MF-LSTM | 0.0145 | 0.0176 | 0.0167 | 0.0186 | 0.0135 |
Results of robustness tests
Robustness is crucial for determining the effectiveness of an algorithm, as well as its applicability for practitioners. This attribute should be demonstrated well on an independent but similar dataset. Correspondingly, we evaluate the ten approaches on the out-of-time data further collected from 1/1/2012 to 12/31/2014, where the previously utilized dataset (1/1/2015 to 4/1/2021) is excluded. To align with the previous dataset, we also apply a data partition setting of 6:2:2. The data from 6/1/2014 to 12/31/2014 are selected to test the robustness of these algorithms.
Table 8 shows the detailed results of robustness tests on out-of-time data. It can be observed that the results are consistent with those in the previous subsection. For illustration, the MF-LSTM exhibits superiority over the other nine algorithms with regard to the three technical criteria. In addition, the LSTM-derived models have better forecasting performance than ARIMA, SVR, BPNN, ELM, and CNN models. Notably, the LSTM-market still outperforms the LSTM-sentiment when a six-month window length is applied.
Table 8.
Technical results of different algorithms (robustness tests on out-of-time data)
| Algorithms | R2 | MAE | MSE | RMSE |
|---|---|---|---|---|
| ARIMA | 0.9388 | 0.0275 | 0.0014 | 0.0372 |
| SVR | 0.9587 | 0.0240 | 0.0011 | 0.0328 |
| BPNN | 0.9466 | 0.0261 | 0.0011 | 0.0339 |
| ELM | 0.9580 | 0.0243 | 0.0010 | 0.0317 |
| CNN | 0.9611 | 0.0237 | 0.0009 | 0.0303 |
| LSTM-single | 0.9657 | 0.0233 | 0.0009 | 0.0298 |
| LSTM-sentiment | 0.9691 | 0.0229 | 0.0008 | 0.0282 |
| LSTM-market | 0.9746 | 0.0188 | 0.0006 | 0.0237 |
| LSTM-all | 0.9785 | 0.0147 | 0.0004 | 0.0211 |
| MF-LSTM | 0.9848 | 0.0129 | 0.0003 | 0.0161 |
Six-month window length
Results of statistical tests
Table 9 exhibits the results obtained on the PT test and DM test. A high PT statistic indicates that a model is accurate in predicting the direction of exchange rate movements. Clearly, the MF-LSTM model outperforms all baseline algorithms in terms of forecasting accuracy from a statistical perspective. Specifically, the performance of the LSTM-derived models exceeds that of the other models, which is consistent with the results obtained from the technical perspective. Moreover, the PT statistic of MF-LSTM is significantly higher than that of LSTM-all.
Table 9.
Statistical results of different algorithms
| Algorithms | PT statistic | DM statistic |
|---|---|---|
| ARIMA | 0.8125 | − 5.7468*** |
| SVR | 1.2039 | − 5.2486*** |
| BPNN | 1.1433 | − 5.3276*** |
| ELM | 1.2918* | − 5.1937*** |
| CNN | 1.9922** | − 5.1329*** |
| LSTM-single | 2.6138** | − 4.4173*** |
| LSTM-sentiment | 3.0192*** | − 3.5404*** |
| LSTM-market | 3.9765*** | − 3.0719*** |
| LSTM-all | 5.2011*** | − 2.3561** |
| MF-LSTM | 6.8469*** |
*** denotes rejection of the null hypothesis at 1% significance level. ** denotes rejection of the null hypothesis at 5% significance level. * denotes rejection of the null hypothesis at 10% significance level
As mentioned before, a low DM statistic represents the forecasting discrepancy between a given model and MF-LSTM. From Table 9, it can be concluded that our proposed model is better than all benchmarks except the LSTM-all model under a 99% confidence level since their DM statistics are below -2. The MF-LSTM is still superior to the LSTM-all under a 95% confidence level.
Discussion
Interestingly, four findings can be derived from the previous section. First, it can be easily observed from Tables 6 and 9 that the LSTM-derived models outperform the ARIMA, SVR, BPNN, ELM, and CNN models. In accordance with [2] and [15], this observation confirms the capability of LSTM in depicting both long-term and short-term dependencies in time series analysis. That is, the LSTM-derived models are good at differentiating and capturing the effects of disparate influencing factors within each modality of information. Second, the MF-LSTM model exhibits an overwhelming advantage over the LSTM-based benchmarks regarding forecasting accuracy and error. This is further confirmed in the statistical tests. Here we present our reasoning and explanation. Initially, compared to LSTM-single, the LSTM-sentiment and the LSTM-market performs better, indicating the necessity of including any modalities of data (market indicators and investor sentiments). Additionally, compared to LSTM-sentiment and LSTM-market, the LSTM-all and the MF-LSTM show superiority, revealing the merits of fusing the modalities. Furthermore, between the two fusing methods, the MF-LSTM is better than the LSTM-all, which implies that a deep multimodal fusion structure is more effective than a straightforward fusion. Therefore, we believe it is safe to accredit such improvement of forecasting accuracy to MF-LSTM’s unique property – it takes two modalities of data into account, treats their exclusive characteristics separately, and fuses the hidden abstract features learned from different modalities. As a result, the proposed model is rendered not only capable of capturing couplings within each type of information, it is also adept at reflecting the interaction between different modalities of information. Third, the LSTM-market model is superior to LSTM-sentiment under the six-month window setting. In consideration of the similar findings concluded in [35], we ascribe this phenomenon to the fact that the impact of information obtained from social media is exerted mainly in the short term. This implies that although extreme sentiments can spread quickly on social media platforms, market indicators and exchange rates may not always fluctuate accordingly. Thus, it might not be an excellent idea to forecast Forex rates purely based on social media sentiments. Finally, the advantage that MF-LSTM-US possesses over MF-LSTM-CN implies that the features obtained from the U.S. side might impact the exchange rate more than those derived from the Chinese side. Here, we give two possible explanations for this finding: On the one hand, the U.S. economy is larger and more liquid, and such differences might affect the utilized market indicators. On the other hand, investor sentiments and new information on Twitter might be more easily transmittable to the Forex market.
In addition to these findings, we believe that two main contributions of our work should be emphasized. Initially, we apply the deep MF method to exchange rate forecasting for the first time, and it is demonstrated to be effective. On the one hand, although previous works used various methods (e.g., the ARIMA technique and SVR), they achieved considerably less promising results because of the overgeneralization of various influencing factors, as well as the neglect of the interactions among different modalities of information. On the other hand, although the MF method has achieved success on certain tasks such as disease diagnosis [37], we have not seen any practical applications of MF in the intricate foreign exchange market. Additionally, we adopt BERT for the sentiment analysis task to obtain sentiment time series, which reflect the text modality. Previous studies usually applied lexicon-based [38] or traditional machine learning-based [39] methods to conduct sentiment analysis on social media text. There is no reason not to utilize the BERT model, which has already been recognized as a state-of-the-art tool for NLP tasks, to execute sentiment classification for microblogs related to the financial market. However, limitations still exist in our study. Considering data availability, we only select microblogs from two social media platforms with respect to the text modality. In addition, only two Mandarin keywords remain after preprocessing. Such data might not be sufficient to reflect the text modality comprehensively. Therefore, in the future, we plan to include more types of social media text, such as news and posts on forums.
By building upon this research, future studies can be conducted from three facets. First, further work may investigate different fusion strategies (e.g., gradual fusion and hybrid fusion), optimization techniques, and model structures to achieve better performance. Although the use of a shared representation layer for intermediate fusion is indeed flexible, easy to operate, and efficacious, other strategies still possess certain merits. For example, late fusion (or decision fusion) is another favorable choice since the errors obtained from multiple classifiers are uncorrelated, and the method itself is feature-independent. In addition, reinforcement learning and other approaches can be leveraged to optimize the fusion structure. Furthermore, the possible structures are not confined to LSTM-derived models. We have noticed that some new models (e.g., the temporal convolutional network (TCN) [40] and LSTM with a transformation mechanism [41]) perform remarkably well in tasks such as time series prediction. Second, in terms of the modalities, image data can also be incorporated into exchange rate forecasting. For illustration, a CNN has demonstrated applicability in extracting abstract features (e.g., Bolinger bands) from stock charts [42]. This modality may also be employed to explore exchange rate charts and generate interesting results when used along with other modalities. Moreover, as recent studies have demonstrated the great potential of multimodal sentiment analysis [43, 44], future studies can conduct sentiment analysis on different modalities of data to improve the effectiveness of sentiment classification. Third, extra engineering tasks may be required before applying the findings of our work to the industry. Since current Chinese NLP corpora are still insufficient relative to the English corpora, we strongly recommend the construction of comprehensive corpora with higher quality, especially for informal social media text. If BERT-based models can be fine-tuned on such corpora in advance and exhibit robustness when encountering different types of text, plenty of practitioner effort can be saved.
Conclusion
The forecasting of exchange rates is an onerous task due not only to the distinctive conduction mechanisms of the influencing factors within each type of information but also to the intricate couplings among information modalities. In this study, we introduce the MF technique with the aim of addressing this issue. We first apply BERT to 1,323,956 pieces of social media text and obtain sentiment time series for 16 keywords to represent the text modality. Along with the market indicator data, which reflect the numerical modality, the data are fed into a novel MF-LSTM model, where two parallel LSTM modules in the first layer learn from each modality of information and a shared representation layer fuses the abstract features acquired from the previous layer. Then evaluations from the technical perspective (the MAE, MSE, and RMSE metrics) and the statistical perspective (the PT test and DM test) are leveraged to compare the prediction performance of our proposed model with that of nine baseline algorithms. The experimental results show the superiority of MF-LSTM in terms of both forecasting accuracy and error, demonstrating that it is feasible and effective to introduce MF into financial time series forecasting. Future studies can be conducted on various fusion strategies, optimization techniques, modal structures, modality selections, etc. We hope that our work may provide practical value for international trade practitioners, Forex market investors, and policy makers.
Biographies
Edmure Windsor
is an undergraduate student at the Hefei University of Technology. This year he will begin pursuing his Master’s degree in Financial Engineering at the New York University Tandon School of Engineering. His research interests include machine learning, deep learning, and algorithmic trading.

Wei Cao
is an associate professor in School of Economics at the Hefei University of Technology. Her research interests include data mining, machine learning, deep learning, and coupling analysis in finance. Cao has a PhD in information technology from the University of Technology, Sydney.

Author Contributions
All authors designed and performed this study. Material preparation, data analysis, and draft composition were performed by Edmure Windsor. Wei Cao made substantial contributions to the conceive of conception as well as the critical revision on previous versions of the manuscript. All authors read and approved the final manuscript.
Funding
Our work was supported by the National Natural Science Foundation of China under Project No. 71801072, 71774047, and 71971071.
Code Availability
Codes are available on reasonable request from the authors.
Declarations
Ethics Approval
Not applicable.
Consent for Publication
Not applicable.
Conflict of Interests
The authors declare that they have no conflict of interest.
Footnotes
Availability of Data and Material
Data are available on reasonable request from the authors.
Consent to Participate
Not applicable.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Edmure Windsor, Email: edmurewindsor@mail.hfut.edu.cn.
Wei Cao, Email: weicao@hfut.edu.cn.
References
- 1.Wooldridge P D (2019) Fx and otc derivatives markets through the lens of the triennial survey. BIS Quarterly Review
- 2.Cao W, Zhu W, Wang W, Demazeau Y, Zhang C (2020) A deep coupled lstm approach for usd/cny exchange rate forecasting. IEEE Intell Syst:1–10. 10.1109/MIS.2020.2977283
- 3.Kocenda E, Moravcova M. Intraday effect of news on emerging european forex markets: An event study analysis. Econ Syst. 2018;42(4):597–615. doi: 10.1016/j.ecosys.2018.05.003. [DOI] [Google Scholar]
- 4.Fama E F (2021) Market efficiency, long-term returns, and behavioral finance. University of Chicago Press. 10.7208/9780226426983-009
- 5.Jiao P, Veiga A, Walther A. Social media, news media and the stock market. J Econ Behav Organ. 2020;176:63–90. doi: 10.1016/j.jebo.2020.03.002. [DOI] [Google Scholar]
- 6.Shmilovici A, Kahiri Y, Ben-Gal I, Hauser S. Measuring the efficiency of the intraday forex market with a universal data compression algorithm. Comput Econ. 2009;33(2):131–154. doi: 10.1007/s10614-008-9153-3. [DOI] [Google Scholar]
- 7.Barberis N, Thaler R (2005) A survey of behavioral finance. Princeton University Press. 10.1515/9781400829125-004
- 8.Frank MZ, Sanati A. How does the stock market absorb shocks? J Financ Econ. 2018;129(1):136–153. doi: 10.1016/j.jfineco.2018.04.002. [DOI] [Google Scholar]
- 9.Escudero P, Alcocer W, Paredes J. Recurrent neural networks and arima models for euro/dollar exchange rate forecasting. Appl Sci. 2021;11(12):5658. doi: 10.3390/app11125658. [DOI] [Google Scholar]
- 10.Zolfaghari M, Gholami S. A hybrid approach of adaptive wavelet transform, long short-term memory and arima-garch family models for the stock index prediction. Expert Syst Appl. 2021;182:115149. doi: 10.1016/j.eswa.2021.115149. [DOI] [Google Scholar]
- 11.Moosa I (2016) Exchange rate forecasting: techniques and applications. Springer
- 12.Sun A, Zhao T, Chen J, Chang J. Comparative study: common ann and ls-svm exchange rate performance prediction. Chin J Electron. 2018;27(3):561–564. doi: 10.1049/cje.2018.01.003. [DOI] [Google Scholar]
- 13.Schmidhuber J, Hochreiter S. Long short-term memory. Neural Comput. 1997;9(8):1735–80. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 14.Greff K, Srivastava RK, Koutník J, Steunebrink BR, Schmidhuber J. Lstm: A search space odyssey. IEEE Trans Neural Netw Learn Syst. 2016;28(10):2222–2232. doi: 10.1109/TNNLS.2016.2582924. [DOI] [PubMed] [Google Scholar]
- 15.Baek Y, Kim HY. Modaugnet: A new forecasting framework for stock market index value with an overfitting prevention lstm module and a prediction lstm module. Expert Syst Appl. 2018;113:457–480. doi: 10.1016/j.eswa.2018.07.019. [DOI] [Google Scholar]
- 16.Urolagin S, Sharma N, Datta TK. A combined architecture of multivariate lstm with mahalanobis and z-score transformations for oil price forecasting. Energy. 2021;231:120963. doi: 10.1016/j.energy.2021.120963. [DOI] [Google Scholar]
- 17.Shen M-L, Lee C-F, Liu H-H, Chang P-Y, Yang C-H. Effective multinational trade forecasting using lstm recurrent neural network. Expert Syst Appl. 2021;182:115199. doi: 10.1016/j.eswa.2021.115199. [DOI] [Google Scholar]
- 18.Poria S, Cambria E, Bajpai R, Hussain A. A review of affective computing: From unimodal analysis to multimodal fusion. Inf Fusion. 2017;37:98–125. doi: 10.1016/j.inffus.2017.02.003. [DOI] [Google Scholar]
- 19.Liu H, Wu Y, Sun F, Fang B, Guo D. Weakly paired multimodal fusion for object recognition. IEEE Trans Autom Sci Eng. 2017;15(2):784–795. doi: 10.1109/TASE.2017.2692271. [DOI] [Google Scholar]
- 20.Calhoun VD, Sui J. Multimodal fusion of brain imaging data: A key to finding the missing link (s) in complex mental illness. Biol Psych: Cogn Neurosci Neuroimag. 2016;1(3):230–244. doi: 10.1016/j.bpsc.2015.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Asvadi A, Garrote L, Premebida C, Peixoto P, Nunes UJ. Multimodal vehicle detection: fusing 3d-lidar and color camera data. Pattern Recogn Lett. 2018;115:20–29. doi: 10.1016/j.patrec.2017.09.038. [DOI] [Google Scholar]
- 22.Devlin J, Chang M-W, Lee K, Toutanova K (2019) Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv:1810.04805
- 23.Ramachandram D, Taylor GW. Deep multimodal learning: A survey on recent advances and trends. IEEE Signal Proc Mag. 2017;34(6):96–108. doi: 10.1109/MSP.2017.2738401. [DOI] [Google Scholar]
- 24.Hemalatha I, Varma GPS, Govardhan A. Preprocessing the informal text for efficient sentiment analysis. Int J Emerging Trends Technol Comput Sci (IJETTCS) 2012;1(2):58–61. [Google Scholar]
- 25.Zhao G, Liu Z, Chao Y, Qian X (2020) Caper: Context-aware personalized emoji recommendation. IEEE Trans Knowl Data Eng. 10.1109/TKDE.2020.2966971
- 26.Zhao P, Jia J, An Y, Liang J, Xie L, Luo J (2018) Analyzing and predicting emoji usages in social media. In: Companion Proceedings of The Web Conference 2018. 10.1145/3184558.3186344, pp 327–334
- 27.Cui Y, Che W, Liu T, Qin B, Wang S, Hu G (2020) Revisiting pre-trained models for chinese natural language processing. arXiv:2004.13922
- 28.Liu Y, Ott M, Goyal N, Du J, Joshi M, Chen D, Levy O, Lewis M, Zettlemoyer L, Stoyanov V (2019) Roberta: A robustly optimized bert pretraining approach. arXiv:1907.11692
- 29.Barbieri F, Camacho-Collados J, Neves L, Espinosa-Anke L (2020) Tweeteval: Unified benchmark and comparative evaluation for tweet classification. arXiv:2010.12421
- 30.Pesaran MH, Timmermann A. A simple nonparametric test of predictive performance. J Bus Econ Stat. 1992;10(4):461–465. [Google Scholar]
- 31.Diebold FX, Mariano RS. Comparing predictive accuracy. J Bus Econ Stat. 2002;20(1):134–144. doi: 10.1198/073500102753410444. [DOI] [Google Scholar]
- 32.Zhang Z, Wang H, Xu F, Jin Y-Q. Complex-valued convolutional neural network and its application in polarimetric sar image classification. IEEE Trans Geosci Remote Sens. 2017;55(12):7177–7188. doi: 10.1109/TGRS.2017.2743222. [DOI] [Google Scholar]
- 33.Campos V, Jou B, Giro-i Nieto X. From pixels to sentiment: Fine-tuning cnns for visual sentiment prediction. Image Vis Comput. 2017;65:15–22. doi: 10.1016/j.imavis.2017.01.011. [DOI] [Google Scholar]
- 34.Chen T, Xu R, He Y, Wang X. Improving sentiment analysis via sentence type classification using bilstm-crf and cnn. Expert Syst Appl. 2017;72:221–230. doi: 10.1016/j.eswa.2016.10.065. [DOI] [Google Scholar]
- 35.Hoseinzade E, Haratizadeh S. Cnnpred: Cnn-based stock market prediction using a diverse set of variables. Expert Syst Appl. 2019;129:273–285. doi: 10.1016/j.eswa.2019.03.029. [DOI] [Google Scholar]
- 36.Wang G, Yu G, Shen X. The effect of online investor sentiment on stock movements: An lstm approach. Complexity. 2020;2020:4754025. doi: 10.1155/2020/4754025. [DOI] [Google Scholar]
- 37.Shi J, Zheng X, Li Y, Zhang Q, Ying SH. Multimodal neuroimaging feature learning with multimodal stacked deep polynomial networks for diagnosis of alzheimer’s disease. IEEE J Biomed Health Inf. 2018;22(1):173–183. doi: 10.1109/JBHI.2017.2655720. [DOI] [PubMed] [Google Scholar]
- 38.Dridi A, Atzeni M, Reforgiato Recupero D. Finenews: fine-grained semantic sentiment analysis on financial microblogs and news. Int J Mach Learn Cybern. 2019;10(8):2199–2207. doi: 10.1007/s13042-018-0805-x. [DOI] [Google Scholar]
- 39.Alqmase M, Al-Muhtaseb H, Rabaan H (2021) Sports-fanaticism formalism for sentiment analysis in arabic text. Soc Netw Anal Min 11(1). 10.1007/s13278-021-00757-9
- 40.Bai S, Kolter J Z, Koltun V (2018) An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv:1803.01271
- 41.Hu J, Zheng W. A deep learning model to effectively capture mutation information in multivariate time series prediction. Knowl-Based Syst. 2020;203:106139. doi: 10.1016/j.knosys.2020.106139. [DOI] [Google Scholar]
- 42.Kim T, Kim HY. Forecasting stock prices with a feature fusion lstm-cnn model using different representations of the same data. PLOS One. 2019;14(2):e0212320. doi: 10.1371/journal.pone.0212320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yu W, Xu H, Meng F, Zhu Y, Ma Y, Wu J, Zou J, Yang K (2020) Ch-sims: A chinese multimodal sentiment analysis dataset with fine-grained annotation of modality. In: Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. 10.18653/v1/2020.acl-main.343, pp 3718–3727
- 44.Zhao G, Lou P, Qian X, Hou X. Personalized location recommendation by fusing sentimental and spatial context. Knowl-Based Syst. 2020;196:105849. doi: 10.1016/j.knosys.2020.105849. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Codes are available on reasonable request from the authors.