Abstract
Accurate assessment of LDL-C levels is important, as they are often used for treatment recommendations. For many years, plasma LDL-C levels were calculated using the Friedewald equation, but there are limitations to this method compared with direct measurement via beta-quantification (BQ). Here, we assessed differences between the Friedewald, Martin-Hopkins, and NIH equation 2 methods of calculating LDL-C and the “gold standard” BQ method using pooled phase 3 data with alirocumab. All randomized patients were included irrespective of the treatment arm (n = 6,122). We compared pairs of LDL-C values (n = 17,077) determined by each equation and BQ. We found that BQ-derived LDL-C values ranged from 1 to 397 mg/dl (mean 90.68 mg/dl). There were strong correlations between Friedewald-calculated, Martin-Hopkins–calculated, and NIH equation 2–calculated LDL-C with BQ-determined LDL-C values (Pearson's correlation coefficient = 0.985, 0.981, and 0.985, respectively). Importantly, for BQ-derived LDL-C values ≥70 mg/dl, only 3.2%, 1.4%, and 1.8% of Friedewald-calculated, Martin-Hopkins–calculated, and NIH equation 2–calculated values were <70 mg/dl, respectively. When triglyceride (TG) levels were <150 mg/dl, differences between calculated and BQ-derived LDL-C values were minimal, regardless of the LDL-C level (<40, <55, or <70 mg/dl). However, when TG levels were >150 mg/dl, NIH equation 2 provided greater accuracy than Friedewald or Martin-Hopkins. When TGs were >250 mg/dl, inaccuracies were seen with all three methods, although NIH equation 2 remained the most accurate. In conclusion, LDL-C calculated by any of the three methods can guide treatment decisions for most patients, including those treated with proprotein convertase subtilisin/kexin type 9 inhibitors.
Supplementary key words: alirocumab, beta-quantification, calculated LDL-C, cholesterol, drug therapy/hypolipidemic drugs, Friedewald, LDL, Martin-Hopkins, NIH equation 2, PCSK9
Abbreviations: BQ, beta-quantification; PCSK9, proprotein convertase subtilisin/kexin type 9
The accurate assessment of LDL-C levels is important, as treatment decisions are often based on achievement of a specific LDL-C goal, a risk-based treatment goal, or reduction of LDL-C levels by at least 50% (1, 2). The gold standard reference method for measurement of LDL-C is beta-quantification (BQ) (3); however, the technique is labor-intensive and time-consuming, requiring the use of ultracentrifugation (which is not routinely available in all laboratories) to separate lipoprotein classes.
In clinical practice, plasma LDL-C levels were, for many years, indirectly determined by calculation from total cholesterol, HDL-C, and plasma triglyceride (TG) measurements following the method of Friedewald et al. (4), where LDL-C = total cholesterol – (HDL-C + TG/5) (using values in mg/dl). However, there are several limitations with the Friedewald equation. Most importantly, the equation assumes a fixed TG:cholesterol ratio for estimating the concentration of VLDL-C (represented by TG/5 in the formula). In patients with high TGs, this relationship may no longer hold true, and the Friedewald equation is not reliable when TGs are >400 mg/dl (4). Friedewald-calculated LDL-C values have also been reported to lose accuracy in patients with TGs ≥150 mg/dl or LDL-C <70 mg/dl (5, 6). Other researchers have reported significant loss of accuracy at very-low LDL-C levels (<30 mg/dl) (7).
With the known limitations of the Friedewald equation, more recent methods for calculating LDL-C have been developed. The method developed by Martin et al. (hereafter referred to as the Martin-Hopkins method) uses patient-specific ratios of TGs to VLDL-C derived from direct measurement of the latter by vertical spin density gradient ultracentrifugation (8) to allow estimation of VLDL-C in conjunction with directly measured TGs, total cholesterol, and HDL-C concentrations. The estimated VLDL-C is subtracted from non-HDL-C to obtain the LDL-C level (LDL-C = total cholesterol − HDL-C − TG/novel factor, where the novel factor is an adjustable factor based on a patient's non-HDL-C and TG levels and is derived from a 174-cell 2D table) (9). A more recent method by Sampson et al. (hereafter referred to as the NIH equation 2 method) used TGs and non-HDL-C as independent variables in a least-squares regression to generate an equation for estimation of VLDL-C, which was used in a second equation to calculate LDL-C at both low LDL-C and/or high TG levels (using least-squares regressions, LDL-C = total cholesterol/0.948 − HDL-C/0.971 − (TG/8.56 + [TG × non-HDL-C]/2,140 − TG2/16100) − 9.44) (6).
Discrepancies between calculated and BQ-derived LDL-C have become more important in the era of proprotein convertase subtilisin/kexin type 9 (PCSK9) inhibitors that can reduce LDL-C to very low levels when added to a statin (10, 11, 12, 13). In some phase 3 trials of the PCSK9 inhibitor alirocumab, LDL-C was determined by both Friedewald calculation and BQ methods (14, 15, 16, 17, 18, 19, 20, 21, 22). This provided an opportunity to assess potential differences between those two methods for determining LDL-C and to compare the Friedewald calculation to the Martin-Hopkins and NIH equation 2 methods (>5,000 patients).
Materials and methods
We compared pairs of LDL-C values determined by the Friedewald, Martin-Hopkins, or NIH equation 2 calculations, and BQ, using data from 10 ODYSSEY trials. Trial designs have been reported previously (14, 15, 16, 17, 18, 19, 20, 21, 22) and are summarized in supplemental Fig. S1. All studies were conducted in accordance with the Declaration of Helsinki and the International Conference on Harmonization Guidelines for Good Clinical Practice. All study protocols were approved by the appropriate institutional review board/ethics review committees, and patients provided written informed consent.
Patients were eligible for participation if their LDL-C levels were ≥70 mg/dl or ≥100 mg/dl at screening (depending on cardiovascular risk), except in LONG TERM, where all patients enrolled had LDL-C ≥70 mg/dl. Patients with TGs >400 mg/dl at screening were excluded. The primary endpoint in each trial was the percentage reduction in LDL-C from baseline to week 24.
For the present analysis, data were pooled from patients randomized to alirocumab, placebo, ezetimibe, or statin in the 10 trials (total 6,122 randomized patients; supplemental Fig. S1). Patients from the statin control arms in the ODYSSEY OPTIONS I, OPTIONS II, and ALTERNATIVE studies, and the 75 mg alirocumab every 2 weeks calibration arm in the ODYSSEY CHOICE I and II studies which investigated the alirocumab every 4 weeks dosing regimen, were also included.
Analyses were performed on the pooled intention-to-treat population (all randomized patients, regardless of treatment adherence). BQ and calculated LDL-C values were assessed at weeks 0 and 24 in all trials, and at weeks 12, 52, and 78 in ODYSSEY LONG TERM. If TG values were >400 mg/dl at one of these postrandomization visits, Friedewald calculation of LDL-C was not performed and LDL-C was derived by BQ instead. All available BQ-derived LDL-C values with a corresponding Friedewald-calculated LDL-C value at that timepoint were included in this analysis.
For the LONG TERM trial, central analysis of lipid parameters and BQ were performed by Covance Central Laboratory Services (Indianapolis, IN, and Geneva, Switzerland); BQ analyses were performed as follows. Serum was centrifuged for 20 h and 15 min using a Beckman Ultracentrifuge (model L7-35, L8-70M, or L-80XP). After centrifugation, VLDL-C and chylomicrons were in the upper layer, and HDL-C and LDL-C were in the bottom layer of the tube. The cholesterol in the bottom fraction was removed using a Beckman CentriTube Slicer and assayed using Roche Modular/Cobas analyzers. LDL-C concentration was calculated as the cholesterol level in the bottom fraction minus the HDL-C concentration. HDL-C was determined enzymatically following the chemical precipitation of LDL with a polyanion dextran sulfate and divalent Mg cation solution. For the enzymatic determination of cholesterol, all cholesteryl esters are split into free cholesterol and fatty acids by cholesterol esterase (Roche Diagnostics, Indianapolis, IN). The total free cholesterol is then oxidized by cholesterol oxidase to cholest-4-en-3-one and hydrogen peroxide. The hydrogen peroxide reacts with phenol in the presence of peroxidase and 4-aminophenozone to form an o-quinoneimine dye; the intensity of the color formed is proportional to the cholesterol concentration and can be measured photometrically. The interassay coefficient of variation (reproducibility) of the BQ assay ranged from 1.77% to 2.12% depending on the cholesterol concentration (supplemental Table S1).
For all other trials, lipid analyses were performed by Medpace Reference Laboratories, with BQ analyses performed using preparative ultracentrifugation as outlined in the Lipid Research Clinics method manual (23), described as follows. Serum or plasma was overlaid with normal saline (density 1.006 g/ml) and centrifuged (Beckman Ultracentrifugation model # L-90K and rotor type 50.4) at 40,000 rpm for 18–22 h at 10 °C to separate VLDL in the supernatant from LDL and HDL in the infranatant. The cholesterol concentration of the infranatant was then measured; all apolipoprotein B–containing lipoproteins (VLDL, LDL, and lipoprotein[a]) were precipitated from the serum using 50 kDa dextran sulfate with magnesium ions (MgCl2), and the cholesterol in the remaining HDL fraction was measured by enzymatic methods. The HDL-C concentration was subtracted from the infranatant cholesterol concentration to provide the BQ LDL-C value. The interassay coefficient of variation (reproducibility) ranged from 4.3% to 5.1% (supplemental Table S1).
The accuracy of serum total cholesterol, HDL-C, and TG level determinations (used to calculate LDL-C by the Friedewald, Martin-Hopkins, and NIH Equation 2 methods) was tested by participating in the Centers for Disease Control and Prevention–National Heart, Lung, and Blood Institute Lipid Standardization Program assays. Total cholesterol and TGs were determined by enzymatic methods using a Roche Modular analyzer (Covance Central Laboratory Services) or a Beckman Coulter AU series automatic analyzer (Medpace Reference Laboratories). HDL-C was isolated by chemical precipitation and centrifugation (a polyanion dextran sulfate and divalent Mg cation solution interacts with the LDL and VLDL to form an insoluble complex that is removed by centrifugation) and then analyzed as for total cholesterol. Assays conducted by Covance Central Laboratory Services and Medpace Reference Laboratories conformed to Centers for Disease Control standards; the precision and reproducibility of all lipid parameters for both central laboratories are summarized in supplemental Table S1. Spearman's correlation coefficients were derived to assess the relationship between LDL-C calculated by each of the three methods and BQ-derived LDL-C. The difference between BQ-derived and calculated LDL-C values was determined by calculated minus BQ-derived LDL-C values (both in mg/dl).
Differences between Friedewald-calculated, Martin-Hopkins–calculated, and NIH equation 2–calculated and BQ-derived LDL-C values were further assessed via Bland-Altman–adapted plots (difference vs. BQ LDL-C). Analyses according to quintiles of BQ LDL-C values or according to tertiles of TG values are also presented. In addition, a sensitivity analysis excluding the results from LONG TERM was also performed.
Results
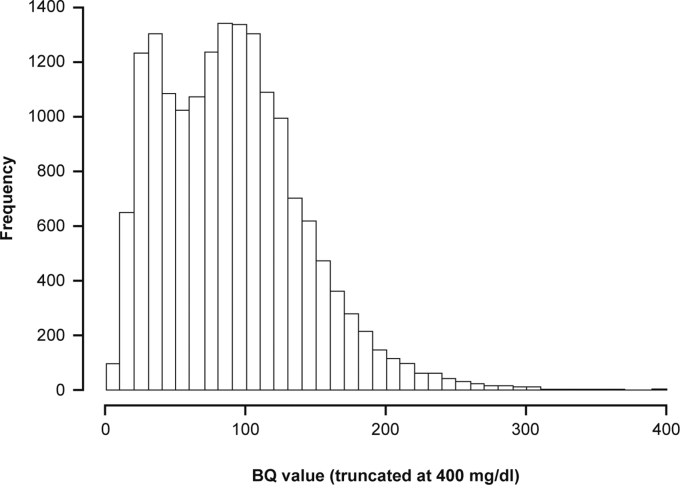
The initial dataset comprised 17,086 pairs of BQ-derived and Friedewald-calculated LDL-C values; nine LDL-C pairs with BQ-derived LDL-C values between 400 and 584 mg/dl were excluded as there was an insufficient number of values to allow for correct estimation of the correlation between LDL-C pairs in this range. Therefore, 17,077 pairs were included in the current analysis (data from 6,007 patients). BQ-derived LDL-C values ranged from 1 to 397 mg/dl (mean 90.68 mg/dl, median 87.00 mg/dl, Q1:Q3 49.03:120.85 mg/dl; Fig. 1).
Fig. 1.
Distribution of BQ-derived LDL-C values. The BQ-derived LDL-C values (n = 17,077) ranged from 1 to 397 mg/dl with the following parameters: mean, 90.68 mg/dl; median, 87.00 mg/dl; and Q1:Q3 49.03:120.85 mg/dl. BQ, beta-quantification.
Overall, there was a strong correlation between Friedewald-calculated and BQ-derived LDL-C (Pearson's correlation coefficient = 0.985); the mean difference was 0.13 mg/dl (median, −0.8 mg/dl; Q1:Q3, −5.4:5.0 mg/dl). A strong correlation between both Martin-Hopkins– and NIH equation 2–calculated LDL-C values with BQ-derived LDL-C values was also observed (Pearson's correlation coefficient = 0.981 and 0.985, respectively); the mean differences were 3.5 mg/dl (median, 1.8 mg/dl; Q1:Q3, −3.0:8.2 mg/dl) for Martin-Hopkins and 3.0 mg/dl (median, 1.7 mg/dl; Q1:Q3, −3.1:7.5, mg/dl) for NIH equation 2. The overall correlation between all four methods is summarized in supplemental Table S2.
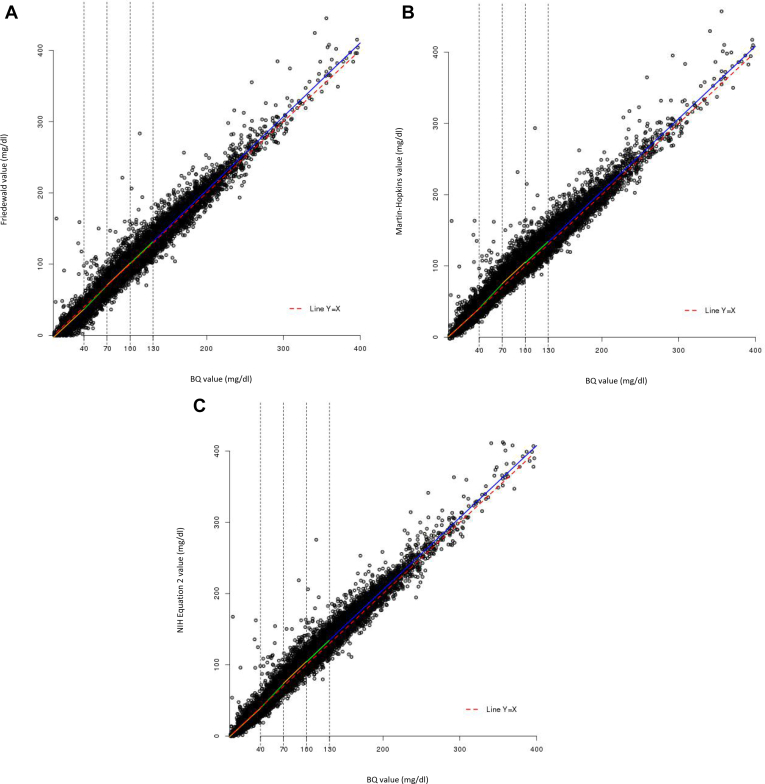
To assess the impact of lower LDL-C levels on the relationship between calculated and measured LDL-C, we examined the correlation by quintile of BQ LDL-C values. The boundaries for the BQ quintiles were 41.7, 73.4, 99.2, and 129.0 mg/dl; however, values rounded to the nearest whole number (40, 70, 100, and 130 mg/dl) were used for the analyses. Although correlations were shown to vary when data were analyzed by quintile of BQ values, there was no observable pattern across quintiles of BQ values with Friedewald-calculated (Fig. 2A), Martin-Hopkins–calculated (Fig. 2B), or NIH equation 2–calculated LDL-C values (Fig. 2C). In addition, the mean differences between Friedewald-calculated and BQ-derived LDL-C values by quintile of BQ LDL-C values for the entire study sample were −3.0, −1.7, 1.0, 1.2, and 2.8 mg/dl for the first to the fifth quintiles, respectively (median differences: −3.0, −2.0, 1.0, 1.0 and 2.0 mg/dl); the interquartile range increased from the first to the fifth quintile (6.9, 8.3, 10.0, 11.0, and 13.6 mg/dl, respectively). The corresponding mean differences between Martin-Hopkins–calculated and BQ-derived LDL-C values by quintile of BQ LDL-C values were 0.4, 2.8, 5.3, 4.3, and 4.3 mg/dl for the first to fifth quintiles, respectively (median differences: −0.9, 1.3, 4.1, 3.0, and 2.4 mg/dl); the interquartile range from the first to the fifth quintile was 6.9, 9.9, 11.0, 12.5, and 15.3 mg/dl, respectively. Similarly, the corresponding mean differences between NIH equation 2–calculated and BQ-derived LDL-C values by quintile of BQ LDL-C values were −0.8, 1.3, 4.4, 4.3, and 5.2 mg/dl for the first to fifth quintiles, respectively (median differences: −1.7, 0.1, 3.5, 3.9, and 4.7 mg/dl); the interquartile range from the first to fifth quintile was 6.3, 8.7, 10.3, 11.3, and 13.6 mg/dl, respectively.
Fig. 2.
Scatter plot of calculated versus BQ-derived LDL-C values according to quintiles of BQ-derived LDL-C values. A: Friedewald-calculated versus BQ-derived LDL-C. B: Martin-Hopkins–calculated versus BQ-derived LDL-C. C: NIH equation 2–calculated versus BQ-derived LDL-C. A: Regression equations (Pearson's correlation) for each quintile of BQ-derived LDL-C values are as follows: Q1 (n = 3,276): y = −2.948 + 0.997x (0.73); Q2 (n = 3,180): y = −7.652 + 1.108x (0.76); Q3 (n = 3,911): y = −1.114 + 1.025x (0.69); Q4 (n = 3,382): y = −1.642 + 1.025x (0.66); and Q5 (n = 3,328): y = −2.592 + 1.032x (0.96). Note that the x = y line is shown as a red dotted line. B: Regression equations (Pearson's correlation) for each quintile of BQ-derived LDL-C values are as follows: Q1 (n = 3,276): y = 0.797 + 0.984x (0.72); Q2 (n = 3,180): y = −5.315 + 1.147x (0.74); Q3 (n = 3,911): y = 4.784 + 1.006x (0.65); Q4 (n = 3,382): y = 4.059 + 1.002x (0.62); and Q5 (n = 3,328): y = 1.477 + 1.016x (0.95). Note that the x = y line is shown as a red dotted line. C: Regression equations (Pearson's correlation) for each quintile of BQ-derived LDL-C values are as follows: Q1 (n = 3,276): y = −0.586 + 0.991x (0.75); Q2 (n = 3,180): y = −6.466 + 1.140x (0.77); Q3 (n = 3,911): y = 1.674 + 1.032x (0.70); Q4 (n = 3,382): y = 1.746 + 1.023x (0.66); and Q5 (n = 3,328): y = 3.567 + 1.010x (0.96). Note that the x = y line is shown as a red dotted line. The boundaries for the quintiles of BQ LDL-C values are 40, 70, 100, and 130 mg/dl (rounded values of the real boundaries were used, which were 41.7, 73.4, 99.2, and 129.0 mg/dl, respectively), with minimum = 1 mg/dl and maximum = 397 mg/dl. BQ, beta-quantification; Q, quintile; x, BQ-derived LDL-C value; y, calculated LDL-C value.
The differences between calculated and BQ-derived LDL-C values were also assessed for subgroups of BQ-derived LDL-C values <40 mg/dl, <55 mg/dl, and <70 mg/dl with TGs >150 mg/dl. The results for all three methods in these subgroups are summarized in Table 1. In the subgroup with LDL-C <40 mg/dl/TGs >150 mg/dl, median differences between calculated and BQ-derived LDL-C values were −9 mg/dl, 3 mg/dl, and −1 mg/dl for the Friedewald, Martin-Hopkins, and NIH equation 2 methods, respectively. For the subgroup with LDL-C <55 mg/dl/TGs >150 mg/dl, the median differences were −8 mg/dl (Friedewald), 4 mg/dl (Martin-Hopkins), and −1 mg/dl (NIH equation 2); for the subgroup with LDL-C <70 mg/dl/TGs >150 mg/dl, the median differences were −7 mg/dl (Friedewald), 5 mg/dl (Martin-Hopkins), and 1 mg/dl (NIH equation 2). Greater median differences were observed for the Friedewald and Martin-Hopkins methods compared with NIH equation 2 for the subgroup with BQ-derived LDL-C <40 mg/dl and TGs >250 mg/dl (Friedewald, −14 mg/dl; Martin-Hopkins, 12 mg/dl; NIH equation 2, 2 mg/dl), the subgroup with BQ-derived LDL-C <55 mg/dl and TGs >250 mg/dl (Friedewald, −14 mg/dl; Martin-Hopkins, 13 mg/dl; NIH equation 2, 2 mg/dl), and the subgroup with BQ-derived LDL-C <70 mg/dl and TGs >250 mg/dl (Friedewald, −10 mg/dl; Martin-Hopkins, 14 mg/dl; NIH equation 2, 4.0 mg/dl; Table 1).
Table 1.
Analysis of difference between calculated LDL-C values and BQ-derived LDL-C values for several subgroups of patients
| Subgroup | n of LDL-C Pairs | Difference (mg/dl) |
||||
|---|---|---|---|---|---|---|
| Mean | Median | Q1 | Q2 | IQR | ||
| BQ-derived LDL-C <40 mg/dl and TGs >150 mg/dl | ||||||
| Friedewald versus BQ | 626 | ˗7.6 | ˗8.9 | ˗13.0 | ˗4.2 | 8.8 |
| Martin-Hopkins versus BQ | 626 | 5.5 | 3.1 | ˗0.8 | 8.9 | 9.7 |
| NIH equation 2 versus BQ | 626 | 0.9 | ˗0.9 | ˗4.4 | 3.5 | 7.9 |
| BQ-derived LDL-C <40 mg/dl and TGs <150 mg/dl | ||||||
| Friedewald versus BQ | 2,595 | ˗1.9 | ˗2.3 | ˗5.0 | 1.0 | 6.0 |
| Martin-Hopkins versus BQ | 2,595 | ˗0.9 | ˗1.5 | ˗4.3 | 1.7 | 6.0 |
| NIH equation 2 versus BQ | 2,595 | ˗1.2 | ˗1.8 | ˗4.7 | 1.3 | 6.0 |
| BQ-derived LDL-C <40 mg/dl and TGs >250 mg/dl | ||||||
| Friedewald versus BQ | 100 | ˗10.0 | ˗14.3 | ˗19.0 | ˗4.8 | 14.1 |
| Martin-Hopkins versus BQ | 100 | 15.6 | 11.5 | 5.9 | 21.3 | 15.4 |
| NIH equation 2 versus BQ | 100 | 5.4 | 1.7 | ˗3.4 | 9.4 | 12.9 |
| BQ-derived LDL-C <55 mg/dl and TGs <150 mg/dl | ||||||
| Friedewald versus BQ | 3,810 | ˗1.8 | ˗2.0 | ˗5.0 | 1.0 | 6.0 |
| Martin-Hopkins versus BQ | 3,810 | ˗0.8 | ˗1.4 | ˗4.4 | 2.0 | 6.4 |
| NIH equation 2 versus BQ | 3,810 | ˗1.1 | ˗1.6 | ˗4.7 | 1.7 | 6.4 |
| BQ-derived LDL-C <55 mg/dl and TGs >150 mg/dl | ||||||
| Friedewald versus BQ | 1,020 | ˗7.0 | ˗8.0 | ˗13.0 | ˗3.0 | 10.0 |
| Martin-Hopkins versus BQ | 1,020 | 6.4 | 4.0 | ˗0.1 | 10.5 | 10.7 |
| NIH equation 2 versus BQ | 1,020 | 1.4 | ˗0.6 | ˗4.1 | 4.9 | 9.0 |
| BQ-derived LDL-C <55 mg/dl and TGs >250 mg/dl | ||||||
| Friedewald versus BQ | 175 | ˗10.0 | ˗13.5 | ˗20.0 | ˗4.6 | 15.4 |
| Martin-Hopkins versus BQ | 175 | 15.5 | 12.7 | 6.2 | 21.2 | 15.1 |
| NIH equation 2 versus BQ | 175 | 4.9 | 1.9 | ˗3.7 | 9.6 | 13.3 |
| BQ-derived LDL-C <70 mg/dl and TGs <150 mg/dl | ||||||
| Friedewald versus BQ | 4,874 | ˗1.5 | ˗2.0 | ˗5.0 | 1.9 | 6.9 |
| Martin-Hopkins versus BQ | 4,874 | ˗0.4 | ˗1.1 | ˗4.3 | 2.6 | 6.9 |
| NIH equation 2 versus BQ | 4,874 | ˗0.6 | ˗1.3 | ˗4.5 | 2.4 | 6.9 |
| BQ-derived LDL-C <70 mg/dl and TGs >150 mg/dl | ||||||
| Friedewald versus BQ | 1,493 | −5.5 | −7.0 | −12.0 | −1.0 | 11.0 |
| Martin-Hopkins versus BQ | 1,493 | 7.7 | 5.4 | 0.6 | 12.3 | 11.7 |
| NIH equation 2 versus BQ | 1,493 | 2.7 | 0.6 | −3.7 | 6.6 | 10.3 |
| BQ-derived LDL-C <70 mg/dl and TGs >250 mg/dl | ||||||
| Friedewald versus BQ | 274 | −7.2 | −10.0 | −17.0 | −0.8 | 16.2 |
| Martin-Hopkins versus BQ | 274 | 16.8 | 13.5 | 7.2 | 22.8 | 15.6 |
| NIH equation 2 versus BQ | 274 | 6.6 | 4.0 | −2.4 | 12.9 | 15.3 |
BQ, beta-quantification; IQR, interquartile range; TG, triglyceride.
However, when subgroups with BQ-derived LDL-C <40 mg/dl, <55 mg/dl, <70 mg/dl, and TGs <150 mg/dl were examined, the median differences between the three methods were minimal (Friedewald, −2.3, 2.0, and −2.0 mg/dl; Martin-Hopkins, −1.5, −1.4, and −1.1 mg/dl; NIH equation 2, −1.8, −1.6, and −1.3 mg/dl for LDL-C <40 <55, <70 mg/dl, respectively (Table 1).
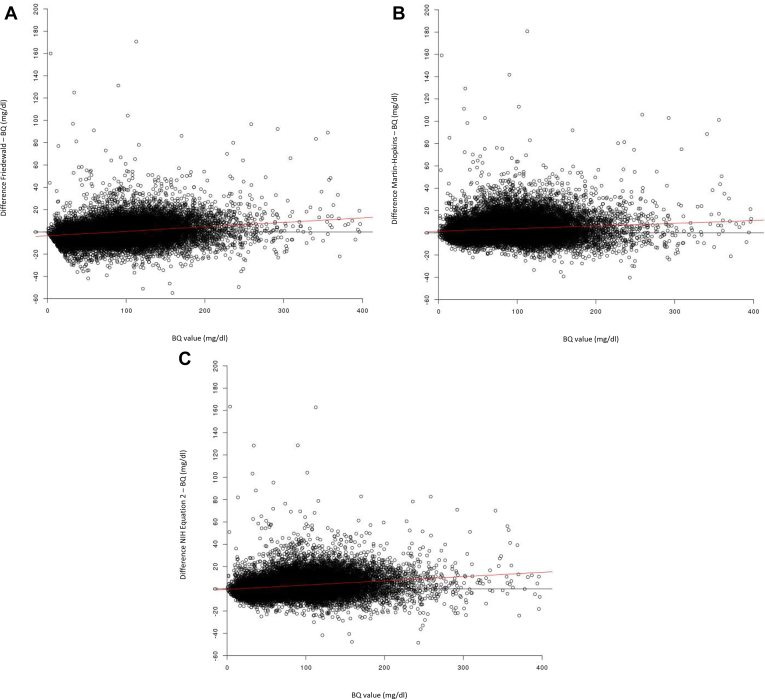
Analyses of the differences between calculated and BQ-derived LDL-C values versus BQ-derived LDL-C values were conducted for the total dataset. Overall, small differences were observed across the range of BQ LDL-C values for all three methods (Fig. 3). Comparison of the differences between Friedewald-calculated and BQ-derived LDL-C and BQ LDL-C values implied that the Friedewald method generally overestimates when BQ values are >87 mg/dl and underestimates when BQ values are <87 mg/dl (Fig. 3A). Similarly, the Martin-Hopkins method was found to overestimate across the entire range of BQ LDL-C values (Fig. 3B), and the NIH equation 2 method was found to overestimate when BQ LDL-C values are >13 mg/dl (Fig. 3C).
Fig. 3.
Bland-Altmann–adapted plots for the difference between calculated and BQ-derived LDL-C values. A: Friedewald-calculated versus BQ-derived LDL-C. B: Martin-Hopkins–calculated versus BQ-derived LDL-C. C: NIH equation 2–calculated versus BQ-derived LDL-C. A: Regression equation (shown as a red line): y = −3.495 + 0.040x. B: Regression equation (shown as a red line): y = 1.338 + 0.0239x. C: Regression equation (shown as a red line): y = −0.497 + 0.0382x. BQ, beta-quantification; TG, triglyceride.
Analyses of the differences between calculated and BQ-derived LDL-C values versus BQ-derived LDL-C values were also analyzed in more detail according to quintiles of BQ-derived LDL-C values (Table 2; supplemental Fig. S2). When comparing the differences between calculated and BQ-derived LDL-C, the smallest difference was observed with the first quintile of BQ values for all three methods (58.1%, 66.5%, and 66.1% of values differed by 0–5 mg/dl; 28.9%, 25.2%, and 27.6% differed by 5–10 mg/dl; and 13.0%, 8.2%, and 6.3% differed by >10 mg/dl for the Friedewald, Martin-Hopkins, and NIH equation 2 methods, respectively; Table 2). By comparison, for the overall dataset, 50.3%, 47.9%, and 49.6% of LDL-C pairs differed by 0–5 mg/dl; 29.4%, 28.1%, and 29.4% differed by 5–10 mg/dl; and 20.3%, 24.1%, and 21.3% differed by >10 mg/dl for the Friedewald, Martin-Hopkins, and NIH equation 2 methods, respectively.
Table 2.
Summary of the differences between calculated and BQ-derived LDL-C values according to quintile of BQ-derived LDL-C values
| Quintile (mg/dl) | Absolute Difference Between Calculated and BQ-Derived LDL-C Values, n (%) of Values | |||
|---|---|---|---|---|
| 0–5 mg/dL | 5–10 mg/dL | >10 mg/dL | Total, n | |
| Friedewald-calculated | ||||
| Q1: ≤40 | 1,902 (58.06) | 947 (28.91) | 427 (13.03) | 3,276 |
| Q2: >40 to ≤70 | 1,754 (55.16) | 908 (28.55) | 518 (16.29) | 3,180 |
| Q3: >70 to ≤100 | 2,001 (51.16) | 1,202 (30.73) | 708 (18.10) | 3,911 |
| Q4: >100 to ≤130 | 1,603 (47.40) | 1,044 (30.87) | 735 (21.73) | 3,382 |
| Q5: >130 to ≤400 | 1,329 (39.93) | 924 (27.76) | 1,075 (32.30) | 3,328 |
| Total, n | 8,589 | 5,025 | 3,463 | 17,077 |
| Martin-Hopkins–calculated | ||||
| Q1: ≤40 | 2,180 (66.54) | 827 (25.24) | 269 (8.21) | 3,276 |
| Q2: >40 to ≤70 | 1,669 (52.48) | 921 (28.96) | 590 (18.55) | 3,180 |
| Q3: >70 to ≤100 | 1,702 (43.52) | 1,171 (29.94) | 1,038 (26.54) | 3,911 |
| Q4: >100 to ≤130 | 1,402 (41.45) | 985 (29.12) | 995 (29.42) | 3,382 |
| Q5: >130 to ≤400 | 1,221 (36.69) | 890 (26.74) | 1,217 (36.57) | 3,328 |
| Total, n | 8,174 | 4,794 | 4,109 | 17,077 |
| NIH equation 2–calculated | ||||
| Q1: ≤40 | 2,166 (66.12) | 905 (27.63) | 205 (6.26) | 3,276 |
| Q2: >40 to ≤70 | 1,803 (56.70) | 927 (29.15) | 450 (14.15) | 3,180 |
| Q3: >70 to ≤100 | 1,805 (46.15) | 1,231 (31.48) | 875 (22.37) | 3,911 |
| Q4: >100 to ≤130 | 1,438 (42.52) | 1,037 (30.66) | 907 (26.82) | 3,382 |
| Q5: >130 to ≤400 | 1,228 (36.90) | 903 (27.13) | 1,197 (35.97) | 3,328 |
| Total, n | 8,440 | 5,003 | 3,634 | 17,077 |
BQ, beta-quantification; Q, quintile.
We examined concordance between calculated and BQ-derived LDL-C values above and below the LDL-C threshold of <70 mg/dl, used as a clinical target for patients at very-high cardiovascular risk (Table 3). Overall, the discordance was 3.6%, 4.0%, and 3.6% for the Friedewald, Martin-Hopkins, and NIH equation 2 methods. For BQ-derived LDL-C values <70 mg/dl, the concordance was 94.7%, 97.4%, and 96.9% for the Friedewald, Martin-Hopkins, and NIH equation 2 methods, respectively. Furthermore, for BQ-derived LDL-C values ≥70 mg/dl, 3.2% had a corresponding Friedewald-calculated LDL-C value <70 mg/dl, 1.4% had a corresponding Martin-Hopkins–calculated LDL-C value <70 mg/dl, and 1.8% had a corresponding NIH equation 2–calculated LDL-C value <70 mg/dl.
Table 3.
Analysis of concordance between calculated and BQ-derived LDL-C values for the LDL-C threshold of 70 mg/dL
| n (%) of LDL-C Pairs | BQ <70 mg/dL | BQ ≥70 mg/dL | Total |
|---|---|---|---|
| Friedewald <70 mg/dL | 6,095 (94.7) | 341 (5.3) | 6,436 |
| Friedewald ≥70 mg/dL | 282 (2.7) | 10,359 (97.3) | 10,641 |
| Total | 6,377 | 10,700 | 17,077 |
| Martin-Hopkins <70 mg/dL | 5,853 (97.4) | 154 (2.6) | 6,007 |
| Martin-Hopkins ≥70 mg/dL | 524 (4.7) | 10,546 (95.3) | 11,070 |
| Total | 6,377 | 10,700 | 17,077 |
| NIH equation 2 <70 mg/dL | 5,960 (96.9) | 191 (3.1) | 6,151 |
| NIH equation 2 ≥70 mg/dL | 417 (3.8) | 10,509 (96.2) | 10,926 |
| Total | 6,377 | 10,700 | 17,077 |
Discordance is 3.6%, 4.0%, and 3.6% for the Friedewald, Martin-Hopkins, and NIH equation 2 methods, respectively.
BQ, beta-quantification.
The number of outliers (absolute difference between calculated and BQ-derived LDL-C values >50 mg/dl) was similar between the Friedewald (45 pairs; 39 distinct patients [6,007 total patients in the analysis]), Martin-Hopkins (63 pairs; 53 distinct patients), and NIH equation 2 (51 pairs; 44 distinct patients) methods. In total, 70 pairs resulted in an absolute difference in LDL-C values >50 mg/dl, of which 49 (70%) pairs were outliers with at least two calculated-LDL-C methods, and 40 (57%) pairs, which were outliers with all three calculated-LDL-C methods. There were 21 LDL-C pairs that resulted in outliers with only one method of LDL-C calculation (Friedewald, two pairs; Martin-Hopkins, 16 pairs; NIH equation 2, three pairs). When the LDL-C outliers were compared for these patients, no obvious patterns were observed over time (supplemental Fig. S3), nor in the lipid parameters used to calculate LDL-C (supplemental Fig. S4).
We further analyzed the data according to TG tertiles to assess whether TG levels affected the results. TGs ranged from 21 to 400 mg/dl, with boundaries of 97 and 150 mg/dl for the tertiles. Overall, no impact on the correlation between calculated versus BQ-derived LDL-C was observed when analyzed by TG tertiles (supplemental Fig. S5). However, there was a trend for Friedewald-calculated LDL-C to be less than BQ-derived LDL-C for the third tertile of TGs (intercept of approximately −7 compared with −1 and −3 for the first and second TG tertiles, respectively; supplemental Fig. S5A). In contrast, there was a trend for Martin-Hopkins–calculated LDL-C to be greater than BQ-derived LDL-C for the third tertile of TGs (intercept of approximately 8 compared with −2 and +2 for the first and second TG tertiles, respectively; supplemental Fig. S5B). A tendency for calculated values to be higher than BQ-derived LDL-C values for the third tertile of TGs was also observed for NIH equation 2–calculated LDL-C values (intercept of approximately 3 for the third tertile vs. −3 and 0 for the first and second TG tertiles, respectively; supplemental Fig. S5C).
Comparison of the difference between calculated and BQ-derived LDL-C values versus BQ LDL-C according to tertiles of TGs is shown in supplemental Fig. S6. The difference between Friedewald-calculated and BQ-derived LDL-C tended to be greater at higher BQ-LDL-C values, with the difference being greater in the third tertile of TGs versus the first and second tertiles of TGs (supplemental Fig. S6A). For the difference between Martin-Hopkins–calculated LDL-C and BQ-derived LDL-C, a larger difference between values was observed in the third tertile versus the first and second tertiles of TGs (supplemental Fig. S6B). There was no obvious trend in the difference between NIH equation 2–calculated LDL-C and BQ-derived LDL-C values when analyzed by TG tertiles (supplemental Fig. S6C).
A sensitivity analysis excluding the results of LONG TERM was also conducted. The BQ-derived LDL-C values (n = 6,667) ranged from 1 to 397 mg/dl (mean 103.2 mg/dl, median 95.0 mg/dl, Q1:Q3 67.0:132.0 mg/dl). As we observed for the total dataset, there was an overall strong correlation between calculated and BQ-derived LDL-C values for all 3 methods (supplemental Tables S3 and S4). When the correlations between calculated and BQ-derived LDL-C levels were assessed by quintile of BQ LDL-C value, the results were overall consistent with that of the total dataset (supplemental Fig. S7). Similarly, when LONG TERM data were excluded, the differences between calculated and BQ-derived LDL-C values were similar to the overall dataset when evaluated by quintiles of BQ-derived LDL-C values (supplemental Table S5). When concordance between calculated and BQ-derived LDL-C values was assessed above and below an LDL-C threshold of 70 mg/dl, the overall discordance after removal of LONG TERM data was 4.2%, 4.2%, and 3.8% for the Friedewald, Martin-Hopkins, and NIH equation 2 methods (supplemental Table S6), respectively, again consistent with the total dataset. Finally, when the LDL-C outliers were compared (absolute difference between calculated and BQ-derived LDL-C values >50 mg/dl) after exclusion of the LONG TERM data, no obvious patterns were observed over time (supplemental Fig. S8).
Discussion
This analysis of the available data in the ODYSSEY trials shows that the discrepancy between Friedewald-calculated, Martin-Hopkins–calculated, and NIH equation 2–calculated LDL-C with BQ-derived LDL-C values is small and clinically insignificant, with approximately 50% or greater of LDL-C values differing by less than 5 mg/dl. This conclusion includes levels in the lowest quintile of BQ-derived LDL-C values (<40 mg/dl) where the majority of LDL-C values also differed by less than 5 mg/dl (58.1%, 66.5%, and 66.1% for the Friedewald, Martin-Hopkins, and NIH equation 2 methods, respectively). Furthermore, even in the lowest quintile of BQ-derived LDL-C values (≤40 mg/dl), the mean difference between calculated and BQ-derived LDL-C values was relatively small compared with the mean difference for the overall dataset for all three methods. In addition, no impact on the overall correlation between calculated and BQ-derived LDL-C values was observed when analyzed by TG tertiles. Although the correlation between Friedewald-calculated and BQ-derived LDL-C diminished as TGs increased, even in the highest tertile of TGs (>150 mg/dl), the correlation remained high (0.98).
The results are in agreement with those of previous analyses (24, 25, 26, 27, 28) as well as current guidelines (1, 2), indicating that Friedewald-calculated LDL-C provides a reasonable estimation of BQ-derived LDL-C in most cases. A previous analysis of samples from patients treated to LDL-C levels <40 mg/dl with the PCSK9 inhibitor evolocumab reported an overall small median absolute difference (4 mg/dl) between Friedewald-calculated and BQ-derived LDL-C values; greater variation was observed for patients with LDL-C <40 mg/dl and TG levels ≥150 mg/dl, with median absolute difference of 10 mg/dl between Friedewald-calculated and BQ-derived LDL-C values (29). Furthermore, in the previous analysis, for the subgroup of patients with LDL-C <40 mg/dl and TG levels ≥150 mg/dl, a smaller median difference between calculated and BQ-derived LDL-C was observed for the Martin-Hopkins versus the Friedewald method (2 vs. −10 mg/dl, respectively) (29). In the present analysis, for the subgroup of BQ-derived LDL-C values <40 mg/dl with TGs >150 mg/dl, a greater median difference between calculated LDL-C values and BQ-derived LDL-C was observed for Friedewald (−9 mg/dl) compared with the Martin-Hopkins (3 mg/dl) and NIH equation 2 (−1 mg/dl) methods. Differences across the three methods were also observed for LDL-C <40, <55, or <70 mg/dl and TGs >150 mg/dl and LDL-C <40, <55, or <70 mg/dl and TGs >250 mg/dl (Table 1). For each set of lipid cut points, Friedewald underestimated, Martin-Hopkins overestimated, and NIH equation 2 was essentially the same as the BQ value. Importantly, when TGs were <150 mg/dl, which was the case in the largest group of subjects by far, differences between the three methods for estimation of LDL-C <40, <55, and <70 mg/dl were minimal to nil.
In the present analysis, we found good concordance between calculated and BQ-derived values of LDL-C <70 or ≥70 mg/dl, with a small proportion (3.6%, 4.0%, and 3.6% for the Friedewald, Martin-Hopkins, and NIH equation 2 methods, respectively) of samples that had a BQ-derived value <70 mg/dl having a corresponding calculated value of ≥70 mg/dl, or vice versa. Importantly, in the lowest quintile of BQ-derived LDL-C values (<40 mg/dl), there were only very small differences between BQ-derived and calculated LDL-C concentrations, with the majority of LDL-C values only differing by 0–5 mg/dl, as noted above.
We identified a number of outliers where the difference between calculated and BQ-derived LDL-C values was >50 mg/dl; the number of outliers was similar between the Friedewald (45 LDL-C pairs), Martin-Hopkins (63 LDL-C pairs), and NIH equation 2 (51 LDL-C pairs) methods. In total, there were 70 LDL-C pairs that were outliers; the majority (70%; 40 LDL-C pairs) were outliers with all three calculated-LDL-C methods. For most patients with an outlier, there was only one outlying value. We cannot exclude the possibility that there were errors in the original lipid panel and/or BQ measurements at certain time points that led to the observed outlying values.
The 2018 US cholesterol management guidelines (2) state that the Friedewald equation loses accuracy at LDL-C levels <70 mg/dl and suggest that alternative calculation methods may be used, such as those of Martin et al. (5, 9) or measurement of direct LDL-C. The 2019 European guidelines note that alternative modes of calculating LDL-C or direct LDL-C measurement may be considered, but the former have not been shown to be superior to the Friedewald equation in estimating cardiovascular risk, and the latter have limitations of precision and accuracy, especially in patients with high TG levels (1). The recent NIH equation 2 method (6) for calculating LDL-C has been shown to have greater accuracy for patients with hypertriglyceridemia (TGs 400–800 mg/dl) compared with both the Friedewald and Martin equations. In the present analysis, NIH equation 2 was found to be more accurate than both other methods with TGs >150 mg/dl. Results to date have not clearly indicated a benefit for using direct LDL-C over Friedewald in routine use (24, 26, 27, 30, 31). As an alternative to LDL-C, guidelines also recommend that analysis of non-HDL-C and apolipoprotein B may be used to estimate cardiovascular risk (1, 2).
The Martin-Hopkins method is now recommended in the 2018 US cholesterol management guidelines (2) when measurement of LDL-C levels is needed at very low LDL-C. In a previous analysis of clinical data from the FOURIER trial with evolocumab, Martin-Hopkins–calculated LDL-C values were found to have a significantly stronger correlation with BQ-derived LDL-C values compared with Friedewald-calculated LDL-C values when Friedewald-calculated LDL-C values were <40 mg/dl (29). In contrast, in the present analysis, an overall similar correlation was observed between Friedewald-calculated, Martin-Hopkins–calculated, and NIH equation 2–calculated LDL-C with BQ-derived LDL-C values (Pearson's correlation coefficient of 0.985 and 0.981, respectively).
As expected, NIH equation 2–calculated and BQ-derived LDL-C values were also shown to be strongly correlated within the current dataset (Pearson's correlation coefficient = 0.985). In a previous comparison with BQ, NIH equation 2–calculated LDL-C values were found to be more accurate than either the Friedewald or Martin-Hopkins methods for calculating LDL-C levels, particularly for patients with hypertriglyceridemia (6). As the present dataset was limited to TG values <400 mg/dl, this may have resulted in the greater similarity in correlation between NIH equation 2–calculated and Friedewald-calculated LDL-C values observed in the present analyses.
Study limitations
The present analysis utilized pooled data from 10 trials in which patients were randomized to alirocumab, placebo, ezetimibe, or statin; we cannot be certain that the various background therapies did not introduce heterogeneity into the dataset. The standard lipid measurements and those derived by the BQ method were carried out in two different laboratories, with a 40/60% split of samples between the two. In addition, all lipid measurements were taken in the fasted state; therefore, conclusions cannot be extended to lipid assessments of nonfasted samples. Furthermore, we did not compare Friedewald-calculated LDL-C with methods that directly precipitate LDL from serum.
Summary
The results of this analysis suggest that the correlations between Friedewald-calculated, Martin-Hopkins–calculated, and NIH equation 2–calculated LDL-C values with BQ-derived LDL-C values are high, with all three methods providing a suitable alternative to BQ-derived LDL-C. This remains true even with LDL-C levels <40 mg/dl, levels that can be achieved in many individuals when PCSK9 inhibitors are added to standard statin therapy. When TG levels are >150 mg/dl, which occurs in the top 25%–30% of the population, NIH equation 2 provides the greatest accuracy.
Data availability
Qualified researchers may request access to study documents (including the clinical study report, study protocol with any amendments, blank case report form, statistical analysis plan) that support the methods and findings reported in this article. Individual anonymized participant data will be considered for sharing once the product and indication have been approved by major health authorities (e.g., FDA, EMA, PMDA, etc), if there is legal authority to share the data and there is not a reasonable likelihood of participant re-identification. Submit requests to https://vivli.org/.
Supplemental data
This article contains supplemental data.
Conflict of interest
H. N. G. has received research grants from Sanofi, Regeneron Pharmaceuticals, Inc., Pfizer, AstraZeneca, and Amgen and modest consultant/advisory board fees from Amarin, Amgen, AstraZeneca, Ionis, Janssen, Kowa, Merck, Novartis, Sanofi, Regeneron Pharmaceuticals, Inc., and Pfizer Inc. R. S. R. has received research grants through his institution from Amgen, Arrowhead, Novartis, and Regeneron Pharmaceuticals, Inc. G. K. H. is a holder of a Vidi Grant (016.156.445) from the Netherlands Organisation for Scientific Research (NWO) and Klinkerpad, has received research support through his institution from Aegerion, Amgen, and Sanofi and speaker fees from Amgen, Aegerion, Sanofi, Regeneron Pharmaceuticals, Inc., and Pfizer. C. P. C. has received research grants from Amgen, Boehringer Ingelheim, Bristol-Myers Squibb, Daiichi Sankyo, Janssen, Merck, and Pfizer and consulting fees from Aegerion, Alnylam, Amarin, Amgen, Applied Therapeutics, Ascendia, Boehringer Ingelheim, Bristol-Myers Squibb, Corvidia, HLS Therapeutics, Innovent, Janssen, Kowa, Merck, Pfizer, and Sanofi. R. S. R. serves on advisory boards from Amgen, Amyrt, C5, CVS Caremark, and Regeneron Pharmaceuticals, Inc., receives honoraria from Amgen, Kowa, and Regeneron Pharmaceuticals, Inc., receives royalties from UpToDate, and has stock ownership in MediMergent. G. K. H. has served as a consultant for Amgen, Aegerion, Sanofi, Regeneron Pharmaceuticals, Inc., and Pfizer and has been employed part-time by Novo Nordisk AS and Copenhagen, Denmark, since April 2019. A. L. is an employee of and stockholder in Sanofi. R. S. is an employee of and stockholder in Regeneron Pharmaceuticals, Inc. Y. P. is employed by a company that is contracted to Sanofi. All other authors declare that they have no conflicts of interest with the contents of this article.
Acknowledgments
The authors thank the patients, their families, and all investigators involved in the ODYSSEY studies included in this analysis. Medical writing support under the direction of the authors was provided by Rachel Dunn, PhD, Susanne Ulm, PhD, and Rob Campbell, PhD, of Prime Global (Knutsford, UK), funded by Regeneron Pharmaceuticals, Inc., according to Good Publication Practice guidelines (http://annals.org/aim/article/2424869/good-publication-practice-communicating-company-sponsored-medical-research-gpp3).
This study was funded by Regeneron Pharmaceuticals, Inc. The sponsors were involved in the study design and collection, analysis, and interpretation of data, as well as data checking of information provided in the article. The authors were involved in the study design and collection, analysis, and interpretation of data. All authors had full access to all the data in this study and take complete responsibility for the integrity of the data and accuracy of the data analysis.
Author contributions
H. N. G. and C. P. C. conceptualization; H. N. G., R. S. R., G. K. H., A. L., R. S., Y. P., and C. P. C. methodology; H. N. G., G. K. H., and C. P. C. investigation; H. N. G., R. S. R., G. K. H., A. L., R. S., Y. P., and C. P. C. writing–review and editing; A. L. and Y. P. formal analysis.
Supplemental data
References
- 1.Mach F., Baigent C., Catapano A.L., Koskinas K.C., Casula M., Badimon L., Chapman M.J., De Backer G.G., Delgado V., Ference B.A., Graham I.M., Halliday A., Landmesser U., Mihaylova B., Pedersen T.R., et al. 2019 ESC/EAS guidelines for the management of dyslipidaemias: lipid modification to reduce cardiovascular risk. Eur. Heart J. 2020;41:111–188. doi: 10.1093/eurheartj/ehz455. [DOI] [PubMed] [Google Scholar]
- 2.Grundy S.M., Stone N.J., Bailey A.L., Beam C., Birtcher K.K., Blumenthal R.S., Braun L.T., de Ferranti S., Faiella-Tommasino J., Forman D.E., Goldberg R., Heidenreich P.A., Hlatky M.A., Jones D.W., Lloyd-Jones D., et al. 2018 AHA/ACC/AACVPR/AAPA/ABC/ACPM/ADA/AGS/APhA/ASPC/NLA/PCNA Guideline on the Management of Blood Cholesterol: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. J. Am. Coll. Cardiol. 2019;73:3168–3209. doi: 10.1016/j.jacc.2018.11.002. [DOI] [PubMed] [Google Scholar]
- 3.Belcher J., McNamara J., Gregory F. In: Methods for clinical laboratory measurement of lipid and lipoprotein risk factors. Rifai N., Warnick G., editors. AACC Press; Washington, DC: 1991. Measurement of low density lipoprotein cholesterol concentration; pp. 80–81. [Google Scholar]
- 4.Friedewald W.T., Levy R.I., Fredrickson D.S. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin. Chem. 1972;18:499–502. [PubMed] [Google Scholar]
- 5.Martin S.S., Blaha M.J., Elshazly M.B., Brinton E.A., Toth P.P., McEvoy J.W., Joshi P.H., Kulkarni K.R., Mize P.D., Kwiterovich P.O., Defilippis A.P., Blumenthal R.S., Jones S.R. Friedewald-estimated versus directly measured low-density lipoprotein cholesterol and treatment implications. J. Am. Coll. Cardiol. 2013;62:732–739. doi: 10.1016/j.jacc.2013.01.079. [DOI] [PubMed] [Google Scholar]
- 6.Sampson M., Ling C., Sun Q., Harb R., Ashmaig M., Warnick R., Sethi A., Fleming J.K., Otvos J.D., Meeusen J.W., Delaney S.R., Jaffe A.S., Shamburek R., Amar M., Remaley A.T. A New Equation for Calculation of Low-Density Lipoprotein Cholesterol in Patients With Normolipidemia and/or Hypertriglyceridemia. JAMA Cardiol. 2020;5:540–548. doi: 10.1001/jamacardio.2020.0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Meeusen J.W., Snozek C.L., Baumann N.A., Jaffe A.S., Saenger A.K. Reliability of calculated low-density lipoprotein cholesterol. Am. J. Cardiol. 2015;116:538–540. doi: 10.1016/j.amjcard.2015.05.013. [DOI] [PubMed] [Google Scholar]
- 8.Kulkarni K.R. Cholesterol profile measurement by vertical auto profile method. Clin. Lab. Med. 2006;26:787–802. doi: 10.1016/j.cll.2006.07.004. [DOI] [PubMed] [Google Scholar]
- 9.Martin S.S., Blaha M.J., Elshazly M.B., Toth P.P., Kwiterovich P.O., Blumenthal R.S., Jones S.R. Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA. 2013;310:2061–2068. doi: 10.1001/jama.2013.280532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Robinson J.G., Rosenson R.S., Farnier M., Chaudhari U., Sasiela W.J., Merlet L., Miller K., Kastelein J.J. Safety of very low low-density lipoprotein cholesterol levels with alirocumab: Pooled data from randomized trials. J. Am. Coll. Cardiol. 2017;69:471–482. doi: 10.1016/j.jacc.2016.11.037. [DOI] [PubMed] [Google Scholar]
- 11.Schwartz G.G., Steg P.G., Szarek M., Bhatt D.L., Bittner V.A., Diaz R., Edelberg J.M., Goodman S.G., Hanotin C., Harrington R.A., Jukema J.W., Lecorps G., Mahaffey K.W., Moryusef A., Pordy R., et al. Alirocumab and cardiovascular outcomes after acute coronary syndrome. N. Engl. J. Med. 2018;379:2097–2107. doi: 10.1056/NEJMoa1801174. [DOI] [PubMed] [Google Scholar]
- 12.Sabatine M.S., Giugliano R.P., Keech A.C., Honarpour N., Wiviott S.D., Murphy S.A., Kuder J.F., Wang H., Liu T., Wasserman S.M., Sever P.S., Pedersen T.R., Fourier Steering Committee Investigators Evolocumab and clinical outcomes in patients with cardiovascular disease. N. Engl. J. Med. 2017;376:1713–1722. doi: 10.1056/NEJMoa1615664. [DOI] [PubMed] [Google Scholar]
- 13.Ray K.K., Ginsberg H.N., Davidson M.H., Pordy R., Bessac L., Minini P., Eckel R.H., Cannon C.P. Reductions in atherogenic lipids and major cardiovascular events: A pooled analysis of 10 ODYSSEY trials comparing alirocumab with control. Circulation. 2016;134:1931–1943. doi: 10.1161/CIRCULATIONAHA.116.024604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bays H., Gaudet D., Weiss R., Ruiz J.L., Watts G.F., Gouni-Berthold I., Robinson J., Zhao J., Hanotin C., Donahue S. Alirocumab as add-on to atorvastatin versus other lipid treatment strategies: ODYSSEY OPTIONS I randomized trial. J. Clin. Endocrinol. Metab. 2015;100:3140–3148. doi: 10.1210/jc.2015-1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Roth E.M., Moriarty P.M., Bergeron J., Langslet G., Manvelian G., Zhao J., Baccara-Dinet M.T., Rader D.J., investigators O.C.I. A phase III randomized trial evaluating alirocumab 300 mg every 4 weeks as monotherapy or add-on to statin: ODYSSEY CHOICE I. Atherosclerosis. 2016;254:254–262. doi: 10.1016/j.atherosclerosis.2016.08.043. [DOI] [PubMed] [Google Scholar]
- 16.Stroes E., Guyton J.R., Lepor N., Civeira F., Gaudet D., Watts G.F., Baccara-Dinet M.T., Lecorps G., Manvelian G., Farnier M., ODYSSEY CHOICE II Investigators Efficacy and safety of alirocumab 150 mg every 4 weeks in patients with hypercholesterolemia not on statin therapy: The ODYSSEY CHOICE II study. J. Am. Heart Assoc. 2016;5 doi: 10.1161/JAHA.116.003421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cannon C.P., Cariou B., Blom D., McKenney J.M., Lorenzato C., Pordy R., Chaudhari U., Colhoun H.M., ODYSSEY COMBO II Investigators Efficacy and safety of alirocumab in high cardiovascular risk patients with inadequately controlled hypercholesterolaemia on maximally tolerated doses of statins: the ODYSSEY COMBO II randomized controlled trial. Eur. Heart J. 2015;36:1186–1194. doi: 10.1093/eurheartj/ehv028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Farnier M., Gaudet D., Valcheva V., Minini P., Miller K., Cariou B. Efficacy of alirocumab in high cardiovascular risk populations with or without heterozygous familial hypercholesterolemia: pooled analysis of eight ODYSSEY Phase 3 clinical program trials. Int. J. Cardiol. 2016;223:750–757. doi: 10.1016/j.ijcard.2016.08.273. [DOI] [PubMed] [Google Scholar]
- 19.Kastelein J.J., Ginsberg H.N., Langslet G., Hovingh G.K., Ceska R., Dufour R., Blom D., Civeira F., Krempf M., Lorenzato C., Zhao J., Pordy R., Baccara-Dinet M.T., Gipe D.A., Geiger M.J., et al. ODYSSEY FH I and FH II: 78 week results with alirocumab treatment in 735 patients with heterozygous familial hypercholesterolaemia. Eur. Heart J. 2015;36:2996–3003. doi: 10.1093/eurheartj/ehv370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kereiakes D.J., Robinson J.G., Cannon C.P., Lorenzato C., Pordy R., Chaudhari U., Colhoun H.M. Efficacy and safety of the proprotein convertase subtilisin/kexin type 9 inhibitor alirocumab among high cardiovascular risk patients on maximally tolerated statin therapy: The ODYSSEY COMBO I study. Am. Heart J. 2015;169:906–915.e913. doi: 10.1016/j.ahj.2015.03.004. [DOI] [PubMed] [Google Scholar]
- 21.Moriarty P.M., Jacobson T.A., Bruckert E., Thompson P.D., Guyton J.R., Baccara-Dinet M.T., Gipe D. Efficacy and safety of alirocumab, a monoclonal antibody to PCSK9, in statin-intolerant patients: design and rationale of ODYSSEY ALTERNATIVE, a randomized phase 3 trial. J. Clin. Lipidol. 2014;8:554–561. doi: 10.1016/j.jacl.2014.09.007. [DOI] [PubMed] [Google Scholar]
- 22.Robinson J.G., Farnier M., Krempf M., Bergeron J., Luc G., Averna M., Stroes E.S., Langslet G., Raal F.J., El Shahawy M., Koren M.J., Lepor N.E., Lorenzato C., Pordy R., Chaudhari U., et al. Efficacy and safety of alirocumab in reducing lipids and cardiovascular events. N. Engl. J. Med. 2015;372:1489–1499. doi: 10.1056/NEJMoa1501031. [DOI] [PubMed] [Google Scholar]
- 23.US Department of Health and Human Services . US Government Printing Office; Washington, DC: 1982. Manual of laboratory operations: lipid and lipoprotein analysis (revised) Report No: (NIH) 75-67815. [Google Scholar]
- 24.Razi F., Forouzanfar K., Bandarian F., Nasli-Esfahani E. LDL-cholesterol measurement in diabetic type 2 patients: a comparison between direct assay and popular equations. J. Diabetes Metab. Disord. 2017;16:43. doi: 10.1186/s40200-017-0326-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tremblay A.J., Morrissette H., Gagne J.M., Bergeron J., Gagne C., Couture P. Validation of the Friedewald formula for the determination of low-density lipoprotein cholesterol compared with beta-quantification in a large population. Clin. Biochem. 2004;37:785–790. doi: 10.1016/j.clinbiochem.2004.03.008. [DOI] [PubMed] [Google Scholar]
- 26.Nauck M., Warnick G.R., Rifai N. Methods for measurement of LDL-cholesterol: a critical assessment of direct measurement by homogeneous assays versus calculation. Clin. Chem. 2002;48:236–254. [PubMed] [Google Scholar]
- 27.Mora S., Rifai N., Buring J.E., Ridker P.M. Comparison of LDL cholesterol concentrations by Friedewald calculation and direct measurement in relation to cardiovascular events in 27,331 women. Clin. Chem. 2009;55:888–894. doi: 10.1373/clinchem.2008.117929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sung K.C., Kwon C.H., Lee M.Y., Kwon M.J., Lee J.H., Jung M.H., Shin J.H. Comparison of low-density lipoprotein cholesterol concentrations by direct measurement and by Friedewald calculation. Am. J. Cardiol. 2020;125:866–873. doi: 10.1016/j.amjcard.2019.12.036. [DOI] [PubMed] [Google Scholar]
- 29.Martin S.S., Giugliano R.P., Murphy S.A., Wasserman S.M., Stein E.A., Ceska R., Lopez-Miranda J., Georgiev B., Lorenzatti A.J., Tikkanen M.J., Sever P.S., Keech A.C., Pedersen T.R., Sabatine M.S. Comparison of low-density lipoprotein cholesterol assessment by Martin/Hopkins estimation, Friedewald estimation, and preparative ultracentrifugation: Insights from the FOURIER trial. JAMA Cardiol. 2018;3:749–753. doi: 10.1001/jamacardio.2018.1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Larsson A., Hagstrom E., Nilsson L., Svensson M.K. Treatment target re-classification of subjects comparing estimation of low-density lipoprotein cholesterol by the Friedewald equation and direct measurement of LDL-cholesterol. Ups J. Med. Sci. 2018;123:94–99. doi: 10.1080/03009734.2018.1465496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jialal I., Inn M., Siegel D., Devaraj S. Underestimation of low density lipoprotein-cholesterol with the Friedewald equation versus a direct homogenous low density lipoprotein-cholesterol assay. Lab. Med. 2017;48:220–224. doi: 10.1093/labmed/lmx023. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Qualified researchers may request access to study documents (including the clinical study report, study protocol with any amendments, blank case report form, statistical analysis plan) that support the methods and findings reported in this article. Individual anonymized participant data will be considered for sharing once the product and indication have been approved by major health authorities (e.g., FDA, EMA, PMDA, etc), if there is legal authority to share the data and there is not a reasonable likelihood of participant re-identification. Submit requests to https://vivli.org/.