TNet: Transmission Network Inference Using Within-Host Strain Diversity and its Application to Geographical Tracking of COVID-19 Spread

Abstract

The inference of disease transmission networks is an important problem in epidemiology. One popular approach for building transmission networks is to reconstruct a phylogenetic tree using sequences from disease strains sampled from infected hosts and infer transmissions based on this tree. However, most existing phylogenetic approaches for transmission network inference are highly computationally intensive and cannot take within-host strain diversity into account. Here, we introduce a new phylogenetic approach for inferring transmission networks, TNet, that addresses these limitations. TNet uses multiple strain sequences from each sampled host to infer transmissions and is simpler and more accurate than existing approaches. Furthermore, TNet is highly scalable and able to distinguish between ambiguous and unambiguous transmission inferences. We evaluated TNet on a large collection of 560 simulated transmission networks of various sizes and diverse host, sequence, and transmission characteristics, as well as on 10 real transmission datasets with known transmission histories. Our results show that TNet outperforms two other recently developed methods, phyloscanner and SharpTNI, that also consider within-host strain diversity. We also applied TNet to a large collection of SARS-CoV-2 genomes sampled from infected individuals in many countries around the world, demonstrating how our inference framework can be adapted to accurately infer geographical transmission networks. TNet is freely available from https://compbio.engr.uconn.edu/software/TNet/.

1. Introduction

The accurate inference of disease transmission networks is fundamental to understanding and containing the spread of infectious diseases [3], [16], [27]. A key challenge with inferring transmission networks, particularly those of rapidly evolving RNA and retroviruses [11], is that they exist in the host as “clouds” of closely related sequences. These variants are referred to as quasispecies [8], [9], [23], [24], [36], and the resulting genetic diversity of the strains circulating within a host has important implications for efficiency of transmission, disease progression, drug/vaccine resistance, etc. [2], [10], [14], [19], [26]. The availability of quasispecies, or sequences from multiple strains per infected host, also has direct relevance for inferring transmission networks and has the potential to make such inference easier and far more accurate [33], [37]. Yet, while the advent of next-generation sequencing technologies has revolutionized the study of quasispecies, most existing transmission network inference methods are unable to make use of multiple distinct strain sequences per host.

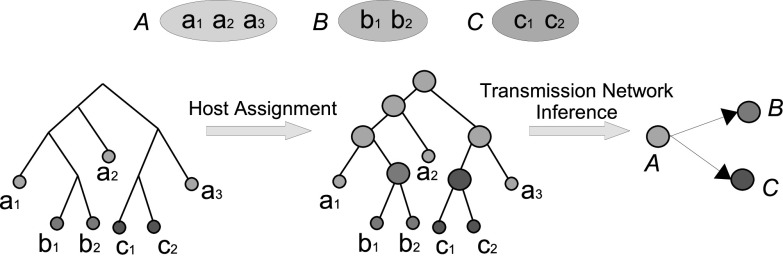
Existing methods for inferring transmission networks can be classified into two categories: Those based on constructing and analyzing sequence similarity or relatedness graphs, and those based on constructing and analyzing phylogenetic trees for the infecting strains. Many methods based on sequence similarity or relatedness graph analysis exist and several recently developed methods in this category are also able to take into account multiple distinct strain sequences per host [15], [22], [32]. However, similarity/relatedness based methods can suffer from a lack of resolution and are often unable to infer transmission directions or complete transmission histories. Phylogeny-based methods [7], [18], [21], [27], [37] attempt to overcome these limitations by constructing and analyzing phylogenies of the infecting strains. We refer to these strain phylogenies as transmission phylogenies. These phylogeny-based methods infer transmission networks by computing a host assignment for each node of the transmission phylogeny, where this phylogeny is either first constructed independently or is co-estimated along with the host assignment. Leaves of the transmission phylogeny are labelled by the host from which they are sampled, and an ancestral host assignment is then inferred for each node/edge of the phylogeny. This ancestral host assignment defines the transmission network, where a transmission event is inferred along any edge connecting two nodes labeled with different hosts. If the phylogeny is rooted then the direction of transmission is also easily inferred. This is illustrated in Fig. 1.

Fig. 1.

Phylogeny-based transmission network inference. The figure shows a simple example with three infected individuals \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C$\end{document}$C$, represented here by the three different colors, where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ has three viral variants while \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C$\end{document}$C$ have two each. The tree on the left depicts the transmission phylogeny for the seven sampled strains, with each of these strains colored by the host from which it was sampled. The tree in the middle shows a hypothetical assignment of hosts to ancestral nodes of the transmission phylogeny. This ancestral host assignment can then be used to infer the transmission network shown on the right, with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ responsible for transmission to both \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C$\end{document}$C$.

Several sophisticated phylogeny-based methods have been developed over the last few years. These include BEASTlier [18], SCOTTI [5], phybreak [21], TransPhylo [7], phyloscanner [37], Nextstrain/Augur [17], and BadTrIP [4]. Among these, only SCOTTI [5], BadTrIP [4], and phyloscanner [37] can explicitly consider multiple strain sequences per host. BEASTlier [18] also allows for the presence of multiple sequences per host, but requires that all sequences from the same host be clustered together on the phylogeny, a precondition that is often violated in practice. Among the methods that explicitly consider multiple strain sequences per host, SCOTTI, BadTrIP, and BEASTlier are model-based and highly computationally intensive, relying on the use of Markov Chain Monte Carlo (MCMC) algorithms for inference. These methods also require several difficult-to-estimate epidemiological parameters, such as infection times, and make several strong assumptions about pathogen evolution and the underlying transmission network. Thus, phyloscanner[37] is the only previous method that is able to take advantage of multiple sequences per host and that is also computationally efficient, easy to use, and scalable to large datasets.

In this work, we introduce a new phylogenetic approach, TNet, for inferring transmission networks. TNet uses multiple strain sequences from each sampled host to infer transmissions and is simpler and more accurate than existing approaches. TNet uses an extended version of the classical Sankoff algorithm [29] from the phylogenetics literature for ancestral host assignment, where the extension makes it possible to efficiently compute support values for individual transmission edges based on a sampling of optimal host assignments where the number of back-transmissions (or reinfections by descendant disease strains) is minimized. TNet is parameter-free and highly scalable and can be easily applied within seconds to datasets with hundreds of strain sequences and hosts. In recent independent work, Sashittal et al. [30] developed a new method called SharpTNI that is based on similar ideas to TNet. SharpTNI is based on an NP-hard problem formulation that seeks to find parsimonious ancestral host assignments minimizing the number of co-transmissions [30]. The authors provide an efficient heuristic for this problem that is based on uniform sampling of parsimonious ancestral host assignments (not necessarily minimizing co-transmissions) and subsequently filtering them to only keep those assignments among the samples that minimize co-transmissions [30]. Thus, both TNet and SharpTNI are based on the idea of parsimonious ancestral host assignments and on aggregating across the diversity of possible solutions obtained through some kind of sampling of optimal solutions. The primary distinction between the two methods is the strategy employed for sampling of the optimal solutions, with SharpTNI minimizing co-transmissions and TNet minimizing back-transmissions.

We evaluated TNet, SharpTNI, and phyloscanner on a large collection of 560 simulated transmission networks of various sizes and representing a wide range of host, sequence, and transmission characteristics, as well as on 10 real transmission datasets with known transmission histories. We found that both TNet and SharpTNI significantly outperformed phyloscanner under all tested conditions and all datasets, yielding more accurate transmission networks for both simulated and real datasets. Between TNet and SharpTNI, we found that both methods performed similarly on the real datasets but that TNet clearly showed better accuracy on the simulated datasets. Furthermore, we show how our transmission network inference framework can be adapted to infer disease transmission across geographical regions, with different countries or geographical regions acting as “hosts”. To demonstrate the feasibility and evaluate the performance of our framework in this setting, we applied our method to a large collection of SARS-CoV-2 genomes sampled from infected individuals in many countries around the world and inferred the international COVID-19 transmission network. Using available epidemiological ground truth data, we found that the COVID-19 transmission network inferred using our framework was significantly more accurate than the corresponding network inferred by the popular Nextstrain tool [17]. SharpTNI could not be applied to this large COVID-19 dataset due to lack of scalability (manifested as runtime errors). TNet is freely available open-source from https://compbio.engr.uconn.edu/software/TNet/.

A preliminary version of this work appeared in the proceedings of ISBRA 2020 [6]. The current manuscript substantially expands upon the preliminary version and includes many additional technical and algorithmic details, several additional figures/tables to better explain the algorithm and results, and more detailed analysis of experimental results. Importantly, we also newly demonstrate how our inference framework can be adapted to infer disease transmission across geographical regions, and apply our method to a large collection of SARS-CoV-2 genomes sampled from infected individuals in many countries around the world to infer the global COVID-19 transmission network as well as a US state-level transmission network (Section 6).

The remainder of this manuscript is organized as follows. The next section provides basic definitions and preliminaries. Section 3 describes our core algorithmic framework. Section 4 describes the simulated datasets, real HCV dataset, and experimental methodology. Experimental results appear in Section 5. Section 6 describes the application of our method to large-scale COVID-19 data and includes the results of this analysis. Section 7 gives concluding remarks.

2. Basic Definitions and Preliminaries

Given a rooted tree \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$, we denote its node set, edge set, and leaf set by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$V(T)$\end{document}$V\left(T\right)$, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$E(T)$\end{document}$E\left(T\right)$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}${Le}(T)$\end{document}$Le\left(T\right)$ respectively. The root node of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ is denoted by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}${rt}(T)$\end{document}$rt\left(T\right)$, the parent of a node \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v \in V(T)$\end{document}$v\in V\left(T\right)$ by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}${pa}_T(v)$\end{document}${pa}_T\left(v\right)$, its set of children by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}${Ch}_T(v)$\end{document}${Ch}_T\left(v\right)$, and the (maximal) subtree of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ rooted at \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v$\end{document}$v$ by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T(v)$\end{document}$T\left(v\right)$. The set of internal nodes of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$, denoted \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$I(T)$\end{document}$I\left(T\right)$, is defined to be \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$V(T) \setminus {Le}(T)$\end{document}$V\left(T\right)\setminus Le\left(T\right)$. A rooted tree is binary if all of its internal nodes have exactly two children. In this work, the term tree refers to a rooted binary tree.

2.1. Problem Formulation

Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ denote the transmission phylogeny constructed from the genetic sequences of the infecting strains (i.e., pathogens) sampled from the infected hosts under consideration. Note that such trees can be easily constructed using standard phylogenetic methods such as RAxML [34]. These trees can also be rooted relatively accurately using either standard phylogenetic rooting techniques or by using a related sequence from a previous outbreak of the same disease as an outgroup. Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H = \lbrace h_1, h_2, \ldots, h_n\rbrace$\end{document}$H=\{h_1,h_2,...,h_n\}$ denote the set of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$n$\end{document}$n$ hosts under consideration. We assume that each leaf of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ is labeled with the host from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H$\end{document}$H$ from which the corresponding strain sequence was obtained. Fig. 1 shows an example of such a tree and its leaf labeling, where the labeling is depicted using the different colors.

Observe that each internal node of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ represents an ancestral strain sequence that existed in some infected host. Moreover, each internal node (or bifurcation) represents either intra-host diversification and evolution of that ancestral strain or a transmission event where that ancestral strain is transmitted from one host to another along one of the child edges. Thus, each node of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ is associated with an infected host. Given \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in V(T)$\end{document}$t\in V\left(T\right)$, we denote the host associated with node \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$ by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t)$\end{document}$h\left(t\right)$. Note that internal nodes may represent strains from hosts that do not appear in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H$\end{document}$H$, i.e., strains from unsampled hosts, and so there may be \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in I(T)$\end{document}$t\in I\left(T\right)$ for which \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) \not\in H$\end{document}$h\left(t\right)\notin H$. Given an ancestral host assignment for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$, i.e., given \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t)$\end{document}$h\left(t\right)$ for each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in I(T)$\end{document}$t\in I\left(T\right)$, the implied transmission network can be easily inferred as follows: A transmission edge is inferred from host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$x$\end{document}$x$ to host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$y$\end{document}$y$ if there is an edge \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$({pa}(t), t) \in E(T)$\end{document}$\left(pa\right(t),t)\in E\left(T\right)$, where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h({pa}(t)) = x$\end{document}$h\left(pa\right(t\left)\right)=x$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = y$\end{document}$h\left(t\right)=y$. Note that each transmission edge in the reconstructed transmission network may represent either direct transmission or indirect transmission through one or more unsampled hosts. Thus, to reconstruct transmission networks it suffices to compute \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t)$\end{document}$h\left(t\right)$ for each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in I(T)$\end{document}$t\in I\left(T\right)$.

TNet (along with SharpTNI) is based on finding ancestral host assignments that minimize the number of inter-host transmission events on \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$. The utility of such parsimonious ancestral host assignment for transmission network inference when multiple strain sequences per host are available was first systematically demonstrated by Romero-Severson et al. [27] and later developed further by Wymant et al. [37] in their phyloscanner method. The basic computational problem under this formulation can be stated as follows:

Problem 1 (Optimal ancestral host assignment). —

Given a transmission phylogeny \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ on strain sequences sampled from a set \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H = \lbrace h_1, h_2, \ldots, h_n\rbrace$\end{document}$H=\{h_1,h_2,...,h_n\}$ of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$n$\end{document}$n$ infected hosts, compute \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t)$\end{document}$h\left(t\right)$ for each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in I(T)$\end{document}$t\in I\left(T\right)$ such that the number of edges \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(t^{\prime }, t^{\prime \prime }) \in E$\end{document}$(t^{\text{'}},t^{\text{'}\text{'}})\in E$ for which \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t^{\prime }) \ne h(t^{\prime \prime })$\end{document}$h\left(t^{\text{'}}\right)\ne h\left(t^{\text{'}\text{'}}\right)$ is minimized.

Problem 1 is equivalent to the well-known small parsimony problem in phylogenetics and can be solved efficiently using the classical Fitch [13] and Sankoff [29] algorithms. In TNet, we solve a modified version of the problem above that considers all possible optimal ancestral host assignments and samples greedily among them to minimize the number of back-transmissions (or reinfections by descendant disease strains). To accomplish this goal efficiently, TNet uses an extended version of Sankoff's algorithm. For completeness, a brief description of Sankoff's algorithm appears below. We later show how to extend that algorithm to perform our special sampling.

2.2. Computing an Optimal Ancestral Host Assignment

Sankoff's algorithm uses a simple bottom-up dynamic programming approach. Given a node \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in V(T)$\end{document}$t\in V\left(T\right)$ and a host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i \in H$\end{document}$h_i\in H$, we define the cost \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(t, h_i)$\end{document}$C(t,h_i)$ to be the minimum number of inter-host transmission events required on subtree \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T(t)$\end{document}$T\left(t\right)$ under the constraint that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = h_i$\end{document}$h\left(t\right)=h_i$. Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(t)$\end{document}$C\left(t\right)$ denote the vector \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\langle C(t, h_i), C(t, h_2), \ldots, C(t, h_n) \rangle$\end{document}$\langle C(t,h_i),C(t,h_2),...,C(t,h_n)\rangle$. The Sankoff algorithm performs a post-order traversal of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ and computes \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(t)$\end{document}$C\left(t\right)$ at each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in V(T)$\end{document}$t\in V\left(T\right)$ using the following recurrence relations.

If \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in {Le}(T)$\end{document}$t\in Le\left(T\right)$, then the dynamic programming table can be initialised as follows:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{} \begin{equation*} C(t, h_i)=\left\lbrace \begin{array}{ll}0, & \text{if } h(t) = h_i, \\ \infty, & \text{otherwise}. \end{array}\right. \tag{1} \end{equation*} \end{document}$$C(t,h_i)=\left\{\begin{array}{cc}0,\hfill & \text{if}h\left(t\right)=h_i,\hfill \\ \infty ,\hfill & \text{otherwise}.\hfill \end{array}\right.\left(\left(1\right)\right)$$

If \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in I(T)$\end{document}$t\in I\left(T\right)$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime }$\end{document}$t^{\text{'}}$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime \prime }$\end{document}$t^{\text{'}\text{'}}$ denote the two children of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$, then

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{} \begin{equation*} \begin{split} C(t, h_i) = & \min _{j \in \lbrace 1, \ldots, n\rbrace } \left\lbrace C(t^{\prime }, h_j) + p(h_i, h_j) \right\rbrace \\ & + \min _{j \in \lbrace 1, \ldots, n\rbrace } \left\lbrace C(t^{\prime \prime }, h_j) + p(h_i, h_j) \right\rbrace, \end{split} \tag{2} \end{equation*} \end{document}$$\begin{array}{cc}\hfill C(t,h_i)=& \underset{j\in \{1,...,n\}}{min}\left\{C(t^{\text{'}},h_j)+p(h_i,h_j)\right\}\hfill \\ & +\underset{j\in \{1,...,n\}}{min}\left\{C(t^{\text{'}\text{'}},h_j)+p(h_i,h_j)\right\},\hfill \end{array}\left(\left(2\right)\right)$$

where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$p(h_i, h_j) = 0$\end{document}$p(h_i,h_j)=0$ if \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$i = j$\end{document}$i=j$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$p(h_i, h_j) = 1$\end{document}$p(h_i,h_j)=1$ if \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$i \ne j$\end{document}$i\ne j$.

This recurrence relation is guaranteed to compute each cost \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(t, h_i)$\end{document}$C(t,h_i)$ correctly (follows from the correctness of Sankoff's algorithm). The minimum number of inter-host transmission events required by any ancestral host assignment on \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ is given by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\min _i \lbrace C({rt}(T), h_i)\rbrace$\end{document}${min}_i\left\{C(rt\left(T\right),h_i)\right\}$, and an actual optimal ancestral host assignment can be easily obtained by backtracking. We point out that the greedy algorithm of Fitch [13] can also be used to compute minimum number of inter-host transmission events required by any ancestral host assignment on \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$; however, Fitch's algorithm cannot be extended to keep track of all possible optimal ancestral host assignments. We therefore use (an extension of) Sankoff's algorithm as the basis for TNet.

It is easy to see that the time complexity of the above algorithm is \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(mn^2)$\end{document}$O\left(m{n}^2\right)$, where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$m = {Le}(T)$\end{document}$m=Le\left(T\right)$, i.e., the total number of strain sequences sampled from all hosts, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$n = |H|$\end{document}$n=\left|H\right|$, i.e., the number of infected hosts in the analysis. In fact, by exploiting the fact that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$p(\cdot, \cdot)$\end{document}$p(·,·)$ is always either 2, 1 or 0, the algorithm can be implemented to run in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(mn)$\end{document}$O\left(mn\right)$ time (details are straightforward and therefore omitted.)

3. Algorithmic Details

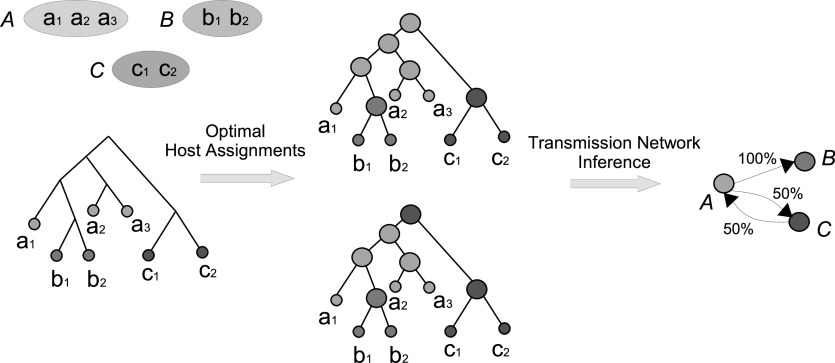
A key methodological and algorithmic innovation responsible for the improved accuracy of TNet (and also of SharpTNI) is the explicit and principled consideration of variability in optimal ancestral host assignments. More precisely, TNet recognizes that there are often a very large number of distinct optimal ancestral host assignments and it samples the space of all optimal ancestral host assignments in a manner that preferentially preserves optimal ancestral host assignments (described in detail below). TNet then aggregates across these samples to compute a support value for each edge in the final transmission network. This approach is illustrated in Fig. 2. Thus, the core computational problem solved by TNet can be formulated as follows:

Fig. 2.

Accounting for multiple optima in transmission network inference. The tree on the left depicts the transmission phylogeny for the seven strains sampled from three infected individuals \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C$\end{document}$C$, represented here by the three different colors. This tree admits two distinct optimal ancestral host assignments as shown in the figure. These two optimal ancestral host assignments can then be together used to infer a transmission network, as shown on the right, in which each edge has a support value. The support value of a transmission edge is defined to be the percentage of optimal ancestral host assignments that imply that transmission edge.

Definition 3.1 (Back-Transmission). —

Given a transmission phylogeny \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ on strain sequences sampled from a set \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H = \lbrace h_1, h_2, \ldots, h_n\rbrace$\end{document}$H=\{h_1,h_2,...,h_n\}$ of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$n$\end{document}$n$ infected hosts and an ancestral host assignment \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$, we say that a host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i$\end{document}$h_i$ has a back-transmission in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ if and only if there exist nodes \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v$\end{document}$v$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v^{\prime }$\end{document}$v^{\text{'}}$ in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$V(T)$\end{document}$V\left(T\right)$ such that (i) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v^{\prime }$\end{document}$v^{\text{'}}$ is a descendant of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v$\end{document}$v$ in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$, (ii) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(v) = h(v^{\prime })$\end{document}$h\left(v\right)=h\left(v^{\text{'}}\right)$ under \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$, and (iii) there exists node \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v^{\prime \prime }$\end{document}$v^{\text{'}\text{'}}$ along the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$v - v^{\prime }$\end{document}$v-v^{\text{'}}$ path for which \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(v^{\prime \prime }) \ne h(v)$\end{document}$h\left(v^{\text{'}\text{'}}\right)\ne h\left(v\right)$. The total number of back-transmissions implied by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ on \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ equals the number of hosts with back-transmissions.

Problem 2 (Minimum back-transmission sampling). —

Given a transmission phylogeny \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ on strain sequences sampled from a set \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H = \lbrace h_1, h_2, \ldots, h_n\rbrace$\end{document}$H=\{h_1,h_2,...,h_n\}$ of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$n$\end{document}$n$ infected hosts, let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\mathcal {O}$\end{document}$\mathcal{O}$ denote the set containing all distinct optimal ancestral host assignments for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$. Further, let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\mathcal {O}^{\prime }$\end{document}${\mathcal{O}}^{\text{'}}$ denote the subset of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\mathcal {O}$\end{document}$\mathcal{O}$ that implies the fewest back-transmissions in the resulting transmission network. Compute an optimal ancestral host assignment from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\mathcal {O}^{\prime }$\end{document}${\mathcal{O}}^{\text{'}}$ such that each element of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\mathcal {O}^{\prime }$\end{document}${\mathcal{O}}^{\text{'}}$ has an equal probability of being computed.

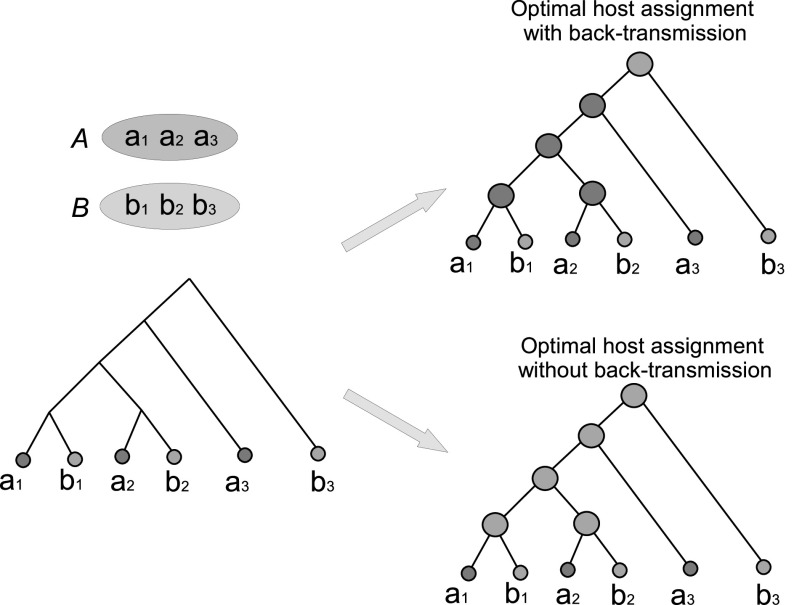
Fig. 3 shows an example of minimum back-transmission sampling. Observe that the actual number of optimal ancestral host assignments (both \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\mathcal {O}$\end{document}$\mathcal{O}$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\mathcal {O}^{\prime }$\end{document}${\mathcal{O}}^{\text{'}}$) can grow exponentially in the number of hosts \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$n$\end{document}$n$. Thus, by solving the sampling problem above instead, TNet seeks to efficiently account for the diversity within optimal ancestral host assignments with minimum back-transmissions, without explicitly having to enumerate them all.

Fig. 3.

Minimizing back-transmissions in transmission network inference. The tree on the left depicts the transmission phylogeny for six strains sampled from two infected individuals \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$, represented by the two different colors. Two possible optimal host assignments for this transmission phylogeny are shown on the right. The optimal host assignment shown on top invokes a back-transmission (transmission from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$ to \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ and later back from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ to \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$). The optimal host assignment shown at the bottom does not invoke any back-transmissions and would be a minimum back-transmission host assignment.

Note that SharpTNI, developed independently and contemporaneously to TNet, performs a similar sampling among all optimal ancestral host assignments, but employs a different optimality objective. Specifically, SharpTNI seeks to sample optimal ancestral host assignments that minimize the number of co-transmissions, i.e., minimize the number of inter-host edges in the transmission network.

3.1. Minimum Back-Transmission Sampling of Optimal Host Assignments

TNet approximates minimum back-transmission sampling by combining uniform sampling of ancestral host assignments with a greedy procedure to assign specific hosts to internal nodes. This is accomplished by suitably extending and modifying Sankoff's algorithm. Note that Sankoff's algorithm computes, at each node \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in V(T)$\end{document}$t\in V\left(T\right)$ and for each host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i \in H$\end{document}$h_i\in H$, the minimum number of inter-host transmission events required on subtree \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T(t)$\end{document}$T\left(t\right)$ under the constraint that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = h_i$\end{document}$h\left(t\right)=h_i$, denoted \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(t, h_i)$\end{document}$C(t,h_i)$. To perform our minimum back-transmission sampling, we must keep track of the number of optimal ancestral host assignments associated with each subproblem \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(t, h_i)$\end{document}$C(t,h_i)$ considered in the dynamic programming algorithm. We therefore define the following: For any \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in V(T)$\end{document}$t\in V\left(T\right)$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i \in H$\end{document}$h_i\in H$, let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t, h_i)$\end{document}$N(t,h_i)$ denote the number of distinct optimal host assignments for the subtree \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T(t)$\end{document}$T\left(t\right)$ under the constraint that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = h_i$\end{document}$h\left(t\right)=h_i$. Each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ can be computed during the same post-order traversal used to compute the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(\cdot, \cdot)$\end{document}$C(·,·)$ values as shown below.

If \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in {Le}(T)$\end{document}$t\in Le\left(T\right)$, then the dynamic programming table for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ can be initialised as follows:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{} \begin{equation*} N(t, h_i)=\left\lbrace \begin{array}{ll}1, & \text{if } h(t) = h_i, \\ 0, & \text{otherwise}. \end{array}\right. \tag{3} \end{equation*} \end{document}$$N(t,h_i)=\left\{\begin{array}{cc}1,\hfill & \text{if}h\left(t\right)=h_i,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right.\left(\left(3\right)\right)$$

If \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in I(T)$\end{document}$t\in I\left(T\right)$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime }$\end{document}$t^{\text{'}}$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime \prime }$\end{document}$t^{\text{'}\text{'}}$ denote the two children of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$, then \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t, h_i)$\end{document}$N(t,h_i)$ can be computed based on optimal host assignments at \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime }$\end{document}$t^{\text{'}}$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime \prime }$\end{document}$t^{\text{'}\text{'}}$ and their corresponding \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ values. Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime } \subseteq H$\end{document}$X^{\text{'}}\subseteq H$ denote the host assignments for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime }$\end{document}$t^{\text{'}}$ that are optimal given a host assignment of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i$\end{document}$h_i$ at \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$. Likewise, let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime \prime } \subseteq H$\end{document}$X^{\text{'}\text{'}}\subseteq H$ denote the host assignments for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime \prime }$\end{document}$t^{\text{'}\text{'}}$ that are optimal given a host assignment of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i$\end{document}$h_i$ at \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$. More precisely, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime } = \lbrace h_j \in H \mid C(t^{\prime }, h_j) + p(h_i, h_j) \text{ is minimized}\rbrace$\end{document}$X^{\text{'}}=\{h_j\in H\mid C(t^{\text{'}},h_j)+p(h_i,h_j)\text{is}\text{minimized}\}$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime \prime } = \lbrace h_j \in H \mid C(t^{\prime \prime }, h_j) + p(h_i, h_j) \text{ is minimized}\rbrace$\end{document}$X^{\text{'}\text{'}}=\{h_j\in H\mid C(t^{\text{'}\text{'}},h_j)+p(h_i,h_j)\text{is}\text{minimized}\}$. Then, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t, h_i)$\end{document}$N(t,h_i)$ can be computed as follows:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{} \begin{equation*} N(t, h_i) = \left(\sum _{x \in X^{\prime }} N(t^{\prime }, x)\right) \times \left(\sum _{x \in X^{\prime \prime }} N(t^{\prime \prime }, x)\right). \tag{4} \end{equation*} \end{document}$$N(t,h_i)=\left(\sum _{x\in X^{\text{'}}}N(t^{\text{'}},x)\right)\times \left(\sum _{x\in X^{\text{'}\text{'}}}N(t^{\text{'}\text{'}},x)\right).\left(\left(4\right)\right)$$

Observe that the total number of distinct ancestral host assignments for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ is given by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\sum _{x \in X} N({rt}(t), x)$\end{document}${\sum }_{x\in X}N(rt\left(t\right),x)$, where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X = \text{argmin}_{y \in H} \lbrace C({rt}(T), y)\rbrace$\end{document}$X={\text{argmin}}_{y\in H}\left\{C(rt\left(T\right),y)\right\}$.

This yields the following theorem.

Theorem 3.1. —

Given a transmission phylogeny \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ on \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$m$\end{document}$m$ strain sequences sampled from a set \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H = \lbrace h_1, h_2, \ldots, h_n\rbrace$\end{document}$H=\{h_1,h_2,...,h_n\}$ of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$n$\end{document}$n$ infected hosts, the number \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t, h_i)$\end{document}$N(t,h_i)$ for each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in V(G)$\end{document}$t\in V\left(G\right)$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i \in H$\end{document}$h_i\in H$ can be correctly computed in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(mn^2)$\end{document}$O\left(m{n}^2\right)$ time.

Proof. —

From the correctness of Sankoff's algorithm (described in Section 2), we already know that all costs \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(\cdot, \cdot)$\end{document}$C(·,·)$ can be correctly computed in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(mn^2)$\end{document}$O\left(m{n}^2\right)$ time. Once all costs \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(\cdot, \cdot)$\end{document}$C(·,·)$ have been computed, the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ numbers can be computed by executing a post-order traversal of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ and applying Equations (3) and (4) at each node of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$.

Correctness. It suffices to prove the correctness of Equations (3) and (4). This is easy to see for (3), where the number of optimal assignments at a leaf is either 1 or 0 depending on whether the specific host under consideration is the true host or not. We therefore focus on establishing the correctness of Equation (4).

Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$ be any node in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$I(T)$\end{document}$I\left(T\right)$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i$\end{document}$h_i$ be some host from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$H$\end{document}$H$. Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime }$\end{document}$t^{\text{'}}$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime \prime }$\end{document}$t^{\text{'}\text{'}}$ denote the two children of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$. Using an induction hypothesis, let us assume that the numbers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t^{\prime }, h_j)$\end{document}$N(t^{\text{'}},h_j)$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t^{\prime \prime }, h_j)$\end{document}$N(t^{\text{'}\text{'}},h_j)$ have been computed correctly for each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_j \in H$\end{document}$h_j\in H$. As in Equation (4), let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime } = \lbrace h_j \in H \mid C(t^{\prime }, h_j) + p(h_i, h_j) \text{ is minimized}\rbrace$\end{document}$X^{\text{'}}=\{h_j\in H\mid C(t^{\text{'}},h_j)+p(h_i,h_j)\text{is}\text{minimized}\}$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime \prime } = \lbrace h_j \in H \mid C(t^{\prime \prime }, h_j) + p(h_i, h_j) \text{ is minimized}\rbrace$\end{document}$X^{\text{'}\text{'}}=\{h_j\in H\mid C(t^{\text{'}\text{'}},h_j)+p(h_i,h_j)\text{is}\text{minimized}\}$. By definition, any host from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime }$\end{document}$X^{\text{'}}$ assigned to \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime }$\end{document}$t^{\text{'}}$ and from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X^{\prime \prime }$\end{document}$X^{\text{'}\text{'}}$ assigned to \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime \prime }$\end{document}$t^{\text{'}\text{'}}$ yields an optimal host assignment for the subproblem associated with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t, h_i)$\end{document}$N(t,h_i)$. Observe that the total number of optimal host assignments for the subtree \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T(t^{\prime })$\end{document}$T\left(t^{\text{'}}\right)$, under the constraint that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$ is assigned host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i$\end{document}$h_i$, is given by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\sum _{x \in X^{\prime }} N(t^{\prime }, x)$\end{document}${\sum }_{x\in X^{\text{'}}}N(t^{\text{'}},x)$. Likewise, the total number of optimal host assignments for the subtree \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T(t^{\prime \prime })$\end{document}$T\left(t^{\text{'}\text{'}}\right)$, under the constraint that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$ is assigned host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i$\end{document}$h_i$, is given by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\sum _{x \in X^{\prime \prime }} N(t^{\prime \prime }, x)$\end{document}${\sum }_{x\in X^{\text{'}\text{'}}}N(t^{\text{'}\text{'}},x)$. Since these optimal host assignments for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime }$\end{document}$t^{\text{'}}$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t^{\prime \prime }$\end{document}$t^{\text{'}\text{'}}$ are independent of each other (they depend only on the host assignment at \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$), the number \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t, h_i)$\end{document}$N(t,h_i)$ must equal the product of the two sums. Thus, Equation (4) correctly computes \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(t, h_i)$\end{document}$N(t,h_i)$. Induction on the nodes of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ completes this proof.

Time Complexity. Observe that there are a total of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(mn)$\end{document}$O\left(mn\right)$ \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ numbers to be computed. Each of these numbers is computed by directly applying either Equations (3) or (4). Equation (3) can be applied in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(1)$\end{document}$O\left(1\right)$ time, while Equation (4) can be applied in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(n)$\end{document}$O\left(n\right)$ time. Thus, computing all \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ requires a total of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$O(mn^2)$\end{document}$O\left(m{n}^2\right)$ time.

After all \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ numbers have been computed, we perform our greedy sampling procedure using probabilistic backtracking. The basic idea is to perform a pre-order traversal of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ and make a final host assignment at the current node based on the number of optimal ancestral host assignments available for each optimal choice at that node, while preferentially preserving the parent host assignment. This is described in detail in Procedure GreedyProbabilisticBacktracking below. This procedure assumes that all costs \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$C(\cdot, \cdot)$\end{document}$C(·,·)$ and numbers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$N(\cdot, \cdot)$\end{document}$N(·,·)$ have already been computed.

Procedure. GreedyProbabilisticBacktracking

• 1:Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\alpha = \min _i \lbrace C({rt}(T), h_i)\rbrace$\end{document}$\alpha ={min}_i\left\{C(rt\left(T\right),h_i)\right\}$.
• 2:for each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \in I(T)$\end{document}$t\in I\left(T\right)$ in a pre-order traversal of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$T$\end{document}$T$ do
• 3:if \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t = {rt}(T)$\end{document}$t=rt\left(T\right)$ then
• 4:Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X = \lbrace h_i \in H \mid C({rt}(T), h_i) = \alpha \rbrace$\end{document}$X=\{h_i\in H\mid C(rt\left(T\right),h_i)=\alpha \}$.
• 5:For each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i \in X$\end{document}$h_i\in X$, assign \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = h_i$\end{document}$h\left(t\right)=h_i$ with probability \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\frac{N(t, h_i)}{\sum _{h_j \in X} N(t, h_j)}$\end{document}$\frac{N(t,h_i)}{{\sum }_{h_j\in X}N(t,h_j)}$.
• 6:if \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t \ne {rt}(T)$\end{document}$t\ne rt\left(T\right)$ then
• 7:Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$X = \lbrace h_i \in H \mid C(t, h_i) + p(h({pa}(t)), h_i) \text{ is minimized}\rbrace$\end{document}$X=\{h_i\in H\mid C(t,h_i)+p(h\left(pa\left(t\right)\right),h_i)\text{is}\text{minimized}\}$.
• 8:if \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h({pa}(t)) \in X$\end{document}$h\left(pa\right(t\left)\right)\in X$ then
• 9:Assign \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = h({pa}(t))$\end{document}$h\left(t\right)=h\left(pa\right(t\left)\right)$.
• 10:if \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h({pa}(t)) \not\in X$\end{document}$h\left(pa\right(t\left)\right)\notin X$ then
• 11:For each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h_i \in X$\end{document}$h_i\in X$, assign \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = h_i$\end{document}$h\left(t\right)=h_i$ with probability \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$\frac{N(t, h_i)}{\sum _{h_j \in X} N(t, h_j)}$\end{document}$\frac{N(t,h_i)}{{\sum }_{h_j\in X}N(t,h_j)}$.

The procedure above preferentially assigns each internal node the same host assignment as that node's parent, if such an assignment is optimal. This strategy is based on the following straightforward observation: If the host assignment of an internal node \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$t$\end{document}$t$ could be the same as that of its parent (while remaining optimal), i.e., \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) = h({pa}(t))$\end{document}$h\left(t\right)=h\left(pa\right(t\left)\right)$ is optimal, then assigning a different optimal mapping \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h(t) \ne h({pa}(t))$\end{document}$h\left(t\right)\ne h\left(pa\right(t\left)\right)$ can result in a transmission edge back to \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h({pa}(t))$\end{document}$h\left(pa\right(t\left)\right)$, effectively implying a reinfection of host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$h({pa}(t))$\end{document}$h\left(pa\right(t\left)\right)$ by a descendant disease strain. Thus, the goal of TNet's sampling strategy is to strike a balance between sampling the diversity of optimal ancestral host assignments but avoiding sampling solutions with unnecessary back-transmissions.

3.2. Aggregation Across Multiple Optima

As illustrated in Fig. 2, aggregating across the sampled optimal ancestral host assignments can be used to improve transmission network inference by distinguishing between high-support and low-support transmission edges. Specifically, each directed edge in the transmission network can be assigned a support value based on the percentage of sampled optimal ancestral host assignments that imply that transmission edge. For example, in Fig. 2, the first sampled optimal host assignment (shown on the top) implies the two transmission edges \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow B)$\end{document}$(A\to B)$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow C)$\end{document}$(A\to C)$, and the second sampled optimal host assignment (shown at the bottom) implies the two transmission edges \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow B)$\end{document}$(A\to B)$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(C \rightarrow A)$\end{document}$(C\to A)$. By aggregating over these two transmission networks, an edge-weighted transmission network can be inferred, as shown on the right of the figure. This aggregated transmission network contains three directed edges, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow B)$\end{document}$(A\to B)$, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow C)$\end{document}$(A\to C)$, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(C \rightarrow A)$\end{document}$(C\to A)$, where the weight of each edge captures the percentage of sampled optimal ancestral host assignments that support that edge. Since \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow B)$\end{document}$(A\to B)$ is inferred by both sampled ancestral host assignments, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow C)$\end{document}$(A\to C)$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(C \rightarrow A)$\end{document}$(C\to A)$ are each inferred by one of the two sampled ancestral host assignments, there support values are 100, 50, and 50 percent, respectively. By executing TNet multiple times on the same transmission phylogeny (100 times per tree in our experimental study), these support values for edges can be estimated very accurately.

3.3. Accounting for Phylogenetic Inference Error

In addition to capturing the uncertainty of minimum back-transmission ancestral host assignments, which we show how to handle above, a second key source of inference uncertainty is phylogenetic error, i.e., errors in the inferred transmission phylogeny. Phyloscanner [37] accounts for such phylogenetic error by aggregating results across multiple transmission phylogenies (e.g., derived from different genomic regions of the samples strains, bootstrap replicates, etc.). We employ the same approach with TNet, aggregating the transmission network across multiple transmission phylogenies, in addition to the aggregation across multiple optimal ancestral host assignments per transmission phylogeny.

4. Datasets and Evaluation Methodology

Simulated Datasets. To evaluate the performance of TNet, SharpTNI, and phyloscanner, we generated a number of simulated viral transmission data sets across a variety of parameters. These datasets were generated using FAVITES [25], which can simultaneous simulate transmission networks, phylogenetic trees, and sequences. The simulated contact networks consisted of 1000 individuals, with each individual connected to other individuals through 100 outgoing edges preferentially attached to high-degree nodes using the Barabasi-Albert model [1]. On these contact networks, we simulated datasets with (i) four types of transmission networks using both Susceptible-Exposed-Infected-Recovered (SEIR) and Susceptible-Infected-Recovered (SIR) [20] models with two different infection rates for each, (ii) number of viruses sampled per host (5, 10, and 20), (iii) three different nucleotide sequence lengths (1000nt, 500nt, and 250nt), and (iv) three different rates of with-in host sequence evolution (normal, half, and double). This resulted in 560 different transmission network datasets representing 28 different parameter combinations. Further details on the construction and specific parameters used for these simulated datasets appear in [33].

These 560 simulated datasets had between 35 and 1400 sequences (i.e., leaves in the corresponding transmission phylogeny), with an average of 287.44 leaves. The maximum number of hosts per tree was 75, with an average of 26.72.

Data From Real HCV Outbreaks. We also evaluated the accuracies of TNet, SharpTNI, and phyloscanner on real datasets of HCV outbreaks made available by the CDC [32]. This collection consists 10 different datasets, each representing a separate HCV outbreak. Each of these outbreak data sets contains between 2 and 19 infected hosts and a few dozen to a few hundred strain sequences. The approximate transmission network is known for each of these datasets through CDC's monitoring and epidemiological efforts. In each of the 10 cases, this estimated transmission network consists of a single known host infecting all the other hosts in that network.

Evaluating Transmission Network Inference Accuracy. For all simulated and real datasets, we constructed transmission phylogenies using RAxML and used RAxML's own balanced rooting procedure to root them [34]. Note that TNet, SharpTNI, and phyloscanner all require rooted transmission phylogenies. To account for phylogenetic uncertainty and error, we computed 100 bootstrap replicates for each simulated and real dataset. For SharpTNI we used the efficient heuristic implementation for evaluation (not the exponential-time exact solution). All TNet results were based on aggregating across 100 sampled optimal host assignments per transmission phylogeny, and all SharpTNI results were aggregated across that subset of 100 samples that had minimum co-transmission cost, per transmission phylogeny. Results for all methods were aggregated across the different bootstrap replicates to account for phylogenetic uncertainty and yield edge-weighted transmission networks. To convert such edge-weighted transmission networks into unweighted transmission networks, we used the same 0.5 (or 50 percent) tree-support threshold used by phyloscanner in [37]. Thus, all directed edges with an edge-weight of at least 0.5 (or 50 percent) tree-support were retained in the final inferred transmission network and other edges were deleted. For a fair evaluation, none of the methods were provided with any epidemiological information such as sampling times or infection times. Finally, since both TNet and SharpTNI build upon uniform sampling procedures for optimal ancestral host assignments (minimizing the total number of inter-host transmissions), we also report results for uniform random sampling of optimal ancestral host assignments, as implemented in TNet, as a baseline.

To evaluate the accuracies of these final inferred transmission networks, we computed precision (i.e., the fraction of inferred edges in the transmission network that are also in the true network), recall (i.e., the fraction of true transmission network edges that are also in the inferred network), and F1 scores (i.e., harmonic mean of precision and recall).

5. Experimental Results

5.1. Simulated Data Results

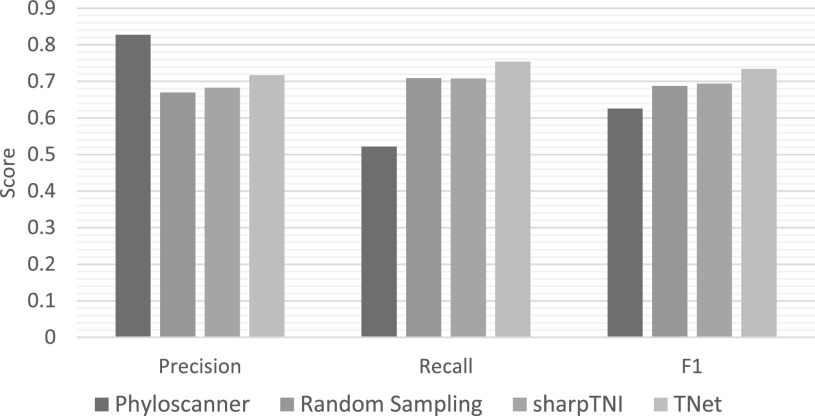
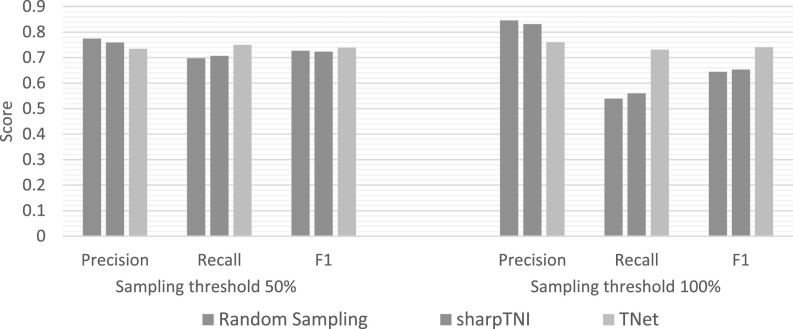
Accuracy of Single Samples. We first considered the impact of inferring the transmission network using only a single optimal solution, i.e., without any aggregation across samples or bootstrap replicates. Fig. 4 shows the results of this analysis. As the figure shows, TNet has by far the best overall accuracy, with precision, recall, and F1 scores of 0.72, 0.75, and 0.73, respectively. Phyloscanner showed the greatest precision at 0.828 but had significantly lower recall and F1 at 0.522 and 0.626, respectively. SharpTNI performed slightly better than a random optimal solution (uniform sampling), with precision, recall, and F1 scores of 0.68, 0.71, and 0.694, respectively, compared to 0.67, 0.71, and 0.687, respectively, for a randomly sampled optimal solution.

Fig. 4.

Accuracy of methods using single samples. This figure plots precision, recall, and F1 scores for the different methods without any aggregation of results across multiple samples or bootstrap replicates. Results are averaged across the 560 simulated datasets.

Impact of Sampling Multiple Optimal Solutions. For improved accuracy, both TNet and SharpTNI rely on aggregation across multiple samples per transmission phylogeny. Note that, when aggregating across multiple optimal ancestral host assignments, the final transmission network is obtained by applying a cutoff for the edge support values. For example, in Fig. 2, at a cutoff threshold of 100 percent, only a single transmission from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A \rightarrow B)$\end{document}$(A\to B)$ would be inferred, while with a cutoff threshold of 50 percent, all three transmission edges shown in the figure would be inferred. We studied the impact of multiple sample aggregation by considering two natural sampling cutoff thresholds: 50 and 100 percent. As Fig. 5 shows, results improve as multiple optimal are considered. Specifically, for the 50 percent sampling cutoff threshold, we found that the overall accuracy of all methods improves as multiple samples are considered. For TNet, precision, recall, and F1 score all increase to 0.73, 0.75, and 0.74, respectively. For SharpTNI, precision and F1 score increase significantly to 0.76 and 0.72, respectively, while recall decreases slightly to 0.706. Surprisingly, we found that uniform random sampling outperformed SharpTNI, with precision, recall, and F1 score of 0.77, 0.70, and 0.73, respectively.

Fig. 5.

Accuracy of methods using multiple samples on a single transmission phylogeny. This figure plots average precision, recall, and F1 scores for random sampling, sharpTNI, and TNet when 100 samples are used on a single transmission phylogeny. Values reported are averaged across all 560 simulated datasets, and results are shown for both 50 and 100 percent sampling cutoff thresholds.

The figure also shows the clear tradeoff between precision and recall as the sampling cutoff threshold is increased. Specifically, for the 100 percent sampling cutoff threshold, the precision of all methods increases significantly, but overall F1 score falls to 0.65 and 0.64 for SharpTNI and random sampling, respectively. Surprisingly, recall only decreases slightly for TNet, and its overall F1 score remains 0.74 even for the 100 percent sampling cutoff threshold.

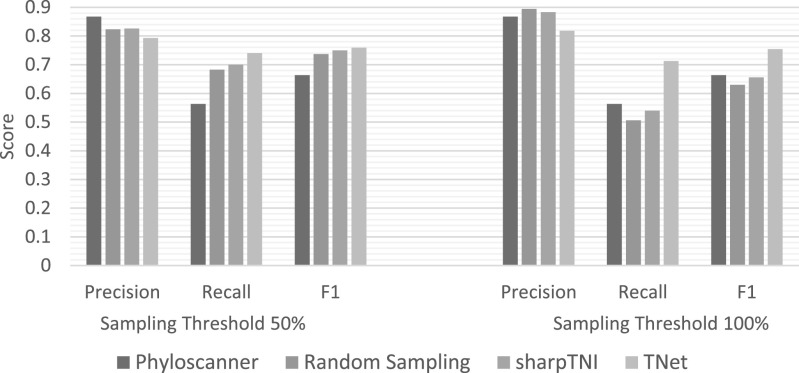
Accuracy on Multiple Bootstrapped Transmission Phylogenies. To further improve inference accuracy, results can be aggregated across the different bootstrap replicates to account for phylogenetic uncertainty. We therefore ran phyloscanner, TNet, and SharpTNI with 100 transmission phylogeny estimates (bootstrap replicates) per dataset. (We tested for the impact of using varying numbers of bootstrap replicates, trying 25, 50, and 100, but found that results were roughly identical in each case. We therefore report results for only the 100 bootstrap analyses.) As Fig. 6 shows, for the 50 percent sampling cutoff threshold, the accuracies of all methods improve over the corresponding single-tree results, with particularly notable improvements in precision. For the 100 percent sampling cutoff threshold, the precision of all methods improves further, but for phyloscanner and SharpTNI this comes at the expense of large reductions in recall. TNet continues to be best performing method overall for both sampling cutoff thresholds, with precision, recall, and F1 score of 0.79, 0.73, and 0.76, respectively, at the 50 percent sampling cutoff threshold, and 0.82, 0.71, and 0.754, respectively at the 100 percent sampling cutoff threshold.

Fig. 6.

Transmission network inference accuracy when multiple transmission phylogenies are used. This figure plots average precision, recall, and F1 scores for phyloscanner, random sampling, sharpTNI, and TNet when 100 bootstrap replicate transmission phylogenies are used for transmission network inference. Values reported are averaged across all 560 simulated datasets, and results are shown for both 50 and 100 percent sampling cutoff thresholds.

Precision-Recall Characteristics of SharpTNI and TNet. The results above shed light on the differences between the sampling strategies (i.e, objective functions) used by SharpTNI and TNet, revealing that SharpTNI tends to have higher precision but much lower recall. Thus, depending on use case, either SharpTNI or TNet may be the method of choice. We also note that random sampling shows similar accuracy and precision-recall characteristics as SharpTNI, suggesting that SharpTNI may not offer much improvement over the much simpler random sampling strategy.

Impact of Transmission Network Parameters. To study the impact of transmission network simulation parameters on relative inference accuracy, we separately partitioned the 560 datasets by transmission network model, mutation rates, number of viruses sampled per host, and sequence length. As expected, we found that the accuracies of all methods increased as sequence length was increased, and that the accuracies of all methods except phyloscanner increased as the number of viruses sampled per host increased. Overall, we found that the relative accuracies of the methods were not significantly impacted by mutation rates, number of viruses sampled per host, and sequence length, i.e., while the accuracies of all methods increased or decreased as these parameters were changed, the relative accuracies of the four methods generally remained the same (results not shown). However, we found that the transmission network model, i.e., SIR or SEIR, had an impact on the relative accuracies of the methods. Specifically, as Table 1 shows, we found that (1) sharpTNI shows a slightly higher F1 score than TNet on the SIR datasets when the 50 percent sampling cutoff threshold is used, and (2) TNet performs substantially better than all other methods under the SEIR model, at both the 50 and 100 percent sampling cutoff thresholds. Notably, TNet clearly remains the most accurate method even for SIR datasets when the 100 percent sampling cutoff threshold is used.

TABLE 1. Transmission Network Inference Accuracy Under SIR and SEIR Models.

	Phyloscanner	Random sampling	SharpTNI	TNet
SIR model at 50% sampling threshold	0.642	0.715	0.727	0.713
SEIR model at 50% sampling threshold	0.684	0.76	0.772	0.806
SIR model at 100% sampling threshold	0.642	0.636	0.65	0.706
SEIR model at 100% sampling threshold	0.684	0.625	0.661	0.802

The table shows average F1 scores for phyloscanner, random sampling, sharpTNI, and TNet when 100 bootstrap replicate transmission phylogenies are used for transmission network inference. Average F1 scores are reported separately for the 280 datasets smulated under the SIR model and the 280 datasets simulated under the SEIR model. Results are shown for both 50 and 100 percent sampling cutoff thresholds.

To understand why TNet shows substantially better accuracy than the other methods on SEIR datasets, we analyzed the SIR and SEIR datasets further. We observed that the key difference between them is that the basic reproduction number, which captures the average number of other individuals infected by any infected individual, and referred to as \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$R_0$\end{document}$R_0$, averaged 1.71 for the SIR datasets but 3.58 for the SEIR datasets. This helps explain the substantially improved performance of TNet on SEIR datasets, since transmission networks with higher \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$R_0$\end{document}$R_0$ may benefit from TNet's host assignment strategy, which preferentially propagates parent host assignments to their children. This analysis suggests that TNet may be especially effective at inferring transmission networks for diseases that spread primarily through super-spreader events [35].

5.2. HCV Dataset Results

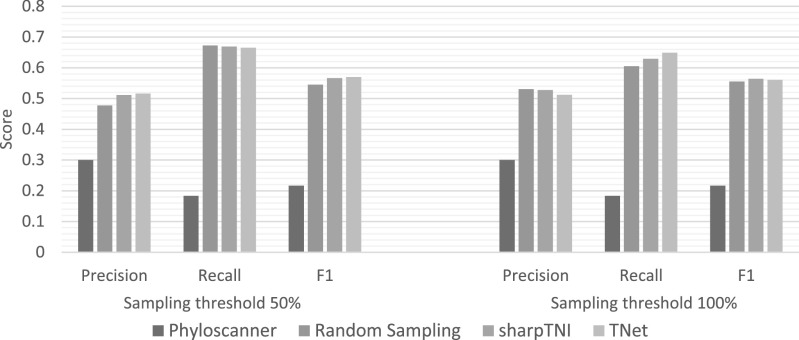
We applied TNet, SharpTNI, and phyloscanner to the 10 real HCV datasets using 100 bootstrap replicates per dataset. We found that both TNet and SharpTNI performed almost identically on these datasets, and that both dramatically outperformed phyloscanner on the real datasets in terms of both precision and recall (and, consequently, F1 scores). Fig. 7 shows these results averaged across the 10 real datasets. As the figure shows, both TNet and SharpTNI have identical F1 scores for the 50 and 100 percent sampling cutoff thresholds, with both methods showing F1 scores of 0.57 and 0.56, respectively. In contrast, phyloscanner shows much lower precision and recall, with an F1 score of only 0.22. Random sampling had slightly worse performance than TNet and SharpTNI at both the 50 and 100 percent sampling cutoff thresholds. At the 100 percent sampling cutoff threshold, we observe the same precision-recall characteristics seen in the simulated datasets, with SharpTNI showing higher precision but lower recall.

Fig. 7.

Transmission network inference accuracy across the 10 real HCV datasets. This figure plots average precision, recall, and F1 scores for phyloscanner, random sampling, sharpTNI, and TNet on the 10 real HCV datasets with known transmission histories. Results are shown for both 50 and 100 percent sampling cutoff thresholds.

6. COVID-19 Analysis

The ongoing COVID-19 pandemic has resulted in the availability of completely sequenced SARS-CoV-2 genomes from thousands of infected individuals across dozens of countries; see, e.g., the GISAID resource [12]. Among a multitude of other uses, this rich dataset allows for the estimation of a global transmission network of the spread of COVID-19. For example, the popular Nextstrain tool (https://nextstrain.org/) computes and provides a regularly updated SARS-CoV-2 phylogeny and associated transmission network between geographical regions [17]. To evaluate the ability of TNet to infer such geographical spread/transmission networks, we applied TNet, along with the random sampling algorithm implemented in TNet, to a large collection of SARS-CoV-2 genomes. For this analysis, countries serve as hosts and the sampled SARS-CoV-2 genomes (only one genome per infected individual) from the infected individuals in each country serve as the sampled strains for that country/host. We also repeated the analysis at the state level for SARS-CoV-2 strains from USA. We compared the resulting transmission networks against those inferred by the widely used Nextstrain tool, evaluating inference accuracy using the available epidemiological information about country of exposure for each SARS-CoV-2 genome used in the analysis. SharpTNI could not be used for this analysis since it was not able to scale to this large dataset and resulted in runtime errors.

6.1. Description of the Dataset

We downloaded all complete, high-coverage SARS-CoV-2 genomes available through GISAID [12] on June 12, 2020. Each of these sequences had between 29000 and 31000 base pairs. We then removed sequences from all countries with fewer than 10 sequences. We then removed duplicate sequences within each country, but keeping at least 10 sequences per country (i.e., if removing duplicates for a country resulted in fewer then 10 sequences for that country, then we allowed some duplicates to remain). Since some countries had a very large number of sequences in the dataset, we then down-sampled sequences from such countries to create a more equitable distribution of sequences per country. Specifically, if a country had more than 100 sequences, we randomly chose 100 sequences for that country. This resulted in a dataset of 2123 SARS-CoV-2 strain sequences from across 59 countries.

We aligned the 2123 sequences using Clustal Omega[31] and reconstructed maximum likelihood phylogenies using RAxML [34] under the GTRGAMMA model. In all, we constructed one maximum likelihood phylogeny along with 10 bootstrap replicates. The resulting 11 phylogenies were rooted and dated using TreeTime [28], which is also used by the Nextstrain pipeline.

This dataset of 2123 SARS-CoV-2 sequences, including sequence alignment, metadata, and reconstructed phylogenetic trees, is freely available from: https://compbio.engr.uconn.edu/global_covid-19_dataset/.

6.2. Geographical Transmission Network Inference

We applied TNet, random sampling, and the Nextstrain/Augur tool to this dataset to infer international (country-to-country) transmission networks. Observe that such geographical transmission networks are distinct from usual disease transmission networks in that (i) most pairs of countries or geographical regions can be expected to be connected through transmission edges, and (ii) transmissions between pairs of counties likely occur in both directions. Thus, the information of interest in geographical transmission networks is not merely the presence of edges between pairs of countries/regions, but the magnitude and time periods of transmission. Accordingly, in our inferred transmission networks, each transmission edge between an ordered pair of countries \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$(A, B)$\end{document}$(A,B)$ is labeled with the following additional information:

• 1)The number of separate transmission events from \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ to \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$.
• 2)The number of such separate transmissions occurring during each month (December 2019 through May 2020).

This information can be directly obtained from the optimal host assignments computed by each method by assigning a date to each internal node of the phylogenetic trees used for the inference (which we obtained using TreeTime, as described above) and then counting the number of edges \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$({pa}(x), x)$\end{document}$\left(pa\right(x),x)$ in the host-assigned phylogeny for which \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}${pa}(x)$\end{document}$pa\left(x\right)$ is assigned host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$A$\end{document}$A$ and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$x$\end{document}$x$ is assigned host \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{upgreek} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} }{}$B$\end{document}$B$.

For TNet and random sampling, we inferred the geographical transmission network by applying those methods to the 10 bootstrap replicate phylogenies, computing 100 samples for each. This resulted in 1000 optimal host assignments for each of these two methods. To compute a single geographical transmission network from these 1000 host assignments, we averaged the numbers of inferred transmission events between ordered pair of countries for each time period over all 1000 host assignments. Since Nextstrain/augur is not based on sampling, we computed the geographical transmission network for Nextstrain by using the maximum likelihood phylogeny from RAxML.

6.3. Evaluation of Geographical Transmission Networks

We performed two kinds of comparisons between the geographical transmission networks inferred by the three different methods. First, we used the available “ground-truth” data available for each strain included in the analysis. Specifically, we used the known country/region of exposure, likely inferred through contact tracing, available in the metadata for each SARS-CoV-2 sequence. This allowed us to use the host assignment for the parent of each leaf node in the host-assigned phylogenies and infer the accuracy of those assignments for each method by comparing to the known country/region of exposure for that leaf. For TNet and random sampling, which use multiple trees and samples, we used the most frequently assigned host for each parent node as its final assignment. Note that for 17 of the 2123 sequences the country of exposure was a country that was not included in our analysis.

Second, we performed a systematic comparison of the geographical transmission networks inferred by the three methods by identifying, for each method, the top five most frequent spreader countries for each time period (month) and the top five receiving countries for each time period. We also repeated this comparative analysis with respect to United States of America (USA) by identifying the top five spreaders to USA and top five recipients from USA during each time period.

6.4. Results

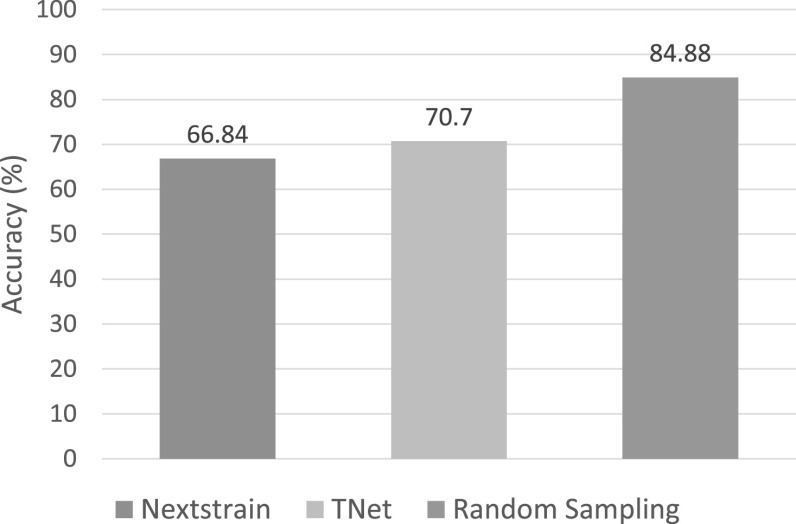
Overall Accuracies of the Methods Based on Ground-Truth. By comparing the international transmission networks inferred by the three methods against the known country of exposure available for each SARS-CoV-2 sequence, we found that TNet significantly outperformed Nextstrain and that random sampling dramatically outperformed both Nextstrain and TNet. Specifically, Nextstrain, TNet, and random sampling were able to correctly determine the country of exposure correctly for 67, 71, and 85 percent of the sequences, respectively. These results are shown in Fig. 8.

Fig. 8.

Accuracy of Nextstrain, TNet, and random sampling on the COVID-19 dataset based on the known country of exposure available for each SARS-CoV-2 sequence.

It is worth noting that the superiority of random sampling over TNet is not surprising for this application. This is because, for geographical transmission networks, there is no expectation that back-transmissions should be rare. In fact, back-transmissions are expected to occur freely and frequently. Thus, random sampling is expected to outperform TNet for geographical transmission network inference. Surprisingly, TNet still outperforms Nextstrain in this analysis. These results suggest that our random sampling framework may prove highly useful for estimating geographical transmission networks as well as for estimating other transmission networks in other settings where back-transmissions can occur freely.

Comparison of Inferred International Transmission Networks. To systematically compare the international transmission networks inferred by the three methods, we computed, for each method, the top five most frequent spreader countries for each time period (month) and the top five receiving countries for each time period. Figs. 9 and 10 show the results of this analysis. As the figures show, there is both agreement and disagreement between the transmission networks inferred by the three methods. Considering spreader countries (Fig. 9), we find that there is agreement among all methods that China was the primary spreader during December 2019 and January 2020, but that it ceases to be among the top five spreaders February 2020 onward. On the other hand, while Nextstrain infers that the majority of spread from China occurred in January 2020, TNet and random sampling both infer that the majority of the spread from China occurred in December 2019. All methods also agree that February 2020 was the most active month for the spread of COVID-19, and that international spread was essentially over by April 2020. For most months, there is considerable variation in the top spreader countries identified by the three methods; for instance, for December 2019, only one country is common among the top five inferred by Nextrain and either of other two methods, and only two are in common between TNet and random sampling. Notably, both TNet and random sampling identity USA as an early and important contributor to the spread of COVID-19, while Nextstrain does not include USA in its top five list until March 2020. Considering receiver countries (Fig. 10), we find that there is generally more agreement between the three methods. For instance, all methods agree that generally Asian countries and Australia acted as major recipients during December 2019 and January 2020, and that European countries became the major receivers during February and March 2020. The methods also mostly agree that USA was a major recipient during all months from December 2019 to March 2020.

Fig. 9.

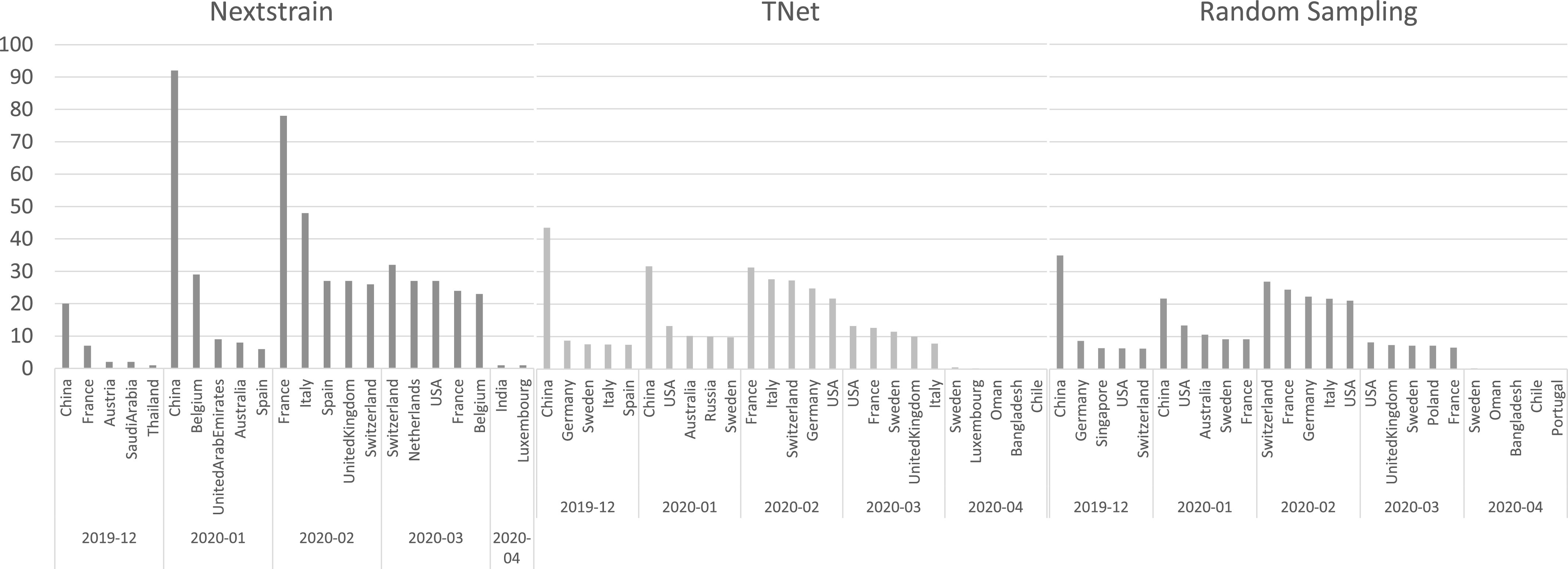
Top five spreader countries inferred by Nextstrain, TNet, and Random Sampling during each month from December 2019 through April 2020.

Fig. 10.

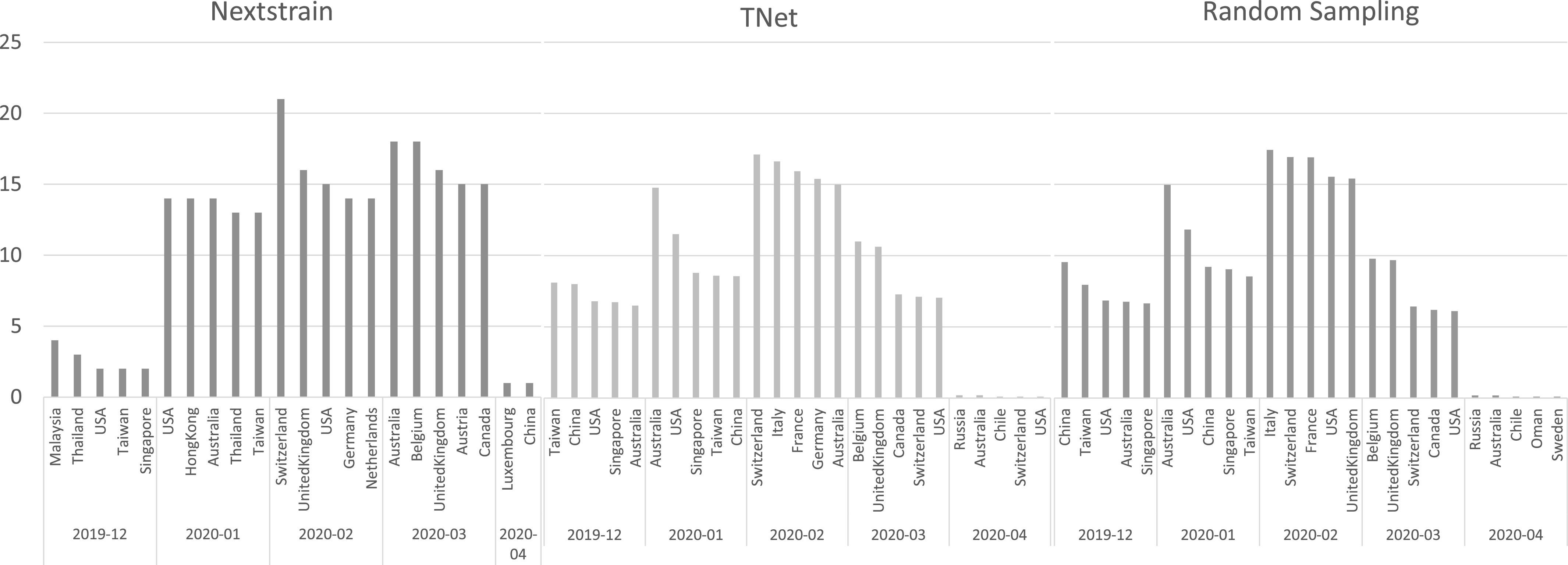
Top five receiver countries inferred by Nextstrain, TNet, and Random Sampling during each month from December 2019 through April 2020.

To further analyse the differences between these transmission networks, we used USA as the “base” country and identified the top five spreaders to USA and top five recipients from USA during each time period. These results are shown in Supplementary Figs. S1 and S2, which can be found on the Computer Society Digital Library at http://doi.ieeecomputersociety.org/10.1109/TCBB.2021.3096455. Considering spreader countries (Supplementary Fig. S1, available online), we find that there is generally good agreement between the top five lists of TNet and random sampling for the months December 2019 through February 2020, but that they have significant differences from the top five lists inferred by Nextstrain for the same periods. However, all methods agree that China was the primary spreader to USA in December 2019 and January 2020 and that France was the primary spreader in March 2020. Considering receiver countries (Supplementary Fig. S2, available online), we find considerable agreement between between the top five lists of TNet and random sampling for the months December 2019 through March 2020. However, as with spreader countries, there are considerable differences between the top five countries for each period inferred by Nextstrain and those inferred by TNet or random sampling. However, all methods identify Canada and France as major receivers of COVID-19 from USA. Notably, TNet and random sampling also identity China as a major recipient of infections from USA during December 2919 and January 2020, and identify Taiwan as one of the top receivers of infections from USA.

State-Level Analysis. We also repeated the above analysis to infer the state-level transmission network within USA. We downloaded available SARS-CoV-2 sequences from USA in July 2020 using the same process as described above, and this resulted in a dataset of 1801 SARS-CoV-2 sequences from 30 states, with each state represented by between 10 and 100 sequences. We applied the three methods to this dataset, computing a sequence alignment and phylogenetic trees using the same methods described before, and obtained the geographical (state-to-state) transmission network implied by each method. We compared the transmission networks inferred by the three methods against the known state of exposure available for each SARS-CoV-2 sequence. (Note that for 10 of the 1801 sequences the state of exposure was a country or state that was not included in our analysis.) As before, we found that TNet significantly outperformed Nextstrain and that random sampling dramatically outperformed both Nextstrain and TNet. Specifically, Nextstrain, TNet, and random sampling were able to correctly determine the state of exposure correctly for 65, 73, and 86 percent of the sequences, respectively.

As before, we also compared the state-level transmission networks inferred by the three method by inferring the top five most frequent spreader and receiver states for each time period (month). These results are shown in Figs. 11 and 12. As these figures show, TNet and random sampling generally agree in their lists of top spreaders and receivers, but that those lists differ significantly from those inferred by Nextstrain. For instance, Nextstrain infers Virginia and Pennsylvania as the top two spreader states during February 2020, but these states do not feature in the top five spreader lists for TNet and random sampling during any time period. All methods agree that the months of February and March 2020 had, by far, the most spread of COVID-19, and that the top spreader states in March were New York and California.

Fig. 11.

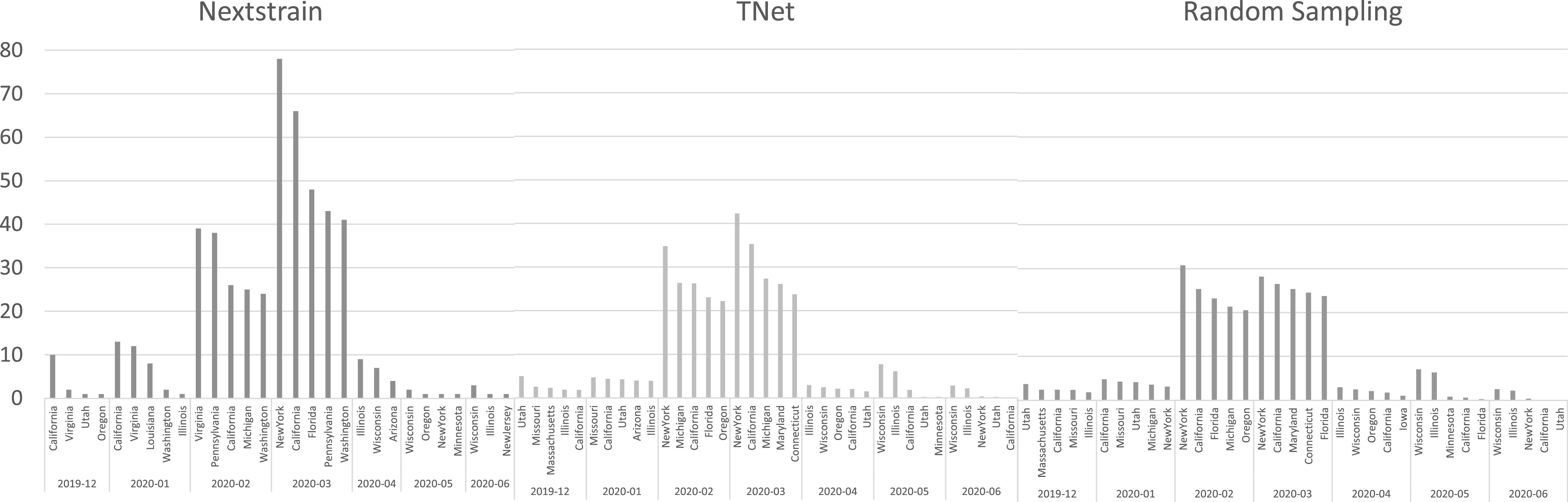
Top five spreader states in USA inferred by Nextstrain, TNet, and Random Sampling during each month from Dec. 2019 through June 2020.

Fig. 12.

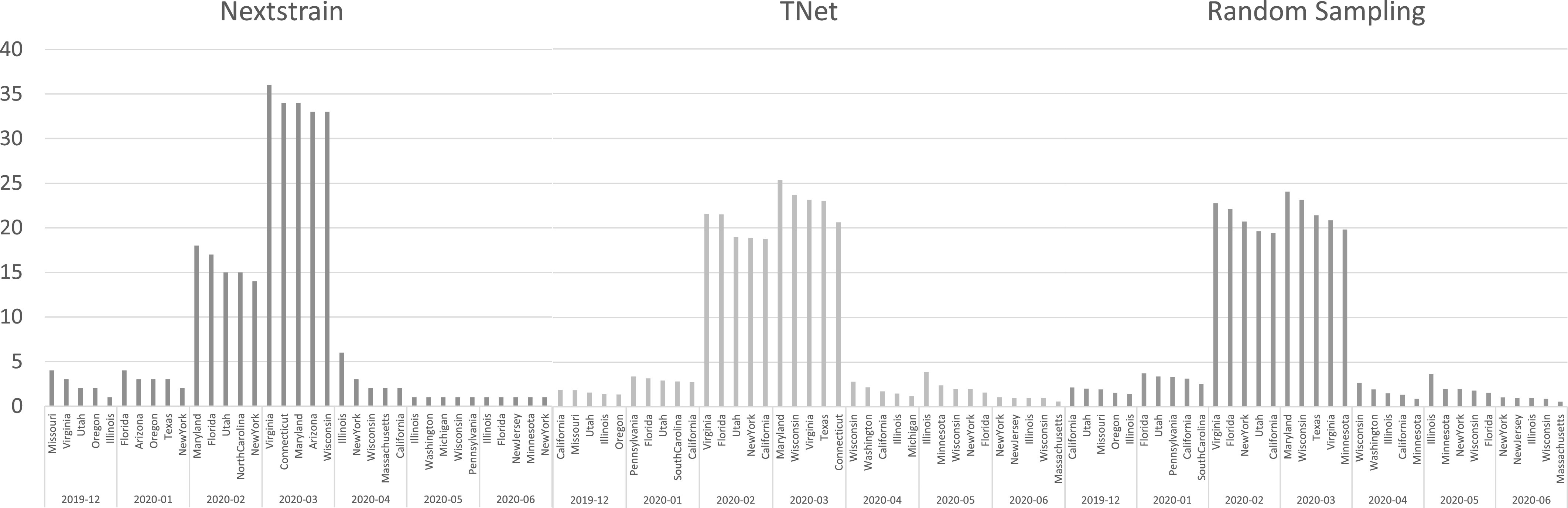
Top five receiver states in USA inferred by Nextstrain, TNet, and Random Sampling during each month from Dec. 2019 through June 2020.

Running Time and Scalability. A key strength of TNet (and also the implementation of the random sampling method in TNet) is that it is extremely fast and highly scalable. For example, each run of TNet on the global COVID-19 dataset with 2123 sequences required only 1.2 seconds using a single core on a commodity desktop computer with a 3.00 GHz 6-core Intel i5-8500 CPU and 16 GB of RAM. Thus, the entire TNet (and also random sampling) analysis consisting of 1000 runs (computing 100 sample host assignments for each of the 10 bootstrap phylogenies) took less than 20 minutes.

7. Discussion

In this paper, we introduced TNet, a new method for transmission network inference when multiple strain sequences are sampled from the infected hosts. TNet has two distinguishing features: First, it systematically accounts for variability among different optimal solutions to efficiently compute support values for individual transmission edges and improve transmission inference accuracy, and second, its objective function seeks to find those optimal host assignments that minimize the number of back-transmissions. TNet is based on a relatively simple parsimony-based formulation and is parameter-free and highly scalable. It can be easily applied within seconds to datasets with many hundreds of strain sequences and hosts. As our experimental results on both simulated and real datasets show, TNet is highly accurate and significantly outperforms phyloscanner. We find that TNet also outperforms SharpTNI, a distinct but very similar method developed independently and published recently. We also show how TNet as well as the closely related random sampling method (also implemented in TNet) can be used to infer geographical transmission networks and our analysis using large-scale COVID-19 data demonstrates how TNet and random sampling both significantly outperform the popular Nextstrain/Augur method.

Going forward, several aspects of TNet can be tested and improved further. The simulated datasets used in our experimental study assume that all infected hosts have been sampled. It would be useful to test how accuracy decreases as fewer and fewer infected hosts are sampled. Phyloscanner employs a simple technique to estimate if an ancestral host assignment may be to an unsampled host, and a similar technique could be used in TNet. Currently, TNet does not make use of branch lengths or of overall strain diversity within hosts, and these could be used to further improve the accuracy of ancestral host assignment and transmission network inference. Likewise, it should be possible to easily model contact-network information within the TNet framework, simply by having different penalties (or costs) for transmissions between connected hosts versus unconnected hosts. Finally, the potential of random sampling for inferring geographical transmission networks is worth investigating and developing further.

Biographies

Saurav Dhar received the BSc degree in computer science and engineering from the Bangladesh University of Engineering and Technology in 2017. He is currently working toward the master's degree in computer science and engineering with the University of Connecticut, USA. His research interests include algorithm development, bioinformatics, and machine learning.

Chengchen Zhang received the BS degree in computer science and engineering and the BA degree in economics from the University of Connecticut, USA, in 2018, and the MS degree in computer science from the University of California at San Diego, USA, in 2020. He is currently a software engineer in San Diego, USA.

Ion I. Măndoiu received the MS degree in computer science from Bucharest University in 1992 and the PhD degree in computer science from the Georgia Institute of Technology in 2000. He is currently a professor of computer science and engineering with the University of Connecticut. He has authored or coauthored more than 130 refereed articles in journals and conference proceedings and 13 book chapters, and has also co-edited 11 conference proceedings and two books published in the Wiley Book Series on Bioinformatics. His research interests include bioinformatics and computational genomics, with a special focus on the development of computational methods for the analysis of high-throughput sequencing data.

Mukul S. Bansal received the PhD degree in computer science from Lowa State University in 2009. He is currently an associate professor with the Department of Computer Science and Engineering, University of Connecticut, USA. His research interests include computational biology and bioinformatics, with an emphasis on computational molecular evolution. He was an Edmond J. Safra postdoctoral fellow with the School of Computer Science, Tel Aviv University till December 2010 and a postdoctoral associate with Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology till August 2013.

Funding Statement

This work was supported in part by U.S National Science Foundation (NSF) Award CCF 1618347 to IM and MSB.