Restoring trilinearity with the purpose of advanced modeling: towards a more effective analysis of Pericarpium Citri Reticulatae during storage periods

Abstract

To accurately quantify Pericarpium Citri Reticulatae samples, trilinear structure was restored in the stacked fingerprints for more robust modeling. Initially, liquid chromatography - diode array detector - mass spectrometry (LC-DAD-MS) and head space-solid phase micro extraction coupled to gas chromatography - mass spectrometry (HS-SPME/GC-MS) were utilized to analyze Pericarpium Citri Reticulatae. Faced with the time-shifts in two-dimensional (2D) matrices across different samples, three algorithms were developed to synchronize them. Furthermore, bilinear and trilinear models were used to realize the quantifications with different principles. Through real cases based on LC-DAD, the advantages and disadvantages of trilinear decomposition over multivariate curve resolution-alternating least-squares can be clarified in the quantification of raw or synchronized fingerprints. Also in the data processing, a modification version of multi-scale peak alignment (^mMSPA) was proved to be more suitable for trilinearity restoring than the other two algorithms. Recognizing these facts, restoring trilinearity were developed for more robust modeling in the application of the Pericarpium Citri Reticulatae fingerprints from different storage periods. After effective analysis, the upward/downward trend of 13 flavonoids were drawn accurately; and several flavour components having the highest contribution rate during storage were outlined reasonably. In conclusion, more robust modeling can be realized in trilinear data synchronized by appropriate algorithms, leading to an accurate quantification in herbal quality researches.

Graphical abstract

Trilinearity restoring; Advanced modeling; Fingerprints; Pericarpium Citri Reticulatae; Storage.

1. Introduction

Storage is an important factor affecting the quality of functional food or herbs [1, 2], such as Pericarpium Citri Reticulatae (Chenpi in mandarin) [3, 4]. The significant differences might be taken place in fingerprints of Pericarpium Citri Reticulatae with different periods [5, 6]. A nondestructive approach has been developed for the rapid classification of different-age Citri Reticulatae Pericarpium using near infrared device [7]. Moreover, other scientific instruments should be utilized to investigate the molecular variations under cover. Presently, second-order analytical instruments have been widely used in the qualitative and quantitative analysis of different species of Pericarpium Citri Reticulatae, such as gas chromatography (GC) combined with mass spectrometry (MS) [8], and liquid chromatography (LC) coupled to diode array detector (DAD) or mass spectrometry (MS) [9]. Nevertheless, multiple scenes with interference are usually observed in the second-order tensor (matrix) for each sample. Thus, multivariate curve resolution and multi-way calibration methodologies [10] should be developed to realize the goals of green and effective analysis in herbal analyse field. But it is worth noting that how to use the best parameters to perform the herbal quality control more efficiently is a core in the application of these methods.

Presently, there are two main solutions for qualitative and quantitative analysis of complex second-order data. Bilinear modeling of an augmented data matrix, such as multivariate curve resolution - alternating least-squares (MCR-ALS) [11], was extensively used to tackle problems about the mixture analysis. Compared with trilinear modeling, it has the advantage of allowing for varying elution-time profiles across samples, especially chromatographic data. To reduce the number of possible solutions, different kinds of constraints were proposed for curve resolution in chromatographic data-set, including non-negativity, unimodality, trilinearity, local rank constraints, and so on. It's worth noting that the use of the trilinearity constraint is considered as the best choice to limit rotation ambiguities (the main source of uncertainty). With such efforts, a correct recovery of the concentration and/or spectra profiles for all the different species can be more easily achieved in MCR-ALS algorithm. Trilinear modeling [12] of three-way data array, as an alternative, is often used for resolving true physical factors and obtaining unique solution. These methods include parallel factor analysis (PARAFAC) [3], alternating trilinear decomposition (ATLD) [13], and so on. It can be seen that both MCR modeling (trilinear-constraint) and trilinear modeling have good results as well as strict requirements for data structure.

In reality, various factors may occur in the process of herbal analysis, leading to subtle/serious differences among a series of outputs from the instrument. Usually the time shifts are usually observed in two-dimensional (2D) matrices across different samples, and they will keep the stacked data-array non-trilinear in herbal data analysis. As a response, MCR-ALS [14] and PARAFAC2 [15] have been used for non-trilinear second-order chromatographic data with non-reproducible elution time profiles, even ATLD [16] can also tolerate very slight time drifts. Another way to solve this problem is to develop synchronization in time-shift fingerprints [17, 18]. At Present, MCR-COW-MCR strategy does not solve the rotational ambiguity issues, and it artificially modifies the raw data without significant improvements in analytical performance [19, 20]. Mazivila etc performed three-way calibration using PARAFAC and MCR-ALS with previous synchronization of second-order chromatographic data through functional alignment of pure vectors (FAPV) [21]. There are many algorithms that can realize synchronization, such as modification version of multi-scale peak alignment (^mMSPA) [22], looping of correlation optimized warping (^LCOW) [23], looping of icoshift (^Licoshift) [24]. They should be discussed in detail, and the core idea can be obtained in the application to perform the herbal analysis more accurately.

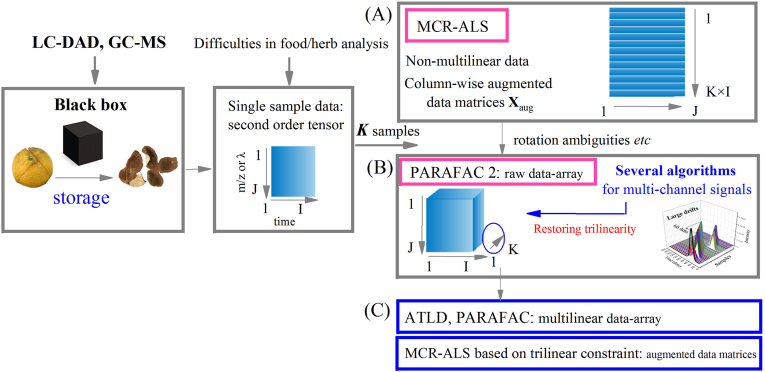
In this paper, three kinds of algorithms were initially developed for restoring trilinearity of the different second-order data. As shown in Figure 1, MCR-ALS (A), PARAFAC2 (B), ATLD and MCR-ALS (trilinear constraint) (C) were used for the quantitative analysis of raw or synchronized fingerprints, respectively. Then, more robust modeling was utilized to realize the quantitative analysis in real fingerprints from Pericarpium Citri Reticulate during storage periods.

Figure 1.

The interrelationship among (A) MCR-ALS model, (B) PARAFAC2 model, (C) MCR model (trilinear constraint) and ATLD model in Pericarpium Citri Reticulatae fingerprint researches.

2. Experimental

2.1. Materials and chemical reagents

The pericarps of Citrus reticulata 'Chachi' (Pericarpium Citri Reticulatae in this paper) were collected at a farm in Xinhui district (N 22°5′15″-22°35′01″, E 112°46′55″- 113°15′43″), Guangdong province. Activated carbon/polydimethylsiloxane/divinylbenzene fiber (40/60μm, CAR/PDMS/DVB) was purchased from Zhengzheng analytical instrument Co., Ltd. (Qingdao, China). HPLC grade n-hexane was purchased from Merk company (Merk, Germany); C₈–C₂₀, the standard of D-limonene were purchased from Sigma-Aldrich (St. Louis, Missouri, USA); Standards of Hesperidin (97%), Nobiletin (98%), Tangeretin (98%) were purchased from Chengdu Ruifensi biotechnology Co., Ltd. (Chengdu, China); Acetonitrile, Methanol and Formic acid were chromatographic grade, and other reagents were analytical pure.

2.2. LC-DAD-MS determination for flavonoids in Pericarpium Citri Reticulatae

2.2.1. Preparation of samples

Ten pericarp samples aged 3 months, ten samples aged 39 months, and other ten samples aged 63 months of period. In the begin 0.3 g of pericarps were weighed and mixed with 1mL Benzoic acid (1 mg/mL, IS) and 10mL Methanol. After ultrasound extraction for 30 min, the supernatant (filtered through 0.22 μm membrane) was diluted twice and subjected to LC analysis. For reference solution, the final concentration of Hesperidin, Nobiletin and Tangeretin were adjusted to appropriate ranges.

2.2.2. LC-DAD-MS determination

A RP-C₁₈ column (4.6 mm × 250 mm, 5 μm) was used to separate flavonoids in a LC-DAD-MS 8045 system (Shimadzu, Japan). The mobile phase was consisted of A (0.1% formic acid acetonitrile) and B (0.1% formic acid water). The gradient program: 0–12 min: 83% B-73% B; 12–24 min: 73% B-50% B; 24–29 min: 50 % B-30% B; 29–43 min: 30% B; 43–48 min: 30% B-83% B. The flow rate was 0.4mL/min and the injection volume was 5 μL. The DAD signals were acquired for each sample. The MS data were collected under positive ion mode, and 3 L min ⁻¹ of atomizer gas flow, 10 L min ⁻¹ of heater flow, 300 °C of interface temperature, 250 °C of DL temperature, 400 °C of heating block temperature and 10 L min ⁻¹ of flow rate of dry gas (N₂) were set. The mass range was set as m/z 100–1000 Da, and the collision energies were set to 15 V, 25 V and 35 V. LC-DAD-MS was measured in random order according to the sample number.

2.3. HS-SPME/GC-MS detection for flavors in Pericarpium Citri Reticulatae

2.3.1. Head space-solid phase micro extraction (HS-SPME)

Thirty pericarp samples (3 months, 39 months, 63 months of storage period) were preprocessed as follow: 0.1 g of Chenpi was added into a 20 mL bottle, and then the fiber was exposed at 50 °C for 40 min.

2.3.2. GC-MS analysis

HP-5MS (30 m × 0.25 mm i.d., film thickness 0.25 um, Agilent) was contained in Shimadzu GC-MS 2010 system (Kyoto, Japan). The HS-SPME fiber was desorbed in the injection port at a split ratio of 1:50 for 5 min. The temperature programme was as follow: 40 °C for 6 min, ascended to 90 °C at 4 °C/min, then increased to 140 °C at 10 ° C/min, finally raised to 280 °C at 25 °C/min for 1 min. The scanning range was 20–500 amu, the ionization energy was 70 eV, and the scanning interval was 0.50 s. The temperature of interface, injection and ion source were maintained at 260 °C, 250 °C and 200 °C, respectively.

2.4. Data processing and statistical analysis

The full spectral data were collected from LC-DAD or GC-MS apparatus at a certain frequency, and they were visualized in MZmine 2 software. The raw data can be transformed into mat file in which each data point is recorded in a matrix (retention time versus response values). Then ^mMSPA [22], ^LCOW [23], ^Licoshift [24], MCR-ALS GUI 2.0 [11,14] and ATLD algorithms [12] worked under MATLAB environment, and their theories was written in detail (Supporting Material). At last, libPLS software was used for the multivariate statistical analysis of the data sets.

3. Result and discussion

3.1. Building trilinear-structure for LC-DAD matrices with slight misalignment

3.1.1. LC-DAD-MS/MS determination for Pericarpium Citri Reticulatae samples

Pericarpium Citri Reticulatae is regarded as having the effect of regulating qi - strengthening spleen (‘Liqi-Jianpi’ in mandarin) and drying dampness - resolving phlegm (‘Zaoshi-Huatan’ in mandarin) after a storage period of 3 years or more. Especially, the aged peel of Citrus reticulata 'Chachi' species is deemed as ‘Daodi’ material with stronger activities. In this research, the peels of Citrus reticulata 'Chachi' were collected as the Pericarpium Citri Reticulatae samples. Due to the previous researches on Citri varieties [25, 26], LC-DAD-MS/MS test was successfully carried out for the known flavone molecules with pharmacological activities in this test. As a result, a good separation performance of Hesperidin, Nobiletin, Tangeretin and unknown peaks was observed in test chromatogram. It is well known that ultraviolet spectrum is not enough to distinguish specific structures of unassigned peaks. Thus herbal scientists need resort to mass spectrum with a set of mass peaks, which is the fingerprint of a small molecule. The procedure is as follows: 1) an in-house database was built for the chemical information of all known flavone molecules in citrus species; 2) adducts of molecular ions were searched against hundreds of structures in an in-house database; 3) experimental MS/MS fragments were utilized to deduct/confirm the target molecules. At last, the peak annotations of ten flavonoids were displayed in Tab S1 (Supplemental Material).

3.1.2. The quantity comparison of bilinear/trilinear modelings

In this section, the researchers quantified each analyte using bilinear or trilinear -decomposition based models. To compare their characteristics, the different cases were illustrated for the two approaches in this section. The first example: different concentrations (0.34 mg/mL and 0.19 mg/mL) of Hesperidin were used to produce 26 simulation matrices with large time-drifts (artificial). Then, an augmented matrix of recorded data over time D_aug (IK× J) and a three-way data array X (I×J×K) were build in Fig. S1 (A) and (B) (Supplemental Material), respectively. As Fig. S1 (C) showed, a good quantification was realized for augmented matrix by MCR-ALS algorithm. That is to say, bilinear modeling can extract the information of the pure analytes through a decomposition of data matrix D_aug into the produce of an elution curves matrix C_aug and a spectral profiles matrix S^T (Supplemental Material). In this case, I, J and K, represent the number of elution points, the number of spectral channels and the number of samples. ATLD is known to be effective in second-order/three way chromatographic data with very slight time shifts. In this process, a three-way data array X (I×J×K) can be decomposed into the elution curve, spectral profile and concentration matrices (A, B and C) (Supplemental Material). Nevertheless, there is no solution for the stacked chromatographic data with large time-drifts. As observed in Fig. S1 (C), a large deviation were observed in the modeling due to trilinear breaking mode (raw data). To make up for this defect, the 26 matrices were synchronized and stacked into a trilinear structure. As observed in Fig. S1 (C), the prediction values of ATLD were stabilized again at 102.0 % and 101.5% of the real values for two kinds of synchronized matrices. In other words, only the data-array with strict trilinearity can be decomposed by trilinear model accurately.

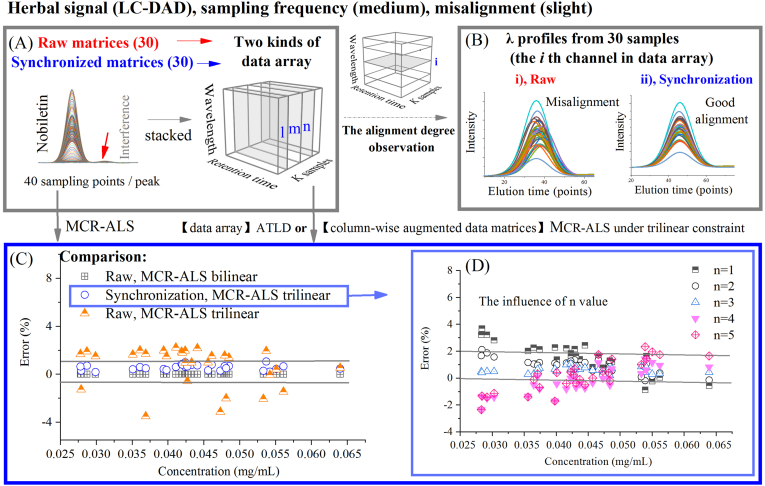
Is there any difference between bilinear decomposition (raw matrices) and trilinear modeling (synchronized matrices) for real LC-DAD data? As shown in Figure 2 (A), the 30 matrices of Nobiletin (37.4–38.4 min) with slight drifts were taken as an example. After the ^mMSPA treatment, the synchronized matrices were reconstructed into another trilinear structure. Because of an overall movement, the linearity observation is mainly considered from a newly assembled side. Here, the alignment of λ profiles from 30 samples (the i th channel in cube) were utilized to evaluate the synchronization. It can be clearly observed from Figure 2 (B) that slight misalignment is observed in a raw slice, while a precise alignment is embodied in a synchronized slice. To better illustrate the trilinearity restoring, MCR models were proposed in a comparison between several approaches with/without trilinear constraint. In this step, the data structure was initially transformed into an augmented data matrix for a further decomposition. As observed from Figure 2 (C), MCR (trilinear-constraint) modeling (blue circles) is satisfactory in the synchronized structure, which is similar to bilinear modeling (grey square) in the raw data. That is to say, the ^mMSPA algorithm doesn't produce harmful effect on peak shape (area), and it is reliable for the restoring of trilinear structure. As seen from Figure 2 (C), a biased prediction (yellow triangles) was inevitably appeared in a trilinear modeling with trilinear breaking mode. It is easy to understand why the researchers often choose an appropriate model to obtain the satisfactory results. In other words, a trilinear structure must be constructed to accommodate trilinear modeling or MCR modeling (trilinearity constraint). The number of components should also be noted, and should be set reasonably in this MCR model. As observed in Figure 2 (D), the errors will be increased significantly using unreasonable n values (n > 4 or n = 1).

Figure 2.

LC-DAD fingerprints of Pericarpium Citri Reticulatae were taken as an example. (A)The 30 raw matrices and the 30 synchronized matrices of Nobiletin (37.4–38.4 min) were reconstructed into another cubes, respectively; (B) The alignment of λ profiles from 30 samples (the i th channel in cube) were utilized to evaluate the synchronization; (C) The comparison results of MCR-ALS bilinear and MCR-ALS trilinear in different matrices, respectively; (D) The influence of n values on the decomposition results.

3.1.3. The necessity of building trilinear structure for LC-DAD data processing

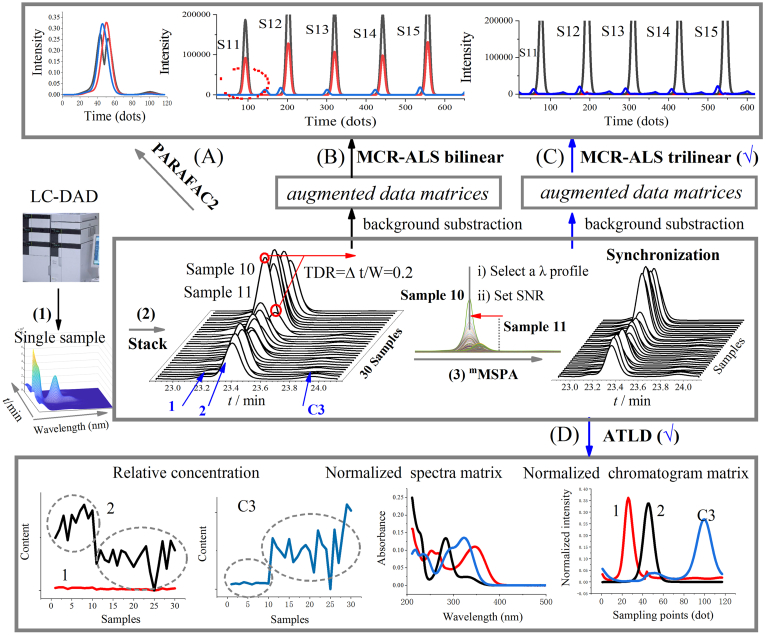
PARAFAC2 and MCR modelings are most widely used for the non-multilinear data. Why should we develop other models requiring more constraints in synchronized data? The main reasons are as follow, the flexible modeling may bring shortcomings. For example, the bilinear modeling is usually require appropriate initial values and restricted by rotation ambiguities. Taking a section of 22.9–24.1 min as an example, the elution profiles are not constant across samples. To obtain more effective analysis, the different modelings of three components (1, 2 and C3) was described in details. (1) PARAFAC2 model was developed for a raw data-array (stacked by thirty matrices), while the result was disappointing in Figure 3 (A). (2) A bilinear decomposition based on MCR modeling was used for a column-wise augmented data matrix (thirty samples), and an imperfect decomposition was observed from red circle in Figure 3 (B). Therefore, this peak-cluster will only resort to MCR model (trilinear constraint) or ATLD model for a perfect resolution. Worse still, the trilinear deviation ratio (TDR) of 0.2 supposed that time shifts may destroy the trilinear structure required in the desired modeling. It meant that the trilinear decomposition does not provide accurate quantitative curves with chemical significance. Therefore, ^mMSPA was utilized to perform a synchronization for multi-channel signals from 30 samples. The 10th sample was set as a reference, and others were deemed as samples to be aligned in the procedure. In this case, a curve of 270 nm was selected as representative profile, and 20 of SNR was set to ensure the detection of peak 2 by Haar CWT. After a synchronization, peak shape can maintain the original state to the maximum extent. (1) Subjected to data rearrangement, a column-wise augmented data matrix was then analyzed by MCR (trilinear-constraint) in Figure 3 (C). Unsurprisingly, the quantitative and qualitative information was accurately calculated even in the presence of overlapped structure (1 and 2). (2) Subjected to data superpose, a data array was further analyzed by trilinear modeling. As observed in Figure 3 (D), normalized chromatogram matrix, normalized spectra matrix and relative concentration matrix can be decomposed by ATLD algorithm. Notably, baseline effects in experimental data can be easily modeled and removed from the scene; and it is not required to correct baseline and to subtract background in raw data. More importantly, the relative concentrations of peak 1, peak 2 and peak C3 were calculated for 30 samples directly. The first ten samples are dried pericarps (3 months), and the last twenty samples are Pericarpium Citri Reticulatae (39, 63 months), respectively. That is, 1 (Diosimin) and 2 (Hesperidin) show a downward trend, whereas C3 (unknown compound) presents an upward trend from pericarps to Pericarpium Citri Reticulatae.

Figure 3.

LC-DAD fingerprints of Pericarpium Citri Reticulatae was used to exemplify the advantages and disadvantages of (A) PARAFAC2 model, (B) MCR-ALS bilinear, (C) ^mMSPA-MCR-ALS trilinear and (D) ^mMSPA-ATLD algorithms. 1: Diosimin; 2: Hesperidin; C3: unknown compound.

3.1.4. Decomposition on LC-DAD data of Pericarpium Citri Reticulatae

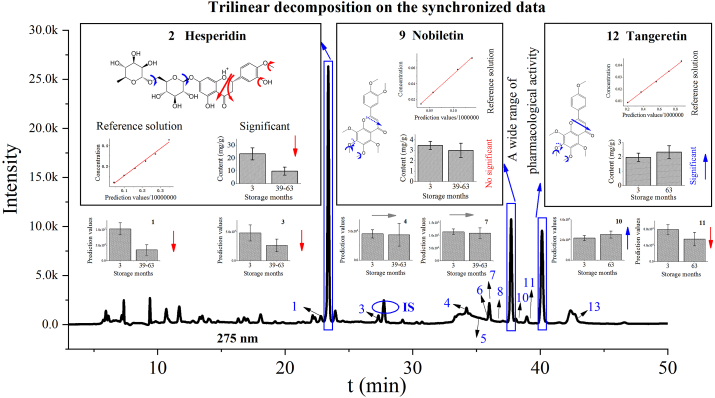
It is a good method that trilinear models can realize the goals of the simultaneous qualitative and quantitative analysis. Initially the LC-DAD fingerprints were normalized, referring to the area of internal standard (IS) peaks. Then the different sample data were stacked into a data-array, and divided into many sub-arrays along the retention time mode. It is important to note that there are less than 5 analytes of interest in each sub-array. After ^mMSPA synchronization, a successful trilinear decomposition can be developed for the target sub-array. In terms of methodology, the three standard curves (trilinear prediction vs real concentration) possessed good linearity for Hesperidin, Nobiletin and Tangeretin. Also the within-day variances, between-day variances and recovery test met the requirements. As a result, the differences of component between dried pericarps (3 months) and Pericarpium Citri Reticulatae (39, 63 months) were displayed for 13 flavonoids in Figure 4. In summary, the contents of Diosmin, Hesperidin and Poncirin decreased significantly after 3–5 years. These flavonoid glycosides may be converted into other compounds during storage, resulting in a decrease trend. On contrary, the contents of 4’, 5,7,8-tetramethoxyflavone and Tangeretin did not change significantly after 3 years of storage, but increased slowly after 5 years storage. In the literature, Tangeretin is deemed as an important active ingredient in Pericarpium Citri Reticulatae. In addition, the contents of Isosinensetin, 5,6,7,4 ′- tetramethoxyflavone and Nobiletin did not change significantly after 3–5 years storage. That is to say, only small changes are taken place in the contents of polymethoxyflavones during storage period.

Figure 4.

The advanced modeling in the synchronized LC-DAD fingerprints of flavonoids from 30 samples. 1: Diosimin; 2: Hesperidin; 3: Poncirin; 4: Isosinensetin; 5:5,7,3′,4′-tetramethoxyflavone; 6: Sinensetin; 7: 5,6,7,4′-tetramethoxyflavone; 8: 5,6,7,8,3′,4′-hexamethoxyflavanone; 9: Nobiletin; 10:4′,5,7,8-tetramethoxyflavone; 11:3,5,6,7,8,3′,4′-heptamethoxyflavone; 12:Tangeretin; 13: 5-hydroxy-6,7,8,3′,4′-pentamethoxyflavone.

3.2. Building trilinear-structure for GC-MS matrices with serious misalignment

3.2.1. HS-SPME/GC-MS test for Pericarpium Citri Reticulatae samples

Electronic nose responses of 18 sensors have been used for the distinction between Pericarpium Citri Reticulatae species [27]. Furthermore, the delicate/herbal fragrances produced in the Pericarpium Citri Reticulatae with 3–5 storage years, should also be investigated in detail.

As we all know, flavor sense is embodied in each volatile odorous compound with different contribution degree. It seems that a significant difference was taken place in the component proportion from the samples at different stages. So the volatile odorous compounds were determined both in dried pericarps (3 months) and Pericarpium Citri Reticulatae (39, 63 months) by HS-SPME/GC-MS. In terms of flavors preparation, HS-SPME has the advantages of easy operation and high selectivity, and it can reduce the oxidation, degradation and other reactions of flavor components. Relying on the property of CAR/PDMS/DVB fiber, a strong enrichment effect on volatile odorous compounds of Citrus was observed in GC-MS data (Fig. S2, Supplementary Material). The similarity searching in a NIST 14 library and retention indices (RIs) confirmation with a collection (https://webbook.nist.gov/chemistry/) have become a qualitative solution. The resulting 49 components were displayed in Tab S2 (Supplementary Material), and they are mainly composed of terpenes, alcohols, esters and aldehydes. Among them, D-Limonene, γ-Terpinene, Methyl methylthranilate, O-cymene and α- Farnesene are the main components of volatile odorous compounds in Pericarpium Citri Reticulatae. The first three components were accounted for 37.23%, 10.28% and 12.61% of the total peak area, respectively. The differences between HS-SPME and steam distillation were also compared in the GC-MS determination. Taking the dried pericarps (3 months) as an example, a total of 54 components were identified by the two methods, of which 12 common components were odorous terpenoids in Tab S2 (Supplementary Material). As shown in the results, the types of compounds adsorbed by HS-SPME are far more than those extracted by SD, but 5 compounds (3-Thujene, β-Phellandrene, β-cis-Ocimene, Terpinolene and Terpinen-4-ol) are only detected in SD product.

3.2.2. Building trilinear structure for the shape-unchanging matrices

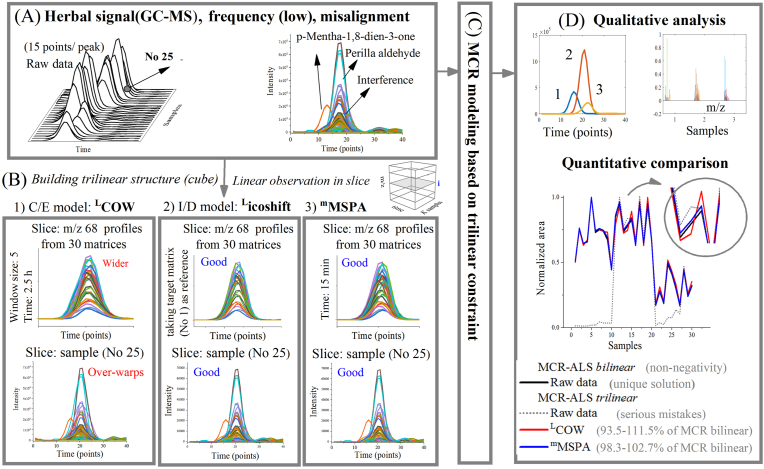
The unknown interference and backgrounds were commonly emerged in the multi-component odor mixture. Faced with the co-eluted peaks, chemometric algorithms were utilized to achieve qualitative/quantitative analysis of interested components in complex samples. At present, MCR modeling (trilinear constraint) and ATLD modeling have been proven effective in resolving the distorted peaks. As an example in Figure 5 (A), a serious misalignment is shown in the segments of 20.8–21.2 min (15 dots/peak, unchanged shape) from 30 samples. In order to obtain a strict trilinear structure, ^LCOW, ^Licoshift and ^mMSPA algorithms were used to synchronize the GC-MS matrices, respectively. As observed in Figure 5 (B), ^LCOW algorithm (C/E model) can ignite a peak-shape change and appear to be time-consuming. The reason is that COW alters the original pair of signals by selectively contracting and expanding the time axes to minimize the distance between them. It usually aligns the signal accurately, and also cause the changes in the peak shape or others in this way. Nevertheless, this change is bound to cause errors in the subsequent quantitative results. Also the researchers used variable penalty dynamic time warping (VPdtw, R language) based on the full signals. In this algorithm, nondiagonal moves are penalized to reduce the number of artificial features in the aligned signals. The pity is that it requires full signals and produces excessive numbers of N/A value. From three kinds of models, the second ^Licoshift (I/D model) and the third ^mMSPA (based on peak detection) were further introduced in the 30 matrices. The results showed that their synchronizations are much faster than that of ^LCOW algorithm here. As observed in Figure 5 (B), the slice of m/z 68 was used to observe the linearity of 30 matrices from the newly assembled side. The sample matrix (No 25) was utilized to check whether the raw data structure (other side of the cube) is damaged. It is glad to observe that two set of slices are both good in the synchronized cubes. But it should also be pointed out that minor misalignment will be observed in weak peaks with a small number of sampling points. That is, because two methods both rely on an efficient fast Fourier transform based computation, and the number of sampling points will affect the quality of synchronization. Just like m/z 161 profiles (slice) in Fig. S3 (A) (Supplemental Material), a slight deviation of can be observed in 30 matrices. Howbeit in Fig. S3 (B), linear interpolation and smoothness may keep the detection errors improved greatly.

Figure 5.

(A) The segments of 20.8–21.2 min (GC-MS, unchanged shape) from 30 Pericarpium Citri Reticulatae samples; (B) ^LCOW, ^Licoshift and ^mMSPA algorithms were used to synchronize the 30 matrices, and the m/z 68 profiles (the i th channel in cube) were utilized to evaluate the synchronization; (C) MCR modeling (trilinear constraint) in the different data array; (D) The quantitative comparison between MCR modeling and MCR modeling (trilinear constraint) in different matrices.

Based on the above data, the qualitative/quantitative profile matrices were then obtained through MCR modeling (trilinear constraint), such as elution-time profiles and mass spectra matrices. As seen in Figure 5 (D), the quantitative comparison was further made for three sets of synchronized data. It was found that a unique solution (gray line) can be obtained from bilinear modeling in the non-multilinear data. Nevertheless the negative result (dotted line) was presented for MCR modeling (trilinear constraint) in raw data. This contrast meant that trilinear structure is the pre-condition to a successful three-way calibration. The next step is to try ^mMSPA and ^LCOW data, and the expected results appeared in the restored structure. That is, ^mMSPA group (98.3–102.7% of MCR bilinear) is significantly better than ^LCOW group (93.5–111.5% of MCR bilinear). In other words, ^mMSPA is more suitable for the sub-matrices (unchanged shape). Howbeit, the ^LCOW algorithm can initiate the changes in the peak shape, leading to the next quantitative errors.

3.2.3. Building trilinear structure for the shape-changing matrices

In the previous studies (Figure 5 A), a trilinear structure is easily maintained for 30 sub-matrices by ^mMSPA algorithm. Even for a complex peak-cluster, the sub-matrices can also be successfully synchronized in a good experimental environment. An example is observed in Fig. S4 (A) that five compounds are overlapped in a segment of 13–14.4 min from LC-DAD signals (Supplemental Material). Faced with the complex structure, ^mMSPA algorithm was successfully developed to synchronize 30 sub-matrices in Fig. S4 (B). Finally, a trilinear decomposition can be realized in Fig. S4 (C), and their variation trends can be observed.

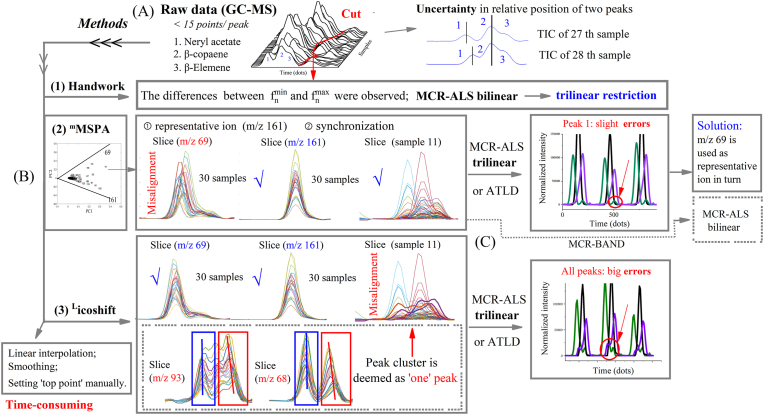
Only limited high-quality data can be obtained in real world, and the researchers often have to face imperfect data. As illustrated in Figure 6 (A), one peak-cluster (23.27 min) of HS-SPME/GC-MS data from Pericarpium Citri Reticulatae was taken as an example. There are three overlapping compounds with large drift in 30 sub-matrices, namely Neryl acetate, β-Copaene and β-Elemene. What's worse, the positional uncertainty (peak 1 and peak 2) was appeared in several matrices. In Figure 6 (A), the distance difference between the two peaks can be observed from the 27th/28th samples clearly. How to perform the qualitative and quantitative analysis of the overlapping system? The first is to use bilinear decomposition of MCR-ALS with non-negativity/unimodality constraints, and it allows modeling non-multilinear data in chromatographic experiments. Nevertheless the differences between ${\text{f}}_n^{\min }$ and ${\text{f}}_n^{\max }$ in MCR-BANDS program represent the rotation ambiguities associated to MCR solutions. In other words, a set of different solutions can fit the experimental data, and they are not real solution. To obtain the satisfied values, the use of the trilinearity constraint in the simultaneous analysis of multiple data sets is the best choice to eliminate this type of ambiguity.

Figure 6.

(A) The distance difference between the two peaks can be observed in the peak-cluster (23.27 min, GC-MS) from the 27 th/28 th samples; (B) The synchronization comparisons of handwork, ^mMSPA and ^Licoshift algorithms; (C) MCR (trilinear constraint) modeling or ATLD modeling in the different data matrices (array), respectively.

Briefly, a strict trilinear structure should be established for the thirty matrices before MCR modeling (trilinear constraint) or ATLD modeling. It is worth reminding that there are several trilinear conditions, e.g. peak shape, retention time. When one or both of them are not met, the data-array superimposed by thirty matrices would sink into breaking modes. In this research, ^mMSPA algorithms were firstly used to synchronize 30 sub-matrices in Figure 6 (B). The key step, representative profile (m/z 161) was sought to calculate the optimal drift, and the overall movement of 30 matrices was realized in ^mMSPA algorithm. That is, it realized the synchronization of m/z profiles from peak 2/peak 3. What's more, it maintained the initial structure of each sample data using the overall movement. Due to this reason, m/z profiles from peak 1 (e.g. m/z 69) were misaligned that the distance deviations were present in the two peaks. As a result, the concentration matrices and spectral matrices of peak 2 (peak 3) could be successfully decomposed by ATLD or MCR model requiring trilinear structures in Figure 6 (C). How to conduct qualitative and quantitative analysis when facing peak 1? As an alternative, representative ion (m/z 69) was selected to synchronize the 30 matrices, and disclose the hidden information of peak 1. That is to say, the researchers can select representative profiles (m/z or λ) to quantify the specific target compound. In addition, if the MCR-BAND test of the synchronized matrices is recovered to normal, the researchers can also use bilinear modeling in an augmentation data matrix.

As an alternative, ^Licoshift was utilized to realize a simultaneous synchronization of multiple peaks in Figure 6 (B). It uses a piece-wise linear correction function based on I/D model, and achieve its ultimate goal. In this test, the different m/z profiles were used to observe the linearity of 30 matrices from the assembled sides in cubes. As can be seen from Figure 6 (B), both slice (profiles) of m/z 69 and slice (profiles) of m/z 161 were aligned in 30 matrices. The pity of it was that slight misalignment was observed in sample slice (No 11), a certain side in cube. Why is there such a thing? For one thing, only one peak top (blue zone) is recognized in peak cluster to be aligned with other samples, e.g, profiles of m/z 93, curves of m/z 68 in Figure 6; another reason is that the deviations is usually occurred in the peak detection of coarse peaks with few sampling-points. Whatever happens, the assembled data was further subjected to a MCR modeling (trilinear constraint). As observed in Figure 6 (C), the result is quite contrary to previous hypothesis, and the apparent errors were observed in all three peaks. In this respect, ^mMSPA is better than ^Licoshift algorithm.

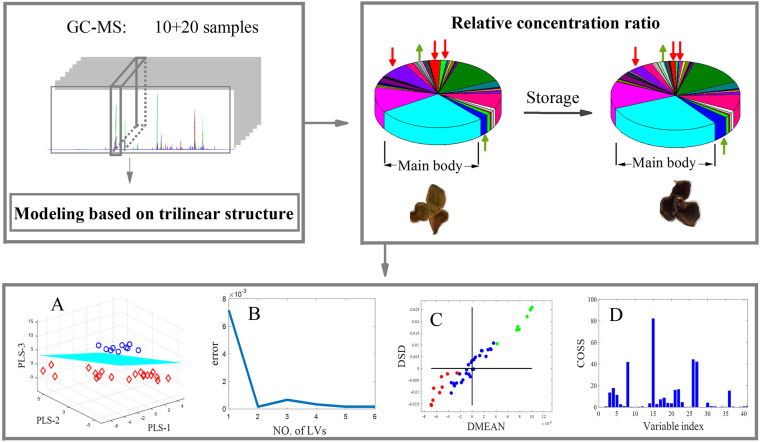
3.2.4. Decomposition on HS-SPME/GC-MS data of Pericarpium Citri Reticulatae

To maintain a strict trilinear structure, ^mMSPA algorithm was introduced to perform synchronization. Then the assembled data were used to achieve the quantitative curves (sample to sample) matrix by trilinear decomposition. As observed from Tab S3 (Supplementary Material), chemical conversion of some terpenes, alcohols and aldehydes must be taken place in storage period. These compounds will display a unique fragrance in a certain proportion at a specific storage period. Due to high content, Limonene was considered to be a great impact on the overall aroma degree, and exert in-apparent change during the 3–5 years of aging. Nevertheless, trans-Sabinene hydrate, cis-Sabinene hydrate, α-Terpineol, cis-Citral, p-Mentha-1,8-dien-3-one, (+)-, Thymol and Antioxine, showed a downward trend. While o-Cymene, p-Cymen-8-ol, cis-Carveol and Citronellol acetate showed an upward trend. In Figure 7, the relative percentage content in fresh pericarps (10 samples)/aged pericarps (20 samples) were then used for PLS-DA modeling [28]. In Figure 7 (A), 30 samples are divided into two categories through a PLS-DA score chart. No outlier values were found, 10 points of dried pericarps (3 months) are gathered in the upper area, whereas 20 points of Pericarpium Citri Reticulatae are gathered in the lower area. As shown in Figure 7 (B), the reliability of PLS-DA model was verified by monte carlo cross validation (MCCV). As observed in Figure 7 (C), phase diagram algorithm (PHADIA) was calculated to find out the key variables affecting fresh pericarps and Pericarpium Citri Reticulatae. Next, subwindow permutation analysis and random frog were used to detect which characteristics had the biggest contribution on the flavors formation of Pericarpium Citri Reticulatae. In Figure 7 (D), the odorous components such as Sabinene hydrate, Antioxine, α-Terpineol and Thymol can be judged as having the highest contribution rate. Although the contents of these components are low, their flavors are considered to be closely involved in the aging procedures.

Figure 7.

The relative content of volatile components were determined by HS-SPME/GC-MS, and their changes between fresh pericarps and old-aged samples were observed. (A) PLS-DA score chart; (B) Monte carlo cross validation; (C) and (D) PHADIA, subwindow permutation analysis and random frog were used to find out the key variables.

4. Conclusion

This paper proposed the necessity of the advanced modeling in Pericarpium Citri Reticulate fingerprints clearly. In some cases, the advantage of trilinear data over the non-trilinear data was proved to achieve more robust calibration models. Nevertheless, it is worth noting that how to restore trilinearity in second-order data by a series of algorithms. The comparison of three algorithms (^LCOW, ^Licoshift, ^mMSPA) showed that their respective characteristics (advantages and disadvantages) are the core of advanced modeling of herbal fingerprints. For example, the ^mMSPA algorithm doesn't produce harmful effect on peak shape (area), and it is reliable for the restoring of trilinear structure. The pity is that all substances cannot be aligned at the same time in the shape-changing matrices. Nevertheless it can also reduce the serious drifts across the different sample data, which is the main cause of MCR error. Facing with this problem, the researchers can resort to other solutions in the quality control of Chinese medicines, e.g, the quantification of target compound (s). Recognizing these facts, trilinear structures were built to be suitable for more robust calibration models in LC-DAD or GC-MS data-sets. Therefore, multiple scenes with different unknown interference were disclosed in this test. Even for those examples with rotation ambiguities in bilinear MCR, more obvious advantages are embodied in the synchronized structure. Furthermore, as an application example, the downward or upward trend was disclosed for the flavone glycoside and polymethoxyflavones from Pericarpium Citri Reticulatae. Also, Sabinene hydrate, Antioxine, α-Terpineol and Thymol were judged as the flavors with large contribution during 3–5 years of storage period. By and large, more effective analysis can be made from MCR modeling (trilinear constraint) or trilinear modeling in qualitative/quantitative data from herbal quality researches.

Declarations

Author contribution statement

Yaping Li: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Qing Cao: Performed the experiments; Analyzed and interpreted the data.

Min He: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.

Xinyue Yang, Pingping Zeng: Analyzed and interpreted the data.

Weiguo Cao: Analyzed and interpreted the data; Contributed reagents, materials and analysis tools.

Funding statement

This work was supported by Hunan 2011 Collaborative Innovation Center of Chemical Engineering & Technology with Environmental Benignity and Effective Resource Utilization, Hunan Province Natural Science Fund (no. 2020JJ4569), the key project of Hunan Provincial Education Department (no. 18A055), the Open Research Funding of Chongqing Key Laboratory of Traditional Chinese Medicine for Prevention and Cure of Metabolic Diseases (no. 2021-1-4) and Hunan Province College Students' innovation and entrepreneurship training program (no.S202110530044).

Data availability statement

Data included in article/supplementary material/referenced in article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix A. Supplementary data

The following is the supplementary data related to this article: