Improving global gross primary productivity estimation by fusing multi-source data products

Abstract

A reliable estimate of the gross primary productivity (GPP) of terrestrial vegetation is essential for both making decisions to address global climate change and understanding the global carbon balance. The lack of consistency in global terrestrial GPP estimates across various products leads to great uncertainty. In this study, we improve the quantification of global gross primary productivity by integrating multiple source GPP products without using any prior knowledge through the Bayesian-based Three-Cornered Hat (BTCH) method to generate a new weighted GPP data set. The fusion results demonstrate the superiority of weighted GPP, which greatly reduces the random error of individual datasets and fully takes advantage of the characteristics of multi-source data products. The weighted dataset can largely reproduce the interannual variation of regional GPP. Overall, the merging scheme based on the BTCH method can effectively generate a new GPP dataset that integrates information from multiple products and provides new ideas for GPP estimation on a global scale.

Gross primary productivity; Bayesian-based three-cornered hat; Multi-source; Validation.

1. Introduction

The total energy for the synthesis organic carbon fixed by vegetation through photosynthesis within a certain area over a given timeframe is called gross primary productivity (GPP) (Gebremichael and Barros, 2006; Zhang et al., 2009). GPP is the largest CO₂ flux component in the ecosystems, acts as a driver of terrestrial ecosystem functions, and plays a pivotal role in the global carbon cycle (Damm et al., 2010; Guo et al., 2020; Wang et al., 2021a; Zhang et al., 2020). With climate change intensifying, the response of terrestrial carbon balance is the great uncertainty affecting the prediction of future climate change, so the estimation of GPP is a central part (Arneth et al., 2010; Friedlingstein et al., 2006). The available regional or global GPP data products rely on assumptions since the targeted measurement of GPP is limited to the leaf level (Damm et al., 2010; Wright et al., 2013). Besides benchmarking is subject to significant uncertainty, leading to the global GPP distribution has not yet reached a consensus (Anav et al., 2015; Parazoo et al., 2014). The reliable methods for indirect estimation of GPP at the ecosystem level with eddy covariance technique through different algorithms depends on the measuring flux tower observations (Baldocchi et al., 2001; Friend et al., 2007). However, the flux sites are sparsely distributed, and the coverage period is different and limited (Jung et al., 2020). Hence, various approaches have been developed to estimate the global GPP values (Chen, 2019; Pei et al., 2020; Yao et al., 2018).

The existing GPP data products can be divided into four main groupings: (1) According to the principle of the light use efficiency (LUE) (Potter et al., 1993; Running et al., 2004); (2) Estimating GPP by machine learning algorithms (ML) (Jung et al., 2019; Tramontana et al., 2015); (3) Using Eddy Covariance (EC) technique to obtain flux tower observations and scaling-up (Gu et al., 2013), Categories 1–3 can be categorized as data-driven models; (4) Utilizing Land surface models (LSM) or ecosystem models (Dunne et al., 2012; Gent et al., 2011; Sun et al., 2019). These products diverge in GPP estimates at different ecosystems and external environments and have advantages and disadvantages in various studies (Chen, 2019; Pei et al., 2020; Zheng et al., 2019). LUE products are good at detecting the spatial distribution pattern of GPP but usually perform poorly on seasonal GPP estimates and overestimate GPP under dry and cold conditions (Chen et al., 2012; Ryu et al., 2011; Wei et al., 2017; Yuan et al., 2012, 2014). While ML products are widely used for benchmarking, which are more dependent on the spatial representation of the flux sites (Anav et al., 2015; Jung et al., 2011). The larger bias in the estimation of the GPP product by scaling-up appears around sparse flux sites (Jung et al., 2020). LSM products are more consistent in spatial and temporal distributions and respond better to climate change, but have large uncertainties caused by various model parameters, input data, model structure (Anav et al., 2015; Bentsen et al., 2013; Williams et al., 2009).

Recent studies have continued to develop many new GPP data products, like using satellite observations of sun-induced chlorophyll fluorescence (SIF) to improve GPP estimates (Liu et al., 2017; Sun et al., 2018; Zhang et al., 2020). The links between SIF and GPP including the sensitivity of GPP against SIF are still being further explored (Ma et al., 2018; Wang et al., 2020, 2021c). Combining various GPP products through the multi-model averaged approach can generate improved GPP products with lower bias. Many studies have indicated that the estimations of GPP from the multi-model averaging approach are better than those of single models (Chen et al., 2019; Yuan et al., 2010). Traditionally, the multi-model averages as the best assessment results are shown in IPCC reports. Empirical evidence from various fields of modeling suggests that multi-model averages eliminating at least some of the bias of individual models can produce better predictions or get closer to observations (Alexandrov, 2020; Eyring et al., 2019; Ichii et al., 2010; Knutti et al., 2010).

The objective of this study is to adopt a new approach to combine the strengths of 45 GPP products without relying on any prior knowledge to produce an improved GPP dataset that achieves consensus on a relative majority of 45 GPP products. The Bayesian-based three-cornered hat (BTCH) method (He et al., 2020) is applied to integrate 45 sets of 4 different types of monthly GPP products into this long-term dataset called BTCH-GPP on the pixel scale, with a period of 1980–2018 and a spatial scale of 0.5°. And we evaluate the performance of the fused dataset in the spatial and interannual variability of GPP from several eddy covariance towers and discuss the effectiveness of the fusion method.

2. Data

2.1. 45 global GPP data sets

This study utilized 45 sets of mainstream global available GPP products, including 5 LUE products (Running et al., 2004; Zhao et al., 2005; Yuan et al., 2010; Madani et al., 2014; Li and Xiao, 2019; Zhang et al., 2017), 9 ML products (Jung et al., 2011, 2019), NGT (Kumar et al., 2016). LUE, ML, and NGT belong to the same category of data-driven models. We divided FLUXCOM GPP into a separate categories for machine learning to better present its features. And 29 LSM products (Running and Hunt, 1993; Oleson et al., 2010; Li et al., 2011; Post et al., 2001; Jain et al., 2013; Sitch et al., 2003; Krinner et al., 2005; Baker et al., 2008; Schaefer et al., 2009, 2008; Hayes et al., 2011; Peng et al., 2013; Zeng et al., 2005; Kato et al., 2013; Huang et al., 2011; Haverd et al., 2017; Lawrence et al., 2019; Tian et al., 2015; Albergel et al., 2017; Ekici et al., 2014; Jules, 1998; Smith et al., 2013; Keller et al., 2017; Zaehle and Friend, 2010; Goll et al., 2017; Woodward et al., 1995; A. B. Harper et al., 2016; Jiang and Ryu, 2016; Zhang et al., 2019) and CMIP6 (Tang et al., 2019). Specific information on each set of GPP data products can be found in Figure 1. To give the BTCH-GPP results a better chance of being optimal, we collected as many GPP products from different categories as possible. The 45 available sets of GPP products were utilized in the study to assimilate their advantages.

Figure 1.

The time periods used in this study of 45 GPP products and their spatiotemporal resolution and category.

2.2. Flux tower data

We marked the location of the EC towers with monthly values in the FLUXNET2015 dataset on the world map and then resampled it at a resolution of 0.5° using the nearest neighbor method. This study screened 140 eddy covariance flux towers (Table S1) worldwide for validation and they are consistent with the pixels of BTCH-GPP dataset. The monthly value data of these flux towers can be found in the FLUXNET2015 dataset (http://fluxnet.fluxdata.org/data/fluxnet2015-dataset/).

2.3. GOME-2 SIF

Monthly GMOE-2 SIF data from 2007 to 2018 are obtained from instruments onboard the EUMETSAT Metop-A satellite, and the data (Joiner et al., 2014) are publicly available. Earth radiation at the top of the atmosphere is captured by GOME-2 in the 715–758 nm spectrum, and the far red peak of the SIF emission at wavelengths around 740 nm was used to retrieve the SIF using a principal component analysis method including atmospheric absorption. the final SIF data were quality controlled to exclude the effects of heavy clouds and aggregated to monthly averages at a spatial resolution of 0.5°.

3. Methods

BTCH-GPP was to improve the estimation of GPP by integrating multi-source GPP products without using any prior knowledge. The long-term GPP product was integrated by 45 sets of GPP gridded products including five categories of LUE, ML, LSM, FLUXNET and CMIP.

3.1. Data processing

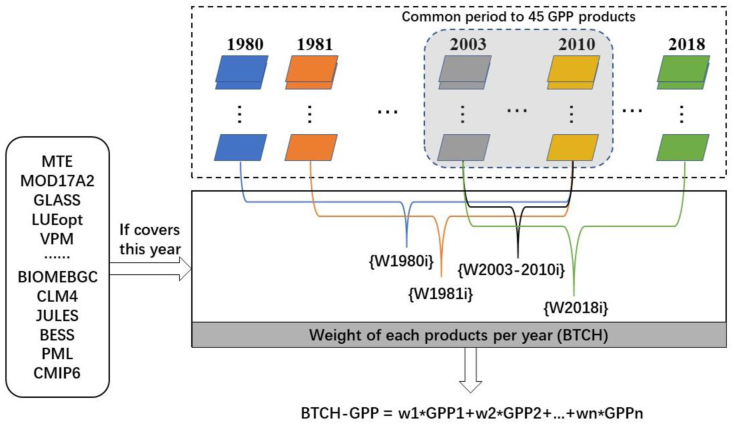
The 45 sets of GPP products collected were resampled to a spatial resolution of 0.5° and monthly GPP values were calculated for integration processing. We used the BTCH method calculate the GPP monthly value data on the pixel scale. The weights of the GPP products in the year from 1980 to 2002 and 2011 to 2018 are obtained (Figure 2). Weight was calculated for 2003–2010 due to the full coverage of 45 sets of GPP products. And the weight value for each year is calculated by extending that year to the common coverage years 2003–2010. For example, the weight for 1980 is calculated from the monthly value data of 1980–2010 containing GPP products for that year, using the BTCH method to derive the weight for each set of GPP products, while the weight for 2011 is calculated from the data for 2003–2011. The specific method for calculating the weights is detailed in 3.2.

Figure 2.

Flowchart showing the BTCH method for integrating 45 GPP products for 1980 to 2018.

3.2. Bayesian-based three-cornered hat (BTCH) method

Suppose there are N sets of GPP products ${\left\{GP{P}_i\right\}}_{i=\mathrm{1,2},\cdots ,N}$, $i$ corresponds to different GPP products (Gray and Allan, 1974; Tavella and Premoli, 1994). In this study, N = 45, that is, 45 GPP products. The time series of each product can be expressed as:

$$GP{P}_i=GP{P}_{\text{ture}}+{\epsilon }_i,\forall i=\mathrm{1,2},\cdots ,N$$ (1)

where $GP{P}_{\text{ture}}$ is the true value of GPP and ${\epsilon }_i$ is the error of the $i^{\text{th}}$ GPP product.

According to the Bayesian, if $GP{P}_{\text{ture}}$, ${\epsilon }_i$ and the error variance ${\mathrm{r}}_{\mathrm{i}}$ of the $i^{\text{th}}$ GPP product is known, the probability of the estimated value can be given by the Gaussian distribution.

$$P\left(GP{P}_i|GP{P}_{\text{ture}}\right)=\frac{1}{r_i\sqrt{2\pi }}\exp \left[-\frac{{\epsilon }_i^2}{2r_i^2}\right]=L\left(GP{P}_{\text{ture}}|GP{P}_i\right)$$ (2)

In the same way, the probability density function of the $j^{\text{th}}$ product can be shown as:

$$P\left(GP{P}_j|GP{P}_{\text{ture}}\right)=\frac{1}{r_j\sqrt{2\pi }}\exp \left[-\frac{{\epsilon }_j^2}{2r_j^2}\right]=L\left(GP{P}_{\text{ture}}|GP{P}_j\right)$$ (3)

The maximum likelihood function of $GP{P}_{\text{ture}}$ is the max value of the joint probability distribution of GPP products can be shown as:

$$\mathrm{maxL}\left(GP{P}_t|GP{P}_i,GP{P}_j\right)=P\left(GP{P}_i|GP{P}_{\text{ture}}\right)P\left(GP{P}_j|GP{P}_{\text{ture}}\right)=\frac{1}{2\pi r_i{r}_j}\exp \left[-\frac{{\epsilon }_i^2}{2r_i^2}-\frac{{\epsilon }_j^2}{2r_j^2}\right]$$ (4)

To obtain the maximum likelihood function value of $GP{P}_{\text{ture}}$, the cost function is defined as:

$$J\left(GP{P}_{\text{ture}}\right)=\frac{{\epsilon }_i^2}{2r_i^2}+\frac{{\epsilon }_j^2}{2r_j^2}=\frac{1}{2}\left[\frac{{\left(GP{P}_i-GP{P}_{\text{ture}}\right)}^2}{r_i^2}+\frac{{\left(GP{P}_j-GP{P}_{\text{ture}}\right)}^2}{r_j^2}\right]$$ (5)

If the first value of $J\left(GP{P}_{\text{ture}}\right)$ is set to 0, $J_0\left(GP{P}_{\text{ture}}\right)=0$, then:

$$GP{P}_{\text{ture}}=\frac{r_i^2}{r_i^2+r_j^2}GP{P}_i+\frac{r_j^2}{r_i^2+r_j^2}GP{P}_j$$ (6)

Define formula (6) as:

$$GP{P}_{\text{ture}}=w_{i}GP{P}_i+w_{j}GP{P}_j$$ (7)

where $w_i$ and $w_j$ are the weight values of different GPP products.

Extending to N sets of GPP products, the formula can be expressed as:

$$GP{P}_{\text{ture}}=w_{1}GP{P}_1+w_{2}GP{P}_2+\cdots +w_{N}GP{P}_N$$ (8)

The weight values of different products are defined as:

$$w_k=\frac{\prod _{i=1,i\ne k}^N{r}_i^2}{\sum _{k=1}^N\left(\prod _{i=1,i\ne k}^N{r}_i^2\right)}$$ (9)

$r_i^2$ in the formula is obtained by the three-cornered hat method (Premoli and Tavella, 1993; Sjoberg et al., 2021).

The time series of any product is selected as the reference since no true GPP values, and the difference series between the time series of the remaining GPP products and the reference product can be obtained as:

$$y_i=GP{P}_i-GP{P}_{\text{ref}}={\epsilon }_i-{\epsilon }_{\text{ref}},i=\mathrm{1,2},\cdots ,N-1$$ (10)

where $GP{P}_{\text{ref}}$ is an arbitrary GPP product as the reference. This study directly selected MTE-GPP as the reference to simplify the calculation. Store the N-1 difference sequence in the following matrix:

$$Y=\left[\begin{array}{llll}{y}_{11}\hfill & y_{12}\hfill & \cdots \hfill & y_{1\left(N-1\right)}\hfill \\ y_{21}\hfill & y_{22}\hfill & \cdots \hfill & y_{2\left(N-1\right)}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ y_{M1}\hfill & y_{M2}\hfill & \cdots \hfill & y_{M(N-1)}\hfill \end{array}\right]$$ (11)

where $M$ is the number of each product. The covariance matrix of the difference sequence can be expressed as:

$$S=\mathrm{cov}\left(Y\right)=\left[\begin{array}{llll}{s}_{11}\hfill & s_{12}\hfill & \cdots \hfill & s_{1\left(N-1\right)}\hfill \\ s_{21}\hfill & s_{22}\hfill & \cdots \hfill & s_{2\left(N-1\right)}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ s_{\left(N-1\right)1}\hfill & s_{\left(N-1\right)2}\hfill & \cdots \hfill & s_{\left(N-1\right)\left(N-1\right)}\hfill \end{array}\right]$$ (12)

where $\mathrm{cov}\left(\right)$ is the covariance operator, and $S\left(s_{i,j}\right)$ is the variance or covariance estimate between different GPP products and the reference product. Introduce the unknown $N\times N$ noise covariance matrix $R$ ($R$ is a symmetric matrix), and its relationship with $S$ can be defined as:

$$S=J\cdot R\cdot J^{\text{T}}$$ (13)

where $J$ and $R$ can be defined as:

$$J_{N-1,N}=\left[\begin{array}{lllll}1\hfill & 0\hfill & \cdots \hfill & 0\hfill & -1\hfill \\ 0\hfill & 1\hfill & \cdots \hfill & 0\hfill & -1\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill & ⋮\hfill \\ 0\hfill & 0\hfill & 0\hfill & \cdots \hfill & -1\hfill \end{array}\right]$$ (14)

$$R=\left[\begin{array}{llll}{r}_{11}\hfill & r_{12}\hfill & \cdots \hfill & r_{1N}\hfill \\ r_{12}\hfill & r_{22}\hfill & \cdots \hfill & r_{2N}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ r_{1N}\hfill & r_{2N}\hfill & \cdots \hfill & r_{NN}\hfill \end{array}\right]$$ (15)

From Eq. (13), the following relationship can be obtained:

$$r_{ij}=s_{ij}-r_{NN}+r_{iN}+r_{jN}$$ (16)

N unknown parameters (the number of elements in $R$) cannot be solved (5) for only N equations (the number of elements in $S$). The N free parameters need the positive definiteness of the covariance matrix $R$ ($\left|R\right|>0$) to obtain the solutions.

$$H_2\left(r_{1N},\cdots ,r_{NN}\right)=-\frac{H_1\left(r_{1N},\cdots ,r_{NN}\right)}{K}<0$$ (17)

Where $K=\sqrt[N-1]{\left|S\right|}$ is introduced to obtain the numerical solution and $H_1\left(r_{1N},\cdots ,r_{NN}\right)$ can be expressed as:

$$H_1\left(r_{1N},\cdots ,r_{NN}\right)=\frac{\left|R\right|}{\left|S\right|}=r_{NN}-\left[r_{1N}-r_{NN},\cdots r_{\left(N-1\right)N}-r_{NN}\right]S^{-1}{\left[r_{1N}-r_{NN},\cdots r_{\left(N-1\right)N}-r_{NN}\right]}^{\text{T}}$$ (18)

To obtain the unique solution of the free parameters, it is necessary to give the optimal standard. By minimizing the "Global relevance" of all products time series, the mean square value of the sum of squares of off-diagonal elements in the upper right or lower left corner of $R$ is introduced as:

$${\left[G\left(r_{iN}\right)\right]}^2=\frac{1}{N}\cdot \sum _{i<j}^N{r}_{ij}^2$$ (19)

The objective function can be expressed as:

$$F_1\left(r_{1N},\cdots ,r_{NN}\right)=\frac{1}{K^2}\cdot \sum _{i<j}^N{r}_{ij}^2$$ (20)

The initial value of the iterative calculation can be set as:

$$r_{iN}^0=0\left(i<N\right)$$ (21)

$$r_{NN}^0=\frac{1}{2s^{\ast }},s^{\ast }=\left[1,\cdots ,1\right]S^{-1}{\left[1,\cdots ,1\right]}^{\text{T}}$$ (22)

Minimize the objective function to obtain a set of free parameter solutions $r_{1N},\cdots ,r_{NN}$, which is the variance of the uncertainty of different GPP products.

3.3. Taylor diagram

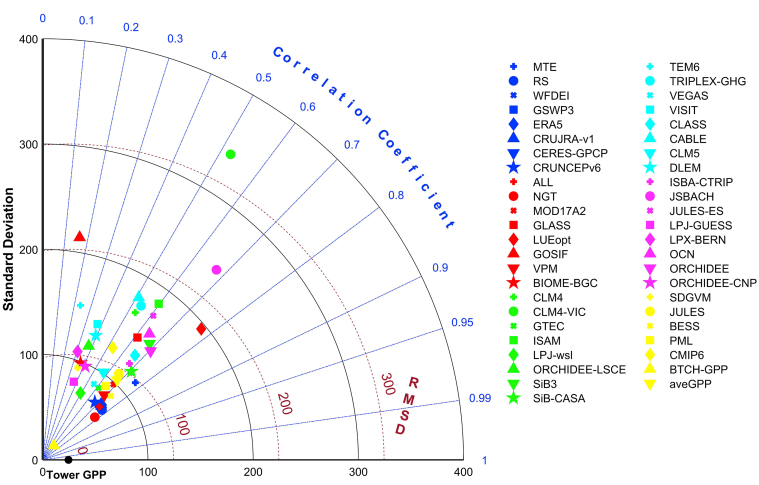
Taylor diagram was first proposed by Karl E. Taylor in 2001 (Taylor, 2001). In short, it is a diagram that can represent three indexes: standard deviation, centered root-mean-square error and correlation coefficient. It is commonly used for model evaluation and testing, comprehensively and clearly reflecting the multi-mode simulation capabilities. The scattered points in the Taylor diagram (Figure 3) represent the models, the radial line represents the correlation coefficient, the horizontal and vertical axis represents the standard deviation, and the dotted line represents the centered root-mean-square error.

Figure 3.

Taylor diagram (Schematic) (Taylor, 2001).

4. Results and discussion

4.1. The BTCH-GPP product

The global average GPP estimated by BTCH-GPP from 1980 to 2018 was 837.98 g C/m²/year (Figure 4). GPP is higher in forests near the equator, especially in areas where plenty of water and heat. This corresponds to the peaks of the annual GPP near the equator and 60°W. Medium-high GPP was found in temperate and semi-humid regions, while the value of GPP is lower in the areas with low temperatures and drought.

Figure 4.

Spatial pattern of annual total GPP and the latitude and longitude of the average throughout 1980 to 2018.

The trend analysis was used to calculate the global distribution pattern of long-term significant trends (p < 0.05) in GPP over the period 1980–2018 (Figure 5). Overall, BTCH-GPP shows an increasing trend in average annual GPP from 1980 to 2018. 86.05% of the vegetated areas (mainly located in the low to mid-latitudes in the Northern Hemisphere) showed a slightly increasing trend (less than 20 g C/m²/year). The GPP decline was found in northern South America as well as in the region near 60°N. The annual GPP in Oceania did not show much change (trends are concentrated between -5 and 5 g C/m²/year) during the entire study period. Annual GPP increased from 827.36 g C/m²/year in 1980 to 969.79 g C/m2/year in 2018, a growth rate of 2.36 g C/m²/year (Figure 6).

Figure 5.

Spatial pattern of global GPP significant trends estimated by BTCH during 1980–2018.

Figure 6.

Long-term changes in global average GPP estimates.

4.2. Data validation

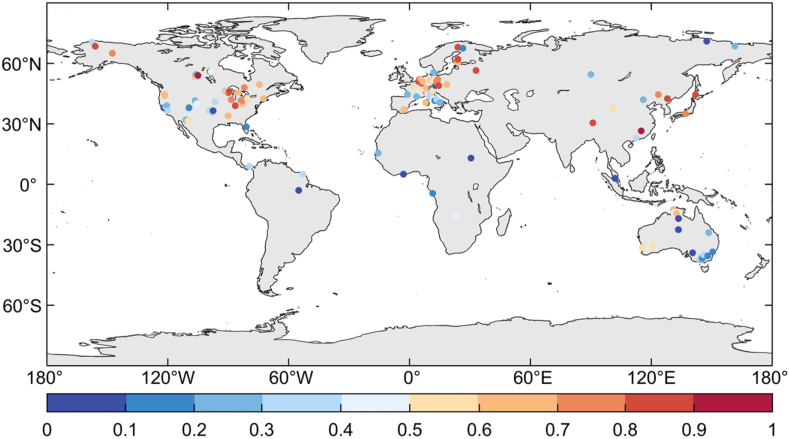
In general, BTCH-GPP can effectively reproduce the spatial distribution and inter-annual variation of tower estimates at most sites. Figure 7 shows the spatial pattern of R² for each site. In terms of BTCH-GPP, 43.57% of sites with the coefficients of determination (R²) were greater than 0.5 with most of them passing the significance test (p-value < 0.05) (Figure 7). BTCH-GPP estimates are closer to the flux towers values in Northern Europe and the Oceania region. We fit the monthly data available for 140 sites during 1980–2018 to the BTCH-GPP (Figure 8). BTCH-GPP estimates were lower than the site data overall. The accuracy of the BTCH-GPP estimates was shown to be rather high, with an R² of 0.79.

Figure 7.

Site validation for GPP (the statistics of R²).

Figure 8.

Regression of BTCH-GPP and tower GPP at a monthly scale.

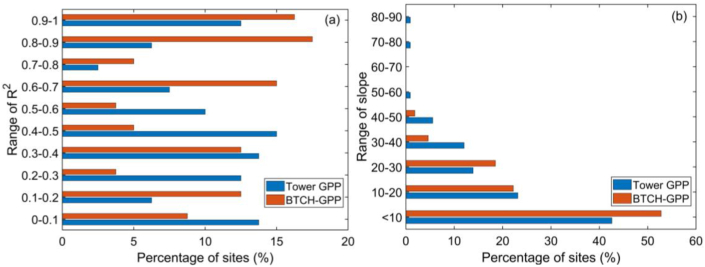
For individual vegetation types, BTCH-GPP products were overall underestimated, with MF, DBF and ENF showing high R² values (>0.5), implying that BTCH-GPP is better estimated on forests (Figure 9). The underestimation was more pronounced in croplands, grasslands and woody savannas, which may be since most products have an underestimated performance in these vegetation types. This may be because the seasonal variation of these vegetation types is strong, while the products are not so sensitive to seasonal capture, which weakens these changes (Stocker et al., 2020; Zhang et al., 2017). We investigated the capability of BTCH-GPP for interannual variation in GPP by selecting sites with more than 5 years of observation among 140 flux towers. The relationship between annual average GPP and observations at each site was examined using correlation coefficients, and the ability to simulate interannual variation in GPP was tested using the coefficient of determination (R²) and regression slopes. The results show that BTCH-GPP can effectively represent the interannual variation of GPP (Figure 10). The overall correlation coefficient of the slope values for the selected sites of BTCH-GPP and tower GPP is 0.8226. 57.5% of the towers have a higher R² value (>0.5), while only 38.75% of tower GPP show R² more than 0.5 (Figure 10a). The distribution of slope values for BTCH-GPP and tower GPP is generally consistent, with 52.78% and 42.59% of sites less than 10 g C/m²/year, respectively (Figure 10b).

Figure 9.

Comparison of BTCH-GPP and Tower GPP for six vegetation types at monthly scale across sites.

Figure 10.

Site percentage with the coefficient of determination (R²) (a) and regression slopes (b) of interannual variation of BTCH-GPP and tower GPP.

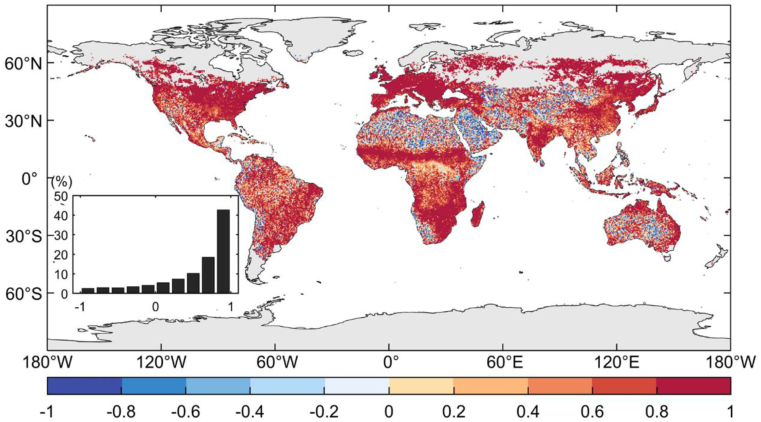
The distribution of the correlation coefficient between BTCH-GPP and GOME-2 SIF shows that the seasonal variation of BTCH-GPP is highly consistent with SIF (Figure 11). 71.38% of the pixels have a correlation coefficient greater than 0.5. The lower correlation coefficient for Northern Africa may be due to the higher uncertainty in the GPP estimates for 45 sets of GPP products in this region.

Figure 11.

Distribution of seasonal linear correlation coefficients for BTCH-GPP and GOME-2 SIF from 2007-2018.

4.3. Comparison with other GPP products

As shown in Figure 12, the BTCH-GPP estimates are closer to the observed values from the flux tower than other GPP products. The GPP estimation for BTCH has higher correlation coefficient (r = 0.77) and lower root-mean-square deviation (RMSD = 7.16 g C/m²/month) and standard deviation (STD = 24.44 g C/m²/month) compared to the average of 45 GPP products (aveGPP) (r = 0.66, RMSD = 16.89 g C/m²/month, STD = 125.60 g C/m²/month), and other individual products.

Figure 12.

Comparison of monthly BTCH-GPP, aveGPP (the ensemble average GPP of 45 GPP products), and 45 GPP products. The tower GPP is used as the reference data.

From the relationship between BTCH-GPP and GOME-2 SIF, it can be seen that the two show a good linear relationship (R² = 0.77) (Figure 13a). Compared with the other 45 sets of products, BTCH-GPP also showed the largest coefficient of determination and a smaller root mean square error (Figure 13b). BTCH-GPP exhibits a stronger linearity than GOME-2 SIF in 46 sets of GPP products. LUE products also show strong linear relationship with GOME-2 SIF by product category.

Figure 13.

Monthly average values of GPP Products in Relation to GOME-2 SIF from 2007 to 2010. (a) BTCH-GPP and GOME-2 SIF. (b) Comparison of deterministic coefficient (R²) and root mean square error (RMSE) of 45 sets of products and BTCH-GPP whose relationship with GOME-2 SIF.

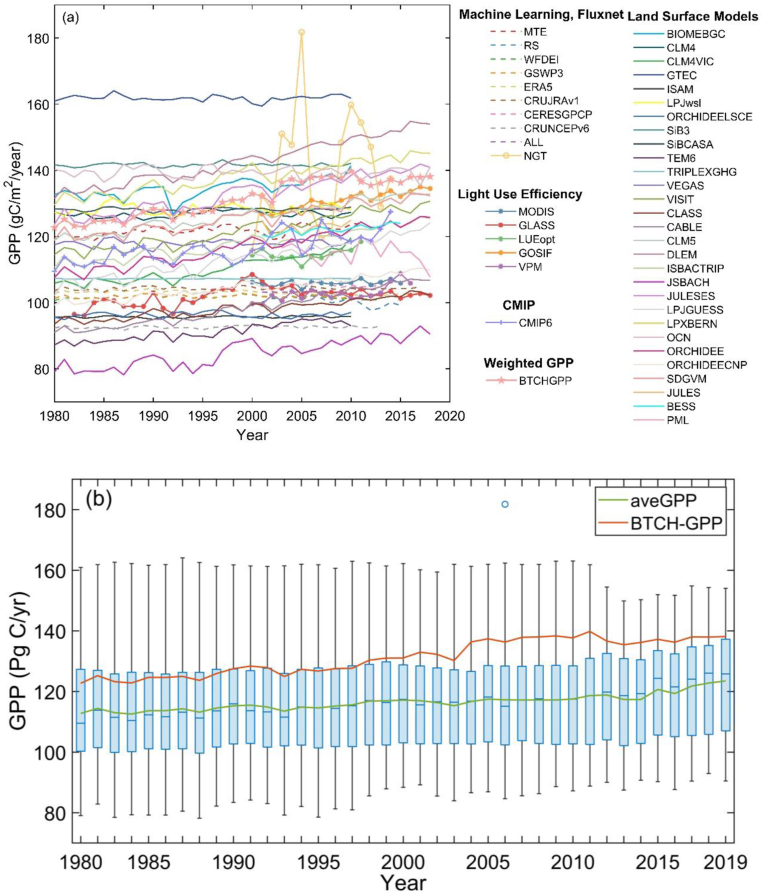
Despite significant advances in flux tower observations, remote sensing observations, and ecological models, global GPP estimates remain highly uncertain. On a global scale (for the same land area), our study shows that the magnitude of the estimated global GPP varies widely across products, from 78.2 to 181.8 Pg C/year (Figure 14). Different categories of GPP products have different interannual variations in the interval (Table 1). Greater variation within LSM categories than ML and LUE. BTCH-GPP estimates global sum GPP values range from 122.7 to 139.8 Pg C/year and quantifies the average GPP of the whole world scope of 1980–2018 as 131.3 ± 1.8 Pg C/year. Some studies have shown that the global total GPP ranges from 112 to 169 Pg C/year, and the BTCH-GPP is almost in the middle of this range (Anav et al., 2015; Zheng et al., 2019). The BTCH method is to select the most optimal solution for the values recognized by the majority of products, which means that the error variance between products is minimized. the value of BTCH-GPP is higher than the ensemble average, indicating that more weight is given to the high-value products and that most products recognize higher values than the ensemble average. Other researches have the same conclusion large uncertainty has existed in GPP estimates as well (Anav et al., 2015; Cai et al., 2014; Zheng et al., 2019).

Figure 14.

Interannual variation of global total GPP value from 1980 to 2019 at the same land area including 45 GPP products and BTCH-GPP. (a) The global sum GPP. (b) The boxplot of 45 GPP products and BTCH-GPP including annual sum GPP change of aveGPP (the average values of 45 GPP datasets).

Table 1.

Minimum (Min), maximum (Max) and average values (Mean) of global sum GPP (Pg C/yr) for different categories of GPP products from 1980 to 2019.

Category	Min	Max	Mean
ML	91.6	124.3	103.8
LUE	96.1	135.0	111.3
LSM	78.2	164.1	119.2
BTCH	122.7	139.8	131.3

Interannual variation and trends in GPP also vary considerably with different products. The standard deviation of interannual variation ranged from 0.087 to 17.92 Pg C/year with a trend of - 0.19 to 0.73 Pg C/year (Figure 15). The LSM products show significant interannual changes with standard deviations ranging from 0.09 to 6.82 Pg C/year. The LUE products estimate interannual changes ranging from 0.84 to 2.82 Pg C/year. While the ML products exhibit smaller interannual changes with a standard deviation of less than 1.50 Pg C/year. The trend of interannual changes of BTCH-GPP was 0.47 Pg C/year. Regarding long-term interannual trends, BTCH-GPP is more consistent with those of GPP_NIRv (Wang et al., 2021b) and the revised EC-LUE GPP (Zheng et al., 2019). Both products reproduce well the long-term interannual variation of GPP. BTCH-GPP avoids the insensitivity of FLUXCOM GPP to the interannual variation (Anav et al., 2015; Jung et al., 2009), and absorbs the consideration of CO2 fertilization effects from other products to better estimate the long-term trend of global GPP (Kolby Smith et al., 2016).

Figure 15.

(a) Comparison of interannual changes in the global sum GPP expressed by standard deviation (SD), and (b) trends of annual global sum GPP among 45 GPP products.

BTCH method cannot avoid the poor performance of the selected products, which is one of its disadvantages. However, with the continuous improvement of new products, the products produced by this method will also be improved.

5. Conclusions

In this study, we utilized a new weighting method, the BTCH method, to fuse multiple GPP data products. The weighting experiments demonstrate that the BTCH method can generate merged GPP datasets with significantly reduced random errors. BTCH-GPP provides improvements in correlation, systematic bias, and random errors over ensemble average values and other products at the monthly scale. BTCH-GPP performs well in the reproduction of spatial and interannual variability of global GPP. The method may not improve GPP accuracy for each grid in the global region, but it can improve overall and also provides new ideas for GPP data products improvement.

Declarations

Author contribution statement

Yahai Zhang: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Aizhong Ye: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by the National Key Research and Development Program of China (2018YFE0196000), the Second Tibetan Plateau Scientific Expedition and Research Program (2019QZKK0405) and the Natural Science Foundation of China (51879009, 41875131, 42171022).

Data availability statement

Data associated with this study has been deposited at https://figshare.com/s/e30ef2b7226f96f9ec60.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix A. Supplementary data

The following is the supplementary data related to this article: