Assessing models of force-dependent unbinding rates via infrequent metadynamics

Abstract

Protein–ligand interactions are crucial for a wide range of physiological processes. Many cellular functions result in these non-covalent “bonds” being mechanically strained, and this can be integral to proper cellular function. Broadly, two classes of force dependence have been observed—slip bonds, where the unbinding rate increases, and catch bonds, where the unbinding rate decreases. Despite much theoretical work, we cannot predict for which protein–ligand pairs, pulling coordinates, and forces a particular rate dependence will appear. Here, we assess the ability of MD simulations combined with enhanced sampling techniques to probe the force dependence of unbinding rates. We show that the infrequent metadynamics technique correctly produces both catch and slip bonding kinetics for model potentials. We then apply it to the well-studied case of a buckyball in a hydrophobic cavity, which appears to exhibit an ideal slip bond. Finally, we compute the force-dependent unbinding rate of biotin–streptavidin. Here, the complex nature of the unbinding process causes the infrequent metadynamics method to begin to break down due to the presence of unbinding intermediates, despite the use of a previously optimized sampling coordinate. Allowing for this limitation, a combination of kinetic and free energy computations predicts an overall slip bond for larger forces consistent with prior experimental results although there are substantial deviations at small forces that require further investigation. This work demonstrates the promise of predicting force-dependent unbinding rates using enhanced sampling MD techniques while also revealing the methodological barriers that must be overcome to tackle more complex targets in the future.

I. INTRODUCTION

Mechanical forces play an important role in a wide range of biological processes.^1–13 Cells have evolved mechanosensing mechanisms by which the behavior of a protein or protein complex changes in a stereotypical way in response to that applied force. In general, these forces produce two types of results: they can have a thermodynamic effect on the conformational landscape of the protein(s) or a kinetic effect, changing reaction rates.^13,14 In this work, we will focus on the kinetic effects of force on protein–ligand unbinding.^1,8,15 Although much work has been performed experimentally and theoretically to understand the role of mechanosensitive unbinding rates in biological processes,^3,8,15–23 much less is known about the molecular details that contribute to the force dependence of the rate. Here, we wish to assess whether molecular dynamics (MD) simulations coupled with enhanced sampling techniques are suitable for this task.

Protein–ligand interactions are essential in mediating cellular adhesion and cell–cell interactions. These non-covalent “bonds” are put under tension due to the action of molecular motors in the cellular cytoskeleton and/or mediated by tension in the cellular membrane.^1,5,24,25 Crucially, at short time scales, we can think of these forces as quasi-static with forces typically in the piconewton scale for each bond. Although MD has been used to probe the effect of force on proteins or even protein–ligand interactions,^26–31 to our knowledge, it has not been used to predict equilibrium unbinding kinetics under these quasi-static, small force conditions. As recently reviewed, this regime is particularly challenging because these small forces are not expected to substantially shift the behavior of the system outside the linear response regime; hence, sampling has to be very accurate to capture the subtle structural changes leading to large changes in the rate.¹³ Theoretical work and coarse grained studies in this area have typically focused on (free) energy surfaces representing the unbound and possibly multiple bound states of the system, given the difficulty in probing these systems at a fully molecular level.^8,18,21,32

The biggest challenge to predicting bond lifetimes is that the relevant time scales for dissociation may be of the order of milliseconds to tens of seconds for systems that we are interested in, meaning that we would not expect to see any unbinding events within a standard MD simulation.¹³ We were inspired by a large amount of recent literature on the development of enhanced sampling MD techniques designed to predict the unbinding time of drug molecules from their protein targets.^33–38 These techniques accelerate the unbinding of the ligand by many orders of magnitude in such a way that many unbinding events can be observed within the limitations of standard computational resources and allow for statistical reweighting of the observed unbinding times to predict their unbiased values. Approaches to accelerate generation of rare unbinding events can be broadly broken into two categories: (1) those that simulate many copies of the system and select only trajectories that advance along some progress variable and (2) those that push the ligand out of its binding pose by applying an energy bias in the bound state.

Here, we report our results from using Infrequent Metadynamics (InfrMetaD), a method that computes unbinding times from reweighted trajectories using an energy bias (see Sec. II B for full details).^39,40 We choose to evaluate this method first because it very quickly produces unbinding trajectories, has a metric for determining whether computed unbinding times are reliable,⁴¹ and because we can compute free energy surfaces (FES) using standard metadynamics (MetaD) to compare the computed changes in a low dimensional free energy surface with applied force to the predicted change in the unbinding rate.

A constant pulling force F on coordinate Q(X) changes the energy of our system to U(X) − FQ(X), where Q is a collective variable (CV) that is a simple function of our molecular configuration X, such as the distance between two atoms on which we are pulling, and U(X) is the potential energy of the system without an applied pulling force.¹³ This has the effect of “tilting” the probability distribution of observed configurations such that the probability of seeing some configuration at force F is given by P_F(X) = P₀(X)e^βFQ(X),¹³ where β = 1/(k_BT), k_B is Boltzmann’s constant, and T is the temperature; k_BT ≈ 4.1 pN nm at room temperature.¹³ Because this is a static change to our probability distribution, standard equilibrium simulation techniques can be applied.

For a simple one dimensional energy surface such as that shown in Fig. 1(a), the rate of transition from bound to unbound follows the Arrhenius law and depends on the exponential of the height of the energy barrier between the two states. Under certain assumptions, this implies that the dependence of an unbinding rate on force should follow

$$k_{\text{off}}(F)=k_{\text{off}}(0)e^{\beta F\mathrm{\Delta }{Q}^{‡}},$$ (1)

where ΔQ^‡ is the distance from the bound to transition state in the coordinate Q and is taken to be constant. This equation was used in a theory of cellular adhesion by Bell and hence is referred to as Bell’s law in the biophysics literature.¹ Bell’s law is an example of a slip bond dependence, where unbinding becomes faster with applied pulling force as we might expect.

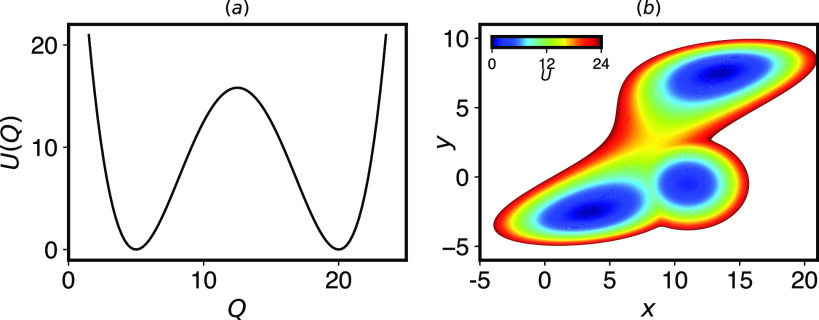
FIG. 1.

(a) A two well potential energy surface serves as a model system for a simple binding/unbinding reaction. (b) A three well potential energy surface, constructed by adding a metastable state to a two well potential from Ref. 8, is designed to exhibit catch bond behavior in escaping from the lower left to the upper right when pulling in the x direction. Details of the potentials are in Sec. V B 1.

It is immediately obvious that the assumptions going into Bell’s law need not hold for real protein systems, and hence, we should not expect Bell’s law to apply. Because of this, several extended theories have been developed to correct the simplest assumptions going into Bell’s law, in particular, that the distance to the transition state does not change with force.^8,20,42,43 From a broader perspective, the reason Bell’s law would not hold is that the unbinding rate should depend not on the energy surface but on the free energy surface, which at a constant volume and temperature would be given by A(Q) = −k_BT log(∫dXδ(Q(X) − Q)P_F(X)). Because many different molecular configurations can contribute to distances in Q intermediate between bound and unbound, the free energy surface could change in unpredictable ways as force varies, and the surface may no longer be represented as a simple double well.¹³

One particularly interesting class of protein–ligand bonds that we wish to study are the so-called catch bonds, where the lifetime of the protein–ligand interaction actually increases with pulling force.^3,15,19,21 Physiologically, catch bonds may play many important roles, including giving cells a tool by which they can adhere strongly in the presence of strong external forces. One example is the FimH–mannose bond, which allows bacteria to adhere to the urinary tract in the presence of large shear forces; here, the effect of shear force is to separate two domains in the protein, which allosterically causes a dramatic increase in ligand binding affinity.^6,15,23,44 A number of general theories have been put forth to explain catch bond behavior,^15,18,19,45 including one type of catch bond where an applied force on the system shifts the stable equilibrium state into one where there is a higher barrier to ligand unbinding, as described for FimH [Fig. 1(b)]. Catch bond kinetics have not been observed directly in atomistic molecular simulation for equilibrium applied forces to date.

An overarching question that we wish to answer in our research is how complex does a molecular system need to be to have behavior that cannot be described by Bell’s law? Our goal here is to check whether InfrMetaD is a sufficiently powerful method to capture expected force-dependent behavior for model systems where we know what the expected result should be and then apply it to more complex molecular systems to gain insight into the molecular dissociation mechanisms that do and do not result in Bell’s law behavior.

An outline of the paper is as follows: in Sec. II, we describe the computational methods to be employed, including MetaD and InfrMetaD; in Sec. III A, we apply these two methods to model potentials in Fig. 1 and confirm that InfrMetaD can capture Bell’s law and catch bond behavior; in Sec. III B, we then apply it to a model of a protein-receptor system, a hydrophobic ball in a hydrophobic cavity surrounded by water, and show that this exhibits Bell’s law behavior, despite having a non-trivial unbinding pathway. In both cases, we evaluate the free energy surfaces to check whether their changes with force are consistent with observed differences in rates; finally, in Sec. III C, we apply these methods to an atomistic protein–ligand system, that of biotin–streptavidin. While InfrMetaD begins to break down in this case, a combination of InfrMetaD and well-tempered MetaD suggests a number of unbinding intermediates that give rise to a breakdown in simple Bell’s behavior, despite being a slip bond overall. We discuss the ramifications of these results and the outlook for future studies in Sec. IV. Finally, we give full details of the simulations performed above in Sec. V.

II. METHODS

A. Metadynamics

Metadynamics (MetaD) is an enhanced sampling method, which allows for the construction of a low dimensional free energy surface (FES) as a function of carefully chosen collective variables (CVs).^46,47 An external history dependent bias that is a function of the CVs is added to the Hamiltonian of the system, pushing the system away from areas already explored.⁴⁷ As a result, a much wider exploration of configuration space is achieved in the same amount of MD steps. The external potential consists of a sum of Gaussians that are deposited along the trajectory of the CVs,

$$V(\mathbf{Q},t)=\omega \sum _{t^{\prime }={\tau }_G,2{\tau }_G\dots }^t{e}^{-\sum _{i=1}^d\frac{{(Q_i(\mathbf{X}(t))-Q_i(\mathbf{X}(t^{\prime })))}^2}{2{\sigma }_i^2}},$$ (2)

where ω is the Gaussian height, τ_G is the time interval at which Gaussians are deposited, Q_i are functions that map the atomic coordinates X(t) onto CV i, and σ_i are the chosen Gaussian widths for each CV.

Well-Tempered Metadynamics (WTMetaD)^47,48 modifies the Gaussian hill heights so that they decrease exponentially as a function of the cumulative bias applied at the current CV position,

$${\omega }^{\prime }(t)=\omega e^{-\frac{V(\mathbf{Q},t)}{k_B\mathrm{\Delta }T}},$$ (3)

where ΔT is the tempering factor. Thus, as ΔT → 0, ordinary MD is recovered, and as ΔT → ∞, standard MetaD is recovered. Effectively, the CV space is sampled at temperature T + ΔT, and as such, WTMetaD balances an increase in the probability of crossing energy barriers with a limitation on the extent of FES exploration. In WTMetaD, the applied bias has been shown to converge asymptotically to $-\frac{\mathrm{\Delta }T}{T+\mathrm{\Delta }T}A(\mathbf{Q})$, where A(Q) is the potential of mean force.⁴⁹

MetaD and many subsequent variations became popular for computing FESs due to its ease of use and the fact that they promote exploration. As with any CV-based enhanced sampling method, the primary difficulty is choosing appropriate CVs that encompass all relevant slow transitions for the system of interest.⁴⁷

B. Infrequent metadynamics

Although MetaD was designed to predict static properties of a system such as the FES, in some situations, it can be adapted to produce an estimate of the rate of slow dynamical events.³⁹ Voter demonstrated that unbiased rates of infrequent barrier crossing processes can be computed very rapidly by applying a bias outside of transition regions to “boost” the system over those barriers.^50,51 Tiwary and Parrinello proposed the idea of infrequent metadynamics (InfrMetaD), where the metadynamics framework described above is used to produce this boost potential on the fly.³⁹ In order to extract unbiased rates, three key conditions must be met: (1) the transitions from one state to the other are rare, but the actual crossing of the transition state is ephemeral, (2) the biased CV is a good reaction coordinate for the transition, and (3) additional Gaussians are added to the bias potential infrequently enough that none are added during the barrier crossing.³⁹

When this is the case, transition state theory says that the ratio of the escape times in the biased and unbiased cases is given by the ratio of the partition functions in the reactant basin. This ratio gives an acceleration factor α, which can be computed as

$$\alpha =⟨e^{\beta V(\mathbf{Q},t)}⟩,$$ (4)

where Q are the collective variables being infrequently biased and V(Q, t) is the metadynamics bias experienced at time t.³⁹

In order to estimate a rate using InfrMetaD, many trajectories are run with different random seeds up to the points where the system was deemed to have reached the unbound state. The unbiased reaction times for each simulation instance are estimated by multiplying the final time in the simulation by the acceleration factor computed up to that point. If unbinding is a rare event with a single dominant barrier, we expect the distribution of transition times to be exponential as for a homogeneous Poisson process and to depend on a single bond lifetime τ.^41,52 In this case, to obtain the unbinding rate, a cumulative distribution function (CDF) from computed unbiased transition times can be built and fit to the ideal CDF,

$$CDF(t)=1-e^{-t/\tau }.$$ (5)

The rate of the process can then be computed as k = 1/τ. The correspondence of the empirical CDF (ECDF) to the ideal CDF can be checked by the Kolmogorov–Smirnov (K–S) test.⁴¹ Here, the standard error in the rates are obtained via the parametric bootstrap method.⁵³ We perform the K–S test and bootstrapping using the python package scipy.stats.⁵⁴ For a real protein system, we do not necessarily expect that the unbinding process should follow this simple rule, and hence, the K–S test will not be passed. For this case, it may be possible to estimate the unbinding time via this fit value or by simple averaging of the boosted escape time if we are only looking for qualitative trends, but more care and comparison with other computational or experimental data must be performed.

III. RESULTS AND DISCUSSION

A. Model potentials

We first wish to confirm that InfrMetaD is an appropriate tool to predict the force dependence of unbinding rates. To do this, we apply InfrMetaD to one- and two-dimensional potentials meant to exhibit slip and catch bond behavior, respectively. As described in Sec. I, a two well potential such as that in Fig. 1(a) is predicted to show Bell’s law dependence of the unbinding rate with force.

To compute the unbinding rates, a total of 20 InfrMetaD runs were performed for forces in the range F = 0–3.32 pN. Both the pulling force and bias were applied to the x coordinate (see Sec. V B 1 with representative CDFs in Fig. S1). Moreover, we explicitly compute the free energy using WTMetaD to see how the change in the underlying FES corresponds to the change in the rate. Here, we do this to be consistent with forthcoming examples and to verify our numerical approaches although it is not necessary for a one dimensional case.

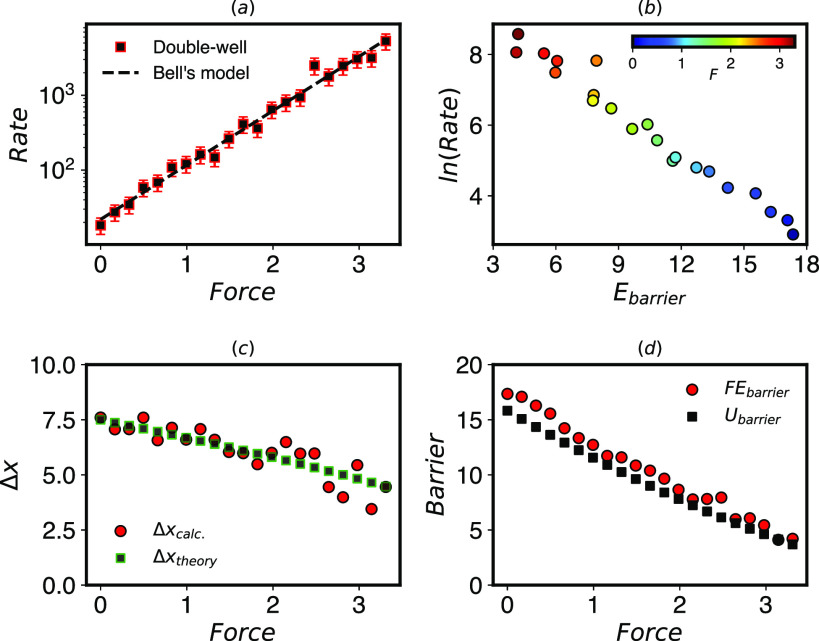
As expected, the rates computed by this approach increase exponentially with applied force and fit very well to Bell’s law [Fig. 2(a)]. How does this connect to the underlying (free) energy surface? Figure 2(b) shows that these rates conform to the Arrhenius law, where the rates are exponentially dependent on the barrier height between the states. Among other assumptions, Bell’s law should hold when the barrier decreases linearly with force and the distance to the transition state is constant.¹³ Figures 2(c) and 2(d) show that the agreement with Bell’s law is a bit fortuitous because the true surface exhibits (an expected) linear shift of the transition state distance with applied force that can be taken into account using extensions of Bell’s law.⁴²

FIG. 2.

(a) Unbinding rates computed by InfrMetaD for the potential in Fig. 1(a) given in μs⁻¹. The log of the rates increases linearly with force (given in pN), apparently following Bell’s law. The fit parameters are k⁰ = 21.90 and Δx^‡ = 6.86 (R² = 0.99). (b) Rates computed by InfrMetaD plotted against the energy barrier computed by WTMetaD exhibit Arrhenius behavior. (c) The transition distances computed from FE calculations shrink with applied force as predicted by extended Bell’s theory,⁴² meaning that not all assumptions of Bell’s law are true. “Theory” values are the shift in the analytical potential with force. (d) The computed energy barrier to unbinding decreases linearly as higher forces are applied in accordance with the assumption going into Bell’s law. U_barrier is the analytical barrier height.

We now move beyond this trivial first test to assess whether InfrMetaD can capture catch bond behavior in a model system. The catch bond potential we have created is adapted from Ref. 8, but we have added a third potential well that has a higher transition barrier to the product (top right) state [Fig. 1(b)]. We predict that upon pulling to the right in x, the intermediate will be stabilized, and the barriers will change such that the most favorable path is through the intermediate, which still has a slower rate of transition to the product.

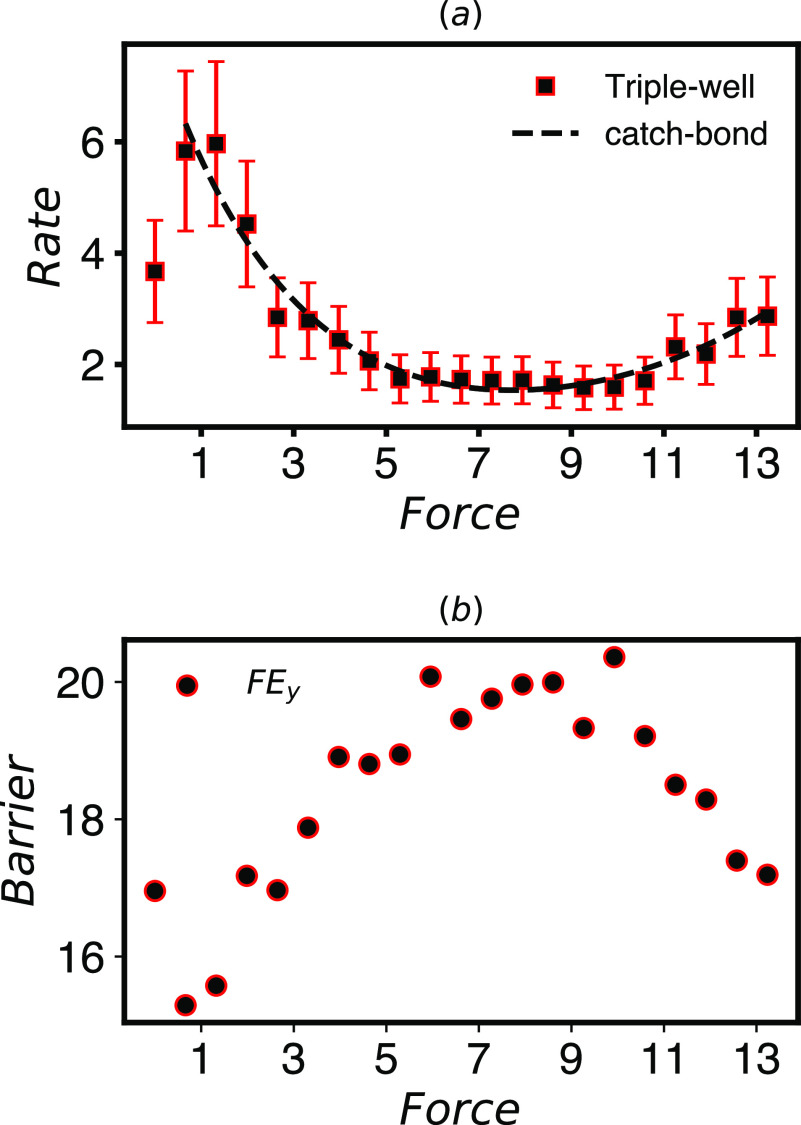
To compute the rates, 20 InfrMetaD runs were performed for forces in the range F = 0–13.3 pN. The forces were applied in the x direction, while the WTMetaD bias was applied symmetrically in both the x and y coordinates (see Sec. V B 1 for simulation details with representative CDFs in Fig. S2). We observe for this model that the rate of unbinding decreases in the range F ∈ {1, 9} and then increases from that point onward, an example of a catch-slip bond [Fig. 3(a)]. The existence of the intermediate state causes the rate dependence to deviate from Bell’s model except at the very smallest forces. We can fit the observed behavior well using a sum-of-exponential catch-slip rate dependence¹⁸ given by $k_{\text{bottom}\to \text{top}}=k_c{e}^{\beta F(-x_c)}+k_s{e}^{\beta F{x}_s}$ where k_c, x_c, k_s, and x_s have values of 7.59, 1.38, 0.22, and 0.80, respectively for the curve in Fig. 3(a).

FIG. 3.

(a) Rates computed by InfrMetaD for the potential in Fig. 1(b) with forces given in pN and rates in μs⁻¹. This system exhibits catch-slip bond behavior, and the rate dependence can be fit well to a catch-slip rate dependence (dashed line) as described in the main text. (b) The free energy barrier in the y direction computed from data in Fig. 4 using Eq. (6) shows an increase and decrease with force mostly commensurate with the rate dependence.

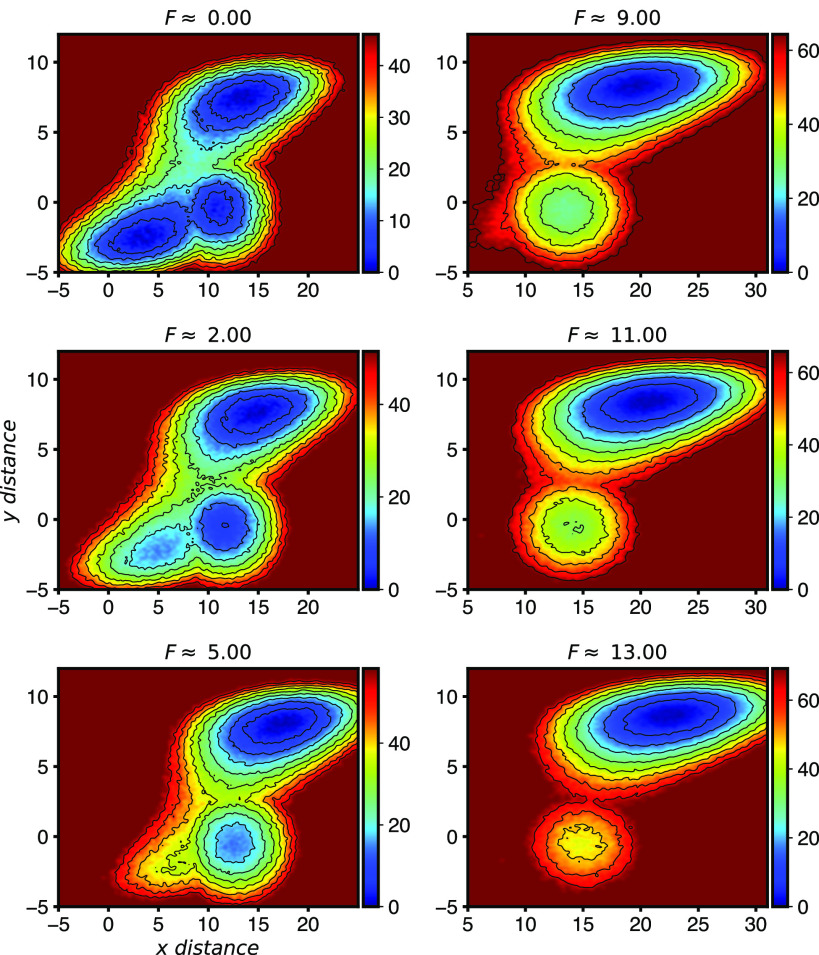
We next use WTMetaD to check our intuition for how the free energy surface is changing. Our results in Fig. 4 show that the situation is similar but more complex than our initial expectations. At small force, it can be seen that all or most MetaD transitions took place directly between the lower and upper state. At F = 2 and F = 5, the force in the x direction makes the intermediate state lower in free energy, which has a higher barrier to escape. Between F = 5 and F = 9, the original stable state has vanished. The rate is still decreasing and the barrier is increasing, but this is due to the shift in relative positions of the two minima. It is only once the upper state is fully to the right of the initial intermediate just above F = 9 that the unbinding rate starts to increase again.

FIG. 4.

Free energy surface for the potential in Fig. 1(b) at different pulling forces. Pulling in the x direction lowers the system’s energy proportional to its x location. This causes the upper state, which is farthest to the right, to become the dominant state at higher forces and also causes the lower-left state to become unstable and vanish.

An effective one dimensional free energy surface in the y direction, A(y), can be computed by integrating out the x dependence,

$$A(y)={\int }_{-\infty }^{\infty }{e}^{-\beta A(x,y)}dx.$$ (6)

The transition barrier between states for A(y) is shown in Fig. 3(b). Here, the change in barrier in the y direction is mostly consistent with the change in observed rates.

B. Cavity-ligand model

Having demonstrated that InfrMetaD and also WTMetaD are capable of extracting the force dependence of unbinding in accordance with our expectations, we now turn to an explicit, all atom but simplified representation of a ligand unbinding process—a hydrophobic sphere contained in a hydrophobic cavity, solvated by water.^52,55,56

We choose this model for two reasons: (1) Through extensive studies, it is known that the unbinding pathway for this system involves first moving sideways before exiting because a direct perpendicular exit requires water molecules to fill in a vacuum created by the fluctuation of the sphere out of the cavity. This means that the unbinding process is not well described by considering the obvious reaction and pulling coordinate (central distance of the ball from the cavity),^52,55,56 and (2) this system has been well characterized at zero force by both WTMetaD and InfrMetaD; hence, we expect our calculations to be converged using the same protocols.

In order to perform InfrMetaD computations for this system, we should have a good estimate of a distance that we consider the sphere to be unbound. Here, we first performed WTMetaD calculations on this model with different applied forces using the same protocol as Ref. 56 (full details in Sec. V B 2). FESs at T = 300 K were obtained for forces F = 0–50 pN in 2 pN intervals, where pulling forces are applied to the full three-dimensional distance between the center of mass (COM) of the cavity and the center of mass of the sphere. The MetaD bias was applied to two CVs, the radial (ρ) and transverse (Z) distances between the COMs of the cavity and sphere (Fig. 5).

FIG. 5.

Solvated cavity-ligand model from Ref. 56. The cyan and orange atoms (CW and CP) form the receptor, and the blue atoms (CF) make up the ligand. The radial and perpendicular distance CVs used for biasing are labeled in the figure.

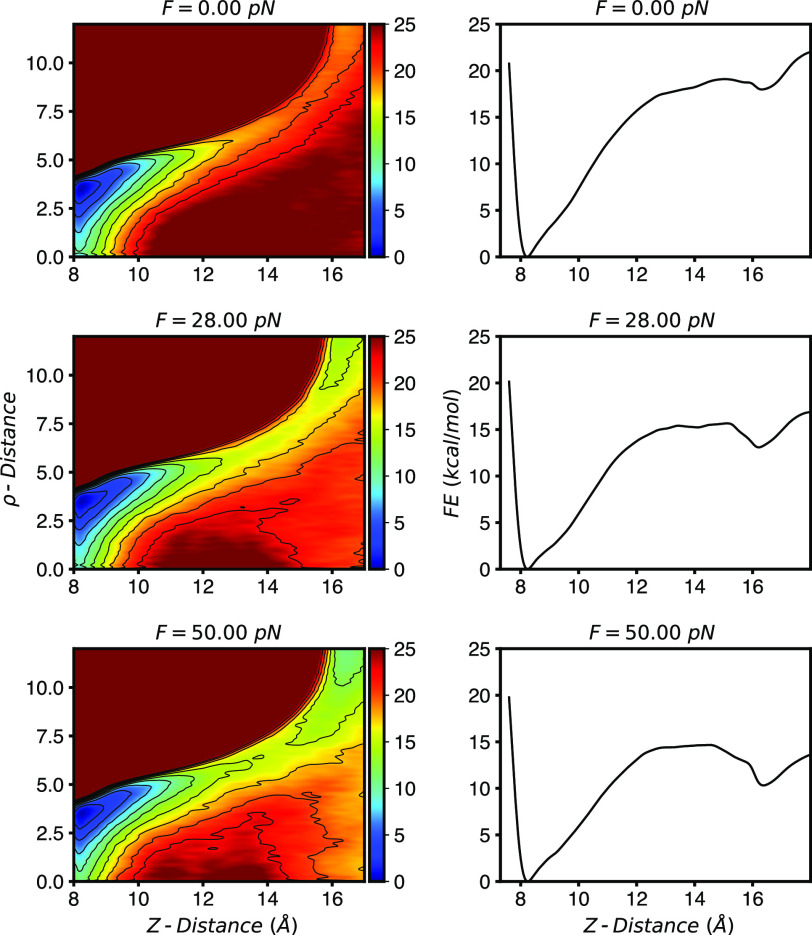
Figure 6 (left) shows the computed FES in our two CVs at three different forces. As described in previous work, the FES at zero force clearly shows that the escape of the sphere involves a radial shift away from the central axis before exiting, which more easily allows water into the cavity.^52,55,56 When projected in just the transverse direction (Z), Fig. 6 (right), we see that the FESs resemble a prototypical double well potential. Application of a pulling force lowers the free energy of the unbound state as well as the barrier between the bound and unbound state.

FIG. 6.

(Left) FESs computed for the cavity-ligand system (Fig. 5) at three different forces. Pulling along a central distance coordinate increases stability of the unbound state. (Right) One dimensional free energy surfaces computed by integrating out the ρ-distance according to Eq. (6).

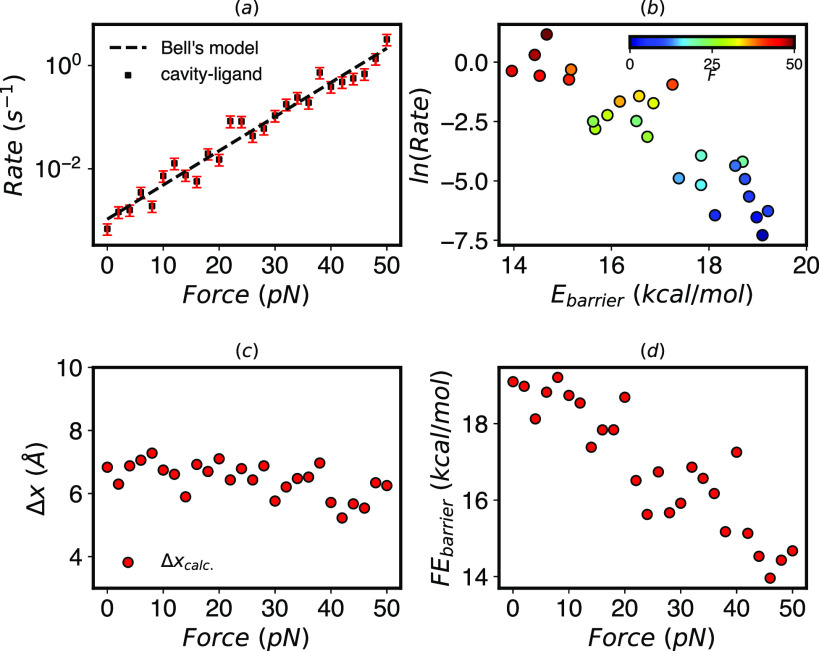
While these FESs can help us understand the mechanism of unbinding at different forces, they do not give us direct access to the unbinding rates. Now that we know the unbound state is at Z = 16 Å and ρ = 6–10 Å, we apply InfrMetaD to this system for the same force range. To be consistent with earlier work, here, we apply InfrMetaD using only a central distance between the ligand and cavity⁵² (see Sec. V B 2 for full details with representative CDFs in Fig. S3). Although the unbinding process is much more complicated than for a two-well potential and we are using only a single bias coordinate, almost all unbinding distributions pass the KS test (Fig. S3). The resulting rates shown in Fig. 7(a) that unbinding rates increase exponentially with increasing force.

FIG. 7.

Cavity-ligand model. (a) Unbinding rates from InfrMetaD increase exponentially with pulling forces. Fit parameters to Bell’s law are k⁰ = 0.0011 s⁻¹ and Δx^‡ = 6.31 Å (R² = 0.96). (b) The rate decreases exponentially with the barrier height computed from WTMetaD projected along the Z-distance using Eq. (6). (c) The distance to the transition state in the Z direction decreases slightly but is relatively constant compared to the two well potential results in Fig. 2(c). (d) The free energy barrier in the Z direction decreases linearly with force.

Again, combining our data from WTMetaD and InfrMetaD, we show that unbinding rates for this cavity model fit well to the Arrhenius law across our range of forces but not nearly so well as for a true one dimensional double well [Fig. 7(d)]. Interestingly, the transition distance in the one-dimensionalized potential is almost constant, as shown in Fig. 7(c), while the barrier shown in (d) decreases linearly; therefore, despite its non-trivial unbinding pathway, in this sense, this cavity-ligand model is closer to ideal Bell’s law behavior than the 1D potential upon which the theory is based. We speculate that the relatively weak dependence of the transition distance on force is due to the rigidity of the cavity and ligand, and this relationship could begin to break down if the cavity were made more flexible.

C. Fully atomistic protein–ligand system

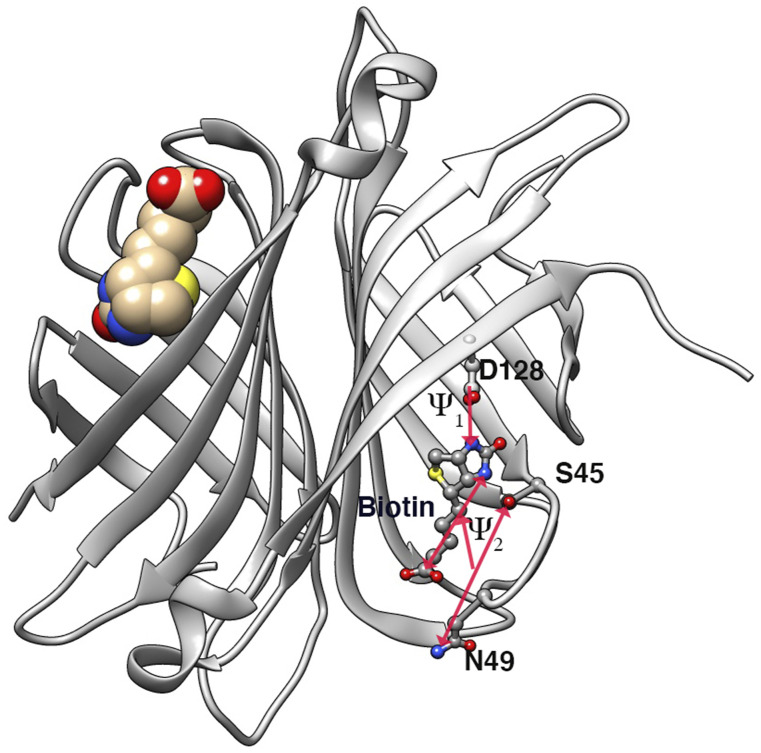
Given the reasonableness of our prior results on the cavity-ligand model, we sought to apply our approach to a fully atomistic protein–ligand system. We chose to study the biotin–streptavidin (SA/b) bond (Fig. 8) for three reasons: (1) it plays an important role in many in vitro biochemical studies and is one of the strongest biological non-covalent bonds known,³¹ (2) its bond rupture has been studied in non-equilibrium pulling experiments and simulations,³¹ and (3) its unbinding kinetics at zero force have been assessed previously using InfrMetaD.⁵⁷

FIG. 8.

Dimeric form of streptavidin in complex with biotin. Only one biotin was chosen to perform InfrMetaD. The other biotin molecule remained in its bound pose throughout the duration of all simulations. Protein residues and distances going into the bias CV are labeled.

Computing unbinding rates of protein–ligand systems is an active area of research and is clearly non-trivial. A major challenge, as discussed above, is choosing a good reaction coordinate. In Ref. 57, Tiwary optimized a slow reaction coordinate using the SGOOP algorithm⁵⁸ for the unbinding of the biotin ligand, which is a linear combination of distances between the ligand and residues in the binding pocket (Fig. 8, Sec. V B 3). This optimized coordinate allowed InfrMetaD unbinding times to pass the statistical test although there are signatures of non-exponential behavior in the data attributed to metastable intermediates along the unbinding pathway (seen also in Ref. 31).

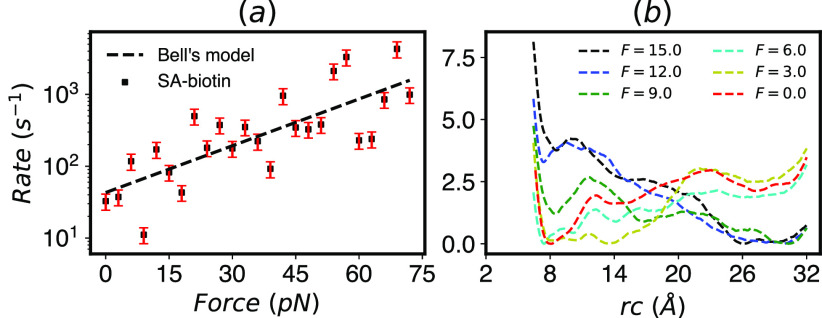
Following Ref. 57, we constructed a dimeric SA/b complex and studied the unbinding of one of the two biotin ligands using InfrMetaD. Using the identical reaction coordinate (rc) and slightly different MetaD parameters (bias was deposited more infrequently, every 15 ps rather than 5 ps as in Ref. 57), we get an unbinding rate of 32.66 ± 8.22 s⁻¹, which as in Ref. 57 is much faster than the measured rate for the full tetrameric complex. We then proceeded to compute the unbinding rates as a function of force with 20 InfrMetaD runs performed for forces in the range F = 0–72 pN, which were applied to the distance between the COMs of the binding pocket and biotin as was performed in steered MD simulations in Ref. 31. The biased rc consists of a couple of distances from key residues to key atoms in biotin (highlighted in Fig. 8), while the pulled CV is a single distance between the entire binding pocket and the entire biotin molecule; see Sec. V B 3 for details. Unfortunately, despite numerous attempts to adjust the InfrMetaD pace, hill height, and width, we were unable to obtain unbinding rate distributions that pass the statistical tests for most forces. The rates obtained from the parameters that gave our closest to exponential results are shown in Fig. 9 with representative CDFs that do and do not pass the KS test shown in Fig. S4.

FIG. 9.

(a) Unbinding rates computed from InfrMetaD show an overall slip bond but a poor fit to Bell’s law. The fit parameters used are Δrc^‡ = 2.1 Å and k⁰ = 43 s⁻¹ (R² = 0.59). This fitted Δrc^‡ is not close to the transition distance observed in the FES estimates. (b) Estimation of free energy surfaces obtained from WTMetaD shows a rough landscape for ligand escape at small force as well as a transition to a tilted landscape favoring unbinding from F = 12 pN and above. Surfaces for other forces can be found in Fig. S8.

Despite the fact that we cannot say with confidence that these unbinding times are accurate or converged, the trend is consistent with experimental results measured by dynamic force spectroscopy in Ref. 31, where the bond lifetime changes exponentially with force by a factor of 30 as force ranges from 0 to 75 pN (see Ref. 31 Fig. 3E) for escape from a putative “outer” binding site. Overall, our predicted rates appear to follow an exponential slip bond; however, there are substantial deviations from the trend, which coincide with what is likely a much more complex unbinding energy landscape in this case. It is unclear whether substantial dips at 9 and 18 pN could correspond to any catchbond like behavior or are simply an indication that our computations are not well converged.

In order to gain some insight into the reason the InfrMetaD breaks down, we compute an approximate FE surface using WTMetaD while restricting the ligand to stay close to its initial monomer using a “wall” constraint (see Sec. V B 3 for full details). We emphasize that these computations are performed in such a way that we can attempt to characterize the unbinding process occurring in our InfrMetaD simulations and not to fully converge an unbinding free energy landscape, which would require a more sophisticated approach such as funnel metadynamics;^59,60 we have plotted the surfaces with dashed lines to help indicate this point.

The approximate average FE surfaces in Fig. 9(b) reveal multiple unbinding intermediates, as previously suggested in Refs. ³¹ and ⁵⁷. Here, we can see that the roughness of the surface becomes more pronounced for intermediate forces, contributing to the breakdown in the assumption of a single high barrier and perhaps resulting in outlier rates in the InfrMetaD computations such as those seen at F = 9 pN. At larger forces in Fig. 9(b), the surface becomes more smooth again and the unbound state is clearly favored. Similar approximate surfaces projected on the pulling coordinate, which is what we would normally tend to show to get insight into the unbinding process, are shown in Fig. S8. However, showing the surface in terms of the reaction coordinate used in InfrMetaD is more appropriate for diagnosing why the assumptions going into the rate computations are not being satisfied. Finally, we note that the variation between runs is quite large and have included Fig. S9 showing each FES estimate shown in Fig. 9(b) separately along with the standard deviation between runs to highlight this point.

In total, these MetaD and InfrMetaD data together suggest that while the coordinate obtained from Ref. 57 was apparently good enough for use at F = 0 pN, it is not sufficiently optimized for higher forces. This poses a challenge going forward as to whether a single CV or set of CVs can be determined that is appropriate for all forces or whether a new reaction coordinate must be determined for each pulling force since the application of force can change the underlying free energy landscape in unpredictable ways.

IV. CONCLUSION

Thermodynamic and kinetics calculations were performed for various models with increasing complexity to determine the force dependence of transition rates. In the case of a simple two-well potential and a hydrophobic ball/cavity system, we showed that unbinding rates increased exponentially with force, while a model catch bond system showed a decrease in unbinding rates corresponding to stabilization of an intermediate. For the biotin–streptavidin interaction, the predicted presence of intermediates causes InfrMetaD to break down as the unbinding process is no longer characterized by a single high energy barrier (using the chosen bias CV). Intriguingly, our rough results for the free energy surface from MetaD show very non-monotonic changes with force that could be indications of metastable unbinding states stabilized by the applied force. Our results also suggest, as described in earlier work, that the failure of unbinding time cumulative distributions to be exponential is reflective of the complexity of the unbinding pathway and can be used to help diagnose whether a good reaction coordinate has been chosen for InfrMetaD in the presence of force.

We believe that our prediction that the hydrophobic cavity system exhibits true Bell’s law behavior is the first such explicit prediction from equilibrium MD simulations. The concordance between MetaD and InfrMetaD results and the relative efficiency of InfrMetaD do suggest that InfrMetaD is a promising technique to evaluate the force dependence of unbinding rates for complex systems. However, its failure to pass statistical sanity checks for most forces in the case of SA/b serves as a warning to those, including us, who hope to apply such techniques to even more complex systems, such as large protein–protein complexes that exhibit catch bond behavior. In our case, we chose the SA/b system because an optimized coordinate had been previously computed for use in InfrMetaD. Yet, this coordinate was insufficient once forces were applied. One possible solution to this problem is to compute new reaction coordinates for each applied force. Although this would be cumbersome, it is certainly a more rigorous approach that we will explore in subsequent work.

Given our current approach though, our results suggest that the overall trend of increasing or decreasing rates computed from InfrMetaD, even in the presence of this breakdown, could be a fingerprint of catch or slip bond behavior, and give some insight into the mechanisms. This would be analogous to the ways in which steered MD has given important insights into unbinding or unfolding reaction mechanisms despite generally producing unrealistically high forces at unrealistically fast rates.

Finally, in the future, we plan to explore other equilibrium methods for computing rates to determine whether they are more suitable for computing force dependence. We are currently evaluating the weighted ensemble approach, which has the advantage of not having to choose a specific reaction coordinate on which to apply an energy bias although a choice of a progress coordinate for unbinding is still needed. Because this method requires performing many cycles of simulation, we can actually predict that it will become more computationally effective for the case of slip bonds as applied forces will result in faster rates, which require fewer cycles to converge. At the same time, catch bonds will require a higher cost than computing a zero force unbinding rate due to the longer lifetime of the bond. Another compelling approach would be to use Markov State Models (MSMs) built from unbiased trajectories as performed for the cavity-ligand model in Ref. 56 as these would not require an a priori choice of a reaction coordinate. Doing so would require computation of an MSM at each force, which would become expensive for fully atomistic models, but this could perhaps be mitigated if we could predict the effect of force on transitions between states as it might be feasible for these small force values.⁶¹ We expect to present a detailed comparison of these approaches in the near future.

V. SIMULATION DETAILS

A. Pulling

The PLUMED plugin library^62,63 was used to apply WTMetaD and pulling forces. A pulling force is achieved via a bias generated by a linear restraint formulated in PLUMED as

$$U_{\text{external}}=F(Q-a),$$ (7)

where F is a force constant in units of energy over length in Q units, Q is the CV to which the force is being applied, and a is the location of the restraint, which only sets the zero of energy but does not change the force applied. Therefore, in order to apply pulling forces, a negative F is fed to PLUMED. For our atomistic simulations, Q is a distance based CV in the protein, and units of kcal/mol and Å were used for energy and distance, respectively; thus, forces were applied in units of 1 kcal/(mol Å). Piconewtons can be computed into this unit system with $\approx 69.48\mathrm{p}\mathrm{N}$ equivalent to 1 kcal/(mol Å).

B. Rate calculation and FES estimates

To compute rates, many simulations must be run for each pulling force. Simulations were run up to the point where the ligand reached the unbound state. The COMMITTOR feature of PLUMED was used to terminate the simulation once specified CVs reached the unbound state. A WTMetaD bias was applied using the METAD feature of PLUMED using the ACCELERATION keyword such that α was computed within each simulation. The time at which the unbound state was reached and the acceleration factor at that time were recorded for each run; the product of the simulation time and acceleration factor gives the scaled residence time for each run. These sets of scaled transition times were used to determine the mean residence time (τ) and unbinding rate (τ⁻¹) for a given force using the following procedure.

ECDFs were built by histogramming the transition times against a set of log-spaced bins and getting a cumulative sum of the histogram divided by the total number of transition times. The ECDFs were fitted to the ideal CDF described by Eq. (5) to obtain τ and subsequently the rate. To determine how well the assumptions of InfrMetaD were met during the simulations and to validate computed rates, the protocol of Ref. 41 was followed. The two sample Kolmogorov–Smirnoff test determines the similarity between the transition time distributions. The null hypothesis is rejected if the transition times obtained from MetaD and the transition times obtained randomly from an exponential CDF with corresponding τ parameter do not come from the same underlying distribution at the 5% significance level. Additionally, the p-value provides a measure of goodness of fit. If the p-value of the KS test is higher than 0.05, then the sample distributions are said to come from the same underlying distribution.

1. Model potentials

Model systems from Fig. 1 were simulated using the PESMD tool in PLUMED. PESMD performs MD using Langevin dynamics.⁶⁴ Inputs are given in reduced units but converted internally to systeme international (SI) units by PLUMED. For both potentials, the temperature was set to 1.0, the friction constant was set to 1.0, the position was set to the corresponding starting point as described in the following, the seed was set to a random number, and the step size was set to 0.002. Inside PLUMED, the timestep was 0.002 ps, k_B = 0.008313 kJ/(mol K), and k_bT = 2.494 where T = 300 K as specified in the METAD command. Temperature in Lennard-Jones (LJ) units is given by (T* = k_BT/ɛ) where ɛ = 2.494. The force applied was in units of kJ/(mol nm); 1 kJ/(mol nm) is equivalent to 1.66 pN. All input files are available in the GitHub repository for this paper.

The potential in Fig. 1(a) is given by U(x) = 0.005(x − 5)²(x − 20)² with a bound state at x = 5 and an unbound state at x = 20 separated by an energy barrier corresponding to 15.8 kJ/mol.

The potential in Fig. 1(b) is constructed as a Gaussian mixture model, combining the two well potential from Ref. 8 with an additional harmonic potential. The potential energy is given by

$$\begin{array}{ll}\hfill U(x,y)=& -\ln \left(e^{{\left.-({(0.4y-1)}^2)-4\right)}^2+\frac{1}{2}{(x-6-y)}^2}+0.2e^{-{(x-11)}^2-2{(y+0.5)}^2}\right).\hfill \end{array}$$ (8)

The starting minima are located at (3.5, −2.5), (13.5, 7.5), and (11, −0.5), representing the bound, unbound, and intermediate states, respectively. The bound and unbound state are separated by a high energy barrier of 16 kJ/mol. The barrier between the intermediate state and unbound state is higher than from the bound state, 21 kJ/mol.

For the double well potential, InfrMetaD was performed with HEIGHT = 1.2, SIGMA = 0.2, BIASFACTOR = 6, and PACE = 4500. A total of 20 simulations were run for each pulling force; simulations were run up to the point at which the unbinding CV reached the unbound state. The unbound state was located at x = 20. FES calculations were performed with WTmetaD for every pulling force using the same parameters as above except for PACE, which was set to 650, and these simulations were performed for 7.5 × 10⁶ MD steps. For both rate and FES calculations, the starting point was the same with the first particle at the origin and the second at x = 5.

For the three well potential, InfrMetaD was performed with HEIGHT = 1.2, SIGMA = 0.2,0.2, BIASFACTOR = 6, and PACE = 7500 and both the x and y components of the distance were biased, but the pulling force was applied only in the x direction. Similarly here, a total of 20 simulations were run at each pulling force until the unbound state was reached.

FES calculations were performed with WTMetaD for every force using the same parameters as above except for PACE and BIASFACTOR, which were set to 500 and 14, respectively. These simulations were performed for 2 × 10⁷ MD steps. For FES calculations, all simulations started at the same point, x = 3.5, y = −2.5. However, for rate calculations, we first determined the coordinates of the minima at each force as these minima shift when forces are applied. For lower forces, the simulation starts at the first minimum, but as forces increase, this minimum disappears, and starting from F = 6, the simulations are initiated from the position of what was the intermediate state (see Fig. S5). The unbound state shifted from x = 13.5, y = 7.5 at zero force to x = 22.6, y = 8.6 at the last force, while the bound state shifted from x = 3.5, y = −2.5 to x = 7.5, y = −1.7 at F = 5; starting from F = 6, this minimum disappears and simulations were started from x = 12, y = −0.5, which continued shifting up to x = 13, y = −0.5 at the last force. The starting positions and COMMITTOR bounds were set accordingly.

2. Cavity-ligand model

The model consists of a semi-hollow cube of pseudo atoms resembling carbon atoms that are ordered in a hexagonally close-packed lattice. Moreover, the cube consists of two categories of hydrophobic atoms; the cavity atoms and the anchor or wall atoms. The radius of the cavity is 8 Å, and the lattice constant a is 2 Å. The ligand is a 60-atom (C60) fullerene (buckyball), which has a weak van der Waals attraction to the cavity. The atoms in the cavity have a higher attraction to the ligand than do the anchor atoms, and the whole complex model is solvated with TIP4P water (Fig. 5). GROMACS⁶⁵ files for this model from Ref. 56 were provided by the Mondal group, and identical GROMACS parameters are employed here (all input information is contained in this paper’s GitHub).

Non-bonded interactions are determined by GROMACS using the OPLS combination rule. The non-bonded interactions of the CP–CP, CW–CP, and CW–CW pairs were excluded by setting their LJ parameters to 0. The entire lattice had its position fixed. The interactions between the different molecules other than water are summarized in Table I.

TABLE I.

Lennard-Jones parameters for cavity and ligand atoms. CW, CP, and CF refer to the anchor, cavity, and fullerene atoms, respectively. The parameters for inter-molecular interactions are described by combination rules: ${\sigma }_{ij}=\sqrt{{\sigma }_i{\sigma }_j}$ and ${\epsilon }_{ij}=\sqrt{{\epsilon }_i{\epsilon }_j}$.

i	j	σ(nm)	$\epsilon (\frac{\mathrm{k}\mathrm{J}}{\mathrm{m}\mathrm{o}\mathrm{l}})$
CF	CF	0.35	0.276 144
CW	CW	0.415 2	0.002 40
CP	CP	0.415 2	0.008 00
CF	CW	0.381 2	0.025 74
CF	CP	0.381 2	0.047 00

InfrMetaD was performed using HEIGHT = 0.287, SIGMA = 0.3, BIASFACTOR = 15, and PACE = 5000. Here, units were set to Å, fs, and kcal/mol for length, time, and energy respectively. Both the InfrMetaD bias and the pulling force were applied on the 3D distance between the COMs of the cavity and ligand. A set of 20 simulations were run for each pulling force until the unbound state at Z = 16 Å and ρ = 6–10 Å was reached. For all forces, each simulation in the set of 20 was started from a different starting point obtained from 20 separate equilibration runs.

FES calculations were performed for all forces using HEIGHT = 0.478, SIGMA = 0.3,0.1, BIASFACTOR = 15, and PACE = 300. The bias was applied to both the transverse and radial distance of the COM of the sphere from the COM of the cavity while the pulling force was applied to the 3D distance. PLUMED walls were applied for the transverse and radial distance CVs at 21 and 12 Å, respectively. A single simulation was performed at each force to obtain the FES. All FES calculations were run for 50 ns. In all cases, a 2 fs MD timestep was used.

3. Streptavidin–biotin complex

In Ref. 57, the dimeric version of the biotin–streptavidin complex was studied to determine an unbinding CV and compute an unbinding rate. Here, we used the same system and calculated unbinding rates at several pulling forces. For the SA/b atomistic system, a bound structure of biotin and a dimeric form of streptavidin was obtained from the protein data bank with PDB ID: 3RY2⁶⁶ (Fig. 8). The all atom AMBER ff99SB*-ILDN⁶⁷ force field was used to describe all bonded and non-bonded interactions in the protein, and the TIP4P model was used for water. The charged biotin ligand was parameterized with AM1-bcc charges and GAFF⁶⁸ parameters as in Ref. 57.

The ligand and protein structures were combined and neutralized with counter ions. The complex was then solvated with TIP4P water, and an ion concentration of 150 mM NaCl was added to the system to approximate physiological/experimental conditions. The full system’s energy was later minimized, and subsequent NVT and NPT 1 ns equilibration was performed while restraining the complex in its bound pose. The Nose–Hoover thermostat⁶⁹ and the Parrinello–Rahman⁷⁰ barostat were used in the NPT production runs at 300 K with a coupling time of 1 ps for temperature and 2 ps for pressure. A short range cutoff of 1.2 nm was employed for the electrostatics. Note that all topology information and Gromacs simulation parameters can be found in the GitHub repository for this paper. For rate calculations, an optimized one dimensional reaction coordinate reported in Ref. 57 was used as the collective variable for InfrMetaD. The reaction coordinate is a linear combination of two distances, rc = ψ₁ + 0.75ψ₂, where ψ₁ is the distance between the COM of the oxygen (OG) in residue S45 and the nitrogen in residue N49 and the COM of the C11 and N2 atoms in biotin and ψ₂ is the distance between the carbon (CG) atom in residue D128 and the N1 atom in biotin. The unbound state was located at rc = 30 Å.

InfrMetaD was performed using HEIGHT = 0.478, SIGMA = 0.2, BIASFACTOR = 15, and PACE = 7500. The ligand was pulled along the distance between the COM of the binding pocket and the COM of the ligand with constant force (binding pocket consists of residues:L25, S27, Y43, S45, V47, G48, A50, W79, R84, A86, S88, T90, W92, W108, L110, and D128 following numbering in 3RY2⁶⁶ as in Ref. 31). A total of 20 runs were performed for each force in the 0–72 pN range in intervals of 3 pN. In this case, we followed the same protocol as in Ref. 52 and started all simulations in the set of 20 from the same equilibrated structure.

FES estimates were obtained by running WTMetaD simulations for each force with HEIGHT = 0.478, SIGMA = 0.2, BIASFACTOR = 12, and PACE = 600. PLUMED walls were applied to both ψ₁ and ψ₂ at 22 and 14 Å, respectively. The ligand was pulled along the distance between the COMs of the binding pocket and the ligand with constant force. The simulations were started from separate equilibrated structures.

The FES estimate for the system at zero force (Fig. 9) was obtained by running 20 such WTmetaD simulations for 100 ns each. Then, the PLUMED function sum_hills feature was used to obtain an FES for each simulation. Then, these surfaces were averaged to obtain the FES estimate. The same procedure was followed for the rest of the forces although only 13 × 50 ns simulations were performed for each. The FES estimates shown in Figs. S8(c) and S8(d) were obtained via last-bias reweighting using PLUMED.⁷¹ For each simulation, the metadynamics bias potential at the end of the simulation was obtained from the file containing the hills. Corresponding weights were obtained via the REWEIGHT_BIAS function, which takes the last-bias potential as its input. The weights were fed to the HISTOGRAM routine to histogram the pulled CV. Finally, the resulting histogram was converted to a FES using the CONVERT_TO_FES command. The PLUMED driver program was used to run all commands using as the input the trajectories of the simulations described above. As for the cavity-ligand model, all units were set to Å, fs, and kcal/mol for length, time, and energy, respectively, and all simulations were performed in GROMACS⁶⁵ using a 2 fs MD timestep.

SUPPLEMENTARY MATERIAL

See the supplementary material for nine additional figures, showing CDF fits for each system at different forces, dependence of the rate on simulation parameters and pulling direction, and additional free energy estimates for the SA/b system.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

DATA AVAILABILITY

Scripts and data to produce all figures in the manuscript as well as input files to generate the data can be found at https://github.com/hocky-research-group/PenaUnbindingPaper.