Abstract
To derive meaning from sound, the brain must integrate information across many timescales. What computations underlie multiscale integration in human auditory cortex? Evidence suggests that auditory cortex analyzes sound using both generic acoustic representations (e.g. spectrotemporal modulation) and category-specific computations, but the timescales these putatively distinct computations integrate over remain unclear. To answer this question, we developed a general method to estimate sensory integration windows – the time window when stimuli alter the neural response – and applied our method to intracranial recordings from neurosurgical patients. We show that human auditory cortex integrates hierarchically across diverse timescales spanning ~50 to 400 milliseconds. Moreover, we find that neural populations with short and long integration windows exhibit distinct functional properties: short-integration electrodes (<200 milliseconds) show prominent spectrotemporal modulation selectivity, while long-integration electrodes (>200 milliseconds) show prominent category selectivity. These findings reveal how multiscale integration organizes auditory computation in the human brain.
Keywords: temporal integration, receptive field, hierarchical organization, auditory cortex, timescale, iEEG, ECoG, electrocorticography, natural sounds, speech, music, epilepsy
Time is the fundamental dimension of sound and temporal integration is thus fundamental to audition. To recognize a complex structure like a word, the brain must integrate information across a wide range of timescales from tens to hundreds of milliseconds (Extended Data Fig 1 plots a histogram of phoneme, syllable and word durations)1–3. At present, the neural computations that underly multiscale integration remain unclear. Prior evidence suggests that the human brain analyzes sound using both generic acoustic computations, such as spectrotemporal modulation filtering4–7, as well as category-specific computations that are nonlinearly tuned for important categories like speech and music8–15. Both modulation filtering and category-specific computations could in principle integrate information across a wide range of timescales, since natural sounds like speech contain temporal modulations and category-specific structure at many temporal scales1,2,16–18(Extended Data Fig 1). Anatomically, there is evidence that modulation tuning and category selectivity are localized to primary and non-primary regions, respectively8,19. But the time window that primary and non-primary regions integrate over is unknown, and thus it remains unclear whether generic and category-specific computations integrate over similar or distinct timescales.
To answer this question, we need to measure the time window over which human cortical regions integrate information. Integration windows are often defined as the time window when stimuli alter the neural response20–22. Although this definition is simple and general, there is no simple and general method to estimate integration windows. Many methods exist for inferring linear integration windows with respect to a spectrogram5,22–24, but human cortical responses exhibit prominent nonlinearities, particularly in non-primary regions19. Flexible, nonlinear models are challenging to fit given limited neural data25,26, and even if one succeeds, it is not obvious how to measure the model’s integration window. Methods for assessing temporal modulation tuning6,7,27–31 are insufficient, since a neuron could respond to fast modulations over either a short or long integration window or respond to a complex structure like a word that is poorly described by its modulation content. Finally, temporal scrambling can reveal selectivity for naturalistic temporal structure11,21,32,33, but many regions in auditory cortex show no difference between intact and scrambled sounds11, presumably because they respond to features that do not differ between intact and scrambled stimuli (e.g. the frequency spectrum).
To overcome these limitations, we developed a method that directly estimates the time window when stimuli alter a neural response (the temporal context invariance or TCI paradigm; Fig 1). We present sequences of natural stimuli in two different random orders such that the same segment occurs in two different contexts. While context has many meanings34, here we simply define context as the stimuli which surround a segment. If the integration window is shorter than the segment duration, there will be a moment when it is fully contained within each segment. As a consequence, the response at that moment will be unaffected by surrounding segments. We can therefore estimate the extent of temporal integration by determining the minimum segment duration needed to achieve a context invariant response.
Fig 1. Temporal context invariance (TCI) paradigm.
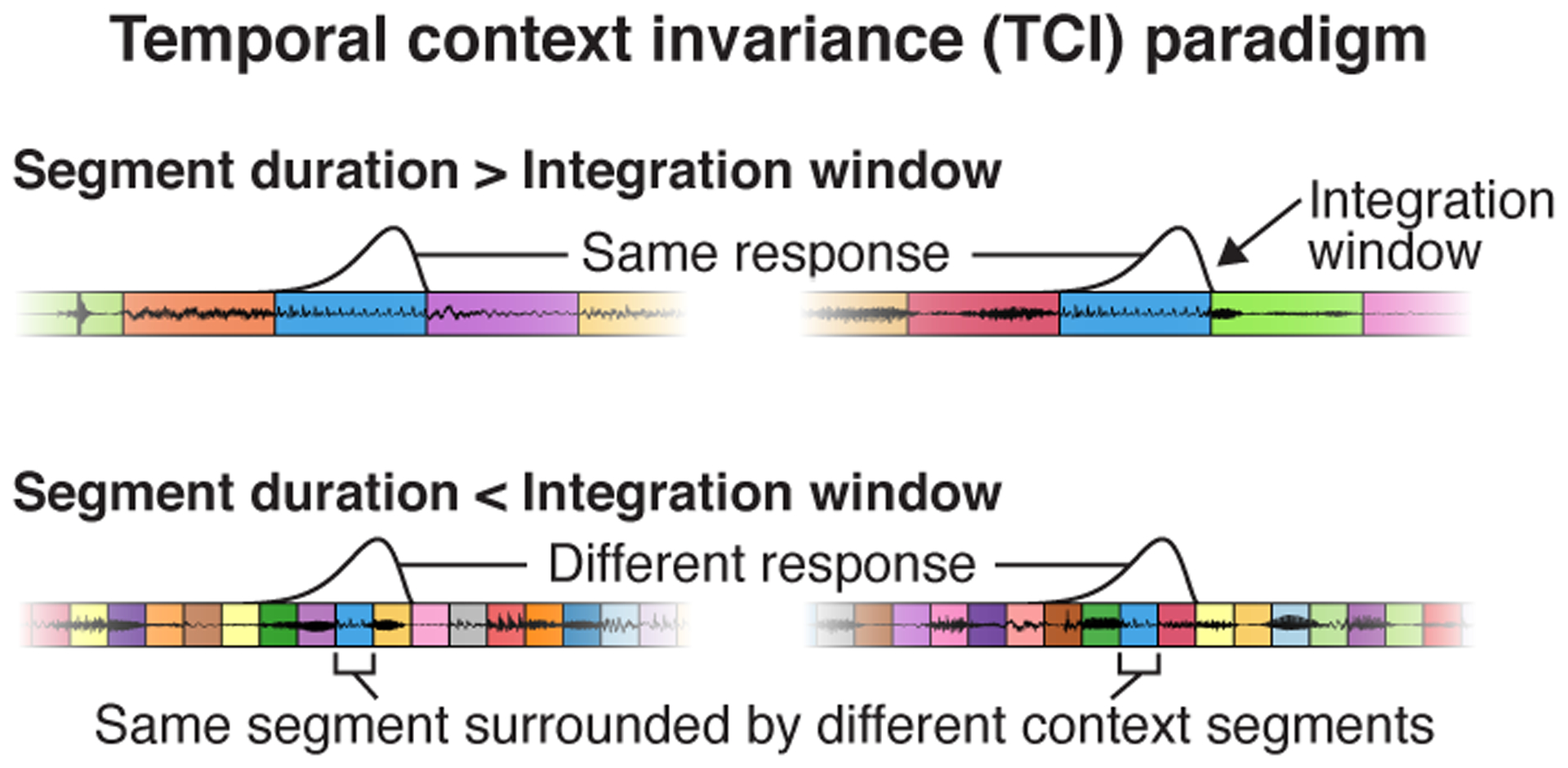
Schematic of the paradigm used to measure integration windows. Segments of natural stimuli are presented using two different random orderings (concatenated using cross-fading). As a consequence, the same segment is surrounded by different context segments. If the segment duration is longer than the integration window (top panel), there will be a moment when the window is fully contained within each segment. As a consequence, the response at that moment will be unaffected by the surrounding context segments. If the segment duration is shorter than the integration window (bottom panel), the integration window will always overlap the surrounding context segments, and they can therefore alter the response. The TCI paradigm estimates the minimum segment duration needed to achieve a context invariant response. This figure plots waveforms for an example sequence of segments that share the same central segment. Segment boundaries are demarcated by colored boxes. The hypothesized integration window is plotted above each sequence at the moment when it best overlaps the shared segment.
TCI does not make any assumptions about the type of response being measured. As a consequence, the method is applicable to sensory responses from any modality, stimulus set, or recording method. We applied TCI to intracranial EEG (iEEG) recordings, collected from patients undergoing surgery for intractable epilepsy. Such recordings provide a rare opportunity to measure human brain responses with spatiotemporal precision, which is essential to studying temporal integration. We used a combination of depth and surface electrodes to record from both primary regions in the lateral sulcus as well as non-primary regions in the superior temporal gyrus (STG), unlike many iEEG studies that have focused on just the lateral sulcus35 or STG5,36. The precision and coverage of our recordings were both essential to revealing how the human auditory cortex integrates across multiple timescales.
Results
Overview of experiment and TCI paradigm.
We recorded intracranial EEG responses to sequences of natural sound segments that varied in duration from 31 milliseconds to 2 seconds (in octave steps). For each segment duration, we created two 20-second sequences, each with a different random ordering of the same segments (concatenated using cross-fading to avoid boundary artifacts). Segments were excerpted from 10 natural sounds, selected to be diverse so they differentially drive responses throughout auditory cortex. The same natural sounds were used for all segment durations, which limited the number of sounds we could test given the limited time with each patient; but our key results were robust across the sounds tested (the results of all robustness analyses are described in the section Human auditory cortex integrates hierarchically across diverse timescales). Because our goal was to characterize integration windows during natural listening, we did not give subjects a formal task. To encourage subjects to listen to the sounds, we asked them to occasionally rate how scrambled the last stimulus sequence was (shorter segment durations sound more scrambled; if patients were in pain or confused we simply asked them to listen).
All of our analyses were performed on the broadband gamma power response timecourse of each electrode (70–140 Hz; results were robust to the frequency range). We focus on broadband gamma because it provides a robust measure of local electrocortical activity37,38 and can be extracted using filters with relatively narrow integration windows, which we verified in simulations had a negligible effect on the estimated neural integration windows (see Simulations in Methods). By contrast, we found that low-frequency, phase-locked activity was substantially biased by the long-integration filters required to extract low-frequency activity and thus was not the focus of our analyses.
Our method has two key components. First, we estimate the degree to which the neural response is context invariant at each moment in time using an analysis we refer to as the “cross-context correlation”. Second, we use a computational model to estimate the integration window from these moment-by-moment estimates.
Cross-context correlation.
The cross-context correlation is measured separately for each electrode and segment duration. First, we organize the response timecourse to all segments of a given duration in a matrix, which we refer to as the segment-aligned response (SAR) matrix (Fig 2a). Each row of the SAR matrix contains the response timecourse surrounding a single segment, aligned to segment onset. Different rows thus correspond to different segments and different columns correspond to different lags relative to segment onset. We compute two versions of the SAR matrix using the two different contexts for each segment, extracted from the two different sequences. The central segment is the same between contexts, but the surrounding segments differ.
Fig 2. Cross-context correlation.
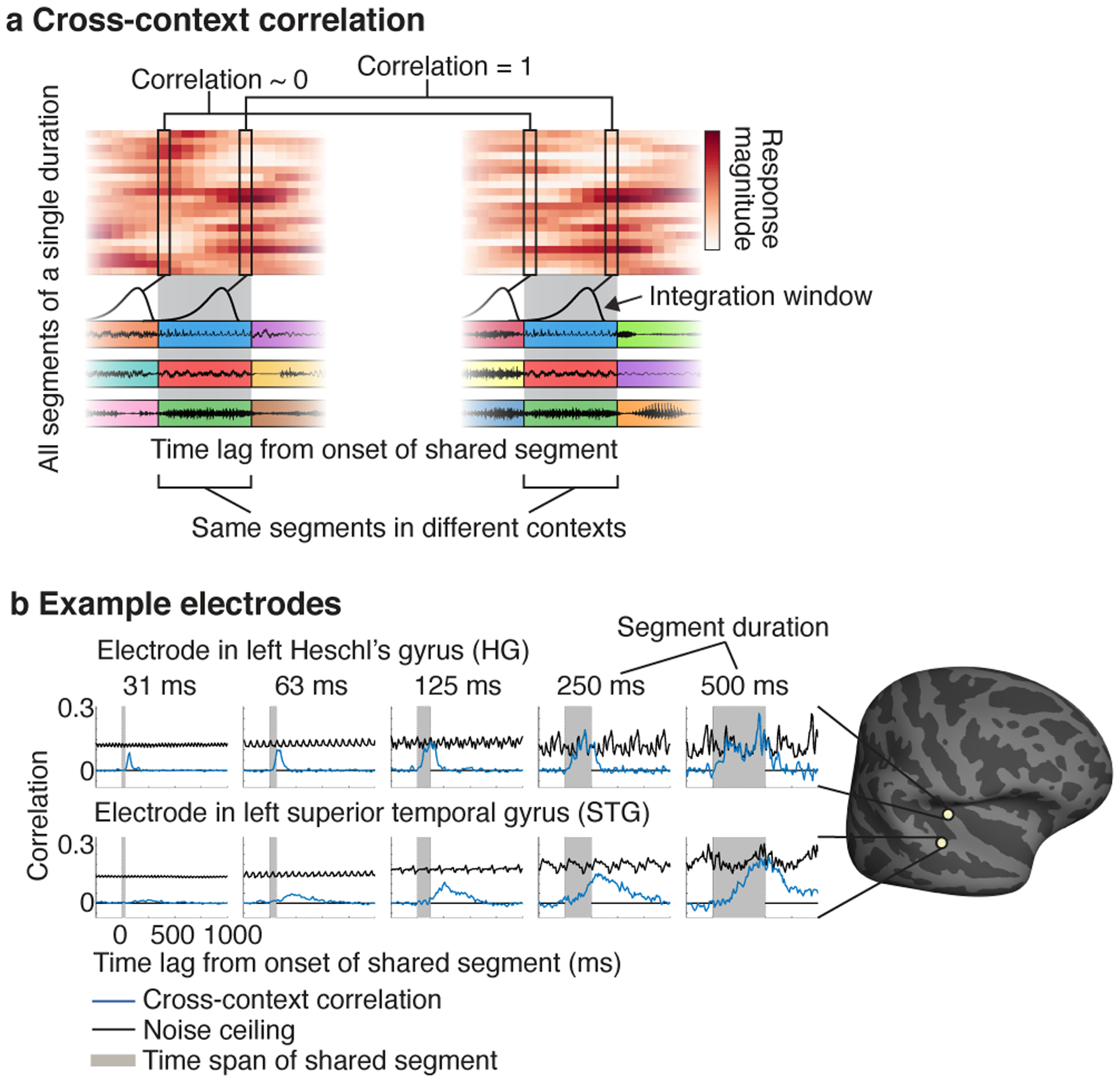
a, Schematic of the analysis used to assess context invariance for a single electrode and segment duration. The response timecourses to all segments of a given duration are organized as a matrix: the segment-aligned response (SAR) matrix. Each row contains the response timecourse to a different segment, aligned to segment onset. A separate matrix is calculated for each of the two contexts. The central segments are the same across contexts, but the surrounding segments differ. The gray region highlights the time window when the shared segments are present. To determine if the response is context invariant, we correlate corresponding columns across SAR matrices from different contexts (the “cross-context correlation”). This analysis is schematized by the linked columnar boxes. For each box, we plot a schematic of the integration window at that moment in time. At the start of the shared segments (first box pair), the integration window will fall on the preceding contexts segments, which are random across contexts and so the cross-context correlation should be approximately zero. As the lag relative to segment onset increases, the integration will begin to overlap the shared central segment. If the integration window is less than the segment duration, there will be a lag when the response is the same across contexts and the correlation will be 1 (second box pair). In practice, noise prevents a correlation value of 1, but we can compute a noise ceiling by measuring the correlation when the context is identical using repeated presentations of each sequence (not depicted). b, The cross-context correlation (blue line) and noise ceiling (black line) for two example electrodes from the left hemisphere of one patient (HG: Heschl’s gyrus, STG: superior temporal gyrus). Each plot shows a different segment duration. The gray region shows the time interval when the shared segment was present. The STG electrode required longer segment durations for the cross-context correlation to reach the noise ceiling, and the build-up/fall-off with lag was more gradual for the STG electrode, consistent with a longer integration window. The plots in this panel were derived from ~40 minutes of data.
Our goal is to determine if there is a lag when the response is the same across contexts. We instantiate this idea by correlating corresponding columns across SAR matrices from different contexts (schematized by the linked columnar boxes in Fig 2a). At segment onset (first box pair in Fig 2a), the cross-context correlation should be near zero, since the integration window must overlap the preceding segments, which are random across contexts. As time progresses, the integration window will start to overlap the shared segment, and the cross-context correlation should increase. Critically, if the integration window is less than the segment duration, there will be a lag where the integration window is fully contained within the shared segment, and the response should thus be the same across contexts, yielding a correlation of 1 modulo noise (second box pair in Fig 2a). To correct for noise, we measure the test-retest correlation when the context is the same, which provides a noise ceiling for the cross-context correlation (not depicted in Fig 2a).
The shorter segments tested in our study were created by subdividing the longer segments. As a consequence, we could also consider cases where a segment was a subset of a longer segment and thus surrounded by its natural context, in addition to the case described so far when a segment is surrounded by random other segments. Since our analysis requires that the two contexts differ, one context has to be random, but the other can be random or natural. In practice, we found similar results using random-random and random-natural contexts, and thus pooled across both types of context for maximal statistical power (results comparing random and natural contexts are described in the section Human auditory cortex integrates hierarchically across diverse timescales).
We plot the cross-context correlation and noise ceiling for segments of increasing duration for two example electrodes from the same subject: an electrode in left posteromedial Heschl’s gyrus (HG) and one in the left superior temporal gyrus (STG) (Fig 2b). The periodic variation evident in the noise ceiling is an inevitable consequence of correlating across a fixed set of segments (see Cross-context correlation in the Methods for an explanation). For the HG electrode, the cross-context correlation started at zero and quickly rose. Critically, for segment durations greater than approximately 63 milliseconds, there was a lag where the cross-context correlation equaled the noise ceiling (or in the case of 63 milliseconds came very close), indicating a context-invariant response. For longer segment durations (e.g. 250 or 500 ms), the cross-context correlation remained yoked to the noise ceiling for an extended duration indicating that the integration window remained within the shared segment for an extended time window. This pattern is what one would expect for an integration window that is ~63 milliseconds, since stimuli falling outside of this window have little effect on the response.
By comparison, the results for the STG electrode suggest a much longer integration window. Only for segment durations of ~250–500 milliseconds did the cross-context correlation approach the noise ceiling, and its build-up and fall-off with lag was considerably slower. This pattern is what one would expect for a longer integration window, since it takes more time for the integration window to fully enter and exit the shared segment. Virtually all electrodes with a reliable response to sound exhibited a similar pattern, but the segment duration and lag needed to achieve an invariant response varied substantially (Extended Data Fig 2 shows 20 representative electrodes). This observation indicates that auditory cortical responses have a meaningful integration window, outside of which responses are largely invariant, but the extent of this window varies substantially across auditory cortex.
Model-estimated integration windows.
In theory, one could estimate the extent of the integration window as the shortest segment duration for which the peak of the cross-context correlation exceeds some fraction of the noise ceiling. This approach, however, would be noise-prone since a single noisy data point at one lag and segment duration could alter the estimate. To overcome this issue, we developed a model that allowed us to pool noisy correlation values across all lags and segment durations to arrive at a single estimate of the integration window.
We modeled integration windows using a Gamma distribution, which is a standard, unimodal distribution commonly used to model temporal windows (Fig 3a)39,40. We varied the width and center of the model window, excluding combinations of widths and centers that resulted in a non-causal window since this would imply the response depends upon the future. The width of the integration window is the key parameter we would like to estimate, and was defined as the smallest interval that contained 75% of the window’s mass. The center of the integration window was defined as the window’s median and reflects the overall latency between the integration window and the response. We also varied the window shape from more exponential to more bell-shaped, but found the shape had little influence on the results.
Fig 3. Model-estimated integration windows.
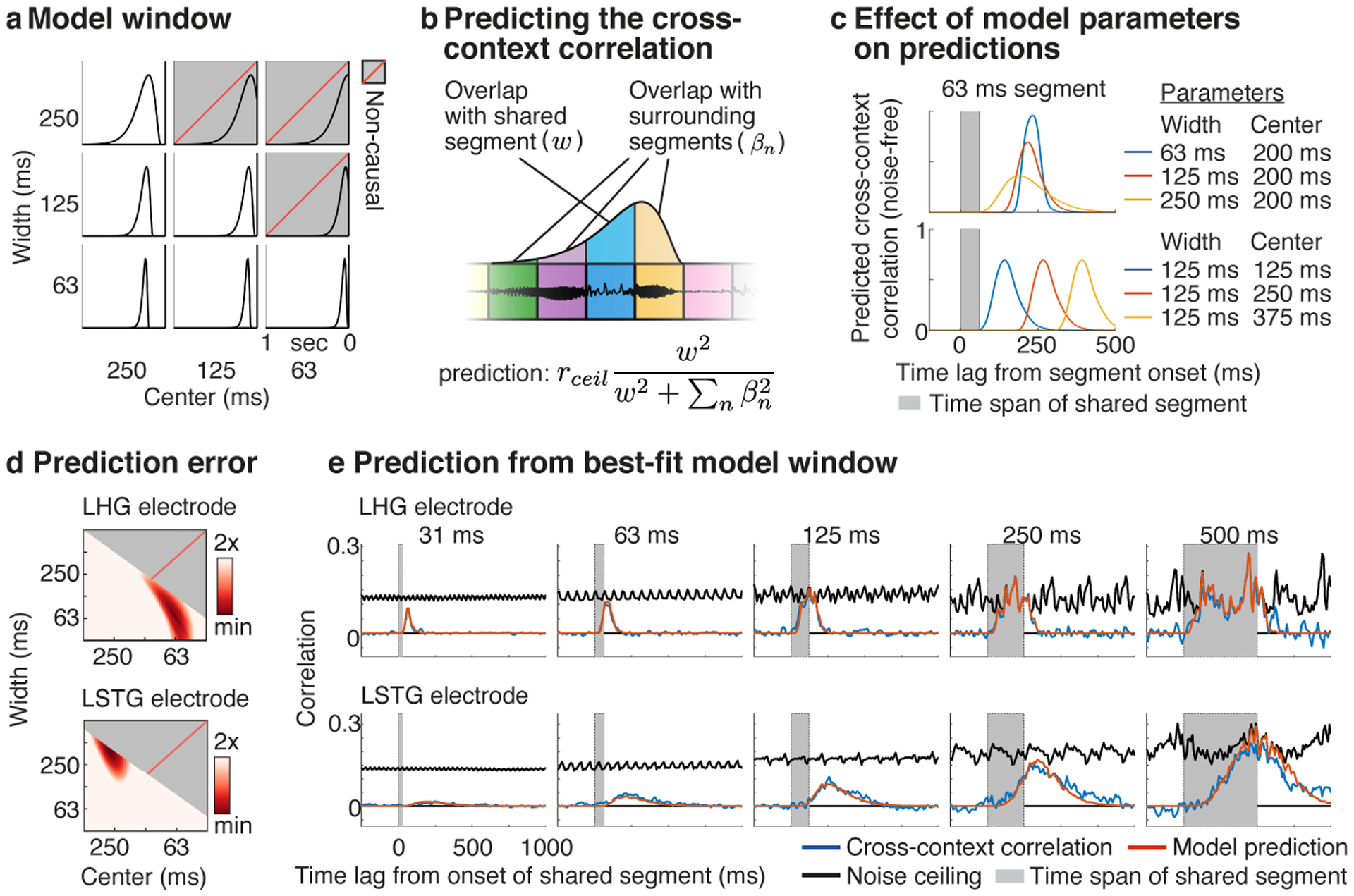
a, Temporal integration windows were modeled using a Gamma distribution. The width and center of the model window were varied, excluding combinations of widths and centers that resulted in a non-causal window (indicated by gray boxes with dashed red line). b, Schematic showing the procedure used to predict the cross-context correlation. For a given lag and segment duration, we measured how much the window overlapped the shared central segment (w, blue segment) vs. all surrounding context segments (βn, yellow, purple, and green segments). The cross-context correlation should reflect the fraction of the response variance due to the shared segment, multiplied by the noise ceiling (rceil). The variance due to each segment is given by the squared overlap with the model window. The overlap measures (w, βn) varied as a function of lag and segment duration and were computed by convolving the model window with boxcar functions representing each segment (tapered at the boundaries to account for cross-fading). c, Illustration of how the width (top panel) and center (bottom panel) of the window alter the model’s prediction for a single segment duration (63 milliseconds). Increasing the width lowers and stretches-out the predicted cross-context correlation, while increasing the center shifts the cross-context correlation to later lags. d, The prediction error for model windows of varying widths and centers for the example electrodes from Figure 2b. Redder colors indicate lower error. e, The measured and predicted cross-context correlation for the best-fit window with lowest error (same format as Fig 2b).
The cross-context correlation depends on the degree to which the integration window overlaps the shared segment vs. the surrounding context segments. We therefore predicted the cross-context correlation by measuring the overlap between the model window and each segment, separately for all lags and segment durations (Fig 3b). The equation used to predict the cross-context correlation from these overlap measures is shown in Figure 3b and described in the legend. A formal derivation is given in the Methods.
Figure 3c illustrates how changing the width and center of the model window alters the predicted correlation. Increasing the width lowers the peak of the cross-context correlation, since a smaller fraction of the window overlaps the shared segment at the moment of maximum overlap. The build-up and fall-off with lag is also more gradual for wider windows since it takes longer for the window to enter and exit the shared segment. Increasing the center simply shifts the cross-context correlation to later lags. We varied these model parameters and selected the window that best-predicted the measured cross-context correlation.
We tested the ability of our complete analysis pipeline to recover ground truth integration windows from a variety models: (1) a model that integrated waveform magnitudes within a known temporal window (2) a model that integrated energy within a cochlear frequency band (3) a standard spectrotemporal model that integrates energy across time and frequency19,40 (4) a simple, deep neural network with a known integration window (see Simulations in Methods for details). Our simulations revealed two upward biases: one present at very low SNRs when using the mean-squared error loss and one present for just the spectrotemporal model due to the presence of strong responses at the boundary between segments. We corrected these two biases by modifying the loss and including an explicit boundary model (see Model-estimated integration windows and Modeling boundary effects in the Methods). With these modifications, we found that we could accurately infer integration widths and centers from all four models using noisy responses with comparable signal-to-noise ratios as those from our electrodes (Extended Data Fig 3).
Figure 3d,e shows the results of applying our model to the example electrodes from Figure 2b. For the example HG electrode, the cross-context correlation was best-predicted by a window with a narrow width (68 ms) and early center (64 ms) compared with the STG electrode, which was best-predicted by a wider, more delayed window (375 ms width, 273 ms center). These results validate our qualitative observations and provide us with a quantitative estimate of each electrode’s integration window. We used these estimates to understand how temporal integration organizes cortical computation in human auditory cortex.
Anatomical organization.
We first examined how different regions of human auditory cortex collectively integrate across multiple timescales. We identified 190 electrodes with a reliable response to sound across 18 patients (test-retest correlation: r > 0.1; p < 10−5 via a permutation test across sound sequences; 128 left hemisphere; 62 right hemisphere). From these electrodes, we created a map of integration widths and centers, discarding a small fraction of electrodes (8 electrodes; 2 right hemisphere; 6 left hemisphere) where the model predictions were not highly significant (p < 10−5 via a phase-scrambling analysis) (Fig 4a). This map was created by localizing each electrode on the cortical surface, and aligning each subject’s brain to a common anatomical template. By necessity, we focus on group analyses due to the sparse, clinically-driven coverage in any given patient. Most electrodes were located in and around the lateral sulcus and STG, as expected9.
Fig 4. Anatomy of model-estimated integration windows.
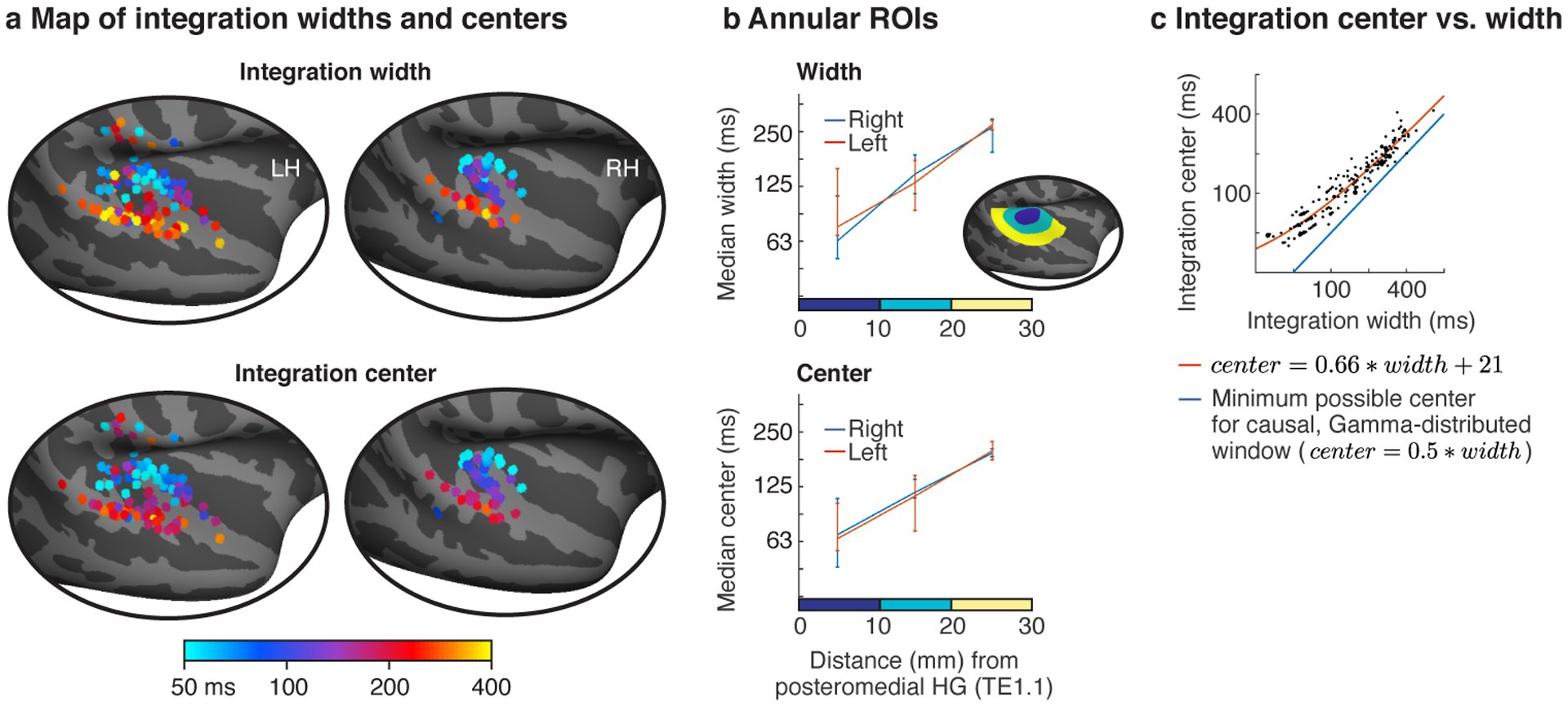
a, Map of integration widths (top) and centers (bottom) for all electrodes with a reliable response to sound. b, Electrodes were binned into ROIs based on their distance to a common anatomical landmark of primary auditory cortex (posteromedial Heschl’s gyrus, TE1.1). This figure plots the median integration width and center across the electrodes in each bin. Inset shows the ROIs for one hemisphere. Error bars plot one standard error of the bootstrapped sampling distribution across subjects and electrodes. c, Scatter plot of integration centers vs. widths for all electrodes. The integration width places a lower bound on the integration center for a causal window (blue line). Integration centers scaled approximately linearly with the integration width and remained relatively close to the minimum possible for a causal window. The orange line shows the affine function that best fit the data (equation shown). The line appears curved because the axes are logarithmically scaled. Each dot corresponds to an electrode and larger dots indicate that multiple electrodes were assigned to that pairing of centers/widths.
We observed a diverse range of integration windows with widths varying from approximately 50 to 400 milliseconds. Moreover, integration windows exhibited a clear anatomical gradient: integration widths and centers increased substantially from primary regions near posteromedial HG to non-primary regions near STG. We quantified this trend by binning electrodes into anatomical regions-of-interest (ROIs) based on their distance to primary auditory cortex (PAC), defined as posteromedial HG (TE1.1) (Fig 4b)19 (this analysis included 154 electrodes across all 18 subjects that were within a 30 mm radius of posteromedial HG; 53 right hemisphere; 101 left hemisphere). Significance was evaluated using a linear mixed effects model trained to predict the electrode integration windows from un-binned distances and hemisphere labels (with random intercepts and slopes for subjects). We controlled for electrode type (depth, grid, strip) by including it as a covariate in the model, although we did not observe any evidence for a difference in integration windows between electrode types (Extended Data Fig 4a).
Our analysis revealed a three- to four-fold increase in integration widths and centers from primary to non-primary regions (median integration width: 74, 136, 274 ms; median integration center: 68, 115, 197 ms). As a consequence, there was a highly significant effect of distance to PAC on the measured integration windows (width: F1,20.85 = 20.56, p < 0.001, βdistance = 0.064 octaves/mm, CI = [0.036, 0.091]; center: F1,20.38 = 24.80, p < 0.001, βdistance = 0.052 octaves/mm, CI = [0.032, 0.073]; N=154 electrodes). There was no significant difference in integration widths or centers between the two hemispheres (width: F1,7.38 = 0.84, p = 0.39, βhemi = 0.16 octaves (left - right), CI = [−0.19, 0.52]; center: F1,10.17 = 1.81, p = 0.21, βhemi = 0.17 octaves (left - right), CI = [−0.08, 0.43]; N=154 electrodes), although we note that intracranial recordings are under-powered for detecting hemispheric differences due to the limited coverage, which is often strongly biased towards one hemisphere in any given patient (the hemisphere where the epileptic focus is thought to arise from). These findings were robust across the specific sounds tested (Extended Data Fig 5a), the type of context used to assess invariance (random vs. natural; Extended Data Fig 5b), the shape of the model window (Extended Data Fig 5c), and the frequency range used to measure broadband gamma (Extended Data Fig 5d).
Across all electrodes, we found that integration centers were an approximately affine function (linear plus constant) of the integration width (Fig 4c; orange line shows the best-fit affine function; note that affine functions unlike linear functions appear curved on a log-log plot like that used in Figure 4c). This dependency is not an artifact of our model since we found that we could independently estimate integration centers and widths in simulations (Extended Data Fig 3a), as expected given that integration widths and centers have distinct effects on the cross-context correlation (Fig 3c). In part as a consequence of this observation, we found that integration centers were relatively close to the minimum possible value for a causal window (blue line, Fig 4c) even when not explicitly constrained to be causal (Extended Data Fig 6). Since the integration center can be thought of as the overall latency between the stimulus and the response, this finding suggests that auditory cortex analyzes sounds about as quickly as possible given the integration time. The fact that our data were well-fit by an affine function (linear plus a constant) rather than a purely linear function suggests that there might be a minimum latency (the constant, which we estimated to be 21 milliseconds) that is independent of the integration width, perhaps reflecting fixed synaptic delays required for information to reach auditory cortex.
Functional organization.
What is the functional consequence of hierarchical temporal integration for the analysis of natural sounds? A priori it seemed possible that spectrotemporal modulation tuning and category-specific computations could both be used to analyze a wide range of timescales. Speech for instance has a wide range of temporal modulations16,17,41, as well as unique phonemic, syllabic, and word-level structure spanning tens to hundreds of milliseconds1,2,42,43 (Extended Data Fig 1). But the anatomical hierarchy revealed by our integration window maps combined with prior evidence that modulation tuning and category selectivity are localized to primary and non-primary regions8,19 suggested an alternative hypothesis: that spectrotemporal modulation and category-specific computations integrate over distinct timescales. We sought to directly test this hypothesis, and if true, determine the specific timescales that modulation and category-specific computations integrate information over.
We measured responses in a subset of 104 electrodes from 11 patients to a larger set of 119 natural sounds (4-seconds in duration), drawn from 11 categories (listed in Fig 5b). We subdivided the electrodes from these patients into three equally sized groups based on the width of their integration window (Fig 5a), and examined the functional selectivity of the electrodes in each group (Fig 5b–c). We pooled across both hemispheres because we had fewer electrodes and because integration windows (Fig 4) and functional selectivity for natural sounds are coarsely similar across hemispheres8,9,11.
Fig 5. Functional selectivity in electrodes with differing integration windows.
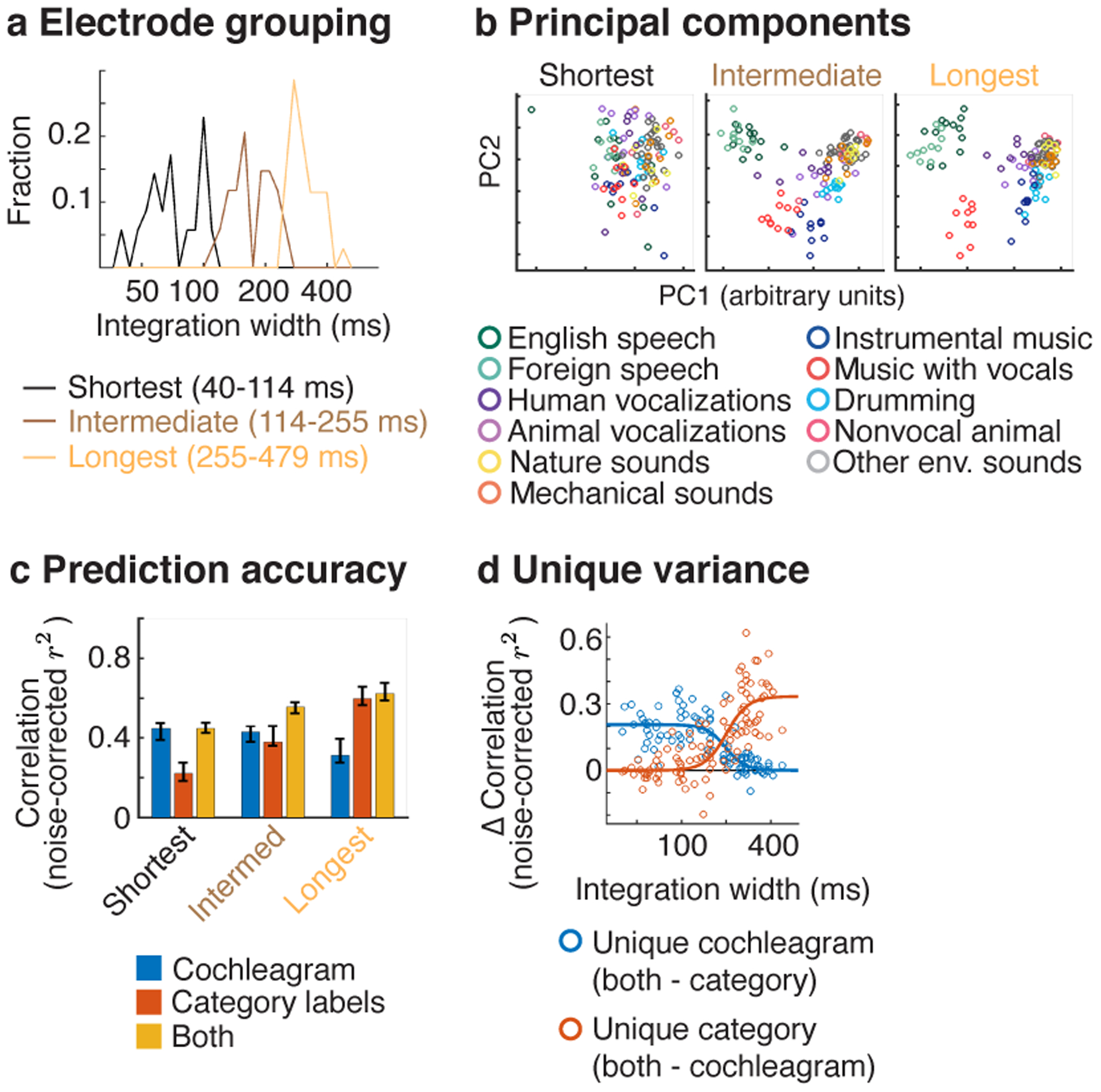
Responses were measured in a subset of patients to a larger collection of 119 natural sounds (4-seconds in duration) from 11 sound categories, listed in panel b. a, Electrodes from these patients were subdivided into three equally sized groups based on the width of their integration window. b, This panel plots the time-averaged response of the electrodes across all 119 sounds, projected onto the top 2 principal components from each group. The population response to sounds from different categories becomes increasingly segregated as integration windows increase. c, The accuracy of cochleagrams (blue line), category labels (red line), and both cochleagrams and categories in predicting electrode response timecourses. This panel plots the median squared correlation for each feature set (noise-corrected) across the electrodes in each group. d, This panel plots the difference in prediction accuracy between the combined model and the individual models (i.e. just cochleagrams or just category labels), which provides a measure of the unique variance explained by each feature type. Each circle corresponds to a single electrode (N=104). A logistic curve has been fit to the distribution of prediction accuracies for each feature set.
To visualize any potential selectivity for sound categories, we projected the time-averaged response of each electrode to each 4-second sound onto the top two principal components from each group (Fig 5b). This analysis revealed a substantial increase in category separation for electrodes with long integration windows. The weak/absent category separation for short integration electrodes is not an artifact of just analyzing the first two principal components, since similar results were obtained when we explicitly selected components with maximum category separation (Extended Data Fig 7).
To quantify selectivity for categories vs. standard acoustic features, we attempted to predict the response timecourse of each electrode (without any averaging) using cochleagrams and category labels (Fig 5c). Cochleagrams are similar to spectrograms but are computed using filters designed to mimic the pseudo-logarithmic frequency resolution of cochlear filtering39. This analysis thus provides an estimate of the fraction of the response that can be predicted using a linear spectrotemporal receptive field5,23. The category labels indicated the membership of each sound in each category for all timepoints with sound energy above a minimum threshold. As is standard, we predicted the response of each electrode using a regression model with temporally delayed copies of each regressor. The delays were selected to span the integration window of each electrode. Prediction accuracies were noise-corrected using the test-retest reliability of the electrode responses, which provides an upper bound on the fraction of the response explainable by any model10,23,44.
For the short-integration electrodes, prediction accuracies were more than twice as high for cochleagrams compared with category labels (cochleagram: median r2 = 0.45, CI = [0.37, 0.53], category labels: median r2 = 0.22, CI = [0.15, 0.31] (Fig 5c). Moreover, the variance explained by both cochleagrams and category labels (median r2 = 0.45, CI = [0.36, 0.50] was very similar to the variance explained by cochleagrams alone, indicating that the category labels added little unique variance. By contrast, category labels explained nearly twice as much response variance in electrodes with long integration windows (cochleagram: median r2 = 0.31, CI = [0.27, 0.43]; category labels: median r2 = 0.60, CI = [0.50, 0.73], and cochleagrams added little unique variance (both cochleagram and category labels: r2 = 0.62, CI = [0.49, 0.74]). As a consequence, there was a highly significant interaction between the integration window of the electrode and the prediction accuracy of the cochleagram vs. category model (F1,12.35 = 104.71, p < 0.001, N=104 electrodes; statistics reflect a linear mixed effects model, where integration widths were used to predict the difference in prediction accuracies between cochleagrams vs. category labels). Figure 5d plots the unique variance explained by cochleagrams and category labels for all individual electrodes as a function of the integration window. This analysis revealed a transition point at ~200 ms, below which cochleagrams explain substantially more variance and above which category labels explain substantially more variance.
We note the absolute prediction accuracies were modest for both the cochleagram and category labels, never exceeding more than 45% and 60% of the explainable response variance, respectively. This fact illustrates the utility of having a model-independent way of estimating integration widths, since even our best-performing models fail to explain a large fraction of the response, and the best-performing model can vary across electrodes.
To ensure that our findings were not an inevitable consequence of increasing temporal integration, we repeated our analyses using integration-matched responses, accomplished by integrating the responses of the short- and intermediate-integration electrodes within a carefully selected window such that their integration windows matched those of the long-integration electrodes (see Integration matching in Methods for details). Results were very similar using integration-matched responses (Extended Data Fig 8), indicating that it is not the integration window itself that drives differences in functional selectivity, but rather the particular features/categories that the electrode responds to within that window.
Discussion
Our study demonstrates that multiscale integration organizes auditory computation in the human brain, both anatomically and functionally. We found that auditory cortex integrates hierarchically across time, with substantially longer integration windows in non-primary regions. Notably, we found that electrodes with short and long integration windows exhibited distinct functional properties. Electrodes with short integration windows (below ~200 ms) responded selectively to spectrotemporal modulations in a cochleagram representation of sound, and exhibited weak selectivity for sound categories, while electrodes with long integration windows (above ~200 ms) exhibited robust category selectivity. This finding suggests that distinct timescales in natural sounds are analyzed by distinct neural computations, with short and long timescales analyzed by generic and category-specific computations, respectively.
These findings were enabled by our TCI method, which makes it possible to estimate the time window over which any neural response integrates sensory information. Unlike prior methods, TCI makes no assumptions about the type of response being measured; it simply estimates the time window when stimuli alter the neural response. As a consequence, the method should be applicable to any modality, stimulus set, or recording method. We applied TCI to intracranial recordings from epilepsy patients, using surface and depth electrodes placed throughout human auditory cortex. The precision and coverage of our recordings were essential to understanding how multiscale integration organizes auditory computation in the human brain.
Relationship to prior methods.
Many methods have been developed for exploring sensory timescales. In the auditory system, it is common to estimate a linear mapping between a spectrogram-like representation and the neural response5,22,23. The extent of the resulting “spectrotemporal receptive field” (STRF) provides an estimate of the integration window. This approach however cannot estimate the temporal extent of nonlinear temporal integration, which is prominent in cortical responses19,23,45. Flexible, nonlinear models such as deep neural networks are often challenging to fit given limited neural data25,26 and are difficult to analyze.
Higher-order cortical regions sometimes respond selectively to naturalistic temporal structure (e.g. the sequence of phonemes that comprise a word) and thus respond more weakly to temporally scrambled stimuli11,21,32. The temporal extent of this selectivity can be estimated by measuring how strongly or reliably a region responds to stimuli that have been scrambled at different timescales. Many neurons however are tuned to features that are similarly present in both intact and scrambled stimuli. For example, a neuron that integrated spectral energy would show similarly strong responses for intact and scrambled stimuli, even for stimuli that are scrambled within its integration window. This insensitivity to scrambling is common in regions in and around primary auditory cortex11.
The stimuli that make-up the TCI paradigm are similar to a standard scrambling paradigm (though note the use of two different scrambled orderings), but the analysis is quite different: standard scrambling paradigms measure the overall strength or reliability of the response across the scrambled sequence, while the TCI paradigm measures the minimum segment duration needed to achieve a context invariant response. Our analysis is related to a recent fMRI study that used a clever approach to examine the delay needed for responses to become synchronized across subjects after a stimulus change46. However, because the timescale of the fMRI response is an order of magnitude slower than auditory cortical integration windows, this study was not able to estimate integration windows within auditory cortex.
Another important concept is the “encoding window” of a neural response, which corresponds to the rate at which the neural response is updated to reflect changes in the stimulus20,22,47. Encoding windows are related to the maximum frequency at which a neural response can synchronize to a stimulus (see ref20 for a more detailed discussion). Synchronization rates however are distinct from integration windows, since fast neural synchronization could be produced by both short (e.g. a delta function) or long integration responses (e.g. a sinusoidal filter that integrates over many cycles of an oscillation).
Modulation frequencies can also be coded by changes in firing rate in the absence of synchronization48–50. Integration windows, however, also cannot be inferred from this type of rate selectivity, since a neuron could respond selectively to a particular modulation frequency by integrating over a single cycle or many cycles of an modulation. In addition, non-primary regions of auditory cortex are poorly described by modulation tuning19, plausibly because they respond to complex structures in speech and music (e.g. words or musical notes) that are not well-described by modulation content51. Integration windows provide a simple way to compare the analysis timescale of primary and non-primary regions, which respond to very different types of structure8–10,13.
Finally, many neurons also exhibit “intrinsic fluctuations” that are not locked to the stimulus, but are nonetheless highly structured52. There is evidence that intrinsic timescales – measured as the decay of the autocorrelation function – exhibit a coarsely similar form of hierarchical organization53. The relationship between intrinsic timescales and stimulus integration windows could be explored in greater detail by measuring both quantities in the same neurons or electrodes and such data could provide a valuable way to test and constrain network models54.
Anatomical organization.
Multiscale temporal analysis has long been thought to play a central role in auditory processing3,22,24,31,55–58. But how multiscale integration is instantiated in the human auditory cortex has remained debated.
Hemispheric models posit that the left and right hemisphere are specialized for analyzing distinct stimulus timescales57,58, in part to represent the distinctive temporal structure of sound categories like speech and music27. Recent evidence for hemispheric specialization comes from studies that have shown that filtering-out fast temporal modulations in speech has a greater impact on responses in left auditory cortex27,28. However, as discussed above, the integration window of a response cannot be inferred from its modulation selectivity, and many non-primary responses are poorly described by modulation tuning19. Another common proposal is that the auditory cortex integrates hierarchically across time3,24,31,55,56. Early evidence for hierarchical temporal organization came from the observation that “phase-locking” slows from the periphery to the cortex48–50, which implies that neurons encode temporal modulations via changes in firing rate rather than synchronized activity. STRF-based analyses have also provided evidence that integration windows grow from the periphery to the cortex22,56, but the presence of prominent nonlinearities in cortex19,23,45 has limited the utility of these types of analyses, particularly in non-primary regions19. Our study demonstrates that integration windows grow substantially (by a factor of ~3 or 4) as one ascends the auditory cortical hierarchy from primary to non-primary regions. While we did not find a significant difference between the two hemispheres, this could be due to the sparse/limited coverage of intracranial recordings.
Across auditory cortex we found that integration centers scaled approximately linearly with integration widths and were close to the minimum possible for a causal window (Fig 4c; Extended Data Fig 7). This finding is not inevitable, since there could have been integration windows with a narrow width but delayed center. The fact that we never observed narrow but delayed integration windows suggests that auditory cortex “never waits”: it integrates information about as quickly as possible given the time window being analyzed1.
Our findings do not rule out the possibility that there might be a small neural population in non-primary auditory cortex with short integration widths and centers59,60, potentially reflecting direct, low-latency projections from the thalamus61. However, our results suggest that the dominant organization is hierarchical: electrodes with short-integration widths and centers are much more likely to be located in primary regions and their response shows little evidence for the type of higher-order category selectivity that characterizes electrodes with long integration windows (Figure 5; Extended Data Fig 7).
The hierarchical organization of temporal integration windows appears analogous to the hierarchical organization of spatial receptive fields in visual cortex62,63, which suggests that there might be general principles that underlie this type of organization. For example, both auditory and visual recognition become increasingly challenging at large temporal and spatial scales, in part because the input space grows exponentially with increasing scale. Hierarchical multiscale analysis may help overcome this exponential expansion by allowing sensory systems to recognize large-scale structures as combinations of smaller-scale structures (e.g. a face from face parts) rather than attempting to recognize large-scale structures directly from the high-dimensional input3,24,55,56.
Functional organization.
How the human brain integrates across the complex multiscale structure that defines natural sounds like speech and music is one of the central questions of audition1–3,64. Prior studies have suggested that the human brain analyzes sounds using both generic acoustic features, such as spectrotemporal modulation4–7, as well as category-specific computations, nonlinearly tuned to the structure of important sound categories like speech and music8–15. But how these different computations integrate across time has remained unclear. A prior fMRI study used a scrambling technique called “quilting” to show that speech-selective regions respond selectively to intact temporal structure up to about 500 milliseconds in duration11. But this study was only able to identify a single analysis timescale across all of auditory cortex, likely because scrambling is a coarse manipulation and fMRI a coarse measure of the neural response. Our paradigm and recordings enabled us to identify a broad range of integration windows from ~50 to 400 ms, and we could thus test how the representation of sound changes as integration windows grow.
We emphasize that our findings are not an inevitable/generic consequence of increasing temporal integration, since we observed very similar results for integration-matched responses (Extended Data Fig 8). Of course, the performance of an ideal observer on any task will always improve as integration windows grow since there is more information available. But this fact cannot explain why neural responses with short integration windows show weak category selectivity, since behaviorally people are excellent at categorizing sounds at short timescales65, and also cannot explain why neural responses with long integration windows show prominent category selectivity, since long-integration responses are perfectly capable of just encoding lower-level acoustic structure, as our matching analysis demonstrates (Extended Data Fig 8).
The shortest integration windows at which we observed category-selective responses (~200 ms) correspond to about the duration of a multiphone syllable, which is substantially longer than duration of most speech phonemes (Extended Data Fig 1). This finding does not imply that speech-selective regions are insensitive to short-term structure such as phonemes, but rather that speech-selective responses respond to larger-scale patterns, such as phoneme sequences, consistent with recent work on phonotactics1,42,43.
Some studies have argued for two distinct processing timescales in auditory cortex29,58,66. The methods and findings from these studies vary widely, but in all cases what is being measured is a specific aspect of the neural tuning, such as modulation synchronization29 or predictive oscillatory activity66, rather than the overall integration window. Our results suggest that integration windows increase in a graded fashion as one ascends the cortical hierarchy, in contrast with what might naively be expected if there were two distinct timescales. However, we do show that neural responses with short and long integration windows exhibit distinct functional properties.
Limitations and future directions.
As with any method, our results could depend upon the stimuli tested. We tested a diverse set of natural sounds with the goal of characterizing responses throughout auditory cortex using ecologically relevant stimuli. Because time is inevitably short when working with neurosurgical patients, we could only test a small number of sounds, but found that our key findings were nonetheless robust to the sounds tested (Extended Data Fig 5a). Nonetheless, it will be important in future work to test whether and how integration windows change for different stimulus classes.
A given neural response might effectively have multiple integration windows. For example, neural responses are known to adapt their response to repeated sounds on the timescale of seconds67 to minutes68 and even hours69, suggesting a form of memory70. TCI measures the integration window of responses that are reliable across repetitions, and as a consequence, TCI will be insensitive to response characteristics that change across repeated presentations. Future work could try and identify multiple integration windows within the same response by manipulating the type of context which surrounds a segment. Here, we examined two distinct types of contexts and found similar results (Extended Data Fig 5b), suggesting that hierarchical temporal integration is a robust property of human auditory cortex.
Our analyses focused on broadband gamma power, which provides an aggregate measure of local neural activity. Although broadband gamma often correlates strongly with spiking37,38, it is likely also influenced by dendritic processes71,72. For example, Leszczyński et al. reported prominent broadband gamma responses in superficial layers of A1 and V1 that was not accompanied by multi-unit spiking and potentially reflected feedback-driven dendritic activity72. Thus, the integration windows measured in our study plausibly reflect a mixture of spiking and dendritic activity, as well as feedforward and feedback responses.
An important question is whether temporal integration windows reflect a fixed property of the cortical hierarchy or whether they are shaped by attention and behavioral demands73. In our study, we did not give subjects a formal task because our goal was to measure integration windows during natural listening without any particular goal or attentional focus. Future work could explore how behavioral demands shape temporal integration windows by measuring integration windows in the presence or absence of focused attention to a short-duration (e.g. phoneme) or long-duration (e.g. word) target.
Our study focused on characterizing integration windows within human auditory cortex, which we showed have integration windows ranging from roughly 50 to 400 milliseconds. Natural sounds, like speech and music, are clearly structured at much longer timescales (e.g. sentences and melodies)18, and this structure may be coded by higher-order cognitive regions with multi-second integration windows21,33,64. Natural sounds also have important structure at much shorter timescales (e.g. pitch periodicity), which are plausibly coded by subcortical nuclei with narrower integration windows22,56. The TCI method provides a conceptually simple tool to measure and compare integration windows across all of these regions, and thus provides a way to better understand how the brain constructs meaning from the complex multiscale structure that defines natural stimuli.
Methods
Participants & data collection.
Data were collected from 23 patients undergoing treatment for intractable epilepsy at the NYU Langone Hospital (14 patients) and the Columbia University Medical Center (9 patients) (12 male, 11 female; mean age: 36 years, STD: 15 years). One patient was excluded because they had a large portion of the left temporal lobe resected in a prior surgery. Of the remaining 22 subjects, 18 had sound-responsive electrodes (see Electrode selection). No formal tests were used to determine the sample size, but the number of subjects was larger than in most intracranial studies, which often test fewer than 10 subjects5,36. Electrodes were implanted to localize epileptogenic zones and delineate these zones from eloquent cortical areas before brain resection. NYU patients were implanted with subdural grids, strips, and depth electrodes depending on the clinical needs of the patient. CUMC patients were implanted with depth electrodes. All subjects gave informed written consent to participate in the study, which was approved by the Institutional Review Boards of CUMC and NYU. NYU patients were compensated $20/hour. CUMC patients were not compensated due to IRB prohibition.
Stimuli for the TCI paradigm.
Segments were excerpted from 10 natural sound recordings, each two seconds in duration (cat meowing, geese honking, cicadas chirping, clock ticking, laughter, English speech, German speech, big band music, pop song, drumming). Shorter segments were created by subdividing the longer segments. Each natural sound was RMS-normalized before segmentation.
We tested seven segment durations (31.25, 62.5, 125, 250, 500, 1000, and 2000 ms). For each duration, we presented the segments in two pseudorandom orders, yielding 14 sequences (7 durations × 2 orders), each 20 seconds. The only constraint was that a given segment had to be preceded by a different segment in the two orders. When we designed the stimuli, we thought that integration windows might be influenced by transients at the start of a sequence, so we designed the sequences such that the first 2 seconds and last 18 seconds contained distinct segments so that we could separately analyze the just last 18 seconds. In practice, integration windows were similar when analyzing the first 18 seconds vs. the entire 20-second sequence. Segments were concatenated using cross-fading to avoid click artifacts (31.25 ms raised cosine window). Each stimulus was repeated several times (4 repetitions for most subjects; 8 repetitions for 2 subjects; 6 and 3 repetitions for two other subjects). Stimuli will be made available upon publication.
Natural sounds.
In a subset of 11 patients, we measured responses to a diverse set of 119 natural sounds from 11 categories, similar to those from our prior studies characterizing auditory cortex9 (there were at least 7 exemplars per category). The sound categories are listed in Figure 5a. Most sounds (108) were 4 seconds. The remaining 11 sounds were longer excerpts of English speech (28–70 seconds) that were included to characterize responses to speech for a separate study. Here, we just used responses to the first 4 seconds of these stimuli to make them comparable to the others. The longer excerpts were presented either at the beginning (6 patients) or end of the experiment (5 patients). The non-English speech stimuli were drawn from 10 languages: German, French, Italian, Spanish, Russian, Hindi, Chinese, Swahili, Arabic, Japanese. We classified these stimuli as “foreign speech” since most were unfamiliar to the patients. Twelve of the sounds (all 4-seconds) were repeated four times in order to measure response reliability and noise-correct our measures. The other 107 stimuli were presented once. All sounds were RMS-normalized.
As with the main experiment, subjects did not have a formal task but the experiment was periodically paused and subjects were asked a simple question to encourage them to listen to the sounds. For the 4-second sounds, subjects were asked to identify/describe the last sound they heard. For the longer English speech excerpts, subjects were asked to repeat the last phrase they heard.
Preprocessing.
Electrode responses were common-average referenced to the grand mean across electrodes from each subject. We excluded noisy electrodes from the common-average reference by detecting anomalies in the 60 Hz power band (measured using an IIR resonance filter with a 3dB down bandwidth of 0.6 Hz; implemented using MATLAB’s iirpeak.m). Specifically, we excluded electrodes whose 60 Hz power exceeded 5 standard deviations of the median across electrodes. Because the standard deviation is itself sensitive to outliers, we estimated the standard deviation using the central 20% of samples, which are unlikely to be influenced by outliers. Specifically, we divided the range of the central 20% of samples by that which would be expected from a Gaussian of unit variance. After common-average referencing, we used a notch filter to remove harmonics & fractional multiples of the 60 Hz noise (60, 90, 120, 180; using an IIR notch filter with a 3dB down bandwidth of 1 Hz; the filter was applied forward and backward; implemented using MATLAB’s iirnotch.m).
We measured integration windows from the broadband gamma power response timecourse of each electrode. We computed broadband gamma power by measuring the envelope of the preprocessed signal filtered between 70 and 140 Hz (implemented using a 6th order Butterworth filter with 3dB down cutoffs of 70 and 140 Hz; the filter was applied forward and backward; envelopes were measured using the absolute value of the analytic signal, computed using the Hilbert transform; implemented using fdesign.bandpass in MATLAB). Results were robust to the frequency range used to measure broadband gamma (Extended Data Fig 5d). We estimated the integration window of the filter to be ~19 ms, calculated as the smallest interval containing 75% of the filter’s mass, where the mass is taken to be the envelope of the impulse response. We found in simulations that the bias introduced by the bandpass filter was small relative to the range of integration windows we observed in human auditory cortex (~50 to 400 ms) (Extended Data Fig 3a). Envelopes were downsampled to 100 Hz (the original sampling rate was 512, 1000, 1024, or 2048 Hz, depending on the subject).
Occasionally, we observed visually obvious artifacts in the broadband gamma power for a small number of timepoints. To detect such artifacts, we computed the 90th percentile of each electrode’s response distribution across all timepoints. We classified a timepoint as an outlier if it exceeded 5 times the 90th percentile value for each electrode. We found this value to be relatively conservative in that only a small number of timepoints were excluded (on average, 0.04% of timepoints were excluded across all sound-responsive electrodes). We replaced the outlier values with interpolated values from nearby non-outlier timepoints (using “piecewise cubic hermite interpolation” as implemented by MATLAB’s interp1 function).
As is standard, we time-locked the iEEG recordings to the stimuli by either cross-correlating the audio with a recording of the audio collected synchronously with the iEEG data or by detecting a series of pulses at the start of each stimulus that were recorded synchronously with the iEEG data. We used the stereo jack on the experimental laptop to either send two copies of the audio or to send audio and pulses on separate channels. The audio on one channel was used to play sounds to subjects, and the audio/pulses on the other were sent to the recording rig. Sounds were played through either a Bose Soundlink Mini II speaker (at CUMC) or an Anker Soundcore speaker (at NYU). Responses were converted to units of percent signal change relative to silence by subtracting and then dividing the response of each electrode by the average response during the 500 ms before each stimulus.
Electrode selection.
We selected electrodes with a reliable broadband gamma response to the sound set. Specifically, we measured the test-retest correlation of each electrodes response across all stimuli (using odd vs. even repetitions). We selected electrodes with a test-retest Pearson correlation of at least 0.1, which we found to be sufficient to reliably estimate integration windows in simulations (described below). We ensured that this correlation value was significant using a permutation test, where we randomized the mapping between stimuli across repeated presentations and recomputed the correlation (using 1000 permutations). We used a Gaussian fit to the distribution of permuted correlation coefficients to compute small p-values74. Only electrodes with a highly significant correlation relative to the null were kept (p < 10−5). We identified 190 electrodes out of 2847 total that showed a reliable response to natural sounds based on these criteria (62 right hemisphere, 128 left hemisphere).
Electrode localization.
Following standard practice, we localized electrodes as bright spots on a post-operative computer tomography (CT) image or dark spots on a magnetic resonance image (MRI), depending on which was available. The post-op CT or MRI was aligned to a high-resolution, pre-operative MRI that was undistorted by electrodes. Each electrode was projected onto the cortical surface computed by Freesurfer from the pre-op MRI, excluding electrodes greater than 10 mm from the surface. This projection is error prone because locations which are distant on the 2D cortical surface can be nearby in 3D space due to cortical folding. To minimize gross errors, we preferentially localized sound-responsive electrodes to regions where sound-driven responses are likely to occur75. Specifically, we calculated the likelihood of observing a significant response to sound using a recently collected fMRI dataset, where responses were measured to a large set of natural sounds across 20 subjects with whole-brain coverage76 (p < 10−5, measured using a permutation test). We treated this map as a prior and multiplied it by a likelihood map, computed separately for each electrode based on the distance of that electrode to each point on the cortical surface (using a 10 mm FWHM Gaussian error distribution). We then assigned each electrode to the point on the cortical surface where the product of the prior and likelihood was greatest (which can be thought of as the maximum posterior probability solution). We smoothed the prior map (10 mm FWHM kernel) so that it would not bias the location of electrodes locally, only helping to resolve gross-scale ambiguities/errors, and we set the minimum prior probability to be 0.05 to ensure every point had non-zero prior probability. We plot the prior map and its effect on localization in Supplemental Fig 1.
Anatomical analyses.
We grouped electrodes into regions-of-interest (ROI) based on their anatomical distance to posteromedial Heschl’s gyrus (TE1.1)77 (Fig 4b), which is a common anatomical landmark for primary auditory cortex (PAC)19,78. Distance was measured on the flattened 2D representation of the cortical surface as computed by Freesurfer. Electrodes were grouped into three 10 millimeter bins (0–10, 10–20, and 20–30 mm), and we measured the median integration width and center across the electrodes in each bin, separately for each hemisphere.
Statistics were computed using a linear mixed effects (LME) model. In all cases, we used logarithmically transformed integration widths and centers, and for our key statistics, we did not bin electrodes into ROIs, but rather represented each electrode by its distance to PAC. The LME model included fixed effects terms for distance-to-PAC, hemisphere, and type of electrode (grid, strip, or depth), as well as a random intercept and slope for each subject (slopes were included for both hemisphere and distance-to-PAC effects)79. Fitting and significance was performed by the matlab functions fitlme and coefTest. A full covariance matrix was fit for the random effects terms, and the Satterwaite approximation was used estimate the degrees of freedom of the denominator80. We report the estimated weight for the distance-to-PAC regressor (and its 95% confidence interval) as a measure of effect size in units of octaves per millimeter. We did not formally test for normality since regression models are typically robust to violations of normality81,82 and our key effects were highly significant (p < 0.001). The relevant data distribution can be seen in Extended Data Figure 4. No a priori hypotheses/predictions were altered after the data were analysed or during the course of writing/revising our manuscript.
Bootstrapping was used to compute errorbars. We resampled both subjects and electrodes with replacement, thus accounting for the hierarchical nature of the data. Specifically, for each subject we sampled a set of electrodes with replacement from that subject. We then sampled a set of subjects with replacement, and for each subject used the previously sampled electrodes. There were a small fraction of samples that were missing data from one of the bins/hemispheres, and we simply discarded these samples (bin 3 in the right hemisphere was missing samples for 4.0% of samples; the rest of the bins/hemispheres were all lower than this percentage). Errorbars plot the central 68% interval (equivalent to 1 standard error).
Component analyses.
To investigate the functional selectivity of our electrodes, we used responses to the larger set of 119 natural sounds that were tested in a subset of 11 patients. There were 104 electrodes from these 11 subjects that passed the inclusion criteria described above. We subdivided these electrodes into three equally sized groups (Fig 5a). We then used component (Fig 5b) and prediction analyses (Fig 5c–d) to investigate selectivity for spectrotemporal modulations and categories.
Component methods are commonly used to summarize responses from a population of electrodes or neurons9,75,83. For each electrode, we measured the average response of each electrode across each 4-second sound (from 250 ms to 4 seconds post-stimulus onset), and projected these time-averaged responses onto the top two principle components (PCs) from each electrode group (Fig 5b). PCs were measured by applying the singular value decomposition (SVD) to the time-averaged electrode responses (demeaned prior to applying the SVD). The orientation of the PCs is arbitrary and so we flipped/rotated the PCs so that they were maximally aligned with each other across the three groups.
Because the first two PCs might obscure category selectivity present at higher PCs, we repeated the analysis using the two components that best separated the categories, estimated using linear discriminant analysis (LDA)84 (Extended Data Fig 7). To avoid statistical circularity, we used half the sounds to infer components and the other half to measure their response. To prevent the analysis from targeting extremely low-variance components, we applied LDA to the top five PCs from each electrode group.
Feature predictions.
As a complement to the component analyses, we measured the degree to which individual electrode response timecourses could be predicted from category labels vs. a cochleagram representation of sound (Fig 5c–d).
Cochleagrams were calculated using a cosine filterbank with bandwidths designed to mimic cochlear tuning19 (29 filters between 50 Hz and 20 kHz, 2x overcomplete). The envelopes from the output of each filter were compressed to mimic cochlear amplification (0.3 power). The frequency axis was resampled to a resolution of 12 cycles per octave and the time axis was resampled to 100 Hz (the sampling rate used for all of our analyses).
For each category label, we created a binary timecourse with 1s for all timepoints/sounds from that category, and 0s for all other timepoints. We only labeled timepoints with a 1 if they had sound energy that exceeded a minimum threshold. Sound energy was calculated by averaging the cochleagram across frequency, and the minimum threshold was set to one fifth the mean energy across all timepoints and sounds.
We predicted electrode responses between 500 milliseconds pre-stimulus onset to 4 seconds post-stimulus onset. We used ridge regression to learn a linear mapping between these features and the response. We included five delayed copies of each regressor, with the delays selected to span the integration window of the electrode (from the bottom fifth to the top fifth quintile). Regression weights were fit using the 107 sounds that were presented once, and we evaluated the fits using the 12 test sounds that were repeated four times each, making it possible to compute a noise-corrected measure of prediction accuracy10,44:
| (1) |
where r1 and r2 are two independent measures of the response (computed using odd and even repetitions) and p is the prediction computed from the training data. One electrode (out of 104) was discarded because of a negative test-retest correlation across the test sounds, making correction impossible. We used cross-validation within the training set to choose the regularization coefficient (testing a wide range of values from 2−100 to 2100 in octave steps). Figure 5c plots the median squared correlation (after noise correction) across the electrodes in each group for each feature set. Bootstrapping across subjects and electrodes was again used to compute errorbars.
Figure 5d plots the difference in squared correlation values for all individual electrodes between a combined model that included both cochleagrams and category labels and the individual feature sets, as a measure of the unique variance contributed by each feature type85. The data in Figure 5d were fit with a three-parameter logistic sigmoid curve (using MATLAB’s implementation of the Levenberg-Marquardt algorithm86 in fit.m):
where x is the logarithmically transformed integration width (log2(i/50), where i is the integration width in milliseconds) and y is the unique variance explained by cochleagram features or category labels (parameters of fit logistic curve for unique cochleagram variance: a = 1.998, b = −4.601, c = 0.206; parameters for unique category variance: a = 2.011, b = 4.125, c = 0.332). The mid-way point of the logistic curve corresponded to 200 and 201 ms for unique cochleagram and category variance, respectively.
Significance was again evaluated using an LME model. The key statistical question was whether category labels explained significantly more variance than the cochleagrams for electrodes with longer integration windows. To test for this interaction between integration window and feature type, we used an LME model to predict the difference between the correlation accuracies for the category vs. cochleagram features. We used the raw prediction accuracies for the two feature sets, rather than trying to measure unique variance to avoid any spurious dependence between the two measures (since estimating unique variance requires subtracting prediction accuracies from the same combined model), and we did not correct for noise, since the goal of this analysis was to assess significance and not effect size. The model included fixed effects terms for the electrode’s integration width and hemisphere, as well as random intercepts and slopes for each subject. A fixed effects regressor was added to control for electrode type (depth, grid, strip). We did not attempt to evaluate the significance of the hemisphere effect for this analysis because we did not have enough subjects with right hemisphere coverage that participated in both the TCI and natural sound experiment (2 subjects, 20 electrodes).
Integration matching.
We tested if the functional changes we observed with increasing integration (Fig 5) could be a generic consequence of greater temporal integration by matching the integration windows of our electrodes. To do this, we grouped the electrodes based on their integration width into three equally sized groups, as in our main analysis. We then increased the integration window of the short and intermediate groups, so that their distribution of integration windows closely matched those for the long-integration group (Extended Data Fig 8). Matching was accomplished by equating the cumulative distribution function across groups, which is a standard way to match the histogram of two distributions19. We manipulated the integration window of an electrode by convolving its response with a Gamma-distributed window, whose width was chosen separately for each electrode to achieve the desired overall integration window. The effective integration window was measured empirically by applying the TCI paradigm to the Gamma-convolved responses. We tested a wide range of Gamma widths (from 50 to 800 ms in ¼-octave steps) and selected the width that yielded the closest match to the desired integration window.
TCI Method
In this section, we give a complete description of our TCI method. We repeat some of the details already described in the Results so that this section is self-contained.
Overview.
Integration windows are defined as the time window when stimuli alter the neural response. Our method involves presenting a set of stimulus segments in two different random orders, such that each segment occurs in two different contexts (Fig 1). If the integration window is less than the segment duration, then there should be a moment when the response is unaffected by the surrounding context segments. We developed an analysis to measure the degree to which the neural response depends upon context at each moment in time for each segment duration (the cross-context correlation). We then developed a model that estimated the overall integration window by pooling across these noisy, moment-by-moment estimates.
Cross-context correlation.
The cross-context correlation is schematized in Figure 2a. For each electrode and segment duration, we compile the responses to all segments into a matrix, aligned to segment onset (the segment-aligned response or SAR matrix) (Fig 2a). A separate SAR matrix is computed for each of the two contexts tested. Each row of the SAR matrix contains the response timecourse to a single segment. Corresponding rows contain the response timecourse to the same segment for two different contexts. We correlate corresponding columns across the two SAR matrices (schematized in Fig 2a by connected columnar boxes). This correlation provides a measure of the degree to which the response is the same across contexts. Before the onset of the shared segments, the integration window will fall on the context segments, which are random, and the correlation should thus be close to 0. After the onset of the shared segment, the integration window will begin to overlap the shared central segment, and if the window is less than the segment duration, there will be a moment/lag when it is fully contained within the shared segment and does not overlap the context. As a consequence, the response at that moment will be the same across the two contexts, yielding a correlation of 1. While noise prevents a correlation of 1, we can measure a noise ceiling for the cross-context correlation by measuring the correlation when the context is the same using repeated presentations of the same sequence.
The noise ceiling shows reliable and periodic variation across lags (see Fig 2b). We know the variation is reliable because it is mirrored in the cross-context correlation when the integration is short relative to the segment duration (evident for example in the HG electrode’s data for 250 and 500 ms segments in Fig 2b). This variation is expected since the sounds that happen to fall within the integration window will vary with lag, and the noise ceiling will depend upon how strongly the electrode responds to these sounds. The periodicity is also expected and is an inevitable consequence of correlating across a fixed set of segments. To see this, consider the fact that the onset of one segment is the offset of the preceding segment. Since we are correlating across segments for a fixed lag, the values being used to compute the correlation are nearly identical at the start and end of a segment (the only difference occurs for the first and last segment of the entire sequence). The same logic applies to all lags that are separated by a period equal to the segment duration.
Because the shorter segments were subsets of the longer segments, we could consider two types of context: (1) random context, where a segment is flanked by random other segments (2) natural context, where a segment is a part of a longer segment and thus surrounded by its natural context (see schematic in Extended Data Fig 5b). Since the two contexts being compared must differ, one of the contexts always has to be random, but the other context can be random or natural. In practice, we found similar results for random-random and random-natural comparisons (Extended Data Fig 5b). This fact is practically useful since it greatly increases the number of comparisons that can be made. For example, each 31 millisecond segment had 2 random contexts (one per sequence) and 12 natural contexts (2 sequences × 6 longer segment durations). The two random contexts can be compared with each other as well as with the other 12 natural contexts. We averaged the cross-context correlation across all of these comparisons for maximal statistical power.
The number of datapoints in the correlation is equal to the number of segments. The number of segments was determined by however many segments could fit in a 20-second sequence, which varied inversely with the segment duration from 640 segments (31 ms duration) to 10 segments (2 second duration). A consequence of this design is that the cross-context correlation will be more reliable for the shorter segment durations, since there are more datapoints. We consider this property useful since for responses with short integration windows there will be a smaller number of lags at the shorter segment durations that effectively determine the integration window, and thus it is helpful if these lags are highly reliable. Conversely, electrodes with longer integration windows exhibit a gradual build-up of the cross-context correlation at the longer segment durations, and as a consequence, there are many more lags that are relevant for determining the integration window. Our model enables us to pool across all of these lags to arrive at a robust estimate of the integration window.
Model-estimated integration windows.
To estimate the neural integration window, we used a parametric window to predict the cross-context correlation across all lags and segment durations, and we selected the parameters that yielded the best prediction.
We parametrized the window using a Gamma distribution (h) and we varied the width and center of the distribution by scaling and shifting the window in time:
| (2) |
| (3) |
The window shape is determined by γ and varies from more exponential to more bell-shaped (Extended Data Fig 5c). The parameters λ and δ scale and shift the window, respectively. The width and center of the integration window do not correspond directly to any of the three parameters (δ, λ, γ), mainly because the scale parameter (λ) alters both the center and width. The integration width was defined as the smallest interval that contained 75% of the window’s mass, and the integration center was defined as the window’s median. Both parameters were calculated numerically from the cumulative distribution function of the window.
For a given integration window, we predicted the cross-context correlation at each lag and segment duration by measuring how much the integration window overlaps the shared central segment (w) vs. the N surrounding context segments (βn) (see Fig 3b for a schematic):
| (4) |
where rceil is the measured noise ceiling, and the ratio on the right is the predicted correlation in the absence of noise. The predicted cross-context correlation varies with the segment duration and lag because the overlap varies with the segment duration and lag. When the integration window only overlaps the shared segment (w = 1, ∑βn = 0), the model predicts a correlation equal to the noise ceiling, and when the integration window only overlaps the surrounding context segments (w = 0, ∑βn = 1), the model predicts a correlation of 0. In between these two extremes, the predicted cross-context correlation equals the fraction of the response driven by the shared segment, with the response variance for each segment given by the squared overlap with the integration window. A formal derivation of this equation is given at the end of the Methods (see Deriving a prediction for the cross-context correlation). For a given segment duration, the overlap with each segment was computed by convolving the model integration window with a boxcar function whose width is equal to the segment duration (with edges tapered to account for segment cross-fading).
We varied the width, center, and shape of the model integration window and selected the window with the smallest prediction error (using a bias-corrected variant of the mean squared error; see Simulations and Deriving the bias-corrected loss for details). Since the cross-context correlation is more reliable for shorter segment durations due to the greater number of segments, we weighted the error by the number of segments used to compute the correlation before averaging across segment durations. Integration widths varied between 31.25 and 1 second (using 100 logarithmically spaced steps). Integration centers varied from the minimum possible given for a causal window up to 500 milliseconds beyond the minimum in 10 millisecond steps. We tested five window shapes (γ = 1,2,3,4,5).
We assessed the significance of our model predictions by creating a null distribution using phase-scrambled model predictions. Phase scrambling exactly preserves the mean, variance and autocorrelation of the predictions but alters the locations of the peaks and valleys. Phase scrambling was implemented by shuffling the phases of different frequency components without altering their amplitude and then reconstructing the signal (using the FFT/iFFT). After phase-scrambling, we remeasured the error between the predicted and measured cross-context correlation, and selected the model with the smallest error (as was done for the unscrambled predictions). We repeated this procedure 100 times to build up a null distribution, and used this null distribution to calculate a p-value for the actual error based on unscrambled predictions (again fitting the null distribution with a Gaussian to calculate small p-values). For 96% of sound-responsive electrodes (182 of 190), the model’s predictions were highly significant (p < 10−5).
For the shape parameters tested (γ = 1,2,3,4,5), the minimum center for a causal window is equal to half the integration width (the blue line in Fig 4c). This value occurs when γ = 1, δ = 0, in which case the window has an exponential distribution. An exponential distribution is monotonically decreasing and takes its maximal value at t = 0, which intuitively fits the notion of a window with minimal delay. We note that for γ < 1, the center can be less than half the integration width, but this is arguably an idiosyncrasy of how the parameters were defined. If we instead define the integration width as the highest-density 50% interval, instead of the highest-density 75% interval, then the center equals the width for all windows with γ ≤ 1, which fits the intuition that all of these windows have minimal delay in the sense that they monotonically decrease from a maximal value at t = 0.
Modeling boundary effects.
The model just described assumes the neural response reflects a sum of responses to individual segments and does not explicitly account for responses that only occur at the boundary between segments. We found in simulations (described below) that strong boundary responses suppressed the cross-context correlation and led to an upward bias in the estimated integration widths when not accounted for. The suppression is likely due to the fact that boundary effects by definition depend upon two segments and thus must be context-dependent.
To correct this bias, we explicitly modeled boundary effects. By definition, boundary effects can only occur when the integration window overlaps two adjacent segments. We captured this fact using the equations below. For every pair of adjacent segments, we compute the magnitude of the boundary effect as:
| (5) |
| (6) |
where α1 and α2 represent how much the integration window overlaps the two adjacent segments being considered. The second term, (α1 + α2), reflects the overall amount of overlap across the two segments, and the third term (raised cosine function, g(α1, α2)) is a nonlinear function that ensures that boundary effects are only present when the window overlaps both segments (taking a value of 1 when overlap is equal across the two adjacent segments and a value of 0 when overlap is exclusive to just one segment). The free parameter η determines the overall strength of the boundary effects, which will depend upon the type of response being measured and thus needs to be estimated from the data. We tested a range of boundary strengths (η = 0, 0.25, 0.5, 1, 2.0) and selected the parameter that yielded the best prediction accuracy for each electrode/response.
For each lag and segment duration, we measured the strength of boundary effects for all pairs of adjacent segments using equation 5. We then summed the boundary effects across all adjacent segments and added this term to the denominator of equation 4, which results in a suppression of the cross-context correlation that depends upon the strength of boundary effect. In simulations, we found this approach substantially reduced the estimated bias for integration windows with substantial boundary sensitivity and had no effect on integration windows without boundary sensitivity (as expected, since η = 0 removes the effect of the boundary).
Simulations.
We tested the ability of our complete analysis pipeline to correctly estimate ground-truth integration windows from a variety of simulated model responses. In all cases, there was a ground-truth, Gamma-distributed integration window. We varied the width and center of the window between 32 and 500 ms, excluding combinations that led to a non-causal window. For simplicity, all windows had the same shape (γ = 3), but we did not assume the shape was known and thus varied the shape along with the width and center when inferring the best-fit window, as was done for the neural analyses.
We simulated responses from four types of models. The first and simplest model integrated waveform magnitudes (absolute value of amplitude) over the specified Gamma window.
The second model integrated energy within a cochlear frequency band. Cochlear energy was computed in a standard manner19,51: the waveform was convolved with a filter whose frequency characteristics were designed to mimic cochlear frequency tuning and the envelope of the filter’s response was then compressed (raised to the 0.3 power) to mimic cochlear amplification. We used filters with five different center frequencies: 0.5, 1, 2, 4, and 8 kHz.
The third model integrated energy across time and frequency in a cochleagram representation of sound (computed in the same manner described above). The spectrotemporal filters were taken from a standard model of cortical responses19,40. The filters are tuned in three dimensions: audio frequency, spectral modulation, and temporal modulation. The temporal envelope of the filters have a Gamma-distributed window, and we varied the width and center of the envelope in the same way as the other models. The temporal modulation rate is determined by the envelope, with the modulation center frequency equal to , where λ is the scale parameter of the Gamma-distributed envelope. We tested five audio frequencies (0.5, 1, 2, 4, and 8 kHz) and four spectral modulation scales (0.25, 0.5, 1, 2 cycles/octave).
The fourth model was a simple deep network, where we first passed the cochleagram through a series of ten pointwise nonlinearities (i.e. applied separately to each timestep) and then integrated the output within a specified time window, thus ensuring that the output had a well-defined integration window and was also a highly nonlinear function of the input. Each nonlinearity involved multiplication by a random, fully connected weight matrix (sampled from a unit-variance Gaussian), mean normalization (setting the mean of the activations at each timepoint to 0), and rectification (setting negative values to 0). We then integrated the output representation across time within a specified time window.
For each model/window, we simulated responses to all of the stimulus sequences from our paradigm (fourteen 20-second sequences; two per segment duration). We then used this response to modulate a broadband gamma carrier (Gaussian noise filtered between 70 and 140 Hz in the frequency domain; 75 dB/octave attenuation outside of the passband), which enabled us to test whether our gamma-extraction frontend had sufficient precision to enable accurate integration estimates (for simulations we used a 512 Hz sampling rate, the minimum sampling rate used for neural data analyses; measured envelopes were downsampled to 100 Hz, again mimicking the neural analyses). Finally, we added wide-band noise to the signal in order to manipulate the SNR of the measurements (Gaussian noise filtered between 1 and 256 Hz in the frequency domain; 75 dB/octave attenuation outside the passband). We generated four repeated measurements per stimulus using independent samples of the carrier and wide-band noise (for most subjects, we also had four independent measurements per stimulus). We set the level of the wide-band noise to achieve a desired test-retest correlation (r = 0.05, 0.1, 0.2, 0.4), the same measure used to select electrodes (the noise level was iteratively increased/decreased until the desired test-retest correlation was attained). We tested the ability of our analysis to recover the correct integration windows from the 4 repeated measurements, as was done for our neural analyses. For each model/window, we repeated this entire process 10 times to generate more samples with which to test our analysis pipeline (each time using different carrier and wide-band noise samples).
We found we were able to recover ground-truth integration windows and centers from the simulated model responses (Extended Data Fig 3a). Accuracy was good as long as the test-retest correlation was greater than 0.1, the threshold we used to select electrodes. The median error in estimated integration widths across all simulations for a test-retest correlation of 0.1 ranged from 11% (waveform model) to 29% (spectrotemporal model). The median error for estimated centers was lower, ranging from 1% (waveform model) to 3% (spectrotemporal model).
For the spectrotemporal filters, the boundary model described above was important for correcting an upward bias induced by the presence of strong responses to spectrotemporal changes at the transition between segments (Extended Data Fig 3b). In addition, we found that our bias-corrected loss helped correct an upward bias present at low SNRs (Extended Data Fig 3c). We used the boundary model and bias-corrected loss for all of our analyses, although the results were similar without them.
Deriving a prediction for the cross-context correlation.
In this section, we derive the equation used to predict the cross-context correlation from a model integration window (equation 4). The cross-context correlation is computed across segments for a fixed lag and segment duration by correlating corresponding columns of SAR matrices from different contexts (Fig 2a). Consider two pairs of cells(es,A, es,B) from these SAR matrices, representing the response to a single segment (s) in two different contexts (A, B) for a fixed lag and segment duration (we do not indicate the lag and segment duration to simplify notation). To reason about how the shared and context segments might relate to the cross-context correlation at each moment in time, we assume that the response reflects the sum of the responses to each segment weighted by the degree of overlap with the integration window (Fig 3b):
| (7) |
| (8) |
where r(s) reflects the response to the shared central segment, r(cs,A,n) and r(cs,B,n) reflect the response to the n-th surrounding segment in each of the two contexts (e.g. the segment right before and right after, two before and two after, etc.), and w and βn reflect the degree of overlap with the shared and surrounding segments, respectively (illustrated in Fig 3b).
Below we write down the expectation of the cross-context correlation in the absence of noise, substitute equations 7 & 8, and simplify (for simplicity, we assume in these equations that the responses are zero mean). Moving from line 9 to line 10 takes advantage of the fact that contexts A and B are no different in structure and so their expected variance is the same. Moving from line 11 to line 12, we have taken advantage of the fact that surrounding context segments are random, and thus all cross products that involve the context segments are zero in expectation, canceling out all of the terms except those noted in equation 12. Finally, in moving from equation 12 to 13, we take advantage of the fact that there is nothing special about the segments that make up the shared central segments compared with the surrounding context segments, and their expected variance is therefore equal and cancels between the numerator and denominator.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
We multiplied equation 13 by the noise ceiling to arrive at our prediction of the cross context correlation (equation 4).
Deriving the bias-corrected loss.
Here, we derive the correction procedure used to minimize the bias when evaluating model predictions via the squared error.
Before beginning, we highlight a potentially confusing, but necessary distinction between noisy measures and noisy data. As we show below, the bias is caused by the fact that our correlation measures are noisy in the sense that they will not be the same across repetitions of the experiment. The bias is not directly caused by the fact that the data is noisy, since if there are enough segments the correlation measures will be reliable even if the data are noisy, which is what matters since we explicitly measure and account for the noise ceiling. To avoid confusion, we use the superscript (n) to indicate noisy measures, (t) to indicate the true value of a noisy measure (i.e. in the limit of infinite segments), and (p) to indicate a “pure” measure computed from noise-free data.
Consider the error between the measured and model-predicted cross-context correlation for a single lag and segment duration (the model prediction is noisy because of multiplication with the noise ceiling which is measured from data):
| (14) |
Our final cost function averages these pointwise errors across all lags and segment durations weighted by the number of segments used to compute each correlation (which was greater for shorter segment durations). Here, we analyze each lag and segment duration separately, and thus ignore the influence of the weights which is simply a multiplicative factor that can be applied at the end after bias correction.
Our analysis proceeds by writing the measured and predicted cross-context correlation in terms of their underlying true and pure measures (equations 15 to 18). We then substitute these definitions into the expectation of the squared error and simplify (equations 19 to 22), which yields insight into the cause of the bias.
The cross-context correlation is the sum of the true cross-context correlation plus error:
| (15) |
And the true cross-context correlation is the product of the pure/noise-free cross-context correlation with the true noise ceiling :
| (16) |
The predicted cross-context correlation is the product of the noise-free prediction times the measured noise ceiling :
| (17) |
And the measured noise ceiling is the sum of the true noise ceiling plus error (eceil):
| (18) |
Below we substitute the above equations into the expectation for the squared error and simplify. Only the error terms (ecross and eceil) are random, and thus in equation 21, we have moved all of the other terms out of the expectation. In moving from equations 21 to 22, we make the assumption / approximation that the errors are uncorrelated and zero mean, which causes all but three terms to dropout in equation 22. This approximation, while possibly imperfect, substantially simplifies the expectation and makes it possible to derive a simple and empirically effective bias-correction procedure, as described next.
| (19) |
| (20) |
| (21) |
| (22) |
The first term in equation 22 is what we would hope to measure: a factor which is proportional to the squared error between the pure cross-context correlation computed from noise-free data and the model’s prediction of the pure cross-context correlation . The second term does not depend upon the model’s prediction and thus can be viewed as a constant from the standpoint of analyzing model bias. The third term is potentially problematic, since it biases the error upwards based on the squared magnitude of the predictions, with the magnitude of the bias determined by the magnitude of the errors in the noise ceiling. This term results in an upward bias in the estimated integration width, because narrower integration windows have less overlap with context and the predicted cross-context correlation tends to be larger in magnitude as a consequence. This bias is only present when there is substantial error in the noise ceiling, which explains why we only observed the bias for data with low reliability (Extended Data Fig 3c).
We can correct for this bias by subtracting a factor whose expectation is equal to the problematic third term in equation 22. All we need is a sample of the error in the noise ceiling, which our procedure naturally provides since we measure the noise ceiling separately for segments from each of the two contexts and then average these two estimates. Thus, we can get a sample of the error by subtracting our two samples of the correlation ceiling and dividing by 2 (averaging is equivalent to summing and dividing by 2 and the noise power of summed and subtracted signals is equal). We then take this sample of the error multiply it by our model prediction, square the result, and subtract this number from the measured squared error. This procedure is done separately for every lag and segment duration.
We found this procedure substantially reduced the bias when pooling across both random and natural contexts (compare Extended Data Fig 3a to Extended Data Fig 3c), as was done for all of our analyses except those shown in Extended Data Figure 5b. When only considering random contexts, we found this procedure somewhat over-corrected the bias (inducing a downward bias for noisy data), perhaps due to the influence of the terms omitted in our approximation (equation 22). However, our results were very similar when using random or natural contexts (Extended Data Fig 5b) and when using either the uncorrected or bias-corrected error. Thus, we conclude that our findings were not substantially influenced by noise and were robust to details of the analysis.
Extended Data
Extended Data Fig. 1. Histogram of phoneme, syllable, and word durations in TIMIT.
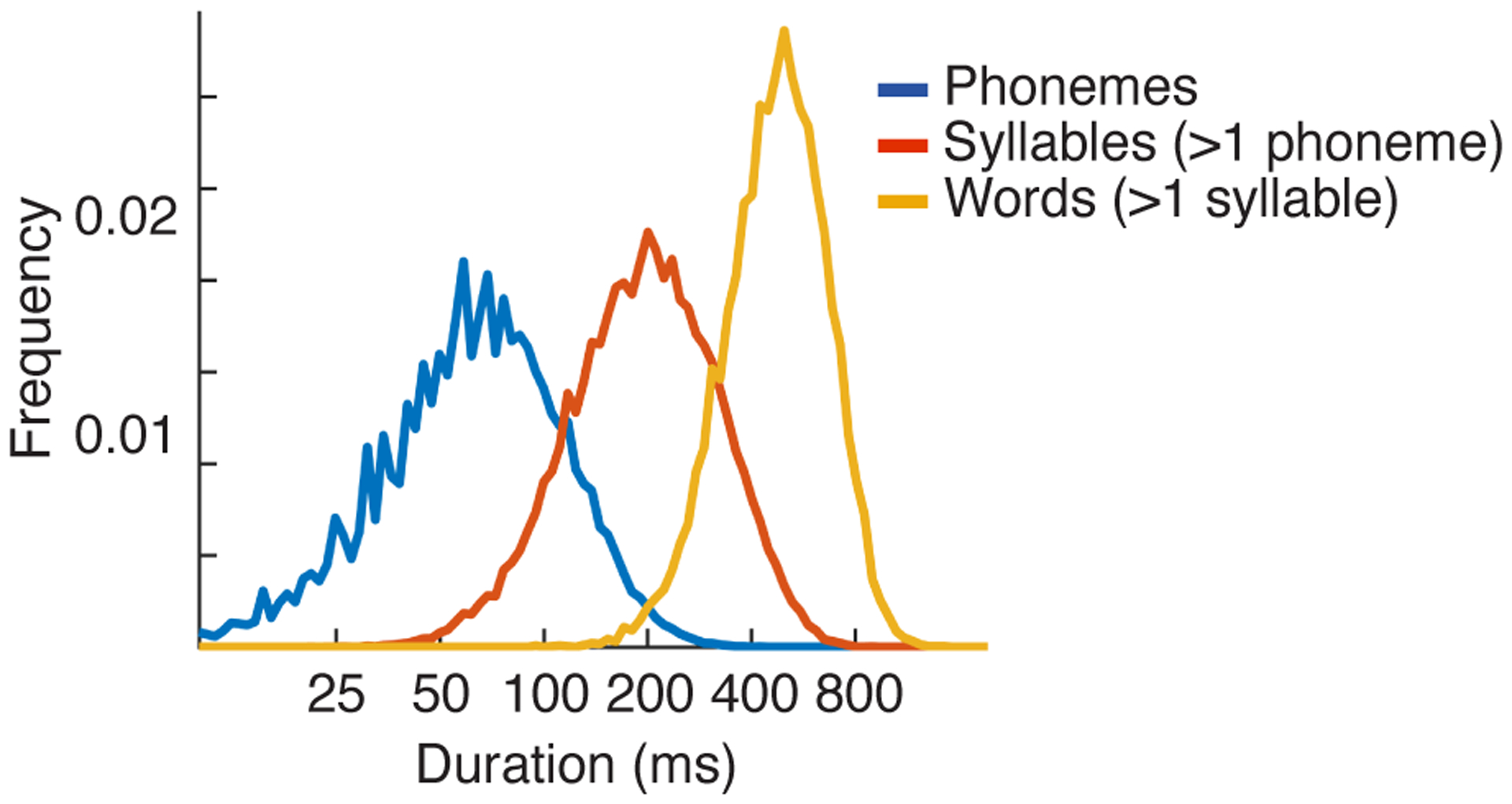
Durations of phonemes, multi-phoneme syllables, and multi-syllable words in the commonly used TIMIT database. Phonemes and words are labeled in the database. Syllables were computed from the phoneme labels using the software tsylb284. The median duration for each structure is 64, 197, and 479 milliseconds, respectively.
Extended Data Fig. 2. Cross-context correlation for 20 representative electrodes.
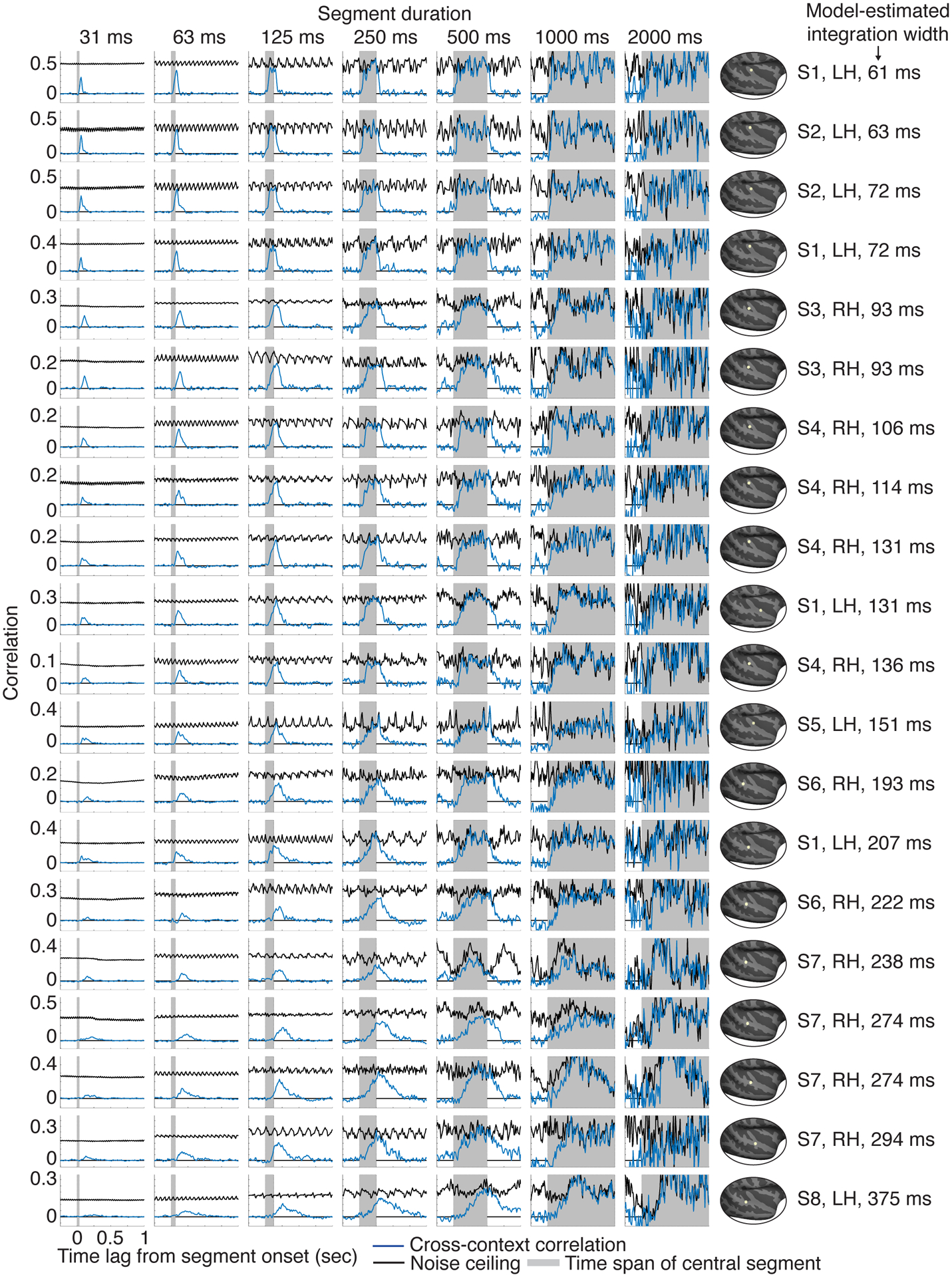
Electrodes were selected to illustrate the diversity of integration windows. Specifically, we partitioned all sound-responsive electrodes into 5 groups based on the width of their integration window, estimated using a model (Fig 3 illustrates the model). For each group, we plot the four electrodes with the highest SNR (as measured by the test-retest correlation across the sound set). Electrodes have been sorted by their integration width, which is indicated to the right of each plot, along with the location, hemisphere and subject number for each electrode. Each plot shows the cross-context correlation and noise ceiling for a single electrode and segment duration (indicated above each column). There were more segments for the shorter durations, and as a consequence, the cross-context correlation and noise ceiling were more stable/reliable for shorter segments (the number of segments is inversely proportional to the duration). This property is useful because at the short segment durations, there are a smaller number of relevant time lags, and it is useful if those lags are more reliable. The model used to estimate integration windows pooled across all lags and segment durations, taking into account the reliability of each datapoint.
Extended Data Fig. 3. Simulation results.
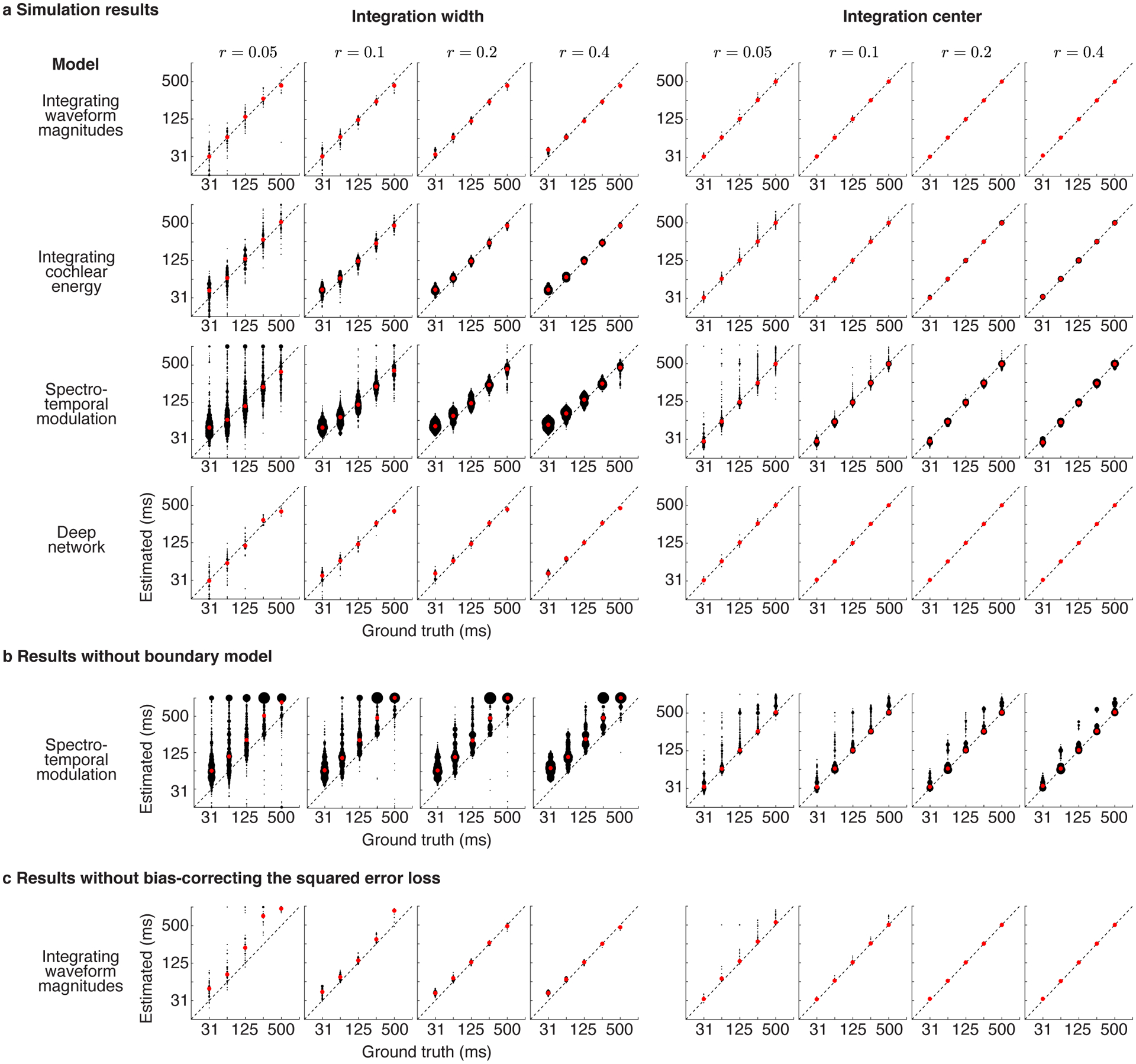
a, Integration windows estimated from four different model responses (from top to bottom): (1) a model that integrated waveform magnitudes within a known window (2) a model that integrated energy within a cochlear frequency band (3) a model that integrated spectrotemporal energy in a cochleagram representation of sound (4) a simple, deep neural network. All models had a ground truth, Gamma-distributed integration window. We independently varied the integration width and center of the models (excluding non-causal combinations) and tested if we could infer the ground truth values. Results are shown for several different SNRs, as measured by the test-retest correlation of the response across repetitions, the same metric used to select electrodes (we selected electrodes with a test-retest correlation greater than 0.1). Black dots correspond to a single model window/simulation. Red dots show the median estimate across all windows/simulations. Some models included more variants (e.g. different spectrotemporal filters), which is why some plots have a higher dot density. There is a small upward bias for very narrow integration widths (31 ms), likely due to the effects of the filter used to measure broadband gamma, which has an integration width of ~19 milliseconds. The integration widths of our electrodes (~50 to 400 ms) were mostly above the point at which this bias would have a substantial effect, and the bias works against our observed results since it compresses the possible range of integration widths. b, Integration windows estimated without explicitly modeling and accounting for boundary effects. Results are shown for the spectrotemporal model, which produces strong responses at the boundary between two segments due to prominent spectrotemporal changes. Note there is a nontrivial upward bias, particularly for integration widths, when not accounting for boundary effects (see Methods for a more detailed discussion). c, Integration windows estimated without accounting for an upward bias in the squared error loss. The bias grows as the SNR decreases (see Methods for an explanation). Results are shown for the waveform amplitude model, but the bias is present for all models since it is caused by the loss. Our bias-corrected loss largely corrected the problem, as can be observed in panel a.
Extended Data Fig. 4. Integration windows for different electrode types and subjects.
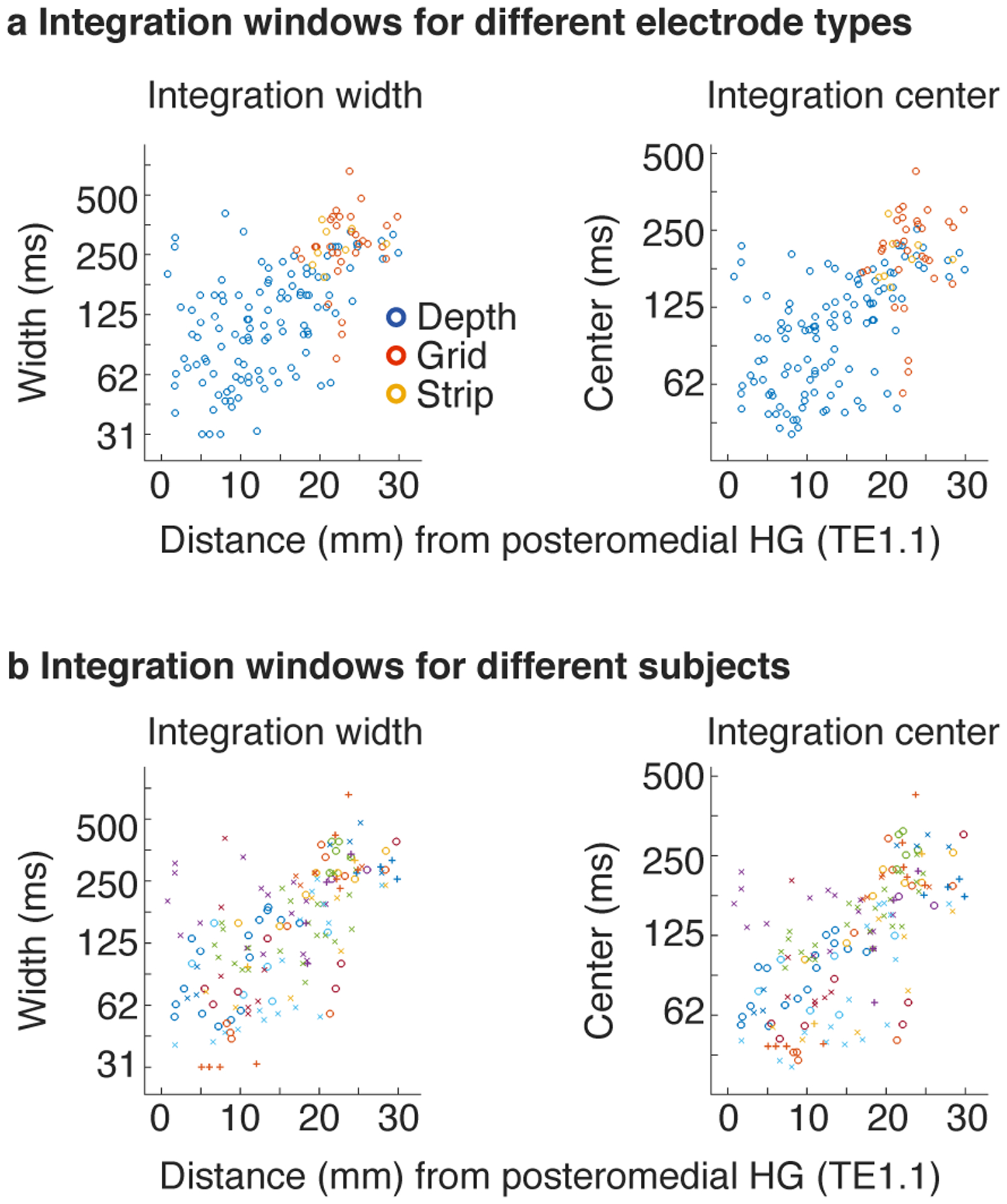
a, This panel plots integration widths (left) and centers (right) for individual electrodes as a function of distance to primary auditory cortex, defined as posteromedial Heschl’s gyrus. The electrodes have been labeled by their type (grid, depth, strip). The grid/strip electrodes were located further from primary auditory cortex on average, but given their location did not show any obvious difference in integration properties. The effect of distance was significant for the depth electrodes alone (the most numerous type of electrode) when excluding grids and strips (width: F1,14.53 = 24.51, p < 0.001, βdistance = 0.065 octaves/mm, CI = [0.039, 0.090]; center: F1,12.83 = 27.76, p < 0.001, βdistance = 0.052 octaves/mm, CI = [0.032, 0.071], N=114 electrodes). To be conservative, electrode type was included as a covariate in the linear mixed effects model used to assess significance as a whole. b, Same as panel a but indicating subject membership instead of electrode type. Each symbol corresponds to a unique subject. The effect of distance on integration windows is broadly distributed across the 18 subjects.
Extended Data Fig. 5. Robustness analyses.
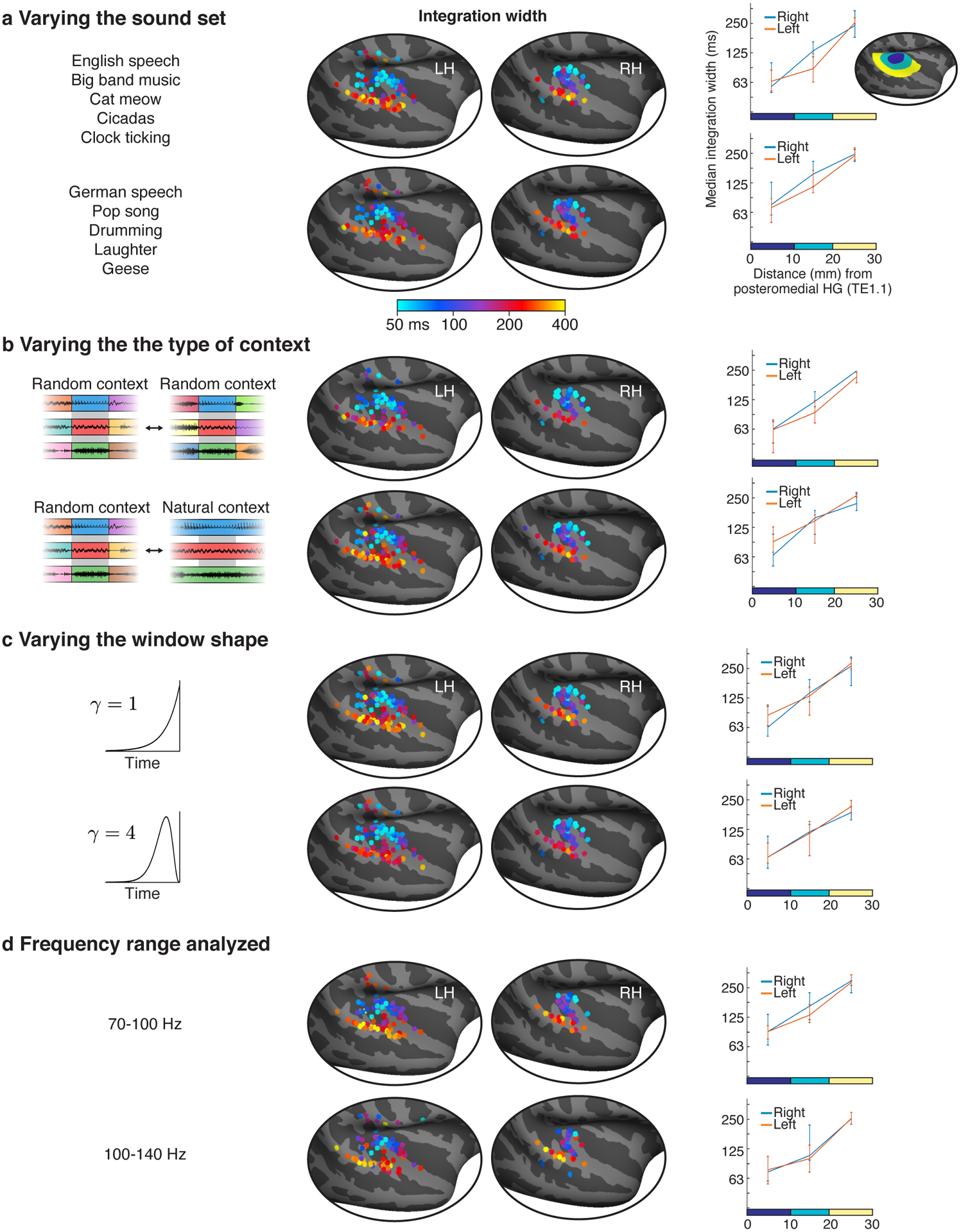
a, Sound segments were excerpted from 10 sounds. This panel shows integration windows estimated using segments drawn from two non-overlapping splits of 5 sounds each (listed on the left). Since many non-primary regions only respond strongly to speech or music8,9,11, we included speech and music in both splits. Format is analogous to Figure 4 but only showing integration widths (integration centers were also similar across analysis variants). The effect of distance was significant for both splits (split1: F1,12.660 = 40.20, p < 0.001, βdistance = 0.069 octaves/mm, CI = [0.047, 0.090], N=136 electrodes; split 2: F1,21.66 = 30.11, p < 0.001, βdistance = 0.066 octaves/mm, CI = [0.043, 0.090], N=135 electrodes). b, Shorter segments were created by subdividing longer segments, which made it possible to consider two types of context (see schematic): (1) random context, in which each segment is surrounded by random other segments (2) natural context, where a segment is a subset of a longer segment and thus surrounded by its natural context. When comparing responses across contexts, one of the two contexts must be random so that the contexts differ, but the other context can be random or natural. Our main analyses pooled across both types of comparison. Here, we show integration widths estimated by comparing either purely random contexts (top panel) or comparing random and natural contexts (bottom panel). The effect of distance was significant for both types of context comparisons (random-random: F1,28.056 = 30.01, p < 0.001, βdistance = 0.064 octaves/mm, CI = [0.041, 0.087], N=121 electrodes; random-natural: F1,18.816 = 27.087, p < 0.001, βdistance = 0.062 octaves/mm, CI = [0.039, 0.086], N=154 electrodes). c, We modeled integration windows using window shapes that varied from more exponential to more Gaussian (the parameter γ in equations 2&3 controls the shape of the window, see Methods). For our main analysis, we selected the shape that yielded the best prediction for each electrode. This panel shows integration widths estimated using two different fixed shapes. The effect of distance was significant for both shapes (γ = 1: F1,21.712 = 24.85, p < 0.001, βdistance = 0.067 octaves/mm, CI = [0.040, 0.093], N=154 electrodes; γ = 4: F1,20.973 = 19.38, p < 0.001, βdistance = 0.055 octaves/mm, CI = [0.031, 0.080], N=154 electrodes). d, Similar results were obtained using two different frequency ranges to measure gamma power (70–100s Hz: F1,21.05 = 19.38, p < 0.001, βdistance = 0.058 octaves/mm, CI = [0.032, 0.083], N=133 electrodes; 100–140 Hz: F1,20.56 = 12.57, p < 0.01, βdistance = 0.051 octaves/mm, CI = [0.023, 0.080], N=131 electrodes).
Extended Data Fig. 6. Relationship between integration widths and centers without any causality constraint.
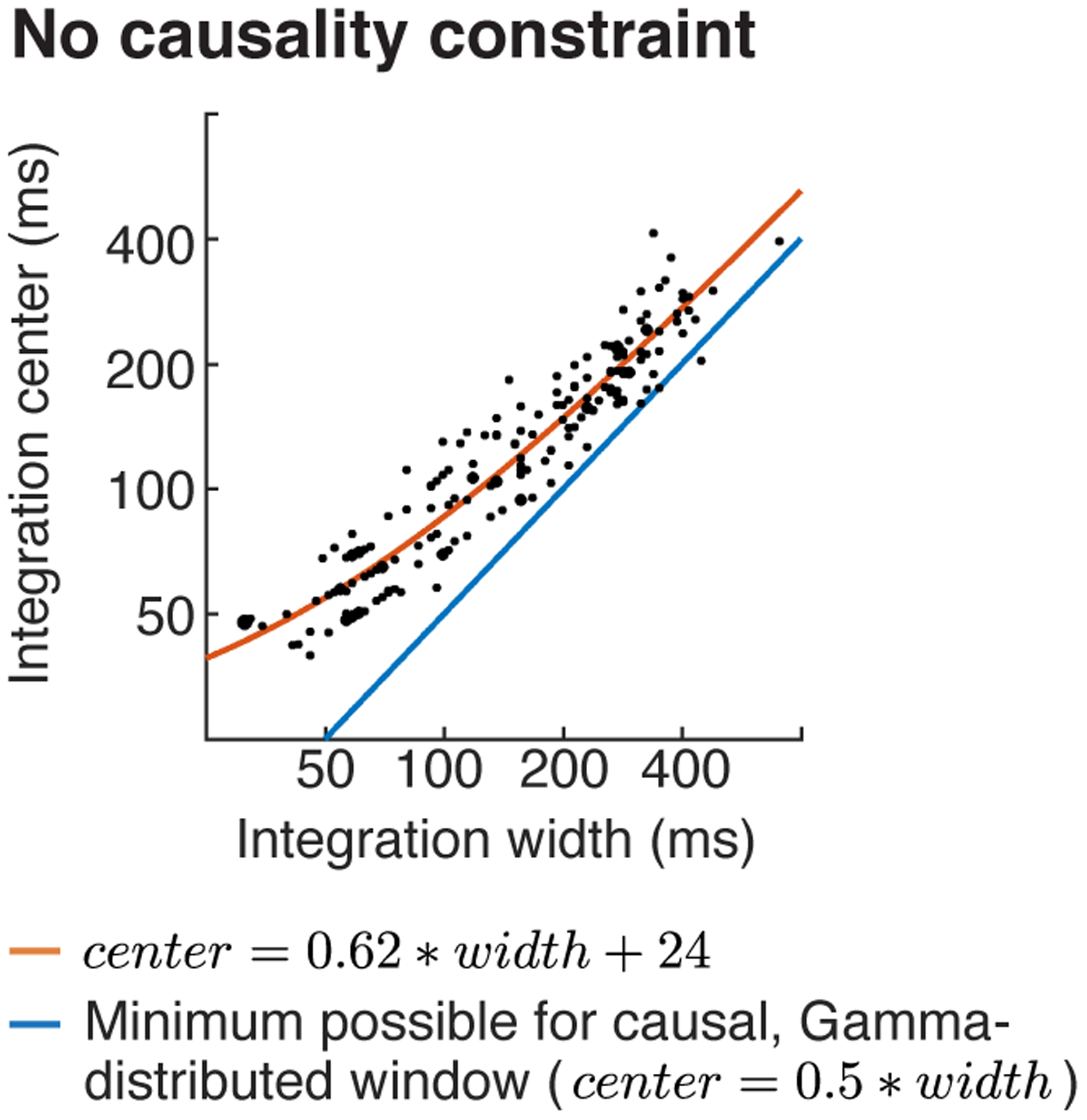
This figure plots integration centers vs. widths for windows that were not explicitly constrained to be causal. Results were similar to those with an explicit causality constraint (Fig 4c). Same format as Figure 4c.
Extended Data Fig. 7. Components most selective for sound categories at different integration widths.
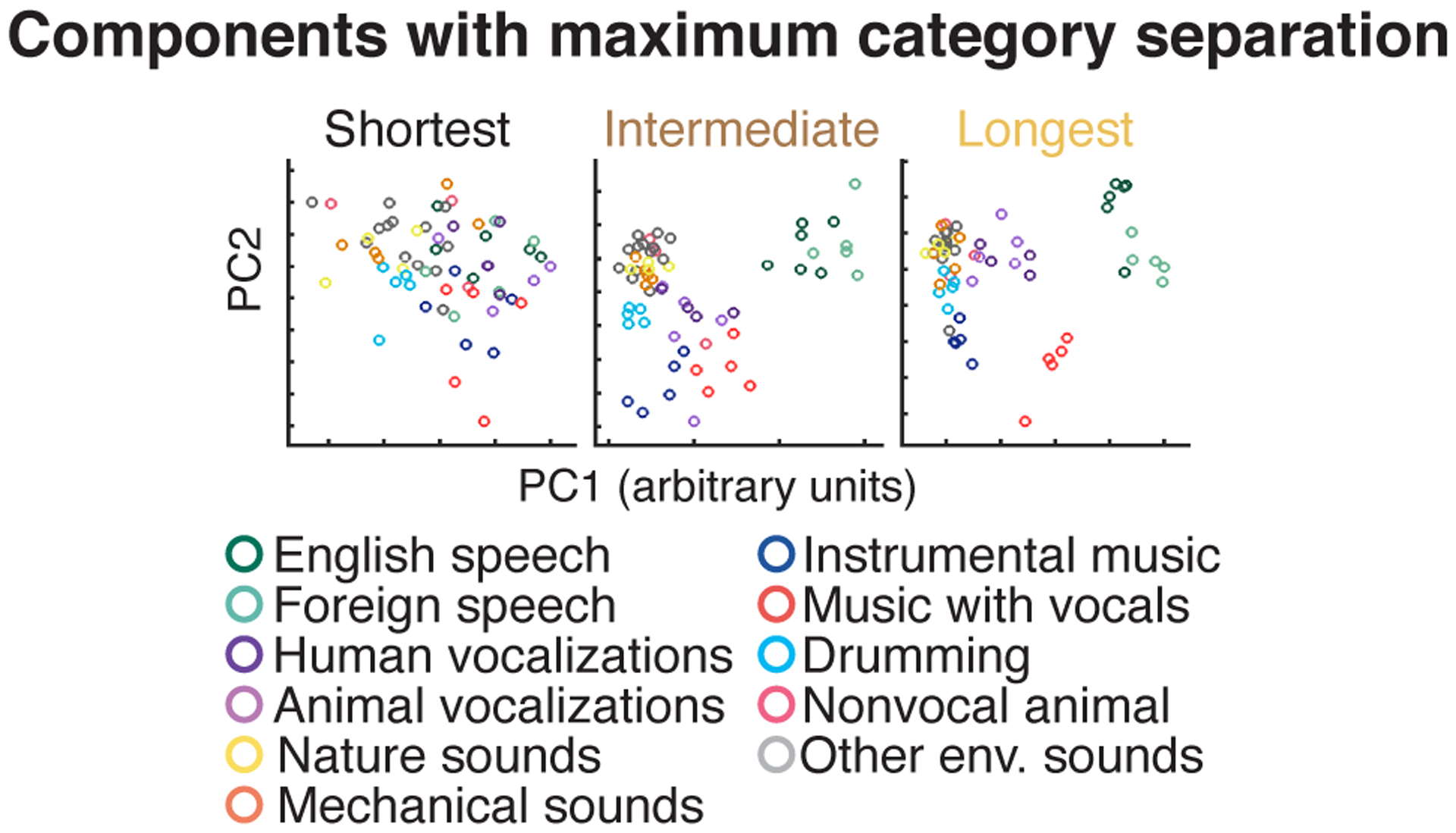
Electrodes were subdivided into three equally sized groups based on the width of their integration window. The time-averaged response of each electrode was then projected onto the top 2 components that showed the greatest category selectivity, measured using linear discriminant analysis (each circle corresponds to a unique sound). Same format as Figure 5b, which plots responses projected onto the top 2 principal components. Half of the sounds were used to compute the components, and the other half were used to measure their response to avoid statistical circularity. As a consequence, there are half as many sounds as in Figure 5b.
Extended Data Fig. 8. Results for integration-matched responses.
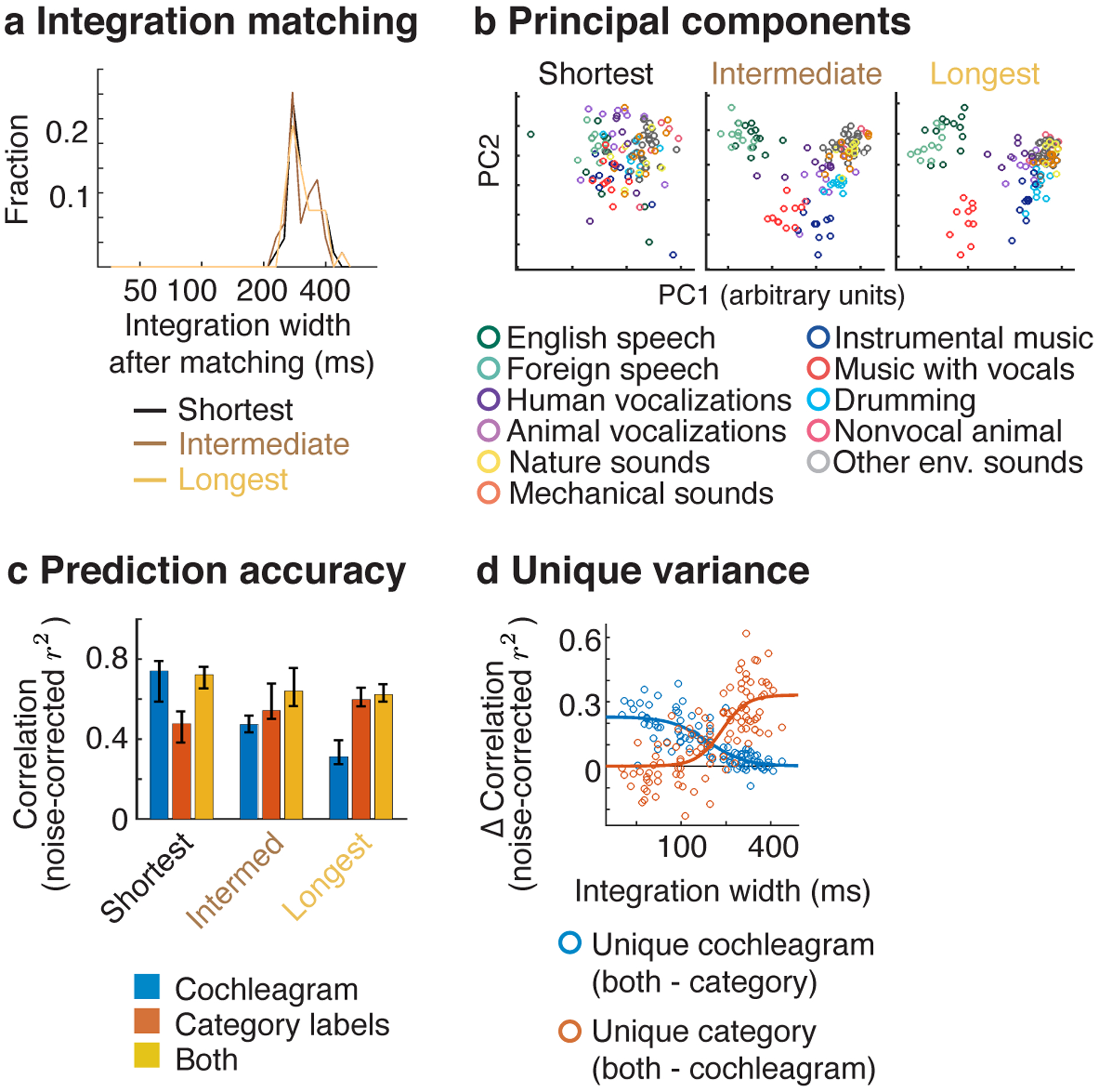
a, For our functional selectivity analyses, we subdivided the electrodes into three equally sized groups, based on the width of their integration window. To test if our results were an inevitable consequence of differences in temporal integration, we matched the integration windows across the electrodes in each group. Matching was performed by integrating the responses from the electrodes in the short and intermediate groups within an appropriately chosen window, such that the resulting integration window matched those for the longest group (see Integration matching in Methods). This figure plots a histogram of the effective integration windows after matching. b-d, These panels show the results of our applying our functional selectivity analyses to integration-matched responses. Format is the same as Figure 5b–d.
Supplementary Material
Acknowledgements
We thank Daniel Maksumov, Nikita Agrawal, Stephanie Montenegro, Leyao Yu, Marcin Leszczynski and Idan Tal for help with data collection. We thank Stephanie Montenegro and Hugh Wang for help in localizing electrodes. And we thank Alex Kell, Stephen David, Josh McDermott, Bevil Conway, Nancy Kanwisher, Nikolaus Kriegeskorte, and Marcin Leszczynski for comments on an earlier draft of this manuscript. This study was supported by the National Institutes of Health (NIDCD-K99-DC018051 to S.V.N.-H., NIDCD-R01-DC014279 to N.M., S10 OD018211 to N.M., NINDS-R01-NS084142 to C.A.S., NIDCD-R01-DC018805 to N.M./A.F.) and the Howard Hughes Medical Institute (LSRF postdoctoral award to S.V.N.-H.). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Footnotes
Code availability
Code implementing the TCI analyses described in this paper is available at: https://github.com/snormanhaignere/TCI
Competing interests
All authors declare no competing interests.
Data availability
The data supporting the findings of this study are available from the corresponding author upon request. Data are shared upon request due to the sensitive nature of human patient data. Source data underlying key statistics and figures (Figures 4 & 5) are available at this repository: https://github.com/snormanhaignere/NHB-TCI-source-data
References
- 1.Brodbeck C, Hong LE & Simon JZ Rapid transformation from auditory to linguistic representations of continuous speech. Current Biology 28, 3976–3983 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.DeWitt I & Rauschecker JP Phoneme and word recognition in the auditory ventral stream. Proceedings of the National Academy of Sciences 109, E505–E514 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hickok G & Poeppel D The cortical organization of speech processing. Nature reviews neuroscience 8, 393–402 (2007). [DOI] [PubMed] [Google Scholar]
- 4.Santoro R et al. Encoding of natural sounds at multiple spectral and temporal resolutions in the human auditory cortex. PLoS computational biology 10, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hullett PW, Hamilton LS, Mesgarani N, Schreiner CE & Chang EF Human superior temporal gyrus organization of spectrotemporal modulation tuning derived from speech stimuli. Journal of Neuroscience 36, 2014–2026 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schönwiesner M & Zatorre RJ Spectro-temporal modulation transfer function of single voxels in the human auditory cortex measured with high-resolution fMRI. Proceedings of the National Academy of Sciences 106, 14611–14616 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barton B, Venezia JH, Saberi K, Hickok G & Brewer AA Orthogonal acoustic dimensions define auditory field maps in human cortex. Proceedings of the National Academy of Sciences 109, 20738–20743 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Leaver AM & Rauschecker JP Cortical representation of natural complex sounds: effects of acoustic features and auditory object category. The Journal of Neuroscience 30, 7604–7612 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Norman-Haignere SV, Kanwisher NG & McDermott JH Distinct cortical pathways for music and speech revealed by hypothesis-free voxel decomposition. Neuron 88, 1281–1296 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kell AJ, Yamins DL, Shook EN, Norman-Haignere SV & McDermott JH A task-optimized neural network replicates human auditory behavior, predicts brain responses, and reveals a cortical processing hierarchy. Neuron (2018). [DOI] [PubMed] [Google Scholar]
- 11.Overath T, McDermott JH, Zarate JM & Poeppel D The cortical analysis of speech-specific temporal structure revealed by responses to sound quilts. Nature neuroscience 18, 903–911 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Davis MH & Johnsrude IS Hierarchical processing in spoken language comprehension. Journal of Neuroscience 23, 3423–3431 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Belin P, Zatorre RJ, Lafaille P, Ahad P & Pike B Voice-selective areas in human auditory cortex. Nature 403, 309–312 (2000). [DOI] [PubMed] [Google Scholar]
- 14.Zuk NJ, Teoh ES & Lalor EC EEG-based classification of natural sounds reveals specialized responses to speech and music. NeuroImage 210, 116558 (2020). [DOI] [PubMed] [Google Scholar]
- 15.Di Liberto GM, O’Sullivan JA & Lalor EC Low-frequency cortical entrainment to speech reflects phoneme-level processing. Current Biology 25, 2457–2465 (2015). [DOI] [PubMed] [Google Scholar]
- 16.Ding N et al. Temporal modulations in speech and music. Neuroscience & Biobehavioral Reviews (2017). [DOI] [PubMed] [Google Scholar]
- 17.Elhilali M Modulation representations for speech and music. in Timbre: Acoustics, Perception, and Cognition 335–359 (Springer, 2019). [Google Scholar]
- 18.Patel AD Music, language, and the brain. (Oxford university press, 2007). [Google Scholar]
- 19.Norman-Haignere SV & McDermott JH Neural responses to natural and model-matched stimuli reveal distinct computations in primary and nonprimary auditory cortex. PLoS biology 16, e2005127 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Theunissen F & Miller JP Temporal encoding in nervous systems: A rigorous definition. J Comput Neurosci 2, 149–162 (1995). [DOI] [PubMed] [Google Scholar]
- 21.Lerner Y, Honey CJ, Silbert LJ & Hasson U Topographic mapping of a hierarchy of temporal receptive windows using a narrated story. Journal of Neuroscience 31, 2906–2915 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen C, Read HL & Escabí MA Precise feature based time scales and frequency decorrelation lead to a sparse auditory code. Journal of Neuroscience 32, 8454–8468 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Meyer AF, Williamson RS, Linden JF & Sahani M Models of neuronal stimulus-response functions: elaboration, estimation, and evaluation. Frontiers in systems neuroscience 10, 109 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Khatami F & Escabí MA Spiking network optimized for word recognition in noise predicts auditory system hierarchy. PLOS Computational Biology 16, e1007558 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Harper NS et al. Network receptive field modeling reveals extensive integration and multi-feature selectivity in auditory cortical neurons. PLoS computational biology 12, e1005113 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Keshishian M et al. Estimating and interpreting nonlinear receptive field of sensory neural responses with deep neural network models. Elife 9, e53445 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Albouy P, Benjamin L, Morillon B & Zatorre RJ Distinct sensitivity to spectrotemporal modulation supports brain asymmetry for speech and melody. Science 367, 1043–1047 (2020). [DOI] [PubMed] [Google Scholar]
- 28.Flinker A, Doyle WK, Mehta AD, Devinsky O & Poeppel D Spectrotemporal modulation provides a unifying framework for auditory cortical asymmetries. Nature human behaviour 3, 393 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Teng X & Poeppel D Theta and Gamma bands encode acoustic dynamics over wide-ranging timescales. Cerebral Cortex 30, 2600–2614 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Obleser J, Eisner F & Kotz SA Bilateral speech comprehension reflects differential sensitivity to spectral and temporal features. Journal of neuroscience 28, 8116–8123 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Baumann S et al. The topography of frequency and time representation in primate auditory cortices. Elife 4, e03256 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rogalsky C, Rong F, Saberi K & Hickok G Functional anatomy of language and music perception: temporal and structural factors investigated using functional magnetic resonance imaging. The Journal of Neuroscience 31, 3843–3852 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Farbood MM, Heeger DJ, Marcus G, Hasson U & Lerner Y The neural processing of hierarchical structure in music and speech at different timescales. Frontiers in neuroscience 9, 157 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Angeloni C & Geffen MN Contextual modulation of sound processing in the auditory cortex. Current opinion in neurobiology 49, 8–15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Griffiths TD et al. Direct recordings of pitch responses from human auditory cortex. Current Biology 20, 1128–1132 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mesgarani N, Cheung C, Johnson K & Chang EF Phonetic feature encoding in human superior temporal gyrus. Science 343, 1006–1010 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ray S & Maunsell JHR Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLOS Biology 9, e1000610 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Manning JR, Jacobs J, Fried I & Kahana MJ Broadband shifts in local field potential power spectra are correlated with single-neuron spiking in humans. Journal of Neuroscience 29, 13613–13620 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Slaney M Auditory toolbox. Interval Research Corporation, Tech. Rep 10, 1998 (1998). [Google Scholar]
- 40.Chi T, Ru P & Shamma SA Multiresolution spectrotemporal analysis of complex sounds. The Journal of the Acoustical Society of America 118, 887–906 (2005). [DOI] [PubMed] [Google Scholar]
- 41.Singh NC & Theunissen FE Modulation spectra of natural sounds and ethological theories of auditory processing. The Journal of the Acoustical Society of America 114, 3394–3411 (2003). [DOI] [PubMed] [Google Scholar]
- 42.Di Liberto GM, Wong D, Melnik GA & de Cheveigné A Low-frequency cortical responses to natural speech reflect probabilistic phonotactics. Neuroimage 196, 237–247 (2019). [DOI] [PubMed] [Google Scholar]
- 43.Leonard MK, Bouchard KE, Tang C & Chang EF Dynamic encoding of speech sequence probability in human temporal cortex. Journal of Neuroscience 35, 7203–7214 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schoppe O, Harper NS, Willmore BD, King AJ & Schnupp JW Measuring the performance of neural models. Frontiers in Computational Neuroscience 10, 10 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mizrahi A, Shalev A & Nelken I Single neuron and population coding of natural sounds in auditory cortex. Current opinion in neurobiology 24, 103–110 (2014). [DOI] [PubMed] [Google Scholar]
- 46.Chien H-YS & Honey CJ Constructing and Forgetting Temporal Context in the Human Cerebral Cortex. Neuron (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Panzeri S, Brunel N, Logothetis NK & Kayser C Sensory neural codes using multiplexed temporal scales. Trends in Neurosciences 33, 111–120 (2010). [DOI] [PubMed] [Google Scholar]
- 48.Joris PX, Schreiner CE & Rees A Neural processing of amplitude-modulated sounds. Physiological reviews 84, 541–577 (2004). [DOI] [PubMed] [Google Scholar]
- 49.Wang X, Lu T, Bendor D & Bartlett E Neural coding of temporal information in auditory thalamus and cortex. Neuroscience 154, 294–303 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gao X & Wehr M A coding transformation for temporally structured sounds within auditory cortical neurons. Neuron 86, 292–303 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.McDermott JH & Simoncelli EP Sound texture perception via statistics of the auditory periphery: evidence from sound synthesis. Neuron 71, 926–940 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cohen MR & Kohn A Measuring and interpreting neuronal correlations. Nature neuroscience 14, 811 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Murray JD et al. A hierarchy of intrinsic timescales across primate cortex. Nature neuroscience 17, 1661 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chaudhuri R, Knoblauch K, Gariel M-A, Kennedy H & Wang X-J A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron 88, 419–431 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Rauschecker JP & Scott SK Maps and streams in the auditory cortex: nonhuman primates illuminate human speech processing. Nature Neuroscience 12, 718–724 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Sharpee TO, Atencio CA & Schreiner CE Hierarchical representations in the auditory cortex. Current opinion in neurobiology 21, 761–767 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zatorre RJ, Belin P & Penhune VB Structure and function of auditory cortex: music and speech. Trends in Cognitive Sciences 6, 37–46 (2002). [DOI] [PubMed] [Google Scholar]
- 58.Poeppel D The analysis of speech in different temporal integration windows: cerebral lateralization as ‘asymmetric sampling in time’. Speech communication 41, 245–255 (2003). [Google Scholar]
- 59.Hamilton LS, Oganian Y, Hall J & Chang EF Parallel and distributed encoding of speech across human auditory cortex. Cell 184, 4626–4639 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nourski KV et al. Functional organization of human auditory cortex: Investigation of response latencies through direct recordings. NeuroImage 101, 598–609 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Bartlett EL The organization and physiology of the auditory thalamus and its role in processing acoustic features important for speech perception. Brain and language 126, 29–48 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gattass R, Gross CG & Sandell JH Visual topography of V2 in the macaque. Journal of Comparative Neurology 201, 519–539 (1981). [DOI] [PubMed] [Google Scholar]
- 63.Dumoulin SO & Wandell BA Population receptive field estimates in human visual cortex. Neuroimage 39, 647–660 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ding N, Melloni L, Zhang H, Tian X & Poeppel D Cortical tracking of hierarchical linguistic structures in connected speech. Nature Neuroscience 19, 158–164 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Suied C, Agus TR, Thorpe SJ, Mesgarani N & Pressnitzer D Auditory gist: recognition of very short sounds from timbre cues. The Journal of the Acoustical Society of America 135, 1380–1391 (2014). [DOI] [PubMed] [Google Scholar]
- 66.Donhauser PW & Baillet S Two distinct neural timescales for predictive speech processing. Neuron 105, 385–393 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ulanovsky N, Las L, Farkas D & Nelken I Multiple time scales of adaptation in auditory cortex neurons. Journal of Neuroscience 24, 10440–10453 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lu K et al. Implicit memory for complex sounds in higher auditory cortex of the ferret. Journal of Neuroscience 38, 9955–9966 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Chew SJ, Mello C, Nottebohm F, Jarvis E & Vicario DS Decrements in auditory responses to a repeated conspecific song are long-lasting and require two periods of protein synthesis in the songbird forebrain. Proceedings of the National Academy of Sciences 92, 3406–3410 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Bianco R et al. Long-term implicit memory for sequential auditory patterns in humans. eLife 9, e56073 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Miller KJ, Honey CJ, Hermes D, Rao RP & Ojemann JG Broadband changes in the cortical surface potential track activation of functionally diverse neuronal populations. Neuroimage 85, 711–720 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Leszczyński M et al. Dissociation of broadband high-frequency activity and neuronal firing in the neocortex. Science advances 6, eabb0977 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Günel B, Thiel CM & Hildebrandt KJ Effects of exogenous auditory attention on temporal and spectral resolution. Frontiers in psychology 9, 1984 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Norman-Haignere SV et al. Pitch-responsive cortical regions in congenital amusia. J. Neurosci 36, 2986–2994 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Norman-Haignere S et al. Intracranial recordings from human auditory cortex reveal a neural population selective for musical song. bioRxiv 696161 (2020). [Google Scholar]
- 76.Boebinger D, Norman-Haignere SV, McDermott JH & Kanwisher N Music-selective neural populations arise without musical training. Journal of Neurophysiology 125, 2237–2263 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Morosan P et al. Human primary auditory cortex: cytoarchitectonic subdivisions and mapping into a spatial reference system. Neuroimage 13, 684–701 (2001). [DOI] [PubMed] [Google Scholar]
- 78.Baumann S, Petkov CI & Griffiths TD A unified framework for the organization of the primate auditory cortex. Frontiers in systems neuroscience 7, 11 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Barr DJ, Levy R, Scheepers C & Tily HJ Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of memory and language 68, 255–278 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Kuznetsova A, Brockhoff PB & Christensen RH lmerTest package: tests in linear mixed effects models. Journal of statistical software 82, 1–26 (2017). [Google Scholar]
- 81.Gelman A & Hill J Data analysis using regression and multilevel/hierarchical models. (Cambridge university press, 2006). [Google Scholar]
- 82.Schielzeth H et al. Robustness of linear mixed-effects models to violations of distributional assumptions. Methods in Ecology and Evolution 11, 1141–1152 (2020). [Google Scholar]
- 83.de Cheveigné A & Parra LC Joint decorrelation, a versatile tool for multichannel data analysis. Neuroimage 98, 487–505 (2014). [DOI] [PubMed] [Google Scholar]
- 84.Murphy KP Machine learning: a probabilistic perspective. (MIT press, 2012). [Google Scholar]
- 85.de Heer WA, Huth AG, Griffiths TL, Gallant JL & Theunissen FE The hierarchical cortical organization of human speech processing. Journal of Neuroscience 3267–16 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Marquardt DW An algorithm for least-squares estimation of nonlinear parameters. Journal of the society for Industrial and Applied Mathematics 11, 431–441 (1963). [Google Scholar]
- 87.Fisher WM tsylb: NIST syllabification software, version 2 revision 1.1. (1997).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author upon request. Data are shared upon request due to the sensitive nature of human patient data. Source data underlying key statistics and figures (Figures 4 & 5) are available at this repository: https://github.com/snormanhaignere/NHB-TCI-source-data


