Modeling Individual Differences in the Timing of Change Onset and Offset

Abstract

Individual differences in the timing of developmental processes are often of interest in longitudinal studies, yet common statistical approaches to modeling change cannot directly estimate the timing of when change occurs. The time-to-criterion framework was recently developed to incorporate the timing of a prespecified criterion value; however, this framework has difficulty accommodating contexts where the criterion value differs across people or when the criterion value is not known a priori, such as when the interest is in individual differences in when change starts or stops. This paper combines aspects of reparameterized quadratic models and multiphase models to provide information on the timing of change. We first consider the more common situation of modeling decelerating change to an offset point, defined as the point in time at which change ceases. For increasing trajectories, the offset occurs when the criterion attains its maximum (“inverted J-shaped” trajectories). For decreasing trajectories, offset instead occurs at the minimum. Our model allows for individual differences in both the timing of offset and ultimate level of the outcome. The same model, reparameterized slightly, captures accelerating change from a point of onset (“J-shaped” trajectories). We then extend the framework to accommodate “S-shaped” curves where both the onset and offset of change are within the observation window. We provide demonstrations that span neuroscience, educational psychology, developmental psychology, and cognitive science, illustrating the applicability of the modeling framework to a variety of research questions about individual differences in the timing of change.

Longitudinal data and growth modeling are widespread within psychology and behavioral sciences (Hox et al., 2017; Singer & Willett, 2003). In longitudinal studies concerned with developmental processes, research questions frequently relate to the timing of when change starts (the change onset) or when change stops (the change offset). As an example from neuroscience, the thickening of the prefrontal cortex is an important maturational process occurring during infancy and there is interest in the change offset rather than solely the level of thickness ultimately attained because the timing of sensitive periods has implications that extend across the lifespan (Goldman-Rakic, 1987). In research on language development in young children, there is an interest in the change onset that demarcates when children start to build their vocabularies, not just the number of words they know (Fenson et al., 1994). And in educational contexts, content mastery is important but so is the change offset, which captures how quickly mastery is acquired to ensure that students continue to progress (Dumas et al., 2019). Despite this interest in questions related to change onsets and change offsets, statistical models for longitudinal data have difficulty incorporating information related to timing.

In the last 20 years, there has been a growing emphasis on selecting and parameterizing growth models so that the coefficients correspond to quantities with useful substantive interpretations (Codd & Cudeck, 2014; McNeish et al., 2019). For instance, common nonlinear models within the family of curves described by Richards (1959) capture growth toward an asymptote, with a primary goal being to predict the ultimate level of the outcome variable. The asymptote of the growth trajectory is included as an explicit parameter and can be directly estimated; however, the trajectory never quite meets the asymptote, only becoming ever closer as time advances. This property makes asymptotic models less useful for questions related to the change offsets such as when studying individual differences in the timing of maturity or mastery in a given domain. That is, researchers often are not only interested in the ultimate level that people reach but also in how fast they get there (Cohen, 2008; Feng et al., 2019). In using an asymptotic model, one must impose a threshold for declaring growth completed, such as 99% to asymptote or 99.9% to asymptote. Such a solution is unsatisfying both for its arbitrariness and for the fact that the quantity of interest – the change offset – is not an explicit parameter of the model.

Johnson and Hancock (2019) introduced the time-to-criterion framework to address research questions specifically about timing. Drawing from Preacher and Hancock (2015), Johnson and Hancock (2019) show how to reparameterize linear and nonlinear growth models such that the timing of a particular value (i.e., the criterion) along the growth trajectory is directly estimable. The time-to-criterion framework is a notable step forward for researchers interested in timing, but it requires that researchers select the criterion of interest a priori. This encompasses situations where there is a predefined benchmark for proficiency such as on standardized educational assessments or a known clinical cut-off. It excludes contexts when the criterion value is unknown ahead of time or where the criterion value varies across people. Using the previous example of prefrontal cortex thickening, the eventual maximum thickness is both unknown a priori and differs across individuals, a situation not accommodated by time-to-criterion models.

To extend research questions about timing to accommodate change offsets or change onsets, this paper outlines how growth models can move from a time-to-criterion framework to time-at-offset or time-at-onset framework. Specifically, we outline a nonlinear time-at-offset model parameterization that includes person-specific parameters for both the ultimate maximum level achieved as well as the time at which this level was achieved (i.e., the change offset). The same approach − with minor differences in model parameterization − can provide a time-at-onset model such there are explicit person-specific change onsets that follow a flat initial level. Additionally, for instances in which both change onset and change offset are present within the observation window, combining the time-at-offset and time-at-onset models produces a model for S-shaped, sigmoidal growth that allows for person-specific coefficients that relate to both aspects of timing.

To outline the structure of the paper, we begin with a short overview of existing growth models and how they struggle to flexibly incorporate aspects of timing, change offsets and change onsets in particular. Then we review reparameterizations discussed by Cudeck and du Toit (2002) and multiphase models discussed by Cudeck and Klebe (2002), elements of which we combine to provide a model for evaluating time-at-offset and time-at-onset. After presenting these models, we provide four empirical examples from different disciplines to demonstrate its utility and versatility for questions that span the behavioral sciences. The first example focuses on the aforementioned example of the maturation of the cortex. The second example is a randomized intervention study concerning early childhood mathematics. The third example demonstrates a time-at-onset model with data on vocabulary acquisition in infancy. Finally, we model S-shaped, sigmoidal growth curves in a strategy learning task, with variability in both individual change onsets and change offsets. We conclude with a discussion of limitations and future directions.

Brief Overview of Growth Modeling

Linear Growth Models

In multilevel notation (Raudenbush & Bryk, 2002), a basic unconditional linear growth model can be written as

$$\begin{gathered} y_{ti}={\beta }_{0i}+{\beta }_{1i}Tim{e}_{ti}+e_{ti} \\ {\beta }_{0i}={\gamma }_{00}+u_{0i} \\ {\beta }_{1i}={\gamma }_{10}+u_{1i} \end{gathered}$$ (1)

The first expression is a typical regression model where the outcome y for the ith person at the tth time is equal to an intercept (β_0i) plus the linear slope (β_1i) times the tth value of Time plus a residual (e_ti) for the ith person at time t. The difference between a standard single-level regression and a growth model is that the regression coefficients (β) have i subscripts, meaning that they vary across people (Laird & Ware, 1982). Correspondingly, each person has a unique intercept and slope which produces person-specific growth trajectories.

These person-specific coefficients are directly modeled in the second and third expressions in Equation 1 and are equal to the average across all people (the fixed effect represented by γ) plus a person-specific random effect (represented by u) which captures the deviation of the ith person’s coefficient from the average. These random effects are not explicitly estimated but instead are assumed to come from a multivariate normal distribution with a mean vector of zero and an estimated covariance matrix: u_i ~ MVN (0, T).

Polynomial Models for Nonlinear Growth

Growth in behavioral sciences is often nonlinear (Grimm et al., 2011) and the model in Equation 1 can be modified to include a quadratic term for Time to reflect nonlinearity such that the first expression becomes $y_{ti}={\beta }_{0i}+{\beta }_{1i}Tim{e}_{ti}+{\beta }_{2i}Tim{e}_{ti}^2+e_{ti}$. The popularity of this second-order polynomial model is that it can model nonlinear relations with models that remain linear in the parameters (Bollen, 1989; Grimm & Ram, 2009). That is, the right side of the regression equation is nonlinear in the variables by including polynomial terms for Time but it remains linear in the parameters such that parameters enter the model in a strictly additive fashion and take the form coefficient × Time + coefficient × Time²… Because the model remains linear in the parameters, it can be fit easily within standard linear model software (Cudeck & du Toit, 2002). Though easy to estimate, polynomial growth models suffer from two major drawbacks, (a) coefficients are difficult to interpret (Grimm et al., 2011) and (b) the implied growth trajectory is unbounded, which rarely matches theories of development (Bollen & Curran, 2006, Ch. 4; Grimm & Ram, 2009).

To expand on these drawbacks, first, a second-degree polynomial growth model with Time and Time² as predictors yields coefficients capturing the instantaneous growth rate at Time = 0 and half the acceleration of the curve (Bollen & Curran, 2006). The sign associated with these coefficients can be useful for discussing concavity, but it is hard to characterize the shape of the growth trajectory in these terms. Further, the effects of predictors of between-person differences in trajectories are difficult to interpret substantively because the coefficients do not have an intuitive scale. Finally, the model neglects important milestones in growth trajectories (Cudeck, 1996) – what is the maximum value of the curve? Does the growth trajectory have an asymptote or does it change concavity? At which time does the maximum take place? Despite the relevance of such questions, answers are difficult to discern in polynomial growth models.

Second-order polynomial models are also symmetric and parabolic (i.e., U-shaped), which implies that the outcome will decline as quickly as it grew (Grimm & Ram, 2009). The idea of a second-order polynomial model is often to locally approximate nonlinearity of a J-shaped or inverted J-shaped curve. This can produce a serviceable local approximation for many monotonic nonlinear growth functions but tends to be unrealistic for defining growth broadly or for generalizing the model to the same phenomena at different times of observations (Blozis, 2004; Pinheiro & Bates, 2000). That is, a polynomial specification necessarily requires that the curve eventually change directions with the rate of decline equal to the rate of ascent, which rarely matches developmental theories of growth. Even for models covering a large portion of the lifespan with outcomes that can decline like memory, the descent is rarely symmetric and as expedient as the initial ascent.

Despite these drawbacks, polynomial models remain widespread. Historically, the use of these models was motivated by the computational challenges of fitting models that are truly nonlinear in their parameters (Blozis & Cudeck, 1999). However, advances in computing have largely mitigated these obstacles and models that are nonlinear in the parameters are a compelling alternative, providing results that more closely match theoretical hypotheses about change over time (Cudeck & Harring, 2007; Ram & Grimm, 2007).

Nonlinear Mixed Effect Models

Nonlinear mixed effect models relax the requirement that the model be linear in the parameters. This means that parameters and random effects can enter the model nonlinearly in exponents, fractions, or as products with other parameters, which allows for unique parameterizations that directly estimate quantities of substantive interest. For instance, the negative exponential model is a popular nonlinear model for decelerating monotonic trajectories (Grimm et al., 2011). The regression equation for the model can be written as y_ti = α_i + (δ_i − α_i)(1 − exp (ϕ_iTime)) + e_ti where α_i is the person-specific intercept, δ_i is the person-specific upper asymptote representing the expected value as Time →∞, and ϕ_i is a person-specific proportional rate of decay in growth that dictates how quickly the data grow from intercept to asymptote. When these models are applied in behavioral science settings, the asymptote and maximum performance are typically the main focus and translate directly to substantive questions (McNeish & Dumas, 2017). However, the rate parameter tends to correspond less closely to quantities that are meaningful to psychologists and does not encode any information about timing.

Some nonlinear growth models improve upon this by directly including parameters corresponding to the timing of particular milestones in the curve. For instance, the Michaelis-Menten model directly estimates the point in time when the outcome is halfway between the intercept and the asymptote such that y_ti = α_i + [(δ_i − α_i) × Time](φ_i +Time)⁻¹ + e_ti for φ_i the person-specific midpoint parameter. So, if the midpoint estimate were 4, that would mean that the outcome y is halfway between the intercept and the asymptote when Time = 4. On this metric, the estimate conveys direct information of substantive relevance and effects of covariates have clear interpretations. Nonetheless, the Michaelis-Menten model is inflexible with respect to the criterion associated with this timing – the model always estimates the timing of the midpoint point between intercept and asymptote. To the extent that the interest in timing deviates from the midpoint, the timing information provided by the Michaelis-Menten model becomes less useful.

Time-to-Criterion Models

Johnson and Hancock (2019) describe an approach for explicitly parameterizing timing of a particular criterion as a parameter in the model. In this time-to-criterion framework, the first step is to respecify the functional form of the intended model in terms of the prespecified criterion. Using Michaelis-Menten as an example, one would solve for a predetermined and substantively interesting criterion value c by substituting c for the outcome y_ti such that c =α_i + [(δ_i − α_i) × ω_i](φ_i + ω_i)⁻¹. Whereas Time was a previously a variable, it now becomes ω_i and is an estimable parameter representing the specific value of Time that yields the desired criterion value c from this function. The equation can be rearranged to solve for ω_i such that ω_i = [φ_i (c − α_i)](δ_i − c)⁻¹.

We can then substitute ω_i back into the original Michaelis-Menten equation to estimate it directly. Unfortunately, one of the original three parameters (α_i, δ_i, φ_i) must be sacrificed to create room for the new parameter ω_i (ω_i is redundant with these three parameters so all four cannot be estimated simultaneously). The midpoint parameter becomes a less useful developmental reference when ω_i is also in the model, so solving for φ_i yields φ_i = [(δ_i − c) ω_i](c − α_i)⁻¹. This expression is then substituted into the original Michaelis-Menten Equation such that $y_{ti}={\alpha }_i+\frac{\left({\delta }_i-{\alpha }_i\right)\times \mathit{\text{Time}}}{\left[\frac{\left({\delta }_i-c\right){\omega }_i}{c-{\alpha }_i}\right]+\mathit{\text{Time}}}$. In essence, the time-to-criterion model trades the ability to estimate the midpoint φ_i for the ability to estimate the more substantively meaningful timing of a researcher-selected criteria ω_i.

The time-to-criterion framework is a useful and clever method for directly estimating the time at which a prespecified criterion occurs; however, some limitations remain. First, the process requires that the criterion be known a priori. Though realistic in settings where there are explicit cutoffs delineating certain pathologies or levels of achievement, an a priori criterion may be less clear-cut in other circumstances. For instance, if the criterion is a person’s maximum value, this is estimated from the data in most cases. Further, the criterion does not have an i subscript and is constant for all people, which is violated for a criterion like maximum development that typically exhibits between-person variability. The next sections discuss how this idea can be generalized to cover a wider set of research questions involving timing of maximum or minimum values in growth trajectories by combining elements of existing models.

Reparameterizing Polynomial Models

The first building block of our proposed model is an idea advanced by Cudeck and du Toit (2002), who noted that polynomial models can often be reparameterized to improve interpretation. They focused on a reparameterized version of the quadratic model that yields coefficients with more substantively meaningful interpretations. Rather than include coefficients to capture the instantaneous rate of change at Time = 0 and half the acceleration as in a polynomial model that is linear in the parameters and includes higher-order polynomials of time as predictors, Cudeck and du Toit (2002) use a nonlinear parameterization that includes coefficients representing the maximum value of the curve and the time at which the maximum occurs (i.e., the vertex coordinates of a parabolic curve). Specifically, the reparameterized quadratic can be written as

$$\begin{gathered} y_{ti}={\beta }_{1i}-\left({\beta }_{1i}-{\beta }_{0i}\right){\left(\frac{Tim{e}_{ti}}{{\beta }_{2i}}-1\right)}^2+e_{ti} \\ {\beta }_{0i}={\gamma }_{00}+u_{0i} \\ {\beta }_{1i}={\gamma }_{10}+u_{1i} \\ {\beta }_{2i}={\gamma }_{20}+u_{2i} \end{gathered}$$ (2)

In this reparameterized model, the intercept (β_0i) remains the expected value of y for person i at Time = 0, but β_1i represents the maximum or minimum expected value of y for person i, and β_2i captures the time at which this maximum or minimum value occurs. As before, each of the β coefficients is then broken down into a fixed effect (γ) and a person-specific random effect (u) so that they can vary across people. A conceptual visual representation of the model with a maximum value is shown in Figure 1.

Figure 1.

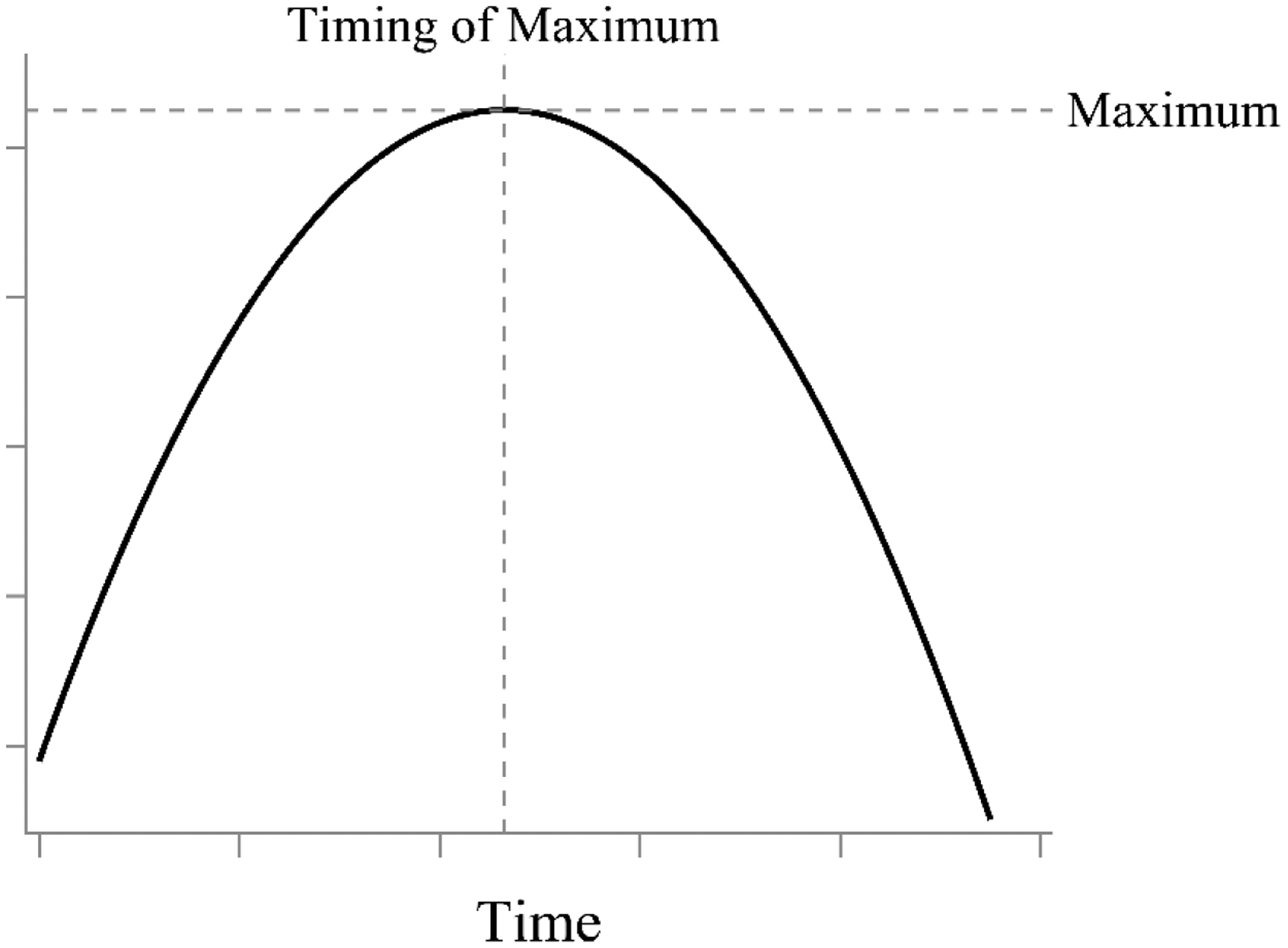
Visual representation of Cudeck and du Toit (2002) model. The model has three parameters to explicitly estimate the intercept (not labeled), the maximum value, and the timing of the maximum value.

Though the Cudeck and du Toit (2002) reparameterized model improves the interpretation of the quadratic growth model by defining the trajectory with more substantively meaningful parameters, a lingering problem of the model is that it remains a symmetric and unbounded parabola with a U or inverted U shape. For many processes, we expect that – once reached – the maximum or minimum will be maintained rather than growth reversing course immediately after. These shortcomings, however, can be addressed by combining the reparameterized quadratic model with multiphase growth models.

Multiphase Growth Models

As described by Cudeck and Klebe (2002), multiphase models allow for different forms of growth in different phases of the observation window. Such models provide flexibility for capturing complex patterns of change using relatively simple functions (Naumova et al., 2001). For instance, in one phase the function might consist solely of an intercept (polynomial of degree zero) whereas in the next phase there might be both an intercept and a slope (polynomial of degree one). Together, these functions would imply an individual trajectory that is initially flat but then – upon hitting the phase transition – shows a linear increase (or decrease). In the special case where growth is characterized by a straight line in each phase, such models are sometimes referred to as piecewise linear growth models. More broadly, they are spline models, where different functions govern growth for different phases of time and the functions are tied together at the phase transitions (typically called knot points) to form one continuous trajectory (Chou et al., 2004). Knot points can either be fixed to particular values corresponding to known transitions (e.g., the transition to high school) or empirically estimated from the data if a transition is expected but its exact timing is unknown (Hall et al., 2001). Knot points can also be modeled as random effects and differ in value from person to person (Harring et al., 2006).

Of particular interest for our purposes here is the quadratic-linear model described by Cudeck and Klebe (2002). In this two-phase model, growth is quadratic in the first phase up to the knot point and then growth proceeds linearly thereafter. Further, the model is specified in a way that ensures that the transition from the quadratic to the linear phases is smooth and that there is no singular point or “elbow” in the trajectory function and the overall trajectory is continuously differentiable. A smooth transition is ensured by parameterizing the model so that the first derivatives of the separate phases are the same at the knot point.

This two-phase quadratic-linear model with equality of first derivatives at the knot point can be written as

$$y_{ti}=\{\begin{array}{ll}{\beta }_{0i}+{\beta }_{1i}Tim{e}_{ti}+{\beta }_{2i}{\left(Tim{e}_{ti}-{\beta }_{3i}\right)}^2+e_{ti}\hfill & \text{if}Tim{e}_{ti}\le {\beta }_{3i}\hfill \\ {\beta }_{0i}+{\beta }_{1i}{\mathit{\text{Time}}}_{ti}+e_{ti}\hfill & \text{if}Tim{e}_{ti}>{\beta }_{3i}\hfill \end{array}$$ (3)

and

$$\begin{gathered} {\beta }_{0i}={\gamma }_{00}+u_{0i} \\ {\beta }_{1i}={\gamma }_{10}+u_{1i} \\ {\beta }_{2i}={\gamma }_{20}+u_{2i} \\ {\beta }_{3i}={\gamma }_{30}+u_{3i} \end{gathered}$$ (4)

Equation 3 shows the trajectory function of the outcome variable y for person i at time t consists of two parts, the first being quadratic (with the conventional polynomial parameterization that is linear in the parameters) and the second being linear. The first part governs the trajectory up to the knot point β_3i and the second part takes over thereafter. The β_0i and β_1i parameters are featured in both phases to ensure equality of the first derivatives. Equation 4 decomposes each growth parameter into its average value (the fixed effect γ) and person-specific deviations (the random effect, u). Figure 2 displays a hypothetical plot of this two-phase quadratic-linear model using β_1i =.05 and β_2i =−.15 as hypothetical values.

Figure 2.

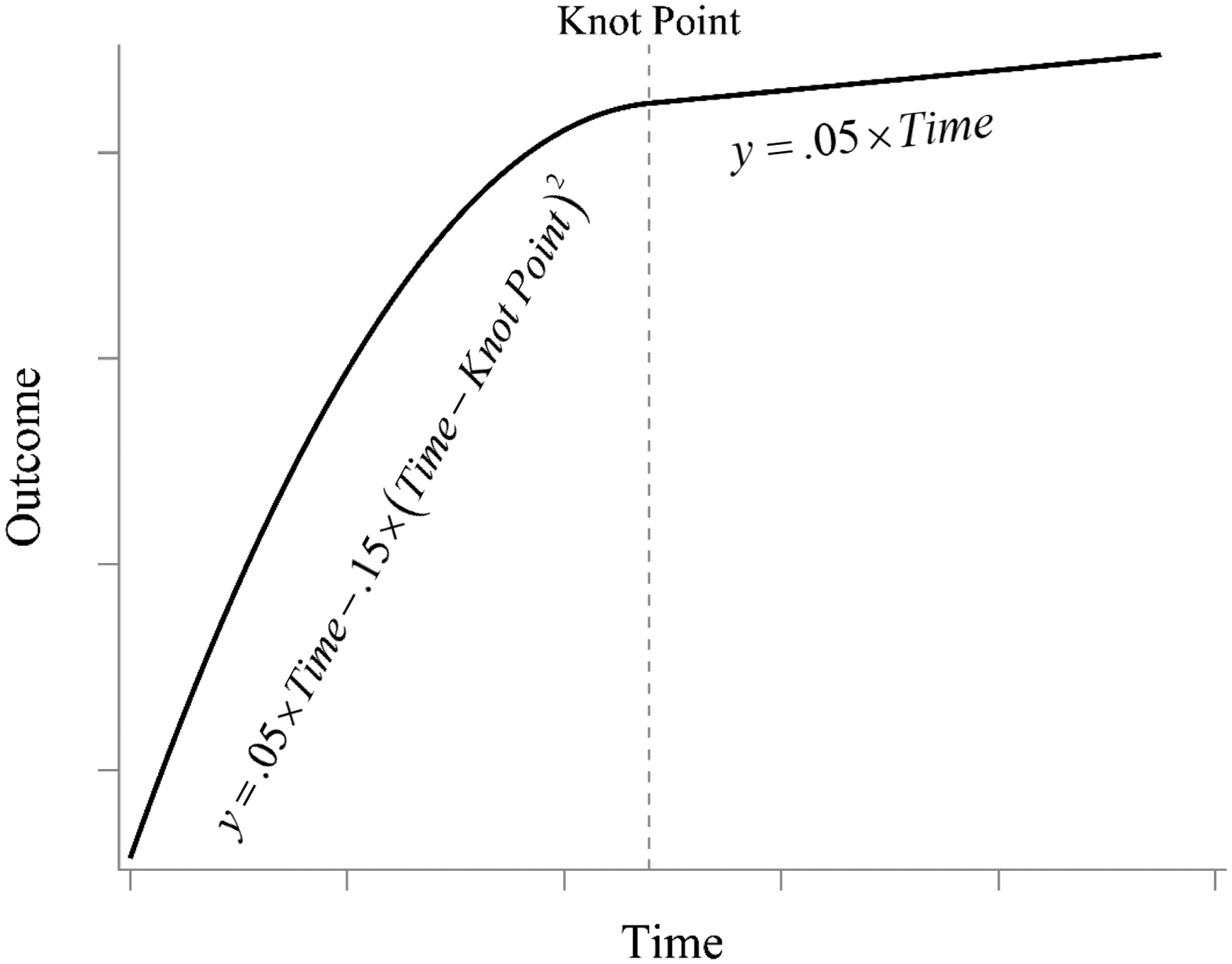
Visual representation of hypothetical two-phase quadratic-linear model from Cudeck and Klebe (2002) with equality of first derivatives across phases. The model changes function form at the knot point, but the equality of the first derivatives leads to a smooth transition between the phases.

Previous studies have considered the standard quadratic-linear multiphase model as a method to incorporate timing of developmental turning points into growth models (e.g., McArdle & Wang, 2008; Wang & McArdle, 2008); however, this idea does not necessarily capture the timing of when change starts or stops. For instance, the function displayed in Figure 2 increases indefinitely. The next section outlines how the multiphase quadratic-linear model can be combined with reparameterized quadratic models discussed in the previous section to capture change offsets such that the knot point directly corresponds with the maximum or minimum of the outcome variable. Subsequently, we extend to the approach to also capture variability in change onsets.

The Time-at-Offset Model

Our proposed time-at-offset model combines multiphase models of Cudeck and Klebe (2002) with the reparameterized quadratic model of Cudeck and du Toit (2002). The first phase is specified as quadratic and the second phase is specified as flat horizontal line (instead of linear growth). Rather than use the conventionally parameterized polynomial quadratic in the first phase, we substitute the Cudeck and du Toit (2002) reparameterization of the quadratic. After this substitution, we have a growth parameter that represents the time at which the maximum or minimum value of y occurs within the first phase. This same parameter serves as an estimate of the knot point. Therefore, the phase transition occurs precisely when individuals reach their maximum value such that the change offset is an explicitly estimated parameter in the model. Following the change offset, the second phase is a horizontal line equal to the maximum or minimum, implying that this value is maintained. The overall trajectory is smooth and continuously differentiable because the first derivative of the quadratic continuously moves to zero at the maximum and then remains at zero from that point forward. Figure 3 provides hypothetical plots of trajectories that would follow the time-at-offset model with the left panel showing growth towards a maximum (e.g., arithmetic skills in primary school children, brain development) and the right panel showing decay towards a minimum (e.g., reaction time over repeated trials, speech errors in young children).

Figure 3.

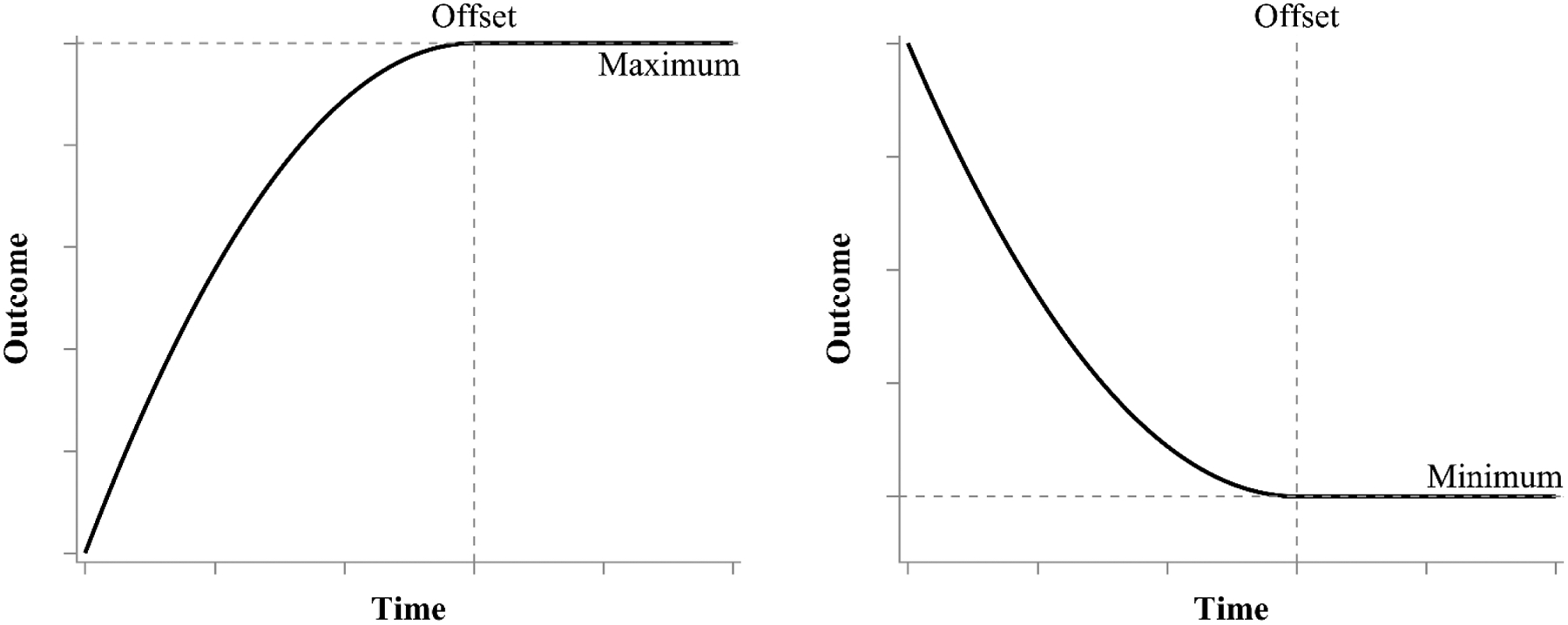
Hypothetical plot of a time-at-offset process growing towards a maximum value (left) and a time-at-offset process decaying towards a minimum value (right). Prior to the change offset, the growth trajectory follows a quadratic function. Once reaching the change offset, which is defined as the extremum of the quadratic function, the growth trajectory becomes a horizontal line at the maximum or minimum value of the quadratic function.

Mathematically, the time-at-offset model can be written as

$$\begin{gathered} y_{ti}=\{\begin{array}{ll}{\beta }_{1i}-\left({\beta }_{1i}-{\beta }_{0i}\right){\left(\frac{Tim{e}_{ti}}{{\beta }_{2i}}-1\right)}^2+e_{ti}\hfill & \text{if}Tim{e}_{ti}\le {\beta }_{2i}\hfill \\ {\beta }_{1i}+e_{ti}\hfill & \text{if}Tim{e}_{ti}>{\beta }_{2i}\hfill \end{array} \\ {\beta }_{0i}={\gamma }_{00}+u_{0i} \\ {\beta }_{1i}={\gamma }_{10}+u_{1i} \\ {\beta }_{2i}={\gamma }_{20}+u_{2i} \end{gathered}$$ (5)

Here the intercept (β_0i) is the expected value of y for person i at Time = 0, β_1i is the maximum or minimum value of y for person i, and β_2i is the time at which the maximum or minimum occurs and serves as transition point between phases (i.e., the change offset).

The first benefit of this parameterization is that the resulting trajectory closely follows decelerating monotonic trajectories like the negative exponential or Michaelis-Menten. The flat second phase resembles an asymptote but has the added advantage in that the maximum is a point that people actually reach rather being an unattainable theoretical upper limit. This removes ambiguity about how close to the asymptote is considered close enough for the growth to be considered to have ceased. It also allows questions about timing of end-point behavior to be addressed rather than relegating timing to the halfway point as in Michaelis-Menten. The second benefit is that the model retains the useful interpretations of the Cudeck and du Toit (2002) reparameterization without requiring a symmetric, U-shaped trajectory. In this way, the model more closely maps onto developmental phenomena where maximal or minimal values are maintained rather than rapidly changing directions after having been achieved. Third, the dual role of β_2i as both a focal parameter and the knot point reduces the number of random effects in the model, which reduces the complexity of the estimation. Because β_2i serves “double-duty”, researchers also do not need to sacrifice any other parameters to enable direct estimation of parameters related to timing as is required in time-to-criterion models.

To demonstrate the generality and usefulness of this modeling approach, we provide two empirical illustrations below where time-at-offset is of primary research interest, something that existing models struggle to address. The first example features two-level data (repeated measures nested in people) and the second example features three-level data (repeated measures nested in people who are nested in schools). Afterwards, we show how we can use the same approach to model individual differences in change onset points and switching the focus to individual differences in where change processes begin rather than end. Then we extend the model to simultaneously include individual differences in both change onset and change offset points for S-shaped, sigmoidal growth processes.¹

Example 1: Prefrontal Cortex Thickening

Background

Decades of work on plasticity in development indicates that the brain is particularly sensitive to environmental inputs during early development. Human and animal models have extensively documented that sensory input received during early sensitive periods (i.e., between 0 and 4 years) fundamentally changes children’s ability to perceive and respond to their environment for the rest of their lives (Goldman-Rakic, 1987; Rakic et al., 1986, Wiesel & Hubel, 1965). Notably, in vivo animal and post-mortem human studies indicate that the timing of sensitive periods differs for neural regions involved in primary sensory versus higher order cognitive function, primarily due to the differences in timing of peak synaptic density across cortex (Bourgeois et al., 1994; Huttenlocher, 1990; Petanjek et al., 2011). Until recently, dense sampling of neural structure in humans in vivo during infancy using neuroimaging was impossible.

Recent technological advances have made it possible to measure cortical thickness in vivo in humans multiple times over the first year of life (Li et al., 2019). Critically, extant literature has not explicitly linked early brain development – especially in regions such as the prefrontal cortex, which are larger and more complex in humans compared to animals – with later cognitive ability. Thus, such formative work is essential in order to advance the promise of neuroimaging as a meaningful tool in the study of developmental plasticity in humans. Using cortical thickness data measured from in vivo neuroimaging during early development, the proposed model captures timing of offset in growth (cortical thickness maturation) as an explicit parameter. The model is thus ideally suited for evaluating how the timing at which areas of the cortex reach maximum thickness in early development may be related to later cognitive abilities. Specifically, we hypothesized that more protracted frontal lobe growth during early development would be related to higher cognitive ability in childhood.

Data

The data come from a longitudinal study of brain development including 51 children who were assessed first at 2 weeks of age, then at 3, 6, 9, 12, 18, and 24 months, and then at 3, 4, 5, and 6 years. The methods for acquisition and analysis of this data were developed by Lin and colleagues, and have been published extensively (Li et al., 2014; Shi et al., 2010, 2011). Given variation in assessment times, for analysis purposes age is computed based on the actual number of days elapsed from birth to when the assessment was made, divided by 365 to make the units years of age. At each time point, T1-weighted and T2-weighted sMRI scans were acquired. Sequences were optimized for imaging neural structure in infants and young children (see Li et al., 2014). Each structural scan was preprocessed and analyzed to quantify gray matter cortical thickness and surface area (Shi et al., 2010, 2011). Thickness was measured in 68 cortical regions of interest defined using a standard atlas (Desikan et al., 2006). The current analysis focused specifically on the thickness of the frontal lobe, defined as the average of thickness within 24 regions of interest located within the right and left frontal lobe. Measures of frontal lobe thickness were available for 50 of 51 children, ranging from 3 to 11 observations with a median of 7 observations per child. Between 5 and 6 years of age (mean = 5.35), a subset of the sample (N=33) also completed the Differential Ability Scales-II (DAS; Elliott, 2007), a standardized assessment similar to an IQ test designed to measure ability in verbal and non-verbal domains. The current analyses focus on the verbal scale, or DAS-II-V.

Model and Results

A spaghetti plot of the data, shown in Figure 4, suggests that the proposed model would be appropriate for capturing changes in frontal lobe thickness. As can be seen in the top panel, gains in thickness are very rapid early in infancy, with decelerating growth observed until approximately year one, after which levels appear steady. To see this pattern more clearly, the bottom panel zooms in on just the first two years, showing that there appears to be a smooth deceleration in growth through the first year. The model proposed in Equation 5 captures precisely this type of trajectory, with the initial quadratic piece capturing smooth deceleration in change and the second flat piece capturing level at the termination of growth. Further, it permits an evaluation of individual differences in starting level, final level, and change offset for frontal lobe thickness.

Figure 4.

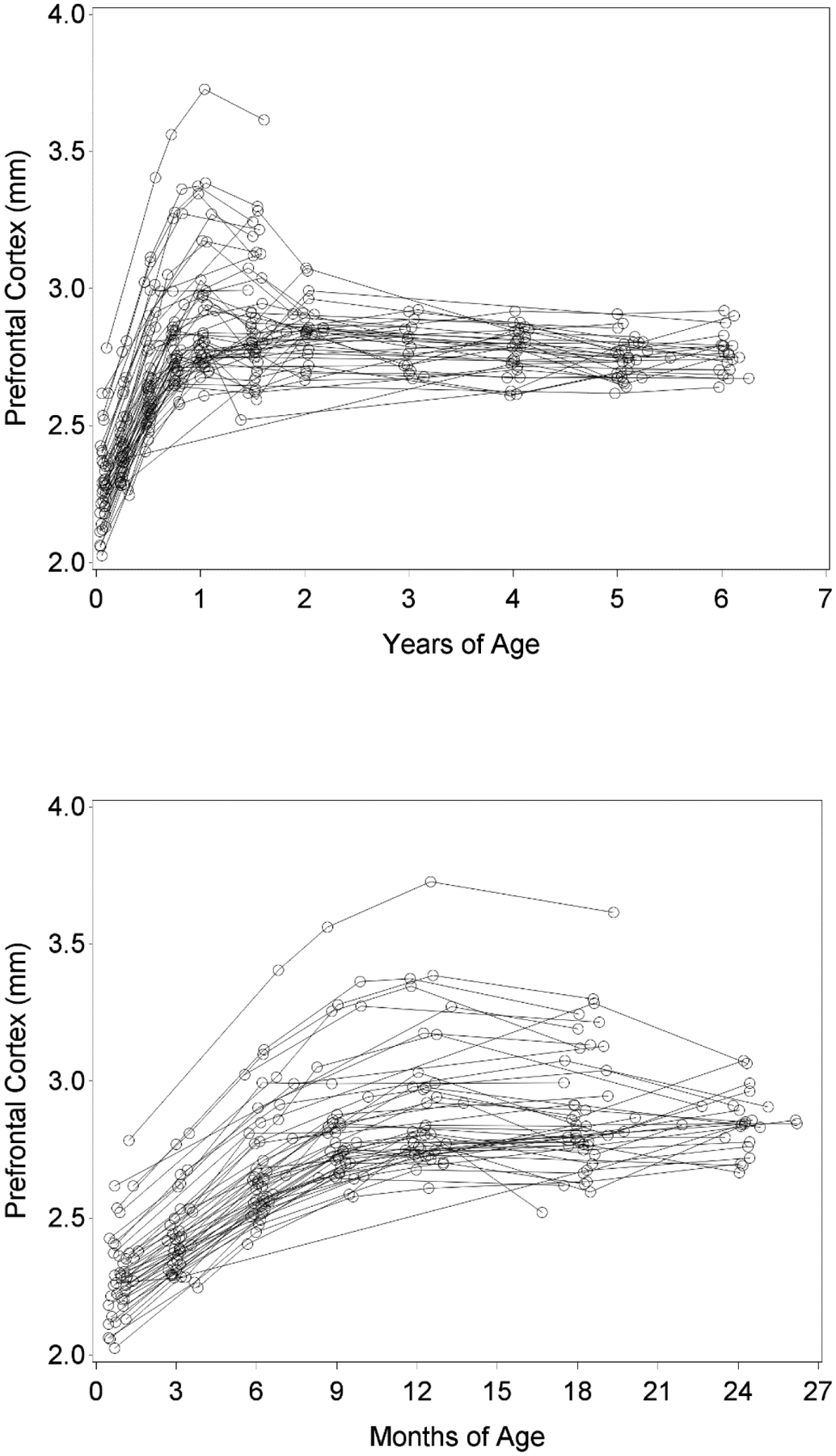
Top panel displays observed values for repeated measures of thickness of the prefrontal cortex over the entire span of the study (age scaled in years). The bottom panel considers only observations within approximately the first two years (age scaled in months) to magnify the rapidly decelerating changes occurring within this period.

We fit two models to the data. The first model included only the repeated measures on frontal lobe thickness, whereas the second model extended this to a multivariate specification to include DAS-II-V. Both models were fit in SAS 9.4 with the NLMIXED procedure, using maximum likelihood estimation via non-adaptive Gaussian quadrature with 7 quadrature points. In each case, the random effects covariance matrix was modeled by estimating the standard deviations and correlations of the random effects to reduce estimation challenges associated with numerically small variances of different magnitudes. Estimation on a standard desktop computer took approximately 9 seconds for Model 1 and 25 seconds for Model 2.

Results from Model 1 (of the form given in Equation 5) are presented in Table 1. The average trajectory was characterized by a predicted frontal lobe thickness at birth of 2.15 mm (SD =.12 mm), a maximum attained thickness level of 2.78 mm (SD =.19 mm), and change offset at 1.12 years of age (SD =.08 years, or approximately 1 month of age). Timing of offset was negatively correlated with both thickness at birth (r = −.41, p =.34) and thickness at maturation (r = −0.68, p <.05), though only the latter correlation was statistically significant. Thickness at birth was positively correlated with ultimate levels at maturation (r = .47, p <.01), but this may simply reflect the common association of these two trajectory features with timing of offset. Indeed, the partial correlation between thickness at birth and thickness at maturation, controlling for timing of offset, was only.28 and not statistically significant (p = .51). The predicted individual trajectories, displayed in Figure 5 for a representative subset of individuals, showed close fit to the observed repeated measures.

Table 1.

Estimates from model for prefrontal cortex thickness, excluding verbal ability criterion

Parameter	Notation	Est.	SE	p
	Growth Trajectory Fixed Effects
Intercept	γ 00	2.15	0.01	<.01
Maximum	γ 10	2.78	0.01	<.01
Change Offset	γ 20	1.12	0.04	<.01
	Random Effects
Intercept Variance	τ 00	0.015	<0.01	<.01
Maximum Variance	τ 11	0.038	<0.01	.01
Change Offset Variance	τ 22	0.007	<0.01	<.01
Int., Max. Correlation	Corr(u0i, u1i)	0.47	0.03	<.01
Int., Offset Correlation	Corr(u0i, u2i)	−0.41	0.42	.34
Max, Offset Correlation	Corr(u1i, u2i)	−0.68	0.32	.04
	Within-Person Residual Variance
Residual Variance	σ 2	0.004	<0.01	<.01

Note: p-values are obtained from a t-distribution with the default degrees of freedom computed as number of upper-level units (50 children) minus the number of estimated random effects (3), which is 47.

Figure 5.

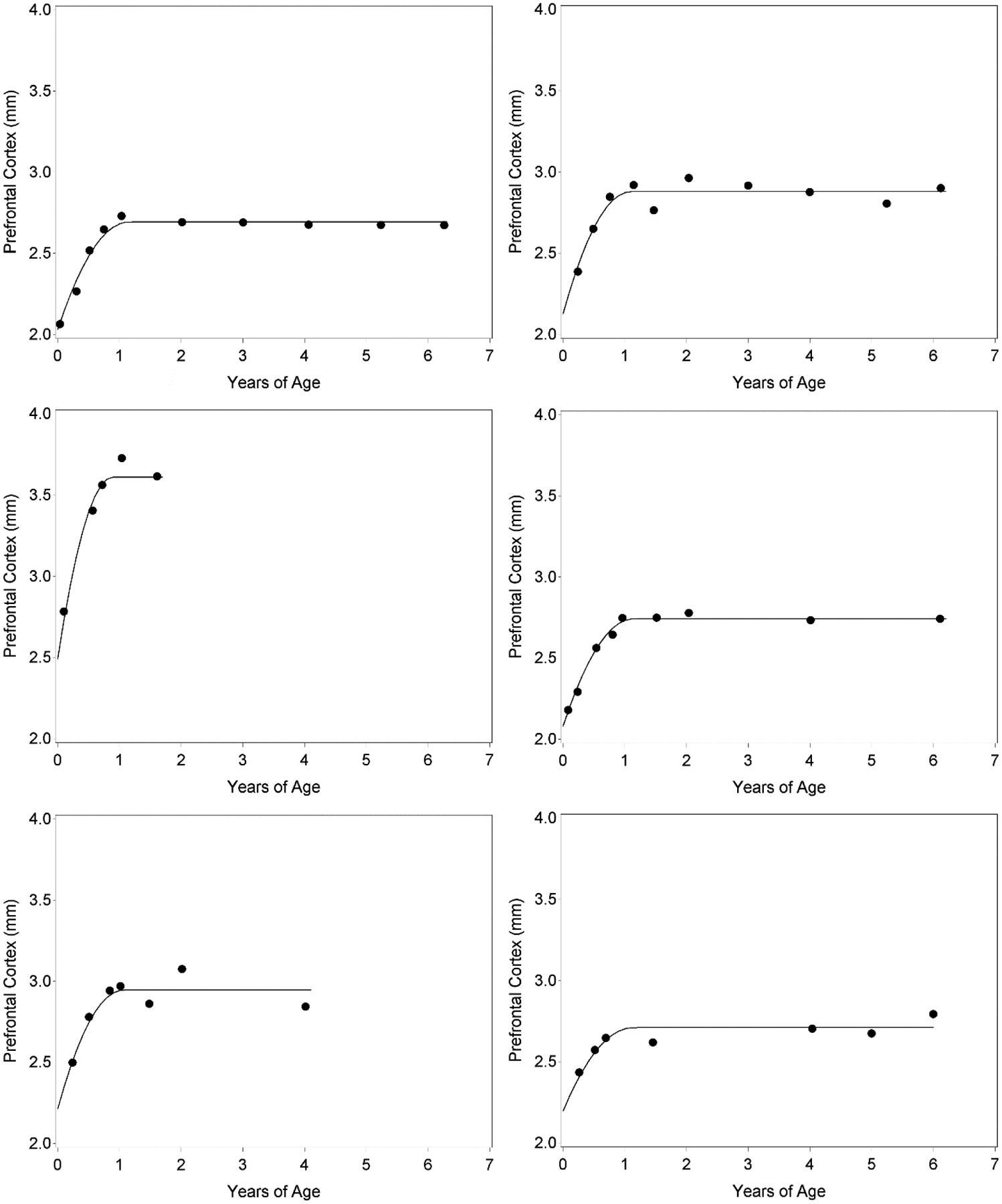
Observed repeated measures (circles) and implied trajectories for six representative children.

In Model 2, we included DAS-II-V as an additional outcome, using the approach described by MacCallum et al (1997) to fit a multivariate multilevel model. For estimation purposes, the model was parameterized with DAS-II-V regressed on the random effects characterizing frontal lobe growth. For interpretation, however, the slopes from this regression were transformed into the implied bivariate correlations between the frontal lobe growth coefficients and DAS-II-V scores. Parameter estimates for the frontal lobe growth process changed little from Model 1 and are thus not reported. DAS-II-V was negatively correlated with frontal lobe thickness at birth (r = −.34, p =.24), virtually uncorrelated with frontal lobe thickness at maturation (r = −.06, p =.88), and positively correlated with age of offset in frontal lobe growth (r =.49, p =.35). Although none of these correlations was statically significant, the tendency for later change offsets to be correlated with higher DAS-II-V scores was consistent with the hypothesis that more protracted growth would be related to higher cognitive ability. This result is intriguing but further research is clearly needed to make more definitive conclusions.

In sum, this example demonstrated that the model fit well to individual trajectories of structural brain development in frontal lobe thickness and provided parameters with appealing interpretations that could be used to obtain direct tests of the hypotheses of interest.

Example 2: Early Childhood Mathematics

Background

Findings on the longitudinal effects of preschool mathematics interventions have been mixed in that effects are typically found immediately following the intervention but fade over the course of elementary school (Natriello et al., 1990). In the absence of intervention effects that persist throughout elementary school, there is debate about the policy ramifications of implementing interventions on a large scale (Bailey et al., 2018). Dumas et al. (2019) applied nonlinear dynamic measurement growth models to data from a clustered randomized trial in children followed from preschool to Grade 5 and similarly found that the difference between the intervention and control groups diminishes over time. To probe aspects of timing, they applied a Michaelis-Menten model which estimated the time at which the outcome had developed to the midpoint between the intercept and asymptote. The intervention group was found to reach the midpoint of their growth trajectory faster than the control group, and the effect was particularly pronounced for black and Latinx students, groups that have been historically under-resourced in mathematics education.

The more interesting question, however, is whether early intervention can help students reach their ultimate level of mastery faster because reaching the midpoint more quickly does not guarantee that mastery will also be achieved more quickly. The Michaelis-Menten model applied by Dumas et al. (2019) is derived from pharmacokinetics where the midpoint of a curve has ramifications for the optimization of chemical reactions, but in education research, the change offset is far more interesting. Because there is between-student variability in ultimate mastery, this situation is not amenable to a single fixed criterion across all students as in the time-to-criterion framework. Consequently, we will fit our proposed time-at-offset model to investigate differences in change offsets between intervention and control groups.

Data

Data for this example come from the TRIAD project (Clements et al., 2013; Clements & Sarama, 2007), the intent of which was to improve mathematics knowledge of students in preschool and early primary school using the Building Blocks curriculum and teacher professional development. The study was a clustered randomized trial where the intervention was applied in preschool and then students were followed through Grade 5, being longitudinally assessed by the vertically scaled Research-based Early Math Assessment (Clements et al., 2008). Measurements occurred twice in preschool (pre- and post-intervention) then once each in kindergarten, Grade 1, Grade 2, Grade 4, and Grade 5. The data contain 1,305 students clustered within 42 schools. Overall attrition was 36% and was about equal for the intervention group (40%) and the control group (33%). At all grade levels, none of the baseline demographic differences between the intervention and control group (i.e., free/reduced price lunch, gender, disability status) were greater than 0.25 standard deviations (in absolute value), which aligns with the reasonable threshold employed by US Institute for Educational Science’s What Works Clearinghouse (Clements et al., 2019).

Model and Results

The model is more complex than previously shown because these data have a three-level structure: repeated measures are nested within people who are nested within schools. The three-level time-at-offset model interested in a Level-3 intervention effect can be written as,

$$\begin{gathered} {\mathit{\text{Math}}}_{tij}=\{\begin{array}{ll}{\beta }_{1ij}-\left({\beta }_{1ij}-{\beta }_{0ij}\right){\left(\frac{{\mathit{\text{Time}}}_{tij}}{{\beta }_{2ij}}-1\right)}^2+e_{tij}\hfill & \text{if}{\mathit{\text{Time}}}_{tij}\le {\beta }_{2ij}\hfill \\ {\beta }_{1ij}+e_{tij}\hfill & \text{if}{\mathit{\text{Time}}}_{tij}>{\beta }_{2ij}\hfill \end{array} \\ {\beta }_{0ij}={\pi }_{00j}+u_{0ij} \\ {\beta }_{1ij}={\pi }_{10j}+u_{1ij} \\ {\beta }_{2ij}={\pi }_{20j}+u_{2ij} \\ {\pi }_{00j}={\gamma }_{000}+{\gamma }_{001}{\mathit{\text{Intervention}}}_j+r_{00j} \\ {\pi }_{10j}={\gamma }_{100}+{\gamma }_{101}{\mathit{\text{Intervention}}}_j+r_{10j} \\ {\pi }_{20j}={\gamma }_{200}+{\gamma }_{201}{\mathit{\text{Intervention}}}_j+r_{20j} \\ {\mathbf{\text{r}}}_j\sim MVN\left(\left[\begin{array}{l}0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right],\left[\begin{array}{lll}{v}_{00}\hfill & \hfill & \hfill \\ v_{10}\hfill & v_{11}\hfill & \hfill \\ v_{20}\hfill & v_{21}\hfill & v_{22}\hfill \end{array}\right]\right) \\ {\mathbf{\text{u}}}_{ij}\sim MVN\left(\left[\begin{array}{l}0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right],\left[\begin{array}{lll}{\tau }_{00}\hfill & \hfill & \hfill \\ {\tau }_{10}\hfill & {\tau }_{11}\hfill & \hfill \\ {\tau }_{20}\hfill & {\tau }_{21}\hfill & {\tau }_{22}\hfill \end{array}\right]\right) \\ {\mathbf{\text{e}}}_{ij}\sim MVN\left(0,{\sigma }^{2}I\right) \end{gathered}$$ (6)

Equation 6 shows that Math scores follow a multiphase model. The first phase is a reparameterized quadratic that has an intercept (β_0ij), maximum value (β_1ij), and change offset (β_2ij) capturing the point in time at which the maximum value occurs. The change offset also functions as the knot point, after which the growth trajectory is characterized by a horizontal line at the maximum value. Each of the three growth parameters are allowed to vary across people via the u random effects and across schools via the r random effects. Each growth parameter is then predicted by the intervention group status of the jth school. Both the person-level and school-level random effects are specified to have an unstructured covariance matrix, meaning that all random effects freely covary with all other random effects at the same level. Consistent with identifiability in multilevel models, random effects across levels are assumed to be independent. The within-person residual variance is modeled to be constant across time.

The model in Equation 6 was fit in SAS 9.4 using the NLMIXED procedure. Maximum likelihood estimation via Gaussian quadrature with 5 quadrature points and double dogleg optimization was used. To improve numerical stability, we used a Cholesky decomposition for the random effect covariance matrix at each level (Kohli et al., 2019). The estimation of the model was rather intensive, requiring about 15 hours of CPU time; however, we were able to greatly reduce real-time computation time by hyperthreading the estimation across 8 cores so that estimation took only about 2 hours.

Results from the model are shown in Table 2 and the growth trajectories of the control group and intervention group are compared in Figure 6. In this context, the change offset is a substantively interesting parameter because it represents the time at which ultimate mastery of basic mathematics occurs (Time = 0 represents the start of pre-school). The intervention effect on the intercept was negligible (γ₀₀₁ = 0.01, t(23) = 0.17, p =.87), as expected because the study was a cluster randomized trial and the first wave of data collection occurred prior to the intervention. As noted in the early childhood mathematics literature, the intervention effect on the maximum value is also negligible and non-significant (γ₁₀₁ =−0.19, t(23) =−1.56, p =.13), indicating that groups are essentially equal at the conclusion of the observation window in Grade 5. Some have considered this equality across groups at the conclusion of the study as evidence that the intervention is not worthwhile. However, the timing at which growth trajectories level off may be more relevant, especially in the elementary school context. That is, if groups have the same maximum values but the intervention group arrives there quicker, that can have a host of psychosocial and educational benefits (e.g., Ahmed et al., 2013; Becker & Neumann, 2018). Indeed, the intervention effect on the change offset parameter is quite large (γ₂₀₁ =−0.74, t(23) =−5.51, p <.01) showing that the practical importance of the intervention is to accelerate mastery. The offset parameter is on the scale of Time, so this effect indicates that the intervention group reaches their maximum 9 months – a full school year – before the control group.

Table 2.

Parameter estimates for modeling intervention effects in the Building Blocks data

Parameter	Notation	Est.	SE	p
	Growth Trajectory Fixed Effects
Intercept	γ 000	−2.99	0.07	<.01
Maximum	γ 100	1.41	0.12	<.01
Change Offset	γ 200	4.78	0.13	<.01
	Intervention Fixed Effects
Intercept on Intervention	γ 001	0.01	0.07	.86
Maximum on Intervention	γ 101	−0.19	0.12	.13
Change Offset on Intervention	γ 201	−0.74	0.13	<.01
	School-Level Random Effects
Intercept Variance	v 00	0.06	0.01	<.01
Maximum Variance	v 11	0.11	0.05	.01
Change Offset Variance	v 22	0.16	0.06	<.01
Int., Max. Correlation	Corr(r00 j, r10 j)	0.89	0.13	<.01
Int., Offset Correlation	Corr(r00 j, r20 j)	0.62	0.19	<.01
Max, Offset Correlation	Corr(r10 j, r20 j)	0.41	0.27	.15
	Person-Level Random Effects
Intercept Variance	τ 00	0.41	0.02	<.01
Maximum Variance	τ 11	0.81	0.04	<.01
Offset Variance	τ 22	0.92	0.09	<.01
Int., Max. Correlation	Corr(u0ij, u1ij)	0.75	0.02	<.01
Int., Offset Correlation	Corr(u0ij, u2ij)	0.67	0.04	<.01
Max, Offset Correlation	Corr(u1ij, u2ij)	0.78	0.03	<.01
	Within-Person Residual Variance
Residual Variance	σ 2	0.22	0.01	<.01

Note: p-values are obtained from a t-distribution with Donald and Lang (2007) degrees of freedom, which is equal to the number of units at the highest level of the hierarchy (42 schools) minus the number of estimated parameters (19), which is 23.

Figure 6.

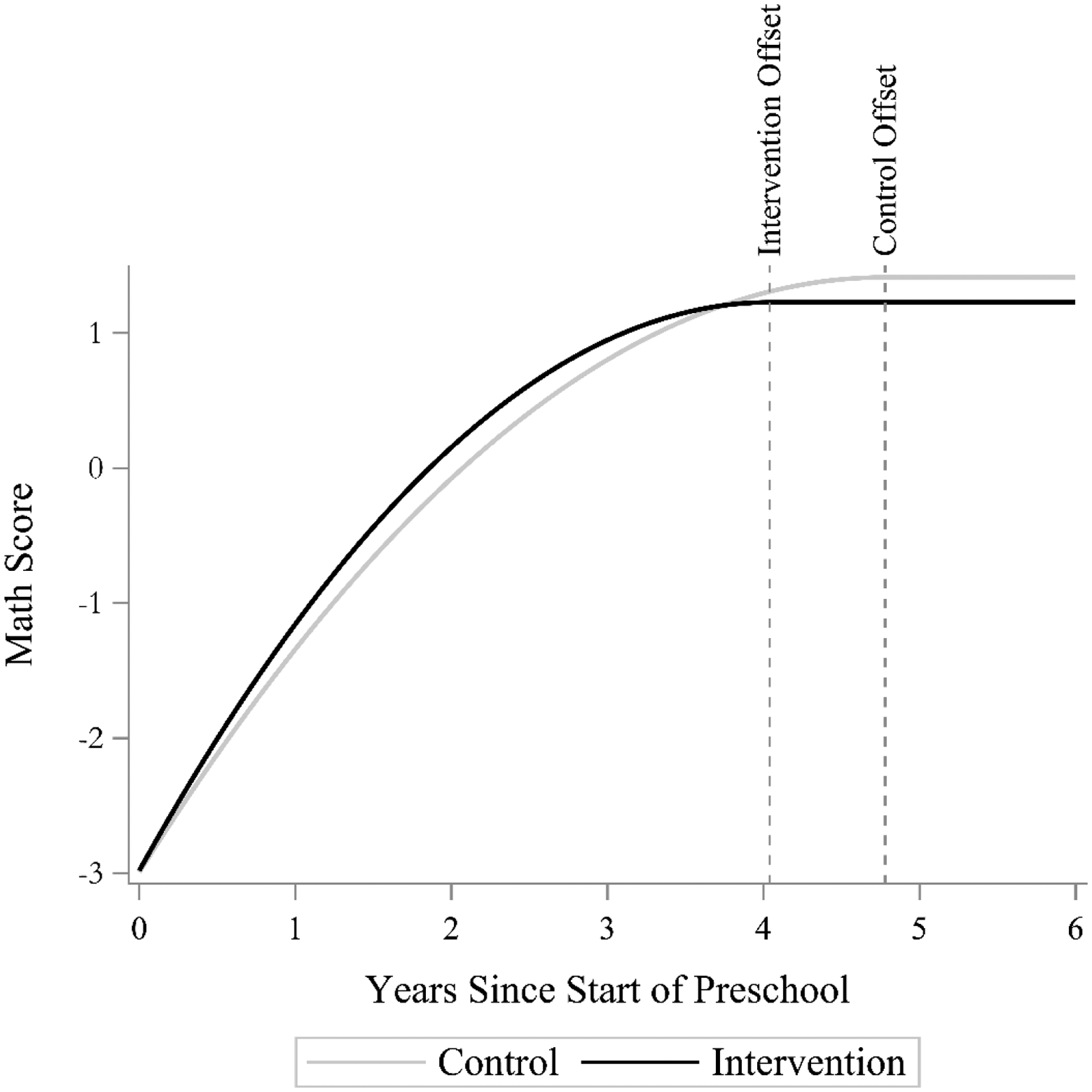
Comparison of the Intervention and Control group for the Building Blocks data. The intercepts and maximum values are not different across groups, but the offset of the intervention occurs 9 months before the offset of the control group.

This example shows the benefit of our proposed time-at-offset model when the timing of maximal development is equally or more important than the level of maximal development itself. Previous analyses of these data have questioned the effectiveness of the intervention based on the equivalence of the groups’ developmental endpoints (Kang et al., 2018), but such a perspective overlooks the importance of timing in learning processes.

Time-at-Onset Model

Examples 1 and 2 demonstrated time-at-offset models where the growth trajectory decelerates towards a maximum value and the change offset represents the point where growth ceases and becomes flat thereafter. In other contexts, one might be concerned with the timing at which a change process begins. A similar model can be applied to address this concern, but the order of the phases is reversed such that growth is initially flat until some change onset point, after which growth accelerates. This type of development occurs, for example, in early childhood studies when the interest is related to timing of development milestones like learning to talk or walk. In such contexts, the number of words known or the number steps per day would be maintained at or near zero for each child until the milestone is reached (i.e., the change onset), after which point rapidly accelerating growth begins. Alternatively, one might be interested in the timing of a process of decline. For example, the interest could be timing of cognitive decline in patients eventually diagnosed with dementia (e.g., Rusmaully et al., 2017). In this case, the first phase would be a relatively stable maximum value while people function typically and the change onset would represent the timing at which cognitive decline begins. Figure 7 provides hypothetical plots of trajectories that would follow the time-at-onset model with the left panel showing an increasing trajectory (e.g., learning to walk or talk) and the right panel showing a decreasing trajectory (e.g., cognitive decline or attention during a task).

Figure 7.

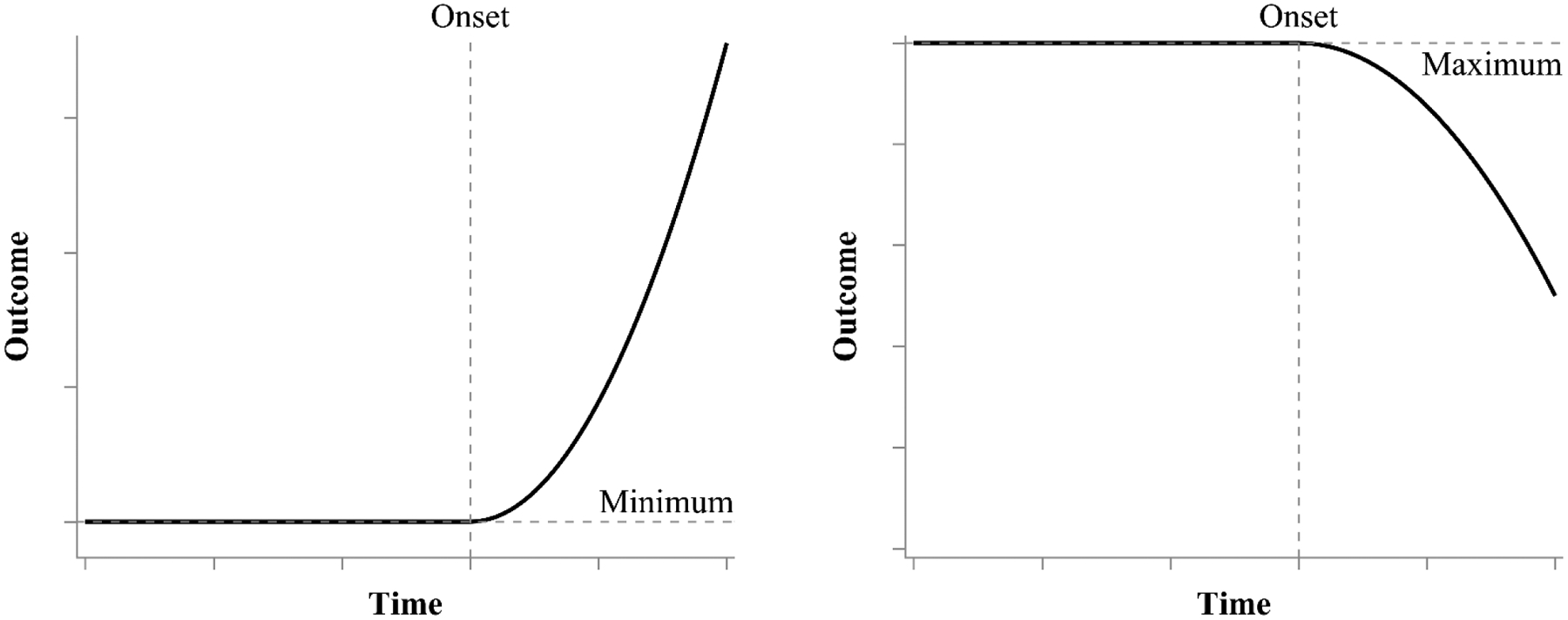
Hypothetical plot of a time-at-onset process that maintains a minimum value until the change onset and grows quadratically thereafter (left) and a time-at-onset process that maintains a maximum until the change onset and decays thereafter (right). Prior to the change onset, the growth trajectory follows a horizontal line at the maximum or minimum value. Once reaching the change onset, the growth trajectory follows a quadratic function.

Mathematically, the time-at-onset model is similar to the time-at-offset model discussed earlier but with the phases reversed such that

$$\begin{gathered} y_{ti}=\{\begin{array}{ll}{\beta }_{1i}+e_{ti}\hfill & \text{if}Tim{e}_{ti}\le {\beta }_{2i}\hfill \\ {\beta }_{1i}-\left({\beta }_{1i}-{\beta }_{0i}\right){\left(\frac{Tim{e}_{ti}}{{\beta }_{2i}}-1\right)}^2+e_{ti}\hfill & \text{if}Tim{e}_{ti}>{\beta }_{2i}\hfill \end{array} \\ {\beta }_{0i}={\gamma }_{00}+u_{0i} \\ {\beta }_{1i}={\gamma }_{10}+u_{1i} \\ {\beta }_{2i}={\gamma }_{20}+u_{2i} \end{gathered}$$ (7)

whereβ_1i is the value of the flat minimum or maximum line prior to the change onset and β_2i is the onset. To be maximally interpretable, Time should be coded such that zero corresponds to an endpoint of interest such as the last measurement occasion. Doing so will make the intercept term β_0i an estimate of the level of the individual’s trajectory at that end point (e.g., expected level of y achieved at the last observation point). The next section provides an example of a time-at-onset model using data on vocabulary development in toddlers.

Example 3: Vocabulary Development

Background & Data

A time-at-onset model will be applied to data originally from Huttenlocher, Haight, Bryk, Seltzer, and Lyons (1991), which can also be found in Chapter 6 of Raudenbush and Bryk (2002). In this data, the vocabulary size is measured repeatedly for 22 children between the ages of 14 months and 26 months. Because the data were originally used for a study with a different purpose, the data consist of 2 groups of 11 children, each with 6 boys and 5 girls. The children in Group 1 were observed every 2 months for 5 hours while the children in Group 2 were observed every 4 months for 3 hours. As a result, children in Group 1 are observed more frequently and were 26 months old at their last measurement occasion whereas children in Group 2 were observed less often and were 24 months old at their last measurement occasion. Given these differences, the children in Group 1 tended to have a higher level of vocabulary as well as greater variability than those in Group 2, particularly at later ages on the raw outcome.

Toddlers begin to produce their first words around 12 months of age and vocabulary grows at an increasing rate thereafter. However, there are individual differences in the timing of this milestone and research questions can revolve around variables that affect the timing of the vocabulary change onset (Bauer, Reznick & Goldfield, 2002; Rescorla et al., 2000). The original analysis in Huttenlocher et al. (1991) fit a quadratic polynomial growth model that did not include fixed or random effects for the intercept or linear slope but did include fixed and random effects for the quadratic slope with Time centered at 12 months. This functional form creates a growth trajectory that is equal to zero at Time = 0 but then increases quickly thereafter. It is indeed effective for rendering a curve that fits through the data points; however, the only coefficient in the model captures growth acceleration. The model coveys no information about individual differences in the timing at which growth begins. The time-at-onset model we fit in the next subsection will explicitly estimate the timing of the onset and its variability across children in addition to testing if exposure more speech by the mother influences this timing.

Model & Results

We fit the time-at-onset model to the Huttenlocher et al. (1991) vocabulary data with the number of words the child knew as the outcome variable and Age (in months) as the time variable. To address differences across groups, we rescaled the outcome by dividing the raw outcome (Vocabulary Size) by the observation hours in each group (5 in Group 1; 3 in Group 2) so that the new outcome is the number of new words produced per hour of observation. We then divided Words per Study Hour by 10 for so that parameters in the model would have similar scaling. Age was centered around the last observed age in Group 2 (24 months), so that zero would correspond to the last measurement occasion common to both groups. The intercept then corresponds to an estimate of expected words per study hour at 24 months of age. The flat minimum line in the first phase was fixed to 0 with no random effect because the change onset represents when vocabulary development begins. The amount of speech (number of words) produced by the mother at 16-months was included as a predictor of the change onset and the endpoint and was divided by 100 and grand-mean centered.² Sex was also included as a predictor. We initially fit a model that included Group as a predictor of the change onset and endpoint as well as of the random effect variances and residual variances. However, after rescaling the outcome, all but one of the effects of Group was non-significant and thus these were dropped from the model. The final fitted model for this example is,

$$\begin{gathered} \mathit{\text{Voca}}{b}_{ti}=\{\begin{array}{ll}0\hfill & \text{if}Tim{e}_{ti}\le {\beta }_{2i}\hfill \\ {\beta }_{0i}{\left(\frac{\left(Ag{e}_{ti}-24\right)}{{\beta }_{2i}}-1\right)}^2\hfill & \text{if}Tim{e}_{ti}>{\beta }_{2i}\hfill \end{array} \\ {\beta }_{0i}={\gamma }_{00}+{\gamma }_{01}{\mathit{\text{Female}}}_i+{\gamma }_{02}\left({\mathit{\text{MomSpeech}}}_i-\overline{\mathit{\text{MomSpeech}}}\right)+u_{0i} \\ {\beta }_{2i}={\gamma }_{20}+{\gamma }_{21}{\mathit{\text{Female}}}_i+{\gamma }_{22}\left({\mathit{\text{MomSpeech}}}_i-\overline{\mathit{\text{MomSpeech}}}\right)+u_{2i} \\ {u}_i~MVN\left(\left[\begin{array}{l}0\hfill \\ 0\hfill \end{array}\right],\left[\begin{array}{ll}{\tau }_{00i}\hfill & \hfill \\ {\tau }_{20i}\hfill & {\tau }_{22}\hfill \end{array}\right]\right) \\ {e}_i~MVN\left(0,{\sigma }_{ti}^{2}I\right) \\ {\sigma }_{ti}^2=\text{exp}\left({\omega }_0+{\omega }_1\times \left(Ag{e}_{ti}-24\right)\right) \\ {\tau }_{00i}=\text{exp}\left({\omega }_2+{\omega }_3\times \mathit{\text{Grou}}{p}_i\right) \\ {\tau }_{20i}=\rho \times {\left({\tau }_{00i}{\tau }_{22}\right)}^{1/2} \end{gathered}$$ (8)

Both the endpoint (β_0i) and change onset (β_2i) have random effects, which are correlated. A variation on the location-scale model proposed by Hedeker et al. (2008) was used to model heteroscedasticity in both the residual variance and endpoint random effect variance. The residual variance is modeled with a log-linear model to preclude negative values with centered Age as the predictor to more parsimoniously allow the residual variance to change as a function Age rather than individually estimating the residual variance of each measurement occasion. The random effect variance of the endpoint was also modeled with a log-linear model with Group as the predictor to account for between-group heteroskedasticity as this was the only parameter that continued to exhibit Group differences after the outcome was rescaled. The random effect correlation was an explicit parameter, meaning that the random effect correlation was constant across Groups but the random effect covariance could differ. The model was fit in SAS 9.4 with the NLMIXED procedure with maximum likelihood via adaptive Gaussian quadrature with 30 quadrature points and double dogleg optimization, which converged in 43 seconds.

Parameter estimates are provided in Table 3. The average onset of vocabulary growth was estimated to be −11.38 for boys, which translates to 12.62 months when converted to the original scale for Age by adding 24. The change onset for girls was slightly later at 12.99 months, but sex differences for the timing of onset were not significant (t(20) =−0.82, p =.42). Individual differences in the timing of onset between children was estimated to have a variance of 0.48, meaning that the 95% interval for person-specific change onsets in boys is (11.26, 13.98) and (11.63, 14.35) for girls, assuming normality. A one-sided t-test for the between-person onset variance was not significant (t(20) =1.67, p =.06). This test is conservative, so we proceeded to test the significance of a variance component with a more appropriate 50:50 mixture of ${\chi }_1^2$ and ${\chi }_2^2$ (because the variance component is part of an unstructured covariance structure; Case 5 in Self & Liang, 1987; Case 2 in Verbeke & Molenberghs, 2012, p. 111). When applying this test using the deviance of a model with a change onset random effect (−2LL =154.5) and without the change onset random effect (−2LL =164.0), the change onset variance is significant $\left({}_{50:50}{\chi }_{1,2}^2=9.5,p=.01\right)$.

Table 3.

Time-at-onset model estimates for Huttenlocher et al. (1991) vocabulary data

Parameter	Notation	Est.	SE	p
	Fixed Effects
Onset Fixed Effect	γ 20	−11.38	0.93	<.01
Onset on Female	γ 21	0.37	0.45	.42
Onset on Mom Speech	γ 22	0.00	0.01	.79
Endpoint Fixed Effect	γ 00	5.20	0.76	<.01
Endpoint on Female	γ 01	4.12	1.13	<.01
Endpoint on Mom Speech	γ 02	0.08	0.03	.03
	Random Effect Variances
Endpoint Variance, Group 1*	exp(ω2)	17.07	7.70	.02
Endpoint Variance, Group 2*	exp(ω2 + ω3)	3.16	1.72	.04
Onset Variance**	τ 22	0.48	0.29	.01
Endpoint, Onset Correlation	ρ	0.41	0.33	.22
	Residual Variances
Residual Variance, 26 Months	exp(ω0 + 2ω1)	11.94	3.78	<.01
Residual Variance, 24 Months	exp(ω0)	3.16	1.73	<.01
Residual Variance, 22 Months	exp(ω0 − 2ω1)	0.84	0.16	<.01
Residual Variance, 20 Months	exp(ω0 − 4ω1)	0.22	0.04	<.01
Residual Variance, 18 Months	exp(ω0 − 6ω1)	0.06	0.01	<.01
Residual Variance, 16 Months	exp(ω0 − 8ω1)	0.02	<0.01	<.01
Residual Variance, 14 Months	exp(ω0 − 10ω1)	<0.01	<0.01	<.01
Residual Variance, 12 Months	exp(ω0 − 12ω1)	<0.01	<0.01	<.01

Note: p-values for fixed effects are obtained from a t-distribution with default degrees of freedom computed as number of upper-level units (22 children) minus the number of estimated random effects (2), which is 20. Estimates for parameters used to calculate the variance terms are ω₀ =1.15, ω₁ = 0.66, ω₂ = 2.84, and ω₃ =−1.69, all of which were statistically significant.

^*p-values are calculated from a one-sided t-test with 20 degrees of freedom

^**p-value is calculated from a 50:50 mixture of ${\chi }_2^1$ and ${\chi }_2^2$

The average endpoint for Words per Study Hour (multiplying by 10 to put it back in the raw frequency scale) was 52.0 for males and 93.2 for females and this difference was statistically significant (t(20) = 3.64, p <.01). The between-person variability in the endpoint was the only parameter that continued to exhibit Group differences after the outcome was rescaled. In Group 1, the estimated between-person variance was 1707 (after multiplying by 100 to put it back in the raw frequency scale), which was statistically significant when assessed with a one-sided t-test (t(20) = 2.22, p =.02). In Group 2, the estimated between-person variance was 317 (on the raw frequency scale), which was also statistically significant when assessed with a one-sided t-test (t(20) =1.83, p =.04). The differences between the Group endpoint variances is also significant (t(20) =16.43, p <.01).The estimated correlation between the endpoint and change onset random effects was 0.41, which was not significant (t(20) =1.26, p =.22).

Mother’s Speech was a significant predictor of the outcome at 24 months (t(20) = 2.29, p =.03), meaning more talkative mothers tended to have children with larger vocabularies. Mother’s Speech did not predict the change onset (t(20) = 0.27, p =.79), meaning that the timing of the child’s vocabulary development was not impacted by exposure to more words from the mother. Figure 8 shows a gradient plot of the model-implied trajectories with line color determined by the value of Mother’s Speech. The top panel shows the entire observation window and the bottom panel shows a detail where the horizontal axis is near the change onset to highlight variability across people. In the top panel, the effect of Mother’s Speech can be seen by a higher density of darker green lines for trajectories with the larger endpoints. In the bottom panel, there is no discernible difference between the line colors and change onsets.

Figure 8.

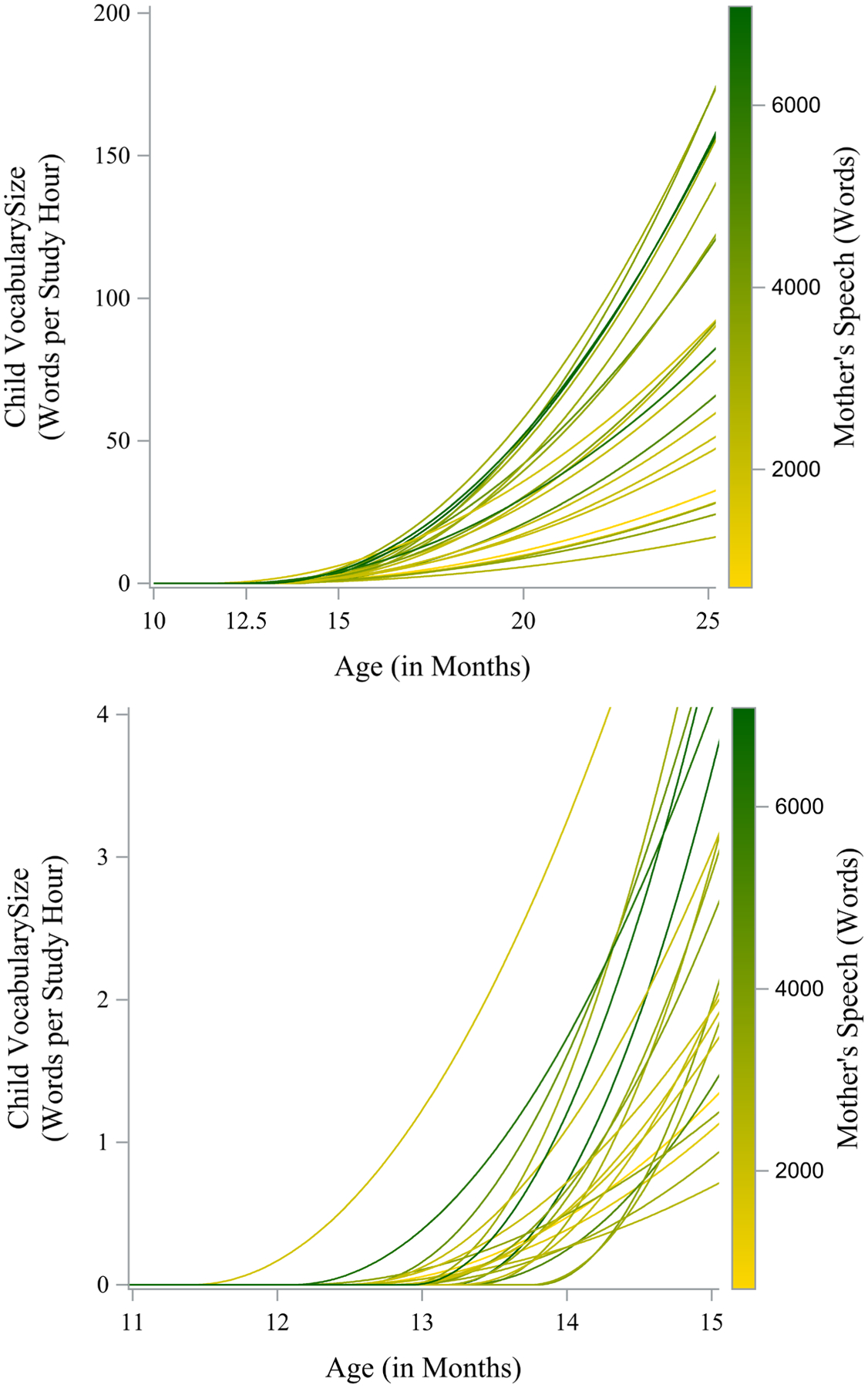
Gradient plot for person-specific model-implied trajectories with color determined by Mother’s Vocabulary across the entire observation window (top panel) and a detail of the change onsets (bottom panel).

Combining Change Onset and Change Offset for Sigmoidal Growth Processes

To this point, we have focused on change offset or change onset in J- or inverted J-shaped growth processes, but the multiphase approach can be further extended to sigmoidal growth processes as well. Sigmoidal processes have an “S” shape such that the process starts off relatively flat, then rapidly accelerates until the curve hits an inflection point, at which point the process decelerates as it approaches an asymptote (Browne & Du Toit, 1991). In psychology, logistic and Gompertz curves are commonly employed functions that follow this shape (Grimm & Ram, 2009). However, these functions are asymptotic and do not provide information on when the onset and offset of change occur. In this section, we discuss how to simultaneously estimate both change onset and offset in a single model with a multiphase double-quadratic model. We then apply this model to a cognitive psychology example that examines how quickly young children learn strategy for a novel game.

The Multiphase Double-Quadratic Model

The top panel of Figure 9 shows a sigmoidal curve. Here we can see that the first half of the curve looks much like the time-at-onset model and the second half (the mirror image of the first) looks much like the time-at-offset model. Combining these two models together, the bottom panel of Figure 9 shows how the S shape can be captured via a spline of two horizontal lines (the minimum or the maximum) and two quadratic curves. Prior to the change onset, the trajectory is a horizontal line at the minimum value. At the change onset, the change is initially accelerating. In the model, the change onset is parameterized as the vertex of a convex quadratic curve which governs change until the inflection point. At the inflection point, change enters a new phase of deceleration governed by a concave quadratic curve which continues until the change offset. The change offset is parameterized as the vertex of the concave quadratic curve. Beyond the change offset, the function again follows a horizontal line, now at the maximum value.

Figure 9.

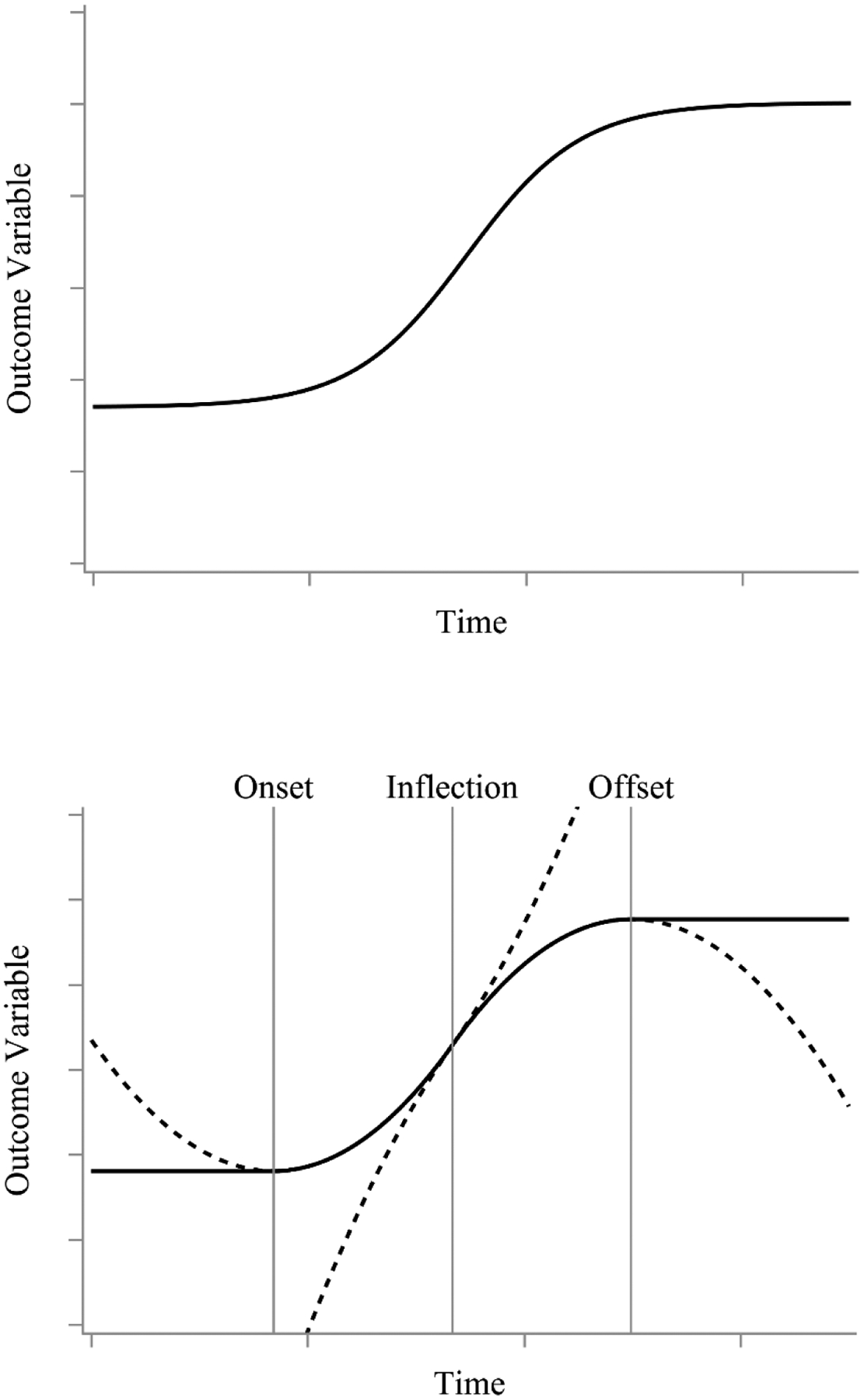
A representative sigmoidal curve (top) and graphical depiction of how sigmoidal curves can be split into two horizontal lines (one before the change onset and one after the change offset) and two quadratic curves represented by dotted lines (one convex and one concave) that intersect at the inflection point. The multiphase double quadratic model breaks a sigmoidal curve into 4 phases (pre-onset, onset to inflection, inflection to offset, post-offset) to incorporate individually varying change onsets and change offsets

The multiphase double-quadratic model corresponding to the bottom panel of Figure 8 can be written as

$$\begin{gathered} y_{ti}=\{\begin{array}{ll}{\beta }_{1i}+e_{ti}\hfill & \text{if }\mathit{\text{Time}}\le {\beta }_{2i}\hfill \\ {\beta }_{1i}-\left({\beta }_{1i}-{\Upsilon }_i\right){\left(\frac{\left(Tim{e}_{ti}\right)}{\left({\beta }_{2i}-{\kappa }_i\right)}-1\right)}^2+e_{ti}\hfill & \text{ if }{\beta }_{2i}<\mathit{\text{Time}}\le {\kappa }_i\hfill \\ {\beta }_{3i}-\left({\beta }_{3i}-{\Upsilon }_i\right){\left(\frac{\left(Tim{e}_{ti}\right)}{\left({\beta }_{4i}-{\kappa }_i\right)}-1\right)}^2+e_{ti}\hfill & \text{ if }{\kappa }_i<\mathit{\text{Time}}\le {\beta }_{4i}\hfill \\ {\beta }_{3i}+e_{ti}\hfill & \text{ if }\mathit{\text{Time}}>{\beta }_{4i}\hfill \end{array} \\ {\beta }_{1i}={\gamma }_{10}+u_{1i} \\ {\beta }_{2i}={\gamma }_{20}+u_{2i} \\ {\beta }_{3i}={\gamma }_{30}+u_{3i} \\ {\beta }_{4i}={\gamma }_{40}+u_{4i} \\ {u}_i~MVN\left(0,T\right) \\ {e}_i~MVN\left(0,{\sigma }^{2}I\right) \end{gathered}$$ (9)

Where β_1i is the minimum value for person i, β_2i is the change onset for person i, β_3i is the maximum value for person i, and β_4i is the change offset for person i. Each of these coefficients can include random effects to allow it to vary across people and the covariance matrix of the random effects is specified in T. The model shows that the outcome variable y is modeled by four different phases. The first phase occurs when Time is less than the person-specific change onset (β_2i) and change is captured by a person-specific horizonal line at the minimum value (β_1i). The second phase occurs when Time is between the person-specific change onset and the timing of the person-specific inflection point (κ_i). In this second phase, change is modeled with a convex quadratic curve using Cudeck and du Toit’s parameterization such that vertex is defined by the minimum value (β_1i) and the time of the change onset (β_2i) so that there is a smooth continuous transition from the first phase to the second. The third phase occurs when Time is between the person-specific timing of the inflection point (κ_i) and the person-specific change offset (β_4i). Change in this phase is modeled with a concave quadratic curve using Cudeck and du Toit’s parameterization with a vertex defined by the maximum value (β_3i) and the time of the change offset (β_4i), again to foster a smooth continuous transition from the third phase to the fourth phase. The fourth phase occurs when Time is greater than the person-specific change offset (β_4i) and change is captured by a person-specific horizonal line at the maximum value (β_3i).

We assume the person-specific inflection point marking the transition from the second to third phase occurs at the midpoint of growth, removing the need to estimate this parameter and making it equal to κ_i = 0.50(β_2i + β_4i). The model in Equation 9 also contains ϒ_i, which is the person-specific value of the outcome variable at the inflection point (i.e., it corresponds to the vertical axis element of the ordered pair defining the inflection point). This parameter is shared in the equations for the second and third phase because it is vital that both quadratic curves intersect at the same point to ensure a smooth transition between the phases (κ_i is also shared in both equations because it is the horizontal element of the ordered pair defining the inflection point). For symmetric sigmoidal curves like the logistic curve, ϒ_i = 0.50(β_1i + β_3i) (Goshu & Koya, 2013). The next section provides a demonstration of how this model can be used to provide information on individual differences in the timing of onset and offset of a sigmoidal change process.

Example 4: Strategy Learning Task

Background & Data

The multiphase double-quadratic model is applied to data originally from Tivnan (1980) which can also be found in Chapter 5 of Singer and Willett (2003). In this data, 17 children ages 6 to 8 years old play a simplified version of chess called Fox and Geese. The game has two players, the experimenter and one child. The experimenter has a single game piece that can move in all directions on a chessboard (the fox) and the child has four game pieces that can only move forward (the geese). The goal of the game is to trap the other player so that they are unable to legally move their piece during their turn. Children complete up to 27 trials and the number of moves made by the child in each game is recorded where a larger number of moves indicates greater skill. The game is useful for studying cognitive skills because (a) there is an optimal strategy, (b) the strategy is not obvious without playing, and (c) the optimal strategy becomes more apparent with trial and error.

Similar to other cognitive tasks that require practice (e.g., second language acquisition), growth across trials of the Fox and Geese game is sigmoidal such that growth is flat in the beginning while children become acquainted with the game, steep in the middle as children start to refine and optimize their strategy, then flat again once their strategy has been fully refined. While the maximum value conveys some information about the quality of the strategy implemented by each child (e.g., not all children discover the optimal strategy), the timing of two events is also useful: how long it takes for children to begin to implement a strategy (learning onset) and how long it takes children to arrive at their best strategy (learning offset). The multiphase double-quadratic model can provide person-specific estimates of the timing of these events in addition to a person-specific maximum value.

Model & Results

We fit the multiphase double-quadratic model to these data with Number of Moves as the outcome variable and Trial Number as the time variable. The model was estimated in SAS in the NLMIXED procedure with maximum likelihood via Gaussian quadrature and double dogleg optimization using 15 quadrature points, which took 3 minutes to converge to a solution. The model is the same as Equation 9 except that we did not include a random effect for the intercept (i.e., u_1i is not present in the β_1i equation) because there was little variation around the outcome during the first trial. This reflects that, without experience, children were uniformly unable to make many moves. Random effects were included for the maximum, the change onset, and the change offset with all random effects being permitted to covary with each other.

Parameter estimates are provided in Table 4. The fixed effect for the minimum is 4.50 moves and children maintained this value until about Trial 9 (the change onset), on average. From Trial 9 (the change onset) until Trial 24 (the change offset), children grew from the minimum moves of 4.50 to the average maximum number of moves of 11.30. There is large between-child variation in the maximum value (τ₃₃ =19.98, implying a SD of 4.47 moves) and the change onset (τ₂₂ = 45.56, implying a SD of 6.75 trials). To a lesser degree, there was also between-child variability in the change offset (τ₄₄ = 9.06, implying a SD of 3.01 trials). Though not explicitly part of the model, we can also calculate the average number of trials in which learning occurs by β_4i − β_2i, which had a mean of 15.58 with a standard deviation of 6.60. These results suggest that children vary widely in the number of elapsed trials before a strategy is implemented and vary in the ultimate number of moves their strategy permits, but there is less variation in how many trials have elapsed when the maximum number of moves is reached.

Table 4.

Double-quadratic multiphase model estimates for Fox and Geese data

Parameter	Notation	Est.	SE	p
	Growth Trajectory Fixed Effects
Minimum	γ 10	4.50	0.21	<.01
Change Onset	γ 20	8.66	2.26	<.01
Maximum	γ 30	11.30	0.39	<.01
Change Offset	γ 40	24.02	1.51	<.01
	Random Effects
Change Onset Variance	τ 22	45.50	17.86	<.01
Maximum Variance	τ 33	19.94	2.32	<.01
Change Offset Variance	τ 44	9.09	6.59	.01
Max., Onset Correlation	Corr(u2i, u3i)	0.42	0.18	.03
Onset, Offset Correlation	Corr(u2i, u4i)	−0.14	0.16	.41
Max., Offset Correlation	Corr(u3i, u4i)	−0.89	<0.01	<.01
	Within-Person Residual Variance
Residual Variance	σ 2	10.79	0.86	<.01

Note: p-values are obtained from a t-distribution with the default degrees of freedom computed as number of upper-level units (17 children) minus the number of estimated random effects (3), which is 14.

The random effect correlations suggest that children with later change onsets have higher maximums, perhaps because they spend more time exploring strategies that do not work in early trials in order to better locate a more optimal strategy whereas children with earlier change onsets might find an adequate – but not optimal – strategy early on and stick to it. The correlation between the change offset and the maximum was highly negative, suggesting that change offset occurs earlier for those who find an optimal strategy and can make the game last many moves.

Figure 10 shows four representative model-implied trajectories plots against the observed data to demonstrate patterns from the parameter estimates. For instance, Child 7 appeared to choose a strategy quickly (change onset at Trial 3) and spent 20 trials refining it (one of the longest in the study) but did not capitalize on the uncovering a strategy quickly and ultimately had an estimated maximum of 11 moves which was near the sample average. Conversely, Child 14 appeared to explore more at the beginning of the study and had a late change onset (Trial 13) but spent only 7 trials refining their strategy with a change offset at Trial 20 in route to reach an above-average estimated maximum of 17 moves. Child 8 started refining their strategy rather early and had fast change offset (Trial 20) with a below-average 12 trial refinement period as well as the highest estimated maximum among all children (18 moves). Child 9 also had a fast change offset (Trial 20) but had an early change onset (Trial 5) and had a long refinement period before reaching one of the higher estimated maximums in the sample at 16 moves.

Figure 10.

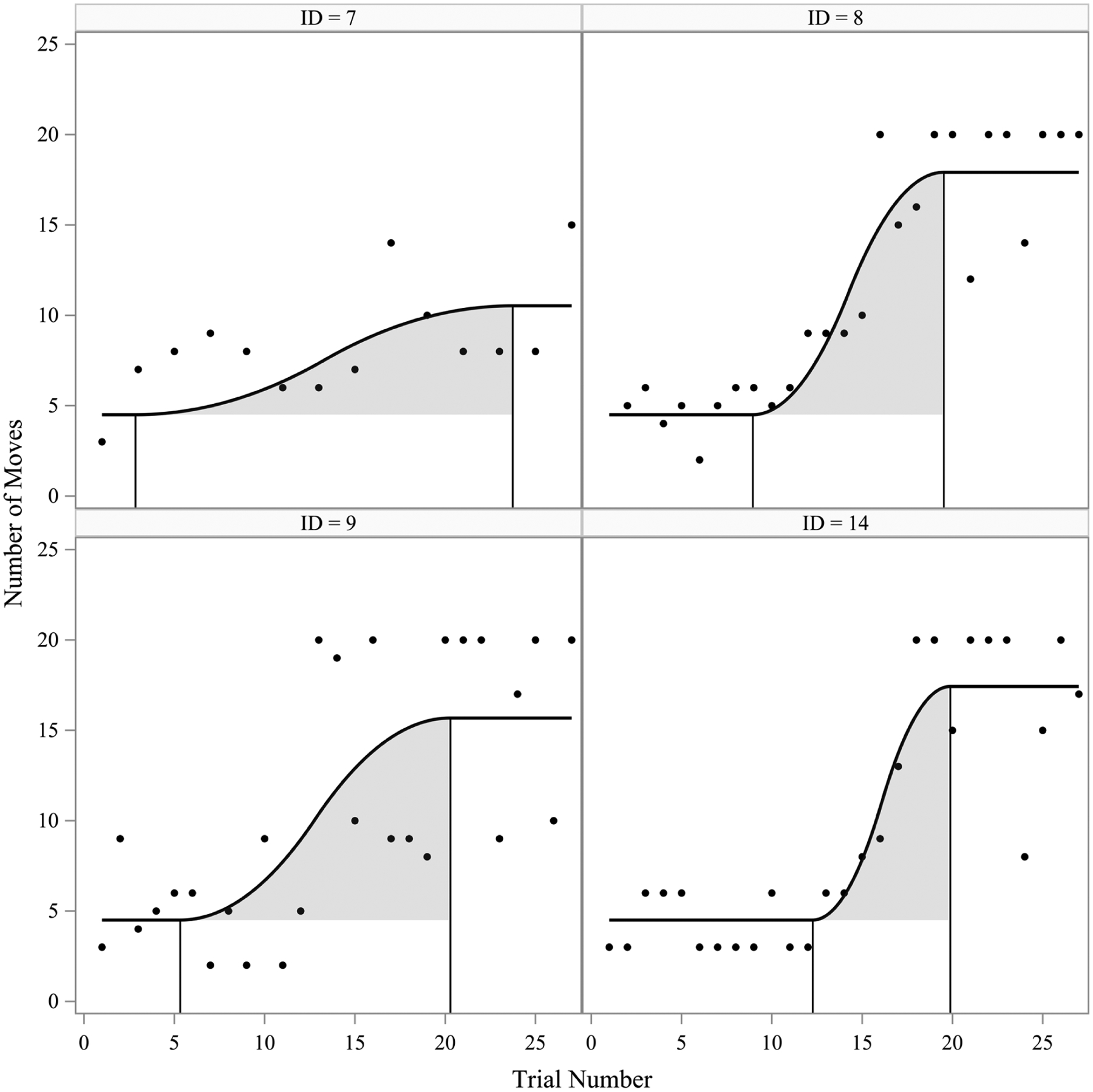
Observed repeated measures (circles) and model-implied trajectories (solid black line) for four children. Solid vertical black lines represent the individual timing of the change onset and change offsets and grey shading represents the refinement period for each child.

Strategy for Variance Component Inference

Tables 1–4 include inferential tests for variance components, the proper handling of which needs additional clarification. Testing whether coefficients have variability across people requires special care in mixed effect models, especially because a main focus lies in individual differences. When testing variance components, a noted issue is that the null hypothesis – whether the variance is equal to zero – falls on the lower boundary of the parameter space because variances typically are not permitted to be negative (Molenberghs & Verbeke, 2007). This boundary problem violates regularity conditions of traditional inferential tests and produces inaccurate p-values (Self & Liang, 1987). A one-sided t-test is an imperfect but simple method to avoid the negative region of rejection that is beyond the boundary (Lin, 1997; SAS Institute, 2018, p. 6641). However, t-tests tend to be too conservative and have low power compared to more theoretically appropriate tests like mixture chi-square tests (also known as modified likelihood ratio tests) for bounded parameters (Berkhoff & Snijders, 2001; Stoel, Garre, Dolan, & van den Wittenboer, 2006). Mixture chi-square tests compute p-values for variance components by combining probabilities from two separate chi-square distributions with different degrees of freedom to create one overall p-value (Stram & Lee, 1994).

Mixture chi-square tests are generally preferable, given their more theoretically appropriate nature, but they do possess some drawbacks. First, mixture chi-square tests compare likelihoods from two nested models and therefore require fitting the model multiple times to obtain the likelihood from each; once with the variance component(s) of interest included (as well as associated covariances) and once with these parameters excluded. The models we discuss include random effects that enter the model nonlinearly, which can lengthen estimation time relative to traditional linear mixed effect models. In cases where computational times are much longer, it may be impractical to refit the model multiple times, especially when testing multiple variance components (SAS Institute, 2018, p. 3774). Second, for models with three or more variance components, there may not necessarily be a proper order for testing and potentially removing variance components. For instance, in the offset model for Example 1, there are three possible models with two variance components and three models with one variance component. Likelihood ratio tests with polynomial growth models typically do not encounter this problem because the variance component associated the highest order polynomial of Time would generally be removed first.

To balance these issues, the strategy we employed here and recommend in practice is to begin by inspecting the one-sided t-tests for the variance components. This test is imperfect, but it is consistently conservative. If the one-sided t-test is significant, there is no need proceed with a mixture chi-square test because the conclusion of such a test would not change if a more conservative test already has reported a significant difference. If the one-sided t-test is not significant, however, then we proceed with the mixture chi-square test to obtain more accurate inference for that particular variance component. This strategy will yield the same conclusions as if we conducted the mixture chi-square test for all variance components, but alleviates potential computational burdens of having to refit slightly different versions of the model multiple times in order to acquire and compare the likelihoods. It also helps to guide uncertainties about ordering of model comparisons by illuminating which variance components should be retained in the model. Inference for variance components presented in Tables 1–4 and in-text clarify which test was used to reach the stated conclusion.

A related issue is whether to remove variance components that are triggering a nonpositive definite covariance matrix. Given that the focus of the models is individual differences, it may be dissatisfying to remove variance components from the model due to the estimates being inadmissible or other convergence issues. Though we did not experience this in our examples, recent literature has noted that reparameterizing the random effect covariance matrix can help reduce the incidence of nonpositive definiteness. Cholesky decompositions have traditionally been the recommended approach (Pourahmadi, 1999), though recent research specific to mixed effect models has found that reparameterizing the random effect covariance matrix with a factor analytic structure can be more effective at combating nonpositive definiteness when there are several random effects present (McNeish & Bauer, 2021).

Discussion

Although piecewise models can be used to gauge the timing of transitions in a developmental process trajectory, these transitions are not tied to specific outcome values corresponding to developmental milestones, such as the beginning or end of the growth process or the attainment of minimum or maximum values. The recently developed time-to-criterion framework is well positioned to model the timing of developmental milestones that are fixed and known, such as when modeling growth to a known benchmark. However, these models cannot accommodate milestone values that are unknown a priori or that vary over persons, such as a person’s maximum development. In particular, no previously developed models of which we are aware provide detailed information on the person-specific timing of the onset or offset of change. The approach we propose incorporates a reparameterized quadratic function within a multiphase growth model that includes person-specific parameters indicating the timing of the minimum or maximum value. This allows researchers to assess variability in the timing across people and to include predictors in the model to determine what factors are associated with earlier or later timing. It also permits researchers to include random effect covariances to determine whether earlier or later timing is related to higher or lower maximum or minimum development.

There are many possible extensions and future directions to consider for our proposed framework. First, we assume that maximum and minimum values are representative of reality rather than artificial floors or ceilings created by limitations of measurement. Nonlinear models in psychology sometimes use scale scores may have artificial bounds (e.g., Marceau et al., 2011) such that minimum and maximum values may reflect properties of a measurement scale rather than the maximum of minimum of the underlying characteristic being studied. Statistically, this is not necessarily problematic because the maximum or minimum parameters in the model can be fixed to specific values or random effects can be removed to prevent estimated values above the scale boundaries. If the truncation due to scale boundaries is large, then a problem may be encountered if distributional assumptions of the model are affected. Interpretation may be affected in some cases if there is a theoretically meaningful difference between when people reach their actual maximum on the underlying construct and when they max out the scale. There is a literature on accommodating ceiling and floor effects in longitudinal models that could be incorporated in our framework in the event that scale boundaries present an issue (Feng et al., 2019; Twisk & Rijmen, 2009; Wang et al., 2008).

Second, we focused on the mixed effect framework given its ability to preserve person-specific interpretations of coefficients in nonlinear models where random effects cannot be integrated out of the likelihood (Blozis & Harring, 2016). A similar approach could be implemented in the structural equation modeling framework, which could have benefits for research questions involving missing covariates, multiple outcomes, distal outcomes, or latent classes (Harring, Strazzeri, & Blozis, 2020; McNeish & Matta, 2018). Most structural equation modeling software cannot accommodate models with nonlinear random effects directly, but the model can be linearized by imposing constraints on the first partial derivatives of the growth trajectory. This approach is referred to as a structured latent curve model and can be used to fit nonlinear models in standard structural equation model software designed for linear models (Blozis, 2004; Browne, 1993). A structured latent curve model will yield coefficients with a population-averaged interpretation rather than a subject-specific interpretation provided by mixed effect models (Harring & Blozis, 2016). Population-averaged coefficients are designed to minimize error between the marginal growth curve and the mean profile whereas the subject-specific coefficients attempt to minimize error between in the person-specific curves. Additionally, the person-specific trajectories will not necessarily follow the prescribed mean trajectory in a structured latent curve model (Blozis & Harring, 2017, p. 799), which could result in inconsistent behavior such as decreases after the maximum in a time-at-offset model. There is no difference between the two interpretations in linear models because the random effects integrate out of the likelihood function, but differences will exist in nonlinear models (Zeger, Liang, & Albert, 1988).

Concluding Remarks

Traditional growth models focus primarily on the shape of the growth trajectory, between-person variability, and predictors that explain differences in growth trajectories. Trajectory shapes can be characterized using a variety of functions, ideally governed by substantively interesting parameters that are amenable to testing theoretically motivated hypotheses. The timing of when a change process begins or ends is theoretically interesting in many developmental contexts but few models include parameters that capture this information directly. Our time-at-onset and time-at-onset models expand the limited literature on this topic by providing models for person-specific timing related to maximum and minimum values. Although there are clearly many interesting areas left to explore regarding how best to model the timing of developmental change processes, our proposed modeling framework offers new opportunities to investigate questions about timing across a variety of research contexts in the behavioral, health, and social sciences.