Point-spread function of the BOLD response across columns and cortical depth in human extra-striate cortex

Abstract

Columns and layers are fundamental organizational units of the brain. Well known examples of cortical columns are the ocular dominance columns (ODCs) in primary visual cortex and the column-like stripe-based arrangement in the second visual area V2.

The spatial scale of columns and layers is beyond the reach of conventional neuroimaging, but the advent of high field magnetic resonance imaging (MRI) scanners (UHF, 7 Tesla and above) has opened the possibility to acquire data at this spatial scale, in-vivo and non-invasively in humans.

The most prominent non-invasive technique to measure brain function is blood oxygen level dependent (BOLD) fMRI, measuring brain activity indirectly, via changes in hemodynamics. A key determinant of the ability of high-resolution BOLD fMRI to accurately resolve columns and layers is the point-spread function (PSF) of the BOLD response in relation to the spatial extent of neuronal activity.

In this study we take advantage of the stripe-based arrangement present in visual area V2, coupled with sub-millimetre anatomical and gradient-echo BOLD (GE BOLD) acquisition at 7T to obtain PSF estimates and along cortical depth in human participants.

Results show that the BOLD PSF is maximal in the superficial part of the cortex (1.78mm), and it decreases with increasing cortical depth (0.83mm close to white matter).

1. Introduction

The cortical column is a prominent organizational feature in primary visual cortex (V1) at the mesoscopic, i.e. millimetre, organization level, and is hypothesized to be a generic organizational feature across the whole human brain (Dumoulin et al., 2017). Columns were first investigated in seminal papers by Mountcastle, Hubel and Wiesel (Hubel and Wiesel, 1968, 1972, 1977; Mountcastle, 1957, 1997). The cortical column is characterized by fine-scale functional specializations, for example V1 neurons responding preferentially to monocular input coming to the left and right eyes are segregated in distinct ocular dominance columns (ODCs).

ODC organization is not the only columnar structure in the early visual system. Data from macaque neurophysiology and human neuroimaging indicates that different visual features are processed in distinct streams, segregated both functionally and anatomically. Data suggests that the magnocellular (M) and parvocellular (P) streams remain predominantly segregated also in the second visual field map V2 (Hubel and Livingstone, 1987; Livingstone and Hubel, 1987) (Felleman and Van Essen, 1991; Hubel and Livingstone, 1987; Merigan and Maunsell, 1993; Zeki and Shipp, 1988) but see also (Sincich and Horton, 2005a) for a different position. The functional segregation in V2 is mirrored in the underlying anatomical organization. V2 contains a stripe-based arrangement as revealed using cytochrome-oxidase and myelin staining (Sincich and Horton, 2005b; Sincich et al., 2007, 2010; Tootell and Taylor, 1995). Recently, we have shown that the functional and anatomical properties of V2 stripes are related (Dumoulin et al., 2017).

The spatial scale of cortical columns and layers is beyond the reach of conventional neuroimaging, limiting studies of these structures to animal studies and post-mortem investigations. The advent of high field magnetic resonance imaging (MRI) scanners (UHF, 7 Tesla and above) has opened the possibility to acquire data at this spatial scale, in-vivo and non-invasively in humans (Berlot et al., 2018; Cheng et al., 2001; Dumoulin et al., 2017; Fracasso et al., 2018; Kemper et al., 2018; Klein et al., 2018b; Nasr et al., 2016; Nasr and Tootell, 2018; Olman et al., 2018; Tootell and Nasr, 2017; Yacoub et al., 2008; Yacoub et al., 2007).

A key determinant of the ability of high resolution fMRI to accurately resolve the columnar and layered organization in human neocortex is the point-spread function (PSF) of the fMRI response, in relation to the spatial extent of neuronal activity. The most prominent MRI technique to measure brain function is blood oxygenation level dependent (BOLD) fMRI. BOLD however measures brain function indirectly via changes in haemodynamic oxygenation levels. BOLD PSF refers to the spatial specificity of the BOLD fMRI signal, characterizing the response that would be generated by a theoretical point stimulus in the neuronal domain, for example a spatially defined group of neurons with approximately identical receptive fields, such as cortical columns.

Here we aim to measure the BOLD PSF function. Accurate estimates of the BOLD PSF however are hard to obtain because the spatial extent of the underlying neuronal activity is typically not known. Previous attempts at characterizing the BOLD PSF focused on the retinotopic organization of V1 or the spatial arrangement of ODC (Chaimow et al., 2018b; Engel et al., 1997; Parkes et al., 2005; Shmuel et al., 2007). Here, we take advantage of the stripe-based arrangement present in human V2. This feature can be observed using both anatomical and functional data, in vivo, in human participants (Dumoulin et al., 2017). As with ODCs, the stripe-based arrangement can be probed to measure the BOLD PSF.

We measured sub-millimetre GE BOLD fMRI at 7T, allowing us to quantify the BOLD PSF across cortical depth in human V2. We compute GE BOLD PSF by fitting a modified cumulative gaussian function across the border between successive stripes and validate our approach using anatomical data of the stripe-based arrangement in human V2.

2. Material and Methods

2.1. Subjects

Four subjects participated in the experiment (age range: 28–39, one female). All subjects had normal or corrected-to-normal acuity. All experimental procedures were conducted in agreement with the 1964 Declaration of Helsinki (amended in 2008, Seoul). Subject informed written consent was obtained and approved by the Human Ethics Committee of the University Medical Center Utrecht. Data were acquired as part of a previously published study (Dumoulin et al., 2017). Stimuli and data acquisition have been reported previously (Dumoulin et al., 2017) and are outlined below.

2.2. Stimuli

Stimuli were generated using Matlab and PsychToolbox on a MacBook Pro. Two stimuli were adopted. In the first experiment (‘V2 stripes’) two visual stimuli were presented that consisted of a concentric circular grating of 20% contrast with a spatial frequency of one cycle per degree and covering a visual field of view of 11 degrees diameter (see Fig. 1). The contrast polarity reversed at a temporal frequency of either 1.5 or 7.5 Hz, alternated in a block design of 13s/block. These two temporal frequencies were chosen to elicit differential responses in parvo- versus magnocellular dominated pathways respectively, and are sufficient to bias activity to parvo- and magnocellular pathways to reveal the stripes (Dumoulin et al., 2017), though there may be considerable mixing of both pathways in each stripe-type. In the second experiment (‘retinotopic scans’) a rotating wedge stimulus was presented to delineate the visual field maps. The parameters of rotating wedge stimuli are described in previous studies (Wandell et al., 2007). During both experiments, subjects fixated a dot in the centre of the display and responded when this changed colour. Stimuli were presented on a back-projection screen and viewed using prisms and an angled mirror. The prisms were used to reflect the image from the screen located at the back of the bore towards participants eyes, allowing the participants to view the visual stimuli.

Figure 1,

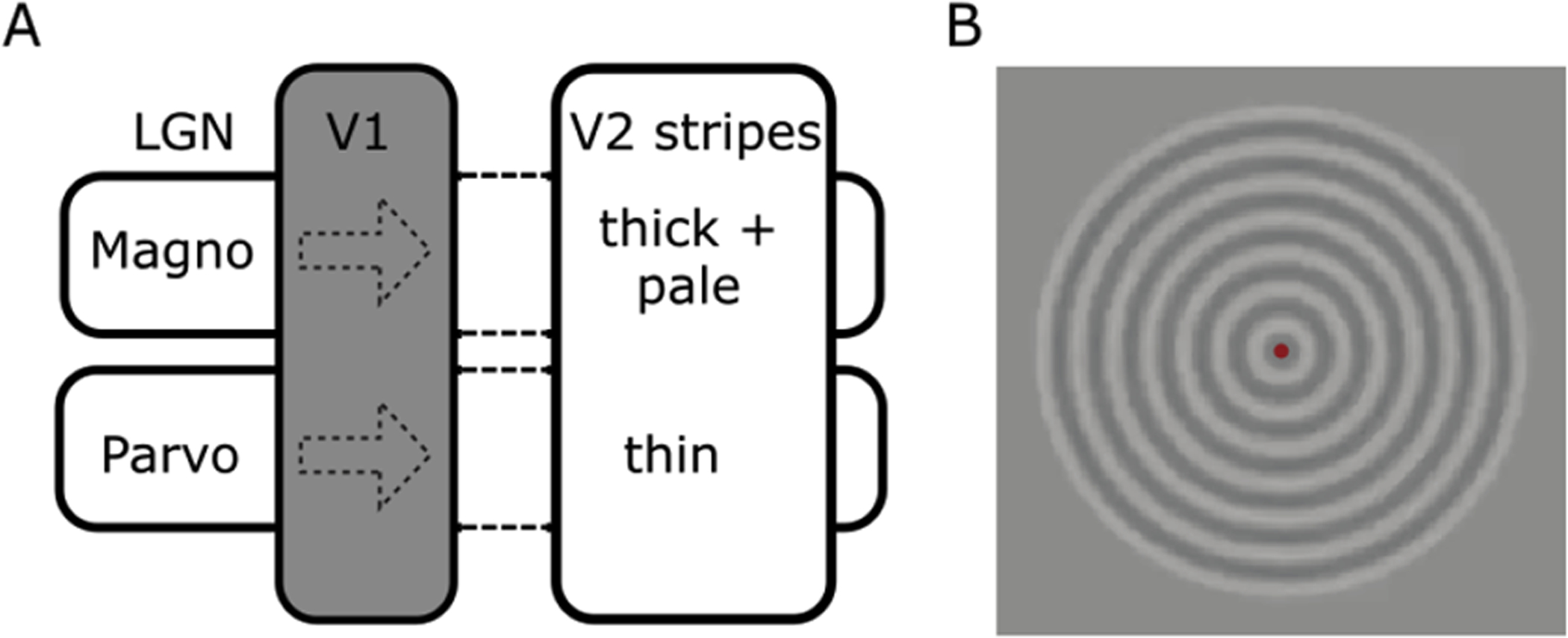
panel A. The second visual area (V2) in non-human primates contains a stripe-based anatomical organization, initially defined using cytochrome-oxidase staining of post-mortem tissue. Neurons in these stripes have been proposed to receive distinct inputs, mainly dominated by the magnocellular and parvocellular pathways (Dumoulin et al., 2017; Tootell and Nasr, 2017). Panel B. Two visual stimuli were presented that consisted of a concentric circular grating of 20% contrast with a spatial frequency of one cycle per degree. The contrast polarity reversed at a temporal frequency of either 1.5 or 7.5 Hz. These two stimuli alternated in a block design (13s/block) and were chosen to elicit responses relatively driven by parvo- versus magnocellular pathways, respectively. Subjects fixated a dot in the centre of the display (red dot in panel B) and responded when this changed colour.

2.3. Magnetic resonance imaging

Functional data were acquired using a 3-dimensional segmented gradient-echo echo-planar-imaging (EPI) sequence with 29 coronal slices and acquisition time of 2.6 s per volume, and the following parameters: TR/TE 35/25 ms, flip angle 20 degrees, SENSE factor 3.5 in the right-left direction, echo planar factor: 17, bandwidth (in the phase-encode direction): 59 Hz/pixel with estimated blurring in the phase-encode direction of ~2% (Haacke et al., 1999) voxel size = 0.9 × 0.9 × 1.0 mm, FOV = 120 (right-left) × 120 (feet-head) × 29 (anterior-posterior) mm³, 80 time-frames, scan duration about 4 min. Each subject participated in at least two fMRI sessions, and each session comprised between 4 and 7 scans. fMRI data were acquired with a 7T Philips Achieva scanner using a volume transmit (Nova Medical, MA, USA) and a 16-channel receive surface-coil (Petridou et al., 2013). Participant’s heads were positioned with foam padding that minimized head motion.

High-resolution T1-weighted (T1-w) anatomical MR images were acquired with the 7T scanner and a 32-channel head coil (Nova Medical, MA, USA) in a separate session. The images were obtained with a 3-dimensional MPRAGE sequence adjusted to obtain a strong myelin contrast in grey matter (GM) (Fracasso et al., 2016b; Fracasso et al., 2016c). Sequence parameters were: inversion delay TI = 1200ms, time delay between inversion pulses TD = 6000ms, TR/TE 8/3 ms, flip angle: 8 degrees, voxel size = 0.5 mm isotropic, FOV: 140 × 140 × 30 mm, 60 coronal slices, bandwidth 202 Hz/pixel, turbo factor: 275, adiabatic inversion, and no acceleration. The imaging volume was placed at about the same location in visual cortex as the functional images.

Because cerebro-spinal fluid (CSF) appears bright in magnitude images using this TI and TD, images from the real component of the complex MR signal were also reconstructed, in which CSF is dark, and were used to mask CSF in the magnitude images by intensity thresholding. The resulting magnitude images were used in subsequent analysis steps.

2.4. Alignment and phase-specified coherence:

Data analysis was performed using AFNI (afni.nimh.nih.gov) and R (https://www.r-project.org/). During the first 13 time-frames in each functional run no visual stimuli was presented, and were discarded to ensure that the signal had reached steady-state. The remaining time-frames were corrected for motion, aligned and interpolated to the anatomical data using the functions 3dVolreg and 3dAllineate using the local Pearson correlation cost function (Fig. 2A–D). The first step in the alignment was to manually align the EPI to the anatomical data using the ‘nudge’ tool in AFNI. After this first step, we ran an automated co-registration algorithm (3dAllineate). We limited the rotation and the shift to 3 mm (flags: -maxrot 3, maxshf 3), and we imposed a single pass only (flag: -onepass). For the alignment we used an affine transformation, estimating shift, rotation, shear, and scaling along 3 dimensions (for a total of 12 parameters). Neither non-linear alignment nor distortion correction (top-up) was used. Baseline drifts of the fMRI time series were removed by high-pass temporal filtering. fMRI data were analysed in the Fourier domain and the coherence and phase-specified coherence was computed per voxel. The coherence of each fMRI series at the fundamental stimulus frequency is a measure of the strength of the BOLD response but does not specify to which stimulus. On the other hand, the phase-specified coherence measures the amplitude of the BOLD response and further distinguishes between the two stimulus types.

Figure 2.

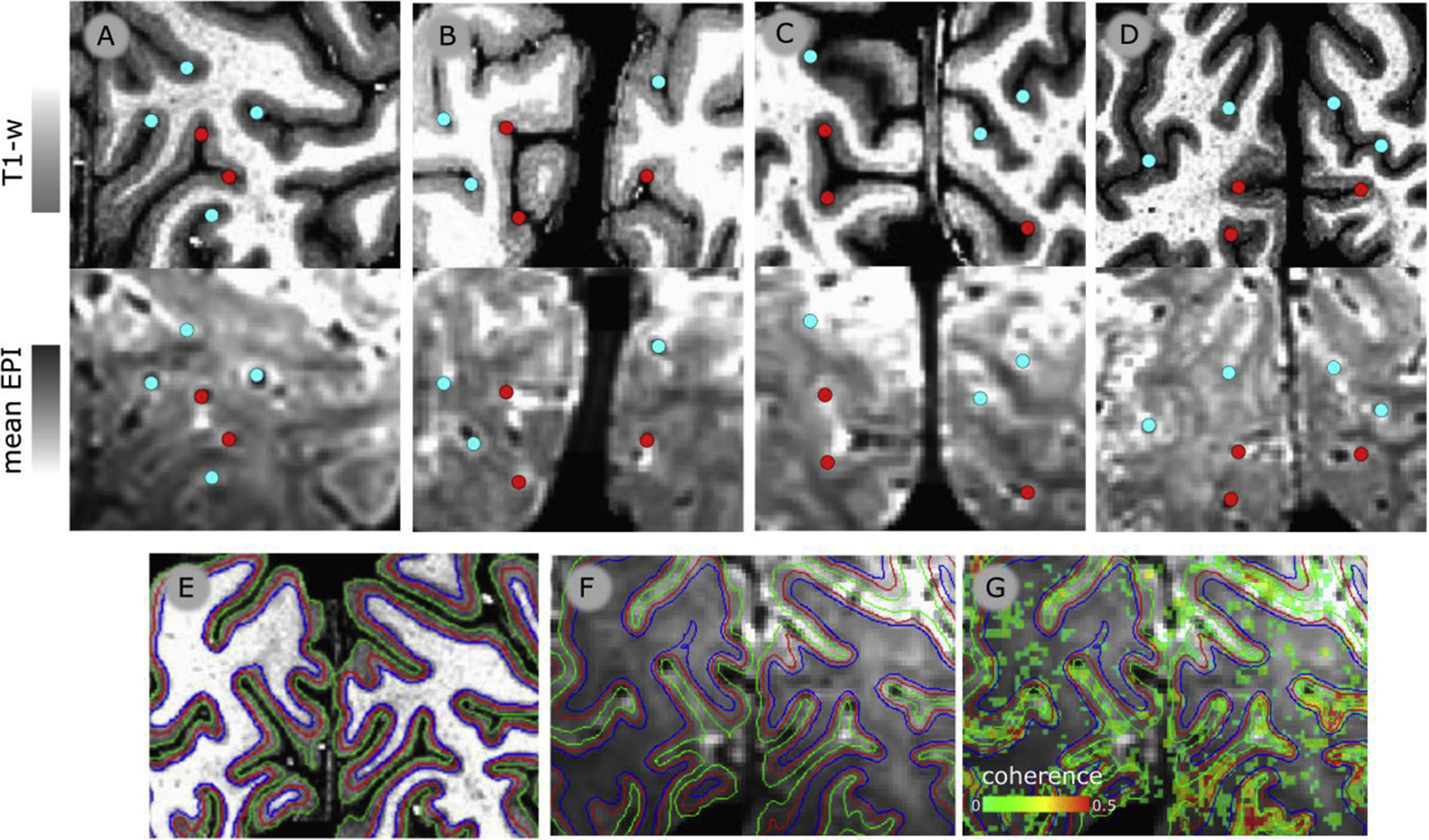
Columns A, B, C & D. First row: Portion of T1-w images for each participant (P1–P4, respectively) with landmark points indicating locations within or outside the calcarine sulcus (red and cyan, respectively). Second row: co-registered mean EPI images from the same portion of the volume as in the first row. The same landmark points are reported as in first row to showcase the correspondence between T1-w and EPI images after co-registration. Third row: anatomical and functional images. Panel E. T1-w image from a representative participant. The green and blue lines represent the GM/WM and GM/CSF border respectively, the red line represents the surface running approximately along the middle of cortical depth. Panel F. Mean 3D-EPI image obtained from the functional time series, co-registered with the T1-w image, and superimposed with the GM/WM GM/CSF and middle of cortical depth surface presented in panel E. Panel G. Mean 3D-EPI image superimposed with coherence map obtained from the ‘stripes’ experiment, thresholded by coherence > 20% and cluster size>20. Only voxels within the 3D-EPI mask are shown. Color scale shown at the bottom left of the panel: ‘coherence’).

The coherence (C) was computed as:

$$C=\frac{A_0}{\sqrt{\sum A_f^2}}$$ Eq. 1:

where A_f are the amplitudes of each Fourier component (f), and A₀ is the amplitude at that stimulation frequency. The coherence values vary between 0% and 100%, where larger values indicate stronger responses to the stimulus manipulation.

The phase-specified coherence (C_φ) was computed as:

$$C_{\phi }=C*\text{cos}\left({\phi }_0-{\phi }_{\mathit{\text{hrf}}}\right)$$ Eq. 2:

where C is the coherence (Eq. 1), φ₀ is the phase of the signal at the stimulation frequency, and φ_hrf is the hemodynamic response delay. The hemodynamic delay (φ_hrf) was estimated based on the response profiles of the data (see below). The phase-specified coherence combines the coherence, i.e. a measure of response amplitude, with phase, i.e. a measure of which stimuli elicited the strongest response. The phase-specified coherence values range between −1 and 1; positive values reflect stronger responses to the 1.5 Hz stimulus presentations, whereas negative values reflect stronger responses to the 7.5 Hz stimulus presentations.

To estimate φ_hrf (or reference phase), we performed an analysis of φ₀ distribution of each participant for area V2. We estimated the probability distribution function of φ₀ via kernel density estimation using the function ‘density’ in R and derived the mode of this distribution. The estimated mode was then used as φ_hrf (or reference phase) to derive the phase-specified coherence (C_φ).

2.5. Segmentation and surfaces

Anatomical volumes were segmented automatically using the function 3dSeg in AFNI and adjusted manually if necessary. The segmentation of the T1-w images was analyzed with nighres (https://nighres.readthedocs.io/en/latest/installation.html). A volume-preserving distance map was computed between the white matter (WM) and gray matter (GM) boundary and the GM/CSF boundary (Dinse et al., 2015; Waehnert et al., 2016; Waehnert et al., 2014) in 8 separate level-set volumes. This equi-volume model provides a coordinate system of cortical depth which is independent from local cortical folding (Waehnert et al., 2014). Local cortical thickness was estimated with nighres and local curvature using the AFNI function SurfMeasures. Cortical surfaces were obtained from the corresponding level-set volumes per subject using the AFNI function IsoSurface (Fig. 2E–G).

First, T1-w signal is known to covary with local curvature (Sereno et al., 2013). Thus, for each ROI, participant and surface along cortical depth, we subtracted the average T1-w signal from the T1-w signal distribution. Because previous post-mortem and in vivo MRI studies have found a significant correlation of myelin density with the folding pattern of the cortex (curvature), we removed the curvature contribution using a procedure similar to the one adopted in previously published papers (Sereno et al., 2013; Sigalovsky et al., 2006). We fit a linear model between the de-meaned T1-w signal and local curvature to obtain the residuals of the model, giving us the de-meaned, de-curved T1-w signal. From now on we refer to the de-meaned, de-curved T1-w signal simply as ‘T1-w signal’.

2.6. Data analysis

2.6.1. Determination of the border between two consecutive V2 stripes from phase-specified coherence (GE BOLD)

To estimate the GE BOLD PSF we started by building a map measuring distance in millimetres from the boundary between consecutive stripes. This distance is computed using the geodesic distance between each two points over the cortical surface for each surface along cortical depth.

First, we used the phase specified coherence to identify the stripes in human V2 responding to high or low temporal frequencies. Phase specified coherence is ideal for this measurement. In our experimental design, a positive phase specified coherence value indicates a relative preference for low temporal frequency, a negative phase specified coherence value indicates a relative preference for high temporal frequency. A phase specified coherence of 0 indicates the shift between a preference for relatively low to relatively high temporal frequency. Hence, 0 demarcates the border between different stripes in human V2.

We identified the nodes on the surface that prefer high or low temporal frequency (‘positive’ and ‘negative’ set of nodes, respectively). We computed the geodesic distance from every node on the positive to every node on the negative group. For each node from the positive group we assigned the smallest distance among all the possible geodesic distances computed towards the negative nodes. We repeated the same operation from the negative to the positive nodes (See Fig. 3). This operation results in a geodesic distance map, indicating the smallest distance from each node to the boundary between successive stripes in V2. A single geodesic distance map was obtained for each surface along cortical depth. We used geodesic distance maps as a basis to estimate the GE BOLD PSF across cortical depth.

Figure 3.

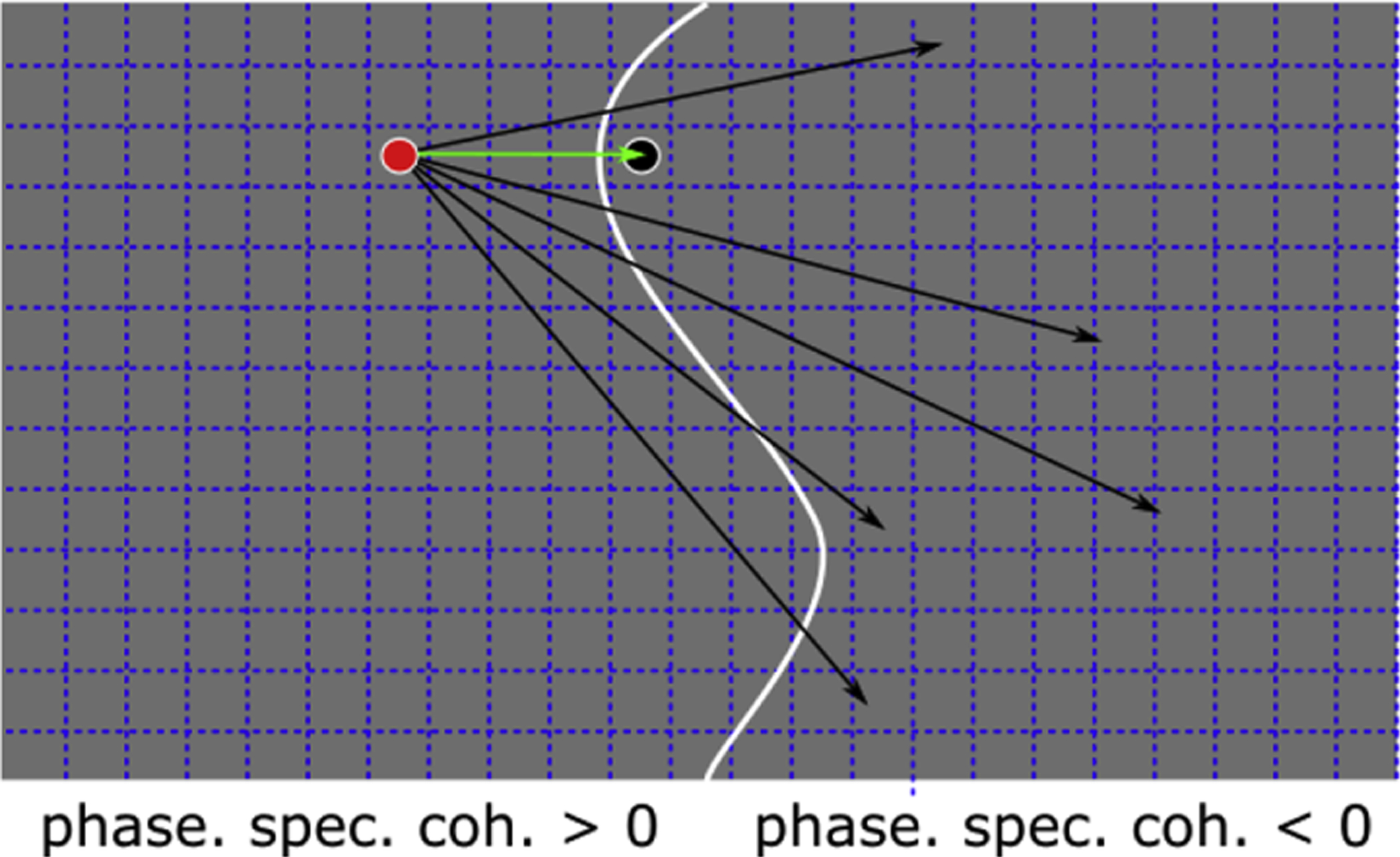
Computing the geodesic distance map (cortical distance)

The grey area depicts a portion of V2 over the cortical surface. Normally, this portion would be a two-dimensional sheet that extends in a three-dimensional space. To simplify, in this example we consider the two-dimensional sheet outlined by the grey area above. The grey area is composed by nodes, represented by the squares delimited by dashed lines. The grey area is divided into two portions (two consecutive stripes), where the phase specified coherence is larger than 0 and smaller than 0, respectively. The border between these two portions is identified by the white line and it divides ‘positive nodes’ form ‘negative nodes’). We computed the geodesic distance from every node in the positive group to every node in the negative group. For each node from the positive group, we assigned the smallest distance among all the possible geodesic distances computed. In the example above we highlight one node among all the positive nodes (red dot) and several distances to negative nodes (arrows). The smallest distance computed from the red dot is represented by the green arrow. We assign the distance depicted by the green arrow to the red node. To obtain a complete geodesic distance map, we repeat the same operation for all positive nodes and negative nodes.

For each surface across cortical depth and each node we obtained the phase specified coherence (ranging between −1 and 1, see Section 2.4) and the geodesic distance (from now on referred to as: ‘cortical distance’), representing the distance from the border between consecutive stripes in human V2 (see Fig. 4). Cortical distance data was binned based on 2% quantile bins. Within each cortical distance bin, we computed the average phase specified coherence as well as cortical distance and plot the former as a function of the latter (see Fig. 4C).

Figure 4.

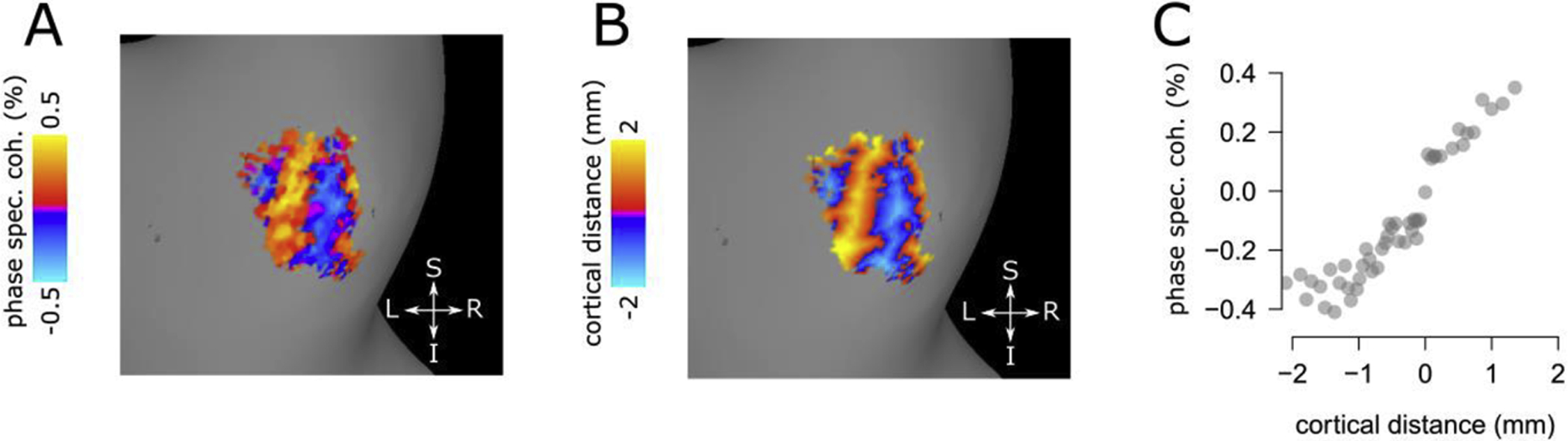
Cortical distance map and phase specified coherence.

We selected a small portion of human V2 (single participant, dorsal V2, left hemisphere), to show the result of our cortical distance measure. Note that the analysis presented in the paper was performed over the entire V2 ROI. Panel A. Phase-specified coherence for a portion of V2. Panel B. Cortical distance derived with the method described in Fig. 3 from the same portion of human V2. The resulting cortical distance ranges between −2 to 2 mm, representing the distance from the border between successive V2 stripes. Panel C. Scatterplot showing the relationship between phase specified coherence and cortical distance. Cortical distance data was binned based on 2% quantile bins and averaged within each bin. Phase specified coherence was averaged within the cortical distance bins. This plot shows the change of phase-specified coherence over cortical distance, across the border between two successive V2 stripes.

2.6.2. Estimation of BOLD PSF

We obtained the binned phase-specified coherence along cortical distance for each surface along cortical depth, for each participant. We fit a model to the measured phase-specified coherence along cortical distance, assuming a Gaussian full-width, half-max (FWHM).

The model followed a similar logic to the analysis introduced by (Shmuel et al., 2007). For a comparison between the current analysis procedure and the one in (Shmuel et al., 2007) see the end of this section and Discussion, section 4.5.3.

The model consisted of a modified cumulative gaussian function (CGF). The standard CGF takes the form reported in equation 3 (Eq. 3). The function ranges from 0 to 1 and has location (μ) and sigma (σ) as parameters. We modified the parametrization of the standard CGF. First, we fixed the location parameter (μ) to zero, as we built the distance map placing the 0 at the cross between successive stripes. Second, we added a scaling constant, to account for different amplitudes of the signal. Third, we added a shift constant to accommodate the range of phase specified coherence values, which naturally varies between −1 and 1. Overall we obtained a model with 3 parameters, CGF_m (Eq. 4): sigma, scaling constant and shift constant (see Fig. 5).

$$\mathit{\text{CGF}}=\frac{1}{2}\left[1+\mathit{\text{erf}}\frac{(x-\mu )}{\sigma \sqrt{2}}\right]$$ Eq. 3:

$${\mathit{\text{CGF}}}_m=\mathit{\text{mult}}*\left(\frac{1}{2}\left[1+\mathit{\text{erf}}\frac{(x)}{\sigma \sqrt{2}}\right]\right)+\mathit{\text{shift}}$$ Eq. 4:

$$\mathit{\text{FWHM}}=2\sqrt{2\text{ln}2}\sigma \approx 2.355\sigma$$ Eq. 5:

Figure 5,

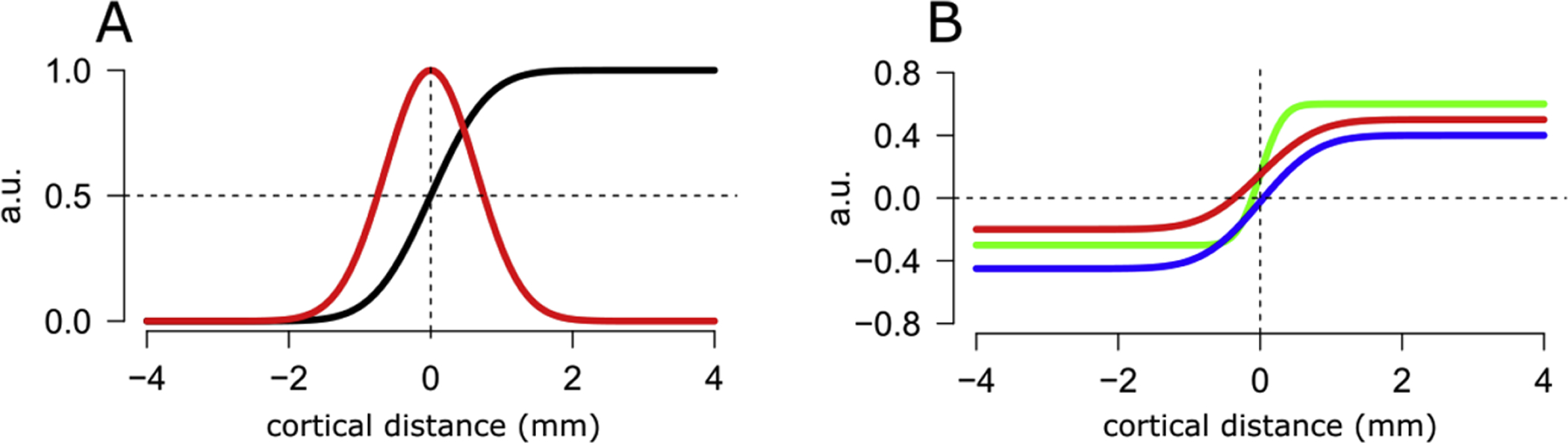
Modelling the GE-BOLD PSF

Panel A. The plot shows a Gaussian PSF (red line). We used the cumulative of the Gaussian (black line, (CGF)) to fit a model to the measured phase-specified coherence along cortical distance, for each surface along cortical depth. Panel B. We modified the parametrization of the standard CGF: we fixed the location parameter (μ) to zero (at the boundary between two successive stripes in human V2); we added a scaling parameter, to account to different amplitudes of the signal; we added a shift parameter to accommodate the range of phase specified coherence [−1, 1], see Eq. 4. The plot shows three CGFs with different parameters: green line: FWHM=0.6mm, scaling parameter: 0.9, shift parameter: −0.3. blue line: FWHM=1.5mm, scaling parameter: 0.85, shift parameter: −0.45. red line: FWHM=1.5mm, scaling parameter: 0.7, shift parameter: −0.2. Please note that the red and blue lines appear to have a different rate of change around the zero crossing along cortical distance, however this difference is accounted for by a difference in amplitude, not FWHM (0.85 and 0.7 for the blue and red lines, respectively). The parametrization adopted in our modelling approach allows to disentangle between different components of the trend between phase specified coherence and cortical distance, and to detect differences that could otherwise be wrongly be ascribed to FWHM alone.

Conveniently, in this parametrization the sigma (σ) represents the width of the Gaussian PSF. We multiplied sigma by 2.355 (Eq. 5) to obtain the Gaussian full-width half-max, representing our estimate GE-BOLD PSF.

There are several differences between the current approach and the analysis of Shmuel and colleagues (2007) that are important to point out. In the current approach, we used functionally defined borders of V2 stripes, and used phase specified coherence to identify stripes in human V2, responding to high or low temporal frequencies. This is different from Shmuel and colleagues, which took advantage of the underlying retinotopic organization of human primary visual cortex and used an estimate of BOLD response based on the 1^st principal component from the activity profiles sampled from the border.

From the modelling perspective, we fit a cumulative Gaussian model with varying width (FWHM), scaling and shift parameter. We allowed the shift parameter to vary to accommodate for negative phase-specified coherence values. On the other hand, Shmuel and colleagues tested two versions of the cumulative Gaussian model. Using three parameters to accommodate Gaussian centre, width, and scaling; or using two free parameters, assuming the edge of the responding region coincides with the edge of the stimulated region.

Lastly, in the current approach we estimate phase-specified coherence and cortical distance at the surface level (for each node on the surface mesh). This, combined with the sub-millimetre resolution acquisition and modelling, allows us to estimate PSFs along cortical depth. Shmuel and colleagues estimated the PSF in voxel space which encompassed a flat part of cortex in human V1.

2.6.3. Validation using anatomical data

In a previous publication we show that human V2 stripes are visible in the underlying anatomy (Dumoulin et al., 2017). We validated our modelling approach fitting T1-w signal to the corresponding cortical distance.

T1-w signal is correlated with phase specified coherence, but the relationship is not perfect (Dumoulin et al., 2017). For this reason, for our validation we re-computed cortical distance based on T1-w signal. The same procedure, estimating the border between two consecutive V2 stripes and the same equations were used to fit the T1-w data. With T1-w data, the parameters were free to vary along a larger range of values, to accommodate the different scaling between the phase specified coherence and T1-w signal. For example, the T1-signal could vary approximately between in the range of [−300, 300] (a.u.), thus the scaling and shift parameters could vary within a larger range, compared to phase specified coherence. Other that this difference, all other aspects of the modelling were identical between the two modalities. See Discussion, 4.3 Anatomical Width for a comment of the different interpretation of the estimated FWHM parameter between the two modalities. In brief, the FWHM fitted on T1-w signal cannot be interpreted as a measure of signal spread, as anatomical features per se do not spread and are not affected by the presence of large draining veins. However, the fitted FWHM for T1-w signal is a useful measure that represents the anatomical variability of the T1-w signal along successive V2 stripes in the absence of venous spread. In the absence of a draining component we hypothesized that the FWHM estimate for T1-w data will remain constant along cortical depth. Note that from now on we refer to the FWHM parameter estimated from T1-w signal as ‘anatomical width’.

2.6.4. Fitting model parameters.

We fit the model described in Eq. 4 to derive an estimate of the scaling parameter, the shift parameter and sigma (σ) for each participant and V2 ROI. We obtained an estimate of Gaussian FWHM applying Eq. 5 to the sigma parameter (σ) for phase specified coherence (GE BOLD) and the T1-w signal.

We ran the model using the software R using an optimization technique (‘optim’ function), selecting the parameters that minimize the sum of squares between our model and the observed data (binned phase-specified coherence / T1-w data along binned cortical distance, see Fig. 4C for example data from a portion of V2, phase-specified coherence).

Fig. 6A shows model fits from the entire V2 at three different levels along cortical depth for one participant. Moving along cortical depth, from WM towards the GM surface, we observe a noticeable difference in the rate of change of phase specified coherence as a function of cortical distance, with a faster rate of change close to the WM and a relatively slower rate of change close to the CSF surface. On the other hand, the rate of change of the T1-w signal remains approximately constant between WM and CSF surface (Fig. 6B).

Figure 6.

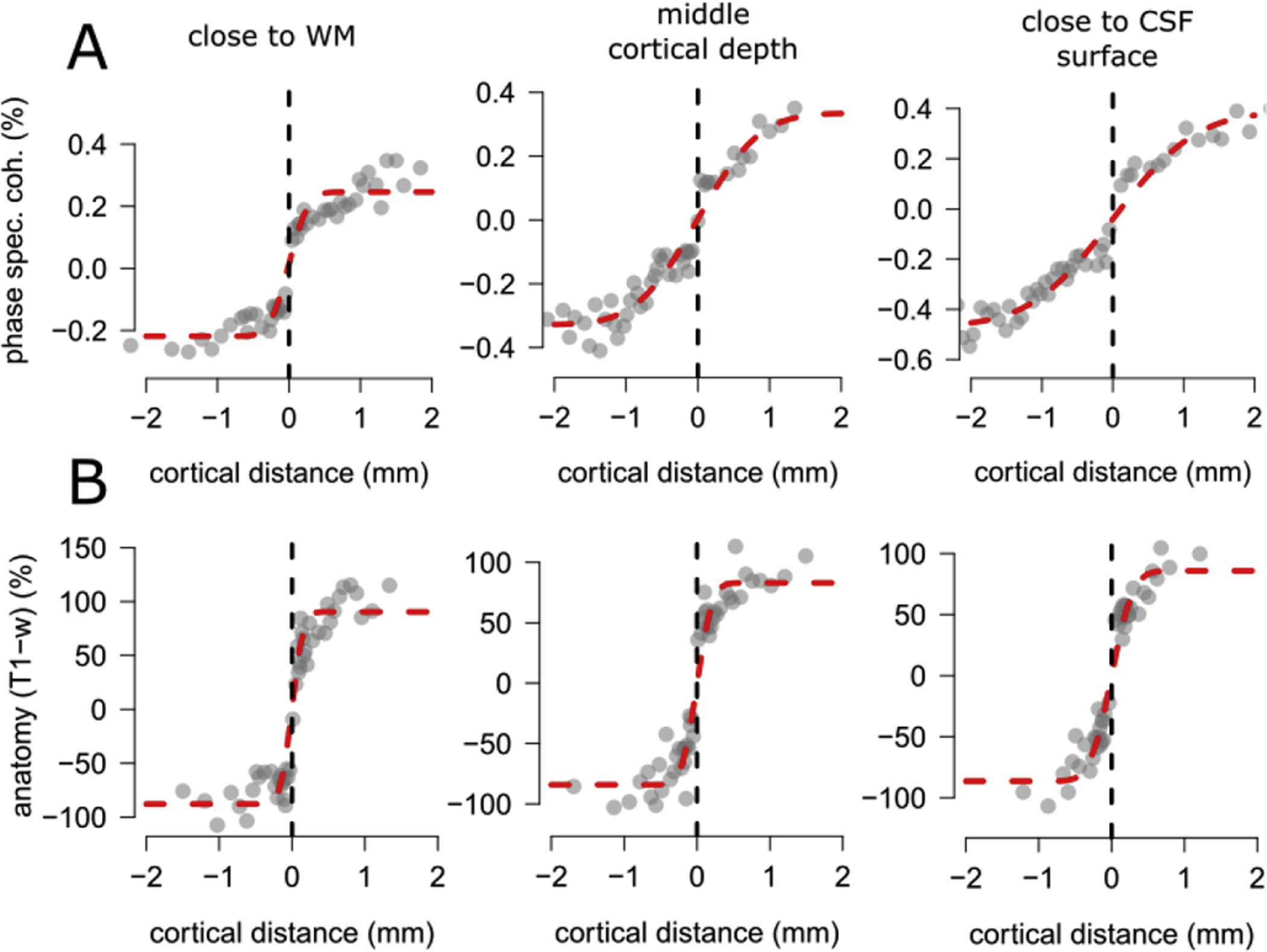
Example fit from the entire V2 from one participant at three different levels along cortical depth (close to WM, around the middle of cortical depth and close to GM surface, see panel titles). Panel A: In the first row we report results from the phase specified coherence. Moving along cortical depth, from WM towards GM surface we notice a difference in the rate of change of phase specified coherence as a function of cortical distance, with a faster rate of change close to the WM and a relatively slower rate of change close to the CSF surface. Panel B: In the second row we report results from the T1-w signal. Moving along cortical depth, from WM towards GM surface we notice an approximately constant rate of change of T1-w signal as a function of cortical distance, between WM and GM surface.

2.7. Statistical analysis

To investigate the relation between the estimated parameters and cortical depth, we performed two separate general linear model analyses.

In the first analysis we tested individually for each participant whether FWHM scales linearly with normalized cortical depth. In this way we obtained an estimate of the intercept and slope of the modelled parameters along cortical depth, at the individual participant level (see Table 1). In the second analysis we pooled parameter estimates from the individual participants in a single analysis (FWHM, scaling and shift parameter), to assess the robustness of the intercept and slope along cortical depth obtained at the single participant level. To account for individual participant variability, we used a generalized linear model with participants as a random factor (see Table 1). The same statistical analysis was performed on the parameters estimates from the T1-w signal, see Table 2 for individual and population results.

Table 1.

summary of the modelled parameters along cortical depth for phase specified coherence. Intercept and slope (Int and sl, respectively) estimates are reported for each participant as well as for the whole dataset.

	P1	P2	P3	P4	All
Gaussian FWHM (GE BOLD PSF)	Int. 0.71** sl: 0.82*	Int. 0.69* sl: 0.91*	Int. 0.92* sl: 1.22*	Int. 0.98*** sl: 0.86***	Int. 0.83*** sl: 0.95***
Scaling parameter	Int: 0.36*** sl: 0.33***	Int: 0.43*** sl: 0.19*	Int: 0.37*** sl: 0.24**	Int: 0.57*** sl: 0.36***	Int: 0.43*** sl: 0.28***
Shift parameter	Int: −0.18*** sl: −0.18***	Int: −0.21*** sl: −0.09	Int: −0.16*** sl: −0.12**	Int: −0.26*** sl: −0.17**	Int: −0.20*** sl: −0.14***

^{* :}significant at the 0.05 level;

^**significant at the 0.01 level;

^{*** :}significant at the 0.001 level.

The sign of the slope indicates whether the parameter (say FWHM) is increasing or decreasing along depth. Overall GE BOLD PSF is maximal in the superficial part of the cortex, and it decreases with increasing cortical depth. Estimates of GE BOLD PSF range from 0.83 mm close to the WM-GM border, to 1.78 mm (0.83mm+0.95mm) closer to the GM/CSF border. The scaling and shift parameters also scale with normalized cortical depth. The former shows a positive linear relationship, with smaller values observed towards WM surface and larger values towards the GM/CSF boundary, the latter shows negative values, with a negative linear relationship with normalized cortical depth, with larger values observed towards WM surface and smaller values towards the GM/CSF boundary.

Table 2.

summary of the modelled parameters along cortical depth for T1-w data. Intercept and slope (Int and sl, respectively) estimates are reported for each participant as well as for the whole dataset.

	P1	P2	P3	P4	All
Gaussian FWHM (T1-w signal)	Int. 0.08* sl: 0.09	Int. 0.11** sl: 0.10	Int. 0.20 sl: 0.15	Int. 0.26** sl: −0.05	Int. 0.38*** sl: 0.17
Scaling parameter	Int: 74.35*** sl: 25.89	Int: 109.24*** sl: −3.97	Int: 49.22*** sl: 12.01	Int: 147.30*** sl: −6.99	Int: 223.79*** sl: 15.86
Shift parameter	Int: −37.36*** sl: −12.62	Int: −54.69*** sl: −2.33	Int: −25.52*** sl: −6.24	Int: −74.30*** sl: 3.65	Int: −117.97*** sl: −7.57

^{* :}significant at the 0.05 level;

^**significant at the 0.01 level;

^{*** :}significant at the 0.001 level.

FWHM, scaling parameter and shift estimated from T1-w signal all remain constant along normalized cortical depth at the single participant level as well as across all participants.

3. Results

3.1. Reconstructing V2 stripes along cortical depth

We recorded fMRI responses while participants viewed concentric gratings with contrast reversing at slow or fast rate (1.5 Hz or 7.5 Hz, respectively). We derived a measure of fMRI response frequency and phase in response to the stimuli, adjusted for the hemodynamic delay (the phase-specified coherence). The values ranged between −1 and 1; positive values reflect stronger responses to the slow-rate stimulus (1.5 Hz) and negative values reflect stronger responses to the fast-rate stimulus (7.5 Hz).

In V2, GE BOLD responses vary in a systematic fashion, i.e. there is an interleaved series of stripes that respond preferentially to slow or fast temporal frequencies. Based on visual inspection, these appear to line up into stripes orthogonal to the V1/V2 border and end at the V1/V2 border (see Fig. 7 for all participants).

Figure 7.

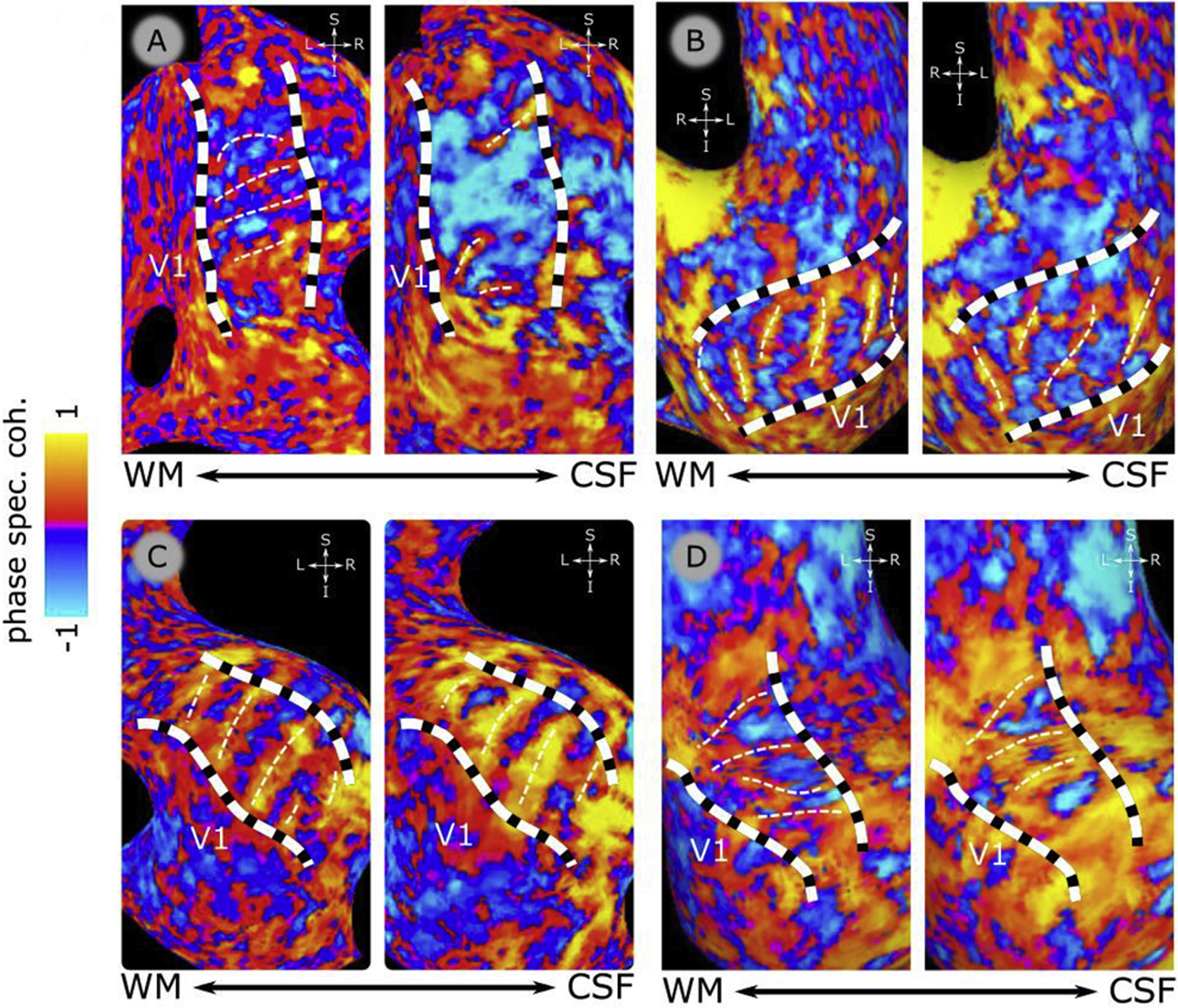
Functional delineation of V2 stripe-based subdivisions. Panels A, B, C & D show phase-specified coherence responses over inflated cortical surfaces for each participant (P1–P4, respectively). On each panel, 2 inflated cortical surfaces are shown, for a location close to WM (on the left of each panel) and a location close to CSF, (on the right of each panel). Panels show the zoomed view of the dorsal occipital lobe with the identified V2 borders (dashed black and white, thick lines). The color bar indicates the phase-specified coherence values, indicating responses dominated by “fast” (7.5 Hz, blue) or “slow” (1.5 Hz, orange) temporal frequencies. White thin dotted lines indicate the manual delineation of the stripes based on the peak of 1.5hz (orange) preference. The location of primary visual cortex (V1) is indicated on each surface.

GE-BOLD also changes systematically across cortical depth as reflected in the coherence which increases monotonically across cortical depth. This is a known behaviour of GE-BOLD due to the draining effect of large pial veins, reflected here on the trend of the scaling parameter along cortical depth (Table 1, scaling parameter).

3.2. BOLD PSF is maximal in the superficial part of the cortex

We observed a positive linear relation between the FWHM estimated from the GE-BOLD data and normalized cortical depth at the single participant level as well as across all participants (Table 1).

Portions of cortex closer to the WM boundary were characterized by a PSF of approximately ~0.8mm, compared to estimates from locations closer to the CSF surface, yielding PSF estimates of approximately ~1.8mm, Figure 8. This linear increase could be expected given the known draining effects of GE BOLD, driven by the influence of large pial veins located at the level of pial surface, leading to marked BOLD gradients towards the pial surface known from the literature (Chen et al., 2013; De Martino et al., 2013; Fracasso et al., 2018; Fracasso et al., 2016a; Havlicek and Uludag, 2020; Kashyap et al., 2018b; Kim and Ress, 2017; Klein et al., 2018a; Lawrence et al., 2019; Siero et al., 2011; van Dijk et al., 2020).

Figure 8.

PSF estimates across cortical depth. Panels A-D, PSF estimates for GE-BOLD across cortical depth (x-axis: 0.0, WM surface, 1.0 GM/CSF border), for each participant (P1–P4), dotted lines indicate best fitting linear relations based on least-square estimation. Panel E. same as A-D, with all participants grouped together. This plot indicates that BOLD PSF is maximal in the superficial part of the cortex, and it decreases with increasing cortical depth. GE-BOLD PSF range from 0.83 mm close to the WM-GM border, to 1.78 mm close to CSF (see Table 1).

The scaling and shift parameters also change along cortical depth. The scaling parameter shows a positive linear relationship with normalized cortical depth, with smaller values observed towards the WM surface and larger values towards the GM/CSF boundary. The shift parameter shows negative values, with a negative linear relationship with normalized cortical depth, with larger values observed towards the WM surface and smaller values towards the GM/CSF boundary (Table 1).

The larger BOLD signal generally observed at the level of the pial surface is reflected in the increasing value of the scaling parameter necessary to accommodate our model to the observed data along cortical depth (Fig. 6A and Table 1, scaling parameter). A similar reasoning can be applied to the shift parameter. The CGF_m model (Eq. 4) with a shift of 0 and a scaling parameter of 1 (Fig. 5A, black line). The phase-specified coherence along cortical depth ranges from negative to positive values (see Fig. 4C and 6A). To accommodate the data, the shift parameter naturally gears towards negative values (Table 1). At the same time, moving along cortical depth, the shift also needs to accommodate for larger phase-specified coherence level, so it tends to become more negative closer to the GM/CSF boundary.

FWHM, scaling parameter and shift estimated from the T1-w signal all remain constant along normalized cortical depth at the single participant level as well as across all participants (see Figure 9 and Table 2). For each surface, the T1-w signal was de-meaned and de-curved (see section 2.5 Segmentation and surfaces), thus this pattern of results along cortical depth was expected for the scaling and shift parameters.

Figure 9.

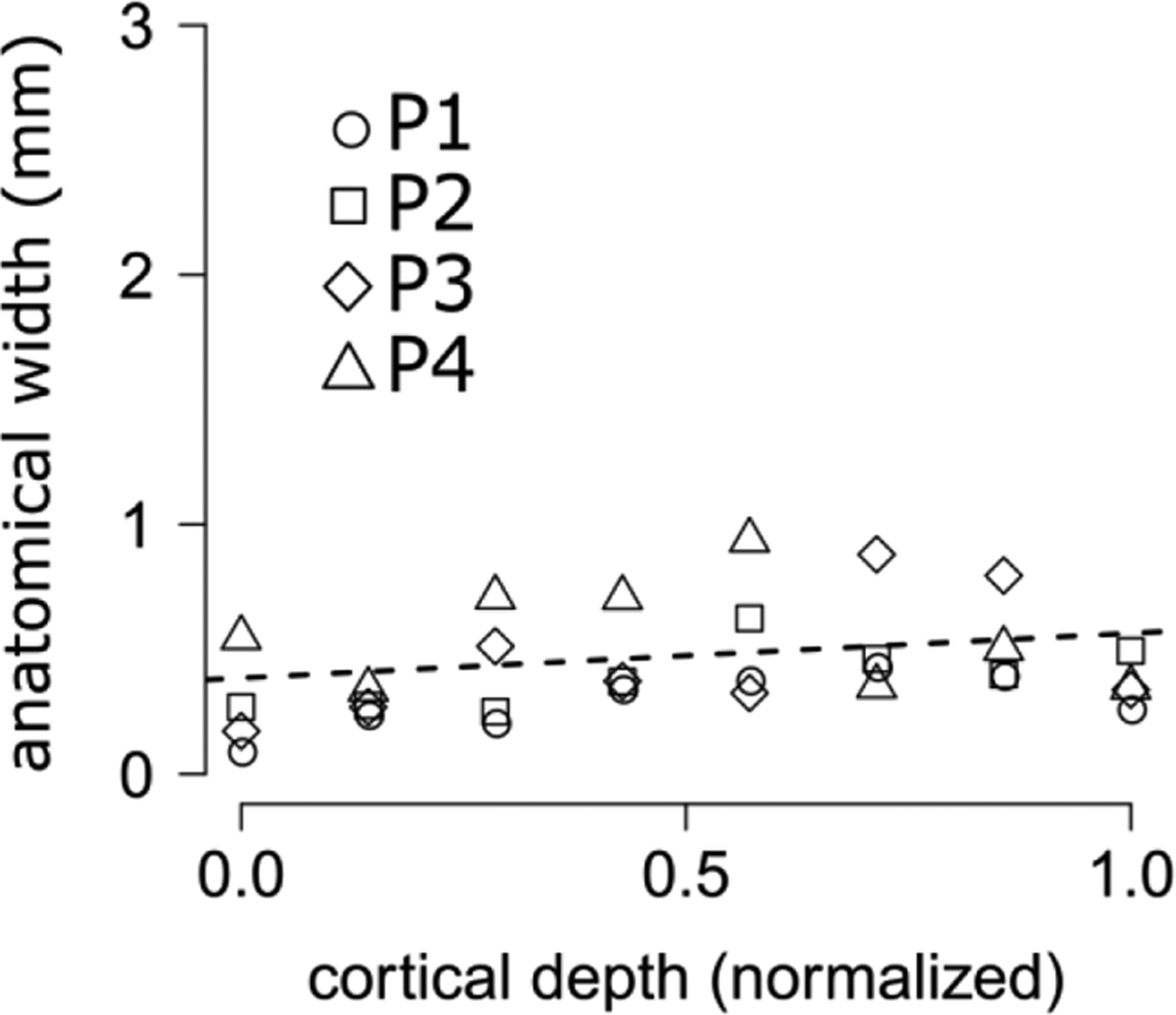
anatomical variability between successive V2 stripes in humans, estimates across cortical depth (x-axis: 0.0, WM surface, 1.0 GM/CSF border). Dotted lines indicate best fitting linear relations based on least-square estimation; all participants grouped together. This plot indicates that anatomical variability between successive stripes remains approximately constant across cortical depth, around a value of 0.38mm (see Table 2).

Results for the FWHM along cortical depth are interesting as they represent the anatomical variability of T1-w signal along successive V2 stripes in the absence of venous spread, thus providing a validation of our modelling approach (the estimate remains constant along cortical depth, Figure 9).

4. Discussion

The ability of high-resolution BOLD fMRI to accurately resolve the columnar and layered organization in human neocortex is determined by the point-spread function of the BOLD response in relation to the spatial extent of neuronal activity. However, this spatial extent is typically not known, making it difficult to accurately estimate the BOLD PSF. In this study we obtained functional estimates of the BOLD PSF using sub-millimetre GE BOLD fMRI data acquired at 7T and taking advantage of the stripe-based organization of visual area V2.

GE BOLD PSF is maximal in the superficial part of the cortex, and it decreases with increasing cortical depth. Portions of cortex closer to the WM boundary are characterized by a PSF of approximately ~0.8mm, compared to estimates from locations closer to the CSF surface, yielding PSF estimates of approximately ~1.8mm. This linear increase could be expected given the known draining effects of GE BOLD, driven by the influence of large pial veins, leading to marked BOLD gradients towards the pial surface (De Martino et al., 2013; Fracasso et al., 2018; Havlicek and Uludag, 2020; Kashyap et al., 2018a; Koopmans et al., 2010; Koopmans et al., 2011; Olman et al., 2012). The anatomical width, that is, anatomical variability between successive V2 stripes (in the absence of a draining component) remains constant along cortical depth, thus validating our modelling approach.

4.1. GE BOLD PSF

In this study we measured the stripe-based organization of visual area V2 to obtain BOLD PSF estimates along cortical depth in human participants. Taking advantage of the fine-grained organization in early visual cortex is advantageous compared to the classical PSF estimation based on V1 retinotopy as it is largely unaffected by several sources of variability such as receptive field scatter and size (Chaimow et al., 2018b; Hetherington and Swindale, 1999).

Recent studies (Chaimow et al., 2018a; Chaimow et al., 2018b) estimated the BOLD PSF taking advantage of the inherent fine-scale organization of ocular dominance columns in primary visual cortex. Using previously published data (Yacoub et al., 2008; Yacoub et al., 2007) these authors modelled the observed ODC patterns using a generative approach, measuring the blurring kernel added to the underlying ODCs pattern as an estimate of PSF independent of neuronal receptive field size and scatter, for both GE and SE BOLD fMRI.

In the present study we measure GE BOLD PSF from the rate of change in phase-specified coherence occurring at the border between successive V2 stripes in humans (Fig. 4,5,6).

V2 stripes were identified using the phase specified coherence to high or low temporal frequencies. Phase specified coherence is ideally suited to identify V2 stripes. In our experimental design, a positive phase specified coherence value indicates a preference for a relatively low temporal frequency, a negative phase specified coherence value indicates a preference for a relatively high temporal frequency. A phase specified coherence of 0 indicates the shift between a preference for low and high temporal frequency. Hence, 0 demarcates the border between different stripes in human V2.

The specific organization of the vasculature across cortical depth leads to systematic GE BOLD signal changes along this dimension. Potentially, simple differences in GE BOLD signal change could be wrongly ascribed to true differences in GE BOLD PSF. In Fig. 5 we show an example of a potential difference in the rate of change of phase-specified coherence along cortical distance between two conditions. The parametrization used in our modelling approach allows to disentangle between different components of GE BOLD PSF, reducing the risk of incurring in spurious PSF estimation due to, for example, changes in signal increase instead of PSF width.

We report an average GE BOLD PSF across participants on the order of 0.83mm (close to WM) to 1.78mm (close to the pial surface), These values are compatible with those reported by Chaimov and colleagues across ODCs (Chaimow et al., 2018b) (between 0.8mm and 1.31mm across different participants). We postulate that GE BOLD measurements can resolve the underlying spatial organization with an accuracy below 1mm deeper in the cortex and become blurred closer to the pial surface.

4.2. V2 stripes

Phase-specified coherence allows us to identify two subdivisions in human V2 (see Figure 7). On the other hand, previous neurophysiology studies distinguish three types of stripes (Horton, 1984; Livingstone and Hubel, 1982; Tootell et al., 1983). In a previous publication (Dumoulin et al., 2017) we interpret our stripe-based subdivisions as collapsing two stripe types into one, speculating that our subdivisions distinguish ‘thick’ versus ‘thin’ and ‘pale’ stripes combined. This speculation is based on previous non-human histological observations suggesting that ‘thick’ stripes in V2 receive a larger projection from layer 4B in V1, dominated by magnocellular input (Shipp and Zeki, 2002; Sincich and Horton, 2005a).

4.3. Anatomical Width

Analysis of T1-w signal was performed for validating our modelling approach. Although we adopt the same modelling strategy for GE BOLD and T1-w signal, it is important to note that the interpretation of the FWHM parameter differs between the two modalities. The fitted FWHM for GE BOLD can be interpreted as an estimate of BOLD PSF, that is the spreading of BOLD signal largely due to the action of draining veins, in response to an otherwise localized neuronal activity (Uğurbil et al., 2003).

On the other hand, the same parameter fitted for the T1-w signal cannot be interpreted as a measure of signal spread, as anatomical features per se do not spread and are not affected by the presence of large draining veins. However, the fitted FWHM for T1-w signal is a useful measure that represents the anatomical variability (‘width’) of the T1-w signal along successive V2 stripes in the absence of venous spread.

We find that anatomical width is about 0.4mm. It is important to highlight that this parameter remains flat along cortical depth, thus providing a validation for our analysis pipeline. Furthermore, the anatomical variation of about 0.4mm might reflect the acquisition resolution of the anatomical data (0.5mm isotropic), so it is possible that voxel size drives the estimates of anatomical width.

4.4. BOLD across cortical depth

One dominant challenge of measuring fMRI signal across cortical depth relates to the cortical vascular organization. While fMRI detects hemodynamic consequences of neuronal activity (Heeger et al., 2000; Logothetis, 2002), the vasculature has a specific organization across cortical depth: blood flows from pial and intracortical arteries and arterioles to the capillary bed, then is drained via venules and intracortical veins to larger pial veins at the cortical surface (Dumoulin et al., 2018; Duvernoy et al., 1981; Kashyap et al., 2018b; Turner, 2002). This specific vascular architecture explains the finding that BOLD signal amplitude is smaller at the WM/GM surface and systematically increases toward the pial surface (Chen et al., 2013; De Martino et al., 2013; Fracasso et al., 2018; Fracasso et al., 2016a; Kim and Ress, 2017; Klein et al., 2018a; Lawrence et al., 2019; Siero et al., 2011; van Dijk et al., 2020), see also Table 1, scaling parameter, slope.

Considering this vascular architecture across cortical depth and how BOLD signal is affected by it, it is important to note that in the current study we report measures of GE BOLD PSF that are tangential to the cortical surface, i.e. across columns (stripes). As pointed out by Polimeni and colleagues (2010) (Polimeni et al., 2010), the tangential PSF may be potentially distinct from the PSF orthogonal to the cortical surface. For example, veins penetrating the cortex could corrupt the PSF across cortical depth while leaving unaltered the tangential PSF. On the other hand, the presence of vessels of relatively large size at the pial surface leads to a corruption of the tangential PSF but may leave the PSF orthogonal to the cortical surface unaltered. Moreover the tangential and orthogonal PSFs could differently affect different voxels, leading to heterogeneous blurring voxel profiles (Kriegeskorte et al., 2010). The two distinct PSFs (tangential and orthogonal) may potentially be observed if the temporal resolution of the measurements is sufficiently high (<<1s) to capture the flow of blood through the (intra)cortical vascular tree upon neuronal activation, avoiding blood pooling in the different venous vessels across cortical depth (Petridou and Siero, 2019). In our experiments each time point was acquired every 2.6s and our PSF estimates reflect the influence of the PSF orthogonal to the cortical surface, as a function of cortical depth. These estimates may be useful for mathematical models of the laminar BOLD PSF that are aimed to correct for the BOLD signal bias toward the pial surface (Havlicek and Uludag, 2020; Markuerkiaga et al., 2016).

4.5. Methodological considerations

4.5.1. The equi-volume model

In this investigation we acquired signal along cortical depth combining sub-millimeter resolution data acquisition, accurate anatomy-functional co-registration, and the generation of multiple intermediate surface reconstructions between the WM boundary and the GM surface.

We could measure GE BOLD fMRI over multiple surfaces that could be processed independently, along cortical depth. A volume-preserving distance map was computed between the WM/GM boundary and the GM/CSF boundary (Waehnert et al., 2016; Waehnert et al., 2014) in 8 steps. This equi-volume model provides a coordinate system of cortical depth which is independent from local cortical folding. The relative thickness of the supra- and infra- layers scales with local curvature and varies over the cortex. The supra-granular layers are thinner within the top of a gyrus and thicker at the bottom, the opposite is true for the infra-granular layers (Fatterpekar et al., 2003; Hilgetag and Barbas, 2006; Van Essen and Maunsell, 1980). Moreover, cortical thickness also varies across the folds which are generally thicker at the top of a gyrus and thinner at the bottom (fundi of sulci) (Fischl and Dale, 2000). The equi-volume model takes these associations between local curvature and thickness into account (given the limitations of the data acquisition resolution) and it represents a good predictor for the location of landmark anatomical features as the stria of Gennari (Waehnert et al., 2016; Waehnert et al., 2014).

It is important to note that an acquisition resolution of about 0.9mm isotropic would at best give us the capacity to measure 2–3 different compartments, assuming a 2mm / 3mm cortical thickness, respectively. However, in Figure 8, we report eight different GE BOLD PSF estimates along normalized cortical depth. We can obtain more that 2–3 different PSF estimates along cortical depth thanks to the folded nature of cortical surface. When measuring MRI signal along cortical depth, we are using a regular grid (the FOV of the acquisition resolution, 0.9×0.9×1mm) to sample signal from an irregular (folded) portion of the cortex. Thus, the centre of a voxel on the regular grid could be located close to the WM surface, close to the CSF surface or anywhere between the two. This comes at the cost of partial volume effects that can especially influence voxels located at the edge of the grey matter (close to the WM surface, close to the CSF surface), and we acknowledge this limitation. From an ROI, taking advantage of the irregular cortical folding, we can sample continuously along cortical depth, obtaining more than 2–3 signal estimates along cortical depth.

4.5.2. Blurring

The accurate estimation of the BOLD PSF is contingent on minimal blurring introduced from data acquisition sampling. The T2* signal decay during data acquisition can cause blurring along the phase encode direction in GE-EPI, which reduces the effective spatial resolution of the images and can introduce blurring in the measured BOLD signal. This effect can be minimized by setting the data acquisition read-out duration equal to the T2* of tissue (Haacke et al., 1999). The read-out duration employed here was 26ms, approximately equal to the T2* of gray matter at 7T (Uludag et al., 2009) which yields a minimal estimated blurring in the phase encode direction of ~2% (Haacke et al., 1999). The impact of this potential blurring on the estimated PSFs is expected to be very small.

4.5.3. Comparison between the current modelling approach and (Shmuel et al., 2007).

The method adopted in (Shmuel et al., 2007) inspired us to implement the modelling analysis used in the current manuscript.

While there are several differences between our model and Shmuel and colleagues (see section 2.6.2), these are introduced to account for the different dependent variable adopted in this study and be able to obtain an estimate of PSF along cortical depth. The main difference between our approach and Shmuel et al., is in the nature of the boundary adopted to measure PSF. In both cases we are in the presence of a functionally defined boundary. However, Shmuel and colleagues take advantage of the retinotopic organization in human primary visual cortex, whereas in the current investigation we take advantage of a different organizational principle, the stripe-based arrangement present in human V2, and validate the model using anatomical data. It is important to point out that there is a discussion as to whether vascularisation is similar between V1 and V2. (Duvernoy et al., 1981; Weber et al., 2008).

4.6. Conclusions

Here we took advantage of the high resolution acquisition afforded at UHF and the stripe-based organization in visual area V2 to obtain BOLD PSF estimates along cortical depth in human participants.

We observed that GE BOLD PSF estimates increase linearly toward the pial surface. Portions of cortex closer to the white matter boundary are characterized by smaller PSF (~0.8mm on average, see Table 1, Figure 8) compared to estimates from locations closer to the pial surface (~1.8mm on average, see Table 1, caption and Figure 8). We postulate that GE BOLD measurements can resolve the underlying neuronal spatial organization with an accuracy below 1mm deeper in the cortex with this spatial specificity degrading closer to the pial surface. Our results provide an estimate of functional PSFs along cortical depth in human participants, useful for studies aimed at probing fine-scale cortical organizations in human neocortex.

Highlights.

• We measured sub-millimetre, 7T T1-weighted and BOLD and reconstructed V2 stripes;

• We used the functionally defined borders of the V2 stripes to compute the BOLD point-spread function (PSF) across cortical depth;

• BOLD PSF increases linearly across cortical depth, ranging between 0.83mm to 1.78mm;