Modeling interaction and dispersion effects in the analysis of gene-by-environment interaction

Abstract

Background:

Genotype-by-environment interaction (GxE) studies probe heterogeneity in response to risk factors or interventions. Popular methods for estimation of GxE examine multiplicative interactions between individual genetic and environmental measures. However, risk factors and interventions may modulate the total variance of an epidemiological outcome that itself represents the aggregation of many other etiological components.

Methods:

We expand the traditional GxE model to directly model genetic and environmental moderation of the dispersion of the outcome. We derive a test statistic, ξ, for inferring whether an interaction identified between individual genetic and environmental measures represents a more general pattern of moderation of the total variance in the phenotype by either the genetic or the environmental measure.

Results:

We validate our method via extensive simulation, and apply it to investigate genotype-by-birth year interactions for Body Mass Index (BMI) with polygenic scores in the Health and Retirement Study (N=11,586) and individual genetic variants in the UK Biobank (N=380,605). We find that changes in the penetrance of a genome-wide polygenic score for BMI across birth year are partly representative of a more general pattern of expanding BMI variation across generations. Three individual variants found to be more strongly associated with BMI among later born individuals, were also associated with the magnitude of variability in BMI itself within any given birth year, suggesting that they may confer general sensitivity of BMI to a range of unmeasured factors beyond those captured by birth year.

Discussion:

We introduce an expanded GxE regression model that explicitly models genetic and environmental moderation of the dispersion of the outcome under study. This approach can determine whether specific GxE interactions identified are specific to the measured predictors or represent a more general pattern of moderation of the total variance in the outcome by the genetic and environmental measures.

1. Introduction

A major goal for epidemiology and public health is to identify measurable factors that predict otherwise unexplained variation in susceptibility or response to environmental risk factors and interventions. Genotype-by-Environment (GxE) interaction studies [1, 2, 3, 4]—which test whether the genotype-phenotype association varies in magnitude across the range of a measured environmental variable (alternatively, whether the environment-phenotype association varies in magnitude across the range of the measured genotype)—are often pursued with this goal in mind. If so, the genotype (alternatively, environment) may serve as an explanatory factor for the variation in susceptibility. It is common for GxE research to interpret any interaction identified between genetic and environmental measures as specific to that pair of variables. However, it may often be the case that identified GxE interactions represent more general patterns of sensitivity of genetic or environmental effects on the outcome to a broad range of factors. Note that our focus here is on the interplay between genetic and/or environment variables and the distribution of the outcome, which is distinct from other types of confounding in GxE that have been raised (e.g., regarding how to properly control for measured confounders in GxE [5]).

Consider the empirical question we focus on here. Suppose a polygenic score [6] is found to be increasingly predictive of a phenotype across birth years. Is it specifically the polygenic score that increases in its predictive power across birth years? Or would many different correlates of the phenotype also increase in their level of prediction of the phenotype across birth year, as would be evidenced by more general changes in the dispersion of the phenotype across birth years? By directly modeling trends in the total variance in the phenotype across birth years we can distinguish between these alternatives.

We develop a formal modeling framework for testing whether an identified GxE interaction represents a pattern specific to the genetic and environmental variables under study, or a more general pattern. In particular, we consider circumstances in which the genetic and/or the environmental measure is associated with the magnitude of variance in the outcome. We expand the standard model for testing GxE (in both single locus and polygenic score settings) to include moderation of the dispersion of the outcome in the form of heteroscedastic residuals. We develop a test statistic for inferring whether an identified GxE between specific genetic and environmental measures represents to a more general effect of the genetic or environmental moderator on the dispersion of the phenotype.

Distinguishing whether an identified GxE interaction is specific to the pair of variables under study versus an instance of a more general pattern is critical to understanding the mechanisms driving the interaction and to policy implications of the effect. All else being equal, when the dispersion of a phenotype is directly controlled by the level of the moderator, the standard regression-based model will identify a significant interaction between that moderator and any correlate of the phenotype, whether genetic or non-genetic. For example, when the effectiveness, intensity, or dosage of a phenotype-altering intervention varies proportionally to baseline levels of the phenotype, then the variance of the phenotype will increase in response to the intervention, and the unstandardized effect sizes for all correlates of baseline levels of the phenotype are expected to increase.

Similarly, when a genetic variant confers greater plasticity in a phenotype, then the variance of the phenotype is expected to differ across alleles (i.e., the variant is a variance quantitative trait locus, vQTL). We would then expect the variant to moderate the effect sizes for all correlates of that phenotype proportionally to their main effects, and a policy or intervention would be most likely to benefit from targeting a suite of determinants of the outcome rather than focusing efforts on the specific predictor studied. Only when a moderator acts preferentially on specific mechanisms of variation in the phenotype are interactions with various predictors expected to depart from expectations that follow from differences in total variance across the range of the moderator. In such circumstances, a policy or intervention that is more specifically targeted may be justified. GxE findings driven by more general moderation of the distribution of the outcome may not justify such interventions. We expect that these questions will be germane to a wide range of GxE investigations, including those relying on individual loci, standard polygenic scores, and “variance polygenic scores” [7, 8] which are derived from vQTL discoveries.

Figure 1 illustrates how GxE can result from heteroscedasticity. At left, we illustrate a scenario in which a polygenic score (PGS) is associated with a constant proportion of variance in the phenotype across the range of the measured environment, but the total variance in the phenotype increases across this range. This indicates that the expected percentile location within the distribution of the phenotype will also be constant across the range of E (assuming that the shape, but not dispersion, of the distribution remains constant across the range of E). At right, we consider an analogous scenario with respect to a single genetic variant that moderates the variance of the phenotype (i.e a vQTL [9, 10, 11, 12, 13]). In both panels, we can observe increasing differentiation of scores on the phenotype across levels of the genetic or environmental predictor, even though the predictor is associated with a constant proportion of variance in the phenotype across the range of the moderator. By directly modeling the heteroscedasticity, we are able to distinguish between scenarios in which GxE represents this general pattern of variance modulation from those representing more specific patterns of GxE. Note that heteroscedasticity has traditionally led to concerns about inaccurate standard errors [14]. This is an important concern, especially because GxE effects are often small. However, our goal here is not merely to obtain more accurate standard errors but rather to directly model the heteroscedasticity in order to gain substantive insight.

Figure 1:

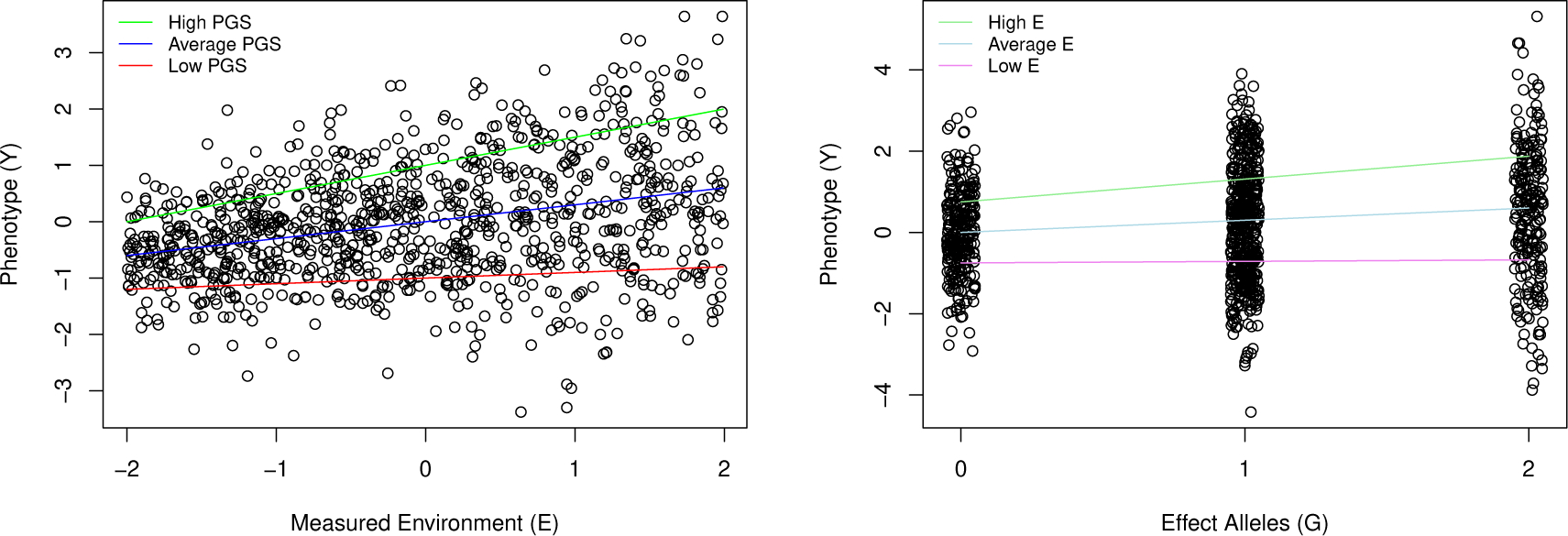
Hypothetical examples of an Environmental moderator (left) or a genetic moderator (right) of total variance in a phenotype producing the impression of GxE. Left: Residuals of the regression of the Phenotype on the Measured Environment are heteroscedastic. high, average, and low polygenic scores (PGSs) are associated with constant percentiles of the phenotype at any given location along the x axis. However, because variance of the phenotype expands across the range of the Measured Environment, the PGS accounts for increasing unstandardized variance across this range. Right: A variance quantitative trait locus (vQTL) in which the effect allele is associated with greater variance in the phenotype. Unstandardized scores on the phenotype that are associated with high, average, and low levels of the measured environment (E) become more distinct with increasing number of effect alleles. However, because the total variance in the phenotype expands across the x axis, the percentile locations of these scores within each genotype (0, 1, or 2) is constant across all levels of the genotype.

After expanding the traditional GxE model to directly model genetic and environmental moderation of the total dispersion of the outcome, we use this model to elucidate the interaction between birth cohort and genetics linked to body mass index (BMI). We test whether observed interactive associations with BMI represent a more general increases in the total dispersion of BMI over historical time. That is, we ask whether birth year is associated specifically with amplification of genetic risk for BMI or more generally with amplification of total variation in BMI.

2. Methods

With a measured genotype, as indexed by a single-locus allele count or a polygenic score (PGS), the standard model for GxE is

$$Y_i={\beta }_0+{\beta }_1{G}_i+{\beta }_2{E}_i+{\beta }_3{G}_i\cdot E_i+e_i,$$ (1)

where Y_i is the phenotype for person i, G_i is the genotype, E_i is the environment, and e_i is an error term. Here, the effect of G_i on Y_i is allowed to vary as a linear function of E_i, as indexed by the regression coefficient β₃. However, a crucial assumption is that the residuals, e_i, are homoscedastic across all levels of $E_i:e_i~\text{N}\left(0,{\sigma }_{ϵ}^2\right)$.

This model (Eqn 1) can be expanded so as to relax the assumption of homoscedasticity of residuals across E_i by specifying the following environmental heteroscedasticity model,

$$Y_i={\tau }_0+{\tau }_1{E}_i+{\pi }_0{G}_i+{\pi }_1{G}_i\cdot E_i+{\lambda }_0{ϵ}_i+{\lambda }_1{E}_i\cdot {ϵ}_i.$$ (2)

Here, τ₁ is the main effect of the measured environment, π₀ is the main effect of G_i, π₁ is the analogue to β₃ in Eqn 1, λ₀ is the main effect of the error ϵ_i (which we assume, without loss of generality given λ₀, to have unit variance), and λ₁ is the coefficient used to index heteroscedasticity. Rather than simply adjusting standard errors and p values of the standard model using a robust estimation method, this model explicitly estimates heteroscedasticity as a model parameter. Such direct modeling of heteroscedasticity allows us to overcome specification bias that would result from estimating a standard homoscedastic GxE model, even with a robust estimator. It allows us to plot, for example, moderation of variance explained by the genetic predictor as a proportion of total variance (both explained plus unexplained variance). Eqn 2 is similar to previous suggestions for modeling heteroscedasticity [15] but note that we are purposeful in choosing a functional form for the heteroscedasticity term, E_i · ϵ_i, that directly parallels the GxE term, G_i · E_i. We provide parallel models for heterogeneity of residuals across G_i (the genetic heteroscedasticity model) and heterogeneity of residuals across both E_i and g_i (the full heteroscedasticity model) in the Supplemental Information (SI; A.3.2).

The heteroscedasticity model is a flexible model allowing for both conventional GxE and heteroscedasticity. In order to test whether this flexibility is necessary, we propose a restricted form version of this model that does not directly include GxE but instead allows for the total variance of the phenotype to vary as a function of E_i. This scaling model represents a scenario wherein GxE—in the sense of a significant estimate of β₃ in Eqn 1—arises as a function of differences in the total variance of Y_i as a function of E_i. We choose this nomenclature given that the model emphasizes the importance of the outcome’s scale. Under this model, the proportional contribution of G_i is constant over the range of E_i, but the scale of Y_i systematically varies across the range of E_i; i.e., E_i acts as a “dimmer” [16].

The scaling model for moderation of the variance of Y_i as a function of E_i takes the form

$$Y_i=a_0+a_1{E}_i+\left(b_0+b_1{E}_i\right)Y_i^{\star }.$$ (3)

Here, $Y_i^{\star }$ is an unobserved factor representing unexplained variation in Y_i incremental of E_i. The b₀ + b₁E_i coefficient on the Y^⋆ term produces heteroscedasticity in Y_i as a function of E_i. We let

$$Y_i^{\star }=h{G}_i+e{ϵ}_i$$ (4)

where G is a measured genotype standardized to have unit variance and ϵ_i is an unobserved error term (we assume it is also scaled to have unit variance). Finally, we identify the units of Y^⋆ by specifying $e=\sqrt{1-h^2}$. The penetrance of the measured genotype is thus controlled via the relative magnitudes of h and e. Note, in particular, that the genotype’s penetrance (in terms of $Y_i^{\star }$) is constant. The test that we introduce relies on this property; i.e., when properly scaled, the penetrance of the measured genotype to Y_i is constant. Suppose that b₁ = 0. In that case, Y_i is affected solely by environmental and genetic main effects. If b₁ ≠ 0, then the role of $Y_i^{\star }$ with respect to Y_i varies as a function of E and so do the raw—but not relative—contributions of G_i and ϵ_i to Y.

We show (SI-A) that the environmental heteroscedasticity model reduces to the environmental scaling model when

$$\frac{{\pi }_0}{{\lambda }_0}=\frac{{\pi }_1}{{\lambda }_1}.$$ (5)

We use this to derive the test statistic ξ_E and associated hypothesis test of whether an empirical estimate of GxE is distinguishable from the scaling model as

$${\xi }_E\equiv \widehat{{\pi }_0}\widehat{{\lambda }_1}-\widehat{{\pi }_1}\widehat{{\lambda }_0},$$ (6)

$$H_0:{\xi }_E=0.$$ (7)

We provide parallel heteroscedasticity and scaling models for moderation of the variance of Y_i as a function of G_i (leading to an analogous test statistic, ξ_G) and illustrate how π₁ can be usefully decomposed into scaling and non-scaling components in SI-A.3.

We conduct a variety of simulation studies (see SI-C). These studies suggest that ξ_E is a reliable indicator of whether the scaling model is the basis for GxE. When a test of the statistic fails to reject H₀ : ξ_E = 0 and there is significant GxE (π₁) observed, we cannot rule out that the scaling model is driving observed GxE. When the test suggests rejection of H₀ : ξ_E = 0, alternative forms of GxE are implicated. Software to estimate the models considered here is described in SI-D. We now apply our heteroscedastic GxE model to the well-studied interaction between birth year and genetics linked to body mass index (BMI) [17, 18, 19, 20, 21], a literal textbook example (see Section 11.3 of [22]).

3. Results

3.1. Data Descriptions

We first test whether previous reports of GxE using a polygenic score can be plausibly attributed to more general increases in the total dispersion of BMI, including variation unique of its genetic etiology, across birth cohorts [23, 24]. We thus ask whether birth year is associated specifically with amplification of genetic risk for BMI or more generally with amplification of all variation in BMI. We consider GxE in the Health and Retirement Study (HRS) [25], a biannual longitudinal study of US adults over 50 (N=11,586). This data has been used in similar previous studies [17, 18, 19]. We use a BMI PGS [26] as constructed by the HRS [27] and analyze mean BMI across all waves. See SI-E for further description of the data.

We then go on to apply our heteroscedastic GxE model to examine individual locus-by-year interactions for BMI. To illustrate how our approach can be used to conduct SNP-level analyses, we apply our technique using the top hits from a recent BMI GWAS [26] to investigate whether they are associated with heteroscedastic GxE. We conducted heteroscedastic regression analyses for 96 marker SNPs for the genome-wide significant loci identified in [26] using independent data from N=380,605 participants from UK Biobank (UKB; not used in the BMI GWAS [26]). Results for all SNPs can be found in Table F.2. The UKB is highly non-representative [28] potentially affecting the generalizability of our results. As with the HRS data, the environmental heteroscedasticity parameter (λ₁) was positive and significant in all models, suggesting greater variance in BMI among those born later in the 20th century. See SI-E for further description of the data.

3.2. Polygenic Score Analysis in the HRS

We first analyze all respondents together and then conduct separate analyses by sex; results are presented in Table 1. Consistent with earlier findings [17, 18, 19], we observe considerable evidence for stronger prediction of BMI by the PGS for more recently born individuals (i.e., π₁ > 0). However, we also observe a birth year-linked increase in non-PGS variance in BMI (i.e., λ₁ > 0); thus, the observed GxE may be attributable to a more general pattern of increasing variance in BMI with birth year. In sex-pooled analyses, the probability associated with a test of H₀ : ξ = 0 is approximately 0.02. We also consider analysis of BMI after normalizing transformations (both Box-Cox [29] and an automated approach [30]) and after controlling for ten PCs and sex; results are similar.

Table 1:

Estimates from parameters of the full heteroscedasticity model (Eqn 49) in analysis of GxE for BMI as a function of birth year in the HRS. The ξ_E and ξ_G estimates reported are obtained from the environmental and genetic heteroscedasticity models, respectively.

Gender	BMIa	N	τ 1	π0 b	π 1	Prπ1	λ0 b	λ1 b	λ 2	Prλ2	PrξE	PrξG
All	Std	11586	0.19	0.25	0.06	1.78e-11	0.93	0.12	0.09	7.49e-50	1.76e-02	7.89e-04
All	BC	11586	0.17	0.26	0.04	1.79e-05	0.95	0.06	0.02	1.15e-03	2.68e-02	5.14e-04
All	BN	11586	0.17	0.26	0.04	2.52e-05	0.95	0.06	0.02	1.14e-03	2.66e-02	6.56e-04
All	Res	11586	0.20	0.26	0.06	3.99e-12	0.93	0.11	0.09	1.01e-53	9.37e-03	5.28e-04
M	Std	5022	0.19	0.26	0.04	4.69e-04	0.93	0.12	0.09	1.63e-22	3.91e-01	2.75e-01
M	BC	5022	0.17	0.26	0.03	2.11e-02	0.95	0.07	0.03	1.33e-03	3.83e-01	1.65e-01
M	BN	5022	0.17	0.26	0.03	3.05e-02	0.95	0.06	0.03	4.84e-03	3.86e-01	1.78e-01
M	Res	5022	0.19	0.26	0.04	4.54e-04	0.93	0.11	0.08	4.70e-22	3.99e-01	2.04e-01
F	Std	6564	0.20	0.25	0.06	6.65e-09	0.93	0.12	0.09	3.51e-31	2.24e-02	1.21e-03
F	BC	6564	0.18	0.26	0.04	2.09e-04	0.94	0.06	0.02	1.11e-02	3.82e-02	1.75e-03
F	BN	6564	0.18	0.26	0.04	2.10e-04	0.94	0.06	0.02	6.43e-03	3.66e-02	1.95e-03
F	Res	6564	0.20	0.26	0.07	1.46e-09	0.92	0.12	0.09	7.91e-33	1.06e-02	8.36e-04

^aWe consider four transformations of BMI. Std denotes the standardized mean BMI shown in the middle panel of Figure E.1. BC denotes the Box-Cox transformation [29]. BN denotes the transformation from bestNormalize [30]. Res denotes analysis of standardized variables after all (BMI, birthyear, PGS) have been residualized on 10 PCs and gender as per Frisch–Waugh–Lovell theorem given previous concerns regarding interaction research [5].

^bWe show probabilities for parameters when the maximal probability in a column is larger than 1e − 6.

Motivated by recent work [21], we also consider sex-stratified analyses. Those results suggest findings vary by sex; for males, we are unable to reject the null of the scaling model. To illustrate the differences in implications in our sex-stratified analyses, we also conduct a posterior predictive check analysis [31], see Figure 2. These findings confirm those of Table 1: for males, the scaling model produces data consistent with the HRS data whereas for females the observed data are inconsistent with both Scaling and GxE approaches (see additional detail in SI–F).

Figure 2:

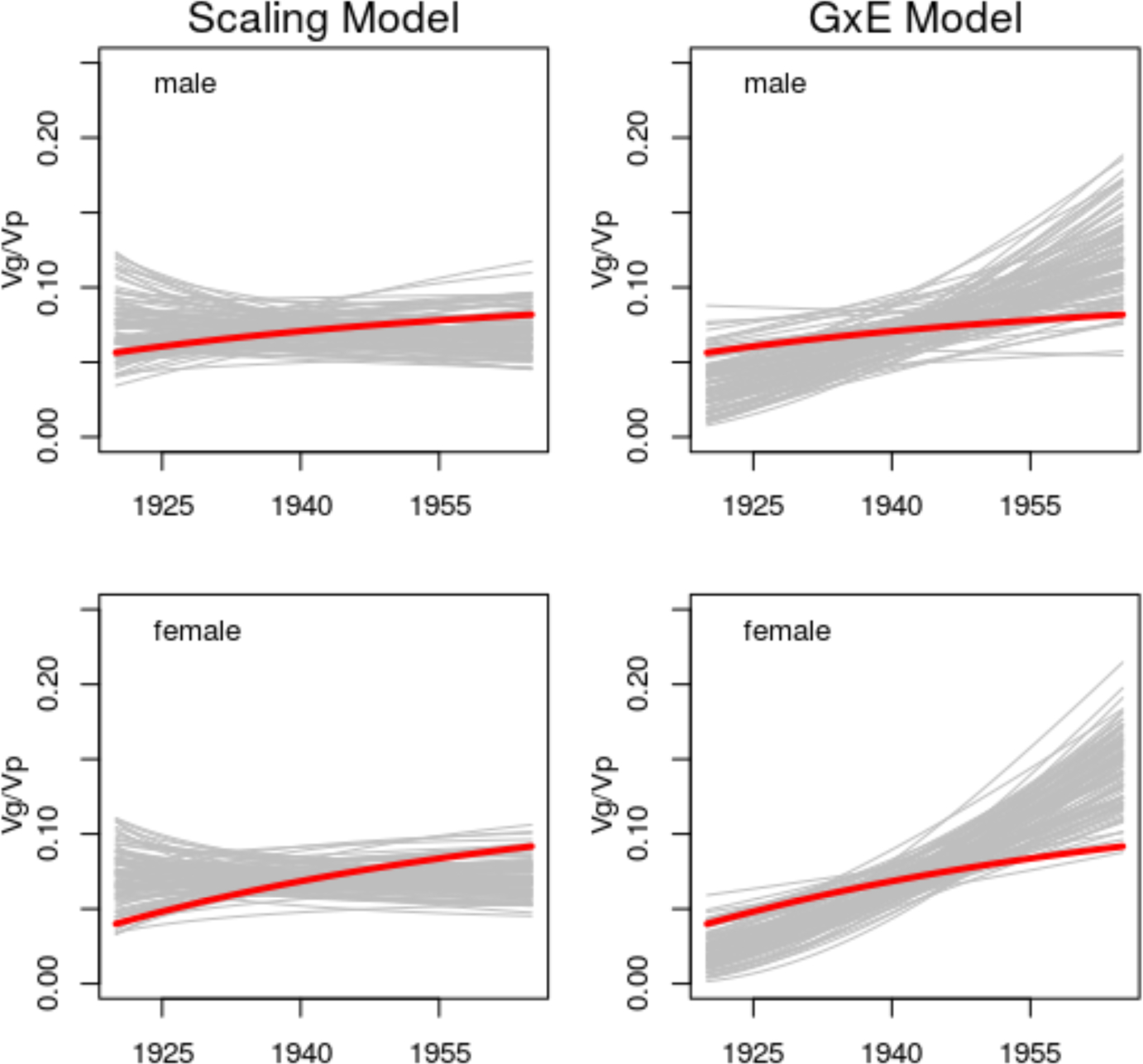
Gray lines represent genetic penetrance as a function of birth year simulated based on either the scaling model (Eqn 13, on left) or the standard homoscedastic GxE model (Eqn 1, on right). Red lines represent genetic penetrance as a function of birth year estimated from the real data using the heteroscedastic regression model (Eqn 2). Analyses based on standardized BMI data.

Finally, decomposing π₁ estimates (i.e., Eqn 43) suggests that, for females and males, 41% (95% CI: 10–57%) and 25% (95% CI: 0–54%) of the GxE (π₁) effect cannot be attributed to a simple scaling term. In an analysis of all respondents, this proportion is 37% (95% CI: 9–52%). We also report λ₂—the coefficient used to index heteroscedasticity as a function of G_i—and ξ_G—a test parallel to ξ_E of genetic heteroscedasticity. We can similarly decompose observed GxE into components related to genetic heteroscedasticity; in sex-pooled analysis, 65% (95% CI: 52–73%) cannot be attributed to a genetic scaling term (see Eqn 44). Additional results on these parameters are included in the SI.

Collectively these results indicate substantial evidence for birth year linked heteroscedasticity in BMI; the simple homoscedastic GxE model does not adequately represent the data. As a final illustration, if we consider the amount of variation in BMI explained by the polygenic score (along the lines of Figure 2), the classic GxE approach in the full data would suggest that this grows from 0.024 in the first birth year to 0.137 in the final birth year. In contrast, analysis under the heteroscedastic regression model suggests much more modest changes, from only 0.045 in the first birth year we observed to 0.088 in the last. We further discuss these findings and evidence related to genetic heteroscedasticity in SI-F.

3.3. SNP Analyses in the UKB

Under the full heteroscedasticity model, four SNPs exhibited significant gene-by-birth year effects as indicated by (Bonferroni-adjusted) p-values for the π₁ parameter. Table 2 contains parameter estimates from the full heteroscedasticity model for these SNPs along with ξ_E and ξ_G estimates obtained from the respective heteroscedasticity models. The main effect of birth year (τ₁) was negative, indicating that later-born UK Biobank participants tend to have lower BMI. Given substantial epidemiological evidence from representative samples indicating increasing BMI with birth year, we speculate that this negative association may be driven by selection bias in the UKB sample [28] (see additional discussion in SI–F). Given that rs1558902 is a variant in the FTO gene locus our finding replicates earlier results [32] which reported increasing penetrance of a variant within FTO over historical time using a different data set. Given that ξ_G was highly significant for each of these four SNPs we reject the null that observed GxE is driven entirely by scaling. In vQTL analysis (see additional discussion in SI–F) we replicate earlier findings [9] suggesting that the FTO gene may act as a vQTL. We note one key limitation: we are unable to distinguish age from cohort effects given the design of the UKB but use birth year to maintain consistency with HRS findings.

Table 2:

Estimates from parameters of the full heteroscedasticity model (Eqn 49) in analysis of GxE for Box-Cox transformed BMI as a function of birth year in the UK Biobank for those SNPs with significant π₁ estimates following Bonferonni adjustment. The ξ_E and ξ_G estimates reported are obtained from the environmental and genetic heteroscedasticity models, respectively.

SNP	π 0 a	π 1	Prπ1	λ 0 a	λ 1 a	λ 2	Prλ2	PrξE	PrξG
rs543874_A	−0.0271	−0.0085	1.90e-07	0.9873	0.0369	−0.0036	1.48e-03	4.39e-06	1.04e-07
rs13021737_G	0.0279	0.0062	1.33e-04	0.9873	0.0369	0.0036	1.53e-03	1.46e-03	1.75e-04
rs1558902_T	−0.0503	−0.0077	2.12e-06	0.9864	0.0368	−0.0096	1.76e-17	2.96e-04	5.14e-07
rs2075650_A	0.0113	−0.0060	2.43e-04	0.9875	0.0371	−0.0002	8.53e-01	2.01e-04	5.78e-04

^aWe show probabilities for parameters when the maximal probability in a column is larger than 1e − 6.

4. Discussion

Identified GxE interactions between specific pairs of genetic and environmental variables may represent specific instances of more general patterns of interaction. This will occur when the genetic or environmental predictor moderates the total variation in a phenotype. For instance, when the phenotypic variation changes as a function of environment, traditional homoscedastic GxE models are likely to detect interactions between that measure and all other correlates of the phenotype, both genetic and non-genetic. Here, we have delineated an expanded heteroscedastic GxE regression model that explicitly models moderation of the dispersion of the the phenotype as a function of the genetic and environmental measures. We use this model to derive a test statistic, ξ, which compares this heteroscedasticity model to a simpler scaling model in which GxE arises from more general differences in phenotypic variance, irrespective of etiology. When the scaling model holds, differences in phenotypic variance across the range of the genetic or environmental moderator induce a form of GxE that is only apparent in unstandardized units; the proportional contribution of the remaining predictors to phenotypic variance remains constant across the range of the moderator. We recommend employing ξ as a formal test of the difference between the GxE and scaling models, and we recommend employing the heteroscedasticity models introduced here for obtaining more accurate estimates and visualizations of the proportions of variance explained in the phenotype across different levels of the genetic or environmental moderators.

We provide an application of the heteroscedastic regression model, replicating previous observations that that genetic predictors of BMI have become increasingly penetrant in recent years. However, we additionally observed that the total variance in BMI increased with participant birth year. We found that, amongst males within the sample, the interaction between PGS and birth year was indistinguishable from a scaling model in which the total variance in BMI increases over birth year. While we reject the null that the scaling model produced data for females, we still estimate that a large proportion of the observed GxE may be due to scaling. In the full sample, only 37% of the estimated π₁ term cannot be attributed to scaling; while this suggests some conventional GxE, it is relatively modest. Other work has considered the potential moderation of genetic risk for BMI as a function of diet [4, 33], other lifestyle characteristics [34], and educational attainment [35]. Our findings may justify reconsideration of these earlier results with an increased focus on outcome variation. Outside of research focused on genetics, our work also dovetails with other empirical evidence [36] suggesting that effectively modeling variation in BMI across contexts may be crucial for accurate understanding of health disparities. We also note that the data considered here focus on older respondents. Such data may have unique characteristics; these data may be shaped by mortality selection [37] or otherwise be non-representative [28]. Moreover, for consistency with past work in this area (e.g., [17]), we interpret effects of birth year in terms of cohort effects, but we have not attempted to formally distinguish between age, period, and cohort effects.

Issues surrounding the scaling of the phenotype not fully explored here have the potential to have additional relevance for study of GxE. For instance, skew in the distribution of the phenotype may produce both GxE and heteroscedasticity by inducing a dependency between the mean and the variance of the distribution of the phenotype. Complications associated with analysis of such outcomes have been of concern since the days of Fischer [38] but we emphasize that heteroscedasticity is not always simply an epiphenomenon of non-normality. For instance, in our empirical analysis of BMI, we report results of GxE analyses after a normalizing (we use both Box-Cox [29] and an algorithmic approach [30]) transformation of BMI, and continue to detect both GxE and heteroscedasticity.

The methods introduced here can be viewed as complementary to those based in other genetic research designs, such as twin/family [39] and genome-wide molecular methods [40] that focus on GxE in the form of differences in the magnitude of of genetic variance or (SNP) heritability across the environmental range. The techniques developed here could be incorporated along with other recently developed GxE techniques [41], as well as techniques to further relax assumptions regarding the parametric form of the likelihood [42, 43], to further enhance the robustness of future GxE work. We also suspect that this approach may prove especially useful in analysis of polygenic scores designed to identify the magnitude of variation in the outcomes, a recently developed tool for genetic prediction [7, 8].

GxE research faces a number of conceptual and statistical challenges [16]. Thoughtfully and rigorously engaging with these challenges is particularly salient given the substantial recent increases in the availability of both genetic resources [44] and computational tools [45] for such research and the well-known failings of earlier epochs of such work [46]. Our proposed test is designed to help clarify the nature of potential GxE findings and to shed additional light on the processes contributing to variation in the phenotype; in particular, we can assess the extent to which the genetic etiology is relatively stable across the range of the environmental measure. Using the model and test statistic presented here, researchers can test for whether variance in the phenotype that is not explained by the genetic predictor shifts across the range of the environment and whether a scaling model may account for the obtained pattern of GxE. When the scaling model holds, we would suggest that the environment largely acts as a “dimming” mechanism on phenotypic variation [16] without altering the proportional contribution of genetic variation to the phenotype.