Unified exact design with early stopping rules for single arm clinical trials with multiple endpoints

Abstract

Adaptive designs are gaining popularity in early phase clinical trials because they enable investigators to change the course of a study in response to accumulating data. We propose a novel design to simultaneously monitor several endpoints. These include efficacy, futility, toxicity and other outcomes in early phase, single-arm studies. We construct a recursive relationship to compute the exact probabilities of stopping for any combination of endpoints without the need for simulation, given pre-specified decision rules. The proposed design is flexible in the number and timing of interim analyses. A R Shiny app with user-friendly web interface has been created to facilitate the implementation of the proposed design.

1. Introduction

Clinical studies to evaluate the toxicity and efficacy of a novel treatment are normally conducted in separate phases. Conventionally, Phase I trials are first-in-human studies aimed at identifying the maximum tolerated dose (MTD) of an experimental agent. In a subsequent Phase II trial, the candidate drug will be evaluated at the MTD to determine whether it has sufficient therapeutic activity to warrant further testing. The majority of Phase II clinical studies are designed as single-arm trials without a control group and are commonly conducted following a two-stage process.¹

The sample sizes of most Phase I trials are too small to allow accurate identification of MTD, so patients in Phase II trials might be exposed to sub-therapeutic doses or overly toxic doses resulting in excessive serious adverse events (SAEs). To overcome these issues, Phase I dose-expansion cohorts (DECs) are now frequently used to assess preliminary efficacy and to further characterize toxicity. In the development of immune checkpoint blockade, for example, the use of DECs serves to generate a continuum of the drug development process, blurring the distinctions between Phase I dose finding, Phase II proof of concept and Phase III comparative efficacy trials.^2,3 Despite its popularity, the majority of DECs are designed without sample size justification or treated as single arm, Phase II trials without statistically accounting for toxicities.⁴ Boonstra et al. state: “Regulatory agencies and others have expressed concern about the uncritical use of dose expansion cohorts (DECs) in Phase I oncology trials.”⁵

Consider a single-arm study to evaluate the efficacy of a novel treatment. We are interested in testing if the response rate to this new treatment is higher than the response rate in historical controls. Hereafter, we refer to this study as our prototype. Based on the commonly used Simon two-stage design, our prototype trial might be conducted in two stages, with the option to terminate accrual after the first stage if the number of responses is below the futility bound. Various extensions to the Simon two-stage design have been developed.^6–11 Notably, Mander and Thompson investigated designs optimal under the alternative hypothesis and constructed two-stage designs with the flexibility to stop early for efficacy, which leads to substantial reductions in expected sample size.⁸ Bryant and Day proposed a two-stage, two-endpoint design by integrating safety considerations into the early stopping rule of Phase II trials.⁷ Based on curtailed sampling procedures, Chen and Chi introduced two-stage designs with two dependent binary endpoints and demonstrated the effectiveness of their method in reducing the expected sample size when the treatment lacks efficacy or is too toxic.⁹ Li et al. proposed new two-stage designs including provisions for early termination due to sufficient effectiveness and safety, ineffectiveness and toxicity.¹⁰

When the outcome of interest can be quickly observed, continuous monitoring designs are particularly useful. With the use of simulated annealing method, Chen and Lee constructed optimal stopping boundaries for the continuous-monitoring of futility.¹² Law et al. proposed curtailed designs allowing a trial to be terminated early for efficacy or futility after evaluating the response of every patient.¹³ Ivanova et al. constructed a Pocock-type boundary to continuously monitor toxicity in Phase II clinical trials.¹⁴ The use of the sequential probability ratio test (SPRT) is not appropriate in this context because the open-ended nature of SPRT.¹⁵ The majority of continuous monitoring designs are proposed in a Bayesian framework based on the posterior or the predictive probability of exceeding the historical response rate.^16–18 A number of Bayesian designs have been proposed to consider both toxicity and response to treatment in Phase II setting based on the Dirichlet-Multinomial Model.^19–22 Sambucini²³ developed predictive probability rules for monitoring bivariate binary outcomes; Teramukai et al.²⁴ proposed a Bayesian adaptive design allowing futility stopping with continuous safety monitoring; Zhong et al.²⁵ applied a copula model to describe the joint probability of efficacy and toxicity. These Bayesian designs rely on extensive simulations to search the optimal design parameters and determine trial operating characteristics. Implementing these methods is also challenging because statisticians need to be informed in real time when new data become available. Complicated computations are often required to provide updated estimates on efficacy or toxicity, and user-friendly software for these previous work are often lacking.

Schulz et al. proposed a recursive formula to calculate the exact probability of accepting or rejecting a null hypothesis for multiple stage designs with a binary endpoint²⁶ and similar approaches have been adopted by some of the previously cited continuous monitoring designs.^12,13 In this work, we extend the univariate recursive relationship to calculate the exact probabilities of making go/no go decisions in single-arm clinical trials with multiple binary valued endpoints. Based on the extended recursive relationship, we propose the unified exact design, which provides a unified statistical framework for making futility, efficacy and/or toxicity stopping decisions in early phase clinical trials with mutiple-stage or continuous monitoring design. The proposed design provides transparent decision rules and is easy to implement because the cut-off values of stopping for toxicity, efficacy, or futility are spelled out a priori without the need to call upon statistical support mid-trial. Barring any of these endpoints, we continue to enroll patients until a maximum sample size is reached. Unlike the previously cited Bayesian methods, which rely on simulation to determine the operating characteristics of their designs, we can calculate the exact frequentist probability of continuing or stopping a trial for any combination of these causes.

The remainder of this paper is organized as follows. We introduce the recursive relationship in Section 2.1 and construct efficacy and futility stopping bounds in Section 2.2. We extend the recursive relationship to accommodate multiple binary endpoints in Section 2.3. In Section 2.4, we describe the identification of design parameters. We apply the unified exact design to our prototype in Section 3 and discuss the properties of the proposed design in Section 4. In Section 5, we present a Shiny application to facilitate the implementation of the proposed design.

2. Method

2.1. The recursive relationship

We denote by i_n the number of responses out the first n patients enrolled, where n = 1, 2, …, N and N is the maximum sample size. Conditional on the unknown response rate p, each i_n has a binomial distribution with parameters n and p in the absence of interim monitoring. We will stop the trial and declare the new treatment worthy of further investigation the first value of n for which i_n exceeds a pre-specified efficacy cut-off value e_n. A clinical study can also be terminated for futility. We stop a trial early for futility if the number of responses i_n observed in the first n patients is less than f_n, the pre-specified futility bound. Similar to Bayesian designs where the stopping bounds is often expressed as the lower and upper quantiles of a beta distribution for response rate, here we define the bounds f_n and e_n based on the lower and upper quantiles of the corresponding binomial distribution of i_n, respectively.

After enrolling and evaluating the first n patients, we can choose to stop for efficacy if the number of responses exceeds e_n or stop for futility if the number of responses falls below f_n. That is, we continue to accrue if f_n ≤ i_n ≤ e_n. Let θ_n(i_n) denote the probability of continuing the study after observing i_n = f_n, …, e_n responses among the first n patients. We define θ_n(i_n) = 0 for other values of i_n. We define θ₀(0) = 1 before any patients are enrolled.

According to Schultz et al.,²⁶ the recursive relationship relating θ_n to θ_n+1 is given by

$${\theta }_{n+1}\left(i_{n+1}\right)=p{\theta }_n\left(i_{n+1}-1\right)+(1-p){\theta }_n\left(i_{n+1}\right)$$ (1)

for f_n+1 ≤ i_n+1 ≤ e_n+1 and zero otherwise. The support for i_n+1 in equation (1) is different from that of a binomial distribution. To enroll one additional patient after having already observed n patients, the number of responses in these n patients cannot exceed e_n and cannot fall below f_n.

The marginal probability of continuing the trial after observing the n-th patient, θ_n, is then

$${\theta }_n=\sum _{i_n=f_n}^{e_n}{\theta }_n\left(i_n\right)$$

2.2. Monitoring efficacy and futility

Consider a study design with pre-specified stopping rules for efficacy (e_n) and futility (f_n). These decision rules can be described as follows:

• After enrolling and evaluating n = 1, …, N − 1 patients, and having not stopped the trial earlier,

• if i_n > e_n, then stop the trial and declare the treatment promising,

• if i_n < f_n, then stop the trial for futility,

• otherwise, continue to enroll the n + 1-th patient.

• After evaluating all the N patients, and having not stopped the trial earlier,

• if i_N > e_N, then reject the null hypothesis,

• if i_N ≤ e_N, then declare the treatment is not worthy of further investigation.

Denote PSE_n(p) the conditional probability of stopping for efficacy with the next patient after the n-th patient has been evaluated, given the trial has not been stopped earlier and the true probability of response is p. Then we have

$$PS{E}_n(p)=p{\theta }_{n-1}\left(e_{n-1}\right)I\left(e_n=e_{n-1}\right)$$

Let PSF_n(p) be the conditional probability of stopping for futility with the next patient after the n-th patient has been evaluated, given the trial has not been stopped earlier. Then we have

$$PS{F}_n(p)=(1-p){\theta }_{n-1}\left(f_{n-1}\right)I\left(f_n>f_{n-1}\right)$$

Figure 1 shows an example of the efficacy and futility stopping bounds. The decision rules sometimes prevent us from stopping at certain points in the trial, regardless of the most recent outcome. Specifically, if e_n > e_n−1 and we do not stop after the n − 1-th patient, then it is impossible to stop after the n-th patient regardless of the outcome of that patient. Similarly, it is impossible to stop the trial at the n-th patient for futility if f_n = f_n−1, regardless of the outcomes of the next patient.

Figure 1.

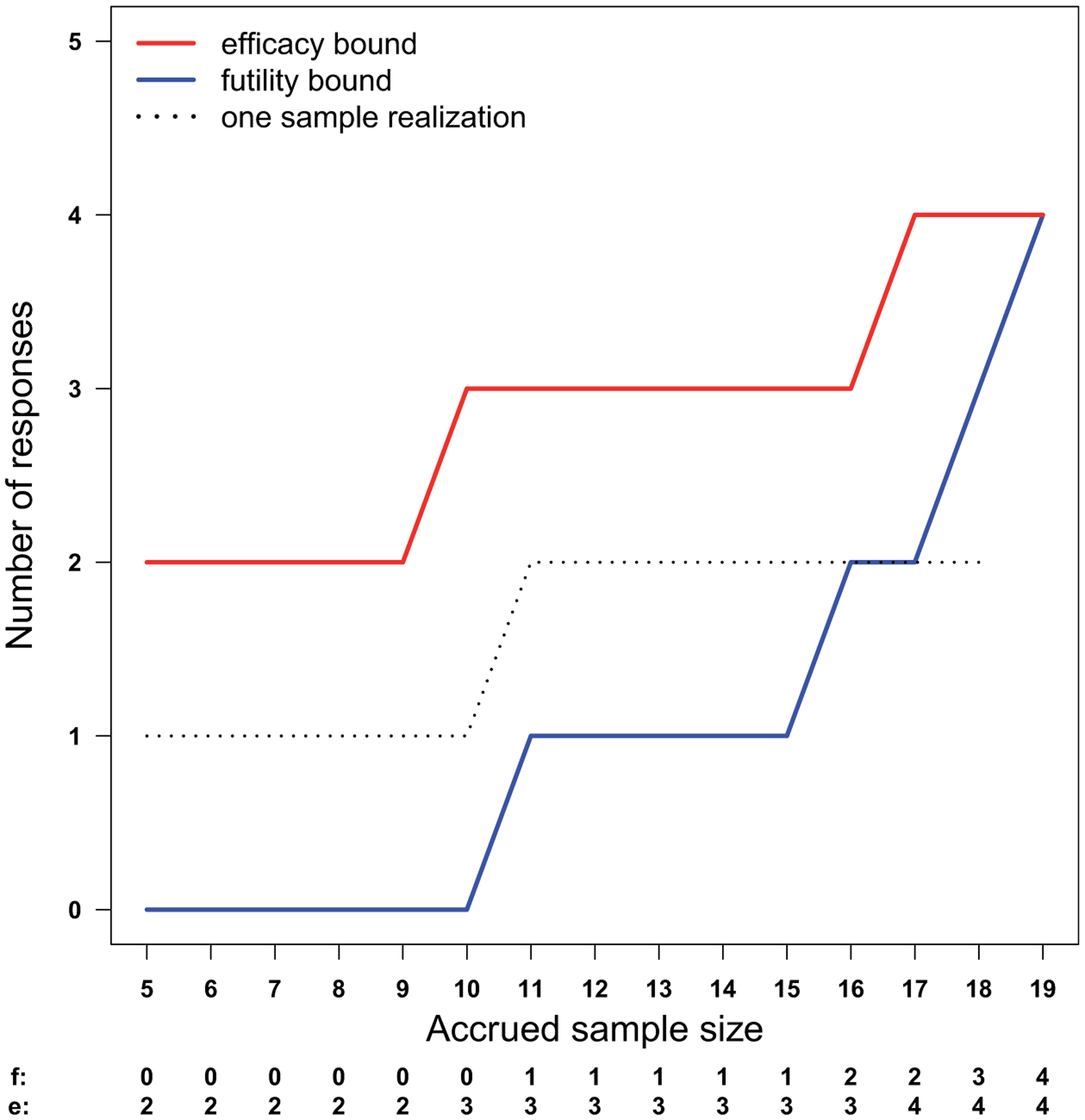
Efficacy and futility stopping bounds for the prototype and a sample path. A study will be stopped for efficacy or futility if the number of responses is above the efficacy bound (e) or below the futility bound (f). The sample path (dotted line) crosses the futility bound when two out of the first 18 patients respond to the treatment, leading to a futility decision. Under the null hypothesis, the response rate is 10%. Under the alternative, the response rate is 35%. This design achieved 90.1% power at a significance level of 0.093.

Denote p₀ as the historic, or standard of care response rate. We are interested in testing

$$H_0:p\le p_0\text{ vs. }{H}_1:p>p_0$$

with a power of at least 1 − β for all p ≥ p₁, where p₁ represents a target response rate of interest (p₁ > p₀). Based on our efficacy and futility stopping rules, the trial-wide statistical significance level is

$$\alpha \left(p_0\right)=\sum _{n=1}^{N}PS{E}_n\left(p_0\right)$$ (2)

the trial-wide type II error rate is

$$\beta \left(p_1\right)=1-\sum _{n=1}^{N}PS{E}_n\left(p_1\right)$$ (3)

and the expected sample size is

$$\mu (p)=\sum _{n=1}^{N-1}nP{S}_n(p)+N\left\{1-\sum _{n=1}^{N-1}P{S}_n(p)\right\}$$ (4)

where PS_n(p) = PSE_n(p) + PSF_n(p).

Based on the recursive relationship, we can calculate the interim conditional power of the study, which is the probability of ever stopping for efficacy after observing x responses out of m patients. We define conditional power as

$$CP(x,m)=\sum _{n=m+1}^{N}p{\theta }_{n-1}\left(e_{n-1}\right)I\left(e_{n-1}=e_n\right)$$

where θ_m(x) = 1 if f_m ≤ x ≤ e_m. We define CP = 1 if x > e_m and CP = 0 if x < f_m.

We suggest choosing stopping bounds e = (e₁, …, e_N)^T and f = (f₁, …, f_N)^T based on an upper or lower quantile of the binomial distribution. The selection of suitable stopping bounds can be accomplished with the use of a grid search to explore the possible combinations of these quantiles. Among all the pairs of vectors e and f defined by quantiles on the grid, we select the set (e, f) minimizing μ(p₀) as the efficacy and futility stopping boundaries for our design, subject to the pre-specified constraints on α(p₀), β(p₁) and N. We consider N fixed, which is determined by accrual rate, budget and other logistic factors. In the case when N is too small, we will need to gradually increase N until a solution is found.

Let us give an example of setting efficacy and futility monitoring bounds based on our prototype. Consider p₀ = 0.10 and p₁ = 0.35. Figure 1 shows the stopping bounds (e and f) and one realized sample path. The efficacy cutoff values e_n are the 93 percentiles of the binomial (n, p₀) distribution. We stop for futility if the number of responses i_n out of n patients is less than the 1.1 percentile of the corresponding binomial (n, p₁) distribution, or if it is impossible to reach the efficacy bound, i.e. i_n < n + e_n − N. The futility bound f_n is the maximum of these two values.

The cumulative probabilities of stopping for efficacy and futility using these bounds are shown in Figure 2. The trial-wide probability of ever crossing the efficacy bound is 0.0932 under p₀. This is the statistical significance of the design. With a maximum sample size of 19, this design yields 90.12% power if the true response rate is 35%. Continuous monitoring is conducted after five patients have been accrued and evaluated. The futility cutoff values f_n of this design is 0 for the first 10 patients, that is, futility stopping is only possible when the outcome for the 11th patient becomes available. Under the null hypothesis, the probability of stopping for futility is 0.3138 when the interim sample size is 11 and 0.5403, when the interim sample size is 16. On the other hand, the proposed design allows earlier decisions on efficacy. If the true response rate is 35%, then the probability of stopping the treatment for efficacy after enrolling nine patients is 0.6627.

Figure 2.

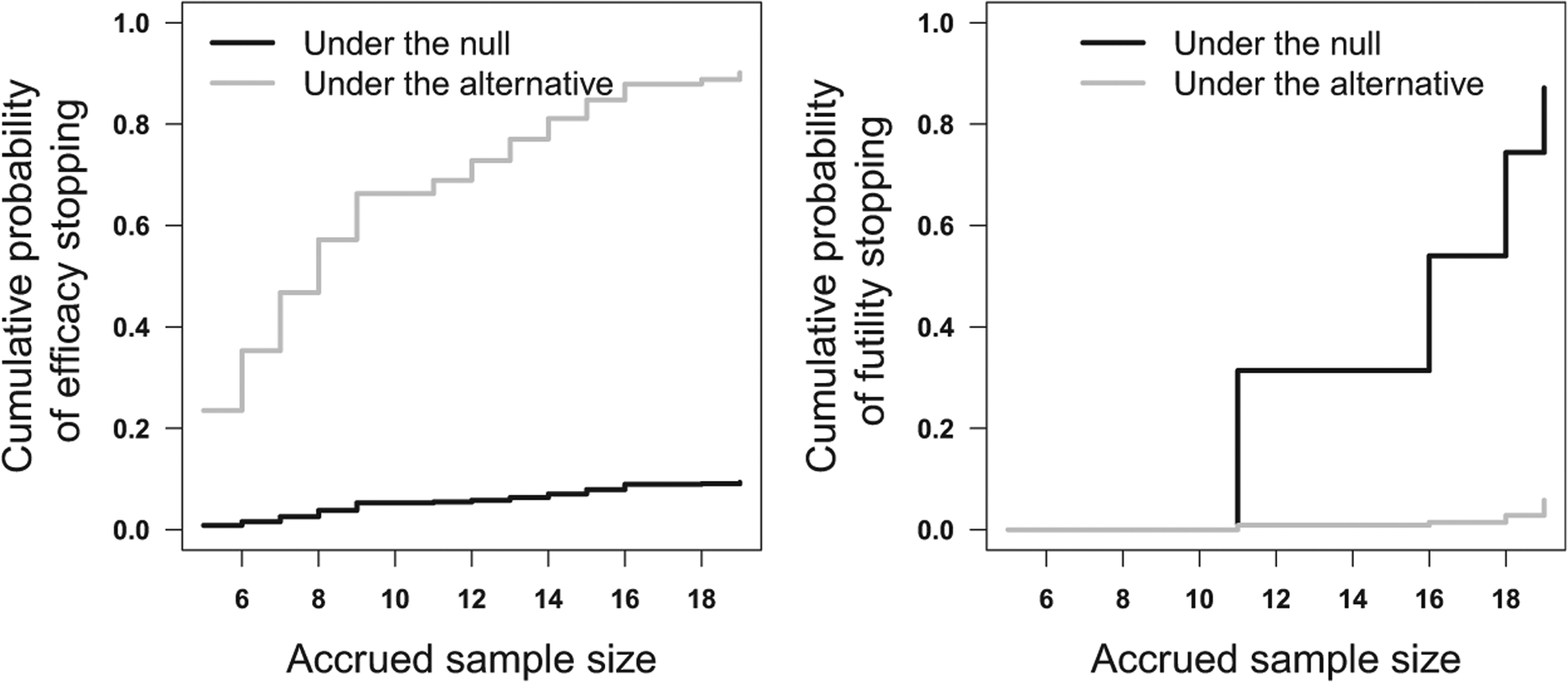
The cumulative probabilities of stopping for efficacy (left panel) and futility (right panel). Under the null hypothesis, the response rate is 10%. Under the alternative, the response rate is 35%. This design achieved 90.1% power at a significance level of 0.093.

Early stopping for efficacy is not always preferred in early phase clinical trials, so the proposed design provides the option to ignore early efficacy stopping by specifying e_n = n for n = 1, …, N − 1.

2.3. The joint monitoring of efficacy, futility and toxicity

In addition to the binary indicator for response, let us assume each patient has a binary valued indication of a SAE. Let π = (π₀₀, π₀₁, π₁₀, π₁₁) denote the probability of a patient in the following categories: no response and no SAE, no response but have SAE, response without SAE, response with SAE. The probability of each category is shown in Table 1. Let y = (y₀₀, y₀₁, y₁₀, y₁₁) be the multinomial distributed random variable with index 1 and probability vector π representing the outcomes for the next patient.

Table 1.

The probability π of a patient with and without response and/or SAE.

	Without SAEs	With SAEs	Marginal
No Response	π 00	π 01	1 − p
Response	π 10	π 11	p
Marginal	1 − q	q	1

Toxicity and efficacy are not generally independent.²⁷ In Immuno-oncology trials, for example, we can expect to see the patient developing a rash as a sign the treatment is taking effect. Define the efficacy-toxicity odds ratio as

$$\lambda =\frac{{\pi }_{00}{\pi }_{11}}{{\pi }_{01}{\pi }_{10}}$$

Define q as the marginal probability of a patient developing a SAE. The joint probability π can be calculated given the marginal probabilities p = π₁₀ + π₁₁ and q = π₀₁ + π₁₁ and a pre-specified λ based on the global cross-ratio model.²⁸

Let j_n be the number of patients with SAEs after n patients have been accrued and evaluated. Let b_n denote the toxicity bound, which is the maximum number of SAE’s we are willing to tolerate among the first n patients and continue to accrue to the trial. Let θ_n(i_n, j_n) denote the probability of continuing to accrue after observing i_n responses and j_n SAEs following the outcomes of the first n patients, for i_n = f_n, …, e_n responses and j_n = 0, …, b_n SAEs. For other values of i_n and j_n, we define θ_n(i_n, j_n) = 0. Then we can write

$${\theta }_{n+1}\left(i_{n+1},j_{n+1}\right)=\sum _{y}Multi\left(y_{00},y_{01},y_{10},y_{11}\right){\theta }_n\left(i_n,j_n\right)$$ (5)

where Multi is the multinomial probability density function, i_n+1 − i_n = y₁₀ + y₁₁ and j_n+1 − j_n = y₀₁ + y_11.

Intuitively the sequences e_n, f_n, b_n are non-decreasing.

After observing the outcomes of each patient, we can take one of four actions: stop for toxicity, stop for efficacy, stop for futility, or continue to accrue based on observed data up to the maximum sample size N. Specifically, a study proceeds as follows according to our design:

• After n = 1, …, N − 1 patients have been enrolled and evaluated, and having not stopped the trial earlier,

• if j_n > b_n, then terminate accrual for excessive SAEs,

• if j_n ≤ b_n and i_n < f_n, then stop the trial for futility,

• if j_n ≤ b_n and i_n > e_n, then stop the trial for efficacy, otherwise, continue to the next stage.

• After all the N patients have been evaluated, and having not stopped the trial earlier,

• if j_N > b_N, then conclude the treatment is too toxic,

• if j_N ≤ b_N and i_N ≤ e_N, then conclude the treatment is not promising, but not toxic,

• if j_N ≤ b_N and i_N > e_N, then conclude the treatment is worthy of further investigation.

Given the pre-specified decision rules, the conditional probability of stopping the trial for toxicity after n patients have been enrolled and evaluated, given the trial has not been stopped earlier, is

$$PS{T}_n(\pi )=\sum _{i_{n-1}}\sum _{j_{n-1}}q{\theta }_{n-1}\left(i_{n-1},j_{n-1}\right)I\left(j_{n-1}+1>b_n\right)I\left(b_n=b_{n-1}\right)$$

for j_n−1 = 0, …, b_n−1, i_n−1 = f_n−1, …, e_n−1.

Likewise, the conditional probability of stopping for efficacy after n patients have been enrolled and evaluated, given the trial has not been stopped earlier, is

$$PS{E}_n(\pi )=\sum _y\sum _{i_{n-1}}\sum _{j_{n-1}}Multi(y){\theta }_{n-1}\left(i_{n-1},j_{n-1}\right)I\left(i_n>e_n\right)I\left(j_n\le b_n\right)I\left(e_n=e_{n-1}\right)$$

and the conditional probability of stopping the trial for futility after n patients have been enrolled and evaluated, given the trial has not been stopped earlier, is

$$PS{F}_n(\pi )=\sum _y\sum _{i_{n-1}}\sum _{j_{n-1}}Multi(y){\theta }_{n-1}\left(i_{n-1},j_{n-1}\right)I\left(i_n<f_n\right)I\left(j_n\le b_n\right)I\left(f_n>f_{n-1}\right)$$

where i_n − i_n−1 = y₁₀ + y₁₁ and j_n − j_n−1 = y₀₁ + y₁₁.

2.4. Selection of design parameters

Bryant and Day considered different approaches to determine the design parameters for the two-stage two-end-point design and recommended the approach assuming independence (λ = 1) between response and safety. This approach is preferred for practical use as it maintains desirable operating characteristics and is easy to convey to investigators.⁷ Chen and Chi also demonstrated that different levels of response-safety correlation have little effect on the selection of design parameters.⁹ Based on these work, we assume λ = 1 and find suitable stopping boundaries for monitoring response and safety separately using the marginal probability of response and safety.

Let q₀ denote the maximum toxicity rate we are willing to tolerate in early phase trials. The value of q₀ can be set based on the maximum-tolerated toxicity rate in Phase I trials or chosen to satisfy specific regulatory requirement. We define the safety stopping bound b_n based on the upper quantiles of the binomial (n, q₀) distribution. Denote γ(q₀) as the probability of falsely stopping for safety when q = q₀, which can be calculated based on the recursive formula given by equation (1). Unlike previous work,^7,9,11 which aimed to establish safety by formally testing an acceptable versus an unacceptable toxicity rate, our objective is to safeguard against excessively toxic agents by controlling the false alarm rate γ(q₀) without overly inflating the maximum sample size (N) of a trial. Similar to Ivanova et al.,¹⁴ we accomplish this objective by choosing values of b_n such that γ(q₀) is as close to the pre-specified value (e.g. 0.1) as possible, but not exceeding it. Figure 3 shows an example of the safety stopping boundary and the cumulative probabilities of safety stopping associated with this boundary, assuming q₀ = 0.10 and γ(q₀) = 0.10.

Figure 3.

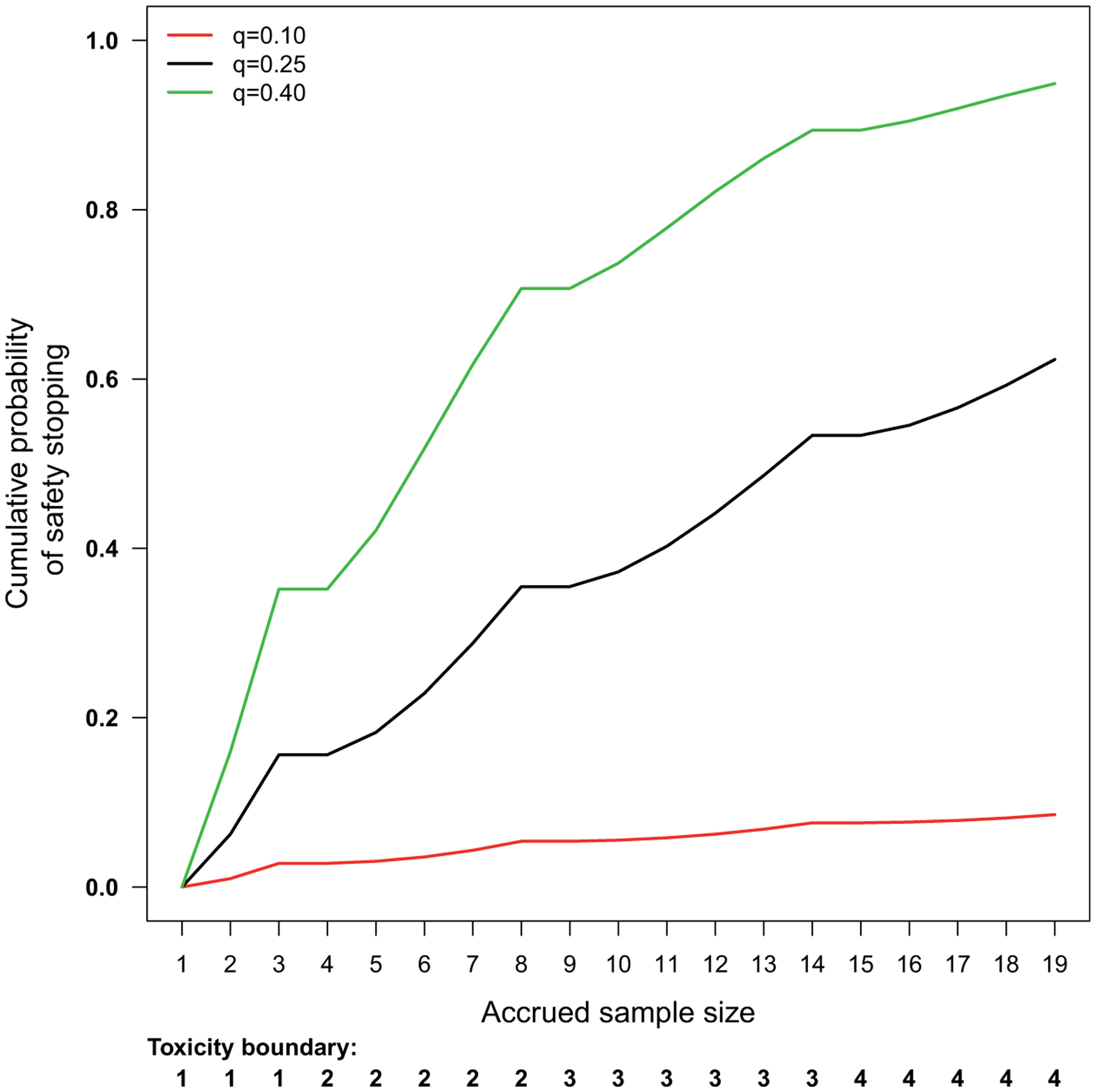
The toxicity bound and the cumulative probability of safety stopping for the prototype. The trial-wide probability of safety stopping is 0.0855, 0.6231 and 0.9489, assuming the true probability of a patient developing SAEs is 0.10, 0.25, and 0.40, respectively. We stop for safety if the number of patients with SAEs exceeds the toxicity bound. The highest SAE rate considered safe is 0.10 and the false alarm rate we are willing to tolerate is 0.10.

The efficacy and futility stopping bounds (e_n, f_n) are determined as described in Section 2.2 by minimizing the expected sample size under H₀ : p ≤ p₀ subject the pre-specified constraints on the marginal error rates α(p₀) and β(p₁).

Given a specific response-toxicity odds ratio λ, the trial-wide type I error rate and false alarm rate considering efficacy, futility and toxicity stopping are defined as

$$\alpha \left(p_0,q,\lambda \right)=\sum _{n=1}^{N}PS{E}_n\left(p_0,q,\lambda \right)$$ (6)

and

$$\gamma \left(p,q_0,\lambda \right)=\sum _{n=1}^{N}PS{T}_n\left(p,q_0,\lambda \right)$$ (7)

The statistical power of a study is given by

$$\alpha \left(p_1,q,\lambda \right)=\sum _{n=1}^{N}PS{E}_n\left(p_1,q,\lambda \right)$$ (8)

Note the false alarm rate γ(p, q₀, λ) is less than the marginal false alarm rate γ(q₀) in those trials which would be stopped for efficacy or futility, for p > 0. Likewise, there is

$$\alpha \left(p_0,q,\lambda \right)<\alpha \left(p_0\right),$$

$$\alpha \left(p_1,q,\lambda \right)<\alpha \left(p_1\right)$$

for q > 0. The statistical power, that is, α(p₁, q, λ) of a study will also be reduced due to the competition of safety stopping and setting γ(q₀) to a small value (0.05 or 0.10) helps to maintain power at an acceptable level.

Yin et al. developed two-stage and multiple-stage designs by identifying the parameter values at which the maximum type I error rate and the minimum power are achieved when safety and response rate are jointly tested.¹¹ In practice, implementation of this approach is difficult due to the intensive computations required to find the stopping boundaries. As detailed in this section, the approach proposed here sacrifices statistical sophistication for practical advantage such that the joint monitoring of response and safety can be implemented in studies with limited sample sizes while reducing the computational complexity in boundary identification.

2.5. Generalize to multiple endpoints

The joint monitoring of multiple endpoints is of special interest in certain disease areas. Monitoring multiple endpoints allows clinical trialists to comprehensively capture complex efficacy or toxicity profiles when a single binary endpoint is not adequate to account for the complexities of outcomes. Consider a clinical trial of prostate cancer with multiple binary endpoints including objective response per RECIST (OR), SAE, and reduction in Prostate-specific antigen (PSA). PSA is a widely used biomarker of tumor burden for patients with prostate cancer. PSA response (PR) is defined as at least 50% reduction in the level of PSA and is known to be a good predictor of overall survival.²⁹ We will use this hypothetical prostate cancer trial to illustrate how to jointly monitor multiple endpoints.

Denote y = (y₀₀₀, y₀₁₀, …, y₁₁₁) as the random variable with eight different categories, representing all the possible combinations of OR (yes/no), SAE(yes/no) and PR(yes/no). For example, y₀₀₀, y₀₁₀, y₁₀₀ and y₁₁₀ represent the following categories: no response and no SAE, no response but have SAE, response without SAE, response with SAE, all in the absence of PSA response. We assume y follows a multinomial distribution

$$y~Multi(1,\pi )$$

where π = (π₀₀₀, π₀₁₀, …, π₁₁₁) denotes the probability of each combinational category.

Denote θ_n the probability of continuing the study after observing i_n ORs, j_n SAEs and k_n PRs after n patients have been accrued and evaluated, for i_n = f_n, …, e_n, j_n = 0, …, b_n and k_n = l_n, …, u_n, with l_n and u_n denoting the lower and upper bound of PSA responses. We define θ_n = 0 for other values of i_n, j_n and k_n. Then the recursive relationship for these endpoints is given by

$${\theta }_{n+1}\left(i_{n+1},j_{n+1},k_{n+1}\right)=\sum _{y}Multi(y){\theta }_n\left(i_n,j_n,k_n\right)$$ (9)

where $i_{n+1}-i_n=\sum y_{\mathrm{1..}}$, $j_{n+1}-j_n=\sum y_{\mathrm{.1.}}$, and $k_{n+1}-k_n=\sum y_{\mathrm{..1}}$ are the marginal sums of y.

The conditional probability of stopping for safety after n patients have been enrolled and evaluated, given the trial has not been stopped earlier, is given by

$$PS{T}_n(\pi )=\sum _{i_{n-1}}\sum _{j_{n-1}}\sum _{k_{n-1}}q{\theta }_{n-1}\left(i_{n-1},j_{n-1},k_{n-1}\right)I\left(j_{n-1}+1>b_n\right)I\left(b_n=b_{n-1}\right)$$

The conditional probability of stopping for efficacy or futility after n patients have been enrolled and evaluated, given the trial has not been stopped earlier, is given by

$$PS{E}_n(\pi )=\sum _y\sum _{i_{n-1}}\sum _{j_{n-1}}\sum _{k_{n-1}}Multi(y){\theta }_{n-1}\left(i_{n-1},j_{n-1},k_{n-1}\right)I\left(i_n>e_n\right)I\left(e_n=e_{n-1}\right)$$

and

$${\text{PSF}}_n(\pi )=\sum _y\sum _{i_{n-1}}\sum _{j_{n-1}}\sum _{k_{n-1}}Multi(y){\theta }_{n-1}\left(i_{n-1},j_{n-1},k_{n-1}\right)I\left(i_n<f_n\right)I\left(f_n>f_{n-1}\right)$$

if j_n ≤ b_n and k_n = l_n, …, u_n

Similarly, we can calculate the conditional probability of stopping for PSA responses when its upper (u_n) or lower bound (l_n) is crossed, given the trial has not been stopped earlier. Specifically, we can write

$$PS{U}_n(\pi )=\sum _y\sum _{i_{n-1}}\sum _{j_{n-1}}\sum _{k_{n-1}}Multi(y){\theta }_{n-1}\left(i_{n-1},j_{n-1},k_{n-1}\right)I\left(k_n>u_n\right)I\left(u_n=u_{n-1}\right)$$

and

$$PS{L}_n(\pi )=\sum _y\sum _{i_{n-1}}\sum _{j_{n-1}}\sum _{k_{n-1}}Multi(y){\theta }_{n-1}\left(i_{n-1},j_{n-1},k_{n-1}\right)I\left(k_n<l_n\right)I\left(l_n>l_{n-1}\right)$$

if j_n ≤ b_n and i_n = f_n, …, e_n.

The expansion from (1) to (9) demonstrates how we can accommodate an arbitrary number of endpoints and their combinations for early stopping. The recursive relationship can be further generalized to allow interim analyses at pre-specified intervals. Let n_g denote the number of patients enrolled and evaluated up to stage g. The recursive formula relating the g + 1-th stage of the trial to the g-th stage is

$${\theta }_{g+1}\left(i_{g+1},j_{g+1},k_{g+1}\right)=\sum _{y}Multi(y){\theta }_g\left(i_g,j_g,k_g\right)$$ (10)

where y~Multi(n_g+1 − n_g, π), with the constrains $i_{g+1}-i_g=\sum y_{\mathrm{1..}}$, $j_{g+1}-j_g=\sum y_{\mathrm{.1.}}$, and $k_{g+1}-k_g=\sum y_{\mathrm{..1}}$.

We would like to test the following hypothesis on PR

$$H_{PR,0}:p_{PR}\le p_{PR,0}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}vs.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{H}_{\text{PR},1}:p_{\text{PR}}>p_{\text{PR},0}$$

with at least 1 − β(p_PR,1) power for p_PR ≥ p_PR,1, where p_PR,1 is a promising PSA response rate worthy of further investigation (p_PR,1 > p_PR,0).

The stopping boundaries for PR are determined in a similar manner as the stopping boundaries for response rate. Specifically, we find the suitable upper (u_n) and lower (l_n) bound for PR stopping subject to the constraints on the marginal error rates α(p_PR,0) and β(p_PR,1), while minimizing the expected sample size under the null H_PR,0. Due to the inclusion of PR stopping, the amount of significance level allocated to objective response per RECIST and PSA response rate need to be carefully adjusted based on the clinical context to maintain the trial-wide significance level.

3. Application

In this section, we retrospectively apply the unified exact design to a Phase II study of Olaparib proposed at our institution. This study aims at evaluating the response rate to Olaparib in patients with acute myeloid leukemia carrying isocitrate dehydrogenase mutations. The MTD has been determined in a Phase I trial. Previous experience suggests the response rate for patients with these tumors is approximately 10%. We are interested in testing

$$H_0:p\le 0.10\text{ vs. }{H}_1:p>0.10$$

with at least 90% power for all p ≥ 0.35. This trial was originally designed using an optimal Simon two-stage design. Initially, 11 patients will be enrolled. If no more than one response is observed, the expansion cohort will be terminated early. If two or more patients respond, an additional eight patients will be enrolled for a total of 19 patients. The null hypothesis will be rejected if four or more responses are observed in these 19 patients. This design yields 90.86% power at an α level of 0.0988, with 0.6974 probability of early negative stopping and an expected sample size of 13.4 under the null. This design can be expressed using our notation with e₁₁ = 11, f₁₁ = 2 for the first stage and e₁₉ = 3, f₁₉ = 3 for the second stage.

The proposed design has the flexibility to include efficacy stopping. Consider a design with interim analysis planed after the first 5, 10, 15, and 20 patients have been accrued and evaluated. The corresponding efficacy bound is e = (2, 2, 3, 4) and the corresponding futility bound is f = (0, 1, 3, 4). We provide the cumulative probabilities of stopping for efficacy and futility assuming different response rates in Table 2. With a maximum sample size of 20, the prototype trial has 90.11% power at a one-sided significance level of 0.0968. Assuming a true response rate of 35%, the probability of stopping the treatment for efficacy after enrolling 10 patients is 0.7384.

Table 2.

The cumulative probabilities of efficacy (CPE) and futility (CPF) stopping for our prototype using the unified exact design.

			p = 0.10		p = 0.20		p = 0.30		p = 0.35
n	f n	e n	CPF	CPE	CPF	CPE	CPF	CPE	CPF	CPE
5	0	2	0.0000	0.0086	0.0000	0.0579	0.0000	0.1631	0.0000	0.2352
10	1	2	0.3487	0.0702	0.1074	0.3222	0.0282	0.6172	0.0135	0.7384
15	3	3	0.8189	0.0893	0.4042	0.4171	0.1314	0.7471	0.0649	0.8558
20	4	4	0.8731	0.0968	0.4628	0.4640	0.1518	0.8044	0.0741	0.9011

Note: In the prototype, we aim to test if the response rate to a novel agent is greater than 10%, assuming a target response rate of 35%. Interim analyses are conducted after 5, 10, 15, and 20 patients have been accrued and evaluated. For each interim sample size n, e_n is the maximum number of treatment successes without stopping for efficacy; and f_n is the minimum number of treatment successes without stopping for futility. The true probability of response rate is assumed to be p = 0.10, p = 0.20, p = 0.30 and p = 0.35.

Consider the continuous monitoring of efficacy and futility after enrolling five patients, and the continuous monitoring of toxicity outcomes for all the patients, with a maximum sample size of 19. To implement a unified exact design for this trial, we specify

$$\alpha \left(p_0\right)<0.10,\beta \left(p_1\right)<0.10\text{ and }\gamma \left(q_0\right)<0.10$$

The efficacy and futility cutoff values for this design are labeled in Figure 1. To include safety monitoring, we consider q₀ = 0.10. That is, the treatment is considered overly toxic if the SAE rate is above 10% and the false alarm rate of stopping for safety when the treatment is safe (q ≤ q₀) is maintained at 0.10. In this example, we assume an efficacy–toxicity odds ratio of 1.5, corresponding to a weak positive correlation coefficient of approximately 0.10. A weak correlation of this magnitude has been suggested by studies of targeted agents³⁰ and adopted by other studies.³¹ The safety cutoff values for this study are labeled in Figure 3. The unified exact design allows users to specify other levels of correlations as well as independence.

This trial can be stopped as early as after two patients are accrued, if the first two patients both develop SAEs. We can also choose to stop this trial if more than two of the first five patients respond to the treatment. We continue to accrue if the number of SAEs is below the toxicity bound, and the number of responses is between the efficacy and the futility bound. If the trial reaches its planned maximum sample size of 19 patients, we conclude the treatment is promising if at least five patients have responded and at most four patients have SAEs.

The probabilities of early stopping using continuous monitoring under different scenarios are shown in Figure 4. Scenarios A and C represent cases when the treatment is safe, whereas scenarios B and D correspond to situations when the treatment is too toxic. The trial-wide probability of safety stopping is less than 0.10 in both scenario A (q = 0.10, p = 0.10) and C (q = 0.10, p = 0.35). When the treatment if safe but not efficacious (Figure 4(a)), the trial-wide probability of stopping for futility and efficacy is 0.8091 and 0.0868, respectively. The trial-wide probability of efficacy stopping is 0.8577 if the treatment is safe and efficacious (Figure 4(c)). When the treatment is overly toxic, the trial-wide probabilities of stopping for toxicity are 0.8608 and 0.6781 in B (q = 0.40, p = 0.10) and D (q = 0.40, p = 0.35), respectively. The trial-wide probabilities of stopping for efficacy are 0.0210 and 0.3126 under scenario B and D, respectively. Table 3 shows the operating characteristics of this design, when interim analysis is planed after 5, 10, 15, and 20 patients have been accrued and evaluated.

Figure 4.

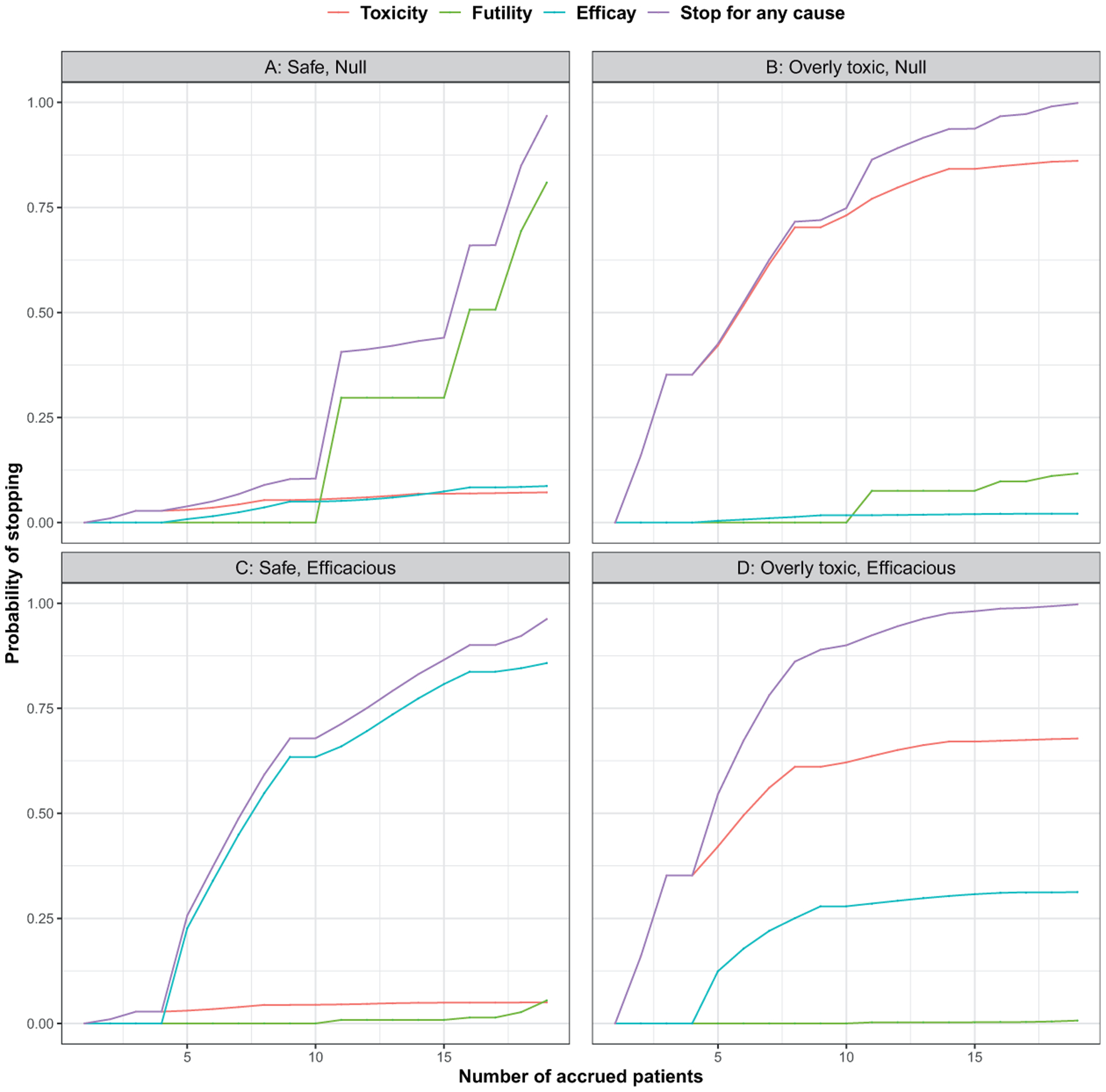
The cumulative probabilities of stopping the prototype for efficacy, futility, toxicity, or any cause in different scenarios. (a) and (c) represent treatment with acceptable toxicity profiles, assuming the probability of SAE is 0.10, whereas (b) and (d) represent treatment with unacceptable toxicity levels, assuming the probability of SAE is 0.40. The probability of response is 0.10 and 0.35 under the null and efficacious scenarios, respectively.

Table 3.

The cumulative probabilities of efficacy (CPE), futility (CPF), and toxicity (CPT) stopping for our prototype using the unified exact design.

				A : q = 0.10, p = 0.10			B : q = 0.40, p = 0.10			C : q = 0.10, p = 0.35			D : q = 0.40, p = 0.35
n	f n	e n	b n	CPF	CPE	CPT	CPF	CPE	CPT	CPF	CPE	CPT	CPF	CPE	CPT
5	0	2	2	0.0000	0.0084	0.0086	0.0000	0.0051	0.3174	0.0000	0.2325	0.0086	0.0000	0.1484	0.3174
10	1	2	2	0.3266	0.0648	0.0696	0.0641	0.0133	0.8287	0.0128	0.6996	0.0540	0.0031	0.2299	0.7182
15	3	3	3	0.7543	0.0819	0.0809	0.0984	0.0144	0.8814	0.0606	0.8076	0.0585	0.0082	0.2394	0.7452
20	4	4	4	0.8027	0.0886	0.0819	0.1001	0.0146	0.8844	0.0690	0.8490	0.0593	0.0087	0.2413	0.7489

Note: The prototype tests if the response rate to a novel agent is greater than 10%, assuming a target response rate of 35%. Any SAE rate greater than 10% is considered overly toxic. For each interim sample size n, e_n is the maximum number of treatment successes without stopping for efficacy; and f_n is the minimum number of treatment successes without stopping for futility; b_n is the maximum number of SAEs without stopping for toxicity. The CPF, CPE and CPT after n patients have been evaluated are calculated in different scenarios, where p and q denote the marginal probability of response and SAE, respectively.

4. Discussion

In this paper, we proposed the unified exact design to simultaneously monitor the efficacy, futility and toxicity outcomes of a single-arm clinical trial. We developed a recursive relationship to calculate the exact probabilities of stopping for any combinations of these outcomes. Compared to the Simon two-stage design, which only allows one futility check and has no provisions for safety monitoring, the unified exact design provides the flexibility to stop the trial early for all the necessary causes. Although we choose stopping bounds based on the tail areas of a binomial distribution in this paper, Bayesian methods can also be used to set the stopping bounds. It is beyond the scope of this paper to discuss other types of stopping bounds; however, it should be noted that the proposed recursive method is valid as long as the stopping bounds is a non-decreasing function of sample size. Our future work will focus on computationally efficient methods to optimize the stopping bounds.

When results from previous studies are available, we can specify the joint probability of efficacy, futility and toxicity based on historical data. Given a correlation structure, it is possible to find stopping bounds producing smaller expected sample sizes compared to the stopping bounds found assuming the independence between response and toxicity. However, these data are not always available and the performance of the unified exact design can be negatively affected if the toxicity-efficacy relationship is mis-specified. To deal with this problem, an adaptive two-stage design similar to Zang and Lee³¹ can be used to learn the efficacy–toxicity relationship in the first stage, assuming independence of these outcomes, and jointly model efficacy toxicity outcomes in the next stage.

The unified exact design allows the stopping boundaries to be completely specified prior to the start of a trial, saving the need for complex computations in the midst of a trial. All possible decision rules can be tabulated, which helps to convey the statistical design to trial practitioners. Continuous monitoring provides clinical trialists the advantage of altering the course of a trial in response to real time data; however, continuous monitoring is difficult to implement if the outcome of interest is not quickly available. The proposed method is flexible in the number and timing of interim analyses, with the flexibility to allow for multiple stage design as well as continuous monitoring design.

5. Software implementation

To provide a more accessible user-interface, we created a web application using Shiny, which can be accessed at https://weiwei-study-design.shinyapps.io/unified_exact_design/. The web interface of our design gives users the option to choose the types of early stopping (efficacy, futility, toxicity, or their combinations), as well as the timing and number of interim looks expressed in terms of interim sample sizes. To monitor response to treatment, users need to specify α, β, p₀ and p₁. To include safety monitoring, users need to provide the values for the efficacy toxicity odds ratio (λ), the highest toxicity level consider safe (q₀) and the chance of falsely stopping for safety (γ) when treatment is safe. After users input their design parameters, the Shiny app generates the stopping bounds and the operating characteristics of the design. A recommended write up summarizing the statistical design will also be generated for use in a protocol.