An analytical framework for interpretable and generalizable single-cell data analysis

Abstract

Scaling single-cell data exploratory analysis with the rapidly growing diversity and quantity of single-cell omics datasets demands more interpretable and robust data representation that is generalizable across datasets. Here we developed a ‘linearly interpretable’ framework that combines the interpretability and transferability of linear methods with the representational power of nonlinear methods. Within this framework, we introduce a data representation and visualization method, GraphDR, and a structure discovery method, StructDR, that unifies cluster, trajectory, and surface estimation and allows their confidence set inference.

Single-cell exploratory analysis methods, including visualization methods and approaches for trajectory estimation, rely on either linear or non-linear data representation, each of which currently presents important limitations to single-cell data analysis. Linear dimensionality reduction methods, including Principal Component Analysis (PCA), provide high interpretability via linear maps. We define linear interpretability as the properties of linear representations that allow intuitively understanding and comparing data in the representation space. Specifically, linear interpretability means any position, direction, or distance in the representation space has a clear meaning in the original data space, for example, the position of a cell may represent a linear combination of expression scores of multiple genes, and such mapping is invariant regardless of position in the representation space. Such invariance further allows comparison of different subregions of a representation, such as comparing cell states in different developmental stages in the same dataset. Moreover, linear interpretability allows applying the same low dimensional projection to different datasets, producing comparable representations. However, linear dimensionality reduction methods typically cannot efficiently represent cell identities in single-cell data: spatial adjacency in low-dimensional representations is not as good predictor of similarity in overall expression state compared to nonlinear methods.

These limitations have led to wide use of nonlinear representations on single-cell omics, including t-distributed stochastic neighbor embedding (t-SNE)¹, UMAP² and others^3–5. Trajectory estimation methods^6–10 can also often be considered specialized nonlinear data representation methods. However, they generally lack the desirable linear interpretability properties enjoyed by linear methods. These limitations present a practical barrier to compare or integrate datasets at scale. Moreover, for most methods it is infeasible to apply statistical inference to analyze uncertainties of extracted structures, making drawing robust conclusions more difficult.

We hypothesize that the difficulty of linear dimensionality reduction for single-cell data arises from high level of noise: high dimensionality is necessary to capture similarities between cells when each individual dimension is noisy, and this renders low dimensional linear representations less appealing. Indeed, all popular nonlinear methods for single-cell omics data use high-dimensional information, which is often represented by distances between cells from high dimensional input, thus effectively reducing the effect of noise. We reasoned that allowing information-sharing across cells leveraging high-dimensional information could improve the quality of cell state representation while preserving the linear space and its interpretability.

We therefore developed a ‘linearly interpretable’ framework for exploratory analysis of single-cell omics data, which includes methods that exactly or approximately preserve the linear interpretability but improve upon linear methods on cell state representation quality or other desired properties. Specifically we developed two methods that complement each other: a dimensionality reduction and visualization method, GraphDR, and a general structure extraction method, StructDR, that unifies cluster, trajectory, and surface estimation under the same framework and enables inference of confidence sets for these structures.

We designed GraphDR to be a graph-based linearly interpretable data representation and visualization method that addresses the limitations of linear representations in single-cell data (Figure 1a, Methods). We achieved these desired properties by considering a flexible class of methods that improves over linear methods but maintains interpretability by introducing nonlinearity specifically for information sharing across cells. Specifically, GraphDR applies: (1) a feature (e.g. gene) space transformation $W$, as in linear methods, and (2) an interpretability-preserving cell space transformation $K$ that introduces nonlinearity and improves cell state representation.

Figure 1. A linearly interpretable data representation method that captures the structure of single-cell data while preserving interpretability and transferability.

a. Schematic overview of the linearly interpretable data representation method GraphDR for single-cell omics data representation and visualization. GraphDR approximately preserves the structure and interpretability of a corresponding linear transform. b. Visualization of two example datasets of developmental trajectory¹¹ (top) and mature cell types¹⁸ (bottom) using GraphDR and representative linear and nonlinear methods, PCA and t-SNE. GraphDR is applied without rotation relative to PCA (Methods). c. Comparison of single-cell data dimensionality reduction methods in representing cell type identity and preserving gene expression space. Y-axis shows the accuracy of recovering cell type information from its nearest neighbor in the representation. X-axis shows preservation of the input linear space measured in correlation of pairwise distance. Both two-dimensional (triangles) and three-dimensional (solid dot) representations are compared. d. Cell type identity representation accuracies in multiple numbers of dimensions for single-cell data dimensionality reduction methods. e-f. Linearly interpretable transform facilitates comparison across datasets, balancing advantages of linear and nonlinear transform. Two planarian single-cell datasets (e. left panel and f. top panel: Fincher et al. 2018; e. right panel and f. bottom panel: Plass et al. 2018) were processed with a representative linear transform PCA, a nonlinear transform t-SNE, and GraphDR.

GraphDR applies a cell space transformation derived from the analytical solution of a graph-based optimization problem that provide information sharing across cells connected in a graph (Figure 1a). The graph can be constructed with cell state similarities in high-dimensional input data and incorporate experimental designs when appropriate. GraphDR then simultaneously optimizes the reconstruction of the input data and the consistency with the graph. The existence of a closed-form solution makes GraphDR analytically tractable and allows ultrafast computation scalable to very large datasets.

We first demonstrated GraphDR, PCA, and t-SNE on two distinct single-cell RNA-seq datasets, representing developing mouse hippocampus cell types¹¹ and mature mouse brain cell types¹² respectively (Figure 1a). GraphDR generated representations that preserved the linear interpretability like PCA and resolved different cell types like t-SNE (Figure 1b, Extended Data Fig. 1). Importantly, this gain of interpretability was achieved without a loss of accuracy: in a benchmark across 339 single-cell datasets with cell type annotations¹⁰, GraphDR distinguished cell types as well as several current state-of-the-art nonlinear methods, measured by consistency of nearest neighbors in dimensionality-reduced embedding with literature-based cell type identities (Figure 1c–d).

GraphDR also facilitates direct comparisons across datasets. To demonstrate, we used GraphDR to analyze two planarian Schmidtea mediterranea whole-animal single-cell RNA-seq datasets by two different labs^13,14. GraphDR generated representations that could both distinguish all cell types and be compared across datasets (Figure 1e, Extended Data Fig. 2–3). In contrast, PCA representations were comparable across the two datasets but did not resolve specific cell types, whereas t-SNE representations resolved cell types but were not comparable across datasets (Figure 1f).

GraphDR can incorporate experimental design information into the analysis by encoding them into graph construction (Extended Data Fig. 3). To illustrate this, we applied GraphDR to single-cell RNA-seq datasets from developing zebrafish embryos scRNA-seq dataset (time-series design; Extended Data Fig. 4) and Xenopus embryos (batch + time-series design; Extended Data Fig. 5). Interestingly, the visualization of each developmental landscape revealed extruding branches of lineages from a continuum cell states, suggesting a more complex paradigm than the traditional branch view of cell fate specification.

While visualization methods provide an intuitive and flexible representation of the structure of the data, quantitatively defined structures such as clusters and trajectories often need to be extracted to perform detailed analysis of cell types and developmental trajectories. Existing single-cell analysis methods^6–10 are still limited in the types of structures that they can represent and, for example, do not allow for unsupervised detection of two-dimensional surface structure (Figure 2a). Furthermore, current state-of-the-art methods do not allow statistical inference of uncertainties of the trajectories such as through constructing confidence sets, which is essential for assessing the robustness of the inferred trajectories.

Figure 2. Density-based generalized trajectory estimation and inference.

a. Schematic overview of the StructDR framework. Left panel: zero-, one-, and two-dimensional density ridges and examples of corresponding biological structures. Mid panel: an example of trajectory estimation (1-dimensional density ridge) based on myoblast single-cell RNA-seq data⁶. The original cell positions are shown in black dots; the projected positions are shown in blue; and the projection lines are shown in dotted lines. Gray shades show confidence sets of trajectory positions. Right panel: the top plot shows an annotated example of confidence set estimation. The bottom plot depicts the elements of the subspace constrained mean-shift algorithm¹⁶; the arrows indicate gradient vectors of the probability density function; the bars indicate the directions of first eigenvectors of the Hessians of the log probability density function; the kernel density estimator-based density function is shown with the contour plot; the estimated trajectory positions are shown in blue dots. b. Performance of StructDR+GraphDR and StructDR+PCA tested on a published large-scale benchmark of 339 datasets. The performance scores are computed based on Saelens et al. 2019¹⁰. StructDR is applied with 1D density ridge estimation and automated graph construction for cells projected onto the density ridge. c. Density ridge identification with adaptive dimensionality example on a hippocampus developmental trajectory single-cell dataset¹¹. Cells projected to one-dimensional (black dots) and two-dimensional density ridges (blue dots) are shown, where the dimensionality of density ridge is adaptively determined based on the data. Insets show the gene expression levels of the indicated genes in sub-regions of the representation.

We thus developed StructDR, a unified framework for single-cell cluster, trajectory, and surface structure discovery based on the nonparametric density ridge estimation (NRE) method^15–17 (Methods). NRE also allows estimation of statistical confidence sets of these structures (Figure 2a). More specifically, StructDR casts the problem of structure discovery in single-cell data as estimating a smooth density function of cells and subsequently projecting cells to their corresponding positions on a set of mathematical structures called density ridges (Extended Data Fig. 6, 7).

In StructDR, we map the problems of discovering clusters, trajectories, and surfaces to identifying zero-, one-, and two-dimensional density ridges of the density function, which are geometrically points, curves, and surfaces respectively. Density ridges are generalizations of local maxima¹⁵ and are uniquely defined given any smooth density function of cells estimated from single-cell data (Extended Data Fig. 7). Trajectory or 1D density ridge analysis is appropriate for representing cell populations that have one dominant direction of variation or when the top one principal direction of variation is of interest, such as in terminally differentiating cells. In contrast, surface or 2D density ridge analysis is appropriate for representing cell populations with two dominant directions of variation or when the top two principal directions of variation are of interest, such as differentiating cells that are also in cell cycle. StructDR can further connect density ridges via graph construction to represent the global topological structure of the data. Thus, in the context of StructDR, we consider trajectory estimation as the inference of 1D density ridges or connected graph of 1D density ridges.

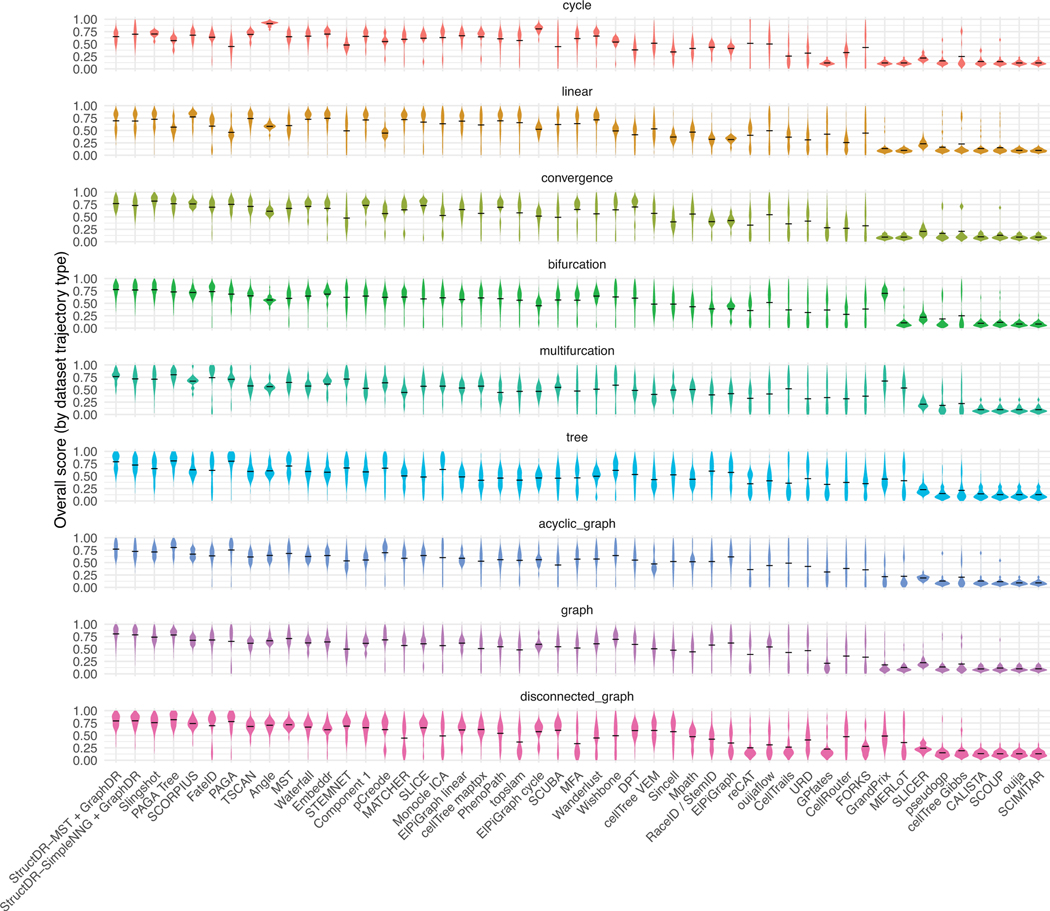
We evaluated the trajectory estimation performance with a large benchmark dataset created by Saelens et al¹⁰ including 339 single-cell datasets. StructDR showed the top overall performance across all datasets (Figure 2b, Extended Data Fig. 8).

In addition to allow capturing the complexity of single-cell data with zero, one, two-dimensional density ridge representations (Figure 2a, c, Extended Data Fig. 9), StructDR can adaptively select density ridge dimensionality for each cell based on the data. For example, when analyzing hippocampus development scRNA-seq data, StructDR captured the cellular heterogeneity of neuronal progenitor cells going through cell cycle by a two-dimensional surface instead of arbitrarily mapping these cells to one-dimensional trajectories (Figure 2c). Furthermore, this analysis identified a CCK+ neurons population between CA1 and CA2/3/4 branches within the hippocampus (Figure 2c), which was not reported in the previous analysis of this dataset with standard methods¹¹.

StructDR can estimate confidence sets of ridge positions when applied with linear representations such as PCA as input (Figure 2a). We demonstrated that StructDR-inferred confidence sets effectively controlled coverage probability of ground-truth trajectory positions in trajectory estimation (Extended Data Fig. 10) as expected from theoretical results.

Taken together, our work presented a linearly interpretable single-cell data analysis framework that provides interpretable, scalable, and robust representations and facilitates dataset comparison and integration. With the rapid growth of single cell datasets, we expect linear interpretability to become increasingly important. We also developed a feature-rich interactive analysis interface that supports 3D visualization, Trenti (Supplementary Figure 1), to facilitate exploratory analysis and make our tools broadly accessible. We also envision these methods to be potentially applicable to other high-dimensional data beyond single-cell omics data applications.

Methods

GraphDR: a linearly interpretable data representation method

We propose a class of linearly interpretable dimensionality reduction methods, which are nonlinear methods that produce representations that aims to maximally preserve the interpretability of a corresponding linear subspace, while allowing other desired properties unachievable by linear method such as information sharing across cells. We believe it is beneficial to provide a unified viewpoint for this class of methods sharing the same properties.

To design a linearly interpretable representation method, we first propose the form $Z=KXW$, analogous to the linear dimensionality reduction $Z=XW$, to allow fast computation and analytical tractability. $Z$ represents the data representation output matrix ($n\times d$, where $n$ is the number of samples and $d$ is the number of output dimensions), $X$ is the input data ($n\times c$, where $n$ is the number of samples and $c$ is the number of input dimensions). $W$ and $K$ are matrices that apply feature (e.g. gene) space and cell space linear transformations that are of shape $d\times c$ and $n\times n$ respectively. In other words, we apply both a linear projection on feature space $W$ like linear methods, and an additional linear transform on cell space $K$ which is also derived from $X$. The addition of cell space operator $K$ allows much greater flexibility in the transformation, which can be exploited to improve the quality of the representation. For example, setting $K$ to a block-diagonal matrix with all entries within a block equal to 1/block-size can move all cells within one block to their average position, leading to clustering-like behavior. In theory, an ideal $K$ can move all cells within the same ground truth state to the same position asymptotically in the limit of large number of cells.

For the design of K in GraphDR, we use ${K=\left(I+\lambda L\right)}^{-1}$, which is motivated by the solution to loss function

$$\begin{array}{c}\\ minimize\\ W,Z\end{array}{‖XW-Z‖}_2^2+\lambda {\sum }_{\{i,j\}\in G}{G}_{ij}{‖Z_i-Z_j‖}_2^2, s.t. W^{T}W=I$$

where the first term is the typical PCA loss, and the second term is a graph-based regularization term that encourages cells connected in the graph to be close to each other. $L$ is the graph Laplacian matrix of graph $G$. The second loss term is also shared by a related nonlinear representation method Laplacian eigenmap. Compared to Laplacian eigenmap, it allows a linear interpretation not available to Laplacian eigenmap and avoids the difficulty when the graph contains disconnected components. The analytical solution to the optimization problem is $Z={\left(I+\lambda L\right)}^{-1}XW$, where $W$ is the top-n eigenvectors of ${X^T\left(I+\lambda L\right)}^{-1}X$ where $n$ is the dimensionality of $Z$. The existence of an analytical solution makes it much easier to be analyzed, modified, and incorporated in downstream analyses compared to methods that do not.

For graph $G$, a practical and empirically well-performing choice for GraphDR is the nearest-neighbors graph. The graph construction process can also incorporate experimental design or prior knowledge information (see next section for more details).

GraphDR can also be applied with a predefined $W$ matrix or without reducing the dimensionality. If $W$ is fixed to be identity matrix in order to preserve the original input space, the problem becomes

$$\begin{array}{c}\\ minimize\\ Z\end{array}{‖X-Z‖}_2^2+\lambda {\sum }_{\{i,j\}\in G}{G}_{ij}{‖Z_i-Z_j‖}_2^2$$

The solution is also simplified as $Z=KX$, while K remains unchanged as ${\left(I+\lambda L\right)}^{-1}$. Notably, preserving the input data dimensionality allows preserving the ability of choosing a linear subspace to visualize after applying the transformation, allowing more flexible comparison of datasets processed separately. For example, a user can construct $G$ from PCA transformed data and apply GraphDR to the full gene by cell matrix in order to obtain Z without reducing dimensionality. Apply any linear transform $W$ to this representation Z is equivalent to applying GraphDR with $W$ being the predefined features space linear transformation matrix.

GraphDR reduce to linear representation when regularization parameter $\lambda$ is 0 and the value of $\lambda$ controls the tradeoff between nonlinear regularization which contributes to better cell type representation and preserving the interpretation of the corresponding linear representation. Note that choosing very high values of $\lambda$ may lead to some distortion and compression of the span of the data compared to the linear representation. Smooth interpolation between any GraphDR representation and the corresponding linear representation can be obtained by generating a series of representations by gradually reducing $\lambda$ to 0.

For large-scale evaluation of GraphDR method, we used the data and cell type annotations from the Saelens et al. 339-dataset benchmark¹⁰. Specifically we measured the local cell type representation quality score by the average accuracy of predicting the cell type identity of each cell by the cell type of its nearest neighbor by Euclidean distance in the representation. We measured the global gene expression space preservation score by computing the Pearson correlation between the pairwise distances in the input data space and the pairwise distances in the representation space. The relative global gene expression space preservation score is further computed by dividing the global gene expression space preservation score of the PCA representation at the same dimensionality.

GraphDR graph construction incorporating experimental design

The graph construction step in GraphDR can flexibly incorporate specific experimental design information, such as batch and time-series design (Extended Data Fig. 3), for better representing the biological variations of interest. We provide a few examples here which can be generalized to other scenarios: for experiments performed in two or multiple batches, nearest-neighbor connections (if the batches contain the same cell types) or mutual nearest neighbor connections¹⁹ (if the batches may contain different cell types) between all pairs of batches can be introduced in addition to the nearest-neighbor graphs constructed for each batch; for experiments with a time-series design, the graph can be constructed by combining the nearest neighbor graphs for each time point and the k-nearest neighbor connections between all adjacent time points; for experiments with both batch and time series design, in addition to constructing graph for each batch in the same way as the time-series design, nearest neighbor connections between two batches in the same or adjacent time points can be added.

Computational efficiency optimization for GraphDR

With the constant growth in single-cell dataset size, it is important to design fast algorithms that scale with the dataset size. We have optimized the performance of GraphDR, resulting in an ultrafast method that takes only 1.5 min for 1.3 million cell datasets. With only CPU computing, GraphDR takes 5 minutes to analyze a large 1.3 million cells dataset on a typical modern server machine (2x Xeon Gold 6148), which is 10x faster than UMAP (52 minutes), currently one of the fastest nonlinear dimensionality reduction methods. For very large datasets that will likely become available in the near future, we developed a GPU-accelerated version of GraphDR, which takes only 1.5 minutes to analyze 1.3 million cells dataset and 18 minutes for 10 million cells simulated dataset (1x Tesla V100). To achieve this speed, each major step of computation was optimized to use fast algorithms and implementations.

The two major steps in the GraphDR algorithms are the graph construction and the step of solving the output Z. To speed up the graph construction step, we leveraged recent progresses in fast approximate KNN algorithms (ANN). Exact KNN algorithms based on ball-tree or KD-tree fit the need for small to medium-sized datasets but do not scale to very large number of cells. For ANN algorithms, we support both the HNSW method²⁰ from NMSlib written in C++ with python binding, and an alternative pure python implementation of NN-descent method²¹ built into the package (originally implemented by the UMAP package²). The HNSW option is faster and used for our performance test.

In the final step of computing $Z$, for problems with a large number of cells, it is much faster to avoid explicit computation of $K$ but solving $Z$ with a linear solver. This is because the inverse of $K, I+\lambda G$ is sparse and thus allows fast computation. To implement the linear solver efficiently with modern multicore architecture we used libraries with highly optimized linear algebra routines, including taking advantage of CUDA-based GPU computation which gives the best performance.

StructDR: unified framework for structure discovery

We propose to unify cluster, trajectory, and surface estimation by formulating it as a nonparametric density ridge estimation problem. The nonparametric density ridge estimation problem can be solved via the subspace constrained mean shift (SCMS) algorithm^16,22. The statistical theory of nonparametric density ridge estimation is described in detail in ^15,17.

Briefly, density ridge generalizes the concept of local maxima in probability density functions, whereas zero-dimensional density ridges are local maxima of the density functions, one-dimensional or two-dimensional ridges are curves or surfaces which have maximum density locally except for one or two orthogonal directions with the least negative curvature (formal mathematical definition can be found below). Gradient based algorithms can be generalized to identify density ridges of arbitrary dimensionality. Specifically, the mean-shift algorithm which projects any points to zero-dimensional density ridges / local maxima can be generalized to subspace constrained mean-shift (SCMS) algorithm which projects points to density ridges or arbitrary dimensionality¹⁶. Therefore, zero-dimensional ridge estimation is equivalent to clustering with mean-shift algorithm, and one- and two-dimensional ridge estimation can be considered trajectory and surface identification algorithms.

More formally, in a N-dimensional space and positions of cells in this space representing cell states from single-cell data, nonparametric ridge estimation identifies positions that satisfy the condition $R=\{x:‖G_d\left(x\right)‖=0,{\lambda }_{d+1}(x)<0\}$,¹⁵ where $d$ is the dimensionality of the density ridge. $‖G_d\left(x\right)‖=0$ is the key condition that requires the projected gradient of the density function at any position on the $d$-dimensional density ridges to be zero. The projected gradient at any position $x$ can be computed from the gradient by setting the values on the directions of the top-d eigenvectors of the Hessian of the log density function at $x$ (eigenvalues ranked in descending order). Kernel density estimator with Gaussian kernel is used to estimate the probability density function as it provides a smooth density function that also allows fast computation of derivatives. ${\lambda }_{d+1}\left(x\right)<0$ is a stability condition that requires trajectory to include points which are ‘local maxima’ instead of ‘local minima’ in probabilistic density function, where ${\lambda }_{d+1}\left(x\right)$ is the $d+1$ th largest eigenvalue of the Hessian matrix of probability density function. This condition is automatically satisfied with the SCMS algorithm.

We use the subspace-constrained mean-shift (SCMS) algorithm (Supplementary Information) to simultaneously solve the problem of identifying the density ridges and projecting individual cells to the trajectory. Notably, an additional advantage of this approach is that not only all estimated trajectory positions can be directly interpreted as cell states in the input space, all possible cell states, including cell states not observed in the input set, can be mapped to their corresponding positions on the density ridges.

The algorithm iteratively moves any point toward the projected gradient direction, until it converges to a point at which the projected gradient is zero. To allow fast convergence, the step size of each update along the projected gradient direction is decided based on the step size of the mean-shift algorithm, which is a fix-point iteration algorithm with good empirical convergence properties. To integrate over the projected gradient curve and project single-cells more accurately, we prefer to use a smaller step size than the standard mean-shift and introduce a multiplication factor $a$ for step size which is usually set to values <1. StructDR can be applied with arbitrary density ridge dimensionality $d$, and $d$=0 (cluster),1 (trajectory), or 2 (surface) are the most interpretable. As $d$ increases the projected cell positions on density ridges approaches the input data point.

StructDR can in principle be used with any data representation, but we recommend using it with GraphDR or linear representations such as PCA, as they allow clear interpretation of the output by allowing any position and direction on the trajectory to have a clear meaning in the original data space. GraphDR synergizes with StructDR by addressing the limitation of applying the original NRE method to single cell omics data. Specifically, the original NRE method becomes less statistically efficient when applied to single-cell data with higher dimensionality (e.g. when the number of principal components used is > 6), limiting the method from utilizing all available information. To address this challenge, we utilize GraphDR to generate a linearly interpretable representation of the data, which reduces high-dimensional noise and enables StructDR to effectively use all informative principal components for density ridge structure estimation.

Even though GraphDR and StructDR methods aim to preserve linear interpretability, they provide nonlinear representations that do not replace linear representations in all cases. For example, the representations for individual cells in GraphDR or StructDR representations are not independent and statistical methods that require such assumption should not be applied.

Estimation of confidence set of density ridge with StructDR

As described in Chen et al.¹⁷, the bootstrap confidence set can be constructed through the following procedure: 1. first generate $N$ bootstrap samples by via sampling with replacement; then estimate density ridges for each bootstrap sample; 2. for each position in the density ridge set estimated from the original sample, calculate the distance to its nearest position in each bootstrap sample density ridge set; 3. take $a$-upper quantile of the distances $t_{\alpha }$, and the $a$-confidence set of each estimated ridge position is constructed as a sphere of radius $t_{\alpha }$ centered at the estimated ridge position.

For interpretation of the confidence sets constructed, two properties of this approach of constructing confidence sets for density ridge positions should be noted. First, the true density ridges considered are the density ridges of the smoothed true data distribution after applying the same KDE kernel. Second, the theoretical asymptotic properties of bootstrap statistical inference are only valid for linear representations for which no cell-to-cell dependencies have been introduced. Most nonlinear representations, including GraphDR, introduce dependencies across cells and generalizing the bootstrap procedure to methods such as GraphDR awaits further work. Finally, even though resampling-based methods can be widely applied, and have indeed been applied for the analysis of stability of trajectory estimation methods¹⁰, not all resampling estimates can be used to construct confidence sets. In fact, in most cases they do not correspond to confidence sets, and StructDR is specifically motivated by the statistical works on nonparametric ridge estimation^15,17 which showed the theoretical properties of bootstrap-based inference of confidence sets with these algorithms.

Adaptive density ridge dimensionality

To allow flexible representations of data containing complex structure with different dimensionalities, we propose the use mixed-dimensionality representation that adaptively determines ridge dimensionality. Empirically, we find mixed one and two-dimensional density ridges to be a robust and informative representation of data structure. In this mode, cells with one dominant direction of variation based on the curvature of the density function are projected onto one-dimensional density ridge, while the rest are projected onto two-dimensional density ridges. Specifically, we modified the SCMS method to adaptively determine, for any position in the space, the ridge dimensionality between $d$ =1 (trajectory) mode vs $d$ =2 (branch point or surface) mode at every iteration. This decision is based on the eigengap between the first and second eigenvalues of the Hessian matrix of the log probability density function: if $\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_1-{\lambda }_{-1}}$ surpassed the specified threshold $d$ =1 is used, otherwise $d$ =2 is used, where ${\lambda }_1, {\lambda }_2$, and ${\lambda }_{-1}$ represent the first, second, and last eigenvalues.

Simulation study for evaluation of confidence set

We used inferred trajectory from a real dataset¹¹ as the ground truth to generate synthetic datasets. 100 simulated datasets are generated by adding independent Gaussian noise to the samples from ground truth trajectory density function. For each simulated dataset, 20 bootstraps were used to construct confidence set of trajectory positions based on distance from bootstrapped trajectories to the estimated trajectory as described in ¹⁷. The estimated confidence sets with a coverage probability were then compared with the ground truth to decide the true proportion of times any point at the ground truth trajectory is covered by the confidence set constructed.

Graph construction from density ridge positions

In StructDR output, density ridges are represented by positions of data points projected to these ridges. To allow more flexible applications we construct graph representations from these projected points. To do so, we first construct a candidate graph connecting k-nearest neighbors in both the projected cell space and in the input cell space. The candidate graph is then simplified by choosing only the one nearest neighbor in $2^d$ orthogonal or opposite directions in the projected cell space, where $d$ is the density ridge dimensionality (e.g. two nearest neighbors are chosen for $d=1$ or trajectories, and 4 are chosen for $d=2$ or surfaces). We chose the directions based on first-d eigenvectors of the Hessian, leveraging the observation that density ridges typically extend on same directions as these eigenvectors. Optional filters can be applied to remove edges based on edge length and direction. The output of this step is a graph representation of density ridges, without imposing prior assumption on its structure type and does not require all cells to be connected, and we call this algorithm SimpleNNG and implemented it in our python package. To construct a minimal graph representation that is guaranteed to connect every cell, we construct a minimum spanning tree graph based on SimpleNNG output with two additional steps: 1. Add edges to connect every connected component to its nearest neighbor in each of the other connected components. 2. Extract a minimum spanning tree of the whole graph. The MST algorithm is robust but assumes tree structure. The SimpleNNG algorithm does not make such assumption and are thus more suitable for cyclic trajectory types or disconnected graph. For simplicity, the MST algorithm is used in all analyses in this manuscript unless otherwise indicated. For use with dynbenchmark package, we further convert a graph to a dynbenchmark-compatible graph format with backbone cells assigned based on betweenness centralities. Cells that passed a betweenness centrality threshold of 10 times the total number of cells are assigned as backbones of the graph.

Reporting Summary. Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

The 339-dataset benchmark dataset published by Saelens et al.¹⁰ was downloaded from https://zenodo.org/record/1443566. The unnormalized performance scores were extracted from https://github.com/dynverse/dynbenchmark_results/blob/1ac55e6c54a950890208b1f7730092d39783dfd2/06-benchmark/benchmark_results_unnormalised.rds. The normalized scores were computed as in ¹⁰, with the scaling factors kept to the same values as the original methods benchmarked. Other singe-cell datasets analyzed in this manuscript were from the following publications^{6,13,14,18,23–26}. Scanpy package⁸ was used for preprocessing steps as described in ²⁷ when needed. We created a Zenodo record for https://zenodo.org/record/3710980²⁸ that contains all the input data used in this manuscript.

Code availability

All methods described in this manuscript are implemented in an open-source python package quasildr https://github.com/jzthree/quasildr. A Code Ocean capsule of the package is provided (https://doi.org/10.24433/CO.9410876.v1)²⁹.

Extended Data

Extended Data Fig. 1. Visualization of first two principal components in PCA, GraphDR, and tSNE visualizations.

We compared the PCA, GraphDR, and tSNE representations by the values of first two principal components (PCs, shown by color) on a developing mouse hippocampus dataset (a-b) (Hochgerner et al. 201811) and a mature mouse brain dataset (c-d) (Zeisel et al. 201818). The top weighted genes by absolute values for the first two PCs are also shown (b, d).

Extended Data Fig. 2. Dataset alignment with GraphDR further improves dataset comparison.

Comparison with applying GraphDR without (a, c) and with (b, d) graph-based dataset alignment on two hematopoietic datasets (Nestorowa et al. 201625 and Paul et al. 201526). The GraphDR visualizations are colored by cell types (a, b) and by datasets (c, d). The cell types are common myeloid progenitors (CMPs), granulocyte-monocyte progenitors (GMPs), lymphoid multipotent progenitors (LMPPs), long-term HSCs (LTHSC), megakaryocyte-erythrocyte progenitors (MEPs), multipotent progenitors (MPPs). Specifically, GraphDR with graph-based dataset alignment constructs a joint graph that also connects the nearest neighbors between datasets (see batch design in Extended Data Fig. 3).

Extended Data Fig. 3. Experimental design encoding through graph construction.

Experimental design information can be encoded through graph construction in GraphDR. Each arrow indicates that nearest-neighbor connections are established between the two groups, where two connected cells are in the two different groups. Self-loop indicates nearest-neighbor connections from cells within a group. Basic design constructs a nearest neighbor graph using all cells, which is suitable for single-batch experiments or experiments with minimal batch effects. Batch design addresses batch effects by introducing nearest-neighbor connections between all pairs of batches, in addition to with-in batch nearest-neighbor connections. Time-series design extends basic design by only allowing connections between the same and adjacent time points. Batch + time series design introduces nearest neighbor connections between two batches in the same or adjacent time points.

Extended Data Fig. 4. Visualization of zebrafish whole embryo single-cell developmental landscape with GraphDR.

Application of GraphDR to a single-cell dataset (Farrell et al. 201823) with a time-series design. a. Single-cell visualization by GraphDR, colored by developmental stages. b. Comparative visualization of developmental stages. This shows the “cross-section” view by visualizing the second and third dimensions. c-d. Single-cell visualization by GraphDR, colored by cell origins.

Extended Data Fig. 5. Visualization of Xenopus tropicalis whole embryo single-cell developmental landscape with GraphDR.

This is an example of applying GraphDR to a single-cell dataset with a batch+time-series design (Briggs et al. 201824). a. Single-cell visualization by GraphDR, colored by developmental stages. b. Comparative visualization of developmental stages. This shows the “cross-section” view by visualizing the second and third dimensions. c-d. Single-cell visualization by GraphDR, colored by cell origins.

Extended Data Fig. 6. Schematic overview of StructDR density ridge estimation procedures with the SCMS algorithm.

(a-b) StructDR starts from performing kernel density estimation with Gaussian kernel on the input cells. (c) Based on the estimated density function, and a selected density ridge dimensionality d (d=1 in this example), the SCMS update can be derived for any position in the space from the gradient and Hessian of the log density function. For any data point or position of interest, iteratively updating the position with the SCMS update will project the data point or position to density ridges of chosen dimensionality. (d). Optional step: construct graph connecting points on the density ridges with one of two optional methods (Methods). The backbone of the graph can be specified based on a betweenness centrality threshold.

Extended Data Fig. 7. Overview of the unified framework of cluster, trajectory, and surface analysis with StructDR.

(a) StructDR uses the SCMS update for the estimation of clusters, trajectories, and surfaces, which can all be derived based on gradient and Hessian of log density function. (b) Examples of projection paths by SCMS updates for zero, one, and two-dimensional density ridges. (c). Comparisons of SCMS algorithms for 0, 1, 2, or k-dimensional density ridges. The SCMS update can identify any k-dimensional density ridges, by projecting a gradient-based update onto subspace spanned by the k+1 th to last eigenvector of the Hessian of log density function.

Extended Data Fig. 8. Performance score distributions on the 339-dataset benchmark shown by dataset type.

Per-dataset performance scores are computed based on Saelens et al. 2019. The performance score distributions are shown with violin plots, separated into panels by dataset types. The performance of applying StructDR + GraphDR with two graph construction algorithms, MST and SimpleNNG, are shown along with the performance of other algorithms benchmarked in Saelens et al. 2019¹⁰.

Extended Data Fig. 9. Trajectory identification with zero, one, and two-dimensional density ridges example on a developmental hippocampus single-cell dataset.

The circle symbols indicate zero-dimensional density ridge positions (local maxima of density function). The red dots indicate one-dimensional density ridge positions (trajectory). The black dots indicate two-dimensional density ridge positions.

Extended Data Fig. 10. Simulation studies of confidence sets construction with nonparametric ridge estimation.

100 simulation datasets were generated. For each dataset the confidence sets for each estimated trajectory were estimated with 20 bootstraps. x-axis shows the expected coverage probabilities of the constructed confidence sets. y-axis shows the observed proportion that the true trajectory position is covered by the confidence set.