¹³C-Optimized HTS NMR RF Coil Design at 21.1 T

Abstract

We present the design of a novel high-temperature superconductor double-sided racetrack resonator for a ¹³C optimized nuclear magnetic resonance (NMR) transmitter/receiver coil. The coils operate in a 21.1 T magnet and accommodate a 3 mm × 6.2 mm cross-section rectangular sample tube. The design includes the incorporation of revised finger lengths to improve the homogeneity of current density across the fingers, a new laser trimming approach for adjusting the resonance frequency, and improved ability to shift higher-order modes for suitability in ¹H/¹³C NMR probes. Resonator design methodology, simulations and experimental results are presented.

I. Introduction

Nuclear magnetic resonance (NMR) detection of ¹³C is inherently a low-sensitivity process because of its low natural abundance, and small gyromagnetic ratio [1]. Increasing the sensitivity of ¹³C NMR has the potential to be enabling for metabolomics and structural biology. We can improve the sensitivity of the probe by enhancing the quality factor of the coil and increasing the magnetic field of the magnet [2]. Using high-temperature superconductor (HTS) material for the coil significantly increases the quality factor of the resonator [3]. Different types of substrates for growing HTS films are already proposed in [4]. Many microwave applications use YBa₂Cu₃O₇ films on the r-cut sapphire substrate [5].

Multiple split-ring resonators (MSRR), known as racetrack resonators, are widely used in metamaterial [6]-[7] and HTS NMR coil designs [8]-[10]. In [6], the authors modeled MSRR with a simple LC equivalent circuit which only works for the first resonance frequency. In [8], the authors incorporate a four-capacitor racetrack for the ¹H-channel with a 1.5 mm sample tube at 14.1 T. The racetrack coil design in [9] is for the ¹H-channel with a 1 mm sample tube at 14.1 T. In [10], the authors used HTS coil design based on the racetrack for microscopy at 9.4 T. All the above articles used the racetrack for the ¹H-channel, which is the channel with the highest frequency, so the higher-order modes of the racetrack were not a concern.

We propose to use novel double-sided racetrack coils for ¹³C-channel, which is at almost exactly a quarter of the frequency of the ¹H-channel, and so the higher-order modes of the structure are critical to proper operation. We refined the design to improve current distribution and allow for laser trimming to adjust the resonance frequency without damage to the film on the opposite side of the substrate. We also use a rectangular sample tube to allow for more sample volume which should increase the maximum achievable signal-to-noise [2].

We begin our discussion by describing the simulation and fabrication process, followed by the NMR coil design criteria.

II. Simulation and Fabrication

In this paper, the electromagnetic simulations are of two types: first, eigenmode solution of finite element method (FEM) by ANSYS HFSS, and second, the discrete frequency sweep of S-parameters simulation by Planar EM in ANSYS HFSS 3D Layout, which implements mixed potential integral equation with the aid of method of moments (MoM) for the surface current approximation [11]. For simplicity, we refer to these simulations as FEM, and MoM, respectively in this text.

We obtained double-sided YBCO films on 76.2 mm diameter, 432 μm thick, r-plane sapphire from Ceraco GmbH (Ismaning, Germany). Star Cryoelectronics (Santa Fe, NM) performed the patterning and dicing. We used normal-metal inductively-coupled loops to measure S-parameters and matched quality factor of the resonance with a C2409 Copper Mountain Technologies (Indianapolis, IN) vector network analyzer with the coil cooled down to ≈30 K inside a test chamber connected to a Conductus (Sunnyvale, CA) closed-cycle cryocooler.

III. Coil Design Criteria and Results

In this section, we summarize important HTS NMR coil design criteria, and we compare the FEM and MoM simulation results with the measured data for the uneven gap-size racetrack.

A. Surface current distribution

To generate the large NMR excitation field needed for ¹³C spectroscopy, we need to develop a resonator that carries as much current as possible. As superconducting materials are limited by a critical current density J_c, we propose to modify the racetrack design to spread the current out more evenly across the resonator. In the even gap-size racetrack design, inner fingers carry much less current than outer fingers since outer fingers are longer, and they have higher capacitance. Based on the equivalent circuit of [6] for the first mode, one way to compensate is by shortening the outer fingers [12]. A further step is to include another coil on the other side of the substrate to form a double-sided design.

Fig. 1 shows the coil design and its trace width, mean width, and ending gap size. We optimized the current distribution by decreasing the capacitance on the outer fingers. One side of the substrate has 30 fingers whereas the other side has 28 fingers. We call the former the front side, and the latter the back side. Two additional outer fingers are introduced only on the front side (Fig. 1a) for fine adjusting of the resonance frequency. Moreover, the front and back-side coils are rotated by 180 degrees (Fig. 1a and Fig. 1b), so parts of the fingers that are on the symmetry plane do not have any overlap with the other side to allow laser trimming of each side without damage to the opposite side. Reduction of the magnetization and eddy current on the fingers promotes sharper linewidth in the NMR spectrum [3]; therefore, we divide each finger into six fingerlets with a width of 8.8 μm each (Fig. 1c). Since including all the fingerlets in the frequency calculations is impractical due to time and memory constraints, we used only two fingerlets in the simulations. We found that adding an additional fingerlet led to only a minimal change (less than 0.5% for FEM and less than 2% for MoM) in the simulated resonance.

Fig. 1.

¹³C double-sided racetrack coil. (a) 30-finger side or front side. This side has two non-overlapping fingers with the other side, sketched in yellow. (b) 28-finger side or back side. (c) Each finger consists of six fingerlets. A and B show the trace width and the mean width, respectively. L shows the ending gap size for innermost finger. Dashed lines determine the symmetry plane passing through the midpoints of the fingers.

Fig. 2 compares the magnitude of the surface current density of two double-sided coils by MoM simulation. Both have the same trace width, mean width, and mean length. The only difference between these two designs is the ending gap size of the fingers of the coil. For the even gap-size racetrack (Fig. 2a), 14 inner fingers have lower than 75% of the maximum current density, but for uneven gap-size (Fig. 2b), only four inner fingers have lower than 75% of the maximum current density (Fig. 2c). So, increasing the ending gap size which shortens the outer fingers leads to a more evenly distributed current.

Fig. 2.

MoM simulation of surface current density magnitude for the first resonance frequency on (a) even gap-size racetrack, and (b) the double-sided uneven gap-size racetrack. Two coils have the same mean width, mean length, and trace width; moreover, they have 30 fingers on one side and 28 fingers on the other. Simulation space is also the same and both coils modeled as perfect conductors. The simulated surface current density’s unit is arbitrary as we set the input power to have the same maximum current density in both simulations. (c) shows magnitude of finger’s current on the symmetry plane in (a) and (b)..

B. Adjusting the coil’s dimensional parameters

The coil’s dimensions determine the resonance frequencies. Increasing the number of fingers [6] and increasing the ending gap size lowers the resonance frequency but increasing the gap size between the fingers and finger width moves it to higher frequencies. Increasing the mean width and the mean length of the coil reduces the resonance frequency. We chose the active sample length of the coil to be 18 mm as in [2] and [8] to match the design of commercially available NMR magnets.

Changing the coil’s dimensions to adjust the resonance frequency also changes the magnetic field inside the sample tube. It is important to have a homogenous magnetic field inside the sample tube for NMR applications. Fig. 3 demonstrates the FEM simulation of the magnetic field of the proposed resonator through a cross-section taken midway down the sample tube. The magnetic field drops abruptly outside of the sample tube along the long side. The magnitude of magnetic field changes 18% along the long side whereas it changes 2% along the short side in the sample tube. This level of homogeneity is slightly better than our previously reported ¹³C-optimized probe [8] which has been successfully used for routine NMR experiments. We can have a more homogenous magnetic field inside the sample tube by making the mean width wider or making the long side of the sample tube shorter. But as this resonator is part of a multichannel probe where the outer coils limit the width of the inner ¹³C coils, we did not increase the width further. Also, as the HTS coil’s substrates are planar, we used a rectangular sample tube as large as we could to improve the NMR sensitivity.

Fig. 3.

FEM simulation of the magnetic field distribution of the ¹³C coil in the symmetry plane for the first mode. The distance between sapphire bars is 5 mm. Arrows and colors show the direction and magnitude of magnetic field, respectively. A: the front side. B: the back side. C: Sapphire substrate. D: Sample tube 3 mm × 6.2 mm with 0.4 mm wall thickness.

C. Adjusting the higher-order modes

A racetrack coil, like any resonator, has several modes beyond its useful fundamental mode. This is of importance in the design of multi-channel NMR probe resonators since the presence of a spurious mode of a low-frequency resonator at the Larmor frequency of a high-frequency nuclei of interest can cause interference. We refined the ¹³C resonator design so that it has no mode at 900.130 MHz which is the ¹H Larmor frequency in a 21.1416 T magnet after the frequency adjustment.

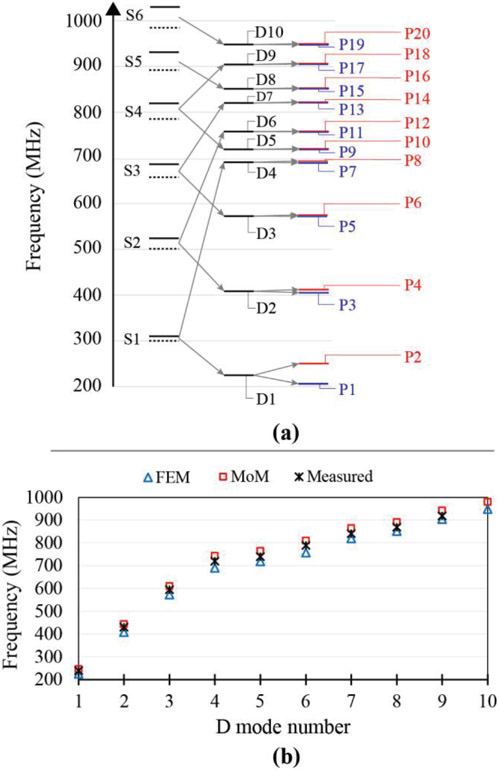
To understand how to adjust higher-order modes, we characterize each mode of the Helmholtz configuration. Each single-sided racetrack coil mode has a unique current and magnetic field distribution. It is beyond the scope of this paper to describe them. Instead, we will denote these modes as S1, S2, and so on, and discuss how these modes interact when double-sided racetrack coils are in a pair. Fig. 4a shows the formation of the first twenty modes of a pair of double-sided racetrack coils. S1–S6 show the first six single-sided modes. The front side has two more fingers than the back side, thus its single-sided modes are slightly lower in frequency (dotted lines in Fig. 4a). The single-sided mode interacts with its counterpart on the opposite side of the substrate to generate two separate modes (D). For example, S1 modes couple to form D1 and D4 modes. In the D1 mode, the currents on the two sides of the substrate are co-rotating, whereas in the D4 mode, the current on the two sides are counter-rotating. The substrate thickness and coil design affect the coupling and splitting between the modes. Each of the double-sided modes interacts with its peer on the other substrate to generate two distinct pair modes (P) e.g., D1 modes interact to make P1 and P2. We note from Fig. 4a that since the distance between the substrates is much larger than the substrate thickness, the splitting between P modes is smaller than the splitting between D modes. Moreover, the higher-order modes have a smaller dipole moment and hence a lower coupling factor, and splitting between the modes get very small like P15 and P16, and it becomes very hard to identify these higher-order modes with S11 spectra from MoM simulations or experiments; however, they are clear with FEM eigenmode simulation, and we assigned these modes with FEM simulations.

Fig. 4.

(a) Mode splitting in the pair of double-sided racetrack coils based on FEM simulations. Solid lines S1–S6 show the first six modes of the single-sided racetrack for the back side, and dotted lines are for the front side. D1–D10 are the first ten modes of the double-sided racetrack. P1–P20 are the first twenty modes of the pair of double-sided racetrack coils. (b) FEM and MoM simulation comparison with the measured data from the test chamber for the double-sided racetrack.

Fig. 4b compares MoM and FEM simulations with the measured data for the double-sided racetrack. The measured modes are close to the simulation, and in this particular example they are between the MoM and FEM simulation. So, we could predict the measured modes by having those simulation results before the fabrication. MoM simulated resonance frequencies are within ≈3% of the measured data and FEM simulated D1 mode frequency is in ≈6% of the experimental result (Fig. 5a) and FEM simulated D9 mode is within ≈2% of the measurement. As shown in Fig. 4b, the closest mode below the ¹H Larmor frequency is D8. The measured D8 mode is 868 MHz and FEM simulation is 850.7 MHz. Other modes are either higher than the ¹H Larmor frequency or lower than D8.

Fig. 5.

Simulation and experimental resonances of a double sided resonator as a function of trimmed fingers. (a) FEM, and MoM simulation comparison with the experimental data shown by Exp. 1, Exp. 2, and Exp. 3 for D1 mode in the trimming process mentioned in the text. (b) FEM simulation of D8 mode in the trimming process described in the text. Lines are only connecting the data points to help us see the trend and do not convey any other information.

D. Frequency adjustment after fabrication

It is typical to design a HTS coil below the target frequency and adjust the final frequency of the resonator by laser trimming of the YBCO fingers as described in [13]. This is due to uncertainties in the fabrication process, such as substrate thickness, film defects, and under or over-etching of YBCO. These can change the modes’ frequencies of the resonator from its designed resonance frequency. The ¹³C Larmor frequency is 226.338 MHz at 21.1416 T and the Helmholtz-like pair’s resonance frequency was 220 MHz before any adjustment of the frequency by laser trimming. Its quality factor was ≈1.7×10⁴ at a CW power level of 15 dBm with a cylindrical brass shield of 35 mm diameter when measured inside the cryogenic test chamber at 30 K.

The novel trimming approach of the resonator involves a coarse and a fine step:

1- In the coarse step, we nullify one finger at a time to produce discrete frequency shifts. To do this, we cut each finger in the symmetry plane shown by the dashed line in Fig. 1. Our procedure was to trim one innermost finger at a time on each side starting by the front side i.e., 1: one cut for the front side, 2: one cut for the front, and one cut for the back, 3: two cuts for the front and one cut for the back side, etc. Fig. 5a shows the resulting frequency shift of the D1 mode of a single double-sided coil for the first eight cuts which is about a 1 MHz increase per cut. In Fig. 5a, the trend of simulation data either by MoM or FEM agrees well with the experimental data, and by fitting the simulation results to the measured resonance frequency before trimming, we could estimate the resonance frequency after the trimming with 0.1 MHz accuracy. In section C, we mentioned the importance of the D8 mode, and it is crucial that it does not interfere with the ¹H Larmor frequency after the trimming process. Fig. 5b shows the shift of the D8 mode in the coarse trimming. The D8 mode has its current concentrated in the back side fingers, and so D8 shifts less when we trim the front side. In contrast, current in the D1 mode is split evenly and so responds similarly to trims on either side. This asymmetric behavior helps us to provide a trimming plan either with a small or large shift of the D8 mode depending on the frequency shifts observed from fabrication uncertainties.

2- The fine trimming involves cutting the ending points of two outermost fingers in Fig. 1a. By FEM simulations, we predict that if we start to just do the fine trimming, after 1 mm trimming of both outer fingers, the first mode upshifts ≈0.53 MHz, and the D8 mode increases ≈2.8 MHz, and for 2 mm trimming, the D1 shifts by ≈0.95 MHz and the D8 mode increases ≈5.2 MHz.

IV. Conclusion

We described a new design, and we showed the simulation and experimental results of ¹³C HTS coils with a double-sided racetrack Helmholtz pair. In our design and simulations, the performed MoM simulation was closer to our measurement of lower-order modes whereas the eigenmode FEM was more efficient computationally for identifying the higher-order modes. Design simulations show expected improvement in the current distribution, higher-order modes, and fine adjusting of the resonance frequency by laser trimming. These coils are a part of our ¹³C-optimized NMR probe which has potential use in a wide range of research areas, especially in metabolomics and protein structural studies.