A comparison of statistical methods to predict the residual lifetime risk

Abstract

Lifetime risk measures the cumulative risk for developing a disease over one’s lifespan. Modeling the lifetime risk must account for left truncation, the competing risk of death, and inference at a fixed age. In addition, statistical methods to predict the lifetime risk should account for covariate-outcome associations that change with age. In this paper, we review and compare statistical methods to predict the lifetime risk. We first consider a generalized linear model for the lifetime risk using pseudo-observations of the Aalen-Johansen estimator at a fixed age, allowing for left truncation. We also consider modeling the subdistribution hazard with Fine-Gray and Royston-Parmar flexible parametric models in left truncated data with time-covariate interactions, and using these models to predict lifetime risk. In simulation studies, we found the pseudo-observation approach had the least bias, particularly in settings with crossing or converging cumulative incidence curves. We illustrate our method by modeling the lifetime risk of atrial fibrillation in the Framingham Heart Study. We provide technical guidance to replicate all analyses in R.

1. Background

The cumulative incidence of a disease is defined as the probability of developing disease while accounting for the competing risk of death. When age is the time scale, the lifetime risk for developing the disease is then defined as the cumulative incidence function at a fixed advanced age. Lifetime risk is a tractable quantity that can motivate changes in lifestyle behavior, particularly among younger individuals or those who may not be at short-term risk of disease [1]. The residual lifetime risk is especially of interest when the risk for developing the disease of interest, for example atrial fibrillation, increases markedly only after a certain age. The residual lifetime risk is the cumulative incidence of the disease among individuals who attained a given index age τ₀ disease-free, up to an advanced age τ, e.g. 95 years. We refer to this quantity as the lifetime risk for short.

Prediction of the lifetime risk uses age as the time scale, combines information on participants entering the risk set at different ages, and accounts for the competing risk of death [3–5]. Short-term risk predictions may often neglect the competing risk of death. However, the competing risk of death increases with age and must be accounted for in order to avoid overestimation when predicting lifetime risk. Accurate lifetime risk prediction can quantify burden of disease over the lifecourse, facilitate identification of risk factors in mid-life, and help target interventions which prevent disease in the long-term [2].

Beiser et al. [3] previously described a modified Kaplan-Meier estimator to allow delayed entries, based on estimators introduced by Gaynor et al. [4] and Larson and Dinse [6]. Brookmeyer et al. [5] developed estimating equations for the lifetime risk using a Markov multi-state model with age as the time scale. Carone et al. [7] developed an estimator of the lifetime risk for a cross-sectional survey augmented with prospective follow-up.

In this paper, we focus on methods for predicting the lifetime risk based on covariates measured at the index age. We consider that participants are observed at periodic examinations and covariates are not collected exactly at the index age. Thus, we allow a window of time for participants to enter the risk set, but we restrict the window so covariates are not measured too far from the index age [9]. The literature on methods for predicting the lifetime risk conditional on covariates is scarce. Here, we describe and compare the performance of three statistical methods.

First, we model directly the lifetime risk using the pseudo-observation technique. We derive the pseudo-observations at a fixed age, τ, which avoids assumptions about the functional form of risk factors over time, and incorporate left truncation in the Aalen-Johansen estimator of the cumulative incidence function (CIF) [10]. Second, we consider the Fine-Gray model for the association between covariates and the CIF and we use the estimated model coefficients to predict the lifetime risk at a fixed age, τ [11]. Because age is the time scale, we use the approach of Geskus [12] to allow left truncation by using inverse probability of right censoring and left truncation weights (IPCLW). Third, we consider the Royston-Parmar flexible parametric model to allow a more complex baseline subdistribution hazard by using restricted cubic splines [13, 14]. We also show how to use the approach of Geskus to account for left truncation. For both Fine-Gray and Royston-Parmar models, we show how to include time-covariate interactions to model time-varying effects and predict lifetime risk. While the applications of Fine-Gray and Royston-Parmar models to competing risks data are widespread, we are not aware of published work describing how to implement these approaches for lifetime risk prediction.

In Section 2, we briefly remind about the non-parametric estimator of the lifetime risk and its connection to the Aalen-Johansen estimator. In Section 3, we describe the regression model for the lifetime risk using pseudo-observations. In Section 4, we describe the IPCLW approach of Geskus [12] to allow left truncation in subdistribution hazard models. In Sections 5 and 6, we describe how to use Fine-Gray and Royston-Parmar flexible parametric models to predict the lifetime risk at a fixed age, τ. In Section 7, we present a simulation study to compare the methods’ finite sample performance under a wide range of scenarios. We also compare the computing time of each method. In Section 8, we use the described methods to predict the lifetime risk of atrial fibrillation with data from the Framingham Heart Study. We provide the R programs to replicate our analyses at https://github.com/s-conner/lifetimerisk.

2. Non-parametric estimation of the lifetime risk

We consider two causes of failure, ϵ ∈ {1, 2} where ϵ = 1 is the disease of interest (for example, atrial fibrillation) and ϵ = 2 is the competing event (for example, death without atrial fibrillation). With age as the time scale, let L be the entry age, T be the age at failure, C be the age at censoring, δ = I(T < C), and assume C and L are independent of T and ϵ. We consider an index age, τ₀, so that L ≥ τ₀. We observe X = T ∧ C, the age at disease diagnosis, death, or censoring. Moreover, individuals are observed conditional on L < X. We denote Z a n × p matrix of covariates. Then, we observe (L_i, X_i, δ_i · ϵ_i, Z_i) for individuals i = 1, …, n.

The lifetime risk is the cumulative incidence of the disease from index age τ₀ (e.g. 55 years) until an advanced age, τ (e.g. 95 years),

$$\begin{gathered} F_1\left(\tau \mid T>{\tau }_0\right)=P\left(T\le \tau ,ϵ=1\mid T>{\tau }_0\right) \\ ={\int }_{{\tau }_0}^{\tau }S\left(t\mid t>{\tau }_0\right){\alpha }_1(t)dt, \end{gathered}$$

in which α₁(t) is the cause-specific hazard function for event 1, A(t) is the cumulative all-cause hazard function, and $S\left(t\mid t>{\tau }_0\right)=exp\left(-{\int }_{{\tau }_0}^{t}A(u)du\right)$ is the overall survival function (of being alive and disease-free) [15].

The lifetime risk is estimated non-parametrically by

$${\widehat{F}}_1\left(\tau \mid T>{\tau }_0\right)=\sum _{{\tau }_0<t_j\le \tau }\widehat{S}\left(t_{j-1}\right)\frac{\Delta N_1\left(t_j\right)}{Y\left(t_j\right)}$$

where $N_k(t)={\sum }_{i=1}^{n}I\left(L_i<X_i\le t,{\delta }_i=1,{ϵ}_i=k\right)$ is the number of events of cause k by age t, N(t) = N₁(t) + N₂(t) is the number of total events by age t, ΔN_k(t) is the increment N_k(t) − N_k(t−), $Y(t)={\sum }_{i=1}^{n}I\left(L_i<t\le X_i\right)$ is the number at risk just before age t allowing delayed entries, t_j, j = 1, …, J are the unique ages at diagnosis of the disease of interest, and $\widehat{S}(t)={\prod }_{{\tau }_0<t_j\le t}\left(1-\frac{\Delta N\left(t_j\right)}{Y\left(t_j\right)}\right)$ is the Kaplan-Meier estimator of being alive and event-free at age t allowing delayed entries [3, 4, 16, 17]. The variance is estimated using Greenwood’s formula (see Section 10.1 of Appendix). [4, 18] In the case of one binary exposure (Z is n × 1), we are interested in estimating the difference in lifetime risk between the exposed and unexposed groups,

$$\mu =F_1\left(\tau \mid T>{\tau }_0,Z=1\right)-F_1\left(\tau \mid T>{\tau }_0,Z=0\right).$$

The non-parametric estimator of the lifetime risk, ${\widehat{F}}_1\left(\tau \mid T>{\tau }_0\right)$, is an element of the Aalen-Johansen estimator with three states (alive and disease-free, disease, and death) and allowing left truncation (i.e., age as the time scale) [17, 19]. Connecting the lifetime risk to the Aalen-Johansen estimator allows us to explore statistical methodologies for competing risks data, which have not yet been used for modeling the lifetime risk [20, 21].

3. Pseudo-observation model for the lifetime risk

We first consider a regression model for the lifetime risk using the pseudo-observation technique [20, 22, 23]. Let a generalized linear model for the lifetime risk be

$$g\left[E\left\{\mathbb{1}\left(T_i\le \tau ,{ϵ}_i=1\mid T_i>{\tau }_0\right)\mid Z_i^{\prime }\right\}\right]=g\left\{F_1\left(\tau \mid T_i>{\tau }_0,Z_i^{\prime }\right)\right\}=Z_i^{\prime }\beta$$

where g(·) is a link function and $Z_i^{\prime }=\left(1,Z_i\right)$ is the covariate matrix allowing an intercept term. Here we let g(θ) denote a logit link function, $g(\theta )=\text{ln}\left(\frac{\theta }{1-\theta }\right)$. Other link functions can be used, such as the complementary log-log link function, g(θ) = ln{−ln(1 − θ)}, or the identity link function, g(θ) = θ. We replace $\mathbb{1}\left(T_i\le \tau ,{ϵ}_i=1\mid T_i>{\tau }_0\right)$ with pseudo-observations for the ith individual at age τ. In the presence of left truncation, the pseudo-observation for individual i at age t is given by

$$\begin{gathered} {\widehat{\theta }}_i(t)=\left\{\sum _{i=1}^n\mathbb{1}\left(L_i\le t\right)\right\}{\widehat{F}}_1\left(t\mid T_i>{\tau }_0\right) \\ -\left\{\sum _{i=1}^n\mathbb{1}\left(L_i\le t\right)-1\right\}{{\widehat{F}}_1}^{-(i)}\left(t\mid T_i>{\tau }_0\right) \end{gathered}$$

for individuals who have entered the study by age t (L_i ≤ t), where ${{\widehat{F}}_1}^{-(i)}\left(t\mid T_i>{\tau }_0\right)$ is the estimated CIF at time t without the ith individual [10] The lifetime risk is evaluated at a fixed age, τ, so we estimate the pseudo-observations at a single age τ [20, 24, 25]. Since all individuals have entered the study before τ, the pseudo-observation simplifies to

$${\widehat{\theta }}_i(\tau )=n{\widehat{F}}_1\left(\tau \mid T_i>{\tau }_0\right)-(n-1){{\widehat{F}}_1}^{-(i)}\left(\tau \mid T_i>{\tau }_0\right),$$

where ${{\widehat{F}}_1}^{-(i)}\left(\tau \mid T_i>{\tau }_0\right)$ is the estimated lifetime risk without the ith individual. We then model

$$g\left[E\left\{{\widehat{\theta }}_i(\tau )\mid Z_i^{\prime }\right\}\right]=Z_i^{\prime }\beta .$$

In the presence of independent right-censoring, it has been previously shown that the pseudo-observations at τ are asymptotically unbiased for the CIF at τ given the covariates $Z_i^{\prime }$ [21, 51]. Graw et al. [21] and Jacobsen and Martinussen [51] showed the pseudo-observations can be rewritten with influence functions by Von Mises expansion. The second-order terms converge in probability to 0, while the expectation of the CIF at τ plus the first-order influence function yields the CIF at τ conditional on covariates [21, 51].

The β coefficients are estimated by solving an unbiased estimating equation. A generalized estimating equation

$$U(\beta )=\sum _i{\left\{\frac{\partial }{\partial \beta }{F}_1\left(\tau \mid T_i>{\tau }_0,Z_i^{\prime }\right)\right\}}^T{V}_i^{(-1)}\left\{{\widehat{\theta }}_i-F_1\left(\tau \mid T_i>{\tau }_0,Z_i^{\prime }\right)\right\}=0,$$

is commonly used to estimate β, where V_i denotes the variance function. When using the logit link, the coefficients β are interpreted as log lifetime odds ratios. When using the identity link, the coefficients are interpreted as differences in lifetime risk. The covariance matrix of $\widehat{\beta }$, Σ, may be estimated with a sandwich estimator [21].

If inference at a fixed age is of interest, such as the lifetime risk, the pseudo-observation approach is advantageous because we can focus on the age of interest without imposing assumptions on other ages. However, multiple ages or timepoints can also be accommodated with this approach [20].

We derive the predicted lifetime risk by inverting the link function. With the logit link, the predicted lifetime risk is

$${\widehat{F}}_1^P\left(\tau \mid T_i>{\tau }_0,Z_i^{\prime }\right)=\frac{1}{1+\text{exp}\left(-Z_i^{\prime }\widehat{\beta }\right)}.$$ (1)

The estimated difference in lifetime risk between individuals with covariate profiles Z_i and Z_j is ${\widehat{\mu }}^P={\widehat{F}}_1^P\left(\tau \mid T_i>{\tau }_0,Z_i^{\prime }\right)-{\widehat{F}}_1^P\left(\tau \mid T_i>{\tau }_0,Z_j^{\prime }\right)$. To obtain confidence intervals, we estimate the variance with the multivariate delta method, $\nabla {(\widehat{\mu })}^T\widehat{\Sigma }\nabla (\widehat{\mu })$, where $\nabla (\widehat{\mu })$ is the gradient. Although the pseudo-observations are calculated at one timepoint and are independent, we use the multivariate delta method because the regression model includes multiple coefficients.

4. Inverse probability of right censoring and left truncation weights

In Sections 5 and 6, we use the approach of Geskus [12] to incorporate left truncation with inverse probability of right censoring and left truncation weights. Individuals receive time-dependent weights which are defined at the unique ages of the disease of interest, t_j, j = 1, …, J, as

$$w_i\left(t_j\right)=\{\begin{array}{ll}1\hfill & \text{ if}{L}_i<t_j<X_i\hfill \\ \frac{\widehat{G}\left(t_j-\right)\widehat{H}\left(t_j-\right)}{\widehat{G}\left(X_i-\right)\widehat{H}\left(X_i-\right)}\hfill & \text{ if}{X}_i<t_j\text{and}{ϵ}_i=2\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

where G(t_j−) and H(t_j−) are the probabilities of not being censored and of entering the study with delay at age t_j− (just before age t_j), each estimated by Kaplan-Meier estimators. In the absence of ties between X_i and L_i or C_i, G(t_j−) = G(t_j) and H(t_j−) = H(t_j) [12]. Essentially, an individual i receives weight w_i(t_j) = 1 while at risk. If an individual experiences the competing event ϵ = 2, they remain in the risk set after age X_i but with a time-dependent weight, w_i(t_j) = Ĝ(t_j−)Ĥ(t_j−)/Ĝ(X_i−)Ĥ(X_i−). The weights w_i(t_j) are evaluated at each unique age of disease, t_j.

We provide an example of IPCLW data in Table 1, based on a subset of the aidssi dataset from the R package mstate [29, 59]. Briefly, the aidssi dataset contains time from HIV infection to AIDS or syncytium-inducing (SI) switching in 329 males from the Amsterdam Cohort studies [59]. We consider a subset of 6 individuals to simplify the example. We also consider AIDS as the event of interest and SI switching as the competing event, so that event status takes value 1 for AIDS, 2 for SI switching, and 0 for censoring.

Table 1.

Example of inverse probability of right censoring and left truncation weighted data

ID	Exposed	Start	Stop	Event	$\frac{\widehat{G}\left(t_j-\right)}{\widehat{G}\left(X_j-\right)}$	$\frac{\widehat{H}\left(t_j-\right)}{\widehat{H}\left(X_j-\right)}$	wi (tj)
1	1	0.6	3.8	1	1.0	1.0	1.0
2	0	2.7	6.8	1	1.0	1.0	1.0
3	1	0.2	5.0	1	1.0	1.0	1.0
4	1	1.2	5.1	0	1.0	1.0	1.0
5	0	3.0	6.5	0	1.0	1.0	1.0
6	1	1.4	2.3	2	1.0	1.0	1.0
6	1	2.3	3.8	2	1.0	1.3	1.3
6	1	3.8	5.0	2	1.0	1.3	1.3
6	1	5.0	6.8	2	0.3	1.3	0.4

Event takes value 1 for AIDS, 2 for SI switching, and 0 for censoring. $\frac{\widehat{G}\left(t_j-\right)}{\widehat{G}\left(X_j-\right)}$ is the right censoring weight, $\frac{\widehat{H}\left(t_j-\right)}{\widehat{H}\left(X_j-\right)}$ is the left truncation weight, and $w_i\left(t_j\right)=\frac{\widehat{G}\left(t_j-\right)\widehat{H}\left(t_j-\right)}{\widehat{G}\left(X_j-\right)\widehat{H}\left(X_j-\right)}$ is the inverse probability of censoring and left truncation weight.

In this subset, we observe three individuals who develop AIDS at times 3.8, 5.0, 6.8, one individual who experiences SI switching at time 2.3, and two individuals who are censored at times 5.1, 6.5. The entry times are 0.2, 0.6, 1.2, 1.4, 2.7, 3.0. The individuals who developed AIDS (IDs 1,2,3) have a single row with event time and weights of 1, since they developed the event of interest. Similarly, the individuals who were censored (IDs 4,5) also have a single row with their censoring time and weights of 1.

Individual ID 6 died at 2.3 years and has four rows in the IPCLW dataset. For their first row, the follow-up time is their time from entry to death, [1.4, 2.3) years, and the weight is 1. However, the individual remains in the risk set until the maximum event time, 6.8, with follow-up time broken up over 3 rows according to the AIDS event times 3.8, 5.0, 6.8. In this artifical time after death, the individual is upweighted or downweighted according to their probability of entering with delay or being censored. We see that the weights change at [2.3, 3.8) and [5.0, 6.8). At [2.3, 3.8), the weights change because individuals ID 2 and 5 entered the data at times 2.7 and 3.0, so the left truncation weight Ĥ(3.8−)/Ĥ(2.3−) = 1.3. Note that the right censoring weight is 1, since the censoring times have not yet occurred. At [5.0, 6.8), the weights change again because individuals ID 4 and 5 were censored at times 5.1 and 6.5. As a consequence, the right censoring weight Ĝ(6.8−)/Ĝ(2.3−) = 0.3 and the overall weight is the product of the right censoring and left truncation weights, w₅ = {Ĝ(6.8−)Ĥ(6.8−)}/{Ĝ(2.3−)Ĥ(2.3−)} = 0.3 · 1.3 = 0.4.

5. Fine-Gray model of the subdistribution hazard with left truncation

We use the Fine and Gray model of the subdistribution hazard to predict the CIF [11]:

$${\lambda }_1\left(t\mid T_i>{\tau }_0,Z_i\right)={\lambda }_{1,0}\left(t\mid T_i>{\tau }_0\right)\text{exp}\left(Z_i\pi \right)$$

where

$$\begin{gathered} {\lambda }_1\left(t\mid T>{\tau }_0,Z\right)=\underset{\Delta t\to 0}{\text{lim}}\frac{P\{t\le T<t+\Delta t,ϵ=1\mid (T>t)\cup (\tau <T<t,ϵ\ne 1),Z\}}{\Delta t} \\ =-\frac{d}{dt}\text{log}\left\{1-F_1\left(t\mid T>{\tau }_0,Z\right)\right\} \end{gathered}$$

is the subdistribution hazard, λ_1,0(t|T > τ₀) is the baseline subdistribution hazard, which is left unspecified, and π are the regression coefficients, which are interpreted as log subdistribution hazard ratios. To account for right-censoring and left truncation, we estimate the Fine-Gray model on the IPCLW data described in Section 4 [12]. Then, we obtain the lifetime risk by predicting the CIF at τ,

$$\begin{gathered} {\widehat{F}}_1^{FG1}\left(\tau \mid T_i>{\tau }_0,Z_i\right)=1-\text{exp}\left\{-{\int }_{{\tau }_0}^{\tau }{\widehat{\lambda }}_1\left(t\mid T_i>{\tau }_0,Z_i\right)dt\right\} \\ =1-\text{exp}\left\{-{\int }_{{\tau }_0}^{\tau }{\widehat{\lambda }}_{1,0}\left(t\mid T_i>{\tau }_0\right)\text{exp}\left(Z_i\widehat{\pi }\right)dt\right\} \\ =1-\text{exp}\left\{-{\widehat{\Lambda }}_{1,0}\left(\tau \mid T_i>{\tau }_0\right)\text{exp}\left(Z_i\widehat{\pi }\right)\right\} \end{gathered}$$ (2)

where ${\widehat{\Lambda }}_{1,0}\left(t\mid T_i>{\tau }_0\right)$ is a weighted Breslow estimator of the baseline cumulative subdistribution hazard (Appendix 10.2). The difference in lifetime risk between individuals with covariate profiles Z_i and Z_j is ${\widehat{\mu }}^{FG1}={\widehat{F}}_1^{FG1}\left(\tau \mid T_i>{\tau }_0,Z_i\right)-{\widehat{F}}_1^{FG1}\left(\tau \mid T_i>{\tau }_0,Z_j\right)$. For a single covariate profile in the absence of left truncation, Fine and Gray [11] described a resampling technique to obtain confidence intervals of the predicted CIF. To our knowledge, there is no closed form for the variance of the predicted CIF with left truncation, nor the difference in two predicted CIFs, due to the IPLC weights. Therefore, we construct 95% confidence intervals for the difference in lifetime risk between covariate profiles with bootstrap resampling.

If the Fine-Gray model is misspecified, e.g. the proportional subdistribution hazards assumption is violated, subsequent prediction of the CIF will be affected. However, the assumption of proportional hazards is complex in the competing risk framework. If a covariate has a proportional effect on the cause-specific hazards, it will not have a proportional effect on the subdistribution hazards and vice versa. Therefore, one cannot assume proportional cause-specific hazards and proportional subdistribution hazards simultaneously [30–33]. We provide an example in Section 10.3 of the Appendix.

To accommodate non-proportional subdistribution hazards, we include time-covariate interactions in the Fine-Gray model:

$${\lambda }_1\left(t\mid T_i>{\tau }_0,Z_i\right)={\lambda }_{1,0}\left(t\mid T_i>{\tau }_0\right)\text{exp}\left\{Z_i{\pi }_1+Z_i\text{log}(t){\pi }_2\right\}$$

where π₁ denotes the time-fixed covariate effects and π₂ denotes the effects for the interactions between the covariates and time. Here we consider log(t), but other functions of t can be implemented, for example I(t > t₀) where t₀ is a pre-specified timepoint. It is also possible to include time-varying effects for only a subset of Z, in which the corresponding coefficients π₂ would be 0. We again transform the model coefficients to predict the lifetime risk,

$$\begin{gathered} {\widehat{F}}_1^{FG2}\left(\tau \mid T_i>{\tau }_0,Z_i\right) \\ =1-\text{exp}\left\{-{\int }_{{\tau }_0}^{\tau }{\widehat{\lambda }}_1\left(t\mid T_i>{\tau }_0,Z_i\right)dt\right\} \\ =1-\text{exp}\left[-{\int }_{{\tau }_0}^{\tau }{\widehat{\lambda }}_{1,0}\left(t\mid T_i>{\tau }_0\right)\text{exp}\left\{Z_i{\widehat{\pi }}_1+Z_i\text{log}(t){\widehat{\pi }}_2\right\}dt\right]. \end{gathered}$$ (3)

The difference in lifetime risk between individuals with covariate profiles Z_i and Z_j is ${\widehat{\mu }}^{FG2}={\widehat{F}}_1^{FG2}\left(\tau \mid T_i>{\tau }_0,Z_i\right)-{\widehat{F}}_1^{FG2}\left(\tau \mid T_i>{\tau }_0,Z_j\right)$, and 95% confidence intervals are obtained using the bootstrap.

Equation (3) does not simplify like Equation (2). The linear predictor is now a function of time, so the integral does not simplify and we cannot plug in the Brewslow-like estimator of the cumulative baseline subdistribution hazard and linear predictor.

Instead, we numerically evaluate the integral and predict the lifetime risk, using the counting process approach of Thomas and Reyes [34] that we extended to the IPCLW data setting. First, we split the IPCLW data into intervals defined by t_j, where the likelihood is evaluated. Each interval receives the weights described in Section 4. Second, we create a time-covariate interaction. Third, we fit the model using the stacked dataset. Finally, we predict the lifetime risk for a covariate profile by evaluating the increments in the subdistribution hazard, $\Delta {\widehat{\Lambda }}_1(t\mid Z)$. If the original dataset is large, this will yield a very large stacked IPCLW dataset which will impact the computing time and model fitting. In Section 7.6, we further explore the computing time with various sample sizes.

In Table 2, we illustrate the approach with our previous example from Table 1 using R’s survSplit(). Note that IDs 2,3,4,5 now have multiple rows, broken up by intervals defined by AIDS event times, t_j. ID 1 still only has 1 row, since their event time 3.8 is the first event 1 time, so it is not possible to break this into further intervals. Although the original rows from Table 1 have been split into multiple rows, the corresponding weights stay the same. Now, we can create the time-covariate interaction as a new variable in our stacked dataset, Exposed × log(Stop), which takes changes values with each row. We provide detailed R syntax for this step on Github.

Table 2.

Example of stacked right censoring and left truncation weighted data to allow prediction with time-covariate interactions

ID	Exposed	Start	Stop	Event	$\frac{\widehat{G}\left(t_j-\right)}{\widehat{G}\left(X_j-\right)}$	$\frac{\widehat{H}\left(t_j-\right)}{\widehat{H}\left(X_j-\right)}$	wi (tj)	Exposed × log(Stop)
1	1	0.6	3.8	1	1.0	1.0	1.0	1.3
2	0	2.7	3.8	1	1.0	1.0	1.0	0.0
2	0	3.8	5.0	1	1.0	1.0	1.0	0.0
2	0	5.0	6.8	1	1.0	1.0	1.0	0.0
3	1	0.2	3.8	1	1.0	1.0	1.0	1.3
3	1	3.8	5.0	1	1.0	1.0	1.0	1.6
4	1	1.2	3.8	0	1.0	1.0	1.0	1.3
4	1	3.8	5.0	0	1.0	1.0	1.0	1.6
4	1	5.0	5.1	0	1.0	1.0	1.0	1.6
5	0	3.0	3.8	0	1.0	1.0	1.0	0.0
5	0	3.8	5.0	0	1.0	1.0	1.0	0.0
5	0	5.0	6.5	0	1.0	1.0	1.0	0.0
6	1	1.4	2.3	2	1.0	1.0	1.0	0.8
6	1	2.3	3.8	2	1.0	1.3	1.3	1.3
6	1	3.8	5.0	2	1.0	1.3	1.3	1.6
6	1	5.0	6.8	2	0.3	1.3	0.4	1.9

Event takes value 1 for AIDS, 2 for SI switching, and 0 for censoring. $\frac{\widehat{G}\left(t_j-\right)}{\widehat{G}\left(X_j-\right)}$ is the right censoring weight, $\frac{\widehat{H}\left(t_j-\right)}{\widehat{H}\left(X_j-\right)}$ is the left truncation weight, and $w_i\left(t_j\right)=\frac{\widehat{G}\left(t_j-\right)\widehat{H}\left(t_j-\right)}{\widehat{G}\left(X_j-\right)\widehat{H}\left(X_j-\right)}$ is the inverse probability of censoring and left truncation weight.

6. Flexible parametric model of the cumulative subdistribution hazard with left truncation

We now describe how to model the CIF by fitting the Royston-Parmar flexible parametric model to IPCLW data [13, 14]. Unlike the Fine-Gray model, the flexible parametric approach directly models the cumulative baseline subdistribution hazard and employs restricted cubic splines to allow more complexity. Since the model estimates the baseline subdistribution hazard, transforming model coefficients to predict the lifetime risk or other summary measures is straightforward.

We model the log cumulative subdistribution hazard as

$$\begin{gathered} \text{log}\left[-\text{log}\left\{1-F_1\left(t\mid T_i>{\tau }_0,Z_i\right)\right\}\right] \\ =\text{log}\left\{{\Lambda }_1\left(t\mid T_i>{\tau }_0,Z_i\right)\right\} \\ =\text{log}\left\{{\Lambda }_{1,0}\left(t\mid T_i>{\tau }_0\right)\right\}+Z_i{\mathit{\text{ϕ}}}_1+Z_{i}s\left\{\text{log}(t)\mid {\mathit{\text{ϕ}}}_0,k_0\right\}{\mathit{\text{ϕ}}}_2 \\ =s\left\{\text{log}(t)\mid k_0\right\}{\mathit{\text{ϕ}}}_0+Z_i{\mathit{\text{ϕ}}}_1+Z_{i}s\left\{\text{log}(t)\mid k_1\right\}{\mathit{\text{ϕ}}}_2, \end{gathered}$$

where ϕ₀, ϕ₁, and ϕ₂, are the regression coefficients (interpreted as log cumulative subdistribution hazard ratios), and the log baseline subdistribution hazard, log{Λ_1,0(t|T_i > τ₀,)}, is modeled by s{log(t)|k₀}, a restricted cubic spline function with a vector of knots, k₀ ∈ {k₁, …, k_K} and basis functions η. The restricted cubic spline function and its coefficients are s{log(t)|k₀}ϕ₀ = ϕ_0,0 + ϕ_0,1η₁ + ⋯ + ϕ_0,K−1η_K−1 where η₁ = log(t), η_j = (log(t) − k_j)³ − ν_j (log(t) − k₁)³ − (1 − ν_j)(log(t) − k_K)³ for j = 2, …, K − 1, and ${\nu }_j=\frac{k_K-k_j}{k_K-k_1}$. Previous studies have demonstrated robust estimation with sufficient number of knots [57, 58]. In practice, one may select the number of knots using criteria such as Akaike’s Information Criterion (AIC) or Bayesian Information Criterion (BIC). Although we consider the complementary log-log link here, one may also consider other link functions. The logit, probit, and Aranda-Ordaz link functions are also commonly implemented with flexible parametric models [13].

We model time-dependent effects, ϕ₂ by including interaction terms between covariates and the restricted cubic spline for log(t) with knots k₁. The model is estimated with IPCL weights, as described in Section 5 [13]. After creating IPCLW data using crprep(), flexible parametric models can be estimated using stpm2() from the R package rstpm2.

The lifetime risk is predicted by applying the inverse link function,

$$\begin{gathered} {\widehat{F}}_1^{FP}\left(\tau \mid T_i>{\tau }_0,Z_i\right) \\ =1-\text{exp}\left[-\left\{{\widehat{\Lambda }}_1\left(\tau \mid T_i>{\tau }_0,Z_i\right)\right\}\right] \\ =1-\text{exp}\left(-\text{exp}\left[s\left\{\text{log}(\tau )\mid k_0\right\}{\widehat{\mathit{\text{ϕ}}}}_0+Z_i\widehat{\mathit{\text{ϕ}}}+Z_{i}s\left\{\text{log}(\tau )\mid k_1\right\}{\widehat{\mathit{\text{ϕ}}}}_2\right]\right). \end{gathered}$$ (4)

The difference in lifetime risk between individuals with covariate profiles Z_i and Z_j is ${\widehat{\mu }}^{FP}={\widehat{F}}_1^{FP}\left(\tau \mid T_i>{\tau }_0,Z_i\right)-{\widehat{F}}_1^{FP}\left(\tau \mid T_i>{\tau }_0,Z_j\right)$. Confidence intervals can be obtained with the multivariate delta method.

7. Simulation studies

We conducted Monte Carlo simulation studies to assess and compare the performance of the pseudo-observation, Fine-Gray, and flexible parametric models in predicting the lifetime risk and its difference between groups. We generated data under both cause-specific hazards [30,35] and subdistribution hazards frameworks [36,37] to assess if our findings depend on the data generation mechanism. Our data generation scenarios covered a variety of patterns, including non-proportional subdistribution hazards. In the presence of non-proportional subdistribution hazards, one group’s CIF may initially be higher than the other group’s CIF, but the two CIFs may cross at a later timepoint or ultimately converge to the same cumulative incidence. We compared the bias, relative bias, mean squared error, and empirical coverage rate for all methods. We also assessed the Type I error and power of the pseudo-observation model in detecting a difference in lifetime risk. Finally, we compared the mean computing times for one setting with varying sample sizes.

7.1. Data generation

7.1.1. Cause-specific hazard framework

We first generated a single binary covariate, Z, from a Bernoulli distribution. To generate event times, we set the cause-specific hazard α_ϵ(t; Z), ϵ ∈ {1, 2} to follow a Weibull form, ${\alpha }_{ϵ}(t;Z)=\frac{a_{ϵ,Z}}{{\left(b_{ϵ,Z}\right)}^{a_{ϵ,Z}}}{t}^{a_{ϵ,Z}-1}$ with shape parameter α_ϵ,Z and scale parameter b_ϵ,Z. We then determined the cumulative all-cause hazard, $A(t;Z)={\int }_0^t{\alpha }_1(u;Z)+{\alpha }_2(u;Z)du$ and its inverse function, A⁻¹(t; Z). We obtained the generated times using an inversion method, where we generated a random variable U ~ Uniform(0, 1) and the simulated time to event was then T = A⁻¹(−ln(1−U)) [30]. To determine the inverse function A⁻¹, we used the uniroot() function in R. Then, we assigned the event type, ϵ, by a Bernoulli experiment, with probability $p=\frac{{\alpha }_1(T;Z)}{{\alpha }_1(T;Z)+{\alpha }_2(T;Z)}$ for cause ϵ = 1.

To use age as the time scale, we generated entry times L ~ Uniform(0, 5) for 50% and 80% of individuals and 0 otherwise. We shifted times by adding 55 to L and T, to be consistent with our motivating example in which we examine residual lifetime risk from age 55. We included independent right-censoring by generating censoring times C ~ Uniform(c, d), where the parameters (c, d) were chosen to yield approximately 25% and 75% probability of censoring at τ = 95. Observed event ages were given by X = T ∧ C. Then, we determined if the event time was censored, δ = I(T ≤ C), and the final observed event type, δ · ϵ. Participants entered the study at entry age L if L < X; otherwise, they were not observed. This yielded (L, X, δ · ϵ, Z).

7.1.2. Subdistribution hazard framework

We first generated a single binary covariate, Z, from a Bernoulli distribution. Let λ₁₀(t) = γ exp(ρt) denote the baseline subdistribution hazard function which follows a Gompertz distribution, and λ₁(t; Z) = λ₁₀(t) exp{(ψ₁ + ψ₂ · t)Z} denote the subdistribution hazard function, where (ψ₁, ψ₂) are the covariate and time-dependent covariate effects on the subdistribution hazard of event 1. We assumed the CIF for event 1 with non-proportional subdistribution hazards to be given by $F_1(t;Z)=P(T\le t,ϵ=1\mid Z)=1-\text{exp}\left[-{\int }_0^t\gamma \text{exp}\left\{\left(\rho +{\psi }_{2}Z\right)s+{\psi }_{1}Z\right\}ds\right]$, and the CIF for event 2 to be given by $F_2(t;Z)=P(T\le t,ϵ=2\mid Z)=\text{exp}\left\{\frac{\gamma \text{exp}\left({\psi }_{1}Z\right)}{\rho +{\psi }_{2}Z}\right\}\left[1-\text{exp}\left\{-t\text{exp}\left({\psi }_{3}Z\right)\right\}\right]$, where ψ₃ is the covariate effect on the subdistribution hazard of event 2 [36].

We assigned the event type by generating a Bernoulli variable with probability $P(ϵ=1\mid Z)=1-\text{exp}\left\{\frac{\gamma \text{exp}\left({\psi }_{1}Z\right)}{\rho +{\psi }_{2}Z}\right\}$ where ρ + ψ₂Z < 0, which is the limit of F₁(t|Z) with respect to t. We generated times for the event of interest from the conditional CIFs for event 1, $P(T\le t\mid ϵ=1,Z)=\left(1-\text{exp}\left[-{\int }_0^t\gamma \text{exp}\left\{\left(\rho +{\psi }_{2}Z\right)s+{\psi }_{1}Z\right\}ds\right]\right)/\left[1-\text{exp}\left\{\gamma \text{exp}\left({\psi }_{1}Z\right)/\rho +{\psi }_{2}Z\right\}\right]$, and event 2 P(T ≤ t|ϵ = 2, Z) = 1 − exp{−t exp(ψ₃Z)}. We generated the event times by simulating a random variable U ~ Uniform(0, 1) and determining the inverse of the conditional CIF with respect to t. We rescaled all times by multiplying by 40 [36]. We included independent right-censoring and delayed entry times as described in Section 4. We shifted times by adding τ₀ = 55 to L and X, in order to be consistent with our motivating example in which we examine residual lifetime risk from age 55 years. Participants entered the study at entry age L if L < X; otherwise, they were not observed. This yielded (L, X, δ · ϵ, Z).

7.2. Scenarios

The true CIFs under cause-specific and subdistribution hazard data generation are available in Fig. 4 of the Appendix. A description of each setting, including the parameters of the Weibull scenarios for cause-specific hazard settings 1–4 and the parameters for the Gompertz scenarios for subdistribution hazard settings 5–8, are provided in Tables 3 and 4.

Table 3.

Settings for cause-specific hazards data generation

	Setting 1	Setting 2	Setting 3	Setting 4
Z associated with AF	Yes	Yes	Yes	No
Z associated with death	No	Yes	No	Yes
Proportional CSHs	No	No	Yes	Yes
CSHR for atrial fibrillation	0.006*t1.9	.059*t	0.5	1.0
CSHR for death	1.0	.043*t	1.0	0.5
Weibull distribution of CSH				c
CSH of AF, Z=0	W(1.2, 39.5)	W(2, 50)	W(2, 35)	W(2, 35)
CSH of AF, Z=1	W(3.1, 29.5)	W(3, 40)	W(2, 49.5)	W(2, 35)
CSH of death, Z=0	W(1.4, 23.4)	W(2, 60)	W(1.4, 30)	W(1.4, 30)
CSH of death, Z=1	W(1.4, 23.4)	W(3, 50)	W(1.4, 30)	W(1.4, 49.22)
Lifetime risk, Z=1	0.34	0.52	0.23	0.33
Lifetime risk, Z=0	0.34	0.39	0.38	0.38
Difference in lifetime risk	0.00	0.12	−0.15	−0.05

AF: atrial fibrillation, CSH: cause-specific hazard function. CSHR: cause-specific hazard ratio, W: Weibull. Sample size before left truncation was set to n=500 and n=1,000. Right censoring was generated from a Uniform(c,d) distribution, where parameters c and d were set to obtain 25% and 75% probability of censoring at τ. Left truncation times were generated from a Uniform(0,5) distribution for 50% and 80% of individuals.

Table 4.

Settings for non-proportional subdistribution hazards data generation

	Setting 5	Setting 6	Setting 7	Setting 8
Main effect of Z on AF	Yes	Yes	Yes	No
Time-varying effect of Z on AF	Yes	Yes	Yes	Yes
Main effect of Z on death	Yes	Yes	Yes	Yes
Subdistribution HR for AF	1.649e−1.72t	1.649e−2.2t	1.6487e0.5t	e 0.5t
Gompertz parameters
γ	1.2	1.2	1	1
ρ	−2	−2	−3	−3
Effect of Z on AF, ψ1	0.5	0.5	0.5	0
Time-varying effect of Z on AF, ψ2	−1.72	−2.2	0.5	1
Effect of Z on death, ψ3	0.5	0.5	0.5	0.5
Lifetime risk, Z=1	0.40	0.37	0.45	0.35
Lifetime risk, Z=0	0.40	0.40	0.27	0.27
Difference in lifetime risk	0.00	−0.03	0.18	0.08

AF: atrial fibrillation, HR: cause-specific hazard ratio. Sample size before left truncation was set to n=500 and n=1,000. Right censoring was generated from a Uniform(c,d) distribution, where parameters c and d were set to obtain 25% and 75% probability of censoring at τ. Left truncation times were generated from a Uniform(0,5) distribution for 50% and 80% of individuals.

Parameters were selected to obtain a variety of shapes in the CIF (converging, diverging, and crossing curves), and a lifetime risk of approximately 40%, similar to the actual lifetime risk of atrial fibrillation in our motivating example [9]. The cumulative incidence curves in settings 1 and 5 converge, which shows an association with the CIF but not the lifetime risk. The cumulative incidence curves in settings 2 and 6 cross. In the cause-specific hazard setup, we also varied if Z was associated with one or both events. In the subdistribution hazard setup, we varied how the association changes with time; the associations in settings 5–7 include a main effect ψ₁ and time-varying term ψ₂, whereas in setting 8, the association is null at baseline (ψ₁ = 0) and then non-null and completely dependent on time (ψ₂ = 1).

We assessed 64 unique scenarios, with varying censoring (25%, 75%), left truncation (50%, 80%), and sample size (500, 1000). We generated 2000 datasets of size n = 500 and n = 1000 for each scenario. The number of replicates was determined to obtain precision of 0.01 in detecting a 0.05 probability of type I error. Due to left truncation, the effective sample sizes are smaller; we report the average sample size for each scenario.

7.3. Statistical analysis

We predicted the lifetime risk at τ = 95 years from an index age of τ₀ = 55 years in each group and the difference in lifetime risk between groups. We applied our R function pseudo() to create pseudo-observations, and fit models using geese() from the R package geepack [38]. We created the IPCLW data with crprep() from the R package mstate. [29] We first fit Fine-Gray models assuming proportional subdistribution hazards using coxph() from the survival R package with the IPCLW data [39]. Then, we fit Fine-Gray models with a time-varying effect by applying survSplit() to the IPCLW data to create a stacked dataset, then creating an interaction term between Z and log(age), and finally fitting the model with coxph(). We used stpm2() from the R package rstpm2 to fit flexible parametric models to the IPCLW data [40]. We fit flexible parametric models with time-varying effects by including an interaction between the covariate Z and the restricted cubic spline for log(age) with 2, 3, and 4 knots. We rescaled age to age – 55 to facilitate model convergence. All models included 4 knots for the baseline cumulative subdistribution hazard. We chose the number of knots by comparing the AIC when fitting models with 2 to 6 knots for the baseline subdistribution hazard in a random sample of 10 simulated datasets. There was little change in AIC between 4, 5, and 6 knots, which justified our choice to use 4 knots.

The pseudo-observation model should be correctly specified for the lifetime risk in all settings, since our data generation only includes one binary covariate. The Fine-Gray and flexible parametric methods model the subdistribution, thus they will be misspecified when data is generated from cause-specific hazards (scenarios 1–4). However, the Fine-Gray with log(age) interaction and flexible parametric models should be correctly specified for the subdistribution hazard when data is generated from subdistribution hazards (scenarios 5–8).

7.4. Assessment of performance

For all methods, we compared prediction of the lifetime risk in each group and the difference in lifetime risk between groups according to mean bias, mean relative bias, and root mean squared error (RMSE). We compared the empirical coverage rate for the pseudo-observation and flexible parametric models only, since the Fine-Gray models require bootstrapping the confidence intervals. We also assessed the type I error and power of the estimated coefficient (log odds ratio) for the pseudo-observation method. The true lifetime risk at τ is given by $F_1\left(\tau \mid T>{\tau }_0,Z\right)={\int }_{{\tau }_0}^{\tau }{e}^{-A(u;Z)}\cdot {\alpha }_1(u;Z)du=1-\text{exp}\left[-{\int }_{{\tau }_0}^t\gamma \text{exp}\left\{\left(\rho +{\psi }_{2}Z\right)s+{\psi }_{1}Z\right\}ds\right]$, where the parameters are given in Tables 3 and 4. Then, the true difference in lifetime risk, δ, between two groups is μ = F₁(τ|T > τ₀, Z = 1) − F₁(τ|T > τ₀, Z = 0).

7.5. Results

The nested loop plots in Figures 1 and 2 present the mean bias and RMSE using the pseudo-observation, Fine-Gray, and flexible parametric methods [42]. Figures for the mean relative bias, coverage, Type I error, and power are available in the Appendix (Figures 5–7). We assessed relative bias and power for scenarios where the true difference in lifetime risk was not 0, and type I error in scenarios where the true difference in lifetime risk was 0; all other criteria were assessed for all scenarios. The flexible parametric model did not reach convergence in all simulated datasets; the presented results include only datasets where the model converged. The convergence rate for this method ranged from 73% to 100%. It is possible that models would converge with different specification of the spline function (e.g. fewer or additional knots or changing the location of the knots).

Fig. 1.

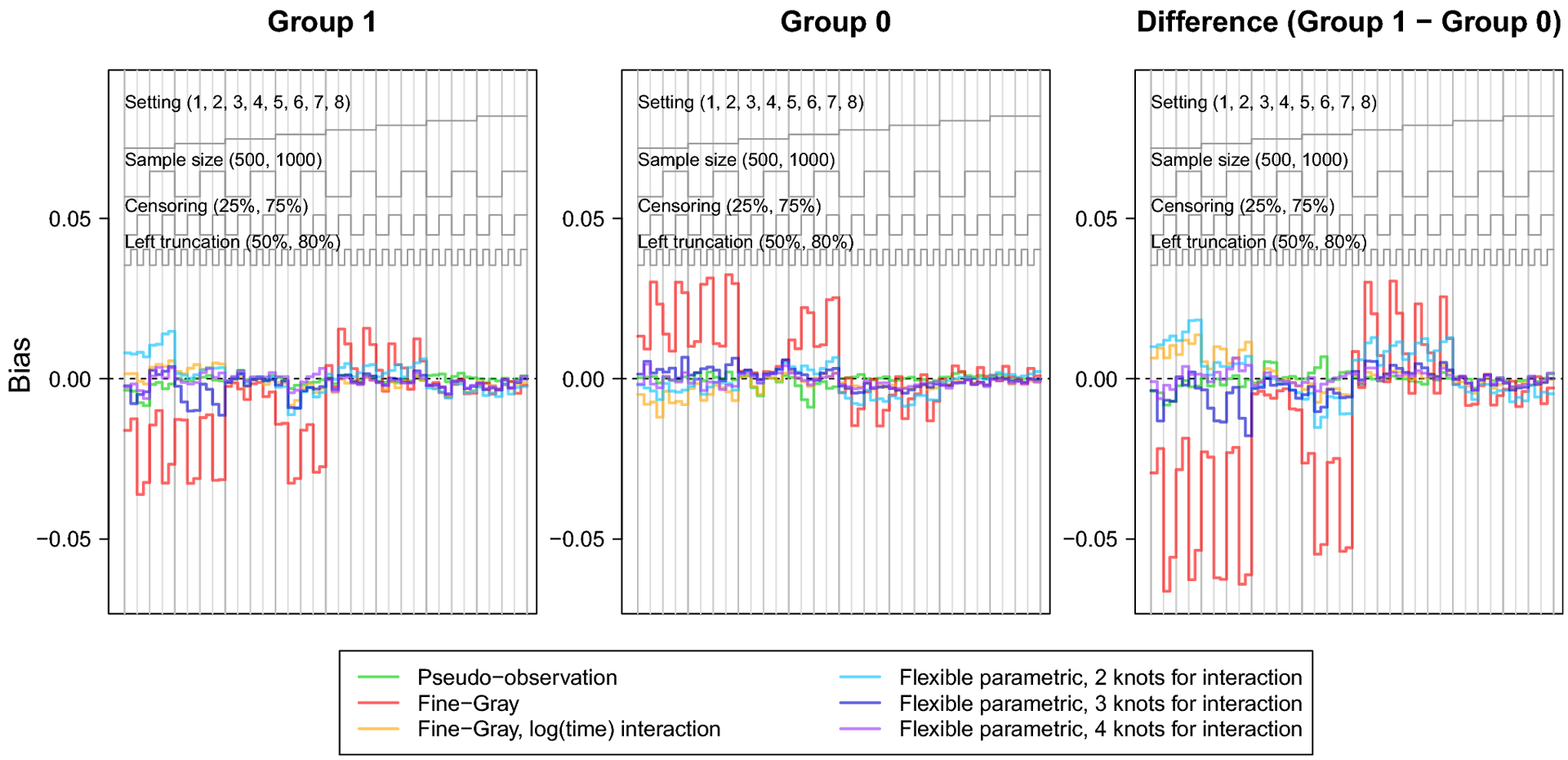
Nested loop plot showing the simulation study results: bias.

The legend at the top describes the organization of results by setting, sample size, censoring, and left truncation. Each vertical panel is a unique scenario, with a total of 64 scenarios.

Fig. 2.

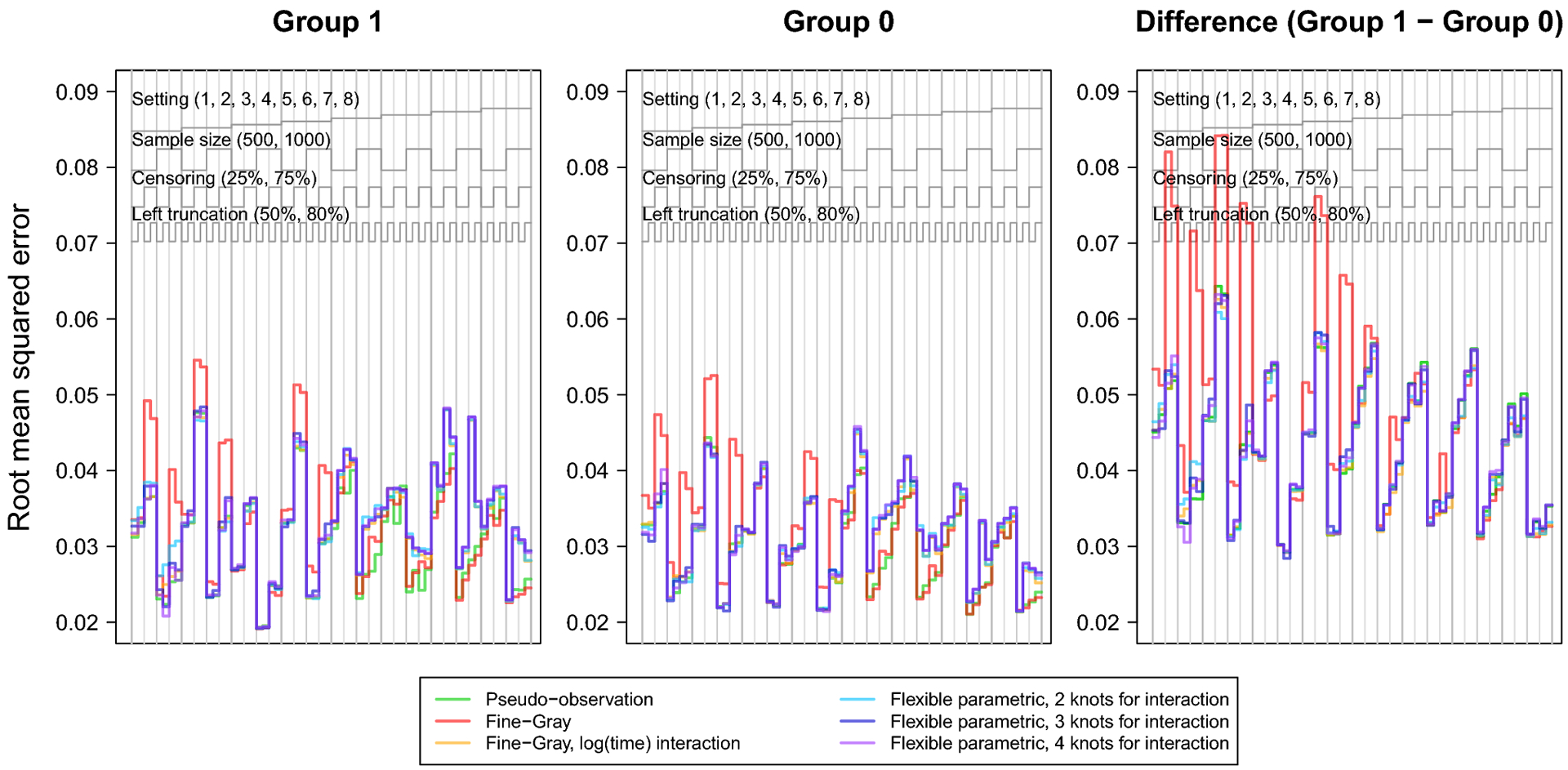
Nested loop plot showing the simulation study results: root mean squared error.

The legend at the top describes the organization of results by setting, sample size, censoring, and left truncation. Each vertical panel is a unique scenario, with a total of 64 scenarios.

The bias and relative bias were similar for all methods except for the Fine-Gray model without log(age) interaction, which demonstrated visibly greater bias across scenarios, particularly in settings with heavy censoring and where the CIFs cross or converge (settings 1, 2, 4, 5 and 6). The flexible parametric model with 2 knots for the covariate-spline interaction showed slight relative bias for the difference in lifetime risk in settings 1, 5, and 6, where the CIFs cross or converge. Sample size did not appear to heavily influence bias of any method. Both the flexible parametric and Fine-Gray models sometimes showed increased bias with heavy right censoring and lighter left truncation.

The RMSE followed a consistent pattern across all methods, except the Fine-Gray without log(age) interaction which displayed notably greater RMSE. Overall, RMSE increased with smaller sample size, heavy right censoring, or heavy left truncation. The Fine-Gray model’s fluctuation in RMSE was greater in settings generated from cause-specific hazards (settings 1–4); but fairly equal among all methods in settings generated from subdistribution hazards (settings 5–8).

The coverage of the pseudo-observation approach hovered around 95% for all scenarios. The coverage of the flexible parametric models was close to 95% for many scenarios, but varied with number of knots for the covariate-spline interaction. For instance, the model with 2 knots for covariate-spline interaction demonstrated undercoverage in setting 1, where the CIFs converged. This undercoverage was more severe in settings with heavy right censoring and/or greater left truncation. This may be explained by this method’s bias in setting 1. Overall, these results suggest that the confidence intervals of the flexible parametric model perform reasonably well, even though they do not account for estimation of the IPCL weights.

Finally, the Type I error of the pseudo-observation method hovered around 5%. The power of the pseudo-observation method was high for most scenarios, but was low for scenarios with both smaller sample size and heavy censoring, as well as when the difference in lifetime risk was small (setting 6).

7.6. Computing time

We also compared the mean computing time for 1,000 simulated datasets, generated from setting 1 at sample sizes 500, 1,000, 5,000, and 10,000. We did not include the bootstrap when fitting Fine-Gray models, as this would depend on the number of bootstrap samples and computing resources.

We observed that calculating the pseudo-observations may take considerable computing time in larger datasets (Table 5). However, once this step is complete, the pseudo-observation model fitting is quick. In contrast, creating IPCLW data for the Fine-Gray and flexible parametric models was less computationally intensive than calculating pseudo-observations. However, the model fitting computing time increased by 12-fold to 112-fold for the Fine-Gray model fit to stacked IPCLW data, and increased by 25-fold to 150-fold for the flexible parametric model. When combining data preparation and model fitting, the total computing time was longer for the pseudo-observation method than the Fine-Gray without bootstrap and flexible parametric models. However, these results do not reflect the common practice of model selection, during which one would fit many models to select a final model. In that case, the total computing time of repeating the Fine-Gray data preparation and model fitting in bootstrap samples would exceed the total computing time of the pseudo-observation approach. In addition, our results do not apply to situations with multiple covariates.

Table 5.

Mean computing time for 1,000 simulated datasets

Dataset preparation
Sample size	Pseudo-observation	Fine-Gray (no bootstrap)	Flexible parametric
500	2.45 sec.	0.18 sec.	0.12 sec.
1,000	17.09 sec.	0.70 sec.	0.45 sec.
5,000	8.26 min.	0.62 min.	0.33 min.
10,000	5.42 hr.	2.58 min.	0.67 min.
Fit model and predict lifetime risk
Sample size	Pseudo-observation	Fine-Gray (no bootstrap)	Flexible parametric
500	0.02 sec.	1.15 sec.	1.18 sec.
1,000	0.03 sec.	3.60 sec.	4.87 sec.
5,000	0.38 sec.	4.68 sec.	9.54 sec.
10,000	0.42 sec.	15.36 sec.	21.21 sec.

sec: seconds, min: minutes, hr: hours.

Our results suggest it may be difficult to calculate the pseudo-observations in larger datasets, but subsequent model fitting remains quick despite the large sample size. In contrast, the IPCLW datasets needed for the Fine-Gray and flexible parametric models can become quite large, which affects computing time and memory usage. These issues should be considered when fitting many models, e.g. models with time-covariate interactions, different numbers of knots, or different functional forms of the covariates. Furthermore, it may be difficult to bootstrap confidence intervals for the Fine-Gray model in larger datasets. We recommend that researchers consider the computing time, available memory and computation resources, and total number of candidate models when choosing a statistical method for larger datasets.

8. Illustrative example: lifetime risk of atrial fibrillation

Staerk et al. [9] previously estimated the lifetime risk of atrial fibrillation by calculating the Aalen-Johansen estimator in various risk factor strata. We apply the pseudo-observation, flexible parametric, and Fine-Gray methods to model the lifetime risk of atrial fibrillation in the Framingham Heart Study [43, 44].

The Framingham Heart Study is a longitudinal, prospective study in the community of Framingham, Massachusetts. We included 5,993 Framingham Heart Study participants who were free of atrial fibrillation at an index age of 55 years and attended an examination between ages 50 and 60 years. Risk factors were measured at the examination closest to age 55 years. Participants were followed until atrial fibrillation or flutter, death, age 95 years, loss to follow-up, last visit or medical contact in which the participant was free of atrial fibrillation, or December 31, 2017. In all, 875 participants developed new-onset atrial fibrillation over a median follow-up of 15.4 years. We included the following risk factors: biological sex (male vs. female), height, weight, current smoking status, elevated vs. optimal alcohol use (elevated defined as more than 14 drinks per week for males and more than seven drinks per week for females), systolic and diastolic blood pressure, hypertensive medication use, prior diabetes, prior heart failure, and prior myocardial infarction [8,9]. Participant characteristics are available in the Appendix (Table 8).

To protect the confidentiality of the Framingham Heart Study participants, the data from our illustrative example are not publicly available. Participant level data from the Framingham Heart Study are available at the database of Genotypes and Phenotypes (https://www.ncbi.nlm.nih.gov/gap/) and BioLINCC (https://biolincc.nhlbi.nih.gov/home/).

8.1. Model fitting and lifetime risk prediction

We fit the pseudo-observation model with a logit link, the Fine-Gray model, and the flexible parametric model for the lifetime risk of atrial fibrillation. All models employed age as the time scale.

When fitting the pseudo-observation model, we considered if any interactions between sex and other covariates improved model fit. Since the pseudo-observation model is fit by solving an generalized estimating equation, we assess model fit by reduction in Quasi-likelihood Information Criterion (QIC) [41]. We prespecified a threshold of QIC reduction of at least 4 to justify including an additional term in the model, but no interactions achieved this threshold [60].

When fitting the Fine-Gray model, we first considered whether time-varying effects improved the model fit according to AIC. We included the additional term in the model if it reduced AIC by at least 4 [60]. We fit additional models, each with an interaction between log(age–55) and a single covariate. In a forward fashion, we selected the model with the lowest AIC that exceeded our prespecified threshold, and repeated this process for the remaining covariates [45] until no further AIC reduction reached the threshold. Then, we considered if any interactions between sex and other covariates improved model fit, but none dramatically improved the AIC. The final model contained interactions between log(age – 55) and weight, smoking status, and prior myocardial infarction.

When fitting the flexible parametric model, we considered models with 2 to 6 knots for the baseline cumulative subdistribution hazard and chose the number that reduced AIC by at least 4, which was 5 knots [14]. Next, we fit additional models allowing time-varying covariate effects with 2 knots (which corresponds to an interaction between the covariate and log(age)) in a forward fashion as described for the Fine-Gray model. Then, we considered if an additional knot for the spline in the time-covariate interaction term improved model fit, but none dramatically improved AIC. Finally, we considered if any interactions between sex and other covariates improved model fit. The final model contained interactions between log(age) and weight, diabetes, and height, and between sex and systolic blood pressure and prior heart failure.

To better understand the competing risk, we also fit models for incident death without atrial fibrillation with a similar approach. The Fine-Gray model including interactions between log(age) and sex, smoking status, hypertension, and prior heart failure. The flexible parametric model included interactions between log(age) and sex, hypertensive medication, smoking status, prior diabetes, and prior heart failure.

For all models, we predicted the lifetime risks by back-transforming the estimated model coefficients. For each binary covariate, we predicted the lifetime risk in each group and the difference between groups, while all other covariates were set to the sample average or proportion. For continuous covariates, we predicted the lifetime risk at the mean and the difference in lifetime risk for one standard deviation increase from the mean, while all other covariates were set to the sample average or proportion. We obtained 95% confidence intervals using the delta method for the pseudo-observation model with logit link and flexible parametric models, and the 0.025 and 0.975 percentiles of 1,000 bootstrap resamples for the Fine-Gray model. We also plot the predicted lifetime risks and cumulative incidence curves.

We performed sensitivity analyses using BIC instead of AIC. We obtained the same Fine-Gray model, but the chosen flexible parametric model included 3 knots for the baseline cumulative subdistribution hazard and interactions between log(age) and weight and prior MI, and no interactions with sex. The flexible parametric model selected with BIC and predicted lifetime risks are available in Table 9 of the Appendix.

8.2. Results

In Table 6, we present the predicted differences in lifetime risk of atrial fibrillation at age 95 from an index age of 55. We also plot the predicted lifetime risks from the pseudo-observation model and predicted CIFs from the Fine-Gray and flexible parametric models in Figure 3.

Table 6.

Predicted differences in lifetime risk of atrial fibrillation at age 95, from index age 55

Risk factor	Pseudo-observation	Cumulative incidence models
		Fine-Gray	Flexible parametric
Sex, male - female	4.54 (−2.29, 11.36)	5.15 (0.24, 10.60)	8.66 (1.95, 15.37)
Height, 70 – 66.2 in.	0.48 (−3.00, 3.96)	2.80 (−0.15, 5.82)	−4.72 (−7.77, −1.66)
Weight, 213.3 – 173.8 lb.	3.49 (1.09, 5.90)	2.68 (0.19, 5.55)	3.08 (1.41, 4.75)
Systolic BP, 142.8 – 125.7 mmHg	5.53 (1.66, 9.41)	5.84 (3.04, 8.82)	4.29 (−0.73, 9.31)
Diastolic BP, 88.2 – 78.4 mmHg	−2.59 (−5.95, 0.77)	−2.21 (−4.67, 0.13)	−0.86 (−5.00, 3.27)
Hypertension, yes - no	5.57 (0.46, 10.67)	7.23 (2.99, 11.45)	0.00 (−0.07, 0.06)
Current smoker, yes - no	−6.93 (−13.34, −0.52)	−1.30 (−5.56, 3.00)	−5.64 (−8.69, −2.59)
Elevated alcohol use, yes - no	5.39 (−0.98, 11.76)	6.88 (2.50, 11.15)	6.52 (−1.18, 14.21)
Prior diabetes, yes - no	−9.18 (−15.48, −2.88)	−3.35 (−10.25, 3.20)	6.21 (−3.63, 16.05)
Prior heart failure, yes - no	2.67 (−24.73, 30.08)	9.93 (−20.79, 43.11)	−13.01 (−42.37, 16.35)
Prior myocardial infarction, yes - no	−11.11 (−21.66, −0.56)	−6.13 (−15.10, 4.18)	4.95 (−6.16, 16.06)

BP: blood pressure. Results are % differences in lifetime risk (95% confidence interval). Differences in lifetime risk for continuous risk factors are for one standard deviation increase from the mean. Differences in lifetime risk were obtained by transforming model coefficients at the mean value of other covariates. 95% CIs are obtained with the delta method for the pseudo-observation and flexible parametric models, and the .025 and .975 percentile of bootstrap resamples for the Fine-Gray model.

Fig. 3.

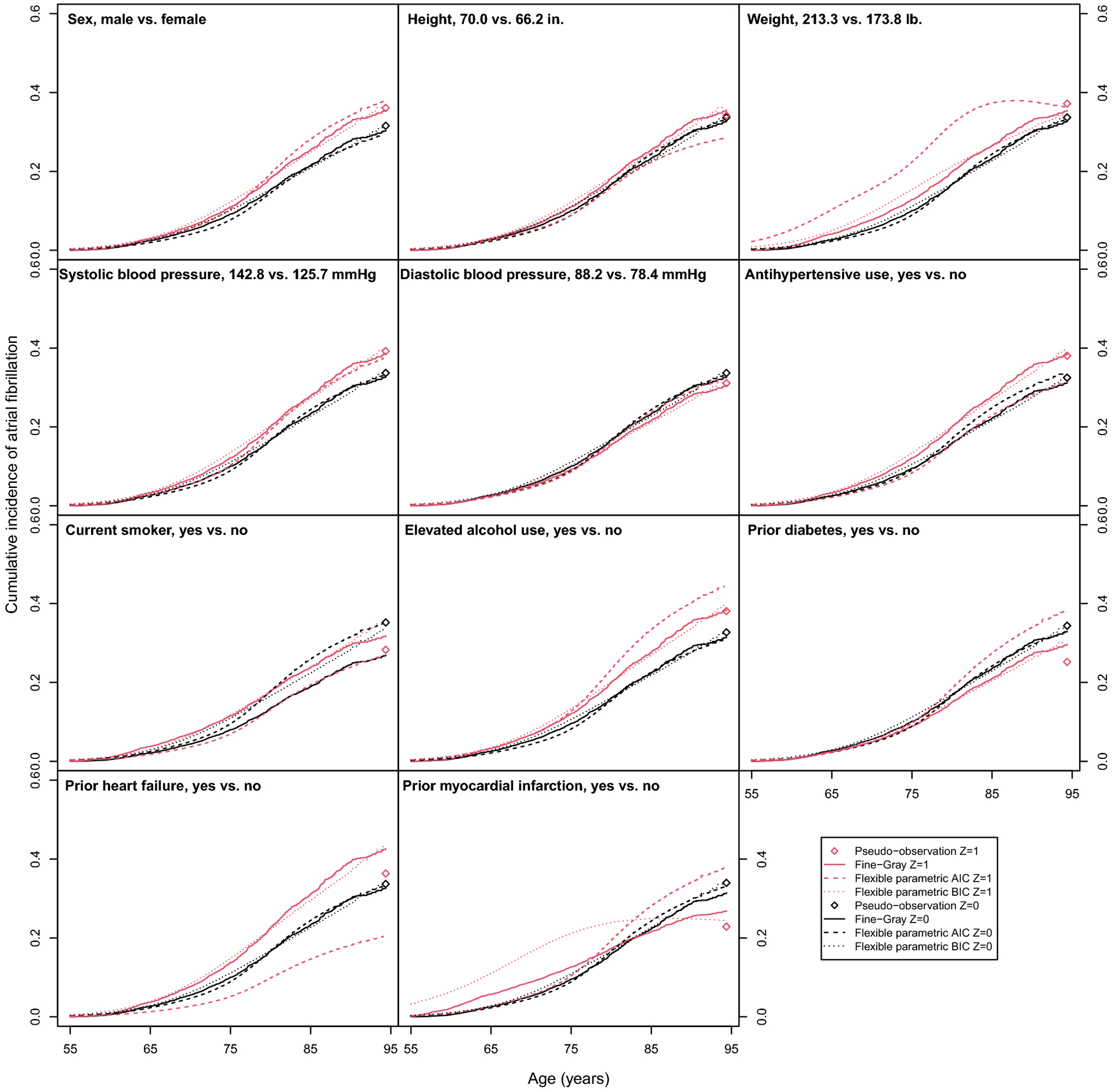
Predicted cumulative incidence functions and lifetime risks of atrial fibrillation in the Framingham Heart Study.

The cumulative incidence functions (Fine-Gray and flexible parametric models) and lifetime risk (pseudo-observation model) for continuous risk factors are predicated at the mean value of the covariate (Z = 0, black) and at 1 SDU increase in the covariate (Z = 1, red), while all other covariates are set to the sample average or proportion. Cumulative incidence function and lifetime risk predictions were obtained by transforming model coefficients at the mean value of other covariates.

All three methods found increased lifetime risk of atrial fibrillation with increased weight. In the pseudo-observation model, there was also evidence of increased lifetime risk associated with (difference in lifetime risk [95% CI]) higher systolic blood pressure (5.5% [1.7, 9.4]) and use of hypertension medication (5.6% [0.5, 10.7]). There was evidence of decreased lifetime risk associated with smoking (−6.9% [−13.3, −0.5]), prior diabetes (−9.2% [−15.5, −2.9]), and prior MI (−11.11%, [−21.7, −0.6]). The Fine-Gray and flexible parametric models both predicted increased lifetime risk in males compared to females. The Fine-Gray model also predicted increased lifetime risk with systolic blood pressure, hypertension, and elevated alcohol use. The flexible parametric predicted a decrease in lifetime risk with increased height and smoking status.

The varying results and wide confidence intervals for prior myocardial infarction and heart failure varied by method, which may be explained by the small number of participants with these risk factors (Appendix, Table 8). Furthermore, the predicted cumulative incidence curves and lifetime risks help illustrate where the methods agree and disagree (Appendix, Figure 3). The exponentiated model coefficients, which are lifetime odds ratios for the pseudo-observation model, subdistribution hazards ratios for the Fine-Gray model, and cumulative subdistribution hazards ratios flexible parametric models, are available in the Appendix (Table 10).

In Table 11 of the Appendix, we present the exponentiated model coefficients for the competing event, death without atrial fibrillation. The inverse associations of smoking status and diabetes with the lifetime risk of atrial fibrillation may be explained by these variables’ strong associations with the competing risk, death without atrial fibrillation. If individuals who smoke have a greater hazard of death, they may die before they can develop atrial fibrillation. In any competing risk analysis, one should examine both competing events to fully understand if results are explained by the event of interest, the competing event, or both [55]. However, the cumulative incidence of disease and any seemingly inverse associations are still important results from a public health or prognostic perspective [48]. In quantifying the burden of atrial fibrillation at advanced ages, individuals who smoke or with diabetes may not develop atrial fibrillation because they did not live long enough to develop atrial fibrillation. The individuals we observe developing atrial fibrillation later in life may not exhibit these risk factors from the very fact that they have survived to a later age due to the absence of these risk factors.

8.3. Computing time

It took approximately 22 minutes to create the pseudo-observation data, but less than 1 second to fit each model (we fit 11 total pseudo-observation models). In contrast, preparing the IPCLW datasets for the Fine-Gray and flexible parametric model was quick (5.4 and 1.7 seconds, respectively) but yielded extremely large datasets. In order to explore all time-covariate interactions, sex-covariate interactions, and spline terms (flexible parametric model only), we fit 60–80 versions of the Fine-Gray and flexible parametric models each. Furthermore, we refit the final Fine-Gray model in 1,000 bootstrap samples. Each Fine-Gray model took approximately 3 minutes to fit without bootstrapping, while each flexible parametric model took approximately 4 minutes. The computing time of the Fine-Gray and flexible parametric models was longer than observed in our simulation study, which may be explained by the increased number of covariates (11 covariates in illustrative example vs. 1 covariate in simulation study).

9. Discussion

In summary, we demonstrate how the pseudo-observation technique can be used to fit a multivariable model for the lifetime risk and how to predict lifetime risk from models for the CIF. Unlike models for the CIF, the pseudo-observation approach avoids the challenges of the proportional subdistribution hazards assumption and complex time-varying effects by targeting the timepoint of interest. Models for the CIF are designed to estimate the subdistribution hazard ratio over all time points, whereas we leverage the pseudo-observation technique to focus on our timepoint of interest. In simulation studies, the pseudo-observation approach and flexible parametric models with sufficient complexity for time-varying associations demonstrated little bias. In the Framingham Heart Study, we identified mid-life risk factors associated with the residual lifetime risk of atrial fibrillation.

The flexible parametric model and Fine-Gray model with log(time) interaction also performed well in predicting the lifetime risk in many scenarios. However, we observed considerable bias and error when the Fine-Gray model did not include an interaction term between the covariate and log(age) and, as a consequence, did not account for a time-varying association. This bias was particularly large in settings where the CIFs crossed or in the presence of heavy censoring. Both the flexible parametric and Fine-Gray models performed better in settings with less right censoring. Additionally, both the flexible parametric and Fine-Gray models sometimes showed improved performance in the presence of heavier left truncation as compared to lighter left truncation. This may be explained by the weights, which require estimation of the entry distribution, H(t). If the amount of left truncation is small, Ĥ(t) may not be estimated correctly which in turn affects the weights.

The regression coefficients are log subdistribution hazard ratios for the Fine-Gray model and log cumulative subdistribution hazard ratios for flexible parametric models. Regression coefficients can be transformed to predict the lifetime risk at τ. Confidence intervals for the Fine-Gray predicted lifetime risk require resampling techniques, such as the bootstrap. When including time-dependent effects in the Fine-Gray model, prediction of the lifetime risk is not always straightforward [46]. On GitHub, we share our R code for predicting the CIF at a fixed time point from the Fine-Gray model with left truncation and time-varying effects using the stacked IPCLW data described in Section 4. The long dataset divides follow-up time into smaller increments and can be considerably large, which makes bootstrapping the confidence intervals very computationally intensive.

In contrast, when fitting a flexible parametric model, confidence intervals or hypothesis tests can be easily obtained with the delta method. Although the confidence intervals do not account for the estimated left truncation and right censoring weights, our simulation study found adequate coverage in most settings. Instances of poor coverage are likely explained by misspecification of the model, such as incorrect number of knots for the time-varying term. These closed-form confidence intervals may be appealing to researchers when bootstrapping becomes too cumbersome in larger datasets.

Interpretations of associations in the competing risk setting require careful consideration. It is possible for a variable to appear to have an association with an event’s CIF even when the variable is only associated with the competing event’s cause-specific hazard, and not the event of interest’s cause-specific hazard. In agreement with previous works, we recommend examining both competing events to fully understand if results are explained by the event of interest, the competing event, or both [30,55]. We recognize that modeling the lifetime risk of death without the event of interest using the pseudo-observation approach may not be as informative as other approaches. Instead, one might model cumulative incidence of the competing event over time and report subdistribution hazard ratios, which may be a more meaningful summary measure.

Our simulation study compared three methods, but was not exhaustive of all methods for modeling the CIF. In Section 1, we described several alternative models for modeling the CIF, which could be fit to obtain predictions of the lifetime risk at τ. Furthermore, the CIF can also be estimated with other approaches to the flexible parametric model. For example, one can fit a flexible parametric model for each log cumulative cause-specific hazard or for the cause-specific CIF using a direct likelihood approach [49, 50].

Grand et al. [10] studied the performance of pseudo-observations for the survival function and restricted mean survival time in the presence of left truncation, but not the CIF. Grand et al. considered two methods of calculating the pseudo-observations, using either the total sample size or a ‘stopped’ approach with the number of entries at each timepoint. Our results confirm their finding that using the number of entries, rather than the total sample size, performs better. When predicting the lifetime risk, we avoid issues that may usually arise with left truncation, such as small numbers at risk at early event times. However, such issues may arise in other applications.

Jacobsen et al. [51] and Overgaard et al. [27] recently examined the asymptotic properties of pseudo-observations and found that the sandwich estimator of the variance is conservative, as it neglects some second-order terms of the influence function. However, they found the sandwich estimator still performed well in settings with low to moderate censoring, and found the bias may be minor. Overgaard et al. [52] proposed an alternative variance estimator, which was found to perform well in large samples but poorly in smaller samples. Here, we only consider the sandwich estimator variance, so the confidence intervals may be conservative. However, the pseudo-observation model demonstrated adequate coverage in our simulation study.

Each method has its own strengths and limitations, which we summarize in Table 7. As shown in our assessment of computing time in simulated data, it may take substantial time to initially compute the pseudo-observations in larger datasets. Future work will explore methods to calculate pseudo-observations for massive sample sizes. However, this step only needs to be performed once. Once this step is complete, fitting models with the pseudo-observations is as quick as fitting any generalized linear model. There are no computational burdens when fitting multiple models, e.g. exploring different confounders, interaction terms, or functional forms of the covariates. In contrast, preparing IPLCW data for the Fine-Gray and flexible parametric models yields a potentially very large dataset. Then, fitting models to this large dataset becomes computationally intensive, especially when fitting multiple models to explore time-varying effects or interactions. Furthermore, the Fine-Gray model requires bootstrapping confidence intervals, which will also increase computational time.

Table 7.

Comparison of strengths and limitations of each method

Method	Strengths	Limitations
Pseudo-observation model	Model coefficients facilitate inference at a fixed timepoint Avoids modeling assumptions over time, thus less prone to misspecification Confidence intervals obtained with the delta method demonstrate adequate performance Model fitting is quick, even with large sample sizes	Does not allow estimating other quantities of interest, e.g. subdistribution hazard ratios Does not leverage the full data over time Assumes completely independent censoring Calculating the pseudo-observations may be computationally intensive for large sample sizes
Fine-Gray model with time-covariate interactions with IPCLW data	Allows estimating other quantities of interest, e.g. subdistribution hazard ratios Assumes conditionally independent censoring Leverages the full data over time	May be difficult to correctly specify complex patterns over time (violations of proportional subdistribution hazards assumption) More prone to misspecification Bootstrap for confidence intervals on predicted lifetime risk adds to computational burden Stacked IPCLW dataset will be very large for large sample sizes, which increases the model fitting computing time
Flexible parametric model with IPCLW data	Can model complex patterns over time with restricted cubic splines Allows estimating other quantities of interest, e.g. subdistribution hazard ratios Confidence intervals on predicted lifetime risk obtained with the delta method demonstrate adequate performance Assumes conditionally independent censoring Leverages the full data over time	More prone to misspecification Stacked IPCLW dataset will be very large for large sample sizes, which increases the model fitting computing time

IPCLW: inverse probability of censoring and left truncation weighting.

Second, if a single timepoint is of interest, the pseudo-observation approach is advantageous because it avoids assumptions for all timepoints. If multiple timepoints or the entire lifespan is of interest, the Fine-Gray and flexible parametric models may be useful, and can readily accommodate time-varying effects. Furthermore, these methods can be used to estimate other quantities of interest, e.g. subdistribution hazard ratios.

Third, the pseudo-observation approach assumes that left truncation and right censoring are completely independent of the event time and covariates, which is more restrictive than commonly used survival models. In the presence of conditional independence, the Fine-Gray and flexible parametric models may have an advantage over the pseudo-observation model. However, dependent truncation or censoring could be accommodated by modeling pseudo-observations of a modified Aalen-Johansen estimator, inverse probability of censoring weights which allow dependent censoring, or adjusting for the entry time as a covariate [52–54, 56].

Our study has some limitations. For all methods, we consider risk factors in mid-life (at baseline). We have not extended the models to account for risk factors which may change over time. We also do not consider alternative functional forms for the continuous variables, which would be important in practice. Finally, we presented predicted differences in lifetime risk of atrial fibrillation based on predicted means. For binary covariates, we acknowledge that such predictions do not correspond to any real-world individuals. Marginal standardization could be used in this context [61].

In conclusion, our approach using pseudo-observations produces unbiased predictions of the lifetime risk and allows hypothesis testing directly on the lifetime risk, rather than the CIF. Furthermore, by focusing on one age τ, we avoid specifying complex patterns over time, such as the baseline subdistribution hazard function or time-varying associations.

10. Appendix

10.1. Variance of non-parametric estimator of lifetime risk

The variance of the lifetime risk is estimated using Greenwood’s formula, [4, 18]

$$\begin{gathered} \widehat{\text{var}}\left\{{\widehat{F}}_1\left(\tau \mid T>{\tau }_0\right)\right\} \\ =\sum _{{\tau }_0<t_j\le \tau }{\left\{\widehat{S}\left(t_{j-1}\right)\frac{\Delta N_1\left(t_j\right)}{Y\left(t_j\right)}\right\}}^2 \\ \times \left\{\frac{Y\left(t_j\right)-\Delta N_1\left(t_j\right)}{Y\left(t_j\right)\Delta N_1\left(t_j\right)}+\sum _{t_l<t_{tj}}\frac{\Delta N\left(t_l\right)}{Y\left(t_l\right)\left(Y\left(t_l\right)-\Delta N\left(t_l\right)\right)}\right\} \\ +2\sum _{{\tau }_0<t_j<\tau }\sum _{t_k\in \left(t_j,\tau \right]}\widehat{S}\left(t_{j-1}\right)\frac{\Delta N_1\left(t_j\right)}{Y\left(t_j\right)}\widehat{S}\left(t_{k-1}\right) \\ \times \frac{\Delta N_1\left(t_k\right)}{Y\left(t_k\right)}\left\{-\frac{1}{Y\left(t_j\right)}+\sum _{t_l<t_j}\frac{\Delta N\left(t_l\right)}{Y\left(t_l\right)\left(Y\left(t_l\right)-\Delta N\left(t_l\right)\right)}\right\}. \end{gathered}$$

10.2. Weighted Breslow estimator of the baseline cumulative subdistribution hazard

The weighted Breslow estimator of the baseline cumulative subdistribution hazard is given by

$$\begin{gathered} {\widehat{\Lambda }}_{1,0}\left(t\mid T_i>{\tau }_0\right)={\int }_{{\tau }_0}^{\tau }{\widehat{\lambda }}_{1,0}\left(t\mid T_i>{\tau }_0\right)dt \\ =\frac{1}{n}\sum _{i=1}^n{\int }_{{\tau }_0}^{\tau }\frac{w_i(u)}{{\widehat{S}}^0(\widehat{\pi },u)}d{N}_i(u) \end{gathered}$$

where ${\widehat{S}}^0(\widehat{\pi },u)={\sum }_{i=1}^n{w}_i(u)T_i(u)\text{exp}\left\{{\widehat{\pi }}^T{Z}_i(u)\right\}$ [11].

10.3. Illustration of non-proportional subdistribution hazards with proportional cause-specific hazards

Let the cause-specific hazards take Weibull form, ${\alpha }_1(t;Z)=\frac{a_1}{b_1^{a_1}}{t}^{a_1-1}{e}^{{\gamma }_{1}Z}$ and ${\alpha }_2(t;Z)=\frac{a_2}{b_2^{a_2}}{t}^{a_2-1}{e}^{{\gamma }_{2}Z}$, where Z is a binary covariate with a proportional effect on both cause-specific hazards. The all-cause cumulative hazard is $A(t;Z)={\frac{t}{b_1}}^{a_1}{e}^{{\gamma }_{1}Z}+{\frac{t}{b_2}}^{a_2}{e}^{{\gamma }_{1}Z}$. The proportional effect of Z on the cause-specific hazard can be verified by deriving the cause-specific hazard ratio (CSHR),

$$\begin{gathered} \frac{{\alpha }_1(t;Z=1)}{{\alpha }_1(t;Z=0)}=\frac{\frac{a_1}{b_1^{a_1}}{t}^{a_1-1}{e}^{{\gamma }_1}}{\frac{a_1}{b_1^{{\alpha }_1}}{t}^{a_1-1}} \\ =e^{{\gamma }_1}. \end{gathered}$$

The subdistribution hazard can be represented as a function of the cause-specific hazard, ${\lambda }_1(t)={\alpha }_1(t)/\left(1+\frac{F_2(t)}{S(t)}\right)$, where $F_k(t)={\int }_0^{t}S(u){\alpha }_k(u)du=1-\text{exp}\left(-{\int }_0^t{\lambda }_k(u)du\right)$. The subdistribution hazard ratio (SHR) is then

$$\begin{gathered} \frac{{\lambda }_1(t;Z=1)}{{\lambda }_1(t;Z=0)}=\frac{{\alpha }_1(t;Z=1)/\left(1+\frac{F_2(t;Z=1)}{S(t;Z=1)}\right)}{{\alpha }_1(t;Z=0)/\left(1+\frac{F_2(t;Z=0)}{S(t;Z=0)}\right)} \\ =e^{{\gamma }_1}\cdot \left(\frac{1+\frac{F_2(t;Z=0)}{S(t;Z=0)}}{1+\frac{F_2(t;Z=1)}{S(t;Z=1)}}\right). \end{gathered}$$

The SHR is not constant, but equal to the CSHR multiplied by a function of time.

10.4. Supplemental tables and figures

Table 8.

Participant characteristics at index age 55 in the Framingham Heart Study

Risk factor	n=5,993
Atrial fibrillation	875 (14.60%)
Death without atrial fibrillation	1,278 (21.32%)
Male sex	2,846 (47.49%)
Height, inches	66.22 (3.73)
Weight, pounds	173.83 (39.52)
Systolic blood pressure, mmHg	125.66 (17.08)
Diastolic blood pressure, mmHg	78.42 (9.83)
Hypertension	1,320 (22.03%)
Current smoker	1,262 (21.06%)
Elevated alcohol use	1,128 (18.82%)
Prior diabetes	421 (7.02%)
Prior heart failure	21 (0.35%)
Prior myocardial infarction	144 (2.40%)

Values are means (standard deviation) or frequency (%).

Table 9.

Sensitivity analysis: predicted differences in lifetime risk of atrial fibrillation at age 95, from index age 55 using BIC

Risk factor	Flexible parametric BIC
Male	5.32 (−0.25, 10.89)
Height, SDU	2.83 (−0.30, 5.95)
Weight, SDU	0.70 (−2.20, 3.59)
Systolic blood pressure, SDU	6.04 (3.13, 8.94)
Diastolic blood pressure, SDU	−2.25 (−4.79, 0.29)
Anti-hypertensive use	1.84 (−1.58, 5.26)
Current smoker	1.97 (−2.05, 5.99)
Elevated alcohol use	2.22 (−0.02, 4.46)
Prior diabetes	−4.63 (−13.92, 4.65)
Prior heart failure	11.46 (−17.68, 40.60)
Prior myocardial infarction	−9.36 (−17.52, −1.20)

SDU: standard deviation unit. Results are % differences in lifetime risk (95% confidence interval). Differences in lifetime risk for continuous risk factors are for one standard deviation increase from the mean. Differences in lifetime risk were obtained by transforming model coefficients at the mean value of other covariates. 95% CIs are obtained with the delta method.

Table 10.

Multivariable models for incident atrial fibrillation in the Framingham Heart Study, from index age 55 to age 95

Risk factor at entry age	Pseudo-observation	Cumulative incidence models
		Fine-Gray	Flex. param. AIC	Flex. param. BIC
	OR (95% CI)	SHR (95% CI)	Cml. SHR (95% CI)	Cml. SHR (95% CI)
Male	1.23 (0.90, 1.66)	1.21 (0.99, 1.49)	4.94 (1.35, 18.06)	1.21 (0.99, 1.49)
Male × Systolic BP, SDU			0.84 (0.71, 1.00)
Male × Prior HF			0.21 (0.01, 4.85)
Height, SDU	1.02 (0.88, 1.19)	1.11 (0.99, 1.23)	1.29 (1.11, 1.50)	1.11 (0.99, 1.23)
Height, SDU × log(age)			0.58 (0.53, 0.63)
Weight, SDU	1.17 (1.05, 1.29)	2.52 (2.06, 3.07)	8.99 (8.19, 9.87)	2.22 (1.83, 2.69)
Weight, SDU × log(age)		0.77 (0.71, 0.83)	0.07 (0.06, 0.09)	0.38 (0.28, 0.51)
Systolic BP, SDU	1.27 (1.08, 1.49)	1.23 (1.12, 1.35)	1.26 (1.10, 1.45)	1.23 (1.12, 1.35)
Diastolic BP, SDU	0.89 (0.76, 1.04)	0.92 (0.84, 1.01)	0.97 (0.83, 1.13)	0.92 (0.83, 1.01)
Hypertension	1.28 (1.02, 1.59)	1.30 (1.11, 1.52)	0.91 (0.74, 1.13)	1.28 (1.09, 1.51)
Current smoker	0.73 (0.53, 0.99)	3.06 (1.65, 5.68)	0.72 (0.60, 0.86)	1.08 (0.93, 1.25)
Current smoker × log(age)		0.69 (0.55, 0.85)
Elevated alcohol use	1.27 (0.96, 1.66)	1.28 (1.09, 1.50)	1.59 (1.36, 1.85)	1.27 (1.09, 1.49)
Prior diabetes	0.64 (0.46, 0.89)	0.88 (0.68, 1.14)	0.96 (0.73, 1.26)	0.88 (0.68, 1.14)
Prior diabetes × log(age)			1.34 (1.17, 1.55)
Prior HF	1.12 (0.34, 3.68)	1.40 (0.57, 3.46)	1.19 (0.12, 12.20)	1.47 (0.60, 3.62)
Prior MI	0.58 (0.32, 1.04)	8.27 (3.49, 19.56)	1.18 (0.82, 1.70)	9.14 (4.72, 17.70)
Prior MI × log(age)	1/4	0.46 (0.33, 0.62)		0.04 (0.02, 0.09)

SDU: standard deviation unit, OR: odds ratio, SHR: subdistribution hazard ratio, Flex. param.: flexible parametric, Cml: cumulative, BP: blood pressure, HF: heart failure, MI: myocardial infarction. Model coefficients for continuous risk factors are presented as a 1 SDU increase (height SD=3.7 inches, weight SD=39.5 pounds, systolic blood pressure SD=17.1 mmHg, diastolic blood pressure SD=9.8 mmHg). Time-covariate interactions are specified as covariate × log(age – 55) for the Fine-Gray model and covariate × log(age) for the flexible parametric model. The flexible parametric model with AIC included 5 knots for the restricted cubic spline of the cumulative baseline hazard, while the model with BIC included 3 knots.

Table 11.

Multivariable models for incident death without atrial fibrillation in the Framingham Heart Study, from index age 55 to age 95

Risk factor at entry age	Pseudo-observation	Cumulative incidence models
		Fine-Gray	Flexible parametric
	OR (95% CI)	SHR (95% CI)	Cml. SHR (95% CI)
Male	0.98 (0.72, 1.32)	3.14 (1.96, 5.04)	5.29 (8.26, 3.39)
Male × log(age)		0.41 (0.30, 0.57)	0.17 (0.31, 0.09)
Height, SDU	0.92 (0.78, 1.08)	0.94 (0.86, 1.03)	0.94 (1.03, 0.86)
Weight, SDU	0.99 (0.89, 1.11)	0.90 (0.82, 0.98)	0.90 (0.98, 0.83)
Systolic blood pressure, SDU	0.86 (0.73, 1.02)	1.05 (0.96, 1.14)	1.04 (1.13, 0.96)
Diastolic blood pressure, SDU	1.24 (1.05, 1.46)	1.13 (1.04, 1.24)	1.13 (1.22, 1.04)
Hypertension	0.79 (0.63, 1.00)	1.77 (1.19, 2.63)	3.02 (4.89, 1.87)
Hypertension × log(age)		0.76 (0.65, 0.89)	0.24 (0.44, 0.13)
Current smoker	2.47 (1.71, 3.56)	3.85 (2.60, 5.68)	3.92 (5.23, 2.94)
Current smoker × log(age)		0.80 (0.69, 0.92)	0.44 (0.62, 0.31)
Elevated alcohol use	0.98 (0.72, 1.32)	1.17 (1.03, 1.33)	1.17 (1.33, 1.03)
Prior diabetes	1.66 (1.14, 2.41)	1.90 (1.55, 2.32)	7.65 (12.42, 4.71)
Prior diabetes × log(age)		0.81 (0.70, 0.92)	0.20 (0.35, 0.11)
Prior HF	1.16 (0.39, 3.48)	9.53 (3.92, 23.17)	0.68 (1.75, 0.27)
Prior HF × log(age)			2.71 (6.31, 1.16)
Prior MI	2.62 (1.29, 5.31)	2.07 (1.60, 2.68)	2.08 (2.69, 1.60)

SDU: standard deviation unit, OR: odds ratio, SHR: subdistribution hazard ratio, Cumul: cumulative, BP: blood pressure, HF: heart failure, MI: myocardial infarction. Model coefficients for continuous risk factors are presented as a 1 SDU increase (height SD=3.7 inches, weight SD=39.5 pounds, systolic blood pressure SD=17.1 mmHg, diastolic blood pressure SD=9.8 mmHg). Time-covariate interactions are specified as covariate × log(age – 55) for the Fine-Gray model and covariate × log(age) for the flexible parametric model. The flexible parametric models also included 4 terms for the restricted cubic spline of the baseline hazard.

Fig. 4.

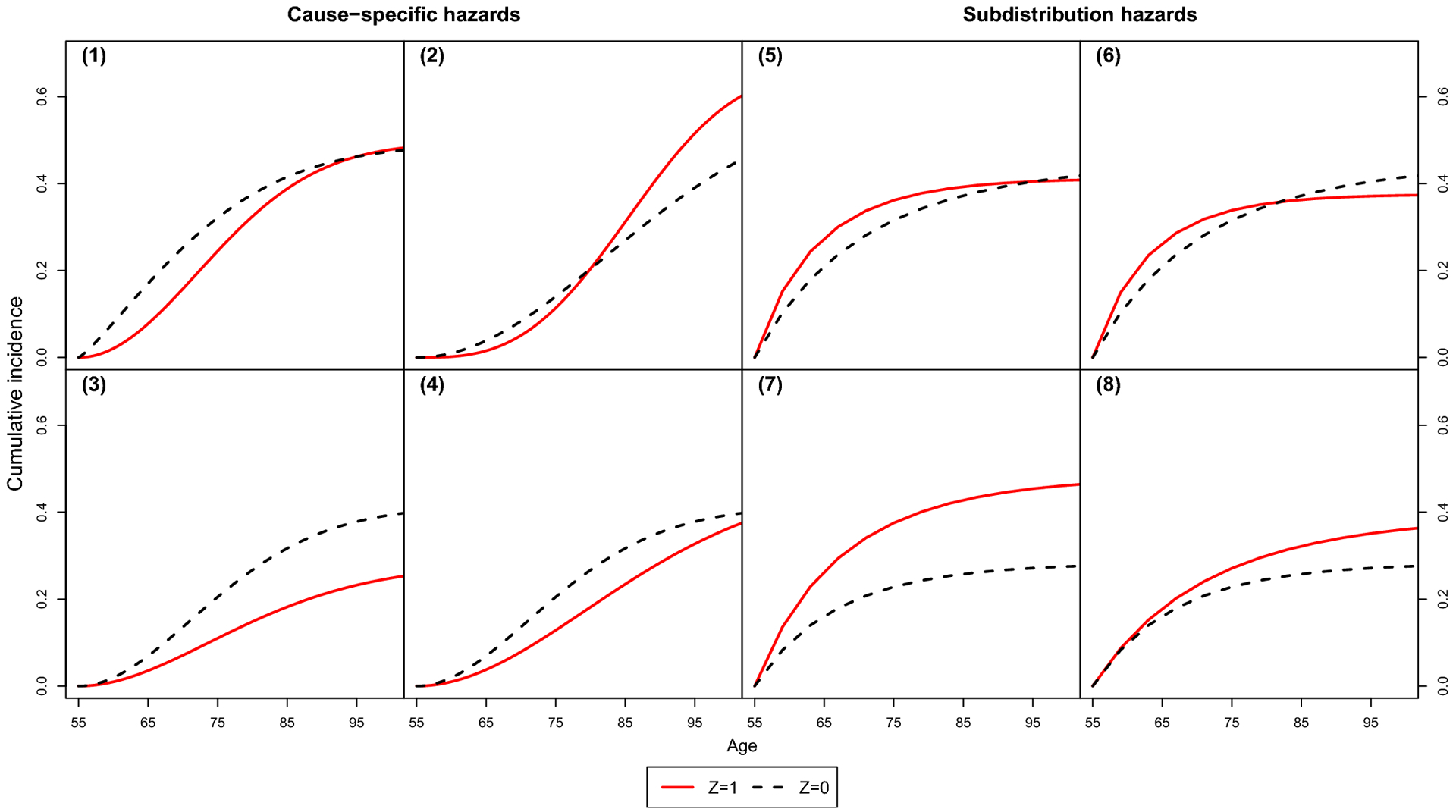
True cumulative incidence functions in simulation study

Fig. 5.

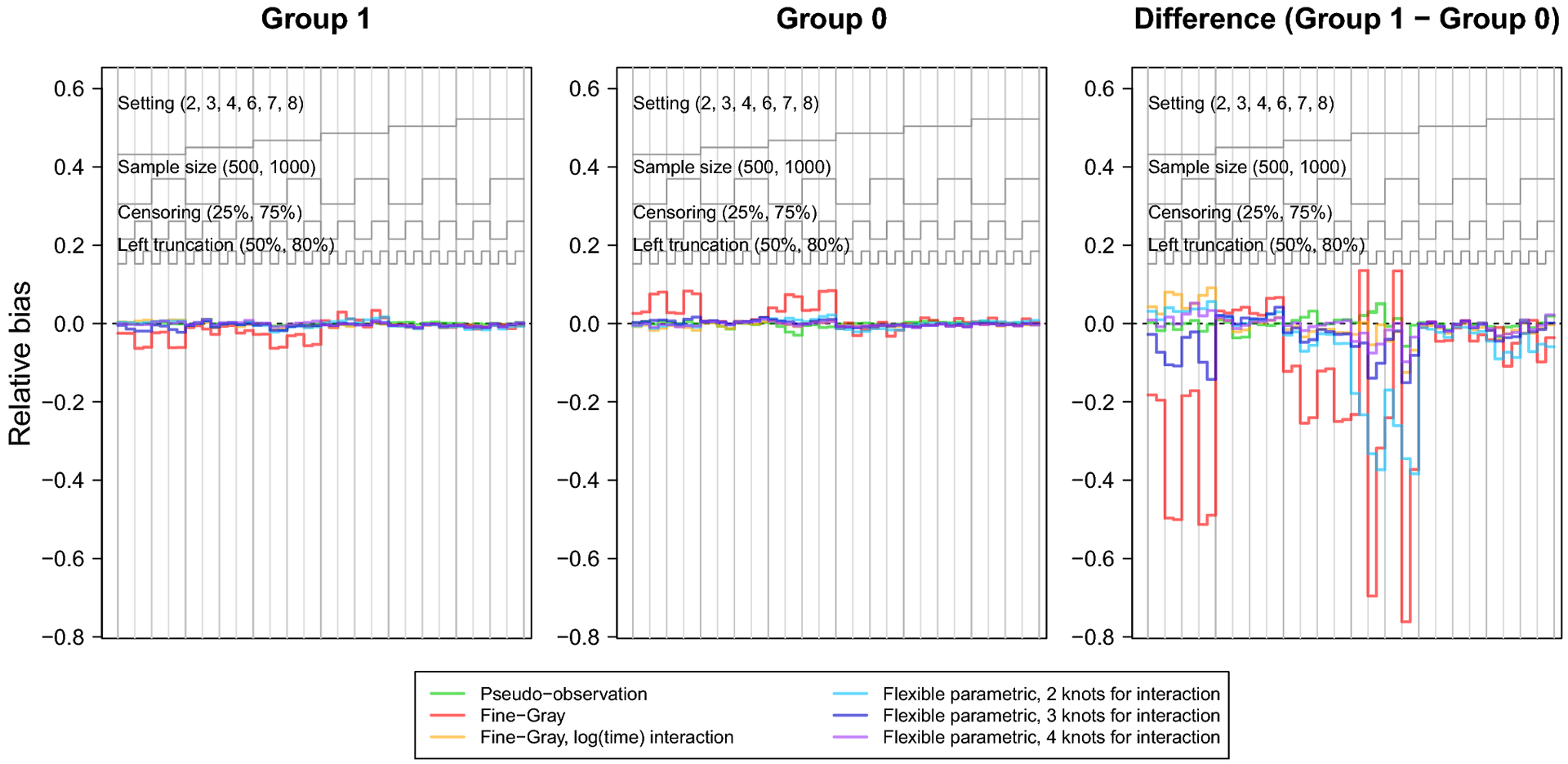
Nested loop plot showing the simulation study results: relative bias

Fig. 6.

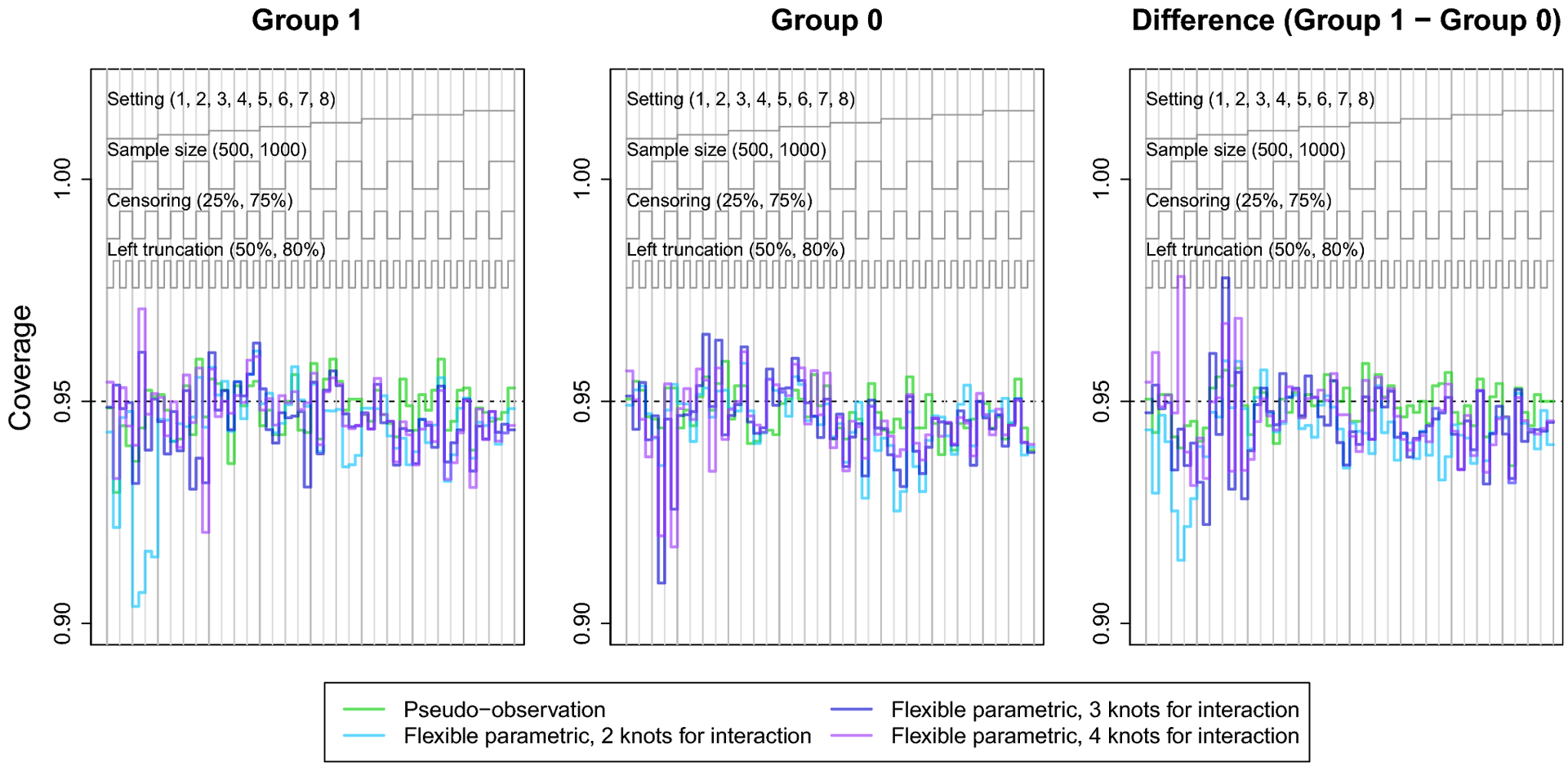
Nested loop plot showing the simulation study results: coverage

Fig. 7.

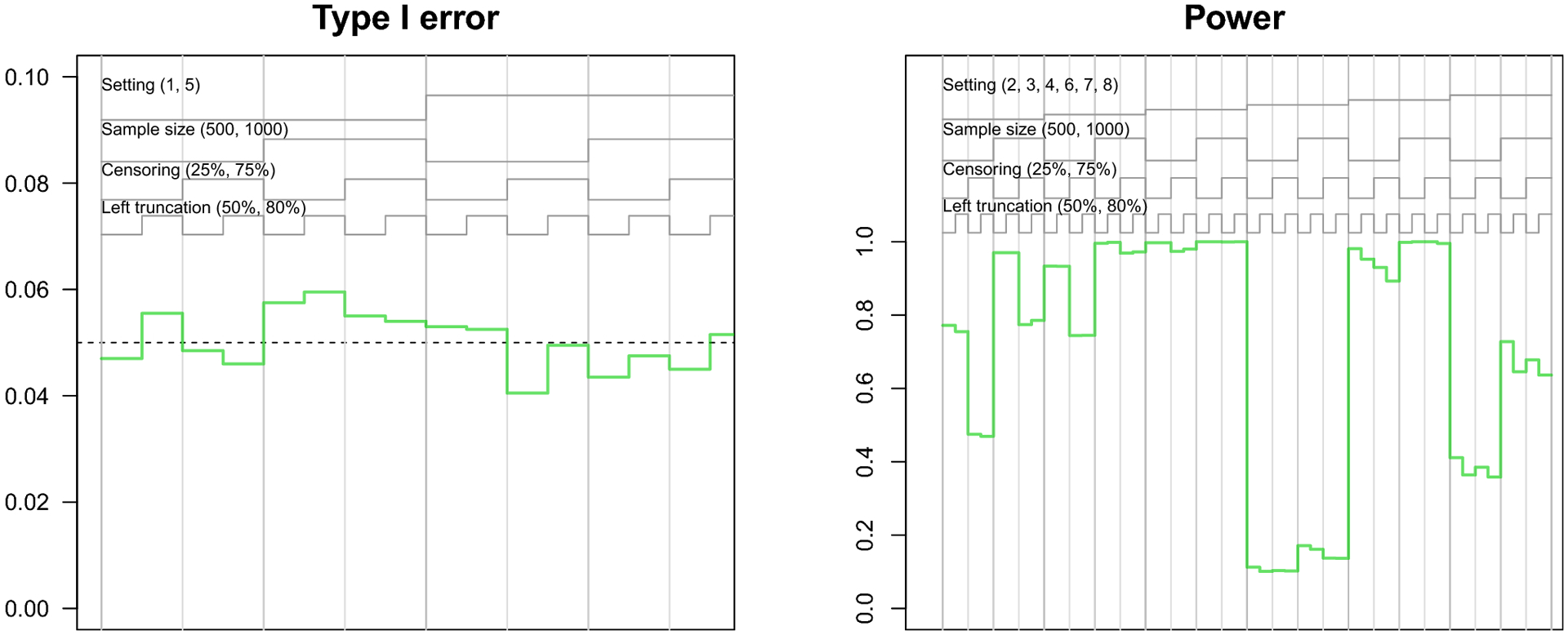
Nested loop plot showing the simulation study results: type I error and power of pseudo-observation method

Availability of data and material

To protect the confidentiality of the Framingham Heart Study participants, the data from our illustrative examples are not on our GitHub page. Participant level data from the Framingham Heart Study are available at the database of Genotypes and Phenotypes (https://www.ncbi.nlm.nih.gov/gap/) and BioLINCC (https://biolincc.nhlbi.nih.gov/home/).