A correlation between cavitation bubble temperature, sonoluminescence and interfacial chemistry – A minireview

Highlights

• •A brief overview on the correlation between sonoluminescence and bubble temperature.
• •Both theoretical and experimental estimation of bubble temperatures discussed.
• •The importance of interfacial chemistry in acoustic cavitation process discussed.
• •The mini-overview is aimed at benefiting new comers to this field.

Abstract

Ultrasound induced cavitation (acoustic cavitation) process is found useful in various applications. Scientists from various disciplines have been exploring the fundamental aspects of acoustic cavitation processes over several decades. It is well documented that extreme localised temperature and pressure conditions are generated when a cavitation bubble collapses. Several experimental techniques have also been developed to estimate cavitation bubble temperatures. Depending upon specific experimental conditions, light emission from cavitation bubbles is observed, referred to as sonoluminescence. Sonoluminescence studies have been used to develop a fundamental understanding of cavitation processes in single and multibubble systems. This minireview aims to provide some highlights on the development of basic understandings of acoustic cavitation processes using cavitation bubble temperature, sonoluminescence and interfacial chemistry over the past 2–3 decades.

1. Introduction

The interaction between bubbles in a liquid and ultrasound induces acoustic cavitation under specific experimental conditions [1]. Detailed mechanistic information on the acoustic cavitation process is covered extensively in several books, review papers and book chapters [2], [3], [4], [5]. Briefly, small bubble nuclei present in a liquid oscillate in response to the pressure variations caused by (ultra)sound waves. The bubbles expand during the rarefaction pressure cycle (negative acoustic force) and shrink during compression pressure cycle. The bubbles grow in size during these oscillations due to rectified diffusion. When bubbles reach a resonance size range, they grow to a maximum and collapse, which is a near adiabatic process. Extreme temperatures and pressures are generated within the collapsing bubbles that lead to the formation of highly reactive redox radicals that may be used to initiate a variety of chemical reactions. The acoustic cavitation process is also accompanied by several physical effects such as the generation of shock waves, microjets, shear forces, etc. These physical forces can also be helpful to initiate chemical and physical processes and for enhancing rates of chemical reactions by mass transfer effects.

Acoustic cavitation is found to be useful in many applications. The redox radicals have been used to generate functional nanomaterials and for the degradation of organic pollutants in an aqueous environment [6], [7], [8], [9], [10]. For example, synthesis of biofunctional polyphenolic nanoparticles has been reported for use in targeted drug delivery [11]. The physical and chemical effects of acoustic cavitation have been used for the conversion of polyphenol molecules into functional nanoparticles. It has been shown in this study that the hot interfacial zone of the cavitation bubbles plays a major role in the crosslinking of polyphenolic molecules to generate nanoparticles. The use of such nanoparticles as drug carriers has also been demonstrated in this report, where the intracellular trafficking and dissipative dissolution of the nanoparticles have been studied. The oxidative radicals (^.OH,^.HO₂) generated during the cavitation process have been used to oxidise aqueous pollutants. A review by Cao et al. [9] discusses the sonochemical degradation of poly- and perfluoroalkyl substances. A substantial amount of work has been progressed on the applications of ultrasound in food processing and flavour/nutrient delivery [5], [12], [13], [14], [15]. In majority of the processing applications, including food processing, the physical forces generated by acoustic cavitation play a significant role. Examples include extraction and emulsification applications. It should also be noted that 20 kHz ultrasound is efficient for applications that need strong physical forces such as shear, microstreaming, shockwaves, etc. For applications that require redox reactions, higher frequency ultrasound in the range of 200 kHz–800 kHz is recommended. The amount of radicals generated in this frequency range is significantly higher due to the formation of greater number of active cavitation bubbles [5]. While the majority of such studies have been carried out on a lab-scale, significant progress has also been made to transform lab-scale research into large-scale processes [16], [17].

One of the hurdles for the development of industrial-scale applications of ultrasound is the optimisation/customisation of the cavitation process for specific applications, which involves maximising the cavitation efficiency at minimal energy consumption. The cavitation efficiency as a function of various experimental parameters could be evaluated using several methodologies. For example, for chemical applications, the amount of radicals generated by cavitation could be quantified [18], [19], [20]. Sonoluminescence, sonochemiluminescence, acoustic emission and acoustic pressure distribution could also be measured to quantify cavitation efficiency [21], [22], [23], [24]. The effect of surface active solutes on cavitation bubbles is extensively discussed by Ashokkumar and Grieser [25].

At a fundamental level, cavitation efficiency, which in turn depends upon collapse intensity, bubble temperature, number of cavitation bubbles, etc., could be quantified using sonoluminescence (SL). SL refers to light emission observed during acoustic cavitation [2], [26]. It is generally accepted, based on hotspot theory, that sonoluminescence intensity is strongly dependent upon the maximum bubble temperature reached when a cavitation bubble collapses. This is valid for a single bubble case. Based on various theories and experimental work, SL spectral profiles could be used to estimate cavitation bubble temperatures, for a single bubble system, which will be discussed in the next sections. In a multibubble (MB) environment, the total SL emission is also governed by the number of cavitation bubbles in addition to the maximum temperature generated in each bubble.

The aim of this minireview is to provide a historical view of selected fundamental work on SL, SL quenching and the role of interfacial chemistry in understanding acoustic cavitation processes in the presence of surface-active solutes. It is worth noting that number of research and review articles are available that provide an advanced level discussion on the theoretical and experimental aspects of acoustic cavitation, sonoluminescence and sonochemistry [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40]. Yasui has written excellent review articles on these topics [27], [28], [29]. The numerical simulations for sonochemistry were discussed for single and multibubble sonochemistry. It is noted that an optimal bubble temperature range exists to maximize the production of oxidants such as OH radicals. At very high temperatures, these oxidants are consumed within the bubble for other reactions resulting in an overall reduction in the amount of oxidizing radicals for reactions in the bulk. A detailed discussion on acoustic cavitation and bubble dynamics [27] provides the readers to get an advanced understanding of this topic. Yasui also discussed [29] that the cavitation bubbles may be filled with a relatively higher amount of water vapour or noncondensable gases depending upon the acoustic frequency and power. The light emission from a plasma formed inside a bubble and the possibility of liquid droplet injection leading to atomic and molecular emissions contributing to SL is discussed. The liquid injection model was first proposed by Suslick and coworkers [30], which has been discussed in a later section.

Suslick and coworkers [31] have recently provided an excellent review on ‘The Chemical History of a Bubble’ where they have discussed the fundamental aspects of cavitation, single and multibubble SL, bubble temperature estimation using SL spectral measurements and chemical reactions arising from bubble collapse. Lohse [32], in his recent review, has discussed his personal scientific journey in bubble dynamics area that includes fundamentals and applications of acoustic cavitation. Other major contributions from many senior researchers that include Crum, Putterman, Brennan, Lauterborn, Mettin, Nikitenko, Pflieger and others [33], [34], [35], [36], [37], [38], [39], [40] also serve as excellent resource articles for the readers who may wish to get an advanced level understanding of acoustic cavitation and bubble dynamics.

The current minireview covers primarily our work on the correlation between cavitation bubble temperature, sonoluminescence and interfacial chemistry. Readers who are interested in learning bubble dynamics and acoustic cavitation at an advanced level are encouraged to refer to other references cited in this article.

2. Theoretical considerations

One may consider Eq. (1) [1], [2], [3] for understanding some key parameters that may control cavitation bubble temperatures.

$$T_m=T_0\left\{\frac{{\text{P}}_{\text{v}}\left(\gamma -1\right)}{{\text{P}}_v}\right\}$$ (1)

where, γ is the heat capacity ratio, viz, $\gamma =\frac{{\text{C}}_p}{{\text{C}}_v}$, T_max = maximum bubble T; T_o = solution T; P_m = Liquid P (can be assumed to be P_hydrostatic; P_acoustic + P₀) and P_v = P inside the bubble before collapse (when the bubble is at its max size). C_p and C_v are heat capacities of gas molecules at constant pressure and volume, respectively. P_hydrostatic represents the total hydrostatic pressure, which could be assumed to be equal to the sum of acoustic pressure (P_acoustic) and atmospheric pressure (P₀).

Equation 1 originates from the original model developed by Rayleigh [2], who derived a mathematical solution for bubble wall velocity and the time of bubble collapse. The model predicted that the collapse time of a cavitation bubble is in the order of microsecond and suggested that the bubble collapse could be considered as an adiabatic process that led to the development of a simplified Equation 1 to estimate the maximum temperature generated when a bubble collapses. Further details on Rayleigh model are available in Ref. 2. A review on SL by Walton and Reynolds [41] has also provided the full analysis of Eq. 1. It should also be noted that Eq. 1 cannot be used to calculate the bubble temperature in a strict sense. The model calculations discussed below are for understanding the importance of each parameter used in Eq. 1, in particular γ and P_v terms. For those interested in determining cavitation bubble temperatures should use advanced equations provided in various references discussed above [1], [2], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41]. Eq. 1 is derived based on certain assumptions (For example, when ultrasound frequency is altered, the resonance size of cavitation bubbles is altered, the bubble collapse is an adiabatic process and no endothermic chemical reactions occur) and does not provide the means to determine the bubble temperature as a function of frequency, acoustic power, etc.

Assuming the bubble core contains a noble gas, γ = 1.66, T_o = 298 K, P_m = 2 atm and P_v = 0.031 atm, Equation 1 yields a T_max of about 12,700 K. It should be noted that Eq. 1 assumes that the bubble collapse is a pure adiabatic process and no endothermic chemical reactions occur within the hot core of the bubble (which may be true if only noble/inert gases are present within the bubble). There is ample evidence available for endothermic chemical reactions leading to radical and other product formation within the bubble. We will get back to this discussion later.

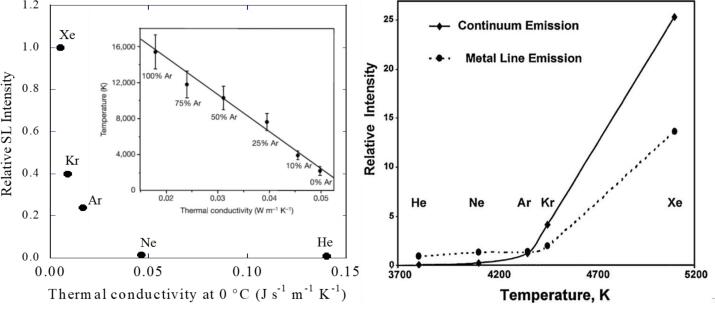
First, let us look at the SL data [26] observed in water saturated with noble gases (Fig. 1). If Eq. 1 is considered, the T_max should not be affected by the nature of noble gas, in other words, SL intensity should be the same for all noble gases. However, it is clear from Fig. 1 that the SL intensity decreases with a decrease in the atomic weight of the noble gas. It can be observed that the SL intensity observed from an Xe cavitation bubble is the highest and that from a He bubble is the lowest. More specifically, the SL intensity decreases with a decrease in atomic size of the noble gas. In order to clarify this observation, let us consider the thermal conductivities of noble gases. The noble gas with the lowest atomic weight has the highest thermal conductivity [42]. Considering kinetic molecular theory, where it has been predicted that the root mean square velocity of atoms/molecules is inversely proportional to molar mass, helium (He), with lowest molar mass, moves much faster than other noble gases and can transfer the heat energy to the surroundings at a faster rate. It should be noted that the data provided in the insert of Fig. 1A was obtained from a unique system consisting of concentrated sulfuric acid [43]. However, a similar observation was reported by Didenko et al. [44] using a system containing a mixture of octanol and dodecane (Fig. 1B) where SL intensities and cavitation bubble temperatures were observed to be different for different noble gases.

Fig. 1.

(A) The dependence of SL intensity, observed at 20 kHz, on thermal conductivity of noble gases [Adapted from Ref [26]]. The insert shows that the cavitation bubble temperature has a linear dependence on the thermal conductivities [43] of gases contained within a cavitation bubble; (B) Relative SL intensity as a function of bubble temperatures observed in a mixture of octanol and dodecane saturated with different noble gases [44].

As noted in Fig. 1, the thermal conductivity of He is higher than that of other noble gases. The data shown in Fig. 1 also indicates that the SL intensity decreases with an increase in thermal conductivity. Note that other equations incorporating thermal conductivity and other parameters are available for the prediction of T_max. Readers may find such equations/discussion in References 1 and 2. A key inference from Fig. 1 is that Equation 1 has limitations and one of the major assumptions made, namely pure adiabatic collapse of the bubble, may not be valid. However, Equation 1 is very useful to understand the effect of other parameters on cavitation bubble temperature, discussed later. Fig. 1 data shows that bubble collapse is not a pure adiabatic process. Flannigan and Suslick [43] provided further experimental evidence for the dependence of T_max on thermal conductivity of gases present within collapsing bubbles at 20 kHz. Using mixtures of Ar and Ne they were able to systematically control the SBSL (single bubble sonoluminescence) emission temperature from ∼15,000 K down to ∼1,500 K. It is also worth noting that the investigation by Flannigan and Suslick [43] also provides some evidence for the existence of a plasma in the bubble core. The existence of a plasma was also confirmed by Putterman and coworkers [45]. A recent review by Nikitenko and Pflieger [46] provides a details discussion on the existence of a plasma based on MBSL spectroscopic data.

Now, let us get back to Equation 1 and explore what other parameters are important for T_max. Assuming a cavitation bubble has only water (vapour) molecules, using γ = 1.32 (for water) and keeping other parameters as noted earlier, the calculated T_max is about 6,150 K. It can be immediately realized that γ plays a major role in controlling T_max. In simple terms, γ indicates the complexity of the molecules present inside the bubble and indirectly indicates the consumption of thermal energy for endothermic processes such as decomposition of molecules. For example, O–H bonds in water could be broken by thermal energy leading to the formation of intermediates and stable products (H, OH, H₂, H₂O₂, etc) [3], [4], [5]. We will get back to this discussion involving endothermic chemical reactions later.

3. Experimental considerations

The question now is whether the T_max range predicted by Equation 1 could be experimentally measured. It is impossible to physically measure the T_max since the volume of the ‘hot zone’ is tiny (less than a micrometer in radius) and the heat stays in this hot zone for less than a microsecond (SL lifetime has been predicted to be less than a few hundred nanoseconds). There are a number of indirect techniques used as ‘chemical thermometers’. Some key techniques used for the estimation of cavitation bubble temperatures in multibubble (MB) systems are listed in Table 1.

Table 1.

Selected techniques for the estimation of cavitation bubble temperatures.

Experimental Technique	Cavitation Bubble Temperature, K	Reference
Molecular emissions observed in multibubble sonoluminescence (20 kHz)	∼2,000–4,300	[47], [48]
Comparative rate thermometry (20 kHz)	∼5,200	[49]
Radical quantification – ESR (20 kHz)	1000–4600 K	[50], [51]
Product quantification – Methyl radical recombination method (20 kHz–1 MHz)	∼2,000–∼7,000	[52], [53], [54], [55]
Molecular emissions observed in single bubble sonoluminescence	15,000–30,000	[56]
Molecular emissions in ionic liquids to determine vibrational and rotational temperatures	4,000–6,000	[57]
Molecular emissions observed from symmetrically and asymmetrically collapsing bubbles (nanodroplet injection model)	4,000–9,500	[30], [59]

Suslick and coworkers [48] developed a MBSL-based technique to determine the T_max of cavitation bubbles at 20 kHz. The emission from the excited state of C₂, generated when a mixture of benzene/water was sonicated at 20 kHz was used to determine the cavitation bubble temperature to be ∼ 4300 K in water. More specifically, the temperature determination was made by comparison of the relative intensities of the two most intense C₂ Swan bands, namely, Δν = 1 and Δν = 2 bands. C₂ molecule in its excited state is generated by thermal decomposition of benzene within the hot zone of the cavitation bubbles. Molecular emission from SBSL was also used to estimate the temperature observed in single bubble systems. Didenko et al. [56] estimated T_max of about 15,000 K in a moving single bubble case and suggested that the T_max reached could be 30,000 K in stable single bubble systems. Pflieger et al. [57] used molecular emissions observed in an ionic liquid and estimated rotational and vibrational temperatures in the range 4000–6000 K.

Suslick et al. [49] used comparative rate thermometry and determined the gas-phase temperature of the collapsing bubble to be about 5,200 K. Using sonochemical ligand substitution rates of volatile metal carbonyls, they proposed two regions of sonochemical reactivity, namely, the gas-phase mentioned above and a thin liquid shell at the bubble interface with an effective temperature of 1,900 K.

The approach is similar to that was established by Henglein and coworkers [52] where they used the relative rate constants of chemical reactions to determine cavitation bubble temperature. This commonly known as methyl radical recombination (MRR) method is based on the decomposition of methane to generate methyl radicals. Briefly, a small amount of methane was dissolved in argon-saturated water. During the acoustic cavitation process, methane diffused into cavitation bubbles and methyl radicals were generated within the ‘hot zone’. The methyl radicals combine to form either ethane or ethylene in two competing reaction pathways. The rate constant for the ethylene formation reaction is highly temperature dependent, whereas that for the formation of ethane is almost independent of the temperature. The ratio between these two rate constants is equal to the ratio between the amounts of the two products. Thus, by measuring the quantities of ethane and ethylene produced after sonication for a given time, cavitation bubble temperatures could be estimated to be around 2,000–7,000 K under various experimental conditions. A few other studies followed the MRR method and determined the temperatures to be in a similar range [53], [54]. Misik et al. [50], [51] independently developed a similar method by sonicating 50/50 H₂O/D₂O and determined the cavitation bubble temperature to be in the range of 1,000–4,600 K.

What is interesting is that, despite the involvement of various methodologies and independent systems, all estimations reported a similar range of cavitation bubble temperatures. Let us get back to the theoretical temperature calculated for water in the discussion above using Equation 1. Under the assumptions that bubble contains only water vapor, the theoretical temperature was estimated to be about 6,150 K. Based on the MRR method, we can make another assumption that the bubble is full of hydrocarbons (methane, ethane, ethylene, etc.) and replace γ from 1.34 to 1.1–1.2 (hydrocarbons), the estimated temperature would be in the range 2,000–4,000 K. This is in agreement with what was determined using MRR method for systems containing volatile organic solutes [53], [54].

From the above discussion, the importance of the γ (heat capacity ratio) of gases present within a collapsing bubble could be understood. Both the thermal conductivity and heat capacity ratio of bubble contents are found to be important in governing the cavitation bubble temperature. Other factors such as ultrasound frequency, power, physical properties of the sonicated liquid, etc., have also been shown to affect the cavitation bubble temperatures [54], [58].

Okitsu et al. [55] investigated the effect of rare gas atmosphere on bubble temperatures at high frequencies using MRR method and reported that the estimated temperatures were similar independent of the nature of rare gas. This is not surprising since the MRR method relies on the fact that hydrocarbon products accumulate over many cycles and the bubble contents are primarily hydrocarbons irrespective of the nature of the dissolved gas. The readers may also benefit by a review article published by Rooze et al. [ref] on the effect of dissolved gas on cavitation.

As mentioned earlier, Suslick and coworkers [49] identified two different ‘hot zones’ when cavitation bubbles collapse, namely hot gas-zone (interior of the bubble) and a thin liquid shell at the interface. Suslick and coworkers [30], [59] have also reported the existence of two distinct bubble populations based on their investigation on SL spectral studies in phosphoric acid under inert gas atmosphere. They observed that the bubbles near the tip of the ultrasonic horn collapsed symmetrically generating a relatively higher temperature (9,500 K). They could observe excited state OH. emission from these bubbles. However, bubbles at the bottom of the clouds showed PO. emission only due to the generation of a relatively lower temperature (4,000 K), which collapse asymmetrically resulting in the injection of liquid nanodroplets from the bubble surface (bubble/solution interface).

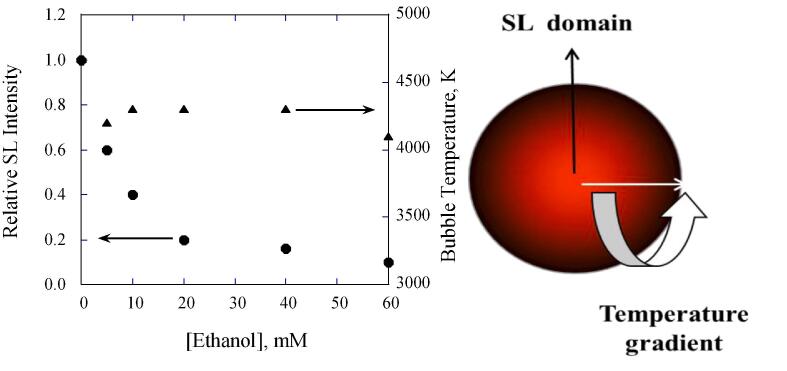
Another important factor that needs to be considered is the peak temperature that can be attained on bubble collapse. The T_max is different from the ones measured above using experimental techniques. Theoretical calculations often report the peak temperatures whereas the experimentally determined temperatures can be considered as time- and volume- average temperatures. Ashokkumar and Grieser [60] compared the extent of (multibubble) sonoluminescence quenching (SL quenching discussed in detail later) and the relative changes in bubble temperatures measured by the MRR method. It can be seen in Fig. 2 that the MBSL (multibubble sonoluminescence) intensity is about 90% quenched by the addition of about 50 mM ethanol and the bubble temperature is not affected by the addition of the same amount of ethanol.

Fig. 2.

Left. The dependence of SL intensity and bubble temperatures measured by MRR method on the bulk concentration of a surface active solute, ethanol. Frequency. 515 kHz. Right: A schematic representation of SL domain at the centre of a collapsing bubble where peak T is reached. The possibility of the existence of a temperature gradient is proposed [60].

It is well known that SL occurs at the last stages of the bubble collapse when the bubble radius reaches its minimum and the bubble T reaches its peak (see the schematic shown in Fig. 2). The peak temperature could be significantly affected by the presence of a small amount of gaseous compounds within the collapsing bubble. Whereas, the temperature measured by the MRR method, which is based on chemical reactions indicates that this method reports on the volume and time averaged temperature, is not significantly affected by the gas contents on a relative basis. The authors speculated that the maximum temperature is reached at the centre of the collapsing bubble, SL domain in Fig. 2, which has a relatively smaller volume and can be easily quenched by gaseous molecules present in the bubble. The authors [60] have also suggested that there exists a temperature gradient as shown in Fig. 2, and the MRR method simply reports on the average temperature, which could be as high as 5000 K where chemical reactions can still proceed without SL. SL is a combination of hot body emission and fluorescence arising from excited state molecules present within cavitation bubbles. The presence of gaseous molecules may also deactivate excited state species via non-radiative processes leading to SL quenching.

4. Sonoluminescence quenching

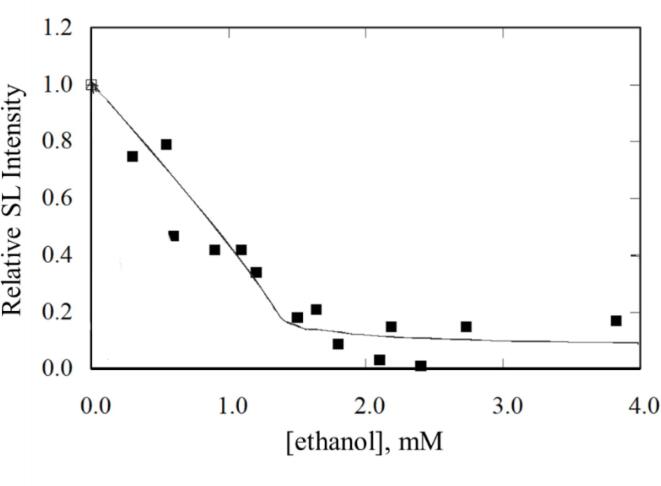
In Fig. 2, the quenching of sonoluminescence by the presence of volatile solutes is shown in relation to cavitation bubble temperature. In a MB system, the SL (MBSL: multibubble sonoluminescence) intensity depends on two factors, namely, the amount of light emitted by each bubble and the total number of cavitation bubbles. The addition of solutes such as ethanol or any volatile compound is found to decrease SL intensity [61], which could be attributed to either a decrease in maximum bubble temperature or a decrease in the number of cavitation bubbles or a combination of both. In order to identify the importance of these factors for SL quenching, further experiments were carried out using a single bubble system [62], [63]. As shown in Fig. 3, the presence of an alcohol in water seems to quench single bubble SL (SBSL) as well [62], suggesting the SL quenching observed in a MB system is due to a decrease in T_max and not due to a decrease in bubble numbers.

Fig. 3.

Sonoluminescence quenching by a volatile solute in a single bubble (22 kHz) system [62].

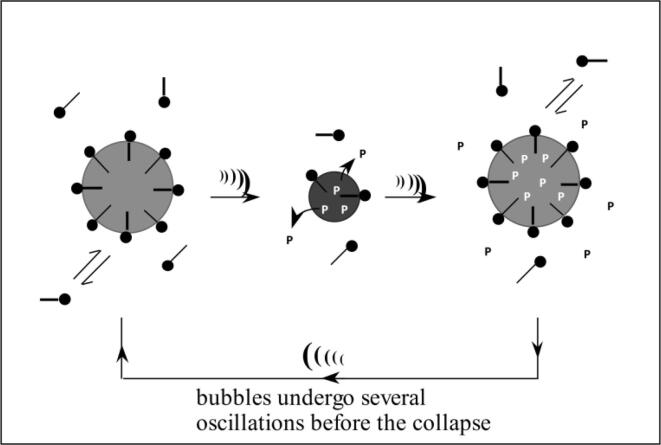
Now, we need to think about why the addition of a small amount of a volatile solute should decrease T_max and quench SL. Let us bring back the T_max equation to see what could be responsible for a decrease in T_max. In Eq. (1), T_max is related to T_o, P_m, γ and P_v. It is obvious that the addition of a few mM of a volatile solute would not affect T_o and P_m. γ represents the heat capacity ratio of solutes that diffuse into the bubble during the expansion phase. Considering the fact that the solubility of air may not be influenced by the presence of a few mM of a volatile solute and the bubble/solution interface will still be dominated by water (55.5 M H₂O vs a few mM volatile solute), the amount and nature of solutes that evaporate/diffuse into the bubble will not be affected. For example, in aqueous solutions, the bubble content will still be dominated by water vapor and only a few volatile solute molecules (such as alcohol) will be diffusing into the bubble during a single expansion cycle. What this means is that both γ and P_v will not be affected by the presence of a small amount of alcohol in the solutions when a single oscillation is considered. Then, why does the temperature and hence the SL intensity should decrease? The answer to this question was proposed by Grieser and coworkers [25]. They suggested that bubbles can undergo stable (repetitive transient) or transient cavitation [64]. Stable bubbles oscillate over several hundred cycles. As schematically shown in Fig. 4 [65], during each expansion cycle, a few alcohol molecules evaporate/diffuse into the bubble, undergo thermal degradation under the extreme heat generated on bubble collapse and generate stable gaseous hydrocarbon products such as methane, ethane, etc.

Fig. 4.

Schematics showing product buildup over several acoustic cycles [65].

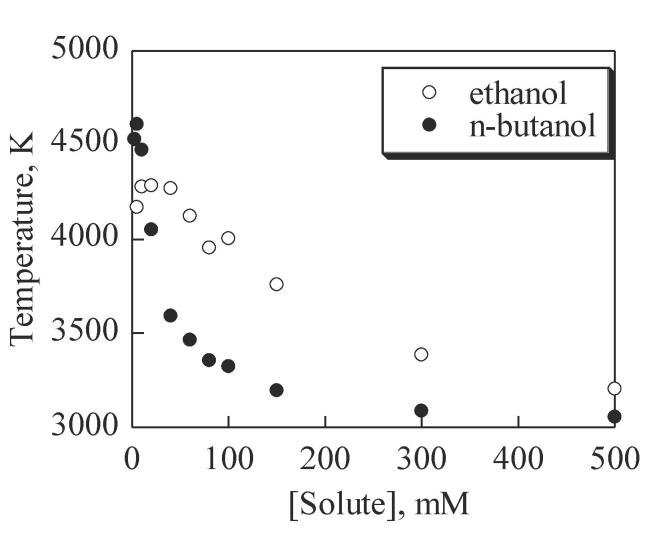
These hydrocarbon products stay inside the bubble due to their hydrophobic nature. This leads to the accumulation of hydrocarbon gases within cavitation bubbles over several cycles, leading to a significant lowering of γ (for hydrocarbons, γ is 1.1–1.2) and an increase in P_v (internal pressure). This ultimately decreases the T_max as predicted by Equation 1. In fact, the lowering of γ from 1.34 for water to 1.1–1.2 for hydrocarbon gases results in a theoretical maximum temperature of about 2,000–4,000, which is in agreement with the temperature measured by the MRR method at 355 kHz (Fig. 5).

Fig. 5.

Cavitation bubble temperatures measured by MRR method in aqueous solutions containing alcohols at various concentrations [Adapted from Ref [54]]. (355 kHz).

The speculative mechanism proposed in Fig. 4 is based on the assumption that volatile solutes should evaporate/diffuse into the cavitation bubbles and hydrocarbon gaseous products should buildup over several acoustic cycles. In order to validate this hypothesis, Ashokkumar et al. carried out both single [62] and multibubble [65] sonoluminescence quenching in the presence of a weak acid or a weak base in aqueous solutions. A weak carboxylic acid or a base can be kept in 100% ionized or neutral forms depending upon the solution pH. For example, propanoic acid has a pKa of about 4.8. The acid exists in neutral form or ionized forms when the solution pH is kept below and above pKa, respectively.

CH₃CH₂COOH + H₂O ↔ CH₃CH₂COO– + H₃O⁺ Reaction 1

CH₃CH₂CH₂NH₂ + H₂O ↔ CH₃CH₂CH₂NH₃⁺ + OH^– Reaction 2

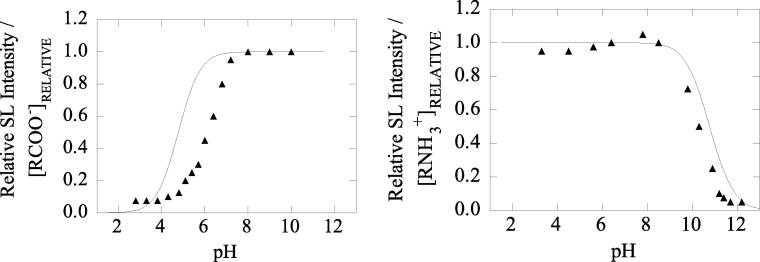
In Fig. 6, the MBSL quenching behavior observed in aqueous solutions containing a weak acid or a base is shown as a function of solution pH. It can be clearly seen that SL quenching occurs only when solute molecules are in their neutral forms. The ionized forms of the molecules have insignificant volatility compared to the highly volatile neutral forms. This study unequivocally demonstrated that the volatility of solutes is important for SL quenching to occur.

Fig. 6.

MBSL quenching as a function of pH in aqueous solutions containing a weak acid or a base [65]. The solid line shows the relative concentration of the ionized form, calculated using Henderson Equation [66] and the solid data points represent experimentally measured SL intensity relative to pure water. Frequency. 515 kHz.

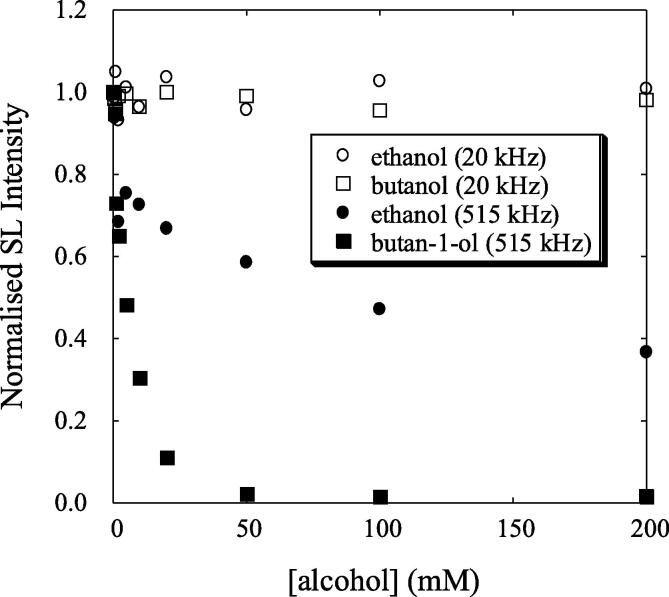
Another speculation that was made when the SL quenching mechanism was proposed is that the bubbles need to oscillate for several acoustic cycles. By providing additional experimental evidence using low frequency (20 kHz) and high frequency (515 kHz) MBSL studies, Grieser and coworkers could demonstrate that SL quenching could only occur under stable (repetitive transient) cavitation conditions [64]. At 20 kHz, where transient cavitation dominates, they could not observe SL quenching, whereas significant SL quenching was observed at 500 kHz under similar experimental conditions. It could be seen in Fig. 7 that the addition of ethanol or butanol quenched more than 90% of SL intensity at 515 kHz whereas no SL quenching could be observed at 20 kHz under similar experimental conditions. The authors have suggested that the cavitation bubbles generated at 20 kHz are primarily transient in nature and exist for only a few acoustic cycles where no product accumulation is possible. Whereas cavitation bubbles generated at 515 kHz are stable bubbles due to the formation of standing waves where hydrocarbon product accumulation is possible. The same authors also carried out further experiments in the frequency range 200 kHz – 1 MHz in order to provide further support to the proposed mechanism for SL quenching [67], [68], [69].

Fig. 7.

MBSL behaviour at 20 kHz and 515 kHz in the presence of volatile solutes [Adapted from Ref. [64]].

Guan and Matula [70] provided a strong experimental support to the speculation that SL quenching occurs due to product accumulation over several acoustic cycles. Using SBSL studies, they reported that it requires 8000 acoustic cycles to completely quench SBSL. In a single bubble setup, a cavitation bubble can be kept ‘alive’ in a standing wave for millions of cycles and the SL intensity is shown to be constant in water for several hours.

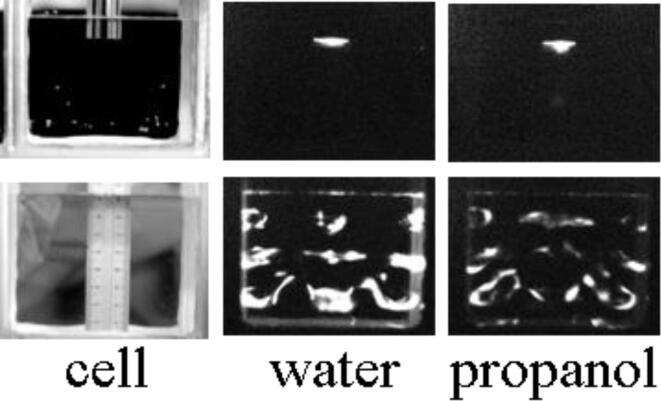
Ashokkumar et al. [71], [72] later showed that MBSL quenching is primarily observed when a standing wave is established, irrespective of the frequency and suggested that stable cavitation dominates when a standing wave is established. They used a 20 kHz horn arrangement and a 20 kHz plate transducer for investigating the SL quenching behavior. The images shown in Fig. 8 shows that SL quenching occurs when a standing wave is established with a plate transducer where the existence of 3 antinodes could be clearly seen. The addition of a small amount of propanol led to the quenching of SL that could be visually observed in the images in Fig. 8. On the other hand, the SL intensity was not influenced by the presence of the same amount of propanol when a horn system was used. It can be seen that majority of cavitation occurs at the tip of the horn and no evidence for the establishment of a standing wave could be seen in the images.

Fig. 8.

SL quenching by propanol could be seen when a plate transducer is used to establish a standing wave and a horn system normally generates transient cavitation where no SL quenching could be observed [Adapted from Ref. [71]].

Thus, it is clear that SL quenching occurs in a stable cavitation environment and stable cavitation could be established when a standing wave is formed. Further experimental evidence in support of this statement could be found in References 52 and 53. The existence of two groups of bubbles, namely sonoluminescence and chemically active bubbles has also been demonstrated [71], [72]. Using sonoluminescence and sonochemiluminescence images, it was shown that a higher acoustic power is required to generate sonoluminescence bubbles [72].

5. Interfacial/surface chemistry

Grieser and coworkers did some pioneering work and established a strong correlation between sonochemistry/sonoluminescence and interfacial chemistry [73], [74], [75], [76], [77], [78], [79]. Since the focus of this review is on SL, the rest of the discussion will focus on how cavitation bubble number and SL quenching are affected by the surface activity of solutes.

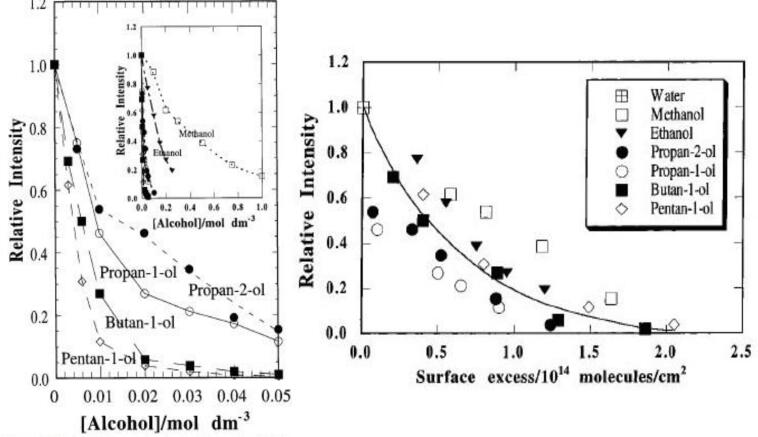
First let us focus on SL quenching. The MBSL quenching data shown in Fig. 7, Fig. 9 show that the extent of SL quenching increases with an increase in the bulk concentration of the alcohol. The differences observed between MBSL quenching data shown in Fig. 7, Fig. 9 are due to different experimental conditions used in these studies [61], [64]. This could be expected since an increase in bulk concentration would increase the interfacial concentration of the solutes. Due to the presence of a hydrocarbon chain (R = (CH₃-CH₂)_n where n = 0, 1, 2, 3, etc.), the alcohol molecules are interfacially active. They adsorb at the bubble/solution interface and diffuse into the bubble during bubble oscillations. With an increase in bulk concentration, the interfacial concentration increases leading to an increase in the number of molecules that diffuse into the bubble during each oscillation cycle. This would ultimately increase the formation of more hydrocarbon products leading to a greater SL quenching as per the mechanism discussed earlier (Fig. 4). What is interesting in the data shown in Fig. 9 is that the extent of SL quenching seems to increase with an increase in the chain length of the alcohol. In other words, for a specific bulk concentration, the extend of SL quenching increases with an increase in the chain length of the alcohol.

Fig. 9.

MBSL quenching observed at 515 kHz in aqueous solutions containing aliphatic alcohols. Left. The extend of SL quenching increases with an increase in bulk concentration and chain length of the alcohols. Right. SL quenching is a function of surface excess, not bulk concentration, of the alcohols [Adapted from Ref. [61]].

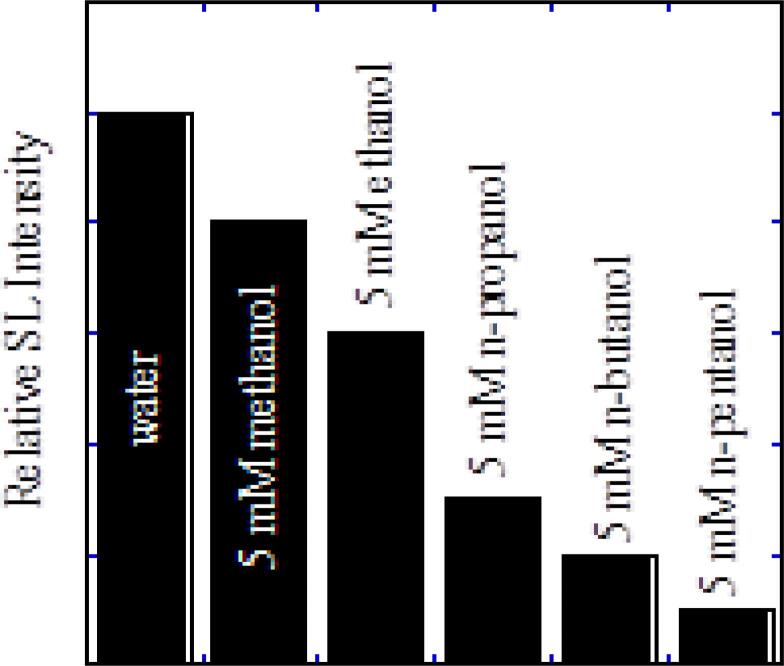
For clarity and to reemphasize the fact that interfacial chemistry plays an important role in the acoustic cavitation process, the SL quenching data is presented in a different form in Fig. 10, where SL quenching by a specific bulk concentration (5 mM) of all alcohols is compared.

Fig. 10.

MBSL quenching at 515 kHz as a function of the chain length of aliphatic alcohols [61].

When the bulk concentration of the alcohols is kept constant, the SL quenching seems to significantly increase with an increase in the chain length of the alcohol. This is due to an increase in hydrophobicity of the alcohols with an increase in chain length. The longer the hydrocarbon chain, greater is the hydrophobicity [80].

The interfacial activity of a solute could be quantified using surface tension measurements. Gibbs equation can then be used to convert surface tension data to surface excess data [80]. Surface excess represents the two-dimensional concentration of surface-active solutes at air/water interface. When the MBSL quenching data shown in Fig. 9 as a function of bulk concentrations of the alcohols were replotted using surface excess data, the differences observed between different alcohols seem to have disappeared. It can be seen in Fig. 9 that the SL quenching is well correlated with the surface excess of the alcohols rather than their bulk concentrations. Ashokkumar and coworkers also showed a similar dependence of SL quenching on surface excess for a single bubble system.

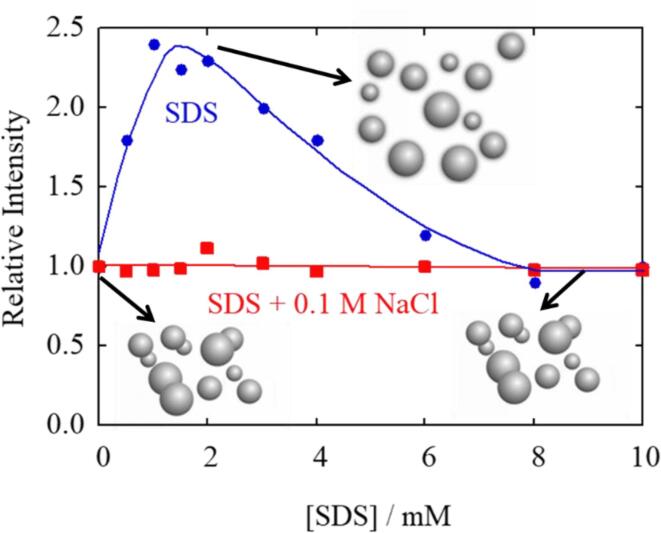
The basic interfacial chemistry knowledge also helped to develop our understanding of the formation of cavitation bubble clusters that leads to ‘acoustic shielding’ and reduced cavitation activity. In a standing wave environment, cavitation bubbles tend to cluster at antinodes. The ‘inner bubbles’ in a cluster are shielded by outer bubbles resulting in a reduced number of ‘active’ cavitation bubbles. The presence of ionic surfactants such as sodium dodecyl sulphate (SDS) was found to increase the number of cavitation bubbles by ‘de-clustering’ them. It was shown that the addition of 1 mM SDS (or any ionic non-volatile surfactant) in water resulted in an increase in MBSL intensity by a factor of 2, as shown in Fig. 11.

Fig. 11.

The addition of a charged surfactant results in an increased cavitation activity [61]. Frequency: 515 kHz.

The adsorption of charged surfactant molecules at the bubble/solution interface results in electrostatic repulsion between bubbles. The role of electrostatic repulsion was demonstrated by the addition of a background electrolyte (0.1 M NaCl for example). In the presence of the salt, the electrostatic repulsion between cavitation bubbles is nullified resulting in the formation of bubble clusters. The discussion that bubble clustering plays a major role in MBSL is further supported by Hatanaka et al. [81].

6. Summary

In this minireview, the role of thermal conductivity and heat capacity ratio of gaseous molecules present within a cavitation bubble in controlling cavitation bubble temperature is discussed. A slight reduction in heat capacity ratio has been shown to lower the cavitation bubble temperature significantly. The importance of the thermal conductivity of gases in controlling cavitation bubble temperature has been discussed using sonoluminescence intensity and other experimental work. Based on various experimental procedures, it has been shown that the cavitation bubble temperatures are of the order of a few thousand degrees. Using MBSL quenching data in the presence of volatile solutes, a detailed mechanism for SL quenching is discussed. Experimental evidence for the existence of transient and stable (repetitive transition) cavitation is provided from relevant literature. Finally, the formation of cavitation bubble clouds and the role of charged surfactants to avoid such bubble clustering during sonication have been discussed.

While the minireview focussed on limited literature, the historical perspectives provided highlight the fact that there has been a significant expansion of fundamental knowledge on the cavitation process over the past 25 years or so. Such a fundamental understanding may be critical for developing practical uses of acoustic cavitation, which have not been fully explored. The primary purpose of this minireview is to provide a quick overview of the historical development of the understanding of the correlation between acoustic cavitation, sonoluminescence and interfacial chemistry that may be beneficial for newcomers to this field.

CRediT authorship contribution statement

Nor Saadah M. Yusof: Data curation, Formal analysis, Validation, Writing – original draft. Sambandam Anandan: Data curation, Formal analysis, Validation. Palani Sivashanmugam: Data curation, Formal analysis, Validation. Erico M.M. Flores: Data curation, Formal analysis, Validation. Muthupandian Ashokkumar: Conceptualization, Resources, Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.