Abstract
SARS-CoV-2 virus is the cause of COVID-19 pandemic and belongs to RNA viruses, showing great tendency to mutate. Several dozens of mutations have been observed on the SARS-CoV-2 virus, during the last two years. Some of the mutated strains show a greater infectivity and are capable of suppressing the earlier strains, through interference. In this work, kinetic and thermodynamic properties were calculated for strains characterized by various numbers and locations of mutations. It was shown that mutations lead to changes in chemical composition, thermodynamic properties and infectivity. Through competition, the phenomenon of interference of various SARS-CoV-2 strains was explained, which results in suppression of the wild type by mutant strains. Standard Gibbs energy of binding and binding constant for the Omicron (B.1.1.529) strain were found to be ΔBG⁰ = −45.96 kJ/mol and KB = 1.13 ∙ 10+8 M−1, respectively.
Keywords: Hu-1 strain, Alpha strain, Beta strain, Gamma strain, Delta strain, Omicron strain
1. Introduction
In 2019, a new disease was reported, named COVID-19 (Zhou et al., 2020). Very soon, the virus was isolated and named SARS-CoV-2. The genetic sequence of SARS-CoV-2 was determined (Wu et al., 2020). The wild type virus strain has been named Hu-1. The morphology of coronaviruses is known (Riedel et al., 2019; Neuman and Buchmeier, 2016; Neuman et al., 2011, 2006). It belongs to RNA viruses, showing a great tendency to mutate (Duffy, 2018). Hu-1 strain has been characterized chemically and thermodynamically (Popovic and Minceva, 2020b; Şimşek et al., 2021). Interactions between the Hu-1 strain with other respiratory viruses is described in (Popovic and Minceva, 2021a). However, interactions between various SARS-CoV-2 strains was not described at the molecular level.
Very soon after the beginning of the pandemic, other strains appeared in various regions, labelled B.1.1.7 (Alpha), B.1.351 (Beta), B.1.36, P.1 (Gamma) and B.1.617 (Delta). With appearance of new strains, competitive interactions occur between the viruses and host (Popovic and Minceva, 2021a). Whenever two viral strains appear in the same time and space, they compete for soil. What soil is for plants, host organisms are for viruses. Various virus strains are characterized by different chemical and thermodynamic properties (Şimşek et al., 2021; Gale, 2021; Popovic and Minceva, 2020a, 2020b). Every virus strain has its own characteristic empirical formula. A specific empirical formula determines thermodynamic properties of virus strains. During mutations, changes occur in the genetic sequence of the virus, leading to changes in the order and type of amino acids determined by the genetic information. Thus, change in genetic information leads to change in chemical composition. Change in chemical composition leads to change in enthalpy, entropy and Gibbs energy of the virus. As a rule, lower Gibbs energy leads to greater spontaneity of a chemical reaction or process (Atkins and de Paula, 2014, 2011; Demirel, 2014).
Gibbs energy and elemental composition of viruses are influenced by mutations, meaning that they differ for various strains. Barton et al., (2021) analyzed the change in Gibbs energy of binding of various mutated strains of SARS-CoV-2, compared to the wild type. It was found that mutations lead to various differences in Gibbs energy of binding, some of which are positive, while others are negative (Barton et al., 2021). Negative changes in Gibbs energy of binding lead to greater spontaneity of binding. The changes in Gibbs energy of binding are accompanied by changes in dissociation, K D, and binding, K B, equilibrium constants, due to mutations (Barton et al., 2021). However, while the changes in thermodynamic parameters K D and K B have been studied in great detail, the kinetic aspect of this process has not been considered. Thus, one of the goals of this paper is to analyze the influence of kinetics on infectivity of SARS-CoV-2 strains, through binding phenomenological coefficients, L B. Moreover, a model is made that includes both thermodynamic and kinetic perspectives, using nonequilibrium thermodynamics and phenomenological equations.
Mutations lead to change in genetic sequence, which in turn lead to changes in viral proteins. Since viral proteins are present in many copies in virus particles, mutations can lead to change in empirical formulas of viruses. The change in empirical formulas lead to changes in thermodynamic properties of virus live matter and growth (Popovic and Minceva, 2020a, 2020b, 2021). In particular, Gibbs energy represents the driving force for most chemical reactions (Demirel, 2014). Gibbs energy of growth is the driving force of growth of organisms (Von Stockar, 2013a, 2013b; Demirel, 2014; Hellingwerf et al., 1982; Westerhoff et al., 1982). Gibbs energy of binding represents the driving force for virus attachment and entry into host cell (Popovic and Minceva, 2021; Popovic and Popovic, 2022; Gale, 2021, 2020, 2019).
Viruses represent open thermodynamic systems, which exhibit growth through multiplication (Popovic and Minceva, 2020a). Thus, it is necessary to use nonequilbrium thermodynamics to analyze processes performed by viruses (Popovic and Minceva, 2021c; Popovic, 2018). Phenomenological equations are an important part of nonequilibrium thermodynamics and are often used to analyze nonequilibrium processes (Demirel, 2014). They relate the rate of a process to its thermodynamic driving force (Demirel, 2014). Phenomenological equations have proved themselves as a useful tool in thermodynamics and engineering (Müller, 2007). Thus, in this paper, phenomenological equations will be used to analyze interactions between SARS-CoV-2 strains and their host.
Determining elemental composition of viruses is required to find their biothermodynamic properties (Popovic, 2022). Biothermodynamics combined with nonequilibrium thermodynamics have been used in analysis of phenomena related to SARS-CoV-2 infection. Lucia et al., (2020a) analyzed the influence of change in pH on homeostasis of host cells during SARS-CoV-2 infections, using the quantitative biothermodynamic approach. Lucia et al., (2020b) developed a model based on thermodynamics, for predicting spreading of epidemics and pandemics through host populations. This kind of model is very important for taking measures against epidemics, as well as organization of health service and fundamental research. A nonequilibrium thermodynamic approach has been used to analyze post-COVID-19 neurological syndrome, explaining mechanistically changes in electrolyte concentrations induced by pH changes during infection by SARS-CoV-2 (Lucia et al., 2021). This is a good example of the intersection of biothermodynamics and clinical studies of post-COVID-19 neurological syndrome, which has been appearing more and more often. Moreover, nonequilibrium thermodynamics and phenomenological coefficients have been used to explain life processes (Lucia and Grisolia, 2020). SARS-CoV-2 has shown a great tendency to mutate. Mutations lead to change in information content in the viral nucleic acid. Change in information and entropy in biological systems has been analyzed in (Popovic, 2014; Hansen et al., 2018).
The aim of this paper is to calculate binding constants, as well as standard enthalpies, entropies and Gibbs energies of binding of various SARS-CoV-2 strains. For the first time, the values were determined of binding phenomenological coefficients, L B, and binding rates, r B, of the spike protein to the ACE2 receptor. The variation in these properties between various SARS-CoV-2 strains are due to mutations, which lead to changes in amino acid sequences and chemical composition of virus particles. The rate of entry of various strains of SARS-CoV-2 is different and depends on temperature, Gibbs energy of SGP-ACE2 binding, and binding phenomenological coefficient, L B.
2. Methodology
This section begins with a discussion of the method used to find binding phenomenological coefficients, using nonequilibrium thermodynamics (Section 2.1.). Then methods are presented for finding the binding constant and Gibbs energy of binding, using classical thermodynamics (Section 2.2.). Then enthalpy and entropy determination are discussed, using the Van ‘t Hoff equation (Section 2.3.). Finally, the sources of input parameters are presented (Section 2.4.).
2.1. Binding phenomenological coefficients
Antigen-receptor binding can be described by the chemical reaction
| (1) |
where A is the free virus antigen, R the host cell receptor and AR the antigen-receptor complex. As any other chemical reaction, antigen-receptor binding consists of a forward and a backward part. In the forward part the antigen and receptor bind to form the antigen receptor complex, in a second order reaction. The concentrations of the free antigen [A] and free receptor [R] determined the rate of the forward reaction, r on, which is described by the law of mass action
| (2) |
where k on is the forward rate constant, also known as the on-rate constant. On the other hand, in the backward reaction, the antigen-receptor complex dissociates into the free antigen and receptor. The rate of the backward reaction, r off, depends only on the concentration of the antigen-receptor complex, [AR], and follows first order kinetics
| (3) |
where k off is the first order rate constant for dissociation of the antigen-receptor complex, also known as the off-rate constant. Therefore, the overall binding rate, r B, is the difference of the forward and backward rates.
| (4) |
The reaction rate becomes zero at equilibrium, implying that the equilibrium forward, r on eq , and backward, r off eq, rates are equal.
| (5) |
This represents the kinetic perspective on antigen-receptor binding.
A similar complementary perspective is given by nonequilibrium thermodynamics. Binding of the spike protein to the host cell receptor represents a chemical reaction. The Gibbs energy of binding, ΔB G, can be related to the forward and backward reaction rates (Demirel, 2014)
| (6) |
(at equilibrium r on eq = r off eq and this equation reduces to ΔB G = 0, which means that at equilibrium Gibbs energy cannot decrease further and is hence at a minimum). This equation can be rearranged into (Demirel, 2014)
| (7a) |
| (7b) |
This equation can be combined with equation (4) to find (Demirel, 2014)
| (8) |
which can be rearranged into
| (9) |
Equation (9) is a general equation of nonequilibrium thermodynamics, relating the rate of a process to its thermodynamic driving force – Gibbs energy change (Demirel, 2014). This equation is applicable to any chemical process (Demirel, 2014). In this case, it relates overall binding rate, r B, to Gibbs energy of binding, ΔB G. Equation (9) contains both thermodynamic parameters (ΔB G and T) and kinetic parameters (r B and r on). Thus, equation (9) bridges thermodynamic and kinetics aspects of a process, using nonequilibrium thermodynamics.
The bridge equation (9) is applicable to all chemical processes under all conditions (Demirel, 2014). However, it was found to take a much simpler form under conditions close to equilibrium. First, close to equilibrium the forward reaction rate, r on, becomes the forward equilibrium reaction rate, r on eq. Second, close to equilibrium, the thermodynamic driving force, ΔB G, is low (Demirel, 2014). This means that the ratio ΔB G/RT is very small. For very small numbers the exponent can be turned into a linear function, using the formula ex = 1 + x for small x. This means that in equation (9), eΔBG/RT = 1 + ΔB G/RT. Thus, equation (9) simplifies into
| (10a) |
| (10b) |
| (10c) |
The fraction on the right hand side can be simplified, by introducing the binding phenomenological coefficient, L B. The binding phenomenological coefficient is defined as the equilibrium forward reaction rate, r on eq, divided by the universal gas constant R g (Demirel, 2014).
| (11) |
Thus, equation (10c) simplifies into the binding phenomenological equation
| (12) |
where L B is the binding phenomenological coefficient and T is temperature (Demirel, 2014; Popovic and Popovic, 2022; Popovic and Minceva, 2021). Thus, the rate of the antigen-receptor binding reaction, r B, is a linear function of Gibbs energy of binding, ΔB G, given by the binding phenomenological equation. The binding phenomenological equation (11) belongs to the family of linear phenomenological equations (Demirel, 2014; Glassman et al., 2014; Kuo, 2005; Annamalai and Puri, 2007). The binding phenomenological equation will be considered in more detail in the Discussion section.
The value of the binding phenomenological coefficient can be found by combining equations (11), (2), resulting in
| (13) |
The dissociation equilibrium constant, K D, is given by the equation
| (14) |
Combining equations (13), (14) results in
| (15) |
Values for k on and K D values were reported by Laffeber et al., (2021) and are given in Table 1 . Since the reported K D values are very small, the equilibrium is shifted towards antigen-receptor binding (Skoog et al., 2013). Thus, most virus particles in the body will be bound to host cells, implying that the equilibrium antigen-receptor complex concentration is approximately equal to the total virion concentration in the organism [AR]eq ≈ [V]tot. Thus, equation (15) becomes
| (16) |
Table 1.
Binding phenomenological coefficients and Gibbs energies of binding of various SARS-CoV-2 strains. The reference column gives references from which the values of on-rate constant, kon, off-rate constant, koff, dissociation constant, KD, and temperature T were taken. In all the references, KD was calculated from kon and koff, using the equation KD = koff /kon. The data reported by Laffeber et al., (2021) and Augusto et al., (2021) were collected at 25 °C, while the data from Barton et al., (2021) were collected at 37 °C. These data were used to calculate the binding phenomenological coefficients, LB, binding constant, KB, and standard Gibbs energy of binding, ΔBG⁰, using equations (16), (17), (18), respectively. The LB values have been multiplied by 1018, to make comparison easier. Zhang et al., (2021) reported the dissociation equilibrium constant of the Omicron strain to be 8.85 nM. Based on this value, equation (17) was used to determine the binding constant, KB, which was found to be 1.13 ∙ 10+8 M−1. The binding constant was used to find standard Gibbs energy of binding, ΔBG⁰, which was found to be −45.96 kJ/mol for the Omicron strain. Moreover, ΔBG⁰ values of all the strains are more negative at 25 °C than at 37 °C. This is in good agreement with the negative standard entropies of binding in Table 2, Table 3, which give the temperature dependence of ΔBG⁰, according to the equation (∂G/∂T)p = - S (Atkins and de Paula, 2011, 2014).
| Mutations | kon (M−1s−1) | koff (s−1) | KD (M) | T (°C) | Reference | LB ∙ 1018 (mol2 K /J s dm³) | KB (M−1) | ΔBG⁰ (kJ/mol) |
|---|---|---|---|---|---|---|---|---|
| Wild type (Hu-1) | 4.50E+05 | 7.80E-03 | 1.70E-08 | 25 | Laffeber et al., 2021 | 16.05 | 5.88E+07 | −44.35 |
| N501Y | 5.70E+05 | 1.30E-03 | 2.40E-09 | 25 | Laffeber et al., 2021 | 2.87 | 4.17E+08 | −49.20 |
| E484K | 8.90E+05 | 1.10E-02 | 1.30E-08 | 25 | Laffeber et al., 2021 | 24.27 | 7.69E+07 | −45.01 |
| K417 N | 3.50E+05 | 2.40E-02 | 7.50E-08 | 25 | Laffeber et al., 2021 | 55.07 | 1.33E+07 | −40.67 |
| E484K/N501Y | 1.10E+06 | 1.50E-03 | 1.40E-09 | 25 | Laffeber et al., 2021 | 3.23 | 7.14E+08 | −50.54 |
| K417 N/E484K/N501Y | 7.60E+05 | 4.30E-03 | 5.80E-09 | 25 | Laffeber et al., 2021 | 9.25 | 1.72E+08 | −47.01 |
| Wild type (Hu-1) | 1.50E+05 | 3.20E-03 | 2.13E-08 | 25 | Augusto et al. (2021) | 6.70 | 4.69E+07 | −43.79 |
| E484K | 1.60E+05 | 3.10E-03 | 1.97E-08 | 25 | Augusto et al. (2021) | 6.61 | 5.08E+07 | −43.98 |
| L452R/E484Q | 7.20E+05 | 3.30E-03 | 4.60E-09 | 25 | Augusto et al. (2021) | 6.95 | 2.17E+08 | −47.59 |
| N440K | 3.10E+05 | 3.10E-03 | 9.90E-09 | 25 | Augusto et al. (2021) | 6.44 | 1.01E+08 | −45.69 |
| Wild type (Hu-1) | 9.00E+05 | 6.68E-02 | 6.26E-08 | 37 | Barton et al. (2021) | 118.20 | 1.60E+07 | −42.77 |
| K417 N | 4.90E+05 | 1.77E-01 | 3.49E-07 | 37 | Barton et al. (2021) | 358.76 | 2.87E+06 | −38.34 |
| K417T | 5.50E+05 | 1.26E-01 | 2.26E-07 | 37 | Barton et al. (2021) | 260.77 | 4.42E+06 | −39.46 |
| S477 N | 8.10E+05 | 3.48E-02 | 4.26E-08 | 37 | Barton et al. (2021) | 72.39 | 2.35E+07 | −43.76 |
| E484K | 1.54E+06 | 8.18E-02 | 5.26E-08 | 37 | Barton et al. (2021) | 169.94 | 1.90E+07 | −43.22 |
| N501Y (Alpha) | 1.59E+06 | 1.11E-02 | 5.50E-09 | 37 | Barton et al. (2021) | 18.35 | 1.82E+08 | −49.04 |
| K417 N/E484K | 1.02E+06 | 2.51E-01 | 2.51E-07 | 37 | Barton et al. (2021) | 537.10 | 3.98E+06 | −39.19 |
| K417T/E484K | 1.10E+06 | 1.68E-01 | 1.47E-07 | 37 | Barton et al. (2021) | 339.23 | 6.80E+06 | −40.57 |
| E484K/N501Y (UK2) | 2.33E+06 | 1.18E-02 | 3.70E-09 | 37 | Barton et al. (2021) | 18.09 | 2.70E+08 | −50.06 |
| K417 N/E484K/N501Y (Beta) | 1.46E+06 | 2.91E-02 | 1.74E-08 | 37 | Barton et al. (2021) | 53.29 | 5.75E+07 | −46.07 |
| K417T/E484K/N501Y (Gamma) | 1.56E+06 | 2.11E-02 | 1.22E-08 | 37 | Barton et al. (2021) | 39.93 | 8.20E+07 | −46.99 |
The value of [V]tot was reported by Sender et al., (2021a; 2021b), to be 1 ∙ 107 RNA copies per gram of tissue. It seems reasonable to assume that one RNA copy corresponds to one virion. In that case, the concentration of virions is 1 ∙ 107 per gram of tissue. The density of tissues is 1050 g/dm³ (IT'IS Foundation, 2021). Thus, the concentration of virions is 1.74∙ 10−14 M.
2.2. Binding constants and Gibbs energies of binding
Dissociation constants were used to calculate binding constants, K B, using the equation (Du et al., 2016)
| (17) |
The binding constants were used to find Gibbs energy of binding, ΔB G⁰, using the equation (Du et al., 2016)
| (18) |
2.3. Enthalpies and entropies of binding
Binding constants were used to determine enthalpies of binding, using the Van ‘t Hoff equation. Van ‘t Hoff equation states that the temperature dependence of the binding constant is proportional to the standard enthalpy of binding, ΔB H⁰
| (19) |
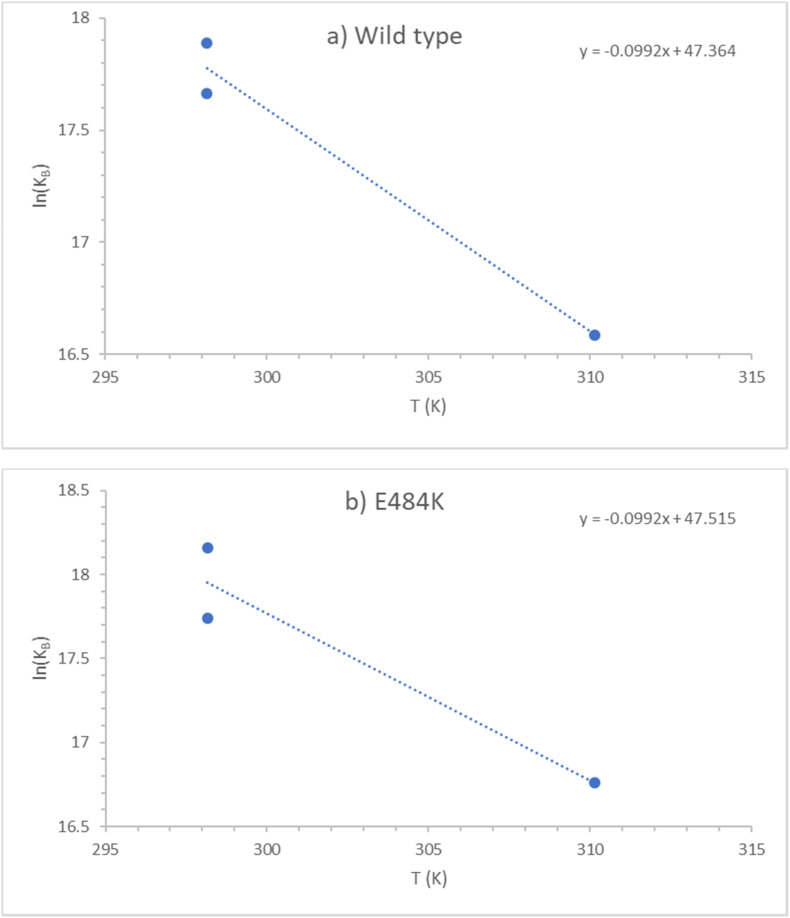
where R g is the universal gas constant and T is temperature (Atkins and de Paula, 2011). Binding constants, K B, from Table 1 were used to calculate enthalpies of binding, ΔB H, using the Van ‘t Hoff equation. First, for every strain, natural logarithms were taken of K B, at 25 and 37 °C. Then, ln(K B) were plotted as a function of temperature for every strain, resulting in Van ‘t Hoff plots. Van ‘t Hoff plots for the Wild type and E484K strain are shown in Fig. 3. Through the plotted data, linear functions were fitted for every strain. The slopes of the fitted functions correspond to d[ln(K B)]/dT term in the Van ‘t Hoff equation (19). Thus, using equation (19), the slopes of the fitted functions were used to find ΔB H at 25 °C and 37 °C.
Fig. 3.
Van't Hoff plots for antigen-receptor binding of SARS-CoV-2 strains: (a) Wild type and (b) E484K. The blue dots ( ) represent experimental data, while the blue dotted lines (
) represent experimental data, while the blue dotted lines ( ) represent the linear fits. The equations for each fit are given in the top right corner. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
) represent the linear fits. The equations for each fit are given in the top right corner. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
The calculated enthalpies of binding were combined with Gibbs energies of binding, to find entropies of binding, ΔB S. Enthalpies of binding, ΔB H, have been calculated using the Van ‘t Hoff equation (19), at 25 °C and 37 °C. Gibbs energies of binding, ΔB G, have been calculated at 25 °C and 37 °C, using equations (17), (18), based on literature K D data. The ΔB H and ΔB G data were combined to find ΔB S at 25 °C and 37 °C, using the equation (Atkins and de Paula, 2011)
| (20) |
The values of ΔB H, ΔB S and ΔB G were calculated at 25 °C and 37 °C (Atkins and de Paula, 2011).
2.4. Input parameters
Dissociation constants, on-rate constants and off-rate constants were taken from Augusto et al., (2021), Barton et al., (2021) and Laffeber et al., (2021). The data reported by Augusto et al., (2021), and Laffeber et al., (2021) are at 25 °C, while the data by Barton et al., (2021) are at 37 °C. The data by Auguesto et al., (2021) were collected using Biolayer Interferometry. Barton et al., (2021) and Laffeber et al., (2021) used surface plasmon resonance. Zhang et al., (2021) reported the dissociation constant for the Omicron (B.1.1.529) strain, which was measured using surface plasmon resonance.
3. Results
Using the described methodology, binding phenomenological coefficients, L B, binding constants, K B, and standard Gibbs energies of binding, ΔB G⁰, were calculated, for various SARS-CoV-2 strains. They are given in Table 1. Binding phenomenological coefficients, L B, were calculated using equation (16), K B using equation (17) and ΔB G⁰ using equation (18). The analyzed strains include Hu-1 (Wild type), B.1.1.7 (Alpha), B.1.351 (Beta), P.1 (Gamma), B.1.617 (Delta) and B.1.36. Moreover, standard enthalpies, ΔB H⁰, and entropies, ΔB S⁰, of binding were calculated and are given in Table 2, Table 3 . The data have been calculated at 25 °C and 37 °C.
Table 2.
Standard Gibbs energies, ΔBG⁰(37 °C), enthalpies, ΔBH⁰(37 °C), and entropies, ΔBS⁰(37 °C), of binding at 37 °C of spike protein to the ACE2 receptor, for various SARS-CoV-2 strains. ΔBH⁰(37 °C) values were calculated using the van't Hoff equation (19), from the experimental KB data (Table 1). ΔBG⁰(37 °C) values were calculated from KB values in Table 1, using equation (18). Calculated ΔBH⁰(37 °C) and ΔBG⁰(37 °C) values were combined to find ΔBS⁰(37 °C) values, using equation (20). All the data are at 37 °C.
| Mutations | ΔBG⁰(37 °C) (kJ/mol) | ΔBH⁰(37 °C) (kJ/mol) | ΔBS⁰(37 °C) (J/mol K) |
|---|---|---|---|
| Wild type (Hu-1) | −42.77 | −79.34 | −117.90 |
| E484K | −43.22 | −79.34 | −116.45 |
| N501Y | −49.04 | −55.27 | −20.08 |
| E484K/N501Y | −50.06 | −64.77 | −47.42 |
| K417 N/E484K/N501Y | −46.07 | −73.22 | −87.53 |
| K417 N | −38.34 | −102.47 | −206.79 |
Table 3.
Standard Gibbs energies, ΔBG⁰(25 °C), enthalpies, ΔBH⁰(25 °C), and entropies, ΔBS⁰(25 °C), of binding at 25 °C of spike protein to the ACE2 receptor, for various SARS-CoV-2 strains. Enthalpies of binding were calculated using the Van ‘t Hoff equation (19) from the experimental KB data (Table 1). ΔBG⁰(25 °C) values were calculated from KB values in Table 1, using equation (18). ΔBH⁰(25 °C) and ΔBG⁰(25 °C) values were combined to find ΔBS⁰(25 °C) values, using equation (20). The “Reference” column contains sources from which the KB data were taken to find ΔBG⁰(25 °C) values. All the data are at 25 °C.
| Mutation | Reference | ΔBG⁰(25 °C) (kJ/mol) | ΔBH⁰(25 °C) (kJ/mol) | ΔBS⁰(25 °C) (J/mol K) |
|---|---|---|---|---|
| Wild type (Hu-1) | Laffeber et al., 2021 | −44.35 | −73.31 | −97.16 |
| Wild type (Hu-1) | Augusto et al. (2021) | −43.79 | −73.31 | −99.04 |
| E484K | Laffeber et al., 2021 | −45.01 | −73.31 | −94.93 |
| E484K | Augusto et al. (2021) | −43.98 | −73.31 | −98.39 |
| N501Y | Laffeber et al., 2021 | −49.20 | −51.07 | −6.29 |
| E484K/N501Y | Laffeber et al., 2021 | −50.54 | −59.86 | −31.26 |
| K417 N/E484K/N501Y | Laffeber et al., 2021 | −47.01 | −67.66 | −69.26 |
| K417 N | Laffeber et al., 2021 | −40.67 | −94.70 | −181.22 |
The data in Table 1 shows that every mutation leads to change in the binding phenomenological coefficient, binding constant, as well as Gibbs energy, enthalpy and entropy of binding. Some mutations lead to increase in L B, while other mutations lead to decrease in L B. The L B values greatly depend on temperature, because they include the kinetic factors, which strongly depend on temperature (Demirel, 2014). The L B values at 37 °C are an order of magnitude greater than those at 25 °C.
Binding constants of all strains were found to decrease with temperature. For all strains, binding constants at 37 °C are lower than at 25 °C (Table 1). This is in accordance with the negative enthalpies of binding, reported in Table 2. Negative enthalpy of binding, through the Van ‘t Hoff equation (19), implies that the binding constant will decrease as temperature increases.
Gibbs energies of binding were found to become less negative at higher temperatures, implying less thermodynamically favorable antigen-receptor binding. Gibbs energies of binding in Table 1 were found to slightly decrease with temperature. This is in good agreement with enthalpies and entropies of binding, given in Table 2, Table 3 Table 2, Table 3 give standard enthalpies and entropies of binding of SARS-CoV-2 strains, at 25 °C and 37 °C, respectively. Standard enthalpies of binding, ΔB H, were calculated using the Van ‘t Hoff equation (19). The calculated ΔB H were then combined with ΔB G values to find ΔB S, using equation (20). Entropies of binding are negative, due to the decrease in the number of independent particles during receptor-antigen binding. The negative entropy of binding implies that Gibbs energy of binding will be less negative at higher temperatures. Moreover, this is in good agreement with the decrease in binding constants with temperature, since Gibbs energy of binding and binding constants are related through equation (18). Thus, antigen-receptor binding becomes less thermodynamically favorable as the temperature increases.
Antigen-receptor binding is a simple process, similar to protein-ligand binding (Du et al., 2016; Popovic and Popovic, 2022). It occurs in only one step, which can be described using reaction (1) (Du et al., 2016; Popovic and Popovic, 2022). Thus, analogously to protein-ligand binding, antigen-receptor binding is characterized by a set of thermodynamic properties of binding, including standard enthalpy of binding, ΔB H⁰, standard entropy of binding, ΔB S⁰, and standard Gibbs energy of binding, ΔB G⁰ (Gale, 2021, 2020, 2019). A particular set of thermodynamic properties of binding is characteristic of every virus species or strain (Popovic and Popovic, 2022). Since the binding process is a simple process, it is not coupled to other processes such as ATP hydrolysis (Gale, 2021, 2020, 2019). Thus, for the binding process to occur spontaneously, Gibbs energy of binding must be negative. This is confirmed by the data in Table 1. Gibbs energy of binding is negative for all considered strains.
Gibbs energy of binding has an enthalpic and entropic component, as can be seen from equation (20) (Gale, 2020). The enthalpic component originates from interactions between the active sites of the antigen and receptor proteins. Since these interactions are energetically favorable, enthalpy of binding is negative (Atkins and de Paula, 2011). On the other hand, during binding, the number of free particles decreases, implying a decrease in entropy (Atkins and de Paula, 2011). Namely, in reaction (1), two reactant molecules (A standing for SGP and R standing for ACE2) combine into one product molecule (SGP-ACE2 complex). Thus, the total number of molecules decreases during the reaction. A reaction decreasing the number of free particles has a negative entropy change (Atkins and de Paula, 2011).
The negative entropy changes are also in agreement with the temperature dependence of Gibbs energy. Most biological processes occur at constant pressure. Under constant pressure, p, entropy determines the temperature dependence of Gibbs energy, according to the well-known equation (∂G/∂T)p = - S (Atkins and de Paula, 2011, 2014). Thus, since all standard entropies of binding in Table 2, Table 3 are negative, standard Gibbs energy of binding should become less negative with temperature. This can indeed be observed from the data in Table 2, Table 3
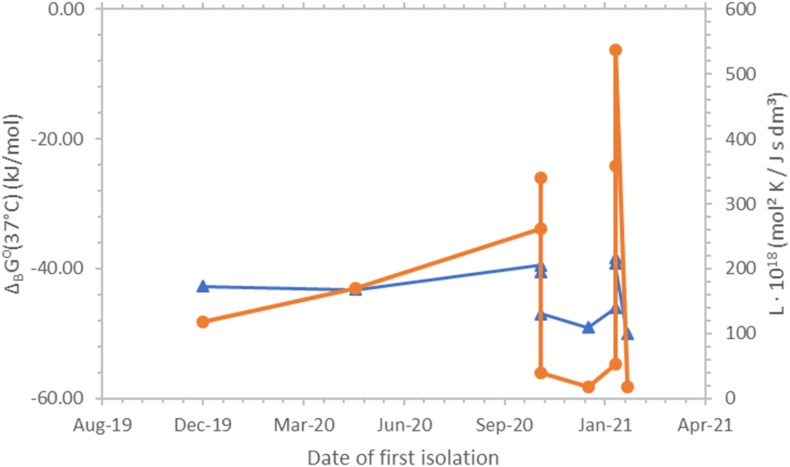
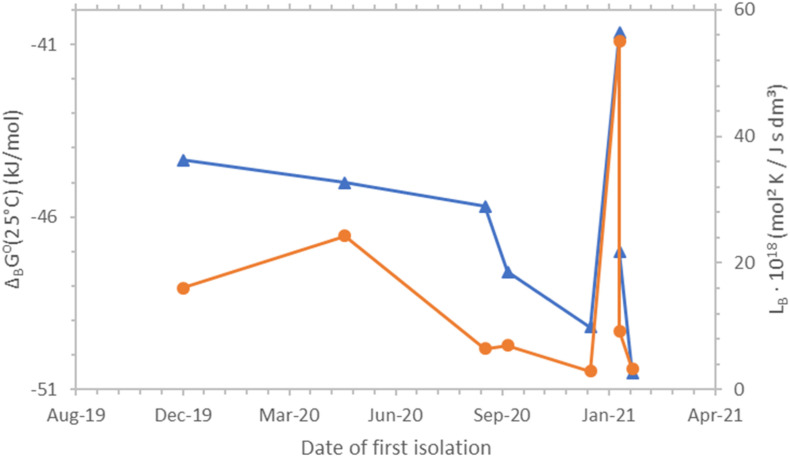
Fig. 1, Fig. 2 show Gibbs energies of binding and binding phenomenological coefficients of SARS-CoV-2 strains at 37 °C and 25 °C, respectively. The data in both figures shows the same general trend: curves representing Gibbs energies of binding and binding phenomenological coefficients behave in the same way. Both curves rise and fall at the same places. However, Gibbs energy of binding and the binding phenomenological coefficient are two independent properties.
Fig. 1.
Gibbs energies of binding and binding phenomenological coefficients, LB, of SARS-CoV-2 strains and their dates of first isolation. The blue triangles ( ) represent Gibbs energies of binding, while the orange circles (
) represent Gibbs energies of binding, while the orange circles ( ) represent LB coefficients. All binding phenomenological coefficient values were multiplied by 1018 to make the presentation simpler. Both Gibbs energies of binding and binding phenomenological coefficients are at 37 °C. ΔBG⁰(37°C) represents standard Gibbs energy of binding at 37 °C, with unit concentrations and at a pressure of 105 Pa (IUPAC, 1997). ΔBG⁰(37°C) is the standard Gibbs energy change of reaction (1). ΔBG⁰(37°C) is related to the binding equilibrium constant at 37 °C, through the equation ΔBG⁰(37°C) = - Rg ⋅ (310.15 K) ⋅ ln[KB(37 °C)]. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
) represent LB coefficients. All binding phenomenological coefficient values were multiplied by 1018 to make the presentation simpler. Both Gibbs energies of binding and binding phenomenological coefficients are at 37 °C. ΔBG⁰(37°C) represents standard Gibbs energy of binding at 37 °C, with unit concentrations and at a pressure of 105 Pa (IUPAC, 1997). ΔBG⁰(37°C) is the standard Gibbs energy change of reaction (1). ΔBG⁰(37°C) is related to the binding equilibrium constant at 37 °C, through the equation ΔBG⁰(37°C) = - Rg ⋅ (310.15 K) ⋅ ln[KB(37 °C)]. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Fig. 2.
Gibbs energies of binding and binding phenomenological coefficients, LB, of SARS-CoV-2 strains and their dates of first isolation. The blue triangles ( ) represent Gibbs energies of binding, while the orange circles (
) represent Gibbs energies of binding, while the orange circles ( ) represent binding phenomenological coefficients. All binding phenomenological coefficient values were multiplied by 1018 to make the presentation simpler. Both Gibbs energies of binding and binding phenomenological coefficients are at 25 °C. ΔBG⁰(25°C) represents standard Gibbs energy of binding at 37 °C, with unit concentrations and at a pressure of 105 Pa (IUPAC, 1997). ΔBG⁰(25°C) is the standard Gibbs energy change of reaction (1). ΔBG⁰(25°C) is related to the binding equilibrium constant at 37 °C, through the equation ΔBG⁰(25°C) = - Rg ⋅ (298.15 K) ⋅ ln[KB(25 °C)]. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
) represent binding phenomenological coefficients. All binding phenomenological coefficient values were multiplied by 1018 to make the presentation simpler. Both Gibbs energies of binding and binding phenomenological coefficients are at 25 °C. ΔBG⁰(25°C) represents standard Gibbs energy of binding at 37 °C, with unit concentrations and at a pressure of 105 Pa (IUPAC, 1997). ΔBG⁰(25°C) is the standard Gibbs energy change of reaction (1). ΔBG⁰(25°C) is related to the binding equilibrium constant at 37 °C, through the equation ΔBG⁰(25°C) = - Rg ⋅ (298.15 K) ⋅ ln[KB(25 °C)]. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Zhang et al., (2021) reported the dissociation equilibrium constant of the SARS-CoV-2 Omicron strain to be 8.85 nM. Based on this value, equation (17) was used to determine the binding constant, K B, to be 1.13 ∙ 10+8 M−1. The binding constant was used to find standard Gibbs energy of binding, ΔB G⁰, which was found to be −45.96 kJ/mol, using equation (18).
4. Discussion
Various SARS-CoV-2 strains were observed epidemiologically to fight each other for survival (Nextstrain, 2021; Hadfield et al., 2018). This fight is a consequence of competition for resources (Popovic and Minceva, 2021a, 2020b). A virus that has a competitive advantage obtained through a mutation can suppress its predecessor with less favorable mutations or the original strain. The original Hu-1 virus has spread very fast and led to a pandemic. Before mutations appeared and with them new strains, Hu-1 didn't have a competitor strain. Unfortunately, SARS-CoV-2 has showed a tendency to mutate. This led to appearance of multiple strains with a single or multiple mutations, mostly on the spike protein gene (Nextstrain, 2021; Hadfield et al., 2018). Mutations lead to changes in binding kinetics (Augusto et al., 2021; Barton et al., 2021; Laffeber et al., 2021). To fully utilize the data on dissociation constants, k on and k off, it is necessary to know other kinetic and thermodynamic properties, including binding phenomenological coefficients, enthalpies of binding, entropies of binding and Gibbs energies of binding. Antigen-receptor binding represents a chemical reaction. Gibbs energy of binding is of particular importance, since Gibbs energy is the driving force of all chemical reactions (Demirel, 2014; Atkins and de Paula, 2014, 2011). Change in enthalpy is important because is shows the temperature dependence of the process (Atkins and de Paula, 2014, 2011). However, binding phenomenological coefficients also play a significant role in antigen-receptor binding (Popovic and Minceva, 2021a).
In this paper, for the first time, calculated binding phenomenological coefficients were presented. This opens an opportunity to calculate the rate of binding of the wild type virus and other mutant strains. Greater rate of binding and entry into host cells gives an advantage to one of the competing strains, allowing it to multiply faster. This results in domination or complete suppression (interference) of one of the competing strains (Popovic and Popovic, 2022; Popovic and Minceva, 2021a). Thus, knowledge of binding rates can explain the appearance of interference between the strains of a single virus or interference between different virus species (Popovic and Popovic, 2022; Popovic and Minceva, 2021a).
Infectivity and infection outcome of SARS-CoV-2 depend on susceptibility and permissiveness (Hou et al., 2017; Kwiatkowski, 2000). Susceptibility depends on rate of binding of the viral antigen to the receptor (Kwiatkowski, 2000; Hickson and Roberts, 2014). The rate of binding to the receptor is essentially a chemical reaction rate. The rate of the chemical reaction depends, according to the phenomenological equation (12), on several factors: temperature, Gibbs energy of binding and binding phenomenological coefficient (Demirel, 2014).
The first factor is temperature (Demirel, 2014; Atkins and de Paula, 2014, 2011). In this paper, properties were determined at two temperatures: standard 25 °C and physiological 37 °C. They are presented in Table 1, Table 2, Table 3 and Fig. 1, Fig. 2. Physiological temperature is important for application in life sciences and medicine, while standard temperature is important in natural sciences. The temperature dependence of binding rate is taken into account by the binding phenomenological coefficient, L B (Demirel, 2014). The L B coefficient depends on k on, according to equation (16), while k on itself depends on temperature, according to the Arrhenius equation (Atkins and de Paula, 2014, 2011).
The second factor is the Gibbs energy of binding (Demirel, 2014). Gibbs energy of binding of various strains of SARS-CoV-2 (every strain characterized with its mutations) are also given in Table 1, Table 2, Table 3 and Fig. 1, Fig. 2. Mutations lead to changes in empirical formulas of viruses. Changes in virus empirical formulas lead to changes in Gibbs energy. As a rule, strains with greater infectivity are characterized by more negative Gibbs energy of binding (Khan et al., 2021a, 2021b). The results of this research are in agreement with those of Han et al., (2021), who found that the difference in Gibbs energies of binding between Hu-1 and 501Y (ΔΔB G) is between 10.61 kJ/mol and 19.97 kJ/mol.
The third factor required to calculate the rate of antigen-receptor binding is the binding phenomenological coefficient, L B (Demirel, 2014). The calculated L B values are given in Table 1, and Fig. 1, Fig. 2. To the extent of authors’ knowledge, phenomenological coefficients have been published in the literature only for plants (Popovic and Minceva, 2021b). Knowing these three parameters, it is relatively simple to calculate the binding rate for various strains of viruses. However, to accurately find virus binding rates, it is necessary to have data on virus and ACE2 concentrations. In this work, the results obtained for the binding phenomenological coefficients show that, except for Gibbs energy which was expectable, binding phenomenological coefficients also change with mutations. Thus, it is not enough to just know the Gibbs energy of binding or the binding constant, to estimate the rate of entry of viruses into host cells and infectivity.
The discussion in this paper uses standard Gibbs energy of binding, ΔB G⁰, to approximate Gibbs energy of binding, ΔB G. This approximation stems from two assumptions, on which the discussion is based.
-
1.
Concentration of ACE2 receptors is approximately equal in all host organisms.
-
2.
A minimum inoculation dose exists, required to start an infection. A small number of viruses is not able to make an infection. The minimum dose is expressed through the concentration of the viruses in the inoculum. Since this analysis is theoretical, we will assume that the inoculum size is the same for all strains. This means that all strains in the inoculum have the same concentration. This assumption is supported by (Sender et al., 2021a, 2021b).
These two assumptions have been introduced to remove the influence of virion and receptor concertation, and enable to use ΔB G⁰ to calculate binding rates. Reaction Gibbs energy depends on two properties: the chemical nature of reactants and products, and the conditions in the reaction mixture (Atkins and de Paula, 2014, 2011). The chemical nature of reactants and products is taken into account by standard reaction Gibbs energy (Atkins and de Paula, 2014, 2011). On the other hand, the conditions in the reaction mixture are taken into account by the reaction quotient, Q (Atkins and de Paula, 2014, 2011). Thus, the reaction Gibbs energy is given by the equation (Atkins and de Paula, 2014, 2011)
| (21) |
The reaction quotient takes into account the reactant and product concentrations, and intermolecular forces between reaction participants (Atkins and de Paula, 2014, 2011). The reaction quotient is hence defined through concentrations, C, activity coefficients, γ, and stoichiometric coefficients, ν, of reactants and products
| (22) |
where the product is over all reaction participants (Atkins and de Paula, 2014, 2011). Thus, the reaction quotient, Q, describes conditions in the reaction mixture, the influence of which on biological processes has been studied in detail by Meurer et al., (2016, 2017), Wangler et al., (2018) and Greinert et al., (2020a, 2020b). In this work, strains of SARS-CoV-2 are considered, which are very similar and use the same receptor. Thus, it is reasonable to make assumptions (1) and (2), which simplify equation (21) into ΔB G ≈ ΔB G⁰. This means that the Gibbs energies of binding of the viruses are mostly dependent on the nature of their spike proteins, quantified by the standard Gibbs energy of binding ΔB G⁰. Thus, standard Gibbs energy of binding is required to find the influence of mutations on virus entry into host cells and infectivity. Similar assumptions, about approximating ΔB G with ΔB G⁰, have been applied in the past, when discussing processes involving multiplication of viruses (Popovic and Minceva, 2020a, 2020b, 2021a; Popovic and Popovic, 2022) and other microorganisms (von Stockar and Liu, 1999; Von Stockar et al., 2013), as well as plant growth (Popovic and Minceva, 2021b).
Another point that needs to be addressed is application of the linear phenomenological equation (12) to the binding process. The linear phenomenological equation is applicable in the linear region of nonequilibrium thermodynamics, where driving forces of processes are small (Demirel, 2014). While this criterion is fulfilled for most processes of heat transfer and diffusion, they are not necessarily met in all chemical reactions (Demirel, 2014). Thus, the application of the linear phenomenological equation (12) needs to be justified. There are four reasons that make the linear phenomenological equation a good choice for studying antigen-receptor binding. First, antigen-receptor binding has already been studied using the linear phenomenological equation (Popovic and Minceva, 2021a; Popovic and Popovic, 2022). Second, linear phenomenological equations have been used to study other processes involving viruses, like their multiplication in the host cell cytoplasm (Popovic and Minceva, 2020a, 2020b; 2021a). Third, linear phenomenological equations have been successfully applied to other processes involving microorganisms (Westerhoff et al., 1982; Hellingwerf et al., 1982; Von Stockar, 2013a; Demirel, 2014) and plant growth (Popovic and Minceva, 2021b). Finally, fourth, linear phenomenological equation is a simplification of the more complex bridge equation (9) of nonequilbrium thermodynamics, which describes the dependence of chemical reaction rate on its driving force (Demirel, 2014, Section 3.9). The simplification can be used when the driving force is not very high, that is in the linear region (Demirel, 2014). However, both the general and simplified equations lead to same conclusions: chemical reaction rate is proportional to its driving force (Demirel, 2014). Thus, using the more complex bridge equation (9) would yield no fundamentally different conclusions, but would make the mathematical treatment much more complicated.
Gibbs energies of binding are negative for all analyzed strains, implying spontaneous antigen-receptor binding. In case two virus strains appear at the same time and place, the strain characterized by a more negative Gibbs energy has an advantage when entering the host cell. However, according to equation (12), the rate of entry depends not only on Gibbs energy of binding, but also on the binding phenomenological coefficient. Thus, at a given temperature, a virus with a more optimal combination of Gibbs energy of binding and binding phenomenological coefficient will dominate.
Table 4 gives binding rates of various SARS-CoV-2 strains. The calculations were made at room and physiological temperatures, using equation (12). The table shows that the rate of binding changes differently with various mutations. Some mutations lead to increase in binding rate, while others lead to decrease in binding rate. Moreover, the binding rate strongly depends on temperature. A comparison can be made between the Wild type and Beta strains. At physiological temperatures, the calculated binding rates are 162.99 M/s for the Wild type and 443.48 M/s for the Beta strain. Obviously, due to greater binding rate, the beta strain has an advantage, enabling it to suppress the original Hu-1 strain, though interference. A similar situation appears, when we consider the binding rates of the original Hu-1 strain and P.1 strain. The strain with the mutation K417T/E484K has a binding rate of 443.72 M/s, while the strain with just the K417T mutation has a binding rate of 331.77 M/s. Other strains have a lower binding rate.
Table 4.
Binding rates, rB, calculated at 25 °C and 37 °C. An assumption was made that the inoculum size is the same for all strains. The rates were calculated using equation (12), with the L and ΔBG⁰ values from Table 1.
| Mutations | Reference | T (°C) | rB ∙ 1019 (M/s) |
|---|---|---|---|
| At 25°C | |||
| Wild type (Hu-1) | Laffeber et al., 2021 | 25 | 22.95 |
| N501Y | Laffeber et al., 2021 | 25 | 4.55 |
| E484K | Laffeber et al., 2021 | 25 | 35.23 |
| K417 N | Laffeber et al., 2021 | 25 | 72.21 |
| E484K/N501Y | Laffeber et al., 2021 | 25 | 5.26 |
| K417 N/E484K/N501Y | Laffeber et al., 2021 | 25 | 14.02 |
| Wild type (Hu-1) | Augusto et al. (2021) | 25 | 9.46 |
| E484K | Augusto et al. (2021) | 25 | 9.38 |
| L452R/E484Q | Augusto et al. (2021) | 25 | 10.66 |
| N440K | Augusto et al. (2021) | 25 | 9.48 |
| At 37°C | |||
| Wild type (Hu-1) | Barton et al. (2021) | 37 | 162.99 |
| K417 N | Barton et al. (2021) | 37 | 443.48 |
| K417T | Barton et al. (2021) | 37 | 331.77 |
| S477 N | Barton et al. (2021) | 37 | 102.14 |
| E484K | Barton et al. (2021) | 37 | 236.80 |
| N501Y (Alpha) | Barton et al. (2021) | 37 | 29.01 |
| K417 N/E484K | Barton et al. (2021) | 37 | 678.65 |
| K417T/E484K | Barton et al. (2021) | 37 | 443.72 |
| E484K/N501Y (UK2) | Barton et al. (2021) | 37 | 29.19 |
| K417 N/E484K/N501Y | Barton et al. (2021) | 37 | 79.17 |
| K417T/E484K/N501Y (Gamma) | Barton et al. (2021) | 37 | 60.49 |
The results of this research are in agreement with those of Barton et al., (2021), who found that various changes in Gibbs energy of binding correspond to different strategies used by viruses. Some mutations lead to more negative Gibbs energy of binding and hence increase in binding rate. However, other mutations lead to less negative in Gibbs energy of binding, but also to decrease in binding rate. The explanation of this phenomenon was given by Barton et al., (2021). Some mutations lead to increased binding affinity and hence more efficient transmission (Barton et al., 2021). Other mutations lead to decreased binding affinity, which facilitates immune escape (Barton et al., 2021). The same principle most likely applies to binding rates. Some viruses bind faster to host cells, but also to antibodies. On the other hand, others bind less effectively to both, meaning that they transmit slower but also better avoid immune response.
Except for susceptibility, permissiveness influences the size of infective reservoir, contributing to greater infectivity. Permissiveness depends on the virus multiplication rate. Virus multiplication represents a chemical process of polymerisation, including nucleic acid and protein synthesis. The rate of polymerisation depends on Gibbs energy of growth (Popovic and Minceva, 2020a). Growth rate of microorganisms depends on their Gibbs energy of growth (Hellingwerf et al., 1982; Westerhoff et al., 1982; Von Stockar et al., 2013; Demirel, 2014). The dependence of growth rate, r g, on Gibbs energy of growth, Δg G, is given by the growth phenomenological equation
| (23) |
where L g is the growth phenomenological coefficient (Popovic and Minceva, 2020a, 2020b, 2021a; Von Stockar, 2013a, 2013b; Demirel, 2014; Hellingwerf et al., 1982; Westerhoff et al., 1982). Both the growth phenomenological equation (23) and binding phenomenological equation (12) belong to the general family of phenomenological equations (Demirel, 2014). Δg G is the Gibbs energy change of growth the growth reaction describing the growth of the virus (Popovic and Minceva, 2020a, 2020b; 2021a).
Microorganisms grow through multiplication of cells, through chemical reactions of polymerisation and biosynthesis. In a similar way, viruses also grow through multiplication and reactions of polymerisation. The building blocks and biosynthesis pathways are obtained by hijacking their host cell's metabolism (Popovic and Minceva, 2020a). Thus, mechanism of the growth rate and its dependence on Gibbs energy is universal for all microorganisms, including viruses (Popovic and Minceva, 2020a; Popovic, 2019). In the literature, it was not possible to find data on mutations of different strains of SARS-CoV-2, except for the spike protein. Thus, for now, it was not possible to determine the potential influence of mutations on other parts of the SARS-CoV-2 genome, including those encoding other proteins. These mutations would not affect binding, but would influence chemical composition and thermodynamic properties of growth.
Under laboratory conditions, at 25 °C, similar tendencies have been found as at 37 °C. The binding rate changes, depending on change in Gibbs energy of binding and binding phenomenological coefficients. Some mutations lead to increase in binding rate, for example K417 N. Notice that at 37 °C, K417 N mutation also leads to increase in binding rate. However, the mutation N501Y leads to a decrease in binding rate at 25 °C, compared to the wild type, as can be seen from Table 4. The same phenomenon can be seen at 37 °C.
The Gibbs energy of binding of the Omicron strain is slightly more negative than that of the wild type, both at 25 °C and 37 °C (Table 1). However, the binding rate could not be calculated in this research, because no data was available on the L B coefficient of the Omicron strain.
As can be seen from the discussion above, it seems that except for knowing the nature and number of mutations, k on, k off and dissociation constants, K D, it is necessary to know other parameters, like binding constants, K B, enthalpies of binding, ΔB H, entropies of binding ΔB S, Gibbs energies of binding, ΔB G, and binding phenomenological coefficients, L B. Since all parameters change with appearance of new mutations, it is necessary to know all parameters that can influence the rate of binding.
5. Conclusions
Antigen-receptor binding is a complex phenomenon, which depends on multiple factors: k on, k off, dissociation constants, K D, binding constants, K B, enthalpies of binding, ΔB H, entropies of binding ΔB S, Gibbs energies of binding, ΔB G, and binding phenomenological coefficients, L B. With appearance of mutations in SARS-CoV-2, all these properties change. Thus, to correctly estimate the influence of mutations on infectivity and spreading of the pandemic, it is necessary to know all these parameters. As a rule, mutations lead to decrease in Gibbs energy of binding, making the process more spontaneous. The change in binding phenomenological coefficient is related to change in composition of the viral S-protein. It seems that changes in Gibbs energy and binding rate correspond to epidemiological observations during the pandemic. The results of this research confirm the hypothesis that some mutations lead to decrease in Gibbs energy of binding and increase in binding rate, while other mutations lead to avoiding immune response. Both mechanisms contribute to greater infectivity of mutated strains.
CRediT authorship contribution statement
Marko Popovic: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Writing – original draft, Writing – review & editing, Visualization.
Declaration of competing interest
The author declares no conflict of interest.
List of symbols
- A
Free virus antigen (spike glycoprotein, SGP)
- [A]
Concentration of the free virus antigen
- [A]eq
Concentration of the free virus antigen at equilibrium
- AR
Antigen-receptor complex (SGP-ACE2 complex)
- [AR]
Concentration of the antigen-receptor complex
- [AR]eq
Concentration of the antigen-receptor complex at equilibrium
- C
Concentration of a substance
- KD
Dissociation equilibrium constant
- KB
Binding equilibrium constant
- kon
Forward rate constant (on-rate constant, association rate constant)
- koff
Backward rate constant (off-rate constant, dissociation rate constant)
- LB
Binding phenomenological coefficient
- Lg
Growth phenomenological coefficient
- Q
Reaction quotient
- R
Free host cell receptor (ACE2)
- [R]
Concentration of the free host cell receptor
- [R]eq
Concentration of the free host cell receptor at equilibrium
- Rg
Universal gas constant
- rB
Overall binding rate (difference of forward and backward binding rates)
- rg
Growth (multiplication rate)
- ron
Forward binding reaction rate
- roneq
Forward binding reaction rate at equilibrium
- roff
Backward binding reaction rate
- roffeq
Backward binding reaction rate at equilibrium
- T
Temperature
- [V]tot
Total virus particle concentration in the organism
- γ
Activity coefficient
- ΔBG
Gibbs energy of binding (dependent on temperature and concentrations, at pressure of 105 Pa)
- ΔBG⁰
Standard Gibbs energy of binding (dependent on temperature, at pressure of 105 Pa, at unit concentrations)
- ΔgG
Gibbs energy of growth (multiplication)
- ΔBH⁰
Standard enthalpy of binding (dependent on temperature, at pressure of 105 Pa, at unit concentrations)
- ΔBS⁰
Standard entropy of binding (dependent on temperature, at pressure of 105 Pa, at unit concentrations)
- ν
Stoichiometric coefficient
References
- Annamalai K., Puri I.K. CRC Press; Boca Raton, FL: 2007. Combustion Science and Engineering. [Google Scholar]
- Atkins P.W., de Paula J. second ed. W. H. Freeman and Company; 2011. Physical Chemistry for the Life Sciences. [Google Scholar]
- Atkins P.W., de Paula J. tenth ed. W. H. Freeman and Company; New York: 2014. Physical Chemistry: Thermodynamics, Structure, and Change. [Google Scholar]
- Augusto G., Mohsen M.O., Zinkhan S., Liu X., Vogel M., Bachmann M.F. Vitro Data Suggest that Indian Delta Variant B.1.617 of SARS-CoV-2 Escapes Neutralization by Both Receptor Affinity and Immune Evasion. Allergy. Advance online publication; 2021. 10.1111/all.15065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton M.I., MacGowan S.A., Kutuzov M.A., Dushek O., Barton G.J., van der Merwe P.A. Effects of common mutations in the SARS-CoV-2 Spike RBD and its ligand, the human ACE2 receptor on binding affinity and kinetics. Elife. 2021;10 doi: 10.7554/eLife.70658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demirel Y. third ed. Elsevier; Amsterdam: 2014. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems. [Google Scholar]
- Du X., Li Y., Xia Y.-L., Ai S.-M., Liang J., Sang P., Ji X.-L., et al. Insights into protein–ligand interactions: mechanisms, models, and methods. Int. J. Mol. Sci. 2016;17(2):144. doi: 10.3390/ijms17020144. MDPI AG. Retrieved from. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy S. Why are RNA virus mutation rates so damn high? PLoS Biol. 2018;16(8) doi: 10.1371/journal.pbio.3000003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gale P. Towards a thermodynamic mechanistic model for the effect of temperature on arthropod vector competence for transmission of arboviruses. Microb. risk anal. 2019;12:27–43. doi: 10.1016/j.mran.2019.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gale P. How virus size and attachment parameters affect the temperature sensitivity of virus binding to host cells: predictions of a thermodynamic model for arboviruses and HIV. Microb. risk anal. 2020;15 doi: 10.1016/j.mran.2020.100104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gale P. Advance online publication; 2021. Using Thermodynamic Equilibrium Models to Predict the Effect of Antiviral Agents on Infectivity: Theoretical Application to SARS-CoV-2 and Other Viruses. Microbial Risk Analysis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glassman I., Yetter R.A., Glumac N.G. fifth ed. Academic Press; Cambridge, MA: 2014. Combustion. [Google Scholar]
- Greinert T., Baumhove K., Sadowski G., Held C. Standard Gibbs energy of metabolic reactions: IV. Triosephosphate isomerase reaction. Biophys. Chem. 2020;258 doi: 10.1016/j.bpc.2020.106330. [DOI] [PubMed] [Google Scholar]
- Greinert T., Vogel K., Seifert A.I., Siewert R., Andreeva I.V., Verevkin S.P., Maskow T., Sadowski G., Held C. Standard Gibbs energy of metabolic reactions: V. Enolase reaction. Biochim. Biophys. Acta Protein Proteonomics. 2020;1868(4) doi: 10.1016/j.bbapap.2020.140365. [DOI] [PubMed] [Google Scholar]
- Hadfield J., Megill C., Bell S.M., Huddleston J., Potter B., Callender C., Sagulenko P., Bedford T., Neher R.A. Nextstrain: real-time tracking of pathogen evolution. Bioinformatics. 2018;34(23):4121–4123. doi: 10.1093/bioinformatics/bty407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Y., Wang Z., Wei Z., Schapiro I., Li J. Binding affinity and mechanisms of SARS-CoV-2 variants. Comput. Struct. Biotechnol. J. 2021;19:4184–4191. doi: 10.1016/j.csbj.2021.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen L.D., Popovic M., Tolley H.D., Woodfield B.F. Laws of evolution parallel the laws of thermodynamics. J. Chem. Therm. 2018;124:141–148. doi: 10.1016/j.jct.2018.05.005. [DOI] [Google Scholar]
- Hellingwerf K.J., Lolkema J.S., Otto R., Neijssel O.M., Stouthamer A.H., Harder W., van Dam K., Westerhoff H.V. Energetics of microbial growth: an analysis of the relationship between growth and its mechanistic basis by mosaic non‐equilibrium thermodynamics. FEMS (Fed. Eur. Microbiol. Soc.) Microbiol. Lett. 1982;15(1):7–17. doi: 10.1111/j.1574-6968.1982.tb00028.x. [DOI] [Google Scholar]
- Hickson R.I., Roberts M.G. How population heterogeneity in susceptibility and infectivity influences epidemic dynamics. J. Theor. Biol. 2014;350:70–80. doi: 10.1016/j.jtbi.2014.01.014. [DOI] [PubMed] [Google Scholar]
- Hou W., Armstrong N., Obwolo L.A., Thomas M., Pang X., Jones K.S., Tang Q. Determination of the cell permissiveness spectrum, mode of RNA replication, and RNA-protein interaction of zika virus. BMC Infect. Dis. 2017;17(1):239. doi: 10.1186/s12879-017-2338-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- It'Is Foundation Tissue properties – density. 2021. https://itis.swiss/virtual-population/tissue-properties/database/density/ [Online], Available at:
- Iupac . In: Compendium of Chemical Terminology. second ed. McNaught A.D., Wilkinson A., editors. Blackwell Scientific Publications; Oxford: 1997. (the "Gold Book"). Compiled by. (1997). Online version (2019-) created by S. J. Chalk, 0-9678550-9-8. [DOI] [Google Scholar]
- Khan A., Mohammad A., Haq I., Nasar M., Ahmad W., Yousafi Q., Suleman M., Ahmad S., Albutti A., Khan T., Marafie S.K., Alshawaf E., Ali S.S., Abubaker J., Wei D.Q. Structural-Dynamics and binding analysis of RBD from SARS-CoV-2 variants of concern (VOCs) and GRP78 receptor revealed basis for higher infectivity. Microorganisms. 2021;9(11):2331. doi: 10.3390/microorganisms9112331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan A., Gui J., Ahmad W., Haq I., Shahid M., Khan A.A., Shah A., Khan A., Ali L., Anwar Z., Safdar M., Abubaker A., Uddin N.N., Cao L., Wei D.-Q., Mohammad A. The SARS-CoV-2 B.1.618 variant slightly alters the spike RBD–ACE2 binding affinity and is an antibody escaping variant: a computational structural perspective. RSC Adv. 2021;11(48):30132–30147. doi: 10.1039/D1RA04694B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo K.K.-Y. second ed. Wiley; Hoboken, NJ: 2005. Principles of Combustion. 13: 978-0471046899. [Google Scholar]
- Kwiatkowski D. Science, medicine, and the future: susceptibility to infection. Br. Med. J. Int. Ed. 2000;321(7268):1061–1065. doi: 10.1136/bmj.321.7268.1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laffeber C., de Koning K., Kanaar R., Lebbink J. Experimental evidence for enhanced receptor binding by rapidly spreading SARS-CoV-2 variants. J. Mol. Biol. 2021;433(15) doi: 10.1016/j.jmb.2021.167058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucia U., Grisolia G. How life works—a continuous Seebeck-Peltier transition in cell membrane? Entropy. 2020;22(9):960. doi: 10.3390/e22090960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucia U., Grisolia G., Deisboeck T.S. Atti della Accademia Peloritana dei Pericolanti-Classe di Scienze Fisiche, Matematiche e Naturali. Vol. 98. 2020. Seebeck-like effect in SARS-CoV-2 bio-thermodynamics; p. 6. 2. [DOI] [Google Scholar]
- Lucia U., Deisboeck T.S., Grisolia G. Entropy-based pandemics forecasting. Front. Phy. 2020;8:274. doi: 10.3389/fphy.2020.00274. [DOI] [Google Scholar]
- Lucia U., Grisolia G., Deisboeck T.S. Thermodynamics and SARS-CoV-2: neurological effects in post-Covid 19 syndrome. 2021. arXiv preprint arXiv:2107.12006. [DOI]
- Meurer F., Bobrownik M., Sadowski G., Held C. Standard Gibbs energy of metabolic reactions: I. Hexokinase reaction. Biochemistry. 2016;55(40):5665–5674. doi: 10.1021/acs.biochem.6b00471. [DOI] [PubMed] [Google Scholar]
- Meurer F., Do H.T., Sadowski G., Held C. Standard Gibbs energy of metabolic reactions: II. Glucose-6-phosphatase reaction and ATP hydrolysis. Biophys. Chem. 2017;223:30–38. doi: 10.1016/j.bpc.2017.02.005. [DOI] [PubMed] [Google Scholar]
- Müller I. Springer; Berlin: 2007. A History of Thermodynamics: the Doctrine of Energy and Entropy. [Google Scholar]
- Neuman B.W., Buchmeier M.J. Supramolecular architecture of the coronavirus particle. Adv. Virus Res. 2016;96:1–27. doi: 10.1016/bs.aivir.2016.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman B.W., Adair B.D., Yoshioka C., Quispe J.D., Orca G., Kuhn P., Milligan R.A., Yeager M., Buchmeier M.J. Supramolecular architecture of severe acute respiratory syndrome coronavirus revealed by electron cryomicroscopy. J. Virol. 2006;80(16):7918–7928. doi: 10.1128/JVI.00645-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman B.W., Kiss G., Kunding A.H., Bhella D., Baksh M.F., Connelly S., Droese B., Klaus J.P., Makino S., Sawicki S.G., Siddell S.G., Stamou D.G., Wilson I.A., Kuhn P., Buchmeier M.J. A structural analysis of M protein in coronavirus assembly and morphology. J. Struct. Biol. 2011;174(1):11–22. doi: 10.1016/j.jsb.2010.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nextstrain Genomic epidemiology of novel coronavirus - global subsampling. 2021. https://nextstrain.org/ncov/gisaid/global [Online], Available at:
- Popovic M. Comparative study of entropy and information change in closed and open thermodynamic systems. Thermochim. Acta. 2014;598:77–81. doi: 10.1016/j.tca.2014.11.002. [DOI] [Google Scholar]
- Popovic M. Living organisms from Prigogine's perspective: an opportunity to introduce students to biological entropy balance. J. Biol. Educ. 2018;52(3):294–300. doi: 10.1080/00219266.2017.1357649. [DOI] [Google Scholar]
- Popovic M. Thermodynamic properties of microorganisms: determination and analysis of enthalpy, entropy, and Gibbs free energy of biomass, cells and colonies of 32 microorganism species. Heliyon. 2019;5(6) doi: 10.1016/j.heliyon.2019.e01950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovic M. Atom counting method for determining elemental composition of viruses and its applications in biothermodynamics and environmental science. Comput. Biol. Chem. 2022;96 doi: 10.1016/j.compbiolchem.2022.107621. [DOI] [PubMed] [Google Scholar]
- Popovic M., Minceva M. A thermodynamic insight into viral infections: do viruses in a lytic cycle hijack cell metabolism due to their low Gibbs energy? Heliyon. 2020;6(5) doi: 10.1016/j.heliyon.2020.e03933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovic M., Minceva M. Thermodynamic insight into viral infections 2: empirical formulas, molecular compositions and thermodynamic properties of SARS, MERS and SARS-CoV-2 (COVID-19) viruses. Heliyon. 2020;6(9) doi: 10.1016/j.heliyon.2020.e04943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovic M., Minceva M. Coinfection and interference phenomena are the results of multiple thermodynamic competitive interactions. Microorganisms. 2021;9(10):2060. doi: 10.3390/microorganisms9102060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovic M., Minceva M. Standard thermodynamic properties, biosynthesis rates, and the driving force of growth of five agricultural plants. Front. Plant Sci. 2021;12 doi: 10.3389/fpls.2021.671868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovic M.E., Minceva M. Comment on: “A critical review on heat and mass transfer modelling of viral infection and virion evolution: the case of SARS-COV2. Therm. Sci. 2021;25(6B):4823–4825. doi: 10.2298/TSCI211021329P. [DOI] [Google Scholar]
- Popovic M., Popovic M. Strain Wars: competitive interactions between SARS-CoV-2 strains are explained by Gibbs energy of antigen-receptor binding. Microb. Risk Anal. 2022 doi: 10.1016/j.mran.2022.100202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riedel S., Hobden J.A., Miller S., Morse S.A., Mietzner T.A., Detrick B., Mitchell T.G., Sakanari J.A., Hotez P., Mejia R. 28th ed. McGraw-Hill; New York: 2019. Jawetz, Melnick and Adelberg's Medical Microbiology. [Google Scholar]
- Sender R., Bar-On Y.M., Gleizer S., Bernshtein B., Flamholz A., Phillips R., Milo R. The total number and mass of SARS-CoV-2 virions. Proceedings of the National Academy of Sciences of the United States of America. 2021;118(25) doi: 10.1073/pnas.2024815118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sender R., Bar-On Y.M., Gleizer S., Bernsthein B., Flamholz A., Phillips R., Milo R. The total number and mass of SARS-CoV-2 virions. medRxiv : the preprint serv. health sci. 2021 doi: 10.1101/2020.11.16.20232009. 2020.11.16.20232009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Şimşek B., Özilgen M., Utku F.Ş. How much energy is stored in SARS‐CoV‐2 and its structural elements? Energy Storage. 2021 doi: 10.1002/est2.298. [DOI] [Google Scholar]
- Skoog D.A., West D., Holler F., Crouch S. ninth ed. Cengage Learning Emea; Boston, MA: 2013. Skoog and West's Fundamentals of Analytical Chemistry. -13: 978-1285056241. [Google Scholar]
- Von Stockar U. In: Biothermodynamics: the Role of Thermodynamics in Biochemical Engineering. Urs von Stockar, editor. EPFL Press; Lausanne: 2013. Live cells as open non-equilibrium systems; pp. 475–534. [Google Scholar]
- Von Stockar U. In: Biothermodynamics: the Role of Thermodynamics in Biochemical Engineering. Urs von Stockar, editor. EPFL Press; Lausanne: 2013. Biothermodynamics of live cells: energy dissipation and heat generation in cellular cultures; pp. 475–534. [Google Scholar]
- von Stockar U., Liu J. Does microbial life always feed on negative entropy? Thermodynamic analysis of microbial growth. Biochim. Biophys. Acta. 1999;1412(3):191–211. doi: 10.1016/s0005-2728(99)00065-1. [DOI] [PubMed] [Google Scholar]
- Von Stockar U., Maskow T., Vojinovic V. In: Biothermodynamics: the Role of Thermodynamics in Biochemical Engineering. Urs von Stockar, editor. EPFL Press; Lausanne: 2013. Thermodynamic analysis of metabolic pathways; pp. 581–604. [Google Scholar]
- Wangler A., Schmidt C., Sadowski G., Held C. Standard Gibbs energy of metabolic reactions: III. The 3-phosphoglycerate kinase reaction. ACS Omega. 2018;3(2):1783–1790. doi: 10.1021/acsomega.7b01704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerhoff H.V., Lolkema J.S., Otto R., Hellingwerf K.J. Thermodynamics of growth. Non-equilibrium thermodynamics of bacterial growth: the phenomenological and the Mosaic approach. Biochim. Biophys. Acta Rev. Bioenerg. 1982;683(3–4):181–220. doi: 10.1016/0304-4173(82)90001-5. [DOI] [PubMed] [Google Scholar]
- Wu F., Zhao S., Yu B., Chen Y.M., Wang W., Song Z.G., Hu Y., Tao Z.W., Tian J.H., Pei Y.Y., Yuan M.L., Zhang Y.L., Dai F.H., Liu Y., Wang Q.M., Zheng J.J., Xu L., Holmes E.C., Zhang Y.Z. A new coronavirus associated with human respiratory disease in China. Nature. 2020;579(7798):265–269. doi: 10.1038/s41586-020-2008-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X., Wu S., Wu B., Yang Q., Chen A., Li Y., Zhang Y., Pan T., Zhang H., He X. SARS-CoV-2 Omicron strain exhibits potent capabilities for immune evasion and viral entrance. Signal Transduct. Targeted Ther. 2021;6:430. doi: 10.1038/s41392-021-00852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou P., Yang X.L., Wang X.G., Hu B., Zhang L., Zhang W., Si H.R., Zhu Y., Li B., Huang C.L., Chen H.D., Chen J., Luo Y., Guo H., Jiang R.D., Liu M.Q., Chen Y., Shen X.R., Wang X., Zheng X.S., Shi Z.L. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020;579(7798):270–273. doi: 10.1038/s41586-020-2012-7. [DOI] [PMC free article] [PubMed] [Google Scholar]