Combining multiple imputation with raking of weights: An efficient and robust approach in the setting of nearly true models

Abstract

Multiple imputation (MI) provides us with efficient estimators in model-based methods for handling missing data under the true model. It is also well-understood that design-based estimators are robust methods that do not require accurately modeling the missing data; however, they can be inefficient. In any applied setting, it is difficult to know whether a missing data model may be good enough to win the bias-efficiency trade-off. Raking of weights is one approach that relies on constructing an auxiliary variable from data observed on the full cohort, which is then used to adjust the weights for the usual Horvitz-Thompson estimator. Computing the optimally efficient raking estimator requires evaluating the expectation of the efficient score given the full cohort data, which is generally infeasible. We demonstrate MI as a practical method to compute a raking estimator that will be optimal. We compare this estimator to common parametric and semi-parametric estimators, including standard MI. We show that while estimators, such as the semi-parametric maximum likelihood and MI estimator, obtain optimal performance under the true model, the proposed raking estimator utilizing MI maintains a better robustness-efficiency trade-off even under mild model misspecification. We also show that the standard raking estimator, without MI, is often competitive with the optimal raking estimator. We demonstrate these properties through several numerical examples and provide a theoretical discussion of conditions for asymptotically superior relative efficiency of the proposed raking estimator.

1 |. BACKGROUND

In many settings, variables of interest maybe too expensive or too impractical to measure precisely on a large cohort. Generalized raking is an important technique for using whole population or full cohort information in the analysis of a subsample with complete data,^1–3 closely related to the augmented inverse probability weighted (AIPW) estimators of Robins et al.^4–6 Raking estimators use auxiliary data measured on the full cohort to adjust the weights of the Horvitz-Thompson estimator in a manner that leverages the information in the auxiliary data and improves efficiency. The technique is also, and perhaps more commonly, known as “calibration of weights,” but we will avoid that term here because of the potential confusion with other uses of the word “calibration.” An obvious competitor to raking is multiple imputation (MI) of the non-sampled data.⁷ While MI was initially used for relatively small amounts of data missing by happenstance, it has more recently been proposed and used for large amounts of data missing by design, such as when certain variables are only measured on a subsample taken from a cohort.^8–12

In this article, we take a different approach. We use MI to construct new raking estimators that are more efficient than the simple adjustment of the sampling weights³ and compare these estimators to direct use of MI in a setting where the imputation model may be only mildly misspecified. Our work has connections to the previous literature, where MI and empirical likelihood are used in the missing data paradigm to construct multiply robust estimators that are consistent if any of a set of imputation models or a set of sampling models are correctly specified.¹³ We differ from this work in assuming known subsampling probabilities, which allows for a complex sampling design from the full cohort, and in evaluating robustness and efficiency under contiguous (local) misspecification following the “nearly true models” paradigm.¹⁴ Known sampling weights commonly arise in settings, such as retrospective cohort studies using electronic health records (EHR) data, where a validation subset is often constructed to estimate the error structure in variables derived using automated algorithms rather than directly observed. Lumley¹⁴ considered the robustness and efficiency trade-off of design-based estimators vs maximum likelihood estimators in the setting of nearly true models. We build on this work by comparing MI with the standard raking estimator, and examine to what extent raking that makes use of MI to construct the auxiliary variable may affect the bias-efficiency trade-off for this setting.

We first introduce the raking framework in Section 2. In Section 3, we describe the proposed raking estimator, which makes use of MI to construct the potentially optimal raking variable. In Section 4, we compare design-based estimators with standard MI estimators in two examples using simulation, a classic case-control study and a two phase study where the linear regression model is of interest and an errorprone surrogate is observed on the full cohort in place of the target variable. For this example, we additionally study the relative performance of regression calibration, a popular method to address covariate measurement error.¹⁵ In Section 5, we consider the relative performance of MI vs raking estimators in the National Wilms Tumor Study (NWTS). We conclude with a discussion of the robustness efficiency trade-off in the studied settings.

2 |. INTRODUCTION TO RAKING FRAMEWORK

Assume a full cohort of size N and a probability subsample of size n with known sampling probability π_i for the ith individual. Further, assume we observe an outcome variable Y, predictors Z, and auxiliary variables A on the whole cohort, and observe predictors X only on the sample. Our goal is to fit a model P_θ for the distribution of Y given Z and X (but not A). Define the indicator variable for being sampled as R_i. We assume an asymptotic setting in which as n → ∞, a law of large numbers and central limit theorem exist. In some places, we will make the stronger asymptotic assumption that the sequence of cohorts are iid samples from some probability distribution and that the subsamples satisfy inf_i π_i > 0.^3,6,14

With full cohort data with complete observations we would solve an estimating equation

$$\sum _{i=1}^{N}U\left(Y_i,X_i,Z_i;\theta \right)=0,$$ (1)

where $U_i(\theta )=U\left(Y_i,X_i,Z_i;\theta \right)$ is an efficient score or influence function for giving at least locally efficient estimation of θ. We write ${\tilde{\theta }}_N$ for the resulting estimator with complete data from the full cohort and assume it converges in probability to some limit θ*. If the cohort is truly a realization of the model P_θ, it follows that ${\tilde{\theta }}_N$ would be a locally efficient estimator of θ in the model P_θ. The Horvitz-Thompson-type estimator ${\widehat{\theta }}_{HT}$ of θ solves

$$\sum _{i=1}^N\frac{R_i}{{\pi }_i}U\left(Y_i,X_i,Z_i;\theta \right)=0.$$ (2)

Under regularity conditions, for example, the existence of a central limit theorem and sufficient smoothness for U_i(θ), it is also consistent for θ*.

A generalized raking estimator using auxiliary information H(Y_i, Z_i, A_i) available for all 1 ≤ i ≤ N, which may depend on some extra parameters, is given by the solution of a weighted estimating equation

$$\sum _{i=1}^N\frac{g_i{R}_i}{{\pi }_i}U\left(Y_i,X_i,Z_i;\theta \right)=0,$$ (3)

where the weight adjustments g_i are chosen to minimize the distance between the original and new weights ${\sum }_{i=1}^N{R}_{i}d\left(g_i/{\pi }_i,1/{\pi }_i\right)$ subject to the calibration constraints

$$\sum _{i=1}^N\frac{R_i{g}_i}{{\pi }_i}H\left(Y_i,Z_i,A_i\right)=\sum _{i=1}^{N}H\left(Y_i,Z_i,A_i\right).$$ (4)

In literature, the idea of weight adjustments g_i was discussed as weighting control procedures through a generalized weighting algorithm in survey¹⁶ to reduce the variance of estimates without making additional assumptions.⁶ Deville and Särndal¹ proposed a family of calibration estimators defined by specifying a distance measure and corresponding calibration constraint (4). Deville and Särndal¹ discuss considerations for the choice of the distance measure. For example, choosing $d_1(a,b)={(a-b)}^2/2b$ leads to the generalized regression estimator, but the calibrated weights may be negative. Choosing $d_2(a,b)=a\log (a/b)-a+b$ results in positive weights, and the resulting estimator is referred to as the generalized raking estimator.⁶ Though, asymptotically the choice of distance function will not matter, in the empirical studies that follow, we will study the use of $d_2(a,b)$, otherwise known as the Poisson deviance. It is worth mentioning that sometimes one may wish to restrict the range of new weights to avoid extreme values. For further details regarding calibration and generalized raking, we refer the reader to Deville and Särndal¹ and Deville et al.¹⁷

3 |. IMPUTATION FOR CALIBRATION

3.1 |. Estimation

In the standard MI approach, one may use a regression model for X given Z, Y, and A. For this, M samples are generated from the predictive distribution to produce MIs $\left({\widehat{X}}_1^{(m)},\dots ,{\widehat{X}}_N^{(m)}\right)$ for $m=1,\dots ,M$, giving rise to M complete imputed datasets that represent samples from the unknown conditional distribution of the complete data given the observed data. Then, it is straightforward to solve an imputed estimating equation (1)

$$\sum _{i=1}^{N}U\left(Y_i,{\widehat{X}}_i^{(m)},Z_i;\theta \right)=0$$ (5)

for each of the mth imputed dataset, giving M values of ${\tilde{\theta }}_{(m)}$ with estimated variances ${\tilde{\sigma }}_{(m)}^2,1\le m\le M$. The imputation estimator ${\widehat{\theta }}_{\text{MI}}$ of θ is the average of the ${\tilde{\theta }}_{(m)}$, and the variance can also be estimated from sum of the variance of ${\tilde{\theta }}_{(m)}$ and the average of ${\tilde{\sigma }}_{(m)}^2$.⁷

We propose a raking estimator using MI. The optimal calibration function $H\left(Y_i,Z_i,A_i\right)$ incorporating the auxiliary variable A_i is given by $E\left[h\left(Y_i,X_i,Z_i;\theta \right)\mid Y_i,Z_i,A_i\right]$, where $h_i(\theta )=h\left(Y_i,X_i,Z_i;\theta \right)$ is the influence function for the target parameter under P_θ, which gives the efficient design-consistent calibrated estimator of θ.³ However, the explicit form of such an optimal function is typically not available.^3,18 We estimate the calibration function through MI. Specifically, for the mth imputation, we generate ${\widehat{X}}_i^{(m)}={\widehat{X}}_i^{(m)}\left(Y_i,Z_i,A_i\right)$, the imputed value of X_i given Y_i, Z_i, and A_i for every subject index $i=1,\dots ,N$, where the imputation model is constructed based on all individuals who have the complete observations $\left(Y_i,X_i,Z_i,A_i\right)$;¹⁹ we calculate ${\tilde{\theta }}_{(m)}$ by solving the imputed estimating equation (5). Then, the optimal calibration function is estimated by the average of the M resulting $h_i\left({\tilde{\theta }}_{(1)}\right),\dots ,h_i\left({\tilde{\theta }}_{(M)}\right)$, estimated as

$$\widehat{H}\left(Y_i,Z_i,A_i\right)=\frac{1}{M}\sum _{m=1}^{M}h\left(Y_i,{\widehat{X}}_i^{(m)},Z_i;{\tilde{\theta }}_{(m)}\right)$$ (6)

for each $i=1,\dots ,N$. If the true regression model associated with Y, X, and Z and the MI model are both correctly specified using all the available variables, the empirical average in (6) will converge to the optimal calibration function $E\left[h\left(Y_i,X_i,Z_i;\theta \right)\mid Y_i,Z_i,A_i\right]$ as both the sample size and the number of MIs increase. Finally, we solve the original weighted estimating equation (3) with respect to θ, where the weight adjustments g_i are derived using the calibration constraints (4) with ${\widehat{H}}_i\left(Y_i,Z_i,A_i\right)$ in place of $H_i\left(Y_i,Z_i,A_i\right)$. We propose the final solution, denoted by ${\widehat{\theta }}_{\text{MIR}}$, as the raking estimator of θ via MI.

3.2 |. Efficiency and robustness

When all three of the sampling probability, the imputation model, and the regression model are correctly specified, the proposed raking estimator gives a way to compute the efficient design-consistent estimator. In this case, the standard MI estimator ${\widehat{\theta }}_{\text{MI}}$ will also be consistent and typically more efficient than a design-based approach. However, if we are willing to only assume the regression model and imputation model are correct, there appears to be no motivation for requiring a design-consistent estimator. Also, it is unreasonable in practice to assume that both the regression and imputation models are exactly correct. Recently, in the special case where the full cohort is an iid sample and the subsampling is independent, so-called Poisson sampling, it has been shown that the inverse probability weighting adjusted by MI attains the semi-parametric efficiency bound for a model that assumes only $E\left[U\left(Y_i,X_i,Z_i;\theta \right)\right]=0$ and $E\left[R_i\mid Y_i,Z_i,A_i\right]={\pi }_i$.¹³ Since the proposed estimator ${\widehat{\theta }}_{\text{MIR}}$ also solves a weighted estimating equation (3) subject to the calibration constraints (4) computed by MI, one may expect similar theoretical results after careful development.

In this article, we argue one step further that the interesting questions of robustness and efficiency arise when the imputation model and potentially also the regression model are slightly misspecified: Under what conditions are ${\Vert {\widehat{\theta }}_{\text{MIR}}-{\theta }^{\ast }\Vert }_2^2$ and ${\Vert {\widehat{\theta }}_{\text{MI}}-{\theta }^{\ast }\Vert }_2^2$ comparable, and do these correspond to plausible misspecifications of the regression model, the imputation model, or both? Recall that θ* is the limit of the resulting estimator ${\tilde{\theta }}_N$ in (1), where the complete data are available for the full cohort. These questions were considered in a more abstract context.¹⁴ More precisely, let P_N be the sequence of likelihood functions for the true regression model and Q_N the sequence corresponding to a misspecified model chosen to be contiguous to P_N. Since ${\widehat{\theta }}_{\text{MI}}$ is an asymptotically efficient estimator of θ*, given that ${\widehat{\theta }}_{\text{MIR}}$ is still asymptotically unbiased, ${\text{Δ}}_N=\sqrt{N}\left({\widehat{\theta }}_{\text{MIR}}-{\widehat{\theta }}_{\text{MI}}\right)$ converges to $N\left(0,{\omega }^2\right)$ for some $\omega >0$ under P_N. Then, it follows from Le Cam’s third lemma^20,21 that Δ_N converges to $N\left(\kappa \rho \omega ,{\omega }^2\right)$ under Q_N, where κ² is the limiting variance of the Kullback-Leibler divergence from Q_N to P_N. Then, we measure the asymptotic magnitude of the model misspecification by ρ, the limiting correlation between Δ_N and log Q_N − logP_N under P_N. Consequently, under the misspecified outcome model Q_N, we have

$$\sqrt{N}\left({\widehat{\theta }}_{\text{MIR}}-{\theta }^{\ast }\right)\stackrel{Q_N}{\to }N\left(0,{\sigma }^2+{\omega }^2\right)$$

and

$$\sqrt{N}\left({\widehat{\theta }}_{\text{MI}}-{\theta }^{\ast }\right)\stackrel{{\text{Q}}_N}{\to }N\left(\kappa \rho \omega ,{\sigma }^2\right)$$

for some ${\sigma }^2>0$. We note that the asymptotic mean-squared error of ${\widehat{\theta }}_{\text{MI}}$ is greater than that for ${\widehat{\theta }}_{\text{MIR}}$ under model misspecification, that is, ${\kappa }^2{\rho }^2{\omega }^2+{\sigma }^2>{\sigma }^2+{\omega }^2$, whenever $|\kappa \rho |>1$.¹⁴

Typically, $|\rho |$ is bounded away from 1 for Horvitz-Thomson type estimators, and therefore the generalized raking estimator with optimal calibration is beneficial for the large amount of model misspecification. In addition, there may also be only small misspecification such that $|\rho |$ is arbitrarily close to 1, the worst-case scenario for MI with respect to mean-squared error. The advantage of a design-based estimator may not be readily evident in a single data set if the model misspecification was not reliably detectable. Hence, in the next section, we study the relative numerical performance of these two estimators and several competitors under “nearly true” model misspecification. See Lumley¹⁴ for further discussion of nearly true models for two-phase study setting.

4 |. SIMULATIONS

In this section, we are interested in three questions; how much precision is gained by multiple vs single imputation in raking, whether imputation models can maintain an efficiency advantage while being more robust, and how these affect the efficiency-robustness trade-off between weighted and imputation estimators. Source code in R for these simulations is available at https://github.com/kyungheehan/calib-mi.

4.1 |. Case-control study

We first demonstrate numerical performance of MI for the case-control study, where calibration is not available but the maximum likelihood estimator can be easily computed. Specifically, we examine the sensitivity of MI for the design-based method when a working regression model is slightly misspecified for the analysis.

Let X be a standard normal random variable and Y be a binary response taking values in {0, 1} such that for a given X = x the associated logistic model is given by

$$\text{logit}\mathrm{\mathbb{P}}(Y=1\mid X=x)={\alpha }_0+{\beta }_{0}x+{\delta }_0(x-\xi )\mathbb{I}(x>\xi )$$ (7)

for some fixed δ₀ and $\xi$, and $\text{logit}(p)=\log \left(\frac{p}{1-p}\right)$ for $0<p<1$. In accordance with the usual case-control study design, we assume Y is known for everyone, but X is available with sampling probability of 1 when Y = 1 and a lower sampling probability when Y = 0. To be specific, we first generate a full cohort ${\mathcal{X}}_N=\left\{\left(Y_i,X_i\right):1\le i\le N\right\}$ following the true model (7) and denote the index set of all the n-case subjects in ${\mathcal{X}}_N$ by $S_1\subset \{1,\dots ,N\},n<N$. Thus, $Y_i=1$ if $i\in S_1$, otherwise $Y_i=0$. Then a balanced case-control design is employed which consists of observing $\left(Y_i,X_i\right)$ for all the subjects in S₁ and a randomly chosen n-subsample S₀ from $\{1,\dots ,N\}\setminus S_1$. For cohort members $\{1,\dots ,N\}\setminus S_0\cup S_1$, only Y_i is observed. Define ${\mathcal{X}}_n^{\ast }=\left\{\left(Y_i,X_i\right):i\in S_0\cup S_1\right\}$.

For a practical definition of a nearly true model,¹⁴ we consider a working model that may not be reliably rejected, even when using the oracle test statistic of the likelihood ratio with the true model (7) used to generate the data as the null. In other words, instead of fitting the true model (7), we employ a simpler outcome model

$$\text{logit}\mathrm{\mathbb{P}}(Y=1\mid X=x)=\alpha +\beta x.$$ (8)

We note that when ${\delta }_0=0$ the working model (8) is correctly specified, but misspecified when ${\delta }_0\ne 0$. It is worth while to mention that the simple linear logistic model (8) misspecifies the single knot linear spline logistic model (7) with $\rho \approx 0.92$ given ${\alpha }_0=-5$, ${\beta }_0=1$, and $\xi$ ≈ 1.8, which may represent the worst-case misspecification scenario under the commonly fit linear model (8).¹⁴ In this case, the maximum likelihood estimator of (8) is the unweighted logistic regression²² for the complete case analysis only with ${\mathcal{X}}_n^{\ast }$.

Four different methods are compared in our example for estimating the nearly true slope β in (8); (i) the maximum likelihood estimation (MLE), (ii) a design-based inverse probability weighting (IPW) approach, (iii) an MI with a parametric imputation model (MI-P), and (iv) an MI with nonparametric imputation based on bootstrap resampling (MI-B). Formally, the parametric MI (MI-P) imputes covariates $X_i,i\notin S_0\cup S_1$, from a parametric model such that $X\mid Y=y$ is assumed to be distributed as $N\left(\mu +\eta y,{\sigma }^2\right)$, where $\mu =\mathbb{E}(X\mid Y=0)$, $\eta =\mathbb{E}(X\mid Y=1)-\mu$, and ${\sigma }^2=\mathbb{V}\text{ar}(X)$. Here, the parameters μ, η, and σ² are estimated from ${\mathcal{X}}_n^{\ast }$. On the other hand, the bootstrap method (MI-B) resamples covariates $X_i,i\notin S_0\cup S_1$, from the empirical distribution of X given Y = 0. We note that MLE only utilizes the sub-cohort information ${\mathcal{X}}_n^{\ast }$ but the other estimators additionally use response observations $\left\{Y_i:i\notin S_0\cup S_1\right\}$ so that efficiency gains can be expected for estimating the nearly true slope β, depending on the level of model misspecification.

Using Monte Carlo iterations, we summarized the empirical performance of the four different estimators based on fitting the nearly true model (8) with the mean squared error (MSE) of the target parameter β,

$$\text{MSE}(\widehat{\beta })=\frac{1}{K}\sum _{k=1}^K{\left({\widehat{\beta }}^{[k]}-\beta \right)}^2,$$ (9)

where ${\widehat{\beta }}^{[k]}$ is the estimate of β from the kth Monte Carlo replication, $1\le k\le K$. Similarly the empirical bias-variance decomposition,

$$\text{Bias}(\widehat{\beta })=\text{E}\widehat{\beta }-\beta \text{and}\text{Var}(\widehat{\beta })=\frac{1}{K}\sum _{k=1}^K{\left({\widehat{\beta }}^{[k]}-\text{E}\widehat{\beta }\right)}^2,$$ (10)

was also reported to compare precision and efficiency, where $\text{E}\widehat{\beta }=K^{-1}{\sum }_{k=1}^K{\widehat{\beta }}^{[k]}$. For all simulations, we fixed β = 1, α₀ = −5, ${\xi }_0$ = 1.8, N = 10⁴, and the number of cases was around n = 110 in average. We used M = 100 MIs and K = 1000 Monte Carlo simulations. Results are provided in Table 1.

TABLE 1.

Relative performance of the semiparametric efficient maximum likelihood (MLE), design-based estimator (IPW), parametric imputation (MI-P), and bootstrap resampling (MI-B) imputation estimators in the case-control design with cohort size N = 10⁴, case-control subset with n = 110 in average, M = 100 imputations, and 1000 Monte Carlo runs

		Estimation performance				Empirical powera
$\left({\beta }_0,{\delta }_0\right)$	Criterion	MLE	IPW	MI-P	MI-B	MP test	Lin. test
(1.0)	$\sqrt{\text{MSE}}$	0.145	0.239	0.140	0.240	0.046	0.042
	Bias	0.014	0.071	0.011	0.071
	$\sqrt{\text{Var}}$	0.144	0.229	0.140	0.229
(0.844, 0.700)	$\sqrt{\text{MSE}}$	0.148	0.229	0.147	0.229	0.202	0.042
	Bias	−0.067	0.064	−0.077	0.064
	$\sqrt{\text{Var}}$	0.132	0.219	0.125	0.219
(0.692,1.400)	$\sqrt{\text{MSE}}$	0.199	0.217	0.204	0.217	0.410	0.061
	Bias	−0.156	0.054	−0.168	0.054
	$\sqrt{\text{Var}}$	0.124	0.211	0.116	0.211
(0.541, 2.100)	$\sqrt{\text{MSE}}$	0.257	0.201	0.262	0.201	0.683	0.156
	Bias	−0.233	0.047	−0.242	0.047
	$\sqrt{\text{Var}}$	0.109	0.196	0.102	0.195
(0.381, 2.800)	$\sqrt{\text{MSE}}$	0.317	0.206	0.320	0.206	0.905	0.382
	Bias	−0.301	0.056	−0.306	0.056
	$\sqrt{\text{Var}}$	0.098	0.199	0.093	0.199

Note: We report the root-mean squared error ($\sqrt{\text{MSE}}$) for β = 1, its bias and variance decomposition (10), and the empirical power to reject the nearly true model (8) through the most powerful (MP) test and the goodness-of-fit test of linear fits.^42,43

^aP_N and Q_N are likelihood functions at θ₀ = (α₀, β₀, δ₀) and θ* = (α, β), respectively.

Table 1 demonstrates two principles. First, the parametric MI (MI-P) estimator closely matches the maximum likelihood estimator, but the resampling (MI-B) estimator closely matches the design-based estimator. Second, more importantly, the design-based estimator is less efficient than the maximum likelihood estimator when the model is correctly specified, but has lower mean squared error when δ₀ was greater than about 1.6. In this case, even the most powerful one-sided test of the null δ₀ = 0 based on the alternative model (8) would have power less than approximately 0.5, so that any model diagnostic used in a practical setting would have lower power. Figure 1 shows the relative efficiency of the methods as a function of the level of misspecification. In summary, the model-based analysis is not robust even to mild forms of misspecification that would not be detectable in practical settings, while MI would be beneficial for the efficiency gain of the design-based analysis through the bias-variance trade-off. This preliminary result motivates us to calibrate raking of weights through MI which is less sensitive to the design-based method under the misspecified model.

FIGURE 1.

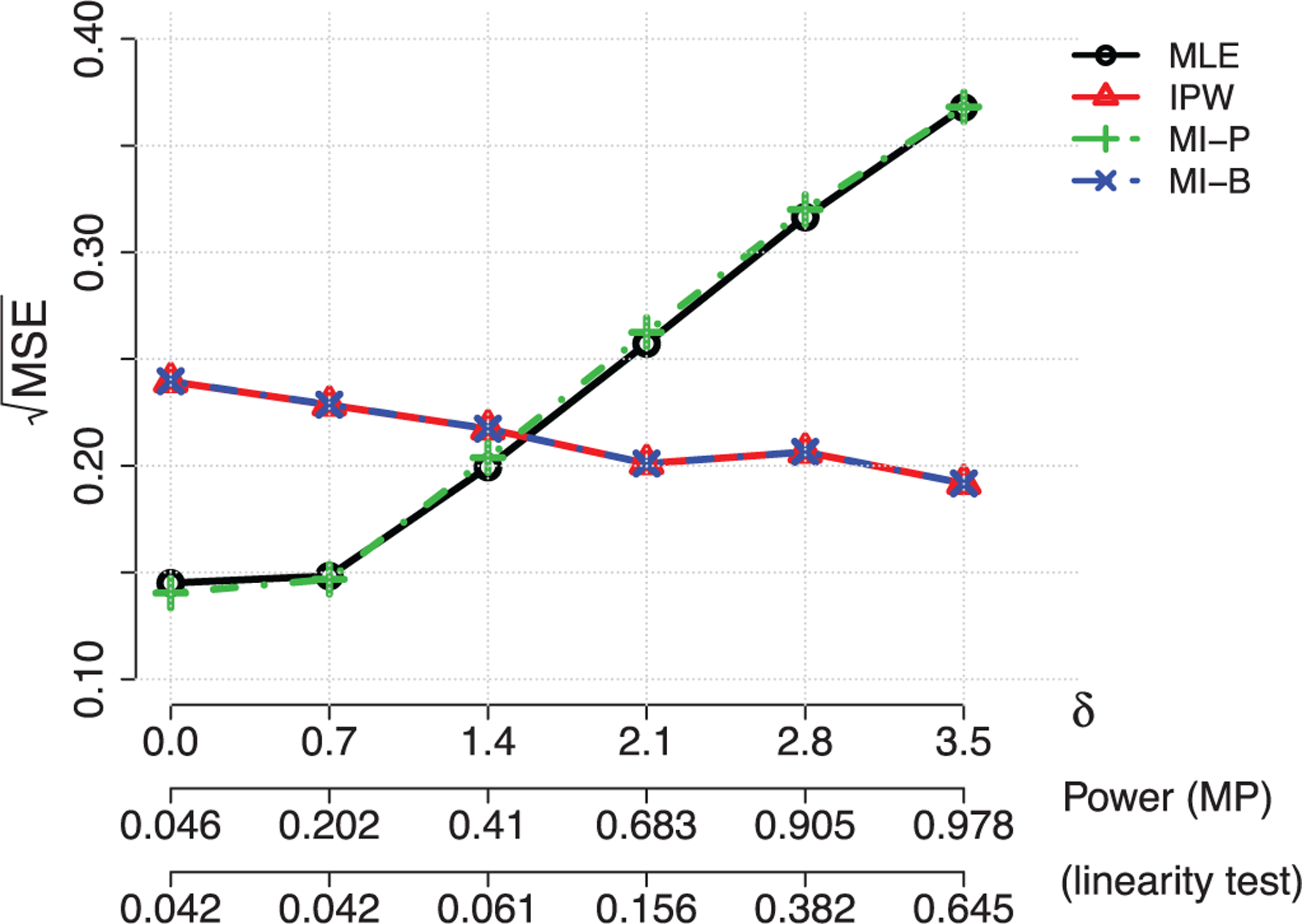
Illustration of Table 1. Relative performance of the semiparametric efficient maximum likelihood (MLE), design-based estimator (IPW), parametric imputation (MI-P), and bootstrap resampling (MI-B) imputation estimators in the case-control design

4.2 |. Linear regression with continuous surrogate

We now evaluate the performance of the MI raking estimator in a two-phase sampling design. Let Y be a continuous response associated with covariates X = x and Z = z such that

$$\mathbb{E}(Y\mid X=x,Z=z)={\alpha }_0+{\beta }_{0}x+{\delta }_{0}x\cdot \mathbb{I}\left(\left|z\right|>{\zeta }_0\right),$$ (11)

for some fixed δ₀ and ${\zeta }_0=F_Z^{-1}(0.95)$, where $\mathbb{V}\text{ar}(Y\mid X,Z)=1$, X is a standard normal random variable, Z is a continuous surrogate of X and $F_Z^{-1}$ is the inverse cumulative distribution function for Z. Similarly to the simulation study in Section 4.1, instead of the true model (11) which generally will not be known in a real data setting, we are interested in the typical linear regression analysis with an outcome model

$$\mathbb{E}(Y\mid X=x)=\alpha +\beta x.$$ (12)

Two different scenarios of the surrogate variable Z are considered such that (a) $Z=X+\epsilon$ for $\epsilon \sim N(0,1)$ and (b) $Z=\eta X$ for $\eta \sim \text{Γ}(4,4)$, which represent additive and multiplicative error, respectively. In the first phase of sampling, we assume that outcomes Y and auxiliary variables Z are known for everyone, whereas covariate measurements of X are available only at the second stage. The sampling for the second phase will be stratified on Z. Specifically, we will observe X_i for all individuals if $\left|Z_i\right|>{\zeta }_0$, otherwise 5% of subjects in the intermediate stratum $\left|Z_i\right|\le {\zeta }_0$ are randomly sampled, where $1\le i\le N$. We write $S_2\subset \{1,\dots ,N\}$ to be the index set of subjects collected in the second phase so that ${\mathcal{X}}_I=\left\{\left(Y_i,Z_i\right):1\le i\le N\right\}$ and χ_II = {(Y_i, X_i, Z_i) : i ∈ S₂} denote the first and second stage samples, respectively.

We compare five different methods of estimating the nearly true parameter β: (i) maximum likelihood estimation (MLE), (ii) a standard generalized raking estimation using the auxiliary variable, (iii) regression calibration (RC), a single imputation method that imputes the missing covariate X with an estimate of $\mathbb{E}[X\mid Z]$,¹⁵ (iv) multiple imputation without raking (MI), and (v) the proposed approach combining raking and the multiple imputation (MIR). We note that when Y is Gaussian, the semi-parametric efficient maximum likelihood estimator of β is available in the missreg3 package in R,²³ using the stratification information.²⁴ We employ this for the MLE (i).

For the standard raking method (ii), we construct a design-based efficient estimator³ as below:

R1. Find a single imputation model $X=a+bY+cZ+ϵ$, where $ϵ\sim N\left(0,{\tau }^2\right)$ based on the second phase sample χ_II.

R2. Fit the nearly true model (12) using $\left(Y_i,{\widehat{X}}_i\right)$ for $1\le i\le N$, where ${\widehat{X}}_i$ are fully imputed from (R1).

R3. Calibrate sampling weights for raking using the influence function induced from the nearly true fits in (R2).

R4. Fit the design-based estimator of the nearly true model (12) with the second phase sample χ_II and calibrated sampling weights from (R3).

We used the distance function $d_2(a,b)=a\log (a/b)-a+b$ to calibrate sampling weights in (R3). For the numerical implementation in calibration, we used calibrate function in the R package survey that provides numerical implementation of calibrating sampling weights with non-negative values.²⁵ For the conventional regression calibration approach (iii), we simply fit a linear model regressing X_i on Z_i for i ∈ S_i and then impute missing observations ${\widehat{X}}_i$ in the first phase so that the nearly true model (12) is evaluated using $\left\{\left(Y_i,{\widehat{X}}_i\right):i\notin S_2\right\}$ and $\left\{\left(Y_i,X_i\right):i\in S_2\right\}$.

We consider two resampling techniques for the MI method (iv): the wild bootstrap^26–28 and a Bayesian approach with a non-informative prior. Note, the wild bootstrap gives consistent estimates for settings where the conventional Efron’s bootstrap does not work, such as under heteroscedasticity and high-dimensional settings. We refer to Appendix A for implementation details of MI with the wild bootstrap and a parametric Bayesian resampling. We now illustrate the proposed method that calibrates sampling weights using MI.

M1. Resample ${\widehat{X}}_i^{\ast }$ independently for all $1\le i\le N$ by using either the wild bootstrap or the parametric Bayesian resampling.

M2. Fit the nearly true model (12) based on a resample $\left\{\left(Y_i,{\widehat{X}}_i^{\ast }\right):1\le i\le N\right\}$.

M3. Repeat (M1) and (M2) in multiple times, and take the average of influence functions, induced by the nearly true models fitted in (M2).

M4. Calibrate sampling weights using the average influence function as auxiliary information.

M5. Fit the design-based estimator of the nearly true model (12) with the second phase sample χ_II and calibrated sampling weights obtained from (M4).

Setting N = 5000, we ran M = 100 MIs over 1000 Monte Carlo replications. For all simulations, β = 1, α₀ = 0, ${\zeta }_0$ ≈ 2.3 when Z is a surrogate of X with an additive measurement error but ${\zeta }_0$ ≈ 1.8 with a multiplicative error in our simulation settings, and the phase two sample with |S₂| = 750 in average. We considered several values of δ₀ and the level of misspecification is described by the empirical power to reject the misspecified model for the level 0.05 likelihood ratio test comparing the null (11) and alternative (12).

The numerical results with additive measurement errors are summarized in Table 2 and Figure 2. In this scenario, regression calibration (RC) performed the best for δ₀ less than approximately 0.15, since RC correctly assumes a linear model for imputing X from Z. The two standard MI had estimation bias due to a misspecified imputation model and had a larger MSE than the RC method. However, we note once again the model diagnostic for linearity, that is, δ₀ = 0, had at most 20% power for the level of misspecification studied, which means one may not reliably reject the misspecified model even when δ₀ = 0.3 and imputation with the correctly specified model is also unlikely. Indeed the standard and proposed MIR raking estimators achieved lower MSE when δ₀ ≥ 0.15. Thus, raking successfully leveraged the information from the cohort not in the phase two sample while maintaining its robustness, as seen in previous literature.^1–3 We further found that the raking estimator can be improved by using MI to estimate the optimal raking variable, with efficiency gains of about 10% in this example. Table 3 and Figure 3 summarize the results for the multiplicative error scenario. In this case, even for δ₀ = 0, the RC and MIs have appreciable bias and worse relative performance compared to the two raking estimators, because of the misspecified imputation model. The two raking estimators outperformed all estimators for all levels of misspecification. In this scenario, the MIR had smaller gains over the standard raking estimator. We also verified that M = 50 MIs produced similar results as reported through all the scenarios (data not shown), but the larger number of MIs is preferred for its potential to provide better numerical stability more generally.²⁹

TABLE 2.

Multiple imputation in two-stage analysis with continuous surrogates when Z = X + ϵ for independent ϵ ∼ N(0, 1)

		Estimation performance
					MI		MIR			Empirical powera
$\left({\beta }_0,{\delta }_0\right)$	Criterion	MLE	Raking	RC	Boot	Bayes	Boot	Bayes	Abs corra	MP test	Lin. test
(1.0)	$\sqrt{\text{MSE}}$	0.019	0.038	0.017	0.019	0.019	0.034	0.034	-	0.052	0.065
	Bias	0.004	0.000	0.000	0.002	−0.003	0.001	0.001
	$\sqrt{\text{Var}}$	0.019	0.038	0.017	0.018	0.018	0.034	0.034
(0.951, 0.068)	$\sqrt{\text{MSE}}$	0.033	0.037	0.022	0.023	0.026	0.033	0.033	0.480	0.140	0.078
	Bias	−0.027	0.000	−0.014	−0.014	−0.019	0.001	0.001
	$\sqrt{\text{Var}}$	0.018	0.037	0.017	0.018	0.018	0.033	0.033
(0.904. 0.131)	$\sqrt{\text{MSE}}$	0.058	0.036	0.032	0.034	0.039	0.033	0.033	0.496	0.407	0.089
	Bias	−0.056	0.000	−0.027	−0.029	−0.034	0.001	0.001
	$\sqrt{\text{Var}}$	0.018	0.036	0.017	0.018	0.018	0.033	0.033
(0.861,0.191)	$\sqrt{\text{MSE}}$	0.084	0.036	0.042	0.047	0.052	0.032	0.032	0.497	0.698	0.108
	Bias	−0.082	−0.001	−0.038	−0.043	−0.048	0.001	0.001
	$\sqrt{\text{Var}}$	0.018	0.036	0.017	0.018	0.018	0.032	0.032
(0.820, 0.247)	$\sqrt{\text{MSE}}$	0.108	0.035	0.052	0.059	0.064	0.032	0.032	0.496	0.893	0.142
	Bias	−0.107	0.000	−0.049	−0.057	−0.062	0.001	0.001
	$\sqrt{\text{Var}}$	0.017	0.035	0.017	0.018	0.018	0.032	0.032
(0.781, 0.3)	$\sqrt{\text{MSE}}$	0.132	0.035	0.062	0.072	0.077	0.032	0.032	0.495	0.978	0.189
	Bias	−0.131	−0.001	−0.060	−0.069	−0.074	0.001	0.001
	$\sqrt{\text{Var}}$	0.017	0.035	0.017	0.018	0.018	0.032	0.032

Note: We compare relative performance of the semiparametric efficient maximum likelihood (MLE), standard raking, regression calibration (RC), multiple imputations (MI) using either the wild bootstrap or Bayesian approach, and the proposed multiple imputation with raking (MIR) estimators for a two-phase design with cohort size N = 5000, phase 2 subset $\left|S_2\right|=750$ in average, M = 100 imputations, and 1000 Monte Carlo runs. We report the root-mean squared error ($\sqrt{\text{MSE}}$) for β = 1, its bias and variance decomposition (10), and the empirical power to reject the nearly true model (12) through the most powerful (MP) test and the goodness-of-fit test of linear fits.^42,43

^aThe absolute value of the correlation between ${\widehat{\beta }}_{\text{MLE}}-{\widehat{\beta }}_{\text{Raking}}$ and $\log Q_N-\log P_N$, where P_N and Q_N are likelihood functions at ${\theta }_0=\left({\alpha }_0,{\beta }_0,{\delta }_0\right)$ and ${\theta }^{\ast }=(\alpha ,\beta )$, respectively.

FIGURE 2.

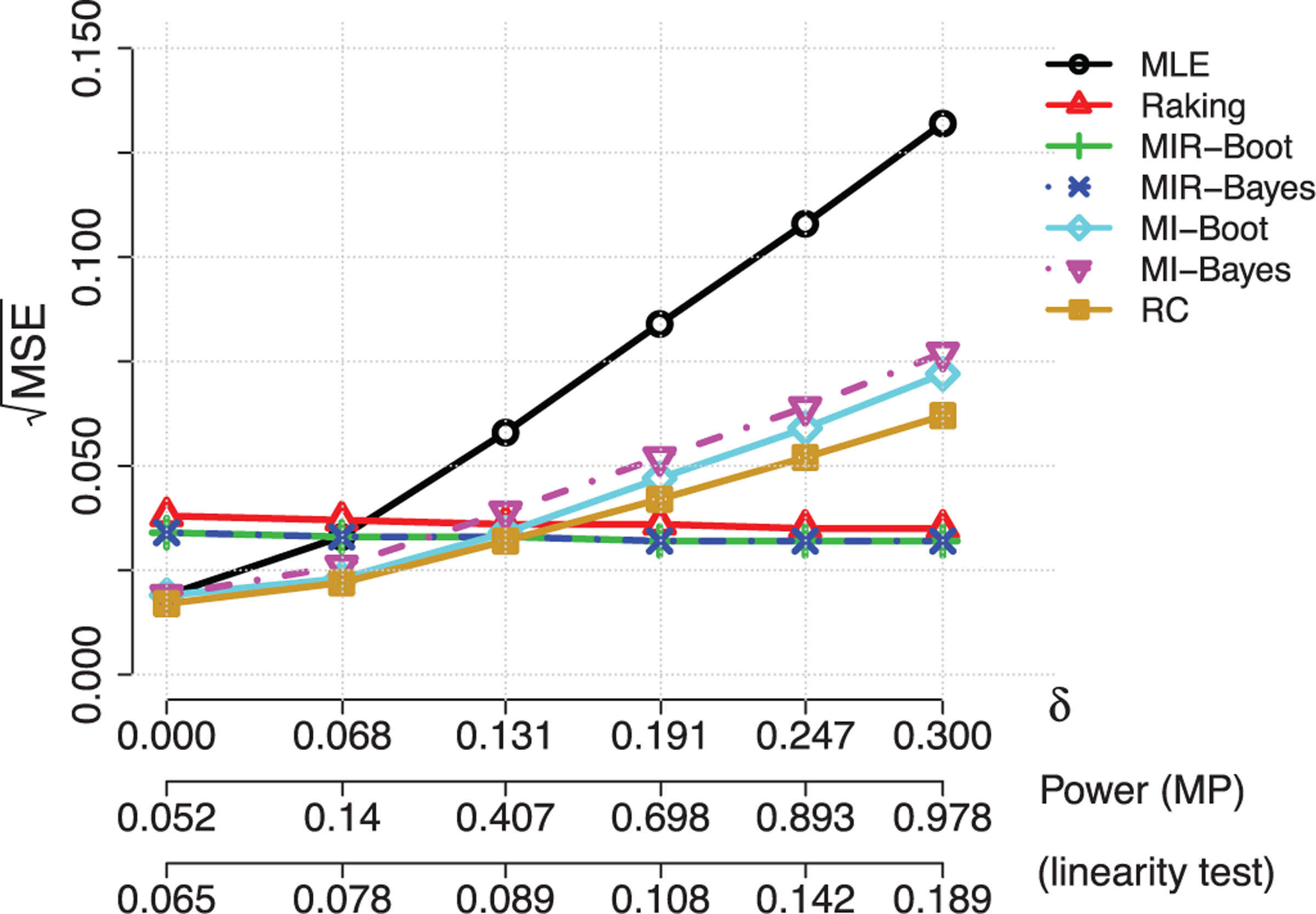
Illustration of Table 2. Relative performance of the semiparametric efficient maximum likelihood (MLE), standard raking, regression calibration (RC), multiple imputations (MI) using either the wild bootstrap or Bayesian approach, and the proposed multiple imputation with raking (MIR) estimators in two-stage analysis with continuous surrogates when $Z=X+\epsilon$ for independent $\epsilon \sim N(0,1)$

TABLE 3.

Multiple imputation in two-stage analysis with continuous surrogates when Z = ηX for independent η ∼ Γ(4, 4)

		Estimation performance
					MI		MIR			Empirical powera
$\left({\beta }_0,{\delta }_0\right)$	Criterion	MLE	Raking	RC	Boot	Bayes	Boot	Bayes	Abs corra	MP test	Lin. test
(1, 0)	$\sqrt{\text{MSE}}$	0.018	0.030	0.216	0.099	0.094	0.029	0.029	-	0.048	0.056
	Bias	0.006	0.001	0.215	0.097	0.092	0.002	0.002
	$\sqrt{\text{Var}}$	0.017	0.030	0.013	0.018	0.018	0.029	0.029
(1.045,−0.068)	$\sqrt{\text{MSE}}$	0.040	0.030	0.227	0.111	0.106	0.029	0.029	0.585	0.149	0.062
	Bias	0.036	0.001	0.227	0.109	0.104	0.002	0.002
	$\sqrt{\text{Var}}$	0.018	0.030	0.013	0.018	0.018	0.029	0.029
(1.087, −0.131)	$\sqrt{\text{MSE}}$	0.068	0.031	0.239	0.123	0.117	0.030	0.030	0.584	0.427	0.075
	Bias	0.065	0.001	0.238	0.121	0.116	0.002	0.002
	$\sqrt{\text{Var}}$	0.018	0.031	0.013	0.018	0.018	0.030	0.030
(1.127, −0.191)	$\sqrt{\text{MSE}}$	0.095	0.032	0.249	0.134	0.128	0.031	0.031	0.585	0.697	0.099
	Bias	0.093	0.001	0.249	0.133	0.127	0.002	0.002
	$\sqrt{\text{Var}}$	0.018	0.032	0.014	0.018	0.018	0.030	0.031
(1.165, −0.247)	$\sqrt{\text{MSE}}$	0.121	0.032	0.259	0.144	0.139	0.031	0.031	0.583	0.890	0.136
	Bias	0.119	0.001	0.259	0.143	0.138	0.002	0.002
	$\sqrt{\text{Var}}$	0.019	0.032	0.014	0.019	0.019	0.031	0.031
(1.200, −0.3)	$\sqrt{\text{MSE}}$	0.146	0.033	0.269	0.155	0.149	0.032	0.032	0.580	0.967	0.179
	Bias	0.145	0.001	0.268	0.154	0.148	0.003	0.002
	$\sqrt{\text{Var}}$	0.019	0.033	0.014	0.019	0.019	0.032	0.032

Note: We compare relative performance of the semiparametric efficient maximum likelihood (MLE), standard raking, regression calibration (RC), multiple imputations using (MI) either the wild bootstrap or Bayesian approach, and the proposed multiple imputation with raking (MIR) estimators for a two-phase design with cohort size N = 5000, phase 2 subset $\left|S_2\right|=750$ in average, M = 100 imputations, and 1000 Monte Carlo runs. We report the root-mean squared error ($\sqrt{\text{MSE}}$) for β= 1, its bias and variance decomposition (10), and the empirical power to reject the nearly true model (12) through the most powerful (MP) test and the goodness-of-fit test of linear fits.^42,43

^aThe absolute value of the correlation between ${\widehat{\beta }}_{\text{MLE}}-{\widehat{\beta }}_{\text{Raking}}$ and $\log Q_N-\log P_N$, where P_N and Q_N are likelihood functions at ${\theta }_0=\left({\alpha }_0,{\beta }_0,{\delta }_0\right)$ and ${\theta }^{\ast }=(\alpha ,\beta )$, respectively.

FIGURE 3.

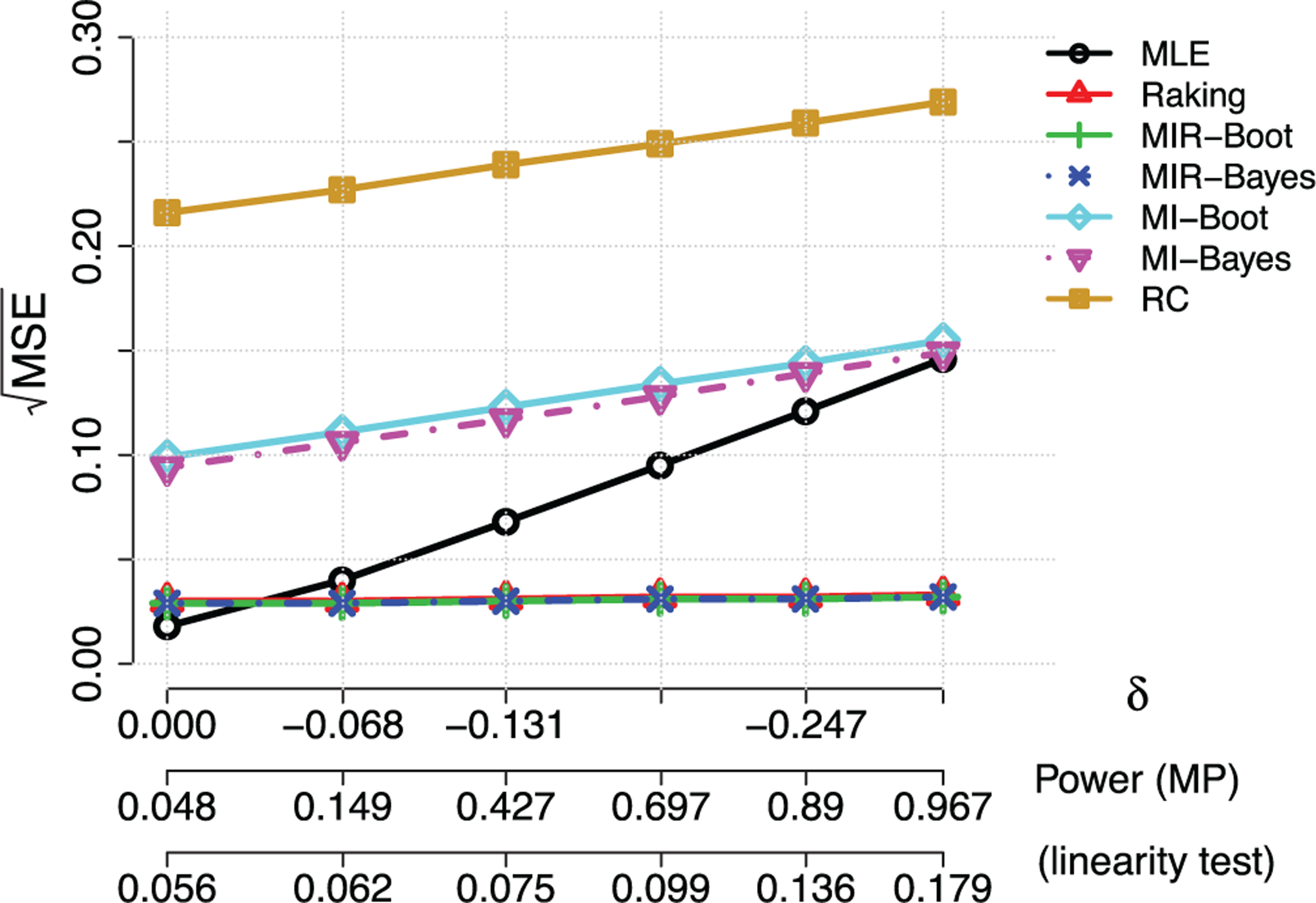
Illustration of Table 3. Relative performance of the maximum likelihood (MLE), standard raking, regression calibration (RC), multiple imputations (MI) using either the wild bootstrap or Bayesian approach, and the proposed multiple imputation with raking (MIR) estimators in two-stage analysis with continuous surrogates when $Z=\eta X$ for independent $\eta \sim \text{Γ}(4,4)$

5 |. DATA EXAMPLE: THE NWTS

We apply our proposed approach to the data from NWTS. In this example, we assume a key covariate of interest is only available in a phase 2 subsample, and compare the proposed MIR method with other standard estimators for this setting. In the data example with NWTS, we are interested in the logistic model for the binary relapse response with predictors histology (UH: unfavorable vs FH: favorable vs), the stage of disease (III/IV vs I/II), age at diagnosis (year) and the diameter of tumor (cm) as

$$\begin{gathered} \text{logit}\mathrm{\mathbb{P}}(\text{Relapse}\mid \text{Histology, Stage, Age, Diameter}) \\ =\alpha +{\beta }_1(\text{Age})+{\beta }_2(\text{Diameter})+{\beta }_3(\text{Histology})+{\beta }_4(\text{Stage})+{\beta }_{3,4}(\text{Histology}\ast \text{Stage}), \end{gathered}$$ (13)

where β_3,4 indicates an interaction coefficient between histology and stage.^30,31 We consider (13) is a nearly true model of the relapse probability associated with covariates, as it is difficult to specify the true model in this real data setting.

Histology was evaluated from both a central laboratory and a local laboratory, where the latter is subject to misclassification due to the difficulty of diagnosing this rare disease. For the first phase data, we suppose that the N = 3915 observations of outcomes and covariates are available for the full cohort, except that the histology is obtained only from the local laboratory. Central histology is then obtained on a phase 2 subset. By considering the outcome-dependent sampling strategies,^30,31 we sampled individuals for the second phase by stratifying on relapse, local histology, and disease stage levels. Specifically, all the subjects who either relapsed or had unfavorable local histology were selected, while only a random subset in the remaining strata (non-relapsed and favorable histology strata for each stage level) were selected so that there was a 1:1 case-control sample for each stage level.³⁰

In this data example, we consider the regression coefficient obtained from the full cohort analysis of the model (13) as the “nearly true parameters.” Similarly to previous numerical studies, we compared four estimators: (i) the maximum likelihood estimates (MLE) of the regression coefficients in (13) based on the complete case analysis of the second phase sample; (ii) the standard generalized raking estimator (specified by the Poisson deviance distance function d₂(a, b)), which calibrates sampling weights by using the local histology information in the first phase sample, where the raking variable was generated by the influence functions. We imputed (unobserved) a central histology path by using a logistic model regressing the second phase histology observations on the age, tumor diameter, and three-way interaction among the relapse, stage, and local histology together with their nested interaction terms. The reason for introducing interaction in the imputation model is that subjects at advanced disease stage or with unfavorable histology were mostly relapsed in the observed data. We note that the data analysis is more closely related to the case-cohort study in Section 4.1 except for the two-phase analysis setting, where the gold standard central histology results are available only for a subset of patients. Recall from Table 1, the bootstrap-based multiple imputation (MI-B) showed more robust results against the nearly true model misspecification than the multiple imputation with a parametric approach (MI-P). Motivated by this simulation result, we consider (iii) the bootstrap procedure for MI with the second phase sample and (iv) combining the raking and multiple imputation (MIR) as proposed in the previous section.

The relative performance of the methods were assessed by obtaining estimates for 1000 two-phase samples. For each two-phase sample, 100 MIs were applied. Table 4 summarizes the results. Similarly to the numerical illustration in the previous section, we found that the proposed method (MIR) had the best performance in terms of achieving lowest MSE for the target parameter available only on the subset. While raking does not provide the lowest MSE for all parameters, in this example, MIR had the lowest squared error summed over the model parameters.

TABLE 4.

The National Wilms Tumor Study data example

		Estimation performance by regressor					Sum of squares
Method	Criterion	Hstga	Stageb	Agec	Diamd	H*Se
MLE	$\sqrt{\text{MSE}}$	1.765	0.776	0.014	0.014	0.602	4.080
	Bias	−1.765	−0.776	−0.007	−0.012	0.600	4.076
	$\sqrt{\text{Var}}$	0.031	0.023	0.012	0.008	0.050	0.004
Raking	$\sqrt{\text{MSE}}$	0.132	0.021	0.006	0.003	0.205	0.060
	Bias	0.032	0.000	0.000	0.001	−0.064	0.005
	$\sqrt{\text{Var}}$	0.128	0.021	0.006	0.003	0.195	0.055
RC	$\sqrt{\text{MSE}}$	0.040	0.004	0.004	0.002	0.183	0.196
	Bias	0.403	0.003	0.004	0.002	−0.179	0.195
	$\sqrt{\text{Var}}$	0.022	0.003	0.001	0.001	0.036	0.001
MI	$\sqrt{\text{MSE}}$	0.148	0.015	0.003	0.002	0.173	0.052
	Bias	0.062	−0.003	0.002	0.002	−0.050	0.006
	$\sqrt{\text{Var}}$	0.134	0.014	0.002	0.001	0.166	0.046
MIR	$\sqrt{\text{MSE}}$	0.125	0.019	0.006	0.003	0.182	0.049
	Bias	0.032	0.004	0.001	0.001	−0.047	0.003
	$\sqrt{\text{Var}}$	0.121	0.019	0.006	0.003	0.175	0.046
Full cohort	Estimate	1.193	0.285	0.089	0.028	0.816	−
	SE	0.156	0.105	0.017	0.012	0.227	−

Note: We compare relative performance of the semiparametric efficient maximum likelihood (MLE), standard raking, regression calibration (RC), multiple imputation using the bootstrap (MI), and the proposed multiple imputation with raking (MIR) estimators for a two-phase design with cohort size N = 3915, phase 2 subset $\left|S_2\right|$ = 1338, M = 100 imputations, and 1000 Monte Carlo runs. We report the root-mean squared error ($\sqrt{\text{MSE}}$) for the parameter estimate obtained from the full cohort analysis of the outcome model (13), and its bias and variance decomposition (10).

^aUnfavorable histology vs favorable.

^bDisease stage III/IV vs I/II.

^cYear at diagnosis.

^dTumor diameter (cm).

^eHistology*Stage.

6 |. DISCUSSION

There are many settings in which variables of interest are not directly observed, either because they are too expensive or difficult to measure directly or because they come from a convenient data source, such as EHR, not originally collected to support the research question. In any practical setting, the chosen statistical model to handle the mismeasured or missing data will be at best a close approximation to the targeted true underlying relationship. A general discussion of the difficulty of testing for model misspecification demonstrates that the data at hand cannot be used to reliably test whether or not the basic assumptions in the regression analysis hold without good knowledge of the potential structure.³²

Here, we have considered the robustness-efficiency trade-off of several estimators in the setting of mild model misspecification, where idealized tests with the correct alternative have low power. When the misspecification is along the least-favorable direction contiguous to the true model, the bias will be in proportion to the efficiency gain from a parametric model.¹⁴ We studied the relative performance of design-based estimators for a nearly true regression model in two cases, logistic regression in a case-control study and linear regression in a two-phase design, where the misspecification was approximately in the least favorable direction. In both cases, the misspecification took the form of a mild departure from linearity, and as expected, the raking estimators demonstrated better robustness compared to the parametric MLE and standard MI models.

In the recent literature, Han³³ discussed that modifying the propensity scores as inverse weights essentially agrees with Deville and Särndal¹ in survey literature and showed that directly optimizing an objective function under calibration constraints leads to improving efficiency and robustness.^34,35 Likewise, a number of AIPW estimators have been proposed to calibrate the propensity scores by paring estimating equations and augmentation terms so that they achieve certain efficiency as well as dealing with double robustness.^13,36–38 Our approach to local robustness is rather related to that of Watson and Holmes,³⁹ who consider making a statistical decision robust to model misspecification around the neighborhood of a given model in the sense of Kullback-Leibler divergence. Our approach is simpler than theirs for two reasons: we consider only asymptotic local minimax behavior, and we work in a two-phase sampling setting where the sampling probabilities are under the investigator’s control and so can be assumed known. In this setting, the optimal raking estimator is consistent and efficient in the sampling model and so is locally asymptotically minimax. In more general settings of nonresponse and measurement error, it is substantially harder to find estimators that are local minimax, even asymptotically, and more theoretical work is needed.

Another contribution of our study is that we demonstrated a practical approach for the efficient design-based estimator under contiguous misspecification. Without an explicit form of an efficient influence function, the characterization of the efficient estimator may not always lead to readily attainable computation of the efficient estimator in the standard raking method. We examined the use of MI to estimate the raking variable that confers the optimal efficiency.¹³ Our proposed raking estimator is easy to calculate and provides better efficiency than any raking estimator based on a single imputation auxiliary variable. In the two cases studied, the improvement in efficiency was evident, though at times small. On the other hand, the degree of improvement of the MI-raking estimator over the standard raking approach is expected to increase with the degree of nonlinearity of the score for the target variable. In additional simulations, not shown, we did indeed see larger efficiency gains for MI-raking over single-imputation raking with large measurement error in Z.

In many real-life examples, we may prefer to choose simpler models when there is a lack of evidence to support a more complicated approach, because of the clarity of interpretation with simpler models.^40,41 In such settings, design-based estimators are easy to implement in standard software and provide a desired robustness. However, as we demonstrated in our numerical results with the nearly true models, the simpler models may not be reliably rejected as an incorrect model. More efforts in characterizing the performance of the simpler models are needed under a class of mild (difficult to detect) misspecification, the nearly true models. The proposed method would provide better efficiency without imposing extra assumptions to the standard techniques, but further theoretical work is also needed to find a more practical representation of the least-favorable contiguous model for the general setting in order to better understand how much of a practical concern this type of misspecification may be. The bias-efficiency trade-off we describe is also important in the design of two-phase samples. The optimal design for the raking estimator will be different from the optimal design for the efficient likelihood estimator, and the optimal design when the outcome model is “nearly true” may be different again.

APPENDIX. DETAILS OF IMPLEMENTATION

A.1. IMPUTATION

The wild bootstrap MI estimator is computed as follows:

W1. Generate $X_i^{\ast }={\widehat{X}}_i+V_i{\widehat{e}}_i$ for $i\in S_2$, where ê_i are residuals from (R2) and V_i is an independent dichotomous random variable that takes on the value $(1+\sqrt{5})/2$ with probability $(\sqrt{5}-1)/(2\sqrt{5})$, otherwise $(1-\sqrt{5})/2$, so that $\mathbb{E}V=0$ and $\text{Var}(V)=1$.

W2. Find an imputation model regressing $X_i^{\ast }$ on Y_i and Z_i for $i\in S_2$.

W3. Resample ${\widehat{X}}_i^{\ast }\sim N\left(v\left(Y_i,Z_i\right),{\tau }^2\left(Y_i,Z_i\right)\right)$ independently for $i\in S_1$, where the mean and variance functions $v\left(Y_i,Z_i\right)\equiv \mathbb{E}(X\mid Y=y,Z=z)$ and ${\tau }^2\left(Y_i,Z_i\right)\equiv \text{Var}(X\mid Y=y,Z=z)$ are estimated from the model in (W2).

W4. Fit the nearly true model (12) using $\left\{\left(Y_i,{\widehat{X}}_i^{\ast }\right):1\le i\le N\right\}$, where ${\widehat{X}}_i^{\ast }=X_i$ for $i\in S_2$.

W5. Repeat (W1) to (W4) and take the average of multiple estimates of parameters.

We employ a parametric Bayesian resampling technique as follows:

B1. Find a posterior distribution of parameters $\left(a,b,c,{\tau }^2\right)$ for the imputation model used in (R1) given the second phase sample χ_II.

B2. Generate $\left(a^{\ast },b^{\ast },c^{\ast },{\tau }_{\ast }^2\right)$ from the posterior distribution in (B1).

B3. Resample $X_i^{\ast }\sim N\left(a^{\ast }+b^{\ast }{Y}_i+c^{\ast }{Z}_i,{\tau }_{\ast }^2\right)$ independently for i ∈ S₁.

B4. Fit the nearly true model (12) using $\left\{\left(Y_i,{\widehat{X}}_i^{\ast }\right):1\le i\le N\right\}$, where ${\widehat{X}}_i^{\ast }=X_i$ for $i\in S_2$.

B5. Repeat (B1) to (B4) and take the average of multiple estimates of parameters.

For the prior distribution of $\left(a,b,c,{\tau }^2\right)$, we adopt a non-informative prior $p\left(a,b,c,{\tau }^2\right)\propto 1/{\tau }^2$. In (B2), we first generate ${\tau }_{\ast }^2\mid {\mathcal{X}}_{II}\sim {\text{Γ}}^{-1}\left(a_n/2,b_n/2\right)$, where $a_n=\left|S_2\right|-3$ and b_n is the residual sum of squares from the linear regression model.

Then, we generate ${\left(a^{\ast },b^{\ast },c^{\ast }\right)}^{\top }\mid {\tau }_{\ast }^2,{\mathcal{X}}_{II}\sim N_3\left({(\widehat{a},\widehat{b},\widehat{c})}^{\top },{\tau }_{\ast }^2{\left({\text{Ξ}}^{\top }\text{Ξ}\right)}^{-1}\right)$, where Ξ is the design matrix of the linear regression model in (R1) and $(\widehat{a},\widehat{b},\widehat{c})$ is the corresponding estimate of the regression coefficient.

A.2. GOODNESS-OF-FIT TEST

We use the wild bootstrap^26–28 together with kernel smoothing techniques in testing model specification of the parametric model. Suppose the true model is given by

$$Y=m(X;\theta )+\epsilon ,$$ (A1)

where m is a known function depending of the parameter θ and ϵ is a noise uncorrelated to X, that is $\mathbb{E}(\epsilon \mid X)=0$. In our study, we are mainly interested in in testing the null hypothesis such that

$$H_0:m(X;\theta )=\alpha +\beta X(a.e.)$$

for some $\theta ={(\alpha ,\beta )}^{\top }\in {\mathbf{R}}^2$. We note that under the null hypothesis H₀, estimation of $\mathbb{E}(Y\mid X=\cdot )$ in a fully nonparametric way regressing iid observations Y_i on $X_i,1\le i\le N$, is less efficient than we directly fit the parametric model (A1) based on the same sample. However, fitting the parametric model may suffers from inevitable bias when the model is misspecified as the sample size is increasing.^42,43

From the above observation, we may test if the mean squared error quantifying the goodness-of-fit of the specified model (A1) is small compared to the nonparametric fits. Specifically, we measure ${\mathcal{l}}_N=\text{MSE}(\widehat{\theta })-\text{MSE}(\widehat{m})$ and examine if the observed quantity ${\mathcal{l}}_N$ is significantly small, where $\widehat{m}(\cdot )$ is a univariate kernel regression estimator of $\mathbb{E}(Y\mid X=\cdot )$. Here, we choose the bandwidth for kernel smoothing based on leave-one-out cross validation criterion which empirically optimizes prediction performance of the kernel smoothed estimates and it can be easily implemented by using the npregbw function of the np package in R.⁴⁴ Similarly to the previous ideas of the bootstrap resampling, the p-value of testing the null hypothesis H₀ is computed as below:

T1. Generate $Y_i^{\ast }=\widehat{\alpha }+\widehat{\beta }{X}_i+V_i{\widehat{e}}_i$, $1\le i\le N$, where ${\widehat{e}}_i=Y_i-\widehat{\alpha }+\widehat{\beta }{X}_i$ and V_i are random copies of an independent random variable V which takes binary values by $(1+\sqrt{5})/2$ with probability $(\sqrt{5}-1)/(2\sqrt{5})$, otherwise $(1-\sqrt{5})/2$ so that $\mathbb{E}V=0$ and $\text{Var}(V)=1$.

T2. Fit the parametric model with $\left(Y_1^{\ast },X_1\right),\dots ,\left(Y_N^{\ast },X_N\right)$ and let ${\widehat{\theta }}^{\ast }={\left({\widehat{\alpha }}^{\ast },{\widehat{\beta }}^{\ast }\right)}^{\top }$ be the resulting estimate of the parameter θ. Compute the mean squared error $\text{MSE}\left({\widehat{\theta }}^{\ast }\right)=N^{-1}{\sum }_{i=i}^N{\left(Y_i^{\ast }-{\widehat{\alpha }}^{\ast }-{\widehat{\beta }}^{\ast }{X}_i\right)}^2$.

T3. Find kernel smoothed its ${\widehat{Y}}^{\ast }={\widehat{m}}^{\ast }\left(X_i\right)$, $1\le i\le N$ and compute the mean squared error $\text{MSE}\left({\widehat{m}}^{\ast }\right)=N^{-1}{\sum }_{i=i}^N{\left(Y_i^{\ast }-{\widehat{m}}^{\ast }\left(X_i\right)\right)}^2$.

T4. Repeat (L1) to (L3) independently to obtain ${\mathcal{l}}_n^{\ast }=\text{MSE}\left({\widehat{\theta }}^{\ast }\right)-\text{MSE}\left({\widehat{m}}^{\ast }\right)$ in multiple times to get an empirical distribution of ${\mathcal{l}}_N$.

T5. Compute the empirical p-value as the fraction of events ${\mathcal{l}}_N^{\ast }>{\mathcal{l}}_N$ occurred among repeated runs in (L4).