massNet: integrated processing and classification of spatially resolved mass spectrometry data using deep learning for rapid tumor delineation

Abstract

Motivation

Mass spectrometry imaging (MSI) provides rich biochemical information in a label-free manner and therefore holds promise to substantially impact current practice in disease diagnosis. However, the complex nature of MSI data poses computational challenges in its analysis. The complexity of the data arises from its large size, high-dimensionality and spectral nonlinearity. Preprocessing, including peak picking, has been used to reduce raw data complexity; however, peak picking is sensitive to parameter selection that, perhaps prematurely, shapes the downstream analysis for tissue classification and ensuing biological interpretation.

Results

We propose a deep learning model, massNet, that provides the desired qualities of scalability, nonlinearity and speed in MSI data analysis. This deep learning model was used, without prior preprocessing and peak picking, to classify MSI data from a mouse brain harboring a patient-derived tumor. The massNet architecture established automatically learning of predictive features, and automated methods were incorporated to identify peaks with potential for tumor delineation. The model’s performance was assessed using cross-validation, and the results demonstrate higher accuracy and a substantial gain in speed compared to the established classical machine learning method, support vector machine.

Availability and implementation

https://github.com/wabdelmoula/massNet. The data underlying this article are available in the NIH Common Fund’s National Metabolomics Data Repository (NMDR) Metabolomics Workbench under project id (PR001292) with http://dx.doi.org/10.21228/M8Q70T.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Mass spectrometry imaging (MSI) is a rapidly growing technology that can provide spatial mapping of a wide range of biomolecular classes (such as proteins, metabolites and lipids) simultaneously and directly from a tissue section in a label-free manner (McDonnell and Heeren, 2007). These make MSI a promising discovery tool with the potential to impact the accuracy and speed of cancer diagnosis and complement the current practice of anatomic pathology (Dewez et al., 2020; Norris and Caprioli, 2013). In support providing information that can complement anatomic pathology, MSI can detect molecular alterations in diseased tissues prior to the manifestation of observable morphological changes (Abdelmoula et al., 2016; Addie et al., 2015; Randall et al., 2020). Recent developments have also enabled automated multimodal integration between MSI and histology (Abdelmoula et al., 2014; Patterson et al., 2018; Race et al., 2021). Such multimodal integration can harness complementary molecular and anatomical information from biological systems, enabling, e.g. a better understanding of molecular mechanisms and pathology of various diseases (Chaurand et al., 2004; Veselkov et al., 2014), more informed drug metabolite distribution (Castellino et al., 2011; Randall et al., 2018), and more sensitive surgical guidance (Eberlin et al., 2014; Santagata et al., 2014).

Matrix-assisted laser desorption ionization (MALDI) is a promising sample introduction technique for the development of diagnostic applications based on MSI (Basu et al., 2019; Calligaris et al., 2015; Drake et al., 2017; Huizing et al., 2019). Acquisition of spectral data from different molecular classes depends largely on the tissue preparation and matrix selection (Carreira et al., 2015). MSI data acquisition is done through laser scanning of a tissue surface for desorption and ionization of molecules using a predefined spatial resolution grid, which defines pixel dimensions. The mass-to-charge ratio (m/z) and relative intensity of the released ions are detected by a mass analyzer. Each pixel then provides a mass spectrum that would be considered as a high-dimensional data point for machine learning purposes. The quality and complexity of mass spectral data depend upon the mass analyzer. Fourier-transform ion cyclotron resonance mass spectrometry imaging (FT-ICR MSI) offers the highest mass resolving power (Bowman et al., 2020). Such ultrahigh mass resolution technology significantly improves the mass identification accuracy, but at the cost of concomitant increases in data complexity and volume (McDonnell et al., 2010b).

The complexity of raw MSI data poses challenges for classical machine learning approaches, where prone to the curse of dimensionality-related issues and slow processing (Alexandrov, 2020). These complexities can be described in terms of massive dimensionality (e.g. ${10}^5-{10}^7$m/z values) and a large number of spectra—that can exceed one million spectra per image, depending on both spectral and spatial resolutions—which can reduce clustering and classification quality (Van Der Maaten et al., 2009). MSI data preprocessing such as peak picking has been a fundamental step that, to avoid the aforementioned limitations, preceded the analysis routines of classical machine learning (McDonnell et al., 2010b). This fundamental preprocessing step aims to significantly reduce the original data dimensionality through identification of as many relevant peaks as possible while minimizing the noise. However, the available implementations of currently established peak picking approaches are highly sensitive to the selection of parameters that require expert optimization (e.g. peak shape, signal-to-noise ratio, full-width-half-maximum, peak frequency, baseline subtraction and spectral smoothing; Donnelly et al., 2019; Murta et al., 2021). In addition, the computational performance of peak picking approaches implemented in widely used commercial software is typically quadratic (Alexandrov, 2012), resulting in slow analysis that can take several hours or even a few days depending on mass resolving power and the number of mass spectra processed. A faster alternative but less sensitive approach is to base the peak picking analysis on the mean spectrum (Alexandrov, 2012). McDonnell et al. (2010a) showed that peak picking on the base peak spectrum, which displays the maximum intensity of each m/z value across the dataset, could improve results compared to the analysis of the mean spectrum, although this analysis is still depended upon expert optimization of peak picking parameters. Spectral preprocessing and the effect of parameters selection do not only impact the downstream analysis (e.g. dimensionality reduction, clustering and classification) but can also affect the overall biological interpretation (Murta et al., 2021; Seddiki et al., 2020).

Deep learning methods have revolutionized many application areas of biomedical imaging (Esteva et al., 2017; Hosny et al., 2018; Ronneberger et al., 2015). Unlike well-established classical approaches that require feature engineering (Balluff et al., 2015; Calligaris et al., 2015), deep learning can perform automatic learning of predictive features (Lecun et al., 2015). Deep learning techniques offer scalability, nonlinearity and efficiency that can accommodate the complexity of MSI data (Abdelmoula et al., 2020; Inglese et al., 2017; Thomas et al., 2016). For example, convolutional neural networks (CNN) were successfully applied to preprocessed and peak picked MSI data for tumor classification (Behrmann et al., 2018; Guo et al., 2020; van Kersbergen et al., 2019). Recently, CNN methods revealed promising results when applied on small scale MSI data without prior processing (Seddiki et al., 2020). Despite the promising results of these CNN architectures, the classification process is sensitive to a user defined, hyperparameter at the input layer that is referred to as the receptive field. The receptive field defines a convolutional kernel window in these CNN architectures to identify salient mass spectral patterns that depend on the selected size of the receptive field (Behrmann et al., 2018). Fully connected neural networks (FCNN) were applied on MSI data to perform nonlinear dimensionality reduction (Dexter et al., 2020; Inglese et al., 2017; Thomas et al., 2016), and we recently applied FCNN-based architecture to capture spatial patterns and learn underlying m/z peaks of interest from large-scale MSI data while bypassing conventional preprocessing (Abdelmoula et al., 2020).

In this work, we extend our recent deep learning development of msiPL (Abdelmoula et al., 2020) to enable tissue classification while avoiding potential bias from the user’s parameter optimization in spectral preprocessing. We propose, massNet, a scalable deep learning architecture to perform probabilistic pixel-based classification directly from mass spectral data with massive dimensionality (e.g. tens of thousands of m/z values) and without prior preprocessing such as peak picking. Unlike classical machine learning methods, massNet is capable of automatically learning predictive features from large-scale MSI data. We demonstrate our method on a MALDI 9.4 Tesla FT-ICR MSI dataset from a patient-derived xenograft (PDX) mouse brain tumor model of glioblastoma (GBM). The model stability was evaluated using 5-fold cross-validation, and the classification speed and robustness were assessed on a test set using various established machine learning metrics such as receiver operating characteristic curve (ROC), accuracy, recall, precision and F1-score. Moreover, the classification performance of massNet was benchmarked by comparison to support vector machine (SVM) a widely used classical machine learning method.

2 Materials and methods

2.1 MALDI FT-ICR MSI data

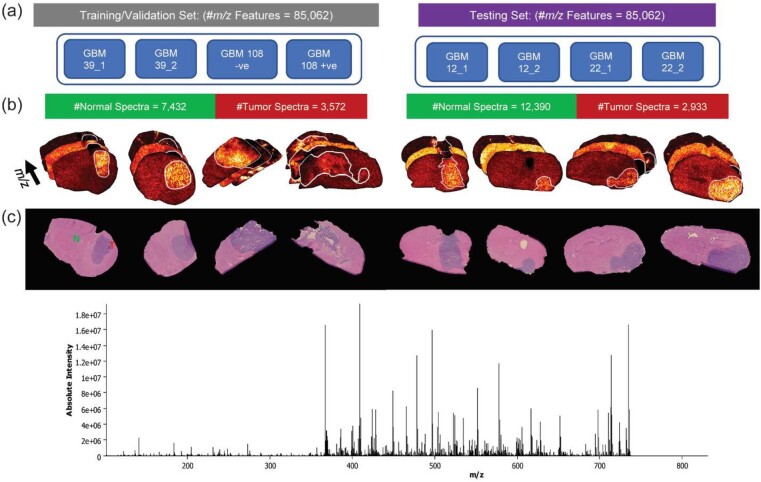
MALDI FT-ICR MSI data acquisition was performed on tissue sections from five different intracranial GBM PDX models (Fig. 1). This MSI data and acquisition process were previously published in another study from our group (Randall et al., 2020). Briefly, eight GBM tissue sections of 12-µm thickness were prepared and analyzed using a 9.4 Tesla SolariX mass spectrometer (Bruker Daltonics, Billerica, MA) in the positive ion mode with spatial resolution of 100 µm. The MSI data were exported from SCiLS lab 2020a (Bruker, Bremen, Germany) in the standardized format imzML (Race et al., 2012) and converted to the HDF5 format (Folk et al., 2011) for deep learning analysis. The data underlying this article are available in the NIH Common Fund’s National Metabolomics Data Repository (NMDR) Metabolomics Workbench (Sud et al., 2016) under project id (PR001292).

Fig. 1.

Tissue sections from five intracranial GBM PDX models were divided into training/validation and testing sets: (a) schematic distribution of tissue sections from different GBM models, (b) annotated tumor regions in the MSI datasets which were guided by the H&E annotations (c)

2.2 Microscopy imaging and tumor annotation

Five tissue sections consecutive to those used for the MSI analysis were thaw mounted onto glass slides for hematoxylin and eosin (H&E) staining. The H&E images were acquired using a Zeiss Observer Z.1 microscope equipped with 20× Plan-APOCHROMAT lens and AxioCam MR3 camera. The tumor regions in these H&E images were annotated by an expert pathologist and the annotations were manually transferred to annotate the MSI data as demonstrated in Randall et al. (2020; Fig. 1).

2.3 Deep learning architecture of massNet

The hyperspectral image from MSI encompasses a set of high-dimensional data points $X=\left\{x^{\left(1\right)},\mathrm{ }{x}^{\left(2\right)},\mathrm{ }\dots ,\mathrm{ }{x}^{\left(N\right)}\right\}$, where $N$ is the total number of spectra (or pixels) and each spectrum is a $d$-dimensional point $x^{\left(i\right)}\in R^d$ where $d$ is the total number of m/z variables. The pixel-wise annotation of the hyperspectral image is represented by a binary vector $Y=\left\{y_1,\mathrm{ }{y}_2,\mathrm{ }\dots ,\mathrm{ }{y}_N\right\}$, where $y_i\in {\left[\mathrm{0,1}\right]}^C$ is the ground truth class label of spectrum $x^{\left(i\right)}$ which belongs to one of the total two-class labels $C$ which are here normal and tumor. Our proposed massNet architecture shown in Figure 2 aims to learn a predictive function $\mathcal{F}$ that would establish the relationship between each spectrum $x^{\left(i\right)}$and its associated class label $y_i$ as depicted in

$${\widehat{y}}_i=\mathcal{F}(\mathcal{H},x^{\left(i\right)})),$$ (1)

where$\mathrm{ }{\widehat{y}}_i\in {\left[\mathrm{0,1}\right]}^C$ is a probabilistic estimate of the predicted class labels $C$ that is computed based on the optimized artificial neural network hyperparameter set $\mathcal{H}$. Class prediction of normal and tumor for a given spectrum $x^{\left(i\right)}$ can then be, respectively, represented as $P\left(N\right)\in {{\widehat{y}}_i}^{c=1}$ and $1-P\left(N\right)=\mathrm{ }P\left(T\right)\in {{\widehat{y}}_i}^{c=2}$. The massNet architecture has two main modules to optimize the hyperparameter set $\mathcal{H}$, namely the variational autoencoder (VAE) and probabilistic classification modules. The VAE module aims to learn a nonlinear manifold of the original complex MSI data through optimizing two functions: a probabilistic encoder $P_{\mathrm{\varnothing }}\left(z|x\right)$ and a probabilistic decoder $P_{\theta }\left(z\right|x)$ for data reconstruction. The learned nonlinear manifold represents a latent variable $z\in R^k;k\ll d$ which is of lower dimensions ($k$) and assumed to be sampled from a normal distribution (Coombes et al., 2005) as such $z\mathrm{ }\sim \mathrm{ }N\left({\mu }_{\mathrm{\varnothing }}\left(x\right),\mathrm{ }{\sigma }_{\mathrm{\varnothing }}\left(x\right)\right).$ The VAE parameters $\mathrm{\varnothing }$ and $\theta$ are optimized based on maximizing the variational lower bound ($\mathcal{L})$ that is given in Equation (2). For more information on VAE we refer readers to Kingma and Welling (2013)  

$$\mathcal{L}\left(\varphi ,\theta ;x^{\left(i\right)}\right)=-\mathrm{ }KL\left(q_{\varphi }\left(z|x^{\left(i\right)}\right)\parallel p_{\theta }\left(z\right)\right)+\mathrm{ }{E}_{q_{\varphi }\left(z|x^{\left(i\right)}\right)}\left[\log p_{\theta }\left(x^{\left(i\right)}|z\right)\right].$$ (2)

Fig. 2.

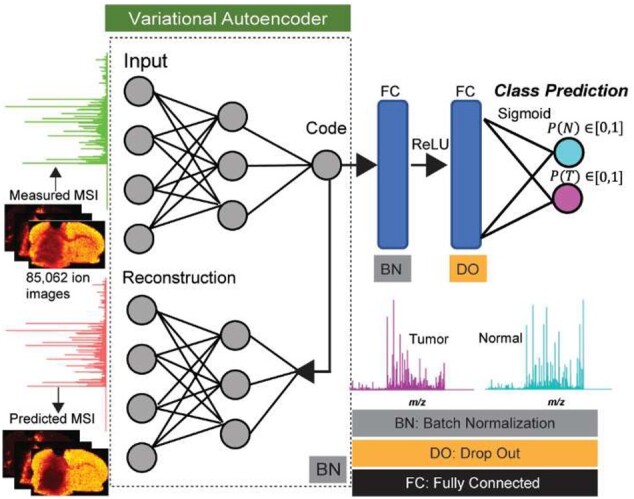
Deep learning-based architecture of massNet for probabilistic two-class classification of large-scale MSI data without prior preprocessing and peak picking. The artificial neural network is based on spectral-wise analysis and consists of two modules, namely: VAE for nonlinear manifold learning that is captured at the ‘Code’ layer, and two fully connected layers that take input from the ‘Code’ layer to yield probabilistic predictions at the output layer using the sigmoid activation. massNet is regularized based on batch normalization and drop out to maintain learning stabilization and faster optimization

The second module of massNet performs probabilistic classification, which is activated with a sigmoid function ($p\left(a\right)=1/(1+e^{-a}))$, where $a$ is an arbitrary variable at the output layer. This classifier module is parametrized by a hyperparameter $\zeta$ and consists of two fully connected hidden layers and an output layer of two classes (normal and tumor; Fig. 2). These two hidden layers are activated based on a rectified linear unit (ReLU) and take their input from the optimized latent variable ($z)$ of the VAE. The classification result is based on optimizing a loss function of the binary cross-entropy (E), shown in Equation (3), to maximize the similarity between the real and predicted class labels. Finally, the hyperparameters $\mathcal{H}$, given in Equation (1), consist of hyperparameters from these two optimized modules $\mathcal{H}=\{\mathcal{\varnothing },\zeta \}$  

$$E(y,\widehat{y})=\mathrm{ }-[y\left(\log \left(\widehat{y}\right)+\left(1-y\right)\log \left(1-\widehat{y}\right)\right].$$ (3)

2.4 Data visualization and feature localization

Uniform Manifold Approximation and Projection (UMAP) is a nonlinear dimensionality reduction method for data visualization in a single map representation in which it preserves both local and global data structures from higher dimensional space (McInnes et al., 2018). UMAP has been found promising in visualizing different types of omics data (Becht et al., 2019). The UMAP algorithm was applied on the learned $k$-dimensional latent variable ($z$) to enable data visualization in a two-dimensional space. Of note, applying the UMAP on the latent variable instead of the original hyperdimensional MSI data is a more efficient way to avoid the curse of dimensionality (Van Der Maaten et al., 2009).

The classification predictions were spatially visualized (based on the location of each corresponding mass spectra in the image space) to gain insight into the molecular interpretability of the predicted classes. This enabled the predicted class labels to be mapped back into the image space to reveal spatial patterns associated with each of the predicted classes. Image-based Pearson correlation was then applied on each of these spatial patterns and the identified peaks from the VAE module using the msiPL method (Abdelmoula et al., 2020). The highly colocalized m/z peaks are those that achieved the highest Pearson correlation coefficient ($r\ge 0.7$).

2.5 Model evaluation

The model’s learning stability was evaluated using 5-fold cross-validation on the training set (80% training and 20% validation), and the best model was finally applied and assessed on an independent test set. The classification speed and robustness were assessed on a test set using various established machine learning metrics such as ROC, accuracy, recall, precision and F1-score. Moreover, the classification performance of massNet was benchmarked by comparison to SVM a widely used classical machine learning method. The SVM was based on a linear kernel and implemented in python using the default values provided by the public machine learning library of Scikit-learn in which the regularization parameter was set to 1.

3 Results

3.1 Hyperparameters and implementation details of the massNet architecture

The massNet architecture, shown in Figure 2, consists of an input layer $\left(L_{\mathrm{in}}\right)$, five hidden layers $\left(h_1,h_{\mathrm{code}},\mathrm{ }{h}_3,\mathrm{ }{h}_4,\mathrm{ }{h}_5\right)$ and two output layers ($L_{\mathrm{out}1},\mathrm{ }{L}_{\mathrm{out}2})$. The input layer $\left(L_{\mathrm{in}}\right)$ takes its input signal from total-ion-count (TIC) normalized mass spectra. The VAE module has three hidden layers ($h_1,h_{\mathrm{code}},\mathrm{ }{h}_3$) and an output layer ($L_{\mathrm{out}1})$. The lower dimensional latent variable ($z)$ is captured at the Code layer ($h_{\mathrm{code}})$, which is then used by the generative model for spectral data reconstruction at the output layer ($L_{\mathrm{out}1}$). The Code layer ($h_{\mathrm{code}})$ also provides an input to the classification module which has two fully connected hidden layers ($h_4,\mathrm{ }{h}_5)$ and eventually yields a probabilistic estimate of class prediction at the output layer ($L_{\mathrm{out}2})$. The layer size of each $L_{\mathrm{in}}$ and $L_{\mathrm{out}1}$ is equivalent to the number of m/z variables, whereas the size of $L_{\mathrm{out}2}$ is equivalent to the number of class labels. The size of hidden layers is a user tunable parameter, and it was empirically set as $\left(h_1=512,{\mathrm{ }h}_{\mathrm{code}}=5,\mathrm{ }{\mathrm{ }h}_3=512,\mathrm{ }{h}_4=128,\mathrm{ }{h}_5=128\right)$ in which the VAE parameter settings were adopted from our former msiPL method (Abdelmoula et al., 2020). The ReLU was used as an activation function for all layers except for the two output layers ($L_{\mathrm{out}1},\mathrm{ }{L}_{\mathrm{out}2})$ which were activated using the sigmoid function. The proposed neural network architecture was regularized using batch normalization and dropout to stabilize the learning process, fasten the convergence and significantly reduce overfitting (Ioffe and Szegedy, 2015; Srivastava et al., 2014). A 20% dropout was added to the two hidden layers of the classification module. The cost function was optimized based on minibatch processing (batch size = 100) using the adaptive stochastic gradient descent method of Adam optimization (with default learning rate = 0.001) and the total number of epochs for VAE and classification modules were, respectively, 100 and 30. The architecture was implemented in python using the publicly available deep learning platforms of Keras (Chollet, 2017) and TensorFlow (Abadi et al., 2016), and it was trained on a PC workstation (Windows 10, Intel Xenon 3.3 GHz, 64-bit Windows and NVIDIA TITAN XP Graphics Card).

3.2 UMAP visualization of the VAE latent variable reveals separation between normal and tumor spectra

The deep learning model was optimized on a training set acquired by MALDI FT-ICR MSI from three different intracranial GBM PDX models, as demonstrated in the left column of Figure 1. This training set encompasses mass spectra with 85 062 m/z variables that were collected from two different classes of normal and tumor tissue types with total number of spectra 7432 and 3572, respectively. The VAE model optimization revealed stable convergence distribution in 100 epochs with random shuffling of data batches (Supplementary Fig. S1) and a total running time of 42.77 min. The optimized model captured the latent variable ($z)$ of five-dimensions at the Code layer (Supplementary Fig. S2) which was then used to efficiently reconstruct the original TIC-normalized MSI data with a total mean squared error (MSE) of $5.31\times {10}^{-5}$ (Fig. 3a). The UMAP visualization of the latent variable in two-dimensional space revealed separation of mass spectra from normal and tumor tissues as shown in Figure 3b. The UMAP features were also colored based on different GBM models to reveal intertumor heterogeneity and visualizing the learning efficiency in capturing similarities based on the molecular phenotype and assess potential batch effect (Fig. 3b).

Fig. 3.

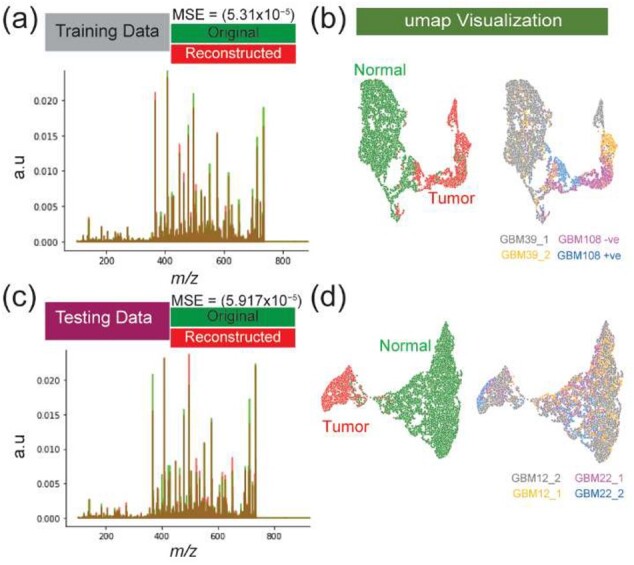
Performance of the VAE module and nonlinear data visualization: overlay of the TIC-normalized average spectrum of original and reconstructed data for both training (a) and testing (b) datasets. UMAP visualization of the five-dimensional latent variable captured by the VAE model reveals distinction between normal and tumor mass spectra from different GBM models for both training (b) and testing (d) dataset

3.3 Pretrained VAE enables optimization of the classification module

The pretrained and optimized VAE provides input to the classifier module through the latent variable that was captured at the Code layer ($h_{\mathrm{code}})$. The classification module was optimized in 30 epochs which also included random shuffling of data batches and the total running time of 4.5 min. To avoid potential overfitting and provide unbiased estimate of out-of-sample error (i.e. on test data), the model was evaluated using 5-fold cross-validation. For each of the cross-validation folds, the entire training dataset (shown in Fig. 1a and b) was randomly divided into 80% training and 20% validation. The robustness and evaluation of the different cross-validation models are shown in Supplementary Table S1, in which the best model with maximum accuracy and minimum loss values was eventually selected to be further independently evaluated on the withheld test set. The best model was benchmarked by comparison to SVM where both models showed comparable performance but massNet was faster (Table 1). Of note, the total running time shown in Table 1 for optimizing the overall massNet model included the running time for both the VAE and the classification modules.

Table 1.

Classification performance during both training and testing phases on MALDI FT-ICR MSI dataset without peak picking

Phase	Class	Spectra #	Precision (%)	Recall (%)	F1-score (%)	Accuracy (%)	Time (min)
Training phase: massNet	Normal	7432	100	100	100	100	47.27
	Tumor	3572	100	100	100
Training phase: SVM	Normal	7432	94	98	96	94	97.95
	Tumor	3572	95	87	91
Test phase: massNet	Normal	12 390	100	97	98	97.6	0.59
	Tumor	2933	90	98	94
Test phase: SVM	Normal	12 390	100	96	98	96.14	117.14
	Tumor	2933	84	98	91

3.4 Rapid and efficient classification performance on MALDI MSI test set of large dimensions

The optimized massNet model was evaluated on the withheld test set of MALDI FT-ICR MSI data from four tissues from two different intracranial GBM PDX models as demonstrated in the right column of Figure 1. This test set encompasses mass spectra with 85 062 m/z variables that were collected from two different classes of normal and tumor tissue types with total number of spectra 12 390 and 2933, respectively. The optimized VAE module took 61.8 s to analyze the entire test set as such the latent variable was captured (Supplementary Fig. S3) and the original TIC-normalized MSI test data were reconstructed with an overall MSE of $5.917\times {10}^{-5}$ (Fig. 3c). The UMAP visualization of the five-dimensional latent variable revealed separation between molecularly distinct phenotypes of normal and tumor tissues, as shown in Figure 3d.

The optimized massNet took about 35.34 s to provide spectral-wise probabilistic prediction of the entire test set. The robustness of this ultrafast classification (compared to SVM, Table 1) is supported by ROC analysis (AUC values for normal and tumor classes were 99.54% and 99.55%, respectively) and the confusion matrix which revealed true negative and true positive values of 97% and 98% respectively, as demonstrated in Figure 4. This classification performance was further benchmarked by comparison to an SVM classifier using different machine learning evaluation metrics shown in Table 1. Of note, both the massNet and SVM models were first optimized on the training set and then applied on this test set. The overall performance of massNet was slightly higher than SVM with respective accuracy of 96.8% and 95.26%, but more significantly, the massNet was substantially faster than SVM as shown in Table 1. Here, the slow running time of SVM was mainly due to the massive dimensionality of MSI data and the computational complexity of SVM is at least quadratic $O(n_{\mathrm{features}}\times m_{\mathrm{samples}}^2)$ during either training or prediction stages (Chang and Lin, 2011).

Fig. 4.

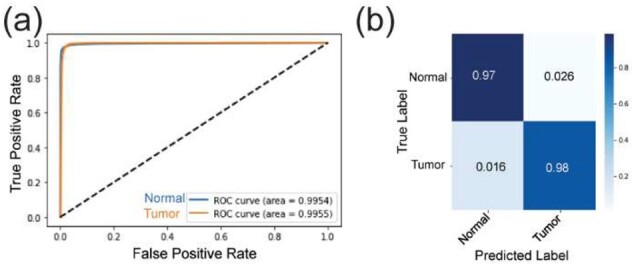
Classification performance on the MALDI FT-ICR MSI test set: (a) ROC curve distribution for both normal (blue) and tumor (orange) classes with an AUC of 99.54% and 99.55%, respectively. (b) Confusion matrix showing the prediction performance compared to the ground truth labels

3.5 Spatial mapping of predicted scores reveals uncertainty at the tumor margin

The probabilistic scores of the predicted class labels were spatially mapped to enable their visualization in the image space (Fig. 5a and b). Despite the massNet model being quite accurate in predicting the true class labels in most of the tissue regions, it showed a higher level of uncertainty at the tumor margin (Fig. 5c). This could reflect that the tumor margin has a convoluted molecular signature likely resulting from mixtures of normal and tumor cells compared to either the tumor core or normal tissue types, therefore representing an infiltrative edge. This observation is in accordance with other studies that studied mass spectral signatures from tumor margins (Calligaris et al., 2014). Identification of m/z peaks that are highly correlated with each of the predicted class labels were determined through the Pearson correlation coefficient. This coefficient was computed by correlating each of the predicted spatial maps with each of the 716 m/z values that were identified by msiPL. A list of top correlated m/z values correlated with the tumor region were identified and presented in Table 2, whereas the highest correlated values for normal tissue are shown in Supplementary Table S2. One of the highest correlated peak with the tumor class was at m/z $480.9211\pm 0.01$ which is elevated in the tumor region (Fig. 5e). The automated nonlinear image registration method (Abdelmoula et al., 2014) was applied to nonlinearly warp this ion image and fuse it with an image of the H&E stained tissue section (Fig. 5d and e). This multimodal integration can provide a reference system for pathologists to further study and gain more insight about the tissue that can go beyond tissue anatomy (Caprioli, 2019).

Fig. 5.

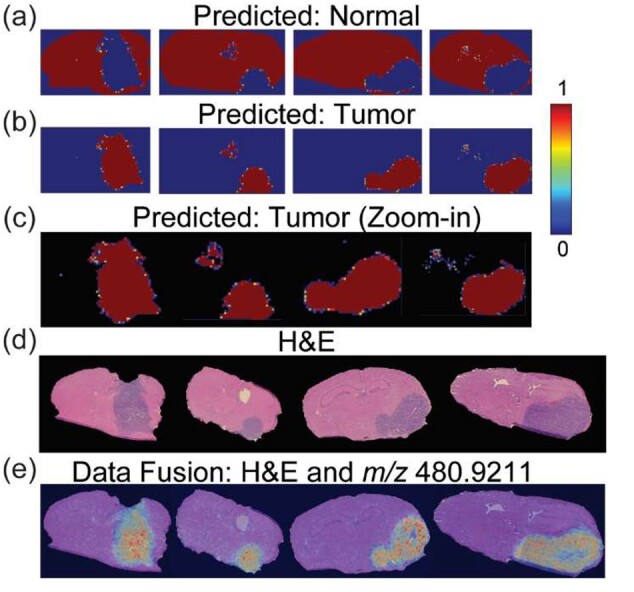
Spatial mapping of the classification predictions and multimodal integration: spatial distribution of the spectral-wise probabilistic predictions for normal (a) and tumor (b) classes. (c) Closeup visualization of the spatially mapped tumor prediction scores reveals a higher level of uncertainty at the interface between normal and tumor (i.e. tumor margins). (d) The H&E microscopy images show tumor regions in different GBM models (columns). (e) Multimodal integration of the H&E images and ion image at m/z 480.9211 ± 0.01 which is highly correlated and elevated in the tumor region

Table 2.

A list top correlated m/z values with the tumor tissue

m/z	Correlation	Tentative assignment	Molecular formula	Adduct	m/z calculated	Database	Error (ppm)
450.29788	0.894
468.3084	0.845
480.9211	0.841	Uridine diphosphate (UDP)	C9H14N2O12P2	[M + 2K − H]+		HMDB	−0.21
730.537	0.824
428.3732	0.8	Stearoylcarnitine	C25H49NO4	[M + H]+		HMDB	0.47
518.8773	0.79
400.9546	0.7807	Uridine monophosphate (UMP)	C9H13N2O9P	[M + 2K − H]+	400.9554553	HMDB	−2.1
545.9591	0.775	Adenosine triphosphate (ATP)	C10H16N5O13P3	[M + K]+	545.9589	Metlin	0.36
703.57416	0.7235	SM (34:1)/PE-Cer (37d/1)	C39H79N2O6P	[M + H]+	703.5749	Metlin	−1.05
583.91437	0.717	Adenosine triphosphate (ATP)	C10H16N5O13P3	[M + 2K − H]+	583.9148	HMDB	−0.74

4 Discussion

We presented massNet, a fully connected deep learning architecture for spectral-wise classification of large-scale MSI data without prior preprocessing and peak picking. The massNet architecture consists of two main modules, namely: VAE and classification modules. The VAE module learns a lower dimensional latent variable that was used to reconstruct the original MSI data and assess the learning quality of the VAE module. That optimized latent variable provides an input to the classification modules which was activated at the output layer using a sigmoid function to provide a probabilistic estimate of the predicted class membership. Unlike other architectures for MSI data classification, massNet is based on a fully connected artificial neural network and does not rely on optimizing a receptive field parameter, which is inherently associated with convolutional artificial neural networks and has an impact on the learning process (Behrmann et al., 2018; Guo et al., 2020; van Kersbergen et al., 2019). The optimized model showed high accuracy and ultrafast performance (<1 min) on the full MSI test data that encompassed a total of 15 323 mass spectra with 85 062 m/z variables. When compared for analysis of the same test dataset, the trained massNet model achieved higher accuracy and was substantially faster than a trained SVM model that took about 117.14 min to provide prediction during the testing phase (Table 1).

The performance of massNet methods was also benchmarked on preprocessed MALDI FT-ICR MSI GBM data after peak picking in SCiLS lab 2020a (Bruker, Bremen). The peak picking algorithm is based on the orthogonal matching pursuit (OMP) algorithm which has a quadratic computational complexity (Alexandrov et al., 2010). The peak picking analysis took 2 h and 58 min on the same workstation (Windows 10, Intel Xenon 3.3 GHz, 64-bit Windows and NVIDIA TITAN XP Graphics Card) and resulted in a reduction of the feature space from 85 062 to 243 dimensions. The overall training time of the massNet model on the preprocessed data was faster (Supplementary Table S3) compared to the analysis of MSI data without preprocessing (Table 1). The massNet training convergence distribution is shown in Supplementary Figure S4a, and the optimized model captured latent variables that revealed structural information (Supplementary Fig. S4b). The two-dimensional UMAP visualization of these latent variables is given in Supplementary Figure S4c and d and shows separation between normal and tumor. The trained model was then applied on the unseen and peak picked test set, and classification performance shows higher AUC scores for both normal and tumor classes, respectively (Supplementary Fig. S5). These results are in agreement with the MSI analysis without classical preprocessing (Figs 3 and 4). While the model training was faster on preprocessed data for both massNet and SVM (Table 1 and Supplementary Table S3), the peak picking step is more computationally expensive and sensitive to parameter settings that can impact downstream analysis and biological interpretation (Murta et al., 2021).

While the proposed model showed promising results for binary class classification, the model could be extended in future development to enable multiclass classification. We envision a slight change in the massNet architecture mainly at the output layer ${(L}_{\mathrm{out}2})$ in which its size will be defined based on the new number of class labels and it must be activated using a different function such as softmax. The ground truth annotations could be defined using microscopy images and then mapped into the MSI space using image registration (Heijs et al., 2015). Depending on the application and tissue types, different stainings could be investigated to provide increased structural annotations compared to the most common H&E staining. MSI and microscopy imaging are complementary modalities and annotating the MSI data based solely on annotated histology is an approximation approach which might not be optimal especially in case of intratumor heterogeneity (Balluff et al., 2015). This is mainly because the MSI data could reveal molecular intratumor heterogeneity that is not yet observed in the microscopic image (Jones et al., 2012; Randall et al., 2020).

The proposed model was applied to the analysis of MALDI FT-ICR MSI data here but the massNet architecture is independent of the mass spectral ionization nature and could be applied to the analysis of MSI data from different platforms with distinct ionization and mass analyzer technologies. The massNet architecture could also be applied to the classification of different tissues and tumor types where the challenging task becomes the establishment of ground truth annotation of the MSI data. For instance, the massNet revealed a higher level of uncertainty around tumor margins in the binary classification task as shown in Figure 5b and c. This could reflect distinct molecular signatures in the tumor margin area compared to either the tumor core or normal tissue types. Tumor margins could therefore either be treated as an independent class or deconvoluted to extract signal from tumor and normal cells; however, the ground truth annotation is a challenging task that would require more pathological investigation and could be enhanced by integrating with multiplexed immunofluorescence to clearly delineate cell types from the tumor and microenvironment.

Funding

This work was supported by the NIH Grants U54-CA210180 (N.Y.R.A.), P41-EB028741 (N.Y.R.A.) and T32EB025823 (S.A.S.).

Conflict of Interest: In compliance with Harvard Medical School and Partners Healthcare guidelines on potential conflict of interest, we disclose that N.Y.R.A. is a scientific advisor to BayesianDX and inviCRO.

Data availability

Additional data are available from the corresponding author on reasonable request.