Automatic detection of pneumonia in chest X-ray images using textural features

Abstract

Fast and accurate diagnosis is critical for the triage and management of pneumonia, particularly in the current scenario of a COVID-19 pandemic, where this pathology is a major symptom of the infection. With the objective of providing tools for that purpose, this study assesses the potential of three textural image characterisation methods: radiomics, fractal dimension and the recently developed superpixel-based histon, as biomarkers to be used for training Artificial Intelligence (AI) models in order to detect pneumonia in chest X-ray images. Models generated from three different AI algorithms have been studied: K-Nearest Neighbors, Support Vector Machine and Random Forest. Two open-access image datasets were used in this study. In the first one, a dataset composed of paediatric chest X-ray, the best performing generated models achieved an 83.3% accuracy with 89% sensitivity for radiomics, 89.9% accuracy with 93.6% sensitivity for fractal dimension and 91.3% accuracy with 90.5% sensitivity for superpixels based histon. Second, a dataset derived from an image repository developed primarily as a tool for studying COVID-19 was used. For this dataset, the best performing generated models resulted in a 95.3% accuracy with 99.2% sensitivity for radiomics, 99% accuracy with 100% sensitivity for fractal dimension and 99% accuracy with 98.6% sensitivity for superpixel-based histons. The results confirm the validity of the tested methods as reliable and easy-to-implement automatic diagnostic tools for pneumonia.

1. Introduction

Pneumonia is an acute respiratory infection caused by viruses or bacteria. Although it affects people of all ages and is typically a mild disease, it is one of the leading infectious causes of death among vulnerable groups, such as the elderly and children. Thus, in 2017, this disease was associated to the deaths of over 808,000 children under the age of five, worldwide, accounting for 15% of all deaths in the mentioned age group [1]. This is particularly prominent in developing countries, where poor sanitary conditions, lack of medical and radiological personnel and air pollution make the country's population particularly vulnerable to this condition [2,3]. Early detection and treatment of pneumonia is essential [4]. Unfortunately, the time available for physicians to perform this analysis is limited. The situationhas been exacerbated by the conditions imposed by the recent COVID-19 pandemic. Therefore, the development of tools to support the diagnosis of pneumonia, particularly when based on a common imaging modality such as X-rays, represents a vital and interesting opportunity for the application of artificial intelligence (AI) techniques.

Given the relevance of the problem, a wide range of research related to the automatic detection of pneumonia in X-ray images has been developed; the widespread adoption of convolutional neural network (CNN)-based deep learning algorithms in image analysis indicates that most of the recent developments in detection of pneumonia in X-ray images rely on different approaches to this concept, with remarkable results. Examples of CNNs developed specifically for pneumonia detection were presented in Refs. [[5], [6], [7]]. Models derived from the DenseNet-121 architecture [8] form the foundation for the studies presented in Refs. [9,10]; an ensemble of multiple models based on transfer learning is used in Ref. [11] for the detection of pneumonia in X-ray images. Notably, the studies conducted on pneumonia detection developed as a result of the recent COVID-19 pandemic, also generally focused on CNN models. During the early stages of the pandemic, these studies focused on the implementation of models optimized for use with small databases, owing to the limited availability of training images, for example, in Ref. [12] or [13]. Over time, the implementation derived to more general CNNs, such as those in Ref. [14] or [15].

Although CNN-based deep learning algorithms currently represent the most common line of research in the automatic detection of pneumonia in X-ray images, other methods, typically based on machine learning algorithms combined with handcrafted textural features, have been part of numerous related studies, as they present certain advantages as a tool for image analysis. Textural characterisation covers a heterogeneous set of techniques based on the parameterisation of changes in textural patterns associated with potential pathologies present in different medical modalities. Textural image characterisation offers good performance with very low computational complexity, and typically does not require large training datasets [16]; moreover, as it is based on well-known methods, its implementation is fairly straightforward.

Different texture-based analysis techniques have been widely used in X-ray analysis for the detection of pneumonia. In Ref. [17], a study on interstitial pneumonia, the images were represented by second-order textural attributes derived from co-occurrence and run length matrices. Two studies aimed at diagnosing childhood pneumonia using radiological images [18,19], compared the performance of different machine learning algorithms using a heterogeneous set of simple first- and second-order textural features. In Ref. [20], a set of textural attributes similar to those used in Refs. [18,19] was used in combination with different dimensionality reduction techniques. Haar wavelets have been used to describe images for pneumonia detection has been used both in Ref. [21] and in the development of the Pneumo-CAD system [21]. There is a wide range of related research, and image texture characterisation is an open, rapidly progressing field. Recent developments [22], as well as results obtained in studies with classical but barely explored methods in the field of automatic pneumonia detection in X-ray images, such as Ref. [23] and Ref. [24], provide new opportunities for simple and robust pneumonia detection methods that are easy to implement and adapt to specific cases.

Therefore, in the context of a COVID-19 pandemic, wherein the major symptom of the infection is pneumonia, we further explored the possibilities provided by the textural characterisation of chest X-ray images aimed at the detection of this disease, to improve prognostic predictions for triage and patient care management. For this purpose, three substantially different methods of texture characterisation were selected: radiomics, fractal dimension, and superpixel-based histon. Fractal dimension represents a well-known descriptor, that has been used in many medical image classification work (see Ref. [25]). Superpixel-based histon is a novel image descriptor based on the image segmentation study proposed in Ref. [26], developed in its current form as an imaging biomarker in Ref. [27]. Finally, we will evaluate the use of a set of classic image descriptors grouped under the general term of radiomics [28]. Because there are multiple prior studies where this set of descriptors were used in a complete or partial manner for pneumonia detection in X-ray images [29] (although not in the specific configuration proposed in this study), this study will serve both as a reference and an assessment of previous studies.

The main contributions of this study are as follows: (a) a comparative analytical study of three different textural feature extraction techniques, radiomics, fractal dimension, and superpixel-based histon, for detection of pneumonia in chest X-rays, and (b) as part of the study, the influence of multiple factors on the performance of the generated models was examined. Thus, the results achieved with different machine learning techniques are compared, and the impact of hyperparameter optimisation on the different generated models is tested. Where possible, the differences in the results achieved with unbalanced training sets and SMOTE-balanced [30] training sets were examined. The performance of the generated machine learning models was evaluated using models generated from two X-ray image datasets, one composed of paediatric images and the other derived from an image repository developed primarily as a tool for the study of COVID-19.

The rest of the paper is organised as follows: Section 2 briefly reviews the textural characterisation methods used in this study: radiomics, fractal dimension, and superpixel-based histon. In Section 3, we provide a description of the datasets employed, the image preprocessing process, and specific implementation details associated with the experimental setup. The experimental results are presented in Section 4. Section 5 discusses the results achieved, the limitations of this study and the possible future work related to the tested characterizations method. Finally, Section 6 concludes this study.

2. Background

This section briefly presents the image characterisation methods used in this study.

2.1. Radiomics

In the field of precision medicine, radiomics studies the associations between qualitative and quantitative information extracted from clinical images and data [28]. Grouped under the general term “radiomics” is a set of classical image descriptors. Radiomics takes advantage of advances in AI, to use them as an aggregate for image characterisation. The concept behind the radiomic approach is the assumption that the parameters that define tissue, genomic and proteomic patterns and even underlying pathologies can be reflected in the different forms of quantitative/qualitative information contained in a clinical macroscopic image. The features on which radiomics is based do not represent original or innovative descriptors [31]. This indicates that the main innovation of radiomics lies in the simultaneous use of numerous parameters derived from a single lesion. This combination of parameters is expected to be able to express tissue properties relevant to the diagnosis and treatment of individual patients. The concept of radiomics is applicable to all modalities of medical imaging, both two- and three-dimensional.

Different types of features, which express different properties of the image, can be derived from clinical Images. The features employed in radiomics are usually classified into the following subgroups:

• ●Shape features describe the shape of the defined region of interest (ROI) and its geometric properties, such as area, maximum diameter along different orthogonal directions, and region compactness.
• ●First-order statistical features describe the distribution of individual pixel values without considering spatial relationships. These properties are based on the intensity values present in the image and encompass the well-known statistics such as mean, median, maximum, minimum, and kurtosis.
• ●Second-order statistical features are obtained by calculating the statistical interrelationships between the neighbouring pixels or voxels. They measure the spatial arrangement of the pixel/voxel intensities and, therefore the heterogeneity of the image. Depending on how we define the spatial relationships between elements, the second-order statistical features can be extracted from the grey-level co-occurrence matrix (GLCM), grey-level run length matrix (GLRLM), grey-level size zone matrix (GLSZM) and/or neighbourhood grey tone difference matrix (NGTDM).
• ●Higher-order statistical features are derived by statistical methods after applying filters or mathematical transformations, including Minkowski functions, waveform transformation and Laplacian image transformations using Gaussian filters.

Although radiomics has emerged as part of the domain of oncology [28], which has led to a significant number of studies focusing on different types of cancer, such as brain [32], breast [33] or lung cancer [34], the versatility of this approach has made it possible to use it in other areas of medicine, such as neurology [35] or pneumonology [36]. The popularity of radiomics in the field of medical image analysis has led to the development of multiple studies in which this set of descriptors is used in a complete or partial manner for pneumonia detection in X-ray images [29,37].

2.2. Fractal dimension

Fractal dimension [38] represents a widely used textural descriptor that measures the complexity of an irregular contour. The fractal dimension of an image increases as it becomes increasingly complex. This allows the detection of the presence of noise, spots, or unusual structures in a set of images.

The concept of fractal dimension defines a measure of statistical complexity, which estimates the evolution of the details of a pattern (strictly speaking, a fractal pattern) in relation to the scale on which it is measured. Fractal dimension provides a tool for describing complex patterns. Within these complex patterns it is possible to define the concept of self- similarity, which indicates that even after enlarging an object in detail with a variable scale, each individual portion is similar to the whole. This measurement of the fractal geometry has been proven to be capable of quantifying irregular patterns, as irregular lines, crumpled faces, and intricate shapes, and estimates the ruggedness of systems [38].

There are multiple definitions of self-similarity, each of which fits best in a particular situation. These methods can be classified into three main categories [39]: box-counting, variance-based, and spectral methods. In particular, the box-counting method is the most widely used computational tool for the calculation of fractal dimensions in complex systems [40] because it is easy to implement and can be used with any type of image regardless of its complexity.

In terms of box-counting, the fractal dimension is commonly referred to as the Minkowski–Bouligand or Kolmogorov dimension. Box-counting approaches the concept of self-similarity by minimising the number of components n, “box”, of edge length r required to cover all the components present in a set. The size of the box is then reduced to determine the dependence of n on length r, that is, n(r). The box-counting approach defines the fractal dimension as ${\lim }_{s\to 0}\log (\frac{n(r)}{\log 1/r})$, generally estimated as the slope of log(n) versus log(1/r). Fractal dimension is a very popular approach in medical imaging characterisation; most biological structures show geometrically complex structural properties; therefore, it is difficult to characterise them using only metrics based on Euclidean geometry. Although these structures cannot be considered true geometric fractals because their property of self-similarity does not extend to infinity, it is possible to define it, to a certain degree, where the concept of repetition is limited to a biologically relevant spatial scale window [41]. The use of fractal dimension for X-ray image analysis has focused on the study of bone tissue [42,43], but examples of its use can be observed in a wide variety of clinical settings such as brain structures analysis [44] or vascular patterns studies [45]. However, the application of the fractal dimension for pneumonia detection in X-ray image has seldom been explored [46].

2.3. Superpixels based histon

Superpixel-based histon is a novel image descriptor based on the image segmentation study proposed in Ref. [26]. It has been developed in its current form as imaging biomarker in Ref. [27]. A histon [47] describes the local relationships of intensity levels in an image, acting as an extension of the histogram concept.

A histon is defined by a similar colour sphere, known as a similarity threshold or expanse, E, and spatial distance measurement $d_t\left(x,y\right)$ that defines which pixels should be inserted into each bin of a histogram. To generate a histon, the number of points encapsulated in an expanse of each intensity category g in the base histogram is added to that category in the histogram. For an image I(x, y, s) of size M × N, where S _p represents the set of colour channels of the image, a histon $H_{s_i}$ for each colour channel s _i can be expressed as follows:

$$\begin{array}{cc}{H}_{s_i}=& \sum _{x=1}^N\sum _{y=1}^M\left(1+S\left(x,y\right)\right)\delta \left(I\left(x,y,s_i\right)-g\right)\\ & \text{for }0\le g\le L-1\text{and}{s}_i\in S_p\end{array}$$ (1)

where, for each of the spectral components, L represents the number of intensity levels, $\delta \left(\cdot \right)$ represents the Kronecker delta, and $S\left(x,y\right)$ represents a similarity function that tests whether or not an element of the neighbourhood is part of the expanse. Typically, the neighbourhood of a pixel is defined by a pre-determined sized sliding window. However, in Ref. [22], the use of superpixel segmentation as a neighbourhood was proposed to generate a set of spatial components that guarantee a direct relationship between a pixel and its neighbourhood.

A superpixel can be defined as a perceptually uniform region in an image (see Ref. [48]). A superpixel segmentation represents a tool for local-scale estimation of features in an image, as it results in a set of small spectrally restricted areas, an image over-segmentation. Calculating histons using a superpixel segmentation as a neighbourhood enables establishing a direct association between the expanse and the pixel whose membership is tested, because a superpixel over-segmentation conforms to the boundaries and features present in the image. In addition, it is possible to quantify the overall local homogeneity of an image using the standard deviation of the mean intensity of the space defined by the superpixel set because a superpixel segmentation already produces locally homogeneous areas. Thus, the expanse concept can be redefined dynamically.

Let us denote the set of superpixels resulting from an image segmentation as Cs = {Cs ₁, Cs ₂, …, Cs _Ns}, whereNs represents the total number of superpixels and $I(x_{C{s}_j},y_{C{s}_j},s_i)$ represents the centroid of the superpixel Cs _j in colour channel s _i ∈ S _p; the similarity function $S\left(x,y\right)$ is defined as follows:

$$S\left(x,y\right)=\left\{\begin{array}{ll}1& \text{if }\forall s_i\in S_p{d}_{t{s}_i}\left(x,y\right)<E_{s_i}\\ 0& \text{otherwise }\end{array}\right)$$ (2)

$$\begin{array}{cc}{d}_{t{s}_i}\left(x,y\right)=& \left|I(x,y,s_i)-I(x_{C{s}_j},y_{C{s}_j},s_i)\right|\\ & I(x,y,s_i)\in C{s}_j\end{array}$$ (3)

$$E_{s_i}=\frac{1}{Ns}\sum _{j=1}^{Ns}\frac{1}{N{p}_j}\sum _{I\in C{s}_j}I(x,y,s_i)$$ (4)

A histon takes advantage of the correlation between neighbouring pixels, both in the same and in other spectral planes, for image characterisation. Compared to other texture features, a histon is particularly sensitive to subtle variations in intensity in the spatial distribution of the image [49], such as those associated with changes in opacity or size of the structures present in an image.

3. Materials and methods

In this section, the datasets selected to test the effectiveness of the proposed features are presented, as well as the preprocessing of the images prior to the classification model generation. A description of the setup of the experiments conducted and the validation criteria used to evaluate them are also included.

3.1. Datasets

Two different datasets are used in this study. The first (referred to as GWCMCx) is compiled by the Guangzhou Women and Children Medical Center (Guangzhou, China) as part of the routine clinical care of paediatric patients [50]. The latest version of this dataset is composed of 5856 X-rays images. It was divided into a training set consisting of 3883 X-rays corresponding to cases of pneumonia and 1349 X-rays without detected pathologies, and a test set with 234 images labelled as pneumonia and 390 without detected pathologies.

The second dataset (referred to as Josep-NIH) combines images from two datasets: the COVID-19 collection [51] and the National Institutes of Health Clinical Center (NIH) dataset [52]. The COVID-19 collection is an open-source collection, made available and maintained by Dr. Joseph Paul Cohen. This repository contains images of different medical modalities collected from multiple public sources, all of which have a diagnosis of pneumonia, mainly a result of COVID-19 infection. At the time of preparing this study, the COVID-19 collection contained, among other images, a total of 728 CXRs, which constitute the set of pneumonia-positive images in our second dataset. Although the COVID-19 collection is regularly maintained and updated, it does not contain images with a negative pneumonia diagnosis. For this purpose, a set of images from the NIH dataset was selected. This dataset consists of 112.120 X-ray images labelled with different diseases, from 30.805 unique patients. From this group, 728 CXRs with no detected pathologies were randomly selected, under the criterion of minimizing, as far as possible, the differences in gender and age compared to the group of cases with pneumonia, with the purpose of limiting the biases that these differences could cause. Together with the CXRs with pneumonia, the Josep-NIH produces a total of 1456 images. These images were randomly divided into training and test set of 1156 and 300 images, respectively, with non-pathological and pneumonia cases balanced in both sets. It should be noted that at least some of the images in the COVID-19 collection are likely to correspond to examples that have been released because they are medically relevant images or correspond to very representative examples, which would indicate a degree of selection bias in the Josep-NIH dataset.

Considering the differences in both the demographics of the subjects covered and overall appearance and quality of the images, separate models were trained for the GWCMCx and Josep-NIH datasets.

This study used images from open-access public databases; we were not responsible for collecting patient informed consent, and therefore, no ethics committee approval was required. For further information, please refer to the original sources. These datasets were provided pre-processed from their original sources, clinical image headers and metadata were removed for anonymisation. Images were converted to either the joint photographic experts group (JPEG) or portable network graphics (PNG).

Examples from both datasets are shown in Fig. 1 . A summary of the demographic characteristics of the datasets used is presented in Table 1 . Files with the names and metadata of the images used to assemble this dataset are provided as supplementary materials.

Fig. 1.

X-ray image samples from both datasets. (a) and (b) correspond to pneumonia cases from the Josep-NIH dataset, (c) and (d) are pneumonia cases from the GWCMCx dataset, (e) and (f) correspond to non-pneumonia cases from the Josep-NIH dataset, and (g) and (h) are non-pneumonia cases corresponding to the GWCMCx.

Table 1.

Datasets demographic information. Age ranges, mean and standard deviation (±) is presented (where this information is available). No age information is reported for 223 pneumonia cases in the Josep-NIH database; thus, in this dataset those values are approximate.

	GWCMCx
Pneumonia	Normal
N. Samples	4273	1583
Age	1–5	1–5
Gender	No data	No data
Diagnosis	Bacterial: 2538 Viral: 1345	No findings
	Josep-NIH
Pneumonia	Normal
N. Samples	728	728
Age	20-94 (55.3 ± 16.7)	20-88 (54.6 ± 15.8)
Gender	Male: 421 Female: 245	Male: 456 Female: 272 No Data: 62
Diagnosis	Bacterial: 45 Fungal: 26 Viral/Covid: 457 Viral/Other: 37 No Data: 163	No findings

3.2. Image preprocessing

Image preprocessing techniques are useful for improving the quality of an image and/or to reveal more relevant information on the targeted object. The preprocessing steps in this study included intensity normalization, masking of obvious non-lung areas and image texture enhancement. This study is conducted on 8-bit grey-scale images (255 intensity levels). The images are converted to this format when necessary. As a first preprocessing step, the histogram of the radiological images are equalized to adapt the set of intensity levels of each image to a reference histogram, defined as the average histogram of the images included in the corresponding training sets. Subsequently, a simple masking process is applied to limit the presence of parts of the image not relevant to this study. This process includes removing the background of the image (identified as regions of intensity equal to zero in contact with the image edges), magnifying the contrast differences between brighter and darker regions using a balance contrast enhancement technique (BCET) [53], and adjusting the mean of the output image to an intensity of 60. The areas corresponding to bone and higher density tissue (defined as the pixels on the top 25% percentile of the image intensity) are then masked.

Finally, to emphasize the textural information available in the ROI, contrast-limited adaptive histogram equalisation (CLAHE) was used [54]. This algorithm enhances the contrast of the input image operating on the local histogram information of the image, dividing the entire image into small nonoverlapping cells (in this study, 16 cells in a 4x4 grid). Therefore, it is suitable for improving the local contrast and enhancing the definitions of edges and details in each region of the image. The individual steps of the preprocessing pipeline are shown in Fig. 2 .

Fig. 2.

Image examples of the different steps in the pre-processing pipeline. (a) is the original X-ray, (b) is the histogram equalised image, (c) is the balance contrast enhancement technique filtered image, (d) is the generated mask, and (e) corresponds to the original image masked and processed using contrast-limited adaptive histogram equalisation.

3.3. Image characterization

In this study, three textural feature extraction methods were evaluated: radiomics, fractal dimension, and superpixel-based histon.

For fractal dimension computation, the method proposed in Ref. [55] is used. This method calculates the fractal distance of the binary images. These binary images are generated by applying different thresholds to the image under analysis (in this implementation, 3 different binary images are generated using the well-known Otsu thresholding method). Thus, it is possible to compose a textural signature of the image from the changes in image complexity, as the threshold used for binarisation varies. This method is based on a simple box-counting implementation [56], where the fractal dimension FD is the slope of the relation between the size r used in a grid of squares overlaying an image C, and the number of squares, N(r), where the box sizes r are powers of two P being the smallest integer that satisfies max(size(C)) < = 2^P, necessary to cover the binary blobs contained in C, or.

$$FD=\underset{r\to 0}{\lim }\frac{\log \left(N\left(r\right)\right)}{\log \left(r\right)}r=1,2,4\dots 2^P$$ (5)

If the size of C in each dimension is lower than 2^P, C is padded with zeros in each dimension up to 2^P. The output vector is sized P + 1. A flowchart of this characterisation method is shown in Fig. 4.

Fig. 4.

Flowchart corresponding to radiomics image textural characterisation method.

To estimate radiomics characteristics, we used an available radiomics analysis package [57]. The full set of features was composed of textural first-order statistical and higher-order textural features based on the GLCM, GLRLM, GLSZM, and NGTDM of the image. Higher-order textural features were generated from a 64-level resampled image, considering the full 8-pixel connectivity neighbourhood (four directions for the GLRLM). A full description of the specific texture features and general configuration of the radiomics analysis package can be found in Ref. [58]. A flowchart of this characterisation method is presented in Fig. 3 .

Fig. 3.

Flowchart corresponding to the fractal dimension image textural characterisation method.

The method presented in Ref. [27] is used for superpixel-based histon image characterisation, although, in this case, as we are studying grey-scale images, the histon will only encode a spatial relationship between pixels, not a spectral relationship between colour bands. The over-segmentation process is conducted by modifying the SLIC superpixel generation method [59] adapted to 8-bit grey-scale images. Fig. 5 shows a flowchart of this characterisation method.

Fig. 5.

Flowchart corresponding to the superpixels based histon image textural characterisation method.

All experiments have been carried out using MATLAB® 2020a.

3.4. Classification strategy

To prevent potential biases arising from the machine learning technique applied, three different machine learning methods have been tested, including k-nearest neighbours (KNN) [60], support vector machine (SVM) [61], and random forests (RF) [62]. The application of these three techniques to a multitude of diagnostic problems is well-documented in the literature [[63], [64], [65]]. The results include a hyperparametric optimisation process and, if necessary, a data balancing process.

3.4.1. K-nearest neighbours

KNN algorithm classification [60], an instance-based learning algorithm, is one of the simplest and oldest nonparametric pattern-classification techniques. Essentially, the KNN algorithm is based on the formation of a majority vote among the K closest instances to a given unclassified data point. Formally, given working out data $\left(x_1,\dots ,x_N\right)$, vectors in space x _i ∈ R ^d, with labels $\left(y_1,\dots ,y_N\right)$ where $y_i\in \left(1,-1\right)$, a classifier aims to attribute a label y′ to an unclassified data point x′. For a defined distance metric d(x _n, x _m) between two data points, KNN runs through the set of training data points and returns set $\mathcal{A}$ containing the K-nearest data points according to metric d. It then estimates the conditional probability for each class, defined as follows:

$$\begin{array}{c}{y}^{\prime }=argma{x}_y\sum _{i\in \mathcal{A}}\delta \left(y=y^{(i)}\right)\\ \delta \left(y=y^{(i)}\right)=\left\{\begin{array}{c}1,y=y^{(i)}\\ 0,y\ne y^{(i)}\end{array}\right)\end{array}$$ (6)

The x′ data point is assigned to the y′ class with the largest probability.

3.4.2. Support vector machine

SVM [61] is a general supervised learning method that can perform binary group separation. A SVM performs classification by constructing an N-dimensional hyperplane that optimally separates the data into two categories. The SVM provides an optimally separating hyperplane to obtain the maximum margin on each side of the hyperplane, by selecting an equidistant separation hyperplane from the borders of each class. Only data that define the borders (support vectors) of these margins are considered. To determine the optimal hyperplane, we can define a hyperplane $y_i\left(w\cdot x_y+b\right)>0$, where w corresponds to a weight vector and b indicates the trend value or bias. It is possible to rescale w and b; so the distance to its closed data point is $1/‖w‖$. The goal of SVM is then to find the optimal separation hyperplane for which the distance to the nearest point is the largest. Because the distance to the nearest point is $1/‖w‖$, finding the optimal separating hyperplane indicates minimising ${‖w‖}^2$ under the constraints $y_i\left(w\cdot x_y+b\right)\ge 0$. As ${‖w‖}^2$ is convex, it is possible to minimise it under linear constraints with Lagrange multipliers. Using $\alpha =\left({\alpha }_1,\dots ,{\alpha }_N\right)$ as the N non-negative Lagrange multipliers, the optimisation problem corresponds as follows:

$$W\left(\alpha \right)=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j$$ (7)

where α _i ≥ 0 and under the constraint ${\sum }_{i=1}^N{y}_i{\alpha }_i=0$; solvable using standard quadratic programming methods. If the dataset is too complex to be properly addressed using a linear solution, it is possible to map the dataset into a high-dimensional feature space where the data can be separated using a linear decision boundary. The resulting optimisation problem is formally similar to the base linear case, except that every dot product is replaced by a symmetric positive nonlinear kernel function K as follows:

$$W\left(\alpha \right)=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i{x}_j\right)$$ (8)

The SVM classification function is then stated by

$$y^{\prime }=sign\left(\sum _{i-1}^N{\alpha }_i{y}_{i}K(x_i,x^{\prime })+b\right)$$ (9)

SVM generally yields good results and is remarkably robust to model bias or model variance [66].

3.4.3. Random forest

RF [62] is a supervised learning method based on the application of the general bootstrap aggregation, or bagging, ensemble technique that uses multiple individual decision trees. The predictions from all the trees were aggregated to produce the final prediction. The concept of bagging aims to reduce variance by averaging noisy but approximately unbiased models. Decision trees, if large enough, have a relatively low bias but are quite noisy, making them ideal candidates for bagging. The trees generated for a random forest classifier are identically distributed, but cannot be considered independent. This indicates that the expectation of an average of B trees is the same as the expectation of any one of them, and that the ensemble of bagged trees has the same bias as the individual trees, therefore the only hope for improvement is variance reduction. For a mean of B random variables each with variance σ ², with positive pairwise correlation ρ, the variance of the mean is as follows:

$$\rho {\sigma }^2+\frac{1-\rho }{B}{\sigma }^2$$ (10)

and therefore, the size of the correlation of the bagged tree pairs restricts the averaging returns. The concept behind RF is to improve the variance reduction of bagging by reducing the correlation between trees without increasing the variance significantly. This is accomplished in the tree-growing process, both by randomly selecting a subset of the features as input for each decision tree, and by selecting the features with which to make successive splits of the tree using the Gini index [67]. For a classification tree of a dataset that contains samples from k classes, the probability of samples belonging to class y _i at a given node can be denoted as $p_{y_i}$. The Gini impurity is then defined as $G=1-{\sum }_{i=1}^k{p}_{y_i}^2$. The Gini index estimates the probability that a specific feature is misclassified when randomly selected; therefore, using the feature with the lowest Gini index to split a node allows the growth of homogeneous child nodes, that is, nodes with target labels that belong to roughly the same class. After B trees are grown, $\widehat{C_b}\left(x^{\prime }\right)$ defined as the class prediction of the bth random forest tree, the RF classification function is then stated as follows:

$$y^{\prime }=maxarg{\left\{\widehat{C_b}\left(x^{\prime }\right)\right\}}_1^B$$ (11)

3.4.4. Data balancing

The GWCMCx dataset is not a balanced dataset; it contains almost three times more pneumonia images than pathology-free images. Models generated using machine learning techniques on an imbalanced dataset may not accurately predict the minority class. Although some methods may find an acceptable balance between true- and false-positive rates, other methods simply learn to prioritise the majority class [68,69]. It is difficult to predict how the models generated from imbalanced datasets will perform, as they depend on factors, such as the degree of imbalance between classes, complexity of the data, the overall size of the dataset or the classification method involved [70]. There are several techniques for balancing datasets when these differences exist [70]. In this study, we compared the differences between unbalanced and balanced datasets. Balancing was performed using the synthetic minority oversampling technique (SMOTE) [30].

SMOTE is a non-destructive algorithm in which the number of samples of each class is equalised by generating virtual data points between the existing points of the minority class, by means of linear interpolation. It should be noted that using SMOTE for oversampling represents a trade-off between sensitivity and specificity. A better-balanced training set represents an increase in the number of items correctly classified for the minority class but also tends to indicate an increase in the number of classification failures associated with that class.

3.4.5. Hyperparameter optimisation

For each dataset (balanced and unbalanced), we compared the results obtained with the default configuration ($K=\sqrt{N}$, where N is the size of the training set for KNN; linear kernel and the cost parameter equal to 1 for SVM; 100 learning cycles and 2 leaf per node observations, for RF) of these algorithms, and with the parameters obtained after a process of hyperparameter optimisation [72].

The purpose of hyperparameter optimisation is to find a set of parameters for a model that can optimally solve a specific machine learning problem. Bayesian optimisation has been used for hyperparametric optimisation [71]. Unlike other methods, Bayesian optimisation keeps track of previous evaluation results that are used to form a probabilistic model mapping hyperparameters to the probability of a score on the objective function. This probabilistic model is significantly easier to optimise compared to the objective function and allows the generation of more promising parameter sets than to directly testing the objective function. By evaluating the hyperparameters that seem more promising from previous results, Bayesian methods can find better model fits in fewer iterations than random searches.

3.5. Validation strategy

To generate each classification model, we applied a 10-fold cross-validation methodology using the training sets. The best model, as measured by the achieved F-scores, was evaluated using the datasets tests sets. The goal is to test whether the model can generalise an independent dataset while avoiding problems, such as overfitting or selection bias [73]. It should be noted that SMOTE is only applied after splitting the test set into folds, and only on the training subsets, to avoid generating biased models that may yield overly optimistic error estimates [74].

We compared both the results achieved using the test sets and those obtained by cross-validation, both using the default parameters and those obtained by hyperparameter optimisation. For the GWCMCx dataset, both the results of the original test set and those achieved from the SMOTE-balanced dataset are reported. To assess whether the differences between the models' performances are statistically significant, and thus, we can truly compare their performance, we used McNemar's chi-square test [75]. The significance level was set at 0.05.

As performance measures, we reported the accuracy (Acc), negative prediction value (NPV), positive prediction value (PPV), sensitivity (Sen), specificity (Spe) and F1-Score (F1),

$$\begin{array}{cc}Acc=\frac{(TP+TN)}{(P+N)}& NPV=\frac{TN}{(TN+FN)}\\ PPV=\frac{TP}{(TP+FP)}& Sen=\frac{TP}{(TP+FN)}\\ Spe=\frac{TN}{(TN+FP)}& F1=2*\frac{(Sen*PPV)}{(Sen+PPV)}\end{array}$$ (12)

where P represents the total number of pneumonia positive patients in the dataset, N represents the normal patients in the dataset, true positives (TP) are the pneumonia disease correctly identified, true negatives (TN) are the number of normal images correctly classified, false positives (FP) represent images uncorrected classified as normal cognitive patients, and (FN) are normal cognitive classified as pneumonia disease patients. Area under the curve (AUC) score, receiver operating characteristics (ROC) curve, and detection error trade-off (DET) curve have also been reported.

4. Results

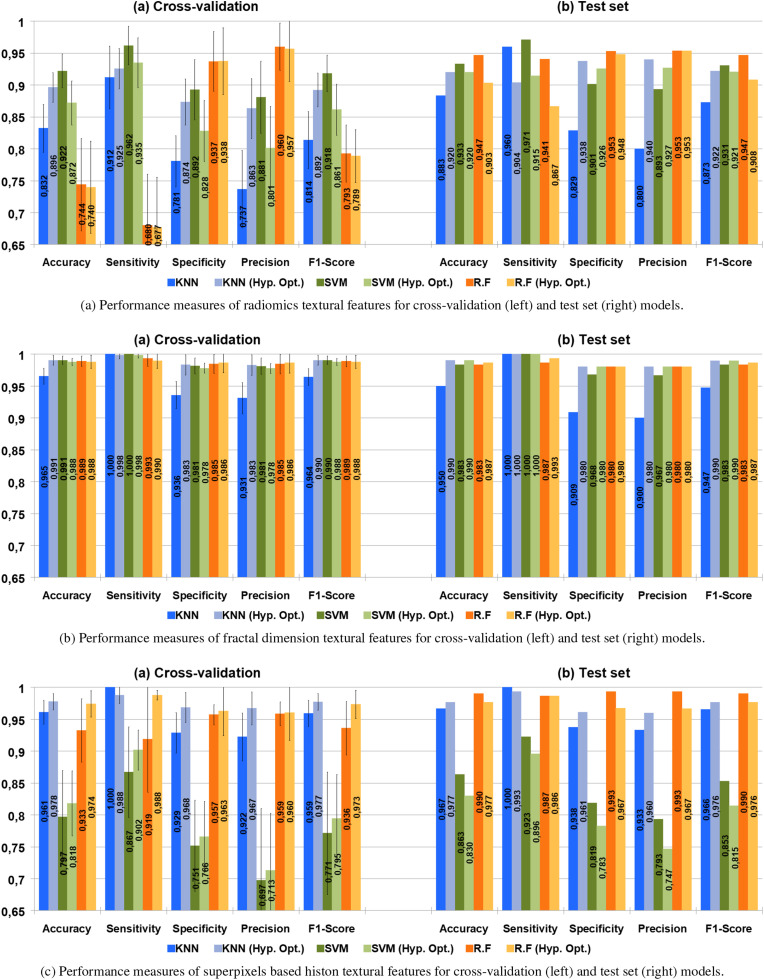
The performance result1 for the models generated for the three types of features, using the unbalanced GWCMCx dataset are presented in Fig. 6 . The best results (F-Score 91–92%, McNemar's test p < 0.05, compared to the rest of the approaches) were achieved by models generated from a histon-based superpixel characterisation using KNN, with no significant differences in the use of hyperparameter optimisation (McNemar p < 0.05). For the remaining generated models, the differences in performance are minor and can only be considered statistically significant (McNemar p < 0.05) for the models generated for radiomics (Fig. 6a) with KNN and SMV, the poorest performance results.

Fig. 6.

Performance measures for the models trained from the unbalanced GWCMCx dataset, for radiomics (upper diagram), fractal distance (middle diagram) and superpixels based histon (lower diagram); both for cross-validation and best model achieved by this process (selected according to its F-Score). The results of the models generated by cross-validation show the mean values of the performance measures of the 10 folds, including its standard deviation.

Fig. 9 compares the ROC and DET curves of the models obtained by radiomics and RF with hyperparameter optimisation (AUC = 0.919), fractal dimension and KNN with hyperparameter optimisation (AUC = 0.923), and histon and KNN (AUC = 0.943), which correspond to the highest F-scores for each characterisation of the unbalanced GWCMCx test set. As can be observed, for the GWCMCx test set, for all the generated models, the sensitivity of the models was significantly lower than the specificity, indicating that the failures obtained by the models tended to be false-positives. Considering that this is an unbalanced dataset, this tendency could be attributed to the presence of a bias toward the majority class, pneumonia cases, in the generated models.

Fig. 9.

Comparison between the receiver operating characteristics (ROC) and detection error trade-off (DET) of the best models achieved with the unbalanced GWCMCx dataset. Includes radiomics and RF with hyperparameter optimisation, fractal dimension and KNN with hyperparameter optimisation and histon and KNN.

The performance results achieved using the GWCMCx test set were not entirely coherent with those achieved by cross-validation. In this case, regardless of the characterisation or the classifier involved, the overall performance evaluation using cross-validation was significantly better than the performance evaluation achieved using the GWCMCx test set. In addition, errors tend to be false-negatives. Since a certain pessimistic bias is generally expected when performing cross-validation [76], this suggests that there are differences between the training and the validation sets, either related to the type of images selected for the GWCMCx training and test set or to the differences in the class bias between the two sets..

Fig. 7 shows the performance results for the models generated from the GWCMCx SMOTE balanced dataset. Similar to the previous case, the best result (F-Score 93%) was achieved by a model trained from a superpixel-based histon characterisation using KNN (McNemar's test p < 0.05, compared to the other approaches). The rest of the models trained from both superpixel-based histon (Fig. 7c) and fractal dimension (Fig. 7b) achieved equivalent performance; the minor differences between them cannot be considered statistically significant (McNemar p < 0.05). The poorest results were again obtained using radiomics (Fig. 7a), although in this case, when compared with the rest of the models, the differences were relevant and statistically significant (McNemar p < 0.05) for all the generated models.

Fig. 7.

Performance measures for the models trained from the balanced GWCMCx dataset, for radiomics (upper diagram), fractal distance (middle diagram) and superpixels based histon (lower diagram); both for cross-validation and best model achieved by this process (selected according to its score). The results of the models generated by cross-validation show the mean values of the performance measures of the 10 fold, including its standard deviation.

Fig. 10 shows the ROC and DET curves belonging to the models with the highest F-score for each characterisation of the balanced GWCMCx test set: radiomics and RF with hyperparameter optimisation (AUC = 0.912), RF and fractal dimension (AUC = 0.949), and histon and KNN (AUC = 0.954). In the case of the image characterisations by radiomics, it can be observed that the miss-classifications produced by the models now tend to be false-negatives. This tendency is maintained, although not as pronounced, in the case of image characterisation using the fractal dimension. Finally, for the models generated from histon based on superpixels, the differences between sensitivity and specificity are narrowed, with the misclassification types moving toward equilibrium.

Fig. 10.

Comparison between the receiver operating characteristics (ROC) and detection error trade-off (DET) of the best models achieved with the SMOTE balanced GWCMCx dataset. Includes radiomics and RF with hyperparameter optimisation, RF and fractal dimension and histon and KNN.

With the exception of the models generated using radiomics (Fig. 7a), the results achieved using the GWCMCx SMOTE balanced dataset were similar to those obtained using cross-validation. Considering this, we can argue that, at least, part of the differences between the test set and cross-validation results in the unbalanced CWCMCx dataset are because of the different biases between classes in the training and test sets, as unbalanced datasets lead to unbalanced folds in cross-validation. Generating models from unbalanced training subsets and evaluating them with testing subsets that share the same bias typically leads to problems such as overfitting and over-optimism in the results [74].

Overall, the results achieved with the balanced GWCMCx test set using radiomics and histon characterisations showed an improvement over their counterparts in the unbalanced GWCMCx test set (McNemar p < 0.05). Although there is an increase in the number of false-negatives, this is compensated by a decrease in false-positives, resulting in a better general performance. However, in the case of the models generated with radiomics, the increase in true-positives does not compensate for the increase in false-positives, with the performance of the generated models being worse (McNemar p < 0.05). In this case, the exception is the models generated with RF, where there are no statistically significant differences in the performance of the models generated with the balanced and unbalanced ensembles (McNemar p < 0.05).

The performance result for the models generated using the Josep-NIH dataset is shown in Fig. 8 . The best results (F-Score 98–99%) are associated with the models generated using superpixel-based histon (Fig. 8c) through the RF algorithm, and with those generated with fractal dimension as textural features (Fig. 8b), using SVM, RF and KNN with hyperparameter optimisation. The differences in the performance measures between the model cannot be considered statistically significant (McNemar p < 0.05). The weakest results, although still remarkable, were once again achieved using of radiomics (Fig. 8c).

Fig. 8.

Performance measures for the models trained Josep-NIH dataset, for radiomics (upper diagram), fractal distance (middle diagram) and superpixels based histon (lower diagram); both for cross-validation and best model achieved by this process (selected according to its score). The results of the models generated by cross-validation show the mean values of the performance measures of the 10 folds, including its standard deviation.

Fig. 11 compares the ROC and DET curves of the models generated using radiomics and RF (AUC = 0.985), fractal dimension, and KNN with hyperparameter optimisation (AUC = 0.990), and histon and RF (AUC = 0.995), corresponding to the highest F-score for each characterisation of the Josep-NIH test set. There was no apparent bias in the types of observed misclassification.

Fig. 11.

Comparison between the receiver operating characteristics (ROC) and the detection error trade-off (DET) of the best models achieved with the with the Josep-NIH dataset. Includes RF and radiomics, fractal dimension and KNN with hyperparameter optimisation and histon and RF.

The results obtained using cross-validation on the Josep-NIH training set were consistent with those obtained in the evaluation of the test set, with the exception of the models generated using radiomics (Fig. 8a), where the cross-validation models showed significant deviations between folds.

5. Discussion

This study assesses the possibilities provided by textural characterisation of chest X-ray images for pneumonia detection by comparing the performance of three different textural feature extraction techniques: radiomics, fractal dimension, and superpixel-based histon. As a general concept, machine learning methods based on textural image characterisation provide remarkable performance, easy implementation and low computational requirements. In this context both radiomics and fractal dimension represent well-known methods with multiple implementations available that enable the quick development of reliable approximations to this and other problems, while superpixel-based histon is a novel method that has shown remarkable potential. Considering the importance of early detection and diagnosis of pneumonia, particularly in context of the COVID-19 pandemic at the time of this study, the development of such machine learning methods to support diagnosis is necessary.

The evaluation of the performance of the models trained with different types of features confirms the validity of the proposed biomarkers. The best results are associated with the use of both fractal dimension and superpixel-based histon, with a slight edge for the latter, although the differences were minor. Models generated from radiomics have consistently provided the weakest results, although they can by no means be considered to perform poorly. Regarding the classifiers used to develop the models, the results obtained using RF are particularly noteworthy, and, in some cases, the use of KNN. Comparing the results with previous studies on the subject we can see that some of the models developed, histon based on superpixel and fractal dimension, provide similar performance to analogous study on both datasets (however it is difficult to directly compare the results obtained in the case of the Josep-NIH dataset, given the dynamic nature of the image repository and the different sources from which the set of pathology-free images can be collected), a remarkable feature considering the nature of this study.

The performance results show the impact of using training sets where the classes are not balanced compared with the balanced training sets. Overall, there is an improvement in the performance results when using a balanced GWCMCx dataset for training. In addition, the use of balanced datasets also affects the behaviour of the obtained errors; models trained with an unbalanced dataset show a strong bias to misclassify an image as the dominant class in the training set regardless of the type of characterisation or the classifier used. This tendency disappeared when a balanced set was used. On the contrary, hyperparameter optimisation has been found to have a minimal or, in some cases, negative effect on the models performance. This suggest that the tested textural characterisations provide a good separability between classes “out of the box”, although it is not possible to conclude this without a detailed analysis.

The results of this study must be understood in the light of several limitations. Although the data are from public sources and are widely used in similar studies, they exhibit a variety of shortcomings in terms of the populations covered. Although the images have undergone a normalization process, there may be some bias between the non-pathological and pneumonia sets, particularly when they are obtained from different sources. In addition, the demographic data provided are very limited, or have not been collected in a standardised or rigorous manner, and are incomplete; therefore, that an analysis beyond the medical image is not possible. In particular, when analysing the Josep-NIH dataset we can observe that, considering the sources from which the pneumonia cases are obtained (online publications, web pages, etc.), corresponding to patients with severe symptomatology, there is a possible selection bias. Furthermore, the nature of the COVID-19 collection implies that the ages may contain annotations, artefacts or medical objects, outside the area of interest, not directly related to the presence of pneumonia, but sufficient to identify the image as part of a specific dataset [77]. Despite our efforts to mask out the non-relevant parts of the image and try to complement the dataset with a group of demographically similar images, we cannot guarantee the extent to which the corresponding biases have been eliminated; therefore, the results obtained using this dataset must be interpreted according to its limitations. On the other hand, the GWCMCx dataset was exclusively paediatric. Considering the radiological and anatomical differences between paediatric images and images from the general population [78], the results of this study should be understood in that context.

It is also necessary to mention that the masking process applied is designed as a simple method to limit the presence of non-relevant areas of the image, and cannot be regarded as a lung segmentation method for chest X-ray images. Furthermore, there are multiple approaches for model development, both based on classifiers not used in this study and alternative approaches to those used, and multiple methods of preparing and processing the feature sets that would certainly affect the results and have not been explored in this study. In addition, the analysis of differences in results between balanced and unbalanced datasets is based only on the use of SMOTE (although studies on the behaviour of different data balancing methods [79] suggest that the results produced using these methods would be approximately similar to those produced using SMOTE). Finally, the tests performed did not attempt to distinguish between different causes of pneumonia or between different infiltration patterns, limiting the usefulness of this study to some extent.

The results achieved highlighted a number of directions for potential future research related to this project. Improvements in the masking process would help to properly isolate the lungs within the image, minimizing both the bias introduced by tissues outside the areas of interest and the possibility of losing parts of them. Moreover, in the same manner as proposed in Ref. [20], there are multiple dimensionality reduction/feature selection techniques (PCA, LDA, multidimensional scaling, statistically based feature selection, etc.) that can result in classification performance improvements for different feature vectors, particularly in the case of radiomics, provided the heterogeneous nature of the generated features. Considering into account the results, it would be interesting to expand the study to test the ability of the methods used to discriminate the different patterns of infiltration associated with different causes of pneumonia. However, the results demonstrated the possibility of applying the characterisation methods used for the identification of other pathologies in X-ray images.

6. Conclusion

In this study, we explore the possibility of using textural image characterisation techniques as a tool for the detection of pneumonia in chest X-ray images. We evaluated several classification models generated from three different types of textural features: fractal dimension, superpixel-based histon and radiomics; and three machine learning algorithms: KNN, SVM and RF. Two different open-access image datasets are used in this study: one paediatric and other COVID-19 related. In addition, we studied the influence of class balancing on model performance, applying SMOTE. The evaluated models confirmed the validity of the proposed methods. While all characterisation methods achieve remarkable results, those obtained with both superpixel-based histon and, to a lesser extent, fractal dimension are particularly noteworthy. Compared to the more classical approach based on radiomics features, the best models trained with these approaches resulted in improvements in both accuracy and F-Score between 6% and 8% for the first dataset. For the second dataset, the accuracy improvements were between 4% and 5%, and approximately 4% for the F-score.

CRediT authorship contribution statement

César Ortiz-Toro: Research, software, data curation, writing: original draft preparation, writing: review & editing. Angel García-Pedrero: Research, writing: original draft preparation, writing: review & editing. Mario Lillo-Saavedra: Research, writing: original draft preparation, writing: review & editing. Consuelo Gonzalo-Martín: Research, writing: original draft preparation, writing: review & editing.

Funding

This work has been partially funded by the Water Research Center For Agriculture and Mining, CRHIAM (ANID/FONDAP/15130015), and by the UPM project RP200060107.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: