Soft robotic origami crawler

Abstract

Biomimetic soft robotic crawlers have attracted extensive attention in various engineering fields, owing to their adaptivity to different terrains. Earthworm-like crawlers realize locomotion through in-plane contraction, while inchworm-like crawlers exhibit out-of-plane bending-based motions. Although in-plane contraction crawlers demonstrate effective motion in confined spaces, miniaturization is challenging because of limited actuation methods and complex structures. Here, we report a magnetically actuated small-scale origami crawler with in-plane contraction. The contraction mechanism is achieved through a four-unit Kresling origami assembly consisting of two Kresling dipoles with two-level symmetry. Magnetic actuation is used to provide appropriate torque distribution, enabling a small-scale and untethered robot with both crawling and steering capabilities. The crawler can overcome large resistances from severely confined spaces by its anisotropic and magnetically tunable structural stiffness. The multifunctionality of the crawler is explored by using the internal cavity of the crawler for drug storage and release. The magnetic origami crawler can potentially serve as a minimally invasive device for biomedical applications.

A bioinspired, untethered, and small-scale origami crawler achieves effective locomotion and steering in severely confined spaces.

INTRODUCTION

Crawling motion is a navigation strategy that is commonly observed in animals, especially in worms. In these animals, body contraction paired with inhomogeneous friction between the surfaces of contact enables forward motion. Worm-based crawling motion shows high adaptivity to complicated terrains (1–3) because of the soft deformable body. By engineering effective crawling, robotic crawlers on various scales have attracted extensive efforts for applications, including planetary subsurface exploration (4, 5), in-pipe inspection (6, 7), and gastrointestinal endoscopy (8, 9), where the operating space is limited or confined.

On the basis of the observed crawling mechanisms, earthworm-like crawlers have been designed to realize locomotion through in-plane contraction (10, 11), while inchworm-like crawlers are designed to exhibit out-of-plane bending-based motions (12, 13). In confined spaces where out-of-plane motion is constrained, the in-plane contraction crawling mechanism surpasses the bending-based counterpart. The contraction of in-plane crawlers is usually achieved through contractile structures (14–16) or soft materials (17–19). Most of the crawlers based on contractive mechanisms only demonstrate straight motion by actuating either the whole body with a single actuator (20, 21) or several individual segments synergistically with multiple actuators (22, 23). On the other hand, the steering function requires additional mechanisms with added actuators (24). These actuators, including motors and pneumatic pumps, commonly lead to bulky systems with extensive wires or tubes. The complicated structures and control systems pose challenges for small-scale applications such as those in the biomedical field. To this effect, an alternative is crawlers made of stimuli-responsive soft materials that generate contraction via large deformation of the soft crawler body (25, 26), which usually has a relatively simple structure that permits small-scale design. Some recent crawlers with a millimeter-sized beam structure have demonstrated the capabilities of effective locomotion and cargo transportation for open biomedical environments, such as the stomach (27, 28). Although soft materials allow easy deformation for contraction, their low material stiffness makes it challenging for the crawler to overcome the large environmental resistance introduced by confined spaces, such as those in the gastrointestinal tract and abdomen, where contacts between tissues or organs are common. To navigate in these environments, systems that allow effective contraction for crawling while having the capability to overcome external load in the lateral direction are desirable.

Origami provides a seamless and effective way of generating contraction by means of structural folding and thus has been adopted to engineer robotic crawlers (29–31). Origami structures demonstrate anisotropic structural stiffness along folding directions and lateral directions, which is beneficial for effective crawling in confined spaces (32, 33). The inherently low stiffness in the foldable direction allows for easy contraction, while the appreciably higher stiffness in the lateral direction makes the crawler more immune to unexpected disturbances from working environments. The Kresling pattern (34–36) is a specific type of origami that generates axial contraction under either torque or compressive force. Its contraction is coupled with a twist from the relative rotation between the two ends of the unit (Fig. 1A). When using the Kresling unit for crawler contraction, the twist induces undesired lateral movement, which prohibits the straight motion of the crawler and limits its application to specific environments, such as in a tube (37). Although some works adopt two parallel Kresling assemblies with reverse crease directions to cancel out twists in the system (38, 39), the clumpy structure and multiple wired actuators hinder the miniaturization of the robotic crawler for applications in environments with limited access.

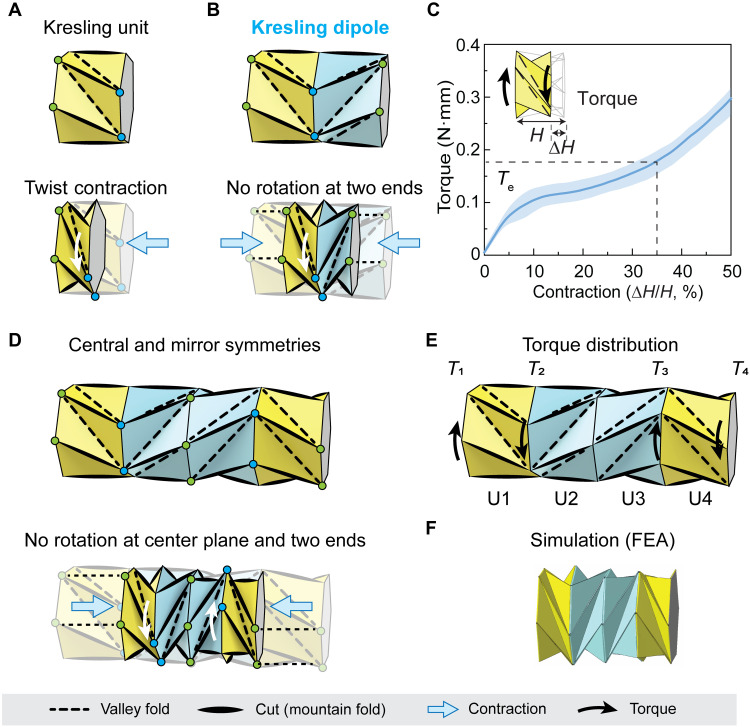
Fig. 1. Mechanism of the four-unit Kresling crawler based on the Kresling dipole.

(A) Schematic of a Kresling unit, showing contraction coupled with a twist deformation. (B) Schematic of a Kresling dipole made of two standard Kresling units with reverse crease directions, showing no rotation at the two ends (green circles) but rotation at the center plane (blue circles) during contraction. (C) The experimentally measured torque contraction curve of the Kresling unit. Contraction is defined as ∆H/H, where H is the initial height of the unit and ∆H is the difference between the initial and contracted heights. Parameter T_e is defined as the corresponding torque at 35% contraction of the unit for effective crawling motion. The solid line is the averaged responses of three Kresling unit samples, and the shaded region represents the range of responses. (D) Schematic of the Kresling crawler made of two Kresling dipoles, showing no rotation at the center plane and two ends. (E) The required torque distribution to actuate the Kresling crawler for simultaneous contraction of all units. (F) FEA verification of the derived torque distribution for simultaneous contraction of all units.

In this work, we report a magnetically actuated small-scale origami crawler for effective in-plane crawling motion. The crawler is made of a four-unit Kresling assembly with a rationally designed structure to avoid the relative rotation between the two ends of the assembly and to cancel out internal twists for efficient straight motion. The required torque distribution on the crawler is theoretically derived and verified by finite element analysis (FEA) to obtain simultaneous contraction of all four Kresling units for the crawling motion. The torques are then realized by distributed magnetic actuation. By controlling the magnitude and direction of the external magnetic field, the Kresling crawler can achieve contraction for forward motion and instantaneous steering. The untethered magnetic actuation eliminates the need for bulky and wired actuators, enabling a small-scale and neat robotic system. The measured anisotropic and magnetically tunable structural stiffness along the axial and lateral directions of the Kresling crawler helps the crawler achieve effective locomotion in severely confined spaces. In addition, drug storage and release capabilities are demonstrated to illustrate the multifunctionality of the crawler.

RESULTS

The Kresling unit shows a coupled twist contraction motion (blue and green circles in Fig. 1A) under either a pair of torques or compressive forces. The twisting direction is either clockwise (CW) or counterclockwise (CCW) on the basis of the crease direction of the Kresling unit (fig. S1). To have a purely translational crawling motion, the Kresling-based crawler design needs to avoid the lateral movement that can be caused by the relative rotation between the two ends of a Kresling unit. To address this, the Kresling dipole is introduced to eliminate the overall twist during contraction. As illustrated in Fig. 1B, the Kresling dipole is composed of two Kresling units with the same geometry and reverse crease directions, showing mirror symmetry. Note that the crease direction only decides the twisting direction without influencing the magnitude of force/torque required to fold the unit. The two units with reverse crease directions can achieve equal amounts of contraction when compressing the two ends of the Kresling dipole (Fig. 1B). Because of the same relative rotation angles with reverse directions of two Kresling units, the two ends of the Kresling dipole are free of relative rotation, as indicated by green circles, while its middle interface shows a rotation, as indicated by blue circles (movie S1). In this way, the Kresling dipole serves as a robust alternative to build crawlers by providing effective in-plane contraction for translational motion while maintaining contacts of two end points with the ground for stick-slip motion, which is usually necessary for crawling motion (28, 40, 41).

The Kresling unit can be designed to be monostable or bistable (35, 42). For the in-plane crawling motion with contraction phase and recovery phase, the Kresling assembly is designed to be monostable for smooth and continuous deformation. Meanwhile, monostability allows automatic recovery to the stress-free initial state of the crawler after releasing the applied loading. By choosing appropriate geometric design (fig. S1) and material (fig. S2), a fabricated Kresling unit shows monostable behavior from the measured force contraction curve (figs. S3 and S4A) and torque contraction curve (Fig. 1C). Under a pair of reasonably small torques of T_e = 0.18 N·mm, the fabricated unit can generate a 35% contraction for effective crawling motion (Fig. 1C).

To further cancel out the contraction-induced rotational motion at the middle interface of the Kresling dipole (white arrow in Fig. 1B), a crawler made of two Kresling dipoles aligned in the axial direction is designed, as shown in Fig. 1D. Here, we define directions perpendicular and parallel to hexagonal planes as the axial and lateral directions of the Kresling assembly, respectively. The structure has two levels of symmetry, including central symmetry of the whole structure and mirror symmetry of each Kresling dipole. With this configuration, the second and fourth hexagonal planes of the crawler from left to right have the same degree of rotation in reverse directions (white arrows in Fig. 1D) when the four units contract simultaneously. The Kresling crawler shows no rotation at both the center (third hexagonal plane) and two ends (first and fifth hexagonal planes) during contraction (movie S1).

To achieve such deformations for effective in-plane crawling motion, a well-designed torque distribution (Fig. 1E) is needed to ensure simultaneous contraction of the four units based on three requirements.

1)A purely translational crawling motion requires torque balance of the whole system, which can be expressed as

$$T_1+T_3=T_2+T_4$$ (1)

where T₁, T₂, T₃, and T₄ are the magnitudes of applied torques at first, second, fourth, and fifth hexagonal planes of the crawler from left to right.

2)The simultaneous and equal contraction of all four Kresling units requires the torque exerted to each Kresling unit to be the same, which can be expressed as

$$T_{\mathrm{U}1}=T_{\mathrm{U}2}=T_{\mathrm{U}3}=T_{\mathrm{U}4}$$ (2)

where T_U1, T_U2, T_U3, and T_U4 are torque magnitudes on units U1, U2, U3, and U4, respectively. On the basis of the structural symmetry and the torque balance analysis from free body diagrams (see the Supplementary Materials and fig. S5 for more details), we have

$$T_2=2T_1,T_3=T_2,T_4=T_1$$ (3)

3)The torque on each Kresling unit needs to reach a sufficient value to generate effective contraction, and we define this torque as T_e, which comes from the mechanical characterization of the Kresling unit (Fig. 1C). Note that T_e for the yellow and blue units have the same magnitude but opposite directions. Upon fulfilling the three aforementioned requirements, the crawler can generate contraction by simultaneously folding the four units, while the two ends remain free of relative rotation.

To verify the derived torque distribution, we simulated the contraction of the Kresling crawler via FEA, as shown in Fig. 1F (see fig. S6 for the comparison between FEA results and analytical derivation). On the basis of the relative rotation angle contraction curve of the Kresling unit (fig. S4C), a 32° relative rotation between the two ends of the Kresling unit corresponds to 35% contraction for effective crawling motion. Rotation angles of 0°, 32°, −32°, and 0° are then enforced to the first, second, fourth, and fifth hexagonal planes of the crawler from left to right in the FEA, with all hexagonal planes free to move along the axial direction. In the simulation, we record the corresponding reaction torques T₁, T₂, T₃, and T₄ at the first, second, fourth, and fifth hexagonal planes of the crawler from left to right and compare their relations with the theoretical derivation. Under the applied boundary conditions, the four units of the crawler contract simultaneously and show no rotation at the center plane (the third hexagonal plane) and the two ends of the crawler (movie S1). The simulated reaction torque relations (T₂/T₁ and T₃/T₂) shown in fig. S6D follow Eq. 3 during the entire contraction process, which verifies the analytically derived torque distribution. By applying the distributed loadings cyclically, the monostable Kresling crawler can provide repeatable contraction for continuous crawling motion.

An appropriate actuation method is necessary to provide the torque distribution for the crawler to achieve desired simultaneous contraction. Compared to other actuation methods, such as motor (33, 38) and pneumatic actuation (11, 19), magnetic actuation is an ideal option, as outlined next. First, magnetic actuation permits untethered and fast response, allowing real-time manipulation of the crawler in an environment with limited access. Second, magnetic actuation isolates the power and controlling system from the crawler, making miniaturization of the crawler feasible for applications in small and confined spaces (27). Figure 2A shows an image of the fabricated Kresling crawler on a fingertip, illustrating the miniaturized robot for potential applications in environments with limited access, such as drug delivery in the intestines and stomach. Third, magnetic control has recently demonstrated distributed actuation for selective or sequential actuation of functional deformable units of origami assembly (34, 43). This further provides the possibility of using the magnetic field to program the torque distribution on the Kresling crawler to have simultaneous contraction of all Kresling units for effective crawling motion.

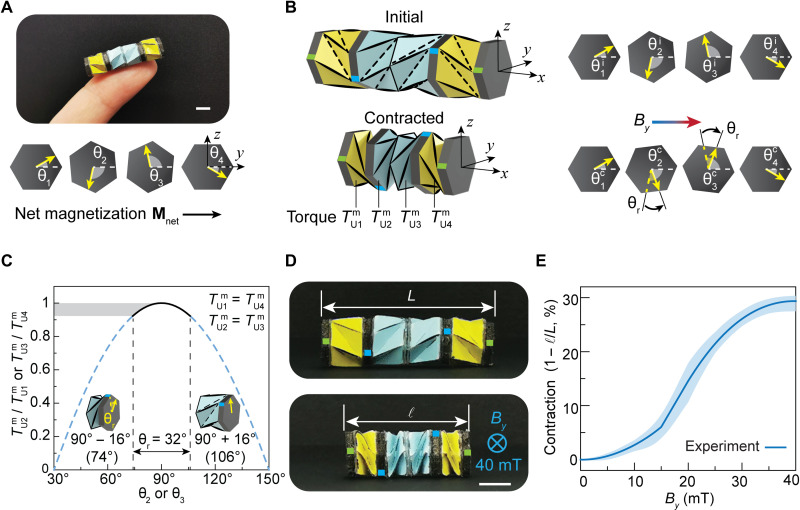
Fig. 2. Magnetic actuation mechanism of the Kresling crawler.

(A) Image of a fingertip holding the fabricated Kresling crawler and designed magnetization directions of attached four magnetic plates for distributed torques. (B) Crawler configurations and magnetization directions at the initial state and the contracted state. B_y is the magnetic field applied to the crawler along its net magnetization direction. Angle θ_r is the total rotation angle of θ₂ or θ₃ during contraction. $T_{\mathrm{U}1}^{\mathrm{m}}$, $T_{\mathrm{U}2}^{\mathrm{m}}$, $T_{\mathrm{U}3}^{\mathrm{m}}$, and $T_{\mathrm{U}4}^{\mathrm{m}}$ are torque magnitudes on units U1, U2, U3, and U4 under magnetic actuation, respectively. Green marks on the vertices of the magnetic plates indicate no rotation at the two ends of the Kresling crawler. (C) Torque ratio between units U1 and U2 (U4 and U3) during contraction. Contraction of the unit of 35% (rotation angle θ_r of 32°) is defined as an effective crawling motion under a reasonably small torque. Note that angles θ₁ and θ₄ stay unchanged during contraction. Angles θ₂ and θ₃ are designed to swing between 106° and 74° to minimize the dynamic fluctuation of magnetic torques during contraction. (D) The magnetically actuated contraction under a magnetic field of 40 mT. (E) Characterization of the Kresling crawler contraction at different magnetic field magnitudes. Contraction is defined as 1 − ℓ/L, where L and ℓ are lengths of the crawler at the initial state and after contraction, respectively. The solid line is the averaged responses of three Kresling crawler samples, and the shaded region represents the range of responses. Scale bars, 5 mm.

As shown in Fig. 2A, four magnetic plates are attached to the first, second, fourth, and fifth hexagonal planes of the crawler from left to right, where distributed torques are needed according to the theoretical derivation. Each magnetic plate is made of silicone embedded with hard magnetic particles so that the magnetization density is tunable by adjusting the volume fraction of the magnetic particles. The magnetic plate has a predetermined magnetization M with a specific direction. Under a uniform magnetic field B, the magnetic plate generates a torque T = V(M × B), which tends to align its M with the applied B by rigid body rotation of the magnetic plate. V is the volume of the magnetic plate. Both the direction and magnitude of the torque can be programmed by specially designing the magnetic plate magnetization and manipulating the applied magnetic field. Here, the four magnetic plates have the same magnetization density but different magnetization directions (Fig. 2A) to provide local and distributed torques that satisfy the derived torque relations in Eq. 3.

To better describe the magnetic actuation and relative rotation of the magnetic plates, we define a local right-handed coordinate system whose origin sits at the center of the rightmost magnetic plate of the crawler. The y axis and the z axis are parallel and perpendicular to the top edge of the rightmost magnetic plate, respectively, as shown in Fig. 2A. The x axis is along the axial direction of the crawler and faces outward. The magnetization directions of the four magnetic plates are all in the yz plane of the local coordinate system with relative angles of θ₁, θ₂, θ₃, and θ₄ to the y axis. Under a uniform magnetic field along the y axis, the generated distributed torques of the four magnetic plates have magnitudes of

$$T_i^{\mathrm{m}}=\mid {\mathbf{T}}_i^{\mathrm{m}}\mid =V\mid {\mathbf{M}}_i\times \mathbf{B}\mid ={\mathit{BM}}_{\mathrm{r}}V\text{sin}{\mathrm{\theta }}_i(i=1,2,3,\text{and} 4)$$ (4)

where M_i is the magnetization of each magnetic plate, B is the applied magnetic field with a magnitude of B, and M_r and V are the measured remanent magnetization and volume of each magnetic plate, respectively. The magnetization directions of the first and fourth (second and third) plates indicate mirror symmetry about the y axis to assure that $T_1^{\mathrm{m}}$ and $T_4^{\mathrm{m}}$, or $T_2^{\mathrm{m}}$ and $T_3^{\mathrm{m}}$ have the same torque magnitude but reverse directions under the uniform magnetic field applied along the y axis. Note that the crawler always aligns its net magnetization M_net (y axis) with the applied magnetic field, and the corresponding torque distribution would then provide simultaneous contraction of all four Kresling units. By substituting Eq. 4 into Eq. 3, we have

$$\text{sin}{\mathrm{\theta }}_1=\frac{1}{2}\text{sin}{\mathrm{\theta }}_2=\frac{1}{2}\text{sin}{\mathrm{\theta }}_3=\frac{1}{2}\text{sin}{\mathrm{\theta }}_4$$ (5)

However, the magnetization directions θ₂ and θ₃ change during the continuous contraction of the crawler, as shown in Fig. 2B. Thus, in practice, the torque distribution would deviate from the ideal torque relations. Taking the left Kresling dipole of the crawler as an example, we derive the torques on units U1 and U2 as

$$\{\begin{array}{c}{T}_{\mathrm{U}1}^{\mathrm{m}}=T_1^{\mathrm{m}}={\mathit{BM}}_{\mathrm{r}}V\text{sin}{\mathrm{\theta }}_1\\ T_{\mathrm{U}2}^{\mathrm{m}}=T_2^{\mathrm{m}}-T_1^{\mathrm{m}}={\mathit{BM}}_{\mathrm{r}}V\text{sin}{\mathrm{\theta }}_2-{\mathit{BM}}_{\mathrm{r}}V\text{sin}{\mathrm{\theta }}_1\end{array}$$ (6)

where $T_{\mathrm{U}1}^{\mathrm{m}}$ and $T_{\mathrm{U}2}^{\mathrm{m}}$ are torque magnitudes on units U1 and U2 under magnetic actuation, respectively. Assuming that the four units of the Kresling crawler still contract simultaneously and its two ends do not rotate during this dynamic process, θ₂ gradually decreases, while θ₁ remains unchanged. To ensure that the torque $T_{\mathrm{U}2}^{\mathrm{m}}$ follows $T_{\mathrm{U}1}^{\mathrm{m}}$ as much as possible, the change of sin θ₂ should be minimized to limit the torque fluctuation during the crawler contraction. In this way, $T_{\mathrm{U}1}^{\mathrm{m}}$ and $T_{\mathrm{U}2}^{\mathrm{m}}$ are close enough to guarantee nearly simultaneous and equal contraction. This is possible when θ₂ swings around 90°, as the change rate of sin θ₂ reaches zero at this point and stays very small within a moderate angle variation. The corresponding θ₁ is obtained to be 30°. Therefore, the ideal angles of the magnetizations are

$${\mathrm{\theta }}_1={\mathrm{\theta }}_4=30°,{\mathrm{\theta }}_2={\mathrm{\theta }}_3=90°$$ (7)

Because θ₂ and θ₃ are changing during contraction, the idealized 90° is set to be the angle at the half-way contraction of the unit. Then, the angle swing during the whole contraction process is expressed as

$${\mathrm{\theta }}_2^{\mathrm{i}}=90°+{\mathrm{\theta }}_{\mathrm{r}}/2,{\mathrm{\theta }}_2^{\mathrm{c}}=90°-{\mathrm{\theta }}_{\mathrm{r}}/2$$ (8)

where ${\mathrm{\theta }}_2^{\mathrm{i}}$ is the angle of θ₂ at the initial state of the Kresling crawler, ${\mathrm{\theta }}_2^{\mathrm{c}}$ is the angle of θ₂ at the contracted state of the Kresling crawler, and θ_r is the total rotation angle of θ₂ during contraction.

For the Kresling crawler, a 35% contraction of each unit could provide effective crawling motion under a reasonably small torque, which corresponds to a rotation angle θ_r of 32° from the relative rotation angle contraction curve of the Kresling unit in fig. S4C. For θ₂ and θ₃ swinging from 106° (90° + 16°) to 74° (90° − 16°), sin θ₂ and sin θ₃ range within 0.96 to 1, and sin θ₁ = sin θ₄ = 0.5. This follows the magnetization angle requirement in Eq. 5 with a small deviation. In this case, the ratio $T_{\mathrm{U}2}^{\mathrm{m}}$/$T_{\mathrm{U}1}^{\mathrm{m}}$ ($T_{\mathrm{U}3}^{\mathrm{m}}$/$T_{\mathrm{U}4}^{\mathrm{m}}$) ranges from 0.92 to 1 during crawler contraction, as shown in Fig. 2C, exhibiting an acceptable torque fluctuation. Therefore, we finalize the magnetization directions for magnetic plates as

$${\mathrm{\theta }}_1={\mathrm{\theta }}_4=30°,{\mathrm{\theta }}_2={\mathrm{\theta }}_3=106°$$ (9)

The derived crawler contraction is then experimentally verified by magnetic actuation (see fig. S7 for experimental setup of magnetic actuation). Upon applying the magnetic field in the y axis, the four units of the crawler start to contract simultaneously (movie S2). For the sake of illustration, Fig. 2D displays the initial and contracted states of the crawler under a 40-mT magnetic field. It can be seen that the four units of the crawler have roughly the same magnitude of contraction, and the magnetic plates on the two sides remain rotation free (green marks), while the middle planes of the two Kresling dipoles rotate in reverse directions (blue marks). The magnetically actuated contraction of the crawler is characterized as shown in Fig. 2E. Here, the contraction of the crawler is defined as 1 − ℓ/L, where L and ℓ are the lengths of the crawler at the initial state and contracted state, respectively. The magnitude of contraction increases with the increasing magnetic field. The crawler can achieve a contraction of about 30% under the 40-mT magnetic field.

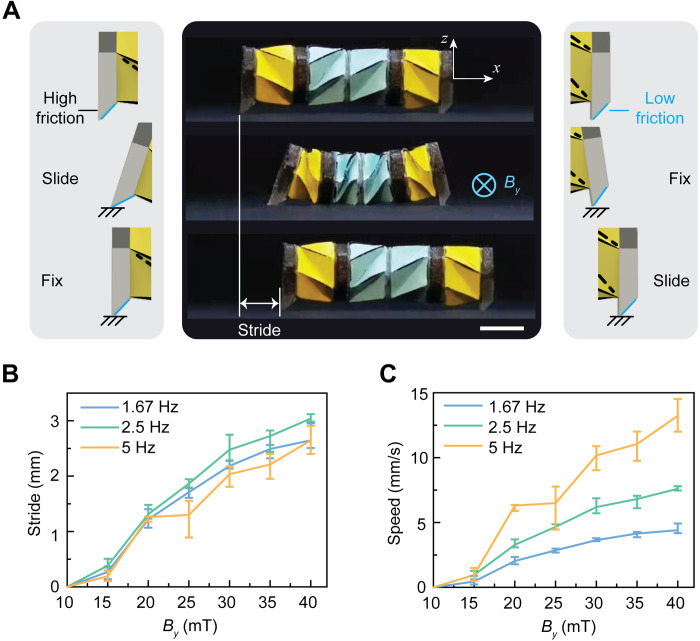
The magnetic actuation permits a well-regulated torque distribution that enables an effective in-plane contraction of the Kresling crawler. To use the friction with the ground for forward motion, we design two feet with anisotropic friction to the front and rear of the crawler. The foot design has a high-friction portion and a low-friction portion, which are made by polydimethylsiloxane (PDMS) and acetate tape, respectively (see the Supplementary Materials for more details). Their friction coefficients are measured and shown in fig. S8. The directional friction converts the contraction/recovery deformations of the crawler into translational motion, as shown in Fig. 3A. During the contraction phase, the rear foot moves forward, while the front foot stays stationary, as low-friction and high-friction portions of the rear and front feet contact the substrate, respectively. During the recovery phase, the rear foot has larger friction, and only the front foot moves forward (movie S2). After one cycle of contraction and recovery, the crawler can move forward along the x axis with a distance, which is defined as the stride length. Continuous crawling motion can be obtained by cyclically applying and removing the magnetic field (movie S2), which is realized by repeating the magnetic field profile shown in fig. S9. The crawling speed can be easily tuned by changing applied magnetic field magnitude and frequency.

Fig. 3. Crawling mechanism of the Kresling robot.

(A) Single stride of the Kresling crawler under a magnetic field of 40 mT. Scale bar, 5 mm. (B) Stride and (C) speed characterization of crawling motion at various magnetic field magnitudes and frequencies.

The strides and speeds of the crawler are characterized under magnetic fields with different magnitudes and frequencies, as shown in Fig. 3 (B and C, respectively). The magnetic field magnitudes range from 0 to 40 mT with a 5-mT interval, and the frequencies are set as 1.67, 2.5, or 5 Hz. As shown in Fig. 3B, there is no locomotion when the magnetic field magnitude is smaller than 15 mT, because the magnetic field is insufficient to overcome the friction between feet and substrate. Then, the stride length increases with a stronger magnetic field and achieves a maximum value of 3 mm under a 40-mT magnetic field. Increasing the magnetic field frequency while keeping the same magnitude does not influence the stride length much. However, the crawling speed can be enhanced by increasing either magnitude or frequency of the applied magnetic field, as evidenced in Fig. 3C. The crawling speed reaches 13.2 mm s⁻¹ when the magnitude and frequency of the magnetic field are 40 mT and 5 Hz, respectively. Notice that the crawling speed can be further enhanced by increasing the magnitude and frequency of the magnetic field. A comparison between the Kresling crawler here and some existing crawlers in terms of their actuation mechanisms, size, weight, and crawling speed can be found in table S1.

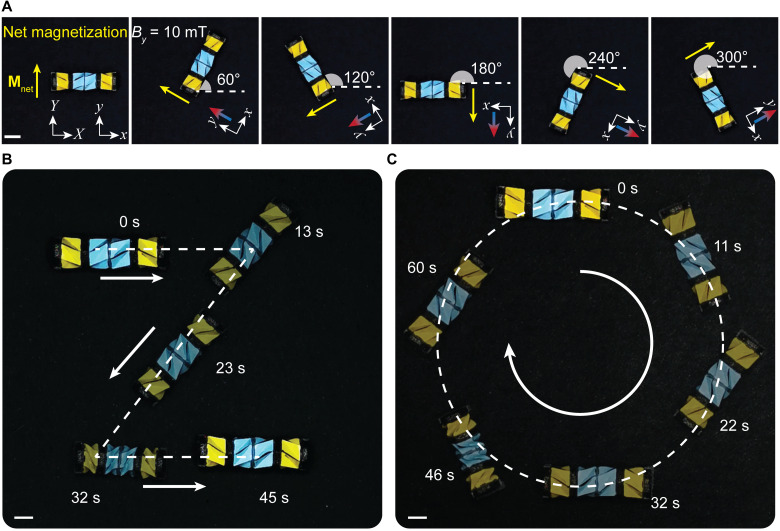
In addition to the locomotion along a straight line, the steering capability is crucial for robots to navigate in complex environments. Compared to some crawlers with other actuation methods (3, 16, 38), the magnetically actuated Kresling crawler in this paper shows advantages in navigation with multiple degrees of freedom, which do not require extra mechanism design or actuators (44–46). As shown in Fig. 4A, the crawler has a net magnetization M_net along the local y axis of the crawler due to the specially designed magnetization distribution. Because the net magnetization always tends to align with the applied magnetic field, the crawler can instantaneously steer by rigid body rotation upon the change of external magnetic field direction in the global XY plane. In Fig. 4A, the crawler is initially positioned with its local coordinate coinciding with the global coordinate. When we change the angle between the magnetic field and the Y axis CCW to 60°, 120°, 180°, 240°, and 300° in sequence, the crawler can immediately rotate to the corresponding directions to align its net magnetization direction with the external magnetic field direction (movie S3). Here, a 10-mT magnetic field is enough for the rigid body rotation of the crawler.

Fig. 4. Steering and navigation of the Kresling crawler.

(A) The steering mechanism. (X and Y) and (x and y) refer to the global and local (deformed) configurations, respectively. The crawler always tends to align its net magnetization M_net with the applied magnetic field direction. (B) The “Z” crawling path (three straight segments) at selected times. (C) The “O” crawling path (continuous angular changes) at selected times. Scale bars, 5 mm.

Figure 4B demonstrates the crawler navigation with a “Z” path, consisting of three discrete straight segments (movie S3). Segments 1 and 3 are along the X axis. Segment 2 is 130° CW from the X axis. In each segment, the magnetic field of 40 mT is cyclically applied and removed along the net magnetization direction of the crawler for it to crawl along the local x axis. The transition from segment 1 to segment 2 or from segment 2 to segment 3 requires the crawler to pause and then steer to the new crawling direction by applying a 10-mT magnetic field along the desired direction, which is 130° CW or CCW from the current net magnetization direction, respectively.

The crawler can also change moving direction during crawling. For instance, Fig. 4C demonstrates the navigation of the crawler about an “O” crawling path by continuously changing the angle between the magnetic field direction and the Y axis from 0° to 360° CW over time (movie S3). Because the net magnetization direction of the crawler always tends to align with the external magnetic field direction, the crawler can keep changing its crawling direction to follow the desired circular path. The magnitude of the magnetic field for crawling in this demonstration is 40 mT. These two paths show the precise maneuverability and omnidirectional locomotion capability of the Kresling crawler.

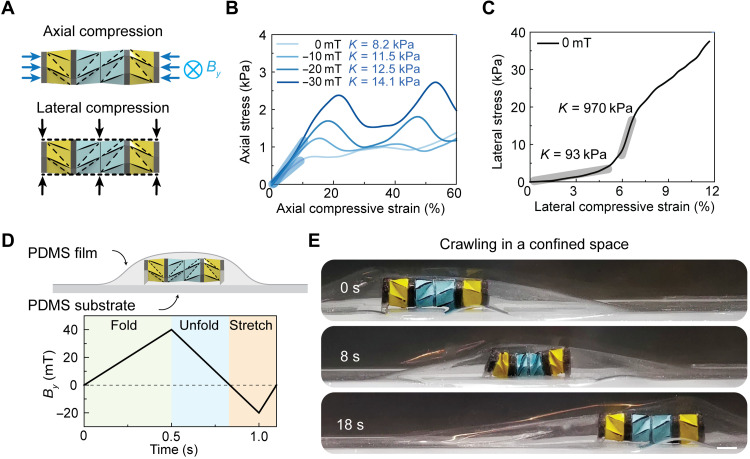
In biomedical environments, the large resistance from the contact between tissues and organs can hinder the motion and function of soft machines because of their low material and structure stiffness (47, 48). The Kresling crawler has a unique anisotropic stiffness that is important to promote crawling motion and maintain the integrity and function of the crawler in confined spaces. In addition, the magnetic field can tune the crawler structure stiffness along its axial direction for enhanced crawling performance. When we compress the crawler along its axial and lateral directions, as shown in Fig. 5A (see fig. S10 for experimental setup), a considerable stiffness difference is observed, regardless of whether a magnetic field is applied or not. Figure 5 (B and C) shows the stress-strain curves from the axial and lateral compression tests, respectively. When no magnetic field is applied, the low axial stiffness of 8.2 kPa (measured at 10% strain from the lightest blue curve in Fig. 5B) enables easy contraction under relatively small magnetic fields for effective locomotion. On the contrary, the stiffness in the lateral direction is as high as 93 kPa, even at a small strain of 5% (Fig. 5C). Once reaching complete contact under increasing compression (from 6% strain), its lateral stiffness increases greatly to 970 kPa, preventing potential structural damage from the high lateral resistance. Furthermore, the mechanical behavior of the crawler in its axial direction is tunable when applying a magnetic field opposite to the net magnetization direction of the crawler, stretching and stiffening the structure from its initial stress-free configuration. The stiffness (measured at 10% strain) can be reinforced to 11.5, 12.5, and 14.1 kPa under −10-, −20-, and −30-mT magnetic fields, respectively. These results demonstrate the tunable structure stiffness to help the crawler overcome the resistance from the axial direction during the crawling motion. We remark that the lateral stiffness of the crawler is also tunable by the magnetic field, as shown in fig. S11. When the negative magnetic field is applied, the crawler is stretched, and its lateral stiffness is almost unchanged. When the positive magnetic field is applied, the crawler contracts, and its lateral stiffness is enhanced with an increasing magnetic field.

Fig. 5. Anisotropic and magnetically reinforced structure stiffness of the Kresling crawler.

(A) Schematic of the compression tests along axial and lateral directions of the crawler. Compressive stress-strain curves for the crawler (B) along the axial direction under different magnetic fields and (C) along the lateral direction. The negative value of the magnetic field indicates that the magnetic field has the opposite direction with the net magnetization of the Kresling crawler, tending to stretch the crawler. (D) Schematic of crawling in a confined space and corresponding magnetic field profile. (E) The crawler gradually cracks the open front space and moves forward in a timely fashion. Scale bar, 5 mm.

The crawler is sandwiched between a PDMS substrate and a PDMS film to demonstrate that the anisotropic stiffness and magnetically assisted reinforcement of the crawler allow it to move in severely confined spaces (Fig. 5D). For the magnetic field profile in Fig. 5D, the positive 40-mT magnetic field is for the crawler contraction, and the negative 20-mT field is for the reinforced axial stiffness to help stretch the crawler. During the crawling motion, as shown in Fig. 5E, the crawler moves forward by effectively cracking open the contact area at the interface of the substrate and film. Meanwhile, its deployment under the negative magnetic field generates a large pushing force, which is essential to open and extend the crack front at the substrate-film interface (movie S4). The stride length in Fig. 5E is comparable to that of crawling motion in open spaces (~3 mm in Fig. 3B), indicating the capability of the crawler to move in confined spaces.

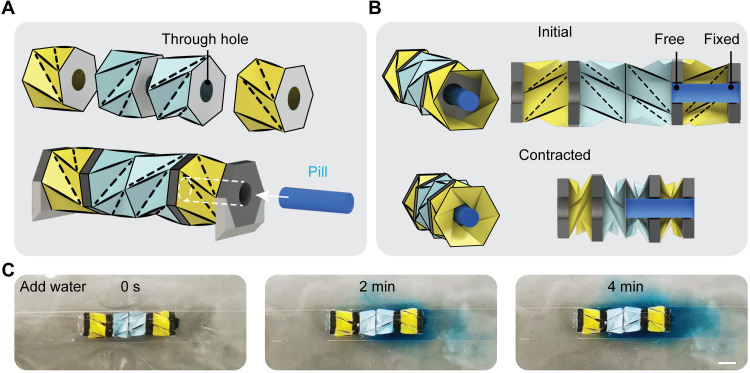
With the capability to agilely crawl and steer under precise magnetic control and move in confined spaces, the miniaturized Kresling crawler could potentially be used for biomedical applications like endoscopy, biopsy, or on-demand drug release. Components such as mini cameras, forceps, or drug pills can be integrated into the system to enable these functions. Note that the Kresling unit is a thin shell structure whose inner cavity permits the loading of functional components without increasing the overall dimension of the system, which is especially favored for environments with limited space. In Fig. 6, we demonstrate the drug storage and release of the Kresling crawler. As shown in Fig. 6A, to use the Kresling origami inner cavity as storage, the crawler is modified with a through hole in its axial direction by assembling Kresling units and magnetic plates with holes. Then, a cylinder-shaped pill is inserted into the crawler for drug storage. Here, the pill has a length equal to the total thickness of two magnetic plates and one Kresling unit, illustrated by the cross-sectional view of the crawler (Fig. 6B). The pill is fixed to the rightmost magnetic plate, having a diameter slightly smaller than the diameter of the through hole. When the crawler contracts, the pill can be pushed into the adjacent unit without influencing the crawling motion, as illustrated in Fig. 6B. Although the internal space of the Kresling unit shrinks during the contracting process, the triangular panels do not interfere with the central cylindrical pill. To illustrate the on-demand drug release capability of the crawler, we fabricate the pill by encapsulating blue dye inside the cylindrical water-soluble paper. Once the crawler reaches the target position, water is poured to surround the crawler (movie S4). Then, the pill gradually dissolves in the water environment, as indicated by the intensity of the blue dye for 4 min (Fig. 6C). On the basis of various applications, alternative drug release mechanisms are also available such as using pH-responsive or protein-sensitive materials in further works.

Fig. 6. Conceptual scheme for drug storage and release using the Kresling crawler.

(A) Exploded view and assembly of the modified Kresling crawler with a through hole. The internal cavity of the front Kresling unit is used for pill storage. (B) Pill positions at initial and contracted states of the Kresling crawler. The crawler contracts without interfering with the cylindrical pill. (C) Pill gradually dissolves in water as indicated by the intensity of the blue dye for 4 min. Scale bar, 5 mm.

DISCUSSION

In this work, we have demonstrated a magnetically actuated small-scale Kresling crawler for effective in-plane crawling motion in confined spaces. The Kresling dipole is introduced as the building block of the crawler, canceling out the relative rotation between the two ends of the crawler for contraction-only motion. Rationally designed torque distribution for simultaneous contraction of the Kresling units is implemented by magnetic actuation for crawling. Magnetic actuation also provides the capability of steering by driving the rigid body rotation of the crawler. In addition, the anisotropic and magnetically tunable structure stiffness helps the crawler effectively overcome the large resistance from severely confined spaces during crawling. Last, we demonstrate the drug storage and release capabilities of the crawler by using the inherent internal cavity of the Kresling unit. To expand the work, advanced fabrication methods, such as small-scale three-dimensional printing (49), stress-controlled folding (50), and mechanically guided assembly (51), can further downsize the origami crawler, bringing forth potential applications in more narrow and confined environments. Highly autonomous biomedical robots based on the presented design are promising for future disease diagnoses and treatment by integrating the functionalities of sensing, vision, computing, and drug storage into the Kresling origami internal cavity.

MATERIALS AND METHODS

Fabrication of the Kresling crawler

The four-unit Kresling crawler is fabricated by assembling Kresling units, magnetic plates, and feet with anisotropic friction. The Kresling unit is folded from the designed Kresling pattern (fig. S1) using polyethylene film (0.05 mm thick). Hexagonal Mylar plates (0.127 mm thick) are attached to the top and bottom planes of the unit to provide high stiffness. Hexagonal magnetic plate (edge length of 3.9 mm and thickness of 1.4 mm) is made of Ecoflex 00-30 silicone (Smooth-On Inc., USA) embedded with 40 volume % hard magnetic particles (NdFeB, average size of 100 μm; Magnequench, Singapore). The feet are molded by PDMS (base to curing agent in a ratio of 5:1; Sylgard 184, Dow Corning, USA) with dimensions shown in fig. S8A. Acetate tape is attached to the inclined surface of the feet to provide lower friction than PDMS.

Finite element analysis

The commercial software Abaqus 2020 (Dassault Systèmes, France) is used for the FEA of the Kresling crawler contraction. Linear elastic material models are used for hexagonal bases, triangular panels, and hinges connecting the panels with the C3D8 element for the whole model discretization. More details about sample fabrication, FEA, material characterization, and experimental setup are provided in the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S11

Table S1

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S4