Direct measurement of nanoscale filamentary hot spots in resistive memory devices

Abstract

Resistive random access memory (RRAM) is an important candidate for both digital, high-density data storage and for analog, neuromorphic computing. RRAM operation relies on the formation and rupture of nanoscale conductive filaments that carry enormous current densities and whose behavior lies at the heart of this technology. Here, we directly measure the temperature of these filaments in realistic RRAM with nanoscale resolution using scanning thermal microscopy. We use both conventional metal and ultrathin graphene electrodes, which enable the most thermally intimate measurement to date. Filaments can reach 1300°C during steady-state operation, but electrode temperatures seldom exceed 350°C because of thermal interface resistance. These results reveal the importance of thermal engineering for nanoscale RRAM toward ultradense data storage or neuromorphic operation.

Direct measurement reveals that nanoscale memory filaments heat up to over 1000°C during operation.

INTRODUCTION

Future information technologies will need ultrahigh storage densities to process unprecedented amounts of data (1, 2), beyond the capabilities of today’s computing systems. Resistive random-access memories (RRAM) (3, 4) promise such densities by being stackable in three dimensions (3D) (5) and by storing data in nanoscale (6–8) conductive filaments (CFs). RRAM can also be used at the heart of neuromorphic computing as a gradually programmable, synapse-like device (9–11). Typical RRAM cells have a compact crossbar structure (4F² footprint, where “F” is the minimum technology half-pitch) and benefit from low-temperature fabrication, compatible with standard complementary metal-oxide semiconductor (CMOS) technology (12). An RRAM cell includes a switching layer, e.g., a metal-oxide like HfO₂, Ta₂O₅ (3), or even emerging 2D materials like hexagonal boron nitride (h-BN) (11) or MoTe₂ (13), sandwiched between metallic top and bottom electrodes (TE and BE, respectively). RRAM operates through forming, partially breaking (reset), and reconnecting (set) nanoscale CFs with diameters as low as ~7 nm (6–9) in the switching layer. With enormous power densities (>10¹³ W/cm³) in such nanoscale volumes, the corresponding temperature rise has been estimated to be as high as 1000 K across multiple studies (14–16) exclusively through electrothermal models of device behavior.

However, measurements of CF heating in RRAM devices have been very challenging, needing either destructive sample processing or indirect estimation. For instance, postmortem analysis of an RRAM device by transmission electron microscopy (17) suggested that the material could have heated to as much as 850 K. Other studies used a microthermal stage (18) or pulse-based electrical thermometry (19) to indirectly estimate RRAM thermal properties, without spatial resolution. Efforts to spatially resolve the localized heating in resistive memory have used optical techniques that are diffraction-limited and require nonstandard cells (20, 21), or scanning probe techniques without quantifying the temperature (22, 23).

In this work, we quantify individual hot spots in realistic metal-oxide RRAM devices and directly attribute them to Joule heating in sub–10-nm diameter CFs under electrical bias. We achieve nanoscale temperature maps using scanning thermal microscopy (SThM) with a novel calibration approach (24), while comparison with detailed simulations reveals that the electrode materials and their thermal coupling with the CF ultimately determine heat spreading in RRAM devices and, thus, thermal cross-talk in RRAM arrays.

RESULTS

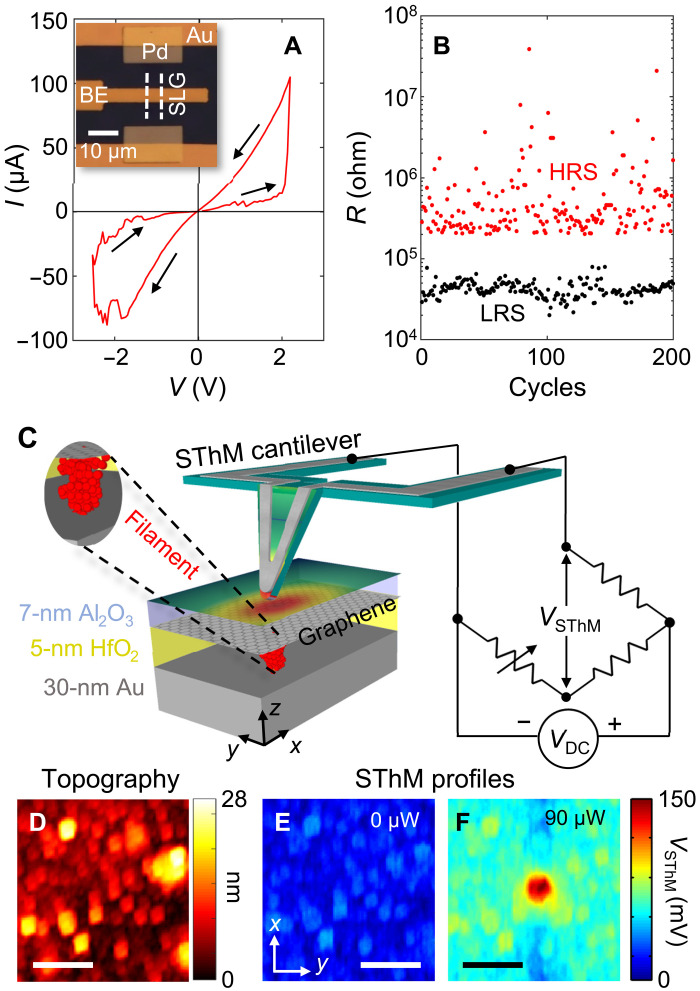
Our crossbar RRAM devices use HfO₂ as the switching metal oxide and TEs that are either conventional metals (TiN), single-layer graphene (SLG), or two-layer graphene (2-LG). All devices are capped with a thin layer of Al₂O₃ (see Materials and Methods). The ultrathin graphene TEs are used because they allow the most intimate thermal coupling between the SThM tip and the buried CF, as further described below. As an example, Fig. 1A displays repeatable switching current versus voltage (I-V) for an RRAM device with SLG as TE, shown in the optical image inset. The CF in this RRAM cell is initially formed at ~4 V under 1-μA current compliance (see Materials and Methods), and Fig. 1B displays >200 switching cycles (also see fig. S1).

Fig. 1. Graphene-contacted RRAM and SThM.

(A) Measured I-V of RRAM device with SLG as the TE using adaptive pulsed switching. Inset: Optical image of such a device. (B) Best devices switched >200 cycles with 1-μs adaptive pulsed switching (see section S1). (C) Schematic of SThM measurement on RRAM devices, showing a Wheatstone bridge connected to a typical SThM cantilever. The cantilever scans with a low V_DC in physical contact with the top surface of the device. For the axes displayed: x and y are in and perpendicular to the SThM scan direction, respectively, while z is in the vertical direction. (D) Topography scan and (E and F) steady-state SThM on SLG TE device from (A) in the LRS at 0 and 90 μW, respectively. Scale bar, 500 nm.

Figure 1C shows a schematic of the SThM scanning probe technique (25–28) that enables temperature measurements with nanoscale resolution, using a sharp V-shaped thermoresistor in direct contact with the sample surface. Our SThM setup can simultaneously map the topography and heating (in terms of the SThM voltage V_SThM; see Materials and Methods) at the top surface of the sample under steady-state bias conditions. We compare V_SThM scans and quantify top temperature rise (ΔT_S) above the ~20°C ambient for multiple bias conditions, to study self-heating in our RRAM crossbars. Figure 1D shows the topography of the 1.5 × 1.5 μm² cell area, while Fig. 1 (E and F) corresponds to V_SThM surface maps of the SLG device in the low-resistance state (LRS) with 0- and 90-μW dissipated electrical power (P) in the device, respectively.

We detect a single hot spot on the TE surface (Fig. 1F), a clear signature of highly localized Joule heating from the CF. This represents the first direct observation of a CF hot spot with sub–100-nm resolution in a crossbar RRAM device. We note that this surface hot spot is not the same as the highest temperature in the entire device, which is likely within the buried CF. We also note that hot spots are not detected in the high-resistance state (HRS) for devices with higher resistance ratio (R_HRS/R_LRS > 10), further underscoring the CF origin of self-heating. The steady-state power in HRS can be too small to enable any hot spot observation under SThM, and at higher electrical power, the device typically switches to the LRS.

Despite the direct surface measurement, extracting the CF temperature from the measured V_SThM remains challenging at first sight. The SThM tip temperature rise ΔT_tip is lower than the sample surface temperature rise ΔT_S (29), which itself is lower than the temperature rise of the CF, ΔT_CF. We first discuss our approach to quantify ΔT_S from V_SThM. Thermal coupling of the sample to the SThM tip occurs not only by direct heat conduction but also through convection (30) and a water meniscus (30, 31) at the tip-sample interface. The result is a net thermal exchange radius (r_th) around the tip-sample contact as shown in Fig. 2A. These effects can be combined through an SThM calibration factor F(w) = [V_SThM,Δ(w) − V_SThM,0(w)]/ΔT_S, where the first term is the measured SThM voltage at the center of an isothermal calibration line of width w and temperature ΔT_S, and the second term is the SThM voltage at the same position with ΔT_S = 0.

Fig. 2. SThM calibration and validation with Raman thermometry.

(A) Tip-sample thermal exchange on metal line heaters of different widths (w), showing an effective thermal exchange radius r_th due to tip-sample conduction (Q_S) shown in red arrow, by convection (Q_conv) shown in black, and by water meniscus (Q_water) in blue. (B) Extracted calibration factors using SThM scans indicating an r_th ≈ 100 nm by individual linear fits (black, error bars show 95% confidence intervals), simple deconvolution (blue), and Wiener deconvolution (orange). See section S3. (C) Combined schematic of SThM and Raman thermometry measurement on same RRAM crossbar with single-layer (1 liter) MoS₂ as Raman-active layer. (D) Extracted SThM (blue squares) and Raman (maroon circles) top temperature rise normalized by applied electrical power. The gray “band” replots the SThM data by averaging it across the Gaussian laser spot size (~600 nm), revealing good agreement with the Raman thermometry. Inset images show SThM (left) and Raman ΔT_S (right). Temperature color range for insets is from 0 to 38 K. Scale bars, 750 nm.

Because of the nanoscale hot spots in these RRAM devices, calibration of the SThM tip on micrometer-scale isothermal lines is insufficient. Thus, we calibrated the SThM tips on metal heater lines of nominal widths ranging from 50 to 750 nm, as detailed in Materials and Methods and figs. S2 and S3. The extracted calibration factors in Fig. 2B indicate F(w) ≈ 6.5 ± 1 mV/K for w > 200 nm, while F(w) decreases for w < 200 nm, in good agreement with an expected r_th ≈ 100 nm from previous work (31). Nearly 46% of heat transfer from sample to SThM tip is through the thermal exchange radius instead of direct conduction. Because the hot spot measured in Fig. 1F was < 200 nm (full width at half maximum) and not an isothermal feature, we implement two deconvolution approaches, simple and Wiener (32), to numerically extract arbitrary temperature profiles from V_SThM (see section S3 for details), as verified against measured values for F(w) in Fig. 2B. We also validate our SThM calibration by comparison to Raman thermometry on the same device using a single MoS₂ layer transferred on top because of its higher Raman sensitivity (33), as shown in Fig. 2C. Good agreement between the Gaussian-averaged SThM temperature and the Raman thermometry data for the same device (Fig. 2D) validates our SThM calibration.

In Fig. 3 (A to D), we reveal how the hot spot generated by the CF changes with different TEs, including TiN/Ti/Pt, TiN, 2-LG, and SLG. A single, nanoscale hot spot imaged in all devices is shown in the corresponding figures. However, the TE vertically and laterally spreads the heat generated by the CF, thus reducing ΔT_S below ΔT_CF. With the ultrathin graphene TE, we minimize the temperature drop across the thickness of the TE, allowing the most intimate thermal coupling between the SThM tip and the buried CF. Imaging RRAM devices with TE thickness from 50 to sub–1 nm (Fig. 3, A to D) reveals that the hot spot width appears >120 nm, but the true diameter of the buried CF is expected to be smaller, even below ~10 nm as observed for HfO₂-based RRAM by Celano et al. (6). The normalized ΔT_S at similar power levels are shown in Fig. 3E for all four device types. The narrowest hot spot is imaged in the device with the thinner TiN electrode (Fig. 3B), confirming more lateral heat spreading in the thicker metal TE (Fig. 3A) and in devices with 2-LG and SLG TE (Fig. 3, C and D), due to the larger thermal healing length (L_H) in these configurations (see section S5).

Fig. 3. Comparison between four different RRAM types measured.

RRAM device stacks and typical SThM extracted temperature with the following: (A) 15-nm TiN/2-nm Ti/33-nm Pt and (B) 15-nm TiN TE. For graphene devices, we measured the following: (C) 2-LG and (D) SLG as TE. All devices are capped by ~7-nm Al₂O₃. Scale bars, 500 nm. (E) Normalized ΔT_S across hot spots at 100- to 200-μW electrical power (symbols), corresponding to the different TEs shown in (A) to (D). Each temperature profile is normalized to its peak value, with the baseline subtracted. Dashed lines show Gaussian fits to the corresponding data. Lateral heat spreading is least for the device type in (B), with 15-nm TiN TE. (F) Estimated top surface temperature rise versus electrical power for devices with different TE. Proximity of SThM tip to filament has a weak effect on ΔT_S, pointing to high thermal interface resistance in all four cases. Power shown on the x axis is after subtracting the power dissipated in the series resistance and electrodes (see section S10).

DISCUSSION

Our observations point to heat spreading in the TE and not the CF diameter, being most important for thermal cross-talk in dense RRAM arrays. Figure 3F displays ΔT_S as a function of applied power. Because of the combined TE and Al₂O₃ capping thickness, the ΔT_S is evaluated ~55 nm above the CF for the device with 50 nm TE and ~7 nm above the CF for the devices with graphene TE (see Materials and Methods). Here, we observe three trends: First, among devices with graphene TE, the one with 2-LG displays similar ΔT_S within variability as compared with the device with SLG. This is due to slightly better lateral heat spreading in the 2-LG countered by the slightly higher series resistance due to interlayer resistance. Second, among devices with metal TE, the one with 50-nm thickness displays lower ΔT_S than the device with 15-nm metal TE. This is consistent both with better lateral heat spreading and with wider initial CF diameter in the device with 50 nm TE, because of the lower series resistance of this TE (6). Third, between the graphene and metal TE devices, our simulations (described below) suggest that effects from different L_H and filament diameter are insufficient to explain their different ΔT_S values. Instead, we find that the thermal boundary conductance (TBC) of the CF-TE interface (34), denoted by G_CF-TE, and the combined effect of the shape and thermal conductivity of the CF (k_CF) itself play important roles in determining the temperature difference between the CF and top surface.

We also perform SThM measurements during device operation, as shown in Fig. 4A, simultaneously with the measured I-V, here for an SLG TE for the most intimate coupling between SThM tip and CF. An example of SThM measurement on relatively conductive, ohmic HRS is also seen in Fig. 4A. We clearly observe a transition from HRS to LRS at ΔT_S ≈ 330 K (i.e., a surface temperature of ~350°C), with the (buried) ΔT_CF expected to be much higher. This observation is not predicted from electrothermal RRAM models in the literature (15, 16) and demands further investigation. This high ΔT_S can elevate neighboring RRAM device temperatures in an array through the electrodes every switching cycle, to result in a substantial array reliability challenge as thermal cross-talk. To gain insight into heat spreading from the CF and to estimate ΔT_CF, we perform electrothermal simulations, displayed in Fig. 4B at three different input electrical powers. This electrothermal model is agnostic to electronic transport mechanisms within the CF while attempting to derive a thermal understanding of the RRAM device and CF material stacks to match SThM measurements and measured voltages. We match our simulations to measured ΔT_S profiles at P ~ 100 μW (applied during SThM measurement) with CF diameter d_CF ~4 nm for the device with TiN TE and ~13 nm for the device with SLG TE, simultaneously fitting the measured electrical resistance of the device as well. Further details are in section S6.

Fig. 4. Maximum filament temperature during operation.

(A) Simultaneously measured I-V and ΔT_S during device operation, here with SLG TE. Symbol colors represent ΔT_S directly at the hot spot above the CF. The SThM is relatively slow compared with the CF time scale, which can cause device failure during this measurement. (B) Simulated device temperature cross sections, axisymmetric around the CF, at three different power levels. Temperatures at the top surface of the Al₂O₃ (ΔT_S) and in the filament center (ΔT_CF) differ depending on power and TBC of the CF-TE interfaces. (C) Maximum surface and filament temperature rise, as a function of input electrical power. Blue symbols are the simulated ΔT_S, in good agreement with the measured values corresponding to both LRS and HRS in (A) (black symbols). Orange symbols display the ΔT_CF (i.e., the maximum CF temperature rise). Simulated temperatures of ΔT_CF,max from individual panels in (B) are shown as (i), (ii), and (iii) in (C), respectively.

We compare measurements during device operation with our simulations in the LRS, as shown in Fig. 4C. The best agreement is found using a double conical filament shape in our simulations (see inset), consistent with direct measurements on HfO₂ RRAM devices by Celano et al. (6). Further filament properties and possible shape-related effects are addressed in section S8. The calculated maximum ΔT_CF during operation is also plotted in Fig. 4C, reaching up to ~1100 K at the filament constriction. The thermal resistance of the filament-TE interface (1/G_CF-TE) contributes more than the thermal resistance of the nanoscale filament (see sections S7 and S8) at all power levels, while the thermal resistance of the TE itself is significantly lower in all cases. G_CF-TE ~75 MW m⁻² K⁻¹ at 550 K for TiN as TE can be estimated by matching the simulations to measured ΔT_S and the electrical resistance and is found to be in the range of typical TiN interfaces (35). The same approach finds slightly higher TBC at the CF-SLG interface, and additional details about this thermal analysis are given in sections S8 and S9.

While the mechanism of resistance change in an RRAM device could be caused by changes of defect concentration (36) or changes in CF diameter (37), both effects require self-heating to cause chemical and structural changes in the CF region. Our work points to the most effective knob to control self-heating: the thermal interfaces to the CF. Lower G_CF-TE increases heat confinement in the CF, creating a larger initial d_CF during forming or a higher initial defect density within a similar d_CF. RRAM cells with wider or more defect-rich initial CF are more easily programmed into analog memory states (10) with varying CF diameter or CF defect density, respectively. On the other hand, more heat confinement during switching provides more power per CF volume, thus making switching more abrupt. Our work shows a first proof of concept that the thermal properties of the CF-TE interface primarily determine heat confinement within a CF and, thus, RRAM device behavior for analog or digital memory operation.

In summary, these represent the first direct measurements of nanoscale hot spots caused by individual filaments in functioning metal-oxide RRAM devices. Using TEs ranging from conventional TiN (~50 nm thick) to SLG (sub–1 nm thick) enabled the most intimate thermal coupling of the SThM with the CF, while elucidating the heat spreading role of the TE. We also uncovered that the thermal resistance of the filament-TE interface is a more important limiter of heat confinement within a CF than the thermal resistance of the TE itself. From simulations, our study reveals a CF diameter of 4 nm with TiN TE and 13 nm with SLG TE at P ~ 100 μW with temperature rise as high as ~1100 K above ambient (i.e., over 1300°C). These results suggest that dense, future RRAM arrays can be made more tolerant to thermal cross-talk by using electrodes with low thermal conductivity. Individual devices could also be made more energy efficient by choosing electrodes with a TBC that is low at the filament-electrode interfaces to confine the CF heating, and high at the surrounding oxide interfaces to minimize lateral heat spreading. Nanoscale thermal engineering at the filament-electrode interfaces could also control heat confinement toward analog versus digital switching in RRAM devices.

MATERIALS AND METHODS

Device fabrication

We use commercially purchased Si wafers coated with thermally grown 30-nm SiO₂ as our starting substrates. Using a lift-off layer (Shipley LOL 1000) and standard Shipley 3612 photoresist-based optical lithography, we first define 5-μm-wide BE strips and contact pad patterns. Then, for fabricating the standard metal-insulator-metal devices, we deposit 30-nm-thick Pt in the defined BE pattern using electron-beam (e-beam) evaporation. For fabricating the devices with graphene as TE (or graphene-insulator-metal devices), we deposit 30-nm-thick Au as the BE material instead, using e-beam evaporation. We dissolve the unexposed photoresist, in each case, using N-methyl pyrrolidone (NMP) treatment at 70°C for 25 min, followed by successively rinsing our samples in acetone and isopropanol (IPA) for 2 min each, and drying with an N₂ blow gun. The metal (Pt or Au) coating the unexposed photoresist is lifted-off because of this process, leaving behind the patterned BE metal features. As Au is more ductile compared with Pt, the Au patterns show negligible lift-off edge features after lithography. We then deposit 5-nm-thick HfO₂ using atomic layer deposition (ALD) at 200°C on both sets of samples using tetrakis(dimethylamido)hafnium and deionized (DI) water as precursors.

To fabricate the standard metal-insulator-metal devices, after the HfO₂ ALD step, we use physical vapor deposition to sputter ~15-nm-thick TiN TE directly on the HfO₂ in a blanket manner. The TiN sputter process is done from a Ti target in a 3:1 Ar:N₂ ambient under 65-W dc bias. The TE is deposited in a different tool, within the quickest time allowed by the laboratory layout, i.e., a few minutes.

To fabricate the graphene-insulator-metal devices, after the HfO₂ ALD step, we wet transfer the SLG on top of the blanket HfO₂ by using DI water and chemical vapor deposited (CVD) graphene monolayers. For a subset of these devices, we wet transfer a second layer of graphene in a subsequent step to get devices contacted by 2-LG. The negligible lift-off features for the Au BE edges in this case ensure smooth graphene coverage after the wet transfer.

For the metal-insulator-metal devices, we pattern 5-μm-wide TE patterns and contact pads on top of the blanket TiN with optical lithography, on one subset as lift-off patterns, and on the remainder as etch patterns. The first subset of the TiN-sputtered samples is top contacted by ~2-nm-thick Ti followed by 33-nm-thick Pt, both deposited sequentially by e-beam evaporation and subsequently lifted off using NMP at 70°C for 25 min, followed by rinsing in acetone and IPA. These samples and the remainder of the TiN-sputtered samples are subjected to a SF₆ reactive ion etch plasma (to etch the remainder of the exposed TiN film), resulting in metal-insulator-metal crossbars. For the graphene-contacted devices, we pattern the SLG and 2-LG into 5-μm-wide TE stripes with optical lithography and a gentle 15-W O₂ plasma dry etch for 30 s. We contact the SLG and 2-LG TE strips with 30-nm-thick Pd on both ends, followed by 2-nm Ti/30-nm Au contact pad lithography. The Pd contacts to graphene are defined away from the crossbar area, so SLG or 2-LG serves as the TE to our RRAM devices, resulting in graphene-insulator-metal crossbars. We thus have four different RRAM crossbars: two as metal-insulator-metal devices—those with 50-nm-thick (Pt/Ti/TiN/HfO₂/Pt) and 15-nm-thick (TiN/HfO₂/Pt) metal TEs, and two as graphene-insulator-metal devices—those with transferred two-layer (2-LG/HfO₂/Au) and single-layer (SLG/HfO₂/Au) graphene TEs.

Last, we cap all our devices with 5-nm Al₂O₃ deposited by ALD at 200°C with trimethylaluminum and DI water as precursors. To ensure good Al₂O₃ coverage on the graphene-insulator-metal devices, we deposit a thin (~1.5 to 1.7 nm thick) Al “seeding” layer using e-beam evaporation, before the ALD step. This seeding layer partially oxidizes post-air exposure and pre-ALD deposition, adding ~2 nm to the ALD Al₂O₃ thickness, thus leading to the eventual ~7-nm-thick AlO_x only on top of the graphene TE devices. The metal-insulator-metal devices have a blanket 5-nm-thick Al₂O₃ layer on top.

For fabricating the metal line heaters in the SThM calibration sample (details of calibration are in section S2), we used 90-nm SiO₂/Si substrates. We first patterned four probe contact pads using optical lithography and lift-off of e-beam evaporated 2-nm Ti/50-nm Pd. We then fabricated heater patterns ranging from 50 to 750 nm with e-beam lithography using poly-methyl methacrylate with molecular weight 950 k in anisole (2% weight/volume) as resist layer. After patterning the metal lines, we deposited 2-nm Ti/30-nm Pd using e-beam evaporation and performed lift-off with NMP, acetone, and isopropanol. The final sample was coated with 10-nm Al₂O₃ deposited via ALD at 200°C.

Sample handling and preparation before SThM

The entire measurement setup and the experimenter follow careful electrical grounding protocols to prevent any electrostatic discharge (ESD) problems before mounting and manipulating the sample and the memory device. For biasing the devices, we used a probe station from Asylum Research and a Keithley 4200 parameter analyzer. The probe station is retrofitted on top of the vibration dampening stage of a MFP-3D atomic force microscopy (AFM) setup from Asylum Research before mounting samples. As-fabricated samples are mounted on this probe station on a glass slide to prevent any electrical leakage into the conductive stage. The sample is secured onto the glass slide with Kapton tape, while the glass slide is secured onto the metallic base of the probe station with permanent magnets to minimize spatial drift during SThM measurements.

Using micromanipulators for the probe station, the measurement probes are positioned within the measurement area of interest. The SThM tip (details further below) is brought into physical proximity of the area of interest by moving the entire stage but still >100 μm above the sample surface. The probes are then brought into physical contact with the device under test (DUT). The ground probe (connected to source-measure unit SMU2) is lowered on the BE pad for the DUT, while the bias probe (connected to SMU1) is lowered on the TE pad.

First, a low-voltage test is performed on the DUT for two reasons: one, to check for probing issues and, two, to ensure that the device is not in a preformed state because of unforeseen fabrication or ESD issues. For this test, a slow, dual-voltage sweep (from 0 to 2.5 V) is applied to the bias probe, and current measured at the ground probe is observed. If subpicoampere current is observed with negligible dependence on bias voltage, the micromanipulators are used to lower probes by a few micrometers to overcome any probing issue. If high current (>100 pA) is observed, the DUT is considered damaged, and micromanipulators are used to move to a different DUT. As-fabricated DUTs that show current in the range 10 to 20 pA with an increasing dependence on voltage within this voltage range are considered for the second step.

Second, the SThM tip is lowered for a topography measurement on the top surface of the DUT. This step ensures a relatively flat topography before electrical measurements, indicating a suitable device for SThM measurements with minimal topography artifacts and the absence of any surface features from ESD damage during preparation and handling.

Third, a forming and preliminary switching step is performed on the DUT that has passed the first two steps. For this purpose, we use a 10-kilohm off-chip series resistor for metal (TiN/Ti/Pt) TE devices to prevent current compliance overshoot and subsequent device breakdown during forming. For the TiN, SLG, and 2-LG TE devices, the on-chip series resistance from the respective TEs prevents current overshoot. Further forming details for devices shown in this study are in section S1. An intermediate topography check is performed after the forming step to confirm no topography damage due to current overshoot.

Fourth, the SThM tip is configured for SThM measurements and scanned over the device surface to ensure steady-state thermal signal from the setup before device heating measurements. RRAM device power across all measurements is calculated as shown in section S10.

SThM measurement setup

The scanning thermal microscope is an add-on from Anasys Instruments that was added to the MFP-3D AFM from Asylum Research. The probes were purchased from Anasys Instruments and consist of a thin Pd line on Si₃N₄. Each probe is connected to one of the arms of a Wheatstone bridge. This bridge is initially matched; an increase in temperature at the SThM probe tip causes a change in the resistance of the Pd line and subsequently a voltage mismatch in the bridge. This voltage change across the Wheatstone bridge is read out as the SThM voltage signal (V_SThM). A higher V_SThM indicates a higher SThM probe resistance and, qualitatively, a higher temperature at the SThM tip. To electrically isolate our device from the Pd line of the SThM tip, we cap our devices with Al₂O₃ as shown in the schematic in Fig. 1C. During all our measurements, we apply the same force to the surface of the devices and account for the thermal drift (see section S3). We used a gain of 1000× while extracting tip voltage change and a relative deflection set point of −0.5 V. Images were analyzed with MATLAB and Asylum Research software.

For steady-state measurements, the SThM tip moved with a scan rate of ≈0.7 to 0.8 Hz over a ≈5-μm scan line (corresponding to width of the scan image), while the device biasing voltage is held constant. Each scan line has 256 pixels. A total of 256 such scan lines taken in succession led to ≈5-μm length of the scan image.

For measurements during device operation, the SThM tip is stationary, in contact with the sample surface, while a slow (0.1 V step every 0.5 s) voltage sweep is applied to the device, to allow ample time for the sample + tip system to thermally equilibrate. The SThM tip is positioned at the observed location of the hot spot from prior steady-state scans of the same device to consequently observe ΔT_S directly above the CF.

Raman measurement setup

Raman spectroscopy was carried out using a Horiba LabRam instrument with a 532-nm laser and 100× long working distance objective with numerical aperture of 0.6 and gratings of 1800 gr/mm. Step sizes in the Raman maps were 0.25 μm, and the acquisition time of device thermal map was ~20 min. The laser spot radius is ~0.3 μm, and with 4-s acquisition time at each point with 5% laser power, the incident laser power is 150 μW (<10-μW absorbed power) to avoid laser heating in excess of the electrical heating. Temperature calibration was done with a Linkam THMS600 stage, following the procedure outlined elsewhere (33).

Supplementary Materials

This PDF file includes:

Sections S1 to S10

Figs. S1 to S9

Tables S1 to S3

References