Modeling the Impacts of Clinical Influenza Testing on Influenza Vaccine Effectiveness Estimates

Abstract

Background

Test-negative design studies for evaluating influenza vaccine effectiveness (VE) enroll patients with acute respiratory infection. Enrollment typically occurs before influenza status is determined, resulting in over-enrollment of influenza-negative patients. With availability of rapid and accurate molecular clinical testing, influenza status could be ascertained before enrollment, thus improving study efficiency. We estimate potential biases in VE when using clinical testing.

Methods

We simulate data assuming 60% vaccinated, 25% of those vaccinated are influenza positive, and VE of 50%. We show the effect on VE in 5 scenarios.

Results

Vaccine effectiveness is affected only when clinical testing preferentially targets patients based on both vaccination and influenza status. Vaccine effectiveness is overestimated by 10% if nontesting occurs in 39% of vaccinated influenza-positive patients and 24% of others. VE is also overestimated by 10% if nontesting occurs in 8% of unvaccinated influenza-positive patients and 27% of others. Vaccine effectiveness is underestimated by 10% if nontesting occurs in 32% of unvaccinated influenza-negative patients and 18% of others.

Conclusions

Although differential clinical testing by vaccine receipt and influenza positivity may produce errors in estimated VE, bias in testing would have to be substantial and overall proportion of patients tested would have to be small to result in a meaningful difference in VE.

To improve study efficiency, clinical influenza testing may be used to estimate vaccine effectiveness, as long as the majority of acute respiratory infection patients are tested, and testing does not preferentially target patients based on both vaccination and influenza status.

Evaluating the performance of influenza vaccines after routine vaccination in a population is an important component of understanding and improving the effects of influenza vaccines. The test-negative design (TND), which is adapted from case-control methodology, is the most commonly used approach for evaluating influenza vaccine effectiveness (VE). The TND approach involves comparing the frequency of prior receipt of the current season’s vaccine among patients who seek care and meet a prespecified definition of an acute respiratory infection (ARI) who test positive for influenza against ARI patients who test negative for influenza [1, 2]. Historically, accurate classification of influenza case versus noninfluenza control status has required reference laboratory molecular testing with higher sensitivity and specificity than clinical diagnostic assays available from clinically oriented laboratories [3]. Thus, common methodology enrolls ARI patients, collects study respiratory specimens, and uses a reference laboratory for molecular influenza testing [4–7]. Using this approach, the TND departs from traditional case-control methodology in 2 major ways: (1) ARI patients are enrolled before confirmation of their influenza status, and (2) on the basis of laboratory confirmation completed after enrollment, ARI patients are classified as influenza cases (if they test positive) or test-negative controls (if they test negative) [1, 2]. This approach to enrollment often leads to a large number of influenza-negative controls compared with influenza-positive cases [8], reducing study efficiency.

With widespread availability of affordable and rapid molecular testing for influenza in inpatient clinical settings, accurate influenza infection status can be ascertained for patients who are eligible for inpatient influenza VE studies. Targeting patient enrollment in influenza VE studies based on clinical molecular testing has the potential to increase the efficiency of these studies by (1) enabling timely identification and selection of influenza cases and noncases and (2) avoiding reliance on reference laboratory testing [9]. Clinical influenza testing results could potentially be incorporated with electronically linked data on vaccination history, clinical course of illness, and demographics, to conduct large and efficient inpatient VE studies.

Although such an approach is appealing, clinical influenza testing may not be systematic, and potential biases introduced by different clinical testing practices should be carefully considered. The choice of whom to test in a clinical setting, which is mainly determined by clinicians who are not part of research studies, may vary within a site and across sites. As a result, only a subset of ARI patients may be tested and therefore become eligible for VE studies relying on clinical testing. Patients who undergo clinical influenza testing may differ from those who are not tested with regard to influenza status and vaccination status, potentially introducing biases into VE estimates. Our objective is to quantify the effects of differential testing on VE estimates.

METHODS

Overview

Our simulation assumes a TND analogous to a case-control study, with the estimate of VE computed by comparing odds of vaccination between influenza-positive cases and test-negative controls, controlling for key confounders such as age, race/ethnicity, geographic location, interval from symptom onset to testing, seasonality, and underlying conditions. We compare influenza VE in the “fully tested group” versus a “clinically tested group” (ie, those tested at clinician’s discretion) of ARI patients. Based on previously conducted studies, we envisaged different clinical testing scenarios (Table 1) [10–13]. Using VE from the fully tested group as reference, we examine the departures in VE estimates introduced by different testing practices. For simplicity, other variables relevant for VE estimates, including healthcare-seeking behavior, vaccine-mediated disease attenuation, temporal confounding, and sensitivity of the ARI case definition, were not examined.

Table 1.

Rationale and Descriptions of Influenza Clinical Testing Scenarios 1–5 Among Acute Respiratory Infection (ARI) Patients

Two-by-Two Tables of Scenarios 1–5, With 25% Overall Reduction in Testing		Description of Clinical Testing Scenarios	Rationale
Scenario 1: Influenza Negative Patients Tested Less Than Others		Less testing in patients without influenza, independent of vaccination (targeted cells are b and d) by increasing C’pb and C’pd from baseline by 5%, 10%, and 15% (scenarios 1a–c)*. The proportionate reductions in C’pb:pb, C’pc:pc, and C’pd:pd can be computed by: $C^{\prime }{p}_a:p_a=C^{\prime }{p}_c:p_c=[1-((p_{b}xv)+(p_{d}xv))]/(p_a+p_c)$ Where v = 0.05, 0.10, or 0.15	Clinicians may be less likely to test ARI patients who are less likely to have influenza and/or more likely to test patients with more severe symptoms (influenza causes more severe symptoms on average than other etiologies of ARI [19, 20]).
Vaccinated, influenza positive case Cell a	Vaccinated, influenza negative control Cell b
Unvaccinated, influenza positive case Cell c	Unvaccinated, influenza negative control Cell d
Scenario 2: Vaccinated Patients Tested Less Than Others		Less testing in vaccinated patients, independent of influenza status by increasing C’pa and C’pb from baseline by 10%, 25%, and 50% (targeted cells a and b, scenarios 2a–c)* The proportionate reductions in C’pb:pb, C’pc:pc, and C’pd:pd can be computed by: $C^{\prime }{p}_c:p_c=C^{\prime }{p}_d:p_d=[1-((p_{a}xv)+(p_{b}xv))]/(p_c+p_d)$ Where v = 0.1, 0.25, or 0.5	Clinicians may ask about influenza vaccination, believe influenza infection is more likely in unvaccinated patients, and therefore target influenza testing for unvaccinated patients. Factors related to healthcare-seeking behavior could also result in this pattern of testing; for example, patients with primary care physicians may be more likely to be vaccinated and may be less likely to undergo influenza testing for an ARI because clinicians treating the ARI may opt for less testing for patients who have established providers for close follow-up.
Vaccinated, influenza positive case Cell a	Vaccinated, influenza negative control Cell b
Unvaccinated, influenza positive case Cell c	Unvaccinated, influenza negative control Cell d
Scenario 3: Vaccinated Influenza Positive Patients Tested Less Than Others		Less testing in vaccinated patients with influenza by increasing C’pa by 10%, 25%, and 50% from baseline (targeted cell a, scenarios 3a–c)* C’pa = pa (1+i) The proportionate reductions in C’pb:pb, C’pc:pc, and C’pd:pd can be computed by: $C^{\prime }{p}_b:p_b=C^{\prime }{p}_c:p_c=C^{\prime }{p}_d:p_d=(1-p_{a}xv)/(p_b+p_c+p_d)$ Where v = 0.1, 0.25, and 0.50	Clinicians may be less likely to test ARI patients who are vaccinated and likely to have influenza if influenza vaccination attenuates the severity of ARI symptoms [21, 22], and clinicians preferentially test patients with higher severity.
Vaccinated, influenza positive case Cell a	Vaccinated, influenza negative control Cell b
Unvaccinated, influenza positive case Cell c	Unvaccinated, influenza negative control Cell d
Scenario 4: Vaccinated Influenza Negative Patients Tested Less Than Others		Less testing in vaccinated patients without influenza by increasing C’pb by 10%, 25%, and 50% (targeted cell b, scenarios 4a–c) from baseline*. The proportionate reductions in C’pb:pb, C’pc:pc, and C’pd:pd can be computed by: $C^{\prime }{p}_a:p_a=C^{\prime }{p}_c:p_c=C^{\prime }{p}_d:p_d=(1-p_{b}xv)/(p_a+p_c+p_d)]$ Where v = 0.1, 0.25, or 0.5	In this situation, clinicians may be less likely to test vaccinated patients with milder symptoms less indicative of influenza (and more indicative of other respiratory viruses).
Vaccinated, influenza positive case Cell a	Vaccinated, influenza negative control Cell b
Unvaccinated, influenza positive case Cell c	Unvaccinated, influenza negative control Cell d
Scenario 5: Unvaccinated Influenza Positive Patients Tested More Than Others		More testing (less nontesting) in unvaccinated patients with influenza by decreasing C’pc by 10%, 25%, and 50% (targeted cell c, scenarios 5a–c) from baseline*. The proportionate changes in C’pb:pb, C’pc:pc, and C’pd:pd can be computed by: $C^{\prime }{p}_a:p_a=C^{\prime }{p}_b:p_b=C^{\prime }{p}_d:p_d=(1-p_{c}xv)/(p_a+p_b+p_d)]$ Where v = −0.1, −0.25, or −0.5	Clinicians may be more likely to suspect influenza and test ARI patients who are unvaccinated and more likely to have influenza.
Vaccinated, influenza positive case Cell a	Vaccinated, influenza negative control Cell b
Unvaccinated, influenza positive case Cell c	Unvaccinated, influenza negative control Cell d

^aBlack arrows represent the targeted reduction in testing.

*With accompanying increases or decreases in testing among other patients to maintain overall proportion nontested of 25%.

NOTE: C’pa, C’pb, C’pc, and C’pd: denote the proportion of nontested ARI patients that are in cells a, b, c, and d, respectively; C’ denotes proportion untested overall; number nontested overall = N*C’; p_a, p_b, p_c, p_d denote the proportion of total ARI patients in each cell.

Prevalence of Clinical Testing From the Influenza Vaccine Effectiveness in the Critically Ill (IVY) 2019–2020 Study

To gain a better understanding of the prevalence of clinical influenza testing in intensive care unit (ICU) settings, investigators from 10 ICU Influenza Vaccine Effectiveness in the Critically Ill (IVY) sites across the United States calculated the proportion of enrolled patients meeting study ARI criteria (defined in the Supplement), who received a clinical test for influenza during an early period of the 2019–2020 influenza season (December 28, 2019–January 26, 2020). Clinical testing prevalence among the 10 IVY study sites ranged from 73% to 92%, with a median prevalence of 81%. Based on testing prevalence from the IVY study sites and previous studies [12, 13], the range in overall proportion of ARI patients clinically tested was incorporated into the scenarios to provide realistic and worst-case scenario estimates of estimated VE (eVE) (Supplement Table S3).

Analysis

Our simulation includes 2000 ARI patients with vaccination prevalence of 60% (based on national vaccine coverage estimates among children [14]). We assumed VE of 50% and that prevalence of influenza infection among unvaccinated ARI patients was 25%. Thus, using cell designations as per Table 1, 2 × 2 table values were a = 171, b = 1029, c = 200, and d = 600; influenza positivity was 18.6% overall and 14.5% among those vaccinated (Supplement Table S1). In sensitivity analyses, we varied the range of values for vaccine coverage from 10% to 90% and percentage of ARI patients with influenza from 16% to 23% (Supplement Tables S4 and S5) [8, 15]. We assumed use of a clinical diagnostic test with perfect sensitivity and specificity.

Using these assumptions, we calculated the number of patients in each 2 × 2 table cell for 5 scenarios (Table 1). We generated VE estimates as 1 – (odds ratio [OR] of vaccination in influenza-positive versus influenza-negative patients) × 100 or 1 − OR × 100, where OR is specified in Equation 1. We report “target VE (tVE)” for the fully tested group and an “eVE” for the various clinically tested groups.

Equation 1:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{O}\mathrm{R}=\frac{(\mathrm{a}\times \mathrm{d})}{(\mathrm{b}\times \mathrm{c})}}\end{array}}$$

We specify C’ as the overall proportion not tested and v as the additional change in proportion not tested in 1 or more cells (designated “targeted cell(s)”), which differed among the scenarios. We assumed that if nontesting in the targeted cells is increased by v, then nontesting in other cells would decrease, such that the total nontesting for all cells combined remained at C’. Equations for these calculations are in Table 1 and the Supplement. For example, in scenario 3, where cell a was the targeted cell, if C’ = 0.25 and v = 0.1, the proportion not tested in cell a = C’*(v + 1) = 0.25*1.1 = 0.275. Using equations in Table 1, we calculate the proportion nontested in the other cells (cells b, c, and d) = 0.248, resulting in overall proportion not tested C’ = 0.25. The difference in nontesting between the targeted cell and the other cells is 0.275 – 0.248 = 0.027 or 2.7%.

We designated “baseline” as overall proportion not tested = C’ = 0.25. First, we made calculations maintaining C’ at 0.25 and varying the values of v, eg, v = 0, 0.05, 0.10, 0.15, and 0.50. For some scenarios, high values of v produce impossible results (ie, negative cell values), and so a ceiling value for v that avoids impossible results was specified. Second, we made calculations varying C’ from 0 to 1.0 and for each value of C’ varying the values of v similar to above.

We defined a baseline scenario and 5 clinical scenarios. In the baseline scenario, nontesting in all cells was the same (25%). As per equation 1, this produced proportionate decreases in the OR numerator and denominator (equation 1), resulting in eVE = tVE = 50%. The 5 scenarios are outlined in Table 1. In brief, decreased testing was assumed in influenza-negative patients (cells b and d) in scenario 1, in vaccinated patients (cells a and b) in scenario 2, in vaccinated influenza-positive patients (cell a) in scenario 3, and in vaccinated influenza-negative patients (cell b) in scenario 4. Increased testing was assumed in unvaccinated influenza-positive patients (cell c) in scenario 5.

RESULTS

The baseline scenario produced the same decreases in the numerator and denominator of the OR (equation 1) and thus eVE = tVE = 50% (Table 2). In scenario 1, testing is less frequent in patients without influenza resulting in lower values in cells b and d, and, because we fix C’, higher values of cells a and c. Again, because proportionate changes occur in the OR numerator and denominator, eVE remains unchanged from tVE at 50%. In scenario 2, testing is less frequent in vaccinated patients resulting in lower values in cells a and b and higher values in cells c and d, proportionate changes in the OR numerator and denominator, and unchanged values of eVE at 50%.

Table 2.

Estimated Vaccine Effectiveness for Various Levels of Clinical Nontesting in a Simulated Group of 2000 ARI Outpatients* With the Overall Proportion Not Tested = 25% (C’)

% Nontesting Variation Compared With Baselinea (v)	Vaccinated Influenza (+) (Cell a, n = 172)	Vaccinated Influenza (−) (Cell b, n = 1028)	Unvaccinated Influenza (+) (Cell c, n = 200)	Unvaccinated Influenza (−) (cell d, n = 600)	eVE Among Clinically Tested
Baselineb: 75% of All Patients Are Tested in All 4 Cells, 25% Not Tested = C’
Not tested N (%)
0%	43 (25)	257 (25)	50 (25)	150 (25)	50%
Scenario 1b: Influenza-Negative Patients Tested Less Than Baseline
5%	34 (20)	270 (26)	39 (20)	157 (26)	50%
10%	25 (15)	282 (27)	28 (15)	165 (27)	50%
15%	15 (9)	295 (29)	17 (9)	173 (29)	50%
Ceiling, 23%	1 (0.6)	315 (31)	1 (0.6)	183 (31)	50%
Scenario 2b: Vaccinated Patients Tested Less Than Baseline
10%	48 (28)	282 (28)	42 (21)	128 (21)	50%
25%	54 (31)	321 (31)	31 (16)	94 (16)	50%
50%	65 (38)	385 (38)	12 (6)	38 (6)	50%
Ceiling, 65%	71 (41)	424 (41)	1 (0.5)	4 (0.5)	50%
Scenario 3b: Vaccinated Influenza-Positive Patients Tested Less Than Baseline
10%	48 (28)	254 (25)	50 (25)	149 (25)	52%
25%	54 (31)	251 (24)	49 (24)	146 (24)	54%
50%	65 (38)	245 (24)	48 (24)	143 (24)	59%
57%	68 (39)	243 (24)	47 (24)	142 (24)	60%
Ceiling, 100%	86 (50)	233 (22)	45 (22)	136 (22)	68%
Scenario 4b: Vaccinated Influenza-Negative Patients Tested Less Than Baseline
10%	39 (23)	282 (26)	45 (23)	134 (23)	46%
25%	32 (19)	321 (30)	37 (19)	110 (19)	41%
26%	31 (18)	324 (32)	36 (18)	109 (18)	40%
50%	21 (12)	385 (36)	24 (12)	71 (12)	29%
Ceiling, 94%	1 (0.6)	498 (46)	0 (0)	1 (0.2)	3%
Scenario 5b: Unvaccinated Influenza-Positive Patients Tested More Than Baseline
10% reduction	43 (25)	260 (25)	45 (23)	152 (25)	52%
25% reduction	44 (26)	264 (26)	38 (19)	154 (26)	54%
50% reduction	46 (27)	276 (27)	17 (8)	161 (27)	58%
67% reduction	46 (27)	276 (27)	17 (8)	161 (27)	60%
Ceiling, 100%	48 (28)	286 (28)	0 (0)	167 (28)	64%

Abbreviations: ARI, acute respiratory infection; C’, the overall proportion not tested; eVE, estimated vaccine effectiveness; v, the additional change in proportion not tested in 1 or more cells.

*Overall percentage vaccinated is 60%, prevalence of infection in vaccinated patients is 25%, true vaccine effectiveness is 50%.

^aRefers to changes in proportion of not-tested ARI patients in the targeted cells compared with the baseline scenario of 25% not tested in all cells.

^bCells with targeted changes in nontesting are bolded.

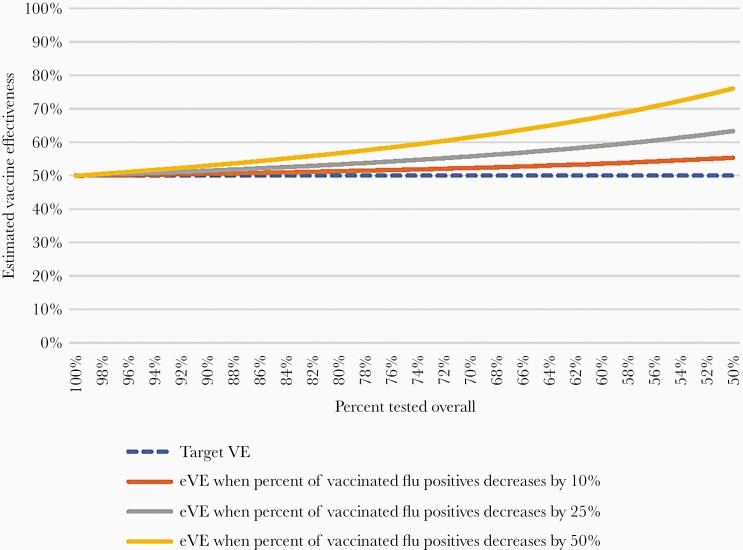
In scenario 3, vaccinated patients with influenza are less likely to be tested resulting in lower values in cell a and higher values in other cells. These changes result in lower OR values and higher eVE values. When the overall proportion not tested (C’) is held constant at 25% and the increase in nontesting for cell a (v) varied from 10% to 100%, eVE increases from 52% to 68% (Table 2). When C’ is varied from 100% to 50%, for v = 50%, eVE increases from 50% to 76%; smaller values of v produce smaller increases in eVE (Figure 1). Estimated VE will be 60% (ie, bias 10%) when the proportion not tested is 39% for cell a (vaccinated cases) and 24% for the other cells (15% absolute difference in testing frequency) (Table 2).

Figure 1.

Changes in estimated vaccine effectiveness (eVE) when overall percentage tested decreases by 50%–100% and when less testing occurs among vaccinated influenza cases (scenario 3).

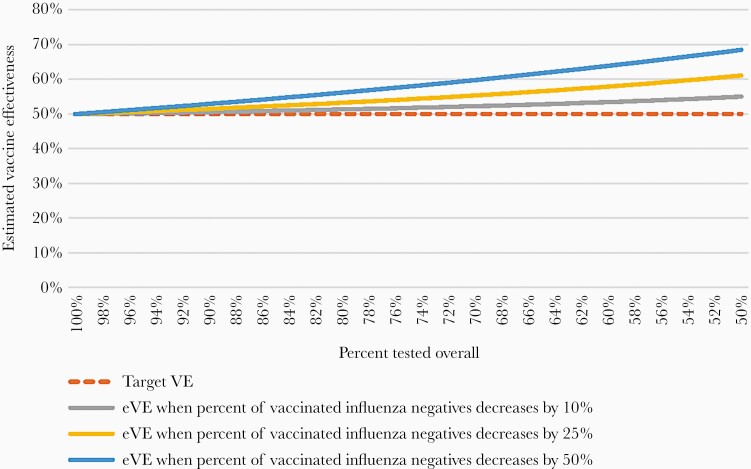
In scenario 4, vaccinated patients without influenza are less likely to be tested resulting in lower values in cell b, higher values in other cells, and lower eVE. When C’ is held constant at 25% and v varied from 10% to 94%, eVE decreases to 46% to 3% (Table 2). When C’ is varied from 100% to 50%, for v = 50%, eVE decreases from 50% to −53%; smaller values of v produce smaller decreases in eVE (Figure 2). Estimated VE will be 40% (ie, bias −10%) when the proportion not tested is 32% for cell b (vaccinated noncases) and 18% for the other cells (14% absolute difference in testing frequency) (Table 2).

Figure 2.

Changes in estimated vaccine effectiveness (eVE) when overall percentage tested decreases by 50%–100% and when less testing occurs among vaccinated acute respiratory infection patients without influenza (scenario 4).

In scenario 5, unvaccinated patients with influenza are more likely to be tested resulting in higher values in cell c, lower values in other cells, and higher eVE. When C’ is held constant at 25% and v varied from 10% to 100%, eVE increases from 52% to 64% (Table 2). When C’ is varied from 100% to 50%, for v = 50%, eVE increases from 50% to 68%; smaller values of v produce smaller increases in eVE (Figure 3). Estimated VE will be 60% (ie, bias +10%) when the overall proportion not tested is 25%, 8% for cell c (unvaccinated cases), and 27% for the other cells (19% absolute difference in testing frequency) (Table 2).

Figure 3.

Changes in estimated vaccine effectiveness (eVE) when overall percentage tested decreases by 50%–100% and when more testing occurs among unvaccinated acute respiratory infection patients with influenza (scenario 5).

To account for variability in vaccination coverage and the proportion of ARI patients with influenza by season and healthcare setting, we provided estimates of eVE for a range of vaccine coverage and influenza prevalence (Supplement Tables S4 and S5). For scenario 3, as vaccine coverage increased, the magnitude of bias for eVE increased only slightly (Supplement Table S4). Likewise, when the proportion of vaccinated ARI patients with influenza decreased (and thus tVE was >50%), the magnitude of bias decreased (Supplement Table S4). When the proportion of vaccinated ARI patients with influenza increased to 90%, however (and thus tVE was <50%), the magnitude of bias increased substantially (by ≥10%) (Supplement Table S4).

DISCUSSION

Widespread use of molecular influenza testing in the clinical setting could be leveraged to increase efficiency of the TND for estimating influenza VE. However, it is likely that clinical testing is obtained only on a subset of ARI patients. Our scenarios highlight 4 findings relevant to VE studies using clinical testing for influenza case and control detection. First, aside from random error, clinical testing of a random subset of patients will not affect VE estimates (baseline scenario). Second, variation in influenza testing based on probability of either influenza (scenario 1) or vaccination (scenario 2) status (but not both) will not affect VE estimates because biases in the OR numerator and denominator cancel out. Third, influenza testing based on both the probability of influenza and vaccination will affect VE estimates. Vaccine effectiveness estimates will be inflated if vaccinated patients with influenza (cell a) are less likely to be tested (scenario 3) or if unvaccinated patients with higher likelihood of influenza (cell c) are more likely to be tested than others (scenario 5). Likewise, if vaccinated patients without influenza (cell b) are less likely to be tested, VE estimates will be biased downward and could be negative (scenario 4). Finally, we observed that the error in VE estimates increased as the overall proportion tested decreased with a fixed degree of testing variation in any one 2 × 2 table cell. If the proportion not tested overall was 25% and testing was 13%–19% different for any of the five scenarios, then we found that eVE was biased ±10%.

Empirical data related to factors influencing variation in influenza testing practices are scarce. Three studies during multiple influenza seasons showed that vaccination status was not significantly associated with clinician-ordered influenza testing [11–13]. However, one of the studies did observe a larger proportion of testing among unvaccinated patients compared with vaccinated patients in physicians’ offices and emergency departments compared with hospitals [11]. Another study among adults >65 years during a single season found that unvaccinated patients were 13% (95% confidence interval [CI], 4%–23%) more likely to be clinically tested than vaccinated individuals, and, after adjusting for confounders, they were 21% (95% CI, 11%–32%) more likely to be tested [16]. Several studies note that clinical testing could be driven by a wide array of factors, including a clinician’s desire to determine the etiology of an illness, need to justify antiviral treatment and isolation measures, severity and duration of illness, and presence of fever or respiratory symptoms [11, 17, 18]. A published study from 2011 used simulations to examine the effects of several factors on VE estimates. The study showed, on average, when considering diagnostic test characteristics, as well as likelihood of being vaccinated, influenza positive, and of being tested, VE was underestimated by 12% [10]. We also show that extreme scenarios of testing practices (up to 50% of preferential testing in certain groups) result in a measured VE that varies from true protection.

Realistically, testing practices in a group of ARI patients reflect a wide range of clinician decision making, patient characteristics, and institutions depending on the study settings. For example, influenza testing may be more frequent in ICU settings where critically ill patients are tested for a broader range of etiology. Even if clinicians’ knowledge of vaccination status does not play a role in who is tested [12], the likelihood of having influenza may factor into decision making. If another factor, such as underlying health conditions, is correlated with vaccination status and likelihood of influenza, then potential biases in VE could be introduced. One way to minimize bias and still increase VE study efficiency is to use clinical testing supplemented by reference laboratory testing for ARI patients who are not otherwise clinically tested, thereby increasing proportion tested.

Our analysis has certain limitations. We purposely designed a simple theoretical example to isolate effects of clinical testing practices without examining other factors that may bias VE estimates, such as sensitivity and specificity of diagnostic testing, healthcare-seeking behavior, vaccine-mediated disease attenuation, testing practices variation within the season, and sensitivity of the ARI case definition. In addition, our analysis assumed vaccination prevalence among medically attended ARI patients was 60% and the proportion of ARI patients with influenza was 19%. However, these assumptions were based on literature review and we performed sensitivity analyses varying them. Furthermore, the empirical estimates from the IVY study of the proportion of ARI patients clinically tested are from an ICU setting, and they are likely not representative of outpatient settings, where clinical testing may not be as prevalent and where many TND studies are conducted. Finally, our calculations assume differential testing based on true influenza and vaccination status. In clinical situations, bias in testing would be based on perceived rather than actual influenza and vaccination status, producing less contrast in nontesting among groups and less bias in VE estimates. Thus, our results may overestimate the bias likely in clinical situations.

CONCLUSIONS

Clinical testing for influenza that preferentially targets patients based solely on vaccination status or likelihood of influenza does not bias VE estimates. Clinical testing that targets patients based on both vaccination status and likelihood of influenza leads to biased VE estimates. It is unlikely that clinical testing is substantially driven by vaccination status. However, prudence dictates that data on the proportion of ARI patients who are clinically tested should be collected in advance of deciding whether use of clinical testing in a TND study setting is appropriate. Identifying cases and test-negative controls by incorporating clinical testing data into VE studies could facilitate rapid, efficient, and broad influenza VE evaluations.

Supplementary Data

Supplementary materials are available at The Journal of Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.

Notes

Disclaimer. The findings and conclusions in this report are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention.

Financial support. This work was funded by the Centers for Disease Control and Prevention (75D301-19-C-05670; to W. H. S.) and National Institutes of Health (R37 AI032042; to M. E. H.).

Potential conflicts of interest. C. G. G. has been paid by Pfizer, Merck, and Sanofi-Pasteur for consulting services and has received research funding from Centers for Disease Control and Prevention (CDC), National Institutes of Health (NIH), Food and Drug Administration, and Agency for Health Care Research and Quality; M. E. H. received research funding from National Institute of Allergy and Infectious Diseases; I. D. P. reports grants from the National Institutes of Health and Janssen Pharmaceuticals and research funding to his institution from Asahi Kasei Pharma and Regeneron; S. M. B. has been paid by Janssen for services for research related to the treatment of influenza; N. H. has been paid by Sanofi-Pasteur, Quidel, Karius, and Moderna for consulting services and research related to influenza and received research funding from the CDC; A. G. R. has received research funding from the CDC and Genentech, Inc. and has been paid by La Jolla Pharma for consulting services and has received royalties from UpToDate; T. W. R. is Director of Medical Affairs for Cumberland Pharmaceuticals, serves on a Data and Safety Monitoring Board (DSMB) for Sanofi, and has received research funding from the CDC, NIH, and Department of Defense (DoD); A. K. received research funding from United Therapeutics, Johnson & Johnson, Actelion, and Eli Lilly; W. H. S. has received research funding from the CDC and has been paid by Merck and Gilead Sciences for work on pneumococcal disease and hepatitis C virus. A. A. G. received support from National Institutes of Health and Department of Defense outside the submitted work and investigator-initiated funding from AbbVie and Faron Pharmaceuticals for coronavirus disease 2019 (COVID-19) research not related to the submitted work; C. J. L. has received research funding to his institution outside of the submitted work from NIH, DoD, CDC, AstraZeneca, bioMerieux, Endpoint Health, and Entegrion Inc.; M. N. G. has received research funding from NHLBI, AHRQ, and Regeneron and has been paid for services on the DSMB for Regeneron trials on monoclonal antibodies in COVID-19 and scientific advisory board for Philips Healthcare; M. C. E. has been paid by Abbott for speaking on nutrition in intensive care unit; H. K. T. served on the Seqirus DSMB.