On physical analysis of topological indices via curve fitting for natural polymer of cellulose network

Abstract

Plant materials are processed in a variety of ways to produce biologically active compounds. Cellulose (natural polymer) has the ability to deliver physiologically active compounds to organ targets that have been extracted by ${\text{CO}}_2$. Researchers have recently become interested in polymers that can transport biologically active compounds into human bodies. For appropriately selecting bearers of biologically active chemicals, knowledge of the thermodynamic properties of cellulose is required. In QSPR/QSAR modelling, which provides the theoretical and optimum foundation for costly experimental drug discovery, molecular descriptors are extremely important. In this article, we investigated a natural polymer of cellulose network which has interesting pharmacological applications, outstanding characteristics, and a novel molecular structure. We plan to look into and compute a variety of closed-form formulas of various K-Banhatti indices along with their respective K-Banhatti entropies and the heat of formation. The numerical and graphical characterization of computed results was combined with curve fitting between calculated thermodynamic properties and topological indices. This presentation will provide a complete description of potentially important thermodynamic features that could be useful in modifying the structure of natural polymer of cellulose network ${\text{CN}}_y^x$.

Introduction

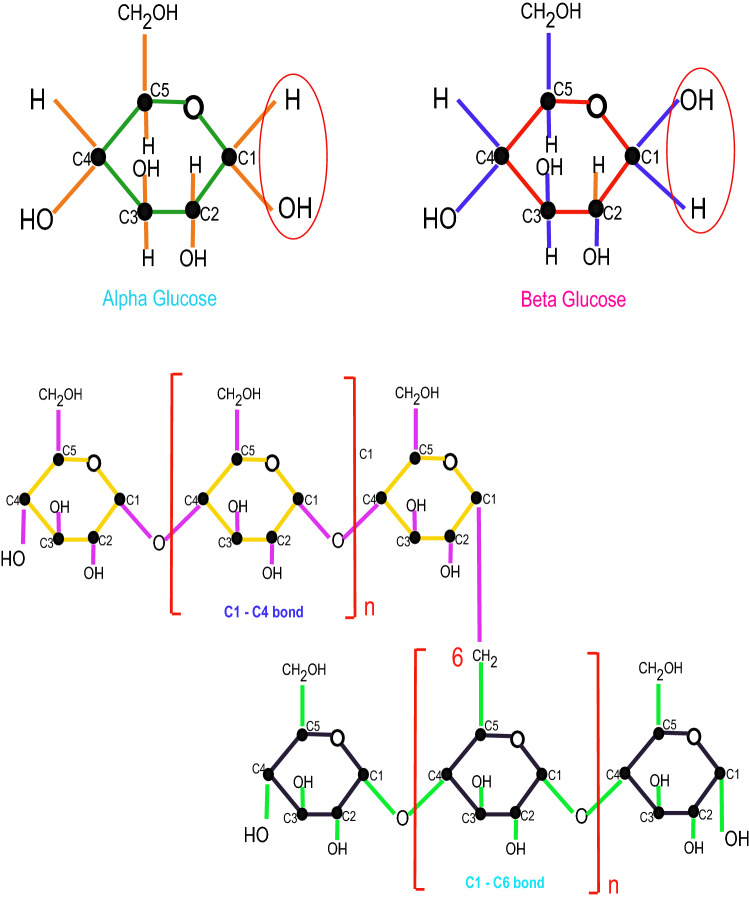
A polymer is a material comprised of numerous tedious subunits and comprises extremely gigantic atoms. Both manufactured and normal polymers perform pivotal and inescapable person in day to day events because of their broad scope of qualities. Drug delivery and prosthodontic substances both depend on polymers, which have remarkable ubiquity. Polymeric organizations have highlights that are resolved by their synthetic structure, yet additionally by how isomer fastens are associated together to shape an organization [1]. Polymers serve a significant job in prosthodontic materials, and their prominence has been marvellous. With respect to their atomic chains, polymers are arranged into four significant classifications, see Fig. 1. In amylopectin and glycogen, there are two sorts of glycosidic bonding: $\alpha ({\text{C}}_1-{\text{C}}_4)$ and $\beta ({\text{C}}_1-{\text{C}}_6)$ glycosidic bonding. The substance recipe of cellulose is ${({\text{C}}_6{\text{H}}_{10}{\text{O}}_5)}_n$. Regular polymers, particularly those got from starches, have been demonstrated to have a wide scope of drug applications [2–4]. See Fig. 2.

Fig. 1.

Depiction of polymers in terms of structural chains [5]

Fig. 2.

Fundamental unit of $\alpha$-glucose and $\beta$-glucose with their connections [5]

Assume $\mathcal{Z}$ which has p vertices and q edges. And let ${\mathcal{Z}}_V$ and ${\mathcal{Z}}_E$ be vertex and edge sets, respectively, i.e. $\mid {\mathcal{Z}}_V\mid =p$ and $\mid {\mathcal{Z}}_E\mid =q$. The amount of neighbouring vertices to a vertex g is called its degree $d_g$. gh stands for the edge e that connects the vertices g and h. For an edge $e=gh$ of $\mathcal{Z}$, the vertex g and edge e, as well as h and e, are incident. We signify the degree of an edge e in $\mathcal{Z}$ by $d_e$. This is calculated by subtracting two from the sum of neighbouring vertices g and h’s degree. The elements of a graph are the vertices and edges. In QSPR/QSAR research, a number of topological indices have been used [6–8].

To count for considerations from pairs of nearby vertices, the first and the second Zagreb indices were added in [9]. Following that, Kulli [10] developed the first and the second K-Banhatti indices, which were designed to account for the contribution of pairs of affiliated elements. In 2016, the first and second K-Banhatti indices [11] were published.

$$\begin{array}{cc}\hfill B_1(\mathcal{Z})=& \sum _{ge\in \mathcal{Z}}(d_g+d_e).\hfill \\ \hfill B_2(\mathcal{Z})=& \sum _{ge\in \mathcal{Z}}(d_g\times d_e).\hfill \end{array}$$

In [12], the modified first and second K-Banhatti indices are established as a result of the formulation of the modified Zagreb type indices. These indices were first derived for certain standard graphs, and later they were extended to include $TU{C}_4{\text{C}}_8$ and $TU{C}_4$ nanotubes. Following that, this work was expanded to include a variety of chemically intriguing networks such as chain silicate, oxide, and honeycomb networks [13] and also for the drugs chloroquine and hydroxychloroquine which were used to stop the spread of the coronavirus disease-19 [14].

$$\begin{array}{cc}\hfill {}_1^{\text{mB}}(\mathcal{Z})=& \sum _{ge\in \mathcal{Z}}\frac{1}{d_g+d_e}.\hfill \\ \hfill {}_2^{\text{mB}}(\mathcal{Z})=& \sum _{ge\in \mathcal{Z}}\frac{1}{d_g\times d_e}.\hfill \end{array}$$

In 2017, harmonic K-Banhatti index was suggested, which is based on Favaron et al. [15] and Zhong’s [16] description of the harmonic index and earlier topological indices research.

$$\begin{array}{cc}\hfill {\text{H}}_b(\mathcal{Z})=& \sum _{ge\in \mathcal{Z}}\frac{2}{d_g\times d_e}.\hfill \end{array}$$

The sum connectivity index is one of the most well-known and commonly used topological indices. In terms of vertex-edge incident, Kulli et al. [17] developed a roughly related form of $\mathcal{Z}$ connectivity indices.

$$\begin{array}{cc}\hfill \text{SB}(\mathcal{Z})=& \sum _{ge\in \mathcal{Z}}\frac{1}{\sqrt{d_g+d_e}}.\hfill \end{array}$$

For the graph $\mathcal{Z}$, the general first and second K-Banhatti indices for real $a\in R$, are specified as:

$$\begin{array}{cc}\hfill B_1^{\eta }(\mathcal{Z})=& \sum _{\mathit{ge}}{[d_g+d_e]}^{\eta }.\hfill \end{array}$$ 1

$$\begin{array}{cc}\hfill B_2^{\eta }(\mathcal{Z})=& \sum _{\mathit{ge}}{[d_g·d_e]}^{\eta }.\hfill \end{array}$$ 2

Shannon [18] was the first to introduce the concept of entropy . It is a measure of a system’s information content’s unpredictability. After this, it’s been employed in chemical networks and graphs. Rashevsky entrenched the entropy of a graph [19]. Graph entropy is now employed in a variety of domains, see [20–22].

Intrinsic and extrinsic graph entropy measurements are used to correlate probability distributions with graph invariants (vertices, edges, and so on) [23]. Dehmer [24, 25] researched the features of graph entropies, which are established on information functionals. See [26–28] for more information.

The information entropy [29] based on Shannon’s entropy [18] is described as:

$$\begin{array}{c}\hfill E_w(\mathcal{Z})=-\sum _{i=1}^m{F}_i\frac{w(x_i{y}_i)}{T_d}{log}_2\frac{w(x_i{y}_i)}{T_d}=log(T_d)-\frac{1}{T_d}\sum _{i=1}^m{F}_{i}w(x_i{y}_i){log}_{2}w(x_i{y}_i),\end{array}$$ 3

where $T_d={\sum }_{i=1}^m{F}_{i}w(g_i{h}_i)$ denotes the topological descriptor, m is the number of edge types, $F_i$ is the frequency or number of repetition, and w(gh) is the weight of the edge gh.

Formation of cellulose network planar graph ${\text{CN}}_y^x$

Natural cellulose is a non-aromatic, hydrophilic, chiral, and biodegradable organic molecule. Anselme Payen, a French scientist, discovered a strong fibrous solid that persists after treating miscellaneous plant tissues with acid and ammonia, then extracting it with water, alcohol, and ether [30]. It is the major constituent of tough cell walls that protect plant cells, resulting in robust and rigid plant stems, leaves, and branches. Plants can stay erect because of the strong cellulose structure, which is tough to digest and break down. Recently, both the government and business have shown a keen interest in items made from sustainable and renewable energy sources that pose minimal dangers to human health and the environment [31]. In the compounding of pharmaceuticals, cellulosics (cellulose-based materials) are utilized as major excipients. Due to several appealing features such as low cost, biocompatibility, repeatability, and recyclability, it has attracted a lot of attention.

Cellulose is a glucose-based natural linear polymer (polysaccharide) with the formula ${({\text{C}}_6{\text{H}}_{10}{\text{O}}_5)}_x$. Plants produce it in the majority of cases. The leaves and stems of the most plants contain this biopolymer. Primitively, the general chemical structure of cellulose, made up of over $3\times {10}^3$ D-glucose units connected by glycosidic bonds $\beta (({\text{C}}_1{\text{C}}_4))$, will be discussed. Unlike glycogen and starch, cellulose is a non-coiling, straight unbranched polymer. Hydrogen–oxygen bonding (on a linear chain that is the same as or similar to another linear chain) is formed by multiple hydroxyl groups on the glucose ring from one chain, resulting in the development of high-tensile-strength microfibrils. Now, we’ll show how to build a ${\text{CN}}_y^x$ molecular graph from the scratch. ${({\text{C}}_6{\text{H}}_{10}{\text{O}}_5)}_2$, illustrated in Fig. 3, is the basic construction unit of the cellulose network, characterized by three hexagons and one octagon with three pendant edges. One of these pendants is made of fixed carbon, while the other two are made of OH (hydroxyl group) pendants, one on the upper side and one on the lower side for additional bonding.

Fig. 3.

The 2D framework of cellulose’s basic units [5]

The number of hexagons in basic units is represented by x, and when one monomer is added to the basic unit, we get seven hexagons. In the same manner, each monomer addition resulted in a four-hexagon increment. The cellulose network ${\text{CN}}_y^x$ has y hexagonal chains, and each hexagonal chain with t isomeric units has x hexagons. Each chain has an odd number of hexagons. $x=4t+3$, $t\in \mathbb{W}$ describes the relationship between hexagons in one chain and isomeric units t. Figure 4 depicts cellulose $C{L}_7^4$’s three-dimensional network as well as its planar network. In the cellulose molecular graph, we may see polygons with 6, 8, and 10 sides.

Fig. 4.

Cellulose’s chemical structure and corresponding molecular graph ${\text{CN}}_4^7$ [5]

We can see the order and size of the cellulose network ${\text{CN}}_y^x$, $x=4t+3$, are $\mid {{\text{CN}}_y^x}_V\mid =2[y(11t+10)-1]$ and $\mid {{\text{CN}}_y^x}_E\mid =5y(6t+5)-2(t+2)$. [32] presents an edge split of the cellulose network with various parameters. Imran et al. determined the metric dimension of the cellulose network in that paper. They did so because networks and metric dimensions are so important in everyday life. Subsequently, in [5] many degree based topological indices were calculated.

Entropies in terms of topological indices for cellulose network ${\text{CN}}_y^x$

Firstly, we compute general first and second K-Banhatti indices by using Eq. (1) and Eq. (2) with Table 1

$$\begin{array}{cc}\hfill B_1^{\eta }({\text{CN}}_y^x)=& [{(1+2)}^{\eta }+{(3+2)}^{\eta }]+[{(2+2)}^{\eta }+{(2+2)}^{\eta }][4(y+t)+1]\hfill \\ \hfill & +[{(2+3)}^{\eta }+{(3+3)}^{\eta }][12y(t+1)-2]+[{(3+4)}^{\eta }+{(3+4)}^{\eta }][9y(2t+1)-2(3t+2)]\hfill \\ \hfill =& (3^{\eta }+5^{\eta })+(2\times 4^{\eta })[4(y+t)+1]+(5^{\eta }+6^{\eta })[12y(t+1)-2]+(2\times 7^{\eta })[9y(2t+1)-2(3t+2)].\hfill \end{array}$$ 4

$$\begin{array}{cc}\hfill B_2^{\eta }({\text{CN}}_y^x)=& [{(1\times 2)}^{\eta }+{(2\times 3)}^{\eta }]+[{(2\times 2)}^{\eta }\times {(2\times 2)}^{\eta }][4(y+t)+1]\hfill \\ \hfill & +[{(2\times 3)}^{\eta }+{(3\times 3)}^{\eta }][12y(t+1)-2]+[{(3\times 4)}^{\eta }\times {(3\times 4)}^{\eta }][9y(2t+1)-2(3t+2)]\hfill \\ \hfill =& (2^{\eta }+6^{\eta })+(2\times 4^{\eta })[4(y+t)+1]+(6^{\eta }+9^{\eta })[12y(t+1)-2]+[2\times {12}^{\eta }][9y(2t+1)-2(3t+2)].\hfill \end{array}$$ 5

We introduce generalized first and second K-Banhatti entropies by using Eq. (3):

$$\begin{array}{cc}\hfill E_{B_1^{\eta }}({\text{CN}}_y^x)=& {log}_2(B_1^{\eta }({\text{CN}}_y^x))-\frac{1}{B_1^{\eta }({\text{CN}}_y^x)}\sum _{i=1}^4\sum _{gh\in {\text{CN}}_y^x}(d_g+d_e){log}_2[d_g+d_e]\hfill \\ \hfill =& {log}_2(B_1^{\eta }({\text{CN}}_y^x))-\frac{1}{(B_1^{\eta }({\text{CN}}_y^x))}[(3^{\eta }+5^{\eta }){log}_2(3^{\eta }+5^{\eta })+(2\times 4^{\eta })[4(y+t)+1]{log}_2(2\times 4^{\eta })\hfill \\ \hfill & +(5^{\eta }+6^{\eta })[12y(t+1)-2]{log}_2(5^{\eta }+6^{\eta })+(2\times 7^{\eta })[9y(2t+1)-2(3t+2)]{log}_2(2\times 7^{\eta })].\hfill \end{array}$$ 6

$$\begin{array}{cc}\hfill E_{B_2^{\eta }}({\text{CN}}_y^x)=& {log}_2(B_2^{\eta }({\text{CN}}_y^x))-\frac{1}{B_2^{\eta }({\text{CN}}_y^x)}\sum _{i=1}^4\sum _{gh\in {\text{CN}}_y^x}(d_g\times d_e){log}_2[d_g\times d_e]\hfill \\ \hfill =& {log}_2(B_2^{\eta }({\text{CN}}_y^x))-\frac{1}{(B_2^{\eta }({\text{CN}}_y^x))}[(2^{\eta }\times 6^{\eta }){log}_2(2^{\eta }\times 6^{\eta })+(2\times 4^{\eta })[4(y+t)+1]{log}_2(2\times 4^{\eta })\hfill \\ \hfill & +(6^{\eta }+9^{\eta })[12y(t+1)-2]{log}_2(6^{\eta }+9^{\eta })+(2\times {12}^{\eta })[9y(2t+1)-2(3t+2)]{log}_2(2\times {12}^{\eta })].\hfill \end{array}$$ 7

• The first K-Banhatti index and entropy of ${\text{CN}}_y^x$

For $\eta =1$ in Eq. (4) and Eq. (6), we estimated the first K-Banhatti index and entropy as listed below:

$$\begin{array}{cc}\hfill B_1({\text{CN}}_y^x)=& -62+32y-52t+132y(t+1)+126y(2t+1).\hfill \\ \hfill E_{B_1}({\text{CN}}_y^x)=& {log}_2(-62+32y-52t+132y(t+1)+126y(2t+1))\hfill \\ \hfill & -\frac{8{log}_2(8)}{(-62+32y-52t+132y(t+1)+126y(2t+1))}-\frac{8[4(y+t)+1]{log}_2(8)}{(-62+32y-52t+132y(t+1)+126y(2t+1))}\hfill \\ \hfill & -\frac{11[12y(t+1)-2]{log}_2(11)}{(-62+32y-52t+132y(t+1)+126y(2t+1))}-\frac{14[9y(2t+1)-2(3t+2)]{log}_2(14)}{(-62+32y-52t+132y(t+1)+126y(2t+1))}.\hfill \end{array}$$

• The first K-hyper-Banhatti index and entropy of ${\text{CN}}_y^x$

For $\eta =2$ in Eq. (4) and Eq. (6), we estimated the first K-hyper-Banhatti index and entropy as listed below:

$$\begin{array}{cc}\hfill {\text{HB}}_1({\text{CN}}_y^x)=& -448+128y-460t+732y(t+1)+882y(2t+1).\hfill \\ \hfill E_{{\text{HB}}_1}({\text{CN}}_y^x)=& {log}_2(-448+128y-460t+732y(t+1)+882y(2t+1))\hfill \\ \hfill & -\frac{34{log}_2(34)}{(-448+128y-460t+732y(t+1)+882y(2t+1))}-\frac{32[4(y+t)+1]{log}_2(32)}{(-448+128y-460t+732y(t+1)+882y(2t+1))}\hfill \\ \hfill & -\frac{61[12y(t+1)-2]{log}_2(61)}{(-448+128y-460t+732y(t+1)+882y(2t+1))}-\frac{98[9y(2t+1)-2(3t+2)]{log}_2(98)}{(-448+128y-460t+732y(t+1)+882y(2t+1))}.\hfill \end{array}$$

• The sum connectivity Banhatti index and entropy of ${\text{CN}}_y^x$

For $\eta =\frac{-1}{2}$ in Eq. (4) and Eq. (6), we estimated the sum connectivity Banhatti index and entropy as listed below:

$$\begin{array}{cc}\hfill \text{SB}({\text{CN}}_y^x)=& (\frac{1-\sqrt{2}}{\sqrt{3}}-\frac{1}{\sqrt{5}}-\frac{8}{\sqrt{7}}+1)+4y+(4-\frac{12}{\sqrt{7}})t+12y(t+1)\left(\frac{1}{\sqrt{5}},+,\frac{1}{\sqrt{6}}\right)+\frac{18y}{\sqrt{7}}(2t+1).\hfill \\ \hfill E_{\text{SB}}({\text{CN}}_y^x)=& {log}_2((\frac{1-\sqrt{2}}{\sqrt{3}}-\frac{1}{\sqrt{5}}-\frac{8}{\sqrt{7}}+1)+4y+(4-\frac{12}{\sqrt{7}})t+12y(t+1)\left(\frac{1}{\sqrt{5}},+,\frac{1}{\sqrt{6}}\right)+\frac{18y}{\sqrt{7}}(2t+1))\hfill \\ \hfill [3mm]& -\frac{\left(\frac{1}{\sqrt{3}},+,\frac{1}{\sqrt{5}}\right){log}_2\left(\frac{1}{\sqrt{3}},+,\frac{1}{\sqrt{5}}\right)}{((\frac{1-\sqrt{2}}{\sqrt{3}}-\frac{1}{\sqrt{5}}-\frac{8}{\sqrt{7}}+1)+4y+(4-\frac{12}{\sqrt{7}})t+12y(t+1)\left(\frac{1}{\sqrt{5}},+,\frac{1}{\sqrt{6}}\right)+\frac{18y}{\sqrt{7}}(2t+1))}\hfill \\ \hfill [3mm]& -\frac{\left(\frac{1}{\sqrt{5}},+,\frac{1}{\sqrt{6}}\right)[12y(t+1)-2]{log}_2\left(\frac{1}{\sqrt{5}},+,\frac{1}{\sqrt{6}}\right)}{((\frac{1-\sqrt{2}}{\sqrt{3}}-\frac{1}{\sqrt{5}}-\frac{8}{\sqrt{7}}+1)+4y+(4-\frac{12}{\sqrt{7}})t+12y(t+1)\left(\frac{1}{\sqrt{5}},+,\frac{1}{\sqrt{6}}\right)+\frac{18y}{\sqrt{7}}(2t+1))}\hfill \\ \hfill [3mm]& -\frac{\frac{2}{\sqrt{7}}[9y(2t+1)-2(3t+2)]{log}_2\left(\frac{2}{\sqrt{7}}\right)}{((\frac{1-\sqrt{2}}{\sqrt{3}}-\frac{1}{\sqrt{5}}-\frac{8}{\sqrt{7}}+1)+4y+(4-\frac{12}{\sqrt{7}})t+12y(t+1)\left(\frac{1}{\sqrt{5}},+,\frac{1}{\sqrt{6}}\right)+\frac{18y}{\sqrt{7}}(2t+1))}.\hfill \end{array}$$

• Modified first K-Banhatti index and entropy of ${\text{CN}}_y^x$

For $\eta =-1$ in Eq. (4) and Eq. (6), we estimated modified first K-Banhatti index and entropy as listed below:

$$\begin{array}{cc}\hfill {}_1^{\text{mB}}({\text{CN}}_y^x)=& -\frac{59}{70}+2y+\frac{2t}{7}+\frac{22}{5}y(t+1)+\frac{18}{7}y(2t+1).\hfill \\ \hfill E_{{}_1^{\text{mB}}}({\text{CN}}_y^x)=& {log}_2(-\frac{59}{70}+2y+\frac{2t}{7}+\frac{22}{5}y(t+1)+\frac{18}{7}y(2t+1))\hfill \\ \hfill & -\frac{\frac{8}{15}{log}_2\left(\frac{8}{15}\right)}{(-\frac{59}{70}+2y+\frac{2t}{7}+\frac{22}{5}y(t+1)+\frac{18}{7}y(2t+1))}-\frac{\frac{1}{2}[4(y+t)+1]{log}_2\left(\frac{1}{2}\right)}{(-\frac{59}{70}+2y+\frac{2t}{7}+\frac{22}{5}y(t+1)+\frac{18}{7}y(2t+1))}\hfill \\ \hfill & -\frac{\frac{11}{30}[12y(t+1)-2]{log}_2\left(\frac{11}{30}\right)}{(-\frac{59}{70}+2y+\frac{2t}{7}+\frac{22}{5}y(t+1)+\frac{18}{7}y(2t+1))}-\frac{\frac{2}{7}[9y(2t+1)-2(3t+2)]{log}_2\left(\frac{2}{7}\right)}{(-\frac{59}{70}+2y+\frac{2t}{7}+\frac{22}{5}y(t+1)+\frac{18}{7}y(2t+1))}.\hfill \end{array}$$

• The second K-Banhatti index and entropy of ${\text{CN}}_y^x$

For $\eta =1$ in Eq. (5) and Eq. (7), we estimated the second K-Banhatti index and entropy as listed below:

$$\begin{array}{cc}\hfill B_2({\text{CN}}_y^x)=& -110+32y-112t+180y(t+1)+216y(2t+1)\hfill \\ \hfill E_{B_2}({\text{CN}}_y^x)=& {log}_2(-110+32y-112t+180y(t+1)+216y(2t+1))\hfill \\ \hfill & -\frac{8{log}_2(8)}{(-110+32y-112t+180y(t+1)+216y(2t+1))}-\frac{8[4(y+t)+1]{log}_2(8)}{(-110+32y-112t+180y(t+1)+216y(2t+1))}\hfill \\ \hfill & -\frac{15[12y(t+1)-2]{log}_2(15)}{(-110+32y-112t+180y(t+1)+216y(2t+1))}-\frac{24[9y(2t+1)-2(3t+2)]{log}_2(24)}{(-110+32y-112t+180y(t+1)+216y(2t+1))}.\hfill \end{array}$$

• The second K-hyper-Banhatti index and entropy of ${\text{CN}}_y^x$

For $\eta =2$ in Eq. (5) and Eq. (7), we estimated the second K-hyper-Banhatti index and entropy as listed below:

$$\begin{array}{cc}\hfill {\text{HB}}_2({\text{CN}}_y^x)=& -1314+128y-1600t+1404y(t+1)+2592y(2t+1).\hfill \\ \hfill E_{{\text{HB}}_2}({\text{CN}}_y^x)=& {log}_2(-1314+128y-1600t+1404y(t+1)+2592y(2t+1))\hfill \\ \hfill & -\frac{40{log}_2(40)}{(-1314+128y-1600t+1404y(t+1)+2592y(2t+1))}\hfill \\ \hfill & -\frac{32[4(y+t)+1]{log}_2(32)}{(-1314+128y-1600t+1404y(t+1)+2592y(2t+1))}\hfill \\ \hfill & -\frac{117[12y(t+1)-2]{log}_2(117)}{(-1314+128y-1600t+1404y(t+1)+2592y(2t+1))}\hfill \\ \hfill & -\frac{288[9y(2t+1)-2(3t+2)]{log}_2(288)}{(-1314+128y-1600t+1404y(t+1)+2592y(2t+1))}.\hfill \end{array}$$

• Modified second K-Banhatti index and entropy of ${\text{CN}}_y^x$

For $\eta =-1$ in Eq. (5) and Eq. (7), we estimated modified first K-Banhatti index and entropy as listed below (Figs. 5, 6; Tables 2, 3, 4, 5, 6):

$$\begin{array}{cc}\hfill {}_2^{\text{mB}}({\text{CN}}_y^x)=& \frac{-1}{18}+2y+t+\frac{10}{3}y(t+1)+\frac{3}{2}y(2t+1).\hfill \\ \hfill E_{{}_2^{\text{mB}}}({\text{CN}}_y^x)=& {log}_2(\frac{-1}{18}+2y+t+\frac{10}{3}y(t+1)+\frac{3}{2}y(2t+1))\hfill \\ \hfill & -\frac{\frac{2}{3}{log}_2\left(\frac{2}{3}\right)}{(\frac{-1}{18}+2y+t+\frac{10}{3}y(t+1)+\frac{3}{2}y(2t+1))}-\frac{\frac{1}{2}[4(y+t)+1]{log}_2\left(\frac{1}{2}\right)}{(\frac{-1}{18}+2y+t+\frac{10}{3}y(t+1)+\frac{3}{2}y(2t+1))}\hfill \\ \hfill & -\frac{\frac{5}{18}[12y(t+1)-2]{log}_2\left(\frac{5}{18}\right)}{(\frac{-1}{18}+2y+t+\frac{10}{3}y(t+1)+\frac{3}{2}y(2t+1))}-\frac{\frac{1}{6}[9y(2t+1)-2(3t+2)]{log}_2\left(\frac{1}{6}\right)}{(\frac{-1}{18}+2y+t+\frac{10}{3}y(t+1)+\frac{3}{2}y(2t+1))}.\hfill \end{array}$$

• Harmonic K-Banhatti index and entropy of ${\text{CN}}_y^x$

$$\begin{array}{cc}\hfill H_b({\text{CN}}_y^x)=& \left(\frac{2}{3},+,\frac{2}{5}\right)+\left(\frac{2}{4},+,\frac{2}{4}\right)[4(y+t)+1]+\left(\frac{2}{5},+,\frac{2}{6}\right)[12y(t+1)-2]+\left(\frac{2}{7},+,\frac{2}{7}\right)[9y(2t+1)-2(3t+2)]\hfill \\ \hfill [3mm]=& \frac{-59}{39}+4y+\frac{4t}{7}+\frac{44}{5}y(t+1)+\frac{36}{7}y(2t+1).\hfill \\ \hfill E_{H_b}({\text{CN}}_y^x)=& {log}_2(H_b({\text{CN}}_y^x))-\frac{1}{H_b({\text{CN}}_y^x)}\sum _{i=1}^4\sum _{gh\in {\text{CN}}_y^x}(\frac{2}{d_g+d_e}){log}_2\left[\frac{2}{d_g+d_e}\right]\hfill \\ \hfill =& {log}_2(\frac{-59}{39}+4y+\frac{4t}{7}+\frac{44}{5}y(t+1)+\frac{36}{7}y(2t+1))-\frac{\frac{16}{15}·{log}_2\left[\frac{16}{15}\right]}{(\frac{-59}{39}+4y+\frac{4t}{7}+\frac{44}{5}y(t+1)+\frac{36}{7}y(2t+1))}\hfill \\ \hfill & -\frac{\frac{11}{15}[12y(t+1)-2]·{log}_2\left[\frac{11}{15}\right]}{(\frac{-59}{39}+4y+\frac{4t}{7}+\frac{44}{5}y(t+1)+\frac{36}{7}y(2t+1))}-\frac{\frac{4}{7}[9y(2t+1)-2(3t+2)]·{log}_2\left[\frac{4}{7}\right]}{(\frac{-59}{39}+4y+\frac{4t}{7}+\frac{44}{5}y(t+1)+\frac{36}{7}y(2t+1))}.\hfill \end{array}$$

Table 1.

Edge partition of ${\text{CN}}_y^x$ established on degree of terminal vertices of every edge

$(d_g,d_h)$	$d_e$	Frequency ($F_i$)
(1, 3)	2	1
(2, 2)	2	$4(y+t)+1$
(2, 3)	3	$12y(t+1)-2$
(3, 3)	4	$-2(3t+2)$

Fig. 5.

Comparison of $B_1$, $B_2$ and $H_b$ indices for ${\text{CN}}_y^x$

Fig. 6.

Comparison of ${\text{mB}}_1$, ${\text{mB}}_2$ and $m{H}_b$ indices for ${\text{CN}}_y^x$

Table 2.

Comparison of $B_1$, $B_2$, ${\text{HB}}_1$, ${\text{HB}}_2$, and $\text{SB}$ indices for ${\text{CN}}_y^x$

[y, t]	$B_1$	$B_2$	${\text{HB}}_1$	${\text{HB}}_2$	$\text{SB}$
[1, 1]	560	818	3330	7798	31.4299
[2, 2]	1950	2970	12,100	30,086	92.7835
[3, 3]	4108	6346	25,862	65,550	181.3504
[4, 4]	7034	10,946	44,616	114,190	297.1308
[5, 5]	10,728	16,770	68,362	176,006	440.1246
[6, 6]	15,190	23,818	97,100	250,998	610.3319
[7, 7]	20,420	32,090	130,830	339,166	807.7526

Table 3.

Comparison of ${}_1^{\text{mB}}$, ${}_2^{\text{mB}}$, and $H_b$ for ${\text{CN}}_y^x$

[y, t]	${}_1^{\text{mB}}$	${}_2^{\text{mB}}$	$H_b$
[1, 1]	10.2429	12.1111	34.9443
[2, 2]	30.1286	36.9444	109.5729
[3, 3]	58.8143	74.4444	222.3729
[4, 4]	96.3000	124.6111	373.3443
[5, 5]	142.5857	187.4444	562.4872
[6, 6]	197.6714	262.9444	789.8015
[7, 7]	261.5571	351.1111	1055.2872

Table 4.

Comparison of $E_{B_1}$, $E_{B_2}$, $E_{{\text{HB}}_1}$, and $E_{{\text{HB}}_2}$ for ${\text{CN}}_y^x$

[y, t]	$E_{B_1}$	$E_{B_2}$	$E_{{\text{HB}}_1}$	$E_{{\text{HB}}_2}$
[1, 1]	5.5876	5.5196	5.5175	5.3196
[2, 2]	7.3189	7.2679	7.2663	7.1217
[3, 3]	8.3700	8.3262	8.3249	8.2002
[4, 4]	9.1335	9.0937	9.0925	8.9784
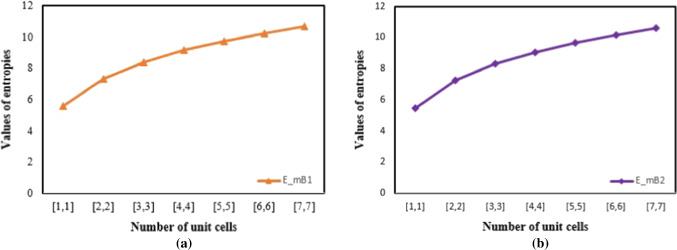
[5, 5]	9.7347	9.6975	9.6964	9.5889
[6, 6]	10.2312	10.1958	10.1948	10.0917
[7, 7]	10.6543	10.6202	10.6192	10.5195

Table 5.

Comparison of $E_{{\text{mB}}_1}$, $E_{{\text{mB}}_2}$, and $E_{\text{SB}}$ for ${\text{CN}}_y^x$

[y, t]	$E_{{\text{mB}}_1}$	$E_{{\text{mB}}_2}$	$E_{\text{SB}}$
[1, 1]	5.5831	5.4846	5.6070
[2, 2]	7.3137	7.2290	7.3336
[3, 3]	8.3653	8.2907	8.3826
[4, 4]	9.1293	9.0614	9.1449
[5, 5]	9.7309	9.6678	9.7454
[6, 6]	10.2276	10.1681	10.2413
[7, 7]	10.6509	10.5941	10.6639

Table 6.

HoF for various formula units of cellulose network ${\text{CN}}_y^x$

[y, t]	Formula unit	Heat of formation
[1, 1]	4	$-639.64\times {10}^{-20}$
[2, 2]	16	$-2558.56\times {10}^{-20}$
[3, 3]	36	$-5756.76\times {10}^{-20}$
[4, 4]	64	$-10234.24\times {10}^{-20}$
[5, 5]	100	$-15991.37\times {10}^{-20}$
[6, 6]	144	$-23027.04\times {10}^{-20}$
[7, 7]	196	$-31342.36\times {10}^{-20}$

Heat of formation for cellulose network ${\text{CN}}_y^x$

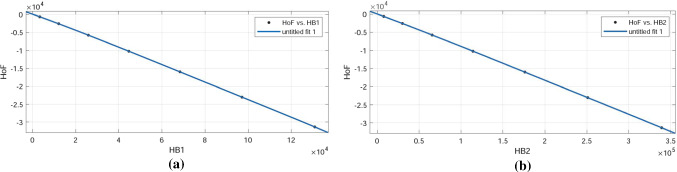
For varying number of unit cells in a cellulose network, the K-Banhatti topological indices $B_1(\mathcal{Z})$, $B_2(\mathcal{Z})$, ${\text{HB}}_1(\mathcal{Z})$, ${\text{HB}}_2(\mathcal{Z})$, $\text{SB}(\mathcal{Z})$, $H_b(\mathcal{Z})$, ${}_1^{\text{mB}}(\mathcal{Z})$, and ${}_2^{\text{mB}}(\mathcal{Z})$, were measured. These indices are connected to the thermodynamic properties of the cellulose network, like heat of formation (enthalpy) and entropy. The change in enthalpy during the creation of 1 mole of a material from its constituent elements is known as the standard enthalpy of formation or standard heat of formation of a compound (all materials are in their natural states). Cellulose network has a typical molar enthalpy of $963\times {10}^{3}kJmo{l}^{-1}$. Avogadro’s number was used to derive the standard molar enthalpy for one formula unit. By multiplying this value by the number of formula units in the cell, the enthalpy of the cell was obtained. The enthalpy of cellulose network ${\text{CN}}_y^x$ is inversely proportional to its crystal size, according to these calculations. It reduces from $-639.64\times {10}^{-20}$ to $-10234.24\times {10}^{-20}$ as the number of cells increases from [1, 1] to [4, 4] (Figs. 7, 8, 9, 10).

Fig. 7.

a First K-Banhatti Entropy and b second K-Banhatti Entropy, for ${\text{CN}}_y^x$

Fig. 8.

a First K-hyper-Banhatti Entropy and b second K-hyper-Banhatti Entropy, for ${\text{CN}}_y^x$

Fig. 9.

a The modified first K-Banhatti entropy and b the modified second K-Banhatti entropy, for ${\text{CN}}_y^x$

Fig. 10.

a The harmonic K-Banhatti entropy and b the sum connectivity K-Banhatti entropy, for ${\text{CN}}_y^x$

Rational curve fitting between entropy (and HoF) and the indices

One of the most powerful and extensively used analysis techniques is curve fitting. The link between one or more predictors and a response variable is investigated using curve fitting with the purpose of developing a “best fit” relationship model. When fitting curves, rational functions are utilized as an empirical technique. Interpolatory, extrapolatory, and asymptotic features of rational function models are superior to polynomial models. Rational function models are frequently used to model complex structures with low degrees in the numerator and denominator. Data visualization as well as to sum up the links between two or more variables can be aided by fitted curves. This analysis is performed to investigate the relationship between entropy/HoF and several K-Banhatti indices. Curve fitting can be done in a variety of ways, including linear, power, polynomial, and rational. To evaluate the association between HoF/ entropy and indices, we apply rational curve fitting. Root mean squared error (RMSE), sum of squared error (SSE), and coefficient of determination ($R_2$) are the accuracy measures that are employed in the analysis. The lower the RMSE, the better the model performance; on the other hand, the higher the $R_2$ (closer to 1), the better the regression line is fitting to the data and that the model’s performance is improved. In this article, RMSE has been our primary focus. We have used MATLAB to conduct all simulations. Tables 7 and 8 show integrity of fit for all K-Banhatti indices vs heat of formation and all K-Banhatti indices vs K-Banhatti entropy of ${\text{CN}}_y^x$, respectively. Also, $r_{\mathit{ij}}$ demonstrates the rational fit in which i represents the degree of numerator while j represents the degree of denominator.

Table 7.

Integrity of fit for K-Banhatti entropy vs K-Banhatti indices of ${\text{CN}}_y^x$

Indices	Fit-type	SSE	$R^2$	RMSE
$B_1({\text{CN}}_y^x)$	r22	3.512e–05	1	0.00419
$B_1({\text{CN}}_y^x)$	r32	4.351e–07	1	0.0006597
${\text{HB}}_1({\text{CN}}_y^x)$	r41	1.238e–05	1	0.003519
${\text{HB}}_2({\text{CN}}_y^x)$	r22	4.435e–05	1	0.004709
$\text{SB}({\text{CN}}_y^x)$	r41	5.258e–06	1	0.002293
$H_b({\text{CN}}_y^x)$	r32	2.913e–07	1	0.0005398
${}_1^{\text{mB}}({\text{CN}}_y^x)$	r32	1.732e–07	1	0.0004161
${}_2^{\text{mB}}({\text{CN}}_y^x)$	r41	8.419e–06	1	0.002902

Table 8.

Integrity of fit for K-Banhatti indices vs heat of formation of ${\text{CN}}_y^x$

Indices	Fit-type	SSE	$R^2$	RMSE
$B_1({\text{CN}}_y^x)$	r13	1073	1	23.17
$B_2({\text{CN}}_y^x)$	r41	671.3	1	25.91
${\text{HB}}_1({\text{CN}}_y^x)$	r41	666	1	25.81
${\text{HB}}_2({\text{CN}}_y^x)$	r41	421.3	1	20.52
$\text{SB}({\text{CN}}_y^x)$	r31	30.32	1	3.894
$H_b({\text{CN}}_y^x)$	r32	0.254	1	0.504
${}_1^{\text{mB}}({\text{CN}}_y^x)$	r22	1160	1	24.08
${}_2^{\text{mB}}({\text{CN}}_y^x)$	r21	474.7	1	12.58

General models for indices vs entropy

The following are general models for the fitted curves for all indices vs entropy. This comparison is also shown graphically.

$$\begin{array}{c}\hfill \text{Entropy}(B_1)=\frac{{\aleph }_1·{B_1}^2+{\aleph }_2·B_1+{\aleph }_3}{{B_1}^2+{\vartheta }_1{B}_1+{\vartheta }_2},\end{array}$$

where $B_1$ is normalized by mean 8570 and standard deviation 7293. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=13.19$, with $\text{CB}=(12.67,13.71)$, ${\aleph }_2=54.7$ with $\text{CB}=(43.67,65.73)$, ${\aleph }_3=47.34$ with $\text{CB}=(34.18,60.5)$, ${\vartheta }_1=5.161$ with $\text{CB}=(4.156,6.166)$, ${\vartheta }_2=5.03$ with $\text{CB}=(3.629,6.43)$.

$$\begin{array}{c}\hfill \text{Entropy}(B_2)=\frac{{\aleph }_1·{B_2}^3+{\aleph }_2·{B_2}^2+{\aleph }_3·B_2+{\aleph }_4}{{B_2}^2+{\vartheta }_1\ast B_2+{\vartheta }_2},\end{array}$$

where $B_2$ is normalized by mean $1.339\text{e+}04$ and standard deviation $1.149\text{e+}04$. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=0.1818$, with $\text{CB}=(0.01896,0.3445)$, ${\aleph }_2=12.3$ with $\text{CB}=(11.58,13.02)$, ${\aleph }_3=38.86$ with $\text{CB}=(25.84,51.88)$, ${\aleph }_4=29.3$ with $\text{CB}=(14.64,43.96)$, ${\vartheta }_1=3.738$ with $\text{CB}=(2.553,4.923)$, ${\vartheta }_2=3.124$ with $\text{CB}=(1.56,4.689)$ (Fig. 11).

$$\begin{array}{c}\hfill \text{Entropy}({\text{HB}}_1)=\frac{{\aleph }_1·{({\text{HB}}_1)}^4+{\aleph }_2·{({\text{HB}}_1)}^3+{\aleph }_3·{({\text{HB}}_1)}^2+{\aleph }_4·({\text{HB}}_1)+{\aleph }_5}{({\text{HB}}_1)+{\vartheta }_1},\end{array}$$

where ${\text{HB}}_1$ is normalized by mean $5.46\text{e+}04$ and standard deviation $4.685\text{e+}04$. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=0.04698$, with $\text{CB}=(-0.08107,0.175)$, ${\aleph }_2=-0.1752$ with $\text{CB}=(-0.3438,-0.006524)$, ${\aleph }_3=0.5568$ with $\text{CB}=(0.4194,0.6942)$, ${\aleph }_4=10.96$ with $\text{CB}=(10.88,11.05)$, ${\aleph }_5=12.13$ with $\text{CB}=(11.21,13.06)$, ${\vartheta }_1=1.294$ with $\text{CB}=(1.193,1.395)$.

$$\begin{array}{c}\hfill \text{Entropy}({\text{HB}}_2)=\frac{{\aleph }_1·{({\text{HB}}_2)}^2+{\aleph }_2·{\text{HB}}_2+{\aleph }_3}{{({\text{HB}}_2)}^2·{\vartheta }_1+{\vartheta }_2},\end{array}$$

where ${\text{HB}}_2$ is normalized by mean $1.405\text{e+}05$ and standard deviation $1.218\text{e+}05$. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=13.01$, with $\text{CB}=(12.48,13.54)$, ${\aleph }_2=52.44$ with $\text{CB}=(41.71,63.16)$, ${\aleph }_3=44.35$ with $\text{CB}=(31.85,56.85)$, ${\vartheta }_1=5.023$ with $\text{CB}=(4.03,6.015)$, ${\vartheta }_2=4.785$ with $\text{CB}=(3.434,6.136)$ (Fig. 12).

$$\begin{array}{c}\hfill \text{Entropy}{(}_1^{\text{mB}})=\frac{{\aleph }_1·{({}_1^{\text{mB}})}^3+{\aleph }_2·{({}_1^{\text{mB}})}^2+{\aleph }_3·{}_1^{\text{mB}}+{\aleph }_4}{({{}_1^{\text{mB}})}^2+{\vartheta }_1·{(}_1^{\text{mB}})+{\vartheta }_2},\end{array}$$

where ${}_1^{\text{mB}}$ is normalized by mean 113.9 and standard deviation 91.97. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=0.1729$, with $\text{CB}=(0.03934,0.3064)$, ${\aleph }_2=12.52$ with $\text{CB}=(11.87,13.17)$, ${\aleph }_3=42.07$ with $\text{CB}=(29.42,54.71)$, ${\aleph }_4=33.63$ with $\text{CB}=(18.56,48.71)$, ${\vartheta }_1=4.008$ with $\text{CB}=(2.873,5.143)$, ${\vartheta }_2=3.583$ with $\text{CB}=(1.976,5.19)$.

$$\begin{array}{c}\hfill \text{Entropy}{(}_2^{\text{mB}})=\frac{{\aleph }_1·{({}_2^{\text{mB}})}^4+{\aleph }_2·{({}_2^{\text{mB}})}^3+{\aleph }_3·({}_2^{\text{mB}}{)}^2+{\aleph }_4·({}_2^{\text{mB}})+{\aleph }_5}{({}_2^{\text{mB}})+{\vartheta }_1},\end{array}$$

where ${}_2^{\text{mB}}$ is normalized by mean 149.9 and standard deviation 124.3. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=0.04297$, with $\text{CB}=(-0.06928,0.1552)$, ${\aleph }_2=-0.1651$ with $\text{CB}=(-0.3167,-0.01359)$, ${\aleph }_3=0.5504$ with $\text{CB}=(0.4373,0.6636)$, ${\aleph }_4=10.99$ with $\text{CB}=(10.91,11.08)$, ${\aleph }_5=12.45$ with $\text{CB}=(11.51,13.4)$,${\vartheta }_1=1.334$ with $\text{CB}=(1.231,1.437)$ (Fig. 13).

$$\begin{array}{c}\hfill \text{Entropy}(\text{SB})=\frac{{\aleph }_1·{(\text{SB})}^4+{\aleph }_2·{(\text{SB})}^3+{\aleph }_3·{(\text{SB})}^2+{\aleph }_4·(\text{SB})+{\aleph }_5}{(\text{SB})+{\vartheta }_1},\end{array}$$

where $\text{SB}$ is normalized by mean 351.6 and standard deviation 284.1. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=0.03826$, with $\text{CB}=(-0.05705,0.1336)$, ${\aleph }_2=-0.1526$ with $\text{CB}=(-0.2846,-0.02056)$, ${\aleph }_3=0.5386$ with $\text{CB}=(0.4491,0.628)$, ${\aleph }_4=11.12$ with $\text{CB}=(11.03,11.21)$, ${\aleph }_5=13.01$ with $\text{CB}=(12.03,13.98)$, ${\vartheta }_1=1.383$ with $\text{CB}=(1.278,1.488)$.

$$\begin{array}{c}\hfill \text{Entropy}(H_b)=\frac{{\aleph }_1·{(H_b)}^3+{\aleph }_2·{(H_b)}^2+{\aleph }_3·(H_b)+{\aleph }_4}{{(H_b)}^2+{\vartheta }_1·(H_b)+{\vartheta }_2},\end{array}$$

where $H_b$ is normalized by mean 449.7 and standard deviation 374.2. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=0.1792$, with $\text{CB}=(0.03168,0.3267)$, ${\aleph }_2=12.4$ with $\text{CB}=(11.72,13.08)$, ${\aleph }_3=40.12$ with $\text{CB}=(27.41,52.84)$, ${\aleph }_4=30.98$ with $\text{CB}=(16.3,45.66)$, ${\vartheta }_1=3.839$ with $\text{CB}=(2.69,4.987)$, ${\vartheta }_2=3.295$ with $\text{CB}=(1.733,4.857)$ (Fig. 14).

Fig. 11.

a First K-Banhatti index vs Entropy and b second K-Banhatti index vs Entropy, for ${\text{CN}}_y^x$

Fig. 12.

a First K-hyper-Banhatti index vs entropy and b second K-hyper-Banhatti index vs entropy, for ${\text{CN}}_y^x$

Fig. 13.

a Modified first K-Banhatti index vs Entropy and b modified second K-Banhatti index vs Entropy, for ${\text{CN}}_y^x$

Fig. 14.

a Sum connectivity K-Banhatti index vs Entropy and b harmonic K-Banhatti index vs Entropy, for ${\text{CN}}_y^x$

General models for indices vs heat of formation

The following are general models for the fitted curves for all indices vs heat of formation. This comparison is also shown graphically.

$$\begin{array}{c}\hfill \text{HoF}(B_1)=\frac{{\aleph }_1·B_1+{\aleph }_2}{{B_1}^3+{\vartheta }_1·{B_1}^2+{\vartheta }_2·B_1+{\vartheta }_3},\end{array}$$

where $B_1$ is normalized by mean 8570 and standard deviation 7293. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=1.404\text{e+}06$, with $\text{CB}=(-8.049\text{e+}05,3.613\text{e+}06)$, ${\aleph }_2=1.63\text{e+}06$ with $\text{CB}=(-9.241\text{e+}05,4.184\text{e+}06)$, ${\vartheta }_1=-3.416$ with $\text{CB}=(-5.602,-1.23)$, ${\vartheta }_2=5.63$ with $\text{CB}=(-2.062,13.32)$, ${\vartheta }_3=-129.2$ with $\text{CB}=(-332.1,73.7)$.

$$\begin{array}{c}\hfill \text{HoF}(B_2)=\frac{{\aleph }_1·{B_2}^4+{\aleph }_2·{B_2}^3+{\aleph }_3·{B_2}^2+{\aleph }_4·B_2+{\aleph }_5}{B_2+{\vartheta }_1},\end{array}$$

where $B_2$ is normalized by mean $1.339\text{e+}04$ and standard deviation $1.149\text{e+}04$. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=5.447\text{e+}06$, with $\text{CB}=(-5.679\text{e+}12,5.679\text{e+}12)$, ${\aleph }_2=-1.241\text{e+}07$ with $\text{CB}=(-1.294\text{e+}13,1.294\text{e+}13)$, ${\aleph }_3=1.035e+07$ with $\text{CB}=(-1.08\text{e+}13,1.08\text{e+}13)$, ${\aleph }_4=9.066\text{e+}08$ with $\text{CB}=(-9.453\text{e+}14,9.453\text{e+}14)$, ${\aleph }_5=1.006\text{e+}09$ with $\text{CB}=(-1.049\text{e+}15,1.049\text{e+}15)$, ${\vartheta }_1=-7.956\text{e+}04$ with $\text{CB}=(-8.295\text{e+}10,8.295\text{e+}10)$ (Fig. 15).

Fig. 15.

a First K-Banhatti index vs HoF and b second K-Banhatti index vs HoF, for ${\text{CN}}_y^x$

$$\begin{array}{c}\hfill \text{HoF}({\text{HB}}_1)=\frac{{\aleph }_1·{B_2}^4+{\aleph }_2·{B_2}^3+{\aleph }_3·{B_2}^2+{\aleph }_4·B_2+{\aleph }_5}{B_2+{\vartheta }_1},\end{array}$$

where ${\text{HB}}_1$ is normalized by mean $5.46\text{e+}04$ and standard deviation $4.685\text{e+}04$. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=5.484\text{e+}06$, with $\text{CB}=(-5.783\text{e+}12,5.783\text{e+}12)$, ${\aleph }_2=-1.249\text{e+}07$ with $\text{CB}=(-1.317\text{e+}13,1.317\text{e+}13)$, ${\aleph }_3=1.041\text{e+}07$ with $\text{CB}=(-1.099\text{e+}13,1.099\text{e+}13)$, ${\aleph }_4=9.165\text{e+}08$ with $\text{CB}=(-9.665\text{e+}14,9.665\text{e+}14)$, ${\aleph }_5=1.017\text{e+}09$ with $\text{CB}=(-1.073\text{e+}15,1.073\text{e+}15)$, ${\vartheta }_1=-8.043\text{e+}04$ with $\text{CB}=(-8.481\text{e+}10,8.481\text{e+}10)$.

$$\begin{array}{c}\hfill \text{HoF}({\text{HB}}_2)=\frac{{\aleph }_1·{B_2}^4+{\aleph }_2·{B_2}^3+{\aleph }_3·{B_2}^2+{\aleph }_4·B_2+{\aleph }_5}{B_2+{\vartheta }_1},\end{array}$$

where ${\text{HB}}_2$ is normalized by mean $1.405\text{e+}05$ and standard deviation $1.218\text{e+}05$. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=3.311\text{e+}06$, with $\text{CB}=(-2.762\text{e+}12,2.762\text{e+}12)$, ${\aleph }_2=-7.497\text{e+}06$ with $\text{CB}=(-6.253\text{e+}12,6.253\text{e+}12)$, ${\aleph }_3=5.99\text{e+}06$ with $\text{CB}=(-5.006\text{e+}12,5.006\text{e+}12)$, ${\aleph }_4=7.041\text{e+}08$ with $\text{CB}=(-5.873\text{e+}14,5.873\text{e+}14)$, ${\aleph }_5=7.848\text{e+}08$ with $\text{CB}=(-6.547\text{e+}14,6.547\text{e+}14)$, ${\vartheta }_1=-6.188\text{e+}04$ with $\text{CB}=(-5.162\text{e+}10,5.162\text{e+}10)$ (Fig. 16).

Fig. 16.

a First K-hyper-Banhatti index vs HoF and b second K-hyper-Banhatti index vs HoF, for ${\text{CN}}_y^x$

$$\begin{array}{c}\hfill \text{HoF}{(}_1^{\text{mB}})=\frac{{\aleph }_1·{({}_1^{\text{mB}})}^2+{\aleph }_2{·}_1^{\text{mB}}+{\aleph }_3}{({{}_1^{\text{mB}})}^2+{\vartheta }_1·{(}_1^{\text{mB}})+{\vartheta }_2},\end{array}$$

where ${}_1^{\text{mB}}$ is normalized by mean 113.9 and standard deviation 91.97. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=-4.221\text{e+}09$, with $\text{CB}=(-6.314\text{e+}13,6.313\text{e+}13)$, ${\aleph }_2=-1.268\text{e+}10$ with $\text{CB}=(-1.896\text{e+}14,1.896\text{e+}14)$, ${\aleph }_3=-9.148\text{e+}09$ with $\text{CB}=(-1.368\text{e+}14,1.368\text{e+}14)$, ${\vartheta }_1=3.427\text{e+}05$ with $\text{CB}=(-5.125\text{e+}09,5.126\text{e+}09)$, ${\vartheta }_2=7.384\text{e+}05$ with $\text{CB}=(-1.104\text{e+}10,1.104\text{e+}10)$.

$$\begin{array}{c}\hfill \text{Entropy}{(}_2^{\text{mB}})=\frac{{\aleph }_1·{({}_2^{\text{mB}})}^2+{\aleph }_2{·}_2^{\text{mB}}+{\aleph }_3}{{(}_2^{\text{mB}})+{\vartheta }_1},\end{array}$$

where ${}_2^{\text{mB}}$ is normalized by mean 149.9 and standard deviation 124.3. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=-1.188\text{e+}04$, with $\text{CB}=(-1.199\text{e+}04,-1.177\text{e+}04)$, ${\aleph }_2=-3.427\text{e+}04$ with $\text{CB}=(-3.717\text{e+}04,-3.136\text{e+}04)$, ${\aleph }_3=-2.39\text{e+}04$ with $\text{CB}=(-2.714\text{e+}04,-2.065\text{e+}04)$, ${\vartheta }_1=1.906$ with $\text{CB}=(1.646,2.166)$ (Fig. 17).

Fig. 17.

a Modified first K-Banhatti index vs Entropy and b modified second K-Banhatti index vs Entropy, for ${\text{CN}}_y^x$

$$\begin{array}{c}\hfill \text{HoF}(\text{SB})=\frac{{\aleph }_1·{(\text{SB})}^3+{\aleph }_2·{(\text{SB})}^2+{\aleph }_3·(\text{SB})+{\aleph }_4}{(\text{SB})+{\vartheta }_1},\end{array}$$

where $\text{SB}$ is normalized by mean 351.6 and standard deviation 284.1. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=-108.2$, with $\text{CB}=(-160.5,-55.78)$, ${\aleph }_2=-1.203\text{e+}04$ with $\text{CB}=(-1.214\text{e+}04,-1.193\text{e+}04)$, ${\aleph }_3=-3.201\text{e+}04$ with $\text{CB}=(-3.384\text{e+}04,-3.019\text{e+}04)$, ${\aleph }_4=-2.133\text{e+}04$ with $\text{CB}=(-2.328\text{e+}04,-1.937\text{e+}04)$, ${\vartheta }_1=1.719$ with $\text{CB}=(1.561,1.877)$.

$$\begin{array}{c}\hfill \text{HoF}(H_b)=\frac{{\aleph }_1·{(H_b)}^3+{\aleph }_2·{(H_b)}^2+{\aleph }_3·(H_b)+{\aleph }_4}{{(H_b)}^2+{\vartheta }_1·(H_b)+{\vartheta }_2},\end{array}$$

where $H_b$ is normalized by mean 449.7 and standard deviation 374.2. The coefficients with $95\%$ confidence bound are: ${\aleph }_1=-1.211\text{e+}04$, with $\text{CB}=(-1.248\text{e+}04,-1.174\text{e+}04)$, ${\aleph }_2=-7.399\text{e+}04$ with $\text{CB}=(-1.302\text{e+}05,-1.781\text{e+}04)$, ${\aleph }_3=-1.291\text{e+}05$ with $\text{CB}=(-2.757\text{e+}05,1.737\text{e+}04)$, ${\aleph }_4=-6.931\text{e+}04$ with $\text{CB}=(-1.647\text{e+}05,2.604\text{e+}04)$, ${\vartheta }_1=5.286$ with $\text{CB}=(0.4965,10.08)$, ${\vartheta }_2=5.526$ with $\text{CB}=(-2.074,13.13)$ (Fig. 18).

Fig. 18.

a Sum connectivity K-Banhatti index vs Entropy and b harmonic K-Banhatti index vs Entropy, for ${\text{CN}}_y^x$

Conclusion

In this article, we investigated a natural polymer of cellulose network which has interesting pharmacological applications, outstanding characteristics, and a novel molecular structure. Natural polymers are preferable to synthetic polymers because they are nontoxic, biocompatible, free of side effects, and cost-effective. We calculated the K-Banhatti indices as well as their entropies. Tables 2, 3, 4, and 5 demonstrate the numerical comparison while Figs. 5, 6, 7, 8, 9, and 10 illustrate pictorial comparison of K-Banhatti indices and K-Banhatti entropies. Following that, curve fitting was performed between several K-Banhatti indices and their respective entropies and heat of formation. We analysed the performance of other mean square error-based strategies and discovered that the rational method produced the best results in all circumstances. The findings show a strong link between the dimensionality of a system and thermochemical properties.

Author Contributions

This work was equally contributed by all writers.

Data Availability

The data used to support the findings of this study are cited at relevant places within the text as references.

Declarations

Conflict of interest

The authors declare that they have no conflicts of interest.