Abstract
BACKGROUND:
Brainstem gliomas are aggressive and difficult to treat. Growth of these tumors may be characterized with MRI methods.
PURPOSE:
To visualize longitudinal changes in tumor volume, vascular leakiness and tissue microstructure in an animal model of brainstem glioma.
STUDY TYPE:
Prospective animal model.
ANIMAL MODEL:
Male Sprague-Dawley rats (n = 9) were imaged with 9L gliosarcoma cells infused into the pontine reticular formation of the brainstem. The MRI tumor microenvironment was studied at 3- and 10-days post-implantation of tumor cells.
FIELD STRENGTH/SEQUENCE:
Diffusion tensor imaging (DTI) and dynamic contrast enhanced (DCE)-MRI were performed at 4.7T using spin-echo multi-slice echo planar imaging and gradient echo multi-slice imaging, respectively.
ASSESSMENT:
Tumor leakiness was assessed by the forward volumetric transfer constant, , estimated from DCE-MRI data. Tumor structure was evaluated with fractional anisotropy (FA) obtained from DTI. Tumor volumes, delineated by T1 map, T2-weighted image, FA and DCE signal enhancement, were compared.
STATISTICAL TESTS:
Changes in the assessed parameters within and across the groups (i.e. rats 3- and 10-days post tumor cell implantation) were evaluated with Wilcoxon rank-sum tests.
RESULTS:
Day 3 tumors were visible mainly on contrast enhanced images, while day 10 tumors were visible in both contrast enhanced and diffusion weighted images. Mean at day 10 was 41% lower than at day 3 (p = 0.23). In day 10 tumors, FA was regionally lower in the tumor compared to normal tissue (p = 0.0004), and tumor volume, segmented based on FA map, was significantly smaller () than that obtained from other contrasts.
DATA CONCLUSION:
Contrast enhanced MRI was found to be more sensitive in detecting early-stage tumor boundaries than other contrasts. Areas of the tumor outlined by DCE-MRI and DTI were significantly different. Over the observed period of tumor growth, average vessel leakiness decreased with tumor progression.
Keywords: Tumor leakiness, Tumor volume, Dynamic contrast enhanced MRI, Brainstem glioma, Diffusion imaging
INTRODUCTION
Brainstem gliomas are aggressive tumors accounting for roughly 20% of pediatric brain tumors (1). The tumor location, close to brain regions controlling such vital bodily functions, such as breathing and heart rate, complicates treatment (2). This treatment can consist of surgical resection (3), radiation (4), chemotherapy and local infusion of drugs directly at the target site, i.e. convection enhanced delivery (5), or a combination of the above. MR imaging is often used to characterize perfusion and microstructural changes inside the tumor as early indicators of therapeutic response (6).
Gliomas often have a leaky blood-brain-barrier (BBB), mainly due to angiogenesis of new blood vessels to supply nutrients. This can lead to a buildup of interstitial fluid pressure, which reduces drug influx into the interstitial space from blood vessels following systemic delivery, as in chemotherapy. Dynamic contrast enhanced MRI (DCE-MRI) has been extensively used to quantify a key measure of BBB leakiness, the forward volumetric transfer constant () along with the extravascular-extracellular space (EES) volume fraction (), and plasma volume fraction () in tumors (7). However, DCE-MRI measures in brainstem gliomas are uncommon, with only one DCE-MRI study reporting on a rodent model of brainstem glioma. That study by Subashi et al. compared MR measured between cortical and focal brainstem gliomas within a genetic mouse model using DF1 cells (8). Using the extended Tofts model (9), they found to increase with tumor volume for relatively large volumes of up to 200 mm3. They also found cortical tumors to be leakier than brainstem tumors.
MR diffusion tensor imaging (DTI) has been used to study tissue microstructure in brainstem gliomas. DTI tractography has proven useful in surgical planning, and post-operatively to assess the regional extent of white matter tracts (10). DTI measures have also been used to quantify response to therapy. Following gene therapy treatment, Steagman and co-workers found that the measure of apparent diffusion coefficient (ADC) of water increased in 9L gliosarcomas tissue 8 days after implantation in the rodent forebrain (11). Several studies have reported marked changes in DTI measures of directional water diffusion that could be attributed with loss of fiber tracts or more complex fiber branching (12). Helton and co-workers found increases in ADC in focal (n = 1) and diffuse (n = 6) human pontine glioma compared to surrounding brain tissue (13). They also reported reductions in fractional anisotropy (FA) compared with normal tissue. Presently lacking are longitudinal studies in rodent models of brainstem glioma and of the evolution of DTI metrics with tumor growth.
Given that tumor models are often used to evaluate promising therapies, there is a need for further MR characterization of the tumor microenvironment in model systems as a prelude to application of a therapy in humans. The goal of this study is to provide insight into vascular and microstructural properties in a rat model of focal brainstem glioma (9L gliosarcoma).
MATERIALS AND METHODS
9L Tumor Cells
Tumor cells were prepared based on the protocol developed by Jallo et al. (14) and Barth et al. (15). Briefly, 9L gliosarcoma cells were cultured to confluence in T175 cell culture flasks in Dulbeco’s modified Eagle’s medium (DMEM) low glucose media supplemented with 10% fetal bovine serum and 10% penicillin-streptomycin. Cells were cultured and incubated at 37 °C in 5% CO2 atmosphere. Prior to surgery, cells were harvested using 0.25% trypsin-EDTA, washed twice and suspended in serum free medium until a concentration of cells/μL was achieved.
Animal Surgery
Animal experiments were performed on 2-month old male Sprague-Dawley rats (n = 9) weighting approximately 250 g using protocols and procedures approved by the Institutional Animal Care and Use Committee. Anesthesia was induced using xylazine (10 mg/kg subcutaneous) and 4% isoflurane in 1 L/min oxygen and maintained using 1.5% isoflurane in 1 L/min oxygen. 2 mL of saline was injected subcutaneously for hydration prior to imaging. For surgery, the anesthetized animals were fixed in position using a stereotaxic frame (Kopf Model 900, David Kopf Instruments, Tujunga, CA, USA), and a burr hole was drilled (AP: +1.0 mm, ML: −1.4 mm and DV: −7.0 mm from the interaural line) above the pontine reticular formation (PnO) to provide access for the 32-gauge needle (small hub RN needle, Hamilton, Reno, NV) that was mounted on a 50 μL gas tight syringe (Hamilton, Reno, NV). 3 μL of a solution containing approximately 105 tumor cells were infused at a constant rate of 0.5 μL/min using a syringe pump (Cole-Parmer, Vernon Hills, IL) into the PnO of each of the animals. Animals were monitored daily for general health and presentation of deleterious effects of tumor inoculation.
MR Imaging
In-vivo MR measurements were performed 3- and 10-days post-implantation of tumor cells. All measures were collected on a 330 mm ID Oxford 4.7 Tesla (T) horizontal bore magnet with a RRI BFG-200/115-S14 gradient set (Resonance Research, Billerica, MA) connected to an Agilent VNMRS imaging console controlled by VnmrJ3.1A software (Agilent Technologies, Santa Clara, CA). Rats were placed in a 39 mm ID quadrature transmit/receive birdcage RF probe (Animal Imaging Research, Holden, MA).
Prior to MR imaging, the tail vein of the rat was catheterized and an approximately 1.5 m long intra-venous line attached to a 1 mL tuberculin syringe was connected to the catheter to inject 0.24 mmol/kg body weight of the gadolinium-based gadodiamide (Omniscan, GE Healthcare, USA) contrast agent. After positioning the rat in the bore, the syringe was placed external to the bore for bolus injection by hand. Respiration was continuously monitored during the imaging session via a pneumatic pillow attached to the animal monitoring system (SA Instruments, Model 1025, Stony Brook, NY).
Ten axial slices of 1 mm thickness were acquired with a field of view of 24 mm x 24 mm and a matrix size of 96 × 96 for all the four MRI sequences employed. T1, the time constant of longitudinal relaxation, was quantified with an inversion recovery based rapid acquisition with relaxation enhancement (RARE) sequence using the following imaging parameters: TR = 10 s, TEeff = 8.51 ms, RARE factor = 4, TI = 100, 500, 1,000, 1,500, 2,000 and 4,000 ms, and NEX = 1. Weighted images based on the time constant of the transverse relaxation, T2, were acquired using a RARE sequence with TR = 10,000 ms, TEeff = 120 ms, RARE factor = 4 and NEX = 3. High angular resolution diffusion imaging (HARDI) data was acquired using a fat suppressed, spin echo diffusion-weighted, multi-shot echo planar imaging (EPI) sequence with TR = 5,000 ms, TEeff = 40 ms, number of shots = 3 and NEX = 8. Diffusion weighted images were obtained in 24 directions (6 with b-value ≈ 80 s/mm2 and 18 with b-value ≈ 800 s/mm2) which were distributed following a scheme of electrostatic repulsion (16). The duration of the diffusion gradient pulse, δ, and the diffusion time, Δ, between gradient pulses were 3 ms and 14 ms, respectively. Diffusion weighted images were fitted to a rank-2 tensor model using an in-house software package written in IDL programming language (Harris Geospatial Solutions, Broomfield, Colorado), from which scalar FA and ADC (i.e. trace of the diffusion tensor divided by 3) values were obtained. A serial T1-weighted spoiled gradient-echo sequence (TR = 100 ms, TE = 2.39 ms, flip angle = 90° and NEX = 3) was used for DCE-MRI with a temporal resolution of 29 seconds per slice pack. Three pre-scans were acquired before the bolus tail-vein injection of gadodiamide, and 122 scans were acquired following the tail-vein injection.
Contrast Agent Concentration
Because gadodiamide does not enter cells due to its size and hydrophilicity (17), brain tissue was modeled as two compartments: blood plasma and EES. Arterial blood carrying the contrast agent flows into the plasma compartment within each voxel and leaves without entering the EES unless the blood-brain barrier is leaking.
To quantify contrast agent dynamic distribution, measured signal enhancement was first converted to estimate concentration of contrast agent in tissue using methods similar to those described by Chen et al. (18). MR signal, S, from a conventional spoiled gradient-echo sequence is given by,
| (1) |
where represents the spin density, α is the flip angle, TR and TE are the repetition and echo times, and is the time constant of reversible transverse relaxation. Assuming the tissue relaxes with a single relaxation time (i.e. fast exchange of protons between blood plasma and EES compartments), the effect of contrast agent on the relaxation rate of nearby nuclei, ignoring the effect of the contrast agent on T2* (18), is approximated by the following relation,
| (2) |
where is the relaxation time of the tissue without the presence of the contrast agent, is the relaxivity of the contrast agent, which quantifies the rate of relaxation time reduction of nearby nuclei, and C is the contrast agent concentration. Using Equations 1 and 2, MR signal enhancement due to the presence of contrast agent is given by,
| (3) |
Assuming is constant, and thus ignoring trans-vascular and trans-cellular water exchange effects on relaxivity, the above equation can be simplified and rearranged to obtain an estimate of tracer concentration,
| (4) |
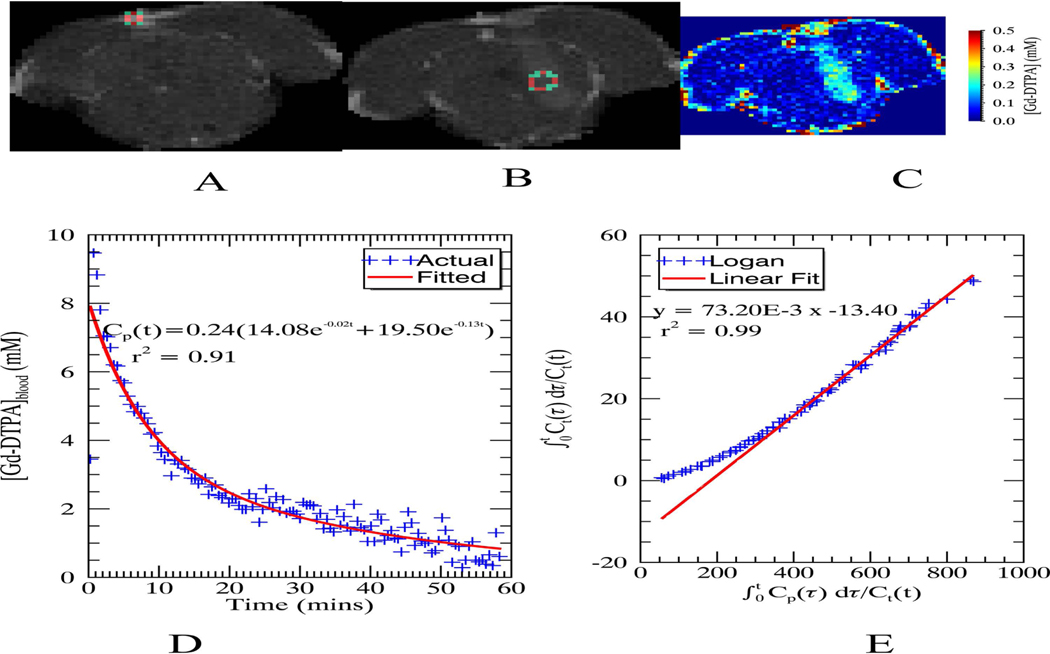
At 4.7T and normal rat body temperature (36–37 °C), relaxivity values are 2.8 sec−1mM−1 and 3.9 sec−1mM−1 in brain tissue and blood plasma, respectively (19,20). Blood vessel voxels were assigned a constant of 2.7 seconds (19) to circumvent inaccuracies in the measured due to flow, and for tissue was calculated by fitting the polarity corrected signal magnitude from the variable inversion time RARE acquisition (i.e. sign of the signal magnitude before the null point is flipped) to the standard inversion recovery model. An example of the estimated concentration map using Equation 4 is shown in Figure 1, Part C at time of peak enhancement in the tumor region.
Figure 1:
(A) Region of interest (ROI) in the superior sagittal sinus used for calculating the arterial input function (AIF), (B) ROI used to generate the Logan plot at the center of the tumor, (C) Calculated concentration map when the relative signal enhancement peaks in the Logan ROI (approximately 7.5 minutes after injecting the contrast agent), (D) and (E) AIF and Logan plots, respectively, with the fitted equation and goodness of fit measure (r2)
Exchange Model
The calculated concentration of the contrast agent was fitted into a two-compartmental exchange model introduced by Tofts and Kermode (21). Vascular leakiness of contrast agent was assumed to be small compared to the incoming blood flow. This allows two distinct compartments for plasma and tissue to exist within some voxels. Within each compartment, the contrast agent was assumed to be well-mixed, and mass flux across a leaking blood vessel was proportional to concentration difference between the two compartments (21),
| (5) |
Where subscripts t, p, e refer to tissue, plasma and EES, are the contrast agent concentrations in plasma and EES compartments respectively, is the volume fraction of the EES in the tissue, is the tissue volume, P is the permeability coefficient of the blood vessel, which is the contrast agent diffusion coefficient per unit blood vessel thickness (22), and S is the surface area of the leaking blood vessel. Equation 5 can be expressed in terms of MR measured tissue concentration, , which is a weighted sum of the individual compartment concentration (, where is the blood plasma volume fraction). Replacing the proportionality factor on the right in Equation 5 with the rate constant, , results in the following relation,
| (6) |
This equation can be further simplified to the following, when and is the reverse rate constant, for exchange from the tissue to plasma compartment,
| (7) |
The exact solution to this linear differential equation is obtained by superposition of solutions for source terms, , and , in the extended Tofts model (9),
| (8) |
where is the convolution operator, is the Dirac delta function, and is the impulse response describing tissue response to a short bolus of contrast agent in the vasculature such that,
| (9) |
is also interpreted as the amplitude of the tissue impulse response. The above model assumes the system is linear and the tissue parameters are time invariant. Linearity is violated at high blood concentrations of contrast agent due to nonlinear relation between contrast agent concentration and T2* dephasing (23). An appropriate dose of contrast agent was chosen to ensure system linearity based on of the contrast agent, T10 of the blood and imaging parameters. Time invariance is typically not violated since the contrast agent is inert and animal physiological conditions are typically well regulated during the experiment.
The arterial input function (AIF) was approximated as bi-exponential (21),
| (10) |
where and represent the amplitude and rate constant, respectively, of the fast equilibrium between plasma and extracellular space, and represent the amplitude and rate constant of the slow component of the clearance, and d is the dose of the bolus injection. Arterial concentration measures per se are hampered, due to flow since the flowing blood both enhances the MR signal, similar to the effect of contrast agent due to the time-of-flight (TOF) effect (24), and decreases the MR signal due to T2* dephasing. In this study, the shape of the AIF was estimated from the signal in a region of the superior sagittal sinus shown in Figure 1, Part A. A venous output function (VOF) was used instead of AIF due to the difficulties, mentioned above, in measuring contrast agent concentration in fast flowing arterial blood and the shape of the AIF has been shown to match with that of the VOF (25). The amplitude was adjusted by scaling with a known 1% plasma volume fraction in caudate-putamen (26). While T2* dephasing due to high contrast agent concentration in the blood may introduce errors in the measured AIF, the resulting signal loss is less than 12% based on the peak concentration calculated in the venous sinus (C = 10 mM), r2 relaxivity of contrast agent at 4.7T (r2 = 5.3 mM−1 sec−1 (19)) and the echo time. An example of the calculated AIF is shown in Figure 1, Part D.
Model Case Selection
Rather than assume leaky vessels and that reflux exists in every voxel, an alternative approach, developed by Ewing et al. (23), was used, which allows for four different model cases. Briefly, Case 1 corresponds to necrotic tissue ( = 0) with no vasculature, Case 2 corresponds to normal perfused brain tissue ( = 0, ≠ 0) without leaking blood vessels, Case 3 corresponds to leaky vessel without reflux ( ≠ 0, = 0, ≠ 0), and Case 4 is the full model with leaky vessel and reflux ( ≠ 0, ≠ 0, ≠ 0). Parametric estimates from cases were combined using a multi-model statistical approach. Akaike information criterion (AIC) was used to derive the probability, that a particular case best fits the data (27),
| (11) |
| (12) |
| (13) |
where SSRi is the sum of square residuals for case i, N is the sample size, is the number of parameters in the case i, and p is the fitted parameter, which is either or . MR measured concentration time-series data from each voxel was fitted with each of the four cases using a non-linear least squares routine, MPFIT (28) in the IDL. AIC weights were computed to calculate and .
The sample size, N, (number of fitted points) was determined by the end-time point in DCE scans when contrast agent concentration equilibrated in both compartments. This was determined graphically using a Logan plot (29), which required integrating Equation 7, assuming a zero-initial condition,
| (14) |
The non-linear part of the Logan plot (y versus x as labeled in the above equation) was used to determine N. The linear portion was fitted to the equation above to determine the distribution volume. An example of the tumor region of interest and the corresponding Logan plot is shown in Figure 1, Part B and Part E respectively.
Tumor Segmentation
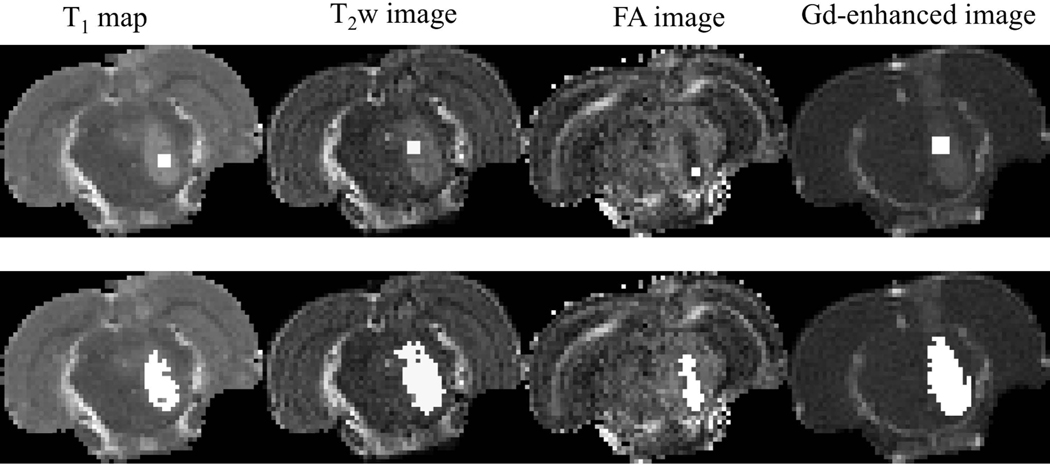
Pontine tumors were individually segmented using quantitative T1 maps, T2 weighted images, fractional anisotropy images obtained from diffusion tensor fitting, and contrast enhanced images obtained at peak relative signal enhancement. Segmentation was performed using IDL’s region grow method. A seed region was selected inside the tumor and grown to encompass voxels that fell within 1 to 3 standard deviations from the average image voxel intensity computed within the seed (Figure 2). A lower standard deviation multiplier such as one was chosen for smaller tumors where the difference in the signal between normal and tumor tissue was small due to partial volume effect. Seed size and number of standard deviations for each imaging slice were selected to i) restrict the tumor within the pons, ii) exclude surrounding normal tissues and iii) exclude cortical tumor regions growing outside the brainstem tumor. The seed position varied due to differences in the outlined tumor region. The cerebrospinal fluid (CSF) boundary between the brainstem and cortex was used to make sure the selected region of interest (ROI) was inside the brainstem, and that image contrast between normal and tumor regions was enough to visually confirm that the ROI laid within the tumor. Most rats (6 out of 9) developed a secondary tumor in the cortex ten days post-implantation of the tumor cells. This tumor most likely grew due to seeding of cells along the needle track during inoculation. These cortical tumor regions were excluded as they were outside of the brainstem.
Figure 2:
An example of tumor segmentation using data acquired ten days post implantation of the tumor. (Top row) Seeds used to grow the tumor region; (Bottom row). Segmented tumor regions are shown in white.
Statistical Analysis
Assuming MR signal is a random variable, a chance exists for some voxels to randomly appear hyper or hypointense relative to its surroundings which might be misinterpreted as tumor. Thus, two statistical tests were performed on kinetic model estimates and calculated tumor volumes based on T1, T2, FA and DCE; 1) to assess if the measures across rats within each group (day 3 and day 10) could have been a random effect and, 2) to assess if there is any statistically significant difference between groups. Since the tumor volumes were not normally distributed and of limited sample sized, Wilcoxon rank-sum test which does not assume the underlying distribution was used for all analyses.
RESULTS
Tumor Segmentation
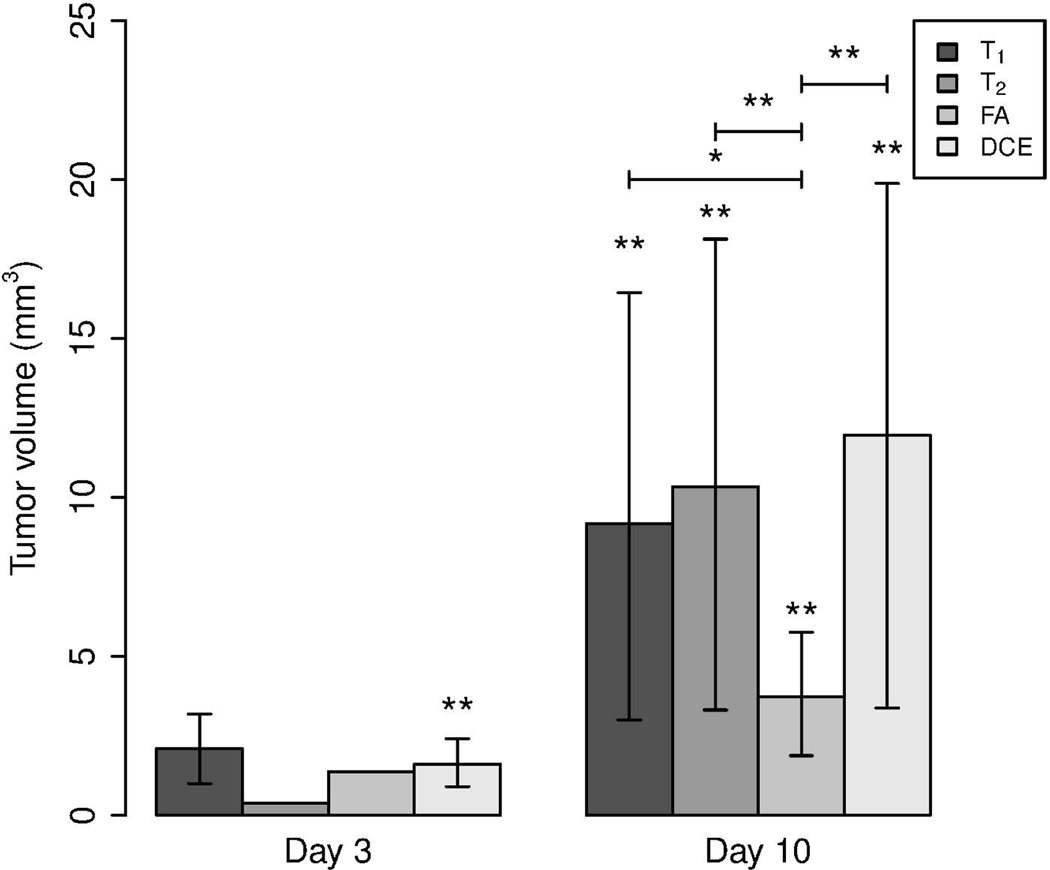
Results of the tumor volumetric analysis are shown in Figure 3. Contrast enhanced images provided the best contrast for all the tumors imaged in this study. At day 3, tumors were detected mainly in contrast enhanced MR images (p = 0.0091). Tumor volumes segmented based on T1 maps (p = 0.5), T2 images (p = 1) and FA maps (p = 1) at day 3 were not statistically significant as the tumor was visible only in a small fraction of rats imaged.
Figure 3:
Bar chart showing average tumor volumes segmented from different MR imaging methods 3 and 10 days post implantation of the tumor. The 95% confidence interval is given by error bars. Statistical significance was analyzed using Wilcoxon rank sum test with p-values denoted by *** for , ** for , * for , and none for
At day 10, tumors were clearly visible on both structural and contrast enhanced scans, but with differences in segmented areas. Tumor volumes within all the groups were found to be statistically significant with p-values of 0.0039, 0.0039, 0.0091 and 0.0039 for T1, T2, FA and DCE-MRI, respectively. Across groups, tumor volumes segmented based on FA were significantly lower than those obtained with other MR contrast mechanisms investigated in this study with p-values of 0.064, 0.022, 0.022 when compared against T1, T2 and DCE, respectively. Tumor volumes segmented based on contrast mechanisms other than FA showed no statistically significant differences, with resulting p-values of 0.51, 0.39, 0.73 between T1 and T2, T1 and DCE, T2 and DCE, respectively.
Tumor Structure
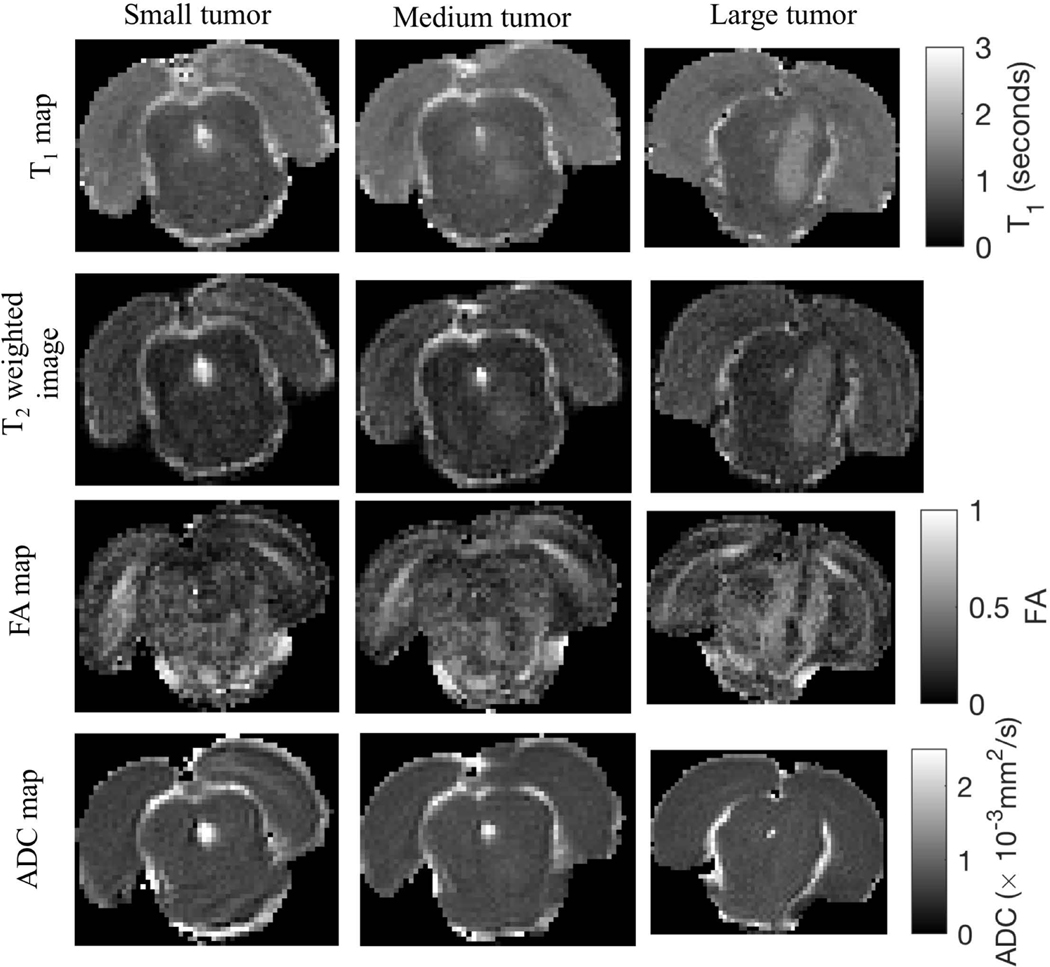
Representative images of tumor structure are shown in Figure 4. T1 and FA values in regions ipsilateral and contralateral to the tumor are given in Table 1. The mean T1 inside the tumor on the ipsilateral side was 15% (p = 0.33) and 45% (p = 0.0004) higher than the contralateral side at 3 and 10 days post implantation of the tumor cells, respectively. This is shown by hyperintense regions in the first and second row images. Areas with elevated T1 matched those with elevated T2. The mean FA on the ipsilateral side was 27% (p = 0.0004, Wilcoxon rank sum test) smaller than the contralateral side at 10 days post implantation of tumor cells, as exhibited by hypointense regions in FA images. FA differences between day 3 and day 10 tumors was not quantified since only one tumor was visible in the FA map at day 3. The ADC did not exhibit enough contrast to distinguish between normal and tumor tissue and hence was excluded in the tumor structural analysis.
Figure 4:
Structural images of small (day 3), medium (day 10) and large (day 10) size tumors representative of those in the study cohort. (First row) Map of T1 relaxation times in the brain, (Second row) T2-weighted images, (Third and fourth row) Map of fractional anisotropy (FA) and apparent diffusion coefficient (ADC) obtained from fitting the diffusion weighted MR data to the tensor model, respectively.
Table 1:
Statistical data for structural MRI scans analyzed using Wilcoxson rank-sum test along with number of tumors and p-value given in brackets: T1 before the injection of contrast agent and FA in regions ipsilateral and contralateral to the tumor 3 and 10 days post implantation of tumor cells. N/A indicates there is only one data point.
| Parameter | Mean | Standard deviation | Median | ||||
|---|---|---|---|---|---|---|---|
| Ipsilateral | Contralateral | Ipsilateral | Contralateral | Ipsilateral | Contralateral | ||
| Pre-contrast T1 (seconds) | Day 3 | 1.062 (2, 0.500) | 0.922 (2, 0.500) | 0.004 | 0.027 | 1.062 | 0.922 |
| Day 10 | 1.372 (9, 0.004) | 0.944 (9, 0.009) | 0.114 | 0.017 | 1.346 | 0.943 | |
| FA | Day 3 | 0.217 (1, 1.000) | 0.299 (1, 1.000) | N/A | N/A | 0.217 | 0.299 |
| Day 10 | 0.250 (9, 0.009) | 0.334 (9, 0.004) | 0.03 | 0.035 | 0.250 | 0.326 | |
Tracer Kinetic Analysis
Out of the 9 rats imaged, 3 (small, medium and large) were selected for display as representative of the entire cohort of rats. The volume of the small (day 3), medium (day 10) and larger (day 10) tumors based on Gd-enhanced images were 2.12, 11.31 and 19.87 mm3, respectively. Results of tracer kinetic analysis are shown in Figure 5, and statistics of kinetic parameters for tumors at day 3 and 10 are given in Table 2. Gd-enhanced images clearly show tumors on both day 3 and 10. Case selection maps were used to further identify the tumor regions; Case 2 is the most frequently selected, representing normal brain tissue with an intact blood brain barrier. Case 3 (leaky vessel without reflux) is at the tumor boundary and Case 4 (leaky vessel with reflux) is selected in the tumor core. The map suggests leakiness within designated tumor regions. An elevated is also found in CSF spaces including the ventricles and sub-arachnoid space, possibly due to leakiness of choroid plexus capillaries. EES volume fraction, ve, suggests that cells within the tumor are tightly packed (ve < 10%). Plasma volume fraction, vp, is not reported as it was an unstable parameter.
Figure 5:
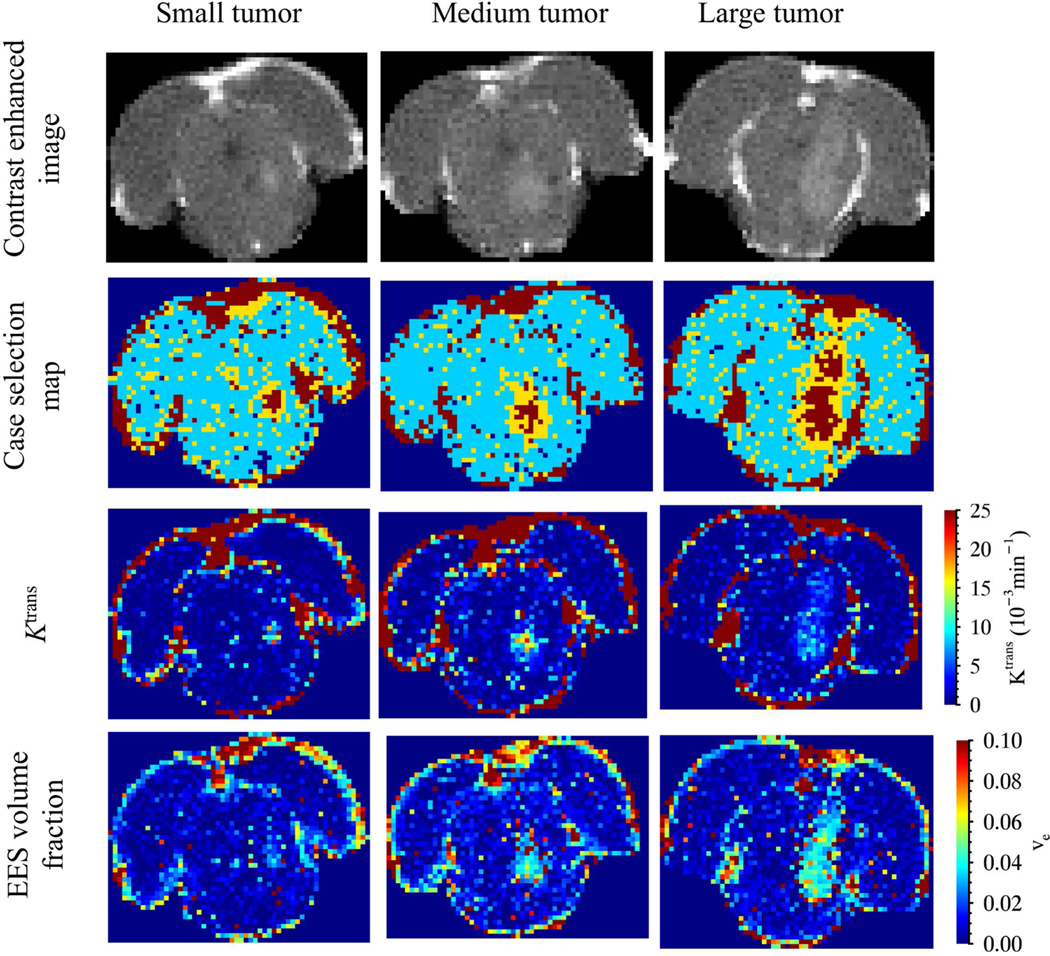
Results of tracer kinetic analysis from rats with small (day 3), medium (day 10) and large (day 10) tumors representative of those in the study cohort. (First row) Contrast enhanced image at peak signal enhancement inside the tumor (roughly within 5–10 minutes after injection of the contrast agent). (Second row) Case selection map with dark blue for case 1, turquoise for case 2, yellow for case 3 and dark red for case 4. (Third row) map and (Fourth row) map of EES volume fraction
Table 2:
Statistical data for DCE-MRI data analysis using Wilcoxson rank-sum test (n = 9, p = 0.0039 for and EES volume fraction on both days) showing mean, median and standard deviation of and EES volume fraction.
| Parameter | Mean | Standard deviation | Median | |||
|---|---|---|---|---|---|---|
| Day 3 | Day 10 | Day 3 | Day 10 | Day 3 | Day 10 | |
| (min−1) | 0.032 | 0.019 | 0.016 | 0.007 | 0.025 | 0.019 |
| EES volume fraction (%) | 3.94 | 4.42 | 1.48 | 1.62 | 4.09 | 4.43 |
and ve are found to be heterogeneous within the tumor. The average at day 10 is approximately 41% lower than that at day 3 (p = 0.23). The mean ve at day 10 tumors is 12% larger than that at day 3, although the differences were not statistically significant (p = 0.82, paired Wilcoxon rank sum test). A plot of these parameters versus the tumor volume based on the case selection map for all 18 data sets along with p-values is shown in Figure 6, Part A and Part B. In this data, the tumor boundary determined by Case 3 voxels in the tumor (selective for voxels at tumor boundary) was not included since it added greater uncertainty due to partial volume effects. Results indicate mean reduced significantly with tumor size, while ve remained approximately the same over time. The histogram of for Case 4 regions at day 10 is shown in Figure 6, Part C is right skewed with 75% quartile point at 0.0359 min-1.
Figure 6:
(A) Plot of average Ktrans, (B) average EES volume fraction versus tumor volume calculated based on the number of case 3 and case 4 voxels within the tumor along with p-values for each data point computed using Wilcoxon rank-sum test, and (C) histogram of Ktrans from case 4 regions for day 10 tumors. Error bars in A & B represent 95% confidence intervals for the mean Ktrans and EES volume fraction.
DISCUSSION
This study provides longitudinal DCE-MRI and DTI measures of focal brainstem glioma in rodents. The 9L allogenic rat brainstem glioma model chosen for this study has been widely used to study cerebral gliomas, especially in the caudate, but less frequently in the brainstem. Of note, previous glioma studies have shown vascular leakiness and tumor microstructure depend on implantation location (8,30). Tumors embedded within regions of high vascularity, such as the cortex are expected to exhibit higher than more fibrous regions, such as the brainstem. Also, changes in FA depend on the extent of white matter disruption, edema and cellularity/vascularity of the tumor which in turn depend on the tumor location. To the best of our knowledge, the present study provides the first demonstration using diffusion-perfusion MRI to assess tumor microenvironment features for allogeneic focal brainstem glioma in rodents.
Rather than using the standard Tofts model for pharmacokinetic analysis of DCE-MRI data (21), a graphical analysis and a multi-case model approach was used. This approach has been previously shown to balance bias versus variance of estimated parameters in the extended Tofts model (23). DCE data analysis shows vascular leakiness, as quantified by , to reduce significantly with tumor volume, and EES volume fraction is found to be independent of the tumor volume. reduction differs from the previous DCE-MRI study by Subashi et al. that reported to increase linearly with brainstem tumor size in mice injected with DF1 cells (8). In their study, MRI was performed once symptoms began to appear (40 ± 10 days post implantation of tumor cells) and the much larger tumor volumes reported may in part explain the difference in trends. Other study differences include implantation of a different tumor cell line. Use of a different DCE-MRI model (standard extended Tofts model) also may result in a higher than we predicted.
The reduction in may result from vascular collapse and initiation of necrosis. It is known that necrosis occurs in 9L gliosarcomas grown in rats, especially at later time points (31). We observed a right skewed histogram for larger tumors (day 10) which may indicate initiation of such a necrotic core. Previous modeling studies have indicated that vascular collapse should precede development of necrosis, mainly due to the combination of compressive stresses within the tumor interior that develop with rapid cell proliferation and reduced trans-vascular pressure gradients driven by elevated interstitial fluid pressure (32). Although DCE-MRI model fits did not identify necrotic regions (Case 1) with , EES and plasma volume fraction equal to 0, later time points (> 10 days) might show Case 1 regions within tumors. However, these results are consistent with an earlier study by Bagher‐Ebadian et al. Case selection for tracer kinetic analysis in human glioblastoma found case numbers to reduce in necrotic regions but not necessarily reaching Case 1 (33). Results of our study suggest an optimal timing window for systemic delivery of drugs to the brainstem glioma before leakiness reduces beyond a threshold to have a therapeutic effect.
In future studies, direct correlations between and plasma volume fraction may be further investigated. Plasma volume fraction was not reported in this study because the mean transit time of contrast agent in normal rat brain cortex (1.41 s (34)) required a very high temporal resolution (< 1 s) to measure blood flow. Also, plasma volume fraction in the brain has been measured to be small (≈ 0.5 to 3% (35)) making it difficult to reliably measure with the signal-to-noise ratio of DCE scans. These problems may be circumvented using parallel imaging and measurements at a higher magnetic field strength to get better temporal resolution or by using arterial spin labeling as an alternate technique to measure blood flow.
In DTI analyses, FA in the focal brainstem tumor was found to be lower compared to normal brainstem tissue. Reduced FA may result from a reduction in the ratio of water diffusion parallel and perpendicular to fiber tracts. Lower FA has been previously measured in regions with loss of fiber tracts or more complex fiber branching (12). Reductions in FA within tumor regions have been reported in other studies of cerebral gliomas. These reductions have been attributed to disruptions to the white matter fiber tracts passing through the region, edema, or necrosis (13,30). In this study, FA was found to be lower in a small sub-region of the tumor only at later stages which may also indicate initiation of necrosis (36), as suggested by reductions in .
Using DCE-MRI, we found interstitial space in brainstem glioma was decreased compared to normal tissue ( ≈ 0.22 in normal mouse brainstem (37)). However, ADC was not reduced inside the tumors, as expected from increased cellularity. Increased diffusion weighting in the DTI scans may be required to increase ADC contrast between normal and tumor tissues.
Different MRI contrast mechanisms were used to segment the tumor in order to evaluate early-stage imaging markers and compare the tumor regions delineated at late-stage tumors. Gd-enhanced imaging was able to detect focal brainstem glioma at an earlier stage better than normal relaxation or diffusion weighted imaging. The reason for higher sensitivity of DCE-MRI for this glioma might be due to the time course of tumor pathophysiology with microscopic angiogenesis preceding more macroscopic structural changes. As the tumor progressed, we found no statistically significant differences in segmented tumor volumes, except for those segmented using FA, which delineated a smaller volume. This suggests that FA changes with white matter fiber track disruption or edema may lag other vascular and microstructural measures at the tumor periphery, as measured with MR.
The study however has several limitations. Firstly, the time course for measuring changes in vascular leakiness and tissue microstructure was not completely resolved since the number of time points in the study was two. This limitation was mainly due to the collapse of veins and the resulting necrosis of the tail observed with frequent tail vein injections closely spaced in time. This limited the number of imaging procedures on the same animal given the limited mean survival time (38). Secondly, the accuracy of the Ktrans maps was limited by the temporal resolution of DCE-MRI scans which were longer than the first pass time of the contrast agent and hence might not fully capture the contrast agent dynamics within an imaging voxel. Thirdly, microstructural changes within the tumor might not be fully captured due to the limited diffusion weighting in the DTI scans which was chosen based on the signal-to-noise ratio of scans. Finally, it is known that rodent brain tumor models do not fully replicate the characteristics of human brain tumors due to the absence of genomic and phenotypic signatures of human tumors (39), hence care should be taken when considering clinical translation of model results.
In conclusion, MR imaging of model tumors can be used to better understand tumor physiology. In this study, results reflect early stages of tumor growth with a loss of vascular leakiness and fiber microstructure within the brainstem. Gd-enhanced imaging is able to detect focal brainstem glioma at an earlier stage compared to relaxation or diffusion weighted imaging. Such MR information may be used to inform the response to new drug therapies. and diffusion tensor data has been previously incorporated in computational transport models to predict interstitial fluid velocity, pressure and drug/tracer distribution following systemic or local delivery (40).
ACKNOWLEDGEMENTS
We thank Dr. Rintaro Hashizume, Northwestern University for providing us with the 9L gliosarcoma cell line used in this study. A portion of this work was performed in the Advanced MRI/S (AMRIS) Facility at the McKnight Brain Institute of the University of Florida, which is part of the National High Magnetic Field Laboratory (supported by National Science Foundation Cooperative Agreement DMR-1157490, the State of Florida, and the U.S. Department of Energy).
Grant Support: The project described was supported by award number R01NS063360 from the National Institute of Neurological Disorders and Stroke.
REFERENCES
- 1.Smith MA, Freidlin B, Ries LA, Simon R. Trends in reported incidence of primary malignant brain tumors in children in the United States. J Natl Cancer Inst 1998;90(17):1269–1277. [DOI] [PubMed] [Google Scholar]
- 2.Donaldson SS, Laningham F, Fisher PG. Advances toward an understanding of brainstem gliomas. J Clin Oncol 2006;24(8):1266–1272. [DOI] [PubMed] [Google Scholar]
- 3.Teo C, Siu TL. Radical resection of focal brainstem gliomas: is it worth doing? Childs Nerv Syst 2008;24(11):1307–1314. [DOI] [PubMed] [Google Scholar]
- 4.Yen CP, Sheehan J, Steiner M, Patterson G, Steiner L. Gamma knife surgery for focal brainstem gliomas. J Neurosurg 2007;106(1):8–17. [DOI] [PubMed] [Google Scholar]
- 5.Murad GJ, Walbridge S, Morrison PF, et al. Image-guided convection-enhanced delivery of gemcitabine to the brainstem. J Neurosurg 2007;106(2):351–356. [DOI] [PubMed] [Google Scholar]
- 6.Yankeelov TE, Lepage M, Chakravarthy A, et al. Integration of quantitative DCE-MRI and ADC mapping to monitor treatment response in human breast cancer: initial results. Magnetic Resonance Imaging 2007;25(1):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aryal MP, Nagaraja TN, Keenan KA, et al. Dynamic Contrast Enhanced MRI Parameters and Tumor Cellularity in a Rat Model of Cerebral Glioma at 7T. Magn Reson Med 2014;71(6):2206–2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Subashi E, Cordero FJ, Halvorson KG, et al. Tumor location, but not H3.3K27M, significantly influences the blood-brain-barrier permeability in a genetic mouse model of pediatric high-grade glioma. J Neurooncol 2016;126(2):243–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tofts PS. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. J Magn Reson Imaging 1997;7(1):91–101. [DOI] [PubMed] [Google Scholar]
- 10.Chen X, Weigel D, Ganslandt O, Buchfelder M, Nimsky C. Diffusion tensor imaging and white matter tractography in patients with brainstem lesions. Acta Neurochir (Wien) 2007;149(11):1117–1131; discussion 1131. [DOI] [PubMed] [Google Scholar]
- 11.Stegman LD, Rehemtulla A, Hamstra DA, et al. Diffusion MRI detects early events in the response of a glioma model to the yeast cytosine deaminase gene therapy strategy. Gene Ther 2000;7(12):1005–1010. [DOI] [PubMed] [Google Scholar]
- 12.Johansen-Berg H, Behrens TEJ. Diffusion MRI: From quantitative measurement to in-vivo neuroanatomy. London: Elsevier, Inc.; 2009. [Google Scholar]
- 13.Helton KJ, Phillips NS, Khan RB, et al. Diffusion tensor imaging of tract involvement in children with pontine tumors. AJNR Am J Neuroradiol 2006;27(4):786–793. [PMC free article] [PubMed] [Google Scholar]
- 14.Jallo GI, Volkov A, Wong C, Carson BS, Penno MB. A novel brainstem tumor model: functional and histopathological characterization. Child’s Nervous System 2006;22(12):1519–1525. [DOI] [PubMed] [Google Scholar]
- 15.Barth RF, Kaur B. Rat brain tumor models in experimental neuro-oncology: the C6, 9L, T9, RG2, F98, BT4C, RT-2 and CNS-1 gliomas. Journal of Neuro-Oncology 2009;94(3):299–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med 1999;42(3):515–525. [PubMed] [Google Scholar]
- 17.Weinmann HJ. Characteristics of gadolinium-DTPA complex-a potential NMR contrast agent. 3 ed: Amer Roentgen Ray Soc, Reston; 1984. p. 619–624. [DOI] [PubMed] [Google Scholar]
- 18.Chen X, Astary GW, Sepulveda H, Mareci TH, Sarntinoranont M. Quantitative assessment of macromolecular concentration during direct infusion into an agarose hydrogel phantom using contrast-enhanced MRI. Magn Reson Imaging 2008;26(10):1433–1441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rohrer M, Bauer H, Mintorovitch J, Requardt M, Weinmann HJ. Comparison of magnetic properties of MRI contrast media solutions at different magnetic field strengths. Invest Radiol 2005;40(11):715–724. [DOI] [PubMed] [Google Scholar]
- 20.Pickup S, Wood AK, Kundel HL. Gadodiamide T1 relaxivity in brain tissue in vivo is lower than in saline. Magn Reson Med 2005;53(1):35–40. [DOI] [PubMed] [Google Scholar]
- 21.Tofts PS, Kermode AG. Measurement of the blood-brain barrier permeability and leakage space using dynamic MR imaging. 1. Fundamental concepts. MagnResonMed 1991;17(2):357–367. [DOI] [PubMed] [Google Scholar]
- 22.Truskey GA, Yuan F, Katz DF. Transport phenomena in biological systems. 2004. [Google Scholar]
- 23.Ewing JR, Bagher-Ebadian H. Model selection in measures of vascular parameters using dynamic contrast-enhanced MRI: experimental and clinical applications. NMR in Biomedicine 2013;26(8):1028–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Haacke EM, Brown RW, Thompson MR, Venkatesan R. Magnetic Resonance Imaging Physical Principles and Sequence Design. New York: John Wiley & Sons: 1999. [Google Scholar]
- 25.Claire Foottit GOC, Mercier Jean Francois, Thanh-Van Nguyen Viviane, Cameron Ian, Schweitzer Mark E., Sinclair John, Woulfe John, Hogan Matthew J., Nguyen Thanh B.. Optimizing Perfusion Imaging of Brain Tumors: Validation of Venous Output Function Used as a Surrogate AIF. International Society for Magnetic Resonance in Medicine. Montreal, Canada; 2011. p. 2038. [Google Scholar]
- 26.Bereczki D, Wei L, Otsuka T, et al. Hypercapnia slightly raises blood volume and sizably elevates flow velocity in brain microvessels. Am J Physiol 1993;264(5 Pt 2):H1360–1369. [DOI] [PubMed] [Google Scholar]
- 27.Burnham KP, Anderson David R. Model Selection and Multimodel Inference - A Practical Information-Theoretic Approach: Taylor & Francis: 2003. [Google Scholar]
- 28.Markwardt CB. Non-linear least squares fitting in IDL with MPFIT. Volume 411. Quebec, Canada: Astronomical Society of the Pacific: San Francisco; 2009. p. 251–254. [Google Scholar]
- 29.Logan J, Fowler JS, Volkow ND, et al. Graphical analysis of reversible radioligand binding from time-activity measurements applied to [N-11C-methyl]-(−)-cocaine PET studies in human subjects. J Cereb Blood Flow Metab 1990;10(5):740–747. [DOI] [PubMed] [Google Scholar]
- 30.Beppu T, Inoue T, Shibata Y, et al. Measurement of fractional anisotropy using diffusion tensor MRI in supratentorial astrocytic tumors. J Neurooncol 2003;63(2):109–116. [DOI] [PubMed] [Google Scholar]
- 31.Stojiljkovic M, Piperski V, Dacevic M, Rakic L, Ruzdijic S, and Kanazir S. Characterization of 9L Glioma Model of the Wistar Rat. 2003;63(1):1–7. [DOI] [PubMed] [Google Scholar]
- 32.Sarntinoranont M, Rooney F, Ferrari M. Interstitial Stress and Fluid Pressure Within a Growing Tumor. Annals of Biomedical Engineering 2003;31(3):327–335. [DOI] [PubMed] [Google Scholar]
- 33.Bagher‐Ebadian H, Jain R, Nejad‐Davarani SP, et al. Model selection for DCE‐T1 studies in glioblastoma. Magnetic resonance in medicine 2012;68(1):241–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shockley RP, LaManna JC. Determination of rat cerebral cortical blood volume changes by capillary mean transit time analysis during hypoxia, hypercapnia and hyperventilation. Brain Res 1988;454(1–2):170–178. [DOI] [PubMed] [Google Scholar]
- 35.Fenstermacher J, Gross P, Sposito N, Acuff V, Pettersen S, Gruber K. Structural and functional variations in capillary systems within the brain. Ann N Y Acad Sci 1988;529:21–30. [DOI] [PubMed] [Google Scholar]
- 36.Sinha S, Bastin ME, Whittle IR, Wardlaw JM. Diffusion Tensor MR Imaging of High-Grade Cerebral Gliomas. 2002. [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang H, Verkman A. Microfiberoptic Measurement of Extracellular Space Volume in Brain and Tumor Slices Based on Fluorescent Dye Partitioning. Biophys J. Volume 99; 2010. p. 1284–1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wu Q, Tyler B, Sukay L, et al. Experimental Rodent Models of Brainstem Tumors. Veterinary Pathology 2002;39(3):293–299. [DOI] [PubMed] [Google Scholar]
- 39.Huszthy PC, Daphu I, Niclou SP, et al. In vivo models of primary brain tumors: pitfalls and perspectives. Neuro-Oncology 2012;14(8):979–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Magdoom KN, Pishko GL, Rice L, Pampo C, Siemann DW, Sarntinoranont M. MRI-Based Computational Model of Heterogeneous Tracer Transport following Local Infusion into a Mouse Hind Limb Tumor. PLoS One. Volume 9; 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]