Inter-regional BOLD signal variability is an organizational feature of functional brain networks

Abstract

Neuronal variability patterns promote the formation and organization of neural circuits. Macroscale similarities in regional variability patterns may therefore be linked to the strength and topography of inter-regional functional connections. To assess this relationship, we used multi-echo resting-state fMRI and investigated macroscale connectivity-variability associations in 154 adult humans (86 women; mean age = 22yrs). We computed inter-regional measures of moment-to-moment BOLD signal variability and related them to inter-regional functional connectivity. Region pairs that showed stronger functional connectivity also showed similar BOLD signal variability patterns, independent of inter-regional distance and structural similarity. Connectivity-variability associations were predominant within all networks and followed a hierarchical spatial organization that separated sensory, motor and attention systems from limbic, default and frontoparietal control association networks. Results were replicated in a second held-out fMRI run. These findings suggest that macroscale BOLD signal variability is an organizational feature of large-scale functional networks, and shared inter-regional BOLD signal variability may underlie macroscale brain network dynamics.

Introduction

Local intrinsic variability and connectivity are two fundamental elements that characterize spontaneous brain activity, both at the micro- and macro-scale. Often studied in isolation, variability arises from moment-to-moment fluctuations in the activity of single neurons, and connectivity is determined from a set of synaptic connections between neurons (Faisal, Selen, & Wolpert, 2008; Uddin, 2020). Increasingly, electrophysiological studies show that these two core features of neural functioning are co-dependent. Variability provides the moving energy that allows neurons to interact with each other and form functional networks (Deco et al., 2009, 2011; Fuchs et al., 2007; Honey et al., 2007; McIntosh et al., 2010; Mišić et al., 2011; Shafiei et al., 2019; Vakorin, Lippe & McIntosh, 2011). Neurons that belong to the same functional population present shared spiking variability (Doiron & Litwin-Kumar, 2014; Goris, Movshon, & Simoncelli, 2014; Lin et al., 2015). Yet, it remains unclear how the interaction between local neuronal variability and distributed connectivity translates to the study of the regional fMRI BOLD signal, and how it impacts the architecture of large-scale functional brain networks.

A parallel between neuronal recordings and the fMRI BOLD signal has been drawn by a recent line of evidence suggesting that variability measured in any given brain region is directly related to the region’s functional embeddedness (Garrett et al., 2018). The more a brain area is integrated with other brain areas, the greater the variability in its BOLD signal. This observation is consistent with the idea that a fragmented biological system has a small dynamic range (Pincus, 1994). While these findings extend our understanding of BOLD signal dynamics and provide substantial innovation linking local moment-to-moment variability to whole-brain network dimensionality, there remains a need to characterize whether and how inter-regional coherence in variability patterns is associated with macroscale network architecture.

If at a microscale, neurons that belong to the same neuronal population show coordinated intrinsic variability, and such variability patterns in turn relate to their synaptic connections; then, we may expect that at a macroscale, brain regions embedded in the same functional network should also show similar BOLD signal variability patterns. In other words, similarities in BOLD signal variability patterns may be proportional to the strength and topography of functional connections. To date, this hypothesis has not been tested, primarily due to the different ways that BOLD variability and macroscale functional connectivity have been conceptualized in the literature. Namely, BOLD signal variability has been typically derived within single brain areas (intra-regionally; Garrett et al., 2010, 2011, 2013, 2018; Nomi et al., 2017), whereas functional connectivity has been estimated as the Pearson’s correlation between mean regional timeseries (inter-regionally; Craddock et al., 2013). If one wishes to assess the correspondence in magnitude and topography between macroscale variability and connectivity patterns, then one needs to estimate BOLD variability at the inter-regional level, in a manner similar to how functional connectivity is computed. In this way, similarities in mean regional timeseries can be related to similarities in the variability of regional timeseries. Pearson’s correlation, Euclidean distance and absolute difference are all equivalent methods usually applied to derive measures of similarity (for more information see Kriegeskorte, Mur & Bandettini, 2008). Here, we introduce a new measure, inter-regional BOLD signal variability, calculated as the absolute value of the difference between regional variability scores, that can be readily associated with functional connectivity metrics. Delineating inter-regional BOLD variability patterns might hold the key to address macroscale connectivity-variability associations.

Recent resting-state fMRI investigations have characterized the architecture of macroscale cortical networks using gradient mapping techniques that decompose functional connectivity profiles into low-rank components representing different cortical axes of functional organization (Hong et al., 2019; Huntenburg, Bazin & Margulies, 2018; Larivière et al., 2019; Vos de Wael et al., 2020). Studies using this approach have consistently reported functional connectivity patterns organized according to functional hierarchies that span from low-level sensory-motor regions to higher-level cognitive brain areas (Bethlehem et al., 2020; Margulies et al., 2016). Whether BOLD signal variability patterns and consequently connectivity-variability associations, also unfold along functional hierarchies remains unclear.

In the present study, we used multi-echo resting-state fMRI data to characterize inter-regional BOLD signal variability patterns and their relationship with resting-state functional connectivity. We determined whether regions that showed high connectivity strength also uniquely showed similar BOLD variability patterns, independently of their inter-regional distance and structural similarities (morphometric similarity). Finally, we assessed the topographical distribution of connectivity-variability interactions by comparing within- and between-network profiles, and by testing whether inter-regional BOLD variability-connectivity similarities were organized along a set of low-dimensional macroscale cortical gradients.

Materials and Methods

Sample and study description

Data from 154 healthy young adults were included in the present study (mean age=22y; age range=18-34y; 56% women). Participants underwent one structural MRI scan and two multi-echo resting-state fMRI scans of 10-min duration each, within the same session. The main analyses reported here were performed on the first run only. The second run was used as a held-out replication set. Data were collected at the Cornell Magnetic Resonance Imaging Facility, at Cornell University (New York, US). All participants provided written informed consent. Research protocols were approved by the Cornell University Institutional Review Board.

MRI data acquisition and preprocessing

MRI data were acquired on a 3T GE750 Discovery series MRI scanner using a 32-channel head coil. Anatomical scans were acquired using a T1-weighted volumetric magnetization-prepared rapid gradient-echo sequence (TR=2500s; TE=3.4ms; 7° flip angle; 1mm isotropic voxels, 176 slices, duration=5m25s) with 2x acceleration and sensitivity encoding. Two resting-state fMRI scans were acquired using a multi-echo EPI sequence with online reconstruction (TR=3000ms; TE1=13.7ms, TE2=30ms, TE3=47ms; 83° flip angle; matrix size=72x72; FOV=210mm; 46 axial slices; 3mm isotropic voxels; 204 volumes) with 2.5x acceleration and sensitivity encoding. During these two functional scans, participants were asked to keep their eyes open, and to blink and breath normally in the darkened scanner bay.

Anatomical images were skull stripped in FSL BET (Smith, 2002) using the default parameters. Whole-brain cortical reconstruction and volumetric segmentation were completed using FreeSurfer v6.0.1 (Fischl & Dale, 2000).

Functional images were preprocessed using multi-echo independent components analysis (ME-ICA v3.2 beta: https://github.com/ME-ICA/me-ica; Kundu et al., 2012). Our study is the first, to our knowledge, to use multi-echo resting-state fMRI data to model BOLD signal variability and its relationship to functional connectivity. Multi-echo resting-state fMRI has been shown to provide better spatial coverage compared to single-echo resting-state fMRI by combining data from three different echoes, and higher tSNR by relying on the unique TE-dependence of the BOLD signal (Kundu et al., 2012). ME-ICA uses spatial ICA to distinguish between BOLD signal and non-BOLD artifact sources (Kundu et al., 2012). As a result, (1) motion artifacts that are likely still present in single-echo data (Gotts, Gilmore & Martin, 2020) and can greatly impact variability estimations (Millar et al., 2020), are significantly mitigated (high sensitivity); and (2) the ability to map whole-brain functional connections is significantly increased (high specificity; Kundu et al., 2013, 2017; Lynch et al., 2020). ME-ICA applied to multi-echo resting-state fMRI data thus allowed us to obtain reliable estimations of both functional connectivity and BOLD signal variability. Importantly, global signal regression, smoothing or filtering are not required on multi-echo data.

In the present study, minimal preprocessing was done on each echo prior to ME-ICA. Motion parameter estimation was also carried out at this step and later incorporated into ME-ICA. Visual inspections were performed on post-processed data to ensure accuracy in anatomo-functional co-registration, removal of noise, temporal signal to noise ratio (tSNR), and amount of BOLD-like data retained. Participants were excluded in cases of abnormal patterns of tSNR (5 participants), having high DVARS (i.e., high motion; 1 participant) and having fewer than 10 components of BOLD-like data following denoising (1 participant) resulting in the final sample of 154 participants.

Experimental design and statistical analyses

In this study, we examined inter-regional measures of BOLD signal variability via mean squared successive difference (MSSD) and related them to resting-state functional connectivity via Pearson’s correlation and dot product estimations. In the next sections we will refer to resting-state functional connectivity as rsFC, to inter-regional BOLD signal variability as irsMSSD (inter-regional similarity in MSSD), and to the Connectivity (rsFC) − Variability (irsMSSD) Association as CoVA (CoVA_cor via Pearson’s correlation and CoVA_dp via dot product).

rsFC calculations.

ME-ICA outputs containing the denoised ICA coefficient (i.e., “mefc” files) were used for the computation of rsFC via Pearson’s correlation. “Mefc” files are component maps of accepted BOLD ICA components (i.e., components that show BOLD-like profiles) and are used to derive functional connectivity estimations (see Kundu et al., 2013 for full details). The “mefc” nomenclature stands for multi-echo functional connectivity.

rsFC values were generated through the CONN toolbox (Whitfield-Gabrieli & Nieto-Castanon, 2012) using the 7-Network, 200 node Schaefer group-parcellation solution (Figure 1A; Schaefer et al., 2018; Yeo et al., 2011). Following Kundu et al. (2013), Pearson’s correlation values were then transformed to z scores (Fisher transformation) and adjusted for degrees of freedom (i.e., number of accepted BOLD signal components; see Eq. 1).

Figure 1. Inter-regional matrices.

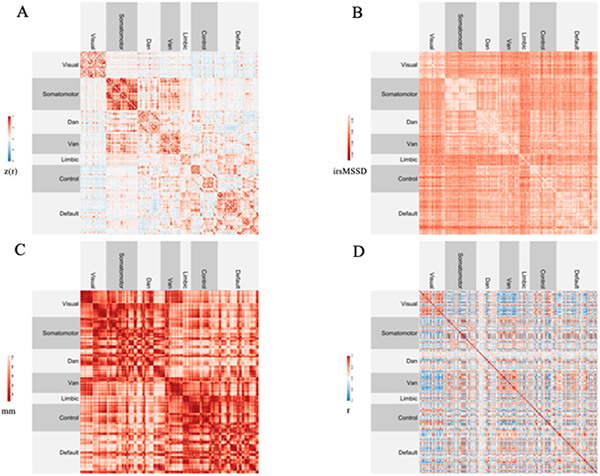
(A) Resting-state functional connectivity (rsFC). Higher values (in red) indicate stronger functional connections.

(B) Inter-regional BOLD signal variability (irsMSSD). Higher values (in lighter red) indicate greater inter-regional similarity in BOLD signal variability scores.

(C) Euclidean distance between regional centroids. Higher values (in lighter red) indicate greater inter-regional distance.

(D) Similarity in grey matter structural profiles (morphometric similarity, MS). Higher values (in red) indicate greater similarity in grey matter profiles.

$$z=\text{arctanh}(r)\times \sqrt{d.f.-3}$$ (1)

Intra-regional BOLD signal variability calculations.

ME-ICA outputs containing the denoised timeseries for the accepted BOLD ICA components (i.e., “hikts” files) were used for the computation of intra-regional BOLD signal variability. “Hikts” stands for high kappa time series. Kappa is a T2* weighting metric derived for each ICA component. High Kappa indicates high TE-dependency. Hence, components that have high kappa values are classified as BOLD signal components.

BOLD signal variability was estimated using MSSD given its ability to model the temporal continuity of resting-state fMRI and thus capturing the variability in signal amplitude between successive time points (von Neumann et al., 1941), and its independence from shifts in the mean (Garrett et al., 2011). Similar to previous work (Nomi et al., 2017), MSSD was calculated by first z scoring each regional timeseries, subtracting each time point from its preceding time point, and then calculating the square root of the average of all subtractions for each timeseries (Eq 2: i and i+1 are two successive time points belonging to the same regional time course). Importantly, differently from our rsFC computations, MSSD scores were not adjusted for the number of components, as the number of accepted BOLD components was not significantly related to the average subject-level variability (Figure S1).

$$\text{Intra-regional MSSD}=\sqrt{\frac{{\sum }_{i=1}^{n-1}(x_{i+1}-x_i{)}^2}{n-1}}$$ (2)

We would like to draw the reader’s attention to our choice of normalizing each regional timeseries prior to MSSD calculations. Typically in the variability literature, independently of the variability metric used (e.g., SD or MSSD), timeseries data are mean centered (to have a mean of 100; see e.g., Garrett et al., 2010) and not normalized (mean = 0; SD = 1; see Nomi et al., 2017). Temporal variability, calculated on centered timeseries data, reflects the dynamic range of a system and likely underpins mechanisms of information transfer in the brain (Garrett et al., 2013). Normalizing timeseries data implies instead disregarding the absolute dynamic range of regional timeseries, in that all regions are now constrained to have a standard deviation of 1. Yet, what we obtain is still to be considered variability. We expand on this matter in the discussion section. In the section “Control Analysis” below, we report additional analyses comparing our approach to previously published literature.

irsMSSD calculations.

Inter-regional BOLD signal variability was obtained by taking the absolute value of the difference in MSSD scores between pairs of regions, multiplied by −1 (a constant of 1 was also added; Figure 1B). Greater inter-regional variability values indicate greater similarity in BOLD signal variability between regions. irsMSSD scores, similarly to rsFC, were also constrained on the 7-Network, 200 node Schaefer group-parcellation scheme. irsMSSD is calculated following Eq. 3 (note: MSSD_X and MSSD_Y are intra-regional MSSD values for region X and region Y respectively).

$$irsMSSD=-\mid MSS{D}_X-MSS{D}_Y\mid +1$$ (3)

CoVA_cor computations and significance testing.

To evaluate the association between rsFC and irsMSSD, we took the lower triangles of each subject’s rsFC and irsMSSD matrices and computed the Pearson’s correlation between each rsFC edge and the corresponding irsMSSD score, across subjects. In doing so, we obtained a group-level CoVA correlation (CoVA_cor) matrix depicting the group-level association between the connectivity strength and the similarity in variability scores for each pair of regions. In order to determine which CoVA_cor values were reliable, we implemented the spin test technique (Alexander-Bloch et al., 2018; Vázquez-Rodríguez et al., 2019). We generated 400 spherical projection null models by randomly permuting network labels of the Schaefer parcellation, while preserving spatial autocorrelation. New parcellations were hence obtained at each repetition (200x for rsFC and 200x for irsMSSD) and rsFC and irsMSSD values were reassigned according to the new network labels. We then correlated (Pearson’s correlation) our unpermuted rsFC matrices with our permuted irsMSSD matrices and our permuted rsFC matrices with our unpermuted inter-regional MSSD matrices, across subjects. In both cases, we assessed how many original correlation values were greater than the obtained null correlation values and divided by the total number of permutations (p-value). We then averaged across the two resulting sets of p-values. Notably, the main goal in this set of analyses was to characterize the larger patterns in the data, rather than identifying the significance of any individual correlation (hence the lack of multiple comparisons correction).

Nuisance variables.

Next, we addressed the possibility that CoVA could be explained by confounding factors, namely the Euclidean distance between regions and the similarity in their grey matter profiles, morphometric similarity (MS). Inter-regional Euclidean distance measures were calculated between regions’ centroids (Figure C). Regions were once again defined using the 7-Network, 200 node Schaefer group-parcellation scheme. One single 200x200 distance matrix was thus generated for the whole sample. Individual inter-regional structural similarity, morphometric similarity (MS), was derived following prior work (Morgan et al., 2019; Seidlitz et al., 2018; Figure 1D). First, each participant’s default FreeSurfer fsaverage surfaces were resampled onto the Schaefer group atlas, allowing us to label the anatomy of each individual’s T1 image using the 7-Network, 200 node Schaefer group-parcellation scheme. Next, FreeSurfer’s default anatomical recon-all outputs were recalculated on the Schaefer parcellation, for each participant. Surface area, brain volume, cortical thickness, mean curvature, Gaussian curvature measures were then extracted for each region, for each individual, and each parameter was z-scored separately. Lastly, for each pair of regions, Pearson’s correlation across these six parameters was computed for each subject (Morgan et al., 2019; Seidlitz et al., 2018).

Hierarchical regression & dominance analysis.

To quantify the potential contribution of Euclidean distance and MS to connectivity-variability interactions, we built a node-wise hierarchical regression model on group-level data, predicting rsFC from inter-regional Euclidean distance, morphometric similarity (MS) and irsMSSD. Similar to previous work (Vázquez-Rodríguez et al., 2019), we used group rsFC between each node i and all other nodes (i ≠ j), as our dependent variable. As independent variables, our baseline model included measures of Euclidean distance between nodes. We then added group MS scores between nodes (model 1), and lastly group irsMSSD values (model 2). Finally, we estimated the node-wise goodness of fit for all three models, by calculating node-wise adjusted R² and adjusted R² change scores. In summary, (i) the hierarchical regression model did not include subject-wise data; (ii) at each step, the model was fitted on each node separately, excluding the node itself and collapsing across all other nodes; and (iii) the primary aim of the hierarchical regression was to determine the contribution of each predictor, rather than model selection. For this latter reason, statistical tests between the various models were not performed.

To expand on our hierarchical regression model and quantify the node-level contribution of each predictor to functional connectivity, we ran a node-wise dominance analysis (DA). DA was run predicting functional connectivity from Euclidean distance, morphometric similarity and inter-regional variability. Dominance analysis allowed us to complement our hierarchical regression by estimating the relative importance of each predictor in a single multiple regression model. Several pairwise comparisons were performed: two predictors at a time were compared against all possible sub-models (i.e., a total of 2^p-1 sub-models, with p being the number of predictors). The incremental contribution of a predictor was then quantified as the increase in R² obtained when the predictor was added to each subset of the remaining predictors. For each predictor, a Total Dominance score can be derived, which represents the additional contribution of each predictor to all subset models. Typically, the Percentage Relative Importance of each predictor is reported and is expressed as the percent value of the Total Dominance score. In our case, we calculated a node-wise Percentage Relative Importance value for each predictor separately (for more information on dominance analysis: Budescu, 1993; Azen and Budescu, 2003; https://github.com/dominance-analysis/dominance-analysis).

CoVA_dp calculations.

Our CoVA_cor analyses allowed us to assess magnitude similarities between rsFC strength and shared BOLD signal variability at the regional level. We were next interested in characterizing network-level CoVA patterns, more specifically in assessing whether within- and between-network connections exhibited different CoVA patterns. To this end, we identified whole brain within- and between-network measures in our subject-level rsFC and irsMSSD matrices and vectorized them. For each individual and for both rsFC and irsMSSD, we concatenated our 7 vectors of within-network connections and z scored them together and repeated this step for our 21 vectors of between-network connections. Doing so resulted in four final normalized vectors: two (one rsFC and one irsMSSD) depicting all within-network connections (3093) and two depicting all between-network connections (16807). We next computed the dot product between our within rsFC and our within irsMSSD vectors by multiplying each element of the former by each element of the latter and dividing by the total number of within-network connections (see Eq. 4: I = total number of within-network edges; i = single within-network edge). We applied the same dot product computations on the between rsFC and between irsMSSD vectors. Differences between average within- and between-network CoVA_dp scores were assessed across participants via paired t-test. Notably, dot product calculations were also repeated for each network separately resulting in 28 correlation coefficients for each subject (z scoring happened for each network separately). For each network, within- and between-network CoVA_dp (CoVA via dot product) measures were contrasted against each other across individuals via repeated measures ANOVA.

Finally, we averaged within- and between-network CoVA_dp values across individuals. We thus obtained a 7x7 group-level CoVA_dp matrix that was used to assess whether our 28 CoVA_dp values were reliably non-zero via one-sample t-tests with Bonferroni correction.

$$ccorr(rsFC,irsMSSD)=\sum _{i=1}^I\frac{rsF{C}_{i}irsMSS{D}_i}{I}$$ (4)

Whole-brain CoVA topographic organization.

Building on our region-wise CoVA_cor and network-wise CoVA_dp calculations, we wanted to further delineate the topographic distribution of our CoVA patterns. First, we applied a linear hierarchical clustering algorithm with Ward’s linkage on our CoVA_dp group matrix. Second, we implemented gradient mapping on our unpermuted CoVA_cor group matrix using BrainSpace, a toolbox implemented in MATLAB (https://github.com/MICA-MNI/BrainSpace; Vos de Wael et al., 2020). Gradient mapping is a nonlinear dimensionality reduction technique that relies on unsupervised manifold learning approaches, diffusion map embedding in the case of the present study (Coifman et al., 2005; Margulies et al., 2016), to project high-dimensional brain-derived similarity matrices into a lower dimensional manifold space (Huntenburg, Bazin & Margulies, 2018; Margulies et al., 2016). Our input matrix was transformed into a normalized angle affinity matrix prior to diffusion map embedding calculations. Similar to PCA, but with the additional benefit of capturing non-linear trends in the data, diffusion map embedding allowed us to identify and locate components (i.e., gradients) that described the greatest amount of variance in our CoVA_cor patterns. Each node of our transformed matrix was represented as a point in the embedded space with nodes showing high functional association between rsFC and irsMSSD being closer together, and nodes with low CoVA being farther apart. Diffusion maps were set to use an α parameter of 0.5, in line with previous studies using gradient mapping on functional connectivity data (Hong et al., 2019; Margulies et al., 2016). Gradients were mapped and visualized onto the conte69 cortical surface template (Van Essen et al., 2012). Analyses were restricted to the first two gradients.

As last step, to place our gradients in the context of the current gradient literature, we sought to quantify the degree of overlap between our first gradient obtained on CoVA_cor and the first gradient obtained by Margulies and colleagues (2016). To do so, we downloaded Margulies and colleagues’ first gradient volume data (available here: https://www.neuroconnlab.org/data/index.html), and constrained them to the 7-Network, 200 node Schaefer group-parcellation solution. We finally correlated (Spearman’s r) our 200 gradient values with the 200 gradient values obtained by Margulies and colleagues (2016).

Replication and control analyses

Intra-run replication.

To assess the robustness of our CoVA findings, we repeated both our CoVA_cor and CoVA_dp computations on our second, held-out, resting-state fMRI run. We correlated CoVA_cor and CoVA_dp patterns from the second run with our CoVA_cor and CoVA_dp from the first run (Pearson’s and Spearman’s). Our replication sample consisted of the same subjects included in the primary analyses (n=154). Resting-state data were acquired and preprocessed in the same fashion across the two runs. rsFC and irsMSSD calculations were conducted identically across the two runs. CoVA_cor computations on our replication set only included those connections that survived permutation testing on the first run. CoVA_dp computations were carried out on the full set of 28 within/between network connections.

Inter-run replication.

Replicating CoVA on a second held-out run did not however address the possibility that CoVA patterns simply derived from the dependency of rsFC and irsMSSD on the same timeseries data (i.e., same run). To address this potential confound, we estimated our CoVA_cor and CoVA_dp metrics from rsFC and irsMSSD measures that belonged to different runs. In other words, we looked at how rsFC patterns derived from our first run were related to irsMSSD scores computed on our second run (case 1), and vice versa (case 2). CoVA_cor and CoVA_dp estimations together with CoVA_dp statistics (one sample t-tests; paired t-tests) and hierarchical clustering calculations were conducted analogously to the main CoVA analyses.

Control analysis.

Variability results and the interpretation of variability effects depend heavily on the methodological approaches taken (Waschke et al., 2021), both in terms of (1) how timeseries data are normalized prior to variability calculations, and of (2) what type of metric is used to estimate BOLD variability. In this work, BOLD variability was calculated using MSSD on z-scored regional timeseries. To assess the validity of our methodological choices, we ran two sets of control analyses taking different (1) regional timeseries normalization and (2) variability metric approaches.

(1) Intra-regional MSSD was calculated on mean centered regional timeseries data (whole brain mean was set to 100; mean centered MSSD), similarly to previous work (Garrett et al., 2010, 2011b, 2013; Wutte et al., 2011). Mean centered MSSD was compared to MSSD estimated on normalized timeseries data (our main approach; z-scored MSSD). Specifically, single-subject mean centered MSSD scores were correlated with their correspondent z-scored MSSD values across the 200 brain parcels (Pearson’s r). Fisher z-transformation was then applied to the within-subject correlation values and a one sample t-test was run to assess whether the resulting correlation values were significantly different from zero, across subjects. Lastly, region-level (CoVA_cor) and network-level (CoVA_dp) associations were recomputed between functional connectivity and mean centered MSSD.

(2) Intra-regional variability was calculated via standard deviation (SD) on mean centered timeseries data, as in prior work (see Garrett et al., 2010, 2011b, 2013; Wutte et al., 2011) and compared with z-scored MSSD calculations and with mean centered MSSD calculations, using the same statistical steps outlined above.

Data and code availability

Analyses were implemented in MATLAB and R. The resampling procedure used to permute rsFC and irsMSSD data was instead coded in Python following existing documentation (https://netneurotools.readthedocs.io/en/latest/auto_examples/plot_perm_pvals.html). Scripts are available at the following link: https://github.com/lbc-spreng/Baracchini_CoVA. Data is being compiled for release in a forthcoming publication.

Results

Inter-regional measures of BOLD signal variability are associated with rsFC patterns

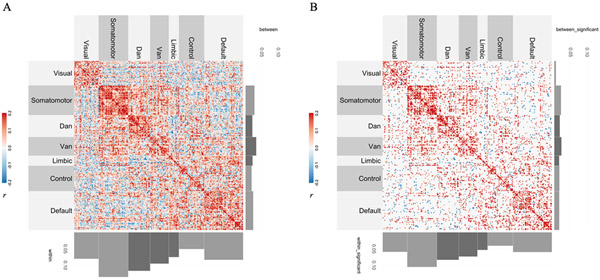
To evaluate the association between connectivity and variability, we computed the Pearson’s correlation between each rsFC edge and each corresponding irsMSSD value across participants (CoVA_cor). Across the brain, patterns of CoVA were revealed (Figure 2A) wherein regions that are highly correlated with one another also show similar variability patterns. The strength of the association between rsFC and irsMSSD was highest within the canonical seven functional networks (i.e., along the diagonal) relative to their between-network counterparts (i.e., off diagonals). Figure 2B shows those CoVA_cor values that survived permutation testing (3512/19900; p<.05). This second matrix highlights again the predominance of positive CoVA_cor patterns and the presence of a stronger diagonal (CoVA_cor within networks) and weaker off diagonals (CoVA_cor between networks).

Figure 2. Functional association between connectivity and variability via Pearson’s correlation (CoVA_cor).

(A) Group-level unpermuted CoVA_cor matrix. Each rsFC edge was correlated (Pearson’s r) with each irsMSSD score across subjects. CoVA_cor patterns were predominantly driven by regions with high rsFC and high irsMSSD. Histograms at the bottom and at the right of the matrix represent the average correlation values for each of the 7 canonical large-scale networks’ within- (bottom) and between-connections (right). Histograms confirm stronger CoVA_cor for regions belonging to the same network. (B) Group-level permuted CoVA_cor matrix. To assess the statistical significance of CoVA_cor patterns, we implemented the spin test technique (Alexander-Bloch et al., 2018; Vázquez-Rodríguez et al., 2019). Out of the 19900 edge values constituting our unpermuted CoVA_cor matrix, 3512 survived permutation testing. Permuted CoVA_cor patterns were again primarily driven by positive connectivity-variability associations and, more specifically, by connections between regions belonging to the same network (histograms on the bottom vs on the right). Note: the average of the between-community correlation values for the visual network is below 0.

Inter-regional measures of BOLD signal variability uniquely explain rsFC patterns

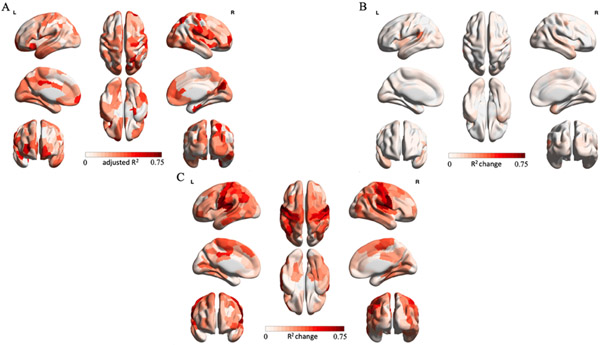
To quantify the potential contribution of Euclidean distance and inter-regional structural similarity to CoVA patterns, we built a node-wise group-level hierarchical regression model predicting rsFC from Euclidean distance, Euclidean distance and morphometric similarity (MS) and finally from irsMSSD holding Euclidean distance and MS constant. Figure 3 summarizes our three-stage hierarchical regression results. Panel A captures node-wise adjusted R² scores when predicting rsFC solely from Euclidean distance measures between brain regions (baseline model). On average, distance explained 22% of rsFC variance across all nodes. Overall, the pattern of associations between distance and rsFC was variable across the brain (interquartile range = 0.21). Panel B depicts node-wise adjusted R² change scores when adding MS measures to the baseline model. On average, MS only accounted for an increment of 4% in the variation in rsFC over the baseline model (interquartile range = 0.05; average adjusted R² = 0.26). Finally, panel C shows the node-wise adjusted R² change scores obtained from entering irsMSSD into the final regression model holding distance and MS constant. Introducing irsMSSD explained an additional 27% of rsFC variance (interquartile range = 0.21; average adjusted R² = 0.53). Together, these results indicate that irsMSSD uniquely adheres to rsFC patterns over and above measures of Euclidean distance and morphometric similarity.

Figure 3. Three-stage hierarchical regression model.

To control for the influence of inter-regional Euclidean distance and similarity in grey matter profiles on our connectivity-variability associations, we built a three-stage node-wise hierarchical regression model on group-level data. Node-wise adjusted R² scores were calculated for the baseline model. For model 1 and 2 adjusted R² change scores are reported. (A) Baseline model. Euclidean distance between regions explained on average 22% of rsFC variance across all nodes. (B) Model 1. Adding morphometric similarity only accounted for an extra 4% of rsFC variance across all regions, over the baseline model. (C) Model 2. Introducing inter-regional MSSD (irsMSSD) explained an additional 27% of rsFC variance.

To expand on our hierarchical regression findings and better delineate the node-level contribution of each predictor to functional connectivity, we ran a Dominance Analysis on a single multiple regression model, predicting functional connectivity from Euclidean distance, morphometric similarity and inter-regional variability. The relative importance of each predictor was quantified for each node (note: nodes were rearranged to have left and right hemispheres together; Table S1). To aid interpretation, we report the Percentage Relative Importance per network for each predictor (Figure 4).

Figure 4. Dominance Analysis.

Network-wise Percentage Relative Contribution values derived from a Dominance Analysis run on a single node-wise multiple regression model (FC = distance + structure + irsMSSD). Panels A-C represent the Percentage Relative Contribution values for each predictor. (A) Relative contribution of distance in explaining functional connectivity. (B) Relative contribution of morphometric similarity in explaining functional connectivity. (C) Relative contribution of inter-regional variability in explaining functional connectivity. Table D shows the network-wise mean Percentage Relative Contribution values for each predictor.

In line with our hierarchical regression results, DA findings revealed how overall inter-regional MSSD contributed the most to functional connectivity, followed by Euclidean distance and lastly by morphometric similarity.

Within network connections exhibit the strongest associations between rsFC and inter-regional BOLD signal variability

Next, we extended our region-wise CoVA_cor findings to empirically assess whether within- and between-network connections exhibited different CoVA patterns. Network-level CoVA metrics were obtained by calculating the dot product between within-network rsFC and within-network irsMSSD scores and between-network rsFC and between-network irsMSSD values, respectively.

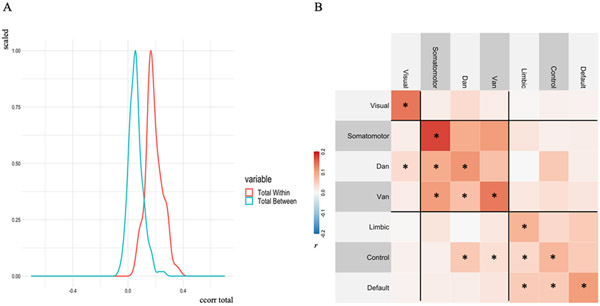
We first observed a significant overall difference in CoVA between within-network and between-network connections across participants (t(153) = 27.87, p < .001; 95% C.I. = [0.12 0.14]; mean of the differences = 0.13; Cohen’s d = 2.25; Figure 5A). Within-network connections displayed overall greater CoVA_dp, in line with our exploratory CoVA_cor findings (Figure 2). Next, we examined CoVA_dp for each network separately (Figure 5B). For each of the seven canonical networks, CoVA_dp values were higher for within- compared with between-network connections across participants (all F’s > 20, p’s < .001). One sample t-tests (Bonferroni adjusted p-values < .005) revealed that all 7 within-network CoVA_dp scores were reliably non-zero, in addition to some between-network connections (see Figure 4B).

Figure 5. Within- vs between-network CoVA patterns.

(A). Subject-level within- and between-network dot-product correlation values were averaged across networks, resulting in one within- (red) and one between-network (blue) distribution of dot product values. Within-network connections showed overall greater CoVA_dp, consistent with our CoVA_cor findings. (B) Group-level CoVA_dp matrix within- and between-network CoVA_dp values (28 in total) across individuals. One sample t-test computed on each element of CoVA_dp, revealed that all 7 within-network CoVA_dp scores were significantly different from zero, in addition to some between-network connections (reported as *). Three clusters, depicted by black lines, reveal the topographical distribution of CoVA_dp patterns: (1) visual, (2) somatomotor/dorsal attention/ventral attention, and (3) limbic/frontoparietal control/default network.

To assess the spatial organization of CoVA_dp patterns, we implemented a hierarchical clustering algorithm with Ward’s linkage on our CoVA_dp matrix. Three separate clusters were identified: (1) visual (occipital), (2) somatomotor/dorsal attention/ventral attention (pericentral, dorsal frontoparietal, midcingulo-insular), and (3) limbic/frontoparietal control/default networks (lateral and medial frontoparietal; network nomenclature in brackets follows recent work by Uddin, Yeo & Spreng, 2019). These results highlight a functional segregation between unimodal visual, somatomotor/attention and heteromodal/associative networks in CoVA_dp patterns.

Associations between rsFC and inter-regional BOLD signal variability follow a unimodal-heteromodal topographical organization

Motivated by our CoVA_dp linear hierarchical clustering results, we decided to further investigate the topographical distribution of CoVA patterns through the implementation of gradient mapping on our unpermuted node-wise group-level CoVA_cor matrix (Figure 2A).

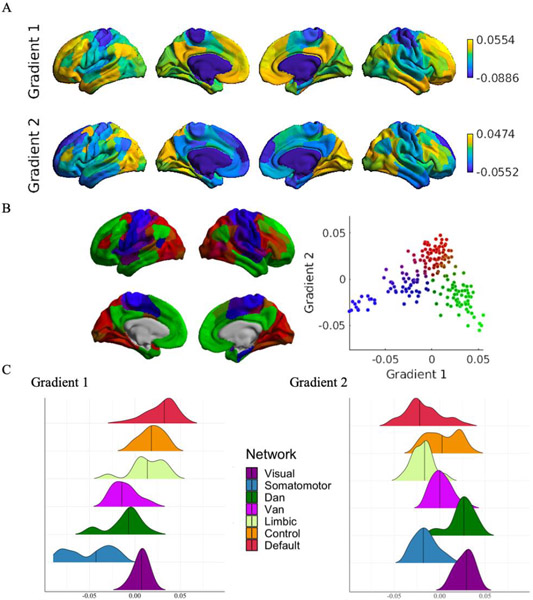
The first gradient (14% of the variance in the CoVA_cor matrix explained; Figure 6A-C), separated nodes of the somatomotor, dorsal and ventral attention networks from nodes of the limbic, frontoparietal control and default networks. Nodes belonging to the visual network were near zero. The second gradient (11% variance explained; Figure 6A-C) separated visual and dorsal attention network nodes from nodes belonging to the somatomotor, limbic and default networks. Nodes located in the ventral attention and frontoparietal control networks had values closer to zero.

Figure 6. Gradient mapping of CoVA patterns.

Gradient mapping was implemented on our unpermuted node-wise group-level CoVA_cor matrix using the diffusion map embedding algorithm. (A) Results for the first two gradients. The first gradient separated sensory, motor and attentional regions from higher-order cognitive nodes. The second gradient separated visual and dorsal attention network nodes from nodes belonging to the somatomotor, limbic and default networks. (B) Embedded space for the first two gradients. Each point is a node of the transformed matrix. Nodes showing high functional association between rsFC and irsMSSD are closer together in the embedded space, whereas nodes with low CoVA are farther apart (Visual: red; Somatomotor: blue; DAN: brown; VAN: purple; Control: dark green; Default: light green). (C) Ridge plots depicting the network-wise distribution of values for the two gradients.

As last step, to place our gradient results in the context of the current gradient literature, we correlated our first gradient obtained on CoVA_cor with the first gradient obtained by Margulies and colleagues (2016). We found a high correspondence between our gradient and Margulies gradient scores (Spearman’s rho = 0.82, p<.001; Figure S2).

Together, these results complement our linear hierarchical clustering findings from the CoVA_dp group matrix and show how CoVA patterns unfold along a unimodal-transmodal topographical organization, which has previously been determined on a fundamentally different input matrix (Margulies et al., 2016).

CoVA patterns are stable features

Intra-run replication.

We repeated both our CoVA_cor and CoVA_dp computations on our second, held-out, resting-state fMRI run. Replication effects were moderate for CoVA_cor (Pearson’s r = 0.44; Spearman’s r = 0.39; p < .001) and strong for CoVA_dp (Pearson’s r = 0.98; Spearman’s r = 0.96; p < .001).

Inter-run replication.

Our second set of replication analyses involved calculating CoVA patterns across runs. We estimated CoVA_cor and CoVA_dp metrics from rsFC and irsMSSD measures that belonged to different runs. In other words, we looked at how rsFC patterns derived from our first run were related to irsMSSD scores computed on our second run (case 1), and vice versa (case 2). We found that in both cases CoVA_cor and CoVA_dp metrics recapitulated our main intra-run estimations (Figure S3 and S4). Namely, nodes belonging to the same network exhibited the strongest CoVA_cor scores. Within-network connections that showed the highest CoVA_dp scores, were significantly different from zero (one sample t-test results with Bonferroni adjusted p-values < .005) and from between-network connections (case 1: t(153) = 29.04, p < .001; 95% C.I. = [0.11 0.13]; mean of the differences = 0.12; Cohen’s d = 2.34; case 2: t(153) = 22.84, p < .001; 95% C.I. = [0.10 0.12]; mean of the differences = 0.11; Cohen’s d = 1.84). Lastly, hierarchical clustering with Ward’s linkage revealed a unimodal-heteromodal network organization that distinguished visual, from attentional and somatomotor networks and limbic, control and default networks. Taken together, these results highlight the stability and generalizability of CoVA patterns.

CoVA patterns depend on how BOLD variability is computed

Given the presence of different analytic approaches to estimate BOLD variability both in terms of (1) how timeseries data are normalized prior to variability calculations, and of (2) what type of variability metric is used, we sought to validate our choice of computing variability via MSSD on z-scored regional timeseries.

(1) First, we assessed whether measures of intra-regional z-scored MSSD were related to measures of intra-regional mean centered MSSD. We found a weak negative correlation between the two (r mean (SD) = −0.04 (±0.16); t(153) = −2.82, p = .005; 95% C.I. = [−0.06, −0.01]). Second, we recalculated inter-regional variability scores by taking the absolute value of the difference between regional mean centered MSSD scores. We observed high similarity in inter-regional mean centered variability across the whole brain (Figure S5A). Third, we recomputed region-level (CoVA_cor) and network-level (CoVA_dp) associations between functional connectivity and inter-regional mean centered MSSD. In both cases, connectivity-variability patterns showed a weaker segregation of within- from between-network CoVA scores, dominated by an overall stronger between-network connectivity-variability coupling than our results using z-scored MSSD (Figure S6A and S6C).

(2) Next, we recalculated intra-regional variability via SD on mean centered timeseries data. Mean centered SD values showed a strong positive correlation with mean centered MSSD calculations (r mean (SD) = 0.97 (±0.01); t(153) = 138.8, p = <.001; 95% C.I. = [2.17, 2.23]), but a moderate negative correlation with z-scored MSSD calculations, as expected (r mean (SD) = −0.23 (±0.15); t(153) = −18.58, p = <.001; 95% C.I. = [−0.27, −0.22]). Furthermore, inter-regional mean centered SD values (Figure S5B) highly overlapped with inter-regional mean centered MSSD scores. Similarly, CoVA_cor and CoVA_dp associations on mean centered SD data (Figure S6B and S6D) replicated CoVA_cor and CoVA_dp patterns obtained on mean centered MSSD data.

As a final step, we submitted the CoVA_cor group matrix obtained on mean centered SD data, to gradient analysis. The spatial hierarchy we initially observed using z-scored MSSD, which aligned with gradient findings previously reported (e.g., Margulies et al., 2016), was disrupted when calculating gradients on mean centered SD values (Figure S7A-C).

Together, these findings show how CoVA patterns are impacted by how timeseries normalization is conducted, independently of the variability metric used.

Discussion

Variability of neural signals permits the nervous system to explore a greater range of network configurations and achieve a dynamic range of responses (Uddin, 2020; McIntosh et al., 2010). Functional connectivity between brain regions is thought to underlie cognition and behavior (Reid et al., 2019). Still, the relationship between inter-regional BOLD signal variability and inter-regional functional connectivity has not been explored. In this study, we used multi-echo resting-state fMRI to reliably characterize resting-state functional connectivity and resting-state BOLD signal variability patterns. We determined that region-level macroscale intrinsic dynamics adhere to the configuration of intrinsic functional networks. We examined local macroscale fluctuations in terms of inter-regional interactions in BOLD signal variability measures and we related them to inter-regional rsFC measures. We found that pairs of brain regions that showed high functional connectivity strength also showed similar moment-to-moment BOLD signal variability patterns. We demonstrated that connectivity-variability associations, CoVA, were predominant within all networks and followed a unimodal-heteromodal topographical organization that separated sensory, motor and attention systems, from higher-order association networks. Our observations were robust to different statistical approaches, replicated in a second held-out resting-state fMRI run and were invariant to inter-run estimations.

Temporal variability in the present study was estimated on z-scored regional timeseries via MSSD (first derivative of a timeseries). We showed how different timeseries normalization and variability approaches yielded distinct inter-regional variability scores that differently cohered with functional connectivity patterns. These findings confirm recent work highlighting how variability results and the interpretation of variability effects depend heavily on the methodological approaches taken (Waschke et al., 2021). Further work is needed to comprehensively examine and compare the different analytic approaches used in the literature to compute BOLD temporal variability. However, in the context of the present study, how should one interpret intra- and inter-regional temporal variability?

The factor to consider when interpreting our findings is how regional timeseries are normalized. In previous reports (e.g. Garrett et al., 2010), mean-centered timeseries data are used, whereby timeseries’ variance is preserved. This approach permits inferences on the dynamic range of a system. In the present study, regional timeseries were z-scored, with variance constrained and equal across regions. Our variability can be considered conceptually related to permutation entropy used in electrophysiology. Permutation entropy maintains the temporal structure of the timeseries and estimates the frequency of occurrence of ranks or “motifs”, signal patterns created by grouping neighbouring timepoints (Bandt and Pompe, 2002). While permutation entropy, unlike z-scored MSSD, is calculated on such motifs (see Figure 1 of Riedl et al., 2013) and thus ignores the value range of the data, it detects transitions between signal patterns, capturing dynamic changes in timeseries data (Cao et al., 2004). Similarly, z-scored MSSD also allows for the characterization of moment-to-moment transitions in regional signal patterns, while taking into account the continuous, scaled regional signal.

Intra-regional z-scored MSSD can be interpreted as capturing a brain region’s normalized rate of change and thus “profiles” regional signal patterns. Greater variability (i.e., higher rate of change) indicates a more noisy/random regional timeseries. Less variability (i.e., slower rate of change) instead indicates a more repetitive/regular regional timeseries. Inter-regional z-scored MSSD can be interpreted as quantifying the similarity between regional rates of change, or signal patterns. Greater inter-regional variability (i.e., smaller absolute difference between two regional MSSD scores) is found between regions that present similar, generally lower, overall signal complexity. We consider two possible scenarios to illustrate this point: (1) regions A and B both have low intra-regional normalized MSSD values, and (2) regions C and D both have high intra-regional normalized MSSD values. Inter-regional variability in scenario (1) will likely be lower in magnitude than inter-regional variability calculated in scenario (2), due to a floor effect. This implies that regions with more regular timeseries (scenario 1) are likely to oscillate together more regularly. We preliminarily show that this is indeed the case (see Figure S8). Further work, however, is needed to expand upon the relationship between variance patterns and phase synchrony among brain regions.

At rest, our brain waxes and wanes between recurring multistable states and network configurations that may allow the system to transfer information between regions (Avena-Koenigsberger, Mišić & Sporns., 2018; Beckmann et al., 2005; Smith et al., 2012). In doing so, brain dynamics have been shown to underpin and explain the integration and segregation patterns that characterize canonical large-scale networks, as assessed via functional connectivity (Bullmore & Sporns, 2012; Kaboodvand, Iravani, & Fransson, 2020; Sporns, 2011; Tognoli & Kelso, 2014). Here, we expanded on this view by showing how similarity in BOLD signal variability patterns between region pairs might be associated with similarities in mean regional timeseries measures between region pairs (i.e., functional connectivity).

Variability has been hypothesized to drive the formation of network configurations (McIntosh et al. 2010; Rubinov et al., 2009) and is related to the functional embeddedness of a brain region (Garrett et al., 2018). In this study, we expanded on such intra-regional findings and demonstrated that higher similarity in BOLD signal variability patterns between regions (i.e., similar overall signal complexity) was associated with stronger functional connections. This was the case mainly for regions that belonged to the same network. Similarly, when analyses were carried out on network- rather than region-level variability estimates, we found that within-network connectivity-variability associations were higher compared with their between-network counterparts. These results are consistent with the foundational observation that functional connections between regions that are part of the same network are more stable and higher in magnitude than connections between regions that belong to different networks (Fox et al., 2005; Shen et al., 2015; Zalesky et al., 2014). Here, we conceptualized stability in terms of higher similarity in BOLD signal variability patterns between region pairs. Greater inter-regional entrainment may indeed facilitate information transfer in the brain. Entrainment may thus be present between regions that show similar overall signal complexity and more likely regularly oscillate.

Entrainment at the microscale level has been shown to result from phase coherence processes among neuronal oscillations (Fries 2005, 2015; Griffiths, McIntosh & Lefebvre, 2019). Neurons receive inputs from different neuronal groups, yet they preferentially respond to and interconnect with those whose phase relation is tuned to their excitability cycle (Fries 2005, 2015). Recent dynamic functional connectivity studies on resting-state fMRI and MEG data have successfully translated inter-neuronal coherence concepts to notions of inter-regional phase coherence of BOLD signal oscillations. Similar to how neurons interact with each other, brain regions have been found to primarily communicate with those brain areas whose BOLD signal oscillates in the same frequency band (Cabral et al., 2017; Marzetti et al., 2013, 2019). If variability drives network configurations and underlies connectivity dynamics, then inter-regional BOLD signal variability measures should also be governed by inter-regional phase coherence of BOLD oscillations. While our variability calculations do not allow for fine-grained inferences on the intrinsic moment-to-moment variability of regional timeseries, we speculate that our inter-regional MSSD measures may reflect the overall rhythmic synchronization of BOLD signal oscillations between region pairs. In other words, such rhythmic inter-regional synchronization may manifest itself at a broader level, in similarities in overall signal complexity between regions.

At the intra-regional level, neural signal complexity has been widely shown to relate to information transfer mechanisms in the brain (Honey et al., 2007; Ghosh et al., 2008; Friston et al., 2012). A recent simulation study using EEG-fMRI data found that multi-scale entropy, a proxy of neural complexity, relates to functional connectivity (Wang et al., 2018). The authors showed that the greater the signal complexity in any one given region, the greater its functional connectivity with other brain regions (Wang et al., 2018). Our work builds on these findings by characterizing complexity (i.e., variability)-connectivity associations between region pairs (i.e., inter-regionally). In our study, connectivity and variability were tightly coupled, over and above influences of distance and structural similarity between regions, and their associations were robustly captured via both Pearson’s correlation on group-level data and dot product estimations on single-subject data.

Consistent with our speculations on connectivity-variability associations, electrocorticographic measures of local phase synchronization processes among neuronal populations have been shown to follow a spatially-organized hierarchical structure (Hasson et al., 2008; Honey et al., 2012). Low-level sensory regions show less neuronal synchronization, suggesting more rapid and isolated regional dynamics (Hasson et al., 2008; Honey et al., 2012). Conversely, higher-order cognitive areas show greater neuronal synchronization, given that activity in these areas is influenced by information collected from different brain regions (Hasson et al., 2008; Honey et al., 2012). Similarly, in resting-state fMRI, BOLD signal dynamics have been found to follow a unimodal-heteromodal hierarchical organization (e.g., Müller et al., 2020; Shafiei et al., 2020; Vidaurre, Smith & Woolrich, 2017). Resting-state functional connectivity patterns have also been separately shown to unfold along such precise spatial hierarchy (e.g., Bethlehem et al., 2020; Margulies et al., 2016). Our work begins to bring together these lines of research.

In the current study, connectivity-variability associations followed a unimodal-transmodal gradient separating visual, somatomotor/dorsal/ventral attention, and limbic/frontoparietal/default networks. The degree of segregation of these three topographical clusters was maximal for the visual network and weaker for heteromodal regions, potentially reflecting a gradual shift from local to distributed processing. Higher-order cognitive networks serve as high centrality networks, and as such, they need to optimally integrate signals coming from multiple sources (Cole, Pathak & Schneider, 2010; Margulies et al., 2016; Zalesky et al., 2014; Zuo et al., 2012). Our findings corroborate and expand on previous electrocorticographic, fMRI BOLD dynamics and dynamic functional connectivity literatures and replicate work showing how the synchronization of BOLD oscillations manifests as a highly spatially organized phenomenon unfolding from sensorimotor areas to higher-level regions (Baria et al., 2011; Raut, Snyder, & Raichle, 2020). The convergence between our observations and this extensive and diverse body of evidence further supports our speculations that greater inter-regional similarity in MSSD scores (i.e., inter-regional similarity in BOLD signal complexity) may represent greater inter-regional BOLD signal phase coherence and thus lead to stronger functional connections. In this scenario, the observed topographical hierarchy of CoVA may thus be dictated by regional differences in microscale neuronal phase coherence properties that are captured, at a macroscale, by differences in BOLD signal complexity modeled via z-scored MSSD.

Conclusions

Variability has been conceptualized as the driving mechanism that allows our brain to maximize information exchange between neurons on a moment-to-moment basis and contribute to the formation and spatio-temporal organization of resting-state functional networks (Deco et al., 2009; McIntosh et al., 2010; Mišić et al., 2011). At a macroscale, dynamic functional connectivity investigations have conceived resting-state functional networks as assemblies of brain regions that coherently fluctuate together over time in the low frequency range. This study reconciles extensive microscale literature with classic macroscale brain dynamics findings by modeling, for the first time, whole-brain moment-to-moment intrinsic fluctuations via inter-regional BOLD signal variability estimations and showing how they uniquely adhere to resting-state functional network configurations. To date, BOLD signal variability has only been studied as an intra-regional phenomenon. Collectively, our findings offer new perspectives on the overarching principles governing the interaction between resting-state fMRI BOLD signal dynamics and functional connections. Furthermore, the convergence of different statistical approaches coupled with the use of multi-echo resting-state data further highlights the robustness of our inter-regional variability characterizations and ultimately opens up possibilities for future studies to assess the behavioral and clinical relevance of connectivity-variability associations.