Scan-less machine-learning-enabled incoherent microscopy for minimally-invasive deep-brain imaging

Abstract

Deep-brain microscopy is strongly limited by the size of the imaging probe, both in terms of achievable resolution and potential trauma due to surgery. Here, we show that a segment of an ultra-thin multi-mode fiber (cannula) can replace the bulky microscope objective inside the brain. By creating a self-consistent deep neural network that is trained to reconstruct anthropocentric images from the raw signal transported by the cannula, we demonstrate a single-cell resolution (< 10μm), depth sectioning resolution of 40 μm, and field of view of 200 μm, all with green-fluorescent-protein labelled neurons imaged at depths as large as 1.4 mm from the brain surface. Since ground-truth images at these depths are challenging to obtain in vivo, we propose a novel ensemble method that averages the reconstructed images from disparate deep-neural-network architectures. Finally, we demonstrate dynamic imaging of moving GCaMp-labelled C. elegans worms. Our approach dramatically simplifies deep-brain microscopy.

1. Introduction

Imaging biological processes from depths > 1mm inside the rodent brain is important for fundamental studies of the neural circuits that underlie behavior [1]. Optical imaging plays a crucial role in these studies by enabling targeted labelling of cells and spatio-temporally resolved imaging of neuronal activity at single cell resolution. However, accessing the deep brain remains challenging. Current solutions come in two flavors. Two-photon microscopy exploits the simultaneous absorption of two long-wavelength photons (that can penetrate deep into tissue) to excite fluorescence, a nonlinear process [2]. Background fluorescence is avoided, since each single photon does not have sufficient energy to excite fluorescence. This approach suffers from two basic problems. First, the penetration depth of 2-photon microscopy is limited to about 0.45 mm due to scattering and absorption in tissue [3]. Three- or more photon microscopy can penetrate slightly deeper (∼0.6 mm), [4,5] but at the expense of requiring much higher laser power, with possibility of photo-toxicity. A second fundamental problem is the requirement of scanning to create images, which makes this approach potentially too slow to monitor fast neural processes. We note that this disadvantage is being addressed by very clever, yet complex approaches like temporal focusing of the excitation beam [6]. The second solution relies on inserting a miniaturized microscope into the brain subsequent to craniotomy [1,7]. This approach has been very successful, particularly for studying the neuronal circuits of freely moving and behaving animals over long time scales [8]. In order to minimize the trauma related to the surgery, it is highly desirable to miniaturize the inserted portion as much as possible. Traditionally, this is achieved by using gradient-index (GRIN) lenses to relay the image from the brain to an intermediate image plane that can then be imaged using conventional microscope objectives. The smallest GRIN lenses today have a diameter of about 0.5 mm, [1] with typical probes being 0.6 mm to 1 mm in diameter [7]. Here, we show that by foregoing the imaging requirement (and compensating via computational post-processing), it is possible to reduce the size of the probe to 0.22 mm (or even smaller), while still achieving imaging at depths > 1 mm. We note that recently, multi-mode fibers have been used in conjunction with 2-photon fluorescence excitation to achieve volumetric imaging, [8] but this requires a significantly more complex illumination system as well as scanning.

Our approach utilizes a surgical cannula, which is the short segment of a step-index glass fiber with outer diameter of 0.22 mm that is inserted into the brain. Excitation light is piped into the brain through the cannula, and is engineered to ensure uniform illumination of the region of the brain in close proximity to the distal end of the cannula (section 1 of Supplement 1 ^{(4.2MB, pdf)} ). All illuminated fluorophores will emit fluorescence, a portion of which is collected by the same cannula (a type of epi-configuration) and routed back to the proximal end. Since the cannula can support a large number of electromagnetic modes and the signal is not coherent, the information containing the location and brightness of each emitting fluorophore is encoded into an intensity distribution on the proximal face of the cannula. By creating a training dataset of ground truth and cannula-based images, one can either use linear algebraic methods, [9–12] or a variety of machine learning algorithms [13,14] to invert the image on the proximal end of the cannula, and discern the distribution and brightness of the fluorophores near the distal end of the cannula (which is inserted into the brain). The depth of imaging is primarily determined by the length of the cannula, and depths greater than 1 mm are readily achievable with the 0.22 mm-diameter cannula.

We note that image transport through the rigid cannula is analogous to incoherent imaging through a deterministic scattering medium. It has been shown that a simple auto-correlation of the captured image, followed by the solution of a phase-retrieval problem can reproduce the image, thereby allowing for imaging through scattering [15,16]. This method is independent of the details of the scattering process and is therefore, generally applicable. The method was also recently extended to multi-mode fibers [17]. However, the latter approach required holographic calibration of the transmission matrix, which can be challenging due to the large number of supported modes and incoherent light. Here, we show that by using machine-learning algorithms, it is possible to perform imaging through the cannula (a short-length multi-mode fiber) with only intensity measurements and requiring no guide-stars (as is necessary in Ref. [16]). Image transmission through multi-mode fibers has also been achieved recently using machine-learning-based post-processing of the recorded intensity images with both coherent [18] and incoherent [19] illumination. Here, we extend the latter work to deep-brain microscopy with single-cell resolution.

2. Setup

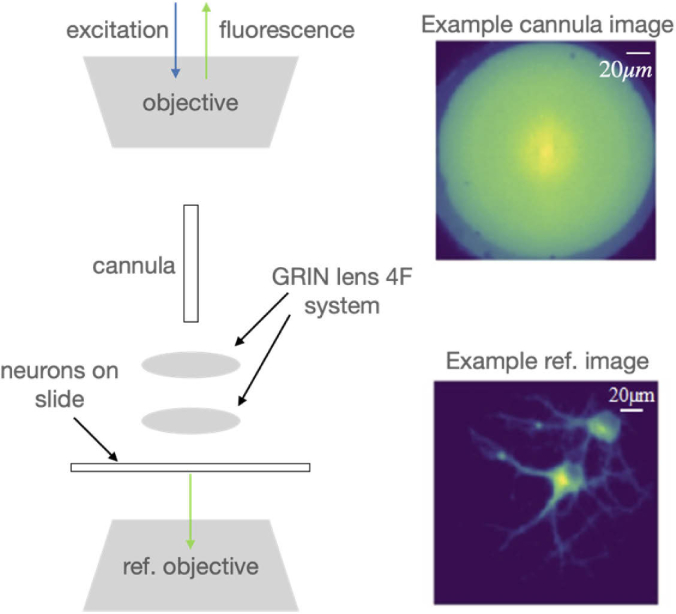
A portion of the experimental setup used to collect training data is illustrated in Fig. 1 (see full details in section 1 of Supplement 1 ^{(4.2MB, pdf)} ). Light from a blue LED (center wavelength = 470 nm, Thorlabs M470L3) is conditioned and focused onto the proximal end of the cannula (maximum insertion length = 2 mm, diameter = 0.22 mm, Thorlabs CFM12L02) via an objective lens (working distance = 1.2 mm, Olympus PLN 20X). An excitation filter (FF02-472/30-25, BrightLine) is used to center the illumination spectrum at λ = 472 nm to maximize excitation efficiency for GFP. The image formed at the distal end of the cannula is relayed using a two-lens 4F system into the cultured neurons (see section 3 of Supplement 1 ^{(4.2MB, pdf)} for preparation) sandwiched between a coverslip (thickness = 0.08 to 0.13 mm) and a glass slide (thickness = 1 mm). The fluorescence is relayed back through the 4F system, cannula and the objective lens, and recorded on an sCMOS camera (pixel size = 6.5 μm, Hamamatsu C11440). The recorded intensity image is referred to as the cannula image (see top-right inset in Fig. 1 for an example). A conventional widefield microscope is placed underneath the sample focused on the same plane as the 4F system to produce the ground truth (see bottom-right inset in Fig. 1). For testing, the 4F system is removed, and the cannula is inserted directly into the brain, where the cannula will be imaging cells in the vicinity of its distal end. In training, the cannula is unable to penetrate the cultured neurons due to the top cover slip. The 4F system allows us to overcome this limitation by relaying the image from inside the cultured neurons to the distal end of the cannula. In addition, the cultured neuron samples are mounted on a 3D stage that allows us to not only translate in the transverse plane to collect a diversity of images, but also in the axial direction, which enables multi-plane imaging. A total of 88,538 image-pairs were collected. The distance between the distal end of the cannula and the effective image plane was set to 0, 40 μm, 80 μm and 120 μm. The number of recorded images were 23,940 (0 μm), 22,001 (40 μm), 22,157 (80 μm), and 20,440 (120 μm). For each distance, 1000 images were set aside for testing the machine-learning algorithms. The sizes of the recorded cannula and ground truth images were 447 × 447 pixels and 788 × 788 pixels, respectively. In order to reduce the computational burden (hardware: Intel Core i7-4790 CPU and NVIDIA GeForce GTX 970), all images were down-sampled to 128 × 128 pixels before being processed by the machine-learning algorithms.

Fig. 1.

Experimental System for training data. The system is comprised of an epifluorescence microscope coupled to the proximal end of a cannula. A 4-F system using two lenses is used to relay the image from under the coverslip to the distal end of the cannula. The fluorescence is recorded on an sCMOS camera (example image shown in top-right inset, scale bar = 20 μm). A conventional widefield fluorescence microscope images the same plane as the cannula, but from underneath to produce the ground truth (bottom right-inset). Pairs of such images serve as training data for the machine learning algorithms.

3. Results and discussion

Since it is very challenging to obtain ground-truth images from inside the brain, we decided to use an ensemble-learning approach by training three different machine-learning algorithms (using the training data from the cultured neurons). If each network produces similar output images from the brain, then we can have high confidence in the results. The first network is identical to what we used previously, a U-network comprised of encoder and decoder blocks concatenated by skip connections [13,14] (also see section 2 of the Supplement 1 ^{(4.2MB, pdf)} ). Dense blocks, which include 2 convolutional layers with RELU activation function and a batch-normalization layer, are used to build each encoder and decoder.

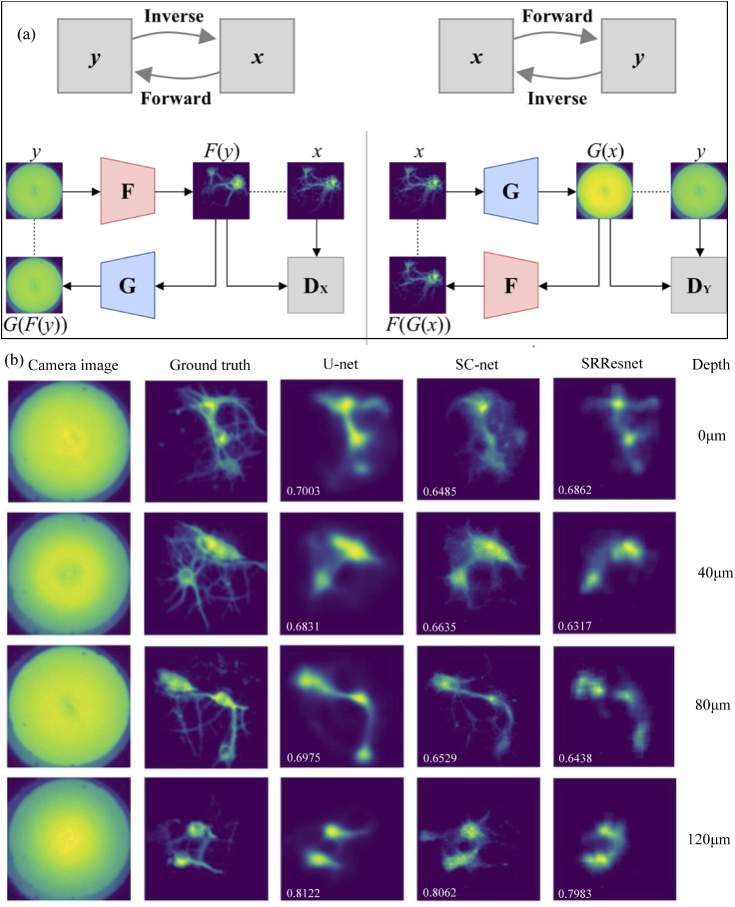
The second network is based on a recent idea of imposing self-consistency in solving inverse problems [20]. For this model we train two Generative Adversarial Networks (GANs) [21] simultaneously in a cycle consistent model (see Fig. 2(a)). One generator, F is trained to learn the inverse mapping from the cannula to the ground-truth images, and another generator, G is trained to learn the forward mapping from ground-truth to the cannula images. We then enforce that $F(G(x))=\widehat{\stackrel{ˆ}{x}}\approx x\text{and}GF(y)=\widehat{\stackrel{ˆ}{y}}\approx y,\text{where}x$ and y are the ground truth and cannula images, respectively. The networks predicted image and the sensor data are $\hat{x}$ and $\hat{y}$ , and the corresponding cycled images, $\widehat{\stackrel{ˆ}{x}}$ and $\widehat{\stackrel{ˆ}{y}}$ Second a least squares GAN loss where we utilize two discriminators DX and $D_Y$ to discriminate between the reconstructed, $G(x)=y$ and $F(y)=x$ , and ground truth images, y and x, respectively. In addition to cycle consistency, we further constrain the model with an L1 loss term between x and x, and y and y. This CycleGAN model [20] has been applied previously to map unpaired images from one domain to another. We found that applying it directly to paired images consistently led to mode collapse. To enable the use of the CycleGAN on paired images we further constrained the model with an additional L1 loss term between x and x, and y and y. The final overall objective is:

$$\begin{array}{cc}l(F,G,D_X,D_Y)& =\lambda [\Vert x-\hat{x}{\Vert }_1+\Vert y-\hat{y}{\Vert }_1+\Vert x-\widehat{\stackrel{ˆ}{x}}{\Vert }_1+\Vert y-\widehat{\stackrel{ˆ}{y}}{\Vert }_1]+E_x[{(D_X(x)-1)}^2]\\ & +E_y[D_X{(\hat{x})}^2]+E_y[{(D_Y(y)-1)}^2]+E_x[D_Y{(\hat{y})}^2],\end{array}$$

where $\lambda$ weights the relative importance of the cycle and reconstruction losses to the adversarial losses, and is set to 100 in all experiments. Both F and G have the same network design, which is similar to the modified U-net used above with a few differences. First, dilated convolutions are used to increase the receptive field of the network. Second, skip connections are not used as they did not improve performance. Third, the number of filters at each block in the encoder is 64, 128, 256 and in the decoder is 256, 128, 64, where the bottom bottleneck contains 3 residual blocks of 256 convolutions each. The generators are trained using an Adam optimizer with a learning rate of $2\times {10}^{-4}$ . Batch norm is left on at test time to utilize the test set statistics, which has been shown to help with image generation [22]. The discriminators use 70×70 PatchGAN architecture, [23] and are trained using an Adam optimizer with a learning rate of $2\times {10}^{-5}$ . The models are trained for 40 epochs with a batch size of 8. Using the same train and test cultured images as above, the model achieved mean absolute error (MAE) of 0.013, structural similarity index (SSIM) of 0.77, and peak signal-to-noise ratio (PSNR) of 32 on the test set. Reconstruction results on the cultured neurons and brain images are shown in Fig. 2(b).

Fig. 2.

Imaging of cultured neurons through the cannula. (a) Schematic of the self-consistent network (SC-net). (b) Exemplary results showing the cannula, ground-truth, U-net and SC-net output images. The SSIM values (compared to the ground truth) are noted in each reconstructed image. Also see additional images in Supplement 1 ^{(4.2MB, pdf)} . All images have size of 200μm x 200μm.

The third network is the SRResNet [24]. Designed for super-resolution, the network does not utilize an encoder-decoder style architecture as the other two networks, but is instead a flat structure of residual blocks, providing us with a third diverse model. The sub-pixel convolution layers used for upsampling at the end of the network were replaced with batch-normalization layers and the model was trained with L1 instead of the L2 loss used in the original paper, as this was more stable when training. The SRResNet is trained with the Adam optimizer for 45 epochs at a learning rate of ${10}^{-3}$ and a batch size of 16.

In all cases, we used a classification network to identify the depth (within 40 μm based on training data) of each image, similar to previous work [14]. The depth-prediction accuracy was 98.65%.

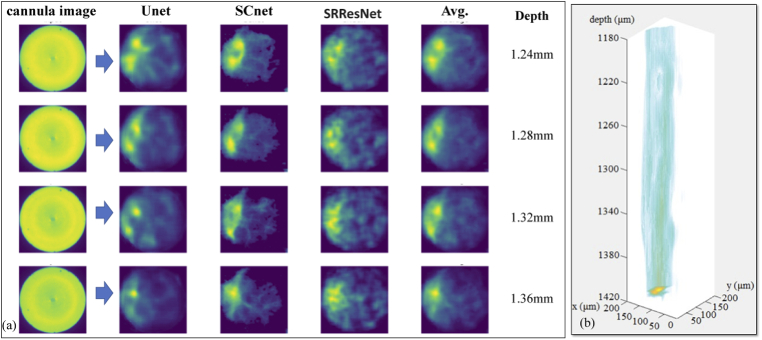
After the machine-learning algorithms were trained and tested against cultured neurons, the cannula was inserted in a fixed whole mouse brain, which was glued onto a glass slide (see Supplement 1 ^{(4.2MB, pdf)} ). The recorded cannula images were processed using the three ML-algorithms as described above, and the results are summarized in Fig. 3(a). By collecting 2D images as the cannula is inserted into the brain, post-processing these images and collating these into a 3D stack, a 3D visualization of the region of the brain can be attained as shown in Fig. 3(b) (also see Visualization 1 ^{(652.3KB, mp4)} ).

Fig. 3.

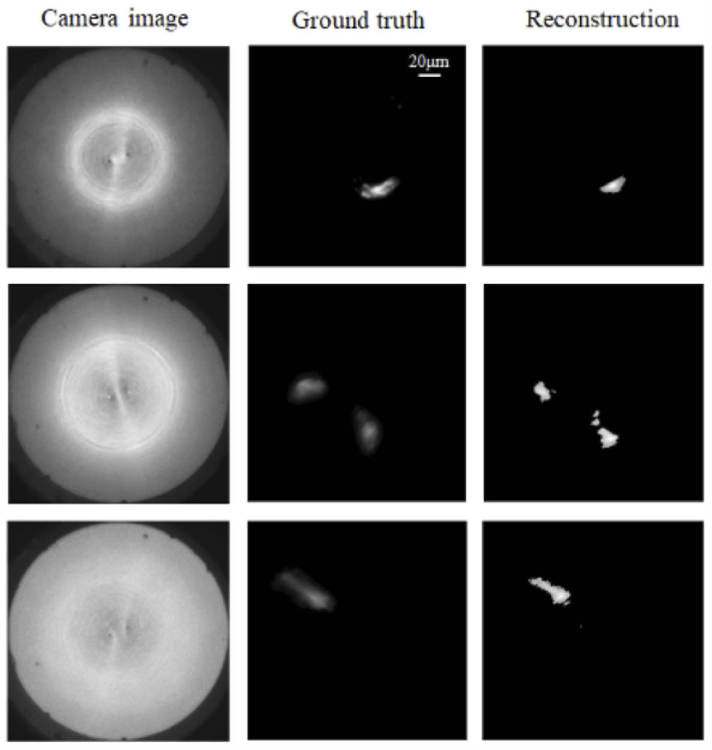
Deep-brain imaging using the cannula. The cannula was inserted into the fixed whole mouse brain at various depths. (a) Each recorded cannula image was post-processed using Unet, SCnet and SRResnet. All 3 networks predicted similar images, which can then be averaged (Avg.) to produce a final result. The depth of the images were predicted from the known location of the cannula (Z stage position) + the network predicted layer depth. Since it is challenging to obtain ground truth images from these depths, we used an ensembling method of using images from 3 separate networks to achieve confidence in the results. (b) Collated stack of images with interpolation in the Z axis to create a 3D image (see Visualization 1 ^{(652.3KB, mp4)} ). All images have scale of 200 μm x 200 μm.

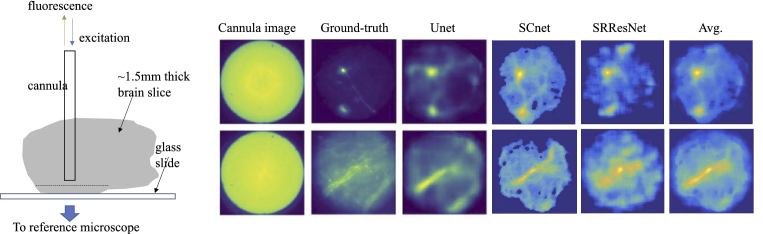
One of the main challenges of deep-brain imaging using machine-learning algorithms is the unavailability of ground truth images. Here, we used an ensemble-learning approach with multiple neural networks predicting the same image as a means to increase confidence in the results. In order to further validate our machine-learning algorithms, we used thick (∼1.5 mm) brain slices mounted on glass slides. We then inserted the cannula to a depth close to, but slightly less than 1.5 mm to image the opposite surface of the slices. The reference microscope can then be used to image the same surface from below. Using this approach, we were also able to verify the performance of the ML algorithms as indicated by examples in Fig. 4.

Fig. 4.

Validating our approach using thick brain slices. The cannula was inserted into ∼1.5 mm-thick brain slices until its distal end was close to the bottom surface, which was also imaged by the reference microscope. This allowed us to compare the ground-truth images against the ML predicted images under conditions that would be similar to those found in the whole brain. All images have scale of 200 μm x 200 μm.

Since our post-processing is very fast (and can also be done after image acquisition, average time ∼ 3.5 ms, see section 4 of Supplement 1 ^{(4.2MB, pdf)} ), the imaging speed is limited primarily by the frame rate of the sensor and the brightness of our fluorophores. Preliminary experiments done with fixed samples indicate that frame rates of 40 Hz should be feasible (Supplement 1 ^{(4.2MB, pdf)} ).

In order to demonstrate dynamic imaging, we also imaged live worms (C. elegans) with GCaMP expressed in their brains. The C. elegans strain was grown and maintained on nematode growth media with OP50 E. coli using standard methods [25]. The strain used was OH15500 otIs672 [rab-3::NLS::GCaMP6s + arrd-4:NLS:::GCaMP6s] [26]. The worms were placed in a drop of water on a slide and covered with a coverslip. Because the lifetime of worms is short on slides, and they move relatively fast, it was difficult to build a dataset with alive worms. Therefore, we used a regularization-based matrix inversion method using measured point spread functions for image and video reconstructions (see Visualization 2 ^{(3MB, mp4)} ), summarized in Fig. 5 (also see Supplement 1 ^{(4.2MB, pdf)} where centroid tracking is also demonstrated) [10].

Fig. 5.

Imaging of GCAMP-labelled C-elegans worms. Fluorescence is present only in the brains. Worms were placed in water on a glass slide with a coverslip. A drop of mucinol was added to the water to slow the motion of the worms. Due to the relatively fast motion of the worms, the ground truth images are slightly blurred. Also see Supplement 1 ^{(4.2MB, pdf)} and Visualization 2 ^{(3MB, mp4)} .

4. Conclusion

In this work, we describe microscopy of fluorescent labeled neurons from depths as large as 1.36 mm inside the rodent brain using a 0.22 mm-diameter surgical cannula as the sole inserted element. Single-cell resolution, depth discrimination (40 μm), full field of view (200 μm diameter) and fast imaging (40 Hz frame rates) are all possible with minimally invasive surgery compared to alternatives (such as micro-endoscopes). We showcased the use of a novel self-consistency network for image reconstructions, which learns the forward and inverse physics of the optical problem, and analyzed its performance to prior auto-encoder networks. Using data from cultured neurons, we trained multiple ML algorithms for image reconstructions, and successfully tested these against data from the deep brain, emphasizing the robustness of our approach. We further note that the fluorescence lifetime is a factor limiting speed in all fluorescence microscopies, but it is generally a more severe limitation for scanning approaches, since pixel dwell time must be larger than this lifetime. Widefield techniques such as compressed fluorescence lifetime microscopy can exploit this temporal dynamics to gain additional sample information [27]. Finally, we note that although scanning techniques impose a trade-off between field-of-view and speed, recent approaches using frequency combs are beginning to mitigate this [28].

Funding

National Institutes of Health10.13039/100000002 (1R21EY030717); National Science Foundation10.13039/100000001 (1533611).

Disclosures

The authors declare that there are no conflicts of interest related to this article.

Data availability

Data and code underlying the results presented in this paper are freely available in Ref. [29].

Supplemental document

See Supplement 1 ^{(4.2MB, pdf)} for supporting content.