BEBIG ⁶⁰Co HDR brachytherapy source dosimetric parameters validation using GATE Geant4-based simulation code

Abstract

Purpose

This study aims to validate the dosimetric characteristics of High Dose Rate (HDR) ⁶⁰Co source (Co0.A86 model) using GATE Geant4-based Monte Carlo code. According to the recommendation of the American Association of Physicists in Medicine (AAPM) task group report number 43, the dosimetric parameters of a new brachytherapy source should be verified either experimentally or by Monte Carlo calculation before clinical applications. The validated ⁶⁰Co source in this study will be used for the simulation of intensity-modulated brachytherapy (IMBT) of vaginal cancer using the same GATE Geant4-based Monte Carlo code in the future.

Materials and methods

GATE (version 9.0) simulation code was used to model and calculate the required TG-43U1 dosimetric data of the ⁶⁰Co HDR source. DoseActors were defined for calculation of dose rate constant, radial dose function, and anisotropy function in a water phantom with an 80 cm radius.

Results

The dose rate constant was obtained as $1.070\pm 0.008\text{cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$ which shows a relative difference of 2.01% compared to the consensus value, 1.092 $\text{ cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$. The calculated results of anisotropy and radial dose functions starting from 0.1 cm to 10 cm around the source showed excellent agreement with the results of published studies. The mean variation of the radial dose and anisotropy functions values from the consensus data were 1% and 0.9% respectively.

Conclusion

Findings from this investigation revealed that the validation of the HDR ⁶⁰Co source is feasible by the GATE Geant4-based Monte Carlo code. As a result, the GATE Monte Carlo code can be used for the verification of the brachytherapy treatment planning system.

GATE Monte Carlo code; HDR ⁶⁰Co source; TG-43 dosimetric parameters.

1. Introduction

High dose rate (HDR) brachytherapy is now an accepted treatment modality for cervix, prostate, breast, skin, head and neck, oesophagus, and several other types of cancers [1]. The convenient application of HDR brachytherapy for outpatient is one of its significant advantages over Low Dose Rate (LDR) brachytherapy.

The technical possibility for the manufacturing of small size ¹⁹²Ir HDR sources in the past resulted in the widespread use of ¹⁹²Ir HDR brachytherapy around the world. Recently, ⁶⁰Co HDR sources with the same size of ¹⁹²Ir HDR source also became available on the shelves. Studies have confirmed that there is no significant clinical difference between using ⁶⁰Co source compared to ¹⁹²Ir source in HDR brachytherapy. However, due to the shorter half-life (74 days) of the ¹⁹²Ir radioisotope, the ¹⁹²Ir HDR afterloading brachytherapy system is categorized as a costly treatment modality. Therefore, the ⁶⁰Co HDR afterloading brachytherapy system is introduced as an interesting alternative. The ⁶⁰Co HDR source due to its longer half-life (5.3 years) offers significant logistical and financial benefits compared to the ¹⁹²Ir HDR source [1, 19, 20].

Before the application of a brachytherapy source in practice, its dosimetric validation should be carried out based on Task Group No. 43 first revised (TG-43U1) [4] report either “experimentally or by Monte Carlo (MC)” simulation codes. The verified characteristics of the source “can then be used as input in the HDR treatment planning system” [3, 5]. MC simulation codes can reproduce the geometry of the source, simulate the physics of radiation interaction with matters and the process of dose absorption. The major advantage of the MC over the experimental validation is that the “MC allows obtaining dose data even at points where conducting an experimental measurement would be very difficult” [3]. Calculation of the dosimetric parameters of a brachytherapy source should be performed in water based on the TG-43 update report of the AAPM [4].

The dosimetric characteristics of the BEBIG ⁶⁰Co (model Co0.A86) have been calculated by several researchers using different Monte Carlo codes. Granero et al. [2] using GEANT4, Reddy et al. [6] using EGSnrc, Guerrero et al. [3] using PENELOPE, Islam et al. [7] using EGSnrc, Selvam et al. [8] using EGSnrc, Badry et al. [9] using EGS5 and Elboukhari et al. [21] using MCNPX calculated those data by their turns.

In this study, the validation of the BEBIG ⁶⁰Co (Co0.A86 model) source's dosimetric data was performed using GATE Geant4-based Monte Carlo code, and the obtained results were compared with published studies and consensus data. The validated source can be used in IMBT simulation of vaginal cancer via the same Monte Carlo code in the future.

2. Materials and methods

2.1. BEBIG ⁶⁰Co source description

The ⁶⁰Co encapsulated source (Co0.A86 model) manufactured by Eckert & Ziegler BEBIG Company was simulated in this study. The diameter and length of the ⁶⁰Co active core (8.9 g/cm³) are 0.5 mm and 3.5 mm respectively. The active part of the source is enclosed in a 316L type stainless steel capsule (8.03 g/cm³) with a thickness of 0.15 mm. The total length and diameter of the encapsulated source are 5 mm and 1 mm respectively. A stainless steel type 304 (5.75 g/cm³) cable with a 0.9 mm diameter and 2 mm long is also attached to the source capsule. The active core is surrounded by a 0.1 mm thick air layer (Figure 1).

Figure 1.

Cross section of BEBIG ⁶⁰Co source (model Co0.A86) generated by GATE code.

2.2. BEBIG ⁶⁰Co source modeling

The geometry of any volume (body) creates through writing several macro commands in the user interface of GATE software. GATE follows the tree structure that each body should be defined as a subset of a bigger volume, like world (the biggest volume in the simulation) or calculation volume (phantom), etc. The center of the world is the origin of the three-dimensional coordinate system. The geometry of the complex bodies is formed via the combination of simple bodies such as cubes, cylinders, spheres, semi-spheres, etc. GATE follows a symmetrical nature around a body center. So, for an accurate and precise combination, one should always take into account the half-height of the two connected bodies. Each body is given a name, shape, three dimensional size, center's coordinate, material, visualization capability, color, etc.

The aforementioned ⁶⁰Co HDR source was successfully modeled as a combination of six cylinders by GATE Geant4-based Monte Carlo code. Two full 316L stainless steel cylinders (disks) with the diameters of 1 mm and heights of 0.75 mm were created in the right and left sides of the source active core. Three concentric cylinders were simulated to represent the 316L stainless steel outer cover, air layer, and active core, each with 3.5 mm height and 1 mm, 0.7 mm and 0.5 mm diameters respectively. Finally, a 2 mm long 304 stainless steel cylindrical cable with 0.9 mm diameter was also defined and attached to the left side desk (Figure 1). A radioactive feature or beam was also created and attached to the source active part which contains the dosimetric properties of the ⁶⁰Co source such as energy spectrum, type of the particle generated, irradiation direction, etc.

The emstandard_opt3 physics which is a standard electromagnetic physics sub-package with the highest precision was used in the whole steps of this simulation based study. This physics list includes all kinds of radiation interactions with matters such as Compton scattering, gamma conversion, photoelectric effect for photons, multiple scattering, ionization, and bremsstrahlung for electrons and positrons which is important for ⁶⁰Co gamma photon interaction [12].

2.3. Dose rate constant calculation

According to the TG43-U1 formalism, the dose rate constant (Λ) is obtained by the division of the source dose rate in water at 1 cm, $\dot{\text{D}}\left({\text{r}}_0,{\text{θ}}_0\right)$ from the source center on the transverse plane $\text{p}(1\text{ cm},{90}^{°})$ to the air-kerma strength, (S_k).

$$\text{Λ}=\dot{\text{D}}\left({\text{r}}_0,{\text{θ}}_0\right)/{\text{S}}_{\text{k}}$$ (1)

The dose rate constant has the unit of $\text{cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$ which reduces to ${\text{cm}}^{-2}$ because the symbol U is defined as $1\text{U}=\text{cGy}.{\text{cm}}^2.{\text{h}}^{-1}=\text{μGy}.{\text{m}}^2.{\text{h}}^{-1}$.

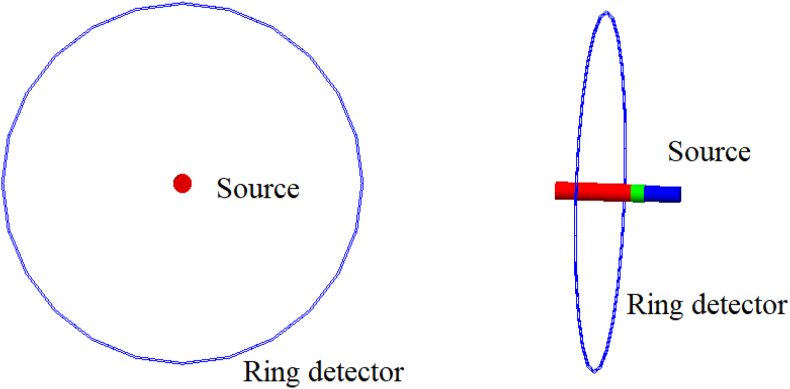
For the calculation of air kerma strength of ⁶⁰Co source, S_k, an air sphere (0.0012 g/cm³) phantom with a radius of 4 m was defined and simulated inside a (10 × 10 × 10 m³) rectangular vacuum (0.000001 mg/cm³) world by GATE Geant4-bases Monte Carlo code. Only the ⁶⁰Co gamma-energy spectrum was taken from the National Nuclear Data Center (NNDC) [10] and introduced to the simulation code. Because it is verified that the existence of stainless steel cover around the active part of the ⁶⁰Co source absorbs the electrons and beta particles, therefore, the contribution of electron spectra and beta spectrum to the absorbed dose is neglected [23].

Track Length Estimator DoseActors (TLEDoseActors) were used for improving speed and efficiency of Monte Carlo simulation [5] and was attached to the air ring detectors for recording absorbed doses in air phantom. DoseActors have the potential to score three dimensional (3D) energy or dose distribution in different output formats such as .txt, .root, .mhd, etc. [11]. The format of output dose was chosen as .mhd in the current study. For all simulation tasks in this study, “a cutoff energy of 10 keV for photons was used because the contribution to the absorbed dose of photons with energy lower than 10 keV is negligible and the Monte Carlo simulation is more efficient” [22]. Meanwhile, for decreasing the level of statistical uncertainties, the number of particles (history) was set to $2\times {10}^9$ and the code was run by a supercomputer (15.5 GB RAM; 3.4 GHz × 8 Intel® Core™ i7-6700; Mesa Intel® HD Graphics 530 (SKL GT2)), Linux operating system, imaging research center, Imam Khomeini Hospital, Tehran, Iran.

The output .mhd images were read out with Python (3.9.0) software (Anaconda3). The mean of calculated values by the ring detectors were used for determining air kerma rate value, ${\text{K}}_{\text{δ}}^{·}\left(\text{d}\right)$. Then, the air kerma strength was calculated using Eq. (1) to compensate for the inverse square law dose fall-off.

$${\text{S}}_{\text{k}}={\text{K}}_{\text{δ}}^{·}\left(\text{d}\right).{\text{d}}^2$$ (2)

For calculation of dose rate in water, $\dot{\text{D}}\left({\text{r}}_0,{\text{θ}}_0\right)$, a spherical water phantom (1.0 g/cm³) with a radius of 80 cm was simulated inside a 4 × 4 × 4 m³ rectangular world by GATE software. A ring with 0.1 mm thickness and 0.1 mm width was defined to score absorbed dose at 1 cm from the source center on the transverse plane in water (Figure 2). The corresponding DoseActor was attached to the defined ring to score the dose in .mhd output format. Then, the output file was read out with Python (3.9.0) software.

Figure 2.

The geometry of dose rate calculation in water at 1 cm from the source center by GATE.

2.4. Radial dose function calculation

The radial dose function ${\text{g}}_{\text{L}}\left(\text{r}\right)$, based on the TG-43U1 report, is defined as;

$${\text{g}}_{\text{L}}\left(\text{r}\right)=\dot{\text{D}}\left(\text{r},{\text{θ}}_0\right).{\text{G}}_{\text{L}}\left({\text{r}}_0,{\text{θ}}_0\right)/\dot{\text{D}}\left({\text{r}}_0,{\text{θ}}_0\right).{\text{G}}_{\text{L}}\left(\text{r},{\text{θ}}_0\right)$$ (3)

Where L shows the length of the source active part, θ is the polar angle between source longitudinal axis and the line which connects the calculation point to the source center, $\dot{\text{D}}\left({\text{r}}_0,{\text{θ}}_0\right)$ and $\dot{\text{D}}\left(\text{r},{\text{θ}}_0\right)$ are dose rates on the transverse plane at 1 cm and r cm away from the source center, ${\text{G}}_{\text{L}}\left({\text{r}}_0,{\text{θ}}_0\right)$ and ${\text{G}}_{\text{L}}\left(\text{r},{\text{θ}}_0\right)$ are the geometry functions on the transverse plan at 1 cm and r cm respectively. Geometry function is a theoretical quantity that is calculated by the following formulas:

$${\text{G}}_{\text{L}}\left(\text{r},\text{ θ}\right)=\left(\begin{array}{l}\frac{\text{β}}{\text{L}.\text{r}.\text{sinθ}}\text{ if θ}\ne 0\hfill \\ {\left({\text{r}}^2-\frac{{\text{L}}^2}{4}\right)}^{-1}\text{ if θ}=0\hfill \end{array}\right)\text{ line}-\text{source approximation }\left[4\right]$$ (4)

$$\text{β}={\text{tan}}^{-1}\left(\frac{\text{rsinθ}}{\text{rcosθ}-\frac{\text{L}}{2}}\right)-{\text{tan}}^{-1}\left(\frac{\text{rsinθ}}{\text{rcosθ}+\frac{\text{L}}{2}}\right)$$

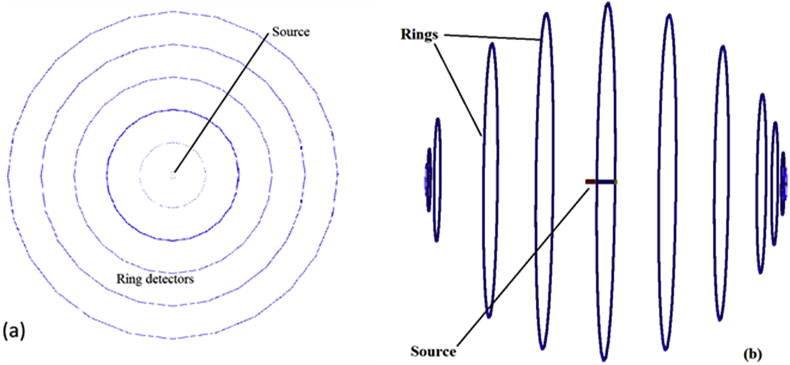
For calculating radial dose function, water rings were simulated at radial distances of 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 1, 1.5, 2, 3, 4, 5, 6, 8, 10 cm around the source inside the water phantom (Figure 3). In order to optimize the voxel size effects on the absorbed dose quantity, rings widths and thicknesses were chosen according to the recommendation of an investigation by Tylor et al. [13] on the topic of benchmarking of voxel size in Monte Carlo calculation of TG-43 parameters. As before, DoseActors were defined and attached to the water rings for scoring the absorbed doses in .mhd format. Then, the output files were read out by Python (3.9.0) software and put to Eq. (3) for obtaining the radial dose function values in the given points.

Figure 3.

Ring dosimeters illustration for calculation of radial dose function (a) and anisotropy function (b).

2.5. Anisotropy function calculation

The theoretical anisotropy function, $\text{F}\left(\text{r},\text{θ}\right)$ formula is given in Eq. (5):

$$\text{F}\left(\text{r},\text{θ}\right)=\dot{\text{D}}\left(\text{r},{\text{θ}}_0\right).{\text{G}}_{\text{L}}\left(\text{r},{\text{θ}}_0\right)/\dot{\text{D}}\left(\text{r},{\text{θ}}_0\right).{\text{G}}_{\text{L}}\left(\text{r},\text{ θ}\right)$$ (5)

Calculation of the anisotropy function was conducted for distances of 1, 2, 3, 4, 5, 6, 7, 8, and 10 cm from the source center at angles between 0 to 180°. Similar to the radial dose function calculation, water ring detectors, and DoseAtors were defined for dose calculation at the given points and the simulation outputs were read out by Python (3.9.0) software. Finally, Eq. (5) was used to determine the values of the anisotropy function in defined points (Figure 3).

3. Results

3.1. Dose rate constant

In this study, the brachytherapy BEBIG ⁶⁰Co (Co0.A86 model) was simulated by the GATE Geant4-based Monte Carlo code for obtaining its dosimetric properties. The dose rate constant was found to be $1.070\pm 0.008\text{cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$ compared to the consensus value of 1.092 $\text{cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$ [14]. The relative difference between the two figures is about 2.01%, which means a considerably good agreement. The dose rate constant values obtained using different Monte Carlo codes are listed in Table 1 for relative comparison.

Table 1.

The BEBIG ⁶⁰Co dose rate constant obtained in this study and other studies.

Monte Carlo Code	Λ (cGyh−1U−1)	Relative difference from the current study (%)
Geant4, Granero et al. [2]	1.087 ± 0.011	1.56
EGSnrc, Islam et al. [7]	1.097 ± 0.001	2.46
PENELOPE, Guerrero et al. [3]	1.094 ± 0.003	2.19
EGS5, Badry et al. [9]	1.092 ± 0.008	2.01
MCNPX, Elboukhari et al. [21]	1.092 ± 0.008	2.01
EGSnrc, Selvam et al. [8]	1.097 ± 0.002	2.46
Consensus Data, Perez et al. [14]	1.092 ± 0.005	2.01
GATE, (This work)	1.070 ± 0.008	0.00

3.2. Radial dose function

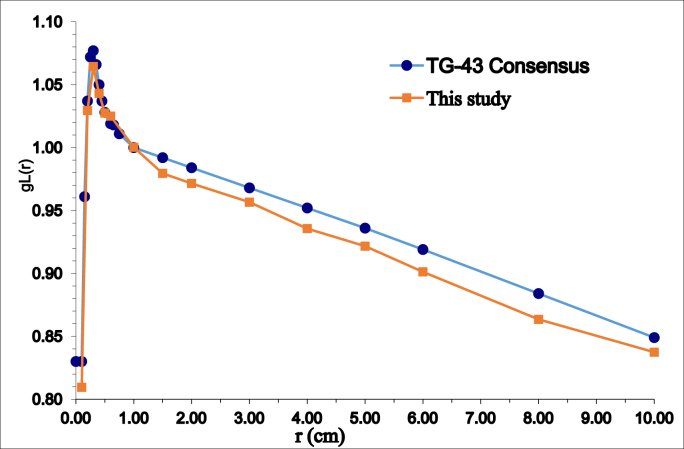
Radial dose function is a unitless quantity that takes into account the reduction of dose as a result of photon attenuation and scattering in water. The radial dose functions were calculated at distances started from 0.1 cm to 10 cm from the source center. The study results showed a remarkably well agreement with the consensus data by a maximum relative difference of 2.5%, while the overall mean deviation from the reference data was about 1% [14]. Table 2 and Figure 4 show the radial dose function values obtained in this study in comparison to the consensus data.

Table 2.

⁶⁰Co HDR source, model Co0.A86 radial dose function.

gL(r)
r (cm)	This study	Perez et al [14]	Relative difference (%)
0.1	0.809	0.830	2.47
0.2	1.029	1.037	0.73
0.3	1.064	1.077	1.17
0.4	1.043	1.050	0.66
0.5	1.027	1.028	0.05
0.6	1.025	1.019	-0.59
1	1.000	1.000	-0.02
1.5	0.980	0.992	1.26
2	0.972	0.984	1.27
3	0.957	0.968	1.18
4	0.936	0.952	1.72
5	0.922	0.936	1.53
6	0.919	0.919	-0.03
8	0.863	0.884	2.32
10	0.837	0.849	1.37

Figure 4.

Radial dose function of ⁶⁰Co (Co0.A86) calculated by GATE.

3.3. Anisotropy function

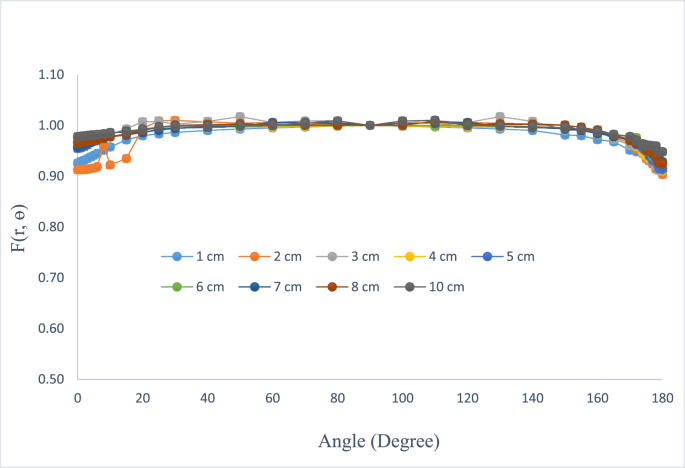
Anisotropy functions were calculated at radial distances 1.0 cm up to 10 cm and angles between 0^° and 180^º around the source. The calculated anisotropy function values are presented in Table 3. Smooth variation in anisotropy function values were observed at the angles $\text{θ}<{10}^{°}\text{ and θ}>{170}^{°}$. The maximum relative difference with reference was 5% for polar point of $\text{ r}=2\text{cm and θ}={10}^{°}$ [2].

Table 3.

⁶⁰Co HDR source, model Co0.A86 anisotropy function values from 1cm to 10 cm.

θ(degrees)	r (cm)
	1 .00	2.00	3.00	4.00	5.00	6.00	7.00	8.00	10.0
0	0.926 ±0.075	0.913 ±0.068	0.957 ±0.081	0.975 ±0.064	0.955± 0.077	0.968 ±0.047	0.958 ±0.054	0.966 ±0.081	0.978 ±0.079
1	0.929 ±0.063	0.913 ±0.065	0.962 ±0.075	0.975 ±0.055	0.956 ±0.066	0.969 ±0.025	0.960 ±0.035	0.966 ±0.055	0.979 ±0.045
2	0.932 ±0.055	0.913 ±0.048	0.971 ±0.063	0.976 ±0.044	0.958 ±0.017	0.970 ±0.013	0.963 ±0.001	0.968 ±0.014	0.979 ±0.017
3	0.935 ±0.044	0.914 ±0.043	0.973 ±0.052	0.976 ±0.043	0.962 ±0.015	0.971 ±0.011	0.965 ±0.012	0.969 ±0.020	0.980 ±0.014
4	0.938 ±0.035	0.915 ±0.040	0.974 ±0.051	0.976 ±0.032	0.9661± 0.0012	0.972 ±0.009	0.967 ±0.010	0.970 ±0.022	0.981 ±0.012
5	0.941 ±0.029	0.916 ±0.035	0.975 ±0.028	0.977 ±0.032	0.971 ±0.011	0.973 ±0.008	0.969 ±0.009	0.971 ±0.012	0.982 ±0.011
6	0.945 ±0.028	0.919 ±0.032	0.976 ±0.024	0.977 ±0.030	0.975 ±0.010	0.974 ±0.008	0.971 ±0.008	0.973 ±0.009	0.982 ±0.010
8	0.951 ±0.017	0.961 ±0.022	0.978 ±0.025	0.978 ±0.021	0.983 ±0.009	0.976 ±0.007	0.975 ±0.007	0.975 ±0.010	0.984 ±0.009
10	0.958 ±0.013	0.922 ±0.015	0.982 ±0.032	0.979 ±0.031	0.986 ±0.008	0.978 ±0.006	0.977 ±0.007	0.978 ±0.012	0.985 ±0.008
20	0.980 ±0.022	0.994 ±0.034	1.007 ±0.023	0.986 ±0.017	0.993 ±0.006	0.987 ±0.005	0.986 ±0.005	0.990 ±0.006	0.992 ±0.008
30	0.986 ±0.013	1.009 ±0.014	1.002 ±0.018	0.995 ±0.022	0.995 ±0.005	0.994 ±0.004	0.994 ±0.004	1.000 ±0.009	0.998 ±0.005
40	0.990 ±0.018	1.007 ±0.014	1.008 ±0.016	0.996 ±0.022	0.997 ±0.004	0.997 ±0.004	0.996 ±0.004	1.001 ±0.004	0.999 ±0.004
50	0.993 ±0.014	1.004 ±0.014	1.017 ±0.016	0.996 ±0.020	0.999 ±0.004	0.998 ±0.003	0.999 ±0.004	1.002 ±0.004	0.999 ±0.004
60	0.995 ±0.013	1.006 ±0.013	1.006 ±0.015	0.997 ±0.020	0.999 ±0.004	0.999 ±0.003	1.005 ±0.003	1.002 ±0.004	0.999 ±0.004
70	0.997 ±0.013	1.005 ±0.015	1.009 ±0.013	0.998 ±0.018	0.999 ±0.004	0.999 ±0.003	1.005 ±0.003	1.003 ±0.004	1.004 ±0.004
80	0.999 ±0.014	1.003 ±0.015	1.009 ±0.012	0.999 ±0.015	1.000 ±0.004	1.000 ±0.003	1.004 ±0.003	1.001 ±0.005	1.008 ±0.004
90	1.000 ±0.014	1.000 ±0.015	1.000 ±0.013	1.000 ±0.010	1.000 ±0.004	1.000 ±0.003	1.000 ±0.003	1.000 ±0.003	1.000 ±0.004
100	0.998 ±0.013	1.000 ±0.014	1.009 ±0.013	0.999 ±0.013	1.000 ±0.004	1.000 ±0.003	1.004 ±0.003	1.001 ±0.029	1.009 ±0.004
110	0.997 ±0.013	1.000 ±0.013	1.009 ±0.014	0.998 ±0.012	0.999 ±0.004	1.000 ±0.003	1.004 ±0.003	1.008 ±0.003	1.010 ±0.004
120	0.995 ±0.020	1.006 ±0.018	1.006 ±0.023	0.997 ±0.019	0.999 ±0.004	1.000 ±0.003	1.004 ±0.003	1.002 ±0.003	0.999 ±0.004
130	0.993 ±0.018	1.004 ±0.017	1.017 ±0.022	0.996 ±0.017	0.999 ±0.004	0.998 ±0.003	0.998 ±0.004	1.002 ±0.004	0.998 ±0.004
140	0.990 ±0.021	1.003 ±0.020	1.008 ±0.019	0.996 ±0.022	0.996 ±0.004	0.997 ±0.004	0.996 ±0.004	1.001 ±0.005	0.997 ±0.004
150	0.981 ±0.014	1.001 ±0.016	0.991 ±0.025	0.993 ±0.014	0.994 ±0.005	0.994 ±0.004	0.993 ±0.004	1.000 ±0.005	0.995 ±0.005
160	0.972 ±0.013	0.988 ±0.024	0.990 ±0.020	0.983 ±0.014	0.990 ±0.006	0.9912 ±0.005	0.984 ±0.005	0.990 ±0.006	0.987 ±0.006
165	0.968 ±0.034	0.976 ±0.030	0.973 ±0.040	0.980 ±0.040	0.980 ±0.007	0.982 ±0.005	0.978 ±0.006	0.981 ±0.007	0.982 ±0.007
170	0.951 ±0.023	0.965 ±0.039	0.966 ±0.054	0.969 ±0.050	0.971 ±0.008	0.978 ±0.006	0.970 ±0.006	0.972 ±0.008	0.978 ±0.008
172	0.948 ±0.035	0.955 ±0.045	0.958 ±0.056	0.960 ±0.060	0.963 ±0.008	0.976 ±0.007	0.964 ±0.007	0.966 ±0.010	0.970 ±0.009
175	0.935 ±0.044	0.934 ±0.063	0.945 ±0.053	0.941 ±0.060	0.950 ±0.011	0.953 ±0.009	0.959 ±0.009	0.951 ±0.011	0.961 ±0.011
178	0.922 ±0.055	0.914 ±0.072	0.921 ±0.068	0.928 ±0.065	0.928 ±0.016	0.940 ±0.013	0.942 ±0.014	0.937 ±0.025	0.959 ±0.017
180	0.916 ±0.087	0.904 ±0.075	0.911 ±0.072	0.912 ±0.070	0.915 ±0.082	0.928 ±0.046	0.928 ±0.053	0.925 ±0.065	0.948 ±0.077

Graphical representation of anisotropy functions for ⁶⁰Co (Co0.A86) source calculated in this study are shown in (Figure 5).

Figure 5.

Anisotropy function of ⁶⁰Co (Co0.A86) source for distances ranged from 1 cm to 10 cm at angles 0–180°.

4. Discussion

4.1. Dose rate constant

The dose rate constant for BEBIG ⁶⁰Co (Co0.A86 model) was obtained as $1.070\pm 0.008\text{cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$ in this study using GATE simulation code. This value is in good agreement with the value of the dose rate constant, 1.087 $\text{ cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$, which was obtained using GEANT4 code by Granero et al. [2] and consensus data, 1.092 $\text{ cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$ [14]. Reddy et al. [6] used EGS-brachy code and reported it as 1.098 ± 0.001 $\text{ cGy}.{\text{h}}^{-1}.{\text{U}}^{-1}$. The BEBIG ⁶⁰Co (Co0.A86 model) dose rate constant was also investigated by several other research groups. Guerrero et al. [3], Islam et al. [7], Selvam et al. [8], and Elboukhari et al. [21] in their respective studies, examined this source dosimetric data using different simulation codes and obtained different results (Table 1). Although, Badry et al. and Elboukhari et al. reported it as equal to the consensus data [9, 14, 21].

According to Table 1, the lowest difference in the value of dose rate constant exist between Granero et al. [2] study based on Geant4 MC code and the current study by GATE. This excellent agreement sounds logical as both codes work based on the Geant4 features. The source of discrepancies between these two studies can be addressed to the usage of different water densities, water phantom radii, and physics lists. Granero et al. [2] used 0.998 g/cm³ water density, a spherical water phantom with 50 cm radius, and Evaluated Photon Data Library (EPDL) and Evaluated Electron Data Library (EEDL) physics libraries for photon and electron respectively. While in the current study, 1.000 g/cm³ water density, a spherical water phantom with 80 cm radius, and emstandard_opt3 physics list were used. Overall, Geant4 and GATE underestimated the dose rate constant as pointed out by Guerrero et al. [3] as well. The higher differences in dose rate constant among this study and those which were performed by EGSnrs [7, 8] and PENELOPE [3] can also be linked to the variation of physics list, water density, and encapsulation material density (Table 1). Meanwhile, some other studies on brachytherapy sources also confirm that GATE produced higher discrepancies compared to other codes which is necessary to be addressed by GATE developers. For example, Thiam et al. [15] study in validating low energy photon sources (¹²⁵I model 6711) using GATE/GEANT4 were reported a 2.6% deviation in dose rate constant from TG-43 consensus data. Similarly, Fardi and Taherparver [16] calculated the dosimetric characteristic of IrSeed-125 by GATE MC code and reported a deviation of 5.5% in dose rate constant compared to the MCNP calculation result by Baghani et al. [17]. Generally, the source of these small dosimetric differences has been addressed to the usage of modified source geometry, different Monte Carlo codes, and physics libraries [8, 18].

4.2. Radial dose function

The radial dose function calculated in this study well followed the common trend and showed great agreement with consensus data and other studies' results. The highest relative difference was 2.5% with the consensus data belonging to 0.1 cm from the source center. The overall mean deviation from consensus data was 1% [14]. Despite, Reddy et al. [6] reported 0.6% as the maximum deviation from consensus data, the study of Selvam et al. [8] using EGSnrc Monte Carlo showed a 9% higher dose rate at 0.25 cm from the source center compared to the Granero et al. [2] study. Similarly, Elbouhkary et al. [21] sated a difference of 5% from the studies of Badry et al. [9] and Guerrero et al. [3] in radial dose function at 0.25 cm distance from the source center. On the other hand, Thiam et al. [15] and Fardi and Taherparver [16] reported a mean relative deviation of 15% and 5% in radial dose functions for ¹²⁵I (Amersham model 671) and IrSeed-125 using GATE code compared to the consensus data and MCNP calculation [17] respectively. As a result, the radial dose function values for the current study maintained an excellent agreement with the consensus data and other studies. Similar to the dose rate constant discussion, the sources of the discrepancies have been linked to the application of different simulation codes, physics lists, different materials’ densities, modified source geometry [3], and dose scoring volume [15].

4.3. Anisotropy function

The overall anisotropy function values relative difference was less than 0.9% compared to the TG-43 consensus data [14] in this study. Smooth variation in anisotropy function values was observed at the angles $\text{θ}<{10}^{°}\text{ and θ}>{170}^{°}$ and was nearly constant at the other angles. The maximum difference of 5% was observed at polar geometry $(2\text{ cm},{10}^{°})$. The agreement was excellent with Granero et al.'s [2] study compared to the other studies. Reddy et al.'s [6] study reported the anisotropy function relative difference within 2% compared to the consensus data. They observed a maximum discrepancy of 10% at angles greater than 175°. The source of the discrepancies in the points close to the source's longitudinal axis was linked to the variation of the source's cable length and capsule oblique radiation filtration. In this regard, Selvam et al. [8] performed an analytical investigation about the effects of the cable size on the dose rate around the BEBIG ⁶⁰Co HDR source and concluded that the reason for respective 9% and 14% variations in radial dose function and anisotropy function in their study is the simulation of 5 mm stainless steel source cable compared to 1 mm by Granero et al. [2]. A small variation of 0.7% in radial dose function and 2% in anisotropy function due to the source geometry simplification were also reported by Guerrero et al. [3]. Furthermore, large gradient dose and oblique source capsule filtration for points close to the source longitudinal axis were also introduced as the reasons for the production of higher discrepancies in anisotropy function values by Sadeghi et al. [18].

Overall, the variation in anisotropy function values in this study falls in the normal range compared to the other studies and consensus data. However, similar to the reasons stated by the other studies, one reason of variation in anisotropy function for this study can be referred to the simulation of 2 mm long cable against the simulation of 1 mm long cable by reference [2]. In addition, the factors mentioned in discussing radial dose function will also contribute in producing descrepancies in anisotropy functions.

5. Conclusion

In the current study, the validation process of the BEBIG ⁶⁰Co brachytherapy source was performed by GATE Geant4-based simulation code. The source geometry was modeled and the required TG-43U1 dosimetric data of the source were calculated [4]. The GATE Geant4-based Monte Carlo code successfully validated the dosimetric characteristics of the BEBIG 60Co HDR source against consensus data [14]. Overall, obtained data showed excellent agreement with the consensus data and other studies' results. The dose rate constant, radial dose function and anisotropy functions mean deviation from the consensus’ respective values were lower than 2.01%, 1.0%, and 0.9% respectively.

The great concordance of the current study results with the consensus data and with the results of other MC based studies is promising. It implies that the user-friendly Monte Carlo code of GATE has the potential to be used as a reliable and standard simulation code in the field of brachytherapy for verification and treatment planning purposes. Therefore, the dosimetric validation data of brachytherapy sources using GATE Geant4-based Monte Carlo code can be used as input data in the brachytherapy treatment planning system. As a result, the authors plan to use the validated ⁶⁰Co HDR source and the GATE Monte Carlo code for simulating intensity-modulated brachytherapy (IMBT) of vaginal cancer in the future.

Declarations

Author contribution statement

Musa Joya: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Hassan Ali Nedaie, Ghazale Geraily: Conceived and designed the experiments.

Mahdi Ghorbani: Contributed reagents, materials, analysis tools or data.

Peyman Sheikhzadeh: Performed the experiments; Analyzed and interpreted the data.

Mahmud Naraqi Arani: Performed the experiments; Contributed reagents, materials, analysis tools or data.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.