Interpersonal synchronization of movement intermittency

Summary

Most animal species group together and coordinate their behavior in quite sophisticated manners for mating, hunting, or defense purposes. In humans, coordination at a macroscopic level (the pacing of movements) is evident both in daily life (e.g., walking) and skilled (e.g., music and dance) behaviors. By examining the fine structure of movement, we here show that interpersonal coordination is established also at a microscopic – submovement – level. Natural movements appear as marked by recurrent (2–3 Hz) speed breaks, i.e., submovements, that are traditionally considered the result of intermittency in (visuo)motor feedback-based control. In a series of interpersonal coordination tasks, we show that submovements produced by interacting partners are not independent but alternate tightly over time, reflecting online mutual adaptation. These findings unveil a potential core mechanism for behavioral coordination that is based on between-persons synchronization of the intrinsic dynamics of action-perception cycles.

Graphical abstract

Highlights

• •Movements show intermittent speed pulses occurring at 2–3 Hz, called submovements
• •Submovements are actively coordinated in counter-phase by interacting partners
• •Submovements coordination depends on spatial alignment but not movement congruency
• •Behavioral coordination occurs both at macro- and microscopic movement scales

Biological sciences; Neuroscience; Behavioral neuroscience; Cognitive neuroscience

Introduction

Motor behavior is the product of coordinated patterns of muscle activations that, in humans, can reach a striking level of variety and complexity. To be effective, behavior needs to be tuned to time-varying changes in the external world. Among the most complex motor activities we are capable of, many arise from a fairly spontaneous tendency to synchronize our movements to periodic or quasi-periodic stimuli (Repp, 2005) or to other people’s movements (Oullier and Kelso, 2009; Noy et al., 2011; Riley et al., 2011; Borroni et al., 2005), providing the basis for perhaps the richest forms of social interactions that exquisitely belong to our species – i.e., playing music and dancing (D'Ausilio et al., 2015).

Interpersonal coordination can indeed be incredibly smooth and accurate, in particular if it is rhythmically organized. Such a capacity has been the object of intense investigation over the last two decades, either by looking at spontaneously emergent patterns of coordination during natural behaviors (Neda et al., 2000) (e.g., walking side by side, hand clapping, postural sway, limb swinging) or, typically, by asking participants to tap jointly according to simple beats or more complex musical rhythms (Keller et al., 2014; Repp and Su, 2013). Many metrics have been put forth to quantify synchrony as well as tempo (co-)adaptation in individual (Haken et al., 1985; Repp, 2005) and joint (Oullier and Kelso, 2009; van der Steen and Keller, 2013) rhythmic performance, showing that, even without any specific training, people are capable of pacing their movements with about 10-ms accuracy.

However, by zooming into the fine structure of movement, another form of rhythmicity becomes apparent at a lower level. Movement is, in fact, organized into smaller units, or primitives (Hogan and Sternad, 2012) – submovements – which combine together to make up full kinematic trajectories (Miall et al., 1993; Navas and Stark, 1968). If observed under the appropriate lens, continuous (non-ballistic) movement is never really smooth, and its elementary units become appreciable as discontinuities in the kinematic profile. Despite being most often filtered out in movement analysis, such discontinuities, or speed breaks, are neither a consequence of biomechanical constraints nor an incidental or erratic phenomenon, but tend to recur with specific periodicity in the range of 2–3 Hz. The presence of submovements has first been noticed more than a century ago (Woodworth, 1899); since then, submovements have been documented in many studies, in human (Doeringer and Hogan, 1998; Miall et al., 1993; Pasalar et al., 2005) as well as non-human primates (Hall et al., 2014; Miall et al., 1986; Roitman et al., 2004; Susilaradeya et al., 2019), and generally ascribed to an intermittent control of movement, deemed as an efficient computational strategy to allow optimal use of sensory feedback in the face of inherently long sensorimotor delays (Gawthrop et al., 2011; Craik, 1947; Navas and Stark, 1968; Neilson et al., 1988; Sakaguchi et al., 2015).

Submovements are thought to consist of pre-programmed (open loop) motor corrections that are being generated in an intermittent fashion. Their dependence on sensory feedback is however unclear (Doeringer and Hogan, 1998; Miall et al., 1993; Vallbo and Wessberg, 1993). Artificially increasing feedback delays during visuomotor control tasks (such as hand tracking of a visual target) alter the submovement frequency in a consistent manner (Miall, 1996; Miall et al., 1985; Susilaradeya et al., 2019). Yet, submovements seem not to be just a mere consequence of extrinsic delays in the visuomotor loop. Recent evidence highlights how the intrinsic oscillatory dynamics within the motor system contributes as well (Hall et al., 2014; Jerbi et al., 2007; Pereira et al., 2017), and in a way that is partly independent of (experimentally manipulated) feedback delays (Susilaradeya et al., 2019). Submovements may thus arise from a more complex interplay between intrinsic and extrinsic constraints on visuomotor loop dynamics (Susilaradeya et al., 2019).

Interpersonal coordination requires continuous corrections based on an accurate (and mostly visually mediated) estimation of others’ behavior toward a joint motor outcome. For such coordination to be successful, information must be flowing within both individual and inter-individual action-perception loops. Movement intermittency opens an empirical window in these action-perception loops, hence providing the opportunity to explore the fabric of how behavioral visuomotor coordination is mechanistically established.

Here, we exploit a movement synchronization task that has been classically used to probe interpersonal coordination (Oullier and Kelso, 2009) but we purposely focus on the faster timescale of movement intermittency. We show that interpersonal synchronization also occurs at a lower level than that pertaining to the sequencing and pacing of movements, i.e., the level of submovements. Importantly, the timing of submovements clearly captures a functional coupling between partners, showing that movement intermittency is actively co-regulated during the interaction.

Results

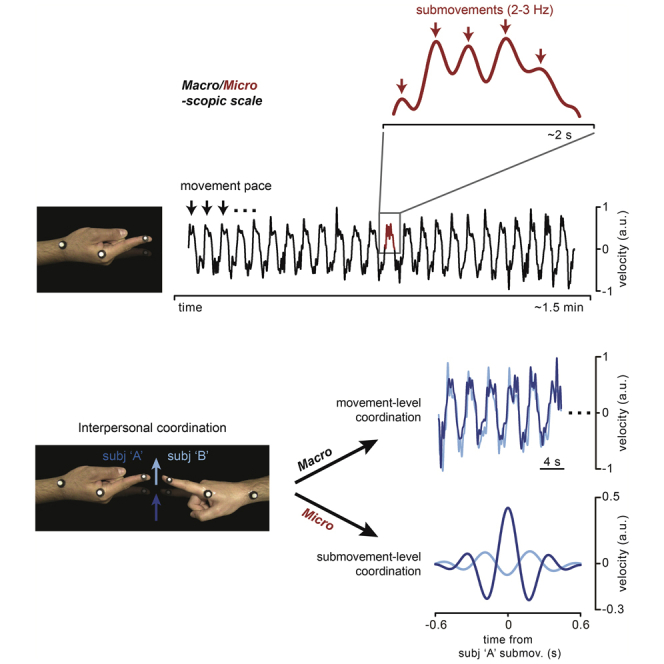
In sum, 60 participants forming 30 couples performed a movement synchronization task. As shown in Figures 1A and 1B, participants were asked to keep their right index fingers pointing toward each other (without touching) and perform rhythmic flexion-extension movements around the metacarpophalangeal joint as synchronously as possible either in-phase (toward the same direction) or anti-phase (toward opposite directions). We instructed participants to keep a slow movement pace (full movement cycle: ∼4 s; single flexion/extension movements: ∼2 s) by having them practice in a preliminary phase with a reference metronome set at 0.25 Hz (metronome was silenced during task performance; see also Figure S3 for results at faster movement paces). Each participant also performed the same finger movements alone (solo condition) with the only requirement of complying with the instructed pace (i.e., 0.25 Hz). Finger movements were recorded using retro-reflective markers tracked by a 3D real-time motion capture system (Vicon), providing continuous kinematic data sampled at 300 Hz (Figure 1C).

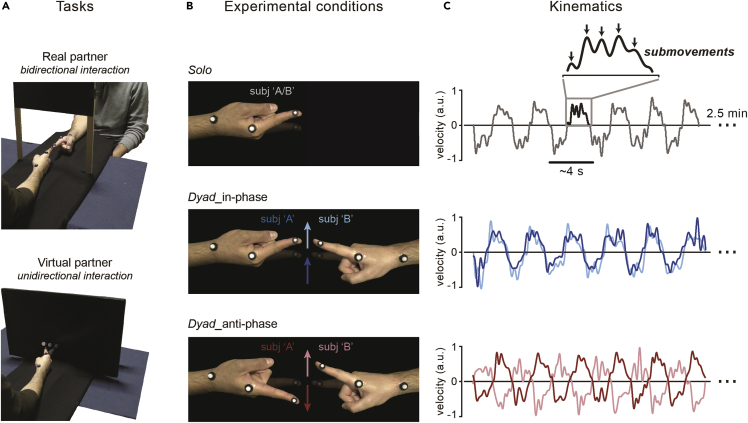
Figure 1.

Experimental setup and procedure

(A) Tasks. Primary task (“Real partner”) and one of the three secondary tasks (“Virtual partner”; for the other tasks, see Figure S2). In both tasks, participants seated at a table with the ulnar side of the right forearm resting on a rigid support and performed rhythmic (0.25 Hz) flexion-extension movements of the index finger about the metacarpophalangeal joint. In the primary task, participants formed couples (n = 30) and were asked to synchronize their movements to one another (dyadic condition; top panel), whereas in the “Virtual partner” task, participants (n = 20) synchronized their movements to a visual dot that moved on a screen according to a pre-recorded human kinematics (bottom panel).

(B) Conditions. Finger movements were performed by each participant alone (solo condition; top panel) as well as together with the (real/virtual) partner (dyadic condition; the middle and bottom panels illustrate the “Real partner” task). In the dyadic condition, participants were required to keep their fingers pointing straight ahead without touching each other (or the screen) and move as synchronously as possible either in-phase (toward the same direction; middle panel) or anti-phase (toward opposite directions; bottom panel).

(C) Kinematics. Movements were recorded in trials of 2.5 min (two trials per condition) using a real-time 3D motion capture system (Vicon; sampling rate: 300 Hz). Examples of the participants’ finger velocity along the main movement (x-)axis, measured at the distal phalanx of the index finger (see markers in Figure 1A), are shown for all conditions. Periodic (2–3 Hz) submovements are highlighted in the inset.

Rhythmicity at movement and submovement levels

By task design, movements are rhythmically organized with periodicity very close to the instructed pace. To highlight the rhythmic components of movement, we transformed the velocity time series into the frequency domain. As expected, all conditions display a major spectral peak around 0.25 Hz – referred to as F0 (Figure 2A). Moving together with a partner leads to a general speed-up (Okano et al., 2017; Thomson et al., 2018; Wolf et al., 2019; Wolf and Knoblich, 2022, but see also Bardy et al. (2020) for an example of the opposite effect) as shown by the F0 frequencies being higher than the instructed movement pace for both dyadic conditions (in-phase: 0.28 ± 0.037 Hz, p < 0.001; anti-phase: 0.27 ± 0.037 Hz, p = 0.002), whereas slightly lower for solo performance (0.24 ± 0.036 Hz, p = 0.059; mean ± SD; one-sample t-tests against 0.25 Hz; see Figure 2A). No difference in pace is, however, observed between in-phase and anti-phase synchronization (p = 0.445; paired samples t-test). Comparable results are obtained by calculating movement pace in a more canonical way as the inverse of the mean inter-movement interval (i.e., between successive flexions/extensions; solo: 0.24 ± 0.03 Hz, in-phase: 0.28 ± 0.02 Hz; anti-phase: 0.27 ± 0.02 Hz) as well as by examining the movement duration (solo: 2.1 ± 0.3 s, in-phase: 1.8 ± 0.2 s; anti-phase: 1.9 ± 0.2 s).

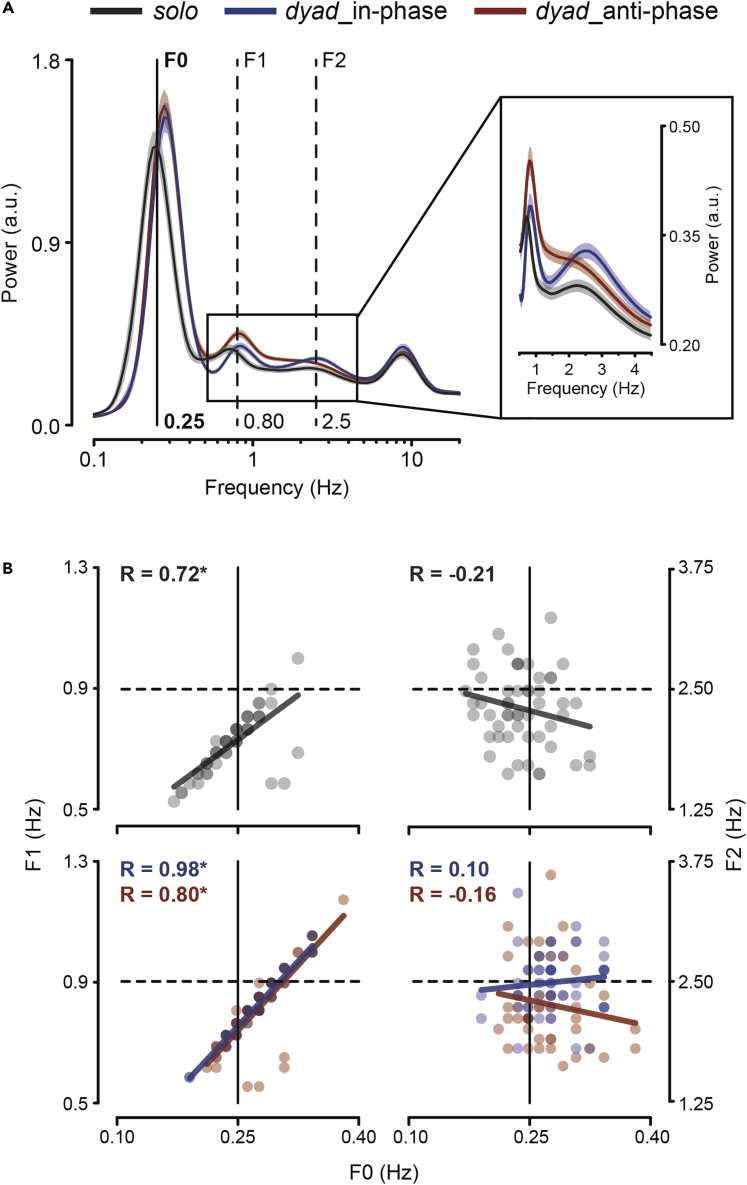
Figure 2.

Rhythmicity at movement and submovement levels

(A) Power spectrum of finger velocity for all conditions (solo, dyad-in-phase/anti-phase; mean ± SEM). The main spectral component peaking around the instructed movement rate (i.e., 0.25 Hz) is denoted as F0 (black solid line). The spectral components peaking around 2.5 Hz (submovement-related) and around 0.8 Hz are denoted as F2 and F1, respectively (dashed lines), and also highlighted in the inset.

(B) Scatter plots showing (across-subjects) correlations of F0 peak frequencies with F1 (left) and F2 (right) peak frequencies for the solo (top) and dyadic (bottom) conditions. Data points represent individual participants. Lines represent the best-fitting linear functions (method of least squares).

Besides the obvious F0 rhythmicity, the velocity profiles are marked by regular pulses that recur every ∼300–500 ms (see Figure 1C for an example), yielding a less prominent but distinct spectral peak also in the 2–3 Hz range – indicated as F2 (Figure 2A). These pulses – otherwise called submovements – are a basic kinematic feature and are indeed present irrespective of the specific coordination mode. However, the increase in power at 2–3 Hz appears to be more sharply defined (narrow-band) for in-phase than anti-phase synchronization (see inset in Figure 2A), suggesting that submovements may be produced more regularly when subjects are engaged in the former rather than the latter type of coordination.

Importantly, the F0 and F2 peak frequencies are not correlated (across-subjects), neither for solo performance (R = −0.21, p = 0.12) nor for in-phase (R = 0.10, p = 0.43) and anti-phase (R = −0.16, p = 0.29) coordination, indicating that submovement periodicity does not have harmonic or other (linear) relationships with the actual pace of the movements (Figure 2B, right column; note that subjects lacking clear peaks in the velocity power spectrum were excluded from the correlation analyses, see STAR Methods).

The velocity power spectrum shows two additional components. One – denoted as F1 – peaks at about 0.8 Hz for dyadic coordination and slightly lower (∼0.7 Hz) for solo performance, which is at about three times the mean F0 frequency in the respective conditions (Figure 2A; p > 0.05 for one-sample t-tests on F1 against 3∗F0 in solo, in-phase and anti-phase). In sharp contrast with the submovement-related F2 component, F1 is indeed strongly and positively correlated with F0 in all conditions (solo: R = 0.72, p < 0.0001; in-phase: R = 0.98, p < 0.0001; anti-phase: R = 0.80, p < 0.0001; Figure 2B, left column) with slopes of the best-fitting lines being close to 3 for both the dyadic conditions (in-phase: 2.87; anti-phase: 2.89) but smaller for the solo condition (1.97). Because of its tight association with the rate of movement (possibly being a harmonic), F1 is of little interest in relation to movement intermittency. Finally, in line with several previous works (Dione and Wessberg, 2019; Vallbo and Wessberg, 1993; McAuley et al., 1999), finger velocity shows a faster component with similar spectral properties across conditions and center frequency of ∼8 Hz, which is known as physiological tremor (Elble, 1996; McAuley and Marsden, 2000).

Partners synchronize at both movement and submovement levels

To quantify coordination at multiple timescales during dyadic interaction, we computed the frequency-resolved phase-locking value (PLV, i.e., a measure of consistency in the phase relationship) between the two partners’ finger velocities. Remarkably, interpersonal synchronization does not occur solely at F0 (and related F1) frequency as prompted by task instructions, but also at F2, which is the frequency of submovements (Figure 3A). That is, the two partners’ submovements happen to be in a stable (phase) relationship. Yet, this is not true for all conditions. Indeed, submovement-level synchronization is present during in-phase coordination – as shown by the distinct F2-peak in the PLV spectrum – but nearly absent during anti-phase coordination.

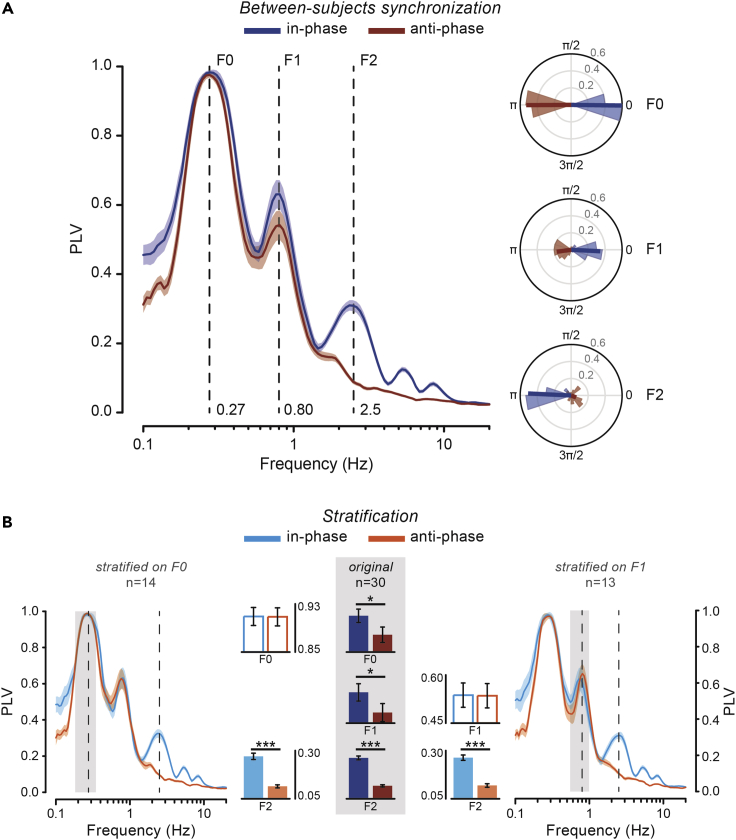
Figure 3.

Partners synchronize at both movement and submovement level

(A) Between-subjects PLV spectrum for the in-phase and anti-phase condition (left; mean ± SEM). Polar plots (right) showing the across-couples distribution of the mean phase difference (phase lag) for F0 (top), F1 (middle), and F2 (bottom).

(B) PLV spectra after data stratification (at the group level) on F0 (left) and F1 (right). Bar plots show mean PLV in the relevant frequency ranges for the original (middle; n = 30) and stratified (left, n = 14; right, n = 13) data. Error bars indicate ± SEM. ∗p < 0.05, ∗∗∗p < 0.001. See also Figures S1 and S2.

We ascertained that the observed synchronization at 2–3 Hz is not artefactual or just trivial – e.g., a mere consequence of doing the same movements at the same time – by performing different control analyses. In principle, the 2–3 Hz discontinuities could be produced in a similar way on each movement, thus retaining a consistent phase across movements. Such a phase-locking of submovements to movement onset is actually very modest and comparable for the in-phase and anti-phase condition (see Figure S1). Yet, because participants are moving simultaneously, submovements could appear as if they were synchronized between the two partners only by virtue of their (albeit weak) phase-locking to each partner’s individual movement. If this was the case, such non-genuine submovement-level synchronization would as well be enhanced during in-phase compared with anti-phase coordination because of the greater synchrony between the two partners’ movements in the former than the latter condition, which is evidenced by the correspondingly higher PLV at both F0 (p = 0.028) and F1 (p = 0.019; see bar plots in Figure 3B). Thus, to ensure that submovement-level synchronization is not a by-product of the overall better in-phase than anti-phase (movement-level) synchronization, we used two complementary analytical strategies. Both of them aim at matching the conditions (in-/anti-phase) for movement-level synchronization, but the first analysis does so at the group level whereas the second one at the couple level. We first used a data stratification approach that consists of subsampling the couples (by means of a random iterative procedure) so that the mean PLV at F0 and (in separate runs) F1 is equated as much as possible between the two conditions (see STAR Methods). As shown in Figure 3B, both types of data stratifications (i.e., on F0 and F1) leave the pattern of results virtually unchanged, with synchronization at the submovement frequency (F2) being significantly stronger during in-phase than anti-phase coordination (p < 0.001; independent samples t-tests). As for the second analysis, we computed again the between-subjects PLV, this time not on the entire velocity time series (shown in Figure 3A) but on shorter 2-s segments (covering approximately the duration of one single movement) that are time-aligned to the onset of each partner’s individual movement. In this way, we artificially compensated for the temporal asynchronies between the two partners’ movements, leveling the discrepancy in synchronization performance between the two conditions. Remarkably, this alignment-on-movement procedure severely disrupts synchronization at 2–3 Hz for the in-phase condition, making it as weak as that observed for the anti-phase condition (p = 0.215; paired-samples t-test; see Figure S1). Altogether, these results decisively exclude that the observed phenomenon is explained by any systematic locking of submovements to movement dynamics and/or the better in-phase vs anti-phase movement synchronization performance; rather, they suggest a true and real-time coadaptation of submovements between the two partners.

Interpersonal synchronization at submovement frequency is also confirmed in two additional experimental conditions. In the first one, we change the hand posture and movement axis (from horizontal to vertical) and show that the effect is independent from the congruency between the two partners’ flexion/extension movements during in-phase and anti-phase coordination (see Figure S2A). In the second one, we show that a similar phenomenon persists when the task involves whole-arm movements (on the horizontal and vertical plane), thereby extending our observations to multi-joint action coordination (see Figure S2B).

Thus, submovement-level synchronization seems to be largely independent from the effector as well as the congruency between the partners’ movements, but highly dependent on their (visuo-)spatial alignment. In fact, the main difference between the two coordination modes is the spatial alignment of the effectors’ endpoints (i.e., the fingertips): a 0° and 180° difference in position is required for in-phase and anti-phase coordination, respectively. Consistently with task requirements, the (across-couples) distribution of the mean phase lag at F0 between the two partners’ kinematics is strongly concentrated around 0-deg for in-phase and 180-deg for anti-phase coordination (Figure 3A, polar plot on top). The same phase relationship as for F0 is also observed for the related F1, although with a less degree of consistency. Surprisingly, synchronization at the submovement level (Figure 3A, polar plot on bottom) is characterized by an opposite, ∼180° relative phase shift with respect to what is established at the movement level (F0) during in-phase coordination (phase lags are relatively scattered during anti-phase coordination, in agreement with the PLV lacking a distinct F2 peak in this condition). In other words, submovements during in-phase synchronization are interlocked in the two partners and seem to follow one another with an alternating, counterphase pattern.

Bidirectional and unidirectional modulation of submovements

To further clarify the nature of submovement-level synchronization, we computed the cross-correlation between the two partners’ (unfiltered) velocities. We first selected data segments that correspond approximately to single movements, i.e., from movement onset to mean movement duration (see STAR Methods). To discard the main contribution deriving from slow and movement-locked components, we subtracted from each segment the mean velocity profile over all segments. We then computed the (between-subjects) cross-correlation either by keeping both partners’ data aligned to the individual movement onset (as just described) and thus misaligned in time (movement-alignment), or by (re)aligning one of the two partners’ data to the other partner’s movement onset (subject “A” by convention) and thus restoring their real alignment (time-alignment). The cross-correlation profile shows a striking difference between the two types of alignments, which is far most apparent for the in-phase condition (Figure 4A). Correlation for the movement-aligned data is maximal at lag zero and slowly declines for lags up to ±0.6 s, reflecting residual (not accounted for by the average subtraction) covariation in movement dynamics between the two partners. Conversely, correlation for the time-aligned data is relatively low at lag zero but sharply increases at symmetrical lags of about ±0.18 s. This curious double-peaked correlation profile most certainly reflects the succession in the partners’ submovements. Indeed, the two cross-correlation peaks are separated by a (lag) interval of almost 0.4 s, closely matching the oscillatory period of submovement production (i.e., 2.5 Hz). Whereas the two peaks are evident in the in-phase condition, two flattened humps are barely detectable at longer lags of about ±0.25 s in the anti-phase condition (Figure 4A, right), reflecting the fact that generation (Figure 2A) and interpersonal locking (Figure 3A) of submovements occurs rather erratically and at a slightly lower frequency in this coordination mode. The rhythmic 2.5-Hz co-variation between the two partners’ kinematics during in-phase coordination and its impairment during anti-phase coordination is further emphasized by taking the difference between the two cross-correlations (time- vs movement-aligned) that yields, for the first condition, an oscillating profile, whereas for the second, an almost flat profile (see Figure 4B).

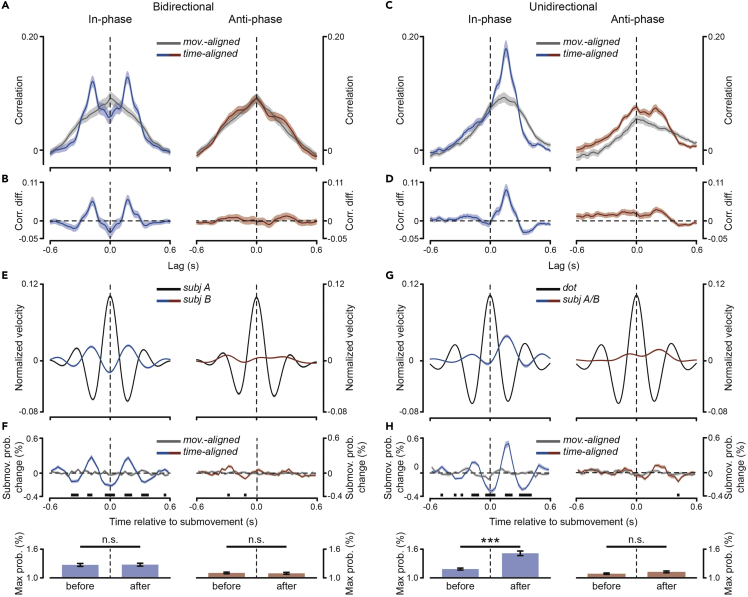
Figure 4.

Bidirectional and unidirectional modulation of submovements

(A) Cross-correlation between the two partners’ (unfiltered) velocities during in-phase (left) and anti-phase (right) synchronization in the “Real partner” task (bidirectional interaction). The cross-correlation is computed between velocity data segments (∼2 s) that are either movement-aligned, i.e., aligned to each partner’s movement onset, or time-aligned, i.e., aligned to one of the two partners (subject “A” by convention) movement onset, thus preserving their real time alignment (mean ± SEM; see STAR Methods).

(B) Difference between the time- and movement-aligned cross-correlation profiles (mean ± SEM).

(C) Cross-correlation as shown in (A) but computed between the participants’ velocity and the dot velocity in the “Virtual partner” task (unidirectional interaction; note that the dot is used as the reference signal for the time alignment; mean ± SEM). Correlation at positive/negative lags indicate that the participants’ (sub)movement follows/precedes the dot (sub)movement.

(D) Same as in (B) but for the “Virtual partner” task.

(E) Velocity for both partners – subjects “A” and “B” – locked to submovements generated by one partner in the couple – i.e., subject “A” by convention (“Real partner” task; mean ± SEM).

(F) Submovement probability (expressed as deviation from mean probability) for one participant (subject “B”) as a function of the actual time (time-aligned) or of time relative to movement onset (movement-aligned) from submovements generated by his/her partner (subject “A”; top panels). The black horizontal bars indicate the time points that survive two-tailed t-test statistics on movement- vs time-aligned data (Bonferroni-corrected for multiple comparisons across time). Maximal submovement probabilities (for subject “B” time-aligned to subject “A”) computed separately before and after time zero (i.e., before and after subject “A” submovements; bottom panels).

(G) Same as shown in (E) but obtained by locking the velocity to the dot submovements (“Virtual partner” task; mean ± SEM).

(H) Same as shown in (F) but obtained by computing the participants submovement probabilities as a function of (actual/movement) time from the dot submovements (time zero). Error bars indicate ± SEM. ∗∗∗p < 0.001. See also Figure S3.

If the two partners’ submovements do alternate with regularity (in-phase condition), by locking the velocity of one participant to his/her own partner’s submovements, the probability of observing a submovement in the former should not be uniform over time but relatively high/low at specific times (corresponding to the lags of high/low cross-correlation and to half period of the submovement frequency). Figures 4E and 4F show that this is exactly what we observe. We identified submovements as velocity peaks occurring within the movements performed by only one of the two participants in the couple (again subject “A” by convention) and then segmented both participants’ velocities based on the identified peaks (from −0.6 to +0.6 s; see STAR Methods). The submovement-locked velocity for subject “A” shows the expected peak at time zero and two smaller peaks at about ±0.35 s, reflecting 2–3 Hz periodicity in submovements generation. Most interestingly, subject “B” velocity (locked to subject “A”submovements) also shows an oscillating pattern, which is apparent for the in-phase and less so for the anti-phase condition (Figure 4E). The probability of observing a submovement (i.e., a velocity peak) in subject “B” is clearly modulated as a function of time relative to his/her partner’s submovements generation (time-aligned data) and is significantly different (higher/lower) than that obtained for movement-aligned data at multiple and regularly interspersed time points, closely matching the submovements rate (Figure 4F; see STAR Methods). Analogously to what was reported for the cross-correlation profiles, subject “B” submovements probability is maximal at relatively shorter (±0.18 s) and longer (±0.3 s) times for in-phase and anti-phase, respectively, suggesting faster (besides tighter) between-subjects alternation of submovements in the former than the latter condition.

We further asked a different sample of couples to coordinate in-phase at multiple movement paces (0.25, 0.5, 0.75, and 1 Hz; Figure S3). The two partners systematically alternate their submovements at 0.25 Hz (replicating the main results) as well as when moving at double this speed, i.e., at 0.5 Hz. Though qualitatively very similar, submovements coordination is however noisier at higher paces (see STAR Methods and Figure S3D). Notably, in line with the known speed-up effect during interpersonal motor coordination (Okano et al., 2017; Thomson et al., 2018; Wolf and Knoblich, 2022; Wolf et al., 2019), partners were always keeping a faster pace than instructed (mean movement duration ±SD: 1.83 ± 0.12 s [p = 0.0016; t-test against 2 s], 0.89 ± 0.15 s [p = 0.046; t-test against 1 s], 0.54 ± 0.09 s [p = 0.0039; t-test against 0.66 s], and 0.4 ± 0.04 s [p = 0.0068; t-test against 0.5 s] for the 0.25-, 0.5-, 0.75-, and 1-Hz pace, respectively). As a consequence, at 0.75 and 1 Hz, actual movement duration de facto approaches the average interval (period) between successive submovements (∼0.4 s), drastically reducing the probability of producing at least one submovement in each single movement. In other terms, movements were most often executed in a one-shot, ballistic way and this could only (and trivially) have detrimental effect on the phenomenon under investigation here.

The alternating pattern of submovements is likely the result of an inherently bidirectional interaction, whereby each participant’s submovements align (with a consistent lag) to those in the respective partner. But are submovements really consequential to one’s own partner submovements? To put this hypothesis to test, we made the interaction no longer bidirectional but purely unidirectional. Ten couples (among the original main sample) were also asked to synchronize their movements (in-phase and anti-phase) to a virtual “partner” – a visual dot shown on a computer screen – which was yet moving according to a pre-recorded human kinematics of the same finger flexion/extension movements (pace: 0.25 Hz; see STAR Methods and Figure 1A). Remarkably, the timing of the participants’ submovements is tightly related to that of the dot submovements. However, both the cross-correlation (Figures 4C and 4D) as well as the submovement-locked (Figures 4G and 4H) profiles are marked by a highly asymmetrical pattern that contrasts with the symmetrical one observed for the real interaction (Figures 4A, 4B, 4E, and 4F). Specifically, for the in-phase condition, submovement probability is systematically higher at times following than preceding the virtual partner’s submovements (p < 0.0001, Figure 4H), whereas it is symmetrical before and after the real partner’s submovements (p = 0.854, Figure 4F); though with a clear reduction in the strength of submovements modulation, a similar trend can also be observed for the anti-phase condition (virtual partner: p = 0.061, Figure 4H; real partner: p = 0.635, Figure 4F; paired samples t-tests on maximal probabilities before vs after time zero; see STAR Methods). The reported pattern exactly fulfisls what is expected based on the bidirectional and unidirectional nature of the real and virtual interaction, respectively. To ascertain that submovements are truly co-modulated in a bidirectional way during the real online interaction, we examined the results also at the single couple level. In fact, the observed (group-level) symmetry might conceal asymmetrical results in individual couples (e.g., subject A’s submovements influencing to a larger extent subject B′ submovements than vice versa) that are mixed up in the average owing to the arbitrary assignment of subject A/B. Yet, significant asymmetry in the cross-correlation and in the submovement-locked profiles is only found in 3 couples out of 30 (paired samples t-tests on maximal correlation/velocity before vs after lag/time zero; see STAR Methods), indicating that a bidirectional co-regulation of submovements is indeed occurring in the great majority of the couples.

Discussion

Whereas an extensive literature looks at the ‘macroscopic’ structure of interpersonal rhythmic coordination – i.e., the sequencing and pacing of movements – the present study looks into its ‘microscopic’ structure – i.e., the intermittency in movement. We show that interpersonal synchronization is not only established at the instructed movement pace – as commonly described (Keller et al., 2014; Oullier and Kelso, 2009) – but also at a faster timescale and lower level of the motor control hierarchy, the one reflected in the production of submovements.

Submovements are a fundamental, long-known feature of movement (Navas and Stark, 1968). They have been primarily studied during sustained and visually guided movements – e.g., hand tracking (Miall et al., 1993) – but their presence is almost ubiquitous in motor behavior as shown in a huge variety of tasks and effectors (Bottaro et al., 2008; Loram et al., 2006; McAuley et al., 1999; Meyer et al., 1988). Early (Craik, 1947; Navas and Stark, 1968) and recent (Gawthrop et al., 2011; Sakaguchi et al., 2015) theoretical accounts mostly consider submovements to be the behavioral sign of underlying intermittency in the control of movement (see also below for an account based on dynamic motor primitives; Hogan and Sternad, 2012). Central to this motor control framework is the idea that measured (or estimated) visual errors are used to update the motor commands in a temporally sparse and not continuous manner, that is, only at discrete moments in time. Once updated, motor commands are executed in a feed-forward fashion, eventually building up (seemingly smooth) movement from a concatenation of motor corrections, so-called submovements. The frequency of submovement production (and possibly that of motor updating) has been variably explained based on either intrinsic, time-dependent factors [e.g., refractory periods (Craik, 1948; Vince, 1948) and neural motor dynamics (Hall et al., 2014; Susilaradeya et al., 2019)], or extrinsic and task-dependent factors, such as delays (Miall, 1996; Miall et al., 1985; Susilaradeya et al., 2019), amount (Roitman et al., 2004; Wolpert et al., 1992), and reliability (Sakaguchi et al., 2015) of actual, estimated, and/or prediction errors, and most often a combination of both factors (Gawthrop et al., 2011; Susilaradeya et al., 2019). However, irrespective of the ongoing debate on the theoretical and computational account of submovements, it is widely agreed that submovements represent a behavioral proxy for the closing of (individual-level) visuo-motor control loops.

When interpersonal movement coordination is demanded, visuomotor control cannot however be closed-up within a single individual. The control loop must be extended to incorporate feedback related to one’s own as well as one’s partner action. In other terms, the relevant visual error signal becomes a joint product of self’s and other’s movements. Crucially, in this case – and not when tracking an external moving stimulus – similar visuomotor machineries are simultaneously at work in the two interacting agents and may thus act in concert. Previous research focusing on joint motor improvisation has considered individual kinematic discontinuities as jittery motion marking epochs of poor coordination performance (Noy et al., 2011, 2017). However, the relational rather than individual control policy of submovement generation was completely overlooked. Strikingly, the present results show that the two partners’ submovements are actually interdependent and time-locked to one another.

Several pieces of evidence indicate that the reported phenomenon does reflect an active co-regulation of submovements between the interacting partners. Submovement-level coordination depends upon the movement-level coordination mode, being it manifest during in-phase coordination but largely impaired during anti-phase coordination. This difference persists regardless of the hand posture, and thus whether the two partners activate simultaneously homologous muscles (flexors/extensors); nor it is a trivial consequence of the greater between-partners synchrony that is observed in this as well as in prior work (e.g., Schmidt et al., 1990; Wolf et al., 2019) during in-phase vs anti-phase coordination. It rather descends most likely from the visuospatial constraints proper to the two modes of coordination. Indeed, moving anti-phase entails a larger (visuo)spatial distance between the endpoints than moving in-phase. This presumably translates into noisier, more unreliable and perhaps delayed computation of visual errors, all known to be important factors in shaping movement intermittency (Miall et al., 1985;Roitman et al., 2004; Sakaguchi et al., 2015; Wolpert et al., 1992). Notably, Reed & Miall (Reed et al., 2003) have shown that progressively increasing the spatial separation between the displayed target and the hand cursor correspondingly reduces intermittency (and accuracy) of tracking, probably by making visual evaluation of positional errors coarser and thus less effective in driving feedback-based motor corrections. Analogously, if interpersonal submovements synchronization is mediated by common access to a mutually controlled visual error signal, we would expect it to be degraded during anti-phase coordination because of the inherent difficulty posed by the 180° alignment in measuring that very same error. In engineering jargon, anti-phase coordination would be deemed to entail a larger “error dead zone”, a concept borrowed by motor control theories to denote the range of inputs to which a system is unresponsive, i.e., which does not bring an update of the (motor) control signals (Wolpert et al., 1992). On the other side, shortening movement duration and/or increasing its speed beyond a certain limit also hampers effective online motor corrections, negatively impacting on interpersonal submovement coordination (Figure S3). Thus, the dependence on movement duration as well as the in-phase vs anti-phase difference are all compatible with functional constrains stemming directly from feedback-based motor control mechanisms.

Yet, it is important to note that submovements are present during dyadic coordination but also during solo performance which only demands temporal (keeping the instructed tempo) but not spatial (keeping one’s finger aligned to the partner’s finger) accuracy, thus minimizing the need for online visual-based motor corrections. This is consistent with evidence showing that submovements are neither abolished nor attenuated when visual feedback is completely removed (Doeringer and Hogan, 1998; Park et al., 2017, but see also Miall et al., 1993; Vallbo and Wessberg, 1993). One alternative account indeed posits that submovements do not reflect feedback-based corrections but rather represent an intrinsic property, or dynamic primitive, of how movement is organized (Hogan and Sternad, 2012). In other words, provided movement duration is not too short (<400 ms), the human motor system cannot avoid but executing it by concatenating multiple, possibly overlapped submovements. Our data reveal that submovements maintain the same periodicity as when moving alone but their actual timing is systematically modulated when interacting with another person. The mechanism controlling submovement production is thus not blind but tuneable, suggesting it is most likely relevant to motor coordination.

Indeed, a major aspect of our results is that submovements alternate in the two partners, i.e., they are produced in a seemingly counterphase relationship. This clearly excludes spurious or trivial forms of ‘passive’ (zero-phase) coupling and rather points to an active co-regulation whereby submovements are consequential and reciprocal adjustments to the partner’s behavior. Indeed, submovement probability is highly non-uniform and maximal ∼200 ms before as well as after one’s partner submovements. This temporal symmetry is clearly broken when interacting with an unresponsive virtual partner: the participants’ submovements more often follow rather than precede the dot submovements, indicating they are effectively tuned to the discontinuities in the dot motion but – obviously – not vice versa. These results corroborate a functional account of interpersonal submovement coordination, making a case for a finely regulated mechanism to generate submovements at specific timing depending on partner’s behavior. Thus, although appearing as subtle features, kinematic discontinuities are nevertheless systematically (and implicitly) read out and, most importantly, used for coordinating with other people’s movement.

We can argue that coupling of movement intermittency in the two partners originates from corresponding coupling of the underlying visuo-motor loop dynamics, though this hypothesis needs further support from physiological data. Many studies examining coherence between brain activities and kinematics have focused on higher level, explicit movement dynamics (e.g., movement pace) during solo (Bourguignon et al., 2019) and interpersonal coordination (Dumas et al., 2020). Coherence between brain activities and motor outputs can yet be observed at multiple timescales beyond the pace of movement. For example, 6–12 Hz oscillations – commonly denoted as physiological tremor (Elble, 1996; McAuley and Marsden, 2000) – are clearly visible in the effector velocity/acceleration (e.g.,Dione and Wessberg, 2019; McAuley et al., 1999; Vallbo and Wessberg, 1993) as well as in the EMG/force (e.g., McAuley and Marsden, 2000; Tomassini et al., 2020), and some studies have shown they are coherent with brain rhythmic activity (Gross et al., 2002; Marsden et al., 2001; Mehta et al., 2014; Raethjen et al., 2002; Tomassini et al., 2020; Williams et al., 2009). However, the anatomo-functional basis of physiological tremor is still highly controversial; some views support a neurogenic origin of alpha tremor, possibly linked to pulsatile motor commands (Bye and Neilson, 2010; Vallbo and Wessberg, 1993), cerebello-talamo-cortical loop activity (Gross et al., 2002), proprioceptive reafference (Williams et al., 2009), or spinal reflex-based loops (Christakos et al., 2006), whereas others suggest a purely peripheral origin related to mechanical resonance of the limb (Lakie et al., 2015; Vernooij et al., 2013). Notably, and in line with our observation (Figure 2), the 10-Hz and the 2–3 Hz (submovements-related) oscillation often co-exist in the kinematic output but appear as functionally dissociated, especially for their susceptibility to manipulations of visual feedback (McAuley et al., 1999; Vallbo and Wessberg, 1993). Remarkably, recent human (Jerbi et al., 2007; Pereira et al., 2017) and monkey (Hall et al., 2014; Roitman et al., 2009; Susilaradeya et al., 2019) evidence has also pointed to distinct neural markers of submovement generation. The spectral fingerprint of such neural activity matches well with the periodicity of submovements (i.e., delta/theta-band: 2–5 Hz; Hall et al., 2014; Jerbi et al., 2007; Susilaradeya et al., 2019); further, this motor activity is phase-locked to submovements and shows consistent dynamics that is unaltered by artificial changes in feedback delays (Susilaradeya et al., 2019). Intrinsic rhythmicity of neural motor dynamics may thus map directly onto submovement periodicity.

Computational and physiological perspectives on movement intermittency have usually attributed it solely to the motor stage: intermittent planning and execution of motor commands is based on otherwise continuous feedback reading (and prediction). Movement-related dynamical changes in sensitivity – e.g., sensory attenuation/suppression – are however very well documented phenomena (Williams et al., 1998). Also, an increasing bulk of evidence shows as well that sampling of sensory data may routinely operate in a discontinuous, rhythmic fashion (VanRullen, 2016). Such rhythmicity is often captured by corresponding fluctuations in neuronal excitability and perceptual performance, and it is interpreted as being of attentional origin (Fiebelkorn and Kastner, 2019; Jia et al., 2017; Landau et al., 2015). However, most recent work suggests that rhythmic sensory sampling can also be specifically coupled to motor behavior/activity (Benedetto et al., 2016, 2021; Nakayama and Motoyoshi, 2019; Tomassini and D'Ausilio, 2018; Tomassini et al., 2015, 2017); for reviews, see Benedetto et al. (2020) and Schroeder et al. (2010). Notably, fluctuations in visual perception are not only synchronized to eye movements (Benedetto and Morrone, 2017; Hogendoorn, 2016; Wutz et al., 2016) but also to oscillatory cortical dynamics subtending upper limb motor planning (Benedetto et al., 2021; Tomassini et al., 2017) and continuous control (Tomassini et al., 2020). Although continuous processing has been called in to explain the fast spinal and transcortical reflexive responses (Crevecoeur and Kurtzer, 2018), intermittency could indeed represent a fundamental property of the more complex sensory and motor functions underlying voluntary behavior, providing an efficient way for synchronizing time-consuming processing within the action-perception loop.

In conclusion, we show that movement intermittency – a basic property of individual-level motor control – is effectively synchronized between interacting partners. Such synchronization is likely to constitute an important building block of the low-level visuomotor machinery underlying interpersonal movement coordination. The present investigation opens up a new window upon the (neuro) behavioral mechanisms enabling joint action coordination. This mechanism can be expected to be of crucial importance whenever the interaction poses an accuracy requirement based on the computation of (visual) errors between one’s own and others’ actions (e.g., passing a small/fragile/dangerous object) as well as when learning new motor skills by imitation of others’ behavior.

Collective or joint action coordination is perhaps the hallmark of human sociality, and a great deal of research is currently pursuing the exploration of its developmental trajectory, comparative origin as well as its relation to pathological conditions (e.g., psychiatric, neurological). The present work has taken a different approach and revealed some core mechanisms of motor control and how they come into play in producing complex coordinated behavior.

Limitations of the study

Research on human as well as animal social behavior has seen increasing leveraging on quantitative methods aimed at modelling the dynamics of complex collective behavior, such as those involving the take-over of leader-follower roles (Calabrese et al., 2021; Couzin et al., 2005; Shahal et al., 2020). Our study was not designed to directly tackle the question of leadership, as we did not assign explicitly nor manipulate implicitly the partners’ roles. Whether leader-follower dynamics possibly emerge (differentially) at multiple macro- and microscopic scales of coordination is, however, an interesting open question. The between-partners symmetrical alternation in submovement production may suggest that no consistent leader-follower dynamics emerged spontaneously at the microscopic level in our task (as supported also by the analysis on single-couple data). However, these results may not be conclusive in this respect: for example, it has been shown that leadership can be associated with different relative phase patterns among the partners engaged in rhythmic coordination (Calabrese et al., 2021). Future studies making use of ad-hoc experimental manipulations and analytical tools apt to quantify informational coupling between the interacting partners are needed to provide further and more compelling insight into this question.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Kinematic data	This paper	https://doi.org/10.17605/OSF.IO/CAGH8
Custom-made analysis code	This paper	https://doi.org/10.17605/OSF.IO/CAGH8
Software and algorithms
Nexus	Vicon Motion Systems Ltd.; https://www.vicon.com/products/software/nexus	RRID: SCR_015001
MATLAB	MathWorks; http://www.mathworks.com/products/matlab/	RRID: SCR_001622
FieldTrip	http://www.fieldtriptoolbox.org	RRID: SCR_004849

Resource availability

Lead contact

Further information should be directed to and will be fulfilled by the lead contact, Alice Tomassini (alice.tomassini@gmail.com).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Participants

Eighty participants (40 females) formed 40 gender-matched couples. Thirty couples (age 23.9 ± 4 years, mean ± SD) took part to the main experiment and 10 couples (age 26.2 ± 4 years) participated in the control experiment. Except two authors (A.T. and G.N.), participants were all naïve with respect to the aims of the study and were paid (€12.5) for their participation. All participants were right-handed (by self-report) and had normal or corrected-to-normal vision. The study and experimental procedures were approved by the local ethics committee (Comitato Etico di Area Vasta Emilia Centro, approval number: EM255-2020_UniFe/170592_EM Estensione). Participants provided written, informed consent after explanation of the task and experimental procedures, in accordance with the guidelines of the local ethics committee and the Declaration of Helsinki.

Method details

Sample size

No power analysis was used to decide on the sample size (i.e., the number of couples). Sample size estimation was based both on pilot studies as well as on previous studies investigating rhythmic interpersonal synchronization (Wolf et al., 2019; Dumas et al., 2020) and submovements in visuo-manual tracking (Susilaradeya et al., 2019).

Setup and procedure

All couples participating in the main experiment (n = 30) performed the same primary task (‘Real partner’) and also one of three different secondary tasks (randomly assigned), so that each secondary task was completed by 10 couples in total. Task details are described in the following.

Primary task – real partner

Participants were seated at a table either alone or in front of each other (∼1 m apart) with their faces hidden from view by means of an interposed panel (Figure 1A). They were asked to keep the ulnar side of the right forearm resting on a rigid support and perform rhythmic flexion-extension movements of the index finger about the metacarpophalangeal joint (Figures 1A and 1B). Movements were performed by each participant alone (solo condition) and by the two participants together (dyadic condition). In the latter condition, participants were required to keep their index fingers pointing straight towards each other (without touching) and move as synchronously as possible either in-phase (towards the same direction) or anti-phase (towards opposite directions, Figure 1B). Given the mirror-like participants’ arrangement and hand posture, in-phase coordination required them to perform simultaneously different movements (i.e., as one participant performed finger flexion, the other performed extension and vice versa). Conversely, anti-phase coordination required the two participants to perform the same type of movement (either flexion or extension; see Figure 1B). In all conditions (solo, dyad-in-phase, dyad-anti-phase), participants were instructed to keep their movement rate around 0.25 Hz (15 bpm; flexion-extension cycle: 4 s; flexion/extension movement duration: 2 s). Before the experiment, they familiarized themselves with the reference rate by listening to a metronome and synchronizing their movements to the auditory beat for a short time (∼1 min). Metronome was also played prior to each experimental condition for a few seconds; during the kinematic recordings the metronome was silenced, and movements were thus self-paced.

Secondary tasks

Ten couples completed a second task (Real partner – Hand prone) that was similar to the primary one, except that they kept their right hand in a prone posture and moved the index finger along the vertical rather than horizontal axis (Figure S2A). As opposed to the main task, during in-phase coordination the two participants had now to perform simultaneously the same type of movement (either flexion or extension), while during anti-phase coordination they had to perform different movements (as one performed flexion, the other performed extension and vice versa). Other 10 couples completed a secondary task (Real partner – Arm) involving movement of the whole forearm, primarily around the elbow joint (Figure S2B). Arm movements were performed (trial-wise) along either the horizontal or vertical inner dimensions of the window (∼40 × 40 cm) delimited by the interposed panel. Only two conditions were tested: participants moved alone (solo) or tracked each other’s movement by keeping the respective fingertips spatially aligned (dyad-in-phase; dyad-anti-phase was not tested in this task). Given the larger movement amplitude, the instructed movement rate was reduced to 10 bpm (i.e., ∼0.17 Hz). The remaining 10 couples completed a secondary task (Virtual partner) whereby hand posture and finger movements were exactly the same as in the primary task. However, instead of coordinating together, participants were now asked to track a visual dot (size: 1.5 cm, position: 7 cm above the bottom screen edge) moving horizontally on a computer screen in front of them (see Figure 1A). The dot velocity corresponded to the velocity of the index fingertip recorded on author A.T. while she was taking part to the primary task. The displayed kinematics belonged to all the three tested conditions (2 trials per condition, see below) – i.e., solo, dyad-in-phase and dyad-anti-phase. Participants tracked the dot kinematics taken from solo performance both in-phase as well as anti-phase; in contrast, the dot kinematics taken from the in-phase and anti-phase conditions were only tracked by the participants in the corresponding modes, that is, in-phase and anti-phase, respectively. Results are shown only for the dot kinematics taken from solo (Figures 4C, 4D, 4G, and 4H) as this provides an unbiased comparison between conditions (same displayed kinematics but tracked in different modes); anyhow, results obtained for the other displayed kinematics are qualitatively comparable and support the same general conclusions.

Control experiment – speed dependency

Couples (n = 10) completed the ‘Real partner’ primary task (in-phase coordination mode only) at different movement paces, including the same pace as tested in the main experiment (i.e., 0.25 Hz) and two additional paces of 0.5 and 0.75 Hz. Five couples of the same sample were additionally tested at a faster movement pace of 1 Hz.

Kinematic data recording

Movements were recorded along three axes (mediolateral, X; anteroposterior, Y; and vertical, Z) using a ten cameras motion capture system (Vicon; Nexus, RRID:SCR_015001; sampling rate: 300 Hz). Three retro-reflective markers were placed at the following anatomical locations on the right hand: on the distal phalanx of the index finger (marker diameter: 6.4 mm), on the metacarpophalangeal joint (marker diameter: 9.5 mm) and on the styloid process of the radius (marker diameter: 9.5 mm; see Figure 1B). The kinematics recorded on author A.T. and used in the ‘Virtual partner’ task corresponds to the x-axis velocity component of the marker attached on the fingertip (distal phalanx). A photodiode (1 × 1 cm) was placed in the bottom right corner of the monitor and was used for accurately aligning the participants’ recorded kinematics with the displayed dot. A white square was drawn on the screen at the position of the photodiode (hidden from view) in synchrony with the start of the dot motion. The signal from the photodiode was acquired with the same system used to record the kinematic data (i.e., Vicon; sampling rate: 1800 Hz).

Data collection

Each couple completed the whole experiment in ∼1.5 h. For all tasks, data were collected in separate trials with short pauses in-between trials. Two trials of 2.5 min each were recorded for each couple and condition (solo, dyad-in-phase/anti-phase) in all tasks except the ‘Arm’ control task (vertical and horizontal) for which three trials of 1.5 min were recorded for each condition (solo, dyad-in-phase). The two/three trials per condition were always performed in succession. Instructions about task/condition were provided verbally before each trial sequence. Tasks and conditions order were randomized across couples.

Quantification and statistical analysis

Analyses were performed within the MATLAB computing environment (RRID:SCR_001622) using custom-made code and the FieldTrip toolbox (RRID:SCR_004849). Analysed data corresponds to position data along the main movement axis for the marker attached on the fingertip. Velocity has been computed as the first derivative of position and normalized (trial-wise) on maximal speed.

Spectral analysis

Spectral content

Spectral analysis was performed by band-pass filtering (FIR filter, order: 3 cycles, two-pass) the continuous (2.5 min) velocity time series applying a sliding window along the frequency axis (range: 0.1–20 Hz) in 100 steps and bandwidths (range: 0.01–3 Hz) that were logarithmically (log10) spaced. Frequency-resolved instantaneous power was derived by means of the Hilbert transform and then averaged over time points (from 5 to 145 s) and trials (Figure 2).

Between-subjects phase-locking value (PLV)

The between-subjects phase-locking value (PLV) was computed as the mean resultant vector of the instantaneous phase differences (Hilbert-derived) between the two partners’ velocity time series (the resulting PLV was then averaged across trials; Figure 3). The (between-subjects) PLV was also computed across shorter 2-s data segments (from all trials) that were time-locked to each partner’s individual movement onsets (see below for details on the algorithm used to identify movement onset time). The resulting PLV was then averaged across time points (Figure S1). To avoid edge artefacts, data segmentation was performed on the already band-passed filtered and Hilbert-transformed signals.

Within-subject phase-locking value (PLV)

Further, to evaluate whether submovements are phase-locked to movement onset, we quantified the within-subject (or inter-movement) PLV on the same data segments as described for the between-subjects PLV but computing the mean resultant vector over the same-participant instantaneous phases (instead of the between-participants phase differences; Figure S1).

Time-domain analysis

Detection of individual movements

To estimate onset/offset of each individual movement, we low pass filtered (3 Hz, two-pass Butterworth, third order) the position data before computing the velocity. Movement onset was defined as the first data sample of a segment equal to 1/4 of the instructed movement duration (0.5 s for the main experiment) where the velocity was positive (or negative, depending on movement direction); movement offset was defined as the first sample after at least half the instructed movement duration (1 s for the main experiment; exact time could be slightly changed according to individual movement duration) from movement onset where the velocity passed through zero. This algorithm was applied iteratively by sliding along the entire velocity time series. Data segmentation was visually checked for each time series and any error was manually corrected (<5%).

Cross-correlation

The cross-correlation analysis was performed on velocity as obtained by taking the first derivative of position data that were low-pass filtered at 40 Hz to remove high-frequency noise. For each couple and condition, we first took velocity segments corresponding approximately to individual movements, i.e., time-locked to the participant-specific movement onsets and with length equal to mean movement duration (velocity segments belonging to movements with duration > or < than mean duration ± 2.5 SD were discarded from the analysis). Velocity sign was adjusted to be positive in all segments. To remove the movement-locked components, we subtracted from each segment the average velocity profile across all the retained segments (subject-wise). After these common preprocessing steps, we computed the cross-correlation (normalized so that the autocorrelations at zero lag are identically 1) by aligning the two partners’ velocity segments in two different ways: 1) movement-aligned, i.e., keeping the data aligned to each participant’s movement onset as just described, and 2) time-aligned, i.e., using the movement onsets of only one of the two participants (subject ‘A’ for convention) as reference temporal markers to re-align her/his partner’s data (subject ‘B’; Figures 4A and 4B). Therefore, only the second type of alignment (time-aligned) preserved the real time relationship between the two partners’ velocities. For the ‘Virtual partner’ task, the analysis pipeline was the same, but the cross-correlation was computed between all participants (‘A’ and ‘B’) and the dot velocity, using the latter as the reference signal for re-aligning the participants’ velocities (time-alignment).

Submovement-locked analysis

For the submovement-locked analysis (Figures 4E, 4F, 4G, and 4H), position data were low-pass filtered (4 Hz, two-pass Butterworth, third order) before computing velocity. Preprocessing of velocity data (i.e., segmentation, change of velocity sign, subtraction of the across-segments average) was identical to that described for the cross-correlation analysis. For one of the two participants (again subject ‘A’ for convention), we identified the submovements as local peaks in the velocity, i.e., data points with values larger than neighbouring values (in each velocity segment). We then segmented the same participant (‘A’) as well as her/his partner (‘B’) velocities based on the identified submovements (from −0.6 to 0.6 s), providing with ‘submovement-triggered’ averages (Figure 4E). Finally, the submovement-aligned data were also used to estimate the probability of producing a submovement given a submovement produced by one’s partner. Specifically, we counted the number of submovements (local velocity peaks) for each time point (from −0.6 to 0.6 s) in subject ‘B’ velocity segments (aligned to subject ‘A’ submovements) and then divided these numbers by the total amount of analysed velocity segments (Figure 4F). In a similar way as performed in the cross-correlation analysis, submovements probabilities were computed for both time-aligned and movement-aligned velocity data segments. We then averaged the computed probabilities within 36 equally spaced and non-overlapping bins between −0.6 and +0.6 s. The same analysis was performed also for the ‘Virtual partner’ task by aligning the participants’ velocities (both ‘A’ and ‘B’) to the submovements contained in the dot kinematics (Figures 4G and 4H). For the control experiment, analyses were limited from −0.3 to 0.3 s to accommodate for the shorter movement durations (Figure S3).

Statistical analysis

Comparison of movement tempo (F0)

We statistically evaluated whether movements are executed at a different pace compared to the instructed one by performing one-sample t-tests (against 0.25 Hz) for all conditions (solo, dyad-in-phase/anti-phase) on the F0 peak frequency, i.e., the frequency with maximal power in the velocity power spectrum. For the solo condition, the test was applied on individual parameter estimates (df = 59), whereas for the dyadic conditions the tests were applied on couple-wise across-subjects averages of the parameter estimates (df = 29). The difference in movement rate between the in-phase and anti-phase condition was tested by means of a paired samples t-test (df = 29).

Correlation between peak frequencies

We computed the Pearson correlation across subjects for all conditions (solo, dyad-in-phase/anti-phase) between, on one side, the F0 peak frequencies and, on the other side, the F1 and (separately) F2 peak frequencies of the individual velocity power spectra. To identify the individual peak frequencies, we used the following criteria. For F0, we just took the frequency with maximal power. For F1 and F2, we sought for local peaks in the power spectrum within frequency ranges comprised between 0.5 and 1.25 Hz and between 1.5 and 4 Hz, respectively. Subjects for which no consistent peak was identified were excluded from the corresponding correlation analysis (F1: 10, 3, 2; F2: 6, 2, 16 excluded subjects out of 60 for solo, dyad-in-phase, dyad-anti-phase, respectively). If more than one peak was identified for a given subject, we included the peak with higher power and frequency closer to the across-subjects average peak frequency (F1: 16, 12, 24; F2: 6, 6, 4 subjects out of 60 for solo, dyad-in-phase, dyad-anti-phase, respectively).

In-phase vs. anti-phase comparison of PLV

Differences in the (between-subjects) PLV between the in-phase and anti-phase conditions were statistically evaluated by means of conventional paired samples t-tests. The tests were applied separately on the PLV averaged between 0.18 and 0.34 Hz for F0, between 0.55 and 0.99 Hz for F1 and between 1.53 and 3.24 Hz for F2 (ranges defined based on the across-couples range of variation – i.e., min-max – in the corresponding PLV peak frequencies; Figure 3B).

Data stratification on F0/F1 PLV

To rule out that the difference between the in-phase and anti-phase condition in the (between-subjects) PLV at F2 depends on corresponding condition differences at F0 and/or F1, we used a data stratification approach. We performed two separate stratifications, one aiming at levelling conditions differences in the mean PLV at F0 (i.e., between 0.18 and 0.34 Hz), and the other in the mean PLV at F1 (i.e., between 0.55 and 0.99 Hz). The distributions across-couples of the PLV at F0/F1 were compiled for the in-phase and anti-phase conditions and binned in 10 equally spaced bins. The number of couples falling in each bin for the in-phase and anti-phase condition was then equated by means of a random subsampling procedure which aims at matching as much as possible the PLV group-level condition averages (as implemented in Fieldtrip, function: ft_stratify, method: ‘histogram’, ‘equalbinavg’). Stratification on F0- and F1-PLV led to the removal of 16 and 17 couples (out of 30), respectively. The condition difference in PLV at F2 (i.e., between 1.53 and 3.24 Hz) after stratification was then statistically evaluated by means of independent samples t-tests.

Time- vs movement-locking of submovements

We tested whether subject ‘B’ submovement probability depended on the (actual) time from subject ‘A’ submovements – and was therefore significantly different from what could be obtained if the two partners’ submovements were locked to the individual movement onsets – by performing two-tailed paired samples t-tests on the probabilities computed for time- vs. movement-aligned data. The obtained p-values were then corrected for multiple comparisons across time by means of the Bonferroni method. We compared submovement probabilities before vs. after time zero by applying paired samples t-tests on the maximal probabilities computed for all subjects (subjects ‘B’; n = 30) in the respective time intervals (i.e., from −0.6 to 0 s and from 0 to +0.6 s).

Single-couple analysis

Finally, we performed analyses at the couple-level. For each couple, we evaluated the symmetry of both the cross-correlation profile as well as the (subject B) submovement-locked profile by applying paired samples t-tests on the maximal values obtained before vs. after lag/time zero, respectively (Bonferroni correction was applied to correct for the multiple individual tests, n = 30).

Published: April 15, 2022

Data and code availability

• •Kinematic data have been deposited at the Open Science Framework Data Repository (osf.io) and is publicly available as of the date of publication. DOIs are listed in the Key resources table.
• •Custom-made analysis code has been deposited at the Open Science Framework Data Repository (osf.io) and is publicly available as of the date of publication. DOIs are listed in the Key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.